No CrossRef data available.
Article contents
A characterization of random analytic functions satisfying Blaschke-type conditions
Published online by Cambridge University Press: 17 January 2024
Abstract
Let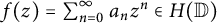 
$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H(\mathbb {D})$ be an analytic function over the unit disk in the complex plane, and let 
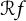$\mathcal {R} f$ be its randomization: 
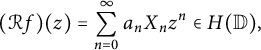$$ \begin{align*}(\mathcal{R} f)(z)= \sum_{n=0}^{\infty} a_n X_n z^n \in H(\mathbb{D}),\end{align*} $$
where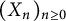 
$(X_n)_{n\ge 0}$ is a standard sequence of independent Bernoulli, Steinhaus, or Gaussian random variables. In this note, we characterize those 
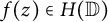$f(z) \in H(\mathbb {D})$ such that the zero set of 
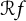$\mathcal {R} f$ satisfies a Blaschke-type condition almost surely: 
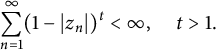$$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n|)^t<\infty, \quad t>1.\end{align*} $$
MSC classification
Secondary:
30B20: Random power series
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
Y. Duan is supported by the NNSF of China (Grant No. 12171075) and Science and Technology Research Project of Education Department of Jilin Province (Grant No. JJKH20241406KJ). X. Fang is supported by the NSTC of Taiwan (112-2115-M-008-010-MY2).
References
Borwein, P. and Erdélyi, T., Polynomials and polynomial inequalities, Springer, New York, 1995.CrossRefGoogle Scholar
Cheng, G., Fang, X., and Liu, C.,
A Littlewood-type theorem for random Bergman functions
. Int. Math. Res. Not. 14(2022), 11056–11091.CrossRefGoogle Scholar
Cinlar, E., Probability and stochastics, Graduate Texts in Mathematics, 261, Springer, New York, 2011.CrossRefGoogle Scholar
Heilper, A.,
The zeros of functions in Nevanlinna’s area class
. Israel J. Math. 34(1979), 1–11.CrossRefGoogle Scholar
Horowitz, C.,
Zeros of functions in the Bergman spaces
. Duke Math. J. 41(1974), 693–710.CrossRefGoogle Scholar
Jevtić, M., Vukotić, D., and Arsenović, M., Taylor coefficients and coefficient multiplier of Hardy and Bergman-type spaces. Vol. 2, RSME Springer Series, Springer, Cham, 2016.CrossRefGoogle Scholar
Kahane, J.-P., Some random series of functions. Vol. 5, 2nd ed., Cambridge Studies in Advanced Mathematics, Cambridge University Press, Cambridge, 1985.Google Scholar
Littlewood, J. E.,
On the mean value of power series
. Proc. Lond. Math. Soc. 25(1926), no. 3, 328–337.CrossRefGoogle Scholar
Littlewood, J. E.,
On mean values of power series (II)
. J. Lond. Math. Soc. 5(1930), no. (2), 179–182.CrossRefGoogle Scholar
McKee, J. and Smyth, C., Around the unit circle: Mahler measure, integer matrices and roots of unity, Springer, Cham, 2021.CrossRefGoogle Scholar
Nazarov, F., Nishry, A., and Sodin, M.,
Log-integrability of Rademacher Fourier series, with applications to random analytic functions
. Algebra i Analiz 25(2013), no. 3, 147–184.Google Scholar
Offord, A. C.,
The distribution of zeros of power series whose coefficients are independent random variables
. Indian J. Math. 9(1967), 175–196.Google Scholar
Smyth, C.,
The Mahler measure of algebraic numbers: A survey
. In: Number theory and polynomials (Conference Proceedings, University of Bristol, 3–7 April 2006), LMS Lecture Notes, vol. 352, Cambridge University Press, Cambridge, 2008, pp. 322–349.CrossRefGoogle Scholar
Ullrich, D. C.,
An extension of the Kahane–Khinchine inequality in a Banach space
. Israel J. Math. 62(1988), 56–62.CrossRefGoogle Scholar
Ullrich, D. C.,
Khinchin’s inequality and the zeroes of Bloch functions
. Duke Math. J. 57(1988), 519–535.CrossRefGoogle Scholar