Abstract
Given two operations \(*\) and \(\circ \) on a set S, an operation \(\star \) on S is said to be a collaboration between \(*\) and \(\circ \) if for all \(a,b \in S\), \(a \star b\) \(\in \{a *b, a\circ b \}\). Another term for collaborations is two-option operations. We are interested in learning what associative collaborations of two given operations \(*\) and \(\circ \) there may be. We do not require that \(*\) and \(\circ \) themselves be associative. For this project, as an initial experiment, we consider Plus-Minus operations (i.e. collaborations between addition and subtraction on an abelian group) and Plus-Times operations (i.e. collaborations between the addition and multiplication operations on a semiring.) Our study of Plus-Minus operations focuses on the additive integers but extends to ordered groups. For Plus Times operations, we make some headway in the case of the semiring of natural numbers. We produce an exhaustive list of associative collaborations between the usual addition and multiplication on the natural numbers \({\mathbb {N}}\). The Plus-Times operations we found are all examples of a type of construction which we define here and that we call augmentations by multidentities. An augmentation by multidentities combines two separate magmas A and B to create another, A(B), having \(A \sqcup B\) as underlying set, and in such a way that the elements of B act as identities over those of A. Hence, B consists of a sort of multiple identities (explaining the moniker multidentities.) When A and B are both semigroups then so is A(B). Understanding the connection between certain collaborations and augmentation by multidenties removes, in several cases, the need for cumbersome computations to verify associativity. A final section discusses connections between group collaborations and skew braces.
Similar content being viewed by others
1 Introduction
The initial focus of this paper is to consider binary operations \(\star \) on the set \({\mathbb {N}}\) of natural numbers such that, for every \(m, n \in {\mathbb {N}}\), \(m \star n\) equals either \(m + n\) or mn. We are interested in the possible associative operations that may be created that satisfy this requirement. We start by giving next the general background and motivation for this question.
A directed graph \(G=(V,E)\) is said to be simple if there is at most one directed edge between any two vertices \(u, v \in V\). As is customary, when G is a simple graph, we identify E with a subset of \(V \times V\) in such a way that, for \(u,v \in V\), \((u,v)\in E\) if and only if E has an edge from u to v.
Given an arbitrary set S and two binary operations \(*\) and \(\circ \) on S, every simple graph \(G=(V,E)\), having \(V=S\) as its set of vertices, induces a new operation \(\star \) on S, as follows. For all \(a,b \in S\), \(a \star b = a *b\) if \((a,b) \in E\) and \(a \star b = a \circ b\) when \((a,b) \notin E\). We shall denote \(\star = G(*,\circ )\).
One may also define two-option algebras in the following way, in which the graph is tacit yet implicit in the definition.
Definition 1
Given an arbitrary set S and two binary operations \(*\) and \(\circ \) on S, an operation \(\star \) on S is said to be a collaboration between \(*\) and \(\circ \) if for all \(x,y \in S\), \(x \star y \in \{ x *y, x \circ y\}\).
Two important examples are those when \(*= \pi _1\) and \(\circ = 0\) (similar to those operations named (one-value) graph magmas in [2]) and those when \(*= \pi _1\) and \(\circ = \pi _2\) (named two-value graph magmas in [1].) To be precise, the one-value graph magmas of [2] and related papers (including [1]) are not collaborations in the sense defined here. The operation there satisfies the definition of a collaboration except for those cases when 0 is a factor since the one-value graph magmas of [2] and related papers require 0 to be an annihilator element. In spite of this slight difference in meaning, we feel that the duplication in terminology is harmless. Therefore, the expression one value graph magmas here refers to straight collaborations between \(\pi _1\) and 0. On the other hand, there is no conflict between our use of the expression two-value graph magmas and that in the prior literature. The two-value graph magmas of [1] and those here are precisely the same.
The authors became interested in this type of situation while studying amenable bases over infinite dimensional algebras. An interesting type of construction, called graph magma algebras is a contracted semigroup algebra over an associative graph magma. Such considerations have been extended to two-value graph magmas, which are semigroup algebras over associative two-value graph magmas. In each case, determining when those two types of two-option magmas are associative was of primordial importance.
The earliest mention we have found of graph magmas is in the doctoral dissertation [14]. We have seen that, for that reason, they are sometimes referred to as Shallon Algebras. Graph magmas resurfaced later, under the moniker graph algebras. The expression graph magmas, which we use, was adopted in [2] when these structures were reintroduced with the precise intention of using them for the exploration of examples an counterexamples in the study of amenability of bases of infinite dimensional algebras. We became first aware of a characterization of associative graph magmas as they appear in [5]. However, the anonymous referee kindly pointed out that this characterization was predated by the work of [11], and it is in fact a corollary of Proposition 1.5(2) in [12]. The first characterization of associative two-value graph magmas is from [8].
The characterizations of one-value and two-value magmas mentioned are the kind of thing we were naively hoping for as we started down this path. Now we realize that the problem seems to be significantly more complex in its complete generality. A journey of a thousand miles begins with a single step; the explorations in this paper are a step. While it is unclear where this is going to take us, we hope the reader will agree that the problem is intriguing and worthy of consideration. The resulting contracted semigroup-algebras corresponding to these semigroups have been instrumental in the classification of amenable algebras (see [2, 9], and [10].)
These types of binary operations have been considered in the context of the study of a certain monoid structure on the set of all binary operations on a fixed set, in [7] and [8]. Adding the qualifier one-value to magma algebras was an afterthought motivated by the advent of two-value (graph) magmas in [8]. Two-value magmas seem destined to also become a fertile ground to answer many questions of these types (see, for instance, [1] for some examples of this phenomenon.)
Considering that algebraic structures with two binary operations acting on the same set one of which distributes over the other are a staple of Modern algebra, it seems reasonable to move in the direction of looking at rings and their two operations (addition and multiplication) as the ingredient operations for our two-option magmas. However, this experiment, our first, considers instead mostly the addition and multiplication the natural numbers (which is not a ring).
Section 3 lists eleven graphs, grouped in three classes (Example 16, Example 17, and Example 18), that induce associative collaborations for \(({\mathbb {N}}, +,-)\), the addition and multiplication of natural numbers. Example 19 shows two graphs which, albeit appearing to be similar to the ones that yield associative operations, yield non-associative ones. Section 4 then aims to prove that the family of graphs that induce associative collaborations between \(+\) and − amounts precisely to those eleven graphs.
An interesting notion has come to the surface, which we have labeled Augmentations by multidentities. Augmentations by multidentities (Definition 14) seem to be interesting magmas in their own right; in particular, Proposition 15 is very useful for our purposes in this paper. We found that many associative two-option operations over antifields (Definition 11) are augmentations by multidentities. In fact, all associative two-option operations that exist for \(({\mathbb {N}}, +, \cdot )\) are of this kind.
2 Associative collaborations between addition and subtraction of integers
In principle, the first step must be to choose pairs of operations that go together well. Given any group G, two natural operations to consider are the product in the group and multiplication by the inverse (i.e. \(a *b= ab^{-1}\)). In spite of the long-standing tradition to reserve additive notation to be used exclusively for abelian groups, we will follow a recent trend in some of the literature about braces and skew-braces and allow its use in the non-commutative setting. With that in mind, we will refer to this type of collaborations as Plus-Minus collaborations. In this first attempt, let us focus on addition and subtraction in the group \({\mathbb {Z}}\). Alternative terminology that removes the risk of inciting an expectation of commutativity is to refer to collaborations of ab and \(ab^{-1}\) as group collaborations. Both expressions are used interchangeably, for instance, in [6].
2.1 Parity-based associative Plus-Minus collaborations: the Plus-Minus group
Clearly, using addition all the time is an associative operation. On the other hand, using subtraction is, more often than not, not an associative operation. Our next example is a non-trivial associative collaboration between addition and subtraction of integers which is in fact a non-abelian group.
Example 2
Define \(*:{\mathbb {Z}} \times {\mathbb {Z}}\rightarrow {\mathbb {Z}}\) such that \(a *b= a - b\) if a is odd and, otherwise, \(a *b= a + b\). Then \(*\) is a Plus and Minus collaboration and, in fact, \(G = ({\mathbb {Z}}, *)\) is a group.
Proof
The first task is to verify associativity. This will have to be done by cases. For convenience, in the following calculations, variables denoted o or \(o_i\) will be odd and variables denoted e or \(e_j\) will be even. Then, the following set of calculations covers all possible cases:
-
1.
\(e_1*(e_2 *e_3) = e_1 + e_2 + e_3 = (e_1*e_2) *e_3\),
-
2.
\(e_1*(e_2 *o) = e_1 + e_2 + o = (e_1*e_2) *o\),
-
3.
\(e_1*(o *e_2) = e_1 + o - e_2 = (e_1*o) *e_2\),
-
4.
\(o *(e_1 *e_2) = o - e_1 - e_2 = (o *e_1) *e_2\),
-
5.
\(o_1*(o_2 *e) = o_1 - o_2 + e = (o_1*o_2) *e\),
-
6.
\(o_1*(e *o_2) = o_1 - e - o_2 = (o_1*e) *o_2\),
-
7.
\(e*(o_1 *o_2) = e + o_1 - o_2 = (e*o_1) *o_2\),
-
8.
\(o_1*(o_2 *o_3) = o_1 - o_2 + o_3 = (o_1*o_2) *o_3\).
Clearly, \(a *0 \in \{a +0, a-0\}=\{a\}\), so 0 is a right identity. Furthermore, since 0 is even, \(0 *a = 0 + a = a\) and therefore 0 is the identity element in \(({\mathbb {Z}}, *)\). In addition, notice that every even integer \(m \in {\mathbb {Z}}\) has its additive inverse \(-m \in {\mathbb {Z}}\) as an inverse under \(*\), while, on the other hand, every odd integer \(n \in {\mathbb {Z}}\) is its own inverse under \(*\). \(\square \)
A better understanding of the structure above is given in the following proposition.
Proposition 3
The group \(G=({\mathbb {Z}}, *)\) is a non-abelian group that has a normal subgroup N isomorphic to \(({\mathbb {Z}}, +)\) such that G/N is isomorphic to \({\mathbb {Z}}/2{\mathbb {Z}}\).
Proof
Note that \(1 *2 = -1\) but \(2 *1 = 3\), so indeed G is not abelian. Let \(N=2{\mathbb {Z}}\), then \((N,\star )=(2{\mathbb {Z}},+)\). To see that \(N \triangleleft G\), note that \(e_1 *e_2 *(-e_1) = e_1 + e_2 - e_1 = e_2\) and \(o *e *o = o + e + o \in N\). To prove that G/N is isomorphic to \({\mathbb {Z}}/2 {\mathbb {Z}}\), it suffices to show that any two odd integers are congruent modulo N. Indeed, \(o_1 *o_2^{-1}=o_1 - o_2 \in N\). \(\square \)
In a case like this one, where the associative collaboration is indeed a group, we say that the collaboration is a Plus-Minus group. When the expression group-collaboration is used instead of Plus-Minus collaboration, Plus-Minus groups are called group group collaborations, which may or may not be pleasant to the reader.
It turns out that \(G=({\mathbb {Z}}, *)\) is the only non-trivial Plus-Minus group over the abelian group \(({\mathbb {Z}},+)\). That is the subject of Theorem 7, which we prove via a series of lemmas. We start, however, with an obvious observation. Note if \(G=({\mathbb {Z}}, \circ )\) is a Plus-Minus group over \(({\mathbb {Z}},+)\) then 0 is the identity for G (since it is always a right identity in any Plus-Minus collaboration) and, also, for any integer a, the inverse \(a^{-1}\) of a must be either a itself or \(-a\).
Our first lemma shows that non-trivial Plus-Minus groups over \({\mathbb {Z}}\) must be non-abelian.
Lemma 4
A Plus-Minus group \(G=({\mathbb {Z}}, \circ )\) over \(({\mathbb {Z}},+)\) is abelian only if \(\circ = +\).
Proof
Suppose \(\circ \ne +\) and assume the group is abelian. Let \(m, n \in {\mathbb {Z}}\) be such that \(m+n \ne m \circ n = m - n\). Then \(n \ne 0\) and \(n \circ m \in \{n+m, n-m\}\) differs from \(m-n\) unless \(m=n\). The abelian assumption implies that \(m \circ n = m -n\) with \(n \ne 0\) only if \(m=n\). If \(m \ne 0\) is such that \(m \circ m=0\) then express m as \(a+b\) for \(0 \notin \{a,b\}\) with \(a\ne b\). Then, as \(a \circ (b \circ m)= (a \circ b) \circ m = m \circ m =0\), it follows that \(a + b + m = 2m\), a contradiction. Thus, G is not abelian. \(\square \)
Lemma 5
Let \(G=({\mathbb {Z}}, \circ )\) be a Plus-Minus group over \(({\mathbb {Z}},+)\). Then,
-
1.
the set \(H = \{ x \in {\mathbb {Z}}\mid x^{-1}=-x\}\) equals \(\{x \in {\mathbb {Z}}\mid \text { for every } y \in {\mathbb {Z}}, \; x\circ y= x+y\}\), and
-
2.
H is a normal subgroup of G.
Proof
-
1.
If x belongs to \(\{x \in {\mathbb {Z}}\mid \text { for every } y \in {\mathbb {Z}}, \; x\circ y= x+y\}\) then, in particular, \(0 = x \circ x^{-1} = x + x^{-1}\) and, therefore, \(x \in H.\) On the other hand, let’s assume that \(x^{-1}=-x\), and consider, on the contrary, \(0 \ne a \in {\mathbb {Z}}\) such that \(x \circ a= x-a\). Then \(a=(x^{-1} \circ x) \circ a = x^{-1} \circ (x \circ a) = -x \circ (x -a) \in \{-a,-2x+a\}\). This would mean that either x or a must be zero. Both of these are cases when \(x \circ a = x+a\) holds, hence we have a contradiction. Notice that this also means that if, for some element \(m \in G\), \(m^{-1}=m\) then, for all \(y \in G\), \(m \circ y= m-y\).
-
2.
The fact that H is closed under inverses is obvious. Now we are ready to show that H is closed under \(\circ \). Let \(b,c \in H\) and consider the inverse of \(b \circ c\). \((b \circ c)^{-1}=c^{-1}\circ b^{-1}=(-c) + (-b) = -(b+c)= -(b \circ c)\). Confirming our claim. Finally, we show that H is normal by considering \(y\circ x \circ y^{-1}\), the conjugate by \(y \in G\) of an element \(x \in H\). We need only consider the case when \(y \notin H\). In that case, \(y^{-1}=y\) and the conjugate in consideration equals \(y\circ x \circ y\) having inverse \(y\circ (-x) \circ y = y-(-x + y) =x \in H\).\(\square \)
Lemma 6
For a Plus-Minus group \(G=({\mathbb {Z}}, \circ )\) over \(({\mathbb {Z}},+)\), other than \(({\mathbb {Z}}, +)\), the normal subgroup \(H = \{x \in {\mathbb {Z}}\mid x^{-1}=-x\}\) consists of all even integers.
Proof
Note that if \(H=\{0\}\) then \(\circ = -\), but \(({\mathbb {Z}}, -)\) is not a group. Therefore, \(H \ne \{0\}.\) Let m be the smallest positive integer in H then \(m^n\), the n-th power of m in G, equals nm for all \(n\in {\mathbb {Z}}\). So, \(m{\mathbb {Z}} \subset H\).
We see \(m \ge 2\), for, if every integer is in H then \(\circ = +\).
We aim to show that \(m=2\). To that avail, note that for any \(a,b \in G {\setminus } H\), \(a \circ b^{-1} = a - b\), which belongs to H since \((a \circ b^{-1})^{-1} = b \circ a^{-1}= b -a\). If m were bigger than 2 we would have \(m-1\) and \(m-2\) to be elements in \(G{\setminus } H\) and that would imply that \((m-1)\circ (m-2)^{-1}\), which equals \((m-1)-(m-2)=1\), belongs to H, contradicting the minimality of m. \(\square \)
Theorem 7
The only group Plus-Minus collaboration over \(({\mathbb {Z}},+)\) are \(({\mathbb {Z}},+)\) and the parity-based associative collaboration \(({\mathbb {Z}}, *)\) featured in Example 2 and Proposition 3.
Proof
Let \(G=({\mathbb {Z}}, \circ )\) be a Plus-Minus group over \(({\mathbb {Z}},+)\) and assume that \(\circ \ne +\). By Lemma 5, whether \(\circ \) adds or subtracts depends completely on whether the first term is in H. By Lemma 6, the elements of H are precisely the even integers. Thus, \(\circ \) coincides with the associative collaboration in Example 2. \(\square \)
The ideas presented here so far can be extended to other groups that have some notion of parity. For instance, if G is an abelian group with a subgroup N such that \(G/N \cong {\mathbb {Z}}_2\) then one can define the following Plus-Minus collaboration. Let \(\varphi : G \rightarrow {\mathbb {Z}}_2\) be an epimorphism with kernel N. Define \(\star : G \times G \rightarrow G\) via \(a \star b = a+b\) if \(\varphi (a)=0\), and \(a \star b = a-b\) if \(\varphi (a)=1\).
This is an example of an associative Plus-Minus collaboration \(\star \) on the finite abelian group \({\mathbb {Z}}_4\) based on the fact that its elements can be divided into even and odd ones, as described above. Notice that addition is carried on the rows labeled 2 and 0, while the rows labeled 3 and 1 correspond to subtraction.
When G does not have \({\mathbb {Z}}_2\) readily as an epimorphic image, one can consider either the direct product \(G \oplus {\mathbb {Z}}\) or \(G \oplus {\mathbb {Z}}_2\) and obtain a Plus-Minus associative collaboration on them, adding when the second entry of the first term is even, and adding when it is odd. We refer to the second term in the elements of \(G \oplus {\mathbb {Z}}\) or \(G \oplus {\mathbb {Z}}_2\) as a pacemaker.
2.2 Order-based associative Plus-Minus collaborations
Our next example is only a monoid, not a group.
Example 8
Define \(\circ :{\mathbb {Z}} \times {\mathbb {Z}}\rightarrow {\mathbb {Z}}\) such that for all \(a,b \in {\mathbb {Z}}^*\), \(a \circ b= a - b\) if a and b have different signs and, \(a \circ b= a + b\) otherwise. Notice that \(b\circ 0 = b\) regardless of our choice of whether \(\circ \) works as addition or subtraction. Our definition will then be complete as soon as we determine the value of \(0 \circ b\). Complete the definition, therefore, by requiring that \(0 \circ b= b\) for every integer b. Then \(\circ \) is an associative Plus-Minus collaboration.
Proof
To confirm associativity, we will proceed by cases. For convenience, in the following calculations, variables denoted p or \(p_i\) will be positive and variables denoted n or \(n_j\) will be negative. Then, the following set of calculations covers all possible cases not involving 0:
-
1.
\(p_1\circ (p_2 \circ p_3) = p_1 + p_2 + p_3 = (p_1\circ p_2) \circ p_3\),
-
2.
\(p_1\circ (p_2 \circ n) = p_1 + p_2 - n = (p_1\circ p_2) \circ n\),
-
3.
\(p_1\circ (n \circ p_2) = p_1 - n + p_2 = (p_1\circ n) \circ p_2\),
-
4.
\(n \circ (p_1 \circ p_2) = n - p_1 - p_2 = (n \circ p_1) \circ p_2\),
-
5.
\(n_1\circ (n_2 \circ p) = n_1 + n_2 - p = (n_1\circ n_2) \circ p\),
-
6.
\(n_1\circ (p \circ n_2) = n_1 - p + n_2 = (n_1\circ p) \circ n_2\),
-
7.
\(p\circ (n_1 \circ n_2) = p - n_1 - n_2 = (p\circ n_1) \circ n_2\),
-
8.
\(n_1\circ (n_2 \circ n_3) = n_1 + n_2 + n_3 = (n_1\circ n_2) \circ n_3\).
Since, under this definition, 0 is an identity element, any expression involving three terms, with at least one 0 will satisfy the associativity requirement. \(\square \)
Our next example is very similar to the previous one but this one is only a semigroup, not a monoid.
Example 9
As in the previous example, define \(*:{\mathbb {Z}} \times {\mathbb {Z}}\rightarrow {\mathbb {Z}}\) such that for all \(a,b \in {\mathbb {Z}}^*\), \(a *b= a - b\) if a and b have different signs and, \(a *b= a + b\) otherwise. Complete the definition by requiring that \(0 *b= - b\) for every positive integer b and \(0 *c = c\), for each negative integer c. Then \(*\) is an associative Plus and Minus collaboration.
Proof
Any expression involving three non-zero elements will satisfy the associativity requirement in exactly the same way that they did in the previous example. The proof of associativity will then be complete once we consider the following cases involving 0, where p’s will denote positives, n’s will denote negatives, and x’s will denote arbitrary (non-zero) elements.
-
1.
\(0*(0 *0) = 0 = (0*0) *0\),
-
2.
\(x*(0 *0) = x = (x*0) *0\),
-
3.
\(0*(x *0) = 0 *x = (0*x) *0\),
-
4.
\(0*(0 *x) = (0*0) *x\),
-
5.
\(0*(p_1 *p_2) = -p_1-p_2 = (0*p_1) *p_2\),
-
6.
\(0*(n_1 *n_2) = n_1+n_2 = (0*n_1) *n_2\),
-
7.
\(0*(p *n) = -p+n = (0*p) *n\),
-
8.
\(0*(n *p) = n-p = (0*n) *p\),
-
9.
\(p_1*(0 *p_2) = p_1+p_2 = (p_1*0) *p_2\),
-
10.
\(n_1*(0 *n_2) = n_1+n_2 = (n_1*0) *n_2\),
-
11.
\(p*(0 *n) = p - n = (p*0) *n\),
-
12.
\(n*(0 *p) = n - p = (n*0) *p\),
-
13.
\(x_1*(x_2 *0) = x_1 *x_2 = (x_1*x_2) *0\).\(\square \)
Two important facts that were used tacitly in the proof for Example 9 are that, for any positive integer p and for all \(x\in {\mathbb {Z}}\), \(p*x\) is also a positive integer, and, similarly, for any negative integer n and for all \(y\in {\mathbb {Z}}\), \(n*y\) is also negative.
Example 10
Example 9 may be modified to get a very similar operation \(*\) changing the behavior of the products with zero as a left factor. Namely, we require that \(0 *n= -n\) for negative n and \(0 *p=p\) for positive p. We will not go over the details of the proof since they are basically the same as those in the previous example.
3 Characterizing certain semirings in terms of their associative Plus-Times collaborations
Remember that a semiring is a set R with two operations \(+\) and \(\cdot \) that behave like those of a ring but with exception that one does not require additive inverses to exist in general. That definition would allow \(R=\{0\}\) to be a trivial semiring but we will always assume \(R \ne \{0\}\) to avoid certain non-sensical consequences.
Definition 11
-
1.
A semiring is said to be semidomain if for all \(\{a,b\} \subset S\), \(ab=0\) if and only if \(0 \in \{a,b\}.\)
-
2.
A semidomain is called an antifield if for all \(\{a,b\} \subset S\), \(ab=1\) if and only if \(\{a,b\} = \{1\}\) and \(a+b = 0\) if and only if \(\{a,b\}=\{0\}\).
Notice that if the semiring is indeed a ring, then it is a semidomain precisely when it is a domain. The semiring of natural numbers is an example of an antifield. This section provides nine non-trivial graphs that induce associative Plus-Times collaborations on an arbitrary antifield R. We show that (some of) these collaborations suffice to precisely characterize antifields. The following section then proves that these eight collaborations are the only ones for the case when \(R= {\mathbb {N}}\).
Since \(2+2= 2(2)=4\) it does not matter whether there is a loop at the vertex corresponding to \(2 \in {\mathbb {N}}\). The same thing happens with the vertex 0. We will choose each time whether to include or not a loop around each one of those vertices in a way that best fits our narrative. We will think of two graphs that are identical other than possibly containing loops (0, 0) or (2, 2) as being the same graph. This is the only possible ambiguity in this setting, as stated in the following lemma, a well-known fact which is part of the folklore.
Lemma 12
If \(m,n \in {\mathbb {N}}\) and \(mn = m+n\) then the set \(\{m,n\}\) equals either \(\{0\}\) or \(\{2\}\).
Another useful well-known fact, concerning the solutions of a similar (but three-fold) Diophantine equation, follows.
Lemma 13
The only positive integer solutions to the Diophantine equation \(a+b+c=abc\) are permutations of \(\{1,2,3\}\).
Definition 14
Let \( (K, \circ ) \& (H, *)\) be two distinct magmas. Define an operation \(\star \) on their disjoint union \(K \sqcup H\) via:
-
1.
\(h_i \star h_j= h_i *h_j \text{ for } \text{ all } h_i, h_j \in H\),
-
2.
\(k_i \star k_j = k_i \circ k_j \text{ for } \text{ all } k_i, k_j \in K\), and
-
3.
\(k \star h= h \star k=k \text{ for } \text{ all } k \in K, h \in H\).
We refer to the underlying set of \(\star \) either as \(K \sqcup H\) or as K(H). The first notation lends itself to writing \((K,\circ ) \sqcup (H,*)\) to refer to this structure, which is quick and convenient. The second notation serves to emphasize, when needed, that there is a difference between the roles of the two components. Likewise, we sometimes write \(\circ (*)\) instead of \(\star \). We say that \((K(H), \circ (*) )\) is the augmentation of K by the multidentities in H. Notice that the elements of H are called the multidentities of K(H) because they act as multiple identities on K, which explains our terminology.
Proposition 15
If \((K, \circ )\) and \((H, *)\) are associative then \((K(H), \circ (*))\) is also associative.
Proof
The proof follows from a straightforward, case-by-case, analysis. \(\square \)
Let \((R,+,\cdot )\) be an arbitrary antifield, the following three examples provide a list of eleven Plus-Times associative collaborations over R. A graph is said to be complete (or full) if any two vertices (including two copies of the same vertex) are joined with an edge. Likewise, the graph is null if no two vertices (including no two copies of the same vertex) are connected with an edge. We use the expressions quasi-complete and roses to roughly describe other graphs appealing to the reader’s intuition but without precise formal definitions. Our eleven examples are thus grouped in three groups. A final fourth example warns the reader about two graphs, which, in spite of their superficial similarity to some that do, do not yield associative operations.
Example 16
-
(a)
The null graph: Let \(G=N_{R}\) be the null graph with vertex set R, then \(G(+,\cdot )=\cdot \) and is, therefore, associative.
-
(b)
The complete graph: When \(G=K_{R}\) is the complete graph, then \(G(+,\cdot )=+\). This, and the previous Example 16, are the two trivial situations that give rise to associative operations in \(\langle +, \cdot \rangle \).
Example 17
Almost complete graphs: We will refer to the following five examples as being quasi-complete in the sense that all but finitely many vertices will be connected to one another. The descriptive titles are an attempt to describe what will be the connection between the large connected subgraph and the remaining vertices.
-
(c)
Quasi-complete with outward multiplicative identity stem: Let G be the graph shown below, such that
 ,
,  for all \( m \in R\), if \(0 \not = m\) then
for all \( m \in R\), if \(0 \not = m\) then  , and, for all \( a,b \in R {\setminus } \{1\}\)
, and, for all \( a,b \in R {\setminus } \{1\}\)  . Then the collaboration \(G(+,\cdot )\) is associative.
. Then the collaboration \(G(+,\cdot )\) is associative.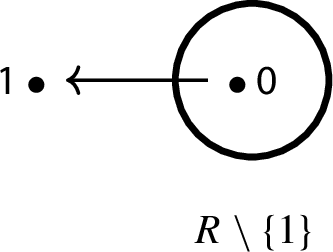
-
(d)
Quasi-complete with inward multiplicative identity stem: Let G be the graph, shown below, such that
 ,
,  and
and  for all \( m \in R {\setminus } \{0\}\), and, for all \( a,b \in R {\setminus } \{1\}\)
for all \( m \in R {\setminus } \{0\}\), and, for all \( a,b \in R {\setminus } \{1\}\)  . Then the collaboration \( G(+,\cdot )\) is an associative operation.
. Then the collaboration \( G(+,\cdot )\) is an associative operation.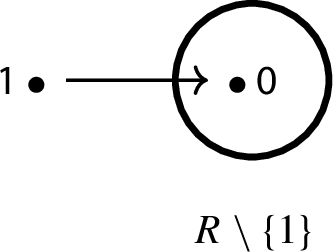
-
(e)
Quasi-complete with multiplicative identity isolated: Let G be the graph, shown below, such that 1 is isolated and all other vertices are fully connected. Then the collaboration \( G(+,\cdot )\) is associative.
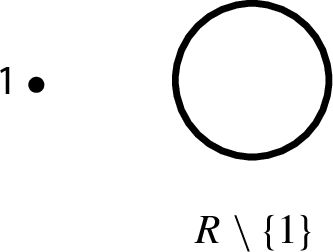
-
(f)
Quasi-complete with additive identity isolated: Let G be the graph, shown below, such that 0 is isolated and all other vertices are fully connected. Then the collaboration \( G(+,\cdot )\) is associative.
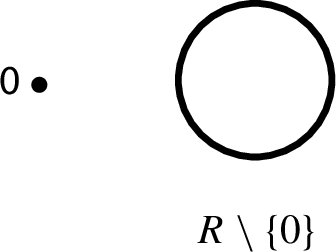
-
(g)
Quasi-complete with both identities isolated: Let G be the graph, shown below, with 0 and 1 isolated and all other elements fully connected. Then the collaboration \( G(+, \cdot )\) is associative.
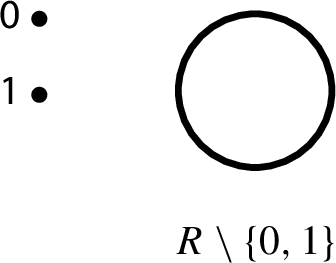
Proof
Proving that the various examples provided here indeed yield associative operations can be done in a straightforward yet tremendously tedious way. Fortunately, as each one of these collaborations can be seen as augmentations by multidentities with associative components, taking advantage of Proposition 15, one may offer proofs that are significantly easier and more insightful. All one needs to observe is that the various operations have the corresponding representations as augmentations by multidentities:
-
(c)
\(( R \setminus \{0,1\}, +) \sqcup (\{0,1\}, \pi _2) \)
-
(d)
\((R \setminus \{0,1\}, +) \sqcup (\{0,1\}, \pi _1) \)
-
(e)
\( ( R \setminus \{1\}, +) \sqcup (\{1\}, \cdot )\)
-
(f)
\((\{0\}, \cdot ) \sqcup ( R \setminus \{0\}, +) \)
-
(g)
\((\{0\},+) \sqcup (R \setminus \{0,1\}, +)\sqcup (\{1\}, \cdot )\) \(\square \)
Our next example lists four other graphs, the roses, that yield associative operations. Once again, the proofs will be aided by Proposition 15.
Example 18
The roses:
-
(h)
Full rose: Let G be the graph, shown below, such that for \(m \in R\),
 and
and  , and, for all nonzero \( u \& v\), then
, and, for all nonzero \( u \& v\), then  . Then \(G(+, \cdot )\) is associative.
. Then \(G(+, \cdot )\) is associative.
-
(i)
Rose with outward stem: Let G be the graph, shown below, such that
 but
but  , for \(m\ne 1\),
, for \(m\ne 1\),  and
and  , and, for all nonzero \( u \ne v\), then
, and, for all nonzero \( u \ne v\), then  . Then \(G(+, \cdot )\) is associative.
. Then \(G(+, \cdot )\) is associative.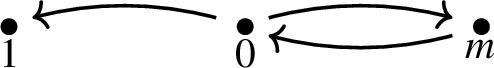
-
(j)
Rose with inward stem: Let G be the graph, shown below, such that
 but
but  , for \(m\ne 1\),
, for \(m\ne 1\),  and
and  , and, for all nonzero \( u \& v\), then
, and, for all nonzero \( u \& v\), then  . Then \(G(+, \cdot )\) is associative.
. Then \(G(+, \cdot )\) is associative.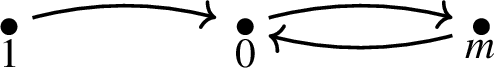
-
(k)
Rose without a stem: Let G be the graph, shown below, such that \(\forall m \in {\mathbb {N}}\),
 and
and  ,for \(m\ne 1\),
,for \(m\ne 1\),  and
and  , and, for all nonzero \( u \& v\), then
, and, for all nonzero \( u \& v\), then  . Then \(\star = G(+, \cdot )\) is associative.
. Then \(\star = G(+, \cdot )\) is associative.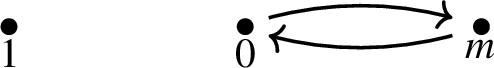
Proof
These four operations are augmentations by identities as follows:
-
(h)
\(( R \setminus \{0\}, \cdot ) \sqcup (\{0\}, \cdot )\)
-
(i)
\((R \setminus \{0,1\}, \cdot ) \sqcup (\{0,1\}, \pi _2) \)
-
(j)
\((R \setminus \{0,1\}, \cdot ) \sqcup (\{0,1\}, \pi _1) \)
-
(k)
\((R \setminus \{0,1\}, \cdot ) \sqcup (\{0,1\}, \cdot ) \) \(\square \)
For completeness, we show two quasi-complete graphs on the set of natural numbers, \({\mathbb {N}}\), that are similar to some of those in Example 17 but do not yield associative operations. Showing that associativity fails boils down to providing an example so it is easy to give proofs for both cases. As promised earlier, further insight will be given in Sect. 4.
Example 19
Non-associative examples:
-
1.
Quasi-complete with inward additive identity stem: Let G be the graph, shown below, such that
 ,
, and
and  for all \( m \in {\mathbb {N}} \setminus \{1\}\), and, for all \( a,b \in {\mathbb {N}} {\setminus } \{0\}\),
for all \( m \in {\mathbb {N}} \setminus \{1\}\), and, for all \( a,b \in {\mathbb {N}} {\setminus } \{0\}\),  . Then \(\star =G(+,\cdot )\) is not an associative operation.
. Then \(\star =G(+,\cdot )\) is not an associative operation.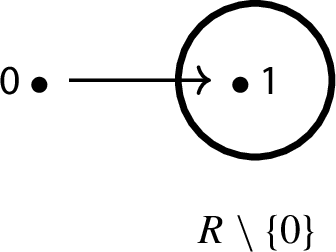
Proof
Consider:
-
\((0 \star 1) \star 2= 1 \star 2=3\), and
-
\(0 \star (1 \star 2)= 0 \star 3=0\).
Therefore \(\star =G(+,\cdot )\) is not an associative operation. \(\square \)
-
2.
Quasi-complete with outward additive identity stem: Let G be the graph, shown below, such that
 ,
, and
and  for all \( m \in {\mathbb {N}}\), and, for all \( a,b \in {\mathbb {N}} {\setminus } \{0\}\)
for all \( m \in {\mathbb {N}}\), and, for all \( a,b \in {\mathbb {N}} {\setminus } \{0\}\)  . Then \(\star =G(+,\cdot )\) is not an associative operation.
. Then \(\star =G(+,\cdot )\) is not an associative operation.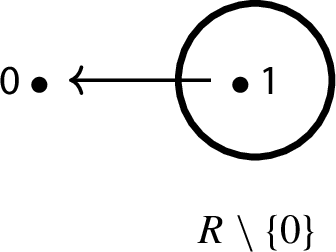
Proof
Consider:
-
\((1 \star 0) \star 2= 1 \star 2=3\), and
-
\(1 \star (0 \star 2)= 1 \star 0=1\).
Therefore \(\star =G(+,\cdot )\) is not an associative operation. \(\square \)
It turns out that the list of associative collaborations given in Examples 17 and 18 suffice to characterize antifields. That will be the subject of Theorem 23 below. We start with three propositions which pinpoint exactly how the various properties of an antifield are determined by specific sets of collaborations.
Proposition 20
Let \((R, +, \cdot )\) be an arbitrary semiring. Then the full rose (Example 18 (e)) is associative if and only if R is a semidomain.
Proof
(\(\Longrightarrow \)) Suppose the graph is associative but the ring is not domain. Then there exist non-zero \(m_1\) and \(m_2 \in R\), such that \(m_1 \cdot m_2=0\). Then \((m_1 \star m_2) \star 1= (m_1 \cdot m_2) \star 1= 0 \star 1=0 + 1=1\), while \(m_1 \star (m_2 \star 1)=m_1 \star (m_2 \cdot 1)= m_1 \cdot m_2 =0\). Therefore the graph is not associative, which is a contradiction.
\(\Longleftarrow \) For the converse, suppose that R is a semidomain. Given \(a,b, c \in R\) if \(0 \notin \{a, b, c\}\) then \(a\star (b\star c) = a \star (bc)\), and, as \(bc \ne 0\), that is equal to a(bc). Similarly, the triple product \((a\star b)\star c\) yield (ab)c, which is the same result since multiplication in a ring is associative. Furthermore, if \(0 \in \{a,b,c\}\) then the triple product equals a single product of the other two factors and associativity is granted. \(\square \)
Proposition 21
Let \((R,+, \cdot )\) be a semiring with identity 1. Then the rose with outward stem below (previously considered in Example 18 (f)) yields an associative collaboration if and only if
-
1.
\((R, +, \cdot )\) is a semidomain, and
-
2.
the only element of R with a multiplicative inverse is 1.
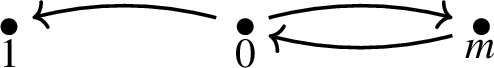
Proof
\((\Longrightarrow )\) By a contradiction suppose that it is not a semidomain or there are multiplicative inverses.
-
1.
Let \(0 \not =a \in R\) be a zero divisor and \(ab=0\), where \(b\ne 0\), and consider \((a \star b) \star 1= (a \cdot b) \star 1= 0 \star 1= 1\) and \(a \star (b \star 1)= a \star b= 0\), and
-
2.
Suppose \(1 \not = x \in R\) is a unit. Then there is \(y \in R\) such that \(xy=1\), now consider \((x \star y) \star 0= 1 \star 0=0\) and \(x \star (y \star 0)= x \star y=1 \).
Therefore, the graph is not associative, which is a contradiction.
\((\Longleftarrow )\) Suppose 1 and 2 hold. Then we can express the semiring \((R,+,\cdot )\) as an augmentation by multidentities, that is \((R, \star )= (R {\setminus } \{0,1\}, \cdot ) \sqcup (\{0,1\}, \pi _2)\), hence the graph is associative. \(\square \)
Proposition 22
Let \((R,+, \cdot )\) be a semiring. Then the quasi-complete graph with outward multiplicative identity stem below (previously considered in Example 17 (a)) yields an associative collaboration if and only if the only element that has an additive inverse is 0.

Proof
\((\Longrightarrow )\) We will show that if an element \(a \in R {\setminus } \{0\}\) has an inverse b then the operation induced by the above graph is not associative. We consider two cases:
If \(a \ne 1\) has an inverse b, then \((a \star b) \star 1= 0 \star 1=1\) and \(a \star (b \star 1)= a \star b=0\). Therefore the operation is not associative.
For the case \(a=1\), suppose that 1 has an inverse b. Notice that
If \(2b+b^2\) were equal to 0, then 0 would be equal to 1, thus, \(2b+b^2 \ne 0\). Consider next the products
and conclude that the operation is not associative.
\((\Longleftarrow )\) Suppose that there are no additive inverses, then we can express the collaboration by addition and multiplication as an augmentation by multidentities of two associative operations, \((R, \star )= (R \setminus \{0,1\}, +) \sqcup (\{0,1\}, \pi _2) \). Therefore, by the graph is associative. \(\square \)
Theorem 23
Given a semiring \((R,+,\cdot )\), the collaborations on Examples 17 and 18 are associative if and only if \((R,+,\cdot )\) is an antifield.
Proof
Examples 17 and 18 show that if R is an antifield then those eight graphs induce associative collaborations. Propositions 20, 22, and 21 show that the converse holds. In fact, it suffices that the collaboration (a) in Example 17, and (e) and (f) in Example 18 (or even just Examples 17(a) and 18(f)) be associative. \(\square \)
In general, as we show in the following example, which closes this section, specific antifields may have associative Plus-Times collaborations beyond the ones in Theorem 23. However, we will show, in Sect. 4, that the list from Theorem 23 is exhaustive in the case of the antifield \({\mathbb {N}}\).
Example 24
The semiring \((A,+,\cdot )=([0,1], \max , \min )\), consisting of the real interval [0, 1] and the usual \(\max \) and \(\min \), is an antifield having an infinite number of associative Plus-Times collaborations.
Proof
It is straightforward to show that this is indeed an antifield. For every \(k \in (0,1)\), one may define a Plus-Times collaboration \(\star \) such that \(a \star b= a\min b\), if \(a,b \in [0,k)\), \(c \star d= c\max d\), if \(c,d \in [k,1]\), and \(x \star y= y \star x = x\max y\), if \(x \in [0,k)\) and \(y \in [k,1]\). \(\square \)
4 There are exactly eleven associative Plus-Times collaborations for the natural numbers
The purpose of this section is to prove that the list of examples provided in the previous section, Example 16 through 18, is a complete enumeration of the associative Plus-Times operations on \({\mathbb {N}}\).
4.1 Connections with 0
We begin with some useful lemmas. Our first lemma shows that, with the possible exception of 1, the relation of elements with 0 is symmetrical.
Lemma 25
Let \(\star \) be associative collaboration on \({\mathbb {N}}\). If \(m \ne 1\), then  if and only if
if and only if  .
.
Proof
Notice that the statement is tautological (and immaterial, since \(0\cdot 0 = 0 +0)\) if \(m=0\). So, we may assume that this is not the case.
Suppose, for the sake of a contradiction, that  but
but  . Since \(\star \) is associative, \((m \star 0)\star m= m \star (0 \star m)\). This implies that \(m \star m\)= m, which means that either \(m^2=m\) or \(2\,m = m\). These possibilities may only hold when \(m \in \{0,1\}\), contrary to our assumptions. They are, therefore, impossible.
. Since \(\star \) is associative, \((m \star 0)\star m= m \star (0 \star m)\). This implies that \(m \star m\)= m, which means that either \(m^2=m\) or \(2\,m = m\). These possibilities may only hold when \(m \in \{0,1\}\), contrary to our assumptions. They are, therefore, impossible.
Similarly, suppose  and
and  and consider the equation \((m \star 0)\star m= m \star (0 \star m)\), which is to hold due to our assumption that \(\star \) is associative. Then, \(m = m \star m\), which yields to the same contradictions as in the first part of the proof. \(\square \)
and consider the equation \((m \star 0)\star m= m \star (0 \star m)\), which is to hold due to our assumption that \(\star \) is associative. Then, \(m = m \star m\), which yields to the same contradictions as in the first part of the proof. \(\square \)
As is customary in graph theory, for any \(m \in {\mathbb {N}}\), we refer to the set  as the outset, out(m), of m. Our second lemma characterizes the possible outsets of 0 for a graph G such that the collaboration \(\star = G(+,\cdot ) \) is associative. Namely, \(out(0) \in \{ \emptyset , {\mathbb {N}}, {\mathbb {N}} {\setminus } \{0\}, {\mathbb {N}} {\setminus } \{0,1\}\}.\)
as the outset, out(m), of m. Our second lemma characterizes the possible outsets of 0 for a graph G such that the collaboration \(\star = G(+,\cdot ) \) is associative. Namely, \(out(0) \in \{ \emptyset , {\mathbb {N}}, {\mathbb {N}} {\setminus } \{0\}, {\mathbb {N}} {\setminus } \{0,1\}\}.\)
Lemma 26
Given an associative collaboration \(\star \) on \({\mathbb {N}}\). Then:
-
1.
For all \(m \ge 1\),
 .
. -
2.
For all \(m \ge 3\),

Proof
-
1.
Suppose
 , then, by Lemma 25,
, then, by Lemma 25,  . For the sake of contradiction, suppose
. For the sake of contradiction, suppose  and consider the triple product \((m \star 0) \star (m+1)\) in two ways. First, \((m \star 0) \star (m+1) = m \star (m+1) \in \{ 2\,m+1, m^2 +m\}\). On the other hand, \(m \star (0 \star (m+1))= m \star 0=m\). These options yield two possible equations, \(2\,m+1=m\) and \(m^2+m=m\), neither of which has a positive integer solution.
and consider the triple product \((m \star 0) \star (m+1)\) in two ways. First, \((m \star 0) \star (m+1) = m \star (m+1) \in \{ 2\,m+1, m^2 +m\}\). On the other hand, \(m \star (0 \star (m+1))= m \star 0=m\). These options yield two possible equations, \(2\,m+1=m\) and \(m^2+m=m\), neither of which has a positive integer solution. -
2.
Assume that for some \(m \ge 3\),
 but
but  . Consider the triple product \((m \star 0) \star (m-1)\) in two ways. First, \((m \star 0) \star (m-1) = m \star (m-1) \in \{ 2\,m-1, m^2 -m\}\). On the other hand, \(m \star (0 \star (m-1))= m \star 0=m\). These options yield two possible equations, \(2\,m-1=m\) and \(m^2-m=m\), neither of which has a solution greater than or equal to 3.\(\square \)
. Consider the triple product \((m \star 0) \star (m-1)\) in two ways. First, \((m \star 0) \star (m-1) = m \star (m-1) \in \{ 2\,m-1, m^2 -m\}\). On the other hand, \(m \star (0 \star (m-1))= m \star 0=m\). These options yield two possible equations, \(2\,m-1=m\) and \(m^2-m=m\), neither of which has a solution greater than or equal to 3.\(\square \)
4.2 Connections among elements larger than or equal to 2
Our next lemma indicates that, for elements bigger than or equal to 2, connectedness (equivalently, disconnectedness) must be mutual.
Lemma 27
For an associative plus-times collaboration, \(\star \), on \({\mathbb {N}}\). Let \(n, m \ge 2\) such that \(n\not = m\): if  then
then  .
.
Proof
Assume that  , and suppose, for the sake of contradiction, that
, and suppose, for the sake of contradiction, that  . Notice that this means, in particular, that \(m \ne n\). Then, since we are assuming that the graph is associative, \(( n \star m) \star n = n \star (m \star n)\). The left hand side \(( n \star m) \star n =(n + m) \star n \in \{2n +m, n^2 + nm \} \), and the right hand side \(n \star (m \star n)= n \star nm \in \{n+nm, n^2\,m\}\). This yields four cases and each leads to either an impossibility or a contradiction, as follows:
. Notice that this means, in particular, that \(m \ne n\). Then, since we are assuming that the graph is associative, \(( n \star m) \star n = n \star (m \star n)\). The left hand side \(( n \star m) \star n =(n + m) \star n \in \{2n +m, n^2 + nm \} \), and the right hand side \(n \star (m \star n)= n \star nm \in \{n+nm, n^2\,m\}\). This yields four cases and each leads to either an impossibility or a contradiction, as follows:
Case i: \(2n +m = n+nm\) then \(n+m =nm\) which, by Remark 12 means that either \(n=m=0\) or \(n=m=2\), a contradiction since \(m \ne n\).
Case ii: \(2n +m = n^2\,m\) then \(2n = m(n^2-1)\). Now, for \(n >2\), \(n< n^2 -2 < n^2-1\). Then, as \(2 \le m\), multiplying these inequalities side by side yields \(2n < m(n^2-1)\), rendering this possibility impossible.
Case iii: \(n^2 + nm = n + nm\) then \(n^2 = n\), which is never the case when \(n \ge 2\).
Case iv: \(n^2+nm = n^2\,m\), then \(n^2 (m-1)= nm\) and therefore \(nm= n + m\), which, can be seen to be an impossibility, arguing as in case i. \(\square \)
Our following lemma shows that every value greater than 2 connects to every such value that is connected (in either direction, because of Lemma 27 ) with 2.
Lemma 28
Let \(\star \) be an associative plus-times collaboration on \({\mathbb {N}}\). For \(n, m > 2\): if  then
then  .
.
Proof
Let \(n, m > 2\). Assume, on the contrary, that  but
but  . Associativity yields that \(( n \star m) \star 2 = n \star (m \star 2)\)
. Associativity yields that \(( n \star m) \star 2 = n \star (m \star 2)\)
Now, \(( n \star m) \star 2= nm \star 2 \in \{ mn +2, 2mn \}\), while \(n \star (m \star 2) = n \star (m+2) \in \{ n+m+2, nm + 2n \}\). Once again, this yields four cases which we show to be impossible.
Case i: If \(mn+2 = n+m+2\) then \(nm= n+m\) which, by Lemma 12, yields a contradiction.
Case ii: If \(mn + 2 = nm +2n\) then \(2=2n\), an impossibility.
Case iii: That \(2mn = m+ n +2\) is a contradiction can be seen from Lemma 13, as the only positive integer solutions to the Diophantine equation \(a+b+c=abc\) are permutations of \(\{1,2,3\}\). This would force either m or n to be 1, contrary to our standing hypothesis.
Case iv: \(2mn = nm + 2n \Longrightarrow mn = 2n\), then \(m=2\), contradicting our assumption that \(m > 2\). Therefore, we must have  . \(\square \)
. \(\square \)
Our final lemma of this subsection shows that if two elements greater than or equal to 3 are connected then every element bigger than or equal to 2 will connect to them. This lemma explains the dichotomy between the roses of Example 18 and the quasi-complete graphs of Example 17. The idea of this lemma is that if there is any arrow between a pair of elements greater than or equal to 2 other than (2, 2) then the graph is the complete graph on the set of elements greater than or equal to 2.
Lemma 29
Given an associative Plus-Times collaboration \(\star \) on \({\mathbb {N}}\), and \(n,m,k \ge 2\) with \(\{m,k\} \ne \{2\}\), then, if \( m \star k=m+k \), then \( n \star m=n+m\).
Proof
Suppose that \(n \star m \not = n+m \) but \(m \star k= m+k\), then \((n \star m) \star k \in \{nm+k, nmk\}\), and \(n \star (m \star k) \in \{n+m+k, n(m +k) \}\). Considering the four possibilities that arise, we get:
-
1.
\(nm+k=n+m+k\), then \(nm=n+m\), therefore \(n \star m=m+n\), a contradiction to our hypothesis.
-
2.
\(nm+k = nm+nk\), then \(nk=k\), which is a contradiction.
-
3.
\(nmk=n+m+k\), a contradiction to Lemma 13 because \(1 \not \in \{m,n,k\}\),.
-
4.
\(nmk=n(m+k)\), then \(mk=m+k\), a contradiction as in part 1.\(\square \)
4.3 Connections with 1
Our final batch of lemmas aims to elucidate the role of 1 in the acceptable graphs.
Lemma 30
Given an associative graph \({\mathbb {N}}(+, \cdot )\). For \(m \not \in \{0,1\}\), \(m \star 1 = m +1\) if and only if \(1 \star m= 1+m\).
Proof
(\(\Longrightarrow \)) Suppose that \(m \star 1= m+1\) but \(1 \star m= 1 \cdot m=m\). Consider, \((m \star 1) \star m= (m+1) \star m \in \{2\,m+1, m^2+m\}\), and \(m \star (1 \star m)= m \star m \in \{2\,m, m^2\}\), which yields a contradiction.
(\(\Longleftarrow )\) Mimicking the steps above. \(\square \)
Lemma 31
Given an associative graph \({\mathbb {N}}(+, \cdot )\). Then for \(m \not \in \{0,1\}\) we have:
-
1.
If
 , and
, and -
2.
If

Proof
-
1.
Let \(m \not \in \{0,1\}\) and suppose that
 , but
, but  . Note that, by Lemma 30,
. Note that, by Lemma 30,  and hence \(m \star 1= m+1\). Then \((m \star 1) \star (m+1) = (m+1) \star (m+1) \in \{ 2\,m+2, (m +1)^2\}\). Also, \(m \star (1 \star (m+1))= m \star (m+1) \in \{2\,m+1, m^2 + m\}\). This yields the following possibilities:
and hence \(m \star 1= m+1\). Then \((m \star 1) \star (m+1) = (m+1) \star (m+1) \in \{ 2\,m+2, (m +1)^2\}\). Also, \(m \star (1 \star (m+1))= m \star (m+1) \in \{2\,m+1, m^2 + m\}\). This yields the following possibilities: -
(a)
\(2m+2=2m+1\), a contradiction.
-
(b)
\(m^2+2m +1= m^2 +m\), a contradiction.
-
(c)
\((m +1)^2=2m+1\), a contradiction.
-
(d)
If \(2m +2= m^2 +m\) then \(m=2\). However, \((2 \star 1) \star 3= 3 \star 3\) and \(2 \star (1 \star 3)= 2 \star 3\). In order to have \(3 \star 3 = 2 \star 3\), 3 must be connected to itself and 2 must not be connected to 3. This would contradict Lemma 29.
-
(a)
-
2.
Let \(m \not \in \{0,1\}\) and assume that
 but
but  . By the first part of this lemma, since
. By the first part of this lemma, since  then
then  and hence, by Lemma 30,
and hence, by Lemma 30,  . Consider the triple product \(((m+1) \star 1) \star (m-1)=(m+2) \star (m-1) \in \{2\,m+1, m^2+m-2\}\). Also, \((m+1) \star (1 *(m-1))= (m+1) \star (m-1) \in \{2\,m, m^2-1\}\). Then there will be the following four possibilities:
. Consider the triple product \(((m+1) \star 1) \star (m-1)=(m+2) \star (m-1) \in \{2\,m+1, m^2+m-2\}\). Also, \((m+1) \star (1 *(m-1))= (m+1) \star (m-1) \in \{2\,m, m^2-1\}\). Then there will be the following four possibilities: -
(a)
\(2m+1 = 2m\), a contradiction.
-
(b)
\(2\,m+1=m^2-1\), then \(m^2-2\,m-2=0\) but then \(m \not \in {\mathbb {N}}\), a contradiction.
-
(c)
\(m^2+m-2= m^2-1\), then \(m=1\) which is a contradiction.
-
(d)
\(m^2+m-2=2m\), which is handled in the exact same way as part (d) in the first part of this lemma.\(\square \)
-
(a)
Lemma 32
Let \(\star \) be associative Plus-Times collaboration on \({\mathbb {N}}\). Then the following are equivalent:
-
1.
\(1 \star 1 =2\) (
 ).
). -
2.
For some \(m>1\), \(1 \star m = 1+m\). (
 ).
). -
3.
For all \(n \not \in \{0,1\}\), \(1 \star n =1+n\). (
 ).
).
Proof
(\(1\implies 3\)) Suppose that \(1 \star 1 =2\) (  ) but \(1 \star n =n\) (
) but \(1 \star n =n\) ( ) for some \(n>1\). Then \((1\star 1 ) \star n= 2 \star n \in \{n+2, 2n \}\). Also, \(1 \star (1 \star n) = n\). Either way, this is a contradiction.
) for some \(n>1\). Then \((1\star 1 ) \star n= 2 \star n \in \{n+2, 2n \}\). Also, \(1 \star (1 \star n) = n\). Either way, this is a contradiction.
(\(3 \implies 2\)) Obvious
(\(2 \implies 1\)) Suppose that \(1 \star m= 1+m\) ( ) but \(1 \star 1 = 1 \cdot 1 =1\) (
) but \(1 \star 1 = 1 \cdot 1 =1\) ( ). By Lemma 31, we have that \(1 \star (m+1)= m+2\) (
). By Lemma 31, we have that \(1 \star (m+1)= m+2\) ( ). Consider the following two contradictory calculations: \((1\star 1 ) \star m= 1 \star m= m+1\), and \(1 \star (1 \star m) = 1 \star (m+1)= m+2\), concluding our proof. \(\square \)
). Consider the following two contradictory calculations: \((1\star 1 ) \star m= 1 \star m= m+1\), and \(1 \star (1 \star m) = 1 \star (m+1)= m+2\), concluding our proof. \(\square \)
Lemma 33
Let \(\star \) be associative Plus-Times collaboration on \({\mathbb {N}}\). If \(1 \star 1=1+1=2\) then \(m \star k= m+k\) for all \(m,k \in \{1,2,3, \dots \}\).
Proof
Suppose \(1 \star 1=2\) but \(m \star k \ne m+k\), for some non-zero m, k.
The case where \(1 \in \{m,k\}\) is settled by Lemmas 32 and 30. Assume that \(1 \not \in \{m,k\} \). By Lemma 32, \(1 \star ( m \star k)= 1 \star mk= 1+mk\). However, also by Lemma 32, \((1 \star m) \star k = (1+m) \star k \in \{1+m+k, k+mk \}\). The first possibility implies \(m \star k = mk=m+k\), which contradicts our assumption. The second possibility implies \(1=k\), which is also a contradiction. \(\square \)
Lemma 34
Let \(\star = {\mathbb {N}}(+, \cdot )\) be an associative Plus-Times collaboration. Then if \(0 \star m=m\) and \(m \star 0=0\) then \(m\in \{0,1\}\)
Proof
By Associativity we have that \((m \star 0) \star m = m \star (0 \star m)\) then \(0 \star m = m \star m\). Hence, \(m=m \star m\). This yields the following possibilities: If  , then \(m=2m \) which implies \(m=0\). If
, then \(m=2m \) which implies \(m=0\). If  then \(m=m^2\), and therefore \(m \in \{0,1\}\). \(\square \)
then \(m=m^2\), and therefore \(m \in \{0,1\}\). \(\square \)
This lemma shows that 1 behaves consistently as a factor for an associative collaboration when the the other factor is bigger than or equal to 2.
Lemma 35
Suppose that \(\star \) is an associative collaboration on \({\mathbb {N}}\). If  and
and  then
then  , where \( m \ne 0\).
, where \( m \ne 0\).
Proof
Suppose that, on the contrary,  , where \(m \ne 0\). By Lemma 26,
, where \(m \ne 0\). By Lemma 26,  for every m bigger than 0. By Lemma 25, \(m \star 0=m\) and \((m+1) \star 0= m+1\). It follows, because \(m \ne 0\), that \((m \star 1) \star 0 = (m+1) \star 0 = m+1\) and \(m \star ( 1 \star 0 )= m \star 0 =m \). This is a contradiction because \(m \ne 0\). \(\square \)
for every m bigger than 0. By Lemma 25, \(m \star 0=m\) and \((m+1) \star 0= m+1\). It follows, because \(m \ne 0\), that \((m \star 1) \star 0 = (m+1) \star 0 = m+1\) and \(m \star ( 1 \star 0 )= m \star 0 =m \). This is a contradiction because \(m \ne 0\). \(\square \)
Theorem 36
The only graphs that are null on \({\mathbb {N}} \setminus \{0,1\}\) and induce associative collaborations on \({\mathbb {N}}\) are the null graph and the following roses:
-
1.

-
2.
-
3.
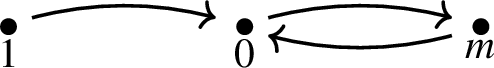
-
4.
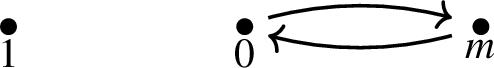
Proof
Suppose that the graph is null on \({\mathbb {N}} \setminus \{0,1\}\) but is not the null graph. The assumption that the graph is null on \({\mathbb {N}} \setminus \{0,1\}\) implies that, for all \(m,n \in {\mathbb {N}} {\setminus } \{0,1\}\), \(m\star n= mn\). On the other hand, Lemmas 32 and 33 allow us to extend that relation to all \(m,n \in {\mathbb {N}} {\setminus } \{0\}\).
The assumption that the graph is not completely null implies that there exist edges connecting 1 or 0 to some element \(n \in {\mathbb {N}}\). We begin by showing that 1 can only be connected to 0 and not to any other n. If \(1 \star n =1+n\) or \(n \star 1=n+1\) for some \(n \ne 0\) then, by Lemmas 32 and 33, the graph is complete on \({\mathbb {N}} {\setminus } \{0\}\), which would be a contradiction.
We show next that, in fact, 0 must connect to every \(m >1\). If, on the contrary, \(0 \star m=0\), where \(m>1\). Then, by Lemmas 25 and 26, \(m \star n=m \cdot n\), where \(m, n \in {\mathbb {N}} \), and the graph is null, contrary to our hypothesis. As \(0 \star m=m\), for all \(m>1\) then, by Lemma 26, \(0 \star k= k \),where \( k > 1\). It follows then, by Lemma 25, that \(k \star 0= k\) and, therefore, the graph will be one of the roses in the statement. \(\square \)
Theorem 37
The only graphs that induce associative collaborations on \({\mathbb {N}}\) and are complete on \(\{2,3, \dots \}\) are the following:
-
1.
The complete graph.
-
2.

-
3.

-
4.

-
5.

In this Graph
 and
and 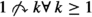 .
. -
6.

In this Graph
 but
but  .
.
Proof
Similar to Theorem 36.
Suppose that the graph on \(\{2,3,4, \dots \}\) is the complete graph. Then consider the following cases:
5 Group collaborations and braces
Contrary to custom, where addition tends to be, by default, a commutative operation, in this section, a group \((G, +)\) will not be assumed to be abelian unless otherwise specified. We will be interested in structures with two operations, \(+\) and \(\circ \), over the same set G and, when writing expressions involving both operations, \(\circ \) will be assumed to take precedence over \(+\).
Braces may be defined in a number of equivalent ways (see [13] and [3], for example). The following definition of a left skew brace is from [4].
Definition 38
A skew left brace is a set G with two binary operations \(+\) and \(\circ \) such that \((G, +)\) and \((G, \circ )\) are groups, and \(\circ \) satisfies the left brace distributive law \(a \circ (b + c) = a \circ b - a + a \circ c\), for all \(a, b, c \in G\). If \((G, +)\) is abelian, then \((G, +, \circ )\) is called a left brace.
Right braces and skew right braces are defined similarly, except in this case \(\circ \) satisfies the right brace distributive law \((a + b) \circ c = a \circ c - c + b \circ c\) for all \(a, b, c \in G\).
Our definition of a collaboration between two binary operations can be naturally extended to a collaboration between a finite number of binary operations. Such an extension, a subject of our next definition, will be instrumental in the remainder of this section.
Definition 39
-
1.
A binary operation \(\circ \) on a set G is said to be a collaboration between the binary operations \(*_1, *_2, \dots , *_n\) on G if, for all \(a, b \in G\), \(a \circ b \in \{a *_1 b, a *_2 b, \dots , a *_n b\}\).
-
2.
Given a collaboration \(\circ \) of \(*_1, *_2, \dots , *_n\) on G, an element \(a \in G\) is said to be left deterministic if there exists an i such that \(a \circ b = a *_i b\) for all \(b \in G\). In other words, the operation chosen to calculate \(a \circ b\) depends only on a.
-
3.
A collaboration \(\circ \) is left deterministic if every \(a \in G\) is left deterministic.
Right deterministic elements and operations are defined similarly.
Note that \(\circ \) is a left deterministic collaboration between the binary operations \(*_1, *_2, \dots , *_n\) if and only if its opposite operation \(\circ ^{op}\) is a right deterministic collaboration between the operations \(*_1^{op}, *_2^{op}, \dots , *_n^{op}\). Also, \(\circ \) is an associative, group, or left brace multiplication if and only if \(\circ ^{op}\) is an associative, group, or right brace multiplication, respectively.
Proposition 40
Let \((G, +)\) be a group, and let \(\circ \) be a Plus-Minus collaboration. Then, the following results hold:
-
1.
If \(\circ \) is associative and left deterministic, then \((G, \circ )\) is a group.
-
2.
If \((G, \circ )\) is a group and \(\circ \) is left deterministic, then either \(\circ = +\) or \((G, +)\) is abelian.
-
3.
If \((G, \circ )\) is a group, and \(\circ \) is right deterministic, then \(\circ = +\).
Proof
-
1.
Since \(a \circ 0 = a \pm 0\), 0 is a right identity. Now if \(0 \circ a = 0 - a = -a\), then \(0 \circ (0 \circ a) = 0 \circ (-a) = 0 - (-a) = a\), but \((0 \circ 0) \circ a = 0 \circ a = -a\), so \(\circ \) is not associative unless \(-a = a\) for all \(a \in G\), in which case \(\circ = +\). Therefore we must have that \(0 \circ a = 0 + a = a\), so 0 is also a left identity. If \(a \circ a = a - a\), then a is its own inverse. Otherwise, \(a \circ (-a) = a + (-a) = 0\), so \(-a\) is a right inverse for a. If \((-a) \circ a = -a - a\), then \(a \circ ((-a) \circ a) = a \circ (-2a) = -a\), but \((a \circ (-a)) \circ a = 0 \circ a = a\), so \(-a = a\). Therefore \((-a) \circ a = (-a) + a = 0\), so \(-a\) is the inverse of a and \((G, \circ )\) is a group.
-
2.
Suppose \(\circ \ne +\), and \(c \circ x = c - x\) for all \(x \in G\). Note that \(a \circ 0 = a \pm 0 = a\) for all \(a \in G\), so 0 is a right identity. Therefore 0 must be the identity for the group \((G, \circ )\). Then \(x = 0 \circ x = (c - c) \circ x = (c\circ c) \circ x = c \circ (c \circ x) = c - (c - x) = c + x - c\), so \(x + c = c + x\). Let a and b be two elements of G such that left multiplication by each of a and b is addition. If \(a = -a\), then left multiplication by \(-a\) is addition. Otherwise \(a \ne -a\), \(a^{-1} = -a\), and \((-a) \circ a = 0 = -a + a \ne -a - a\), and again left multiplication by \(-a\) is also addition since \(\circ \) is left deterministic. Then \(a + b + c = a \circ (b + c) = a \circ (c + b) = a \circ (c -(-b)) = a \circ c \circ (-b) = (a + c) \circ (-b) = (c + a) \circ (-b) = (c - (-a)) \circ (-b) = c \circ (-a) \circ (-b) = c \circ (-a - b) = c - (-a - b) = c + b + a = b + a + c\), so \(a + b = b + a\). Therefore \((G, +)\) is abelian.
-
3.
If \((G, \circ )\) is a group, then 0 must be the identity since it is a right identity. Therefore \(0 \circ b = b = 0 + b\) for all \(b \in G\). Thus if \(\circ \) is right deterministic, then we must have that \(a \circ b = a + b\) for all \(a, b \in G\), and \(\circ = +\).\(\square \)
When the group \((G,+)\) is not commutative, there are two possible candidates for the moniker Plus-Minus collaboration. One can consider collaborations between \(a+b\) and \(a-b\) or collaborations between \(a+b\) and \(-b + a\). The above proposition also holds if we use \(-b + a\) instead of \(a - b\) when we subtract. However, in this paper we use the term Plus-Minus collaboration exclusively for collaborations between \(a+b\) and \(a-b\). Part 2 of the above proposition shows that every non-trivial group Plus-Minus collaboration with a non-abelian addition must be non-deterministic. Infinitely many such examples are known, and are discussed in [6]. The next theorem proves non-deterministic group Plus-Minus collaborations do not exist when \((G, +)\) is abelian.
Theorem 41
Let \((G, +)\) be an abelian group, and let \(\circ \) be a Plus-Minus collaboration. Then \((G, \circ )\) is a group if and only if \(\circ \) is associative and left deterministic. When \((G, \circ )\) is a group, \((G, +, \circ )\) is a left brace.
Proof
Proposition 40 proves the \(\Longleftarrow \) direction. In this case, \((G, +, \circ )\) is a left brace since we either have \(a \circ (b + c) = a + b + c = a + b - a + a + c = a \circ b - a + a \circ c\) or \(a \circ (b + c) = a - (b + c) = a - b - c = a - b - a + a - c = a \circ b - a + a \circ c\). Therefore it is sufficient to show that \(\circ \) is left deterministic when \((G, \circ )\) is a group.
Case i: a has additive order greater than 2 and \(a \circ a = a - a\). Then \(a^{-1} = a\) and \(x = a^{-1} \circ a \circ x = a\circ a \circ x\) for all \(x \in G\). If there exists an x such that \(a \circ x = a + x\), then \(x = a \circ (a \circ x) = a \circ (a + x) \in \{-x, 2a + x\}\). If \(x = 2a + x\), then a has additive order 2, and we have a contradiction. Therefore \(x = -x\), so \(a\circ x = a + x = a - x\) and a is left deterministic.
Case ii: a has additive order greater than 2 and \(a \circ a = a + a\). Then \(a^{-1} = -a\). If there exists an x such that \(a \circ x = a - x\), then \(x = (-a) \circ (a \circ x) = (-a) \circ (a - x) \in \{-x, -2a + x\}\). Again we either have the contradiction that a has order 2, or \(x = -x\), in which case a is left deterministic.
Case iii: a has additive order 2. Then \(a = -a = a^{-1}\). If a is not left deterministic, then there exist x and y of additive order greater than 2 such that \(a \circ x = a + x\) and \(a\circ y = a - y\). Suppose that \(x \circ x = x - x\). Then x is left deterministic by Case 1, and \(a\circ x = a + x = x - a = x \circ a\). Therefore \((a \circ x) \circ y = (x \circ a) \circ y = x \circ (a \circ y) = x \circ (a - y) = x - (a - y) = a + x + y\). On the other hand, \(a \circ (x \circ y) = a \circ (x - y) \in \{a + x - y, a - x + y\}\). This implies that either \(x = -x\) or \(y = -y\), and we have a contradiction.
Suppose instead that \(x \circ x = x + x\). Then x is left deterministic by Case 2, \(x^{-1} = -x\), and \(x \circ x^{-1} = x^{-1} \circ x = -x + x\). Thus left multiplication by \(-x\) is also addition, and \(-x = a \circ (a \circ (-x))\). If \(a \circ (-x) = a - (-x) = a + x = a \circ x\), then \(-x = x\) and we have a contradiction. Therefore \(a\circ (-x) = a + (-x) = a - x\). Now \(a\circ (-x) = a - x = -x + a = (-x) \circ a\), so \((a \circ (-x)) \circ y = ((-x) \circ a) \circ y = (-x) \circ (a \circ y) = (-x) \circ (a - y) = (-x) + (a - y) = a - x - y\). On the other hand, \(a \circ ((-x) \circ y) = a \circ (-x + y) \in \{a - x + y, a + x - y\}\). This again implies that either \(x = -x\) or \(y = -y\), and we have a contradiction. Therefore a must be left deterministic. \(\square \)
Theorem 42
Let \((G, +)\) be an abelian group, and let \(\circ \) be a Plus-Minus collaboration such that \(\circ \ne +\). Then \((G, \circ )\) is a group if and only if there exists a normal subgroup N of both \((G, +)\) and \((G, \circ )\) such that \(\frac{G}{N} \cong {\mathbb {Z}}_2\), \(a \circ b = a + b\) if \(a \in N\), and \(a \circ b = a - b\) if \(a \notin N\).
Proof
(\(\Longrightarrow \)) If \((G, \circ )\) is a group, then \(\circ \) is left deterministic by the previous theorem. Let \(N = \{a \in G \, \mid \, a \circ x = a + x \, \, \forall x \in G\} = \{a \in G | a^{-1} = -a\}\). It is clear that N is closed under inversion. Let \(b, c \in N\). Then \((b \circ c)^{-1} = c^{-1} \circ b^{-1} = (-c) \circ (-b) = -c - b = -(b + c) = -(b \circ c)\). Thus N is closed under \(\circ \). The beginning of the proof of Proposition 40 also shows that 0 is the identity and \(0 \in N\), so N is a subgroup of \((G, \circ )\).
To show that N is normal, we only need to consider the conjugate of an element \(x \in N\) by an element \(y \notin N\). In this case, \(y^{-1} = y\) and \(y \circ x \circ y^{-1} = y \circ x \circ y = y \circ (x + y) = y - (x + y) = -x = x^{-1} \in N\). Therefore N is normal in \((G, \circ )\), and since \(\circ = +\) on N, N is also a normal subgroup of \((G, +)\).
By our definition of N, we have that for all \(a, b \in G\), \(a \circ b = a + b\) if \(a \in N\) and \(a \circ b = a - b\) if \(a \notin N\). It remains to be shown that N and \(G \setminus N\) are the only cosets of \(\frac{G}{N}\). Let \(a \in A\) and \(b \in B\), where A and B are two cosets different from N. Then for any \(c \in G\), \(a \circ (b \circ c) = a \circ (b - c) = a - (b - c) = a - b + c\), and this is equal to \((a \circ b) \circ c = (a - b) \circ c\). Since left multiplication by \(a - b\) is addition, \(a - b = a \circ b \in N\). Therefore \(B = A^{-1} = A\), so \(\frac{G}{N} \cong {\mathbb {Z}}_2\).
(\(\Longleftarrow \)) Suppose there exists a normal subgroup N of \((G, +)\) such that \(\frac{G}{N} \cong {\mathbb {Z}}_2\), \(a \circ b = a + b\) if \(a \in N\), and \(a \circ b = a - b\) if \(a \notin N\). For any \(a \in G\), call a even if \(a \in N\) and call a odd if \(a \in G {\setminus } N\). Then the proof that \(\circ \) is associative is identical to the proof given in Example 2.1. Also since \(0 \in N\), 0 is an identity for \((G, \circ )\). The inverse of a is \(-a\) if \(a \in N\) and it is a if \(a \notin N\). Therefore \((G, \circ )\) is a group, and we have already shown that N is also normal in \((G, \circ )\) in that case. \(\square \)
The group \((G, \circ )\) in the above theorem is isomorphic to the semidirect product of N and \({\mathbb {Z}}_2\), where the non-identity element of \({\mathbb {Z}}_2\) acts on N by inverting its elements. In particular, if N is cyclic then \((G, \circ )\) is dihedral.
Corollary 43
The group \((G, \circ )\) in Theorems 41 and 42 is abelian if and only if \(\circ = +\) or every element of N has order \(\le 2\).
Proof
(\(\Longrightarrow \)) Suppose \((G, \circ )\) is abelian and \(\circ \ne +\). Let \(x \in N\) and let \(y \in G {\setminus } N\). Then \(y \circ y = y - y = 0\), so we only need to show that \(x \circ x = 0\). Since \(x + y = x \circ y = y \circ x = y - x = -x + y\), we have that \(x + x = x \circ x = 0\).
(\(\Longleftarrow \)) If \(\circ = +\), then clearly \((G, \circ )\) is abelian. If every element of N has order \(\le 2\), then every element of \((G, \circ )\) has order \(\le 2\), since every element of \(G \setminus N\) has order 2. Therefore \((G, \circ )\) is abelian. \(\square \)
Example 2 is an example of a group collaboration of the form given in Theorem 42, and Lemma 4 is a special case of Corollary 43.
Note that when \((G, \circ )\) is a group, \((G, +, \circ )\) is a left brace. There may be more than one choice for N, and the braces \(B_1\) and \(B_2\) corresponding to the normal subgroups \(N_1\) and \(N_2\) will be isomorphic if and only if there exists an automorphism \(\varphi \) of \((G, +)\) such that \(\varphi (N_1) = N_2\). To prove this, we will need the following definitions from [3].
Definition 44
A map \(\varphi : B_1 \rightarrow B_2\) is a homomorphism between the left braces \(B_1\) and \(B_2\) if \(\varphi (a + b) = \varphi (a) + \varphi (b)\) and \(\varphi (a \circ b) = \varphi (a) \circ \varphi (b)\) for all \(a, b \in B_1\). A homomorphism between two braces is called an isomorphism if it is bijective. The socle of a left brace B is \(Soc(B) = \{a \in B \,|\, a \circ b = a + b \text { for all } b \in B\}\).
Proposition 45
Let \((G, +)\) be an abelian group, and let \(N_1\) and \(N_2\) be two subgroups of index 2. Let \(B_1\) and \(B_2\) be the corresponding left braces whose form is given by Theorem 42. Then \(B_1\) and \(B_2\) are isomorphic if and only if there exists an automorphism \(\varphi \) of \((G, +)\) such that \(\varphi (N_1) = N_2\).
Proof
(\(\Longrightarrow \)) Suppose \(\varphi \) is an isomorphism from \(B_1\) to \(B_2\). Then \(\varphi \) is an automorphism of \((G, +)\). By the definition of \(N_1\) and \(N_2\), \(N_1 = Soc(B_1)\) and \(N_2 = Soc(B_2)\). Therefore \(\varphi (N_1) \subseteq N_2\), since for any \(a \in N_1\) and any \(b \in B_1\), we have that \(\varphi (a) \circ \varphi (b) = \varphi (a \circ b) = \varphi (a + b) = \varphi (a) + \varphi (b)\). Similarly, \(\varphi ^{-1}(N_2) \subseteq N_1\), so \(\varphi (N_1) = N_2\).
(\(\Longleftarrow \)) If \(\varphi \) is an automorphism of \((G, +)\) such that \(\varphi (N_1) = N_2\), then we only need to show that for all \(a, b \in B_1\), \(\varphi (a \circ b) = \varphi (a) \circ \varphi (b)\). If \(a \in N_1\), then \(\varphi (a) \in N_2\), so \(\varphi (a \circ b) = \varphi (a + b) = \varphi (a) + \varphi (b) = \varphi (a) \circ \varphi (b)\). If \(a \notin N_1\), then \(\varphi (a) \notin N_2\), so \(\varphi (a \circ b) = \varphi (a - b) = \varphi (a) - \varphi (b) = \varphi (a) \circ \varphi (b)\). Therefore \(\varphi \) is a brace isomorphism. \(\square \)
Example 46
Let \((G, +) = {\mathbb {Z}}_4 \times {\mathbb {Z}}_4\), let \(N_1 = 2{\mathbb {Z}}_4 \times {\mathbb {Z}}_4\), and let \(N_2 = {\mathbb {Z}}_4 \times 2{\mathbb {Z}}_4\). Then \(N_1 \cong N_2\), and the map \(\varphi \) that sends each (x, y) to (y, x) is an isomorphism between the braces \(B_1\) and \(B_2\).
Example 47
Let \((G, +) = {\mathbb {Z}}_2 \times {\mathbb {Z}}_4\), let \(N_1 = 2{\mathbb {Z}}_2 \times {\mathbb {Z}}_4\), and let \(N_2 = \{(0, 0), (1, 1), (0, 2), (1, 3)\}\). Then \(N_1 \cong N_2\), and the map \(\varphi \) that sends the generators (0, 1) and (1, 0) to (1, 1) and (1, 0), respectively, is an isomorphism between the braces \(B_1\) and \(B_2\).
In the remainder of this section, we define endomorphism and automorphism collaborations and discuss their connections with braces.
Definition 48
Let \((G, +)\) be a group, and for every map \(\lambda \in End(G, +)\), define a binary operation \(*_\lambda \) on G such that \(a *_\lambda b = a + \lambda (b)\) for all \(a, b \in G\). Let \(\circ \) be a binary operation on G such that \(a \circ b \in \{a *_\lambda b \,|\, \lambda \in End(G, +)\}\) for all \(a, b \in G\). Then we say that \(\circ \) is an endomorphism collaboration on G. If instead we require that each \(\lambda \in Aut(G, +)\), then we say that \(\circ \) is an automorphism collaboration on G. If \(\circ \) is left deterministic, then the map \(\lambda \) chosen to compute \(a \circ b\) depends only on a for all \(a, b \in G\), so we may write \(a \circ b = a + \lambda _a(b)\).
Example 49
Let \(\circ \) be a left deterministic endomorphism collaboration such that \(\lambda _a(b) = 0\) for all \(a, b \in G\). Then \(a \circ b = a\) for all \(a, b \in G\). This makes \((G, \circ )\) a semigroup.
Lemma 50
Let \((G, +)\) be a group, and let \(\circ \) be a left deterministic endomorphism collaboration on G. Then
-
1.
\(a\circ (b + c) = a \circ b - a + a \circ c\) for all \(a, b, c \in G\).
-
2.
\(\circ \) is associative if and only if \(\lambda _{a \circ b} = \lambda _a \circ \lambda _b\) for all \(a, b \in G\).
-
3.
\((G, \circ )\) is a group if and only if \(\circ \) is an associative automorphism collaboration.
Proof
-
1.
For all \(a, b, c \in G\), we have that \(a\circ (b + c) = a + \lambda _a(b + c) = a + \lambda _a(b) + \lambda _a(c) = a + \lambda _a(b) - a + a + \lambda _a(c) = a \circ b - a + a \circ c\).
-
2.
For all \(a, b, c \in G\), we have that \(a \circ (b \circ c) = a \circ (b + \lambda _b(c)) = a + \lambda _a(b + \lambda _b(c)) = a + \lambda _a(b) + \lambda _a(\lambda _b(c))\), and \((a \circ b) \circ c = (a + \lambda _a(b)) \circ c = a + \lambda _a(b) + \lambda _{a + \lambda _a(b)}(c) = a + \lambda _a(b) + \lambda _{a \circ b}(c)\). Therefore \(a \circ (b \circ c) = (a \circ b) \circ c\) if and only if \(a + \lambda _a(b) + \lambda _a(\lambda _b(c)) = a + \lambda _a(b) + \lambda _{a \circ b}(c)\), and this holds if and only if \(\lambda _{a \circ b}(c) = \lambda _a(\lambda _b(c))\).
-
3.
(\(\Longrightarrow \)) Suppose \((G, \circ )\) is a group. Since \(\circ \) is associative, we have that \(\lambda _{a \circ b} = \lambda _a \circ \lambda _b\) for all \(a, b \in G\) by part (2). Also 0 is the identity of \((G, \circ )\) since it is a right identity. Then for any \(a \in G\), \(a = 0 \circ a = \lambda _0(a)\), so \(\lambda _0\) is the identity map. We also have that \(\lambda _0 = \lambda _{a \circ a^{-1}} = \lambda _a \circ \lambda _{a^{-1}}\), so \(\lambda _a\) and \(\lambda _{a^{-1}}\) are inverses of each other. Therefore each \(\lambda _a\) is an automorphism.
(\(\Longleftarrow \)) Suppose \(\circ \) is associative and each \(\lambda _a\) is an automorphism. Then \(a \circ 0 = a + \lambda _a(0) = a + 0 = a\) for all \(a \in G\) since every endomorphism maps 0 to 0. Therefore 0 is a right identity. By statement (2), \(\lambda _a = \lambda _{a \circ 0} = \lambda _a \circ \lambda _0\) for any \(a \in G\). Since \(\lambda _a\) is an automorphism, it has an inverse map, and thus the above equation implies that \(\lambda _0\) is the identity map. Then for all \(a \in G\), \(0 \circ a = 0 + \lambda _0(a) = 0 + a = a\), so 0 is also a left identity. Now we claim that \(b = \lambda _a^{-1}(-a)\) is the inverse of a. We have that \(a \circ b = a + \lambda _a(b) = a + \lambda _a(\lambda _a^{-1}(-a)) = a - a = 0\), and \(b \circ a = b + \lambda _b(a) = \lambda _a^{-1}(-a) + \lambda _{\lambda _a^{-1}(-a)}(a) = x\) for some element \(x \in G\). Applying \(\lambda _a\) to both sides of the last equation gives us \(\lambda _a(x) = \lambda _a(\lambda _a^{-1}(-a) + \lambda _{\lambda _a^{-1}(-a)}(a)) = \lambda _a(\lambda _a^{-1}(-a)) + \lambda _a(\lambda _{\lambda _a^{-1}(-a)}(a)) = -a + \lambda _{a \circ \lambda _a^{-1}(-a)}(a) = -a + \lambda _{a \circ b}(a) = -a + \lambda _0(a) = -a + a = 0\). But \(\lambda _a(x) = 0\) implies that \(x = 0\), so b is the inverse of a, as claimed. Therefore \((G, \circ )\) is a group.\(\square \)
We conclude this section with a theorem that characterizes skew left braces in terms of automorphism collaborations.
Theorem 51
Let \((G, +)\) be a group, and let \(\circ \) be another binary operation on G. Then the following are equivalent:
-
1.
\((G, +, \circ )\) is a skew left brace.
-
2.
\(\circ \) is an associative, left deterministic automorphism collaboration.
-
3.
\(\circ \) is a left deterministic automorphism collaboration such that \((G, \circ )\) is a group.
-
4.
\(\circ \) is a left deterministic automorphism collaboration such that \(\lambda _{a \circ b} = \lambda _a \circ \lambda _b\) for all \(a, b \in G\).
When any of these hold, the map \(\lambda : (G, \circ ) \rightarrow \textrm{Aut}(G, +)\) such that \(\lambda (a) = \lambda _a\) is a group homomorphism.
Proof
By Lemma 50, \((2 \iff 3 \iff 4)\) and (\(3 \implies 1\)). For (\(1 \implies 3\)), it is known that skew left brace multiplications are of the required form (see Remark 1.8 and Proposition 1.9 of [4]). The last statement of the theorem follows immediately from statements (3) and (4). \(\square \)
References
Aydoğdu, P., Díaz-Boils, J.D., López-Permouth, S.R., Muhammad, R.A.: Two value graph magma algebras and amenability, pp. 383–400 (2022). https://doi.org/10.1007/978-981-19-3898-6_30
Aydoğdu, P., López-Permouth, S.R., Muhammad, R.A.: Infinite-dimensional algebras without simple bases. Linear Multilinear Algebra 68(12), 2390–2407 (2020). https://doi.org/10.1080/03081087.2019.1585414
Cedó, F., Jespers, E., Okniński, J.: Braces and the Yang-Baxter equation. Commun. Math. Phys. 327(1), 101–116 (2014). https://doi.org/10.1007/s00220-014-1935-y
Guarnieri, L., Vendramin, L.: Skew braces and the Yang-Baxter equation. Math. Comp. 86(307), 2519–2534 (2017). https://doi.org/10.1090/mcom/3161
Kelarev, A.V., Sokratova, O.V.: Syntactic semigroups and graph algebras. Bull. Austral. Math. Soc. 62(3), 471–477 (2000). https://doi.org/10.1017/S0004972700018992
López-Permouth, S.R., Nicely, A.: Group collaborations and braces (in preparation)
López-Permouth, S.R., Owusu-Mensah, I., Rafieipour, A.: A monoid structure on the set of all binary operations over a fixed set. Semigroup Forum 104(3), 667–688 (2022). https://doi.org/10.1007/s00233-022-10280-8
López-Permouth, S.R., Owusu-Mensah, I., Rafieipour, A.: Binary operations and graphs (in preparation)
López-Permouth, S.R., Stanley, B.: Graph magma algebras have no projective bases. Linear Multilinear Algebra 69(11), 1997–2005 (2021). https://doi.org/10.1080/03081087.2019.1652552
López-Permouth, S.R., Stanley, B.: On the amenability profile of infinite dimensional algebras. Commun. Algebra 49(5), 2253–2264 (2021). https://doi.org/10.1080/00927872.2020.1869245
Poomsa-Ard, T.: Hyperidentities in associative graph algebras. Discuss. Math. Gen. Algebra Appl. 20(2), 169–182 (2000). https://doi.org/10.7151/dmgaa.1014
Pöschel, R., Wessel, W.: Classes of graphs definable by graph algebra identities or quasi-identities. Comment. Math. Univ. Carolin. 28(3), 581–592 (1987). http://eudml.org/doc/17572
Rump, W.: Braces, radical rings, and the quantum Yang-Baxter equation. J. Algebra 307(1), 153–170 (2007). https://doi.org/10.1016/j.jalgebra.2006.03.040
Shallon, C.R.: Non-finitely based binary algebras derived from lattices. Ph.D. Thesis–University of California, Los Angeles (1979)
Acknowledgements
The authors wish to thank the anonymous referee for a meticulous reading of our manuscript. The paper is much better because of their very valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Marcel Jackson.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
López-Permouth, S.R., Nicely, A. & Zailaee, M. Semigroup collaborations between elementary operations. Semigroup Forum 108, 195–220 (2024). https://doi.org/10.1007/s00233-024-10408-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00233-024-10408-y




 ,
,  for all
for all  , and, for all
, and, for all  . Then the collaboration
. Then the collaboration 
 ,
,  and
and  for all
for all  . Then the collaboration
. Then the collaboration 
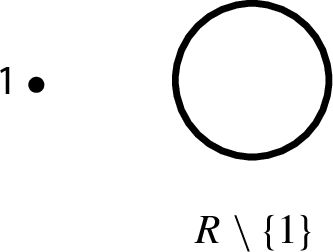
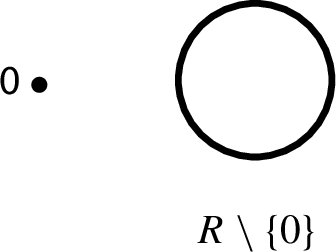
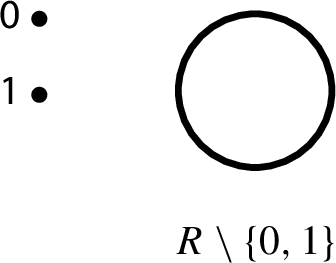
 and
and  , and, for all nonzero
, and, for all nonzero  . Then
. Then 
 but
but  , for
, for  and
and  , and, for all nonzero
, and, for all nonzero  . Then
. Then 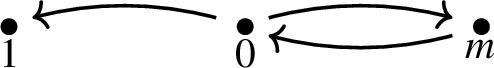
 but
but  , for
, for  and
and  , and, for all nonzero
, and, for all nonzero  . Then
. Then 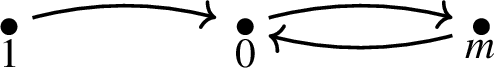
 and
and  ,for
,for  and
and  , and, for all nonzero
, and, for all nonzero  . Then
. Then 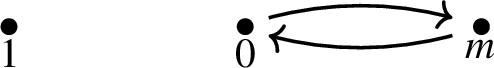
 ,
, and
and  for all
for all  . Then
. Then 
 ,
, and
and  for all
for all  . Then
. Then 
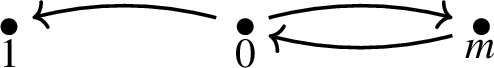
 .
.
 , then, by Lemma
, then, by Lemma  . For the sake of contradiction, suppose
. For the sake of contradiction, suppose  and consider the triple product
and consider the triple product  but
but  . Consider the triple product
. Consider the triple product  , and
, and
 , but
, but  . Note that, by Lemma
. Note that, by Lemma  and hence
and hence  but
but  . By the first part of this lemma, since
. By the first part of this lemma, since  then
then  and hence, by Lemma
and hence, by Lemma  . Consider the triple product
. Consider the triple product  ).
). ).
). ).
).
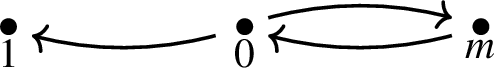
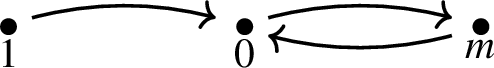




 and
and  .
.
 but
but  .
. and
and  . Then the graph is 3,5 or 6.
. Then the graph is 3,5 or 6.