A particle finite element method approach to model shear cutting of high-strength steel sheets

Abstract

Shear cutting introduces residual strains, notches and cracks, which negatively affects edge-formability. This is especially relevant for forming of high-strength sheets, where edge-cracking is a serious industrial problem. Numerical modelling of the shear cutting process can aid the understanding of the sheared edge damage and help preventing edge-cracking. However, modelling of the shear cutting process requires robust and accurate numerical tools that handle plasticity, large deformation and ductile failure. The use of conventional finite element methods (FEM) may give rise to distorted elements or loss of accuracy during re-meshing schemes, while mesh-free methods have tendencies of tensile instability or excessive computational cost. In this article, the authors propose the particle finite element method (PFEM) for modelling the shear cutting process of high-strength steel sheets, acquiring high accuracy results and overcoming the stated challenges associated with FEM. The article describe the implementation of a mixed axisymmetric formulation, with the novelty of adding a ductile damage- and failure model to account for material fracture in the shear-cutting process. The PFEM shear-cutting model was validated against experiments using varying process parameters to ensure the predictive capacity of the model. Likewise, a thorough sensitivity analysis of the numerical implementation was conducted. The results show that the PFEM model is able to predict the process forces and cut edge shapes over a wide range of cutting clearances, while efficiently handling the numerical challenges involved with large material deformation. It is thus concluded that the PFEM implementation is an accurate predictive tool for sheared edge damage assessment.

1 Introduction

The shear-cutting process is a widely used manufacturing process in sheet metal forming. In high-strength materials, as those used for lightweight construction of vehicles, the process involves high cutting loads, which may induce mechanical damage in the sheared edges. Such damage may result in microscopic defects or evolve to micro-cracks during the part in-service life. Therefore, detailed insight into the shear-cutting process through numerical modelling is highly relevant to the sheet metal industry. A common manufacturing defect in high-strength metallic sheets is edge-cracking. Edge-cracking occurs when a sheet metal edge, produced by shear cutting, is being stretched in a cold-forming operation and sudden fracture of the edge occurs. Conventional sheet metal-forming analyses, such as forming limit diagrams, cannot foresee edge-cracking and the lack of predictive tools lead to costly re-designing and production stops. Investigations by, e.g. Konieczny and Henderson [1], Shih et al. [2], Dykeman et al. [3], Thomas [4] and Frómeta et al. [5] to mention few, declare that the damage imposed to the cut edges of advanced high-strength steels (AHSS) by the shear-cutting operation causes the edge-cracking phenomenon. These studies show significant decrease of stretch-flangeability of sheared edges compared to undamaged edges produced by laser or water jet cutting. Likewise, the work by Lara et al. [6], Paetzold et al. [7], Stahl et al. [8], Shiozaki et al. [9] and Parareda et al. [10] states that the fatigue properties of AHSS grades are reduced on edges produced by shear cutting compared to undamaged edges. The cut edge damage is defined by extensive plastic deformation in the shear-affected zone (SAZ), micro-cracks as reported by Yoon et al. [11] and by micro-notches associated with surface irregularities. Numerical assessment of the shear-cutting process can predict and prevent such defects and enhance the use of AHSS grades. However, shear cutting consists of a few process steps that are challenging to reproduce accurately with numerical modelling. These process steps involve combination of large plastic deformation, material rotation, contact as well as local crack initiation and propagation, which is manifested in the following stages of the shear-cutting process.

• 1. Roll-over, Fig. 1a: Initial bending of the blank, with substantial plastic deformation imposed.

• 2. Shearing, Fig. 1b: Shearing of the blank material. Extre-me plastic deformation and material flow close to the punch edge.

• 3. Fracture, Fig. 1c: After a certain amount of shearing, cracks will initiate at the tool edges which rapidly propagates until separation of the blank.

Fig. 1

Schematic representation of the main stages of the shear-cutting process, starting with (a) Roll-over, followed by (b) Shearing and ends with the (c) Fracture process. d shows the final cut edge morphology and its characteristic zones

The extreme deformations during the roll-over and shearing stages make it difficult to use conventional Lagrangian finite element (FEM) modelling, as severe element distortion is likely to impair the numerical accuracy. Additionally, the crack initiation and propagation require failure modelling and fine mesh discretisation in order to capture such local failure phenomenon. The numerical modelling of crack initiation and propagation using FEM combined with strain-driven failure modelling was discussed by Sandin et al. [12], where it was shown that the presence of cracks impairs the numerical accuracy if crack nucleation and propagation are not appropriately considered.

Various approaches to numerically model the shear cutting have been proposed over the last decades, and the following paragraph provides a brief overview. With early work by Popat et al. [13], the intention of the numerical modelling was to gain knowledge of how the cutting forces were affected by process- and material parameters. This model was limited to elasto-plastic deformation; thus, the sheet fracture process was not modelled. With growing attention to detailed cut edge results, ductile damage modelling was required, such in the work by Hambli and Potiron [14] and Klingenberg and Singh [15]. These articles describe elaborate 2D models of the shear-cutting process using Lagrangian FEM where the ductile damage model defines element erosion or loss of element stiffness where material failure occurs. More recent work by Wang et al. [16] describes a 3D model of the shear-cutting process with a consecutive hole expansion operation in order to assess the damage effect from shear cutting on stretch-flangeability. Although the Lagrangian FEM models described generate results with great significance to the sheet-forming industry, the issue of distorted elements during shearing may limit the predictability of the model due to numerical instability. To address instability related to mesh distortion, re-meshing techniques have been applied as in the work of Thipprakmas et al. [17] and Basak et al. [18]. Similarly, the Arbitrary-Lagrangian–Eulerian (ALE) approach provides an efficient method for modelling of large material deformations as the material may move independently to the blank mesh, thus allowing for large material deformation without causing skewed and distorted elements. This technique has been adopted for modelling of shear cutting by Brokken et al. [19], Gutknecht et al. [20] and Sahli et al. [21]. Additionally, Canales et al. [22] and Pätzold et al. [23] applied both ALE and re-meshing when modelling shear cutting. Even though re-meshing and ALE are excellent strategies for numerical stability in large deformations, both techniques come with drawbacks. Such drawbacks include smoothing of results in the results mapping stages of re-meshing according to Gutknecht et al. [20], while ALE is limited in defining unpredictable deformation of domains which includes fluid splashing, wave breaking or solid material separation as stated by Cremonesi et al. [24]. Regarding re-meshing, they reported unavoidable results diffusion as the field variables are mapped from the old mesh to the new. Results diffusion may reduce the modelling accuracy in localised zones, thus loosing modelling information in important areas. In a shear-cutting context, this might smooth the results along the cut edge and give insufficient information for subsequent forming processes or fatigue life prediction with edge-cracks or in-service failure as consequence.

However, by using particle methods or mesh-free methods for shear-cutting simulation, mesh distortion and related numerical issues may be avoided. Such methods are generally developed for large deformation and failure and circumvents mesh distortion through alternative discretisation procedures. To these groups belong numerical methods such as discrete element method (DEM), smooth particle hydrodynamics (SPH), element-free Galerkin (EFG) and smoothed particle Galerkin (SPG). In DEM, the domain consists of particles which interacts through bonds defined by springs and dampers as stated by Fleissner et al. [25]. The bonded connection allows for robust failure modelling without risk of element distortion as bond breakage simply removes the cohesive forces between the particles. The use of DEM for modelling of metal cutting was presented by Eberhard and Gaugele [26] and He et al. [27] and shows stability in handling material separation, but appears sensitive to particle size and requires extensive bonding parameter calibrations. Similarly, smooth particle hydrodynamics (SPH) is a particle method with the ability to handle material separation without mesh distortions, as SPH uses kernel functions for neighbour particle search and connectivity. SPH has successfully been used for modelling of high-speed metal cutting by Limido et al. [28], Madaj and Píška [29] and Villumsen and Fauerholdt [30], where the results show that SPH is suitable for modelling the material flow around the tool edge in orthogonal cutting. However, as shown by Libersky et al. [31], SPH is prone to tensile instability which limits its use in modelling of ductile metals, such as AHSS, that primarily fails from tensile void growth. To overcome some of the instability issues, EFG was developed by Belytschko et al. [32] and numerous of improvements of the method enables use of EFG in dynamic fracture, crack tip analysis as well as large deformation [33]. The main drawback of EFG consists of the computational inefficiency due to the requirement of background cells for weak form integration as discussed by Garg and Pant [34]. A promising and new particle method, the SPG method developed by Wu et al. [35], provides a robust approach for failure modelling during metal grinding [36] as well as ballistic simulations [37]. Current implementations of SPG are not intended for crack propagation problems, therefore not suitable for modelling of the fracture process during shear cutting which is governed by crack initiation and propagation. However, future development of the method might be of interest for modelling of shear-cutting processes. The benefit in using any of the presented mesh-less methods is in the large deformation analysis that concurrently causes numerical issues in conventional FEM. The drawbacks of the mesh-less methods are issues related to stability and computational inefficiency compared to FEM. A numerical method that benefits from both particle methods and FEM is the particle finite element method (PFEM) developed by Idelsohn et al. [38]. PFEM was developed with the intention to solve fluid dynamic problems in a Lagrangian manner, but using the interpolation functions of FEM for the particle interactions. In this way, Idelsohn et al. [38] avoided troublesome numerical stabilisation related to convective terms of the Lagrangian Navier–Stokes equation. The Lagrangian manner of PFEM makes it suitable for mechanical problems, since it accurately handles large deformations at reasonable computational cost. Rodriguez et al. [39,40,41,42] and Ye et al. [43] applied thermo-mechanical PFEM formulation for modelling of orthogonal cutting with material strain rate sensitivity, showing satisfactory results in terms of accuracy and computational efficiency for such challenging numerical problem. Similarly, Oñate et al. [44] applied PFEM for a two-dimensional shear-cutting problem using a thermo-elastoplastic constitutive law. Modelling of both orthogonal cutting and shear cutting needs to numerically handle severe material deformation along the tool edges. However, the final results of shear-cutting process are to a large extent controlled by the fracture following the shearing, as shown in Fig. 1c, whereas the chip formation of the orthogonal cutting process consists of continuous material flow around the tool edge. Therefore, modelling of shear cutting of AHSS requires the addition of material failure modelling in order to adequately reproduce the fracture process. This modelling feature was, however, not applied in any of the PFEM metal cutting implementations mentioned.

In the present work, a PFEM formulation is used to simulate sheet punching, overcoming the challenges with FEM and shear cut modelling. For computational efficiency, an axisymmetric element formulation is utilised since the material exhibited a near isotropic behaviour. Additionally, the reduced computational effort using axisymmetric modelling compared to a three-dimensional approach makes the suggested PFEM shear-cutting model suitable for industrial applications where part- or process design loops require fast simulations. The PFEM implementation is applied to sheet punching operations with varying cutting clearances to investigate the predictive ability of the numerical model. The significant novelty of the modelling work presented is adding ductile damage modelling to the PFEM scheme. This implementation extends PFEM to also incorporate fracture initiation and propagation that define the final morphology and residual state of the sheared edge. Such edge characteristics are highly relevant to understand edge-cracking resistance and fatigue behaviour during in-service life. Consequently, this work aims to improve shear-cutting modelling of AHSS sheets and provide an accurate description of the sheared edge characteristics.

2 Numerical modelling

This section presents the theoretical framework, material modelling and numerical implementation of the PFEM shear-cutting model.

2.1 The particle finite element method

The particle finite element method (PFEM) is a Lagrangian FE-discretisation for particle connectivity used. The governing equations depend on the problem at hand, but the fundamental steps remain the same, as stated by Oñate et al. [45]:

• Define a domain with particles.

• Connect the particles using a Lagrangian finite element framework and solve the governing equations.

• Store the results and historical data at the particles.

• To avoid element distortion at large deformation, perform re-connectivity between the particles using Delaunay Tessellation continuously during the simulation.

• The $\alpha$-shape method regenerates internal and external boundaries.

These steps are schematically shown in Fig. 2 in a shear-cutting context for visualisation of the PFEM procedure. Figure 2 shows initially that the blank is defined by a particle cloud at time $t_0$. This cloud defines an initial volume, and connectivity of the particles forms an initial mesh. At time $t_n$, as the shear cutting has progressed, the same steps are done but the particle connectivity is rearranged in order to prevent distorted elements. For even larger local blank deformation at time $t_{n+x}$, particles are added in the vicinity of the tool edges and the volume definition and re-connectivity is done continuously.

Fig. 2

Schematic overview of the PFEM procedure for a shear-cutting application. Showing the initial time step, a time step $t_n$ with added nodes and a time step $t_{n+x}$ where nodes are concentrated near the tool edges

A characteristic feature of the PFEM procedure is the $\alpha$-shape method developed by Edelsbrunner and Mücke [46] used for defining internal and external domain boundaries. The $\alpha$-shape method uses geometrical criterion to remove elements that are overly distorted and non-physical because of the Delaunay triangulation. Generally, such elements do not belong to the analysis domain and are therefore removed. Further description of the $\alpha$-shape method and the effect of its input parameters were discussed by Franci and Cremonesi [47]. An alternative approach to the $\alpha$-shape method utilised in the present work is the constrained Delaunay algorithm, described by Shewchuk [48]. This method constrains the external boundaries and thus conserves the domain volume.

2.1.1 Results variable transfer and mesh refinement

In PFEM, the particles move in a Lagrangian manner throughout the numerical modelling and continuous update of the particle re-connectivity ensures satisfactory element quality. To deal with low particle density in localised areas or unwanted particle concentration, the PFEM scheme can add or remove particles to control adequate discretisation, both in terms of simulation time and in terms of solution accuracy. However, as mentioned in Sect. 1, re-meshing often leads to results smoothing as the results variables are being transferred from the old mesh to the updated mesh. The result transfer includes the particle variables, such as pressure and displacement, and the elemental Gauss point variables, such as stress and material damage. The classical approach for variable transfer in PFEM is storing all results variables in the particles in between re-connectivity. This method preserves the particle information between re-connectivity, but elemental variables are inevitably smoothed as they are transferred from the particle to the element Gauss points. To avoid the elemental results smoothing, the PFEM scheme utilised in the present article transfers elemental variables directly from the old to the new elements. This method of elemental variable transfer was proven effective regarding results preservation in the work by Rodríguez et al. [40]. However, as stated by Rodriguez et al. [39,40,41,42], the results preservation between mesh re-connectivity is only valid in areas where no particles are added or removed. Addition of particles requires interpolation between the neighbouring particles which unavoidably lead to a certain degree of smoothing, and the elemental variable transfer is affected by the distance between the old and new Gauss points. In this article, the closest point projection of the Gauss point variables, described by Rodriguez et al. [42] and schematically shown in Fig. 3, was applied to minimise the results smoothing when the particle connectivity was altered due to insertion of particles. Similarly, removing particles will cause results smoothing in variable transfer to a coarser mesh. Consequently, extensive addition or removal of particles should be avoided.

Fig. 3

Closest point projection of Gauss point variables when refining two large elements into four smaller elements

Taking the implications of mesh refinement into consideration, adding particles remain as an effective method for increasing the numerical accuracy in localised areas if done sparingly. The current PFEM implementation applies particle insertion based on prescribed limit values of both geometrical and mechanical criteria. The geometrical criterion is described by Rodriguez et al. [42], are presented in Eq. (1) and define when to refine the discretisation such that the predefined minimum distance between $h_\textrm{min}$ prevails. In Eq. (1), d denotes the tool displacement and r the tool edge radii.

$$\begin{aligned} h_\textrm{min}=\text {max} \Bigl \{ \frac{d}{100},\frac{\pi r}{2\cdot 20} \Bigr \} \end{aligned}$$

(1)

The mechanical criterion for insertion of particles considers the plastic power $G_{mech}$, as described by Rodriguez et al. [39] and shown in Eq. (2), and a predefined value of the accumulated damage parameter D, to be described in Sect. 2.4.

$$\begin{aligned} G_\textrm{mech}= \chi \sqrt{\frac{2}{3}}\bar{\sigma }\frac{\Delta \gamma _{n+1}}{\Delta t} \end{aligned}$$

(2)

Table 1 Tensile properties in different material directions relative to the rolling direction (RD) for CP1000HD with a thickness of $t=1.5$ mm, yield strength (Rp02), tensile strength (Rm), uniform elongation (Ag), total elongation (A80), n-value at uniform elongation (nAg) and r-value (r)

Here, $\chi$ refers to a user-defined dissipation parameter in the range of [0.85, 0.95], $\bar{\sigma }$ is the effective stress, $\Delta t$ is the time step and $\Delta \gamma _{n+1}$ is the updated plastic multiplier presented in Appendix A.

2.2 Governing equations

The development of a PFEM shear-cutting model was started by defining the governing equations of the problem. This was done considering the balance of momentum equation of the blank body occupying the volume V over the time interval [0, T] as stated in Equation (3), which is expressed in tensor notation over indexes $i,j=1,2,3$.

$$\begin{aligned} \rho a_i - \frac{\partial \sigma _{ij}}{\partial x_j} - \rho b_i = 0 \hspace{0.1cm} \text {in}\hspace{0.1cm} V\times [0,T] \end{aligned}$$

(3)

In Eq. (3), $\rho$ defines the material density, $a_i$ is the acceleration, $\sigma _{ij}$ is the Cauchy stress tensor and $\rho b_i$ denotes the external body forces.

In this work, a stabilised mixed formulation of the finite elements was implemented for avoiding volume locking in near-incompressibility $J_2$ plasticity. This was accomplished by decomposing $\sigma _{ij}$ into its deviatoric and volumetric parts according to Eq. (4), where $s_{ij}$ is the deviatoric part of the stress tensor, $\delta _{ij}$ is the Kronecker delta and p is the pressure defined according to Equation (5).

$$\begin{aligned} \sigma _{ij}= & {} s_{ij}+p\delta _{ij} \end{aligned}$$

(4)

$$\begin{aligned} p= & {} \frac{1}{3}\text {tr}(\sigma _{ij}). \end{aligned}$$

(5)

The pressure was rewritten according to the principle described by Simo and Hughes [49], using the hyperelastic potential as shown in Eq. (6) where $\kappa$ is the compressibility modulus of the material and J is the Jacobian.

$$\begin{aligned} p-\kappa \frac{\ln (J)}{J}=0 \hspace{0.1cm} \text {in}\hspace{0.1cm} V\times [0,T] \end{aligned}$$

(6)

The weak form of Eq. (3) is given by Equation (7) and established by multiplication of a test function $\delta u_i$, integration over the defined configuration and applying the divergence theorem according to Bonet et al. [50].

$$\begin{aligned} \int _V \delta u_i \rho a_i \textrm{d}V+\int _V \varepsilon _{ij}\sigma _{ij} \textrm{d}V - \int _V \delta u_i \rho b_u \textrm{d}V - \int _S \delta u_i t_i \textrm{d}S=0 \end{aligned}$$

(7)

In Eq. (7), $t_i$ is the traction force per unit of area acting on the boundary, V is the volume in the current configuration, S is the boundary area for the current configuration and $\varepsilon _{ij} =\frac{1}{2}(\frac{\partial \delta u_i}{\partial x_j}+\frac{\partial \delta u_i}{\partial x_i})$. Meanwhile, the weak form of Eq. (6) was obtained by multiplying a test function $\delta p$ and integration over the reference V configuration as shown in Eq. (8).

$$\begin{aligned} \int _V \delta p \frac{ln(J)}{J}\textrm{d}V - \int _V \delta p \frac{p}{\kappa } \textrm{d}V=0 \end{aligned}$$

(8)

For an axisymmetric formulation of the governing equations, the differential volume dV is expressed as d$V=2\pi r \textrm{d}A$, where r corresponds to the radial position of a discrete point and $\textrm{d}A$ is the differential area. The details of forming the balance equations and weak form of the mixed displacement and pressure mechanical problem are found in work by Rodríguez et al.  [40,41,42] and Reinold and Meschke [51].

2.3 Isotropic plasticity model

A common automotive steel grade, CP1000HD, was investigated in the present article. The material is a cold-rolled, high-ductility complex phase steel with an ultimate tensile strength of 1000 MPa. The CP1000HD tensile mechanical properties are presented in Table 1.

During the shear-cutting process, the blank endures substantial plastic deformation. It is therefore important that the numerical modelling accurately describes the plastic loading response of the blank material for high plastic strains and up until material failure. Generally, cold-rolled AHSS grades show certain anisotropic behaviour regarding the rolling direction, but the fine-grained microstructure of the CP1000HD grade reduces the anisotropic effect. In this work, anisotropy was disregarded due to the limited anisotropic material behaviour of the CP1000HD material, which also enabled the use axisymmetric representation of the numerical modelling. The plastic hardening response of the blank material was governed by the isotropic plasticity model proposed by Stiebler et al. [52] and presented in Eq. (9), where $\varepsilon _p$ is the equivalent plastic strain.

$$\begin{aligned} \bar{\sigma }=c_1+c_2\cdot \varepsilon _p+c_3\cdot (1-e^{c_4\cdot \varepsilon _p}) \end{aligned}$$

(9)

The parameters $c_1$–$c_4$ were calibrated using least-squares fitting against experimental results of effective stress versus plastic strain from hydraulic bulge testing performed according to the ISO 16808 standard [53]. Figure 4 shows the experimental plastic hardening response, experimentally measured up until $\varepsilon _p=0.62{-}0.75$ and extrapolated to $\varepsilon _p=1$, and the corresponding results from the calibrated Stiebler et al. plasticity model. Table 2 states the calibrated values of parameters $c_1$–$c_4$.

Fig. 4

Plastic hardening of CP1000HD from hydraulic bulge testing, extrapolated to $\varepsilon _p=1$ for effective stress $\bar{\sigma }$, and the calibrated Stiebler et al. plasticity model

Table 2 Plasticity model parameters $c_1$–$c_4$

2.4 Ductile damage- and failure model

A local phenomenological ductile damage- and failure model was implemented in the PFEM modelling scheme in order to predict the fracture process. The damage- and failure model was based on the Generalized Incremental Stress State Dependent Damage Model (GISSMO), developed by Neukamm et al. [54] and further enhanced by Effelsberg et al. [55] and Andrade et al. [56, 57]. GISSMO is commonly used in FE models for modelling of ductile damage and fracture in metals, such as aluminium and high-strength steel. Similar to most AHSS grades, the CP1000HD material shows a stress-state-dependent failure behaviour, which was accounted for in the damage- and failure model by relating the equivalent plastic failure strain $\varepsilon _\textrm{eff}^f$ to the stress triaxiality $\eta$ and the normalised Lode angle parameter $\bar{\theta }$. The stress triaxiality and normalised Lode angle parameter are presented in Eqs. (10) and (11) for indexes $i,j,k,m,n=1,2,3$.

$$\begin{aligned} \eta= & {} \frac{\sigma _{kk}}{3 \sqrt{\frac{3}{2} s_{ij}s_{ij}}} \end{aligned}$$

(10)

$$\begin{aligned} \bar{\theta }= & {} \frac{1}{3} \arccos \left( \frac{3\sqrt{3}}{2} \frac{\frac{1}{3}s_{ij}s_{jk}s_{ki}}{(\frac{1}{2}s_{mn}s_{mn})^{3/2}}\right) . \end{aligned}$$

(11)

The damage- and failure model applied an incremental accumulation of the damage parameter D according to Eq. (12). In Eq. (12), $\dot{\varepsilon }_{p}$ denotes the effective plastic strain increment, $\varepsilon _{eff}^f(\eta ,\bar{\theta })$ states the stress-state-dependent equivalent plastic failure strain and the parameter n defines the rate of damage accumulation. When D reached a defined critical value $D_{crit}$, the material was considered failed. The current implementation of the damage- and failure model used $D_{crit}=0.95$, ensuring enough stiffness reduction of the failed element to consider the blank as separated by material fracture. In the post-processing routine, elements reaching $D=D_\textrm{crit}$ were removed for visualisation purposes.

$$\begin{aligned} \dot{D} = \frac{n}{\varepsilon _\textrm{eff}^f \left( \eta ,\bar{\theta } \right) } D^{(1 - \frac{1}{n})} \dot{\varepsilon }_{p} \end{aligned}$$

(12)

Due to void growth during extensive plastic deformation, the load-bearing capacity of a ductile metal is commonly lowered as the load-bearing area is reduced. This phenomenon was accounted for in the damage- and failure modelling by the instability parameter F that accumulated similarly to the damage parameter D, but referred to the stress-state-dependent instability strain $\varepsilon _{ins}(\eta ,\bar{\theta })$.

$$\begin{aligned} \dot{F} = \frac{n}{\varepsilon _{ins}(\eta )} F^{(1-\frac{1}{n})}\dot{\varepsilon }_{p} \end{aligned}$$

(13)

The load-bearing capacity of the material was affected by the accumulated damage parameter $\tilde{D}$ through Eq. (14). The damage value of the element at stress coupling, $D_{c}$, was defined when $F=1$ and from this point the stress tensor was affected by the accumulated damage according to the radial return scheme. In Eq. (14), the parameter m defines the degradation rate.

$$\begin{aligned} \tilde{{\sigma }}={\sigma }(1-\tilde{D})\hspace{0.1cm}\text {where}\hspace{0.1cm}\tilde{D} = \left( \frac{D - D_{c}}{1 - D_{c}} \right) ^m \end{aligned}$$

(14)

2.5 Calibration of damage- and failure model

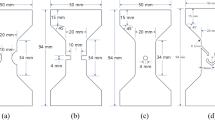
Digital image correlation (DIC) with a 0.1 mm facet grid and 75% overlap enabled measurement of CP1000HD sheet specimen strain field during tensile testing, beyond necking and up until failure. The tensile testing specimen geometries were designed to deform and fail at designated stress-states and were developed by Sjöberg et al. [58]. Schematic images of the specimen are shown in Fig. 5. Using the stepwise modelling method (SMM) by Marth et al. [59], the equivalent plastic strain at failure $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$ and the corresponding stress-state were determined. Based on material data such as yield strength, estimated values of Poisson’s ratio as $\nu =0.3$ and Young’s modulus as $E=210$ GPa, SMM calculated the stress tensor along an integration path of the specimen localisation zone for each DIC frame acquired during the tensile test. With the stress tensor known, the stress triaxiality and effective plastic strain were calculated.

Fig. 5

Tensile specimen geometries

With experimental values of $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$, a failure locus was calibrated. Due to its renowned accuracy in predicting failure of high-strength steel, a modified Mohr–Coulomb (MMC) failure locus was calibrated for the CP1000HD material. The MMC model was developed by Bai and Wierzbicki [60, 61], and its accuracy in prediction of material failure during for shear cutting of high-strength steel was displayed by Wang [62] and Wang et al. [16]. Equation (15) states the expression of the MMC failure locus, reduced for von Mises plasticity, which is formed by the parameters $C_1$, $C_2$ and $C_3$. The parameters were calibrated with a least-squares fit against the experimental values of the effective plastic failure strain at their corresponding stress-state. As the DIC strain field measurements were taken at the specimen surface, plane stress was assumed for the stress and strain calculations. Accordingly, Eq. (16) relates the normalised Lode angle parameter $\bar{\theta }$ to the stress triaxiality $\eta$ for plane stress assumption as described by Bai and Wierzbicki [60, 61]. Given the thin thickness of the CP1000HD sheet steel material, failure strain measurement was limited to plane stress assumption even though punching is reportedly a plane strain process. The use of a three-dimensional failure locus, such as Eq. (15), would therefore generate failure strain data outside the calibrated stress-states.

$$\begin{aligned} \varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })= & {} \Bigg \{ C_2 \Bigg [\sqrt{\frac{1+C_1^2}{3}}\cos \Big (\frac{\bar{\theta }\pi }{6}\Big )\nonumber \\{} & {} +C_1\Big (\eta +\frac{1}{3}\sin \Big (\frac{\bar{\theta }\pi }{6}\Big )\Big ) \Bigg ]\Bigg \}^{-\frac{1}{C_3}} \end{aligned}$$

(15)

$$\begin{aligned} \bar{\theta }= & {} 1 - \frac{2}{\pi }\cos ^{-1} \left( -\frac{27}{2} \eta \left( \eta ^2 - \frac{1}{3} \right) \right) \end{aligned}$$

(16)

Table 3 contains the MMC parameters $C_1$ to $C_3$ after calibration. Meanwhile, Fig. 6 shows the MMC failure locus formed by the calibrated $C_1$ to $C_3$. The experimental values of the effective plastic failure strains are shown in Fig. 6, as well as the plane stress curve formed using the relation between $\bar{\theta }$ and $\eta$ shown in Eq. (16) and the plain strain valley found at $\varepsilon _\textrm{eff}^f(\eta ,0)$.

Table 3 MMC parameters $C_1$–$C_3$

Fig. 6

The modified Mohr–Coulomb failure locus of CP1000HD, where the plane stress failure curve (blue) and the plane strain valley curve defined by $\varepsilon _\textrm{eff}^f(\eta ,0)$ (red), is plotted along with the experimental tensile failure points

The MMC expression is not designated for the instability strain $\varepsilon _\textrm{ins}(\eta )$, and no analytical expression of the instability strain as a function of stress-state was found in the literature. In this work, the values of $\varepsilon _\textrm{ins}(\eta )$ were therefore determined at the maximum force and the corresponding stress triaxiality of the tensile tests shown in Fig. 5. Consequently, $\varepsilon _\textrm{ins}(\eta )$ was input as a tabular function of $\eta$ in the damage- and failure modelling. Table 4 shows the tabulated values of the effective plastic instability strain $\varepsilon _\textrm{ins}(\eta )$. For triaxialities over the last table entry, $\eta =0.51$, the value of $\varepsilon _\textrm{ins}(\eta =0,51)$ was kept constant.

Table 4 Effective plastic instability strain values $\varepsilon _\textrm{ins}(\eta )$

The cut-off value in ductile damage modelling is conventionally assigned at $\eta <-1/3$, as this is the lowest triaxiality at which can failure occur during uniaxial compression, i.e. $\bar{\theta }=-1$ as reported by Bao and Wierzbicki [63] and Lou et al. [64]. However, results by Zhao et al. [65] showed that limited void growth and coalescence occur during shear cutting of ductile metals as the high hydrostatic pressure suppresses the void growth. The study was conducted on a fine blanking process, and Zhao et al. discovered that a shearing penetration of 70% of the blank thickness was required before enough void growth caused final fracture of the material. At this penetration depth, the hydrostatic pressure was significantly lower and the tension dominated stress-state accelerated material failure. Based on these results, the authors of this article defined a cut-off value of $\varepsilon _\textrm{eff}^f(\eta <0,\bar{\theta })$ for creation of the MMC failure surface. Consequently, no failure occurred at negative triaxialities and the burnish zone was formed due to flow of the blank material. The punching processes of this work involved larger cutting clearances than in fine blanking, thus considerably shorter shearing depths and less time in compressive stress-states. Therefore, disregarding ductile damage in compression was considered adequate.

2.5.1 Mesh size dependency and regularisation of damage- and failure modelling

A consequence of using local damage- and failure modelling was mesh dependency related to the effective plastic failure strain. The DIC measurement used a 100 $\upmu$m evaluated facet size during strain field measurement, meaning that the measured failure strain correlated to similar mesh size in the numerical model. Reducing the mesh size led to different element strains compared to the coarse mesh in localisation zones, meaning that smaller elements could reach $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$ earlier in the deformation process than for the larger elements. To reduce the effect of mesh dependency in the failure modelling, the current damage- and failure model used the mesh regularisation technique presented by Andrade et al. [57]. The mesh regularisation technique scaled the value of $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$ based on the individual element size. This means that $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$ for elements smaller than 100 $\upmu$m was increased by a scale factor. The regularisation factors were determined by comparing the numerical traction results from a fictitious notched specimen with varying mesh sizes in the localisation zone. The regularisation factors and their corresponding element sizes are presented in Table 5. Linear interpolation was used in the numerical model for extracting regularisation factors between the points presented in Table 5, whereas linear extrapolation was used for smaller elements than 5 $\upmu$m. Elements larger than 100 $\upmu$m were given a regularisation factor of 1 as mesh regularisation of these elements was redundant.

Table 5 Characteristic element size and the corresponding regularisation factor used for mesh regularisation with respect to $\varepsilon _\textrm{eff}^f(\eta ,\bar{\theta })$

The effect from mesh regularisation is here visualised for a 0.3 $\times$ 0.3 mm square model subjected to simple shear with varying mesh size, as shown in Fig. 7. All the simple shear configurations of Fig. 7 were analysed, and the results in Fig. 8 show for (a) using only the elasto-plastic material model, (b) using the material model with the unregularised damage model and (c) using the material model with the regularised damage model and regularisation factors in Table 5. The analyses show that the elasto-plastic response is independent of mesh size, as shown in Fig. 8a, while the mesh size dependency of the damage modelling is apparent in Fig. 8b as decreased element sizes cause premature failure compared to the reference size of 100 $\upmu$m. Figure 8c demonstrates that by using the regularised damage model, material failure occurred at the same level of $\delta _{shear}$ for all configurations. The element stress level at failure converged with smaller element sizes, indicating that element sizes smaller than 10 $\upmu m$ should give similar stress- and damage response even in larger and more complex geometries.

Fig. 7

The schematic representation of the simple shear model in a and b shows the geometry discretisation using varying element sizes, ranging from 100 to 5 [$\mu$m]

Fig. 8

The effect of applying damage modelling to the simple shear cases of Fig. 7 using varying characteristic element sizes, ranging from 100 to 5 [$\mu m$]. a shows the stress response of the square model subjected to simple shear without applying the damage model, while b shows the stress response until failure with unregularised damage modelling and c using regularised damage model

2.6 Spatial discretisation

For modelling of the mechanical shear-cutting process, discretisation of the governing equations by axisymmetric 2D elements in an updated Lagrangian formulation was done. This gave the FE-formulation of the nodal displacements $\textbf{u}$ and nodal pressure $\textbf{p}$ according to Eqs. (17a) and (17b), where $\textbf{N}_u$ and $\textbf{N}$ denote the corresponding shape functions.

$$\begin{aligned} \textbf{u}= & {} \textbf{N}_u \bar{\textbf{u}} \end{aligned}$$

(17a)

$$\begin{aligned} \textbf{p}= & {} \textbf{N} \bar{\textbf{p}} \end{aligned}$$

(17b)

The finite element discretisation in Eqs. (17a) and (17b) is applied to the weak forms in Eqs. (7) and (8) to yield the discretised system of equations as

$$\begin{aligned} \textbf{R}_u= & {} \textbf{M}_u^{n+1}\bar{\textbf{a}}^{n+1}-\textbf{f}_{u,\textrm{ext}}^{n+1}+\textbf{P}_u^{n+1}(\bar{\textbf{u}}^{n+1})=0 \end{aligned}$$

(18a)

$$\begin{aligned} \textbf{R}_p= & {} \textbf{M}_p\bar{\textbf{p}}^{n+1}+\textbf{f}_{p,\textrm{stab}}(\bar{\textbf{p}}^{n+1})-\textbf{F}_{p,\textrm{vol}}(\bar{\textbf{u}}^{n+1})=0 \end{aligned}$$

(18b)

Here, the nodal accelerations $\bar{\textbf{a}}^{n+1}$ form from the trapezoidal rule following Eqs. (19a) and (19b), where h is the time increment defined as $h=t^{n+1}-t^n$.

$$\begin{aligned} \bar{\textbf{v}}^{n+1}= & {} \bar{\textbf{v}}^n+\frac{2}{h}(\bar{\textbf{u}}^{n+1}-\bar{\textbf{u}}^n) \end{aligned}$$

(19a)

$$\begin{aligned} \bar{\textbf{a}}^{n+1}= & {} \bar{\textbf{a}}^n+\frac{4}{h}\bar{\textbf{v}}^n+\frac{4}{h^2} (\bar{\textbf{u}}^{n+1}-\bar{\textbf{u}}^n) \end{aligned}$$

(19b)

The matrices and vectors in Eqs. (18a) and (18b) are obtained from the standard finite element assembling as

$$\begin{aligned} \begin{aligned}&\textbf{P}_{\textbf{u}}(\textbf{u})= \int _{v} \textbf{B}_{\textbf{u}}^T \overline{\varvec{\sigma }} \textrm{d} v \\&\textbf{f}_{\textbf{u}, \text { ext }}= \int _{v} \textbf{N}_{\textbf{u}}^T \cdot \textbf{b} \textrm{d} v+ \int _{a} \textbf{N}_{\textbf{u}}^T \cdot \overline{\textbf{t}} \textrm{d} a \\&\textbf{M}_{\textbf{u}}= \int _{v} \rho \textbf{N}_{\textbf{u}}^T \textbf{N}_{\textbf{u}} \textrm{d} v \\&\textbf{M}_p= \int _{v} \frac{1}{\kappa } \textbf{N}^T \textbf{N} \frac{\textrm{d} v}{J} \\&\textbf{F}_{p, \textrm{vol}}(\overline{\textbf{u}})= \int _{v} \textbf{N}^T\left( \frac{\ln (J)}{J}\right) \frac{\textrm{d} v}{J} \\&\textbf{F}_{p, \text{ stab } }(\bar{p})= \int _{v} \frac{\alpha }{G} \bar{p}\left( \textbf{N}^T \textbf{N}-\tilde{\textbf{N}}^T \tilde{\textbf{N}}\right) \frac{\textrm{d} v}{J} \end{aligned} \end{aligned}$$

(20)

where $\textbf{B}_{\textbf{u}}$ is the small deformation matrix for axisymmetry, $\overline{\varvec{\sigma }}$ is the Voigt notation of the Cauchy stress tensor. $dv = 2 \pi x dA$ defines the axisymmetric volume as a function of the radial position of the element mid point x.

The linearisation of Eqs. (18a) and (18b) gives Eq. (21) to be solved through iteration, given the time step $n+1$ and iteration number (i).

$$\begin{aligned} \Bigg [ \begin{array}{ll} \frac{4}{h^2}\textbf{M}_u+\textbf{K}_{uu,(i)}^{n+1} &{} \textbf{K}_ {up,(i)}^{n+1} \\ \textbf{K}_{pu}^{n+1} &{} \textbf{K}_{pp}^{n+1} \end{array} \Bigg ]\Bigg [ \begin{array}{l} \Delta \textbf{u}^{n+1}_{(i)}\\ \Delta \textbf{p}^{n+1}_{(i)}\\ \end{array} \Bigg ]=\Bigg [ \begin{array}{l} \textbf{R}_{u,(i)}\\ \textbf{R}_{p,(i)} \end{array} \Bigg ] \end{aligned}$$

(21)

The constituents of the tangent stiffness matrix in Eq. (21) were defined according to Eqs. (22), (24), (25) and (26) for the axisymmetric mixed formulation.

$$\begin{aligned} \textbf{K}_{uu}=\textbf{K}^\textrm{geo}+\textbf{K}^\textrm{mat} \end{aligned}$$

(22)

where

$$\begin{aligned} \textbf{K}^\textrm{mat}= & {} \int _v \textbf{G}^T \bar{\sigma }\textbf{G}\textrm{d}v \end{aligned}$$

(23a)

$$\begin{aligned} \textbf{K}^\textrm{geo}= & {} \int _v \frac{1}{J} \textbf{B}_{\textbf{u}}^T \hat{\textbf{c}}^{ep,\textrm{mix}}\textbf{B}_{\textbf{u}}\textrm{d}v \end{aligned}$$

(23b)

$$\begin{aligned} \textbf{K}_\textrm{up}= & {} \int _v \textbf{B}_{\textbf{u}}^T\textbf{m}\textbf{N}\textrm{d}v \end{aligned}$$

(24)

$$\begin{aligned} \textbf{K}_{pu}= & {} \int _v \frac{(1-ln(J))}{J^2}\textbf{N}^T\textbf{m}^T\mathbf {B_{\textbf{u}}}\textrm{d}v \end{aligned}$$

(25)

$$\begin{aligned} \textbf{K}_{pp}= & {} \int _v \frac{1}{J\kappa }\textbf{N}^T\textbf{N}\textrm{d}v \end{aligned}$$

(26)

and $\textbf{m}$ represents the second-order identity tensor in Voigt notation, $\hat{\textbf{c}}^{ep,\textrm{mix}}$ is the matrix representation of the hyperelasto-plastic fourth-order tensor and J denotes the Jacobian. The expressions of matrices $\hat{\sigma }$ and $\textbf{G}$ for axisymmetry are given by Wriggers [66]. The jacobian J equals the determinant of the deformation gradient $\textbf{F}$, defined as

$$\begin{aligned} F_{ij}=\frac{\partial x_{i}}{\partial X_j} \end{aligned}$$

(27)

where $F_{33}$ is defined as following based on the axisymmetric assumption

$$\begin{aligned} F_{33}=\frac{x}{X} \end{aligned}$$

(28)

The discretisation of the axisymmetric problem presented in this work is here expressed such that it can be interpreted for both plane strain and axisymmetry. Detailed expressions of the ingoing matrices in axisymmetric representation are given in Appendix B.

The hyperelasto-plastic compliance tensor $\textbf{c}^{ep,\textrm{mix}}$ depends on deformation state where the elastic deformation compliance matrix in Eq. (29) or the plastic deformation matrix in Eq. (30) was used for calculation.

$$\begin{aligned} \textbf{c}^{\textrm{elast,mix}}= & {} p[\textbf{I}\otimes \textbf{I}-2\textbf{i}]+\bar{\textbf{C}} \end{aligned}$$

(29)

$$\begin{aligned} c^{\textrm{plast,mix}}= & {} \textbf{c}_{\textrm{elast,mix}}-\beta _1\textbf{c}^{ela}-2\mu \beta _3 \textbf{n}\otimes \textbf{n}\nonumber \\{} & {} -2\mu \beta _4\textbf{n}\otimes dev(\textbf{n}^2) \end{aligned}$$

(30)

In Eqs. (29) and (30), $\bar{\textbf{C}}$ is the deviatoric component of the spatial elasticity tensor, $\textbf{I}$ is the second-order identity tensor, $\textbf{i}$ is the fourth-order identity tensor and $\textbf{c}^{ela}$ is the algorithmic elasticity module according to Eq. (31).

$$\begin{aligned} \textbf{c}^{ela}=\kappa \frac{\textrm{ln}(J)}{J}[\textbf{I}\otimes \textbf{I}-2\textbf{i}]+\kappa \frac{(1-ln(J))}{J}\textbf{I}\otimes \textbf{I}+\bar{\textbf{C}} \end{aligned}$$

(31)

For a time increment $n\rightarrow n+1$, the implicit solution scheme iteratively solved Eq. (21) using a Newton–Raphson scheme further described in Sect. 2.9.

2.7 Radial return mapping

An iterative scheme was used for determining the hyperelastic–plastic loading behaviour of the blank material and calculation of the Cauchy stress tensor. The plasticity calculation followed a radial return mapping method, where the yield stress $\bar{\sigma }_Y$ is described by Eq. (9). The stress calculation scheme was performed according to the work by Rodriguez et al. [42], with the addition of degradation of the stress tensor with respect to the damage parameter D as stated in Eq. (14). The damage parameter D influenced the trial stress, the consistency term $f'$ and the iteration residual during the radial return mapping. Quadratic convergence of the Newton–Raphson schemes assured correct implementation of the proposed mixed axisymmetric mechanical solution. The radial return algorithm of the current implementation is in detail described in Appendix A.

2.8 Time integration of the damage model

Given the staggered, incremental solution of the damage parameter, a time step dependency was present in the damage accumulation. The time step dependency was stronger with higher values of m and n as this increased the nonlinearity of the damage accumulation. To visualise the time step dependency, an analysis of the stress- and damage response of a single element subjected to simple shear using $m=3$ and $n=3$ was performed, and the results are shown in Fig. 9. The results in Fig. 9 show that time steps of $\Delta t=1e{-2}$ [s] gave delayed element failure compared to using time steps of $\Delta t=1e{-3}$ [s], which indicates that the simulation time steps should be kept as small as possible to ensure the accuracy of the numerical modelling. To reduce the time step dependency of the ductile damage modelling, the authors implemented a sub-cycling routine that for each time step divided the plastic strain increment in several sub-steps over which Eq. (12) is calculated. The effect from the sub-cycling routine is apparent in Fig. 9, as the analysis using a time step $\Delta t=1e{-2}$ [s] with $n_\textrm{sub} = 1000$ sub-cycles can reproduce the results of the analysis using $\Delta t=1e{-3}$ [s].

Fig. 9

The evolution of stress (solid lines) and damage (dashed lines) of a single element of 1 mm subjected to simple shear using different time step sizes $\Delta t$ and number of sub-cycles $n_{sub}$ for damage accumulation rate $m=3$ and material degradation rate $n=3$

2.9 Global time integration scheme

For solving the mechanical problem described in Sects. 2.2 and 2.6, an iterative Newton–Raphson scheme using the trapezoidal rule was implemented according to the work by Rodriguez et al. [42]. The implicit solution scheme was executed using the following steps over the time increment $n\rightarrow n+1$:

• 1. Initialize the variables $\textbf{u}_{n+1}=0$, $\textbf{p}_{n+1}=\textbf{p}_n$, $\textbf{x}_{n+1}=\textbf{x}_n$, $\overline{\textbf{b}}_{n+1}^e=\overline{\textbf{b}}_{n}^e$ and $\varepsilon _{p,n+1}=\varepsilon _{p,n}$, where $\textbf{b}^e$ denotes the volumetric preserving part of the elastic left Cauchy–Green tensor and $\varepsilon _p$ is the equivalent plastic strain.

• 2. Compute nodal displacements, pressure increment and contact forces between blank and tool and perform iteration of the problem over iteration numbers $i=1\ldots N_{\textrm{max,iter}}$.

• 3. Update nodal displacements, pressures and nodal coordinates according to Eqs. (32a), (32b) and (32c).

  $$\begin{aligned} \textbf{u}_{n+1,(i+1)}= & {} \textbf{u}_{n+1,(i)}+\gamma \Delta \textbf{u}_{n+1,(i)} \end{aligned}$$

  (32a)
  $$\begin{aligned} \textbf{p}_{n+1,(i+1)}= & {} \textbf{p}_{n+1,(i)}+\gamma \Delta \textbf{p}_{n+1,(i)} \end{aligned}$$

  (32b)
  $$\begin{aligned} \textbf{x}_{n+1,(i+1)}= & {} \textbf{x}_{n+1,(i)}+\gamma \Delta \textbf{u}_{n+1,(i)} \end{aligned}$$

  (32c)

• 4. Calculate the relative deformation gradient $\textbf{F}=\textrm{d}\textbf{x}_n/\textrm{d}\textbf{x}_{n+1}$, the Jacobian and the element areas $A_e$.

• 5. Calculate the Cauchy stress ${\sigma }$, $\overline{\textbf{b}}^e$ and $\varepsilon _p$ using radial return mapping as described in Sect. 2.7.

• 6. Calculate the displacement and pressure residuals $\textbf{R}_u$ and $\textbf{R}_p$ and check convergence according to Eqs. (33a), (33b), (33c) and (33d),

  $$\begin{aligned}{} & {} \parallel \textbf{u}_{n+1,(i+1)}-\textbf{u}_{n+1,(i)} \parallel \le \text {TOL}_u \parallel \textbf{u}_n\parallel \end{aligned}$$

  (33a)
  $$\begin{aligned}{} & {} \parallel \textbf{p}_{n+1,(i+1)}-\textbf{p}_{n+1,(i)} \parallel \le \text {TOL}_p \parallel \textbf{p}_n\parallel \end{aligned}$$

  (33b)
  $$\begin{aligned}{} & {} \parallel \textbf{R}_{u,(i)}\parallel \le \text {TOL}_u \text { max}(\parallel \textbf{P}_{u,n+1}\parallel ,\parallel \textbf{F}^\textrm{ext}_{n+1}\parallel ) \end{aligned}$$

  (33c)
  $$\begin{aligned}{} & {} \parallel \textbf{R}_{p,(i)}\parallel \le \text {TOL}_p \text { max}(\parallel \textbf{F}_{p,\textrm{vol},n+1}\parallel ,\parallel \textbf{F}^\textrm{stab}_{n+1}\parallel ) \end{aligned}$$

  (33d)

• 7. If the conditions of Eqs. (33a)–(33d) are fulfilled, convergence is met. Otherwise, increase $i=i+1$.

• 8. For the updated configuration, the damage calculation and time integration are performed as described in Sects. 2.4 and 2.8.

In Eqs. (32a), (32b) and (32c), $\gamma$ is a line search parameter which defines the magnitude of the increment step in direction of the displacement vector, as stated by Bonet et al. [50]. The value of $\gamma$ can vary between 0 and 1, but the initial value of each increment is 1 which corresponds to standard Newton–Raphson method. For certain cases of severe nonlinearity, other values of $\gamma$ might be necessary and the determination of such vales was described by Bonet et al. [50] and implemented in this work. Otherwise, really small time steps are needed.

2.10 Contact modelling

Accurate contact modelling of the shear-cutting simulations was of high importance as contact force distribution and part penetration substantially affect the blank deformation near the tool edges. In this work, this was achieved by implementation of a penalty-based node-to-segment (NTS) contact formulation based on the work by Rodríguez et al. [40]. The contact formulation distinguished between normal and tangential contact, where the normal NTS contact prevented contact penetration, while the tangential part controlled frictional sticking and sliding states according to a regularised Coulomb friction law.

The principle of the penalty-based NTS contact origins from the axisymmetric normal penalty force $F_{p}$ arising when a blank particle, denoted $\textbf{x}^b$ in Fig. 10, penetrates the tool contact segment between tool particles $\textbf{x}^t_1$ and $\textbf{x}^t_2$ with the normal distance $p_N$ according to Eq. (34), where $\kappa$ is the penalty parameter and r is the radial distance from the symmetry axis.

$$\begin{aligned} F_{p}=2\pi r \kappa p_N \end{aligned}$$

(34)

The discretised form of Eq. (34) forms accordingly,

$$\begin{aligned} \textbf{F}_c=F_{p}\textbf{N}_s \end{aligned}$$

(35)

where $\textbf{N}_s$ is the segment normal vector defined by the nodal vector $\textbf{n}_1$ and the penetrating blank particle projection $\xi$ onto the tool segment surface as

$$\begin{aligned} \textbf{N}_s = \Bigg [ \begin{array}{l} \textbf{n}_1 \\ -(1-\xi )\textbf{n}_1\\ -\xi \textbf{n}_1 \end{array} \Bigg ] \end{aligned}$$

(36)

and the blank particle projection $\xi$ is defined according to Eq. (37).

$$\begin{aligned} \xi =(\textbf{x}^b-\textbf{x}^t_1)\textbf{a}_1/l \end{aligned}$$

(37)

In Eq. (37), $\textbf{a}_1$ is the tangent vector of the tool segment, while l is the length of the tool segment.

Fig. 10

A schematic image of a node-to-segment contact between tool segment formed by particles $\textbf{x}^t_1$ and $\textbf{x}^t_2$ and the penetrating blank particle $\textbf{x}^b$. The red area defines the penetration between the tool and blank

Concurrently, the tangential contact component defined the friction law using a discrete relative tangential velocity, $\dot{p}_T$, according to the work by Rodríguez et al. [40]. $\dot{p}_T$ was defined according to Eq. (38), where the time increment, tool segment length l, the current projection of the particle penetration $\xi$ and the particle projection at the beginning of the time step $\xi _0$ were used.

$$\begin{aligned} \dot{p}_T=(\xi -\xi _0)l/\Delta t \end{aligned}$$

(38)

The regularised Coulomb friction law stated in Eq. (39), defined by $\dot{p}_T$, the friction coefficient $\upmu$, the normal penalty force $P_N$ and a regularisation parameter $V_\textrm{ref}$ furthermore formed the tangential contact force.

$$\begin{aligned} F_T=\mu F_p \text {tanh}\Big (\frac{\dot{p}_T}{V_{ref}}\Big ) \end{aligned}$$

(39)

Similar to Eq. (36), the tangential segment vector $T_s$ is formed as stated in Eq. (40).

$$\begin{aligned} \textbf{T}_s = \Bigg [ \begin{array}{l} \textbf{a}_1 \\ -(1-\xi )\textbf{a}_1\\ -\xi \textbf{a}_1 \end{array} \Bigg ] \end{aligned}$$

(40)

The combined contribution of $F_t\textbf{T}_s$ and $F_{p}\textbf{N}_s$ was linearised and used when iteratively solving the balance of momentum.

3 Application to shear cutting

The axisymmetric PFEM implementation described in Sect. 2 was applied in modelling of sheet punching processes of the CP1000HD grade. Sheet punching is a type of shear cutting process for creating holes on a sheet metal surface and is commonly used in the forming industry prior to collaring operations. Validation of the model was carried out using sheet punching experiments, conducted in a laboratory environment. To investigate the predictive power of the numerical method, different die diameters were used, thus changing the cutting clearance. The cutting clearance is an important process parameter as it reportedly affects the cut edge morphology and consequently the formability of the sheared edge [1, 4, 67]. Table 6 presents the punching process parameters used in both numerical modelling and in experiments.

Table 6 Cutting clearance and the corresponding punch diameter $d_\textrm{Punch}$, die diameter $d_\textrm{Die}$, punch edge radius $r_\textrm{Edge,Punch}$, die edge radius $r_\textrm{Edge,Die}$ and blank thickness $t_\textrm{Blank}$

A schematic overview of the sheet punching process is shown in Fig. 11. The magnified image shows the cutting tools (dark), the blank holder (green) and the blank (light grey) and the cutting clearance is highlighted. In the models, the tools were considered linear elastic using small strain theory, while the blank was assigned the mixed axisymmetric formulation, the isotropic plasticity model and damage model described in Sects. 2.6, 2.7 and 2.4. The tool edges were assumed circular. The numerical model was solved implicitly with no strain rate dependency or thermomechanical coupling. Enough time steps were needed, both for the damage accumulation described in Sect. 2.4 and for avoiding convergence issues related to negative element volumes. The initial time step size was set sufficiently small to ensure modelling accuracy with respect to the time step-dependent damage accumulation while remain feasible simulation time. Therefore, an initial time step size of $\Delta t=6.667e{-5}$ [s] was used along with $n_\textrm{sub}=1e4$ sub-cycles. However, large contact forces and localised results close to the tool edges required reduction of the simulation time steps in late stages of the simulation.

The minimum element length was set to $h_\textrm{min}=8.5$ [$\upmu$m] to give a fine discretisation in the shear-affected zone and to ensure that mesh size dependency of the damage modelling was diminished. The initial particle distribution of the blank was defined to match $h_\textrm{min}$ close to the tool edges. This ensured minimal addition of particles in localised areas in the initial steps of the simulation, thus avoiding initial results smoothing. The threshold values of the plastic power and damage parameter for fulfilling the particle insertion criteria described in Sect. 2.1.1 were set to $G_\textrm{mech}=0.2$ and $D=0.1$ which made sure that the mesh refinement occurred well in advance of the tool displacement, thus far away from localised areas. Additionally, a Hausdorff value of 0.01 was assigned giving refined curvatures, while the graduation value was set to $h=1.3$ which is the default value. The numerical solutions of the shear-cutting problems were solved using a vectorised MATLAB programme. The analyses were performed on a Dell computer with and Intel Core i7-9700 @ 3.00 GHz processor with 16 GB RAM.

Fig. 11

A schematic overview of the sheet punching set-up, showing the active elements of the sheet punching process, the symmetry axis for the axisymmetric assumption and the moving direction of the punch and blank holder. The magnified image shows a close-up of the axisymmetric cutting plane being numerically modelled and the corresponding cutting clearance

3.1 Experimental procedure

The sheet punching experiments were conducted with a punch speed of 0.05–2 mm/min which corresponds to quasi-static conditions. The morphology of the cut edges in the punched holes was experimentally evaluated using a cut edge inspection system (EISYS), first presented by Larour et al. [68], delivering a 360$^\circ$ panoramic view of the cut edge surface for each cutting clearance. The EISYS system captured several images every 2$^\circ$ of the hole circumference with different lightning configurations as can be seen in Fig. 12. The images were then stitched together and image analysis determined the cut edge parameters.

Fig. 12

360$^\circ$ panoramic pictures with different lightning settings and cut edge surface identification, generated by the EISYS system

In order to experimentally discern the cut edge morphology of the three main shear-cutting stages presented in Fig. 1, interrupted punching experiments were conducted. This procedure enabled experimental observation of the creation of the cut edge formations and the corresponding punch displacement at which they were formed. The cut edge morphologies of the intermediate shear-cutting stages along with the corresponding punch stroke provided supplemental validation results for the numerical modelling, which is commonly limited to the final cut edge. The experiments were performed by stopping the punch at different displacement and investigating the cut edge cross section at 0$^\circ$ and 90$^\circ$ to the rolling direction. As this required an immense amount of work, this was only conducted for a single cutting clearance, 9.0%. The displacement of the interrupted punching experiments is presented in Table 7.

Table 7 Punch displacement and force level at the four stops of the interrupted punching experiments

The sheet punching experiments were conducted using two different machines in different laboratories. For creating the punched holes for circumferential cut edge imaging, a servo-hydraulic clinching machine with 150 kN maximum load was used equipped with a dedicated ISO16630 HET 10 mm hole punching tool [69]. The punching tool is a four-column tool with punch and die coaxiality tolerances of $\pm 5$ $\upmu$m and fitting accuracy of $\pm 5$ $\upmu$m for punch and die inserts, which in total allows of a 1% cutting clearance compliance accuracy. The interrupted punching experiments were conducted with a rigid punching tool mounted on an Instron 5900R electromechanical universal testing machine where the load data were recorded using a 200-kN load cell and the displacement was measured using a linear encoder. The use of different punching machines was due to the more precise force output of the Instron 5900R required for interrupted punching. The experimental punching setups are shown in Fig. 13.

Fig. 13

The experimental punching setups used for producing the validation results, where a shows the servo-hydraulic clinching machine equipped with the ISO16630 HET 10 mm hole punching tool that was used for creation of the panoramic cut edge images and b shows the Instron 5900R electromechanical universal testing machine mounted with a rigid punching tool used for interrupted punching experiments

4 Results and discussion

This section presents the results and validations of the shear cutting simulations introduced in Sect. 3, along with a mesh sensitivity study concerning mesh size-dependent failure modelling and tool contact compatibility. Additionally, a stress-state analysis of a punching simulation is showed.

4.1 Cut edge morphology and crack initiation

By comparing the cut edge morphology between numerical modelling and experiments, validation of the plasticity and damage models controlling the cut edge zone distribution is performed. Figure 14 shows the numerical cut edge cross section and the experimental circumferential cut edge image for 12.1% cutting clearance. The numerical result, in terms of cut edge morphology, is in the range of the experimental variation, thus correlating well with the average distribution of the roll-over depth and the length of the burnish and fracture surfaces. Similarly, Fig. 15 shows a corresponding predictive accuracy for 20.5% cutting clearance comparing the numerical results with experiment. For the case of 27.0% cutting clearance, the numerical model predicts burr formation. Meanwhile, the experimental results show partial burr formation over roughly half of the hole circumference. For the part with burr, the numerical and experimental results show good correlation.

Fig. 14

Numerical axisymmetric cut edge cross-section (left) and experimental hole cut edge morphology as a panoramic image (right) of CP1000HD with 12.1% cutting clearance. The experimental cut edge zones were identified with the EISYS system, and the maximum and minimum cut edge zone lengths are annotated

Fig. 15

Numerical axisymmetric cut edge cross-section (left) and experimental hole cut edge morphology as a panoramic image (right) of CP1000HD with 20.5% cutting clearance. The experimental cut edge zones were identified with the EISYS system, and the maximum and minimum cut edge zone lengths are annotated

Fig. 16

Numerical axisymmetric cut edge cross-section (left) and experimental hole cut edge morphology as a panoramic image (right) of CP1000HD with 27.0% cutting clearance. The experimental cut edge zones were identified with the EISYS system, and the maximum and minimum cut edge zone lengths are annotated

The axisymmetric representation of the sheet punching process is a simplification of the actual process where the cut edge morphology will vary in the circumference of the hole, as seen in the experimental results of Figs. 14, 15 and 16. This circumferential variation of the experimental cut edge morphology is caused by a combination of material anisotropy, tool misalignment and uneven tool radii. However, given the limited anisotropic behaviour of the CP1000HD material, it is more likely that the variations are caused by uneven tool edges as this, along with plasticity, influences the roll-over depth. For the 12.1% and 20.5% cutting clearances seen in Figs. 14 and 15, the variation of the experimental cut edge zone distribution is small. However, variation do still exist, thus comparing the numerical cut edge to the circumferential hole cut edge distribution gives a bigger picture of its correlation than comparing to a single experimental cut edge cross section. Considering the circumferential experimental cut edges, it is obvious that a single experimental cut edge cross section may vary in shape depending on where along the circumference the cross section is extracted, and the comparison to numerical results may therefore be misleading. As seen in Fig. 16, a large burr developed over roughly half of the hole circumference. This means that a slight change of cutting parameters, possibly due to the above-mentioned reasons, changed the effective tool clearance such that an uneven burr formation was created. However, in the numerical model no change in process parameters due to misalignment, uneven tool wear or similar was considered and the model could therefore only predict the results from the intended cutting clearance. Consequently, the burr formation was predicted by the numerical model, which is the most likely outcome of a punching process with such large cutting clearance. Considering the experimental results, it is possible that a 3D model of the sheet punching process could provide even better insight to the shear cutting process, with the drawback of significant increase in computational cost and preprocessing detail. For special cases, such as the partial burr formation event in Fig. 16 such analysis appears necessary. For the lower clearances, the presented modelling approach provides sufficient level of detail for justifying the axisymmetric assumption, especially if simulation time is of any importance.

A comparison in terms of force and punch displacement between the numerical results and experimental counterparts was conducted. This was done for a cutting clearance of 9.0% using the laboratory punching setup shown in Fig. 13b. As seen in Fig. 17, the numerical and experimental force–displacement curves follow each other well throughout the entire punching process. The marks $\times$ and $\bullet$ highlight the points of crack initiation for the experiment and modelling, respectively. The initial part of the experimental force versus displacement curve was corrected regarding the machine and tool compliance, since it was omitted in the numerical model.

Fig. 17

Force versus displacement results from punching experiment (dashed) and numerical modelling (solid) for CP1000HD with 8.99% cutting clearance. The point of experimental crack initiation is marked with $\times$ occurring for Exp. Int. 2, while the numerical fracture initiation is marked with $\bullet$

Figure 17 also shows the punch force versus displacement from four interrupted punching experiments that were interrupted in the vicinity to crack initiation and fracture. At each stop, the cut edge cross section was investigated with a scanning electron microscope (SEM). The first experimental crack was detected for the second interrupted punching experiment, denoted Exp. Int. 2 in Table 7. Figure 18 shows the experimental SEM images along with the corresponding numerical results for Exp. Int. 2, where the crack appears at the die side as highlighted in the green boxes of Fig. 18. Accordingly, at this punch displacement the first failed elements are found in the numerical model. The ability of predicting the point of crack initiation is of high relevance when numerically reproducing a correct cut edge morphology and states the accuracy of the damage model implemented in the PFEM scheme. It is worth mentioning that the numerical representation of the crack is blunter than seen in experiments, which inevitably affects the crack tip stress intensity. The width of the crack is controlled by the mesh size, and a finer discretisation would therefore give a more precise representation of the crack tip loading. However, the computational effort when using even finer elements than in this work significantly increased the simulation time.

Fig. 18

SEM images from the interrupted punching experiment Exp. Int. 2 and corresponding numerical results, showing punch edge results (blue boxes) and die edge results (green boxes). Experimental results are shown for cross sections extracted longitudinal (0$^\circ$) and transversal (90$^\circ$) to the rolling direction (RD)

4.2 Mesh sensitivity

Given the converging stress levels with decreased element size shown in Fig. 7c, it was observed that element sizes equal to or smaller than $h_\textrm{min}=$ 10 $\upmu$m were necessary to get accurate results in the fine mesh areas of the shear-affected zone. However, geometrical aspects of the sheet punching process also affected the upper element size limit. The tool edge radii of the current cutting configurations were 30 $\upmu$m for both punch and die, which enforced a maximum element size of 10 $\upmu$m to avoid severe penetration in the tool edge contact with extreme contact forces and convergence issues as consequences. Such penetration is displayed in Fig. 19a for a $h_\textrm{min}=$ 12 $\upmu$m mesh, showing that the blank elements were too large to comply with the tool edge curvature. Figure 19b, c shows the tool edge contact for a 10 $\upmu$m and 8.5 $\upmu$m mesh, respectively, where less penetration was observed.

Fig. 19

Images showing the punch tool and blank contact using element sizes a $h_\textrm{min}=$ 12 $\upmu$m, b $h_\textrm{min}=$ 10 $\upmu$m and c $h_\textrm{min}=$ 8.5 $\upmu$m. The red area highlights the penetration area between the tool and blank domains

To investigate the mesh sensitivity of the numerical modelling with regard to predicted cut edge morphology, cut edges produced with either $h_\textrm{min}=$ 10 $\upmu$m, 8.5 $\upmu$m, or 5 $\upmu$m SAZ discretisation were compared. Due to the extensive simulation time needed for such investigation, this study was limited to the 9.0% cutting clearance. The comparison of the cut edges is shown in Fig. 20 where it is seen that the cut edge morphologies do not vary significantly using SAZ discretisation between 5 and 10 $\upmu$m. Conducting the analyses in this work using $h_\textrm{min}=$ 8.5 $\upmu$m for the SAZ elements was therefore considered a compromise between obtaining the highest possible resolution results in a reasonable simulation time.

As stated in Sect. 2.1.1, the level of results smoothing is dependent on particle addition or removal. As smoothing is an unwanted modelling implication, this was accounted for in the numerical modelling by using a fine particle distribution in the initial configuration and using particle insertion criteria that ensured particle insertion well in advance of the tool displacement. Particle removal was controlled to not occur in the shear affected zone to preserve the results in this area. However, certain particle addition occurred in vicinity of the tool edges during the simulations, but the smoothing effect from this is considered limited. Quantifying the level of results smoothing is troublesome, but the accuracy in predicting the point of crack initiation presented in Figs. 17 and 18 indicates that the material damage parameter appears well preserved close to the tool edges. This statement is supported by the validations of Figs. 14, 15 and 16. The final cut edge morphology is, except from the roll-over formation, controlled by fracture initiation as this event defines the lengths of the burnish- and fracture surfaces. The lengths of these surfaces were accurately predicted over the entire range of cutting clearances, which suggests that the damage accumulation and fracture initiation remained precise, independent of changing cutting clearance and the variation of stress-states thereof.

4.3 Stress-state analysis

An examination of the blank stress-states during the numerical punching process reveals that most of the deformation and fracture occurred at $\bar{\theta }\approx 0$, indicating a plane strain condition. This is seen in Fig. 21, showing the stress-state adjacent to the die and punch edges as the punching progresses. Additionally, this is displayed in Fig. 22, showing that the shear-affected zone close to tool or crack edges experiences deformation for $\bar{\theta }\approx 0$ during the entire cutting process. The stress triaxiality $\eta$ increases with the progress of the cutting, going from plane strain compression $\eta \approx -0.66$ to tension $\eta \approx 0.5$ as seen in Fig. 23. From these results, it appears that the damage model calibration through tensile testing, presented in Sect. 2.4, can be simplified by omitting the Hole and R15 samples as they deform and fail for $\bar{\theta }>0$. The need of calibrating a failure locus depending on Lode angles smaller or larger than $\bar{\theta }\approx 0$ appears redundant as well. Thus, a failure locus of $\varepsilon _\textrm{eff}^f(\eta ,0)$ calibrated by the Shear and R3.75 samples is sufficient, but additional calibration experiments at plane strain could further enrich the failure locus.

Fig. 20

Cut edge comparison for 9.0% cutting clearance using $h_\textrm{min}=$ 5, 8.5 or 10 $\upmu$m

Fig. 21

Analysis of the blank stress-state in adjacent to the a die edge and b punch edge during the shear-cutting process for 9.0% cutting clearance. The colour bar illustrates the time of stress-state analysis and transition between process stages

Fig. 22

Evolution of the normalised Lode angle parameter $\bar{\theta }$ during the numerical shear-cutting process of 9.0% cutting clearance

Fig. 23

Evolution of the stress triaxiality $\eta$ during the numerical shear-cutting process of 9.0% cutting clearance

5 Conclusion

This work shows how axisymmetric PFEM modelling, with the addition of a ductile damage- and failure model, can successfully reproduce the sheet punching process of an AHSS sheet. Following conclusions are drawn based on the modelling results supported by experimental tests:

• PFEM is an efficient and stable numerical approach to model sheet metal-forming processes involving large material deformation. In the present work, such large deformation is associated with the roll-over and burnish formation during sheet punching. The PFEM procedure ensures good element aspect ratios throughout the modelling of the punching process and can with adequate accuracy reproduce the crack geometry during the fracture process.

• The implementation of a ductile damage model enables the prediction of fracture initiation and propagation following the burnish formation. By this, accurate predictions of the punched edge morphologies over several cutting clearances are possible. This extends the use of PFEM and makes this numerical approach suitable for large mechanical deformation with added ductile failure capabilities.

• Due to the preservation of the result variables in the PFEM procedure, the presented shear-cutting modelling approach serves as an accurate numerical tool for study of the sheared edge damage, as local cut edge results may affect large-scale formability properties.

• The accurate force prediction of the PFEM punching model provides the possibility to analyse how tool shapes or tool materials affect the shear-cutting process. By this, tool optimisation is possible with respect to, i.e. process forces or tool wear.

• Given the experimental circumferential variation of the cut edge zones, the authors of this work further declare that 3D PFEM modelling of the punching process should be investigated. Even though the axisymmetric results give a good representation of the sheared edge damage, 3D results could provide valuable inputs for modelling of subsequent forming operations.

Appendices

Radial return mapping algorithm

The radial return mapping algorithm for iterative calculation of the Cauchy stress tensor, which is affected by the damage parameter $\tilde{D}$.

• 1. Initiate ${\varepsilon }_{p,n}$ and $\textbf{n}_n$.

• 2. Define $f^\textrm{trial}_{n+1}$ according to Equation (A1), where $\tilde{D}$ is related to the ductile damage model presented in Sect. 2.4

  $$\begin{aligned} f^\textrm{trial}_{n+1}=\parallel \textbf{s}^\textrm{trial}_{n+1}\parallel -\sqrt{\frac{2}{3}}(c_1+c_2\cdot \alpha _{n}+c_3\cdot (1-e^{c_4\cdot \alpha _{n}}))(1-\tilde{D}_n) \end{aligned}$$

  (A1)

  If $f^\textrm{trial}_{n+1}\le 0$: Elastic deformation, exit scheme

  Else

• 3. Newton–Raphson iteration, while $R_{n+1}>$ Tol & $N_\textrm{iter}<$ $N_\textrm{max,iter}$

  • Define consistency equations:

    $$\begin{aligned} \bar{\mu }= & {} \frac{\mu }{3}tr(\textbf{b}_{n+1}^{trial}) \end{aligned}$$

    (A2a)
    $$\begin{aligned} f'= & {} 2 \bar{\mu } + \frac{2}{3}(c_2+c_3\cdot c_4 e^{-c_4\cdot \alpha _{n}})(1-\tilde{D}) \end{aligned}$$

    (A2b)
    $$\begin{aligned} \Delta ^2\gamma _{n+1}= & {} f_{n+1}^\textrm{trial}/f' \end{aligned}$$

    (A2c)

  • Determine plastic multiplier and update the plastic strains

    $$\begin{aligned} \Delta \gamma _{n+1}= & {} \Delta \gamma _n+\Delta ^2\gamma _{n+1} \end{aligned}$$

    (A3a)
    $$\begin{aligned} \alpha _{n+1}= & {} \alpha _n+\sqrt{\frac{2}{3}}\Delta \gamma _{n+1} \end{aligned}$$

    (A3b)

  • Calculate the iteration residual $R_{n+1}$ according to Eq. (A4)

    $$\begin{aligned} R_{n+1}= & {} \parallel \textbf{s}^\textrm{trial}_{n+1}\parallel -2\bar{\mu }\Delta \gamma _{n+1}\nonumber \\{} & {} -\sqrt{\frac{2}{3}}(c_1+c_2\cdot \alpha _{n+1}\nonumber \\{} & {} +c_3\cdot (1-e^{c_4\cdot \alpha _{n+1}}))(1-\tilde{D}) \end{aligned}$$

    (A4)

  • If the objective is fulfilled, update the state variables and perform next implicit time integration step.

Axisymmetric FE-formulation

The axisymmetric representation of the matrices in Sect. 2.6 is presented in this Appendix along with the corresponding expression for plane strain assumption. This is presented for stating the differences between the axisymmetric and plane strain assumption regarding spatial discretisation.

Beginning with the Cauchy stress tensor written in matrix form, $\hat{\bar{\sigma }}$, the apparent difference between axisymmetry and plane strain assumption is constituted by the out-of-plane stress component in axisymmetry compared to plane strain. This is manifested by a expansion of the Cauchy stress tensor $\hat{\bar{\sigma }}_\textrm{axi}$, where a term associated with out-of-plane stress component is added, thus expanding the size of Cauchy stress tensor $\hat{\bar{\sigma }}_\textrm{axi}$ to a 5-by-5 matrix compared to the 4-by-4 plane strain tensor. This is shown in Eq. (B5).

$$\begin{aligned} \hat{\bar{\sigma }}_\textrm{axi}= & {} \left[ \begin{array}{lllll} \bar{\sigma }_{11} &{}\quad \bar{\sigma }_{12} &{}\quad 0 &{}\quad 0 &{}\quad \quad 0\\ \bar{\sigma }_{21} &{}\quad \bar{\sigma }_{22 }&{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \bar{\sigma }_{33} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \bar{\sigma }_{11} &{}\quad \bar{\sigma }_{12} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \bar{\sigma }_{21} &{}\quad \bar{\sigma }_{22} \\ \end{array}\right] \hspace{2cm}\nonumber \\ \hat{\bar{\sigma }}_{ps}= & {} \left[ \begin{array}{llll} \bar{\sigma }_{11} &{}\quad \bar{\sigma }_{12} &{}\quad 0 &{}\quad 0 \\ \bar{\sigma }_{21} &{}\quad \bar{\sigma }_{22 }&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \bar{\sigma }_{11} &{}\quad \bar{\sigma }_{12} \\ 0 &{}\quad 0 &{}\quad \bar{\sigma }_{21} &{}\quad \bar{\sigma }_{22} \\ \end{array}\right] \end{aligned}$$

(B5)

As for the deformation gradient $\textbf{F}$, the out-of-plane deformation in axisymmetric assumption requires an additional row to account for the circumferential deformation.

$$\begin{aligned} \textbf{F}_\textrm{axi}=\left[ \begin{array}{lll} \frac{\partial x}{\partial X} &{}\quad \frac{\partial x}{\partial Y} &{}\quad 0 \\ \frac{\partial y}{\partial X} &{}\quad \frac{\partial y}{\partial Y} &{}\quad 0 \\ 0 &{}\quad 0 &{} \quad \frac{ x}{ X} \end{array} \right] \hspace{2cm} \textbf{F}_{ps}=\left[ \begin{array}{ll} \frac{\partial x}{\partial X} &{} \frac{\partial x}{\partial Y} \\ \frac{\partial y}{\partial X} &{} \frac{\partial y}{\partial Y} \\ \end{array} \right] \end{aligned}$$

(B6)

In accordance, the displacement–strain matrix $\textbf{B}$ requires an extra row associated with the out-of-plane strain in axisymmetric representation compared to plane strain, as shown in Eq. (B7).

$$\begin{aligned} \textbf{B}_{\textbf{u},\textrm{axi}}=\sum _{i=1}^3\left[ \begin{array}{ll} \frac{\partial N_i}{\partial x} &{} 0 \\ 0 &{} \frac{\partial N_i}{\partial y} \\ \frac{ N_i}{ x} &{} 0 \\ \frac{\partial N_i}{\partial y} &{} \frac{\partial N_i}{\partial x}\\ \end{array}\right] \hspace{2cm} \textbf{B}_{\textbf{u},ps}=\sum _{i=1}^3\left[ \begin{array}{ll} \frac{\partial N_i}{\partial x} &{} 0 \\ 0 &{} \frac{\partial N_i}{\partial y} \\ \frac{\partial N_i}{\partial y} &{} \frac{\partial N_i}{\partial x}\\ \end{array}\right] \end{aligned}$$

(B7)

Similarly, the $\textbf{G}$-matrices differs with regards to the out-of-plane stress, such that an additional row for the circumferential stress component $\sigma _{33}$ is considered. This forms the following expressions for $\textbf{G}$.

$$\begin{aligned} \textbf{G}_\textrm{axi}=\sum _{i=1}^3\left[ \begin{array}{ll} \frac{\partial N_i}{\partial x} &{}\quad 0 \\ \frac{\partial N_i}{\partial y} &{}\quad 0 \\ \frac{N_i}{x} &{}\quad 0 \\ 0 &{}\quad \frac{\partial N_i}{\partial x}\\ 0 &{}\quad \frac{\partial N_i}{\partial y}\\ \end{array}\right] \hspace{2cm} \textbf{G}_{ps}=\sum _{i=1}^3\left[ \begin{array}{ll} \frac{\partial N_i}{\partial x} &{}\quad 0 \\ \frac{\partial N_i}{\partial y} &{}\quad 0 \\ 0 &{}\quad \frac{\partial N_i}{\partial x}\\ 0 &{}\quad \frac{\partial N_i}{\partial y}\\ \end{array}\right] \end{aligned}$$

(B8)

The mass matrix with respect to displacement $\textbf{M}_\textbf{u}$ is of same shape regardless of plane strain or axisymmetry. However, the axisymmetric representation takes radial position into account as follows:

$$\begin{aligned}{} & {} \textbf{M}_{\textbf{u},axi}=\frac{\pi \rho A}{10}\nonumber \\{} & {} \left[ \begin{array}{llllll} \frac{4}{3}x_1+2\bar{x} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_3}{3} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_2}{3}&{}\quad 0\\ &{}\quad \frac{4}{3}x_1+2\bar{x} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_3}{3} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_2}{3} \\ &{}\quad &{}\quad \frac{4}{3}x_2+2\bar{x} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_1}{3} &{}\quad 0\\ &{}\quad &{}\quad &{}\quad \frac{4}{3}x_2+2\bar{x} &{}\quad 0 &{}\quad 2\bar{x}-\frac{x_1}{3}\\ &{}\quad &{}\quad &{}\quad &{}\quad \frac{4}{3}x_3+2\bar{x} &{}\quad 0 \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad \frac{4}{3}x_3+2\bar{x} \end{array}\right] \nonumber \\ \textbf{M}_{\textbf{u},ps}= & {} \frac{t \rho A}{12}\left[ \begin{array}{llllll} 2 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1&{}\quad 0\\ &{}\quad 2 &{}\quad 0 &{}\quad 1&{}\quad 0 &{}\quad 1 \\ &{}\quad &{}\quad 2 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ &{}\quad &{}\quad &{}\quad 2 &{}\quad 0 &{}\quad 1\\ &{}\quad &{}\quad &{}\quad &{}\quad 2 &{}\quad 0 \\ &{}\quad &{}\quad &{}\quad &{}\quad &{}\quad 2 \end{array}\right] \end{aligned}$$

(B9)

where $x_1$ to $x_3$ denotes the nodal radial coordinates and $\bar{x}=\frac{x_1 + x_2 + x_3}{3}$. The mass matrix associated with the pressure term, $\textbf{M}_\textbf{p}$, is formed similarly to $\textbf{M}_\textbf{u}$ for both axisymmetric assumption and plane strain, but all diagonal zero terms are removed such that $\textbf{M}_\textbf{p}$ is a 3-by-3 matrix.

To fulfil stability conditions associated with the mixed FE-formulations, a pressure stability term is subtracted from Eq. (8) according to the work by Dávalos et al. [70]. The stabilisation term is expressed as follows, where $\alpha$ is a dimensionless stabilisation parameter, $\upmu$ is the Lamé parameter and $A^e$ is the element area:

$$\begin{aligned} {\psi }_{axi}=\frac{\alpha A^e}{36\mu }\left[ \begin{array}{lll} 2 &{}\quad -1 &{}\quad -1 \\ -1 &{}\quad 2 &{}\quad -1 \\ -1 &{}\quad -1 &{}\quad 2 \end{array} \right] \end{aligned}$$

(B10)