Skip to main content
SpringerLink
Log in

Analysis of a \(\varvec{P}_1\oplus \varvec{RT}_0\) finite element method for linear elasticity with Dirichlet and mixed boundary conditions

  • Published:
Advances in Computational Mathematics Aims and scope Submit manuscript

Abstract

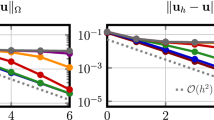
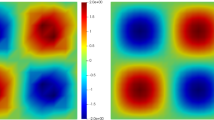
In this paper, we investigate a low-order robust numerical method for the linear elasticity problem. The method is based on a Bernardi–Raugel-like \(\varvec{H}(\textrm{div})\)-conforming method proposed first for the Stokes flows in [Li and Rui, IMA J. Numer. Anal. 42 (2022) 3711–3734]. Therein, the lowest-order \(\varvec{H}(\textrm{div})\)-conforming Raviart–Thomas space (\(\varvec{RT}_0\)) was added to the classical conforming \(\varvec{P}_1\times P_0\) pair to meet the inf-sup condition, while preserving the divergence constraint and some important features of conforming methods. Due to the inf-sup stability of the \(\varvec{P}_1\oplus \varvec{RT}_0\times P_0\) pair, a locking-free elasticity discretization with respect to the Lamé constant \(\lambda \) can be naturally obtained. Moreover, our scheme is gradient-robust for the pure and homogeneous displacement boundary problem, that is, the discrete \(\varvec{H}^1\)-norm of the displacement is \(\mathcal {O}(\lambda ^{-1})\) when the external body force is a gradient field. We also consider the mixed displacement and stress boundary problem, whose \(\varvec{P}_1\oplus \varvec{RT}_0\) discretization should be carefully designed due to a consistency error arising from the \(\varvec{RT}_0\) part. We propose both symmetric and nonsymmetric schemes to approximate the mixed boundary case. The optimal error estimates are derived for the energy norm and/or \(\varvec{L}^2\)-norm. Numerical experiments demonstrate the accuracy and robustness of our schemes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

All data generated or analyzed during this study are included in this manuscript.

References

  1. Akbas, M., Gallouët, T., Gaßmann, A., et al.: A gradient-robust well-balanced scheme for the compressible isothermal Stokes problem. Comput. Methods. Appl. Mech. Engrg. 367(113), 069 (2020)

    MathSciNet  Google Scholar 

  2. Arnold, D., Falk, R., Winther, R.: Mixed finite element methods for linear elasticity with weakly imposed symmetry. Math. Comp. 76(260), 1699–1723 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  3. Arnold, D.N., Winther, R.: Mixed finite elements for elasticity. Numer. Math. 92, 401–419 (2002)

    Article  MathSciNet  Google Scholar 

  4. Arnold, D.N., Brezzi, F., Cockburn, B., et al.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002)

    Article  MathSciNet  Google Scholar 

  5. Babuška, I., Suri, M.: Locking effects in the finite element approximation of elasticity problems. Numer. Math. 62(1), 439–463 (1992)

    Article  MathSciNet  Google Scholar 

  6. Basava, S.R., Wollner, W.: Gradient robust mixed methods for nearly incompressible elasticity. J. Sci. Comput. 95, 93 (2023)

    Article  MathSciNet  Google Scholar 

  7. Bernardi, C., Raugel, G.: Analysis of some finite elements for the Stokes problem. Math. Comp. 44(169), 71–79 (1985)

    Article  MathSciNet  Google Scholar 

  8. Boffi, D., Brezzi, F., Fortin, M.: Mixed finite element methods and applications, Springer Series in Computational Mathematics, vol. 44. Springer, Heidelberg (2013)

    Book  Google Scholar 

  9. Brenner, S.C., Scott, L.R.: The mathematical theory of finite element methods, Texts in Applied Mathematics, vol. 15, 3rd (edn.) Springer, New York (2008)

  10. Brenner, S.C., Sung, L.Y.: Linear finite element methods for planar linear elasticity. Math. Comp. 59(200), 321–338 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  11. Chiumenti, M., Valverde, Q., De Saracibar, C.A., et al.: A stabilized formulation for incompressible elasticity using linear displacement and pressure interpolations. Comput. Methods. App. Mech. Engrg. 191(46), 5253–5264 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  12. Cockburn, B., Shi, K.: Superconvergent HDG methods for linear elasticity with weakly symmetric stresses. IMA J. Numer. Anal. 33(3), 747–770 (2013)

    Article  MathSciNet  Google Scholar 

  13. Cockburn, B., Kanschat, G., Schötzau, D.: A note on discontinuous Galerkin divergence-free solutions of the Navier-Stokes equations. J. Sci. Comput. 31(1–2), 61–73 (2007)

    Article  MathSciNet  Google Scholar 

  14. Cook, R.D.: Improved two-dimensional finite element. J. Structural. Division 100(9), 1851–1863 (1974)

    Article  Google Scholar 

  15. Crouzeix, M., Raviart, P.A.: Conforming and nonconforming finite element methods for solving the stationary Stokes equations i. Revue française d’automatique informatique recherche opérationnelle Mathématique 7(R3), 33–75 (1973)

    Article  MathSciNet  Google Scholar 

  16. Fu, G., Lehrenfeld, C., Linke, A., et al.: Locking-free and gradient-robust H(div)-conforming HDG methods for linear elasticity. J. Sci. Comput. 86(3), 1–30 (2021)

    Article  MathSciNet  Google Scholar 

  17. Gatica, G.N.: Analysis of a new augmented mixed finite element method for linear elasticity allowing \({\mathbb{R}\mathbb{T}}_{0}-\mathbb{P}_{1}-\mathbb{P}_{0}\) approximations. ESAIM: Math. Model. Numer. Anal. 40(1), 1–28 (2006)

  18. Gatica, G.N., Gatica, L.F., Stephan, E.P.: A dual-mixed finite element method for nonlinear incompressible elasticity with mixed boundary conditions. Comput. Methods. Appl. Mech. Engrg. 196(35–36), 3348–3369 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  19. Gatica, G.N., Márquez, A., Meddahi, S.: An augmented mixed finite element method for 3D linear elasticity problems. J. Comput. Appl. Math. 231(2), 526–540 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  20. Hansbo, P., Larson, M.G.: Discontinuous Galerkin and the Crouzeix–Raviart element: application to elasticity. ESAIM: Math. Model. Numer. Anal. 37(1), 63–72 (2003)

  21. Hu, J.: Finite element approximations of symmetric tensors on simplicial grids in \(\mathbb{R}^{n}\): The higher order case. J. Comput. Math. pp. 283–296 (2015)

  22. Hu, J., Schedensack, M.: Two low-order nonconforming finite element methods for the Stokes flow in three dimensions. IMA J. Numer. Anal. 39(3), 1447–1470 (2018)

    Article  MathSciNet  CAS  Google Scholar 

  23. Hu, J., Zhang, S.: Finite element approximations of symmetric tensors on simplicial grids in \(\mathbb{R} ^n\): the lower order case. Math. Model. Method Appl. Sci. 26(09), 1649–1669 (2016)

    Article  Google Scholar 

  24. Jin, S.: Efficient asymptotic-preserving (ap) schemes for some multiscale kinetic equations. SIAM J. Sci. Comput. 21(2), 441–454 (1999)

    Article  MathSciNet  Google Scholar 

  25. John, V.: Finite element methods for incompressible flow problems, Springer Series in Computational Mathematics, vol. 51. Springer, Cham (2016)

    Book  Google Scholar 

  26. John, V., Linke, A., Merdon, C., et al.: On the divergence constraint in mixed finite element methods for incompressible flows. SIAM Rev. 59(3), 492–544 (2017)

    Article  MathSciNet  Google Scholar 

  27. Kouhia, R., Stenberg, R.: A linear nonconforming finite element method for nearly incompressible elasticity and Stokes flow. Comput. Methods Appl. Mech. Engrg. 124(3), 195–212 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  28. Lamichhane, B.P.: Inf-sup stable finite-element pairs based on dual meshes and bases for nearly incompressible elasticity. IMA J. Numer. Anal. 29(2), 404–420 (2009)

    Article  MathSciNet  Google Scholar 

  29. Li, X., Rui, H.: A low-order divergence-free H(div)-conforming finite element method for Stokes flows. IMA J. Numer. Anal. 42(4), 3711–3734 (2022)

    Article  MathSciNet  Google Scholar 

  30. Linke, A.: On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime. Comput. Methods. Appl. Mech. Engrg. 268, 782–800 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  31. Linke, A., Merdon, C.: Pressure-robustness and discrete Helmholtz projectors in mixed finite element methods for the incompressible Navier-Stokes equations. Comput. Methods. Appl. Mech. Engrg. 311, 304–326 (2016). https://doi.org/10.1016/j.cma.2016.08.018

    Article  ADS  MathSciNet  Google Scholar 

  32. Linke, A., Matthies, G., Tobiska, L.: Robust arbitrary order mixed finite element methods for the incompressible Stokes equations with pressure independent velocity errors. ESAIM: Math. Model. Numer. Anal. 50(1), 289–309 (2016)

  33. Malkus, D.S., Hughes, T.J.: Mixed finite element methods-reduced and selective integration techniques: a unification of concepts. Comput. Methods. Appl. Mech. Engrg. 15(1), 63–81 (1978)

    Article  ADS  Google Scholar 

  34. Phillips, P.J., Wheeler, M.F.: Overcoming the problem of locking in linear elasticity and poroelasticity: an heuristic approach. Comput. Geosci. 13, 5–12 (2009)

    Article  Google Scholar 

  35. Qiu, W., Shen, J., Shi, K.: An HDG method for linear elasticity with strong symmetric stresses. Math. Comp. 87(309), 69–93 (2018)

    Article  MathSciNet  Google Scholar 

  36. Rui, H., Sun, M.: A locking-free finite difference method on staggered grids for linear elasticity problems. Comput. Math. Appl. 76(6), 1301–1320 (2018)

    Article  MathSciNet  Google Scholar 

  37. Wang, J., Ye, X.: New finite element methods in computational fluid dynamics by H(div) elements. SIAM J. Numer. Anal. 45(3), 1269–1286 (2007)

    Article  MathSciNet  Google Scholar 

  38. Wihler, T.: Locking-free adaptive discontinuous Galerkin FEM for linear elasticity problems. Math. Comp. 75(255), 1087–1102 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  39. Yi, S.Y.: A study of two modes of locking in poroelasticity. SIAM J. Numer. Anal. 55(4), 1915–1936 (2017)

    Article  MathSciNet  Google Scholar 

  40. Yi, S.Y.: A lowest-order weak Galerkin method for linear elasticity. J. Comput. Appl. Math. 350, 286–298 (2019)

    Article  MathSciNet  Google Scholar 

  41. Yi, S.Y., Lee, S., Zikatanov, L.: Locking-free enriched Galerkin method for linear elasticity. SIAM J. Numer. Anal. 60(1), 52–75 (2022)

    Article  MathSciNet  Google Scholar 

  42. Zdunek, A., Neunteufel, M., Rachowicz, W.: On pressure robustness and independent determination of displacement and pressure in incompressible linear elasticity. Comput. Methods. Appl. Mech. Engrg. 403(115), 714 (2023)

    MathSciNet  Google Scholar 

  43. Zhang, M., Zhang, S.: A 3D conforming-nonconforming mixed finite element for solving symmetric stress Stokes equations. Int. J. Numer. Anal. Model. 14(4–5), 730–743 (2017)

    MathSciNet  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (Grant 12131014).

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, China

    Hongpeng Li, Xu Li & Hongxing Rui

  2. Eastern Institute for Advanced Study, Eastern Institute of Technology, Ningbo, 315200, China

    Xu Li

Authors
  1. Hongpeng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongxing Rui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongxing Rui.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Communicated by: Lourenco Beirao da Veiga

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, H., Li, X. & Rui, H. Analysis of a \(\varvec{P}_1\oplus \varvec{RT}_0\) finite element method for linear elasticity with Dirichlet and mixed boundary conditions. Adv Comput Math 50, 13 (2024). https://doi.org/10.1007/s10444-024-10107-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10444-024-10107-w

Keywords

Mathematics Subject Classification (2010)

Mathematics Subject Classification (2010)

Search

Navigation