Deflection angle and shadow of slowly rotating black holes in galactic nuclei

Abstract

In this paper, we construct the slowly rotating case of an asymptotically flat supermassive black hole embedded in dark matter using Newman–Janis procedure. Our analysis is carried with respect to the involved parameters including the halo total mass M and the galaxy’s lengthscale $a_0$. Concretly, we investigate the dark matter impact on the effective potential and the photon sphere. In particular, we find that the lengthscale $a_0$ controles such potential values. Indeed, for low $a_0$ values, we find that the halo total mass M decreases the potential values significantly while for high $a_0$ values such impact is diluted. Regarding the shadow aspects, we show that the shadow size is much smaller for high values of $a_0$ while the opposite effect is observed when the halo total mass M is increased. By comparing our case to the slowly rotating case, we notice that the former exhibits a shadow shifted from its center to the left side. Finally, we compute the deflection angle in the weak-limit approximation and inspect the dark matter parameters influence. By ploting such quantity, we observe that one should expect lower bending angle values for black holes in galactic nuclei.

A: Energy-momentum, Einstein tensor and energy conditions

1.1 A.1: Energy-momentum and Einstein tensors

The energy-momentum tensor for a general spherically symmetric metric of the form

$$\begin{aligned} ds^2=-f(r) dt^2 + \frac{dr^2}{g(r)}+r^2 \left( d\theta ^2 + \sin ^2\theta d\phi ^2 \right) , \end{aligned}$$

(A.1)

can be given by

$$\begin{aligned} T^{t}_{\, \, \, \, t}=-\rho , \quad T^{r}_{\, \, \, \, r}=p_r,\quad T^{\theta }_{\, \, \, \, \theta }= T^{\phi }_{\, \, \, \, \phi }=p_T. \end{aligned}$$

(A.2)

To determine the explicit expression of the energy-momentum tensor, we rewrite the metric functions f(r) and g(r) in the following way

$$\begin{aligned} g(r)=1-\frac{2m(r)}{r}, \quad f(r)=\frac{g(r)}{\left[ j(r)\right] ^2}, \end{aligned}$$

(A.3)

with

$$\begin{aligned} j(r)=\sqrt{1-\frac{2 M r}{(a_0+r)^2}\left( 1-\frac{2M_{BH}}{r} \right) } \, e^{\frac{\pi }{2}\sqrt{\frac{M}{2a_0-M+4M_{BH}}}-\sqrt{\frac{M}{2a_0-M+4M_{BH}}}\arctan \left( \frac{r+a_0-M}{\sqrt{M\left( 2a_0-M+4M_{BH} \right) }} \right) }. \end{aligned}$$

(A.4)

Using the known definitions of $\rho , p_r$ and $p_T$, we obtain

$$\begin{aligned} \rho&=\frac{m'}{4 \pi r^2}=\frac{M \left( a_0+2M_{BH}\right) \left( 1-\frac{2M_{BH}}{r} \right) }{2\pi r\left( r+a_0\right) ^3}, \end{aligned}$$

(A.5)

$$\begin{aligned} p_r&=-\frac{m'}{4 \pi r^2}-\frac{(r-2m)j'}{4 \pi r^2 j}=0, \end{aligned}$$

(A.6)

$$\begin{aligned} p_T&=-\frac{m''}{4 \pi r^2}+\frac{3r m'-r-m}{8 \pi r^2 j} j'+\frac{(r-2m)(j')^2}{4 \pi r j^2}-\frac{r-2m}{8 \pi r j}j'', \end{aligned}$$

(A.7)

$$\begin{aligned}&=\frac{M(a_0+2M_{BH})(a_0^2 M_{BH}+2a_0 M_{BH} r+ M_{BH}r^2+M\left( r-2M_{BH} \right) ^2 )}{4\pi r^2\left( a_0+r\right) ^3 \left( a_0^2+4M M_{BH}+2a_0r-2Mr+r^2\right) }, \end{aligned}$$

(A.8)

where $m'$ is associated to the first derivative of m while $m''$ is the second derivative. Thus, the non-rotating energy-momentum tensor is

$$\begin{aligned} T^{\mu }_{\, \, \, \, \nu }=diag\left( -\rho ,0,p_T,p_T\right) . \end{aligned}$$

(A.9)

The Newman–Janis algorithm application on the metric (A.1) give rise to a slowly rotating black hole with a spacetime described by the following metric

$$\begin{aligned} ds^2=-f(r) dt^2 + \frac{dr^2}{g(r)}+h(r) d\Omega ^2-2a \, e(r) \sin ^2 \theta dt d\phi . \end{aligned}$$

(A.10)

However, the energy-momentum tensor of such solution is different from the non-rotating one given by (A.9). Using the function j(r), we can rewrite the metric (A.10) as

$$\begin{aligned} ds^2=-f(r) dt^2 + \frac{dr^2}{g(r)}+h(r) d\Omega ^2-2a \left( \frac{1}{j(r)} -\frac{g(r)}{j(r)^2} \right) \sin ^2 \theta dt d\phi . \end{aligned}$$

(A.11)

To establish the expression of the energy-momentum tensor components, we introduce an orthonormal tetrad $e^\alpha _{\widehat{\alpha }}$ adapted to the metric (A.11)

$$\begin{aligned} e^\alpha _{\widehat{\alpha }}=\begin{pmatrix} \frac{j}{\sqrt{1-\frac{2m}{r}}} &{} 0 &{} 0 &{} \frac{a \sin \theta }{r} \\ 0 &{} \sqrt{1-\frac{2m}{r}} &{} 0 &{} 0\\ 0 &{} 0 &{} \frac{1}{r} &{} 0 \\ \frac{a}{r^2 \sqrt{1-\frac{2m}{r}}} &{} 0 &{} 0 &{} \frac{1}{r \sin \theta } \end{pmatrix}, \end{aligned}$$

(A.12)

such that $g_{\widehat{\alpha } \widehat{\beta }}=g_{\alpha \beta } \, e^\alpha _{\, \, \, \, \widehat{\alpha }} e^\beta _{ \, \, \, \,\widehat{\beta }}=diag(-1,1,1,1)$. In this way, the energy momentum tensor component forms become simple. However, the defined tetrad is not the principale frame of the energy momentum where it is diagonal. In this base, the latter is given by

$$\begin{aligned} T_{\widehat{\mu } \widehat{\nu }}=\begin{pmatrix} -\widehat{u}_0 &{} 0 &{} 0 &{} \widehat{\sigma }_{30} \\ 0 &{} \widehat{u}_1 &{} \widehat{\sigma }_{12} &{} 0\\ 0 &{} \widehat{\sigma }_{12} &{} \widehat{u}_2 &{} 0 \\ \widehat{\sigma }_{30} &{} 0 &{} 0 &{} \widehat{u}_3 \end{pmatrix}, \end{aligned}$$

(A.13)

where $\widehat{\sigma }_{12}=\left( r\sqrt{1-\frac{2\,m}{r}} \right) \sin \theta \, \,\widehat{u}_{12}, \widehat{\sigma }_{30}=\left( r\sqrt{1-\frac{2\,m}{r}} \right) \sin \theta \, \, \widehat{u}_{30}$ and the quantities $\widehat{u}_{i}, \widehat{u}_{ij}$ depend on m, j and their derivatives $m', m'', j', j''$. According to [107], the final expressions of the energy-momentum components can be obtained as a function of $\widehat{u}_{i}, \widehat{u}_{ij}$. In the case of a slowly rotating black hole, higher orders in a should be omitted, yielding

$$\begin{aligned} \widehat{u}_{0}&=-\frac{m'}{4 \pi r^2}=-\rho , \end{aligned}$$

(A.14)

$$\begin{aligned} \widehat{u}_{1}&=-\frac{1}{4 \pi r^2 j}\left( j m'+j'(r-2m) \right) =0, \end{aligned}$$

(A.15)

$$\begin{aligned} \widehat{u}_{2}&=\frac{1}{8 \pi r^2 j^2}\left( -rj m''-rj(r-2m)j''+2r(r-2m)-j(m+r-3rm')j' \right) , \end{aligned}$$

(A.16)

$$\begin{aligned}&=\frac{M(a_0+2M_{BH})(a_0^2 M_{BH}+2a_0 M_{BH} r+ M_{BH}r^2+M\left( r-2M_{BH} \right) ^2 )}{4\pi r^2\left( a_0+r\right) ^3 \left( a_0^2+4M M_{BH}+2a_0r-2Mr+r^2\right) }=p_T, \nonumber \\ \widehat{u}_{3}&=\frac{1}{8 \pi r^2 j^2}\left( r^2(2j'-j j'')+r(3j j' m'-j^2 m''-4 j'm +2 j j'' m-j j')-j j' m \right) , \end{aligned}$$

(A.17)

$$\begin{aligned}&=\frac{M(a_0+2M_{BH})(a_0^2 M_{BH}+2a_0 M_{BH} r+ M_{BH}r^2+M\left( r-2M_{BH} \right) ^2 )}{4\pi r^2\left( a_0+r\right) ^3 \left( a_0^2+4M M_{BH}+2a_0r-2Mr+r^2\right) }=p_T, \nonumber \\ \widehat{u}_{30}&= \frac{a}{16 \pi r^4 j^2}\left( -2r j j'+r^2 j^2-r^2j j''-2j(j-1) \right) , \end{aligned}$$

(A.18)

$$\begin{aligned}&=\frac{a}{16 \pi r^4 (a_0+r)^2 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^2} \nonumber \\&\times \left\{ 4 M^2 r^2 (a_0+2 M_{BH})^2+M^2 r^2 (a_0+4M_{BH}-r)^2-2 M^2 r^2 (a_0+r) (a_0+4 M_{BH}-r)\right. \nonumber \\&-2 M r^2 (2 a_0+6 M_{BH}-r) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) \nonumber \\&-2 M r^2 (a_0+r)^2 (a_0-M+r) \nonumber \\&-2 ( a_0+r)^2 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^2 -M^2 r^2 (a_0+r)^2 \nonumber \\&+4 M r^3 (a_0+2 M_{BH}) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \nonumber \\&\times \exp \left( \frac{1}{2} \sqrt{\frac{M}{2 a_0-M+4 M_{BH}}} \left( \pi -2 \arctan \left( \frac{a_0-M+r}{\sqrt{M (2 a_0-M+4 M_{BH})}}\right) \right) \right) \nonumber \\&+2 (a_0+r)^3 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \nonumber \\&\left. \times \exp \left( -\frac{1}{2} \sqrt{\frac{M}{2a_0-M+4 M_{BH}}} \left( \pi -2 \arctan \left( \frac{a_0-M+r}{\sqrt{M (2a_0-M+4 M_{BH})}}\right) \right) \right) \right\} , \nonumber \\ \widehat{u}_{12}&=0. \end{aligned}$$

(A.19)

Regarding the components of the energy-momentum tensor, we obtain

$$\begin{aligned} T^t_{\, \, \, \, t}&=\frac{1}{r^2 j} \left( a \sin ^2 \theta \left( r^2(1+j)-2rm \right) \widehat{u}_{30}+r^4 j^2 \widehat{u}_{0} \right) \simeq \widehat{u}_{0}=-\rho , \end{aligned}$$

(A.20)

$$\begin{aligned} T^t_{\, \, \, \, \phi }&=\frac{\sin ^2 \theta }{r^2 j} \left( a r^2 j \left( \widehat{u}_{3} -\widehat{u}_{0} \right) -r^4 j^2 \widehat{u}_{30} \right) , \end{aligned}$$

(A.21)

$$\begin{aligned}&= \frac{a \sin ^2(\theta )}{16 \pi r^2 (a_0+r)^3 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^2} \times \nonumber \\&\quad \left\{ \exp \left( \alpha \right) \sqrt{(a_0+r)^2+M (4 M_{BH}-2 r)} \right. \nonumber \\&\quad \times \left[ -4 M^2 r^2 (a_0+2 M_{BH})^2-M^2 r^2 (a_0+4 M_{BH}-r)^2\right. \nonumber \\&\quad +2 M^2 r^2 (a_0+r) (a_0+4 M_{BH}-r) \nonumber \\&\quad +2 M r^2 (2 a_0+6 M_{BH}-r) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) \nonumber \\&\quad +2 M r^2 (a_0+r)^2 (a_0-M+r) \nonumber \\&\quad +M^2 r^2 (a_0+r)^2 +2 (a_0+r)^2 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^2 \nonumber \\&\quad -2 (a_0+r)^3 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \times \exp \left( -\alpha \right) \nonumber \\&\quad \left. -4 M r^3 (a_0+2M_{BH}) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \times \exp \left( \alpha \right) \right] \nonumber \\&\quad +4 M (a_0+2 M_{BH}) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) \nonumber \\&\quad \times \left. \left( a_0^2 (2 r-3 M_{BH})+a_0 \left( 4 r^2-6 M_{BH} r\right) -3 M (r-2 M_{BH})^2+r^2 (2 r-3 M_{BH})\right) \right\} , \nonumber \\ T^\phi _{\, \, \, \, t}&= \frac{1}{r^2 j}\left( r ( r-2m) \widehat{u}_{30}-a(\widehat{u}_3 - \widehat{u}_0)\right) , \end{aligned}$$

(A.22)

$$\begin{aligned}&= \frac{a \exp \left( -\alpha \right) }{16 \pi r^5 (a_0+r)^3 \left( a_0^2+2a_0 r+4 M M_{BH}-2 M r+r^2\right) \sqrt{(a_0+r)^2+M (4M_{BH}-2 r)}} \times \nonumber \\&\quad \left\{ 4 M r (a_0+2 M_{BH}) (a_0+r) \left[ a_0^2 (3 M_{BH}-2 r)+2 a_0 r (3 M_{BH}-2 r) \right. \right. \nonumber \\&\qquad \left. +3 M (r-2 M_{BH})^2+r^2 (3 M_{BH}-2 r)\right] \nonumber \\&\quad +(r-2 M_{BH})\left[ 4 M^2 r^2 (a_0+2 M_{BH})^2+M^2 r^2 (a_0+4 M_{BH}-r)^2\right. \nonumber \\&\quad -2 M^2 r^2 (a_0+r) (a_0+4 M_{BH}-r) \nonumber \\&\quad -2 M r^2 (2 a_0+6 M_{BH}-r) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) -M^2 r^2 (a_0+r)^2 \nonumber \\&\quad -2 M r^2 (a_0+r)^2 (a_0-M+r) -2 (a_0+r)^2 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^2 \nonumber \\&\quad +4 M r^3 (a_0+2 M_{BH}) \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \times \exp \left( \alpha \right) \nonumber \\&\quad \left. \left. +2 (a_0+r)^3 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) ^{3/2} \times \exp \left( -\alpha \right) \right] \right\} , \nonumber \\ T^\phi _{\, \, \, \, \phi }&=\frac{1}{r^2 j} \left( -a r \sin ^2 \theta \left( r(1+j)-2m \right) \widehat{u}_{30}+r^2 j \widehat{u}_3 \right) \simeq \widehat{u}_3=p_T, \quad T^r_{\, \, \, \, r} = \widehat{u}_1=0, \end{aligned}$$

(A.23)

$$\begin{aligned} T^r_{\, \, \, \, \theta }&= \left( r^2-2r m \right) \widehat{u}_{12}\sin \theta =0, \quad T^\theta _{\, \, \, \, r} = \widehat{u}_{12}\sin \theta =0, \quad T^\theta _{\, \, \, \, \theta }= \widehat{u}_{2} = p_T, \end{aligned}$$

(A.24)

where $\alpha = \frac{1}{2} \sqrt{\frac{M}{2 a_0-M+4M_{BH}}} \left( \pi -2 \arctan \left( \frac{a_0-M+r}{\sqrt{M (2 a_0-M+4 M_{BH})}}\right) \right)$. We omitted the terms with $a \times \widehat{u}_{30}$ since they are proportional to $a^2$. If we set $T^t_{\, \, \, \, \phi } = a \chi \left( r,\theta \right)$ and $T^\phi _{\, \, \, \, t}= a\Psi (r)$, we can write the energy momentum tensor as follows

$$\begin{aligned} T^\mu _\nu =\begin{bmatrix} -\rho &{} 0 &{} 0 &{} a \chi \left( r,\theta \right) \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} p_T &{} 0 \\ a \Psi (r) &{} 0 &{} 0 &{} p_T \end{bmatrix}. \end{aligned}$$

(A.25)

Thus, such a form can describe a slowly rotating black hole in active galactic nuclei. Taking the limit $a \rightarrow 0$, we recover the non rotating energy momentum tensor given in Eq.(A.9). It is worth noting that the Einstein tensor can also be calculated in the slowly rotating regime. Indeed, with the use of the metric provided in equation (A.11), we obtain the following Einstein tensor components

$$\begin{aligned} G_{t}^{t}&=\frac{r g^{\prime }(r)+g(r)-1}{r^2}, \nonumber \\ G_{t}^{\phi }&=\frac{a }{4 r^4 f(r)^2} \left( 2 r^2 f(r)^2 g(r) e^{\prime \prime } (r)-r^2 f(r) g(r) e^{\prime }(r) f^{\prime }(r)+r^2 f(r)^2 e^{\prime }(r) g^{\prime }(r) \right. \nonumber \\&\left. -2 r^2 e(r) f(r) g(r) f^{\prime \prime }(r) -r^2 e(r) f(r) f^{\prime }(r) g^{\prime }(r)+r^2 e(r) g(r) f^{\prime }(r)^2-4 e(r) f(r)^2\right) , \nonumber \\ G_{\phi }^{t}&=-\frac{a \sin ^2(\theta )}{4 r^2 f(r)^2} \left( 2 r^2 f(r) g(r) e^{\prime \prime }(r)-r^2 g(r) e^{\prime }(r) f^{\prime }(r)+r^2 f(r) e^{\prime }(r) g^{\prime }(r) \right. \nonumber \\&\quad \left. +2 r e(r) g(r) f^{\prime }(r)-2 r e(r) f(r) g^{\prime }(r)-4 e(r) f(r) g(r)\right) , \nonumber \\ G_{\theta }^{\theta }&=\frac{2 r f(r) g(r) f^{\prime \prime }(r)+r f(r) f^{\prime }(r) g^{\prime }(r)+2 f(r) g(r) f^{\prime }(r)-r g(r) f^{\prime } (r)^2+2 f(r)^2 g^{\prime }(r)}{4 r f(r)^2}, \nonumber \\ G_{\phi }^{\phi }&=\frac{2 r f(r) g(r) f^{\prime \prime }(r)+r f(r) f^{\prime }(r) g^{\prime }(r)+2 f(r) g(r) f^{\prime }(r)-r g(r) f^{\prime }(r)^2+2 f(r)^2 g^{\prime }(r)}{4 r f(r)^2}. \end{aligned}$$

(A.26)

From these expressions, we remark that $G_{\phi }^{t}$ depend on $a, \theta$ and r and that $G_{t}^{\phi }$ depend on a and r which agree with the expression of the energy-momentum tensor given above. By taking the limit $a \rightarrow 0$, $G_{\phi }^{t}$ and $G_{t}^{\phi }$ go to zero and the non rotating, symmetrical and diagonal Einstein tensor can be recovered. Besides, by computing the expression of $G_{t}^{t}$ and $G_{\theta }^{\theta }$ or $G_{\phi }^{\phi }$, we obtain

$$\begin{aligned} G_{t}^{t}&= \frac{4 M (a_0+2 M_{BH}) (2 M_{BH}-r)}{r^2 (a_0+r)^3}, \nonumber \\ G_{\phi }^{\phi }=G_{\theta }^{\theta }&= \frac{2 M (a_0+2 M_{BH}) \left( a_0^2 M_{BH}+2 a_0 M_{BH} r+M (r-2 M_{BH})^2+M_{BH} r^2\right) }{r^2 (a_0+r)^3 \left( a_0^2+2 a_0 r+4 M M_{BH}-2 M r+r^2\right) }. \end{aligned}$$

(A.27)

Since the Einstein equation is given by $T^\mu _\nu =\frac{1}{8 \pi } G^\mu _\nu$, we conclude that the computations of $G^\mu _\nu$ agree with the expressions of the quantities $\rho$ in (A.5) and $p_T$ given in equation (A.8) and also the ones derived through the calculation of the energy-momentum tensor.

1.2 A.2: Weak energy condition

The Weak Energy Condition can be used in singularity theorems associated with black holes. In specific terms, the later is exploited to show that under certain conditions, the formation of singularities is indispensable. In the present work, we consider the last energy momentum tensor $T^\mu _\nu$ associated with the slowly rotating solution. Using this tensor, we have derived the quantities $\rho$ and $p_T$ which are given by

$$\begin{aligned} \rho&=\frac{M \left( a_0+2M_{BH}\right) \left( 1-\frac{2M_{BH}}{r} \right) }{2\pi r\left( r+a_0\right) ^3}, \end{aligned}$$

(A.28)

$$\begin{aligned} p_T&=\frac{M(a_0+2M_{BH})(a_0^2 M_{BH}+2a_0 M_{BH} r+ M_{BH}r^2+M\left( r-2M_{BH} \right) ^2 )}{4\pi r^2\left( a_0+r\right) ^3 \left( a_0^2+4M M_{BH}+2a_0r-2Mr+r^2\right) }. \end{aligned}$$

(A.29)

According to the weak energy condition, all classical matter must be non-negative when by any observer in space-time [48], i.e

$$\begin{aligned} T_{\mu \nu } \xi ^\mu \xi ^\nu \ge 0 \end{aligned}$$

for all the time-like vectors $\xi ^\mu$. By decomposing the energy-momentum tensor, we find that the weak energy condition can be written as

$$\begin{aligned} \rho \ge 0, \rho + p_T \ge 0. \end{aligned}$$

Fig. 6

Dependence of matter density $\rho$ and $\rho +p_T$ on the radius for the slowly rotating black hole

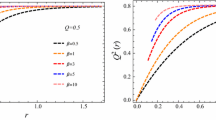
To verify the weak energy conditions, we illustrate the variation of $\rho$ and $\rho + p_T$ as function of the radial coordinate r according to equations (A.28) and (A.29). Indeed, in the Fig. 6 we present the variation of these quantities for different values of the parameters $a_0$ and M. It can be shown that the weak energy condition is violated near the origin which is a common feature for all the rotating black holes. Further investigation shows that the quantity $\rho$ is positive when

$$\begin{aligned} r \ge 2M_{BH}, \end{aligned}$$

(A.30)

while $\rho + p_T$ is positive when

$$\begin{aligned} r \ge \frac{1}{6} \left( \frac{4 a_{0}^2+12 a_{0} (M_{BH}-2 M)+9 \left( M^2-6 M M_{BH}+M_{BH}^2\right) }{\root 3 \of {A}}+\root 3 \of {A}-4 a_{0}+3 M+3 M_{BH}\right) , \end{aligned}$$

(A.31)

where we have

$$\begin{aligned} A&= 9 M \left( 10 a_{0}^2+42 a_{0} M_{BH}+45 M_{BH}^2\right) -27 M^2 (4 a_{0}+9 M_{BH})\nonumber \\&\quad +(2 a_{0}+3 M_{BH})^3+27 M^3 \nonumber \\&\quad + 18 \sqrt{M} (a_{0}+2 M_{BH}) \left( 9 M_{BH} \left( 4 a_{0}^2+2 a_{0} M-M^2\right) +a_{0}^2 (8 a_{0}-3 M) \right. \nonumber \\&\quad \left. + 54 M_{BH}^2 (a_{0}+M)+27 M_{BH}^3 \right) ^{1/2}. \end{aligned}$$

(A.32)

Analysing $\rho + p_T$ numerically for the different values of the involved parameters $a_0$ and M, we find that the quantity $\rho + p_T$ is positive for the values $r > 1.5$ which is observable from Fig. 6. Finally, we remark that $\rho \underset{r \rightarrow +\infty }{\longrightarrow }\ 0$ and $\rho + p_T \underset{r \rightarrow +\infty }{\longrightarrow }\ 0$.