1 Introduction

The bedrock of science and engineering lies in the realm of differential equations, serving as indispensable tools for tackling a wide array of physical problems. Nonlinear oscillator models, integral to engineering and physics, find extensive application across various fields. In the realm of mechanical oscillatory systems, nonlinear differential equations prove invaluable for simulation and control. In the vast landscape of mathematical physics, chemical physics, and astrophysics, second-order nonlinear differential equations are a cornerstone. However, many nonlinear ordinary differential equations resist formulation in compact forms with exact solutions. Consequently, researchers have directed their efforts toward the quest for analytically approximate or numerically derived solutions.

The dynamics of structures have spurred significant interest among scientists and researchers in the realm of nonlinear oscillating systems, particularly those involving nonlinear fractal oscillators. This interest has coincided with the rapid development of nonlinear sciences. A prevalent challenge in the current scientific landscape revolves around the quest for exact solutions to problems involving fractal nonlinear oscillators, with a particular emphasis on avoiding the use of perturbation methods. Obtaining analytic approximations is generally considered more formidable compared to numerical solutions.

Nonlinear dynamics inherently give rise to fractal structures, and their phase space serves as a representation of complex dynamical systems. This knowledge forms the foundation for understanding the intricate relationship between these systems, encompassing aspects of uncertainty and indeterminism. The insights derived from nonlinear dynamics contribute to gathering information about the future behavior of complex dynamic systems. Presently, the utilization of fractal-fractional calculus to capture self-similarities in chaotic attractors has emerged as a valuable tool, enhancing our comprehension of stability, bifurcations, and intermittency in dynamic systems. Applications for nonlinear dynamics can be found in many domains, such as signal analysis, engineering, and theoretical and applied physics like quantum mechanics.

Fractality has become pervasive since its connection with nonlinear dynamics was established [1]. Predicting outcomes in complex systems across various scientific domains remains challenging. Numerous instances of fractal behavior are observed in dissipative systems. Fractal space, grounded in the principles of fractal geometry, provides a unique perspective on spatial structures by challenging traditional Euclidean concepts. Fractals, mathematical constructs exhibiting self-similar patterns across different scales, unveil intricate details upon magnification. Mandelbrot pioneered the concept, highlighting irregularity and complexity in spatial arrangements. Researchers, such as Elias-Zuniga et al. [2], have employed fractal equations to model the dynamic response of non-Gaussian polymer chains, demonstrating the versatility of fractal space in capturing intricate behaviors. Feng and Niu [3] explored the analytical solution of the fractal Toda oscillator, emphasizing the applicability of fractal concepts in nonlinear oscillatory systems. Additionally, Song [4] proposed a thermodynamic model for a packing dynamical system, incorporating fractal considerations. The comprehensive review by Bayat et al. [5] delves into recent developments in asymptotic methods, including their applications in nonlinear vibration equations, contributing to a broader understanding of fractal phenomena. Fractal space not only enriches theoretical discussions but also finds practical applications in diverse scientific domains, ranging from materials science to vibrational analysis and beyond. Fractional differential equations and conventional differential equations can both be effectively solved using the homotopy perturbation method based on the Aboodh transform [6] or Laplace transformation [7].

Fractal nonlinear oscillations, characterized by irregular and self-similar trajectories, offer a captivating insight into the complexity of oscillatory systems. Departing from the traditional smooth and regular paths, these oscillations exhibit self-replicating patterns across different scales, highlighting the inherent nonlinearity and sensitivity to initial conditions in dynamic evolution. Mathematical tools like the homotopy perturbation method (HPM) and other non-perturbative approaches prove valuable in unraveling the intricate nature of fractal oscillations. Researchers, in exploring fractal Toda oscillators, utilize these methods to understand the self-similarity and non-smooth behavior inherent in these systems [8]. Beyond theoretical investigations, the study of fractal nonlinear oscillations extends to practical applications, particularly in vibration analysis. Insight into the complex, self-repeating patterns facilitates improved control and manipulation of oscillatory systems displaying fractal characteristics [9]. Numerous nonlinear oscillators, including the Duffing oscillator, display fractal patterns. Feng introduced a variational principle to derive the fractal frequency formula, obtaining an approximate frequency for the fractal oscillator using the two-scale fractal derivative within a fractal space [3, 10, 11]. In this space, Feng discovered an analytical solution for the Duffing oscillator [12]. Researchers like Ain and He explored the two-scale dimension for applications in fractal theory [13], and Anjum et al. applied the two-scale fractal theory to mathematical models of tsunami waves and population dynamics [14, 15]. The homotopy perturbation method has been employed to solve fractal Duffing oscillators with arbitrary initial conditions [16]. He and colleagues provided a rough solution for the Toda oscillator in fractal space [8], while Feng and Niu [3] derived a fresh analytical solution for a fractal Toda model. He and El-Dib [17] investigated the application of the two-scale fractal calculus to the Shabat-Zhiber fractal model. Additionally, an exact steady-state solution for a damped forced fractal oscillator was calculated [18].

For systems characterized by non-integer dimensions, fractal dimensionality serves as a measure of complexity. However, understanding fractal control mechanisms, physical implications, and connections to nonlinear dynamics remains incomplete. El-Dib et al. proposed a more efficient formula to convert the fractal derivative into the traditional derivative, allowing for the quantification of dynamical system fractals in integer dimensions [19,20,21,22].

Several investigations have focused on the dynamics of a bead traversing a slender, rigid wire [23]. Perturbation methods have been instrumental in analyzing this motion across diverse scenarios. The scenario involving a circular wire revolving around a horizontal diameter was addressed in [24], while the rotation of a circular wire around a vertical diameter was explored in [25] and further examined in [26]. Fractional calculus was employed in [27] to scrutinize the case of a straight wire rotating at a constant angle around a vertical axis. Utilizing fractional calculus, homotopy perturbation, and Laplace transforms, solutions were approximated in [28,29,30] for the scenario involving a heavy bead sliding on a parabolic wire spinning around its vertical axis. In all these mechanical systems, it is assumed that the wire's rate of rotation remains constant, resulting in a single degree of freedom for each system.

The non-homogeneity of angular rotation refers to variations in rotational behavior that deviate from uniform or constant patterns. This phenomenon is particularly evident in complex mechanical systems and fluid dynamics, where angular rotation may exhibit irregularities due to non-uniform distributions of mass, varying forces, or changing environmental conditions. He and El-Dib [31] demonstrated the enhanced homotopy perturbation method for the axial vibration of strings, emphasizing the importance of considering non-homogeneous effects in vibrational analysis. The work of Tian [32] introduced a frequency formula for a class of fractal vibration systems, addressing non-homogeneous characteristics within the context of fractal dynamics. These studies collectively underscore the significance of accounting for non-homogeneity in angular rotation to enhance the accuracy and applicability of theoretical models across diverse fields.

In this paper, we introduce a novel approach to derive an accurate analytical solution for fractal nonlinear conservative oscillators with a single degree of freedom. Leveraging the non-perturbative method proposed by [33, 34] and analytical approximation solutions, we investigate the dynamics of a mechanical system where a bead slides down a rotating wire with the non-homogeneity of angular rotation. The motion of the bead exhibits fractal characteristics, and the system's dynamics are described by a fractal second-order ordinary differential equation, arising from the conservation of energy and rotational momentum. A key contribution of this study is the application of a non-perturbative approach to obtain an analytical solution for the fractal differential equations governing the system's motion.

2 Formulation of the problem

As depicted in Fig. 1, the bead travels along a wire shaped like a vertical parabola. The trajectory of the bead forms a circle with a radius denoted as R. The wire undergoes rotation with an angular velocity \(\omega_{0}\) around its vertical symmetry axis. The coordinates for this scenario are cylindrical \(\left( {r,\,\theta ,\,z} \right)\). Due to the constant c, rotation rate, the equation for the parabola is expressed as \(z = cr^{2}\). Notably, these coordinates are not independent. The explicit temporal dependence on angular rotation is represented by \(\theta = \omega_{0} \tau .\)

Fig. 1
figure 1

Sketch for the problem

Full size image

The equation of motion in the smooth wire is derived as follows [25]:

$$\frac{{d^{2} r}}{{d\tau^{2} }}({ }1 + { }4{ }c^{2} r^{2} { }) + (2gc - \omega_{0}^{2} )r + 4c^{2} r\left( {\frac{dr}{{d\tau }}} \right)^{2} = 0.$$
(1)

Here, the derivatives conserve the independent variable τ in continuous space, and g represents the acceleration due to gravity on Earth. In the stationary case, we have r = R (constant) so that \(\frac{dr}{{d\tau }} = \frac{{d^{2} r}}{{d\tau^{2} }} = 0.\) At this stage, the constant c becomes

$$c = \frac{{\omega_{0}^{2} }}{2g}.$$
(2)

The harmonic balance approach [35] has been used to approximate the solution for the bead moving on a vertically rotated parabola in continuous space, as defined by Eq. (1) with initial conditions r(0) = A and \(\frac{dr\left( 0 \right)}{{d\tau }} = 0\). Moatimid [30] derived an analytical approximate solution by using the Laplace transform approach and the homotopy perturbation method. Furthermore, the current investigation aims to examine the impact of non-homogeneous spatial variation on the sliding bead motion. Assuming that the angular rotation is expressed in fractional form

$$\omega_{0} \tau = t^{\alpha } ;0 < \alpha < 1,$$
(3)

Regarding angular rotation's non-homogeneity, we have

$$\frac{d}{d\tau } \to \omega_{0} \frac{d}{{dt^{\alpha } }}\,\,\,{\text{and}}\,\,\frac{{d^{{^{2} }} }}{{d\tau^{2} }} \to \omega_{0}^{2} \frac{{d^{2} }}{{dt^{2\alpha } }}.$$
(4)

The non-homogeneity of spatial coordinates refers to the variations and irregularities in the distribution of points or locations within a given space. In the context of mathematical modeling and physical systems, accounting for non-homogeneous spatial coordinates is crucial for accurately describing the behavior of complex phenomena [36, 37].

The following is the transformation of the governing equation of motion with fractional temporal variation from the original Eq. (1) using non-homogeneity:

$$({ }1 + { }4{ }c^{2} r^{2} { })\frac{dr}{{dt^{2\alpha } }} + \frac{1}{{\omega_{0}^{2} }}(2gc - \omega_{0}^{2} )r + 4c^{2} r\left( {\frac{dr}{{dt^{\alpha } }}} \right)^{2} { } = 0.$$
(5)

It is believed that the initial circumstances in fractal space take the following form:

$$r\left( 0 \right) = A{ },\frac{dr\left( 0 \right)}{{dt^{\alpha } }} = { }0,$$
(6)

where A is a constant representing the initial radius at t = 0.

Fractional calculus, renowned for its extensive applicability in various scientific and engineering domains, presents a suitable mathematical framework for characterizing the motion of a bead traversing along a dynamically active wire. This field has witnessed a significant surge in scholarly contributions over recent decades, underscoring its growing relevance. In the context of the present challenge, which eludes resolution through traditional methodologies, the application of fractal nonlinear vibration analysis emerges as a promising avenue for investigation.

Employing the fractal dimension parameter α, this study elucidates He’s definition of the derivative within fractal space, as referenced in [38]. This definition is articulated as follows:

$$\frac{dr}{{dt^{\alpha } }} = \Gamma \left( {1 - \alpha } \right)\mathop {\lim }\limits_{{\Delta t = t_{1} - t_{2} \to t_{0} }} \frac{{r\left( {t_{2} } \right) - r\left( {t_{1} } \right)}}{{\left( {t_{2} - t_{1} } \right)^{\alpha } }}.$$
(7)

In the given context, α represents the fractal dimension in the t-direction, and t0 denotes the lowest hierarchical time level. This fractal derivative is conceptualized as a natural progression of Leibniz's derivative, specifically tailored for discontinuous fractal media. Notably, the aforementioned definition of a fractal operator is extensively introduced and discussed in literature sources [39,40,41,42,43,44,45]. The fractal derivative, as formulated in Eq. (7), has been widely applied in various studies [46,47,48,49], demonstrating considerable efficacy. Furthermore, the fractal derivative, as specified in (7), possesses distinct properties, as elaborated in source [17].

$$\mathop {\lim }\limits_{\alpha \to 0} \frac{dr}{{dt^{\alpha } }} = r\,\,,\,\,\mathop {\lim }\limits_{\alpha \to 1} \frac{dr}{{dt^{\alpha } }}\, = \dot{r}\,{\text{and}}\,\,\mathop {\lim }\limits_{\alpha \to 2} \frac{dr}{{dt^{\alpha } }}\, = \ddot{r},\,...$$
(8)

In this framework, the over-dot symbol denotes the traditional derivative of the variable t. A critical inquiry emerges concerning the dynamics in fractal space under two distinct scenarios: when 0 < α < 1 and when 1 < α < 2. Considering the properties delineated in (8), it can be inferred that

$$\frac{dr}{{dt^{\alpha } }}\, = a(\alpha )\dot{r} + b(\alpha )r;\,\,\,\,\,\,\,0 < \alpha < 1,\,$$
(9)

The analysis is structured to address the unknowns \(a(0) \to 0\), \(b(0) = 1\), \(a(1) \to 1\), and \(b(1) = 0.\) To comprehensively encompass this property, it is advisable to refer to the recent publications by El-Dib [19,20,21,22]. Based on these studies, the following proposal is put forward:

$$\frac{dr}{{dt^{\alpha } }} = S^{\alpha } \cos \left( {\tfrac{1}{2}\pi \alpha } \right)\,r + S^{\alpha - 1} \sin \left( {\tfrac{1}{2}\pi \alpha } \right)\,\,\dot{r};\,\,\,\,\,0 < \alpha < 1\,,$$
(10)

Consequently, it can be verified that

$$\frac{dr}{{dt^{2\alpha } }} = S^{2\alpha } \cos^{2} \left( {\tfrac{1}{2}\pi \alpha } \right)\,r + 2S^{2\alpha - 1} \cos \left( {\tfrac{1}{2}\pi \alpha } \right)\sin \left( {\tfrac{1}{2}\pi \alpha } \right)\,\dot{r}\, + S^{2\alpha - 2} \sin^{2} \left( {\tfrac{1}{2}\pi \alpha } \right)\ddot{r},$$
(11)

where S is a real constant indicating a fractalness parameter (non-homogeneity parameter) of the medium, depending on the fractal dimension α to be determined later.

It is noted that when \(\alpha \to 1\), the original Eq. (1) of the sliding bead in the continuous space on a vertically rotated parabola appears, in which case its solution behavior is periodic. This conclusion can be discerned from Eq. (1) where there are no linear damping forces. Fractal oscillation behaves differently from the traditional oscillation such that it describes a damping or un-damping behavior which has been demonstrated in the publications of [19,20,21,22].

2.1 Description of the non-perturbative technique (NPT)

The Non-Perturbative Technique (NPT) represents a significant departure from traditional perturbative methods in the analysis of nonlinear oscillatory systems. As a robust mathematical technique, it is particularly adept at handling a wide range of parameter regimes, demonstrating exceptional prowess in scenarios characterized by pronounced nonlinearity. Recent advancements by El-Dib [33, 50, 51] have positioned the NPT as an essential tool for deriving analytical approximate solutions in the realm of nonlinear oscillators. El-Dib [33, 34] has adeptly applied the NPT, meticulously deriving frequency-amplitude correlations for oscillators with substantial nonlinearity. The primary aim of this approach is to replace the complex nonlinear model with an alternative framework that provides clear, well-defined solutions, thus facilitating an initial approximation of the original system’s behavior. The cornerstone of this methodology is the transformation of a nonlinear equation into a linear equivalent, achieved by minimizing the average discrepancy between the two systems. This is accomplished through an averaging operator with specific properties, enabling the seamless substitution of the nonlinear system with a linear version. The ultimate goal is to linearize the nonlinear oscillation, resulting in a linear oscillator whose solution spans the entire oscillation history. The existence and uniqueness of such a generalized equivalent linear system have been thoroughly investigated in previous research [33].

To ascertain the effectiveness and precision of the NPT, a comparison with numerical solutions was conducted. The results of this comparative analysis demonstrate that the NPT yields more accurate outcomes than similar approximation methods, as evidenced by the minimal absolute error when comparing the numerical solution of the original nonlinear oscillation with the analytical solution of the corresponding linear system. The NPT has shown remarkable potential and adaptability, proving to be effective in solving various strongly nonlinear scenarios and real-world applications. While these practical cases were previously addressed using established analytical methods documented in the literature, the NPT provides a more efficient route to superior results. The computational processes involved in the NPT are significantly simpler than those required by other analytical techniques.

Moreover, the NPT delineates the procedures for deriving approximate solutions, contrasting with other methods that can be complex and time-consuming. Fundamentally, the non-perturbative method simplifies and deepens the understanding of the stability of dynamical systems. Due to its high accuracy and flexibility, the NPT is an invaluable tool for researchers seeking a more profound comprehension of the dynamics of complex nonlinear systems.

2.2 Method of solution

In the realm of physics, the objective is to approximate a suitable solution to Eq. (5) within the context of fractal space, adhering to the constraints specified in Eq. (6). A practical approach involves transforming Eq. (5) into a form that utilizes the traditional derivative in continuous space. This necessitates converting the assignments of the traditional derivative, as delineated in Eqs. (10) and (11), into the format of the equation of motion (5) coupled with the initial conditions (6), resulting in a formulation that can be expressed as:

$$\ddot{r} + 2P\left( {1 + 8c^{2} r^{2} } \right)\dot{r} + \left( {4c^{2} \ddot{r}r + P^{2} + 8c^{2} r^{2} P^{2} + 4c^{2} \dot{r}^{2} + \frac{1}{{\omega_{0}^{2} Q^{2} }}\left( {2gc - \omega_{0}^{2} } \right)} \right)r = 0,$$
(12)
$$r\left( 0 \right) = A,\,\,\,\dot{r}\left( 0 \right) = - AP,$$
(13)

where the notations P and Q are given by

$$P\left( \alpha \right) = S\cot \left( {\tfrac{1}{2}\pi \alpha } \right) ,\,\,\,\, Q\left( \alpha \right) = S^{\alpha - 1} \sin \left( {\tfrac{1}{2}\pi \alpha } \right).$$
(14)

Analysis of Eq. (12) indicates that the nonlinear oscillator described in Eq. (5) has transformed a Duffing-Van der Pol oscillator, a consequence of applying the formulas presented in Eqs. (10) and (11). Additionally, the relatively simplistic initial conditions specified in Eq. (6) have evolved into more comprehensive initial conditions, as elucidated in Eq. (13).

Given that Eq. (12) is a counterpart of Eq. (5), comparing the linear frequency of this transformed equation with the linear frequency of the original nonlinear oscillator yields a significant relation. This relation intricately connects the constant c and the angular frequency ω0 in terms of the fractal parameter α, illustrating a critical linkage between these fundamental parameters within the context of the fractal space.

$$2gc = \left( {\frac{{P^{2} Q^{2} }}{{Q^{2} - 1}} + 1} \right)\omega_{0}^{2} ;\,\,\,\,Q \ne 1$$
(15)

This relationship ceases to exist or becomes nullified when α = 1. In scenarios other than this specific condition, the equation provides a means to determine the constant c concerning the fractal parameters S and α. This formulation is key in illustrating how the characteristics of the fractal space, as encapsulated by these parameters, influence and dictate the value of c in the system's dynamics.

2.3 Establish the linearized form of the nonlinear equation of motion (12)

To derive an approximate solution for the damped nonlinear Van der Pol oscillator using the non-perturbative approach, Eq. (12) can be reformulated into a specific form. This reformulation aims to adapt the equation into a structure that is more amenable to the application of the non-perturbative method. By rewriting Eq. (12), the complexities of the damped nonlinear oscillator are reshaped, making it possible to apply the non-perturbative techniques effectively for an approximate solution.

$$\ddot{r} + 2K\left( {r^{2} } \right)\dot{r} + F\left( {r,\dot{r},\ddot{r}} \right)r = 0,$$
(16)

where \(K\left( {r^{2} } \right)\) and \(F\left( {r,\dot{r},\ddot{r}} \right)\) are defined as

$$K\left( {r^{2} } \right) = P\left( {1 + 8c^{2} r^{2} } \right),$$
(17)
$$F\left( {r,\dot{r},\ddot{r}} \right) = 4c^{2} \left( {{ }\ddot{r}r + \dot{r}^{2} } \right) + P^{2} \left( {1 + 8c^{2} r^{2} } \right) + \frac{1}{{\omega_{0}^{2} Q^{2} }}\left( {2gc - \omega_{0}^{2} } \right).$$
(18)

The damping function in the Van der Pol oscillator, denoted as \(K\left( {r^{2} } \right)\), is notably influenced by the fractal parameter P(α), which is a function of the parameter S. This highlights the unique impact of the fractal dimension on the damping characteristics of the system. Additionally, the stiffness function \(F\left( {r,\dot{r},\ddot{r}} \right)\) encapsulates both the nonlinear contributions and the linear frequency component within the oscillator. These functions are instrumental in estimating the damping coefficient and the conservative (or natural) frequency for the linearized version of the oscillator. Given these insights, the linearized form of the oscillator can be proposed in a specific representation. This representation simplifies the original nonlinear dynamics into a linear framework, making it more tractable for analysis and solution. The linearized form, as suggested, aims to retain the essential dynamical characteristics of the original system while reducing its complexity.

$$\ddot{r}(t) + 2\mu \dot{r}(t) + \omega^{2} r(t) = 0.$$
(19)

In the proposed linearized approach, as mentioned in references [50, 51], the symbol μ is used to represent the damping coefficient, and ω2 signifies the conservative frequency. The primary objective in this context is to estimate these unknown parameters, which are crucial for understanding and accurately representing the dynamics of the system.

To meet this objective and fulfill the necessary conditions, it is assumed that the total frequency of the fractal equation, which is referenced as Eq. (19), is denoted by Ω. With this definition in place, it becomes feasible to introduce a trial solution that aligns with the corresponding initial conditions delineated in Eq. (9). This trial solution is formulated in a specific manner, ensuring that it not only fits the initial conditions but also effectively captures the dynamics of the system as described by the fractal equation. The form of this trial solution is a key step in the process of determining the unknown parameters μ and ω2 in the context of the linearized model.

$$r_{0} (t) = A{\text{cos }}\Omega t - \frac{A}{\Omega }P\sin \Omega t.$$
(20)

To ascertain the values of the unknown parameters \(\mu\) and ω2, a comparison can be made between Eq. (19), which represents the trial solution in the context of the fractal equation, and Eq. (16), which embodies the linearized form of the oscillator. This comparison is aimed at identifying and quantifying the discrepancies between the two equations.

By conducting this comparative analysis, an error function or expression can be derived. This error quantifies the degree of deviation between the trial solution (Eq. 19) and the linearized model (Eq. 16). The evaluation of this error is a critical step in the process of refining the estimates of μ and ω2. It allows for adjustments to be made to these parameters to minimize the error, thereby achieving a more accurate representation of the system's dynamics within the linearized framework.

$$E(\mu ,\omega^{2} ) = \left| {\left( {F(r,\dot{r},\ddot{r}) - \omega^{2} } \right)r(t) + \left( {K\left( {r^{2} } \right) - \mu } \right)\dot{r}(t)} \right|.$$
(21)

The mean square error is defined as

$$\overline{E}^{2} (\mu ,\omega^{2} ) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{2T}\int_{0}^{T} {\left( {\left( {F(r,\dot{r},\ddot{r}) - \omega^{2} } \right)r(t) + \left( {K\left( {r^{2} } \right) - \mu } \right)\dot{r}(t)} \right)^{2} } dt;\,\,T = \frac{2\pi }{\Omega }.$$
(22)

The minimum value requires that

$$\frac{{d\overline{E}^{2} }}{{d(\omega^{2} )}} = \frac{d}{{d(\omega^{2} )}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{2T}\int_{0}^{T} {\left( {\left( {F - \omega^{2} } \right)^{2} r^{2} (t) + \left( {K - \mu } \right)^{2} \dot{r}^{2} (t) + 2\left( {F - \omega^{2} } \right)\left( {K - \mu } \right)r\dot{r}} \right)dt = 0} ,$$
(23)
$$\frac{{d\overline{E}^{2} }}{d\mu } = \frac{d}{d\mu }\mathop {\lim }\limits_{T \to \infty } \frac{1}{2T}\int_{0}^{T} {\left( {\left( {F - \omega^{2} } \right)^{2} r^{2} (t) + \left( {K - \mu } \right)^{2} \dot{r}^{2} (t) + 2\left( {F - \omega^{2} } \right)\left( {K - \mu } \right)r\dot{r}} \right)dt = 0} .$$
(24)

Because of (20), and regarding the vanishing of the integral \(\mathop {\lim }\limits_{T \to \infty } \frac{1}{2T}\int_{0}^{T} {r_{0} } \dot{r}_{0} dt\), the above equations have the following simplification:

$$\,\omega^{2} \int_{0}^{T} {r_{0}^{2} (t)dt - \int_{0}^{T} {r_{0}^{2} (t)F(r_{0} ,\dot{r}_{0} ,\ddot{r}_{0} )dt} } = 0,$$
(25)
$$\mu \int_{0}^{T} {\dot{r}_{0}^{2} (t)dt} - \int_{0}^{T} {\dot{r}_{0}^{2} (t)K(r_{0}^{2} )dt} = 0.$$
(26)

Solving both Eqs. (25) and (26) yields

$$\omega^{2} = \frac{{\int\limits_{0}^{T} {r_{0}^{2} (t)F(r_{0} ,\dot{r}_{0} ,\ddot{r}_{0} )dt} }}{{\int\limits_{0}^{T} {r_{0}^{2} (t)dt} }},$$
(27)
$$\mu = \frac{{\int_{0}^{T} {\dot{r}_{0}^{2} (t)K(r_{0}^{2} )dt} }}{{\int_{0}^{T} {\dot{r}_{0}^{2} (t)dt} }}.$$
(28)

Executing the integrals as described previously results in the determination of the equivalent damping coefficient and the equivalent conservative frequency. These values are derived in a specific form, encapsulating the dynamics of the system under consideration. This process of integration and subsequent calculation is pivotal in translating the complex dynamics of the system into quantifiable and understandable parameters, namely the damping coefficient and conservative frequency. These parameters are essential for comprehensively understanding and accurately modeling the behavior of the system within the framework of the linearized approach.

$$\omega^{2} = P^{2} \left( {1 + 4A^{2} c^{2} } \right) + 2A^{2} c^{2} \left( {\frac{{3P^{4} }}{{\Omega^{2} }} - \Omega^{2} } \right) + \frac{1}{{\omega_{0}^{2} Q^{2} }}\left( {2cg - \omega_{0}^{2} } \right),$$
(29)
$$\mu = P\left( {1 + 2A^{2} c^{2} } \right) + \frac{{2A^{2} c^{2} P^{3} }}{{\Omega^{2} }}.$$
(30)

The simplicity of the proposed Eq. (19) allows for its exact solution to be readily obtained. This solution is expressed in a specific form, reflecting the straightforward nature of the equation. The ability to derive an exact solution from such a simplified equation is advantageous, as it provides clear insights into the system's behavior and aids in validating the effectiveness of the linearization and approximation methods used in the analysis. This exact solution form is a key element in understanding the dynamics and properties of the system as described by Eq. (19).

$$r(t) = Ae^{ - \mu t} \left( {\cos \sqrt {\omega^{2} - \mu^{2} } t + \frac{(\mu - P)}{{\sqrt {\omega^{2} - \mu^{2} } }}\sin \sqrt {\omega^{2} - \mu^{2} } t} \right).$$
(31)

The exact solution mentioned previously is derived by applying the initial conditions specified in Eq. (13). In examining the impact of the damping behavior on the frequency of oscillation, it is possible to distinguish three distinct cases. Each of these cases is characterized by a specific relationship between the conservative frequency ω2 and the square of the damping coefficient μ. These relationships are crucial in defining the nature of the oscillatory behavior of the system and fall under one of the following categories:

$$\omega^{2} > \mu^{2} ,\,\,\,\,\,\omega^{2} = \mu^{2} ,\,\,\,\,\,{\text{and}}\,\,\,\,\omega^{2} < \mu^{2} .$$

The different inequalities on the left, middle, and right-hand sides correspond to distinct damping scenarios in the system:

  1. 1.

    Underdamped Case: The left-hand side inequality characterizes the underdamped case. In this scenario, the system experiences oscillations with a gradually decreasing amplitude over time, a typical behavior in systems where the damping force is not strong enough to prevent oscillations.

  2. 2.

    Critical Damping State: The middle case corresponds to critical damping. This is a unique condition where the system returns to equilibrium as quickly as possible without oscillating. Critical damping represents a precise balance between the damping force and the system's tendency to oscillate.

  3. 3.

    Overdamping Case: The right-hand side inequality signifies the overdamped case, as referenced in [52]. In overdamped systems, the damping force is so strong that it suppresses oscillations entirely, causing the system to return to equilibrium slower than in the critically damped case.

The analytical solution, as shown in Eq. (31), suggests that the oscillator frequency Ω is conventionally related to the conservative frequency ω2 and the damping coefficient μ. This relationship is fundamental to understanding the dynamics of the oscillator, as it links the intrinsic properties of the system (like its natural frequency and damping characteristics) with the observed behavior (the frequency of oscillation).

$$\Omega^{2} = \omega^{2} - \mu^{2} .$$
(32)

At this juncture, incorporating Eqs. (29) and (30) into Eq. (32) and conducting the necessary simplifications, results in the derivation of the frequency-amplitude relationship. This relationship is represented in a specific form, which articulates the connection between the frequency of oscillation and the amplitude of the system. This frequency-amplitude relationship is a fundamental aspect in the analysis of oscillatory systems, providing crucial insights into how the amplitude of oscillation influences or is influenced by the frequency of oscillation in the given system.

$$\left( {1 + 2A^{2} c^{2} } \right)\Omega^{6} + \frac{1}{{\omega_{0}^{2} Q^{2} }}\left( {4P^{2} A^{4} Q^{2} \omega_{0}^{2} c^{4} - 2cg + \omega_{0}^{2} } \right)\Omega^{4} - 2P^{4} A^{2} c^{2} \left( {1 - 4A^{2} c^{2} } \right)\Omega^{2} + 4P^{6} A^{4} c^{4} = 0.$$
(33)

This is a cubic equation in \(\Omega^{2}\) and with its real roots, the trial solution (20) and the exact solution (31) will be completely performed. It is worthwhile to observe that there are no three exchanges of signs for the coefficients of Eq. (33), but there are only two exchanges. Therefore, there is at least one real negative root and two real positive roots. Accordingly, relation (32) with positive \(\Omega^{2}\) should indicate the underdamped case. The critical damping case arises for putting zero value of \(\Omega^{2}\) into (32).

3 The residual Galerkin’s method

The residual Galerkin's method is a numerical technique commonly employed in solving differential equations, especially in the context of approximating solutions to complex or nonlinear problems. This approach typically involves constructing a set of basis functions and then determining the coefficients of these functions such that the residual (the difference between the actual differential equation and the approximated equation) is minimized in a certain sense, often in the least squares sense.

The residual \({\text{Re}} (\Omega ;t) = 0\) can be used to estimate the frequency Ω as well as the parameter S. To establish this residual, one may employ (20) into (19) to yield

$${\text{Re}} (\Omega ;t) = - A\left( {2P\mu - \omega^{2} + \Omega^{2} } \right)\cos \Omega t + \frac{A}{\Omega }\left( {P\left( {\Omega^{2} - \omega^{2} } \right) - 2\mu \Omega^{2} } \right)\sin \Omega t = 0.$$
(34)

Indeed, the residual, denoted here as \({\text{Re}} (\Omega ;t) = 0\), can be utilized to formulate an expression for the frequency Ω. This is achieved through the application of the residual Galerkin’s formula, a method that is particularly effective in such contexts as referenced in [53].

$$\frac{1}{2T}\int_{0}^{T} {\left( {\Omega \left( {2P\mu - \omega^{2} + \Omega^{2} } \right)\cos^{2} \Omega t + \left( {P\left( {\Omega^{2} - \omega^{2} } \right) - 2\mu \Omega^{2} } \right)\sin^{2} \Omega t} \right)} dt = 0;\,\,\,\,T = \frac{2\pi }{\Omega }.$$
(35)

Executing the integral as specified in the residual Galerkin’s formula results in a non-explicit frequency formula. This formula captures the frequency Ω in terms of the integral's output and the system's parameters. Being non-explicit means that the formula does not directly express Ω in a straightforward algebraic form; instead, it may involve implicit relationship structures.

$$\Omega^{3} + \left( {P - 2\mu } \right)\Omega^{2} + \left( {2P\mu - \omega^{2} } \right)\Omega - P\omega^{2} = 0.$$
(36)

To derive the explicit frequency formula, a systematic approach is required. Initially, Eqs. (29) and (30) are applied to Eq. (36). This step integrates specific parameters or relationships into the frequency formula derived from the integral in the residual Galerkin’s method. The explicit frequency formula, as a result, will clearly define the frequency Ω in terms of the known parameters and variables of the system. This transformation from a non-explicit to an explicit formula is significant as it simplifies the representation of Ω and makes it more accessible for practical calculations and analysis.

$$\left( {2P^{2} A^{2} c^{2} + \left( {1 + 2A^{2} c^{2} } \right)\Omega^{2} } \right)\left( {3P^{3} + P^{2} \Omega + P\Omega^{2} - \Omega^{3} } \right) = 0.$$
(37)

In the context of deriving a practical and bounded solution, it is important to consider the implications of the choices made in the formulation of the frequency equation. If the left bracket of the equation leads to an imaginary value for Ω, this indicates an unbounded or physically unrealistic solution for the system being modeled. In oscillatory systems, especially those grounded in physical realities, frequencies should typically be real values to represent bounded and physically meaningful oscillations. Therefore, to ensure a bounded and realistic solution, the focus should shift to the right bracket of the equation. By considering the terms and conditions outlined in this part of the equation, a frequency equation can be derived that ensures Ω remains a real and bounded value. This approach is crucial for maintaining the physical validity and applicability of the model.

In summary, the frequency equation that emerges from the right bracket will define Ω in a way that aligns with the expected physical behavior of the system, offering a realistic and practical representation of the system's dynamics.

$$\Omega^{3} - P\Omega^{2} - P^{2} \Omega - 3P^{3} = 0.$$
(38)

The frequency formula's dependency on the parameter P is a critical aspect of the analysis. In the context of stability behavior for the system, the frequency Ω must assume real values. This requirement is inherently met in the given scenario since the two discriminants in Eq. (49) are based on the squaring of P, a mathematical operation that ensures a non-negative outcome, thereby favoring the real nature of Ω. As a result, the real root of Eq. (48), which represents the physically realistic frequency of the system, can be determined. This real root is crucial for the practical application and understanding of the system's dynamics, as it aligns with the fundamental requirement for real-valued frequencies in stable oscillatory systems. The process of verifying and calculating this real root is an integral part of ensuring the model's validity and applicability to real-world scenarios.

$$\Omega = \frac{1}{3}P\left( {1 + \frac{{2 \times 2^{2/3} }}{{\left( {23 - 3\sqrt {57} } \right)^{1/3} }} + 2^{1/3} \left( {23 - 3\sqrt {57} } \right)^{1/3} } \right) \cong 2.1304P.$$
(39)

At this stage of the analysis, with the real root of the frequency equation determined, the initial solution that was proposed in Eq. (20) can now be effectively implemented. This implementation involves applying the determined values, especially the frequency Ω, into the form of the solution as originally laid out in Eq. (20) as

$$r_{0} (t) = A{\text{cos }}\left( {2.1304P} \right)\,t - \frac{A}{2.1304}\sin \left( {2.1304P} \right)t.$$
(40)

To formulate the final solution for the linearized problem as presented in Eq. (19), a systematic integration of various derived components is required. Specifically, Eq. (37), which presumably contains the real root of the frequency equation or other relevant parameters, should be inserted into Eqs. (29) and (30). This step is crucial as it incorporates the calculated frequency and other parameters into the broader framework of the problem. Following this, Eq. (15) can be utilized. This equation likely provides additional relationships or constraints necessary for the problem. By applying Eq. (15), the coefficients in Eq. (19) can be accurately determined. The outcome of these steps is an alternative form of the coefficients in Eq. (19), which more accurately reflects the dynamics of the linearized system with the incorporated parameters and constraints. This final form of the coefficients is essential for completing the solution to the linearized problem, representing a synthesis of the various elements of the analysis into a cohesive and practical solution.

$$\omega^{2} = 3P^{2} \left( {1 - \frac{{8\left( {23 - 3\sqrt {57} } \right)^{1/3} A^{2} c^{2} }}{{2 \times 2^{2/3} + \left( {23 - 3\sqrt {57} } \right)^{1/3} + 2^{1/3} \left( {23 - 3\sqrt {57} } \right)^{2/3} }}} \right),$$
(41)
$$\mu \cong P\left( {1 + 2.44067A^{2} c^{2} } \right).$$
(42)

In the concluding phase of this analysis, simplifying the argument used in the analytical solution presented in Eq. (31) will lead to a solution for Eq. (19). This final step involves refining or reworking the argument of Eq. (31) in light of the newly determined coefficients and parameters. This process results in an alternative variety of solutions for Eq. (19), which encapsulates the findings and adjustments made throughout the analysis. This alternative solution is expected to provide a more accurate and comprehensive representation of the system's behavior, reflecting the refined understanding of the dynamics achieved through the analytical process.

$$r(t) = Ae^{ - \mu t} \left( {\cos \sigma t + \frac{(\mu - P)}{\sigma }\sin \sigma t} \right).$$
(43)

In the final formulation of the solution for Eq. (19), the argument σ signifies the oscillation frequency. This frequency is expressed in terms of the constant c. This representation links the oscillatory behavior of the system to both the linear and fractal aspects of the model, illustrating the interplay between these different characteristics. The completion of this analysis culminates in the frequency-amplitude relation as follows:

$$\sigma^{2} = \omega^{2} - \mu^{2} = 2P^{2} \left( {1 - 4.3183A^{2} c^{2} - 2.9784A^{4} c^{4} } \right).$$
(44)

3.1 Preformation the fractalness parameter S

To evaluate the suitable value for the fractalness parameter S, a specific approach is followed in this section. The process involves integrating the notation outlined in Eq. (14) into Eq. (15). After this integration, a series of simplifications is carried out, leading to a formulation for S. This relation is aimed at expressing the fractalness parameter S more explicitly in terms of the variables and parameters defined in Eq. (12). The significance of determining a suitable value for S lies in

$$S^{2} = \frac{{\left( {2gc - \omega_{0}^{2} } \right)S^{2\alpha } \sin^{2} \left( {\tfrac{1}{2}\pi \alpha } \right)}}{{\left( {\omega_{0}^{2} S^{2\alpha } \cos^{2} \left( {\tfrac{1}{2}\pi \alpha } \right) + \left( {2gc - \omega_{0}^{2} } \right)} \right)}}.$$
(45)

This is a complicated transcendental representation of the parameter S which it depends on the parameter α as well as the coefficient of the original equation.

Utilizing the residual Eq. (34), one can deduce an alternative representation for the fractal parameter S and concurrently derive a variant form for the constant c. This methodology facilitates deeper insights into the dynamics of the oscillator and substantially enhances the precision in estimating the frequency Ω.

A detailed examination of the residual Eq. (34) reveals its composition of two fundamental, linearly independent functions, denoted here as \(\cos \Omega t\) and \(\sin \Omega t\). The linear independence of these functions necessitates that, for Eq. (34) to be valid, each coefficient associated with \(\cos \Omega t\) and \(\sin \Omega t\) must independently equate to zero. This prerequisite is rooted in the principle of linear independence, which asserts that a linear combination of these functions can only yield a zero result if all corresponding coefficients in that combination are also zero.

Consequently, by setting each of these coefficients to zero, two conditions or equations emerge. These conditions are of paramount importance as they impose the requisite constraints for resolving the system of equations involving \(\cos \Omega t\) and \(\sin \Omega t\). The successful resolution of these conditions is instrumental in determining the parameters or variables pivotal to the problem under consideration, thereby contributing to a comprehensive understanding and solution of the system.

$$2P\mu - \omega^{2} + \Omega^{2} = 0,$$
(46)
$$P\left( {\Omega^{2} - \omega^{2} } \right) - 2\mu \Omega^{2} = 0.$$
(47)

By incorporating Eqs. (29) and (30) into Eqs. (46) and (47), we can eliminate the dependency on the damping coefficient μ and the conservative frequency ω2. This integration leads to a new set of equations that are independent of these two parameters.

$$2P^{4} A^{2} c^{2} + \frac{1}{{Q^{2} }}\left( {2cg - \omega_{0}^{2} - P^{2} Q^{2} } \right)\Omega^{2} - \left( {1 + 2A^{2} c^{2} } \right)\Omega^{4} = 0,$$
(48)
$$\omega_{0}^{2} Q^{2} \left( {1 + 2A^{2} c^{2} } \right)\Omega^{4} + \left( {P^{2} Q^{2} \omega_{0}^{2} \left( {1 + 8A^{2} c^{2} } \right) + 2cg - \omega_{0}^{2} } \right)\Omega^{2} + 6P^{4} A^{2} Q^{2} \omega_{0}^{2} c^{2} = 0.$$
(49)

When Ω is eliminated between Eqs. (48) and (49), the result is a new equation that no longer explicitly includes Ω. This elimination process involves manipulating the two equations to isolate and remove Ω, effectively reducing the number of variables and simplifying the system. The resulting equation will provide a relationship between the remaining variables and parameters, potentially offering a more direct path to solve for specific unknowns in the system or to understand the underlying dynamics. Thus, we have

$$\left( {2cg - \omega_{0}^{2} } \right)\left( {2P^{2} Q^{2} \omega_{0}^{2} - 2cg + \omega_{0}^{2} } \right) = 0;\,\,\,Q \ne 0.$$
(50)

Given that Eq. (2) represents a travel condition applicable to the stationary state, the right bracket of Eq. (50) becomes pertinent in the context of a non-stationary state. This means that when considering situations where the system is not in a stationary state, the focus shifts to this specific part of Eq. (50). Therefore, by comparing the condition where this right bracket vanishes with the previously established relation in Eq. (15), we can conclude or establish a new relationship described as

$$c = \left( {3P^{2} + 1} \right)\frac{{\omega_{0}^{2} }}{2g}\;{\text{and}}\;Q^{2} = \frac{3}{2}.$$
(51)

It is noted that both the conditions (15) and (51) are represent the parameter c as a function in the parameter α. Further, we have three conditions on the notation Q that are \(Q \ne 1\), \(Q \ne 0\) and \(Q^{2} = \frac{3}{2}.\) The first and the second conditions are trivial satisfied because of \(\alpha \ne 1\) nor \(\alpha \ne 0\). The last condition reads as follows:

$$S^{2} = \frac{2}{3}S^{2\alpha } \sin^{2} \left( {\tfrac{1}{2}\pi \alpha } \right);\,\,\,\alpha \ne 1$$
(52)

Equation (52) is unique from its counterpart, Eq. (45), in that it gives the direct relationship between S and α without relying on the coefficients of the original equation under study. The approach to solving Eq. (52) and the subsequent derivation of relations, particularly in the context of the fractal parameter α, is pivotal in the analysis. The dependency of both the frequency Eq. (33) and the exact solution (31) on Eq. (14) highlights the integral role of α in influencing the system's dynamics.

To mitigate this strong dependency on α and enhance the versatility of the model, a key strategy involves revising the relations in Eq. (51). This revision is articulated in

$$P^{2} = \frac{1}{3}\left( {\frac{2gc}{{\omega_{0}^{2} }} - 1} \right)\;\,{\text{and}}\;Q^{2} = \frac{3}{2},$$
(53)

where the parameter P is redefined in a new form. The intention behind this re-expression is to lessen the direct impact of the fractal parameter α on the final solutions, thereby enabling the solutions to be more adaptable and relevant across a wider array of scenarios, not just those confined to specific values of α. This modification increases the flexibility and general applicability of the model, allowing for a more comprehensive analysis under varied conditions. By implementing this revised approach, Eq. (52) can be compared with Eq. (45) yields

$$S^{\alpha } = \sqrt {\frac{1}{2}\left( {\frac{2gc}{{\omega_{0}^{2} }} - 1} \right)} \sec \left( {\tfrac{1}{2}\pi \alpha } \right).$$
(54)

Subsequently, inserting Eq. (54) into Eq. (52) results in

$$S = \sqrt {\frac{1}{3}\left( {\frac{2gc}{{\omega_{0}^{2} }} - 1} \right)} \tan \left( {\tfrac{1}{2}\pi \alpha } \right).$$
(55)

These steps aim to establish a more generalized relation that retains the core of the original equation while diminishing its sensitivity to particular values of α. This broadening of applicability is crucial for a model that aims to accurately represent the system's behavior in a range of settings and conditions, especially in complex systems characterized by nonlinear and fractal dynamics.

Further, employing relations (54) and (55) in the transformation outlined in Eq. (10) allows for the expression of the model without depending on a specific value of α, as indicated in

$$\frac{dr}{{dt^{\alpha } }} = \frac{1}{\sqrt 2 }\left( {\left( {\sqrt {\frac{2gc}{{\omega_{0}^{2} }} - 1} } \right)\,r + \sqrt 3 \,\,\dot{r}} \right).$$
(56)

This step is integral to achieving a model that is robust, versatile, and applicable to a broader range of practical situations. It signifies a significant stride toward a more generalized understanding of the system and extends the model's relevance beyond specific fractal dimensions, making it a valuable tool in the study of complex dynamical systems.

4 Graphical illustration

The extensive analysis of the nonlinear mechanical vibrations of a sliding bead on a wire culminates in a series of graphical representations, which serve as a vital tool for visualizing and understanding the complex dynamics of the system. These graphical illustrations are key to demonstrating the effectiveness and accuracy of the analytical and numerical solutions derived for this problem.

The graphical representation of the frequency given by Eq. (33) is displayed in Figs. 2, 3, and 4. Figure 2 reveals that the maximum frequency is observed when the constant c is valued at 0.65, regardless of the fractal parameter α. A notable trend is that the frequency curve declines as αα increases, broadening the range of c. This suggests that a higher α leads to a lower vibration frequency. Figure 3 demonstrates that lower frequencies occur at smaller values of c, allowing for an expanded range of the amplitude A. Figure 4, akin to Fig. 2 but with arbitrary values of α, shows that lower frequencies are achieved with smaller values of c.

Fig. 2
figure 2

Representation of the frequency Ω given in (33) versus the constant c, for the variation of the parameter α. The system is considered as A = 1, g = 32, ω0 = 1

Full size image
Fig. 3
figure 3

Representation of the frequency Ω given in (33) versus the amplitude A, for the variation of the constant c for a specific value of α = 0.5

Full size image
Fig. 4
figure 4

Representation of the frequency Ω given in (33) versus the amplitude A, for the variation of the constant c without depending on a specific value of α

Full size image

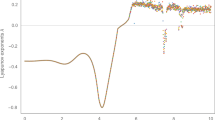
The graphs offer a visual depiction of the exact solution (31) corresponding to the equivalent linear Eq. (19). This highlights the integration of nonlinear contributions from the original Eq. (12) into the solution. These visualizations are crucial in demonstrating the precision and effectiveness of the analytical solutions derived using the non-perturbation technique. Figure 5 compares the numerical solution of Van der Pol’s Eq. (12) with the analytical solution, focusing on varying α values. The system parameters are A = 1, g = 32, ω0 = 1, and c = 0.1. The graph shows solid curves in different colors representing different α values: red for α = 0.9, green for α = 0.8, magenta for α = 0.6, orange for α = 0.4, and cyan for α = 0.2. The results demonstrate a strong agreement across various α values, underlining the robustness of the analytical method. The graph also illuminates the dynamical and damping behaviors as α varies, indicating more effective damping and slight wave profile variations with decreasing α.

Fig. 5
figure 5

Regarding the frequency provided by Eq. (33), a comparison is made between the numerical solution for Eq. (12) and the exact solution (31). In addition to the change in the parameter α, Equation (52) evaluates the argument S. A = 1, g = 32, ω0 = 1, and c = 0.1 make up the system

Full size image

The effect of the constant c on damping and wave profile has been illustrated in Fig. 6. This graph significantly contributes to the visual interpretation of the study's findings. It represents the exact solution (Eq. 31) with the frequency determined by Eq. (33), focusing on the variation of c as defined in Eq. (51). The graph shows that damping behavior is significantly influenced by variations in c, with different c values leading to distinctive damping curve shapes.

Fig. 6
figure 6

Shows how altering the constant c affects the wave profile and damping characteristics. The precise answer (31) is calculated using the frequency provided by Eq. (33) and the connection (51) is utilized. In the system, ω0 = 2, g = 32, and A = 1

Full size image

The advanced frequency σ and the solution comparison is the subject of Fig. 7. This graph compares the numerical solution of the Van der Pol oscillator (Eq. 12) with the alternative exact solution (Eq. 43), which is based on the advanced frequency σ (Eq. 44) and the expansion of cc as defined by α (Eq. 51). The values of c for various α are given as c(α = 0.9) = 0.01564, c(α = 0.8) = 0.01602, c(α = 0.6) = 0.01874, c(α = 0.4) = 0.02331, c(α = 0.2) = 0.02982. This comparison confirms an excellent match between the analytical solution with the advanced frequency σ and the numerical solution, reaffirming the analytical methods' accuracy. The wave profile behavior in Fig. 7 is consistent with the observations in Fig. 5, reinforcing the consistency and reliability of the analytical model.

Fig. 7
figure 7

Represents the linear exact solution (31) in terms of the frequency given by Eq. (44) for the variation of the parameter α which leads to a variation in the constant c that is given by (51). The system has A = 1, g = 32, ω0 = 1

Full size image

Overall, these graphical representations not only validate the theoretical and numerical analyses but also provide a comprehensive view of the system's behavior under varying conditions. They bridge the gap between complex mathematical models and their real-world applications, allowing for a deeper understanding of the dynamics of nonlinear mechanical systems.

5 Conclusion

In this study, a comprehensive approach is taken to analyze the dynamics of a sliding bead on a wire shaped into a vertical parabola and rotating at a constant angular velocity. The salient features of this work include:

  1. 1.

    Fractal Model Description: The movement of the bead is described using a fractal model, encapsulating the complex nature of the motion in fractal space.

  2. 2.

    Nonlinear Oscillator Modeling: The motion is characterized by a nonlinear Duffing-type oscillator within the fractal space, offering a detailed view of the dynamical behaviors involved.

  3. 3.

    Transformation to Continuous Space: Utilizing El-Dib’s et al. formula, the fractal model is transformed into traditional, continuous space. This conversion makes the model more amenable to standard analytical techniques.

  4. 4.

    Duffing-Van der Pol Oscillator: The transformed equation is identified as a Duffing-Van der Pol oscillator, a form well-known for its application in nonlinear dynamics.

  5. 5.

    Non-Perturbative Approach Application: This approach is employed to represent the nonlinear oscillator in terms of a linear damping oscillator. It simplifies the analysis by reducing the nonlinear aspects into a linear framework.

  6. 6.

    Exact Solution and Frequency Determination: An exact solution for the equivalent linear oscillator is provided (Eq. 31), with the frequency Ω determined as outlined in Eq. (32) and derived from Eq. (33).

  7. 7.

    Fractalness Parameter Estimation: The study leverages the properties of fractal space to estimate the fractalness parameter of the medium, a novel approach that incorporates fractal dimensions into the analysis.

  8. 8.

    Galerkin's Method for Nonlinear Frequency: An alternative methodology using Galerkin's approach is adopted to derive the nonlinear frequency, leading to a reformation of the exact solution (Eq. 31) with a modified frequency profile as shown in Eq. (51).

  9. 9.

    Description of the Exact Solution: The exact solution, incorporating these refinements, is detailed in Eq. (50), demonstrating the applicability of the method.

  10. 10.

    Simplicity and Usability: The method presented is fundamental in its concept and is designed to be easy to use, making it accessible for a wide range of applications.

Overall, this work represents a significant contribution to the field of nonlinear dynamics, especially in systems characterized by fractal behaviors. It combines theoretical rigor with practical simplicity, offering a robust and accessible tool for analyzing complex dynamical systems.