Skip to main content
SpringerLink
Log in

Spectral Neural Operators

  • Published:
Doklady Mathematics Aims and scope Submit manuscript

Abstract

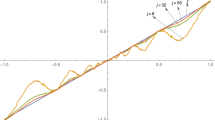
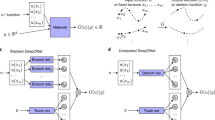
In recent works, the authors introduced a neural operator: a special type of neural networks that can approximate maps between infinite-dimensional spaces. Using numerical and analytical techniques, we will highlight the peculiarities of the training and evaluation of these operators. In particular, we will show that, for a broad class of neural operators based on integral transforms, a systematic bias is inevitable, owning to aliasing errors. To avoid this bias, we introduce spectral neural operators based on explicit discretization of the domain and the codomain. Although discretization deteriorates the approximation properties, numerical experiments show that the accuracy of spectral neural operators is often superior to the one of neural operators defined on infinite-dimensional Banach spaces.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.

Similar content being viewed by others

REFERENCES

  1. T. E. Hull et al., “Comparing numerical methods for ordinary differential equations,” SIAM J. Numer. Anal. 9, 603–637 (1972).

    Article  MathSciNet  Google Scholar 

  2. B. Fornberg and G. B. Whitham, “A numerical and theoretical study of certain nonlinear wave phenomena,” Philos. Trans. R. Soc. London Ser. A: Math. Phys. Sci. 289 (1361), 373–404 (1978).

    Article  MathSciNet  Google Scholar 

  3. T. Yoneyama, “The Korteweg–de Vries two-soliton solution as interacting two single solitons,” Prog. Theor. Phys. 71 (4), 843–846 (1984).

    Article  MathSciNet  Google Scholar 

  4. I. E. Lagaris, A. Likas, and D. I. Fotiadis, “Artificial neural networks for solving ordinary and partial differential equations,” IEEE Trans. Neural Networks 9 (5), 987–1000 (1998).

    Article  Google Scholar 

  5. L. N. Trefethen, Spectral Methods in MATLAB (SIAM, Philadelphia, 2000).

    Book  Google Scholar 

  6. J. P. Boyd, Chebyshev and Fourier Spectral Methods (Dover, Mineola, NY, 2001).

    Google Scholar 

  7. M. L. Saksman, S. Siltanen, et al., “Discretization-invariant Bayesian inversion and Besov space priors” (2009). https://doi.org/10.48550/arXiv.0901.4220

  8. D. J. Kedziora, A. Ankiewicz, and N. Akhmediev, “Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits,” Phys. Rev. E 85 (6), 066601 (2012).

  9. Y. Bar-Sinai et al., “Learning data-driven discretizations for partial differential equations,” Proc. Natl. Acad. Sci. 116, 15344–15349 (2019).

    Article  MathSciNet  Google Scholar 

  10. L. Lu, P. Jin, and G. E. Karniadakis, “DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators” (2019). https://doi.org/10.48550/arXiv.1910.03193

  11. L. N. Trefethen, Approximation Theory and Approximation Practice (SIAM, 2019).

    Book  Google Scholar 

  12. B. Ummenhofer et al., “Lagrangian fluid simulation with continuous convolutions,” in International Conference on Learning Representations (2019).

  13. Z. Li et al., “Fourier neural operator for parametric partial differential equations” (2020). https://doi.org/10.48550/arXiv.2010.08895

  14. Z. Li et al., “Neural operator: Graph kernel network for partial differential equations” (2020). https://doi.org/10.48550/arXiv.2003.03485

  15. G. Gupta, X. Xiao, and P. Bogdan, “Multiwavelet-based operator learning for differential equations,” Adv. Neural Inf. Process. Syst. 34, 24048–24062 (2021). https://doi.org/10.48550/arXiv.2109.13459

    Article  Google Scholar 

  16. N. Kovachki et al., “Neural operator: Learning maps between function spaces” (2021). https://doi.org/10.48550/arXiv.2108.08481

  17. T. Tripura and S. Chakraborty, “Wavelet neural operator: A neural operator for parametric partial differential equations” (2022). https://arxiv.org/abs/2205.02191

Download references

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (project no. 075-10-2021-068).

Author information

Authors and Affiliations

  1. Skoltech, 121205, Moscow, Russia

    V. S. Fanaskov & I. V. Oseledets

  2. AIRI, 105064, Moscow, Russia

    I. V. Oseledets

Authors
  1. V. S. Fanaskov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. V. Oseledets
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. S. Fanaskov or I. V. Oseledets.

Ethics declarations

The authors of this work declare that they have no conflicts of interest.

Additional information

Publisher’s Note.

Pleiades Publishing remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fanaskov, V.S., Oseledets, I.V. Spectral Neural Operators. Dokl. Math. 108 (Suppl 2), S226–S232 (2023). https://doi.org/10.1134/S1064562423701107

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1064562423701107

Keywords:

Search

Navigation