1 Introduction

When explosives are detonated during rock blasting, some rocks are forcefully expelled to distant locations from the blasting area, commonly known as flyrock. The distance that these flyrock fragments travel depends on various factors associated with rock excavation, some of which can be controlled while others cannot. The controllable parameters that have an influence on predicting flyrock include factors such as the depth of the blast hole, powder factor (explosive charge per unit volume of rock), spacing between blast holes, burden (distance between blast hole and rock face), diameter of the blast hole, stemming (material used to plug the blast hole), type of explosive material used, and sub-drilling (depth of additional drilling). On the other hand, uncontrollable parameters that are beyond the control of the blast engineer include rock properties, such as compressive strength, joint spacing, and tensile strength [1, 2]. These uncontrollable parameters play a significant role but cannot be directly manipulated. Several empirical equations have been proposed to simulate the occurrence of flyrock, which is expected to happen as a result of the blasting operation [1,2,3,4]. Furthermore, rock mass characteristics exhibit a significant role in the fragmented rock upheaval throughout blasting [5]. The rock density and some rock mass characteristics have virtually been overlooked in all the empirical models [5, 6]. Amini et al. [7] also conducted research to predict flyrock throw using a support vector machine (SVM) and the following input parameters powder factor (PF), hole length (HL), subdrill (SD), spacing (S), hole diameter (D), burden (B), and stemming length (ST) without considering the velocity of detonation (VOD) and charge per bank cubic meter (CPBCM).

As the explosive moves through the explosive column, its potency is taken into consideration by the VOD. The cost component per bank cubic meter of blast undertaking is taken into account by the CPBCM. The VOD of explosives and CPBCM are not usually considered in the flyrock throw distance prediction. Combining the rarely used input parameter and structural risk minimization (SRM) of SVMs seems novel because it incorporates the concept of finding an upper limit on the generalization error [8]. SVM also deals with a convex quadratic optimization problem, which means it uses the Karush–Kuhn–Tucker (KKT) principles to find the global optimum. This explains why SVM outperforms other algorithms in so many fields [8].

This paper, therefore, seeks to explore the predictive capability of SVM with input parameters such as cost charged per bank cubic meter (CPBCM) and velocity of detonation (VOD), along with traditional geometric parameters of fragmentation and flyrock throw distance. The effectiveness of SVM for predicting flyrock throw distance will help attain innovation and infrastructure protection as well as sustainable cities and communities.

1.1 Overview of Flyrock Throw Distance

Currently, among the recent efficient tools for predicting these flyrock outcomes were hybrid dimensional analysis fuzzy inference system (H-DAFIS), artificial neural network (ANN), biogeography-based optimization (BBO), gene expression programming (GEP), multiple linear regression (MLR), support vector machine (SVM), fuzzy interface system (FIS), fuzzy rock engineering system (FRES), and extreme learning machine (ELM) [1, 9,10,11,12]. Table 1 shows the previous works on AI techniques for fragmentation and flyrock throw distance predictions.

Table 1 Previous works on AI techniques for fragmentation and flyrock throw distance predictions (modified after [13,14,15])
Full size table

Raina et al. [33] determined the pressure-time record of blasts by exploiting a pressure probe, which has been verified and proven. On the other hand, because of these simplifications, the technique proposed pressure probe has proven to be a more efficient method for predicting flyrock distance. Using this method, which gauges pressure-time data, the flyrock distance and blast danger zone can be estimated around mines that carry out blasting operations [33]. The rock mass itself responds to dynamic fracturing via the processes of dynamically moving cracks and crack growth under dynamic loading conditions. Tests are limited in number, but they are used to determine whether flyrock is present and to find out how much pressure is involved. While the aforementioned tests are quite advanced and are meant to demonstrate a single bench with similar lithology, they are still useful in conveying the basics of mineral testing. Not only does this experiment cost a lot, but it is impossible to implement on a large scale for flyrocks, because pressure probes are too expensive [33].

Additionally, Sawmliana et al. [34] tried to replicate the effect of a similar blast in the mines that caused the flyrock incident. A digital video camera was used to record all the blasting trials. Based on the replicated results, the burden relief success rate was at least 80% with adequate delay recesses for the blasted rock movement. If various flight rock prediction models are employed, the maximum possible traveling distance for flinging fragments is 227 m. It was observed that the only upward throws of the flyrock happened to be from about 70 m in elevation in the trial explosion. Since it was hard to discover the actual cause of the flyrock outbreak, it must have been difficult to infer. However, Sawmliana et al. [34] after their extensive investigation concluded that it is highly possible that the source of flying rocks traveling a distance of 280 m could be a weak zone in the rock strata.

Along this line of reasoning, Hasanipanah et al. [35] researched the Ulu Tiram Quarry in Malaysia where risk assessment and the prediction of flyrock were envisaged. It was realized that in order to tackle the first objective of risk associated with flyrock, the fuzzy rock engineering system (FRES) framework needs to be applied. The proposed FRES thoroughly tested parameters that influence flyrock, which can help determine future decisions when situations are ambiguous because of its ability to handle multiple inputs and scenarios. Flyrock’s risk was evaluated with 11 different parameters, and the proposed FRES could take into account these interactions. The parameters are burden (B), powder factor (PF), hole depth to burden ratio (H/B), spacing to burden ratio (S/B), maximum charge per delay (MC), stemming and burden ratio (St/B), burden, diameter ratio (B/D), blastability index (BI), rock mass rating (RMR), and hole diameter (D) and VOD parameters. The most sensitive parameters on the cause-and-effect diagram (C + E or C − E) were PF, B, and H/B, which possess the highest values of C + E (interactive intensity). The RMR, with the maximum C – E, is the dominant system factor, and the system factor with the lowest C – E is the MC. Based on the findings, flyrock risk was found to be moderate to high at Ulu Tiram Quarry. Thus, it was recommended that using a controlled blasting method at Ulu Tiram Quarry is of the essence. Genetic algorithm (GA) was also employed to simulate flyrock, and it was discovered that the GA-based algorithm provided more precise predictions than the particle swam optimization (PSO) and imperialist competitive algorithm (ICA) constructed models.

From the works of previous authors, the most common parameters for flyrock throw prediction are explosives specific gravity (SGe), hole diameter (D), burden (B), spacing (S), hole depth (HD), subdrill (SD), powder factor (PF), stemming (ST), and explosive charge (Q). A review of the various AI techniques, their authors, the input used, the total datasets, and the coefficient of determination achieved for flyrock throw prediction is illustrated in Table 1.

2 Materials and Methods

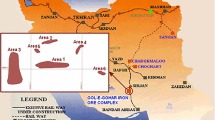
Gold Fields Ghana Limited Damang (GFGLD) mine is located in the southwestern part of Ghana, which is approximately 300 km away from the capital, Accra, by road. GFGLD mine is located at a latitude of 5° 11′ N and longitude of 1° 57′ W [36,37,38] (Fig. 1). To the north of and connected to the Tarkwa concession is the Damang commercial enterprise, which is found near the town.

Fig. 1
figure 1

Location of gold fields Ghana Damang mine [36]

Full size image

2.1 Data Collection

Data was collected for drill and blast parameters and was used to predict flyrock. The whole data set was 2629. The input parameters were summarized in Table 2: explosives specific gravity, hole diameter, burden, spacing, hole depth, subdrill, powder factor, rate charged per bank cubic meter, stemming, velocity of detonation, VOD, and explosive charge while the output was flyrock. This secondary data was collected over 2 years spanning April 2018 to March 2020.

Table 2 Input parameters
Full size table

The dataset was analyzed in Matrix Laboratory (MATLAB) software, and the corresponding results are also indicated in Table 2. The collected data also included the geological condition of the operating mine (see Fig. 2).

Fig. 2
figure 2

Pit lithology domains using rock mass rating (RMR)

Full size image

Figure 2 shows the description of the rock formation as good rock mass with a rating between 70 and 90 (color coded as green), fair rock mass with a rating of 50–70 (color coded yellow), poor rock mass with a rating of between 25 and 50 (color coded brown), and very poor rock mass with a rating of less than 25 (color coded red). The following drill patterns used for the various domains are designated as follows 3.5 m by 3.5 m for (phyllites and diorites), 3.7 m by 4.3 m (all waste zones), and 3.8 m by 3.8 m (huni sandstones) all at depths of 9 m and 6 m as and when needed.

The modeling was carried out using machine learning models in MATLAB and using a Hewlett-Packard (HP) laptop with Intel® Core™ i7. The predictive accuracy of the various spawns of SVM was discovered, and the best-performing posterities were selected.

2.2 Methods

Over the years, a series of empirical methods have been developed and used by several researchers [1, 5, 6, 39,40,41,42,43,44]. It was realized that the predictive performance of empirical models always trails behind AI models [6]. Among the AI techniques are support vector machines (SVM). SVM has proven its robustness in the field of engineering predictions. The standard SVM and least square support vector machines were examined to test their predictive capability using large datasets and input parameters seldom used for flyrock throw distance prediction.

2.3 Support Vector Machine

A support vector machine (SVM) is a sparse technique, like all other nonparametric methods [45]. SVM is a sorting technique built on arithmetical knowledge and the Vapnik–Chervonenkis (VC) dimensional models [46]. The SVM is a set of interrelated controlled learning methods that process data and extricate patterns. It is used for classification and regression studies [47]. In contrast to a neural network, which achieves only a local minimum, SVR introduces a global optimization by applying a methodology that eliminates structural risk [48]. The rudimentary code is fleetingly presented as, for any given sample sets (xi, yi), 1 ≤ i ≤ Tn as training samples, where Tn is the entire number of vectors. Training vectors xi ∈ (Rn) are the random number/(contribution vectors), and Dx is the dimension of the input space. yi denotes the corresponding yield of xi, yi = ± 1, which is designated as precipitation occurrence or not here.

2.3.1 Variants of Support Vector Machine

The parting hyperplane is represented as Ψ* x + γ = 0, where (*) is the inner product. w is the weight vector, and b represents the bias term [49]. Equation (1) represents the classification hyperplane. Any of the training samples that fall on the hyperplane form the equal sign of Eq. (1), called the support vector

$$\left({\varPsi}^{\ast }x+\gamma \right)\ge 0$$
(1)

For better optimization of the range or to take full advantage of the range, one only needs to maximize ‖ Ψ ‖ −1, which is equivalent to minimizing \(\frac{1}{2}\)‖ Ψ ‖ 2. The rudimentary kind of SVM is as revealed in expression (2):

2.3.2 Least Squares Support Vector Machines

The least squares support vector machine (LS-SVM) was spearheaded by An et al. [50]. Furthermore, these techniques have been efficaciously applied to numerous global areas of research. Finally, while the less popular LS-SVM is not quite as widely used as the standard SVM, in a broad range of benchmark information sets, LS-SVM and standard SVM accomplish about the same. A hyperparameter (i.e., kernel parameter or regularization parameter) is used in the design of LS-SVM models.

$$\operatorname{Min}\left[\frac{1}{2}{\left\Vert \varPsi \right\Vert}^2\right]$$
(2)

subject to yi (Ψ* x +γ ) − 1 ≥ 0,where i = 1, 2, · · ·, Tn with reference to Eq. (2), a hyperplane can be obtained as w · xi + b = 0 with the largest margin. Considering the equality constraints in Eq. (2), they can be unconstrained by applying the Lagrangian relation, and this is done by introducing the soft margin, to make a soft margin adapt to noisy data if the case is undivided, leading to Eq. (3):

$$\operatorname{Min}\left[\frac{1}{2}{\left\Vert \varPsi \right\Vert}^2\right]-C\sum\nolimits_{i=1}^{T_n}{l}_o\left[{y}_i\left(\Psi \ast x+\upgamma \right)-1\right]$$
(3)

l0/1 is the 0/1 loss function.

C is a constant bigger than 0, and when C is infinite, the imposition of the constraint that all samples meet the requirements is engaged. Otherwise, a room is created for samples that do not meet the requirements to be used. The two main problems here are the maximization of the objective function and the writing of a quadratic program, both of which must be addressed to solve the problem. If an equation is solvable, then Eq. (4) is arrived at

$${\max}_{\upalpha}\sum\nolimits_{i=1}^{T_n}\alpha -\frac{1}{2}\sum\nolimits_{i=1}^{T_n}\sum\nolimits_{j=1}^{T_n}{y}_i{y}_j{\alpha}_i{\alpha}_j\left({x}_i{y}_j\right)$$
(4)
$$\sum\nolimits_{i=1}^{T_n}{\alpha}_i{y}_i=0$$

Subject to

$$0\le \alpha \le C$$

i = 1,2,……Tn

Vapnik [51] and Du et al. [49] described this as an extremum tricky problem of a quadratic function having inequality variables that present a unique solution. Ai is a Lagrange multiplier for each training sample, and the sample is the support vector for which ai in Eq. (4) = 0, overlay on one of the two hyperplanes:

$$\left({\varPsi}^{\ast }x\right)+\gamma =+1;$$
(5)
$$\left({\varPsi}^{\ast }x\right)+\gamma =-1$$
(6)

The code of the Karush–Kuhn–Tucker (KKT) state indicates that the optimization problem requirement needs to satisfy Eqs. (5) and (6) when dealing with the nonlinear SVM problem. The SVM presents a kernel function to enable easy plotting of the data and transforms the data into a high-dimensional space [49, 51]:

$${\max}_{\upalpha}\sum\nolimits_{i=1}^{T_n}\alpha -\frac{1}{2}\sum\nolimits_{i=1}^{T_n}\sum\nolimits_{j=1}^{T_n}{y}_i{y}_j{\alpha}_i{\alpha}_j\mathrm{KKT}\left({x}_i{x}_j\right)$$
(7)

where the KKT(xi, xj) is the kernel function, KKT(xi, xj) = ϕ(xi) · ϕ(xj).

Once the training algorithm gives the expression ϕ(xi) · ϕ(xj), we can use the K(xi, xj) in its place.

The parameter is identical to Eq. (7), and 0 ≤ αi ≤ C. SVM is grounded upon the learning of the kernel. The kernel function is a crucial component of the algorithm. When choosing a kernel function, a crucial location needs to be selected, and this has a direct impact on the model’s generalization capabilities [46]. Many kernel functions, including the RBF function, are used often (8). An ace, simple, and easy-to-use kernel function that helps the RBF’s nonlinearity issues is the RBF radial basis function (RBF RBF) [50].

2.3.3 Gaussian Support Vector Machine

Until now, the only functions used by the kernel are as follows: fractional Brownian motion, kernel polynomial, kernel function, and sigmoid kernel [52]. No matter the situation in low-dimensional cases or in high-dimensional cases, small sample numbers, or significant sample numbers, the Gaussian kernel function is applied in all three of these kernel functions, a broader area of convergence for the Gaussian kernel and a better classification. According to the fundamental theorem of inner products, which asserts that inner products are essentially equivalent to feature space, the kernel function is well defined as the inner products of feature space. In essence, dot products are interpreted as how closely two features are located to each other in feature space. The level of similar degree differs in positive proportion to the worth of K(xi, x). In model space, Euclidean distance d(x,y) Z(xi − yi)2 (i = l, 2, ..., n) is frequently used to define the similarity in degree between sample x and y, where n is the dimension of sample in Eq. (8) [53].

$$K\left({x}_i{x}_j\right)=\exp \left\{-g\mathrm{P}{x}_j-{x}_i{\mathrm{P}}^2\right\}$$
(8)

where g represents the kernel constraint to quantify the breadth of the kernel function in RBF.

Suppose unfitting occurs with g, the results of the process may outfit or overfit the training data. This function is vigorous and can account for the nonlinear decision border [49].

The Gaussian kernel is based on the notion that similar points in the feature space are close to each other and only depend on the Euclidean distance between x and xi (in terms of Euclidean distance). In many circumstances, this assumption is fair; hence, the Gaussian kernel is frequently utilized in practice. For a Gaussian kernel: K(x, xi) := \({e}^{-g\parallel x-{x}_i{\parallel}^2}\) (for a given parameter γ > 0) it works well [53].

A new constraint is enforced on the optimization problem: the hyperplane must be located far away from the classes. We use the term Gaussian kernel because it services the optimization phase to discover the hyperplane that is situated at the greatest distance from the classes while still being equidistant from them. Training needs to take place on a subset of the overall population. Prediction, on the other hand, requires making predictions on things that have not yet occurred [45].

Awad and Khanna [45] stated that structural risk minimization (SRM) is used in conjunction with structural optimization minimization (SOM) to obtain the two solutions and convexity requirements. The SRM is an inductive code that, from a finite training dataset, selects a learning model. The SRM model suggests a trade-off between the VC extents, which is to say the space required, and the deviation of empirical measurements. In convex optimization, with m constraints and n variables to be maximized, SRM has developed a novel method to solve the problem in polynomial time. The SRM sequenced models are placed in order of increasing complexity [45]. Figure 3 shows the complete model error variation with the involvedness index of any machine learning model.

Fig. 3
figure 3

Connection between error trends and model index

Full size image

Figure 3 illustrates complex models, as evidenced by the elevated error at (B1). Since a basic model does not describe entirely the complexity of the data, a model underfitting the data occurs, which results in a high error and a maximum error (B3). (B3) is overfitting, as described in Fig. 3, and occurs in the early stages of training when the structure begins adapting its learning model to the training data, resulting in overfitting that reduces the training error value while simultaneously increasing the model validation coefficient. B2 has the least amount of error; hence, the best result is obtained at the intersection of the B2 and the test error. When this is achieved, then the best model is ready to be implemented [54].

During the modeling of support vector machines for flyrock throw distance prediction, the procedures undertaken are illustrated in Fig. 4. The process started with the collection of raw secondary data. After the data collection, data processing was carried out by cleaning data and splitting data. The processed data then goes through the SVM model for training, fine-tuning, validation, and testing. If the desired result of prediction was obtained, then the process was truncated, if not, the whole process was repeated.

Fig. 4
figure 4

Flow chart of modeling

Full size image

The empirical equations for flyrock throw prediction are as follows:

Chiapetta (1983) proposed Eqs. (9) to (11) for the distance traveled by the rock from the blast horizontally, the initial velocity of the flyrock at an angle, and the size of the projectile flyrock respectively [41].

$$\mathrm{F}{\mathrm{R}}_1={V}_O\left(\frac{2\sin 2\theta }{g}\right)$$
(9)
$${V}_O=\left(\frac{10D(2600)}{T_b\times {\rho}_r}\right)$$
(10)
$${T}_b=0.1\left({D}^{\frac{2}{3}}\right)$$
(11)

where

FR1:

is the distance traveled (m) by the rock along a horizontal line at the original elevation of the rock on the face,

V0:

is the initial velocity of the flyrock and θ is the angle of departure with the horizontal,

g:

is the gravitational constant,

d:

is hole diameter in inches,

Tb:

is the size of rock fragment (m), and

𝛒r:

is the density of rock in g/cm3.

An empirical model was established by Lundborg et al. (1975) based on hole and rock diameters as follows [43]:

$${\mathrm{FR}}_m=260{\left(\frac{D}{25}\right)}^{\frac{2}{3}}$$
(12)
$${T}_b=0.1{(D)}^{\frac{2}{3}}$$
(13)

where

FRm:

is the maximum rock projection in meters,

D:

is the hole diameter in inches, and

Tb:

is the size of rock fragments in meters.

Gupta (1980) suggested an empirical equation to predict flyrock distance based on stemming length and burden [44].

$$L=155.2{(d)}^{-1.37}$$
(14)
$$\mathrm{FR}={\left(\frac{155.2}{L}\right)}^{{~}^{1}\!\left/ \!{~}_{1.37}\right.}$$
(15)

where

L:

is the ratio of stemming length to burden and

FR:

is the distance traveled by the rocks in meters.

According to McKenzie (2018), the minimum stemming length can be estimated using Eqs. (16) to (18) [55].

$${St}_{\mathrm{min}}=0.03\times \frac{{\left(m\times {\rho}_e\right)}^{0.333}\times {D}^{1.31}}{\left(\frac{{\mathrm{Range}}_{\mathrm{max}}}{\mathrm{FoS}}\right)}-0.0005\times m\times D$$
(16)

Flyrock range with a safety factor of 1 is given as:

$$\mathrm{FR}=\frac{{\left(m\times {\rho}_e\right)}^{0.333}\times {D}^{1.31}}{\mathrm{St}-0.0005\times m\times D}$$
(17)

Scaled depth of burial (SDOB)

$$\mathrm{SDOB}=\frac{\mathrm{St}+0.0005\times m\times D}{0.00923\times {\left(m\times D\times {\rho}_e\ \right)}^{0.333}}$$
(18)

where

St:

is the stemming length,

m:

is the explosive charge length,

D:

is the blast hole diameter,

𝛒e:

is the explosive density,

FoS:

is the factor of safety, and

RangeMax:

is the maximum flyrock range.

3 Results and Discussion

The study and analysis clearly demonstrate the significant role of artificial intelligence in blasting operations and their environmental consequences. In light of this, the utilization of support vector machines (SVMs), which is one form of AI, was investigated.

In order to develop effective models, various types of SVMs were examined, including linear, quadratic, cubic, fine Gaussian, medium Gaussian, and coarse Gaussian. For all these models, automatic kernel functions and kernel scales were employed. The fine Gaussian, medium Gaussian, and coarse Gaussian SVMs utilized optimal kernel scales of 0.79, 3.2, and 13, respectively. The training and testing times ranged from 3.66 s for the fine Gaussian SVM to a maximum of 104.24 s for the coarse Gaussian SVM. The number of observations processed per second varied from 62,000 observations for the medium Gaussian SVM to 150,000 observations for the linear Gaussian SVM. Throughout the analysis, automatic box constant, epsilon, and standardization were enabled for all SVMs. The outcomes of this analysis are presented in Tables 3 and 4, respectively.

Table 3 Training results
Full size table
Table 4 Testing results
Full size table

Following this analysis, an investigation was conducted to determine the influence of the velocity of detonation (VOD) of the explosive and the charge per bank cubic meter (CPBCM) of the blasted material on the model development. Please refer to Table 5 for the results of this investigation.

Table 5 Impact of VOD and CPBCM on overall results
Full size table

According to the data presented in Table 3, it is evident that the fine Gaussian SVM (FGSVM) exhibits the lowest R2 value in both scenarios. Conversely, the linear SVM (LSVM) and quadratic SVM (QGSVM) show the highest R2 values. In terms of root-mean-square error (RMSE) values, the FGSVM has the highest value, while the LSVM has the lowest value.

Furthermore, the influence of VOD and CPBCM were examined, and their impacts are in Table 5. A positive value indicates the sensitivity of the included parameter to the model, while a negative indicates otherwise. Linear support vector machine had a 4% and 80% increase in R2 and RMSE values. The fine Gaussian support vector machine had a − 54% decrease in R2 value, but the RMSE value improved by 94%. An improvement of 14% was observed in the medium Gaussian support vector machine but a 75% improvement in the R2 and RMSE values, respectively. The coarse Gaussian support vector machine improved R2 and RMSE by 3% and 65%, respectively. The respective parity plots for the SVM models are illustrated in Fig. 5a–e. During the training and testing stages, 10-fold cross-validation was engaged. The corresponding plots are indicated in Fig. 5. The predicted value is on the vertical axis, and the true response is on the horizontal axis.

Fig. 5
figure 5

a–e Parity plots for the SVM models

Full size image

From the parity plot, the fine Gaussian support vector machine is indicated in Fig. 5a. Figure 5b represents the linear support vector machine, Fig. 5c is the coarse Gaussian support vector machine, Fig. 5d is the medium Gaussian support vector machine, and Fig. 5e represents the quadratic Gaussian support vector machine respectively.

The results from the SVM models were then compared with the empirical models as shown in Table 6. Based on Eqs. (9) to (18), empirical predictions were made. Afterward, the result was then compared with the actual flyrock throw distance determined using ProAnalyst software. The R2 and RMSE values were then determined as shown in Table 6.

Table 6 Comparisons of statistics of empirical models
Full size table

4 Conclusions

The predictive capability of linear, quadratic, fine Gaussian, medium Gaussian, and coarse Gaussian quadratic support vector machines (LS-SVM, QGSVM FGSVM, MGSVM, and CGSV) have been examined.

The best-examined model for flyrock throw distance prediction is the linear support vector machine with R2 and RMSE values of 1.00 and 0.05, respectively. The achieved result was better than those produced by empirical predictions.

The significant contribution offered by the inclusion of VOD and CPBCM was determined.

The magnitudes of improvement in R2 an RMSE for the LS-SVM, FGSVM, MGSVM, CGSVM, and QGSVM are 0.00% and 80.00%, 39.5.00% and 94.00%, 14.00% and 75.00%, 3.00% and 65.00%, and then 1.00% and 98.00% respectively.

This work is limited to the Ghanaian mining environment but can be replicated elsewhere provided, and collected data has been trained and tested in the model applied.