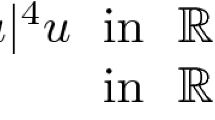Skip to main content
SpringerLink
Log in

Solutions of a quasilinear Schrödinger–Poisson system with linearly bounded nonlinearities

  • Published:
Nonlinear Differential Equations and Applications NoDEA Aims and scope Submit manuscript

Abstract

In this paper, we are concerned with the following quasilinear Schrödinger–Poisson system

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+V(x)u+ K(x)\phi u=f(x,u),\quad &{}x\in {\mathbb {R}}^3,\\ -\Delta \phi -\varepsilon ^4\Delta _4\phi = K(x) u^2, &{}x\in {\mathbb {R}}^3, \end{array}\right. } \end{aligned}$$

where \(\varepsilon \) is a positive parameter and f is linearly bounded in u at infinity. Under suitable assumptions on V, K and f, we establish the existence and asymptotic behavior of ground state solutions to the system. We prove that they converge to the solutions of the classic Schrödinger–Poisson system associated as \(\varepsilon \) tends to zero.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adams, R.: Sobolev Spaces. Pure and Applied Mathematics, vol. 65, p. xviii+268. Academic Press, New York (1975)

  2. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Does the nonlinear Schrödinger equation correctly describe beam equation? Opt. Lett. 18, 411–413 (1993)

    Article  ADS  CAS  PubMed  Google Scholar 

  3. Azzollini, A., d’ Avenia, P., Pomponio, A.: On the Schrödinger–Maxwell equations under the effect of a general nonlinear term. Ann. Inst. H. Poincaré Anal. NonLinéaire 27, 779–791 (2010)

  4. Benci, V., Fortunato, D.: An eigenvalue problem for the Schrödinger–Maxwell equations. Nonlinear Anal. 11, 283–293 (1998)

    MathSciNet  Google Scholar 

  5. Benmilh, K., Kavian, O.: Existence and asymptotic behaviour of standing waves for quasilinear Schrödinger–Poisson systems in \({\mathbb{R} }^3\). Ann. Inst. H. Poincaré Anal. NonLinéaire 25, 449–470 (2008)

    Article  ADS  Google Scholar 

  6. Cai, L., Zhang, F.: Semiclassical states for Schrödinger–Poisson system with Hartree-type nonlinearity. Topol. Methods Nonlinear Anal. 59, 779–817 (2022)

    MathSciNet  Google Scholar 

  7. Cerami, G., Vaira, G.: Positive solutions for some non-autonomous Schrödinger–Poisson systems. J. Differ. Equ. 248, 521–543 (2010)

    Article  ADS  Google Scholar 

  8. Chen, S., Fiscella, A., Pucci, P., Tang, X.: Semiclassical ground state solutions for critical Schrödinger–Poisson systems with lower perturbations. J. Differ. Equ. 268, 2672–2716 (2020)

    Article  ADS  Google Scholar 

  9. Chen, C., Wu, T.-F.: Positive solutions for nonlinear Schrödinger–Poisson systems with general nonlinearity. Nonlinear Differ. Equ. Appl. 29, 58 (2022)

    Article  Google Scholar 

  10. Ding, L., Li, L., Meng, Y.-J., Zhuang, C.-L.: Existence and asymptotic behaviour of ground state solution for quasilinear Schrödinger–Poisson systems in \({\mathbb{R} }^3\). Topol. Methods Nonlinear Anal. 47, 241–264 (2016)

    MathSciNet  Google Scholar 

  11. Du, M., Tian, L., Wang, J., Zhang, F.: Existence and asymptotic behavior of solutions for nonlinear Schrödinger–Poisson systems with steep potential well. J. Math. Phys. 57, 031502 (2016)

    Article  ADS  MathSciNet  PubMed  PubMed Central  Google Scholar 

  12. Fang, X.: Bound state solutions for some non-autonomous asymptotically cubic Schrödinger–Poisson systems. Z. Angew. Math. Phys. 70, 50 (2019)

    Article  CAS  Google Scholar 

  13. Figueiredo, G.M., Siciliano, G.: Quasilinear Schrödinger–Poisson system under an exponential critical nonlinearity: existence and asymptotic behaviour of solutions. Arch. Math. 112, 313–327 (2019)

    Article  MathSciNet  Google Scholar 

  14. Figueiredo, G.M., Siciliano, G.: Existence and asymptotic behaviour of solutions for a quasilinear Schrödinger–Poisson system with a critical nonlinearity. Z. Angew. Math. Phys. 71, 130 (2020)

    Article  Google Scholar 

  15. Fortunato, D., Orsina, L., Pisani, L.: Born–Infeld type equations for electrostatic fields. J. Math. Phys. 43, 5698–5706 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  16. Illner, R., Lange, H., Toomire, B., Zweifel, P.: On quasilinear Schrödinger–Poisson systems. Math. Methods Appl. Sci. 20, 1223–1238 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  17. Illner, R., Kavian, O., Lange, H.: Stationary solutions of quasilinear Schrödinger–Poisson system. J. Differ. Equ. 145, 1–16 (1998)

    Article  ADS  Google Scholar 

  18. Jiang, Y., Wang, Z., Zhou, H.: Positive solutions for Schrödinger–Poisson–Slater system with coercive potential. Topol. Methods Nonlinear Anal. 57, 427–439 (2021)

    MathSciNet  Google Scholar 

  19. Jiang, Y., Zhou, H.: Schrödinger–Poisson system with steep potential well. J. Differ. Equ. 251, 582–608 (2011)

    Article  ADS  Google Scholar 

  20. Li, B., Yang, H.: The modified quantum Wigner system in weighted \(L^2\)-space. Bull. Aust. Math. Soc. 95, 73–83 (2017)

    Article  MathSciNet  Google Scholar 

  21. Li, F., Li, Y., Shi, J.: Existence and multiplicity of positive solutions to Schrödinger–Poisson type systems with critical nonlocal term. Calc. Var. Partial. Differ. Equ. 56, 134 (2017)

    Article  Google Scholar 

  22. Liu, Z., Su, J., Wang, Z.-Q.: Solutions of elliptic problems with nonlinearities of linear growth. Calc. Var. Partial. Differ. Equ. 35, 463–480 (2009)

    Article  MathSciNet  CAS  Google Scholar 

  23. Liu, Z., Su, J., Weth, T.: Compactness results for Schrödinger equations with asymptotically linear terms. J. Differ. Equ. 231, 501–512 (2006)

    Article  ADS  Google Scholar 

  24. Liu, Z., Zhang, Z., Huang, S.: Existence and nonexistence of positive solutions for a static Schrödinger–Poisson–Slater equation. J. Differ. Equ. 266, 5912–5941 (2019)

    Article  ADS  Google Scholar 

  25. Markovixh, P.A., Ringhofer, C., Schmeiser, C.: Semiconductor Equations. Springer, Wien (1990)

    Google Scholar 

  26. Ruiz, D.: The Schrödinger–Poisson equation under the effect of a nonlinear local term. J. Funct. Anal. 237, 655–674 (2006)

    Article  MathSciNet  Google Scholar 

  27. Peng, X., Jia, G.: Existence and asymptotical behavior of solutions for modified quasilinear Schrödinger–Poisson system. Discrete Contin. Dyn. Syst. Ser B. 27, 2325–2344 (2022)

    Article  MathSciNet  Google Scholar 

  28. Sun, T., Chen, H., Nieto, J.: On ground state solutions for some non-autonomous Schrödinger–Poisson systems. J. Differ. Equ. 252, 3365–3380 (2012)

    Article  ADS  Google Scholar 

  29. Sun, M., Su, J., Zhao, L.: Solutions of a Schrödinger–Poisson system with combined nonlinearities. J. Math. Anal. Appl. 442, 385–403 (2016)

    Article  MathSciNet  Google Scholar 

  30. Wang, Z., Zhou, H.: Positive solution for a nonlinear stationary Schrödinger–Poisson system in \({\mathbb{R} }^3\). Discrete Contin. Dyn. Syst. 16, 809–816 (2007)

    Article  Google Scholar 

  31. Wang, Z., Zhou, H.: Sign-changing solutions for the nonlinear Schrödinger–Poisson system in \({\mathbb{R} }^3\). Calc. Var. Partial. Differ. Equ. 52, 927–943 (2015)

    Article  Google Scholar 

  32. Wei, C., Li, A., Zhao, L.: Existence and asymptotic behaviour of solutions for a quasilinear Schrödinger–Poisson System in \({\mathbb{R} }^3\). Qual. Theory Dyn. Syst. 21, 82 (2022)

    Article  Google Scholar 

  33. Wei, C., Li, A., Zhao, L.: Existence of nontrivial solutions for a quasilinear Schrödinger-Poisson system in \(mathbb{R}^3\) with periodic potential. Electron. J. Qual. Theory Differ. Equ. 48, 1–15 (2023)

    Google Scholar 

  34. Wu, T.: Existence and symmetry breaking of ground state solutions for Schrödinger–Poisson systems. Calc. Var. Partial. Differ. Equ. 60, 59 (2021)

    Article  Google Scholar 

  35. Yin, L., Wu, X., Tang, C.: Ground state solutions for an asymptotically 2-linear Schrödinger–Poisson system. Appl. Math. Lett. 87, 7–12 (2019)

    Article  MathSciNet  Google Scholar 

  36. Zhang, J., Marcosdo, O.J., Squassina, M.: Schrödinger–Poisson systems with a general critical nonlinearity. Commun. Contemp. Math. 19, 1650028 (2015)

    Article  Google Scholar 

  37. Yu, M., Chen, H.: Existence and uniqueness of multi-bump solutions for nonlinear Schrödinger–Poisson systems. Adv. Nonlinear Stud. 21, 661–681 (2021)

    Article  MathSciNet  Google Scholar 

  38. Zhao, L., Liu, H., Zhao, F.: Existence and concentration of solutions for the Schrödinger–Poisson equations with steep well potential. J. Differ. Equ. 255, 1–23 (2013)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We are grateful to the referees for the insightful comments and valuable suggestions to our paper. This work is supported by NSFC (12171014, 12071266, 11701346) and Fundamental Research Program of Shanxi Province (202303021212001, 202203021221005, 202103021224013).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Shanxi University, Taiyuan, 030006, Shanxi, People’s Republic of China

    Anran Li & Chongqing Wei

  2. School of Mathematics and Statistics, Beijing Technology and Business University, Beijing, 100048, People’s Republic of China

    Leiga Zhao

Authors
  1. Anran Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chongqing Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Leiga Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Anran Li and Leiga Zhao prepare the manuscript. Chongqing Wei and Leiga Zhao wrote the main manuscript text. All authors reviewed the manuscript.

Corresponding author

Correspondence to Leiga Zhao.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, A., Wei, C. & Zhao, L. Solutions of a quasilinear Schrödinger–Poisson system with linearly bounded nonlinearities. Nonlinear Differ. Equ. Appl. 31, 28 (2024). https://doi.org/10.1007/s00030-023-00912-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00030-023-00912-5

Keywords

Mathematics Subject Classification

Search

Navigation