1 Introduction

Adequate performance of structures under extreme loading, such as seismic, wind (e.g., [1, 2]) or blast loads [3], can be ensured by designing them to have appropriate ductility. This property of a structure provides energy absorption, as well as the necessary warning before failure. Ductility of reinforced concrete (RC) structures can be achieved by appropriate reinforcing details. Another possible way is enhancement of the material (concrete) toughness under tension by addition of fibers to the concrete mixture (e.g., [4,5,6,7]). In view of the enhanced toughness of the material it might have been expected that the addition of fibers (especially steel fibers) to reinforced concrete structural elements (e.g., beams) will also enhance their structural ductility (e.g., [8]). However, relatively recent experimental studies show a decrease of flexural ductility of R/SFRC (reinforced steel fiber reinforced concrete) structural members with low amounts of conventional reinforcement, compared to similar RC members (e.g., beams) without fibers (e.g., plain RC beams) [9,10,11,12,13]. A main reason for this phenomenon is the so-called ‘cracking localization’ (CL), characterized by significant opening of one or few cracks under the ultimate load, out of all cracks that develop prior to yielding of the tension steel [14,15,16,17,18,19]. In the following, the parts along the member that contain these wide cracks are referred to as “weak” (after [20]). CL in R/SFRC structural members leads to strain localization in the rebars that bridge the widened cracks (see Sect. 2 below), which in turn, decreases the flexural ductility of these elements [10, 21, 22] for both normal [21, 23] and high [21, 24] strength concrete. CL has been observed to occur in both axial tension [14, 20, 25] and bending elements with low reinforcement ratios [9, 24, 26].

It has been shown that the occurrence of CL is a result of the non-uniform fibers distribution along the R/SFRC elements [20, 27, 28]. Because of this non-uniform distribution, the effectiveness of the fibers is relatively low in weak segments, compared with their mean effectiveness along the structural element (the term ‘effectiveness’ is explained in Sect. 2.5). Additionally, it has been observed that cracking localization is more pronounced for larger ratios between fiber contents and conventional reinforcement [14, 18, 29]. Consequently, CL intensifies in R/SFRC elements (tensile and flexural) with low conventional reinforcement ratios.

There exist only a few models of cracking localization. Markic et al. [10] proposed a model that predicts whether or not CL is expected to occur. Shao and Billington [11] proposed a method to predict the flexural strength, considering the influence of CL, as well as the rebars hardening, on the failure mechanism. However, these models do not provide quantification of the CL level (CLL).

In a previous work, the authors have developed a probabilistic model to estimate the CLL in R/SFRC tensile elements [27]. The limitations of this model are twofold: (1) it refers only to rebars that are centrally located in the cross-section, which is irrelevant to flexural elements (beams); (2) the model does not refer to the steel rebars mechanical properties but only to the amounts of the fibers and of the conventional reinforcement.

This paper proposes a probabilistic model to quantify the CLL in flexural R/SFRC elements (beams and slabs). The model predicts the CLL, depending on the fibers distribution along the beam, their effectiveness, the reinforcement ratio, the tensile rebar location in the beam’s cross-section, and the mechanical properties of the rebars’ steel. Note that the model refers to CL that develops in structural members that include conventional reinforcement (and not to similar behavior in the material, i.e., concrete without reinforcing bars).

1.1 Role of cracks in ductility of RC beams

For clarity, this section briefly describes the role of cracking in flexural RC elements. It is well-known that flexural ductility of RC beams is enabled by the tensile action of the longitudinal steel and its interaction with the surrounding concrete. The latter is manifested by the concrete cracks that are bridged by the strained tensile rebars. The dominant elongation of the rebars occurs within the cracks (compared with a smaller elongation in the uncracked concrete between the cracks). The formation of a sequence of cracks along the beam, at relatively uniform spacing and crack opening, leads to the so-called ‘plastic hinge’ (e.g., [30, 31]). The plastic hinge maintains steel strains, large enough to provide sufficient curvature but not too large to cause rupture of the rebars. When cracking localization occurs, the rebars’ elongation is concentrated in a single or few wide cracks thus leading to steel strain localization in the wide cracks. This causes increased curvature along a reduced length (i.e., reduced length of the ‘plastic hinge’) and consequently—to reduced displacement ductility.

2 The model

2.1 Description and definitions

Consider a R/SFRC beam of span L that includes fibers, subjected to bending moment M. At a certain level of M a crack is initiated in the tension side of the beam and as M increases, the number of cracks increases as well. Finally, when M reaches the yielding moment My, there are n cracks along the specimen. In the absence of experimental data, the number n can be obtained by dividing the element’s considered length by the crack spacing (which is commonly evaluated in pertinent models or design codes, e.g., [1, 2, 4]). Beyond My some of the cracks widen while the widths of the others remain almost the same [9, 16, 24]. At the ultimate moment, only m out of n cracks are significantly wider. The definition of ‘significantly wide’ cracks is adopted here from the one previously proposed by the authors [14, 21]: ‘significantly wide cracks’ are those whose width at the end of the test is larger by an order of magnitude or more, than the average width of cracks just before yielding of the tension steel. Additionally, based on previous experimental results of R/SFRC specimens, m should be larger than or equal to 1. According to the above definition, the case of uniform crack widening at the ultimate limit state corresponds uniquely to m = n, similarly to plain RC beams.

2.2 Previous model for tensile R/SFRC elements [27]

As mentioned in the Introduction, the authors have previously developed a probabilistic model to evaluate the CLL in R/SFRC axially tensioned elements [27]. Although the new model presented here significantly differs from the previous one, there is a common basis for both. For clarity, this section presents a brief description of the previous model, which is based on the following assumptions that correspond to common characteristics of RC and R/SFRC beams:

  1. 1.

    The conventional reinforcement ratio ρ and the fibers volume ratio Vf are small (ρ << 1.0, Vf << 1.0).

  2. 2.

    A typical fiber is much shorter than a quarter of the tensile bar’s length.

  3. 3.

    The lengths of the shorter parts, embedded in concrete at one of the sides of a crack bridged by the fibers, are uniformly distributed between 0 and half of the fiber length. Therefore, the cumulative function of this distribution is linear (after Bentur and Mindess [6]).

  4. 4.

    The model refers only to the action of fibers pullout.

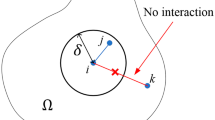
Consider a tensile RC bar with a constant cross-section that includes n cracks. The bar is sub-divided into n sub-elements of equal length, each of which contains a single crack, as described in Fig. 1, where h is the height of the entire cross-section (or its characteristic dimension). Each sub-element is divided into slices with a length that is evaluated as half of the fiber length. A slice that contains a crack is denoted ‘segment’ (such that there are n ‘segments’ along the entire tensile element). A conventional rebar (or a group of rebars) is located at the centroid of the cross-section.

Fig. 1
figure 1

Sub-division of a tensile RC bar

Full size image

The model employed the following non-dimensional random variable, which includes the amounts of the conventional steel (deterministic part) and of the fibers (random part):

$$\xi = { }\frac{{\rho { } + { }V^{\prime}_{f} \left( {1 - \rho } \right)}}{{\rho { } + { }V_{f} \left( {1 - \rho } \right)}},$$
(1)

where V'f is the actual fibers ratio in a specific slice, and its average is equal to Vf.

A cumulative distribution function P(ξ) was proposed to satisfy the following conditions: (1) The probabilities of having more or less fibers than the average content in a slice are equal; (2) The cases of no or all fibers allocated in a single slice have zero probability; (3) The mean value of ξ has the highest probability. This function was defined within a final interval [ξmin, ξmax] of ξ, defined in [27]. To ensure smooth continuity outside this interval (i.e., within the range of \(- \infty\) ≤  ξ  ≤ \(+ \infty\)) the following two conditions were applied:

$$\left. {p(\xi_{{{\text{min}}}} ) \, = \frac{{{\text{d}}{\varvec{P}}\left( \xi \right)}}{{{\text{d}}\xi }}} \right|_{{\xi = \xi_{{{\text{min}}}} }} = 0,$$
(2)
$$p(\xi_{{{\text{max}}}} ) \, = \left. {\frac{{{\text{d}}{\varvec{P}}\left( \xi \right)}}{{{\text{d}}\xi }}} \right|_{{\xi = \xi_{{{\text{max}}}} }} = 0,$$
(3)

Finally, the function that was proposed is:

$${\varvec{P}}\left( \xi \right) = \left\{ {\begin{array}{*{20}c} 0 & { - \infty \le \xi \le \xi_{{{\text{min}}}} } \\ {f\left( {\frac{{\xi - \xi_{{{\text{min}}}} }}{{1 - \xi_{{{\text{min}}}} }}} \right)^{{\frac{{p_{0} \left( {1 - \xi_{{{\text{min}}}} } \right)}}{f}}} } & {\xi_{{{\text{min}}}} \le \xi \le 1.0} \\ {1 - \left( {1 - f} \right)\left( {\frac{{\xi_{{{\text{max}}}} - \xi }}{{\xi_{{{\text{max}}}} - 1}}} \right)^{{\frac{{p_{0} \left( {\xi_{{{\text{max}}}} - 1} \right)}}{1 - f}}} } & {1.0 \le \xi \le \xi_{{{\text{max}}}} } \\ {1.0} & {\xi_{{{\text{max}}}} \le \xi \le + \infty } \\ \end{array} } \right.,$$
(4)

where f is the solution of the following equation:

$$\sigma^{2} = \frac{{2\left[ {\left( {1 - \xi_{{{\text{min}}}} } \right)\left( {2f - 1} \right)\left( {Q - 1} \right)} \right]^{2} \left( {3Qf - 1 - Q} \right)}}{{\left[ {Q^{2} f^{3} + 2Q\left( {Q - 2} \right)f^{2} - \left( {Q^{2} + Q - 3} \right)f + Q - 1} \right]\left[ {\left( {Q + 3} \right)f - Qf^{2} - 2} \right]}},$$
(5)
$$p_{0} = \frac{{f\left( {1 - f} \right)\left[ {Q\left( {1 - f} \right) - 1} \right]}}{{\left( {1 - \xi_{{{\text{min}}}} } \right)\left( {2f - 1} \right)\left( {Q - 1} \right)}},$$
(6)
$$Q = \left\{ {\begin{array}{*{20}c} {\frac{1}{\lambda }} & {; V_{f} \le \lambda } \\ {\frac{1}{{ V_{f} }}} & {; V_{f} \ge \lambda } \\ \end{array} } \right.,$$
(7)

and λ is the slice length normalized with respect to the length of the entire tensile element.

The standard deviation σ of the variable ξ that appears in Eq. (5), was proposed as follows:

$$\sigma = \left( {1 - \xi_{min} } \right)\sigma_{mix}^{{}}$$
(8)

where σmix is the standard deviation of the fibers distribution along a concrete element that does not include a conventional steel rebar.

The mathematic condition for a ‘weak slice’ is when ξ is smaller than a certain value ξw, which is given for a tensile element in [27]. As explained above, the element is sub-divided into slices, and a ‘segment’ is a slice that contains a crack.

The probability that there are m ‘weak segments’ (rather than ‘weak slices’) in a tensile element that includes n segments (i.e., n cracks) is given by the following binomial probability function PA(m):

$${\varvec{P}}_{{\varvec{A}}} \left( m \right) = C_{n}^{m} \left[ {\tilde{P}\left( {\xi_{w} } \right)} \right]^{m} \left[ {1 - \tilde{P}\left( {\xi_{w} } \right)} \right]^{{\left( {n - m} \right)}} ,\;{\text{where}}\;C_{n}^{m} = \frac{n!}{{m!\left( {n - m} \right)!}},$$
(9)

where \(\tilde{P}\left( {\xi_{w} } \right)\) depends on the number of slices in a sub-element. When a sub-element includes a very large numbers of slices, then \(\tilde{P}\left( {\xi_{w} } \right)\) is the probability that the two following conditions are satisfied simultaneously: (1) the given sub-element includes a ‘weak slice’ and (2) the initial crack is developed in this weak slice (and not in the other slices). The probability of each of these conditions P(ξ) is given by Eq. (4) and hence, \(\tilde{P}\left( {\xi_{w} } \right) = {\varvec{P}}\left( {\xi_{w} } \right)^{2}\). However, when a sub-element includes only a single slice (theoretical limit case), the second condition is satisfied automatically and \(\tilde{P}\left( {\xi_{w} } \right) = {\varvec{P}}\left( {\xi_{w} } \right)\), and for any intermediate case \(\tilde{P}\left( {\xi_{w} } \right)\) varies monotonically. According to [27] this variation is given by:

$$\tilde{P}\left( {\xi_{w} } \right) = P\left( {\xi_{w} } \right)^{\gamma \left( \lambda \right)} ,$$
(10)

The power γ depends on λ and as explained above—it ranges between 1 and 2. The expression for γ for a tensile RC bar is given in [27].

2.3 Current model

The proposed model analyzes the cracking localization (CL) in beams. The model quantifies the CL level (CLL) by the n/m ratio, where larger ratios represent larger CLL and vice versa. Unlike the previous model (that refers to tension members [27]), the model refers only to part of the beam’s cross-section, i.e., to its effective tension zone (see below), in which the volumetric contents of the fibers and of the conventional steel are Vf and ρr. Note that the model has been developed only for beams with conventional reinforcement and thus—for ρr that should be more than the minimum value required by the design codes for RC beams. Additionally, in contrary to the previous model, the current model considers not only the volumetric content of the rebars but also their mechanical properties (based on observation and analysis of experimental results [18, 32]). Consequently, to represent the influence of the conventional reinforcement, the following parameter, denoted ‘effective reinforcement ratio’, is proposed:

$$\rho_{{r,{\text{eff}}}} = \rho_{r} \frac{{f_{u} }}{{f_{y} }},$$
(11)

where fu and fy are the maximum and yielding strengths of the steel rebars. ρr represents the ratio between the area of the tensile steel and the concrete effective tension area (see Sect. 2.4). Note that this ratio is different from the commonly used reinforcement ratio ρs, which is the ratio between the area of the tensile steel and the (whole) effective concrete area.

The current model is based on the assumptions 1–4 given in Sect. 2.2, where ρr replaces ρ in assumption 1. Additionally, a slice in the model refers only to the tension part along the beam, with a height, heff, equal to the height of the effective tension zone of the cross-section (rather than to its whole height), see Fig. 2. Accordingly, Fig. 1 represents the tension part along the beam, with h = heff.

Fig. 2
figure 2

Beam rectangular cross-section

Full size image

To consider both geometrical and mechanical properties of the reinforcing steel (see Eq. (11)) a new random variable for R/SFRC beams is proposed as follows:

$$\xi = \frac{{\rho_{{r,{\text{eff}}}} + V^{\prime}_{f} \left( {1 - \rho_{{r,{\text{eff}}}} } \right)}}{{\rho_{{r,{\text{eff}}}} + V_{f} \left( {1 - \rho_{{r,{\text{eff}}}} } \right)}}.$$
(12)

As above, V'f in Eq. (12) is the actual fibers ratio in a specific slice, where the mean value of V'f is equal to Vf, and therefore, the average value of ξ, \(\xi_{avg}\), is equal to 1.0. Note that, as for ρr, also Vf and V’f refer only to the tension part of the beam, i.e., to the effective tension zone.

The minimum value of ξ, which corresponds to a case of no fibers in a specific slice, is given by:

$$\xi_{{{\text{min}}}} = \frac{{\rho_{{r,{\text{eff}}}} }}{{\rho_{{r,{\text{eff}}}} + V_{f} \left( {1 - \rho_{{r,{\text{eff}}}} } \right)}} .$$
(13)

The maximum value of ξ, for practical amounts of fibers (i.e., no more than several percents, see also assumption 1), corresponds to the theoretical limit case when a slice contains all the fibers and it is given by:

$$\xi_{{{\text{max}}}} = \frac{{\rho_{{r,{\text{eff}}}} + V_{f} \frac{{\left( {1 - \rho_{{r,{\text{eff}}}} } \right)}}{\lambda }}}{{\rho_{{r,{\text{eff}}}} + V_{f} \left( {1 - \rho_{{r,{\text{eff}}}} } \right)}}.$$
(14)

where λ is the ratio between the slice length and the considered part, Lb, of the beam span (e.g., for a four-point-bending setup it would be equal to the length of the constant moment zone). According to assumption 3, this orientation has a linear distribution (between 0 and 90°) [6, 33,34,35]. Thus, the average projection length of the fibers to bridge a possible crack is equal to half of the fiber length. Therefore, the width of a slice (see Fig. 1 with L = Lb) is equal to half of a fiber length. Therefore, λ is equal half of the fiber length, normalized with respect to Lb.

2.4 Effective tension area

To assess the dimensions of the above-mentioned effective tension zone, we use the effective tension area (in a cross-section) defined by EC2 [36] for the purpose of evaluation of flexural crack widths along the beam. The code refers to an effective height of this area, heff, as follows (e.g., see Fig. 2 for rectangular cross-sections):

$$h_{{{\text{eff}}}} = {\text{MIN}}\left\{ {{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}},2.5 \cdot d_{s} ,h - x} \right\},$$
(15)

where h is the height of the cross section, x is the height of the compression zone (under service moment) and ds is the depth of the longitudinal reinforcement (measured from the extreme tension cross-section fiber).

In most cases, the effective tension height is equal to \(2.5 \cdot d_{s}\). For this case, the effective reinforcement ratio for a rectangular cross-section with a width b and cross-sectional area of the longitudinal reinforcement As, is given by:

$$\rho_{{r,{\text{eff}}}} = 0.4\frac{{A_{s} }}{{b \cdot d_{s} }} \cdot \frac{{f_{u} }}{{f_{y} }} = 0.4\rho_{s} \frac{d}{{d_{s} }} \cdot \frac{{f_{u} }}{{f_{y} }},$$
(16)

where ρs is the cross-sectional reinforcement ratio and d = h−ds. It follows that ρr in Eq. (11) is equal to \(0.4\rho_{s} \frac{d}{{d_{s} }}\). It is thus evident that using ds is valid only when there is conventional reinforcement, which conforms to the above condition that ρr should be more than the minimum value required by the design codes for RC beams.

2.5 Probabilistic functions to predict CLL

As explained in the Introduction a major reason for cracking localization in R/SFRC elements with low conventional reinforcement ratios is the non-uniform distribution of the fibers’ effectiveness along the tension part of the beam. The effectiveness refers to the ability of the fibers to transfer tensile stresses in the beam axis direction. It depends on the fibers type, length, and on their orientation.

To analyze this fibers effectiveness and non-uniform distribution, the following probabilistic functions are proposed: (1) a cumulative distribution and probability density functions of the variable ξ (Eq. 12) and (2) a binomial probabilistic function to evaluate CLL.

2.5.1 Cumulative distribution and probability density functions

The cumulative distribution function (CDF) has been derived based on the following assumptions:

  1. I.

    The probabilities of having more or less fibers than the average content are equal.

  2. II.

    The cases of no or all fibers allocated in a single slice have zero probability.

  3. III.

    The mean value of ξ (Eq. 12) has the highest probability.

The CDF P(ξ) (within ξmin ≤ ξ  ≤ ξmax, see Eqs. (13) and (14)) should also satisfy the following conditions:

$$P(\xi_{{{\text{min}}}} ) \, = \, 0, P(\xi_{{{\text{max}}}} ) \, = { 1}.0.$$
(17)

Additionally, to ensure smooth continuity of the CDF within the range of \(- \infty\) ≤  ξ  ≤ \(+ \infty\), the probability density function (PDF) p(ξ), should satisfy two more conditions:

$$p(\xi_{{{\text{min}}}} ) \, = \left. {\frac{{{\text{d}}P\left( \xi \right)}}{{{\text{d}}\xi }}} \right|_{{\xi = \xi_{{{\text{min}}}} }} = 0,\;p(\xi_{{{\text{max}}}} ) \, = \left. {\frac{{{\text{d}}P\left( \xi \right)}}{{{\text{d}}\xi }}} \right|_{{\xi = \xi_{{{\text{max}}}} }} = 0.$$
(18)

Based on Eqs. (17) and (18), and on assumption III, the following CDF and PDF within the range \(\xi_{{{\text{min}}}} \le \xi \le \xi_{{{\text{max}}}}\) are proposed (consisting on Eq. (4)):

$$P\left( \xi \right) = \left\{ {\begin{array}{*{20}c} {f\left( {\frac{{\xi - \xi_{{{\text{min}}}} }}{{\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} }}} \right)^{{\frac{{p_{0} \left( {\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} } \right)}}{f}}} } & {\xi_{{{\text{min}}}} \le \xi \le \xi_{{{\text{avg}}}} { }} \\ {1 - \left( {1 - f} \right)\left( {\frac{{\xi_{{{\text{max}}}} - \xi }}{{\xi_{{{\text{max}}}} - \xi_{{{\text{avg}}}} }}} \right)^{{\frac{{p_{0} \left( {\xi_{{{\text{max}}}} - \xi_{{{\text{avg}}}} } \right)}}{1 - f}}} } & {\xi_{{{\text{avg}}}} { } \le \xi \le \xi_{{{\text{max}}}} } \\ \end{array} } \right..$$
(19)
$$p\left( \xi \right) = p_{0} \cdot \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\xi - \xi_{{{\text{min}}}} }}{{\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} }}} \right)^{{\frac{{p_{0} \left( {\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} } \right)}}{f} - 1}} } & {\xi_{{{\text{min}}}} \le \xi \le \xi_{{{\text{avg}}}} { }} \\ {\left( {\frac{{\xi_{{{\text{max}}}} - \xi }}{{\xi_{{{\text{max}}}} - \xi_{{{\text{avg}}}} }}} \right)^{{\frac{{p_{0} \left( {\xi_{{{\text{max}}}} - \xi_{{{\text{avg}}}} } \right)}}{1 - f} - 1}} } & {\xi_{{{\text{avg}}}} { } \le \xi \le \xi_{{{\text{max}}}} } \\ \end{array} } \right.$$
(20)

Note that the smooth continuation of the CDF to the interval [\(- \infty ,\infty ]\) leads to the function in Eq. (4), but with a different variable and parameters. The parameter p0 is equal to p\((\xi_{{{\text{avg}}}} )\) and it is given by:

$$p_{0} = \frac{{f\left( {1 - f} \right)\left( {1 - f - \lambda } \right)}}{{\left( {\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} } \right)\left( {2f - 1} \right)\left( {1 - \lambda } \right)}}$$
(21)

Following the derivation in [27], the parameter f is obtained from the solution to Eq. (22) for the standard deviation (squared) obtained from Eq. (20) (see also Eqs. (13) and (14)), which is given by:

$$\sigma \left( \xi \right)^{2} = \mathop \smallint \limits_{{\xi_{{{\text{min}}}} }}^{{\xi_{{{\text{max}}}} }} \left( {\xi - \xi_{{{\text{avg}}}} } \right)^{2} \cdot p\left( \xi \right)d\xi = \frac{{2\left[ {\left( {\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} } \right)\left( {2f - 1} \right)\left( {1 - \lambda } \right)} \right]^{2} \left( {3f - 1 - \lambda } \right)}}{{\left[ {f^{3} + 2\left( {1 - 2\lambda } \right)f^{2} - \left( {1 + \lambda - 3\lambda^{2} } \right)f + \left( {1 - \lambda } \right)\lambda } \right]\left[ {\left( {1 + 3\lambda } \right)f - f^{2} - 2\lambda } \right]}}.$$
(22)

It is important to note that the relation between the standard deviations of the distribution along a reinforced concrete element and along an element without conventional reinforcement, as given in Eq. (8), is valid only for rebars centrally located in the cross-section (as in a tension RC bar). This is not the case in beams, where 0 < ds ≤ heff/2, and therefore this relation must be modified.

For the theoretical extreme condition of ds = 0 the rebars are located at the very edges of the tensile zone. In this case the tensile zone essentially contains only fiber reinforced concrete with a standard deviation σ = σmix. Another limit case is when the rebars are located at heff/2, where Eq. (8) is valid. Consequently, the following modified equation for σ is proposed, assuming a parabolic transition (with ds) between the two conditions:

$$\sigma = \left[ {\left( {1 - \xi_{{{\text{min}}}} } \right) \cdot \frac{{d_{s} \cdot \left( {h_{{{\text{eff}}}} - d_{s} } \right)}}{{h_{{{\text{eff}}}}^{2} /4}} + \frac{{h_{{{\text{eff}}}} /2 - d_{s} }}{{h_{{{\text{eff}}}} /2}}} \right]\sigma_{{{\text{mix}}}} .$$
(23)

Note that for the above limit conditions of ds = 0 and heff/2 σ/σmix is equal to 1.0 and 1−ξmin (Eq. 8), respectively, as expected. Also, for the most common case of heff = 2.5ds (refer to Eq. (15)) Eq. (23) becomes:

$$\sigma = \left[ {\left( {1 - \xi_{{{\text{min}}}} } \right) \cdot 0.96 + 0.2} \right]\sigma_{{{\text{mix}}}} .$$
(24)

The standard deviation σmix is assumed to be known, e.g., from experimental measurements [28, 33]. Note that σmix refers to the case of a member that contains only fibers and therefore—to the non-dimensional variable ξ = V'f/Vf (see Eq. (12)).

2.5.2 Binomial probabilistic function to evaluate CLL

The binomial probabilistic function to evaluate CLL in beams has the same form given in Eqs. (9) and (10) but with different P(ξw), which is given by Eq. (19) and with the power γ(λ) in Eq. (10), which is given only for the realistic steel fiber lengths (~ 20 to ~ 60 mm) as follows:

$$\gamma = 1 + \frac{1/\lambda - n}{{1/V_{f} - n}}$$
(25)

Here ξw (the limit value of ξ, below which the slice is referred to as ‘weak’) is defined as in Eq. (39) in [27] but with new formulations for its parameters ξmin and ξmax that are given by Eqs. (13) and (14), and σ, which is given by Eqs. (23) or (24). For the reader’s convenience these formulas are given below for the current beam model:

$$\xi_{{\text{w}}} = \left\{ {\begin{array}{*{20}c} {\left( {\xi_{{{\text{max}}}} } \right)^{{1 - \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{\alpha } }} , 0 \le \sigma \le \sigma_{0} } \\ {1 - \left( {\frac{{\sigma - \sigma_{0} }}{{\sigma_{{{\text{max}}}} - \sigma_{0} }}} \right)\left( {\xi_{{{\text{avg}}}} - \xi_{{{\text{min}}}} } \right), \sigma_{0} < \sigma \le \sigma_{{{\text{max}}}} } \\ \end{array} } \right..$$
(26)

where

$$\alpha = \frac{{{\text{ln}}\left[ {1 - {\text{ln}}\left( {\xi_{{{\text{min}}}} } \right)/{\text{ln}}\left( {\xi_{{{\text{max}}}} } \right)} \right]}}{{{\text{ln}}\left( {\sigma_{{{\text{max}}}} /\sigma_{0} } \right)}}.$$
(27)
$$\sigma_{{\text{o}}} = \left( {\frac{{V_{f} }}{\lambda }} \right)^{\kappa } \cdot\left( {\frac{{V_{f} }}{{V_{f} + \rho_{{{\text{cr}}}} { }}}} \right) \sigma_{{\text{mix,max}}}^{{}} ; \rho_{{{\text{cr}}}} = \rho_{{\text{real,max}}} /\left( {1 - \rho_{{\text{real,max}}} } \right).$$
(28)
$$\begin{gathered} \sigma_{{{\text{max}}}}^{{}} = \left[ {\left( {1 - \xi_{{{\text{min}}}} } \right) \cdot \frac{{d_{s} \cdot \left( {h_{{{\text{eff}}}} - d_{s} } \right)}}{{h_{{{\text{eff}}}}^{{2}} /4}} + \frac{{h_{{{\text{eff}}}} /2 - d_{s} }}{{h_{{{\text{eff}}}} /2}}} \right] \cdot \sigma_{{\text{mix,max}}}^{{}} ; \hfill \\ \sigma_{{\text{mix,max}}}^{{}} = \frac{2}{\sqrt 3 }\sqrt {\frac{{\left( {3{\Xi } - 10 + 11\lambda } \right)\left[ {17\left( {1 - 2\lambda } \right) - 6{\Xi }\left( {1 - \lambda } \right) + 18\lambda^{2} } \right]\left( {1 - \lambda } \right)}}{{\left[ {3{\Xi }\left( {1 - 2\lambda } \right) - 8 + 25\lambda - 18\lambda^{2} } \right]\left[ {{\Xi }\left( {7 - 8\lambda } \right) - 20 + 43\lambda - 24\lambda^{2} } \right]}}} ; {\Xi } = \sqrt {8 - 16\lambda + 9\lambda^{2} } . \hfill \\ \end{gathered}$$
(29)

Note that the relation between σmax and σmix,max (maximum value of σmix) in Eq. (29) takes the form of the current model for σmix,max, i.e., according to Eq. (23).

The power κ in Eq. (28) ought to be calibrated from experimental results and the term ρreal,max represents the ratio between the realistic maximum amount of conventional reinforcement in beams and the equivalent tensile concrete zone/area (with a height heff, given in Eq. (15)). The common provision in design codes for the maximum tensile reinforcement in beams (and columns) is 4% of the concrete effective area (e.g., EC2 [36]). Therefore, the corresponding value of ρreal,max is equal to \(\frac{0.04 \cdot d}{{h_{{{\text{eff}}}} }}\) (where d is the effective height of the cross-section).

Note that formally, Eq. (28) can lead to non-realistic results of σ0 > σmax. For these cases, another definition of ξw is required (instead of Eq. (26)). According to Eq. (27), when σ0 approaches σmax, α approaches infinity and therefore, the first row of Eq. (26) yields ξw = ξmax (note that in this case the 2nd range in this equation does not exist). To preserve continuity of ξw, we propose that when Eq. (28) yields σ0 larger than σmax, ξw is set to be equal to ξmax. This conforms to the physical state, where all slices are similar, i.e., all slices are weak (see Sect. 2.1).

3 Model validation

The modified model has been validated against experimental data from published results of four-point-bending tests of R/SFRC beam specimens [16,17,18, 32]. The specimens were made of normal strength concrete with “3D hooked-end” steel fibers and with deformed conventional rebars. The fibers had 35-mm length and a diameter of 0.55 mm with an aspect ratio of 64. The beams had a cross-section with a width b = 240 mm and height h = 300 mm, and a span of L = 3.2 m with a constant moment zone, Lb = 1.5 m (Fig. 3).

Fig. 3
figure 3

Setup of the considered beam

Full size image

The tests included 15 specimen types that comprised 7 types with 40- and 8 types with 60-kg/m3 fibers (volumetric ratios of 0.5 and 0.76%, respectively), and deformed rebars of 400 or 500-MPa nominal yield strengths with reinforcement ratios ρs ranging from 0.0015 to 0.033. Two specimens of each type were tested and when results appeared to vary considerably, an additional specimen was cast and tested [18].

The range of the corresponding ρr,eff (taken by Eq. (16)) was 0.0076 to 0.089. Concrete strengths varied between 25 to 35 MPa (150-mm cube specimens) and the FRC classifications according to EC2 (2021 draft [37]), MC2010 [4] and EN 14651 [38] were ‘2.5d’ and ‘3d’ for the mixes with 40- and 60-kg/m3 fibers, respectively. Specimen details are given in Table 1.

Table 1 R/SFRC reported specimens [16, 18, 32]
Full size table

The middle number (e.g., “015”) in a specimen notation denotes reinforcement ratio ρs (%).

The load in the tests was applied until failure and the number of the cracks, n, formed in the constant moment zone was counted until yielding of the tension steel was reached. The number of significantly wide cracks, m, was counted at the end of the test.

The parameters that were used for the model’s calculations (in addition to the specimen parameters given in Table 1) are listed in Table 2.

Table 2 R/SFRC model’s parameters (corresponding to the data in Table 1)
Full size table

The additional parameters, which are common for all specimens are λ = 0.0117 and σmix which is equal to 0.234 and 0.254 for the mixes with 40- and 60-kg/m3 fibers, respectively [28, 32]. The calibration of the parameter κ in Eq. (28) was done only according to the 60_039 specimens, and it yielded \(\kappa \left( {V_{f} = 0.0076} \right) = - 0.9\). This value of κ was then used for all other specimens with 60 kg/m3 fibers, without any additional calibration. As mentioned above (after Eq. (28)), the parameter κ ought to be calibrated for each mixture type. However, in this example for the specimens with 40 kg/m3 fibers, κ is evaluated, based on the calibration for the mixture with 60 kg/m2 fibers, and according to the following proposed relation:

$$\kappa \left( {V_{f} } \right) = \kappa \left( {V_{{f,{\text{cal}}}} } \right) \cdot \left( {\frac{{V_{f} }}{{V_{{f,{\text{cal}}}} }}} \right)^{2} .$$
(30)

where Vf,cal is the fiber content for which calibration of κ has been performed. In our case, Vf,cal = 0.0076 (and κ (Vf,cal) = − 0.9). For the 40-kg/m3 specimens, these yield κ = − 0.3895.

Equation (30) was proposed based on the following assumed conditions:

  1. 1.

    When there are no fibers (plain concrete, Vf = 0) κ = 0 and dκ/dVf = 0.

  2. 2.

    When Vf = Vf,cal, κ = κ(Vf,cal).

For the model’s prediction of the number of wide cracks (m), the total number of cracks observed in the experiments (n) is used. The binomial probability function PA(m) is calculated (Eq. 9) for each m, varying from 1 to n. The maximum value of this function indicates the predicted value of m. Typical examples of this binomial probability function are shown in Fig. 4.

Fig. 4
figure 4

Typical examples of the binomial probability function

Full size image

The results of the prediction, together with the observed results, are given in Table 3.

Table 3 Results
Full size table

Plots of CLL in terms of n/m (see Table 3) are shown in Fig. 5.

Fig. 5
figure 5

Observed and predicted CLL

Full size image

It is evident from Fig. 5b that good agreement between the predicted and observed results for the specimens with 0.76% fibers was obtained for the entire range of the effective reinforcement ratio ρr,eff. Note that for ρr,eff = 0.023 (specimen type 60_053) there is one result (out of three) with an n/m value, significantly higher than the other two. When disregarding this result, it can be seen that the predictions agree well with the other two. As explained above, after the first two specimens of this type showed a considerable scatter (n/m values of 6.8 and 3.6, Table 3), a third specimen was cast and tested and yielded n/m = 4.9.

For the specimens with 0.5% fibers, Fig. 5a shows that good agreement between the predicted and observed results was obtained for the middle and high values of the effective reinforcement ratio ρr,eff. For ρr,eff = 0.0199 (specimens 40_039), 2 and 4 wide cracks were observed while the model predicts m = 3.5 and 4 (Table 3). For ρr,eff = 0.0076, 2 and 1 wide cracks were observed while the model predicts m = 1. I.e., the observed n/m of these specimens differed by ~ 100% and the model’s prediction agrees very well with one of two observed results for each specimen type.

Overall, the model conforms, both qualitatively and quantitatively, to the empirical result of relatively high levels of cracking localization (large n/m ratios) at the lower range of the effective reinforcement ratio, and vice versa.

4 Conclusions

This paper proposes a probabilistic model that explains the phenomenon of cracking localization in R/SFRC beams where for low conventional reinforcement ratios only a few cracks widen significantly more than the other cracks. The cracking localization is defined quantitatively by the ‘cracking localization level’ (CLL), given as the n/m ratio between the total number of cracks and the number of the significantly wide cracks.

The model considers both the fibers and conventional reinforcement ratios, as well as the steel stress hardening, given in terms of the ratio between the maximum and yielding strengths of the steel rebars, fu/fy. This model overcomes the limitations of the previous model [27] by considering the tensile rebar location in the beam’s cross-section, and the mechanical properties of the rebars’ steel. The fibers distribution in the concrete mix is considered random while the conventional reinforcement—as deterministic. The conventional reinforcement is considered in terms of the ratio ρr between the areas of the tensile steel, As, and of the concrete tensile zone of the beam’s cross-section, rather than the regular ratio between As and the effective concrete area. The deterministic part of the total steel (rebars and fibers) distribution is represented in the model by the multiplication of ρr and fu/fy. Additionally, the model takes into account the common characteristics of RC and R/SFRC beams.

The paper presents a cumulative probability function of the total steel distribution along R/SFRC beams for a newly defined variable that represents the above model’s parameters, as well as a new approach to evaluate the standard deviation σ of the total steel distribution. The latter is based on the standard deviation σmix of the fibers in the FRC mixture (without reinforcement) and on the location of the rebars along the height cross-section.

These derivations allow constructing a binomial probability function, whose maximum value denotes the most expected number of cracks that widen more than the others do. This function depends on the definition of a so-called ‘weak slice’ where the fibers effectiveness is relatively low, compared with their mean effectiveness along the beam. A criterion for the definition of this weak slice is given in terms of a limit value of the cumulative function parameter.

The model was validated with available data from flexural, 4-point-bending experiments of R/SFRC beam specimens. Calibration of the model was performed according to data of a single specimen type (SFRC mixture with 0.76% of fibers and a 0.39% reinforcement ratio). The comparison of the model’s prediction yielded good agreement with results of other 14 specimen types, without any further calibration.

The model shows that the cracking localization level (CLL) is more pronounced in R/SFRC beams with low effective reinforcement ratios (ρr,eff). Moreover, for a given level of ρeff a larger fibers content causes a larger CLL (larger n/m ratios).