1 Introduction

It is well known that nonlinear evolution equations (NLEEs) play some important role in mathematics, physics, chemistry, biology and other fields. It is necessary to construct their explicit solutions in order to understand the mechanisms of their physical phenomena. Some powerful methods, such as inverse scattering transformation (IST) [1], Lie symmetry method [2,3,4], the Möbious invariant form [5], etc. [6,7,8,9,10,11,12,13], have been explored for seeking exact solutions of NLEEs. It is worth mentioning that Lie symmetry method, particulary nonlocal symmetry method, is a very effective method. The research on nonlocal symmetry can be traced back to before 1997 [14, 15]. In fact, the first complete geometric theory of nonlocal symmetries is due to Vinogradov and coworkers in the 1980s. A summary of their work appears in the AMS volume [16] published in the 1990s. With respect to applications, Sergyeyev and Reyes have published papers on nonlocal symmetries in the early 2000s [17,18,19,20,21]. Recently, Lou [22, 23] proposed the consistent Riccati expansion (CRE) method, which is used to find new solutions of NLEEs via the nonlocal symmetry. Based on that, there are many works have been done to study this problem [24,25,26,27,28,29,30,31,32,33,34].

The most general form of the fifth-order Korteweg–de Vries (KdV) equation [35] is usually expressed as

$$\begin{aligned} u_{t}+\rho u_{xxxxx}+\alpha uu_{xxx}+\beta u_{x}u_{xx}+\gamma u^{2}u_{x}=0, \end{aligned}$$
(1.1)

where \(u=u(x,t)\) is a differentiable function with space coordinate x and time coordinate t, \(\rho =\pm 1\), and \(\alpha , \beta , \gamma \) are arbitrary non-zero real parameters. As an important mathematical model, Eq. (1.1) has a wide range of applications in quantum mechanics and nonlinear optics, and reveals motions of long waves in shallow water under gravity and in a one-dimensional nonlinear lattice [36,37,38,39,40]. If we take \(\rho =1, \beta =2\alpha , \gamma =\frac{2}{9}\alpha ^{2}\), Eq. (1.1) can be converted into the generalized Ito equation [41]

$$\begin{aligned} u_{t}+u_{xxxxx}+\alpha uu_{xxx}+2\alpha u_{x}u_{xx}+\frac{2}{9}\alpha ^{2}u^{2}u_{x}=0, \end{aligned}$$
(1.2)

where the parameter \(\alpha \) is non-zero constant. Its soliton solution is derived by Wazwaz in [42] with \(\alpha =3\). In this paper, we will study nonlocal symmetry of the equation via the truncated Painlevé expansion, which have not yet been discussed before. Additionally, its soliton-cnoidal wave interaction can also be obtained.

This paper is organized as follows. In Sect. 2, we obtain the nonlocal symmetry and initial value problem of the generalized Ito equation (1.2) by employing the truncated Painlevé analysis method. In Sect. 3, we use CRE method to the generalized Ito equation, and derive its interaction solution between soliton and cnoidal periodic wave. In Sect. 4, based on the Ibragimov’s theorem, the conservation laws of the equation are presented. The last section is provided for a short summary and discussion.

2 Nonlocal Symmetry and Its Localization

The truncated Painlevé analysis approach, as one of the most effective and power methods, is widely applied to seek nonlinear waves of NLEEs. Based on this method, we will consider the generalized Ito equation (1.2). For Eq. (1.2), we have the following truncated Painlevé expansion of the form

$$\begin{aligned} u=\frac{u_{2}}{\phi ^{2}}+\frac{u_{1}}{\phi }+u_{0}, \end{aligned}$$
(2.1)

where \(\phi =\phi (x,t)\) is a singular manifold, and \(u_{0}, u_{1}, u_{2}\) are functions with x and t to be known later. Substituting the above expression (2.1) into Eq. (1.2), we can get a complicated function in regard to \(u_{0}, u_{1}, u_{2}, \phi \). By vanishing all the coefficients of each powers of \(\phi \) for the obtained equation, we can obtain the following results

$$\begin{aligned}{} & {} u_{2}=-\frac{90\phi _{x}^{2}}{\alpha },~~u_{1}=\frac{90\phi _{xx}}{\alpha },~~u_{0}=-\frac{15(4\phi _{x}\phi _{xxx}-3\phi _{xx}^{2})}{2\alpha \phi _{x}^{2}}, \end{aligned}$$
(2.2)
$$\begin{aligned}{} & {} 3\phi _{xx}^{3}-4\phi _{x}\phi _{xx}\phi _{xxx}+\phi _{x}^{2}\phi _{xxxx}=0, \end{aligned}$$
(2.3)
$$\begin{aligned}{} & {} u_{0t}+u_{0xxxxx}+\alpha u_{0}u_{0xxx}+2\alpha u_{0x}u_{0xx}+\frac{2}{9}\alpha ^{2}u_{0}^{2}u_{0x}=0. \end{aligned}$$
(2.4)

It is obvious that Eq. (2.4) is just Eq. (1.2) with the solution \(u_{0}\) and the residual \(u_{1}\) is the symmetry corresponding to the solution \(u_{0}\) based on the residual symmetry theorem presented in [43]. So we can get a solution of Eq. (1.2) given by

$$\begin{aligned} u=-\frac{90\phi _{x}^{2}}{\alpha \phi ^{2}}+\frac{90\phi _{xx}}{\alpha \phi }+u_{0}, \end{aligned}$$
(2.5)

which is an auto-Bäcklund transformation between u and \(u_{0}\).

In terms of the nonlocal symmetry \(\sigma ^{u}=\frac{90\phi _{xx}}{\alpha }\), the corresponding initial value problem is written as

$$\begin{aligned} \frac{d\overline{u}(\epsilon )}{d\epsilon }=\frac{90\overline{\phi }_{xx}}{\alpha },~~~\overline{u}(\epsilon )|_{\epsilon =0}=u, \end{aligned}$$
(2.6)

where \(\epsilon \) means infinitesimal parameter. Subsequently, we introduce the following new dependent variables

$$\begin{aligned} f=\phi _{x},~~~h=f_{x},~~~\rho =\phi _{t}, \end{aligned}$$
(2.7)

so that the nonlocal residual symmetry becomes the local Lie point symmetry of the closed prolonged system.

For Eq. (2.6), it is not hard to find that the nonlocal residual symmetry for (1.2) can be localized to the Lie point symmetry of form

$$\begin{aligned} \sigma ^{u}=\frac{90h}{\alpha },~~ \sigma ^{\phi }=-\phi ^{2},~~ \sigma ^{f}=-2\phi f, ~~ \sigma ^{h}=-2f^{2}-2\phi h,~~\sigma ^{\rho }=-2\phi \rho , \end{aligned}$$
(2.8)

for the prolonged system

$$\begin{aligned}&u_{t}+u_{xxxxx}+\alpha uu_{xxx}+2\alpha u_{x}u_{xx}+\frac{2}{9}\alpha ^{2}u^{2}u_{x}=0,\nonumber \\&u=-\frac{15(4\phi _{x}\phi _{xxx}-3\phi _{xx}^{2})}{2\alpha \phi _{x}^{2}},\nonumber \\&f=\phi _{x},\nonumber \\&h=f_{x},\nonumber \\&\rho =\phi _{t}. \end{aligned}$$
(2.9)

Therefore the corresponding Lie symmetry vector is derived by

$$\begin{aligned} V=\frac{90h}{\alpha }\frac{\partial }{\partial u}-\phi ^{2}\frac{\partial }{\partial \phi }-2\phi f\frac{\partial }{\partial f}-2(f^{2}+\phi h)\frac{\partial }{\partial h}-2\phi \rho \frac{\partial }{\partial \rho }. \end{aligned}$$
(2.10)

Meanwhile the initial value problem (2.6) becomes

$$\begin{aligned}&\frac{d\overline{u}(\epsilon )}{d\epsilon }=\frac{90h}{\alpha },~~~\overline{u}(\epsilon )|_{\epsilon =0}=u,\nonumber \\&\frac{d\overline{\phi }(\epsilon )}{d\epsilon }=-\phi ^{2},~~~\overline{\phi }(\epsilon )|_{\epsilon =0}=\phi ,\nonumber \\&\frac{d\overline{f}(\epsilon )}{d\epsilon }=-2\phi f,~~~\overline{f}(\epsilon )|_{\epsilon =0}=f,\nonumber \\&\frac{d\overline{h}(\epsilon )}{d\epsilon }=-2 f^{2}-2 \phi h,~~~\overline{h}(\epsilon )|_{\epsilon =0}=h,\nonumber \\&\frac{d\overline{\rho }(\epsilon )}{d\epsilon }=-2\phi \rho ,~~~\overline{\rho }(\epsilon )|_{\epsilon =0}=\rho . \end{aligned}$$
(2.11)

By further calculating the initial value problem, we have the following theorem.

Theorem 1

If \({u, \phi , f, h, \rho }\) is a solution of the prolonged system (2.9), so \({\overline{u}}, \overline{\phi }, \overline{f}, \overline{h}, \overline{\rho }\) can be given by

$$\begin{aligned}&\overline{\phi }(\epsilon )=\frac{\phi }{\epsilon \phi +1}, ~~\overline{f}(\epsilon )=\frac{f}{(\epsilon \phi +1)^{2}},\nonumber \\ {}&\overline{h}(\epsilon )=\frac{h+h\phi \epsilon -2f^{2}\epsilon }{(\epsilon \phi +1)^3},~~\overline{\rho }(\epsilon )=\frac{\rho }{(\epsilon \phi +1)^{2}},\nonumber \\&\overline{u}(\epsilon )=\frac{\alpha \phi ^{2}u\epsilon ^{2}+2\alpha \phi u\epsilon -90f^{2}\epsilon ^{2}+90h\phi \epsilon ^{2}+\alpha u+90h\epsilon }{\alpha (\epsilon \phi +1)^{2}}, \end{aligned}$$
(2.12)

with infinitesimal parameter \(\epsilon \).

3 Consistent Riccati Expansion Method and Interaction Solution

In this section, by employing the CRE approach provided in [44,45,46], we mainly introduce a new form of solution as follows

$$\begin{aligned} u=u_{2}R(w)^{2}+u_{1}R(w)+u_{0}, \end{aligned}$$
(3.1)

where \(u_{2}, u_{1}, u_{0}\) are the determined functions with x and t, and R(w) is a special solution for the following Riccati equation

$$\begin{aligned} R_{w}=a_{0}+a_{1}R+a_{2}R^{2}, \end{aligned}$$
(3.2)

with R(w) being a general solution with respect to \(\tanh (w)\), and arbitrary constants \(a_{0}, a_{1}, a_{2}\). By substituting (3.1) and (3.2) into (1.2), and making coefficients of all the same powers of R(w) to zero, one can find

$$\begin{aligned}&u_{2}=-\frac{90a_{2}^{2}w_{x}^{2}}{\alpha },~~u_{1}=-\frac{90a_{2}(a_{1}w_{x}^{2}+w_{xx})}{\alpha },\nonumber \\&u_{0}=-\frac{15(8a_{0}a_{2}w_{x}^{4}+a_{1}^{2}w_{x}^{4}+6a_{1}w_{x}^{2}w_{xx}+4w_{x}w_{xxx}-3w_{xx}^{2})}{2\alpha w_{x}^{2}}, \end{aligned}$$
(3.3)
$$\begin{aligned} \delta&w_{x}^{4}w_{xx}+4w_{x}w_{xx}w_{xxx}-w_{x}^{2}w_{xxxx}-3w_{xx}^{3}=0, \end{aligned}$$
(3.4)

with \(\delta =a_{1}^{2}-4a_{0}a_{2}\). To clarify the solution more clearly, we introduce a theorem as follows.

Theorem 2

If w is a solution of Eq. (3.4), then

$$\begin{aligned}&u=-\frac{90a_{2}^{2}w_{x}^{2}}{\alpha }R(w)^{2}-\frac{90a_{2}(a_{1}w_{x}^{2}+w_{xx})}{\alpha }R(w)\nonumber \\&\quad ~~~~~-\frac{15(8a_{0}a_{2}w_{x}^{4}+a_{1}^{2}w_{x}^{4}+6a_{1}w_{x}^{2}w_{xx}+4w_{x}w_{xxxx}-3w_{xx}^{2})}{2\alpha w_{x}^{2}}, \end{aligned}$$
(3.5)

is a solution of the generalized Ito equation (1.2) with a solution R(w) for the Riccati equation (3.2).

In next work, we will focus on interaction solutions which can be used to describe some interesting physical phenomena of the generalized Ito equation (1.2). By investigating Eq. (3.4), let us suppose w of the following form

$$\begin{aligned} w=k_{1}x+d_{1}t+W(k_{2}x+d_{2}t), \end{aligned}$$
(3.6)

where

$$\begin{aligned} W=W(X)=W(k_{2}x+d_{2}t) \end{aligned}$$
(3.7)

satisfies the following two expressions

$$\begin{aligned}&W_{1X}^{2}=C_{0}+C_{1}W_{1}+C_{2}W_{1}^{2}+C_{3}W_{1}^{3}+C_{4}W_{1}^{4},\nonumber \\&W_{1}=W_{X}, \end{aligned}$$
(3.8)

with

$$\begin{aligned}&C_{0}=\frac{\delta k_{1}^{4}+2C_{1}k_{1}k_{2}^{3}-C_{2}k_{1}^{2}k_{2}^{2}}{3k_{2}^{4}},\nonumber \\&C_{3}=\frac{4\delta k_{1}^{3}-C_{1}k_{2}^{3}+2C_{2}k_{1}k_{2}^{2}}{3k_{1}^{2}k_{2}},\nonumber \\&C_{4}=\delta . \end{aligned}$$
(3.9)

In order to construct Jacobi elliptic function interaction solutions, we study \(W_{1}\) in the form of

$$\begin{aligned} W_{1}=\mu _{0}+\mu _{1}sn(mX,n). \end{aligned}$$
(3.10)

Moreover, by integrating the above Eq. (3.10), one can obtain W in the form of

$$\begin{aligned} W=\mu _{0}X+\mu _{1}\int _{X_{0}}^{X}sn(mY,n)dY. \end{aligned}$$
(3.11)

Substituting (3.9) and (3.10) into (3.8), we have

$$\begin{aligned}&C_{1}=\frac{4k_{1}\delta \mu _{0}(2k_{1}+k_{2}\mu _{0})}{k_{2}^{2}},~~m=\frac{\sqrt{\delta }(k_{1}+k_{2}\mu _{0})}{k_{2}},\nonumber \\&C_{2}=-\frac{2\delta (k_{1}^{2}+2k_{1}k_{2}\mu _{0}-2k_{2}^{2}\mu _{0}^{2})}{k_{2}^{2}},~~\mu _{1}=\frac{k_{1}+k_{2}\mu _{0}}{k_{2}}, \end{aligned}$$
(3.12)

where \(k_{1}, k_{2}, \mu _{0}\) are arbitrary constants.

Based on the above analysis, an interaction solution between soliton and canoidal periodic wave is expressed by

$$\begin{aligned}&u=\frac{15[8(k_{1}+k_{2}W_{1})^{4}-4k_{2}^{3}W_{1XX}(k_{1}+k_{2}W_{1})]}{2\alpha (k_{1}+k_{2}W_{1})}+\frac{90k_{2}^{2}W_{1X}}{\alpha }\tanh (k_{1}x+d_{1}t+W)\nonumber \\&\quad -\frac{90(k_{1}+k_{2}W_{1})^{2}}{\alpha }\tanh (k_{1}x+d_{1}t+W)^{2}, \end{aligned}$$
(3.13)

where \(W_{1}, W\) are given by (3.10) and (3.11).

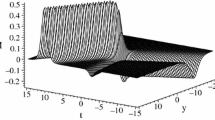
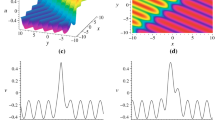
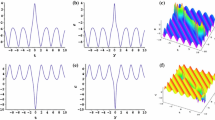
Based on different parameters, Figs. 1 and 2 reveal the propagation situation of interaction solution (3.13) between soliton wave and cnoidal periodic wave, respectively.

Fig. 1
figure 1

Interaction solution (3.13) between soliton waves and cnoidal periodic waves by choosing appropriate parameters: \(k_{1}=-\,0.5, k_{2}=0.9, d_{1}=1, d_{2}=1, \mu _{0}=1, n=0.2, \delta =4\). a Evolution of the soliton-cnoidal structure. b The Profile of the special structure at \(t=0\). \({\textbf {(c)}}\) The Profile of the special structure at \(x=0\)

Full size image
Fig. 2
figure 2

Interaction solution (3.13) between soliton waves and cnoidal periodic waves by choosing appropriate parameters: \(k_{1}=-0.6, k_{2}=1.31, d_{1}=1, d_{2}=1, \mu _{0}=1, n=0.5, \delta =4\). a Evolution of the soliton-cnoidal structure. b The Profile of the special structure at \(t=0\). c The Profile of the special structure at \(x=0\)

Full size image

4 Conservation Laws

In this section, we first present some concepts and formulations to construct the conservation laws of the generalized Ito equation (1.2). We consider a general form of systems

$$\begin{aligned} F_{\alpha }(x,u,u_{(1)},\cdots ,u_{(s)}), ~~~\alpha =1,2,\cdots ,m, \end{aligned}$$
(4.1)

where \(x=(x_{1},x_{2},\cdots ,x_{n})\) are n independent variables, \(u=(u^{1},u^{2},\cdots ,u^{m})\) are m dependent variables and \(u_{(s)}\) is s-th order partial derivatives.

Theorem 3

The adjoint equation of Eq. (4.1) is given by

$$\begin{aligned} F_{\alpha }^{*}(x,u,v,u_{(1)},v_{(1)},\cdots ,u_{(s)},v_{(s)})=\frac{\delta L}{\delta u^{\alpha }}, ~~~\alpha =1,2,\cdots ,m. \end{aligned}$$
(4.2)

with

$$\begin{aligned} \frac{\delta }{\delta u^{\alpha }}=\frac{\partial }{\partial u^{\alpha }}+\sum _{s=1}^{\infty }(-1)^{s}D_{i_{1}}\cdots D_{i_{s}}\frac{\partial }{\partial u_{i_{1}\cdots i_{s}}^{\alpha }}. \end{aligned}$$
(4.3)

Here, the formal Lagrangian for Eq. (4.1) is

$$\begin{aligned} L=\sum _{\beta =1}^{m}v^{\beta }F_{\beta }(x,u,u_{(1)},\cdots ,u_{(s)}), \end{aligned}$$
(4.4)

with \(v=v(v^{1},v^{2},\cdots ,v^{m})\) being new dependent variables about x.

Theorem 4

Each infinitesimal symmetry

$$\begin{aligned} X=\xi ^{j}(x,u,u_{(1)},\cdots )\frac{\partial }{\partial x^{j}}+\eta ^{\alpha }(x,u,u_{(1)},\cdots )\frac{\partial }{\partial u^{\alpha }}, ~~~j=1,2,\cdots ,n, \end{aligned}$$
(4.5)

for Eq. (4.1) leads to a conservation law \(D_{j}(C^{j})=0\) constructed by

$$\begin{aligned}&C^{j}=\xi ^{j}L+W^{\alpha }\Bigg [\frac{\partial L}{\partial u_{j}^{\alpha }}-D_{i}\left( \frac{\partial L}{\partial u_{ji}^{\alpha }}\right) +D_{i}D_{k}\left( \frac{\partial L}{\partial u_{jik}^{\alpha }}\right) -\cdots \Bigg ]+D_{i}(W^{\alpha })\Bigg [\frac{\partial L}{\partial u_{ji}^{\alpha }}\nonumber \\&~~~~-D_{k}\left( \frac{\partial L}{\partial u_{jik}^{\alpha }}\right) +\cdots \Bigg ]+D_{i}D_{k}(W^{\alpha })\Bigg [\frac{\partial L}{\partial u_{jik}^{\alpha }}-\cdots \Bigg ], \end{aligned}$$
(4.6)

with

$$\begin{aligned} W^{\alpha }=\eta ^{\alpha }-\xi ^{i}u_{i}^{\alpha }. \end{aligned}$$
(4.7)

According to the above Theorem, on the one hand, we construct the following Lagrangian form of Eq. (1.2)

$$\begin{aligned} L=v(u_{t}+u_{xxxxx}+\alpha uu_{xxx}+2\alpha u_{x}u_{xx}+\frac{2}{9}\alpha ^{2}u^{2}u_{x}), \end{aligned}$$
(4.8)

where v is a new dependent variables. Substituting (4.8) into (4.2), then the adjoint equation of Eq. (1.2) yields

$$\begin{aligned} F^{*}=\frac{\delta L}{\delta u}=0, \end{aligned}$$
(4.9)

with

$$\begin{aligned} \frac{\delta L}{\delta u}=\frac{\partial L}{\partial u}-D_{x}\frac{\partial L}{\partial u_{x}}-D_{t}\frac{\partial L}{\partial u_{t}}+D_{x}^{2}\frac{\partial L}{\partial u_{xx}}-D_{x}^{3}\frac{\partial L}{\partial u_{xxx}}-D_{x}^{5}\frac{\partial L}{\partial u_{xxxxx}}. \end{aligned}$$
(4.10)

In view of (4.8), the adjoint equation (4.9) can be deduced to

$$\begin{aligned} F^{*}=-v_{t}-v_{xxxxx}-\alpha v_{xxx}u-\alpha v_{x}u_{xx}-\alpha v_{xx}u_{x}-\frac{2}{9}\alpha ^{2}v_{x}u^{2}=0. \end{aligned}$$
(4.11)

If we substitute \(-u\) instead of v in (4.11), Eq. (1.2) is derived.

On the other hand, we represent a general vector formalism of (4.1)

$$\begin{aligned} X=\xi ^{1}\frac{\partial }{\partial t}+\xi ^{2}\frac{\partial }{\partial x}+\eta ^{1}\frac{\partial }{\partial u}. \end{aligned}$$
(4.12)

The corresponding conservation law is constructed by

$$\begin{aligned} D_{t}(C^{t})+D_{x}(C^{x})=0, \end{aligned}$$
(4.13)

where \(C=(C^{t},C^{x})\) means the conserved vector, i.e.,

$$\begin{aligned}&C^{t}=\xi ^{1}L+W^{1}\left( \frac{\partial L}{\partial u_{t}}\right) ,\nonumber \\&C^{x}=\xi ^{2}L+W^{1}\Bigg [\frac{\partial L}{\partial u_{x}}-D_{x}\left( \frac{\partial L}{\partial u_{xx}}\right) +D_{x}^{2}\left( \frac{\partial L}{\partial u_{xxx}}\right) +D_{x}^{4}\left( \frac{\partial L}{\partial u_{xxxxx}}\right) \Bigg ]\nonumber \\&\quad ~~~~+D_{x}(W^{1})\Bigg [\frac{\partial L}{\partial u_{xx}}-D_{x}\left( \frac{\partial L}{\partial u_{xxx}}\right) -D_{x}^{3}\left( \frac{\partial L}{\partial u_{xxxxx}}\right) \Bigg ]\nonumber \\&\quad ~~~~+D_{x}^{2}(W^{1})\Bigg [\frac{\partial L}{\partial u_{xxx}}+D_{x}^{2}\left( \frac{\partial L}{u_{xxxxx}}\right) \Bigg ]\nonumber \\&\quad ~~~~+D_{x}^{3}(W^{1})\Bigg [-D_{x}\left( \frac{\partial L}{\partial u_{xxxxx}}\right) \Bigg ]\nonumber \\&\quad ~~~~+D_{x}^{4}(W^{1})\Bigg [\frac{\partial L}{\partial u_{xxxxx}}\Bigg ], \end{aligned}$$
(4.14)

with

$$\begin{aligned} W^{1}=\eta ^{1}-\xi ^{1}u_{t}-\xi ^{2}u_{x}. \end{aligned}$$
(4.15)

Theorem 5

We can obtain the following three geometric vectors for Eq. (1.2)

$$\begin{aligned}&X_{1}=\frac{\partial }{\partial t},\nonumber \\&X_{2}=\frac{\partial }{\partial x},\nonumber \\&X_{3}=\frac{1}{5}x\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{2}{5}u\frac{\partial }{\partial u}, \end{aligned}$$
(4.16)

by employing the Lie symmetry analysis method.

Then, we can derive the following conserved vectors of Eq. (1.2) by discussing the symmetry generators \(X_{1}, X_{2}, X_{3}\).

Case 1 For the generator

$$\begin{aligned} X_{1}=\frac{\partial }{\partial t}, \end{aligned}$$
(4.17)

the corresponding Lie characteristic function is

$$\begin{aligned} W^{1}=-u_{t}, \end{aligned}$$
(4.18)

then we can obtain the conserved vector of Eq. (1.2)

$$\begin{aligned}&C^{t}=-uu_{xxxxx}-\alpha u^{2}u_{xxx}-2\alpha uu_{x}u_{xx}-\frac{2}{9}\alpha ^{2}u^{3}u_{x},\nonumber \\&C^{x}=\frac{2}{9}\alpha ^{2}u^{3}u_{t}+2\alpha uu_{xx}u_{t}+u_{xxxx}u_{t}-u_{xxx}u_{tx}+\alpha u^{2}u_{txx}+u_{xx}u_{txx}\nonumber \\&\quad ~~~~~~~-u_{x}u_{txxx}+uu_{txxxx}. \end{aligned}$$
(4.19)

Case 2 For the generator

$$\begin{aligned} X_{2}=\frac{\partial }{\partial x}, \end{aligned}$$
(4.20)

the corresponding Lie characteristic function is

$$\begin{aligned} W^{1}=-u_{x}, \end{aligned}$$
(4.21)

then we can obtain the conserved vector of Eq. (1.2)

$$\begin{aligned}&C^{t}=uu_{x},\nonumber \\&C^{x}=-uu_{t}. \end{aligned}$$
(4.22)

Case 3 For the generator

$$\begin{aligned} X_{3}=\frac{1}{5}x\frac{\partial }{\partial x}+t\frac{\partial }{\partial t}-\frac{2}{5}u\frac{\partial }{\partial u}, \end{aligned}$$
(4.23)

the corresponding Lie characteristic function is

$$\begin{aligned} W^{1}=-\frac{2}{5}u-\frac{1}{5}xu_{x}-tu_{t}, \end{aligned}$$
(4.24)

then we can obtain the conserved vector of Eq. (1.2)

$$\begin{aligned}&C^{t}=-tuu_{xxxxx}-\alpha tu^{2}u_{xxx}-2\alpha tuu_{x}u_{xx}-\frac{2}{9}\alpha ^{2}tu^{3}u_{x}+\frac{2}{5}u^{2}+\frac{1}{5}xuu_{x},\nonumber \\&C^{x}=-\frac{1}{5}xuu_{t}+\frac{4}{45}\alpha ^{2}u^{4}+\frac{4}{5}u_{xx}^{2}+\frac{2}{9}\alpha ^{2}tu^{3}u_{t}+\frac{8}{5}\alpha u^{2}u_{xx}+\frac{8}{5}uu_{xxxx}-\frac{8}{5}u_{x}u_{xxx}\nonumber \\&+2\alpha tuu_{xx}u_{t}+tu_{xxxx}u_{t}-tu_{tx}u_{xxx}+\alpha tu^{2}u_{txx}+tu_{xx}u_{txx}-tu_{x}u_{txxx}+tuu_{txxxx}. \end{aligned}$$
(4.25)

5 Conclusions and Discussions

In this work, we have investigated the generalized Ito equation. In view of the truncated Painlevé expansion method, its auto-Bäcklund transformation and nonlocal symmetry have been derived, respectively. By prolonging the generalized Ito equation to a closed prolonged system, its nonlocal symmetry would be localized to the corresponding Lie point symmetry. Moreover, based on CRE method, we have constructed an interaction solution between soliton and canoidal periodic wave with a Jacobi sine function. The dynamic behavior characteristics of interaction solution have been revealed by Figs. 1 and 2. Additionally, three groups of conservation laws for the generalized Ito equation (1.2) have been constructed in detail. It is hoped that the results of this work can help to enrich the dynamic behavior of the equation.