1 Introduction

When designing strip footings in engineering practices, the primary objective is to achieve the prescribed safety level, where one of the fundamental principles is to achieve a uniformly distributed contact pressure beneath the foundation to the greatest extent possible. The most straightforward approach to accomplish this is to align the center of the footing’s surface as closely as possible with the center of external loads. In cases where strip footings are subjected to concentrated loads from columns and walls of varying loading sizes, the effort to achieve uniform contact pressure beneath the foundation may result in irregular (tapered or stepped) shapes of strip footings, most commonly trapezoidal. Tapered strip footings thus provide an effective solution to overcome the challenge of ensuring a suitably uniform distribution of contact pressure. The tapered (as well as stepped) shape of strip footings also offers potential economic benefits by allowing dimensional adjustments where necessary, such as to reduce moments and shear forces. However, stepped footings can lead to issues related to stress concentration at the connections of individual sections.

In studying this problem, all three key components must be properly modeled, namely the soil, the footing and the crack. In those rare situations when analytical solutions are available [1, 2], the utilization of 2D and/or 3D FE meshes is being more or less reduced to verification tools. On the other hand, where analytical solutions are not available, such meshes can provide essential information not obtainable otherwise. This modeling strategy namely ensures the provision of accurate information regarding the response of cracked beams on an elastic medium, as it comprehensively addresses all three previously mentioned components. However, such analyses are extremely time-consuming and usually unsuitable for widespread utilization in practice. The analysis can also be done in a convenient and satisfactory way by using computationally simpler models. Thus, when the main objective is a bending analysis of the transverse response of a cracked slender beam rather than a soil, the Euler–Bernoulli beam on an elastic medium proved to be effective, as confirmed by numerous analytical and numerical studies [3].

Various approaches have been developed for simplified mathematical modeling of cracks in beams. The two well-known approaches for simple crack modeling are the flexural stiffness reduction model and the discrete spring (DS) model. The present study focuses on the latter, which represents the best compromise between accuracy and computational cost in analyses where the exact stress distribution near the crack is not in the interest of the research (i.e., in inverse crack identification [4, 5]). One of the main advantages of the DS model is also the effective representation of the position and the depth of the crack. In this model, two undamaged segments are pinned at the crack location with an equivalent massless rotational spring, which represents the reduced local bending stiffness of the cracked part of the beam.

Cracked beams on elastic medium can be efficiently modeled with the DS model for transverse displacement analyses, as confirmed by a many studies [6,7,8]. The first and also the simplest of all elastic media soil models is the one-parameter Winkler’s model. In this model, the elastic medium is modeled with linear and mutually independent springs that allow deformations only directly under load. Despite an inadequate mechanical description, this conservative model is still widely used for a variety of mechanical analyses, including cracked beam analysis. In a recent study, a new finite element was developed using interpolation functions derived from exact analytical solutions of a cracked beam on an elastic Winkler medium [9]. This allows the computation of analytically accurate transverse displacements under uniform continuous load even for the minimalistic finite element discretization of the structure.

A major shortcoming of the Winkler’s model is that it does not take into account the continuous transverse displacement behavior of the loaded and unloaded part of soil due to the neglect of the shear stresses. Due to the above shortcomings of the Winkler model, a two-parameter (Pasternak) model was later presented in which the shear interaction between the springs is also taken into account by adding a shear layer over the springs [10]. The results of the researches showed that the behavior of the soil is, therefore, more realistically represented by this model [11]. In a recent study, a new finite element for the static analysis of transversely cracked slender uniform prismatic beams on two-parameter elastic medium was derived [12]. Hermitian cubic polynomial functions were utilized to derive the stiffness matrix and the load vector, which include the shear parameter due to the continuity condition of the transverse forces at the crack location. Moreover, another recent study presents a beam finite element for the same type of analysis, which was derived using Winkler’s analytically exact interpolation functions [13]. The finite elements presented in both studies provide great approximate results for nodal values and functions of transverse displacements even for the minimalistic finite element discretization of the structure. Transverse displacement values rapidly converge to exact analytical solutions of the governing differential equation of two-parameter model when the finite element mesh is condensed. The moment functions presented in both of the above-mentioned studies do not take into account the discontinuity conditions at the crack location, which consequently requires a much denser finite element meshing in the vicinity of the crack to achieve the analytical values solidly.

This study extends the finite element for the static analysis of cracked Euler–Bernoulli slender tapered beams on an elastic two-parameter medium. All expressions were derived with the standard (and at the same time the simplest) Hermitian interpolation functions, which have been already applied in numerous analyses of cracked beams and consequently do not include soil parameters. Another novelty of this study is the enhanced bending moment functions that include discontinuity conditions at the crack location.

2 Theoretical background and simplified mathematical model formulation

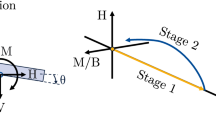
In this paper a transversely cracked strip tapered footing resting on elastic soil for linear static analysis was considered, Fig. 1a. For the transverse response analysis, the strip footing is computationally efficiently modeled as a slender Euler–Bernoulli beam under \(x-y\) plane stress conditions. The beam of length L has a rectangular cross section with a uniform height \(h_{\textrm{0}}\) and linear variation of the width b(x) along the x-axis defined as:

$$\begin{aligned} b\left( x \right) =b_{0} \cdot \left( {1-\beta \cdot x} \right) \end{aligned}$$
(1)

with the width tapering parameter \(\beta =\frac{b_{0} -b_{1} }{b_{0} \cdot L}\), where the \(b_{0}\) and \(b_{1}\) are widths at left and right end of the beam.

The bending stiffness of the beam EI\(_{z}(x)\), which is the product of the Young’s modulus E and the moment of inertia \(I_{z}(x)=h_{\textrm{0}}^{\textrm{3}}\) \(\cdot \) b(x)/12, is thus defined as:

$$\begin{aligned} EI_{z} \left( x \right) =EI_{0} \cdot \left( {1-\beta \cdot x} \right) \end{aligned}$$
(2)

with the bending stiffness \(EI_{0} =\frac{E\cdot b_{0} \cdot h_{0} ^{3}}{12}\) at the left end of the beam.

A crack of depth d is represented by an alternate linear elastic rotational discrete spring of stiffness \(K_{r}\), Fig. 1b. The beam material is isotropic, homogeneous and linearly elastic, and the soil, exhibiting the same material behavior as the beam, is represented by a two-parameter (Pasternak) model.

Fig. 1
figure 1

a Cracked tapered strip footing resting on elastic soil; b corresponding DS model on two-parameter soil

Full size image

2.1 Crack definition

For rectangular sections, many definitions of the stiffness of a rotational spring for a transverse crack have been proposed [14,15,16,17]. Most of them have the same basic mathematical form and differ only in the definition of the compliance function. For this study, we have deliberately chosen Okamura’s definition, which uniquely incorporates Poisson’s ratio [18]. This genuine definition is commendably in agreement with experimental values, particularly for the half-cracked section, providing additional validation for its selection [19]. Okamura’s definition is expressed as follows:

$$\begin{aligned} K_{r} =\frac{EI\left( {L_{1} } \right) }{h\cdot 6\cdot (1-\nu ^{2})\cdot F(\delta ')} \end{aligned}$$
(3)

where: EI\(_{z}(L_{\textrm{1}})\)—bending stiffness of non-cracked cross section, defined as product of the Young’s modulus E and the moment of inertia \(I_{z}\) of the rectangular cross section; \(\nu \)—Poisson’s ratio; \(\delta '=d/h_{0}\)—relative crack depth; \(F(\delta ')\)—compliance function for a rectangular section which is defined as:

$$\begin{aligned} \begin{array}{ll} F(\delta ')&{}=1.98\cdot \delta '^{2}-3.277\cdot \delta '^{3}+14.43\cdot \delta '^{4}-31.26\cdot \delta '^{5}+63.56\cdot \delta '^{6} \\ &{}\quad -103.36\cdot \delta '^{7}+147.52\cdot \delta '^{8}-127.69\cdot \delta '^{9}+61.50\cdot \delta '^{10} \\ \end{array} \end{aligned}$$
(4)

2.2 Governing differential equation of tapered slender beam on two-parameter soil

Reacting pressure \(\bar{{p}}(x)\) in the soil due to Winkler springs and Pasternak shear layer which occurs as a result of the acting distributed continuous load p(x) and the concentrated forces F on the strip footing (modeled as beam) can be written as:

$$\begin{aligned} \bar{{p}}(x)=k(x)\cdot v(x)-\frac{\textrm{d}}{\textrm{d}x}\left( {k_{G} (x)\cdot \frac{\textrm{d}v(x)}{\textrm{d}x}} \right) \end{aligned}$$
(5)

where the transverse load p(x) and any concentrated forces F are assumed to be located act through at the center of the cross section along the beam axis.

In Eq. (5), the k(x) is Winkler proportionality parameter function defined from the product of modulus of the subgrade reaction \(k_{s}\) and beam width b(x) and the \(k_{G}(x)\) is Pasternak proportionality parameter function defined from the product of shear modulus of the shear layer \(G_{p}\) and the beam width b(x). Further, by taking into account b(x) from Eq. (1), both proportionality functions were written in their final form as:

$$\begin{aligned} k(x)=k_{0} \cdot \left( {1-\beta \cdot x} \right) \end{aligned}$$
(6)

and

$$\begin{aligned} k_{G} (x)=k_{G,0} \cdot \left( {1-\beta \cdot x} \right) \end{aligned}$$
(7)

where \(k_{0}\)—product of \(k_{s}\) and \(b_{0}\); \(k_{G,0}\)—product of \(G_{p}\) and \(b_{0}\).

In addition, the elastostatic bending problem of a slender tapered beam on an elastic two-parameter soil with distributed continuous acting load and reacting pressure was formulated by the classical Euler–Bernoulli differential equation:

$$\begin{aligned} \frac{\textrm{d}^{2}}{\textrm{d}x^{2}}\left( {EI_{z} (x)\cdot \,\frac{\textrm{d}v^{2}(x)}{\textrm{d}x^{2}}} \right) =p(x)-\bar{{p}}(x) \end{aligned}$$
(8)

By considering Eq. (5), Eq. (8) was written in the final general form for the presented problem as:

$$\begin{aligned} \frac{\textrm{d}^{2}}{\textrm{d}x^{2}}\left( {EI_{z} \left( x \right) \cdot \,\frac{\textrm{d}v^{2}\left( x \right) }{\textrm{d}x^{2}}} \right) +k(x)\cdot v\left( x \right) -\frac{\textrm{d}}{\textrm{d}x}\left( {k_{G} (x)\cdot \frac{\textrm{d}v\left( x \right) }{\textrm{d}x}} \right) =p\left( x \right) \end{aligned}$$
(9)

There is no existing exact analytical solution to this governing differential equation (GDE), so the solution must be found using numerical methods such as the finite element method (FEM).

3 Finite element model formulation

In this section, the stiffness matrix and load vector of the two-node finite element of the cracked tapered strip footing resting on elastic soil were newly derived for the static analysis. Furthermore, new improved bending moment functions were developed for post-processing analyses, which additionally take into account the discontinuity conditions at the crack location. All the theoretical foundations presented in the previous section also apply to the FE model considered in this section.

The presented FE has two standard nodes 1 and 2 on the endpoints and therefore altogether four degrees of freedom; these are the upwards positive transverse displacements \(Y_{1}\) and \(Y_{2}\) and the anticlockwise rotations \(\varPhi _{1}\) and \(\varPhi _{2}\), Fig. 2.

Fig. 2
figure 2

Two-node finite element model of the cracked beam

Full size image

3.1 Selection of the cracked beam’s interpolation functions

To describe the transverse displacements of both segments \(v_{1}(x)\)    and \(v_{2}(x)\), complete cubic polynomial functions were utilized as approximation functions.

$$\begin{aligned}{} & {} v_{1} (x)=a_{1} +a_{2} \cdot x+a_{3} \cdot x^{2}+a_{4} \cdot x^{3}\,\,\,\,\,\,\,\,\,\,\,\,\,(0\le x\le L_{1} ) \end{aligned}$$
(10)
$$\begin{aligned}{} & {} v_{2} (x)=b_{1} +b_{2} \cdot x+b_{3} \cdot x^{2}+b_{4} \cdot x^{3}\,\,\,\,\,\,\,\,\,\,\,\,\,(L_{1} \le x\le L) \end{aligned}$$
(11)

The eight unknown coefficients (\(a_{\textrm{1}}\), \(a_{\textrm{2}}\), \(a_{\textrm{3}}\), \(a_{\textrm{4}}\), \(b_{\textrm{1}}\), \(b_{\textrm{2}}\), \(b_{\textrm{3}}\) and \( b_{\textrm{4}})\) from Eqs. (10) and (11) were determined from the four standard boundary conditions on both endpoints of the finite element (\(v_{1} (0)=Y_{1} \), \(v_{1} '(0)=\varPhi _{1} \), \(v_{2} (L)=Y_{2} \), \(v_{2} '(L)=\varPhi _{2} )\), three continuity conditions between both elastic segments at the crack location (\(v_{1} (L_{1} )=v_{2} (L_{1} )\), \(v_{1} ''(L_{1} )=v_{2} ''(L_{1} )\), \(v_{1} '''(L_{1} )=v_{2} '''(L_{1} ))\), and the condition of slope discontinuity, which is:

$$\begin{aligned} v_{1} '(L_{1} )+\psi \cdot v_{1} ''(L_{1} )=v_{2} '(L_{1} ) \end{aligned}$$
(12)

where abbreviation \(\psi \) is the ratio between bending stiffness of the non-cracked cross section EI\(_{z}(L_{\textrm{1}})\) at the crack location and the rotational springs stiffness \(K_{r}.\)

$$\begin{aligned} \psi =\frac{EI_{z} \left( {L_{1} } \right) }{K_{r} } \end{aligned}$$
(13)

Furthermore, the interpolation (or shape) functions are consequently complete cubic polynomials, by means of which transverse displacements’ function can be defined as product of interpolation function vector N\(_{i}\) (\(i=1, 2\)) and generalized displacement vector q:

$$\begin{aligned}{} & {} v_{1} (x)=\left\{ {N_{\text{1,1 }},\,N_{\text{2,1 }},\,N_{\text{3,1 }},\,N_{\text{4,1 }} } \right\} \cdot \left\{ {Y_{\text{1 }},\,\varPhi _{\text{1 }},\,Y_{\text{2 }},\,\varPhi _{\text{2 }} } \right\} ^{T}=\mathrm{\textbf{N}}_{1} \cdot \mathrm{\textbf{q}}^{T}\quad \quad \left( {0\le x\le L_{1} } \right) \end{aligned}$$
(14)
$$\begin{aligned}{} & {} v_{\text{2 }} (x)=\left\{ {N_{\text{1,2 }},\,N_{\text{2,2 }},\,N_{\text{3,2 }},\,N_{\text{4,2 }} } \right\} \cdot \left\{ {Y_{\text{1 }},\,\varPhi _{\text{1 }},\,Y_{\text{2 }},\,\varPhi _{\text{2 }} } \right\} ^{T}=\mathrm{\textbf{N}}_{2} \cdot \mathrm{\textbf{q}}^{T}\quad \quad \left( {L_{1} \le x\le L} \right) \end{aligned}$$
(15)

These transverse displacement functions are approximations, as they are modeled using cubic polynomial functions (instead of non-polynomial functions existing in exact GDE solutions). These approximations play a crucial role in obtaining solutions for the analyzed problem, striking a balance between computational efficiency and result accuracy.

The interpolation functions \(N_{i,1} \)and \(N_{i,2} \) (\(i = 1,2, 3, 4\)) from Eqs. (14) and (15) are given as:

$$\begin{aligned} N_{i\text{,1 }} \left( x \right) =\frac{\textrm{d}v_{1} (x)}{\textrm{d}\,q_{i} }=\sum \limits _{j=1}^4 {A_{i,j} \cdot x^{j\mathrm{-1}}} \quad \quad \left( {0\le x\le L_{1} } \right) \end{aligned}$$
(16)

and

$$\begin{aligned} N_{i\textrm{,2}} \left( {\textrm{x}} \right) =\frac{\textrm{d}v_{2} (x)}{\textrm{d}\,q_{i} }=\sum \limits _{j=1}^4 {B_{i,j} \cdot x^{j\mathrm{-1}}} \quad \quad \left( {L_{1} \le x\le L} \right) \end{aligned}$$
(17)

where altogether 16 unknown coefficients \(A_{ij}\) (\(i, j=1, 2, 3, 4\)) of interpolation functions from Eq. (16) were determined by utilization of Dirac \(\delta \) functions as:

$$\begin{aligned} \begin{array}{l} A_{i1} =\delta _{i,1} \\ A_{i2} =\delta _{i,2} \\ A_{i3} =\frac{2\cdot \delta _{i,2} \left( {L^{3}+3\cdot L_{\text{1 }} ^{2}\cdot \psi } \right) -\delta _{i,4} \cdot \left( {L^{3}+6\cdot L_{\text{1 }} \cdot \psi \cdot (L-L_{\text{1 }} )} \right) -3\cdot \delta _{i,1} \left( {L^{2}+2\cdot L_{\text{1 }} \cdot \psi } \right) +3\cdot \delta _{i,3} \left( {L^{2}+2\cdot L_{\text{1 }} \cdot \psi } \right) }{L^{4}+4\cdot L\cdot \psi \cdot \left( {L^{2}-3\cdot L\cdot L_{\text{1 }} +3\cdot L_{\text{1 }}^{2}} \right) } \\ A_{i4} =\frac{\delta _{i,2} \left( {L^{2}+2\cdot L_{\text{1 }} \cdot \psi } \right) +\delta _{i,4} \left( {L^{2}+2\cdot \psi \cdot (L-L_{\text{1 }} )} \right) +2\cdot \delta _{i,1} \cdot (L+\psi )\cdot -2\cdot \delta _{i,3} \cdot (L+\psi )}{L^{4}+4\cdot L\cdot \psi \cdot \left( {L^{2}-3\cdot L\cdot L_{\text{1 }} +3\cdot L_{\text{1 }}^{2}} \right) } \\ \end{array} \end{aligned}$$
(18)

Furthermore, the remaining 16 coefficients \(B_{ij}\) (\(i,j=1, 2, 3, 4\)) in Eq. (17) were expressed (with continuity and discontinuity conditions at the crack location) directly by applying the coefficients \(A_{ij}\) as follows:

$$\begin{aligned} B_{ij} =A_{ij} +2\cdot \psi \cdot (\delta _{2,j} -\text{ L}_{\text{1 }} \cdot \delta _{1,j} )\cdot (3\cdot \text{ L}_{\text{1 }} \cdot A_{i4} +A_{i3} ) \end{aligned}$$
(19)

It may be noted that these functions reduce to standard polynomial interpolation functions for the non-cracked case (\(\delta ^{\prime } =\psi = 0\)).

3.2 Derivation of stiffness matrix

The potential energy U of the work done by the internal forces can be expressed as the sum of the contributions of the beam (for two elastic parts), discrete crack (rotational spring stiffness) and the soil (the Winkler springs and Pasternak shear layer):

$$\begin{aligned} \begin{array}{l} U=\underbrace{\frac{1}{2}\cdot \int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {EI_{z} (x)\cdot \left( {\frac{\textrm{d}^{2}v_{1} (x)}{\textrm{d}x^{2}}} \right) ^{\textrm{2}}} \,\textrm{d}x+\frac{1}{2}\cdot \int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {EI_{z} (x)\cdot \left( {\frac{\textrm{d}^{2}v_{2} (x)}{\textrm{d}x^{2}}} \right) ^{\textrm{2}}} \,\textrm{d}x}_{beam}+\underbrace{\frac{1}{2}\cdot K_{r} \left( {\left. {\frac{\textrm{d}v_{1} (x)}{\textrm{d}x}} \right| _{L_{1} } -\left. {\frac{\textrm{d}v_{2} (x)}{\textrm{d}x}} \right| _{L_{1} } } \right) ^{\textrm{2}}}_{\textrm{crack}} \\ \quad +\underbrace{\frac{1}{2}\cdot \int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {k(x)\cdot v_{1} (x)^{\textrm{2}}} \,dx+\frac{1}{2}\cdot \int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {k(x)\cdot v_{2} (x)^{\textrm{2}}} \,\textrm{d}x}_{Winkler\,springs}+\underbrace{\frac{1}{2}\cdot \int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {k_{G} (x)\cdot \left( {\frac{\textrm{d}v_{1} (x)}{\textrm{d}x}} \right) ^{\textrm{2}}} \,dx+\frac{1}{2}\cdot \int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {k_{G} (x)\cdot \left( {\frac{\textrm{d}v_{2} (x)}{\textrm{d}x}} \right) ^{\textrm{2}}} \,\textrm{d}x}_{Pasternak\,\,shear\,layer}\\ \end{array}\nonumber \\ \end{aligned}$$
(20)

All the potential energy contributions from Eq. (20), taking into account the selected vectors of the interpolation function from Eqs. (14) and (15), were considered together in the complete finite element stiffness matrix K:

$$\begin{aligned} \mathrm{\textbf{K}}&=\int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {EI_{z} (x)\cdot \left( {\frac{\textrm{d}^{2}\mathrm{\textbf{N}}_{1} }{\textrm{d}x^{2}}} \right) ^{T}\left( {\frac{\textrm{d}^{2}\mathrm{\textbf{N}}_{1} }{\textrm{d}x^{2}}} \right) } \,\textrm{d}x+\int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {EI_{z} (x)\cdot \left( {\frac{\textrm{d}^{2}\mathrm{\textbf{N}}_{2} }{\textrm{d}x^{2}}} \right) ^{T}\left( {\frac{\textrm{d}^{2}\mathrm{\textbf{N}}_{2} }{\textrm{d}x^{2}}} \right) } \,\textrm{d}x \nonumber \\&\quad +K_{r} \cdot \left( {\left. {\frac{\textrm{d}\mathrm{\textbf{N}}_{1} }{\textrm{d}x}} \right| _{L_{1} } -\left. {\frac{\textrm{d}\mathrm{\textbf{N}}_{2} }{\textrm{d}x}} \right| _{L_{1} } } \right) ^{T}\cdot \left( {\left. {\frac{\textrm{d}\mathrm{\textbf{N}}_{1} }{\textrm{d}x}} \right| _{L_{1} } -\left. {\frac{\textrm{d}\mathrm{\textbf{N}}_{2} }{\textrm{d}x}} \right| _{L_{1} } } \right) \nonumber \\&\quad +\int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {k(x)\cdot \left( {\mathrm{\textbf{N}}_{1} } \right) ^{T}\left( {\mathrm{\textbf{N}}_{1} } \right) } \,\textrm{d}x+\int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {k(x)\cdot \left( {\mathrm{\textbf{N}}_{2} } \right) ^{T}\left( {\mathrm{\textbf{N}}_{2} } \right) } \,\textrm{d}x \nonumber \\&\quad +\int \limits _{\textrm{x}=0}^{\textrm{L}_{\textrm{1}} } {k_{G} (x)\cdot \left( {\frac{\textrm{d}\mathrm{\textbf{N}}_{1} }{\textrm{d}x}} \right) ^{T}\left( {\frac{\textrm{d}\mathrm{\textbf{N}}_{1} }{\textrm{d}x}} \right) } \,\textrm{d}x+\int \limits _{\textrm{x}=\textrm{L}_{\textrm{1}} }^{\textrm{L}} {k_{G} (x)\cdot \left( {\frac{\textrm{d}\mathrm{\textbf{N}}_{2} }{\textrm{d}x}} \right) ^{T}\left( {\frac{\textrm{d}\mathrm{\textbf{N}}_{2} }{\textrm{d}x}} \right) } \,dx \end{aligned}$$
(21)

After the integration procedure of Eq. (21), the coefficients \(k_{i,j}\) (\(i, j=1, 2, 3, 4\)) of complete stiffness matrix K are finally given in the simple closed-form as:

$$\begin{aligned} k_{\text{ i,j }} =\text{ EI}_{\text{0 }} \cdot \lambda _{2} +K_{r} \cdot (A_{i2} \text{- } B_{i2} )(A_{j2} \text{- } B_{j2} )+\text{ k}_{\text{0 }} \cdot \lambda _{0} +\text{ k}_{\text{ G,0 }} \cdot \lambda _{1} \end{aligned}$$
(22)

with the following abbreviation \(\lambda _{\xi } \) (\(\xi =0, 1, 2\)):

$$\begin{aligned} \lambda _{\xi } =\sum \limits _{m=\xi +1}^4 {\sum \limits _{n=\xi +1}^4 {\left( {I_{\xi } (\text{ L}_{\text{1 }} )\cdot \left( {A_{im} A_{jn} -B_{im} B_{jn} } \right) +B_{im} B_{jn} \cdot I_{\xi } (\text{ L})} \right) } } \end{aligned}$$
(23)

with:

$$\begin{aligned} I_{\xi } (x)=x^{m+n-2\xi -1}\cdot \left( {\prod \limits _{\bar{{\xi }}=1}^\xi {\left( {m-\bar{{\xi }}} \right) } \left( {n-\bar{{\xi }}} \right) } \right) \cdot \left( {\frac{1}{m+n-2\cdot \xi -1}-\frac{\beta \cdot x}{m+n-2\cdot \xi }} \right) \end{aligned}$$
(24)

3.3 Derivation of load vector

The load vector \(\mathrm{\textbf{F}}=\left\{ {F_{1},\,F_{2},\,F_{3},\,F_{4} } \right\} ^{T}\) for the case of a continuously distributed load p(x) over the whole beam was determined from the work W done by the external forces, given by:

$$\begin{aligned} W=\int \limits _{\text{ x }=0}^{\text{ L}_{\text{1 }} } {p(x)\cdot v_{1} (x)} \,\text{ d }x+\int \limits _{\text{ x }=\text{ L}_{\text{1 }} }^{\text{ L }} {p(x)\cdot v_{2} (x)} \,\text{ d }x \end{aligned}$$
(25)

Afterward, the implementation of Eqs. (14) and (15) in Eq. (25) yields:

$$\begin{aligned} \mathrm{\textbf{F}}=\int \limits _{\text{ x }=0}^{\text{ L}_{\text{1 }} } {p(x)\cdot \mathrm{\textbf{N}}_{1} } \,\text{ d }x+\int \limits _{\text{ x }=\text{ L}_{\text{1 }} }^{\text{ L }} {p(x)\cdot \mathrm{\textbf{N}}_{2} } \,\text{ d }x \end{aligned}$$
(26)

In Eq. (26), the load was further defined as an (upwards positive) linear function:

$$\begin{aligned} p(x)=p_{0} \cdot \left( {1-\beta _{p} \cdot x} \right) \end{aligned}$$
(27)

with the load tapering parameter \(\beta _{p} =\frac{p_{0} -p_{1} }{p_{0} \cdot L}\), where the \(p_{0}\) and \(p_{1}\) represent the values of the load at the left and right end of the finite element, respectively. After the integration procedure of Eq. (26), the load vector coefficients \(F_{i}\) (\(i=1, 2, 3, 4\)) were finally defined as:

$$\begin{aligned} F_{i} =\sum \limits _{m=1}^4 {\left( {L_{\text{1 }}^{m}\left( {\frac{1}{m}-\frac{L_{\text{1 }} \cdot \beta _{p} }{1+m}} \right) \cdot \left( {A_{im} -B_{im} } \right) +L^{m}\left( {\frac{1}{m}-\frac{L_{\text{1 }} \cdot \beta _{p} }{1+m}} \right) \cdot B_{im} } \right) } \end{aligned}$$
(28)

3.4 Computation of nodal shear forces and bending moments

After the values of the generalized transverse displacement vector have been processed, the vector of secondary variables Q\(=\){\(V_{y1}\), -\(M_{{z1}}\), -\(V_{{y2}}\), \(M_{{z2}}\)}\(^{\textrm{T}}\) can be calculated from the finite element equilibrium equation:

$$\begin{aligned} \mathrm{\textbf{Q}}=\mathrm{\textbf{K}}\cdot \mathrm{\textbf{q}}-\mathrm{\textbf{F}} \end{aligned}$$
(29)

providing the nodal transverse forces (\(V_{{y1}}\) and \(V_{{y2}})\) and the bending moments (\(M_{{z1}}\) and \(M_{{z2}})\) though a simple selective change of signs.

3.5 Derivation of bending moment functions

In general, the bending moment function \(M_{z}(x)\) is determined by product of bending stiffness and the second derivative of transverse displacements function (\(M_{z} (x)=EI(x)\cdot v''(x))\). However, since there are only approximate functions of the transverse displacements available, this differential relation does not prove to be a quality option, since it gives extremely poor approximations compared to the exact bending moment functions obtained from GDE solution [12]. Consequently, a large number of FEs are required to achieve sufficient accuracy. Therefore, in such cases, the utilization of approximate cubic (H1) or quantic (H2) polynomial functions with the interpolated nodal quantities (bending moments, shear forces and load) proves to be a better alternative [13]. However, it is worth noting that the bending moment polynomial functions H1 and H2 are still limited within the context of the analyzed two-parameter soil model. Although their 1st, 2nd, and 3rd derivatives appear to be continuous at the crack location, this continuity does not persist in the bending moment solutions of the GDE model. To address the discrepancy, a more precise approach involves defining new bending moment functions for each segment that explicitly account for the discontinuities at the crack location in these derivatives.

This work presents the improved cubic polynomial bending moment functions (H1-I) for the two finite element segments in this section. The functions are expressed as follows in the following form:

$$\begin{aligned}{} & {} M_{z,1} (x)=\hbox {c}_{1} +c_{2} \cdot x+c_{3} \cdot x^{2}+c_{4} \cdot x^{3}\,\,\,\,\,\,\,\,\,\,\,\,\,(0\le x\le L_{1} ) \end{aligned}$$
(30)
$$\begin{aligned}{} & {} M_{z,2} (x)=d_{1} +d_{2} \cdot x+d_{3} \cdot x^{2}+d_{4} \cdot x^{3}\,\,\,\,\,\,\,\,\,\,\,\,\,(L_{1} \le x\le L) \end{aligned}$$
(31)

All unknown coefficients (\(c_{\textrm{1}}\), \(c_{\textrm{2}}\), \(c_{\textrm{3}}\), \(c_{\textrm{4}}\), \(d_{\textrm{1}}\), \(d_{\textrm{2}}\), \(d_{\textrm{3}}\), \(d_{\textrm{4}})\) from Eqs. (30) and (31) were determined from the four boundary conditions of nodal bending moments and shear forces expressed from the vector of secondary variables Q, Eq. (29):

$$\begin{aligned}{} & {} M_{z,1} (0)=M_{z1} \end{aligned}$$
(32)
$$\begin{aligned}{} & {} M_{z,1} '(0)=V_{y1} +k_{G,0} \cdot \varPhi _{1} \end{aligned}$$
(33)
$$\begin{aligned}{} & {} M_{z,2} (L)=M_{z2} \end{aligned}$$
(34)
$$\begin{aligned}{} & {} M_{z,2} '(L)=V_{y2} +k_{G} \left( L \right) \cdot \varPhi _{2} \end{aligned}$$
(35)

The remaining four unknown coefficients were derived from the bending moment continuity and discontinuity conditions of 1st, 2nd and 3rd bending moment derivative at the location of the crack:

$$\begin{aligned}{} & {} M_{z,1} (L_{1} )=M_{z,2} (L_{1} ) \end{aligned}$$
(36)
$$\begin{aligned}{} & {} M_{z,2} '(L_{1} )-M_{z,1} '(L_{1} )=k_{G} (L_{1} )\cdot \varDelta \phi \end{aligned}$$
(37)
$$\begin{aligned}{} & {} M_{z,2} ''(L_{1} )-M_{z,1} ''(L_{1} )=k_{G} '(L_{1} )\cdot \varDelta \phi \end{aligned}$$
(38)
$$\begin{aligned}{} & {} M_{z2} '''(L_{1} )-M_{z1} '''(L_{1} )=-\frac{\left( {EI_{z} (L_{1} )\cdot k_{0} (L_{1} )-k_{G} (L_{1} )^{2}} \right) \cdot \varDelta \phi }{EI_{z} (L_{1} )} \end{aligned}$$
(39)

where \(\varDelta \phi =v_{2} '(L_{1} )-v_{1} '(L_{1} )\) is the difference in rotation from the left and right side of the crack. By taking the ratio \(\varDelta \phi =\frac{M_{z,1} (L_{1} )}{K_{r} }\) together with Eqs. (2), (7) and (13), Eqs. (37)–(39) were written in its final form as:

$$\begin{aligned}{} & {} M_{z2} '(L_{1} )-M_{z1} '(L_{1} )=\frac{k_{G,0} \cdot \psi }{EI_{0} }\cdot M_{1} (L_{1} ) \end{aligned}$$
(40)
$$\begin{aligned}{} & {} M_{z2} ''(L_{1} )-M_{z1} ''(L_{1} )=\frac{-k_{G,0} \cdot \beta \cdot \psi }{EI_{0} \cdot \left( {1-L_{1} \cdot \beta } \right) }\cdot M_{z1} (L_{1} ) \end{aligned}$$
(41)
$$\begin{aligned}{} & {} M_{z2} '''(L_{1} )-M_{z1} '''(L_{1} )=\frac{-\left( {EI_{0} \cdot k_{0} -k_{G,0}^{2}} \right) \cdot \psi }{EI_{0}^{2}}\cdot M_{z1} (L_{1} ) \end{aligned}$$
(42)

Unlike the bending moment functions, the shear force functions (\(V_{y} (x)=M_{z} '(x)-k_{G} (x)\cdot v'(x))\) are continuous at the crack location and thus requiring no improvement.

Fig. 3
figure 3

Cracked tapering strip footing resting on two-parametric elastic soil

Full size image
Fig. 4
figure 4

Transverse displacements of FE model compared to GDE solutions

Full size image

4 Numerical example

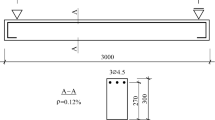
For the static analysis of the strip tapered footing, a verification example with length \(L=10\) m combined with selected various width tapering parameter values (\(\beta =-0.1\), \(-\)0.05, 0, 0.025, 0.05 and 0.075) has been considered to demonstrate the efficiency of the proposed finite element. The example considers two cracks (both with the relative crack depth \(\delta =0,5\)). Other considered data are given in the Fig. 3.

The FE results were compared also with the results of GDE solutions of the simplified model, Eq. (9). As the structure has two cracks, the corresponding computational model of the beam consisted of three elastic segments. Consequently, three coupled differential equations were solved to obtain the model GDE solutions. Since no exact analytical expressions exist, these solutions were obtained by numerical solving using Mathematica software [20].

Several meshes generated with the newly introduced FE were analyzed, starting with the smallest mesh possible. Due to the presence of two cracks, two finite elements of equal lengths were required. As an example, the corresponding complete stiffness matrices and load vectors for the case of a width tapering parameter \(\beta = 0.05\) are as follows:

$$\begin{aligned} \mathrm{\textbf{K}}_{1} =\left[ {{\begin{array}{*{20}c} {0.476803} &{} {0.553547} &{} {-0.048087} &{} {0.213186} \\ {0.553547} &{} {1.191518} &{} {-0.158910} &{} {0.365862} \\ {-0.048087} &{} {-0.158910} &{} {0.406871} &{} {-0.526742} \\ {0.213186} &{} {0.365862} &{} {-0.526742} &{} {1.327764} \\ \end{array} }} \right] ; \quad \mathrm{\textbf{F}}_{1} =\left\{ {{\begin{array}{*{20}c} {-238.176} \\ {-219.242} \\ {-199.324} \\ {174.198} \\ \end{array} }} \right\} \end{aligned}$$
$$\begin{aligned} \mathrm{\textbf{K}}_{2} =\left[ {{\begin{array}{*{20}c} {0.359705} &{} {0.447582} &{} {-0.047517} &{} {0.169129} \\ {0.447582} &{} {1.146672} &{} {-0.194457} &{} {0.326239} \\ {-0.047517} &{} {-0.194457} &{} {0.325955} &{} {-0.408192} \\ {0.169129} &{} {0.326239} &{} {-0.408192} &{} {1.003157} \\ \end{array} }} \right] \quad \mathrm{\textbf{F}}_{2} =\left\{ {{\begin{array}{*{20}c} {-173.438} \\ {-140.625} \\ {-154.688} \\ {132.813} \\ \end{array} }} \right\} \end{aligned}$$

After evaluating the equilibrium equations of the structures for all considered meshes of FEs, the nodal displacements and rotations were initially obtained. These values were further combined with interpolation functions to obtain the displacements also between the nodes, Eqs. (14) and (15). The results of transverse displacements of FE model with 2, 8, 16 and 32 FE discretizations and GDE solution for all considered values of \(\beta \) are presented in Fig. 4. From the figure, it can be seen that FE refinements has a positive effect on convergence, as the difference between approximate and GDE transverse displacements is effectively reduced. It can be seen that for \(\beta =0.075\), the transverse displacements (at the beams right end) are converging most slowly and even with 32 FE meshes, there is still a slight deviation compared to the GDE displacements. One of the reasons for the increase in the deviation (as \(\beta \) increases) is definitely the interpolation functions used, which do not include the width tapering parameter \(\beta \).

Moreover, a comparison of the transverse displacements and their errors for some representative points (i.e., left end (A), left crack (C1), midspan (B), right crack (C2) and right end (C)) for various (2, 4, 8, 16 and 32) FE meshes are given in Table 1. The relative error of FE compared to GDE is also given in brackets. In addition, exclusively for FE convergence control, the last column of the table shows the corresponding GDE solution values of the simplified DS model, obtained numerically using Mathematica software. For representative points A, B, C, the nodal transverse displacement values of FEs were obtained directly for all considered FE meshes, while for the both cracks (C1 and C2) the interpolated values between the FE nodes are presented. From the table, it can be further observed that among the considered values of the parameter \(\beta \), the FE model exhibits the fastest convergence at the \(\beta \) value of 0.025.

Furthermore, the bending moments for the various meshes were analyzed by applying the newly derived approximating cubic functions from Eqs. (30) and (31) and were compared with the GDE bending moment functions. Figure 5 thus shows the convergence of the bending moment functions for the cases \(\beta =0.025\) and \(\beta =-0.05\) for meshes of 2 and 6 FEs. In both figures, it can be noticed that the discrepancy is successfully and rapidly decreasing, and that for the 6-FE mesh the agreement with GDE bending moment function is excellent also in the vicinity of cracks.

Table 1 Results of negative (−) transverse displacements on several locations for various values of beam tapering parameter
Full size table
Fig. 5
figure 5

Bending moments of FE model for \(\beta =\textit{0.025}\) and \(\beta =-0.05\) compared to GDE solutions

Full size image

In addition, in the similar way as the transverse displacement values, a comparison of the bending moment values and their errors for some representative points (i.e., left crack (C1), midspan (B) and right crack (C2)) for various (2, 4, 8, 16 and 32) FE meshes is given in Table 2. The bending moment values at the both ends of the beam are zero and are therefore not included in the table. The relative errors are also given in brackets below the bending moment values. In addition, for FE convergence control, the last column of the table shows the GDE bending moment solution values.

Table 2 Results of negative (−) bending moments [kNm] for various beam tapering parameters and several locations
Full size table

The values of the nodal bending moment at midpoint (point B) for all FE meshes and the values of the tapering parameter considered were evaluated directly from the vector of secondary variables Q, Eq. (29). However, for the both crack points C1 and C2, the interpolated bending moment values between the FE nodes obtained from Eqs. (30) and (31) are presented.

From the table, it can be seen that the bending moments converge to the GDE values at all the points considered. Similar to the transverse displacement values, the nodal bending moment values (point B) are also converging slowly in the case of tapering parameter \(\beta =0.075\), and consequently, the interpolated bending moment values between the FE nodes (in points C1 and C2) are also slower to converge.

If shear forces are of the interest, their functions can be obtained through the derivation of bending moment functions.

5 Conclusions

The following summarizes the main conclusions:

  • FEM bending analysis of cracked tapered beams resting on two-parameter soil was considered.

  • Implemented interpolation functions lead to the simple expressions of the stiffness matrix and the load vector in closed form, which is a major advantage of this choice.

  • The proposed finite element successfully converges to the GDE solution of the problem as the mesh density increases.

  • The further benefit of choosing these interpolation functions is that the presented FE model enables analysis even for prismatic footings, allowing for a broader application of the model in engineering practice. It is worth noting that, if an exact solution were available, calculating transverse displacements for prismatic beams would not be feasible, making the selected interpolation functions particularly advantageous in overcoming this limitation.

  • New bending moment functions (unlike the standard approach by utilizing H1 and H2 interpolations) now provide better agreement with the GDE functions also in the vicinity of the crack since less finite element discretization is required.

Although the presented solutions already give very good results, any potential future studies could focus on improving the interpolation functions by including the width tapering parameter as well as both soil parameters. Researches could also take into account the variation of the foundation height on an inclined soil. Likewise, studies should also focus on very important experimental verifications.

The practical implications of this study extend to various engineering scenarios, empowering engineers to enhance the accuracy and efficiency of their analyses when designing strip tapered footings for various engineering footing structures. The proposed finite element model strikes a delicate balance between computational efficiency and result accuracy, offering cost-effective engineering solutions.

Moreover, the optimized structural designs resulting from this research can play a pivotal role in minimizing the environmental impact. This study, by highlighting the economic benefits of adopting the proposed model over intricate and time-consuming 2D and 3D analyses, contributes to more efficient engineering practices.