Zhang neural networks: an introduction to predictive computations for discretized time-varying matrix problems

Abstract

This paper wants to increase our understanding and computational know-how for time-varying matrix problems and Zhang Neural Networks. These neural networks were invented for time or single parameter-varying matrix problems around 2001 in China and almost all of their advances have been made in and most still come from its birthplace. Zhang Neural Network methods have become a backbone for solving discretized sensor driven time-varying matrix problems in real-time, in theory and in on-chip applications for robots, in control theory and other engineering applications in China. They have become the method of choice for many time-varying matrix problems that benefit from or require efficient, accurate and predictive real-time computations. A typical discretized Zhang Neural Network algorithm needs seven distinct steps in its initial set-up. The construction of discretized Zhang Neural Network algorithms starts from a model equation with its associated error equation and the stipulation that the error function decrease exponentially fast. The error function differential equation is then mated with a convergent look-ahead finite difference formula to create a distinctly new multi-step style solver that predicts the future state of the system reliably from current and earlier state and solution data. Matlab codes of discretized Zhang Neural Network algorithms for time varying matrix problems typically consist of one linear equations solve and one recursion of already available data per time step. This makes discretized Zhang Neural network based algorithms highly competitive with ordinary differential equation initial value analytic continuation methods for function given data that are designed to work adaptively. Discretized Zhang Neural Network methods have different characteristics and applicabilities than multi-step ordinary differential equations (ODEs) initial value solvers. These new time-varying matrix methods can solve matrix-given problems from sensor data with constant sampling gaps or from functional equations. To illustrate the adaptability of discretized Zhang Neural Networks and further the understanding of this method, this paper details the seven step set-up process for Zhang Neural Networks and twelve separate time-varying matrix models. It supplies new codes for seven of these. Open problems are mentioned as well as detailed references to recent work on discretized Zhang Neural Networks and time-varying matrix computations. Comparisons are given to standard non-predictive multi-step methods that use initial value problems ODE solvers and analytic continuation methods.

1 Introduction

We study and analyze a relatively new computational approach, abbreviated occasionally as ZNN for Zhang Neural Networks, for time-varying matrix problems. The given problem’s input data may come from function given matrix and vector flows A(t) and a(t) or from time-clocked sensor data. Zhang Neural Networks use some of our classical notions such as derivatives, Taylor expansions (extended to not necessarily differentiable sensor data inputs), multi-step recurrence formulas and elementary linear algebra in seven set-up steps to compute future solution data from earlier system data and earlier solutions with ever increasing accuracy as time progresses.

In particular, we only study discretized Zhang Neural Networks here. We cannot and will not attempt to study all known variations of Zeroing Neural Networks (often also abbreviated by ZNN) due to the overwhelming wealth of applications and specializations that have evolved over the last decades with more than (estimated) 400 papers and a handful of books. Zhang’s ZNN method has an affinity to analytic continuation methods that reformulate an algebraic system as an ODE initial value problem in a differential algebraic equation (DAE) and standardly solve it by following the solution’s path via an IVP ODE initial value solver. But ZNN differs in several fundamental aspects that will be made clear in this survey. For example, Loisel and Maxwell [28] computed the field of values (FOV) boundary curve in 2018 via numerical continuation quickly and to high accuracy using a formulaic expression for the FOV boundary curve of a matrix A and a single-parameter hermitean matrix flow F(t) for $t \in [0, 2\pi ]$. The Zhang Neural Network method, applied to the matrix FOV problem in [49] in 2020 used the seven step ZNN set-up and ZNN bested the FOV results of [28] significantly, both in accuracy and speed-wise. Unfortunately, the set-up and the workings of Zhang Neural Networks and their success has never been explained theoretically. Since the 1990s our understandings of analytic continuation ODE methods has been broadened and enhanced by the works of [1,2,3, 9] and others, but Zhang Neural Networks appear to be only adjacent to and not quite understood as part of our analytic continuation canon of adaptive multi-step DAE formulas. One obvious difference is the exponential decay of the error function E(t) stipulated by $\dot{E}(t) = - \eta E(t)$ for $\eta > 0$ in Zhang Neural Networks at their start versus just requiring $\dot{E}(t) = 0$ in analytic continuation methods. Indeed Zhang Neural Networks never solve or try to solve their error equation at all.

Discretized ZNN methods represent a special class of Recurrent Neural Networks (RNN) that originated some 40 years ago and are intended to solve dynamical systems. A new zeroing neural network was proposed by Yunong Zhang and Jun Wang in 2002, see [61]. As a graduate student at Chinese University in Hong Kong, Yunong Zhang was inspired by Gradient Neural Networks such as the Hopfield Neural Network [22] from 1982 that mimics a vector of interconnected neural nodes under time-varying neuronal inputs and has been useful in medical models and in applications to graph theory and elsewhere. He wanted to extend Hopfield’s idea from time-varying vector algebra to more general time-varying matrix problems and his Zeroing Neural Networks, called Zhang Neural Networks or ZNN by now, were conceived in 2001 for solving dynamic parameter-varying matrix and vector problems alike.

Both Yunong Zhang and his Ph.D. advisor Jun Wang were unaware of ZNN’s adjacency to analytic continuation ODE methods. For time-varying matrix and vector problems, Zhang and Wang’s approach starts from a global error function and an error differential equation to achieve exponential error decay in the computed solution.

Since then, Zhang Neural Networks have become one mainstay for predictive time-varying matrix flow computations in the eastern engineering world. Discretized ZNN methods nowadays help with optimizing and controlling robot behavior, with autonomous vehicles, chemical plant control, image restoration, environmental sciences et cetera. They are extremely swift, accurate and robust to noise in their predictive numerical matrix flow computations.

A caveat: The term Neural Network has had many uses.

• Its origin lies in biology and medicine of the 1840s. There it refers to the neuronal network of the brain and to the synapses of the nervous system. In applied mathematics today neural networks are generally associated with models and problems that mimic or follow a brain-like function or use nervous system like algorithms that pass information along.

• In the computational sciences of today, assignations that use terms such as neural network most often refer to numerical algorithms that search for relationships in parameter-dependent data or that deal with time-varying problems. The earliest numerical use of neural networks stems from the late 1800s. Today’s ever evolving numerical ‘neural network’ methods may involve deep learning or large data and data mining. They occur in artificial neural networks, with RNNs, with continuation methods for differential equations, in homotopy methods and in the numerical analysis of dynamical systems, as well as in artificial intelligence (AI), in machine learning, and in image recognition and restoration, and so forth. In each of these realizations of ’neural network’ like ideas, different type algorithms are generally used for differing problems.

• Zhang Neural Networks (ZNN) are a special zeroing neural network that differs more or less from the above. They are specifically designed to solve time-varying matrix problems and they are well suited to deal with constant sampling gap clocked sensor inputs for engineering and design applications. Unfortunately, neither time-varying matrix problems and continuous or discretized ZNN methods are listed in the two most recent Mathematics Subject Classifications lists of 2010 or 2020, nor are they mentioned in Wikipedia.

In practical numerical terms, Zhang Neural Networks and time-varying matrix flow problems are governed by different mathematical principles and are subject to different quandaries than those of static matrix analysis where Wilkinson’s backward stability and error analysis are common tools and where beautiful modern static matrix principles reign. ZNN methods can solve almost no static, i.e., fixed entry matrix problems, with the static matrix symmetrizer problem being the only known exception, see [54]. Throughout this paper, the term matrix flow will describe matrices whose entries are functions of time t, such as the 2 by 2 dimensional matrix flow $A(t) = \left( \begin{array}{cc} \sin (t^2) -t&{} \quad - 3^{t-1}\\ 17.56 ~ t^{0.5}&{} \quad 1/(1+t^{3.14} )\end{array}\right)$.

Discretized ZNN processes are predictive by design. Therefore they require look-ahead convergent finite difference schemes that have only rarely occurred anywhere. In stark contrast, convergent finite difference schemes but not look-ahead ones are used in the corrector phase of multi-step ODE solvers.

Time-varying matrix computational analysis and its achievements in ZNN feel like a new and still mainly uncharted territory for Numerical Linear Algebra that is well worth studying, coding and learning about. To begin to shed light on the foundational principles of time-varying matrix analysis is the aim of this paper.

The rest of the paper is divided into two parts: Sect. 2 will explain the seven step set-up process of discretized ZNN in detail, see e.g., Remark 1 for some differences between Zhang Neural Networks and analytic continuation methods for ODEs. Section 3 lists and exemplifies a number of models and applied problems for time-varying matrix flows that engineers are solving, or beginning to solve, via discretized ZNN matrix algorithms. Throughout the paper we will indicate special phenomena and qualities of Zhang Neural Network methods when appropriate.

2 The workings of discretized Zhang Neural Network methods for parameter-varying matrix flows

For simplicity and by the limits of space, given 2 decades of ZNN based engineering research and use of ZNN, we restrict our attention to time-varying matrix problems in discretized form throughout this paper. ZNN methods work equally well with continuous matrix inputs by using continuous ZNN versions. Continuous and discretized ZNN methods have often been tested for consistency, convergence, and stability in the Chinese literature and for their behavior in the presence of noise, see the References here and the vast literature that is available in Google.

For discretized time-varying data and any matrix problem therewith, all discretized Zeroing Neural Network methods proceed using the following identical seven constructive steps—after appropriate start-up values have been assigned to start their iterations.

Suppose that we are given a continuous time-varying matrix and vector model with time-varying functions F and G

$$\begin{aligned} F(A(t),B(t),{x(t)}, \ldots ) = G(t, C(t), u(t), \ldots ) \in {\mathbb {R}}^{m,n} \ \text { or } \ {\mathbb {C}}^{m,n} \end{aligned}$$

(0)

and a time-varying unknown vector or matrix x(t). The variables of Fand G are compatibly sized time-varying matrices $A(t), B(t), C(t),\ldots$ and time-varying vectors $u(t),\ldots$ that are known—as time t progresses—at discrete equidistant time instances $t_i \in {[} t_o,t_f{]}$ for $i\le k$ and $k = 1,\ldots$ such as from sensor data. Steadily timed sensor data is ideal for discretized ZNN. Our task with discretized predictive Zhang Neural Networks is to find the solution $x(t_{k+1})$ of the model equation (0) accurately and in real-time from current or earlier $x(t_{..})$ values and current or earlier matrix and vector data. Note that here the ‘unknown’ x(t) might be a concatenated vector or an augmented matrix x(t) that may contain both, the eigenvector matrix and the associated eigenvalues for the time-varying matrix eigenvalue problem. Then the given flow matrices A(t) might have to be enlarged similarly to stay compatible with the augmented, now ‘eigendata vector’ x(t) and likewise for other vectors or matrices B(t), u(t), and so forth as needed for compatibility.

• Step 1: From a given model equation (0), we form the error function

  $$\begin{aligned} E(t)_{m,n} = F(A(t),B(t),{x(t)},\ldots ) - G(t, C(t), u(t),\ldots ) \ \ \ ({\mathop {=}\limits ^{!}} O_{m,n} \ \text {ideally})\nonumber \\ \end{aligned}$$

  (1)

  which ideally should be zero, i.e., $E(t) = 0$ for all $t \in [t_o,t_f]$ if x(t) solves (0) in the desired interval.

• Step 2: Zhang Neural Networks take the derivative $\dot{E}(t)$ of the error function E(t) and stipulate its exponential decay: ZNN demands that

  $$\begin{aligned} \dot{E}(t) = -\eta \ E(t) \end{aligned}$$

  (2)

  for some fixed constant $\eta > 0$ in case of Zhang Neural Networks (ZNN). [ Or it demands that

  $$\begin{aligned} \dot{E}(t) = -\gamma \ \mathcal{F}(E(t)) \end{aligned}$$

  for $\gamma > 0$ and a monotonically nonlinear increasing activation function $\mathcal F$. Doing so changes E(t) element-wise and gives us a different method, called a Recurrent Neural Network (RNN). ]

The right-hand sides for ZNN and RNN methods differ subtly. Exponential error decay and thus convergence to the exact solution x(t) of (2) is automatic for both variants. Depending on the problem, different activation functions $\mathcal F$ are used in the RNN version such as linear, power sigmoid, or hyperbolic sine functions. These can result in different and better problem suited convergence properties with RNN for highly periodic systems, see [21, 63], or [58] for examples.

The exponential error decay stipulation (2) for Zhang Neural Networks is more stringent than a PID controller would be with its stipulated error norm convergence. ZNN brings the entry-wise solution errors uniformly down to local truncation error levels, with the exponential decay speed depending on the value of $\eta > 0$ and it does so from any set of starting values.

As said before, in this paper we limit our attention to discretized Zhang Neural Networks (ZNN) exclusively for simplicity.

• Step 3: Solve the exponentially decaying error equation’s differential equation (2) at time $t_k$ of Step 2 algebraically for $\dot{x}(t_k)$ if possible. If impossible, reconsider the problem, revise the model, and try again.(3) (Such behavior will be encountered and mitigated in this section and also near the end of Sect. 3.)

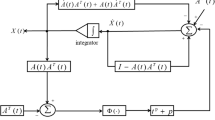
Continuous or discretized ZNN never tries to solve the associated differential error Eq. (2). Throughout the ZNN process we never compute or derive the actual computed error. The actual errors can only be assessed by comparing the solution $x(t_i)$ with its desired quality, such as comparing $X(t_i) \cdot X(t_i)$ with $A(t_i)$ for the time-varying matrix square root problem whose relative errors are depicted in Fig. 1 in Sect. 2. Note that ZNN cannot solve ODEs at all. ZNN is not designed for ODEs, but rather solves time-varying matrix and vector equations.

The two general set-up steps 4 and 5 of ZNN below show how to eliminate the error derivatives from the Zhang Neural Network computational process right at the start. Zhang Neural Networks do not solve or even care about the error ODE (2) at all.

• Step 4: Select a look-ahead convergent finite difference formula for the desired local truncation error order $O(\tau ^{j+2})$ that expresses $\dot{x}(t_k)$ in terms of $x(t_{k+1}), x(t_k),\ldots , x(t_{k-(j+s)+2})$ for $j+s$ known data points from the table of known convergent look-ahead finite difference formulas of type j_s in [45, 46]. Here $\tau = t_{k+1} - t_k = const$ for all k is the sampling gap of the chosen discretization.(4)

• Step 5: Equate the $\dot{x}(t_k)$ derivative terms of Steps 3 and 4 and thereby dispose of $\dot{x}(t_k)$ or the ODE problem (2) altogether from ZNN. (5)

• Step 6: Solve the solution-derivative free linear equation obtained in Step 5 for $x(t_{k+1})$ and iterate in the next step. (6)

• Step 7: Increase $k+1$ to $k+2$ and update all data of Step 6; then solve the updated recursion for $x(t_{k+2})$. And repeat until $t_k$ reaches the desired final time $t_f$. (7)

For any given time-varying matrix problem the numerical Zhang Neural Network process is established in step 6. It consists of one linear equations solve (from Step 3) and one difference formula evaluation (from Step 5) per iteration step. This predictive iteration structure of Zhang Neural Networks with their ever decreasing errors differs from any known analytic continuation method.

Most recently, steps 3–5 above have been streamlined in [35] by equating the Adams–Bashforth difference formula, see e.g. [11, p. 458–460], applied to the derivatives $\dot{x}(t_k)$ with a convergent look-ahead difference formula from [45] for $\dot{x}(t_{k})$. To achieve overall convergence, this new ZNN process requires a delicate balance between the pair of finite difference formulas and their respective decay constants $\lambda$, and $\eta$; for further details see [35] and also [23, 42, 43] which explore the feasibility of $\eta$ and the sampling gap $\tau$ pairs for stability and stiffness problems with ODEs. There the feasible parameter regions are generally much smaller than what ZNN time-varying matrix methods allow. Besides, a new ‘adapted’ AZNN method separates and adjusts the decay constants for different parts of ZNN individually and thereby allows even wider $\eta$ ranges than before and better and quicker convergence overall as well, see [54].

Discretized Zhang Neural Networks for matrix problems are highly accurate and converge quickly due to the intrinsically stipulated exponential error decay of Step 2. These methods are still evolving and beckon new numerical analysis scrutiny and explanations which none of the 400 + applied engineering papers or any of the the handful of Zhang Neural Network books address.

The errors of Zhang Neural Nework methods have two sources: for one, the chosen finite difference formula’s local truncation error order in Step 4 depends on the constant sampling gap $\tau = t_{k+1} - t_k$, and secondly on the conditioning and rounding errors of the linear equation solves of Step 6. Discretized Zhang Neural Network matrix methods are designed to give us the future solution value $x(t_{k+1})$ accurately—within the natural error bounds for floating-point arithmetic; and they do so for $t_{k+1}$ immediately after time $t_k$. At each computational step they rely only on short current and earlier equidistant sensor and solution data sequences depending on $j + s +1$ previous solution data when using a finite difference formula of type $j\_s$.

See formula (Pqzi) for example for the extended matrix eigenvalue problem several pages further down.

Convergent finite difference schemes have only been used in the Adams–Moulton, Adams–Bashforth, Gear, and Fehlberg multi-step predictor–corrector formulas, see [11, Section 17.4], e.g. We know of no other occurrence of finite difference schemes in the analytic continuation literature prior to ZNN. Discrete ZNN methods can be easily transferred to on-board chip designs for driving and controlling robots and other problems once the necessary starting values for ZNN iterations have been set. See [64] for 13 separate time-varying matrix/vector tasks, their Simulink models and circuit diagrams, as well as two chapters on fixed-base and mobile robot applications. Each chapter in [64] is referenced with 10 to 30 plus citations from the engineering literature.

While Zeroing Neural Networks have been used extensively in engineering and design for 2 decades, a numerical analysis of ZNN has hardly been started. Time-varying matrix numerical analysis seems to require very different concepts than static matrix numerical analysis. Time varying matrix methods seem to work and run according to different principles than Wilkinson’s now classic backward stability and error analysis based static matrix computations. This will be made clear and clearer throughout this introductory ZNN survey paper.

We continue our ZNN explanatory work by exemplifying the time-varying matrix eigenvalue problem $A(t)x(t) = \lambda (t)x(t)$ for hermitean or diagonalizable matrix flows $A(t) \in {\mathbb {C}}^{n,n}$ that leads us through the seven steps of discretized ZNN, see [6] also for state of the analytic continuation based ODE methods for the parametric matrix eigenvalue problem and [1, Chs. 9, 10] and [3, Ch. 9] for new theoretical approaches and classifications of ODE solvers that might possibly connect discretized Zhang Neural Networks to analytic continuation ODE methods. Their possible connection is not understood at this time and has not been researched with numerical analysis tools.

The matrix eigen-analysis is followed by a detailed look at convergent finite difference schemes that once originated in one-step and multi-step ODE solvers and that are now used predictively in discretized Zhang Neural Network methods for time-varying sensor based matrix problems.

If $A_{n,n}$ is a diagonalizable fixed entry matrix, the best way to solve the static matrix eigenvalue problem $Ax = \lambda x$ for A is to use Francis’ multi-shift implicit QR algorithm if $n \le$ 11,000 or use Krylov methods for larger sized A. Eigenvalues are continuous functions of the entries of A. Thus taking the computed eigenvalues of one flow matrix $A(t_k)$ as an approximation for the eigenvalues of $A(t_{k+1})$ might seem to suffice if the sampling gap $\tau = t_{k+1} - t_k$ is relatively small. But in practice the eigenvalues of $A(t_k)$ often share only a few correct leading digits with the eigenvalues of $A(t_{k+1})$. In fact the difference between any pair of respective eigenvalues of $A(t_k)$ and $A(t_{k+1})$ are generally of size $O(\tau )$, see [24, 59, 60]. Hence there is need for different methods that deal more accurately with the eigenvalues of time-varying matrix flows.

By definition, for a given hermitean matrix flow A(t) with $A(t) = A(t)^* \in {\mathbb {C}}_{n,n}$ [ or for any diagonalizable matrix flow A(t)) ] the eigenvalue problem requires us to compute a nonsingular matrix flow $V(t) \in {\mathbb {C}}_{n,n}$ and a diagonal time-varying matrix flow $D(t) \in {\mathbb {C}}_{n,n}$ so that

This is our first model equation for the time-varying matrix eigenvalue problem.

Here are the steps for time-varying matrix eigen-analyses when using ZNN.

Step 1 Create the error function

Step 2 Stipulate exponential decay of E(t) as a function of time, i.e.,

for a decay constant $\eta > 0$.

Note: Equation $(2^*)$, written out explicitly is

$$\begin{aligned} \dot{E}(t)&= \dot{A}(t) V(t) + A(t)\dot{V}(t) - \dot{V}(t) D(t) - V(t) \dot{D}(t) \\&{\mathop {=}\limits ^{(*)}} - \eta A(t)V(t) + \eta V(t)D(t) \ =\ - \eta E(t) . \end{aligned}$$

Rearranged with all derivatives of the unknowns V(t) and D(t) gathered on the left-hand side of $(*)$:

Unfortunately we do not know how to solve the full system eigen-equation (#) algebraically for the eigen-data derivative matrices $\dot{V}(t)$ and $\dot{D}(t)$ by simple matrix algebra as Step 3 asks us to do.

This is due to the non-commutativity of matrix products and because the unknown derivative $\dot{V}(t)$ appears both as a left and a right matrix factor in the eigen-data DE (#). A solution that relies on Kronecker products for symmetric matrix flows $A(t) = A(t)^T$ is available in [67] and we will follow the Kronecker product route later when dealing with square roots of time-varying matrix flows in subparts (VII) and (VII start-up) in this section, as well as when solving time-varying classic matrix equations via ZNN in subpart (IX) of Sect. 3.

Now we revise our matrix eigen-data model and restart the whole process anew. To overcome the above dilemma, we separate the global time-varying matrix eigenvalue problem for $A_{n,n}(t)$ into n eigenvalue problems

that can be solved for one eigenvector $x_i(t)$ and one eigenvalue $\lambda _i(t)$ at a time as follows.

Step 1 The error function (0i) in vector form is

Step 2 We demand exponential decay of e(t) as a function of time, i.e.,

for a decay constant $\eta > 0$.

Equation (2i), written out explicitly, now becomes

$$\begin{aligned} \dot{e}(t)&= \dot{A}(t) x_i(t) + A(t)\dot{x}_i(t) - {\dot{\lambda }}_i(t) x_i(t) - \lambda _i(t) \dot{x}_i(t)\\&{\mathop {=}\limits ^{(*)}} - \eta ~ A(t)x_i(t) + \eta ~ \lambda _i (t) x_i(t) = - \eta ~ e(t). \end{aligned}$$

Rearranged, with the derivatives of $x_i(t)$ and $\lambda _i(t)$ gathered on the left-hand side of $(*)$:

$$\begin{aligned} A(t) \dot{x}_i(t) - {\dot{\lambda }}_i(t) x_i(t) - \lambda _i(t) \dot{x}_i(t)= - \eta ~ A(t)x_i(t) + \eta ~ \lambda _i(t) x_i(t) - \dot{A}(t) x_i(t) . \end{aligned}$$

Combining the $\dot{x}_i$ derivative terms gives us

$$\begin{aligned} ( A(t) - \lambda _i(t) I_n) \dot{x}_i(t) - {\dot{\lambda }}_i(t) x_i(t) = (- \eta ~ (A(t) - \lambda _i(t) I_n) - \dot{A}(t)) ~ x_i(t) . \end{aligned}$$

For each $i = 1,\ldots ,n$ this equation is a differential equation in the unknown eigenvector ${x_i(t)} \in {\mathbb {C}}^n$ and the unknown eigenvalue ${\lambda _i(t)} \in {\mathbb {C}}$. We concatenate $x_i(t)$ and $\lambda _i(t)$ in

$$\begin{aligned} z_i(t) = \left( \begin{array}{ll} x_i(t)\\ \lambda _i(t) \end{array}\right) \in {\mathbb {C}}^{n+1} \end{aligned}$$

and obtain the following matrix/vector DE for the eigenvector $x_i(t)$ and its associated eigenvalue $\lambda _i (t)$ and each $i = 1,\ldots , n$, namely

where the augmented system matrix on the left-hand side of formula (Azi) has dimensions n by $n+1$ if A is n by n.

Since each matrix eigenvector defines an invariant 1-dimensional subspace we must ensure that the computed eigenvectors $x_i(t)$ of A(t) do not grow infinitely small or infinitely large in their ZNN iterations. Thus we require that the computed eigenvectors attain unit length asymptotically by introducing the additional error function $e_2(t) = x^*_i(t) x_i(t) - 1$. Stipulating exponential decay for $e_2$ leads to

$$\begin{aligned} \dot{e}_2(t) = 2 x^*_i(t) \dot{x}_i(t) = -\mu ~ ( x^*_i(t) x_i(t) - 1) = -\mu ~ e_2(t)\ \end{aligned}$$

or

for a second decay constant $\mu > 0$. If we set $\mu = 2 \eta$, place equation (e$_2i$) below the last row of the n by $n+1$ system matrix of equation (Azi), and extend its right-hand side vector by the right-hand side entry in (e$_2i$), we obtain an $n+1$ by $n+1$ time-varying system of DEs (with a hermitean system matrix if A(t) is hermitean). I.e.,

Next we set

$$\begin{aligned} P(t_k) = \left( \begin{array}{ll} A(t_k) - \lambda _i(t_k) &{} I_n -x_i(t_k)\\ - x_i^*(t_k) &{} \qquad 0 \end{array}\right) \in {\mathbb {C}}_{n+1,n+1}, \ \ \ z(t_k)= \left( \begin{array}{ll} x_i(t_k)\\ \lambda _i(t_k) \end{array}\right) \in {\mathbb {C}}^{n+1} \, \\ \text { and } \ q(t_k) = \left( \begin{array}{l} ( - \eta ~ (A(t_k) - \lambda _i(t_k) I_n) - \dot{A}(t_k)) x_i(t_k) \\ \qquad \qquad \eta ~ (x_i^*(t_k)x_i(t_k) -1) \end{array}\right) \in {\mathbb {C}}^{n+1} \end{aligned}$$

for all discretized times $t = t_k$. And we have completed Step 3 of the ZNN set-up process.

Step 3 Our model (0i) for the ith eigenvalue equation of $A(t_k)$ has been transformed into the mass matrix/vector differential equation

Note that at time $t_k$ the mass matrix $P(t_k)$ contains the current input data $A(t_k)$ and currently computed eigen-data $\lambda _i (t_k)$ and $x_i(t_k)$ combined in the vector $z(t_k)$, while the right-hand side vector $q(t_k)$ contains $A(t_k)$ as well as its first derivative $\dot{A}(t_k)$, the decay constant $\eta$, and the computed eigen-data at time $t_k$.

The system matrix $P(t_k)$ and the right-hand side vector $q(t_k)$ in formula (3i) differ greatly from the simpler differentiation formula for the straight DAE used in [28] where $\dot{E}(t) =0$ or $\eta =0$ was assumed.

Step 4 Now we choose the following convergent look-ahead finite 5-IFD (five Instance Finite Difference) formula of type j_s = 2_3 with global truncation error order $O(\tau ^3)$ from the list in [46] for $\dot{z}_k$:

Step 5 Equating the different expressions for $18 \tau \dot{z}_k$ in (4i) and (3i) (from steps 4 and 3 above) we have

with local truncation error order $O(\tau ^4)$ due to the multiplication of both (3i) and (4i) by $18 \tau$.

Step 6 Here we solve the inner equation $(*)$ in (5i) for $z_{k+1}$ and obtain the discretized look-ahead ZNN iteration formula

that is comprised of a linear equations part and a recursion part and has local truncation error order $O(\tau ^4)$.

Step 7 Iterate to predict the eigendata vector $z_{k+2}$ for $A(t_{k+2})$ from earlier eigen and system data at times $t_{{\tilde{j}}}$ with

${\tilde{j}} \le k+1$ and repeat. (7i)

The final formula (6i) of ZNN contains the computational formula for future eigen-data with near unit eigenvectors in the top n entries of $z(t_{k+1})$ and the eigenvalue appended below. Only a mathematical formula of type (6i) needs to be derived and implemented in code for any other matrix model problem. In our specific case and for any other time-varying matrix problem all entries in (6i) have been computed earlier as eigen-data for times $t_{{\tilde{j}}}$ with ${\tilde{j}} \le k$, except for the system or sensor input $A(t_k)$ and $\dot{A}(t_k)$. The derivative $\dot{A}(t_k)$ is best computed via a high error order derivative formula from previous $\dot{A}(t_{{\tilde{j}}})$ with ${\tilde{j}} \le k$.

The computer code lines that perform the actual math for ZNN iteration steps for a single eigenvalues from time $t = t_k$ to $t_{k+1}$ and $k = 1, 2,3,\ldots$ are listed below. There ze denotes one eigenvalue of $Al = A(t_k)$ and zs is its associated eigenvector. Zj contains the relevant set of earlier eigen-data for $A(t_j)$ with $j \le k$ and Adot is an approximation for $\dot{A}(t_k)$. Finally eta, tau and $taucoef\!f$ are chosen for the desired error order finite difference formula and its characteristic polynomial, respectively.

The four central code lines above that are barred along the left edge express the computational essence of Step 6 for the matrix eigen-problem in ZNN. Only there is any math performed, the rest of the program code are input reads and output saves and preparations. After Step 6 we store the new data and repeat these 4 code lines with peripherals for $t_{k+2}$ until we are done with one eigenvalue at $t = t_f$. Then we repeat the same code for the next eigenvalue of a hermitean or diagonalizable matrix flow A(t).

What is actually computed in formula (6i) for time-varying matrix eigen-problems in ZNN? To explain we recall some convergent finite difference formula theory next.

It is well known that the characteristic polynomial coefficients $a_k$ of a finite difference scheme must add up to zero for convergence, see [11, Section 17] e.g. Thus for a look-ahead and convergent finite difference formula

$$\begin{aligned} z(t_{k+1}) + \alpha _k z(t_k) + \alpha _{k-1} z(t_{k-1}) + \ \cdots \ + \alpha _{k-\ell } z(t_{k-\ell }) \end{aligned}$$

and its characteristic polynomial

$$\begin{aligned} p(x) = x^{k+1} + \alpha _k x^k + \alpha _{k-1} x^{k-1} + \ \cdots \ + \alpha _{k-\ell } x^{k-\ell } \end{aligned}$$

we must have that $p(1) = 1 + \alpha _k + \alpha _{k-1} +\ldots + \alpha _{k-\ell } = 0$. Plugging $z_{..}$ into the 5-IFD difference formula (4i), we realize that in formula (6i)

due to unavoidable truncation and rounding errors. Thus asymptotically and with the stipulated exponential error decay

with local truncation error of order $O(\tau ^4)$ for the chosen 5-IFD j_s = 2_3 difference formula in (4i).

In step 6 of the above ZNN process, formula (6i)

$$\begin{aligned} z_{k+1} = \dfrac{9}{4} \tau (P(t_k) \backslash q(t_k)) - \dfrac{1}{8} z_k + \dfrac{3}{4} z_{k-1} + \dfrac{5}{8} z_{k-2} - \dfrac{1}{4} z_{k-3} \ \in {\mathbb {C}}^{n+1} \end{aligned}$$

splits the 5-IFD formula (8i) into two nearly equal parts that become ever closer to each other in (9i) due to the nature of our convergent finite difference schemes. The first term $\dfrac{9}{4} \tau (P(t_k) \backslash q(t_k))$ in (6i) adjusts the predicted value of $z(t_{k+1})$ only slightly according to the current system data inputs while the remaining finite difference formula term

$$\begin{aligned} - \dfrac{1}{8} z_k + \dfrac{3}{4} z_{k-1} + \dfrac{5}{8} z_{k-2} - \dfrac{1}{4} z_{k-3} \end{aligned}$$

in (6i) has eventually a nearly identical magnitude as the solution vector $z_{k+1}$ at time $t_{k+1}$.

And indeed for the time-varying matrix square root problem in (VII), our test flow matrix A(t) in Fig. 1 increases in norm to around 10,000 after 6 min of simulation and the norm of the solution square root matrix flow X(t) hovers around 100 while the magnitude of the first linear equations solution term of (6i) is around $10^{-2}$, i.e., the two terms of the ZNN iteration (6i) differ in magnitude by a factor of around $10^4$, a disparity in magnitude that we should expect from the above analysis. This behavior of ZNN matrix methods is exemplified by the error graph for time-varying matrix square root computations in Fig. 1 below that will be discussed further in Sect. 3, part (VII). The ‘wiggles’ in the error curve of Fig. 1 after the initial decay phase represent the relatively small input data adjustments that are made by the linear solve term of ZNN. For more details and data on the magnitude disparity see [54, Fig 6, p.173].

Figure 1 was computed via simple Euler steps from a random entry matrix start-up matrix in tvMatrSquareRootwEulerStartv.m, see Sect. 3(VII start-up). The main ZNN iterations for Fig. 1 have used a 9-IFD formula of type 4_5 with local truncation order 6.

Fig. 1

Typical relative error output for tvMatrSquareRootwEulerStartv.m in Sect. 3(VII)

The 5-IFD formula in equation (4i) above is of type j_s = 2_3 and in discretized ZNN its local truncation error order is relatively low at $O(\tau ^4)$ as $j+2 = 2+2 = 4$. In tests we prefer to use a 9-IFD of type 4_5. To start a discretized ZNN iteration process with a look-ahead convergent finite difference formula of type j_s from the list in [46] requires $j+s$ known starting values. For time-varying matrix eigenvalue problems that are given by function inputs for $A(t_k)$ we generally use Francis QR to generate the $j+s$ start-up eigen-data set, then iterate via discretized ZNN. And throughout the discrete iteration process from $t = t_o$ to $t = t_f$ we need to keep only the most recently computed $j+s$ points of data to compute the eigen-data predictively for $t = t_{k+1}$.

MATLAB codes for several time-varying matrix eigenvalue computations via discretized ZNN are available at [48].

Next we study how to construct general look-ahead and convergent finite difference schemes of arbitrary truncation error orders $O(\tau ^p)$ with $p \le 8$ for use in discretized ZNN time-varying matrix methods. We start from random entry seed vectors and can use Taylor polynomials and elementary linear algebra to construct look-ahead finite difference formulas of any order that may or—most likely—may not be convergent. The constructive first step of finding look-ahead finite difference formulas is followed by a second, an optimization procedure to find look-ahead and convergent finite difference formulas of the desired error order. This second non-linear part may not always succeed as we shall explain later.

Consider a discrete time-varying state vector $x_k = x(t_k) = x(t_o+k \cdot \tau )$ for a constant sampling gap $\tau$ and $k = 0,1,2,\ldots$ and write out $r = \ell + 1$ explicit Taylor expansions of degree j for $x_{k+1}, x_{k-1},\ldots , x_{k-\ell }$ about $x_k$.

Each Taylor expansion in our scheme will contain $j+2$ terms on the right hand side, namely j derivative terms, a term for $x_k$, and one for the error $O(\tau ^{j+1})$. Each right hand side’s under- and over-braced $j-1$ ‘column’ terms in the scheme displayed below contain products of identical powers of $\tau$ and identical higher derivatives of $x_k$ which—combined in column vector form, we will call taudx. Our aim is to find a linear combination of these $r = \ell +1$ equations for which the under- and over-braced sums vanish for all possible higher derivatives of the solution x(t) and all sampling gaps $\tau$. If we are able to do so, then we can express $x_{k+1}$ in terms of $x_l$ for $l = k,k-1,\ldots ,k-\ell$, $\dot{x}_k$, and $\tau$ with a local truncation error of order $O(\tau ^{j+1})$ as a linear combination of the depicted $r=\ell + 1$ Taylor equations (10) through (15) below. Note that the first Taylor expansion (10) for $x(t_{k+1})$ is unusual, being look-ahead. This has never been used in standard ODE schemes. Equation (10) sets up the predictive behavior of ZNN.

$$\begin{aligned} x_{k+1}= & {} x_k ~ +~ \tau {\dot{x}}_k \ \overbrace{ + \ \ \dfrac{\tau ^2}{2!} ~ \ddot{x}_k \ \ ~ + ~ \ \ \dfrac{\tau ^3}{3!} ~ \overset{\dots }{x}_k ~ \ \ldots \ \ \ \ \ \ \ \ \ \ + \ \dfrac{\tau ^{j}}{j!} ~ \overset{j}{{\dot{x}}}_k \ \ \ \ \ \ } \ \ \ + \ ~O(\tau ^{j+1}) \end{aligned}$$

(10)

$$\begin{aligned} x_{k-1}= & {} x_k ~ - ~ \tau {\dot{x}}_k \ + \ \dfrac{\tau ^2}{2!} ~ \ddot{x}_k \ \ ~ - ~ \ \ \dfrac{\tau ^3}{3!} ~ \overset{\dots }{x}_k ~ \ \ldots \ \ \ \ + (-1)^{j}\dfrac{\tau ^{j}}{j!} ~ \overset{j}{{\dot{x}}}_{k} \ \ \ \ \ ~ + \ O(\tau ^{j+1}) \end{aligned}$$

(11)

$$\begin{aligned} x_{k-2}= & {} x_k - 2\tau {\dot{x}}_k \ + \dfrac{(2\tau )^2}{2!} ~ \ddot{x}_k - \dfrac{(2\tau )^3}{3!} ~ \overset{\dots }{x}_k ~\ldots ~ + (-1)^{j} \dfrac{(2\tau )^{j}}{j!} ~ \overset{j}{{\dot{x}}}_{k} \ \ \ + \ O(\tau ^{j+1}) \end{aligned}$$

(12)

$$\begin{aligned} x_{k-3}= & {} x_k - 3\tau {\dot{x}}_k \ + \dfrac{(3\tau )^2}{2!} ~ \ddot{x}_k - \dfrac{(3\tau )^3}{3!} ~ \overset{\dots }{x}_k ~\ldots ~ + (-1)^{j} \dfrac{(3\tau )^{j}}{j!} ~ \overset{j}{{\dot{x}}}_{k} \ \ \ + \ O(\tau ^{j+1}) \end{aligned}$$

(13)

$$\begin{aligned}&\vdots&\hspace{53mm} \vdots \end{aligned}$$

(14)

$$\begin{aligned} x_{k-\ell }= & {} x_k - \ell \tau {\dot{x}}_k \ \ \underbrace{ + \ \dfrac{(\ell \tau )^2}{2!} ~ \ddot{x}_k - \dfrac{(\ell \tau )^3}{3!} ~ \overset{\dots }{x}_k ~\ldots \ + (-1)^{j} \dfrac{(\ell \tau )^{j}}{j!} ~~ \overset{j}{{\dot{x}}}_{k} } \ \ ~ + ~ O \ (\tau ^{j+1})\nonumber \\ \end{aligned}$$

(15)

The ‘rational number’ factors in the ‘braced $j-1$ columns’ on the right-hand side of equations (10) through (15) are collected in the $r = \ell + 1$ by $j-1$ matrix $\mathcal A$:

$$\begin{aligned} \mathcal{A}_{r,j-1} = \left( \begin{array}{llllll} \dfrac{1}{2!} &{} \dfrac{1}{3!} &{} \dfrac{1}{4!} &{} \cdots &{} \cdots &{}\qquad \dfrac{1}{j!}\\ \dfrac{1}{2!} &{} -\dfrac{1}{3!} &{} \dfrac{1}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{1}{j!}\\ \dfrac{2^2}{2!} &{} - \dfrac{2^3}{3!} &{} \dfrac{2^4}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{2^{j}}{j!}\\ \vdots &{} \vdots &{} \vdots &{}&{} &{} \vdots \\ \dfrac{\ell ^2}{2!} &{} - \dfrac{\ell ^3}{3!} &{} \dfrac{\ell ^4}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{\ell ^{j}}{j!} \end{array}\right) _{r,j-1}. \end{aligned}$$

(16)

Now the over- and under-braced expressions in equations (10) through (15) above have the matrix times vector product form

$$\begin{aligned} \mathcal{A} \cdot taudx = \left( \begin{array}{llllll} \dfrac{1}{2!} &{} \dfrac{1}{3!} &{} \dfrac{1}{4!} &{} \cdots &{} \cdots &{}\qquad \dfrac{1}{j!}\\ \dfrac{1}{2!} &{} -\dfrac{1}{3!} &{} \dfrac{1}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{1}{j!}\\ \dfrac{2^2}{2!} &{} - \dfrac{2^3}{3!} &{} \dfrac{2^4}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{2^{j}}{j!}\\ \vdots &{} \vdots &{} \vdots &{}&{} &{} \vdots \\ \dfrac{\ell ^2}{2!} &{} - \dfrac{\ell ^3}{3!} &{} \dfrac{\ell ^4}{4!} &{} \cdots &{} \cdots &{} (-1)^{j}~ \dfrac{\ell ^{j}}{j!} \end{array}\right) _{r,j-1} \hspace{-6.7mm} \cdot \left( \begin{array}{ll} \tau ^2 \ \ddot{x}_k \\ \tau ^3 \ \overset{\dots }{x}_k \\ \tau ^4 \ \overset{4}{{\dot{x}}}_k \\ \vdots \\ \vdots \\ \tau ^{j} \ \overset{j}{{\dot{x}}}_{k} \end{array}\right) _{j-1,1} \end{aligned}$$

(17)

where the $j-1$-dimensional column vector taudx contains the increasing powers of $\tau$ multiplied by the respective higher derivatives of $x_k$ that appear in the Taylor expansions (10) to (15).

Note that for any nonzero left kernel row vector $y \in {\mathbb {R}}^{r}$ of $\mathcal{A}_{r,j-1}$ with $y \cdot \mathcal{A} = o_{1,j-1}$ we have

$$\begin{aligned} y_{1,r} \cdot \mathcal{A}_{r, j-1} \cdot taudx_{j-1,1} = o_{1,j-1} \cdot taudx_{j-1,1} = 0\in {\mathbb {R}}\, \end{aligned}$$

no matter what the higher derivatives of x(t) at $t_k$ are. Clearly we can zero all under- and over-braced terms in equations (10) to (15) if $\mathcal{A}_{r,j-1}$ has a nontrivial left kernel. This is certainly the case if $\mathcal A$ has more rows than columns, i.e., when $r=\ell +1 >j-1$. A non-zero left kernel vector w of $\mathcal A$ can then be easily found via Matlab, see [45] for details. The linear combination of the equations (10) through (15) with the coefficients of $w \ne o$ creates a predictive recurrence relation for $x_{k+1}$ in terms of $x_k, x_{k-1},\ldots , x_{k-\ell }$ and $\dot{x}_k$ with local truncation error order $O(\tau ^{j+2})$ as desired. Solving this recurrence equation for $\dot{x}_k$ gives us formula (4i) in Step 4. Then multiplying by a multiple of $\tau$ in Step 5 increases the resulting formula’s local truncation error order from $O(\tau ^{j+1})$ to $O(\tau ^{j+2})$ in equation (5i).

Thus far we have tacitly assumed that the solution x(t) is sufficiently often differentiable for high order Taylor expansions. This can rarely be the case in real world applications, but—fortunately—discretized computational ZNN works very well with errors as predicted by Taylor even for discontinuous and limited random sensor failure inputs and consequent non-differentiable x(t). The reason is a mystery. We do not know of any non-differentiable Taylor expansion theory. What this might be is a challenging open question for time-varying numerical matrix analysis.

A recursion formula’s characteristic polynomial determines its convergence and thus its suitability for discretized ZNN methods. More specifically, the convergence of finite difference formulas and recurrence relations like ours hinges on the lay of the roots of their associated characteristic polynomials in the complex plane. This is well known for multi-step formulas and also applies to processes such as discretized ZNN recurrences. Convergence requires that all roots of the formula’s characteristic polynomial lie inside or on the unit disk in ${\mathbb {C}}$ with no repeated roots allowed on the unit circle, see [11, Sect. 17.6.3] e.g.

Finding convergent and look-ahead finite difference formulas from look-ahead ones is a non-linear problem. In [45] we have approached this problem by minimizing the maximal modulus root of ‘look-ahead’ characteristic polynomials to below $1 + eps$ for a very small threshold $0 \approx eps\ge 0$ so that they become numerically and practically convergent while the polynomials’ coefficient vectors w lie in the left kernel of $\mathcal{A}_{r,j-1}$.

The set of look-ahead characteristic polynomials is not a subspace since sums of such polynomials may or—most often—may not represent look-ahead finite difference schemes. Hence we must search indirectly in a neighborhood of the starting seed $y\in {\mathbb {R}}^{r-j+1}$ for look-ahead characteristic polynomials with proper minimal maximal magnitude roots. For this indirect root minimization process we have used Matlab’s multi-dimensional minimizer function fminsearch.m that uses the Nelder-Mead downhill simplex method, see [26, 31]. It mimics the method of steepest descent and searches for local minima via multiple function evaluations without using derivatives until it has either found a look-ahead seed with an associated characteristic polynomial that is convergent and for which its coefficient vector remains in the left kernel of the associated $\mathcal{A}_{r,j}$ matrix, or there is no such convergent formula from the chosen look-ahead seed.

Our two part look-ahead and convergent difference formula finding algorithm has computed many convergent and look-ahead finite difference schemes for discretized ZNN of all types j_s with $1 \le j \le 6$ and $j \le s \le j+3$ with local truncation error orders between $O(\tau ^3)$ and $O(\tau ^8)$. Convergent look-ahead finite difference formulas were unavailable before for ZNN use with error orders above $O(\tau ^4)$. And different low error order formulas had only been used before in the corrector phase of predictor-corrector ODE solvers.

In our experiments with trying to find convergent and look-ahead discretization formulas of type j_s where $s = r-j$ we have never succeeded when $1 \le s = r-j <j$. Success always occurred for $s = j$ and better success when $s = j+1$ or $s=j+2$. It is obvious that for $s= r-j= 1$ and any seed $y \in {\mathbb {R}}^1$ there is only one normalized look-ahead discretization formula j_1 and it appears to never be convergent. For convergence we seemingly need more freedom in our seed space ${\mathbb {R}}^{r -j}$ than there is in one dimension or even in less than j-dimensional space.

A different method to find convergent look-ahead finite difference formulas starting from the same Taylor expansions in (10) to (15) above has been derived in [59] for various IFD formulas with varying truncation error orders from 2 through 6 and rational coefficients. These two methods have not been compared or their differences studied thus far.

Remark 1

• Discretized Zhang Neural Networks were originally designed for sensor based time-varying matrix problems. They solve sensor given matrix flow problems accurately in real-time and for on-line chip applications. They are being used extensively in this way today. Yet discretized matrix Zhang Neural Networks are partially built on one differential equation, the error function DE (2), and they use custom multi-step finite difference formulas as our centuries old numerical initial value ODE solvers do in analytic continuation algorithms.

• What are their differences? I.e., can discretized ZNN be used, somehow understood, or interpreted as part of an analytic continuation method for ODEs. Or is the reverse possible, i.e., can numerical IVP ODE solvers be used successfully for function based parameter-varying matrix problems?

• Only the latter seems possible, see [28] for example. There the accuracy and speed comparison of the much more difficult to evaluate field of values boundary curve equation is bettered by an analytic continuation method that integrates the computationally simpler derivative more accurately and quickly.

• Yet for time-varying, both function based and sensor based, matrix flow problems Zhang Neural Networks algorithms are seemingly a breed of their own.

• In Sect. 3(V) we use them to solve time-varying linear systems of nonlinear equations via Lagrange matrix multipliers and linearly constrained nonlinear optimization.

• Here, however, we deliberately focus on the seven step design of Zhang Neural Networks for discretized time-varying matrix flow problems.

• Given an initial value function based ODE problem

  $$\begin{aligned} y'(t) = f(t,y(t)) \ \ \text{ with } \ \ y(t_o) = y_o \ \text { and } t \in [a,b], \end{aligned}$$

  and if we formally integrate

  $$\begin{aligned} \int _{t_i}^{t_{i+1}} y'(t) \ dt = \int _{t_i}^{t_{i+1}} f(t,y(t)) \ dt \ \text { with } t_i \ge a \text { and } t_{i+1} \le b \end{aligned}$$

  we obtain the one-step look-ahead Euler-type formula

  $$\begin{aligned} y(t_{i+1}) = y(t_i) + \int _{t_i}^{t_{i+1}} f(t,y(t)) \ dt \end{aligned}$$

  for all feasible i. The aim of IVP ODE solvers is to compute an accurate approximation for each partial integral of f from $t_i$ to $t_{i+1}$ and then approximate the value of y at $t_{i+1}$ by adding $\int _{t_i}^{t_{i+1}} f(t,y(t)) dt$ to its previously computed value $y(t_i)$. One-step methods use ever more accurate integration formulas to achieve an accurate table of values for y, provided that an antiderivative of $y'$ is not known, cannot be found in our antiderivative tables, and cannot be computed via symbolic integration software.

• The multi-step formulas of Adams–Bashforth, Adams–Moulton and others use several earlier computed y values and integration formulas in tandem in a two-process method of prediction followed by a correction step. The Fehlberg multi-step corrector formula [11, p.464], [14] uses three previous y values and five earlier right-hand side function f evaluations while the Gear corrector formulas [11, p. 480], [17] use up to six previously computed y values and just one function evaluation to obtain $y(t_{i+1})$ from data at or before time $t_i$. Note finally that IVP one- and multi-step ODE integrators are not predictive, since they use the right-hand side function data f(t, y(t)) of the ODE $y' = f(t,y(t))$ up to and including $t = t_{i+1}$ in order to evaluate $y'$’s antiderivative $y(t_{i+1})$.

• The onus of accuracy for classic general analytic continuation ODE solvers such as polygonal, Runge–Kutta, Heun, Prince–Dormand and embedding formulas lies within the chosen integration formula’s accuracy for the solution data as their errors propagate and accumulate from each $t_i$ to $t_{i+1}$ and so forth in the computed solution y(t) as time t increases.

• All Zhang Neural Network based algorithms for time-varying matrix problem differ greatly in method, set-up, accuracy and speed from any analytic continuation method that computes antiderivative data for the given function $y' = f$ approximately, but without exponentially decreasing its errors over time as ZNN does.

• ZNN’s fundamental difference lies in the stipulated (and actually computed and observed) exponential error decay of the solution. ZNN solutions are rather impervious to noisy inputs, to occasional sensor failures and even to erroneous random data inputs (in a limited number of entries of the time-varying input matrix), see [47] e.g., because an external disturbance will become invisible quickly in any solution whose error function decreases exponentially by its very design.

• A big unsolved challenge for both sensor driven matrix flow data acquisition and function based Zhang Neural Networks is their use of Taylor expansions, see formulas (10) through (15) in Sect. 2. Taylor expansions require smooth and multiply differentiable functions. But for Zhang Neural Network algorithms and time-varying matrix problems there is no guarantee of even once differentiable inputs or solutions. Non-differentiable movements of robots such as bounces are common events. Yet discretized ZNN is widely used with success for robot control.

• This dilemma seems to require a new understanding and theory of Taylor formulas for non-differentiable time-varying functions.

• The speed of error decay of ZNN based solutions hinges on a feasibly chosen decay constant $\eta$ in Step 2 for the given sampling gap $\tau$ and on the truncation error order of the look-ahead convergent difference formula that is used. While analytical continuation is best used over small sub-intervals of increasing t values inside [a, b], we have run ZNN methods for seemingly near infinite time intervals $[0,t_f]$ with $t_f = 5, 10, 20, 100, 200,\ldots , 480,$ or 3600 s and up to eight hours and have seen no deterioration in the error, or just the opposite, see Fig. 1 above for the time-varying matrix square root problem, for example, whose relative error decreases continuously over a 6 min span. Note further that time-varying matrix problems can be started from almost any starting value $y_o$ in ZNN and the computed solution will very quickly lock onto the problem’s proper solution.

• But ZNN cannot solve ODEs, nor can it solve static matrix/vector equations; at least we do not know how to. Here the term static matrix refers to a matrix with constant real or complex entries. On the other hand, path following IVP ODE based methods have been used to solve formulaic matrix equations successfully, see [28, 49, 53] e.g., but only implicit and explicit Runge–Kutta formulas can integrate sensor clocked data input while—on the other hand—suffering larger integration errors than adaptive integrators such as Prince–Dormand or ZNN.

Discretized Zeroing Neural Network methods and the quest for high order convergent and look-ahead finite difference formulas bring up many open problems in numerical analysis:

Are there any look-ahead finite difference schemes with $s < q$ in $\mathcal{A}_{q+s,q}$ and minimally more rows than columns? Why or why not?

For relatively low dimensions the rational numbers matrix $\mathcal{A}_{q+s,q}$ in formula (16) above can easily be checked for full rank when $1 \le q \le 6$. Is this true for all integers q? Has the rational $\mathcal{A}$ matrix in (16) ever been encountered anywhere else?

Every look-ahead polynomial p that we have constructed from any seed vector $y \in {\mathbb {R}}^s$ with $s \ge q$ by our method has had precisely one root on the unit circle within $10^{-15}$ numerical accuracy. This even holds for non-convergent finite difference formula polynomials p with some roots outside the unit disk. Do all Taylor expansion matrix $\mathcal{A}_{q+s,q}$ based polynomials have at least one root on the unit circle in ${\mathbb {C}}$? What happens for polynomial finite difference formulas with all of their characteristic roots inside the open unit disk and none on the periphery or the outside? For the stability of multi-step ODE methods we must have $p(1) = \sum p_i = 0$, see [11, p. 473] for example.

For any low dimensional type j_s finite difference scheme there are apparently dozens of convergent and look-ahead finite difference formulas for any fixed local truncation error order if $s \ge j > 1$.

What is the most advantageous such formula to use in discretized ZNN methods, speed-wise, convergency-wise?

What properties of a suitable formula improve or hinder the ZNN computations for time-varying matrix processes?

Intuitively we have preferred those convergent and look-ahead finite difference formulas whose characteristic polynomials have relatively small second largest magnitude roots.

Is that correct and a good strategy for discretized ZNN methods? See the graphs at the end of [49] for examples.

A list of further observations and open problems for discretized ZNN based time-varying matrix eigen methods is included in [47].

The errors in ZNN’s output come from three sources, namely (a) the rounding errors in solving the linear system in (3i) or (6i), (b) the truncation errors of the finite difference formula and the stepsize $\tau$ used, and (c) from the backward evaluation of the derivative $\dot{A}(t_k)$ in the right hand side expression of equation (Azi) or (Pqzi) above. How should one minimize or equilibrate their effects for the best overall computed accuracy when using recurrence relations with high or low truncation error orders? High degree backward recursion formulas for derivatives are generally not very good.

3 Models and applications of discretized ZNN matrix methods

In this section we develop specific discretized ZNN algorithms for a number of selected time-varying matrix problems. Moreover we introduce new matrix techniques to transform matrix models into Matlab code and we point to problem specific references.

Our first example deals with the oldest human matrix problem, namely solving linear equations $A_{n,n} x = b_n$. This model goes back well over 6,000 years to Babylon and Sumer on cuneiform tablets that describe Gaussian elimination techniques and solve static linear equations $Ax=b$ for small dimensions n.

(I) Time-varying Linear Equations and Discretized ZNN:

For simplicity, we consider matrix flows $A(t)_{n,n} \in {\mathbb {C}}_{n,n}$ all of whose matrices are invertible on a time interval $t_o \le t \le t_f \subset {\mathbb {R}}$. Our chosen model equation is $A_{n,n} (t)x(t) = b(t) \in {\mathbb {C}}^n$ for the unknown solution vector x(t). The error function is $e(t) = A(t)x(t) - b(t)$ and the error differential equation is

Solving the inner equation $(*)$ in first for $A(x)\dot{x}(t)$ and then for $\dot{x}(t)$ we obtain the the following two differential equations (DEs,) see also [61, (4.4)]

$$\begin{aligned} A(t) \dot{x}(t) = - \dot{A}(t) x(t) + \dot{b}(t) -\eta ~ A(t)x(t) +\eta ~ b(t)\ \end{aligned}$$

and

To simplify matters we use the simple 5-IFD formula (11i) of Sect. 2 again in discretized mode with $A_k = A(t_k), x_k = x(t_k)$ and $b_k = b(t_k)$ to obtain

Equating derivatives at time $t_k$ yields

Then the inner equation $(*)$ of gives us the predictive convergent and look-ahead ZNN formula

Since equation involves the matrix inverse $A^{-1}_k$ at each time step $t_k$, we propose two different Matlab codes to solve time-varying linear equations for invertible matrix flows A(t). The code tvLinEquatexinv.m in [55] uses Matlab’s matrix inversion method inv.m explicitly at each time step $t_k$ as requires, while our second code tvLinEquat.m in [55] uses two separate discretized ZNN formulas. The tvLinEquat.m code solves the time-varying linear equation with the help of one ZNN method that computes the inverse of each $A(t_k)$ iteratively as detailed next in Example (II) below and another ZNN method that that solves equation by using these two independent and interwoven discretized ZNN iterations.

Both methods run equally fast. The first with its explicit matrix inversion is a little more accurate since Matlab’s inv computes small dimensioned matrix inverses near perfectly with $10^{-16}$ relative errors while ZNN based time-varying matrix inversions give us slightly larger errors, losing 1 or 2 accurate trailing digits. This is most noticeable if we use low truncation error order look-ahead finite difference formulas for ZNN and relatively large sampling gaps $\tau$. There are dozens of references when googling ‘ZNN for time-varying linear equations’, see also [57] or [66].

(II) Time-varying Matrix Inverses via ZNN:

Assuming again that all matrices of a given time-varying matrix flow $A(t)_{n,n} \in {\mathbb {C}}_{n,n}$ are invertible on a given time interval $t_o \le t \le t_f \subset {\mathbb {R}}$, we construct a discretized ZNN method that finds the inverse X(t) of each A(t) predictively from previous data so that $A(t)X(t) = I_n$, i.e., $A(t) = X(t)^{-1}$ is our model here. This gives rise to the error function $E(t) = A(t) - X(t)^{-1} \ (= O_{n,n} \text { ideally})$ and the associated error differential equation

Since $X(t)X(t)^{-1} = I_n$ is constant for all t, $d(X(t)X(t)^{-1})/dt = O_{n,n}$. And the product rule gives us the following relation for the derivative of time-varying matrix inverses

$$\begin{aligned} O_{n,n} =\dfrac{d(X(t)X(t)^{-1})}{dt} = \dot{X}(t) X(t)^{-1} + X(t) \dot{X}(t)^{-1} \, \end{aligned}$$

and thus $\dot{X}(t)^{-1} = -X(t)^{-1} \dot{X}(t) X(t)^{-1}$ . Plugging this derivative formula into establishes

$$\begin{aligned} \dot{E}(t) = \dot{A}(t) - \dot{X}(t)^{-1} = \dot{A}(t) + X(t)^{-1}\dot{X}(t) X(t)^{-1} {\mathop {=}\limits ^{(*)}} -\eta ~ A(t) + \eta ~ X(t)^{-1} = -\eta ~ E(t). \end{aligned}$$

Multiplying the inner equation $(*)$ above by X(t) from the left on both, the left- and right-hand sides and then solving for $\dot{X}(t)$ yields

Fig. 2

Cuneiform tablet (from Yale) with Babylonian methods for solving a system of two linear equations. [Search for CuneiformYBC4652 first to then learn more on YBC 04652 from the Cuneiform Digital Library Initiative in Berlin at https://cdli.mpwg-berlin.mpg.de and from other articles on YBC 4652.]

If—for simplicity—we choose the same 5-IFD look-ahead and convergent formula as was chosen on line (4i) for Step 4 of the ZNN eigen-data method in Sect. 1, then we obtain the analogous equation to (12i) here with $(P\backslash q)$ replaced by the right-hand side of equation . Instead of the eigen-data iterates $z_j$ in (12i) we use the inverse matrix iterates $X_j = X(t_j)$ here for $j = k-3,\ldots ,k+1$ and obtain

Solving $(*)$ in for $X_{k+1}$ supplies the complete ZNN recursion formula that finishes Step 6 of the predictive discretized ZNN algorithm development for time-varying matrix inverses.

This look-ahead iteration is based on the convergent 5-IFD formula of type j_s = 2_3 with local truncation error order $O(\tau ^4)$. The formula requires two matrix multiplications, two matrix additions, one backward approximation of the derivative of $A(t_k)$ and a short recursion with $X_j$ at each time step.

The error function differential equation is akin to the Getz and Marsden dynamic system (without the discretized ZNN $\eta$ decay terms) for time-varying matrix inversions, see [18, 20]. Simulink circuit diagrams for this model and time-varying matrix inversions are available in [64, p. 97].

A Matlab code for the time-varying matrix inversion problem is available in [55] as tvMatrixInverse.m. A different model is used in [62] and several others are described in [64, chapters 9, 12] (Fig. 2).

The image in Fig. 2 above shows how ubiquitous matrices and matrix computations have been across the eons, cultures and languages of humankind on our globe. It took years to learn and translate cuneiform symbols and to realize that ‘Gaussian elimination’ was already well understood and used then. And it is still central for matrix computations today.

Remark 2

(a) Example (II) reminds us that the numerics for time-varying matrix problems may differ greatly from our static matrix numerical approaches for matrices with constant entries. time-varying matrix problems are governed by different concepts and follow different best practices.

For static matrices $A_{n,n}$ we are always conscious of and we remind our students never to compute the inverse $A^{-1}$ in order to solve a linear equation $Ax = b$ because this is an expensive proposition and rightly shunned. But for time-varying matrix flows $A(t)_{n,n}$ it seems impossible to solve time-varying linear systems $A(t)x(t) = b(t)$ predictively without explicit matrix inversions as was explained in part (I) above. For time-varying linear equations, ZNN methods allow us to compute time-varying matrix inverses and solve time-varying linear equations in real time, accurately and predictively. What is shunned for static matrix problems may work well for the time-varying matrix variant and vice versa.

(b) For each of the example problems in this section our annotated rudimentary ZNN based Matlab codes are stored in [55]. For high truncation error order look-ahead convergent finite difference formulas such as 4_5 these codes achieve 12 to 16 correct leading digits predictively for each entry of the desired solution matrix or vector and they do so uniformly for all parameter values of t after the initial exponential error reduction has achieved this accuracy.

(c) General warning: Our published codes in [55] may not apply to all uses and may give incorrect results for some inputs and in some applications. These codes are built here explicitly only for educational purposes. Their complication level advances in numerical complexity as we go on and our explicit codes try to help and show users how to solve time-varying applied and theoretical matrix problems with discretized ZNN methods. We strongly advise users to search the theoretical literature on their specific problem and to test their own applied ZNN codes rigorously and extensively before applying them in the field. This scrutiny will ensure that theory or code exceptions do not cause unintended consequences or accidents in the field.

(III) Pseudo-inverses of Time-varying Non-square Matrices with Full Rank and without:

Here we first look at rectangular matrix flows $A(t)_{m,n} \in {\mathbb {C}}_{m,n}$ with $m \ne n$ that have uniform full rank($A(t)) =$ min(m, n) for all $t_o \le t \le t_f \subset {\mathbb {R}}$.

Every matrix $A_{m,n}$ with $m = n$ or $m \ne n$ has two kinds of nullspaces or kernels

$$\begin{aligned} N(A)_r = \{x \in {\mathbb {C}}^n \mid Ax = 0 \in {\mathbb {C}}^m\} \ \ \ \text {and} \ \ \ N(A)_\ell = \{x \in {\mathbb {C}}^m \mid xA = 0 \in {\mathbb {C}}^n\} \, \end{aligned}$$

called A’s right and left nullspace, respectively. If $m>n$ and $A_{m,n}$ has full rank n, then A’s right kernel is $\{0\} \subset {\mathbb {C}}^n$ and the linear system $Ax=b \in {\mathbb {C}}^m$ cannot be solved for every $b \in {\mathbb {C}}^m$ since the number the columns of $A_{m,n}$ is less than required for spanning all of ${\mathbb {R}}^m$. If $m < n$ and $A_{m,n}$ has full rank m, then A’s left kernel is $\{0\} \subset {\mathbb {C}}^m$ and similarly not all equations $xA=b \in {\mathbb {C}}^n$ are solvable with $x \in {\mathbb {C}}^m$. Hence we need to abandon the notion of matrix inversion for rectangular non-square matrices and resort to pseudo-inverses instead.

There are two kinds of pseudo-inverses of $A_{m,n}$, too, depending on whether $m >n$ or $m<n$. They are always denoted by $A^+$ and always have size n by m if A is m by n. If $m>n$ and $A_{m,n}$ has full rank n, then $A^+ = (A^*A)^{-1}A^* \in {\mathbb {C}}_{n,m}$ is called the left pseudo-inverse because $A^+A = I_n$. For $m<n$ the right pseudo-inverse of $A_{m,n}$ with full rank m is $A^+ = A^*(AA^*)^{-1} \in {\mathbb {C}}_{n,m}$ with $AA^+ = I_m$.

In either case $A^+$ solves a minimization problem, i.e.,

$$\begin{aligned}{} & {} \min _{x\in {\mathbb {C}}^n} ||Ax - b||_2 = ||A^+ b||_2 \ge 0 \ \ \text { for } \ m>n \ \text { and } \\{} & {} \min _{x \in {\mathbb {C}}^m} ||xA - b||_2 = ||bA^+||_2 \ge 0 \ \ \text { for } \ m<n. \end{aligned}$$

Thus the pseudo-inverse of a full rank rectangular matrix $A_{m,n}$ with $m \ne n$ solves the least squares problem for sets of linear equations whose system matrices A have nontrivial left or right kernels, respectively. It is easy to verify that $(A^+)^+ = A$ in either case, see e.g. [39, section 4.8.5]. Thus the pseudo-inverse $A^+$ acts similarly to the matrix inverse $A^{-1}$ when $A_{n,n}$ is invertible and $m=n$. Hence its name.

First we want to find the pseudo-inverse X(t) of a full rank rectangular matrix flow $A(t)_{m,n}$ with $m < n$. Since $X(t)^+ = A(t)$ we can try to use the dynamical system of Getz and Marsden [18] again and start with $A(t)=X(t)^+$ as our model equation.

(a) The right pseudo-inverse model$X(t) = A(t)^+$ for matrix flows $A(t)_{m,n}$ of full rank m when $m<n$:

The exponential decay stipulation for our model’s error function $E(t) = A(t) - X(t)^+$ makes

Since $A(t)X(t) = I_m$ for all t and $A(t) = X(t)^+$ we have

$$\begin{aligned} O_{m,m} = d(I_m)/dt = d(A(t)X(t))/dt = d(X(t)^+X(t))/dt = \dot{X}(t)^+ X(t) + X(t)^+ \dot{X}(t) . \end{aligned}$$

Thus $\dot{X}(t)^+ X(t) = - X(t)^+ \dot{X}(t)$ or $\dot{X}(t)^+ = - X(t)^+ \dot{X}(t) X(t)^+$ after multiplying equation $(*)$ in by $X(t)^+$ on the right. Updating equation establishes

$$\begin{aligned} \dot{A}(t) + X(t)^+\dot{X}(t) X(t)^+= - \eta ~ A(t) + \eta ~ X(t)^+ . \end{aligned}$$

Multiplying both sides on the left and right by X(t) then yields

$$\begin{aligned} X(t)\dot{A}(t) X(t)+ X(t)X(t)^+\dot{X}(t) X(t)^+ X(t)= - \eta ~ X(t) A(t) X(t)+ \eta ~ X(t) X(t)^+ X(t) . \end{aligned}$$

Since $X(t)^+ X(t) = I_n$ we obtain after reordering that

$$\begin{aligned} X(t)X(t)^+\dot{X}(t) = - X(t)\dot{A}(t) X(t) - \eta ~ X(t) A(t) X(t)+ \eta ~ X(t) X(t)^+ X(t) . \end{aligned}$$

But $X X(t)^+$ has size n by n and rank $m<n$. Therefore it is not invertible. And thus we cannot cancel the encumbering left factors for $\dot{X}(t)$ above and solve the equation for $\dot{X}(t)$ as would be needed for Step 3. And a valid ZNN formula cannot be obtained from our first simple model $A(t) = X(t)^+$.

This example contains a warning not to give up if one model does not work for a time-varying matrix problem.

Next we try another model equation for the right pseudo-inverse X(t) of a full rank matrix flow $A(t)_{m,n}$ with $m<n$. Using the definition of $A(t)^+ = X(t) = A(t)^*(A(t)A(t)^*)^{-1}$ we start from the revised model $X(t) A(t)A(t)^* = A(t)^*$. With the error function $E = XAA^* - A^*$ we obtain (leaving out all time dependencies of t for better readability)

Separating the term with the unknown derivative $\dot{X}$ on the left of $(*)$ in , this becomes

$$\begin{aligned} \dot{X} \ AA^* = -X\left( (\dot{A} + \eta ~ A)A^* + A \dot{A}^*\right) + \dot{A}^* + \eta ~ A^* . \end{aligned}$$

Here the matrix product $A(t)A(t)^*$on the left-hand side is of size m by m and has rank m for all t since A(t) does. Thus we have found an explicit expression for $\dot{X}(t)$, namely

The steps , and now follow as before. The Matlab ZNN based discretized code for right pseudo-inverses is tvRightPseudInv.m in [55]. Our code finds right pseudo-inverses of time-varying full rank matrices $A(t)_{m,n}$ predictively with an entry accuracy of 14 to 16 leading digits in every position of $A^+(t) = X(t)$ when compared with the pseudo-inverse defining formula. In the code we use the 4_5 look-ahead convergent finite difference formula from [45] with the sampling gap $\tau = 0.0002$.

Similar numerical results are obtained for left pseudo-inverses $A(t)^+$ for time-varying matrix flows $A(t)_{m,n}$ with $m>n$.

(b) The left pseudo-inverse $X(t) = A(t)^+$ for matrix flows $A(t)_{m,n}$ of full rank n when $m>n$:

Our starting model now is $A^+ = X_{n,m} = (A^*A)^{-1}A^*$ and the error function $E = (A^*A)X - A^*$ then leads to

Solving for $\dot{X}$ similarly as before yields

Then follow the steps from subpart (a) and develop a Matlab ZNN code for left pseudo-inverses with a truncation error order finite difference formula of your own choice.

(c) The pseudo-inverse$X(t) = A(t)^+$ for matrix flows $A(t)_{m,n}$ with variable rank$\mathbf {(A(t)) \ \le \ \min (m,n)}$:

As before with the unknown pseudo-inverse $X(t)_{n,m}$ for a possibly rank deficient matrix flow $A(t) \in {\mathbb {C}}_{m,n}$, we use the error function $E(t) = A(t) - X(t)^+$ and the error function DE

For matrix flows A(t) with rank deficiencies the derivative of $X^+$, however, becomes more complicated with additional terms, see [19, Eq. 4.12]:

$$\begin{aligned} \dot{X}^+ = -X^+\dot{X}X^+ + X^+X^{+^*}\dot{X}^* (I_n-XX^+) + (I_m-X^+X)\dot{X}^* X^{+^*}X^+ \end{aligned}$$

(18)

where previously for full rank matrix flows A(t), only the first term above was needed to express $\dot{X}^+$. Plugging the long expression in (18) for $\dot{X}^+$ into the inner equation (*) of we obtain

which needs to be solved for $\dot{X}$. Unfortunately $\dot{X}$ appears once on the left in the second term and twice as $\dot{X}^*$ in the third and fourth term of above. Maybe another start-up error function can give better results, but it seems that the general rank pseudo-inverse problem cannot be easily solved via the ZNN process, unless we learn to work with Kronecker matrix products. Kronecker products will be used in subparts (VII), (IX) and (VII start-up) below.

The Matlab code tvLeftPseudInv.m for ZNN look-ahead left pseudo-inverses of full rank time-varying matrix flows is available in [55]. The right pseudo-inverse code for full rank matrix flows is similar. Recent work on pseudo-inverses has appeared in [38] and [64, chapters 8,9].

(IV) Least Squares, Pseudo-inverses and ZNN:

Linear systems of time-varying equations $A(t)x(t) = b(t)$ can be unsolvable or solvable with unique or multiple solutions and pseudo-inverses can help us.

If the matrix flow $A(t)_{m,n}$ admits a left pseudo-inverse $A(t)^+_{n,m}$ then

$$\begin{aligned} A(t)^+A(t)x(t)= & {} A(t)^+b(t) \ \text {and} \ x(t)=(A(t)^+A(t))^{-1} A^+(t)b(t) \ \text {or} \ x(t) = A(t)^+b(t) . \end{aligned}$$

Thus $A(t)^+b(t)$ solves the linear system at each time t and $x(t) = A(t)^+b(t)$ is the solution with minimal Euclidean norm $||x(t)||_2$ since according to (18) all other time-varying solutions have the form

$$\begin{aligned} u(t) = A(t)^+b(t) + (I_n - A(t)^+A(t))w(t) \ \ \text { for any } \ \ w(t) \in {\mathbb {C}}^m . \end{aligned}$$

Here $||A(t)x(t) - b(t)||_2 = 0$ holds precisely when b(t) lies in the span of the columns of A(t) and the linear system is uniquely solvable. Otherwise $\min _x(||A(t)x(t) - b(t)||_2) > 0$.

Right pseudo-inverses $A(t)^+$ play the same role for linear-systems $y(t)A(t) = c(t)$. In fact

$$\begin{aligned} y(t)A(t)A(t)^* = c(t)A(t)^* \ \ \text { and } \ \ y(t) = c(t)A(t)^*(A(t)A(t)^*)^{-1} = c(t)A(t)^+ . \end{aligned}$$

Here $c(t)A(t)^+$ solves the left-sided linear system $y(t)A(t) = c(t)$ with minimal Euclidean norm.

In this subsection we will only work on time-varying linear equations of the form $A(t)_{m,n} x(t) = b(t) \in {\mathbb {C}}_m$ for $m > n$ with rank$(A(t)) = n$ for all t. Then the left pseudo-inverse of A(t) is $A(t)^+= (A(t)^*A(t))^{-1}A^*$. The associated error function is $e(t) = A(t)_{m,n} x(t) - b(t)$. Stipulated exponential error decay defines the error function DE

where we have again left off the time parameter t for clarity and simplicity. Solving $(*)$ in for $\dot{x}(t_k)$ gives us

Here the subscripts $\dots _{k}$ remind us that we are describing the discretized version of our Matlab codes where $b_k$ for example stands for $b(t_k)$ and so forth for $A_k, x_k,\ldots$. The Matlab code for the discretized ZNN look-ahead method for time-varying linear equations least squares problems for full rank matrix flows $A(t)_{m,n}$ with $m > n$ is tvPseudInvLinEquat.m in [55]. We advise readers to develop a similar code for full rank matrix flows $A(t)_{m,n}$ with $m < n$ independently.

The survey article [27] describes nine discretized ZNN methods for time-varying different matrix optimization problems such as least squares and constrained optimizations that we treat in subsection (V) below.

(V) Linearly Equality Constrained Nonlinear Optimization for time-varying Matrix Flows:

ZNN can be used to solve parametric nonlinear programs (parameteric NLPs). However, ensuring that the solution path exists and that the extremum is isolated for all t is nontrivial, requiring careful tracking of the active set and avoiding various degeneracies. Simpler sub-classes of the general problem can readily be solved without the extra machinery. For example, optimization problems with f(x(t), t) nonlinear but only linear equality constraints and no inequality constraints, such as

(19)

for $f:~ ({\mathbb {R}}^n \times {\mathbb {R}}) \rightarrow {\mathbb {R}}$, $x(t) \in {\mathbb {R}}^n$, $\lambda (t) \in {\mathbb {R}}^m$, and $A(t) \in {\mathbb {R}}_{m,n}$ and $b(t) \in {\mathbb {R}}^n$ acting as linear equality constraints $A(t)x(t) = b(t)$, we can write out the corresponding Lagrangian (choosing the + sign convention),

$$\begin{aligned} \mathcal{L}(x(t),\lambda (t)) = f(x(t), t) + \lambda (t) (A(t)x(t) - b(t)) \, \ ({\mathbb {R}}^{n} \times {\mathbb {R}}^{m}) \rightarrow {\mathbb {R}}. \end{aligned}$$

A necessary condition for ZNN to be successful is that a solution $x^*(t)$ must exist and that it is an isolated extremum for all t. Clearly the Lagrange multipliers, $\lambda ^*(t)$, must also be unique for all t. Furthermore, due to Step 3 in the ZNN setup, both solution $x^*(t)$ and $\lambda ^*(t)$ must have a continuous first derivatives. Therefore we further suppose that f(x(t), t) is twice continuously differentiable with respect to x and t, and that A(t) and b(t) are twice continuously differentiable with respect to t.

To ensure that the $\lambda ^*(t)$ are not only inside a bounded set but are also unique [16], LICQ must hold, i.e., A(t) must have full rank for all t. If (19) is considered for static entries, i.e., for some fixed $t=t_0$, and we suppose that $x^*(t)$ is a local solution then there exists a Lagrange multiplier vector $\lambda ^*(t)$ such that the first order necessary conditions [5, 33], or ‘KKT conditions’, are satisfied:

$$\begin{aligned}&\nabla _{x} \mathcal{L}(x^*(t),\lambda ^*(t)) = \nabla _{x} f(x^*(t)) + (\lambda ^*(t))^T A(t) = 0 \in {\mathbb {R}}^n, \end{aligned}$$

(20a)

$$\begin{aligned}&A(t) x^*(t) - b(t) =0 \in {\mathbb {R}}^m . \end{aligned}$$

(20b)

Here $\nabla _{x}$ denotes the gradient, in column vector form. A second order sufficient condition must also be imposed here that $y^T \nabla _{xx}^2 \mathcal{L}(x^*(t),\lambda ^*(t)) y > 0$ for all $y \ne 0$ with $Ay = 0$. This ensures the desired curvature of the projection of $f(\cdot )$ onto the constraints. Theorem 2.1 from [13] then establishes that the solution exists, is an isolated minimum, and is continuously differentiable. For the reader’s reference, further development of these ideas can be seen in, e.g. [36], which considers the general parametric NLP under the Mangasarian–Fromovitz Constraint Qualification (MFCQ).

The system of Eqs. (20a, 20b) is the starting point for the setup of ZNN and this optimization problem. For notational convenience, the $x^*(t)$ notation will be simplified to x(t) since it is clear what is meant. We want to solve for time-varying x(t) and $\lambda (t)$ in the predictive discretized ZNN fashion. I.e., we want to find $x(t_{k+1})$ and $\lambda (t_{k+1})$ from earlier data for times $t_j$ with $j = k, k-1,\ldots$ accurately in real time. First we define in Matlab column vector notation and use (20a) and (20b) to define our error function as

To find the derivative $\dot{y}(t)$ of y(t) we use the multi-variable chain rule which establishes the derivative of h(y(t)) as

$$\begin{aligned} {\dot{h}}(x(t), t) = \left( \begin{array}{ll} \left( \nabla _{xx}^2 f(x(t), t) \right) {\dot{x}} &{} A(t)^T \\ A(t) &{}\quad 0 \end{array}\right) {\dot{y}} + \left( \begin{array}{c} \nabla _x f_t(x(t), t) + {\dot{A}}(t)^T \lambda \\ {\dot{A}}(t) x(t) - {\dot{b}}(t) \end{array}\right) , \end{aligned}$$

(21)

where the $\nabla _{xx}^2$ denotes the Hessian. The expression in (21) is a slight simplification of a more general formulation often used in parametric NLPs when the active set is fixed; usually, it is used for numerical continuation directly by setting it equal to zero and integrating, but here we are interested in using it with ZNN.

In our restricted case, we could use an equivalent formulation and suppose that the equality constraints are arising from the Lagrangian by taking gradients with respect to both x and $\lambda$ as follows

$$\begin{aligned} \dot{h}(y(t),t) = J(h(y(t),t)) \ \dot{y}(t) + h_t(y(t), t) . \end{aligned}$$

Here

$$\begin{aligned} J(h(y(t),t)) = \left( \begin{array}{ccc} \dfrac{\partial h_1(t)}{\partial x_1} &{} \cdots &{} \dfrac{\partial h_1(t)}{\partial \lambda _m}\\ \vdots &{} &{} \vdots \\ \dfrac{\partial h_{n+m}(t)}{\partial x_1} &{}\cdots &{} \dfrac{\partial h_{n+m}(t)}{\partial \lambda _m} \end{array}\right) _{n+m,n+m} \ \ \ \text { and } \ \ \ h_t(y(t)) = \left( \begin{array}{c} \dfrac{\partial h_1(y(t))}{\partial t}\\ \vdots \\ \dfrac{\partial h_{n+m}(y(t))}{\partial t}\end{array}\right) _{n+m} \end{aligned}$$

are the Jacobian matrix J of h(y(t), t) taken with respect to the location vector $x(t) = (x_1(t), \dots , x_n(t))$ and the Lagrange multiplier vector $(\lambda _1(t), \dots , \lambda _m(t))$, and the time derivative of h(y(t), t), respectively. This formulation, however, does not apply when we encounter inequality constraints that are non-differentiable on a set of measure zero or further difficulties with active and inactive constraints, etc. For otherwise ‘regular’ linear time-varying optimization problems we simply start from the standard Lagrangian ‘Ansatz’:

which will lead us exponentially fast to the optimal solution y(t) for $t_o \le t \le t_f$. Solving for $\dot{y}(t)$ gives us

Using the 5-IFD look-ahead finite difference formula once again, this time for $\dot{y}_k$ with discretized data $y_k = y(t_k)$, we obtain the following solution-derivative free equation for the iterates $y_j$ with $j \le k$ by equating the two expressions for $\dot{y}_k$ in the 5-IFD discretization formula and in as follows:

Solving $(*)$ in for $y_{k+1}$ supplies the complete discretized ZNN recursion formula that finishes Step 6 of the predictive discretized ZNN algorithm development for time-varying constrained non-linear optimizations via Lagrange multipliers:

The Lagrange based optimization algorithm for multivariate functions and constraints is coded for one specific example with $m = 1$ and $n = 2$ in tvLagrangeOptim2.m, see [55]. For this specific example the optimal solution is known. The code can be modified for optimization problems with more than $n=2$ variables and for more than $m=1$ constraint functions. Our code is modular and accepts all look-ahead convergent finite difference formulas from [45] that are listed in Polyksrestcoeff3.m in the j_s format.

For other matrix optimization processes it is important to reformulate the code development process above and to try and understand the interaction between suitable $\eta$ and $\tau$ values for discretized ZNN methods here in order to be able to use ZNN well, see Remark 3 (a) and (b) below.

An introduction to constrained optimization methods is available at [10]; see also [27]. Several optimization problems are studied in [27] such as Lagrange optimization for unconstrained time-varying convex nonlinear optimizations called U-TVCNO and time-varying linear inequality systems called TVLIS. The latter will be treated in subpart (VI) just below.

Remark 3

(a) The computed results of any Lagrangian optimization algorithm should always be carefully scrutinized against what is well known in optimization theory, see [5, 13, 16, 33, 37] for analytic requirements. Do not accept your ZNN computed results blindly. Our code development here applies to just one specific time-varying discretized matrix.

(b) An important concept in ZNN’s realm is the product $\tau \cdot \eta$ of the sampling gap $\tau$ and the exponential error decrease constant $\eta$ for any one specific problem and any discretized ZNN method which uses a specific suitable finite difference scheme of one fixed type j_s. This product of constants, regularly denoted as $h = \tau \cdot \eta$ in the Zeroing Neural Network literature, seems to be nearly constant for the optimal choice of the parameters $\tau$ and $\eta$ over a wide range of sampling gaps $\tau$ if the chosen difference formula of type j_s stays fixed. Yet the optimal value of the near ’constant’ h varies widely from one look-ahead convergent finite difference formula to another. The reason for this behavior is unknown and worthy of further studies; see the optimal $\eta$ for varying sampling gaps $\tau$ tables for time-varying eigenvalue computation in [49]. It is interesting to note that analytic continuation ODE methods also deal with optimal bounds for a product, namely that of the step-size $\tau$ and the local Lipschitz constant $L_i$ of the solution y, see [11, p. 429].

Thus far in this practical section, we have worked through five models and a variety of time-varying matrix problems. We have developed seven detailed Matlab codes. Our numerical codes all implement ZNN look-ahead convergent difference formula based discretized processes for time-varying matrix and vector problems in seven steps as outlined in Sect. 1. Each of the resulting ZNN computations requires a linear equations solve (or an inverse matrix times vector product) and a simple convergent recursion per time step. Some of the codes are very involved such as for example (V) which relies on Matlab’s symbolic toolbox and its differentiation functionality. Others were straightforward. All of our seven algorithms are look-ahead and rely only on earlier and current data to predict future solutions. They do so with high accuracy and run in fractions of a second over sampling gap $\tau$ time intervals that are 10 to 100 times longer than their CPU run time. This adaptability makes discretized ZNN methods highly useful for real-time and on-chip implementations.

We continue with further examples and restrict our explanations of discretized ZNN methods to the essentials from now on. We also generally refrain from coding further ZNN based programs now, except for one code in subpart (VII start-up) that benefits from a Kronecker product formulation and where we also explain how to generate start-up data from completely random first settings via ZNN steps. We include extended references and encourage our readers to try and implement their own ZNN Matlab codes for their specific time-varying matrix or vector problems along the lines of our detailed examples (I)...(V) above and the examples (VI)...(X) that follow below.

(VI) Time-varying Linear Equations with Linear Equation and Inequality Constraints:

We consider two types of linear equation and linear inequality constraints here:

We assume that the matrices and vectors all have real entries and that the given inequality problem has a unique solution for all $t_o \le t \le t_f \subset {\mathbb {R}}$. Otherwise with subintervals of $[t_o,t_f]$ in which a given problem is unsolvable or has infinitely many solutions, the problem itself would become subject to potential bifurcations and thus well beyond the scope of this introductory ZNN survey paper.

In general, solving parametric NLPs with inequality constraints is a difficult problem. The ‘active set’—the set of inequality constraints at their boundaries—can change, there can be so-called weakly-active constraints where a constraint is active but its associated multiplier is zero or the Lagrange multipliers may not be unique (albeit contained within a bounded convex polytope). For example, Ralph and Dempe [36] addresses the problem of non-unique multipliers by solving a linear program. To avoid such difficulties here, we introduce the idea of ‘squared slack variables’, see, e.g. [40], to replace the given system with linear inequalities by a system of linear equations. This is usually a dangerous move due to the potential for numerical instabilities, e.g. [15, 37], and arguably should not be used in practice. It may suffice as a motivating example.

The slack variable vector $u^{\texttt {.}2} \in {\mathbb {R}}^\ell$ typically has non-negative entries in the form of real number squares, i.e., for in Matlab column vector notation with $\ell = m$ or k, depending on the type of time-varying inequality system (A) or (AC). With u our models (A) and (AC) become

For (ACu), diag(u) denotes the k by k diagonal matrix with the entries of $u \in {\mathbb {R}}^k$ on its diagonal.

The error function for (Au) and $u \in {\mathbb {R}}^k$ is . The product rule of differentiation, applied to each component function of u(t) establishes the error function DE for (Au) as

where the $.*$ product uses the Matlab notation for entry-wise vector multiplication. If the unknown entries of $x\in {\mathbb {R}}^n$ and $u\in {\mathbb {R}}^m$ are gathered in one extended column vector $[x(t);u(t)] \in {\mathbb {R}}^{n+m}$ we obtain the alternate error function DE for (Au) in block matrix form as

Similarly for (ACu), the error function is

and its error function DE is .$_c$

$$\begin{aligned} \dot{E}_c(t)= & {} \left( \begin{array}{lc} \dot{A} &{} O \\ \dot{C} &{} 2\text {diag}(u) \end{array}\right) \left( \begin{array}{ll} \dot{x}\\ \dot{u} \end{array}\right) - \left( \begin{array}{ll} \dot{b}\\ \dot{d} \end{array}\right) ~ {\mathop {=}\limits ^{(*)}} ~ -\eta ~ \left( \left( \begin{array}{lc} A&{} O\\ C &{} \text {diag}(u) \end{array}\right) \left( \begin{array}{ll} x\\ u \end{array}\right) - \left( \begin{array}{ll} b\\ d \end{array}\right) \right) \\= & {} -\eta ~ E_c(t). \end{aligned}$$

Solving the error function DEs $_a$ and $_c$ for the derivative vectors $[\dot{x}(t);\dot{u}(t)]$, respectively, via the built-in pseudo-inverse function pinv.m of Matlab for example, see subsection (III) above, we obtain the following expressions for the derivative of the unknown vectors x(t) and u(t).

For model (Au)

and for (ACu)

The Matlab function pinv.m in uses the Singular Value Decomposition (SVD). The derivative of the vector [x(t); u(t)] can alternately be expressed in terms of Matlab’s least square function lsqminnorm.m in

or

Next choose a look-ahead finite difference formula of type j_s for the discretized problem and equate its derivative $[\dot{x}(t_k);\dot{u}(t_k)]$ with the above value in $_a$, $_{als}$ or $_c$, $_{cls}$ in order to eliminate the derivatives from now on. Then solve the resulting solution-derivative free equation for the 1-step ahead unknown $[x(t_{k+1}); u(t_{k+1})]$ at time $t_{k+1}$.

The Matlab coding of a ZNN based discretized algorithm for time-varying linear systems with equation or inequality constraints can now begin after $j+s$ initial values have been set.

Recent work on discretized ZNN methods for time-varying matrix inequalities is available in [27, TVLIS], [57, 66].

(VII) Square Roots of Time-varying Matrix flows:

Square roots $X_{n,n} \in {\mathbb {C}}^{n,n}$ exist for all nonsingular static matrices $A \in {\mathbb {C}}^{n,n}$, generalizing the fact that all complex numbers have square roots over ${\mathbb {C}}$. Like square roots of numbers, matrix square roots may be real or complex. Apparently the number of square roots that a given nonsingular matrix $A_{n,n}$ with $n \gg 2$ has is not known, except that there are many. Every different set of starting values for our otherwise identical nonsingular matrix flow A(t) example of Fig. 1 did result in a different matrix square root matrix flow X(t) for A(t) when covering $0 \le t \le 360 \ sec$.

For singular matrices A the existence of square roots depends on A’s Jordan block structure and its nilpotent Jordan blocks J(0) and some matching dimension conditions thereof, see e.g. [12, l. 15–18, p. 466; Thm. 4.5, p. 469; and Cor. 11.3, p. 506] or the result in [8, Theorem 2] formulated in terms of the “ascent sequence” of A for details.

Here we assume that our time-varying flow matrices A(t) are nonsingular for all $t_o \le t \le t_f \subset {\mathbb {R}}$. Our model equation is $A(t) = X(t)\cdot X(t)$ for the unknown time-varying square root X(t) of A(t). Then the error function becomes and the error DE under exponential decay stipulation is

where we have again omitted the time variable t for simplicity. Rearranging the central equation $(*)$ in with all unknown $\dot{X}$ terms on the left-hand side gives us

Equation is model (10.4) in [67, ch. 10] except for a minus sign. In we have a similar situation as was encountered in Sect. 1 with the n by n matrix eigenvalue equation for finding the complete time-varying matrix eigen-data. Here again, the unknown matrix derivative $\dot{X}$ appears as both a left and right factor in matrix products. In Sect. 1 we switched our model and solved the time-varying matrix eigenvalue problem one eigenvector and eigenvalue pair at a time. If we use the Kronecker product for matrices and column vectorized matrix representations in —we could have done the same in Sect. 1 for the complete time-varying matrix eigen-data problem—then this model can be solved directly. And we can continue with the global model and discretized ZNN when relying on notions from classical matrix theory, i.e., static matrix theory helps to construct a discretized ZNN algorithm for time-varying matrix square roots.

For two real or complex matrices $A_{m,n}$ and $B_{r,s}$ of any size, the Kronecker product is defined as the matrix

$$\begin{aligned} A \otimes B = \left( \begin{array}{cccc} a_{1,1}B &{} a_{1,2}B &{} \dots &{} a_{1,n}B\\ a_{2.1}B &{}\ddots &{} &{} a_{2,n}B\\ \vdots &{}&{} \ddots &{} \vdots \\ a_{m,1}B&{} \dots &{}\dots &{}a_{m,n}B \end{array}\right) _{m\cdot r,n \cdot s} . \end{aligned}$$

The command kron(A,B) in Matlab creates $A \otimes B$ for general pairs of matrices. Compatibly sized Kronecker products are added entry by entry just as matrices are. For matrix equations a very useful property of the Kronecker product is the rule

$$\begin{aligned} \quad \qquad (B^T \otimes A )X(:) = C(:) \ \ \ \text { where } \ \ C = AXB . \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad \quad (22) \end{aligned}$$

Here the symbols X( : ) and $C(:) \in {\mathbb {C}}^{m n}$ denote the column vector storage mode in Matlab of any matrices $X_{m,n}$ or $C_{m,n}$.

When we combine the Kronecker product with Matlab’s column vector matrix notation M( : ) we can rewrite the left-hand side of equation $\dot{X} X + X \dot{X} = \dot{A} + \eta ~ A - \eta ~ X X$ as

$$\begin{aligned} \qquad \quad (X^T(t) \otimes I_n + I_n \otimes X(t))_{n^2,n^2}\cdot \dot{X}(t)(:)_{n^2,1} \in {\mathbb {C}}^{n^2}\qquad \qquad \qquad \qquad \qquad \quad \quad (23) \end{aligned}$$

while its right-hand side translates into

$$\begin{aligned} \dot{A}(t)(:)_{n^2,1} + \eta \ A(t)(:)_{n^2,1} - \eta \ (X^T(t) \otimes I_n)_{n^2,n^2} \cdot X(t)(:)_{n^2,1} \in {\mathbb {C}}^{n^2} . \end{aligned}$$

And miraculously the difficulty of $\dot{X}$ appearing on both sides as a factor in the left-hand side matrix products in is gone. We generally cannot tell whether the sum of Kronecker products in front of $\dot{X}(t)(:)$ in (22) is nonsingular. But if we assume it is, then we can solve for $\dot{X}(t)(:)$.

Otherwise if $X^T(t) \otimes I_n + I_n \otimes X(t)$ is singular, we simply replace the matrix inverse by the pseudo-inverse

pinv$(X^T(t) \otimes I_n + I_n \otimes X(t))$ above and likewise in the next few lines. A recent paper [60] has dealt with a singular Kronecker product that occurs when trying to compute the Cholesky decomposition of a positive definite matrix via ZNN. With

$$\begin{aligned} P(t) = (X^T(t) \otimes I_n + I_n \otimes X(t)) \in {\mathbb {C}}_{n^2,n^2} \end{aligned}$$

when assuming non-singularity and

$$\begin{aligned} q(t) = \dot{A}(t)(:) + \eta \ A(t)(:) - \eta \ (X^T(t) \otimes I_n) \cdot X(t)(:) \in {\mathbb {C}}^{n^2} \end{aligned}$$

we now have . This formulation is reminiscent of formula (3i) in Step 3 of Sect. 2, except that here the entities followed by ( : ) represent column vector matrices instead of square matrices and these vectors now have $n^2$ entries instead of n in (3i). This might lead to execution time problems for real-time applications if the size of the original system is in the hundreds or beyond, while $n = 10$ or 20 should pose no problems at all. How to mitigate such size problems, see [30] e.g.

To obtain the derivatives $\dot{X}(t_k)$ for each discrete time $t_k = t_o + (k-1) \tau$ for use in Step 5 of discretized ZNN, we need to solve the $n^2$ by $n^2$ linear system $P(t)\backslash q(t)$ and obtain the column vectorized matrix $\dot{X}(t_k)(:)_{n^2,1}$. Then we reshape $\dot{X}(t)(:)_{n^2,1}$ into square matrix form via Matlab’s reshape.m function. Equation then equates the above matrix version $\dot{X}(t_k)_{n,n}$ of step with the difference formula for $\dot{X}(t_k)_{n,n}$ from our chosen finite difference expression in step of ZNN and this helps us to predict $X(t_{k+1})_{n,n}$ in step . This has been done many times before in this paper, but without the enlarged Kronecker product matrices and vectors and it should create no problems for our readers. A plot and analysis of the error function’s decay as time t progresses for 6 min was given in Sect. 2, preceding Fig. 1, for the time-varying matrix square root problem.

For further analyses, a convergence proof and numerical tests of ZNN based time-varying matrix square root algorithms see [67]. Computing time-varying matrix square roots is also the subject of [64, Chs. 8, 10].

(VIII) Applications of 1-parameter Matrix Flow Results to Solve a Static Matrix Problem:

Concepts and notions of classical matrix theory help us often with time-varying matrix problems. The concepts and results of the time-varying matrix realm can likewise help with classic, previously unsolvable fixed matrix theory problems and applications. Here is one example.

Numerically the Francis QR eigenvalue algorithm ’diagonalizes’ every square matrix A over ${\mathbb {C}}$ in a backward stable manner. It does so for diagonalizable matrices as well as for derogatory matrices, regardless of their Jordan structure or of repeated eigenvalues. QR finds a backward stable ‘diagonalizing’ eigenvector matrix similarity for any A. For matrix problems such as least squares, the SVD, or the field of values problem that are unitarily invariant, classic matrix theory does not know of any way to unitarily block diagonalize fixed entry matrices $A \in {\mathbb {C}}_{n,n}$. If such block decompositions could be found computationally, unitarily invariant matrix problems could be decomposed into subproblems and thereby speed up the computations for decomposable matrices A.

An idea that was inspired by studies of time-varying matrix eigencurves in [50] can be adapted to find unitary block decompositions of static matrices A. [52] deals with general 1-parameter matrix flows $A(t) \in {\mathbb {C}}_{n,n}$. If X diagonalizes one very specific associated flow matrix $\mathcal{F}_A(t_1)$ via a unitary similarity $X^*\ldots X$ and $X^* \mathcal{F}_A(t_2)X$ is properly block diagonal for some $t_2 \ne t_1$ with $\mathcal{F}_A(t_1) \ne \mathcal{F}_A(t_2)$, then every $\mathcal{F}_A(t)$ is simultaneously block diagonalized by X and consequently the flow A(t) decomposes uniformly. [53] then applies this specific matrix flow result to the previously intractable field of values problem for decomposing matrices A when using path following methods. Here are the details.

For any fixed entry matrix $A \in {\mathbb {C}}_{n,n}$ the hermitean and skew parts

$$\begin{aligned} {H= (A+A^*)/2 = H^*} \ \ \text{ and } \ \ {K= (A - A^*)/(2i) = K^*} \in {\mathbb {C}}_{n,n} \end{aligned}$$

of A generate the 1-parameter hermitean matrix flow

$$\begin{aligned} \mathcal{F}_A(t) = \cos (t) H + \sin (t) K = (\mathcal{F}_A(t))^* \in {\mathbb {C}}_{n,n} \end{aligned}$$

for all angles $0 \le t \le 2\pi$. This matrix flow goes back to Bendixson [4] and Johnson [25] who studied effective ways to compute matrix field of values boundary curves. Whether there are different associated matrix flows that could enable such matrix computations and what they might look like is an open problem. If two matrices $\mathcal{F}_A(t_1)$ and $\mathcal{F}_A(t_2)$ in this specific flow are properly block diagonalized simultaneously by the same unitary matrix X into the same block diagonal pattern for some $A(t_2) \ne A(t_1)$, then every matrix $\mathcal{F}_A(t)$ of the flow $\mathcal{F}_A$ is uniformly block diagonalized by X and subsequently so is $A = H + iK$ itself, see [53] for details.

The matrix field of values (FOV) problem [25] is invariant under unitary similarities. The field of values boundary curve of any matrix A can be determined by finding the extreme real eigenvalues for each hermitean $\mathcal{F}_A(t)$ with $0 \le t \le 2\pi$ and then evaluating certain eigenvector A-inner products to construct the FOV boundary points in the complex plane. One way to approximate the FOV boundary curve is to compute full eigenanalyses of hermitean matrices $\mathcal{F}_A(t_k)$ for a large set of angles $0 \le t_k \le 2\pi$ reliably via Francis QR as QR is a global method and has no problems with eigen-decompositions of normal matrices. Speedier ways use path following methods such as initial value ODE solvers or discretized ZNN methods. But path following eigencurve methods cannot ensure that they find the extreme eigenvalues of $\mathcal{F}_A(t_k)$ if the eigencurves of $\mathcal{F}_A(t)$ cross in the interval $[0,2\pi ]$. Eigencurve crossings can only occur for unitarily decomposable matrices A, see [32]. Finding eigencurve crossings for decomposing matrices A takes up a large part of [28] and still fails to adapt IVP ODE path following methods for all possible types of decompositions for static matrices A.

The elementary method of [52] helps to solve the field of values problem for decomposable matrices A for the first time without having to compute all eigenvalues of each hermitean $\mathcal{F}_A(t_k)$ by—for example—using the global Francis QR algorithm. Our combined matrix decomposition and discretized ZNN method is up to 4 times faster than the Francis QR based global field of values method or any other IVP ODE analytic continuation method. It depicts the FOV boundary accurately and quickly for all decomposing and indecomposible matrices $A\in {\mathbb {C}}_{n,n}$, see [53] for more details and ZNN Matlab codes.

(IX) Time-varying Sylvester and Lyapunov Matrix Equations:

(S) The static Sylvester equation model

with $A \in {\mathbb {C}}_{n,n}$, $B \in {\mathbb {C}}_{m,m}$, $C \in {\mathbb {C}}_{n,m}$ is solvable for $X \in {\mathbb {C}}_{n,m}$ if A and B have no common eigenvalues.

From the error function $E(t) = A(t) X(t)+ X(t) B(t) - C(t)$ we construct the exponential decay error DE $\dot{E}(t) = -\eta ~ E(t)$ for a positive decay constant $\eta$ and obtain the equation

and upon reordering the terms in $(*)$ we have

where we have dropped all references to the time parameter t to simplify reading. Using the properties of Kronecker products and column vector matrix representations as introduced in Sect. 2 (VII) above we rewrite the left-hand side of as

$$\begin{aligned} (I_m \otimes A(t) + B^T(t) \otimes I_n)_{n\cdot m,n\cdot m} \cdot \dot{X}(t)(:)_{n\cdot m,1} = M(t) \dot{X}(t)(:) \in {\mathbb {C}}^{nm} \end{aligned}$$

and the right-hand side as

$$\begin{aligned} q(t)= & {} ( - (I_m \otimes \dot{A} + \dot{B}^T\otimes I_n)_{nm,nm}\cdot X(:)_{nm,1} + \dot{C}(:)_{nm,1} \\{} & {} - \eta ~ ( (I_m \otimes A + B^T\otimes I_n)\cdot X(:) - C(:))_{nm,1} ) \in {\mathbb {C}}^{n m} . \end{aligned}$$

The Kronecker matrix product is necessary here to express the two sided appearances of $\dot{X}(t)$ on the left-hand side of . The right-hand side of can be expressed more simply in column vector matrix notation without using Kronecker matrices as

$$\begin{aligned} q(t)= & {} (- ((\dot{A} \cdot X)(:)+ (X\cdot \dot{B})(:))_{nm,1} +\dot{C}(:)_{nm,1} \\{} & {} - \eta ~ \left( (A\cdot X)(:)+ (X\cdot B)(:) - C(:)\right) _{nm,1}) \in {\mathbb {C}}^{n m} . \end{aligned}$$

Expressions such as $(A\cdot X)(:)$ above denote the column vector representation of the matrix product $A(t) \cdot X(t)$. Thus we obtain the linear system $M(t) \dot{X}(t) = q(t)$ for $\dot{X}(t)$ in with $M(t) = (I_m \otimes A(t) + B^T(t) \otimes I_n) \in {\mathbb {C}}_{n m, n m}$ when using either form of q(t). And $\dot{X}(t)(:) \in {\mathbb {C}}^{n m}$ can be expressed in various forms, depending on the solution method and the case of (non)-singularity of M(t) as $\dot{X}(t)(:) = M(t)\backslash q(t)$, $\dot{X}(t)(:) = \text {inv}(M(t)) * q(t)$, or

$$\begin{aligned} \dot{X}(t)(:)= & {} \text {inv}(M(t)) \cdot q(t) \ \ \text { or } \ \ \dot{X}(t)(:) = \text {pinv}(M(t)) \cdot q(t) \ \ \text { or } \\ \dot{X}(t)(:)= & {} \text {lsqminnorm}(M(t)), q(t)) \, \end{aligned}$$

with the latter two formulations to be used in case M(t) is singular.

Which form of q(t) gives faster or more accurate results for $\dot{X}(t)(:)$ can be tested in Matlab by opening the $>\!\!>$ profile viewer and running the discretized ZNN method for both versions of q(t) and the various versions of $\dot{X}(t)$. We have also mentioned several methods in Matlab to (pseudo-)solve linear systems with a singular system matrices such as M(t) above. Users can experiment and learn how to optimize such Matlab codes for their specific problems and for the specific version of Matlab that is being used.

Once $\dot{X}(t)(:)$ has been found in column vector form it must be reshaped in Matlab into an n by m matrix $\dot{X}(t)$. Next we have to equate our computed derivative matrix $\dot{X}_k$ in the discretized version at time $t_k$ with a specific look-ahead finite difference formula expression for $\dot{X}_k$ in step . The resulting solution-derivative free equation finally is solved for the future solution $X_{k+1}$ of the time-varying Sylvester equation in step of our standard procedures list. Iteration then concludes the ZNN algorithm for Sylvester problems.

(L) A suitable time-varying Lyapunov equation model is

Its error function is

Here all matrices are complex and square of size n by n. Now we introduce a shortcut and convert the matrix error equation immediately to its column vector matrix with Kronecker matrix product form

where we have used the formula $(AXA^*)(:) = ({\bar{A}} \otimes A)X(:)$ and dropped all mention of dependencies on t for simplicity. Working towards the exponentially decaying differential error equation for $E_K(:)$, we note that derivatives of time-varying Kronecker products $U(t)\otimes V(t)$ follow the product rule of differentiation

$$\begin{aligned} \dfrac{\partial (U(t)\otimes V(t))}{\partial t} = \dfrac{\partial U(t)}{dt} \otimes V(t) + U(t) \otimes \dfrac{ \partial V(t)}{dt} \end{aligned}$$

according to [29, p. 486–489]. With this shortcut to column vector matrix representation, the derivative of the error function for $E_K(:)$ is

$$\begin{aligned} \dot{E}_K(:) = ((\dot{{\bar{A}}} \otimes A) +({\bar{A}} \otimes \dot{A}))X(:) + ({\bar{A}} \otimes A))\dot{X}(:) - \dot{X}(:) + \dot{Q}(:) \in {\mathbb {C}}^{n^2} \end{aligned}$$

And the error function DE $\dot{E}_K(:) = - \eta ~ E_K(:)$ becomes

Upon reordering the terms of the central equation $(*)$ in we have the following linear system for the unknown column vector matrix $\dot{X}(:)$

where ${\bar{A}}$ is the complex conjugate matrix of A. For $M(t) = (I_{n^2} - {\bar{A}} \otimes A) \in {\mathbb {C}}_{n^2,n^2}$ and

$$\begin{aligned} q(t)(:)= & {} ( (\dot{\overline{A(t)}} \otimes A(t) + \overline{A(t)} \otimes \dot{A}(t)) X(t)(:) - \eta ~ (I_{n^2} - \overline{A(t)} \otimes A(t))X(t)(:)\\{} & {} + \eta ~ Q(t)(:) + \dot{Q}(t)(:) ) \in {\mathbb {C}}^{n^2} \end{aligned}$$

we have to solve the system $M(t) \dot{X}(t)(:) = q(t)$ for $\dot{X}(t)(:) \in {\mathbb {C}}^{n^2}$ as was explained earlier for the Sylvester equation. In Step 5 we equate the matrix-reshaped expressions for $\dot{X}$ in and the chosen look-ahead convergent finite difference scheme expression for $\dot{X}$ from Step 4. Then we solve the resulting solution-derivative free equation for $X_{k+1}$ in Step 6 for discrete data predictively and thereby obtain the discrete time ZNN iteration formula. These steps, written out in Matlab commands, give us the computer code for Lyapunov.

Introducing Kronecker products and column vector matrix notations early in the construction of discrete ZNN algorithms is a significant short-cut for solving matrix equations whose unknown solution X(t) will occur in several different positions of time-varying matrix products. This is a simple new technique that speeds up discretized ZNN algorithm developments for such time-varying matrix equation problems.

ZNN methods for time-arying Sylvester equations have recently been studied in [56]. For a new right and left 2-factor version of Sylvester see [69]. For recent work on discretized ZNN and Lyapunov, see [41] e.g.

(X) Time-varying Matrices, ZNN Methods and Computer Science:

The recent development of new algorithms for time-varying matrix applications has implications for our understanding of computer science and of tiered logical equivalences on several levels in our mathematical realms.

The most stringent realm of math is ‘pure mathematics’ where theorems are proved and where, for example, a square matrix either has a determinant equal to 0 or it has not.

In the next, the mathematical computations realm with its floating point arithmetic, zero is generally computed inaccurately as not being 0 and any computed value with magnitude below a threshold such as a small multiple or a fraction of the machine constant eps may be treated rightfully as 0. In the computational realm the aim is to approximate quantities to high precision, including zero and never worrying about zero exactly being 0.

A third, the least stringent realm of mathematics belongs to the engineering world. There one needs to find solutions that are good enough to approach the “true theoretical solution" of a problem as known from the ‘pure’ realm asymptotically; needing possibly only 4 to 5 or 6 correct leading digits for a successful algorithm.

The concept of differing math-logical equivalences in these three tiers of mathematics is exemplified and interpreted in Yunong Zhang and his research group’s recent paper [68] that is well worth reading and contemplating about.

(VII start-up) How to Implement ZNN Methods on-chip for Sensor Data Inputs and Remote Robots:

Let $A(t_k)$ denote the sensor output that arrives at time $t_o \le t_k = t_o + (k-1) \tau \le t_f$ for a given time-varying matrix ‘problem’. Assume further that this data arrives with the standard clock rate of 50 Hz at the on-board chip of a robot and that there is no speedy access to software such as Matlab as the robot itself may be autonomously running on Mars. At time instance $t_k$ the ‘problem’ needs to be solved on-chip predictively in real-t-ime, well before time $t_{k+1}$. We must predict or compute the problem’s solution $x(t_{k+1})$ or $X(t_{k+1})$ on-chip with its limited resources and solve the given problem (at least approximately) before $t_{k+1}$ arrives.

How can we generate start-up data for a discretized ZNN method and the relatively large constant sensor sampling gap $\tau = 0.02\ \text {sec} = 1/50\ \text {sec}$ that is standardly used in real-world applications. How can one create start-up data out of thin air. For real-time sensor data flows A(t), we assume that the robot has no information about the ‘theoretical solution’ or that there may be no known ‘theoretical solution’ at all. Without any usable a priori system information, we have to construct the $j + s$ initial values for the unknown $x(t_k)$ or $X(t_k)$ and $k \le j+s$ that will then be used to iterate with a j_s look-ahead convergent finite difference scheme based discrete ZNN method.

After many tries at this task, our best choice for the first ‘solution’ turned out to be a random entry vector or matrix for $x(t_o)$ or $X(t_o)$ of proper dimensions and then iterating through $j + s$ simple low truncation error order ZNN steps until a higher truncation order predictive ZNN method can take over for times $t_{k+1}$, running more accurately with local truncation error order $O(\tau ^{j+2})$ when $k > j+s$.

Here we illustrate this random entries start-up process for the time-varying matrix square root example of solving $A(t)_{n,n} = X(t) \cdot X(t) \in {\mathbb {C}}_{n,n}$ from subpart (VII) by using

(a) the Kronecker form representation of $\dot{X}(t) (:)$ of (24), denoted here as (23v) for conformity,

(b) the matrix column vector notation $X(:) \in {\mathbb {C}}^{n^2}$ for n by n solution matrices X, and

(c) the Kronecker product rule (21) $(B^T \otimes A )X(:) = C(:)$ for compatible matrix triple products $C = AXB$.

The Kronecker product representation requires two different notations of matrices X here: one as a square array, denoted by the letter m affixed to the matrix name such as in $X\!m$, and another as a column vector matrix, denoted by an added v to the matrix name as in $X\!v$. With these notations, equation (24) now reads as

where we have again dropped all mentions of the time parameter t for ease of reading.

As convergent look-ahead finite difference formula at start-up we use the simple Euler rule of type j_s = 1__2

$$\begin{aligned} \dot{x}(t_k) = \dfrac{x(t_{k+1} ) - x(t_k)}{\tau } \end{aligned}$$

(25)

which gives us the expression $x(t_{k+1}) = x(t_k) + \tau \dot{x}(t_k)$. When applied to the solution matrix X(t) and combined with (23v), we obtain the explicit start-up iteration rule

$$\begin{aligned} X\!v(t_{k+1})= & {} X\!v(t_k) + \tau \cdot (X\!m^T \otimes I_n + I_n \otimes X\!m)^{-1}\cdot \\{} & {} \cdot \left( \dot{A}v(t_k) + \eta \ (Av(t_k) - (I_n \otimes X\!m(t_k)) \cdot X\!v(t_k) ) \right) \ \end{aligned}$$

where $(I_n \otimes X\!m(t_k)) \cdot X\!v(t_k)$ expresses the matrix square $X\!m(t_k) \cdot X\!m(t_k)$ according to the Kronecker triple product rule (22) by observing that $X\!m (t_k)\cdot X\!m(t_k) \cdot I = (I \otimes X\!m(t_k)) \cdot X\!v(t_k)$. Every iteration step in the discretized ZNN algorithm is coded exactly like this equation as done many times before, with time-adjusted expressions of $\dot{A}v$ and for a different look-ahead convergent finite difference formula of type j_s = 4_5 accordingly in the main iterations phase when $k > j+s = 9$.

The Matlab m-file tvMatrSquareRootwEulerStartv.m for finding time-varying matrix square roots ‘from scratch’ is available together with two auxiliary m-files in [55].

To plot the error graph in Fig. 1 of Sect. 2 with our code we compute 18,000 time-varying matrix square roots predictively for 360 sec or 6 min, or one every 50th of a second. This process takes around 1.3 s of CPU time which equates to 0.00007 s for each square root computation step and shows that our discretized ZNN method is very feasible to run predictively in real-time for matrix square roots during each of the 0.02 s sampling gap intervals.

Note that any ZNN method that is based on a finite difference scheme j_s such as 4__5 with $j = 4$ has a local truncation error order of $O(\tau ^{j+2}) = O(0.02^{~6}) \approx O(6.4 \cdot 10^{-11})$. In this example the model equation $A(t) = X(t) \cdot X(t)$ is satisfied from a random Euler based start-up after approximately 20 s with smaller than $10^{-10}$ relative errors. The model’s relative errors decrease to around $10^{-13}$ after about 6 min according to Fig. 1.

As $\tau = 0.02$ sec is the standard fixed 50 Hz clocking cycle for sensor based output, it is important to adjust the decay constant $\eta$ appropriately for convergence: If a look-ahead ZNN method diverges for your problem and one chosen $\eta$, reduce $\eta$. If the error curve decays at first, but has large variations after the early start-up phase and 10 or 20 s have passed, increase $\eta$. The optimal setting of $\eta$ depends on the data input $A(t_k)$ and its variations size, as well as the chosen finite difference formula. The optimal setting for $\eta$ cannot be predicted.

This is one of the many open problems with time-varying matrix problems and both discretized and continuous ZNN methods that needs a deeper understanding of the numerical analysis of time-varying matrix computations.

Eight different model equations for the time-varying matrix square root problem are detailed in [64, Ch. 10].

4 Conclusions

This paper has tried to explain the inner workings and describe the computational phenomena of a recent, possibly new or slightly different branch of numerical analysis for discretized time-varying matrix systems from its inside out. Time-varying discretized ZNN matrix algorithms are built from standard concepts and well known relations and facts of algebra, matrix theory, and also aspects of static numerical matrix analysis. Yet they differ in execution from their near cousins, the analytic continuation IVP differential equation solvers; in speed, accuracy, predictive behavior and more. Zhang Neural Networks do not follow the modern call for backward stable computations that find the exact solution of a nearby problem whose distance from the given problem depends on the problem’s conditioning. Instead Zhang Neural Networks compute highly accurate future solutions based on an exponentially decaying error function that ensures their global convergence from nearly arbitrary start-up data. In their coded versions, the thirteen discretized ZNN time-varying matrix algorithm examples in this paper use just one linear equations solve and a short recursion of earlier systems data per time step, besides some auxiliary set-up et cetera functions. These codes run extremely fast using previous data immediately after time $t_k$ and they arrive well before time $t_{k+1}$ at an accurate prediction of the unknown variable(s) at the next time instance $t_{k+1}$.

The standard version of discretized ZNN methods for time-varying matrix problems proceeds in seven steps. The ZNN steps do mimic standard IVP ODE continuation methods and it is challenging to try and understand the differences between them from the ‘outside’. Here many time-varying problems from matrix theory and optimization have been built from the ground up for ZNN, including working Matlab codes for most of them. This was done with ever increasing levels of difficulty and complexity, from simple time-varying linear equations solving routines to time-varying matrix inversion and time-varying pseudo-inverses; from time-varying Lagrange multipliers for function optimization to more complicated matrix problems such as time-varying matrix eigenvalue problems, time-varying linear equations with inequality constraints, time-varying matrix square roots and time-varying Sylvester and Lyapunov equations. Some of these algorithms require Kronecker product matrix representations and all can be built and handled successfully in the discretized ZNN standard seven steps way.

On the way we have encountered models and error functions for ZNN that do not yield usable derivative information for the unknown variable(s) and for which we have learned how to re-define our model and its error function accordingly for success in ZNN. We have pointed out alternate ways to solve the linear equations part of discretized ZNN differently in Matlab and shown how to optimize the speed of some ZNN Matlab codes. We have dealt with simple random entry early on-chip ‘solutions’ for unknown and unpredictable sensor data as starting values of the discretized ZNN iterations for time-varying matrix square roots in light of Kronecker products.

But we have not dealt with the final, the engineering application of discretized time-varying sensor driven ZNN matrix algorithms or have we created on-chip circuit designs for use in the control of chemical plants and in robots, for autonomous vehicles, and other machinery. That was the task of [64] and this is amply explained in Simulink schematics there. Besides, circuit diagrams appear often in the Chinese engineering literature that we have quoted.

There are many wide open questions with ZNN as, for example, how to choose among dozens and dozens of otherwise equivalent same j_s type look-ahead and convergent finite difference formulas for improved accuracy or speed and also regarding the ability of specific finite difference formulas to handle widely varying sampling gaps $\tau$ well. Neither do we know how to assess or distinguish between high optimal $h = \tau \cdot \eta$ and low optimal h value finite difference formulas, nor why there are such variations in h for equivalent truncation error order formulas. These are open challenges for experts in difference equations.

Many other open questions with discretized ZNN are mentioned here and in some of the quoted ZNN papers.

A rather simple test problem would be to try and solve the mass matrix differential equations for the unknown solution x(t) in Step 3 of some of our ZNN code developments with initial value ODE solvers such as ode23t, ode45, ode15s, ode113 or ode23s in Matlab and see how well and quickly the solution x can be evaluated over time when compared with complete ZNN methods for the same problem. Such a comparison has appeared in [49] where our specific ZNN algorithm was compared to Loisel and Maxwell’s [28] directly differentiated eigendata equation and its IVP ODE solution.

5 The genesis of this paper

The author’s involvement with Zhang Neural Networks (ZNN) began in 2016 when he was sent the book [64], written by Yunong Zhang and Dongsheng Guo from the Zentralblatt for review, see Zentralblatt 1339.65002.

The author of this introductory survey was impressed by the ideas and workings of ZNN. He contacted Yunong Zhang and visited him and his research group at Sun Yat-Sen University in Guangzhou in the summer of 2017. Thanks to this visit and through subsequent exchanges of e-mails, questions and advice back and forth, he began to enter this totally new-to-him area of predictive time-varying matrix numerics. When writing and trying to submit papers on ZNN methods to western matrix and numerical and applied mathematics journals, he soon learned that time-varying numerical matrix methods and predictive solutions thereof had been nearly untouched in the West; there were no suitable referees. This 20 years old, yet new area had come to us from the East. It resides and flourishes outside of our western knowledge and understandings base, with more than 90 $\%$ of its estimated 400 research and engineering papers and all of its at least five books originating in China. Only a few European and even fewer American scientists have begun to contribute to the field, often with publications that include Chinese coauthors; see, e.g., [7, 38, 47]. Moreover, in the emerging global ZNN engineering literature of today there hardly is a hint of theoretical work on ZNN and no published numerical analysis for this new method and area.

In the summer of 2019 the author visited Nick Trefethen and Yuji Nakatsukasa in Oxford. And we conferred for several hours about the numerical ideas that may lie behind discretized Zhang Neural Networks and its error decay.

In October 2020, when the first version of the manuscript was submitted, Nick Trefethen advised the editor to look for a referee with expertise in the vast literature of numerical methods for ODEs. And indeed, the group of referees discovered analogies and possible connections between discretized ZNNs and certain analytic continuation methods, as described in Stephen Robinson’s paper [37] from 1976, and in the books by Peter Deuflhard [9], by Eugene Allgower and Kurt George [1], and by Uri M. Ascher, Hongsheng Chin and Sebastian Reich [2], and in the paper by Ascher and Petzold [3] that all originated in the 1990s. More recent are the optimization books by Jorge Nocedal and Stephen J. Wright [33] from 1999/2006 and by Dimitri Panteli Bertsekas, Angelia Nedić and Asuman E. Ozdaglar [5] from 2003/2006, and the paper by Ellen Fukuda and Masao Fukushima [15] from 2017. In [2] the authors analyzed how to stabilize the DAEs in analytic continuations algorithms and introduced certain analytic continuation limit manifolds that might shed more understanding and light onto their connections with Zhang Neural Networks. But none of these expansive analytic continuation notions in [9] or [1,2,3] were known to Zhang and Wang in 2001 and no numerical analysis studies of their possible connections to ZNN have ever been attempted so far. The second round referee Peter Maxwell proved quite knowledgable on these possibly adjacent method classes. Subsequently Maxwell and the author exchanged a series of extended reviews and rebuttals that eventually lead to the present form of the publication. Unfortunately we could not settle the question of the level or actual kind of interconnectedness between analytic continuation algorithms and the Zhang Neural Network method.

Eventually the seven step set-up structure of discretized Zhang Neural Networks became clear. ZNN starts with a global entry-wise error function for time-varying matrix problems and it stipulates an exponential error decay that makes convergence and noise suppression automatic. Then ZNN continues with an ingenious way to replace the error function differential equation with solving linear equations repeatedly instead and using high error order look-ahead convergent recursion formulas in tandem. Such difference formulas had only been sparingly used in predictor-corrector ODE schemes before with relatively low error orders. To our knowledge, the discretized ZNN solution-derivative free setting has been achieved completely outside of the ODE analytic continuation realm and ZNN converges quite differently, see [54, Figures 3 and 5] for examples with convergence into the machine constant error levels (and below) over time.

This discovery and others such as the disparate term magnitudes of an adapted AZNN algorithm in [54, Table 1] in the predictive computational Zhang Neural Network step have further strengthened this introductory and partial survey paper of Zhang Neural Network methods. As author I am glad and very thankful for the help and patience of my family and for the editor’s and referees’ helpful comments, to Nick and Yuri, to Peter Benner who pointed me to eigencurves and analytic continuation ODE methods (see [49]), and to Peter Maxwell in particular for helping to improve the Lagrange optimization sections (V) and (VI) in Sect. 3.

I do hope that time-varying matrix methods and continuous or discretized ZNN time-varying matrix methods can become a new part of our global numerical matrix analysis research and that they will add to our numerical matrix analysis know-how soon.

For this we need to build a new time-varying matrix numerics knowledge base in the West; just as has been done so many times before for our own ever evolving matrix computational needs, see [44] for example.