Comparison of the symmetric hyperbolic thermodynamically compatible framework with Hamiltonian mechanics of binary mixtures

Abstract

How to properly describe continuum thermodynamics of binary mixtures where each constituent has its own momentum? The Symmetric Hyperbolic Thermodynamically Consistent (SHTC) framework and Hamiltonian mechanics in the form of the General Equation for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC) provide two answers, which are similar but not identical, and are compared in this article. They are compared both analytically and numerically on several levels of description, varying in the amount of detail. Namely, a reduction to a more common one-momentum setting is shown, where the effects of the second momentum translate into diffusive fluxes. Both SHTC and GENERIC can thus be interpreted as a method specifying diffusive flux in standard theory. The GENERIC equations, stemming from the Liouville equation, contain terms expressing self-advection of the relative velocity by itself, which lead to a vorticity-dependent diffusion matrix after the reduction. The SHTC equations, on the other hand, do not contain such terms. We also discuss the possibility to formulate a theory of mixtures with two momenta and only one temperature that is compatible with the Liouville equation and possesses the Hamiltonian structure, including Jacobi identity.

 

"We speak different languages, as usual," responded Woland, "but this does not change the things we speak about. Well?..."

–M. Bulgakov [1]

1 Introduction

Homogeneous mixtures, also known as single-phase mixtures, (for instance, the air, petrol, aqueous solutions, or plasma in fusion reactors) are ubiquitous in everyday life and industry. Although their behaviour can in most cases be well explained by means of equilibrium thermodynamics or fluid mechanics [2, 3], there are processes that are difficult to describe theoretically. For instance, when two species are mixing with high relative velocity, dynamics of the relative velocity affects the overall behaviour of the mixture (stress, heat flux, or possibly even rates of chemical reactions [4]). Our goal is to derive dynamics of binary mixtures with evolving relative velocity. A particular feature of our model is that the relative velocity is advected by itself when it has nonzero vorticity. After a reduction, this leads to a diffusion equation with a vorticity-dependent diffusion matrix. Consequently, the diffusion flux does not need to be aligned with the gradient of chemical potential, in contrast with the standard theory of mixtures [5].

Binary homogeneous mixtures can be described by various non-equilibrium thermodynamic models. These models can be classified based on the chosen state variables (fields that are equipped with their own time evolution equations). In Classical Irreversible Thermodynamics (CIT), the mixture models have only one momentum density or velocity, typically the barycentric one [5], or they have none, being in the mechanical equilibrium [6]. In Rational Thermodynamics, each constituent of the mixture can be equipped with its own momentum [7]. In Extended Rational Thermodynamics and Extended Irreversible Thermodynamics, the constituents can also have different temperatures [8,9,10]. These classical approaches take the conservation laws of mass, momentum, and energy for granted while seeking the undetermined fields like the stress tensor, heat flux, and diffusion flux via an entropic closure. There is, however, no unique way how to find such closure, which is why the theory of mixtures is still an active area of research. Alternative approaches exploit variational principles and the Lagrange$\rightarrow$Euler transformation [11], which are the directions where we also aim. Further comparison can be found at relevant places throughout this paper.

A closure found in [4] leads to a mixture with several velocities and only one temperature, allowing for the diffusion to affect chemical reactions and for identification of partial pressure for non-ideal mixtures [12]. Especially in the non-isothermal case, however, there are many possibilities of finding the closures, and construction of the models is rather cumbersome when relying on the closures. In [13] another theory was developed, leading to similar results, but facing difficulties when identifying the partial pressure of ideal gases in equilibrium. Yet another approach was developed in [14], using a definition of time-reversal parity dependent on the choice of the physical units, making the Onsager–Casimir reciprocal relations dependent on the units as well. In [15] a theory of mixtures is obtained from the kinetic theory of rarefied gases, similarly as in [5], but equations for partial momenta of all components are not provided. All these theories of mixtures are based on entropic closures and share the property that the closure cannot be identified uniquely.

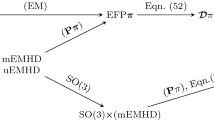
In this article, on the other hand, we show different ways towards theory of mixtures, relying on geometric mechanics or on the requirement of hyperbolicity. We present two approaches to binary mixtures: (i) the Symmetric Hyperbolic Thermodynamically Compatible (SHTC) equations, which is a set of first-order quasilinear hyperbolic equations [16,17,18], and (ii) the General Equation for Non-Equilibrium Reversible-Irreversible Coupling (GENERIC), which relies on geometric mechanics, in particular Hamiltonian mechanics [19,20,21,22].

The SHTC system can be seen as constructed from a Lagrangian master system of equations guaranteeing its mathematical properties [23,24,25]. GENERIC, on the other hand, is constructed from four geometric building blocks: a Poisson bracket, an energy functional, a dissipation potential, and an entropy functional. Both approaches are compatible for the simple continuum [17], where the SHTC form of governing equations possesses the GENERIC structure. In the case of (binary) mixtures, the SHTC equations still possess the GENERIC structure. However, the projection from the Liouville equation (for the N-particle distribution function) within GENERIC leads to additional terms expressing self-advection of the relative velocity, which are not observed in the SHTC framework. We demonstrate the effects of those additional terms both analytically and numerically in this article.

On top of the two momenta, binary mixtures can have two entropies (or temperatures). By direct projection from the (Hamiltonian) Liouville equation, we obtain a Hamiltonian theory of mixtures where each constituent has its own density, momentum density, and entropy density (or temperature) [22]. But models with only one entropy density are more difficult to obtain because it is not straightforward to fulfil the Jacobi identity, which expresses the self-consistency of Hamiltonian mechanics [26]. Therefore, we study two possible solutions to derive a one-temperature model—reduction of the entropy difference by maximisation of entropy and a Jacobi closure relation for the entropy difference, keeping only the overall entropy of the mixture, so that Jacobi identity is satisfied.

To summarise the introduction, this article has three main aims. Firstly, we introduce a two-momenta model for binary mixtures, both with one and two entropies (or temperatures). Albeit being simplified—viscosity and heat conductivity are omitted to keep the technical steps comprehensible—we believe the fundamental properties of the model can be identified. Moreover, the additional terms might be added in future works similarly as in the case of a simple continuum. For instance, viscous terms are added through distortion, see [17]. Secondly, we compare the GENERIC model to SHTC, which is known for its good numerical results, see [27, 28]. Furthermore, SHTC is similar to GENERIC in the sense that, unlike the standard theory based on entropy closures, it relies on Lagrange$\rightarrow$Euler transformation. Finally, through the reduction of both models to one momentum, we derive diffusion flux. Especially in case of GENERIC framework, the resulting flux is rather unique and could be understood as an alternative to the standard-theory-derived closures, based on different foundations.

In Sect. 2, we recall the SHTC approach to binary mixtures. In Sect. 3, we first construct the GENERIC model for binary mixtures by projection from the Liouville equation. In Sect. 4, a GENERIC model with only one entropy is constructed and compared to the SHTC model. Next, both SHTC and GENERIC models are reduced to only one momentum. Some differences between reduced versions of the SHTC and GENERIC models are discussed and compared both analytically and numerically.

2 SHTC framework

The SHTC equations are a class of partial differential equations of continuum physics with two crucial properties. Firstly, they are symmetric hyperbolic in the sense that they can be written, after a possible change of variables, in the form

$$\begin{aligned} A({\textbf{q}})\cdot \frac{\partial {\textbf{q}}}{\partial t} + B_n({\textbf{q}})\cdot \frac{\partial {\textbf{q}}}{\partial x_n} +C({\textbf{q}})\cdot {\textbf{q}}= 0, \end{aligned}$$

(1)

with ${\textbf{q}}$ being the vector of state variables and where the matrices A and $B_n$ are symmetric and A is positive definite [29,30,31]. One of the reasons to work with such restricted class of PDEs is that hyperbolic first-order systems guarantee finite speed of propagation, unlike second-order parabolic equations such as Navier–Stokes, and thus do not violate the concept of relativistic causality. Another reason is that symmetric hyperbolic systems are locally well posed,¹ since a unique and stable solution exists at least locally in time [30, 31].

Secondly, the SHTC equations are compatible with thermodynamics because they satisfy the first and second laws of thermodynamics.

Due to the restriction of SHTC to first-order PDEs, classical models with higher derivatives, such as Navier–Stokes equations, are not within the framework directly. However, it has been shown via an asymptotic expansion in a relaxation parameter that solutions to the Navier–Stokes–Fourier model are approximated by the solutions to the SHTC equations [27, 28].

The above definition is, however, quite general and does not show how to derive and what qualities to expect from the SHTC equations. While a complex description of SHTC is out of scope of this paper, see [17] for details, we briefly present the ideas that gave rise to the framework. Notice that mass and entropy balance are the same equations, at least in reversible processes with no entropy growth, even though the two physical quantities are fundamentally different. Similarly, some non-Fourier heat transports, such as phonon hydrodynamics developed in [32], share many similarities with Navier–Stokes equations even though they describe dramatically different phenomena. In general, many equations in continuum physics are similar to each other even though they describe different quantities in different processes. It is therefore a natural question, what can be actually said about the system of equations and their structure without specifying the exact setting and focusing only on more general qualities such as conservation and invariance principles, causality principle or the laws of thermodynamics. In [24], Godunov, Mikhailova and Romenski proposed a system of Lagrangian conservation laws that would satisfy the above principles, e.g., it is invariant under rotations, admits an additional conservation law, etc. For the full list of qualities and the actual system, see [17] or the original work [24].

After a rather technical Lagrange$\rightarrow$Euler transformation, an Eulerian system for vector of variables ${\textbf{p}}$ is derived, in the form

$$\begin{aligned} \frac{\partial L_{{{\textbf {p}}}}}{\partial t} + \frac{\partial L^k_{{{\textbf {p}}}}}{\partial {{\textbf {x}}}_k} = 0 \end{aligned}$$

(2)

where $L({\textbf{p}})$ and $L^k({\textbf{p}})$ are potentials and lower indices stand for derivatives, i.e., $L_{p_i} = \frac{\partial L}{\partial p_i}$. Chain rule then gives

$$\begin{aligned} L_{p_ip_j}\frac{\partial p_j}{\partial t} + L^k_{p_ip_j} \frac{\partial p_j}{\partial x_k}. \end{aligned}$$

(3)

If L is strictly convex, than the system is symmetric hyperbolic. Example of one equation of the system is

$$\begin{aligned} \frac{\partial L_r}{\partial t} + \frac{\partial (v_kL)_r}{\partial x_k} = 0, \end{aligned}$$

(4)

where $v_k$ and r are some of the state variables ${\textbf{p}}$, $v_k$ typically meaning velocity component of the matter. However, the fundamental quality of SHTC is the fact that it does not need to give precise physical meaning to the fields.

Moreover, one can perform Legendre transformation to get to the energetic representation, namely

$$\begin{aligned} {\textbf{q}}&= L_{{\textbf{p}}}, \end{aligned}$$

(5)

$$\begin{aligned} E(q)&= {\textbf{p}}\cdot L_{{\textbf{p}}} - L({\textbf{p}}) \end{aligned}$$

(6)

or vice versa

$$\begin{aligned} {{\textbf {p}}}&= E{_\textbf{q}}, \end{aligned}$$

(7)

$$\begin{aligned} E(p)&= {\textbf{q}}\cdot E_{{\textbf{q}}} - E({\textbf{q}}). \end{aligned}$$

(8)

Since $E_{{\textbf{q}}{\textbf{q}}} = (L_{{\textbf{p}}{\textbf{p}}})^{-1}$, strict convexity of E once again proves the symmetric hyperbolicity of the system. Denoting $\rho = L_r$ (and therefore $r = E_{\rho }$), one gets the equation

$$\begin{aligned} \frac{\partial \rho }{\partial t} + \frac{\partial (\rho v_k)}{\partial x_k} = 0, \end{aligned}$$

(9)

which typically stands for the mass balance. For more details about the original system of equations, the transformations, other equations in the system, and their qualities, see [24] or [17].

We focus on a simplified setting close to the thermal equilibrium that can be modelled with just one entropy, see [33], and on homogeneous mixtures, neglecting volume fractions. Therefore, we aim neither at multi-temperature mixtures, like electrons and ions in low-temperature plasma, nor at heterogeneous mixtures, like water vapour with droplets. The following section addresses binary one-temperature homogeneous mixtures within the SHTC framework.

2.1 SHTC equations for binary mixtures

Let us consider a homogeneous binary mixture composed of fluids of two kinds, denoted as species 1 and 2. A possible set of state variables describing the mixture are the pairs of densities, momentum densities, and entropy densities of the two species,

$$\begin{aligned}&\rho _1, \rho _2,&\text{ Eulerian } \text{ mass } \text{ densities } \text{ of } \text{ the } \text{ two } \text{ components, }\end{aligned}$$

(10a)

$$\begin{aligned}&{\textbf{u}}_1, {\textbf{u}}_2,&\text{ momentum } \text{ densities } \text{ of } \text{ the } \text{ two } \text{ components, } \end{aligned}$$

(10b)

$$\begin{aligned}&s_1, s_2,&\text{ Eulerian } \text{ entropy } \text{ densities } \text{(per } \text{ volume) } \text{ of } \text{ the } \text{ two } \text{ components. } \end{aligned}$$

(10c)

Within the SHTC framework, binary mixtures are expressed in terms of the following state variables

$$\begin{aligned} \rho _1&= \rho _1 ,&\mathrm {mass \ density \ of \ the \ first \ component} , \end{aligned}$$

(11a)

$$\begin{aligned} \rho&=\rho _1 + \rho _2,&\mathrm {(total) \ mass \ density}, \end{aligned}$$

(11b)

$$\begin{aligned} {\textbf{m}}&= {\textbf{u}}_1 + {\textbf{u}}_2,&\mathrm {(total) \ momentum \ density} ,\end{aligned}$$

(11c)

$$\begin{aligned} {\textbf{w}}&=\frac{{\textbf{u}}_1}{\rho _1} - \frac{{\textbf{u}}_2}{\rho _2},&\mathrm {velocity \ difference},\end{aligned}$$

(11d)

$$\begin{aligned} s&= s_1 + s_2,&\text{ total } \text{ entropy } \text{ density. } \end{aligned}$$

(11e)

Their SHTC time evolution equations are

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 E_{m_i}) - \partial _iE_{w_i}, \end{aligned}$$

(12a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho E_{m_i}), \end{aligned}$$

(12b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i E_{\rho } - \rho _1 \partial _i E_{\rho _1} - s\partial _i E_s - m_j \partial _i E_{m_j} - \partial _j (m_i E_{m_j}) \nonumber \\&+ E_{w_j}\partial _i w_j - \partial _j (w_i E_{w_j}), \end{aligned}$$

(12c)

$$\begin{aligned} \frac{\partial w_i}{\partial t} =&- \partial _i E_{\rho _1} -E_{m_j} \partial _j w_i - w_j \partial _i E_{m_j} - \frac{1}{\tau }E_{w^i}, \end{aligned}$$

(12d)

$$\begin{aligned} \frac{\partial s}{\partial t} =&-\partial _i(s E_{m_i}) +\frac{1}{\tau }\frac{1}{E_s}E_{w^j}E_{w^j}, \end{aligned}$$

(12e)

where E is energy, its lower indices stand for partial derivatives with respect to the state variable, see [34] or [22], and $\tau$ is a positive relaxation parameter specifying the rate of dissipation, see [18]. The dissipation is purely algebraic (involving no spatial gradients). This system of PDEs is written in the language common in SHTC and GENERIC communities with the derivatives of the potential (energy), not in the continuum dynamics language of balance laws. However, as the energy is typically chosen in such a way, that $E_{{\textbf{m}}}$ is equal to the velocity ${\textbf{v}}$, the models are very similar. For example, the second equation gets the form of classical mass conservation, while the third can be rewritten as momentum conservation. As the model and its comparison to classical balance laws isn’t the main goal of this paper, we do not describe the similarities. A more classical formulation of system (12) is presented in [18].

In order to close the system of evolution equations, we have to specify the energy and the relaxation parameter. The theory so far has been independent of the physical system under consideration and thus general. The energy can be obtained by the means of statistical physics or by geometrical arguments based on the maximisation of entropy, see [22]. The dissipation parameter can be obtained, for instance, by a dynamic reduction [22], by the fluctuation–dissipation theorem [21], or, of course, it can be measured experimentally [35].

For binary mixtures the energy is composed from the kinetic and the internal energy,

$$\begin{aligned} E = \underbrace{\frac{{\textbf{u}}_1^2}{2\rho _1}+\frac{{\textbf{u}}_2^2}{2\rho _2}}_{=E_{\textrm{kin}}(\rho _1, \rho , {\textbf{m}}, {\textbf{w}})} + E_{\textrm{int}}(\rho _1, \rho , s) = \frac{{\textbf{m}}^2}{2\rho } + \frac{\rho _1(\rho -\rho _1)}{2\rho }{\textbf{w}}^2 + E_{\textrm{int}} (\rho _1, \rho ,s). \end{aligned}$$

(13)

Therefore, the velocity is conjugate to the momentum density through $E_{{\textbf{m}}} = {\textbf{m}}/ \rho = {\textbf{v}}$. Once the internal energy is prescribed, for instance, by the Sackur–Tetrode relation [36] or in any other way [27], the energy becomes an explicit function of the state variables. Both the energy and $\tau$ will be chosen later in Sect. 4 explicitly. In the following section we discuss the particular properties of SHTC equations like hyperbolicity.

2.2 Properties of the SHTC equations

Evolution Eq. (12) can be written as a symmetric quasilinear system (1) of first-order partial differential equations [17, 33, 37]. Therefore, one can expect local in-time well-posedness of the Cauchy problem for (12), provided that we have regular initial data [31] and convex energy E. The symmetrisation of (12) can be accomplished by introducing a generating potential and generating variables, as described, for example, in [38]. It should be noted that for the presented version of SHTC Eq. (12), it is difficult to define a physically reasonable internal energy that is convex over a wide range of state parameters. To formulate the SHTC model, in which the energy is a convex function, it is necessary to extend the system (12) by including the equation for the evolution of the volume fraction, as it is done in [38], and to define the internal energy of the mixture as the mass averaged internal energy of constituents’ internal energies. In this paper, however, we exclude the volume fraction from the set of state variables and consider simplified versions of both SHTC and GENERIC equations in order to focus on the relative velocity evolution equation, which is the main equation describing transport of the constituents.

Furthermore, the reversible part of the SHTC Eq. (12), obtained by disregarding the relaxation terms with the prefactor $1/\tau$, is a particular realisation of Hamiltonian mechanics [17]. Namely, it is generated by Poisson bracket (21). The validity of the Jacobi identity can be shown, for instance, using program [39].

Finally, system (12) admits the total energy conservation law, see [17, 33, 37], and therefore, it is compatible with the first law of thermodynamics. Additionally, the irreversible part of (12) (the relaxation terms) can be seen as the gradient of a quadratic dissipation potential, see [17], and therefore, the entropy production is guarantied. This implies the compatibility with the second law of thermodynamics. The entropy production can also be inferred directly from (12e), as the equation contains just a time derivative, divergence, and a positive algebraic term ($\tau$ and temperature $E_s$ are positive).

3 GENERIC framework

Within the GENERIC framework, summarised in monographs [21, 22], the time evolution of the vector of state variables ${\textbf{q}}$ is split into reversible and irreversible parts. The reversible part is generated by a Poisson bracket $\{\bullet ,\bullet \}$ with the Hamiltonian (or energy) of the system E, while the irreversible part is described by a dissipation potential $\Xi ,$ and entropy S. The time evolution of any functional A of the state variables is given by

$$\begin{aligned} {\dot{A}} = \{A, E\} + \langle A_{\textbf{q}}, \Xi _{{\textbf{q}}^*} \rangle , \end{aligned}$$

(14)

where subscripts stand for functional derivatives, angle brackets for the $L_2$ scalar product, and ${\textbf{q}}^*=S_{{\textbf{q}}}$ are the conjugate variables. The evolution equation for a state variable $q^i$ is obtained by plugging $A=q^i$ into Eq. (14).

Let us now discuss the GENERIC building blocks in more detail. The Poisson bracket is a skew-symmetric bilinear operator, $\{F,G\} = -\{G,F\}$, and it satisfies the Leibniz rule and the Jacobi identity,

$$\begin{aligned}&\{F,GH\} = G\{F,H\} + \{F,G\}H, \end{aligned}$$

(15)

$$\begin{aligned}&\{F,\{G,H\}\} + \{G,\{H,F\}\} + \{H,\{F,G\}\} = 0 \end{aligned}$$

(16)

for any $F({\textbf{q}})$ and $G({\textbf{q}})$. In particular, the skew-symmetry implies conservation of energy. When the dissipation potential is convex with a minimum at zero in conjugate variables,² entropy is being produced, which guarantees compatibility with the second law of thermodynamics. An interesting feature of GENERIC is the fact that once the given requirements are met, the first and second laws of thermodynamics are automatically satisfied by construction, so every GENERIC model is thermodynamically compatible.

The dissipation potential is usually assumed to be quadratic, which makes it compatible with the concept of dissipative brackets [21, 41], although it does not have to be. The Poisson bracket can be obtained by a series of projections. For instance, Hamiltonian continuum mechanics can be obtained from the N-particle Liouville Poisson bracket, as in this article, or by other geometric techniques like variational principles [42], dynamics on Lie algebra duals [43,44,45], or semidirect products [46, 47]. Once a set of state variables is declared, the Poisson bracket is usually derived in a unique way [48]. When, moreover, entropy or energy density are among the set of state variables, only one of the pair E and S is necessary, since one can be then expressed in terms of the other, similarly as in the so called one-generator framework [49]. The whole model for a chosen set of state variables only requires the knowledge of the energy of the system and of the dissipation potential, since these describe the particular material of the system.

Compared to standard theory based on entropy closures, principles of invariance etc., GENERIC relies a lot on geometry.³ While not being perfect—the choice of energy and dissipation potential is very complicated—we believe that the Hamiltonian theory of the reversible part is convincing and plausible. Since it is, additionally, based on rather different principles and could therefore be better in some matters (and worse in others) than the standard theory, it is natural to use it for complementing the standard results.

In the next section, we show a GENERIC formulation of binary mixtures.

3.1 Hamiltonian mechanics of mixtures by projection from the Liouville equation

Let us briefly summarise the derivation of Hamiltonian mechanics for binary mixtures by projection from the Liouville equation. Any system composed of classical particles can be described by means of the N-particle distribution function, $f_N$, evolution of which is expressed by the Liouville equation [22]. The Liouville equation is a particular realisation of the Lie–Poisson Hamiltonian mechanics and is thus constructed from a Poisson bracket, called Liouville–Poisson bracket, and from an N-particle energy [48, 50].

When the system is composed of particles of two kinds, the $N-$particle distribution function can be projected onto state variables of continuum mechanics (10). Such projection turns the Liouville–Poisson bracket for the N-particle distribution function to another Poisson bracket for state variables (10),

$$\begin{aligned} \{F,G\}^{\textrm{binary}}&= \int \,\textrm{d}{\textbf{r}}\rho _1\left( \partial _i F_{\rho _1} G_{u_{1i}}-\partial _i G_{\rho _1} F_{u_{1i}}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}u_{1i}\left( \partial _j F_{u_{1i}} G_{u_{1j}}-\partial _j G_{u_{1i}} F_{u_{1j}}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}s_1\left( \partial _i F_{s_1} G_{u_{1i}}-\partial _i G_{s_1} F_{u_{1i}}\right) \nonumber \\&\quad + \int \,\textrm{d}{\textbf{r}}\rho _2\left( \partial _i F_{\rho _2} G_{u_{2i}}-\partial _i G_{\rho _2} F_{u_{2i}}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}u_{2i}\left( \partial _j F_{u_{2i}} G_{u_{2j}}-\partial _j G_{u_{2i}} F_{u_{2j}}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}s_2\left( \partial _i F_{s_2} G_{u_{2i}}-\partial _i G_{s_2} F_{u_{2i}}\right) , \end{aligned}$$

(17)

see, for instance, [22, 48]. The resulting reversible evolution equations (before adding dissipative dynamics) are

$$\begin{aligned} \frac{\partial \rho _{a}}{\partial t}&= \partial _i (\rho _{a} E_{u_{a, i}}), \end{aligned}$$

(18a)

$$\begin{aligned} \frac{\partial u_{a i}}{\partial t}&= - \rho _{a}\partial _i E_{\rho _{a}} - u_{a j} \partial _i E_{u_{a j}} - \partial _j (u_{a i} E_{u_{a j}}), \end{aligned}$$

(18b)

$$\begin{aligned} \frac{\partial s_{a}}{\partial t}&= - \partial _i (s_a E_{u_{a i}}), \end{aligned}$$

(18c)

for $a = 1,2$. The total energy of the system is denoted by E and the subscripts stand for functional derivatives. If the energy is of an algebraic type, that is $E=\int e(\rho _1,{\textbf{u}}_1,s_1,\rho _2,{\textbf{u}}_2,s_2) d{\textbf{r}}$, where the volumetric energy density e is a smooth function of its arguments, the functional derivatives become identical with the partial derivatives of the energy density. State variables $\rho _1$, $\rho _2$, ${\textbf{u}}_1$, ${\textbf{u}}_2$, $s_1$, and $s_2$ are, however, not those in which the SHTC equations are usually expressed.

The purpose of the following section is to adapt the variables closer to the SHTC framework.

3.2 Transformation to the SHTC-like variables with two entropies

Let us now transform the state variables so that the total density, total momentum density, and total entropy density are included, [16],

$$\begin{aligned} \rho _1&= \rho _1,&\mathrm {mass \ density \ of \ the \ first \ component} , \end{aligned}$$

(19a)

$$\begin{aligned} \rho&=\rho _1 + \rho _2,&\mathrm {(total) \ mass \ density}, \end{aligned}$$

(19b)

$$\begin{aligned} {\textbf{m}}&= {\textbf{u}}_1 + {\textbf{u}}_2,&\mathrm {(total) \ momentum \ density} ,\end{aligned}$$

(19c)

$$\begin{aligned} {\textbf{w}}&=\frac{{\textbf{u}}_1}{\rho _1} - \frac{{\textbf{u}}_2}{\rho _2},&\mathrm {velocity \ difference,} \end{aligned}$$

(19d)

$$\begin{aligned} s&= s_1 + s_2,&\text{ total } \text{ entropy } \text{ density, }\end{aligned}$$

(19e)

$$\begin{aligned} \Delta s&= \frac{s_1}{\rho _1}-\frac{s_2}{\rho _2},&\text{ specific } \text{ entropy } \text{ difference. } \end{aligned}$$

(19f)

If we excluded the specific entropy difference $\Delta s$, we would have the same state variables as in SHTC.

Poisson bracket (17) then transforms to

$$\begin{aligned} \{F,G\}&= \{F,G\}^{(SHTC)}\nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\frac{\rho }{\rho _1(\rho -\rho _1)}\left( \partial _i\frac{m_j}{\rho }-\partial _j\frac{m_i}{\rho }\right) F_{w_i}G_{w_j}\nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\frac{\partial _i w_j -\partial _j w_i}{\rho _1}F_{w_i}G_{w_j}\nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\frac{\rho }{\rho _1(\rho -\rho _1)}\left( \partial _j\frac{\rho _1 w_i}{\rho }-\partial _i\frac{\rho _1 w_j}{\rho }\right) F_{w_i}G_{w_j}\nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\Delta s \left( \partial _i F_s G_{w_i} - \partial _i G_s F_{w_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\Delta s \left( G_{m_i}\partial _i F_{\Delta s}- F_{m_i}\partial _i G_{\Delta s}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\left( s_1\partial _i \frac{1}{\rho _1}-s_2\partial _i \frac{1}{\rho -\rho _1}\right) \left( F_{\Delta s} G_{m_i}-G_{\Delta s} F_{m_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\left( \frac{s_1}{\rho ^2_1}-\frac{s_2}{(\rho -\rho _1)^2}\right) \left( \partial _i F_{\Delta s} G_{w_i}-\partial _i G_{\Delta s} F_{w_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\left( \frac{s_1}{\rho _1}\partial _i\frac{1}{\rho _1}-\frac{s_2}{\rho -\rho _1}\partial _i\frac{1}{\rho -\rho _1}\right) \left( F_{\Delta s} G_{w_i}-G_{\Delta s} F_{w_i}\right) , \end{aligned}$$

(20)

where $s_1$ and $s_2$ are functions of s, $\Delta s$, $\rho$, and $\rho _1$ accordingly to transformation rules (19). The SHTC part of the bracket is

$$\begin{aligned} \{F,G\}^{(SHTC)}&= \int \,\textrm{d}{\textbf{r}}\rho _1 \left( \partial _i F_{\rho _1} G_{m_i}-\partial _i G_{\rho _1} F_{m_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\rho \left( \partial _i F_{\rho } G_{m_i}-\partial _i G_{\rho } F_{m_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}m_i \left( \partial _j F_{m_i} G_{m_j}-\partial _j G_{m_i} F_{m_j}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}s \left( \partial _i F_{s} G_{m_i}-\partial _i G_{s} F_{m_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}\left( \partial _i F_{\rho _1} G_{w_i}-\partial _i G_{\rho _1} F_{w_i}\right) \nonumber \\&\quad -\int \,\textrm{d}{\textbf{r}}\partial _i w_j \left( F_{w_j} G_{m_i}-G_{w_j} F_{m_i}\right) \nonumber \\&\quad +\int \,\textrm{d}{\textbf{r}}w_i \left( \partial _j F_{m_i} G_{w_j}-\partial _j G_{m_i} F_{w_j}\right) . \end{aligned}$$

(21)

All the terms in bracket (20) not involved in the part designated as SHTC have indeed not been contained within SHTC. As we shall see below, these terms imply significantly different behaviour of the two models.

Dissipation expressing mutual friction of the two species is expressed by terms

$$\begin{aligned} (\partial _t w_i)_{irr}&= -\frac{1}{\tau }E_{w_i}, \end{aligned}$$

(22a)

$$\begin{aligned} (\partial _t \Delta s)_{irr}&= -\frac{1}{\tau _{\Delta s}}E_{\Delta s},\end{aligned}$$

(22b)

$$\begin{aligned} (\partial _t s)_{irr}&= \frac{1}{\tau }\frac{1}{E_s}E_{w^j}E_{w^j} +\frac{1}{\tau _{\Delta s}}\frac{1}{E_s}(E_{\Delta s})^2, \end{aligned}$$

(22c)

so that the total energy is conserved by the dissipative terms and entropy produced.⁴

The resulting system of evolution equations, including the terms expressing the mutual friction, reads

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 E_{m_i}) - \partial _iE_{w_i}, \end{aligned}$$

(23a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho E_{m_i}), \end{aligned}$$

(23b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i E_{\rho } - \rho _1 \partial _i E_{\rho _1} - s\partial _i E_s - m_j \partial _i E_{m_j} - \partial _j (m_i E_{m_j}) \end{aligned}$$

(23c)

$$\begin{aligned}&+ E_{w_j}\partial _i w_j - \partial _j (w_i E_{w_j}) - \boxed {\Delta s\partial _i E_{\Delta s} - \left( s_1 \partial _i \frac{1}{\rho _1} - s_2\partial _i \frac{1}{\rho -\rho _1}\right) E_{\Delta s},} \nonumber \\ \frac{\partial w_i}{\partial t} =&- \partial _i E_{\rho _1} -\partial _j w_i E_{m_j} - w_j \partial _i E_{m_j} \boxed {-\Delta s \partial _i E_s } \end{aligned}$$

(23d)

$$\begin{aligned}&\boxed { - \left( \frac{s_1}{\rho _1^2} - \frac{s_2}{(\rho -\rho _1)^2} \right) \partial _iE_{\Delta s} - \left( \frac{s_1}{\rho _1}\partial _i\frac{1}{\rho _1} - \frac{s_2}{\rho -\rho _1}\partial _i\frac{1}{\rho -\rho _1} \right) E_{\Delta s} } \nonumber \\&\boxed { + \frac{\rho }{\rho _1 (\rho -\rho _1)} \left( \partial _i \frac{m_j}{\rho } - \partial _j \frac{m_i}{\rho } \right) E_{w_j} } \nonumber \\&\boxed { + \frac{1}{\rho _1} (\partial _i w_j - \partial _j w_i)E_{w_j} } \nonumber \\&\boxed { + \frac{\rho }{\rho _1 (\rho -\rho _1)} \left( \partial _j \frac{\rho _1 w_i}{\rho } - \partial _i \frac{\rho _1 w_j}{\rho } \right) E_{w_j}} - \frac{1}{\tau }E_{w^i}, \nonumber \\ \frac{\partial s}{\partial t} =&-\partial _i(s E_{m_i}) \boxed {-\partial _i (\Delta s E_{w_i})}+\frac{1}{\tau }\frac{1}{E_s}(E_{{\textbf{w}}})^2 + \frac{1}{\tau _{\Delta s}}\frac{1}{E_s} (E_{\Delta s})^2, \end{aligned}$$

(23e)

$$\begin{aligned} \boxed { \frac{\partial \Delta s}{\partial t} }=&\boxed {- \partial _i\left( \Delta s E_{m_i} \right) + \left( s_1 \partial _i \frac{1}{\rho _1} - s_2\partial _i \frac{1}{\rho -\rho _1}\right) E_{m_i} }\nonumber \\&\boxed {- \partial _i \left( \left( \frac{s_1}{\rho _1^2} - \frac{s_2}{(\rho -\rho _1)^2} \right) E_{w_i} \right) + \left( \frac{s_1}{\rho _1}\partial _i\frac{1}{\rho _1} - \frac{s_2}{\rho -\rho _1}\partial _i\frac{1}{\rho -\rho _1} \right) E_{w_i}-\frac{1}{\tau _s} E_{\Delta s},} \end{aligned}$$

(23f)

where the boxed terms are not present in the SHTC framework. In particular, we have to eliminate the $\Delta s$ variable from the equations in order to be compatible with the one-temperature SHTC system (12). Even if we do that, however, system (23) stays more complex than (12). The reason for that can be seen in the derivation of the models—while GENERIC model can alternatively be derived using two Lagrange$\rightarrow$Euler transformations [Eq. (18] are essentially two Euler equations derived by Hamilton’s principle, each of them relying on one transformation, see [22]), SHTC employs just one Lagrange$\rightarrow$Euler transformation. As each of the mappings brings inertial terms in the respective momentum equation, the double hydrodynamic (GENERIC) equations are expected to have more convective terms than the SHTC equations.

At the moment, we cannot prove the well-posedness of system (23) via its symmetrisation as it can be done for the SHTC system (12). We hope to clarify this question in the future.

4 Reduction and comparison of SHTC and GENERIC

A few more comments should now be made about Eq. (23). The SHTC model (12) as well as many other models work with one entropy. This is perfectly justifiable as the two components are likely to have nearly equal temperatures in most cases. The system (23) therefore might seem too complex in this respect. We understand the system as an intermediate step in derivation of other systems. We now need to reduce the model to one entropy, both for the sake of comparison and simplification of the overly complex system. Namely, we assume $\Delta s$ is no longer a state variable, but a function of the other variables, and therefore, the total energy does not explicitly depend on it. We thus have

$$\begin{aligned} E_{\Delta s}=0, \end{aligned}$$

(24)

which means that $E_{\Delta s} = \frac{\rho _1 - \rho _2}{\rho }\left( E_{s_1} - E_{s_2} \right) =0$ and consequently $T_1 = E_{s_1} = E_{s_2} = T_2$, which means that the temperatures of the two constituents are equal. Therefore, the restriction to only the overall entropy is possible only if the two constituents of the mixture have the same temperature. This is not satisfied only in rather extreme cases of homogeneous mixtures like electrons and ions in cold plasma [52]. Using results from [22] for a binary mixture of two ideal gases with the same atomic masses m, we obtain that (24) holds if

$$\begin{aligned} \Delta s = \frac{k_B}{m} \ln \left( \frac{\rho }{\rho _1}-1\right) , \end{aligned}$$

(25)

where $k_B$ is the Boltzmann constant. The resulting system (or more specifically its underlying bracket) does not satisfy the Jacobi identity.⁵ Therefore, we have left the Hamiltonian/GENERIC formalism. The resulting one-temperature model reads

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 E_{m_i}) - \partial _iE_{w_i}, \end{aligned}$$

(26a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho E_{m_i}), \end{aligned}$$

(26b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i E_{\rho } - \rho _1 \partial _i E_{\rho _1} - s\partial _i E_s - m_j \partial _i E_{m_j} - \partial _j (m_i E_{m_j}) \end{aligned}$$

(26c)

$$\begin{aligned}&+ E_{w_j}\partial _i w_j - \partial _j (w_i E_{w_j}) , \nonumber \\ \frac{\partial w_i}{\partial t} =&- \partial _i E_{\rho _1} -E_{m_j} \partial _j w_i - w_j \partial _i E_{m_j} \boxed {-\Delta s \partial _i E_s } \end{aligned}$$

(26d)

$$\begin{aligned}&\boxed { + \frac{\rho }{\rho _1 (\rho -\rho _1)} \left( \partial _i \frac{m_j}{\rho } - \partial _j \frac{m_i}{\rho } \right) E_{w_j} }\nonumber \\&\boxed {+ \frac{1}{\rho _1} (\partial _i w_j - \partial _j w_i)E_{w_j} } \nonumber \\&\boxed {+ \frac{\rho }{\rho _1 (\rho -\rho _1)} \left( \partial _j \frac{\rho _1 w_i}{\rho } - \partial _i \frac{\rho _1 w_j}{\rho } \right) E_{w_j}} - \frac{1}{\tau }E_{w^i}, \nonumber \\ \frac{\partial s}{\partial t} =&-\partial _i(s E_{m_i}) \boxed {-\partial _i (\Delta s E_{w_i})}+\frac{1}{\tau }\frac{1}{E_s}(E_{{\textbf{w}}})^2. \end{aligned}$$

(26e)

This is a two-fluid model with one temperature derived from the Liouville equation only through projections and assuming $E_{\Delta s} = 0$, which is equivalent to $\Delta s$ maximising the entropy. The total mass, momentum, and the total energy are conserved by Eqs. (23) and (26).

System (26) is now comparable to (12), once again differing by the additional boxed terms. The Liouville equation leads to the SHTC equations extended by extra terms that express self-advection of the relative velocity field ${\textbf{w}}$ and extra advection of total entropy by that field. This difference is demonstrated below.

Note that in case of isothermal models, i.e., when both $\Delta s$ and s are neglected, only the three last boxed terms in (26d) remain. These represent the “mechanical” differences between the two models and as they are present in the simplest possible setting, we view them as in some sense fundamental. We now focus on their effects.

Note that the models (12) and (26) are still rather complex, keeping two velocities (or more precisely one momentum and the velocity difference), unlike many other models, which work with one velocity or momentum and express the mixing through diffusion fluxes. Bearing in mind that viscosity and heat conductivity are not taken into account, the applicability of such models is limited, even though similar systems are indeed studied, for instance, in the case of superfluids, see [53, 54]. We therefore reduce the models further, namely passing to a one-velocity model, to get closer to the standard theory. Furthermore, this simplification shall highlight the effects of self-advection of ${\textbf{w}}$ which is contained in the difference between SHTC and GENERIC models.

Assuming that the dynamics of the ${\textbf{w}}$ field is fast (relaxation parameter $\tau$ sufficiently small), solutions to the full systems (12), (26) should be close to solutions to reduced systems without ${\textbf{w}}$ as a state variable. Note that in the reduction above, where $\Delta s$ was reduced, we assumed that its effect (or the effect of temperature differences of the two constituents) is completely lost and has no effect. This was different from the current situation where we also assume that the velocity difference becomes negligible, but we want to keep at least some of its effects within the model. That means that before eliminating the equation for ${\textbf{w}}$, we need to extract some information from it. One way to carry out that reduction is asymptotic analysis [27]. Here we follow another way, called the Dynamic Maximum Entropy reduction (DynMaxEnt), which is based on the geometric character of the evolution equations.

4.1 DynMaxEnt reduction of GENERIC

DynMaxEnt is motivated by contact geometry, and it is typically compatible with asymptotic analysis [22, 55, 56]. Let us denote the energetic conjugate variables as $\rho _1^{\dagger }=E_{\rho _1}$, $\rho ^{\dagger }=E_{\rho }$, ${\textbf{m}}^{\dagger }=E_{{\textbf{m}}}$, ${\textbf{w}}^{\dagger }=E_{{\textbf{w}}}$, and $s^{\dagger }=E_{s}$. The DynMaxEnt reduction of ${\textbf{w}}$ is carried out in these steps: (i) Set ${\textbf{w}}$ to its maximum entropy (MaxEnt) value [36] (here ${\textbf{w}}=0$), which corresponds to the minimum of energy (13), (ii) calculate ${\textbf{w}}^{\dagger }$ from the evolution equation of ${\textbf{w}}$, and (iii) plug the calculated ${\textbf{w}}$ and ${\textbf{w}}^\dagger$ into the remaining equations.

From Eq. (26d) we get that

$$\begin{aligned} \tau \Gamma = - ({\mathbb {I}} - \alpha \Omega ){\textbf{w}}^{\dagger }, \end{aligned}$$

(27)

where

$$\begin{aligned} \Gamma = \nabla \rho _1^{\dagger } + \Delta s \nabla s^{\dagger }, \quad \Omega _{i,j} = \partial _i m_j^{\dagger } - \partial _j m_i^{\dagger }, \quad \text {and}\quad \alpha = \frac{\tau \rho }{\rho _1(\rho -\rho _1)}. \end{aligned}$$

(28)

Denoting $\Theta = ({\mathbb {I}} - \alpha \Omega )$, we obtain a relation for ${\textbf{w}}^\dagger$,

$$\begin{aligned} {\textbf{w}}^{\dagger } = - \tau \Theta ^{-1} \Gamma , \end{aligned}$$

(29)

that is to be substituted into the remaining equations (for $\rho$, $\rho _1$, and ${\textbf{m}}$). By introducing quantities

$$\begin{aligned} a = -\alpha (\partial _1m_2^{\dagger } - \partial _2m_1^{\dagger }),\, b = -\alpha (\partial _1m_3^{\dagger } - \partial _3m_1^{\dagger }), \,\text {and}\, c = -\alpha (\partial _2m_3^{\dagger } - \partial _3m_2^{\dagger }), \end{aligned}$$

(30)

which are proportional to the overall vorticity, matrix $\Theta$ can be rewritten as

$$\begin{aligned} \Theta = \begin{pmatrix} 1 &{} a &{} b \\ -a &{} 1 &{} c \\ -b &{} -c &{} 1 \end{pmatrix}. \end{aligned}$$

(31)

Moreover,

$$\begin{aligned} \det (\Theta )&= 1+a^2+b^2+c^2> 0, \ \ \ \Theta > 0, \text { and}\\ \Theta ^{-1}&= \frac{1}{\det (\Theta )} \begin{pmatrix} 1 + c^2 &{} -a-bc &{} -b+ac \\ a-bc &{} 1 + b^2 &{} -c-ab \\ b+ac &{} c-ab &{} 1 + a^2 \end{pmatrix} \approx \begin{pmatrix} 1 &{} -a &{} -b \\ a &{} 1 &{} -c \\ b &{} c &{} 1 \end{pmatrix} {\mathop {=}\limits ^{\text {def}}} \overline{\Theta ^{-1}}, \end{aligned}$$

which is an approximate inverse of matrix $\Theta$ in the regime of low overall vorticity. Matrices $\Theta , \Theta ^{-1}, \overline{\Theta ^{-1}}$ are positive definite because their symmetric parts are positive definite although the eigenvalues of $\Theta$, $\{1, 1\pm \sqrt{-a^2-b^2-c^2} \}$, are not all real (bearing in mind that the matrices are not symmetric).

System of Eq. (26) is then reduced to

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 m_i^{\dagger }) + \nabla \cdot \underbrace{ \left( \tau \Theta ^{-1} \Gamma \right) }_{=-{\textbf{J}}}, \end{aligned}$$

(32a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho m_i^{\dagger }) , \end{aligned}$$

(32b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i \rho ^{\dagger } - \rho _1 \partial _i \rho _1^{\dagger } - s\partial _i s^{\dagger } - m_j \partial _i m_j^{\dagger } - \partial _j (m_i m_j^{\dagger }) \end{aligned}$$

(32c)

$$\begin{aligned} \frac{\partial s}{\partial t} =&-\partial _i(s m_i^{\dagger }) + \nabla \cdot \left( \Delta s \tau \Theta ^{-1} \Gamma \right) + \frac{\tau }{s^{\dagger }} \left( \Theta ^{-1} \Gamma \right) ^{2}, \end{aligned}$$

(32d)

which no longer contains ${\textbf{w}}$ as a state variable.

Let us now discuss the properties of this reduced system of equations. Firstly, entropy is produced because the right-hand side of (32d) consists of divergence terms and positive terms. Secondly, energy is conserved up to the first order in $\delta = \Theta ^{-1}-{\mathbb {I}}$. Finally, Eq. (32a) can be interpreted as advection of $\rho _1$ by the velocity and as diffusion of $\rho _1$ with a vorticity-dependent non-symmetric diffusion matrix. When using the approximate inverse $\overline{\Theta ^{-1}}$ and neglecting the entropies (the isothermal case), the flux ${\textbf{J}}$ becomes

$$\begin{aligned} {\textbf{J}}\approx -\tau \nabla \rho _1^\dagger +\tau \alpha \varvec{\omega }\times \nabla \rho ^\dagger _1, \end{aligned}$$

where $\varvec{\omega }=\nabla \times {\textbf{v}}$ is the overall vorticity. The flux then consists of two terms, one proportional to the gradient of chemical potential and the other perpendicular to that gradient and the vorticity.

It is also noteworthy that the GENERIC system shares many similarities with Extended Rational Thermodynamics (RET) on multiple levels of description. If we stay in the isothermal setting for the sake of comparison, our model is compatible with that from [4], which has been compared with RET, namely [57]. There are no significant difference between the two approaches, as far as two velocities are kept in the model. Once the relative velocity relaxes in its quasi-equilibrium, a difference appears in the possible curl dependence of the diffusion matrix, which was not found in [57]. Outside of the isothermal regime, when one temperature (or entropy) is in the model, maximisation of entropy (or, alternatively the Jacobi closure) restricts the possible thermodynamics quite a lot and the resulting model is then different from [57]. When we keep both the temperatures in the model, [57] has no analogue. Moreover, similar vorticity-dependent terms are discussed in [58] in the case of rotating frames, albeit also in the laboratory frame. Here, we show that the vorticity-dependent terms are present even in non-rotating frames.

We shall study the effects of the latter term in flux ${\textbf{J}}$ later in this section, but first, let us show how the reduction proceeds in the case of usual SHTC equations.

4.2 DynMaxEnt reduction of SHTC

Similarly as in the case of GENERIC, DynMaxEnt reduces the SHTC Eq. (12) to

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 m_i^{\dagger }) + \nabla \cdot \underbrace{\left( \tau \nabla \rho _1^{\dagger } \right) }_{=-{\tilde{{\textbf{J}}}}}, \end{aligned}$$

(33a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho m_i^{\dagger }) , \end{aligned}$$

(33b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i \rho ^{\dagger } - \rho _1 \partial _i \rho _1^{\dagger } - s\partial _i s^{\dagger } - m_j \partial _i m_j^{\dagger } - \partial _j (m_i m_j^{\dagger }) , \end{aligned}$$

(33c)

$$\begin{aligned} \frac{\partial s}{\partial t} =&-\partial _i(s m_i^{\dagger }) + \frac{\tau }{s^{\dagger }} \left( \nabla \rho _1^{\dagger } \right) ^{2}. \end{aligned}$$

(33d)

This model has similar features as model (32).

The main difference between GENERIC and SHTC for binary mixtures is the self-advection of ${\textbf{w}}$. In the following section, we confine ourselves to the isothermal case to highlight this difference.

These are the results of DynMaxEnt reduction. Similar results can be, however, obtained by other reductions, for instance, the above-mentioned asymptotic expansion. However, if applied to the first order only, this reduction reduces both SHTC and GENERIC models into (33). If we want the vorticity-dependent terms to be kept in the GENERIC model, one needs to go up to the second order. That, however, adds other terms, so DynMaxEnt with the linearised $\overline{\Theta ^{-1}}$ gives a result between the first- and second-order asymptotic reduction.

4.3 The isothermal regime in two dimensions

The reduction of both the SHTC and GENERIC models [(33), (32)] to isothermal case (dropping all terms with the entropy) leads to

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&-\partial _i (\rho _1 m_i^{\dagger }) + \nabla \cdot \left( \tau \Theta ^{-1} \nabla \rho _1^{\dagger } \right) , \end{aligned}$$

(34a)

$$\begin{aligned} \frac{\partial \rho }{\partial t} =&-\partial _i (\rho m_i^{\dagger }) , \end{aligned}$$

(34b)

$$\begin{aligned} \frac{\partial m_i}{\partial t} =&-\rho \partial _i \rho ^{\dagger } - \rho _1 \partial _i \rho _1^{\dagger } - m_j \partial _i m_j^{\dagger } - \partial _j (m_i m_j^{\dagger }) , \end{aligned}$$

(34c)

where the difference between the two models is encoded into the “diffusion matrix” $\Theta ^{-1}$. Next, we linearise the “diffusion matrix” $\Theta ^{-1}$ to $\overline{\Theta ^{-1}}$ and restrict ourselves to two dimensions, which gives

$$\begin{aligned} \Theta ^{-1}\approx \begin{pmatrix} 1 &{} -a \\ a &{} 1 \end{pmatrix} \end{aligned}$$

(35)

with

$$\begin{aligned} a&= 0,&\text {for SHTC,} \end{aligned}$$

(36)

$$\begin{aligned} a&= - \alpha \left( \partial _1\left( \frac{m_2}{\rho }\right) - \partial _2\left( \frac{m_1}{\rho }\right) \right) = -\alpha \textrm{curl}\left( \frac{{\textbf{m}}}{\rho }\right)&\text {for GENERIC.} \end{aligned}$$

(37)

Let us now interpret the quantities a and $\alpha$. From the definition (28) it follows that $\alpha \sim \frac{\tau }{\rho }$, the units of $\alpha$ are thus seconds, and $\alpha$ represents the microscopic time scale due to the relative velocity ${\textbf{w}}$, $t_{\text {micro}}$. The units of the vorticity $\Omega$ are $s^{-1}$ and thus the vorticity represents the macroscopic time scale related to the overall vortices, $t_{\text {macro}}$. Quantity a represents the ratio of the microscopic relative velocity time scale and the macroscopic vorticity time scale, $a \sim t_{\text {micro}}/t_{\text {macro}}$.

In order to compare both approaches quantitatively, we have to provide an energy functional and a formula for the relaxation parameter. In the isothermal case the energy can be substituted with the free energy, see [22]. Therefore, we choose a simplified free energy of two ideal gases

$$\begin{aligned} E = \frac{{\textbf{m}}^2}{2\rho } + \frac{\kappa }{\alpha } \left( \rho _1 \log (\rho _1) - (\rho _1 - \rho ) \log (\rho -\rho _1)\right) , \end{aligned}$$

(38)

where $\kappa$ and $\alpha$ are constants. Furthermore, the choice of $\alpha$ also defines the relaxation parameter $\tau$ through relation (28).

We now write (34) in a compact divergence form as

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho } - \tau \Theta ^{-1}\nabla E_{\rho _1}\right) , \end{aligned}$$

(39a)

$$\begin{aligned} \frac{\partial \rho }{\partial t}&= -\textrm{div} ({\textbf{m}}), \end{aligned}$$

(39b)

$$\begin{aligned} \frac{\partial m_i}{\partial t}&= - \textrm{div}\left( \frac{m_i {\textbf{m}}}{\rho } + pe_i \right) , i=1,2, \end{aligned}$$

(39c)

where the pressure p stands for

$$\begin{aligned} p = -E + \rho \frac{\partial E}{\partial \rho } + \rho _1 \frac{\partial E}{\partial \rho _1} + {\textbf{m}}\cdot \frac{\partial E}{\partial {\textbf{m}}}. \end{aligned}$$

(40)

Even more explicitly, we obtain that

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \textrm{div} \left( \tau \Theta ^{-1}\nabla \left( \frac{\kappa }{\alpha }(\log (\rho _1)-\log (\rho -\rho _1)) \right) \right) ,\end{aligned}$$

(41a)

$$\begin{aligned} \frac{\partial \rho }{\partial t}&= -\textrm{div} ({\textbf{m}}), \end{aligned}$$

(41b)

$$\begin{aligned} \frac{\partial m_i}{\partial t}&= - \textrm{div}\left( \frac{m_i {\textbf{m}}}{\rho } + \frac{\kappa }{\alpha }\rho \right) , i=1,2. \end{aligned}$$

(41c)

The pressure can be rewritten as $p= \frac{\kappa }{\alpha }\rho$. Evaluating gradients in the rightmost term of (41a) gives

$$\begin{aligned} \textrm{div} \left( \tau \Theta ^{-1}\nabla \left( \frac{\kappa }{\alpha }(\log (\rho _1)-\log (\rho -\rho _1)) \right) \right)&= \textrm{div} \left( \tau \Theta ^{-1} \nabla \rho _1 - \tau \Theta ^{-1} \frac{\rho _1}{\rho } \nabla \rho \right) \nonumber \\&= \textrm{div} \left( \kappa \Theta ^{-1} \rho \nabla \left( \frac{\rho _1}{\rho } \right) \right) . \end{aligned}$$

(42)

The system of equations then simplifies to

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho } - \kappa \Theta ^{-1} \rho \nabla \left( \frac{\rho _1}{\rho } \right) \right) , \end{aligned}$$

(43a)

$$\begin{aligned} \frac{\partial \rho }{\partial t}&= -\textrm{div} ({\textbf{m}}), \end{aligned}$$

(43b)

$$\begin{aligned} \frac{\partial m_i}{\partial t}&= - \textrm{div}\left( \frac{m_i {\textbf{m}}}{\rho } + \frac{\kappa }{\alpha }\rho \right) , \ i=1,2, \end{aligned}$$

(43c)

which we solve both analytically and numerically.

4.4 Analytical comparison

In this section, we illustrate the difference between SHTC and GENERIC formulations by analytical means, solving the simplified system (43). Equation (43a) gets within the SHTC model the following form,

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 - \kappa \frac{\rho _1}{\rho } \Delta \rho - \kappa \nabla \left( \frac{\rho _1}{\rho } \right) \cdot \nabla \rho . \end{aligned}$$

(44)

On the other hand, within the GENERIC model, we obtain

$$\begin{aligned} \frac{\partial \rho _1}{\partial t} =&- \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 - \kappa \frac{\rho _1}{\rho } \Delta \rho - \kappa \nabla \left( \frac{\rho _1}{\rho } \right) \cdot \nabla \rho \nonumber \\&+ \kappa \left( \frac{\partial a}{\partial y}\frac{\partial \rho _1}{\partial x} - \frac{\partial a}{\partial x} \frac{\partial \rho _1}{\partial y}\right) - \kappa \frac{\rho _1}{\rho }\left( \frac{\partial a}{\partial y}\frac{\partial \rho }{\partial x} - \frac{\partial a}{\partial x} \frac{\partial \rho }{\partial y}\right) \nonumber \\&- \kappa \nabla \left( \frac{\rho _1}{\rho } \right) \cdot \left( -a \frac{\partial \rho }{\partial y}, a \frac{\partial \rho }{\partial x} \right) ^{\top } . \end{aligned}$$

(45)

Realising that the Eqs. (43b) and (43c) are not coupled with (43a), we first search for stationary ${\textbf{m}}$ and $\rho$, solving Eqs. (43b) and (43c), and then for a non-stationary $\rho _1$, solving Eq. (43a). The following functions indeed represent stationary solutions,

$$\begin{aligned} \rho&= 1, \end{aligned}$$

(46)

$$\begin{aligned} {\textbf{v}}&= (v_1,v_2) = (10 \sin (y),0), \end{aligned}$$

(47)

where ${\textbf{v}}$ is the velocity field defined by ${\textbf{m}}=\rho {\textbf{v}}$. Plugging these solutions into Eqs. (44) and (45), we get

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 \quad \text {for SHTC}, \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 + \kappa \left( \frac{\partial a}{\partial y}\frac{\partial \rho _1}{\partial x} - \frac{\partial a}{\partial x} \frac{\partial \rho _1}{\partial y}\right) \quad \text {for GENERIC}. \end{aligned}$$

(49)

We now recall the vorticity diffusion ratio a, that for GENERIC takes the form

$$\begin{aligned} a = -\alpha (\partial _x v_2 - \partial _y v_1) = \alpha \partial _y v_1. \end{aligned}$$

(50)

As a result, $\partial _x a = 0$ and $\partial _y a = \alpha \partial _{yy} v_1 = - 10 \alpha \sin (y) = - \alpha v_1$. Plugging this into Eq. (49) yields

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 - \kappa \alpha v_1 \frac{\partial \rho _1}{\partial x}. \end{aligned}$$

(51)

Since $v_1$ does not depend on x and $v_2=0$, we get

$$\begin{aligned} \frac{\partial \rho _1}{\partial t}&= - (1 + \kappa \alpha ) \textrm{div} \left( \rho _1 \frac{{\textbf{m}}}{\rho }\right) + \kappa \Delta \rho _1 . \end{aligned}$$

(52)

In summary, both SHTC and GENERIC models contain advection and diffusion of $\rho _1$. The advection in GENERIC, however, has a coefficient $1+\kappa \alpha$ while in SHTC the coefficient equals 1, even though the velocity field is identical in both cases. This is an effect of the vorticity-dependent part of the diffusion matrix in the reduced GENERIC model. Let us now examine these effects in more detail numerically.

4.5 Numerical comparison

We now solve the reduced system (43) numerically in order to illustrate the differences between the reduced SHTC and GENERIC systems. The numerical implementation is realised in the software library PyPDE [59], using ADER-WENO [27, 60] method for solution to equations in the form:

$$\begin{aligned} \frac{\partial {\textbf{q}}}{\partial t}+\nabla {\textbf{F}}({\textbf{q}}, \nabla {\textbf{q}})+B({\textbf{q}}) \cdot \nabla {\textbf{q}}={\textbf{S}}({\textbf{q}}), \end{aligned}$$

(53)

where ${{\textbf {q}}}$ is the vector of state variables, S represents the vector of source terms, ${\textbf{F}}$ are the conservative terms, and B the non-conservative terms. In particular, for system (43) we have $B={{\textbf {S}}}=0$.

Fig. 1

Steady laminar flow of a binary mixture with periodic boundary conditions. The density of the first component is diffused and advected by the flow, for three times (from left to right $t = 0,T_{\textrm{final}}/2,T_{\textrm{final}}$) under the SHTC model (top), and the GENERIC model (middle). The bottom line shows one-dimensional density profiles of the first component along x-axis at the middle of the y-axis

Fig. 2

Time evolution of the difference between $\rho _1$ in SHTC model and the GENERIC model, $\rho _1^{SHTC} - \rho _1^{GENERIC}$ for initial data of the Gersho vortex. We present six times, in the reading order, $t = 0,1/5T_{\textrm{final}},2/5T_{\textrm{final}}, 3/5T_{\textrm{final}},4/5T_{\textrm{final}},T_{\textrm{final}}$)

The presented examples are solved with the scheme of third order and the Rusanov flux. For laminar flow and the Gresho vortex, periodic and transitive boundary conditions are applied, respectively. Parameters are chosen as $\kappa =1$ and $\alpha =1$ in Eq. (37). Computational examples run till the final time $T_{\textrm{final}} = 0.5$ in 100 time steps on a $100\times 100$ mesh. Let us now discuss the laminar channel flow.

4.5.1 Laminar channel flow

The first example corresponds to the setting in Sect. 4.4. The computation domain is $\Omega =[0, 2\pi ] \times [-\pi /2, 3\pi /2]$, and initial conditions are

$$\begin{aligned} \rho _1 = 0.5 + 0.25 \sin (x), \end{aligned}$$

(54)

$\rho$ and ${\textbf{v}}$ being prescribed by formulas (46).

Figure 1 shows the numerical solution to the system (43). Similar profiles of SHTC and GENERIC solutions at times $T_{\textrm{final}}$ (Fig. 1 top-right) and $T_{\textrm{final}}/2$ (Fig. 1 middle-bottom), respectively, indicate that advection within the reduced GENERIC model is (with the chosen material parameters $\kappa$ and $\alpha$) twice faster than in the reduced SHTC model.

4.5.2 Gresho vortex

The second computational example is based on the Gresho vortex for the Euler equation, where the centrifugal force is balanced by the pressure gradient, resulting in a stable time-independent vortex [61]. In our case, the mixture density plays the role of the pressure, as can be from Eq.  (43c).

Let the computation domain be a square $\Omega =[0, 1] \times [0,1]$. Initially, we prescribe a Gresho body vortex outside of the origin,

$$\begin{aligned} \rho&= \left\{ \begin{array}{ll} 5 + \frac{25}{2} r^{2}, &{} \quad r<0.2 \\ 9 -4 \ln (0.2) + 4 \ln (r) -20 r+ \frac{25}{2} r^2, &{} \quad 0.2 \leqslant r \leqslant 0.4 \\ 3 + 4 \ln (2), &{} \quad 0.4 < r \end{array}\right. , \end{aligned}$$

(55)

$$\begin{aligned} \rho _1&= 2.5 , \end{aligned}$$

(56)

$$\begin{aligned} {\textbf{v}}&= {\varvec{e}}_{\varphi }\left\{ \begin{array}{ll} 5 r, &{} \quad r<0.2 \\ 2-5 r, &{} \quad 0.2 \leqslant r \leqslant 0.4 \\ 0, &{} \quad 0.4 < r \end{array}\right. , \end{aligned}$$

(57)

where $r=\sqrt{(x-0.5)^{2}+(y-0.5)^{2}}$ and ${\varvec{e}}_{\varphi }=\left( -(y-0.5),x-0.5\right) /r$.

Figure 2 shows the time evolution of the difference in the density of the first component $\rho _1^{SHTC} - \rho _1^{GENERIC}$. We can see that the vorticity-dependent diffusion matrix within the reduced GENERIC model causes extra interaction between the vortex and $\rho _1$. Field $\rho _1$ now flows partly in the direction perpendicular to the (radial) gradient of chemical potential, that is also in the azimuthal direction. Those extra terms break the radial symmetry of the solution.⁶ Comparison with experimental data is, however, out of scope of the present paper.

5 Conclusion

The main goal of this manuscript is to compare two recent frameworks of continuum thermodynamics, the SHTC equations and GENERIC, in the context of binary homogeneous mixtures. Using GENERIC, we can start from the Liouville equation and obtain equations for binary mixtures with additional terms that are not present in the SHTC framework, namely the terms containing the self-advection of the relative velocity.

These terms can be analysed on simplified versions of the SHTC and GENERIC models, letting the relative velocity ${\textbf{w}}$ relax to a quasi-equilibrium value. Within GENERIC, we obtained a vorticity-dependent diffusion matrix, which is not symmetric. Consequently, the density of the first constituent flows not only against the gradient of the chemical potential but also in the direction perpendicular to the gradient and the vorticity pseudovector. This implies, for instance, different advection rates in the two models or symmetry breaking of the solution in the presence of vorticity, see Figs. 1 and 2. The result is interesting also from a more theoretical point of view. The diffusion matrix needs to be a matrix of positive definite bi-linear functional to ensure entropy production. However, it does not need to be symmetric positive definite. Indeed, our model has a non-symmetric diffusion matrix and shows that the assumption of symmetry might not always be suitable. As the SHTC model does not incorporate these effects, it might, albeit being successfully used, be extended in the setting of mixtures.

Apart from the terms with self-advection of the relative velocity, the mixture models can have two entropies, the overall entropy, or no entropy at all. The first option is observed, for instance, in cold plasma, where light electrons and heavy ions absorb electromagnetic energy with different efficiency. Second possibility assumes that the components have the same temperature, and the third option is isothermal. The first option (two entropies) has uniquely determined Poisson bracket, that is derived from the Liouville equation. The second option (one entropy) is, however, much more difficult in the context of Hamiltonian mechanics. We have shown that there is a family of Hamiltonian binary mixture models with only the overall entropy that still contains the self-advection terms of the relative velocity while satisfying the Jacobi identity. The entropy difference $\Delta s$ is given by solutions to (59), for example by formulas (60a), (60b), albeit we have also shown the difficulties and limitations of the derivation. Finally, the isothermal case then again has a unique Poisson bracket.

The structure of the SHTC model (12), which does not contain the self-advection terms, is also Hamiltonian (considering only the reversible part) and furthermore admits constant $\Delta s$ (without violating Jacobi identity), unlike the GENERIC model.

In future, we would like to compare the results with 2D experimental results on diffusion in the presence of vorticity. Furthermore, it remains to generalise the analysis to multiphase mixtures, taking volume fractions among the state variables, as well as adding viscosity and thermal conduction into the model. Finally, we shall explore the possible presence of similar vorticity terms in equations for superfluid helium-4 after the reduction to a Navier–Stokes-like form.

Reduction to only one entropy

In this section we comment on another way to reduce the system (23) to only the overall entropy s, eliminating $\Delta s$. Like in the method from Sect. 4, we assume that $\Delta s$ is no longer a state variable, but a function of other state variables. Instead of focusing on Eq. (23), we work with the bracket (17). The elimination consists of two steps. First, only energy functionals independent of $\Delta s$ are considered, and secondly, the entropy difference is expressed in terms of the remaining state variables, $\Delta s(\rho _1,\rho ,s,{\textbf{m}},{\textbf{w}})$ while keeping Jacobi identity valid. The second step is called a Jacobi closure [62]. The whole bracket (20) of course satisfies the Jacobi identity because it is just a transformation of the Poisson bracket (17), and if we drop the lines with s and $\Delta s$, it still satisfies Jacobi identity.⁷ Such bracket with no entropies is suitable for isothermal mixtures, as shown in [63]. Here, however, we aim at non-isothermal mixtures, keeping s among the state variables.

Since $\Delta s$ is no longer a state variable, the total energy does not explicitly depend on it, so we once again have

$$\begin{aligned} E_{\Delta s}=0, \end{aligned}$$

(58)

and therefore like in Sect. 4 the temperatures of the two constituents are equal.

The last four lines of (20), which generate Eq. (23f), disappear, but the fifth line of (20) still contains $\Delta s$, which translates to the boxed terms in Eq. (23e) and in the first line of (23d). Using a program [39], we now check whether there exists an admissible formula for $\Delta s$ such that the remaining terms of (20) (without the last four lines) fulfil Jacobi identity. We first assume a general dependence $\Delta s(\rho ,\rho _1,{\textbf{m}},{\textbf{w}},s)$ and get a necessary condition that it does not depend on ${\textbf{m}}$ to satisfy the Jacobi identity. Then we consider $\Delta s$ independent of ${\textbf{m}}$ which yields that $\Delta s$ must be independent of ${\textbf{w}}$ as well. Choosing such entropy difference, we get that $\Delta s$ must be 0-homogeneous, that is $\Delta s = \Delta s \left( \varphi , \psi \right)$, where $\varphi = \rho /s$ and $\psi = \rho _1/s$. The next iteration of this procedure gives the condition

$$\begin{aligned} \partial _{\psi }\Delta s - \Delta s \left( \varphi \partial _{\varphi } \Delta s + \psi \partial _{\psi } \Delta s \right) = 0, \end{aligned}$$

(59)

particular solution of which is

$$\begin{aligned} \Delta s = \frac{\varphi _0-\varphi }{\varphi _0\psi - \varphi \psi _0} \end{aligned}$$

(60a)

for arbitrary parameters $\varphi _0, \psi _0$. Note, however, that this class does not contain all solutions. Finally, using again the program [39], it becomes necessary that

$$\begin{aligned} \psi _0=0 \quad \text{ or }\quad \psi _0=\varphi _0 \end{aligned}$$

(60b)

in order that the Jacobi identity be fulfilled. Even though we have not studied all possible solutions of (59), we have found a family of reductions satisfying Jacobi identity. Neither the constant solution, nor (25), however, do not belong to that family.

To sum up, the above choice of $\Delta s$ [conditions (60a) and (60b)] leads to a simplified Poisson bracket which fulfils the Jacobi identity. This condition is, however, not unique and compatible with the initial assumption $E_{\Delta s} = 0$. In terms of equations, system (23) then simplifies to (26) where $\Delta s$ is a function of $\rho /s$ and $\rho _1/s$. Similarly to (26), this is a two-fluid model with one temperature derived from the Liouville equation only through projections and a Jacobi closure. The total mass, momentum, and the total energy are conserved by Eqs. (23) and (26). Moreover, the model is Hamiltonian and fulfils the Jacobi identity.

There is also another way to obtain a Hamiltonian model with only the overall entropy. If we first drop the second, third and fourth lines of (20), which represent the difference between the SHTC evolution and the evolution stemming from the Liouville equation, then, following the above procedure based on the program [39], we get that the Jacobi identity is satisfied as long as $\Delta s$ is constant. In other words, if we drop the three boxed terms not containing $\Delta s$, we can leave the others and reduce the model to single entropy s as long as $E_{\Delta s}=0$ and $\Delta s$ is constant. If actually $\Delta s = 0$, we obtain the SHTC equations as a special case. Thus, the SHTC model is Hamiltonian, and stays Hamiltonian even after adding the boxed terms containing constant $\Delta s$. However, it is derived from the Liouville equation not just by projections, but also by the further neglection of the boxed terms.