A Benders decomposition approach for planning home blood donations

Abstract

Blood donations are crucial for the health system. We consider the problem of planning blood donation services, where the donors are reached at home. The scope is to minimize the penalty for the unserved donors, while guaranteeing that the available resources for implementing the service are not exceeded and that the appointment preferences of the donors are met. We present an offline model for this setting, where the produced solution must be robust with respect to the availability of the donors, which is not known in advance and is managed in a stochastic way using scenarios. A Benders decomposition approach to solve this model is developed. The proposed algorithm is tested on real-life instances coming from the Milan department of the Associazione Volontari Italiani Sangue (AVIS).

1 Introduction

The availability of a sufficient blood supply is crucial for ensuring high-quality and fully-functional health services. Unfortunately, blood and its components are highly perishable: this forbids long term conservation and requires continuous donations by unpaid volunteers, as no successful artificial blood substitutes have been developed so far. Therefore, the policies used to implement and manage the so-called Blood Donation Supply Chain (BDSC) deeply affect the whole healthcare system. BDSC includes four main stages: collection, transportation, storage and final utilization (Pierskalla 2004). Collection consists of finding donors, checking them for eligibility, collecting donations and controlling the produced blood units (Lanzarone and Yalçındağ 2019). Transportation faces the problem of moving blood from where donations are made to the storage place. Storage deals with the blood conservation, considering that the shelf life of blood products is very limited. Final utilization consists of distributing blood units to end-users, but also of predicting the amounts needed from the different health facilities.

Collection is the most critical stage of the whole process and, relying on voluntary donors, it structurally suffers from data uncertainty (Rahmani 2019). Moreover, it is particularly vulnerable to pandemics. In fact, it was calculated that, due to the SARS-CoV-2 pandemic, the production of red blood cells in Italy in April 2020 was reduced by $36.4\%$ with respect to April 2019 (Centro Nazionale Sangue 2020). There were several concurrent reasons that caused this contraction: many donors became unavailable because they were infected; most places used as locations to perform blood donations (schools, churches, offices, clubs, $\ldots$) were shut down because of the pandemic; many donors were scared of reaching hospitals or donation centers, where they could potentially meet SARS-CoV-2 positive individuals (Gupta et al. 2020; Pagano et al. 2020). This supports the policy of relocating health services on the territory instead of concentrating them into hospitals or centers (Lanzarone and Matta 2012; Carello et al. 2018; Govindan et al. 2020; Regis-Hernández et al. 2020), which includes home blood donations (Doneda et al. 2023). The possibility to donate at home can be seen as an incentive: if donating becomes easier for the donors, more donors can be convinced to start (or re-start) donating and to become regular donors

For this reason, this paper is devoted to the presentation of models and algorithms for a home blood donation problem that arises in an urban context. We show that the problem exhibits an underlying network structure that can be exploited to efficiently solve it by a branch-and-cut algorithm based on Benders decomposition. The approach is tested on instances derived from real-life data. In the rest of this section, after a brief review of the existing literature on the blood supply chain and on blood donations, we describe our contribution and provide information and references on data and techniques we use.

1.1 Literature review

While the medical aspects of blood donation are very well-studied, the logistics of the blood supply chain has received less attention in the literature, if compared to other supply chains (Baş Güre et al. 2016, 2018b). Recent surveys can be found in (Beliën and Forcé 2012; Osorio et al. 2015; Pirabán et al. 2019). Starting from Millard (1959), where industrial inventory models were applied to blood collection, several papers considered the blood supply chain, also including vehicles and mobile donations. Gunpinar and Centeno (2016) use vehicles to create temporary blood collection sites in regions that may be far from a collection center. The problem of managing a fleet of vehicles to transport blood from temporary locations to the centers has been considered by Alfonso et al. (2015a), Gülizahinyazan et al. (2015), and Şahinyazan et al. (2015).

Scheduling problems arising in blood donations have also been investigated. Michaels et al. (1993) use simulation to compare donors scheduling strategies. Alfonso et al. (2012) analyze how different donor schedules and workforce planning strategies affect the efficiency of the system. A simulation-optimization approach for capacity planning and appointment scheduling is considered by Alfonso et al. (2015b). Baş Güre et al. (2018a) present a framework for scheduling appointments over a few weeks, considering both booked and non-booked donors, with the aim of balancing the production and reduce the queuing time. The approach was extended to stochastic arrivals by Yalçındağ et al. (2020). Finally, the problem of dimensioning a collection center based on the expected donors arrival patterns is studied by Testik et al. (2010).

However, the assumption that has been made so far in the blood collection literature is that the donors must come to the place of donation (either temporary or permanent) and not the other way around. Although the problem of collecting blood donations at home shares some aspects with the collection of biological samples from patients, which is a common practice in home care (Anaya-Arenas et al. 2021), home donations have been considered for the first time in the literature only recently (Doneda et al. 2023). The authors develop an appointment scheduling system for home donation, with a planning horizon of several weeks, taking into account donors preferences and balanced production. The problem is decomposed into three stages, that are sequentially solved: an offline procedure for selecting the appointments to be opened; an online phase for booking the appointments; an offline routing planner, where the routes are arranged. The online phase is required to obtain information on donors preferences, for which reliable statistical predictions are not available.

1.2 Our contribution

In this paper we consider a short time horizon (e.g., one week) and some statistical knowledge on donors availability and preferences can be exploited. This allows us to model the uncertainty using a set of scenarios that represents the availability of donors over the time horizon, thus deriving a fully offline mathematical model to handle home blood donation in an urban context. Using scenarios in order to manage data uncertainty, is a common approach, that has been already used in many contexts, including healthcare (Lanzarone et al. 2012; Guo et al. 2020). The proposed formulation represents the complex situation that a donation center faces, which includes: the assignment of appointments to donors; the presence of limited resources; the need to ensure some amounts of each blood type; the preferences of the donors and the uncertainty in the availability of the donors. To solve the proposed model, we develop an ad-hoc branch-and-cut (Padberg and Rinaldi 1991) algorithm, based on a Benders decomposition approach (Benders 1962). In particular, we show that an underlying network structure can be exploited to efficiently find violated Benders inequalities, if any.

Benders decomposition has been already proved to be effective in many fields, such as scheduling problems (Mattia et al. 2017), prevention of blackouts in power grids (Bienstock and Mattia 2007) and network design (Avella et al. 2007; Mattia 2012a, b, 2013; Mattia and Poss 2018). There also exist generalizations of this method (Hooker 2019), with application in operating room scheduling (Guo et al. 2020). Discovering and exploiting underlying structures in the solution of mixed integer programming problems, is also a well-known and successful technique. One possibility is to identify submatrices of the original constraint matrix that exhibit a combinatorial structure, that can be used to generate valid inequalities to strengthen the problem formulation. Inequalities from combinatorial structures include, among the others, clique, (lifted) cover, network flows-based (Achterberg and Raack 2010; Avella et al. 2013, 2021) and mod-2 inequalities (Avella et al. 2007; Arbib et al. 2017). Another possibility is to show that a given problem can be transformed into another one, for which efficient algorithms and theoretical results are available. Many applied problems have an underlying network structure that can be exploited, e.g., personnel scheduling (Mattia et al. 2017), pick-up and delivery (Bonomo et al. 2011), wireless network planning (Mannino et al. 2011), assignment and matching (Ahuja et al. 1993). Here we show that we can obtain Benders feasibility and optimality cuts by solving a min cost flow problem on a suitable graph. To our knowledge, this is the first time that this strategy has been used to tackle the home blood donation problem.

Data for the experiments come of the Milan department of the Associazione Volontari Italiani Sangue (AVIS), referred to as AVIS Milan. AVIS is the largest blood donors association in Italy, being responsible for the collection stage of a very large portion of the Italian blood supply chain (about 70% of the national blood demand). AVIS Milan manages about 50 whole blood donations per day and other few units produced by apheresis (AVIS 2020) and serves one of the largest hospitals in Milan, the Niguarda Hospital. This hospital must be replenished with a given amount of units for each blood type, which allows to set target levels for each planning period. It is worth remarking that this situation is common to several blood collection centers, thus making AVIS Milan and its setting of general validity in blood collection.

The rest of the paper is organized as follows. In Sect. 2 we describe the considered problem and present a first mathematical model. In Sect. 3 we provide theoretical results that allow to obtain a second model, based on Benders decomposition. The proposed solution approach is described in Sect. 4. In Sect. 5 we present the computational experience and discuss the results. Conclusions are given in Sect. 6.

2 The problem and the model

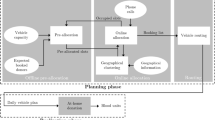
We address the problem of planning a home blood donation service over a given territory assigned to a single blood collection center, considering a fixed time horizon. Its main scope is to serve as many donors as possible, provided that some constraints on production and available resources are satisfied. We assume that the blood center is provided with blood storage facilities and vehicles, which are used to reach the donors at home. It collects the blood from regular blood donors, according to given appointments. Below we detail the considered setting, while an Integer Programming (IP) formulation for the problem is given in Sect. 2.2.

2.1 The considered setting

The territory corresponding to the donation center is partitioned into cells of similar size and population. Each cell is assigned to one vehicle. Each vehicle can make at most two tours in the cell (one in the morning and one in the afternoon), starting from the center and coming back to the center at the end of the route. Each tour is, then, associated with a cell, a vehicle, a day, a part of the day (morning or afternoon) and a set of service stops (donation slots) that can be assigned to the donors (one donor per slot). Therefore, each donation slot has a pre-assigned cell, vehicle, tour, part of the day and time window for the donation. The locations within the cell where the stops must occur (i.e., the actual route that the tour must follow), instead, are not pre-set and depend on the actual location of the donors assigned to the slots, if any.

Each donor can be assigned only to the slots that he/she likes, among those available for his/her cell. The routes are automatically determined given the appointments: each tour starts from the collection center, visits the donors in the appointment order for that tour and then goes back to the collection center. To go from location i to location j, the vehicle will follow an ij shortest path according to the current traffic conditions. The underlying assumption is that the visiting order has no critical effect on the total duration of the tours. This is true if the cells are small enough to guarantee that the travel time from any location i to any location j in the cell plus the donation time at j (which is a fixed time) does not exceed the duration slot.

As an example, consider the case of a cell that has at its disposal a single vehicle and consider a time horizon of one day. The vehicle can make at most one tour ($tour_1$) in the morning and at most one tour ($tour_2$) in the afternoon. Each tour contains three available stops, namely $slot^1_1, slot^1_2$ and $slot^1_3$ for $tour_1$ and $slot^2_1, slot^2_2$ and $slot^2_3$ for $tour_2$. Then, the total number of available slots is six, partitioned into two tours served by the same vehicle (tours are not time-overlapping as $tour_1$ is in the morning and $tour_2$ in the afternoon), that is, up to six donors living in the cell can potentially be served. Assume that there are four donors ($donor_1, \ldots , donor_4$) in the cell. Suppose that $donor_1$ likes only $slot^1_1$, $donor_2$ and $donor_3$ like all the available slots, while $donor_4$ likes $slot^1_1$ and $slot^2_1$. Consider the assignment $ass_1$: $donor_1$ assigned to $slot^1_1$; $donor_2$ assigned to $slot^2_2$, $donor_3$ assigned to $slot^1_2$, $donor_4$ assigned to $slot^2_1$. Assignment $ass_1$ corresponds to the activation of both $tour_1$ and $tour_2$. The route of $tour_1$ visits first $donor_1$ (assigned to $slot^1_1$) and then $donor_3$ (assigned to $slot^1_2$), before coming back to the center. The route of $tour_2$ visits first $donor_4$ and then $donor_2$. Consider now assignment $ass_2$: $donor_4$ assigned to $slot^1_1$; $donor_2$ assigned to $slot^1_2$, $donor_3$ assigned to $slot^1_3$, $donor_1$ not served, as no remaining slot matches the donor’s preferences. Assignment $ass_2$ corresponds to the activation of $tour_1$ only, whose route visits first $donor_4$, then $donor_2$ and finally $donor_3$. Hence, a tour can be seen as a set of slots (input), while the route that each tour must follow (possibly none) depends on the assignment of donors to slots (output).

Each tour needs some resources, the most important of which is the medical personnel, that is, a nurse and a physician are required to be on board of each vehicle. Therefore, at most a given percentage of the available tours can be activated. In our setting, it is enough to have one single constraint to limit the total number of activated tours over the considered time horizon. However, it is possible to impose further limits and side constraints on the tours (e.g., limiting the maximum number of vehicles that can simultaneously be routed), without affecting the theoretical results we present in Sect. 3. Since each tour is related to a very small portion of territory (cell), we assume that the working time of the onboard medical personnel, the fuel and the conservation time of the collected samples are never exceeded, independently of the actual assignment of the slots to the donors. We also suppose that the considered time windows always allow the vehicle to perform the donation and to reach the next donor or come back to the depot.

The center has a target level for each blood type that must be produced in the considered time horizon. Since the donors are unpaid, not serving a donor may discourage the donor from donating again. For this reason, when a donor is not served, a penalty cost must be paid and the corresponding penalty can be increased in the next round of assignments, so that the probability to serve that donor increases, as well. In principle, not all the donors may be available in the considered time horizon. Therefore, a set of scenarios is defined: in each scenario a given subset of the donors is supposed to be available and each scenario has an associated probability to happen. The problem consists of minimizing the mean penalty costs over the set of the considered scenarios, ensuring that the service does not exceeded the available resources and that, in each scenario, the prescribed amounts of blood are produced. Since the planning horizon (1 week) is much shorter than the shelf life of collected whole blood units (6 weeks), the blood amounts to be produced refer to the whole time horizon and there is no need to add production constraints for sub-periods as in Doneda et al. (2023).

2.2 The complete formulation

We consider a discrete time horizon T, where each $t \in T$ refers to a day of the week. Set B contains the blood types that must be produced (namely: A+, A−, B+, B−, AB+, AB-, 0+, 0−), while the set of all possible donors is denoted by J. Let R be the set of the tours and let I be the set of donation slots. For a slot i, we denote by v(i) the tour to which i belongs. Let $0\le \beta \le 1$ be the percentage of tours that can be activated, that is, due to limited resources, we can use only up to $\beta \mid R \mid$ tours.

We denote by $I_j \subseteq I$ the slots that are suitable for donor $j \in J$, based on his/her preferences and cell. A donor $j \in J$ is associated with a unique blood type, denoted by $b_j$. Let $J^b \subseteq J$ be the donors corresponding to blood type $b \in B$ and denote by $LB_b$ and $UB_b$, respectively, the minimum and maximum number of blood units of type $b \in B$ to be produced in the considered time horizon T, that is, the number of donors of type b to be served. A set S of possible scenarios is considered, each one with an associated probability $p_s$ to occur. In a scenario, a donor may or may not be willing to donate. The set of the donors willing to donate in scenario $s \in S$ are denoted by $J_s \subseteq J$. Let $w_j$ be the penalty to be paid if donor j is willing to donate, but not served.

Let $z_v$ be a variable taking value 1 if tour $v \in R$ has been selected and 0 otherwise. Since i belongs to v(i), if $z_{v(i)} = 1$, all slots j belonging to v(i) became available. Let $y^s_{ij}$ be a binary variable taking value 1 if donor $j \in J$ is assigned to slot $i \in I$ under scenario $s \in S$ and 0 otherwise. The problem can be modeled as in the complete formulation (CF) below.

$$\begin{aligned} \text{ CF } \quad&\min \sum _{s \in S} p_s \sum _{j \in J_s} w_j (1-\sum _{i \in I_j} y^s_{ij}) \nonumber \\&\sum _{{v \in R}} z_v \le \beta \mid R\mid \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{i \in I_j} y^s_{ij} \le 1{} & {} j \in J_s, s \in S \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j \in J_s: i \in I_j} y^s_{ij} \le z_{v(i)}{} & {} i \in I, s \in S \end{aligned}$$

(3)

$$\begin{aligned}&LB_b \le \sum _{j \in J^b} \sum _{i \in I_j} y^s_{ij} \le UB_b{} & {} b \in B, s \in S \nonumber \\&\textbf{z}\in \{0,1\}^{\mid R \mid }{} & {} \nonumber \\&y^s_{ij} \in \{0,1\}{} & {} i \in I_j, j \in J_s, s \in S \end{aligned}$$

(4)

The objective function to be minimized measures the expected penalty to be paid for not serving donors. In fact, if donor $j \in J_s$ is not served, then $\sum _{i \in I_j}y^s_{ij} = 0$ and cost $w_j$ is paid. Otherwise, there exists a unique slot i assigned to j, $\sum _{i \in I_j} y^s_{ij} = 1$ and no penalty for not serving j is considered in the objective function. Constraints (1) ensure that we activate at most $\beta \mid R \mid$ tours. Constraints (2) guarantee that each donor j is assigned to at most one time slot in $I_j$. Constraints (3) force a slot to be unassigned (if the corresponding tour has not been selected) or to be assigned to at most one donor per scenario (if the corresponding tour has been activated). Constraints (4) ensure that the number of donations for each blood type is between the prescribed minimum and maximum values. We assume that $\mid J_s \cap J^b\mid \ge LB_b$ for any $b \in B$ and $s \in S$, otherwise the problem is trivially infeasible.

As common in scenario based approaches (Lanzarone et al. 2012; Bacci et al. 2023) the models usually become very difficult to solve when the number of scenarios and, then, the number of constraints and variables of the model, increases. This is true also for model CF. To overcome this issue, we present a second formulation (BF, that we call projected model), where a large part of the variables and the related constraints are projected out according to a Benders decomposition scheme (Benders 1962).

3 The projected formulation

We reformulate the problem by projecting out the $\textbf{y}$ variables and the related constraints, so that the remaining problem only includes the $\textbf{z}$ variables, which do not depend on the scenarios. CF can be restated in a bilevel fashion as follows, where each inner min refers to a single scenario.

$$\begin{aligned}&\min \sum _{s \in S} p_s \lambda _s \\&\sum _{v \in R} z_v \le \beta \mid R \mid \\&\textbf{z}\in \{0,1\}^{\mid R\mid} \end{aligned}$$

$$\begin{aligned}\\\hbox {for any }s\in S, \qquad \lambda _s &=\min \sum _{j \in J_s} w_j \left( 1-\sum _{i \in I_j} y^s_{ij}\right) \\ &\sum _{i \in I_j} y^s_{ij} \le 1{} & j \in J_s \\&\sum _{j \in J_s: i \in I_j} y^s_{ij} \le z_{v(i)}{} & i \in I\\&LB_b \le \sum _{j \in J^b} \sum _{i \in I_j} y^s_{ij} \le UB_b \quad{} & b \in B \\&y^s_{ij} \in \{0,1\}{} & {} i \in I_j, j \in J_s \end{aligned}$$

We now prove that, for a given $\textbf{z}$, each inner min, that we call the lower level problem for s and $\textbf{z}$, can be solved as a linear programming problem.

3.1 Solving the lower level problem as a network flow problem

Fig. 1

Picture of the graph defined in Theorem 1. For some representative arcs, we added into brackets the corresponding cost and capacity values, respectively

Minimizing the original objective function of the lower level problem is equivalent to optimize $\lambda _s = \sum _{j \in J_s} w_j - \max \sum _{j \in J_s} w_j \sum _{i \in I_j} y^s_{ij}$.

Theorem 1

The lower level problem can be solved as a max-cost flow problem on an acyclic graph for any $s \in S$ and $\textbf{z}$.

Proof

Consider the following direct acyclic graph $G(s,\textbf{z})$ (see Fig. 1). The node set V(s) has a source node $\sigma$, a destination node $\tau$, an auxiliary node $\gamma$, a node for any donor $j \in J_s$, a node for any slot $i \in I$ and a node for any blood type $b \in B$. The arc set $E(\textbf{z})$ includes: for any $i \in I$, an arc $(\sigma ,i)$ of cost 0 and capacity $z_{v(i)}$; an arc $(\sigma ,\gamma )$ of cost 0 and capacity $\mid J_s\mid -\sum _{b \in B} LB_b$; an arc $(\gamma ,\tau )$ of cost 0 and capacity $\mid J_s\mid -\sum _{b \in B} LB_b$; for any $b \in B$, an arc $(b, \tau )$ of cost 0 and capacity $LB_b$ and an arc $(b,\gamma )$ of cost 0 and capacity $UB_b-LB_b$; for any $j \in J_s$, an arc $(j,b_j)$ with capacity 1 and cost $w_j$; for any $i \in I_j$ and $j \in J_s$, an arc (i, j) of cost 0 and capacity 1. Suppose that flow $\mid J_s\mid$ must be sent from $\sigma$ to $\tau$ and that one wants to compute the max-cost flow. If all costs and capacities are integer, the flow will be integer. Since each $j \in J_s$ has only one outgoing arc of capacity 1, at most flow 1 can cross it and the flow will be 1 if j is served (i.e., a slot is assigned to it) and 0 otherwise. A flow 1 on arc (i, j) means that slot i is assigned to donor j. The capacities on the $(\sigma ,i)$ arcs guarantee that slot i is crossed by some flow (i.e., i is assigned to some j) only if the corresponding tour has been activated and the flow that can cross i is at most 1. This means that either i is unassigned or it is assigned to at most one donor. The flow can follow three paths in the graph from $\sigma$ to $\tau$: $\{(\sigma ,\gamma ),(\gamma ,\tau )\}$; from $\sigma$ to some b and then to $\tau$ using arcs $(b,\tau )$; from $\sigma$ to some b and then to $\tau$ via the auxiliary node $\gamma$. Node $\tau$ must receive flow $\mid J_s\mid$ and it has to come either from nodes for $b \in B$ or from node $\gamma$. Since the sum of the capacities on the arcs entering $\tau$ is exactly $\mid J_s\mid$, they will be saturated by any feasible solution. Having flow $LB_b$ on arc $(b,\tau )$ means that $LB_b$ donors of type b have been assigned to some slots. Having a positive flow on edge $(b,\gamma )$ means that more than $LB_b$ donors (but less than $UB_b$) have been served. If there is some flow on arc $(\sigma ,\gamma )$, it means that there are some unassigned donors. Since we must maximize the cost of the flow, it would be preferable to follow the second or the third path, since the only arcs with a positive cost are the ones in $\{(j,b_j), j \in J_s\}$. If a feasible solution exists, then we can obtain a solution for the lower level problem by assigning slot i to donor j if the flow on arc (i, j) is 1. If the problem is infeasible, that is, it is not possible to send a flow from $\sigma$ to $\tau$ respecting the given upper and lower bounds on the capacities, this means that it is not possible to obtain the prescribed blood amounts and the lower level problem for the considered s and $\textbf{z}$ is infeasible. $\square$

The reformulation of the lower level problem as a max-cost flow problem and its dual are reported below. The primal problem for s and $\textbf{z}$ is denoted by $low(s,\textbf{z})$ and the dual by $dual(s,\textbf{z})$. We use the convention that a negative supply/demand value for a node denotes a demand, while a positive one a supply. Variable $f_{uv}$ represents the flow on arc $(u,v) \in E(\textbf{z})$, being $E(\textbf{z})$ the arc set defined in the proof of Theorem 1. Symbols on the left in $low(s,\textbf{z})$ ($dual(s,\textbf{z})$) are dual (primal) variables associated with the primal (dual) constraints.

$$\begin{aligned} low(s,\textbf{z}) \quad&\max \sum _{j \in J_s} w_j f_{jb_j}{} & {} \\ (\delta _u) \quad&\sum _{v: (u,v) \in E(\textbf{z})} f_{uv} - \sum _{v: (v,u) \in E(\textbf{z})} f_{vu} = \left\{ \begin{array}{rl} \mid J_s\mid &{} u = \sigma \\ -\mid J_s\mid &{} u = \tau \\ 0 &{} u \in V(s) \setminus \{\sigma ,\tau \} \end{array} \right.{} & {} \\ (\mu _{uv}) \quad&f_{uv} \le \left\{ \begin{array}{ll} LB_b &{} (u,v) \in \{ (b,\tau ), b \in B\}\\ UB_b-LB_b &{} (u,v) \in \{(b,\gamma ), b \in B\}\\ \mid J_s\mid -\sum _{b \in B}LB_b &{} (u,v) \in \{(\sigma ,\gamma ),(\gamma ,\tau )\}\\ z_{v(i)} &{} (u,v) \in \{(\sigma ,i), i \in I\}\\ 1 &{} \text{ otherwise } \end{array} \right.{} & {} \\&\textbf{f}\ge \textbf{0}{} & {} \end{aligned}$$

The constraints corresponding to the dual variable ${\varvec{\delta }}$ are flow conservation constraints, ensuring that the required amount goes from $\sigma$ to $\tau$. The constraints corresponding to dual variables ${\varvec{\mu }}$ are capacity constraints that guarantee that the capacities on the arcs are not exceeded.

$$\begin{aligned} dual(s,\textbf{z}) \quad&\min \mid J_s\mid (\delta _{\sigma } - \delta _{\tau }) + \sum _{b \in B}(LB_b \mu _{b\tau } + (UB_b-LB_b) \mu _{b\gamma }) \\&\quad \quad + (\mid J_s\mid -\sum _{b \in B}LB_b)(\mu _{\sigma \gamma }+\mu _{\gamma \tau }) + \sum _{j \in J_s} \sum _{i \in I_j} \mu _{ij} \\&\quad \quad + \sum _{i \in I} z_{v(i)}\mu _{\sigma i} + \sum _{j \in J_s} \mu _{jb_j}\\ (f_{j b_j}) \quad&\delta _j - \delta _{b_j} + \mu _{jb_j} \ge w_j \quad j \in J_s\\ (f_{uv}) \quad&\delta _u - \delta _v + \mu _{uv} \ge 0 \qquad \, (u,v) \in E(\textbf{z}) \setminus \{(j,b_j), j \in J_s\}\\&{\varvec{\mu }}\ge \textbf{0} \end{aligned}$$

Let $D_s$ be the dual feasible region and let $r(D_s)$ and $e(D_s)$ be its extreme rays and vertices, respectively. Note that $D_s$ does not depend on $\textbf{z}$, which appears only in the objective function of the dual problem. Then, both its rays and its vertices are independent of the current $\textbf{z}$. We can now reformulate CF using a Benders decomposition scheme as follows.

Theorem 2

Problem CF can be reformulated as BF.

$$\begin{aligned} \text{ BF } \quad&\min \sum _{s \in S} p_s \lambda _s \nonumber \\&\sum _{v \in R} z_v \le K \nonumber \\&\mid J_s\mid (\delta _{\sigma } - \delta _{\tau }) + \sum _{b \in B}(LB_b \mu _{b\tau } + (UB_b-LB_b) \mu _{b\gamma }) \nonumber \\&+ (\mid J_s\mid -\sum _{b \in B}LB_b)(\mu _{\sigma \gamma }+\mu _{\gamma \tau }) + \sum _{j \in J_s} \sum _{i \in I_j} \mu _{ij} \nonumber \\&+ \sum _{i \in I} \mu _{\sigma i} z_{v(i)} + \sum _{j \in J_s} \mu _{jb_j} \ge 0 \qquad \qquad \quad ({\varvec{\delta }},{\varvec{\mu }}) \in r(D_s) \end{aligned}$$

(5)

$$\begin{aligned}&\lambda _s \ge \sum _{j \in J_s} w_s - (\mid J_s\mid (\delta _{\sigma } - \delta _{\tau }) \nonumber \\&\quad \sum _{b \in B}(LB_b \mu _{b\tau } + (UB_b-LB_b) \mu _{b\gamma }) \nonumber \\&+ (\mid J_s\mid -\sum _{b \in B}LB_b)(\mu _{\sigma \gamma }+\mu _{\gamma \tau }) \nonumber \\&+ \sum _{i \in I} \mu _{\sigma i}z_{v(i)} + \sum _{j \in J_s} \mu _{jb_j}) \qquad \qquad \qquad \qquad ({\varvec{\delta }},{\varvec{\mu }}) \in e(D_s) \nonumber \\&\textbf{z}\in \{0,1\}^{\mid R\mid }, {\varvec{\lambda }}\ge \textbf{0} \end{aligned}$$

(6)

Proof

Problem $low(s,\textbf{z})$ cannot be unbounded: it may admit a feasible solution or it may be infeasible. On the other hand, problem $dual(s,\textbf{z})$ always admits the feasible solution where all the variables are set to 0, apart from $\mu _{jb_j}$, which are set to $w_j$. Hence, it can be unbounded or it may admit an optimal solution, but it is never infeasible. If there exists at least a scenario $s \in S$ whose corresponding $low(s,\textbf{z})$ is infeasible, then $\textbf{z}$ is infeasible and must be cut off. Requiring that $low(s,\textbf{z})$ is not infeasible for any s for the given $\textbf{z}$, corresponds to requiring that $dual(s,\textbf{z})$ is not unbounded. Hence, the dual objective function must assume a positive value for any extreme ray in $r(D_s)$. This is obtained by the Benders feasibility cuts (5). On the other hand, we must also ensure that the computed $\lambda _s$ values correspond to optimal values for the lower level problem $low(s,\textbf{z})$. The weak duality theory ensures that, for any feasible solution of the primal problem and any feasible solution of the dual problem, the primal objective value is lower than or equal to the dual objective value. This condition is implemented by the Benders optimality cuts (6). The strong duality theory ensures that there is at least one vertex (which may be different for any $\textbf{z}$ and s) for which the constraint is satisfied with equality, guaranteeing that the corresponding primal and dual objective values are optimal. $\square$

Formulation BF has less variables than CF, but an exponential number of constraints. However, the problem can be solved via branch-and-cut, by generating Benders feasibility cuts (5) and Benders optimality cuts (6) dynamically. Usually, the optimization process terminates when only a very limited number of inequalities has been added, without the need to consider each vertex and ray of the dual polyhedron. In problem $dual(s,\textbf{z})$, variables $\textbf{z}$ are parameters, as they are fixed to given values, while ${\varvec{\mu }}$ and ${\varvec{\delta }}$ are the variables whose value must be computed. On the contrary, in constraints (5) and (6), $\textbf{z}$ are variables, while ${\varvec{\mu }}$ and ${\varvec{\delta }}$ are fixed to given values and, hence, they are coefficients. Also note that, if we replace the single inequality (1) by any set of constraints $\textbf{Q}\textbf{z}\le \textbf{q}$ that may limit the available tours and/or add objective costs for the $\textbf{z}$ variables, these modifications do not affect the subproblems and, hence, the results used to derive reformulation BF.

3.2 Benders feasibility cuts

Feasibility has a natural interpretation by network flow arguments. Let a $\sigma \tau$ cut $\{W: V(s) \setminus W\}$ be a partition of the nodes V(s) of graph $G(s,\textbf{z})$, such that $\sigma \in W$ and $\tau \in V(s) {\setminus } W$. The arcs (u, v) of the cut are the ones having $u \in W$ and $v \in V(s) {\setminus } W$. The capacity of the cut is the sum of the capacities on the arcs of the cut.

Theorem 3

The problem of checking if $low(s,\textbf{z})$ is feasible, amounts to test if there is a $\sigma \tau$ cut in $G(s,\textbf{z})$ whose capacity is strictly less than $\mid J_s\mid$.

Proof

By the max-flow min-cut theorem (Ford and Fulkerson 1956), each flow from the source to the destination must cross each cut that separates the source from the destination. If there exists one of such cuts whose capacity is less than the demand that must cross the cut, then the problem is infeasible. Since the costs play no role, as far as feasibility is concerned, suppose that $w_j = 0$ for all $j \in J$. Consider $dual(s,\textbf{z})$. Assume that there exists a $\sigma \tau$ cut $\{W: V(s) \setminus W\}$ whose capacity is less than the demand. Consider the solution having $\mu _{uv} = 1$ for the arcs of this cut and 0 otherwise. Let $\delta _u = 1$ for $u \in V(s)$ and $\delta _u = 0$ otherwise. This solution is feasible for $dual(s,\textbf{z})$ and, since the capacity of the considered cut is less than the demand, the corresponding objective function is negative. Moreover, it can be scaled by an arbitrary factor, leading to unboundedness. Hence, each unbounded ray corresponds to a $\sigma \tau$ cut with capacity less than the demand in $G(s,\textbf{z})$. On the other hand, if each $\sigma \tau$ cut has a capacity greater than or equal to the demand, then the primal problem admits an optimal solution and so it is for the dual by linear duality. It follows that there is no unbounded ray. $\square$

Then, each Benders feasibility cut corresponds to a $\sigma \tau$ cut of graph $G(s,\textbf{z})$. We describe below some Benders feasibility cuts that can be added to the initial model to avoid separating trivially infeasible $\textbf{z}$ vectors.

Theorem 4

The source inequalities (7) are Benders feasibility cuts.

$$\begin{aligned} \sum _{i \in \cup _{j \in J_s} I_j} z_{v(i)} \ge \sum _{b \in B} LB_b \quad s \in S \end{aligned}$$

(7)

Proof

Constraints (7) are valid for BF. In fact, if one does not have the slots to accommodate the minimum number of donors needed to reach the required blood mix, then $low(s,\textbf{z})$ is infeasible. They correspond to the $\sigma \tau$ cuts $\{\{\sigma \}: V(s) {\setminus } \{\sigma \}\}$, for $s \in S$. This cut prescribes that the edges going from $\sigma$ to any node $i \in I$, plus edge $(\sigma ,\gamma )$ have enough capacity to support an amount of flow corresponding to the number of donors of scenario s, that is, $\mid J_s \mid$. Since edge $(\sigma ,\tau )$ can accommodate at most flow $\mid J_s \mid -\sum _{b \in B} LB_b$, then the edges from $\sigma$ to $i \in I$ must have capacity at least $\sum _{b \in B} LB_b$, leading to inequality (7). The cut is illustrated in Fig. 2. $\square$

According to the blood type, we can derive the inequalities below.

Theorem 5

The blood type inequalities (8) are Benders feasibility cuts.

$$\begin{aligned} \sum _{i \in \cup _{J^b \cap J_s} I_j} z_{v(i)} \ge LB_b \quad b \in B, s \in S \end{aligned}$$

(8)

Proof

Constraints (8) are valid for BF. If one does not have enough slots to accommodate the minimum number of donors needed to reach the required minimum amount for blood type b, then $low(s,\textbf{z})$ is infeasible. For a given b and s, inequality (8) corresponds to the $\sigma \tau$ cut $\{V(s)\setminus \{\tau ,b, J(b), I(b)\}:\{\tau ,b, J(b),I(b)\}\}$, where $J(b) = J^b \cap J_s$ are the donors of blood type b and $I(b) = \cup _{j \in J(b)} I_j$ are the slots that can be assigned to these donors. This cut has capacity $\sum _{i \in I(b)} z_{v(i)}$ (edges from $\sigma$ to $i \in I(b)$) $+ \sum _{w \in B {\setminus } \{b\}} LB_w$ (edges from $w \in B {\setminus } \{b\}$ to $\tau$) $+ \mid J_s \mid - \sum _{w \in B} LB_w$ (edge $(\gamma ,\tau )$). This capacity can support a total flow of amount $\mid J_s \mid$ only if $\sum _{i \in I(b)} z_{v(i)} \ge LB_b$, leading to inequalities (8). The cut is illustrated in Fig. 2. $\square$

Algorithm 1

Processing a node of the branch-and-bound tree

Fig. 2

In the picture, the dotted lines represents the cuts associated with an inequality of type (7) (in gray) and with an inequality of type (8) (in black)

4 The algorithm

Since formulation BF has an exponential number of constraints, the problem is solved by branch-and-cut, generating inequalities (5) and (6) dynamically. A branch-and-cut approach (Padberg and Rinaldi 1991) is a branch-and-bound (see, e.g., Wolsey (1998)) that starts from a suitable reduced formulation of the problem and where each node of the tree is processed by applying a user defined policy, which generates additional inequalities to be added to the model on the fly. In our case, the initial formulation that is used to solve BF does not include inequalities (5) and (6) and it only contains the constraint that limits the number of tours that can be activated (1) and inequalities (8), that are polynomially many in the input size.

Indeed, it is well-known that Benders decomposition approaches can be very ineffective in the first iterations, when few constraints are present in the formulation and, hence, the generated solutions are often infeasible or far from the optimum. This effect can be mitigated by adding to the initial formulation a set of cuts, like constraints (8), that allows to generate more reasonable initial solutions, thus reducing the overall time and speeding up convergence. In Sect. 5.3 we discuss how effective these inequalities are, by showing what happens if we remove them from the initial formulation. The user defined policy (separation) is described below, where we discuss further strategies that have been adopted to improve the overall algorithm.

4.1 Separation

Consider a node of the branch-and-bound tree. If it is not the root node and the optimal solution of the linear relaxation $(\textbf{z},{\varvec{\lambda }})$ is fractional, we just branch, as in a standard branch-and-bound. Instead, if we are at the root node or $(\textbf{z},{\varvec{\lambda }})$ is integer, we check if $(\textbf{z},{\varvec{\lambda }})$ violates some inequalities (5) or (6). Therefore, for each scenario $s \in S$, we solve $low(s,\textbf{z})$. If $low(s,\textbf{z})$ is infeasible, the dual is unbounded and a constraint (5) must be generated and added to the current formulation. If $low(s,\textbf{z})$ is feasible, but $\lambda _s$ does not correspond to the optimal value, a constraint (6) must be added to the current model. We add a single inequality (5) at a time but, possibly, multiple inequalities (6).

In fact, if a feasibility cut is violated by a solution $\textbf{z}$ for a scenario s, then there is a high probability that it will be violated for other scenarios r. Indeed, if we cannot satisfy some lower bounds $LB_b$ with $\mid J_s \cap J^b \mid$ potential donors for type b, it is unlikely to satisfy them with $\mid J_r \cap J^b \mid \le \mid J_s \cap J^b \mid$ donors, despite the preferences of those donors could better match the activated tours. This observation was confirmed in the experiments, where, for a given current solution $(\textbf{z}, {\varvec{\lambda }})$, most of the times the different scenarios produced very similar (if not the same) feasibility cuts. Hence, at each iteration, we decided to add only the first violated feasibility cut that we generate among all scenarios. Moreover, fractional solutions are tested only at the root node. This avoids generating many inequalities that: although globally valid, are possibly violated only for one single node, whereas in the others are not needed and just increase the problem size; are possibly violated by small amounts, leading to small changes between one fractional solution and the next, while branching would be more effective. All integer solutions are tested at each node to guarantee the correctness of the algorithm.

If $(\textbf{z},{\varvec{\lambda }})$ is integer and it does not violate any inequality (5) or (6), then it is, indeed, a feasible solution that can be used to possibly update the incumbent solution, that is, the best solution computed so far. The node procedure is illustrated in detail in Algorithm 1, where we denote by bestSol the value of the best solution found so far and by currentSol the value of the current solution $(\textbf{z},{\varvec{\lambda }})$. Step 10 of Algorithm 1 requires checking if $low(s,\textbf{z})$ is feasible and, if the case, producing a violated inequality corresponding to an unbounded ray. As already discussed in Sect. 3, $low(s,\textbf{z})$ can be modeled as a network flow problem, leading to the following result.

Theorem 6

Checking if $low(s,\textbf{z})$ is feasible or generating a violated inequality (5) if not, can be done in polynomial time.

Proof

Checking if $low(s,\textbf{z})$ is feasible amounts to verify if there is a cut whose capacity is less than $\mid J_s\mid$. This can be done by applying a max-flow algorithm to the graph $G(s,\textbf{z})$ corresponding to the current solution. The maximum flow in a graph can be computed in polynomial time (Ahuja et al. 1993). If the maximum flow is less than $\mid J_s\mid$, the corresponding minimum cut has capacity less than $\mid J_s\mid$ and it corresponds to an unbounded ray by Theorem 3. $\square$

If $low(s,\textbf{z})$ is not infeasible, step 13 requires producing an optimal solution of the problem. Again, by the network flow argument illustrated in Sect. 3, the following result holds.

Theorem 7

Computing an optimal solution for $low(s,\textbf{z})$ or generating a violated inequality (6) if any, can be done in polynomial time.

Proof

Problem $low(s,\textbf{z})$ is a max cost flow problem on an acyclic graph. Max cost flows on acyclic graphs and corresponding dual variables can be computed in polynomial time Ahuja et al. (1993). $\square$

4.2 The implementation

We implemented the code in Python and used the Gurobi (gurobipy) libraries 9.1.1 for solving the linear (integer) programming problems. Model BF is solved using Algorithm 1 at each node of the branch-and-bound tree. Model CF is solved using Gurobi with default settings. We ran the code on a 3 GHz Intel Xeon Gold 6136 machine, with 258 GB of RAM. For the solution of each instance, we set a time limit of 3600 s.

5 The computational experiments

Below we present and discuss the computational experiments that have been carried out using the models presented in Sects. 2.2 and 3.

Table 1 Distribution among the blood types of the donors in the dataset

5.1 The test bed

Since home blood donation has not been treated in practice and it was addressed only marginally in the literature, there are no reference instances that can be used as a benchmark. We started from data provided by AVIS Milan, which is not currently offering the possibility of home blood donations, and derived some instances for the home blood donation problem. These same data have been already used by Doneda et al. (2021) and Baş Güre et al. (2018a). According to AVIS Milan, we assume that the 60% of its donors are served by the home donation service, while the others continue to make the donations at the blood collection centers. Therefore, 60% of donation requests have been randomly extracted from the historical data and included in the simulations. In this way, the considered dataset includes a set J of 3865 donors who booked an appointment during a period of 120 days, starting from January 1st 2014. Therefore, in our experiments, we have on average $\pi = 3865 / 120 \approx 32$ donors to be served every day (equal to 60% of the about 50 daily donors of AVIS Milan).

AVIS Milan is located in the Eastern part of the city and collects blood from donors living or working in Milan. The city of Milan has an extension of 181.8 ${\text{km}}^2$ and an almost circular shape. The geodesic positions of the donors are uniformly generated in a circle with radius 7.6 km, where the uniform distribution is in agreement with the characteristics of Milan and the experience of AVIS Milan. The area is divided into 9 zones (cells): the city center, with a radius of 2.5 km and 8 suburban sectors of 45° each. We assume that each cell is visited twice a day by a tour, once in the morning and once in the afternoon. Each tour can serve 3 donors and, therefore, we can serve up to 54 donors per day. The geodesic position of each donor is used to place the donor in the corresponding cell. For the 9 cells we consider, the set R is made by $9 \times 2 = 18$ tours for each day and set I contains $18 \times 3 = 54$ slots per day. We set a penalty $w_j = 1$ for each slot $j \in J$.

The preferences of the donors for the slots (sets $I_j$) are randomly generated by adding to $I_j$ any slot $i \in I$ belonging to a tour that visits the cell of donor j with an independent probability $\alpha$. There are $\mid B\mid =8$ blood types, whose distribution among the donors is illustrated in Table 1. For each $b \in B$, we let $LB_b$ and $UB_b$ be 15% and 150%, respectively, of the values reported in Table 1. For each scenario $s \in S$, we set a uniform probability $p_s = 1/\mid S\mid$ to occur and we construct the set $J_s$ of donors in s by randomly picking each donor in J with probability $7 \pi /\mid J\mid$.

Each group of instances is represented by the triple $\{\mid S\mid ,\beta ,\alpha \}$ and contains 10 instances with the same value of the parameters. Parameter $\mid S\mid$ represents the number of considered scenarios: it takes values in $\{200, 400, 600, 800, 1000\}$ and gives an indication of the size of the instances. Parameter $\beta$ is the percentage of the tours that can be activated: it takes values in $\{50\%, 70\%, 90\%\}$ and corresponds to the available resources. Parameter $\alpha$ is the probability that donor j likes slot i: it takes values in $\{25\%, 50\%, 75\%\}$ and represents a measure of the difficulty of satisfying the donors preferences. Hence, the considered test bed contains a total number of 450 instances. Observe that, as already mentioned, if we activate all available tours, we can serve up to 54 donors per day. On the other hand, the average number of daily donors of each scenario is $\pi \approx 32$. Therefore, any donor has, on average, almost two alternative dedicated slots for donating blood, when all tours are activated, and it is possible to serve a large portion of the donors, even with difficult donors preferences (small values of parameter $\alpha$).

Table 2 Comparison between model CF and model BF on instances with 200 scenarios

5.2 Comparing CF and BF

In Table 2 we present the computational results obtained by solving CF and BF on the instances with 200 scenarios described in Sect. 5.1. We limit to 200 scenarios because CF suffers when $\mid S\mid$ increases and cannot solve any instance with more than 200 scenarios and with a percentage of available tours less than 90%. Each row of the table is associated with the group of 10 instances corresponding to the indicated parameter values $\mid S\mid$, $\beta$, and $\alpha$. For each model, column solved denotes the number of instances of the group that are solved to optimality within the time limit, while column time reports the average computing time (in seconds) on the solved instances. The results show that model BF outperforms CF, both in terms of computing times and of solved instances. Also note that $\beta =90\%$ means that the available slots are about 1.5 times the average number of donors in the scenarios. It follows that most $\textbf{z}$ choices do not exceed the available resources and are sufficient to serve almost all the donors, reducing the importance and the effect of such variables in the model. As we discussed in Theorem 1, the $\textbf{z}$ variables are the only true integer variables of the model, while the $\textbf{y}$ ones can be treated as continuous variables. Therefore, it is to be expected that instances with $\beta = 90\%$ are much easier than the others for both approaches. In fact, both CF and BF can solve all the instances with $\beta = 90\%$, independently of the values of the other parameters.

We also observe that, when neither CF nor BF can solve an instance to optimality, the best solution produced by CF at the time limit serves, on average, about $4\%$ less donors than the corresponding BF solution in the instances with $\mid S \mid = 200$. The difference increases to about $17\%$ on the instances with $\mid S \mid = 400$.

Table 3 Results on the solved instances for BF

Table 4 Results on the unsolved instances for BF

Fig. 3

Percentage of solved instances depending on the number $\mid S\mid$ of scenarios for BF

Fig. 4

Percentage of solved instances depending on parameter $\alpha$ for BF

Fig. 5

Percentage of solved instances depending on parameter $\beta$ for BF

5.3 Statistics on solving BF

Table 5 The role of constraints (8) for BF

Table 6 Served donors on the solved instances for BF (optimal solution)

Table 7 Served donors on the unsolved instances for BF (best available solution)

In Tables 3, 4, we focus on the model BF and present in detail the computational results for it, using instances up to 1000 scenarios. The former refers to the instances solved to optimality, the latter to the ones not solved to optimality within the time limit.

In Table 3, for each group of instances, the number of solved instances is reported in column solved. For such instances, columns time, nodes, F-cuts and O-cuts give, respectively, the average computing time (in seconds), the average number of explored nodes, the average number of generated feasibility cuts (5), the average number of generated optimality cuts (6). Observe that BF can solve most of the instances even when the number of scenarios $\mid S\mid$ goes up to 1000. Because of the cut generation procedure we adopted, the number of feasibility cuts is very limited with respect to the number of optimality cuts.

In Table 4, we analyze the performances of BF over the instances that it could not solve to optimality within the time limit of 3600 s. Here, column unsolved reports the number of the unsolved instances of each group. Column gap (%) is the average percentage optimality gap when the procedure stops and column nodes is the average number of branch-and-bound nodes. These values show that, even when the solution provided within the time limit is not proved to be optimal, it is, nevertheless, definitively a good solution. In fact, with only one exception on an instance with 1000 scenarios, the optimality gap values are always below $0.5\%$.

Table 5 measures the effect of inequalities (8) in solving BF. It reports a comparison on the instances with 200 scenarios between two settings of the algorithm: inequalities (8) added in the initial formulation (column BF with (8)); inequalities (8) separated as feasibility cuts (column BF without (8)). We report the number of instances that are solved to optimality within the 1 h time limit in both settings. If the second setting is used for BF, the number of instances solved to optimality dramatically decreases, even in the easy case where $\beta =90\%$.

In Figs. 3, 4 and 5 we show how the average number of solved instances changes when, respectively, the number of considered scenarios, the value of parameter $\alpha$ and the value of parameter $\beta$ change. The difficulty of the problem grows with the number of scenarios and decreases with the increasing of parameters $\alpha$ and $\beta$. Indeed, the greater is the value of these two parameters, the easier is to assign donors to slots.

Fig. 6

Percentage of served donors depending on the number $\mid S\mid$ of scenarios for BF

Fig. 7

Percentage of served donors depending on parameter $\alpha$ for BF

Fig. 8

Percentage of served donors depending on parameter $\beta$ for BF

5.4 Served donors

The main objective of the blood donation planning described in the present paper is to serve as many donors as possible, provided that some constraints are satisfied. In Tables 6 and 7 we report the average number of served donors (column percentage of served donors), respectively, for the solved instances and for the unsolved ones (served donors in the best solution found). The results show that the number of served donors is always very large, also for the instances not solved to optimality. The only instance where the served donors are less than 81% is the unique unsolved instance with 1000 scenarios with gap around 18% that was discussed before.

In Figs. 6, 7 and 8 we summarize how the percentage of served donors change, depending on the number of scenarios, the donors preferences ($\alpha$) and the percentage of tours that can be activated, given the available resources ($\beta$). Although the preferences of the donors cannot be controlled, it is easy to see that they are not crucial and that it is possible to serve a large number of donors even when each of them only likes 25% of the proposed slots. On the other hand, as expected, the value of parameter $\beta$ largely affects the number of served donors. However, even with a small percentage of available tours ($\beta = 50\%$) it is possible to serve more than 80% of the considered donors. Observe that, when $\beta = 50\%$, the number of available slots is about $84\%$ of the average number of donors in each scenario. An increase in the percentage of available tours from 50 to 70% allows to serve almost all the donors (about 98%). Observe that, further increasing the resources dedicated to the service, that is, increasing $\beta$ from 70 to 90% allows to increase the number of served donors by a maximum of 2%. Also note that, in principle, it may not be possible to serve all the donors, due to the upper bounds on the blood production, independently of the available resources.

6 Conclusions

We considered the problem of planning home blood donations, which has received only a very limited attention in the literature so far. The uncertain availability of the donors is modeled in a stochastic way, by scenarios. The aim was to serve as many donors as possible, while respecting a bound on the available resources, that limits the number of tours that can be activated, and ensuring that prescribed amounts of each blood type are produced in each scenario. For this problem, we proposed an integer programming formulation that is solved using a Benders decomposition approach, via a network flow argument. The results show that the proposed framework can produce good solutions, where a large portion of the donors are served. They also show how to control the resources that are needed to produce the desired level of service. In particular, activating about 50% of the tours already ensures to serve more than 80% of the donors.