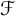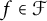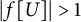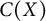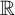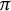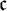1 Introduction
The question about how resolvable are crowded locally connected spaces has been around for some time. Costantini proved in [Reference Costantini1] that regular such spaces are
![]() $\omega $
-resolvable. Actually, it is proved there that local connectedness can be weakened to having a
$\omega $
-resolvable. Actually, it is proved there that local connectedness can be weakened to having a
![]() $\pi $
-base consisting of connected sets. We simply call such spaces
$\pi $
-base consisting of connected sets. We simply call such spaces
![]() $\pi $
-connected.
$\pi $
-connected.
In [Reference Pavlov5], it is stated that Yaschenko proved that every crowded locally connected Tykhonov space is
![]() $\mathfrak {c}$
-resolvable, however, as far as we know, no proof of this has been published.
$\mathfrak {c}$
-resolvable, however, as far as we know, no proof of this has been published.
Dehghani and Karavan claim in [Reference Dehghani and Karavan2] that every crowded locally connected functionally Hausdorff space is
![]() $\mathfrak {c}$
-resolvable. They get this as a corollary of their more general Theorem 2.6, in the proof of which, however, we found a gap, and we do not know if this gap can be fixed. On page 88 of their paper, lines -7 and -6, they claim that
$\mathfrak {c}$
-resolvable. They get this as a corollary of their more general Theorem 2.6, in the proof of which, however, we found a gap, and we do not know if this gap can be fixed. On page 88 of their paper, lines -7 and -6, they claim that
![]() $\bigcup _{\gamma \not =\alpha } A_\gamma = f^{-1}(\bigcup _{\gamma \not =\alpha } D_\gamma )$
is not closed in any nonempty connected open subset V of U. But this can only be concluded in case the restriction of f to V is not constant, and they only assume that some continuous function
$\bigcup _{\gamma \not =\alpha } A_\gamma = f^{-1}(\bigcup _{\gamma \not =\alpha } D_\gamma )$
is not closed in any nonempty connected open subset V of U. But this can only be concluded in case the restriction of f to V is not constant, and they only assume that some continuous function
![]() $g : V \to \mathbb {R}$
is not constant.
$g : V \to \mathbb {R}$
is not constant.
It follows, however, from our results below that their Corollary 2.7 of Theorem 2.6 is correct. In fact, the following property weaker than being crowded and functionally Hausdorff suffices: for every non-empty open set U, there is a continuous map of the whole space to
![]() $\mathbb {R}$
that is not constant on U.
$\mathbb {R}$
that is not constant on U.
We are going to get this from a more general result that will make use of the following concept.
Definition 1.1 Let X be a topological space and Y any set. We call a family
![]() $\mathcal {F}$
of maps from X to Y nowhere constant (
$\mathcal {F}$
of maps from X to Y nowhere constant (
![]() $NWC$
) if for every non-empty open set U in X, there is
$NWC$
) if for every non-empty open set U in X, there is
![]() $f \in \mathcal {F}$
with
$f \in \mathcal {F}$
with
![]() $|f[U]|> 1$
, i.e., f is not constant on U.
$|f[U]|> 1$
, i.e., f is not constant on U.
We note the trivial fact that any space that admits a NWC family of maps is crowded, i.e., has no isolated points.
2 The results
We first present a very general result that connects NWC families of maps and resolvability.
Theorem 2.1 Let
![]() $\mathcal {F}$
be a NWC family of maps of the topological space X to the set Y. Moreover,
$\mathcal {F}$
be a NWC family of maps of the topological space X to the set Y. Moreover,
![]() $\mathcal {B}$
is a
$\mathcal {B}$
is a
![]() $\pi $
-base of X and
$\pi $
-base of X and
![]() $\mathcal {A}$
is a disjoint family of subsets of Y such that, putting
$\mathcal {A}$
is a disjoint family of subsets of Y such that, putting
![]() $\mathcal {B}_f = \{B \in \mathcal {B} : |f[B]|> 1\}$
and
$\mathcal {B}_f = \{B \in \mathcal {B} : |f[B]|> 1\}$
and
![]() $U_f = \bigcup (\mathcal {B} \setminus \mathcal {B}_f)$
for any
$U_f = \bigcup (\mathcal {B} \setminus \mathcal {B}_f)$
for any
![]() $f \in \mathcal {F}$
, we have
$f \in \mathcal {F}$
, we have
Then X is
![]() $|\mathcal {A}|$
-resolvable.
$|\mathcal {A}|$
-resolvable.
Proof We are going to use transfinite recursion to produce a disjoint collection
![]() $\{D(A) : A \in \mathcal {A}\}$
of dense subsets of X.
$\{D(A) : A \in \mathcal {A}\}$
of dense subsets of X.
To do that, we first introduce the following piece of notation. For
![]() $f \in \mathcal {F},\,\,B \in \mathcal {B}_f$
, and
$f \in \mathcal {F},\,\,B \in \mathcal {B}_f$
, and
![]() $A \in \mathcal {A}$
, we let
$A \in \mathcal {A}$
, we let
It follows from our assumptions that
![]() $S(f, B, A) \ne \emptyset $
.
$S(f, B, A) \ne \emptyset $
.
We start our recursive construction by choosing
![]() $f_0 \in \mathcal {F}$
such that
$f_0 \in \mathcal {F}$
such that
![]() $\mathcal {B}_{f_0} \ne \emptyset $
and then define
$\mathcal {B}_{f_0} \ne \emptyset $
and then define
for all
![]() ${A \in \mathcal {A}}$
. Then
${A \in \mathcal {A}}$
. Then
![]() $\{D_0(A) : A \in \mathcal {A}\}$
is disjoint because
$\{D_0(A) : A \in \mathcal {A}\}$
is disjoint because
![]() $D_0(A) \subset {f_0}^{-1}[A]$
for each
$D_0(A) \subset {f_0}^{-1}[A]$
for each
![]() $A \in \mathcal {A}$
, moreover
$A \in \mathcal {A}$
, moreover
![]() $B \cap D_0(A) \ne \emptyset $
whenever
$B \cap D_0(A) \ne \emptyset $
whenever
![]() $B \in \mathcal {B}_{f_0}$
and
$B \in \mathcal {B}_{f_0}$
and
![]() $A \in \mathcal {A}$
.
$A \in \mathcal {A}$
.
Now, assume that
![]() $\alpha> 0$
and we have already defined
$\alpha> 0$
and we have already defined
![]() $f_\beta \in \mathcal {F}$
and the family
$f_\beta \in \mathcal {F}$
and the family
![]() $\{D_\beta (A) : A \in \mathcal {A}\}$
for all
$\{D_\beta (A) : A \in \mathcal {A}\}$
for all
![]() $\beta < \alpha $
, and consider
$\beta < \alpha $
, and consider
If
![]() $\mathcal {B}_\alpha = \mathcal {B},$
then our construction stops. Otherwise, we may pick
$\mathcal {B}_\alpha = \mathcal {B},$
then our construction stops. Otherwise, we may pick
![]() $f_\alpha \in \mathcal {F}$
such that
$f_\alpha \in \mathcal {F}$
such that
![]() $\mathcal {B}_{f\alpha } \setminus \mathcal {B}_\alpha \ne \emptyset $
. In this case, we define
$\mathcal {B}_{f\alpha } \setminus \mathcal {B}_\alpha \ne \emptyset $
. In this case, we define
for each
![]() $A \in \mathcal {A}$
.
$A \in \mathcal {A}$
.
Note that we clearly have
![]() $\bigcup (\mathcal {B}_{f\alpha } \setminus \mathcal {B}_\alpha ) \subset \bigcap \{U_{f_\beta } : \beta < \alpha \}$
, hence it may be verified by straightforward transfinite induction that
$\bigcup (\mathcal {B}_{f\alpha } \setminus \mathcal {B}_\alpha ) \subset \bigcap \{U_{f_\beta } : \beta < \alpha \}$
, hence it may be verified by straightforward transfinite induction that
![]() $\{D_\alpha (A) : A \in \mathcal {A}\}$
is disjoint, moreover, we have
$\{D_\alpha (A) : A \in \mathcal {A}\}$
is disjoint, moreover, we have
![]() $B \cap D_\alpha (A) \ne \emptyset $
whenever
$B \cap D_\alpha (A) \ne \emptyset $
whenever
![]() $A \in \mathcal {A}$
and
$A \in \mathcal {A}$
and
![]() $B \in \mathcal {B}_{f_\beta }$
with
$B \in \mathcal {B}_{f_\beta }$
with
![]() $\beta \le \alpha $
.
$\beta \le \alpha $
.
Of course, this construction must stop at some ordinal
![]() $\alpha $
, in which case putting
$\alpha $
, in which case putting
![]() $D(A) = \bigcup \{D_\beta (A) : \beta < \alpha \}$
the disjoint family
$D(A) = \bigcup \{D_\beta (A) : \beta < \alpha \}$
the disjoint family
![]() $\{D(A) : A \in \mathcal {A}\}$
consists of dense subsets of X because
$\{D(A) : A \in \mathcal {A}\}$
consists of dense subsets of X because
![]() $B \cap D(A) \ne \emptyset $
for any
$B \cap D(A) \ne \emptyset $
for any
![]() $B \in \mathcal {B}$
and
$B \in \mathcal {B}$
and
![]() $A \in \mathcal {A}$
and
$A \in \mathcal {A}$
and
![]() $\mathcal {B}$
is a
$\mathcal {B}$
is a
![]() $\pi $
-base of X.
$\pi $
-base of X.
Now, we deduce from Theorem 2.1 our promised result concerning
![]() $\pi $
-connected spaces.
$\pi $
-connected spaces.
Corollary 2.2 If X is any
![]() $\pi $
-connected space for which
$\pi $
-connected space for which
![]() $C(X)$
, the family of all continuous maps of X to
$C(X)$
, the family of all continuous maps of X to
![]() $\mathbb {R}$
, is NWC then X is
$\mathbb {R}$
, is NWC then X is
![]() $\mathfrak {c}$
-resolvable.
$\mathfrak {c}$
-resolvable.
Proof To apply Theorem 2.1, we of course put
![]() $Y = \mathbb {R}$
and
$Y = \mathbb {R}$
and
![]() $\mathcal {F} = C(X)$
. For
$\mathcal {F} = C(X)$
. For
![]() $\mathcal {B}$
, we choose a
$\mathcal {B}$
, we choose a
![]() $\pi $
-base of X consisting of connected sets, and let
$\pi $
-base of X consisting of connected sets, and let
![]() $\mathcal {A}$
be any disjoint collection of dense subsets of
$\mathcal {A}$
be any disjoint collection of dense subsets of
![]() $\mathbb {R}$
with
$\mathbb {R}$
with
![]() $|\mathcal {A}| = \mathfrak {c}$
.
$|\mathcal {A}| = \mathfrak {c}$
.
Note that for any
![]() $f \in C(X)$
and
$f \in C(X)$
and
![]() $B \in \mathcal {B}_f$
, we have
$B \in \mathcal {B}_f$
, we have
![]() $|f[B]|> 1$
, hence
$|f[B]|> 1$
, hence
![]() $f[B]$
is a nondegenerate interval in
$f[B]$
is a nondegenerate interval in
![]() $\mathbb {R}$
, being a non-singleton connected subset of
$\mathbb {R}$
, being a non-singleton connected subset of
![]() $\mathbb {R}$
, and thus
$\mathbb {R}$
, and thus
![]() $A \cap f[B] \ne \emptyset $
holds for all
$A \cap f[B] \ne \emptyset $
holds for all
![]() $A \in \mathcal {A}$
. Consequently, we shall be done if we prove the following claim.
$A \in \mathcal {A}$
. Consequently, we shall be done if we prove the following claim.
Claim For any
![]() $f \in C(X)$
and
$f \in C(X)$
and
![]() $B \in \mathcal {B}_f$
, we have
$B \in \mathcal {B}_f$
, we have
To see this, pick any
![]() $t \in f[B]$
and note that
$t \in f[B]$
and note that
![]() $B \cap f^{-1}(t)$
is a non-empty proper closed subset of the connected subspace B. Properness follows from
$B \cap f^{-1}(t)$
is a non-empty proper closed subset of the connected subspace B. Properness follows from
![]() $|f[B]|> 1$
. Consequently, the boundary
$|f[B]|> 1$
. Consequently, the boundary
![]() $H_t$
of
$H_t$
of
![]() $B \cap f^{-1}(t)$
in B is non-empty. Also, we have
$B \cap f^{-1}(t)$
in B is non-empty. Also, we have
![]() $H_t \subset B \cap f^{-1}(t)$
, the latter set being closed in B.
$H_t \subset B \cap f^{-1}(t)$
, the latter set being closed in B.
Now, take any
![]() $B' \in \mathcal {B} \setminus \mathcal {B}_f$
, then
$B' \in \mathcal {B} \setminus \mathcal {B}_f$
, then
![]() $f[B'] = \{t'\}$
for some
$f[B'] = \{t'\}$
for some
![]() $t' \in \mathbb {R}$
. If
$t' \in \mathbb {R}$
. If
![]() $t' \ne t$
, then we have
$t' \ne t$
, then we have
![]() $B' \cap f^{-1}(t) = \emptyset $
, hence
$B' \cap f^{-1}(t) = \emptyset $
, hence
![]() $B' \cap H_t = \emptyset $
as well. If, on the other hand,
$B' \cap H_t = \emptyset $
as well. If, on the other hand,
![]() $t' = t$
, then
$t' = t$
, then
![]() $B'\cap B$
is in the interior of
$B'\cap B$
is in the interior of
![]() $B \cap f^{-1}(t)$
in B, hence we have
$B \cap f^{-1}(t)$
in B, hence we have
![]() $B' \cap H_t = \emptyset $
again. This, however, means that
$B' \cap H_t = \emptyset $
again. This, however, means that
![]() $H_t \cap U_f = \emptyset $
, consequently,
$H_t \cap U_f = \emptyset $
, consequently,
![]() $t \in f[H_t] \subset f[B \setminus U_f]$
, completing the proof of the claim.
$t \in f[H_t] \subset f[B \setminus U_f]$
, completing the proof of the claim.
A closer inspection of this proof reveals that we did not use the full force of continuity for the members f of the NWC family
![]() $\mathcal {F} = C(X)$
. What we used was that f preserves connectedness for
$\mathcal {F} = C(X)$
. What we used was that f preserves connectedness for
![]() $B \in \mathcal {B}$
, i.e.,
$B \in \mathcal {B}$
, i.e.,
![]() $f[B]$
is connected in
$f[B]$
is connected in
![]() $\mathbb {R}$
for
$\mathbb {R}$
for
![]() $B \in \mathcal {B}$
, moreover, that
$B \in \mathcal {B}$
, moreover, that
![]() $f^{-1}(t)$
is closed in X for all
$f^{-1}(t)$
is closed in X for all
![]() $t \in \mathbb {R}$
.
$t \in \mathbb {R}$
.
3 Discussion and questions
Corollary 2.2 is clearly sharp in the sense that the cardinal
![]() $\mathfrak {c}$
cannot be replaced with anything bigger because there are very nice crowded and locally connected spaces of cardinality
$\mathfrak {c}$
cannot be replaced with anything bigger because there are very nice crowded and locally connected spaces of cardinality
![]() $\mathfrak {c}$
. The natural question arises, however, if such a space X is maximally resolvable, i.e.,
$\mathfrak {c}$
. The natural question arises, however, if such a space X is maximally resolvable, i.e.,
![]() $\Delta (X)$
-resolvable, where
$\Delta (X)$
-resolvable, where
![]() $\Delta (X)$
is the minimum cardinality of a non-empty open set in X.
$\Delta (X)$
is the minimum cardinality of a non-empty open set in X.
In a recent arXiv preprint [Reference Lipin4], Lipin proved that if
![]() $2^{\mathfrak {c}} = 2^{(\mathfrak {c}^+)}$
, then there is a locally connected and pseudocompact Tykhonov space X such that
$2^{\mathfrak {c}} = 2^{(\mathfrak {c}^+)}$
, then there is a locally connected and pseudocompact Tykhonov space X such that
![]() $\Delta (X)> \mathfrak {c}$
but X is not
$\Delta (X)> \mathfrak {c}$
but X is not
![]() $\mathfrak {c}^+$
-resolvable. So, at least consistently, Corollary 2.2 is sharp in that sense as well.
$\mathfrak {c}^+$
-resolvable. So, at least consistently, Corollary 2.2 is sharp in that sense as well.
As we wrote in the Introduction, Costatini [Reference Costantini1] proved that crowded
![]() $\pi $
-connected regular spaces are
$\pi $
-connected regular spaces are
![]() $\omega $
-revolvable. As usual, in his treatment regular implies
$\omega $
-revolvable. As usual, in his treatment regular implies
![]() $T_1$
. But his proof actually works for all crowded
$T_1$
. But his proof actually works for all crowded
![]() $\pi $
-connected quasi-regular spaces as well, without the use of any additional separation axiom. Recall that a space is quasi-regular if for every non-empty open U, there is a non-empty open V such that
$\pi $
-connected quasi-regular spaces as well, without the use of any additional separation axiom. Recall that a space is quasi-regular if for every non-empty open U, there is a non-empty open V such that
![]() $\overline {V} \subset U$
. The only slight modification we need is that in this case, the definition of crowded has to be replaced by the following assumption: there is no finite indiscrete open subspace. For
$\overline {V} \subset U$
. The only slight modification we need is that in this case, the definition of crowded has to be replaced by the following assumption: there is no finite indiscrete open subspace. For
![]() $T_0$
-spaces, this assumption is clearly equivalent with the usual one, i.e., not having any isolated points.
$T_0$
-spaces, this assumption is clearly equivalent with the usual one, i.e., not having any isolated points.
Hewitt [Reference Hewitt3] gave an example of a regular connected space X of cardinality
![]() $\omega _1$
. Let
$\omega _1$
. Let
![]() $Y=\lambda _f(X)$
be the superextension of X consisting of all finitely generated maximal linked systems consisting of closed subsets of X. Then Y also has size
$Y=\lambda _f(X)$
be the superextension of X consisting of all finitely generated maximal linked systems consisting of closed subsets of X. Then Y also has size
![]() $\omega _1$
, since the collection of all finite subsets of X has size
$\omega _1$
, since the collection of all finite subsets of X has size
![]() $\omega _1$
, moreover, Y is Hausdorff, connected and locally connected (see [Reference Verbeek7, IV.3.4(v) and (viii)]).
$\omega _1$
, moreover, Y is Hausdorff, connected and locally connected (see [Reference Verbeek7, IV.3.4(v) and (viii)]).
We claim that Y is also regular and adopt the terminology of [Reference Verbeek7]. To prove this, let
![]() $m\in Y$
be arbitrary, and let A be a closed subset of Y not containing m. Let
$m\in Y$
be arbitrary, and let A be a closed subset of Y not containing m. Let
![]() $F\subseteq X$
be a finite defining set for m, and let
$F\subseteq X$
be a finite defining set for m, and let
![]() $n = m{\restriction }F$
. There is a finite collection of open subsets
$n = m{\restriction }F$
. There is a finite collection of open subsets
![]() $\mathcal {U}$
of X such that
$\mathcal {U}$
of X such that
![]() $m\in \bigcap _{U\in \mathcal {U}} U^+ \subseteq Y\setminus A$
. For each
$m\in \bigcap _{U\in \mathcal {U}} U^+ \subseteq Y\setminus A$
. For each
![]() $U\in \mathcal {U}$
, let
$U\in \mathcal {U}$
, let
![]() $N_U\in n$
be such that
$N_U\in n$
be such that
![]() $N_U\subseteq U$
. By regularity of X, we may pick an open neighborhood
$N_U\subseteq U$
. By regularity of X, we may pick an open neighborhood
![]() $V_U$
of
$V_U$
of
![]() $N_U$
whose closure is contained in U. Then
$N_U$
whose closure is contained in U. Then
![]() $\bigcap _{U\in \mathcal {U}} V_U^+$
is a closed neighborhood of m that misses A.
$\bigcap _{U\in \mathcal {U}} V_U^+$
is a closed neighborhood of m that misses A.
Hence Y is a connected, locally connected regular space which by Costantini’s result is
![]() $\omega $
-resolvable. (In this special case, there is also a direct proof of this.) But Y has cardinality
$\omega $
-resolvable. (In this special case, there is also a direct proof of this.) But Y has cardinality
![]() $\omega _1$
, hence it is not
$\omega _1$
, hence it is not
![]() $\mathfrak {c}$
-resolvable if the Continuum Hypothesis fails. So, for crowded locally connected regular spaces, a positive answer to the following question is the best we can hope for.
$\mathfrak {c}$
-resolvable if the Continuum Hypothesis fails. So, for crowded locally connected regular spaces, a positive answer to the following question is the best we can hope for.
Problem 3.1 Let X be regular, crowded, and locally connected (respectively,
![]() $\pi $
-connected). Is
$\pi $
-connected). Is
![]() $X \omega _1$
-resolvable?
$X \omega _1$
-resolvable?
We cannot resist mentioning here that it is still a widely open question whether non-singleton connected regular spaces are resolvable (see e.g., [Reference Pavlov and Pearl6] for details and references). This seems to be one of the most central open problems in the area.
We call a space X nowhere 0-dimensional if no non-empty open subspace of X is 0-dimensional. Clearly, any crowded locally connected, even
![]() $\pi $
-connected, space is nowhere 0-dimensional.
$\pi $
-connected, space is nowhere 0-dimensional.
Assume that X is a nowhere 0-dimensional Tykhonov space. We may assume that X is a subspace of
![]() $\mathbb {R}^I$
for some set I. For every
$\mathbb {R}^I$
for some set I. For every
![]() $i\in I$
, let
$i\in I$
, let
![]() $\pi _i\colon \mathbb {R}^I \to \mathbb {R}$
be the ith projection. Then, for every nonempty open subset U of X, there exists
$\pi _i\colon \mathbb {R}^I \to \mathbb {R}$
be the ith projection. Then, for every nonempty open subset U of X, there exists
![]() $i\in I$
such that
$i\in I$
such that
![]() $\pi _i(U)$
has nonempty interior. For otherwise U would be a subspace of a product of 0-dimensional spaces, and so would itself be 0-dimensional. Hence the collection of projections
$\pi _i(U)$
has nonempty interior. For otherwise U would be a subspace of a product of 0-dimensional spaces, and so would itself be 0-dimensional. Hence the collection of projections
![]() $\mathcal {P} = \{\pi _i{\restriction }X : i \in I\}$
is NWC in a (very) strong sense. This observation lead us to the following problem.
$\mathcal {P} = \{\pi _i{\restriction }X : i \in I\}$
is NWC in a (very) strong sense. This observation lead us to the following problem.
Problem 3.2 Is every nowhere 0-dimensional Tykhonov space resolvable (
![]() $\omega $
-resolvable,
$\omega $
-resolvable,
![]() $\mathfrak {c}$
-resolvable)?
$\mathfrak {c}$
-resolvable)?