Abstract
This work investigates a Bregman and inertial extension of the forward–reflected–backward algorithm (Malitsky and Tam in SIAM J Optim 30:1451–1472, 2020) applied to structured nonconvex minimization problems under relative smoothness. To this end, the proposed algorithm hinges on two key features: taking inertial steps in the dual space, and allowing for possibly negative inertial values. The interpretation of relative smoothness as a two-sided weak convexity condition proves beneficial in providing tighter stepsize ranges. Our analysis begins with studying an envelope function associated with the algorithm that takes inertial terms into account through a novel product space formulation. Such construction substantially differs from similar objects in the literature and could offer new insights for extensions of splitting algorithms. Global convergence and rates are obtained by appealing to the Kurdyka–Łojasiewicz property.
Similar content being viewed by others
Notes
Take \(x^k\in {{\,\textrm{dom}\,}}h{\setminus } C\) with \(\Vert x^k\Vert \rightarrow \infty \). Since \({{\,\textrm{dom}\,}}h\) is convex, its interior \(C\) is nonempty, and \(f\) is continuous on \({{\,\textrm{dom}\,}}h\), for each \(k\) there exists \({\tilde{x}}^k\in C\) with \(\Vert x^k-{\tilde{x}}^k\Vert \le 1\) such that \(h({\tilde{x}}^k)-\gamma f({\tilde{x}}^k)\le h(x^k)-\gamma f(x^k)+1\). By 1-coercivity on \(C\ni {\tilde{x}}^k\), \((h({\tilde{x}}^k)-\gamma f({\tilde{x}}^k))/\Vert \tilde{x}^k\Vert \rightarrow \infty \), implying that \((h(x^k)-\gamma f(x^k))/\Vert x^k\Vert \rightarrow \infty \) as well.
The equivalence of the domains follows from the inclusion \({{\,\textrm{dom}\,}}f\supseteq {{\,\textrm{dom}\,}}h\).
Being \({\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}\) defined on \(C\times C\), osc and local boundedness are meant relative to \(C\times C\). Namely, \({{\,\textrm{gph}\,}}{\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}\) is closed relative to \(C\times C\times \mathbb {R}^n\), and
 is bounded for any
is bounded for any  compact.
compact.This also covers the case in which \(f\) is affine on \(C\), although a tighter \(p_{-f,h}=0\) could be considered in this case and improve the range to \(\beta \in (-1/2,0]\) and any \(\gamma >0\).
References
Ahookhosh, M., Themelis, A., Patrinos, P.: A Bregman forward-backward linesearch algorithm for nonconvex composite optimization: superlinear convergence to nonisolated local minima. SIAM J. Optim. 31(1), 653–685 (2021)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137(1), 91–129 (2013)
Azé, D., Penot, J.: Uniformly convex and uniformly smooth convex functions. Annales de la Faculté des sciences de Toulouse: Mathématiques, Ser. 6 4(4), 705–730 (1995)
Bauschke, H.H., Bolte, J., Teboulle, M.: A descent lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications. Math. Oper. Res. 42(2), 330–348 (2017)
Bauschke, H.H., Borwein, J.M., Combettes, P.L.: Essential smoothness, essential strict convexity, and Legendre functions in Banach spaces. Commun. Contemp. Math. 3(04), 615–647 (2001)
Bauschke, H.H., Borwein, J.M., Combettes, P.L.: Bregman monotone optimization algorithms. SIAM J. Control. Optim. 42(2), 596–636 (2003)
Bauschke, H.H., Combettes, P.L.: Iterating Bregman retractions. SIAM J. Optim. 13(4), 1159–1173 (2003)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics, Springer (2017)
Beck, A., Teboulle, M.: Mirror descent and nonlinear projected subgradient methods for convex optimization. Oper. Res. Lett. 31(3), 167–175 (2003)
Bertsekas, D.P.: Nonlinear Programming. Athena Scientific (2016)
Böhm, A., Sedlmayer, M., Csetnek, E.R., Boţ, R.I.: Two steps at a time-taking GAN training in stride with Tseng’s method. SIAM J. Math. Data Sci. 4(2), 750–771 (2022)
Bolte, J., Sabach, S., Teboulle, M., Vaisbourd, Y.: First order methods beyond convexity and Lipschitz gradient continuity with applications to quadratic inverse problems. SIAM J. Optim. 28(3), 2131–2151 (2018)
Boţ, R.I., Dao, M.N., Li, G.: Extrapolated proximal subgradient algorithms for nonconvex and nonsmooth fractional programs. Math. Oper. Res. 47(3), 2415–2443 (2022)
Boţ, R.I., Nguyen, D.: The proximal alternating direction method of multipliers in the nonconvex setting: convergence analysis and rates. Math. Oper. Res. 45(2), 682–712 (2020)
Chen, G., Teboulle, M.: Convergence analysis of a proximal-like minimization algorithm using Bregman functions. SIAM J. Optim. 3(3), 538–543 (1993)
Dragomir, R., d’Aspremont, A., Bolte, J.: Quartic first-order methods for low-rank minimization. J. Optim. Theory Appl. 189(2), 341–363 (2021)
Dragomir, R., Taylor, A.B., d’Aspremont, A., Bolte, J.: Optimal complexity and certification of Bregman first-order methods. Math. Program. 194(1), 41–83 (2022)
Gidel, G., Hemmat, R.A., Pezeshki, M., Le Priol, R., Huang, G., Lacoste-Julien, S., Mitliagkas, I.: Negative momentum for improved game dynamics. In: The 22nd International Conference on Artificial Intelligence and Statistics, pp. 1802–1811. PMLR (2019)
Hanzely, F., Richtarik, P., Xiao, L.: Accelerated Bregman proximal gradient methods for relatively smooth convex optimization. Comput. Optim. Appl. 79(2), 405–440 (2021)
Kan, C., Song, W.: The Moreau envelope function and proximal mapping in the sense of the Bregman distance. Nonlinear Anal.: Theory Methods Appl. 75(3), 1385–1399 (2012)
László, S.C.: A forward-backward algorithm with different inertial terms for structured non-convex minimization problems. J. Optim, Theory Appl (2023)
Li, G., Liu, T., Pong, T.K.: Peaceman-Rachford splitting for a class of nonconvex optimization problems. Comput. Optim. Appl. 68(2), 407–436 (2017)
Li, G., Pong, T.K.: Global convergence of splitting methods for nonconvex composite optimization. SIAM J. Optim. 25(4), 2434–2460 (2015)
Li, G., Pong, T.K.: Douglas-Rachford splitting for nonconvex optimization with application to nonconvex feasibility problems. Math. Program. 159(1), 371–401 (2016)
Liu, Y., Yin, W.: An envelope for Davis-Yin splitting and strict saddle-point avoidance. J. Optim. Theory Appl. 181(2), 567–587 (2019)
Lu, H., Freund, R.M., Nesterov, Y.: Relatively smooth convex optimization by first-order methods, and applications. SIAM J. Optim. 28(1), 333–354 (2018)
Mairal, J.: Incremental majorization-minimization optimization with application to large-scale machine learning. SIAM J. Optim. 25(2), 829–855 (2015)
Malitsky, Y., Tam, M.K.: A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J. Optim. 30(2), 1451–1472 (2020)
Mordukhovich, B.: Variational Analysis and Applications, volume 30. Springer (2018)
Moreau, J.: Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. France 93, 273–299 (1965)
Moreau, J.: Fonctionnelles convexes. Séminaire Jean Leray (2):1–108 (1966–1967)
Nesterov, Y.: Lectures on Convex Optimization, volume 137. Springer (2018)
Nesterov, Y.: Implementable tensor methods in unconstrained convex optimization. Math. Program. 186, 157–183 (2021)
Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1(3), 127–239 (2014)
Reem, D., Reich, S., De Pierro, A.: Re-examination of Bregman functions and new properties of their divergences. Optimization 68(1), 279–348 (2019)
Rockafellar, R.T., Wets, R.J.: Variational Analysis, volume 317. Springer (2011)
Stella, L., Themelis, A., Patrinos, P.: Newton-type alternating minimization algorithm for convex optimization. IEEE Trans, Automatic Control (2018)
Teboulle, M.: A simplified view of first order methods for optimization. Math. Program. 170(1), 67–96 (2018)
Themelis, A.: Proximal Algorithms for Structured Nonconvex Optimization. PhD thesis, KU Leuven (2018)
Themelis, A., Hermans, B., Patrinos, P.: A new envelope function for nonsmooth DC optimization. In: 2020 59th IEEE Conference on Decision and Control (CDC), pp. 4697–4702 (2020)
Themelis, A., Patrinos, P.: Douglas-Rachford splitting and ADMM for nonconvex optimization: Tight convergence results. SIAM J. Optim. 30(1), 149–181 (2020)
Themelis, A., Stella, L., Patrinos, P.: Forward-backward envelope for the sum of two nonconvex functions: further properties and nonmonotone linesearch algorithms. SIAM J. Optim. 28(3), 2274–2303 (2018)
Themelis, A., Stella, L., Patrinos, P.: Douglas-Rachford splitting and ADMM for nonconvex optimization: accelerated and Newton-type algorithms. Comput. Optim. Appl. 82, 395–440 (2022)
Wang, X., Wang, Z.: A Bregman inertial forward-reflected-backward method for nonconvex minimization. J. Glob. Optim. (2023). https://doi.org/10.1007/s10898-023-01348-y
Wang, X., Wang, Z.: The exact modulus of the generalized concave Kurdyka-Łojasiewicz property. Math. Oper. Res. 47(4), 2765–2783 (2022)
Wang, X., Wang, Z.: Malitsky-Tam forward-reflected-backward splitting method for nonconvex minimization problems. Comput. Optim. Appl. 82(2), 441–463 (2022)
Acknowledgements
The authors are deeply thankful to the anonymous reviewers for their thorough reading and many constructive comments that significantly improved the quality and rigor of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Radu Ioan Boţ.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the NSERC Discovery Grants and JSPS KAKENHI grant number JP21K17710.
Appendices
Proof of Theorem 4.6
Throughout this appendix, we remind that the adoption of extended arithmetics is not necessary, since, as a result of Lemma 4.2.(iii), all variables are confined in the open set \(C\) onto which both \(h\) and \(f\) (and consequently \(\hat{h}\) and \(\hat{f}_{\!\beta }\) as well, for any \(\beta \in \mathbb {R}\)) are finite-valued.
1.1 Proof of Theorem 4.6.(i) and 4.6.(ii)
We begin by proving a technical lemma in the setting of Theorem 4.6.(A).
Lemma A.1
Suppose that Assumption 1 holds and let \(\gamma >0\) and \(\beta \in \mathbb {R}\) be such that \(\hat{f}_{\!\beta }\mathrel {{=}}f\mathbin {\dot{-}}\frac{\beta }{\gamma }h{}+{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}\) is a convex function. Then, for every \(x,x^-\in C\) and \(\bar{x}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)\)
Proof
The claimed inequality follows from (4.6) together with the fact that \({{\,\textrm{D}\,}}_{\hat{f}_{\!\beta }}\ge 0\). \(\square \)
In the setting of Theorem 4.6.(A), recall that we set \(c\mathrel {{:}{=}}1+2\beta +3\alpha p_{-f,h}>0\). Then, inequality (A.1) can equivalently be written in terms of  as
as

where the second inequality owes to the fact that \({{\,\textrm{D}\,}}_{\hat{h}-2\hat{f}_{\!\beta }-\frac{c}{\gamma }h}\ge 0\), since \(\hat{h}-2\hat{f}_{\!\beta }-\frac{c}{\gamma }h\) is convex, having

the coefficient of \(h\) being null by definition of \(c\), and \(-f-\sigma _{-f,h}h\) being convex by definition of the relative weak convexity modulus \(\sigma _{-f,h}\), cf. Definition 3.3. This proves (4.10a); inequality (4.10b) follows similarly by observing that
so that

This concludes the proof of Theorem 4.6.(i) and 4.6.(ii) in the setting of Theorem 4.6.(A).
Now we work under the setting of Theorem 4.6.(B), in which case the following lemma will be useful.
Lemma A.2
Additionally to Assumption 1, suppose that \(\hat{f}_{\!\beta }\) is \(L_{\hat{f}_{\!\beta }}\)-Lipschitz differentiable for some \(L_{\hat{f}_{\!\beta }}\ge 0\). Then, for every \(x,x^-\in C\) and \({\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)\) we have
Proof
By means of the three-point identity, that is, by using (4.3a) in place of (4.3b), inequality (4.6) can equivalently be written as
which by using Young’s inequality on the inner product and \(L_{\hat{f}_{\!\beta }}\)-Lipschitz differentiability yields
Rearranging and using the fact that \({{\,\textrm{D}\,}}_{{\mathcal {j}}}(x,y)=\frac{1}{2}\Vert x-y\Vert ^2\) yields the claimed inequality. \(\square \)
Under Theorem 4.6.(B), recall that we define
We will pattern the arguments of the previous case, and observe that inequality (A.2) can equivalently be written in terms of  as
as

Once again, the fact that \({{\,\textrm{D}\,}}_{\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}-\frac{c}{\gamma }h}\ge 0\) owes to the convexity of \(\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}-\frac{c}{\gamma }h\) on \({{\,\textrm{dom}\,}}h\), having

altogether proving (4.10a). Similarly, inequality (4.10b) follows from (A.3) together with the fact that \({{\,\textrm{D}\,}}_{\hat{h}-L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\ge {{\,\textrm{D}\,}}_{\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\ge \frac{c}{\gamma }{{\,\textrm{D}\,}}_h\), as shown above, having

This concludes the proof of Theorems 4.6.(i) and 4.6.(ii).
1.2 Proof of Theorem 4.6.(iii)
We first state a property of the Bregman distance \({{\,\textrm{D}\,}}_h\) that holds when \(h\) is as in the assertion of the theorem. The proof is provided for completeness, though part of it is straightforward and the rest is an easy adaptation of [6, Lem. 7.3(viii)].
Lemma A.3
Let \(h:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}\) be a 1-coercive Legendre kernel. If either \(h\) is strongly convex or \({{\,\textrm{dom}\,}}h=\mathbb {R}^n\), then \({{\,\textrm{D}\,}}_h(x,y)\) is level bounded in \(y\) locally uniformly in \(x\).
Proof
Let \((x^k)_{k\in \mathbb {N}}\) and \((y^k)_{k\in \mathbb {N}}\) be sequences in \(\mathbb {R}^n\) such that \({{\,\textrm{D}\,}}_h(x^k,y^k)\le \ell \) for some \(\ell \in \mathbb {R}\). Suppose that \((x^k)_{k\in \mathbb {N}}\) is bounded; then the proof reduces to showing that also \((y^k)_{k\in \mathbb {N}}\) is. If \(h\) is, say, \(\sigma _h\)-strongly convex for some \(\sigma _h>0\), the claim trivially follows from the fact that \({{\,\textrm{D}\,}}_h(x,y)\ge (\sigma _h/2)\Vert x-y\Vert ^2\) in this case.
Suppose that \({{\,\textrm{dom}\,}}h=\mathbb {R}^n\), then it follows from [6, Thm. 3.4] that \(h^*\) is 1-coercive. Furthermore, observe that
where \(c\mathrel {{:}{=}}\inf h(x^k)\) and \(c'\mathrel {{:}{=}}\sup \Vert x^k\Vert \) are finite. Since \(h^*\) is 1-coercive, it follows that \((\nabla h(y^k))_{k\in \mathbb {N}}\) is bounded, and therefore so is \((y^k)_{k\in \mathbb {N}}\) by virtue of [6, Thm. 3.3]. \(\square \)
We now turn to the proof of Theorem 4.6.(iii). By contraposition, suppose that  is not level bounded, and consider an unbounded sequence \((x_k,x_k^-)_{k\in \mathbb {N}}\) such that
is not level bounded, and consider an unbounded sequence \((x_k,x_k^-)_{k\in \mathbb {N}}\) such that

for some \(\ell \in \mathbb {R}\). Then, it follows from (4.10b) that
and in particular both \(({{\,\textrm{D}\,}}_h({\bar{x}}_k,x_k))_{k\in \mathbb {N}}\) and \(({{\,\textrm{D}\,}}_h(x_k,x_k^-))_{k\in \mathbb {N}}\) are bounded. Moreover, it follows from Lemma A.3 that if \((x_k^-)_{k\in \mathbb {N}}\) is unbounded then so is \((x_k)_{k\in \mathbb {N}}\), and similarly unboundedness of \((x_k)_{k\in \mathbb {N}}\) implies that of \(({\bar{x}}_k)_{k\in \mathbb {N}}\). Since at least one among \((x_k)_{k\in \mathbb {N}}\) and \((x_k^-)_{k\in \mathbb {N}}\) is unbounded, it follows that \(({\bar{x}}_k)_{k\in \mathbb {N}}\) is unbounded. Noticing that this sequence is contained in \([\varphi _{\overline{C}}\le \ell ]\), we conclude that \(\varphi _{\overline{C}}\) is not level bounded.
Proof of Theorem 5.6
In the remainder of this section, we will make use of the norm  on the product space \(\mathbb {R}^n\times \mathbb {R}^n\) defined as
on the product space \(\mathbb {R}^n\times \mathbb {R}^n\) defined as  . For a set \(E\subseteq \mathbb {R}^n\), define \((\forall \varepsilon >0)\) \(E_\varepsilon =\{x\in \mathbb {R}^n:{{\,\textrm{dist}\,}}(x,E)<\varepsilon \}\).
. For a set \(E\subseteq \mathbb {R}^n\), define \((\forall \varepsilon >0)\) \(E_\varepsilon =\{x\in \mathbb {R}^n:{{\,\textrm{dist}\,}}(x,E)<\varepsilon \}\).
Let \((\forall k\in \mathbb {N})\) \(z^k=(x^{k+1},x^k,x^{k-1})\), and let \(\Omega \) be the set of limit points of \((z_k)_{k\in \mathbb {N}}\). Define

Set \((\forall k\in \mathbb {N})\)  for simplicity. Then
for simplicity. Then  , \(\delta _{k}\rightarrow \varphi ^\star \) decreasingly and \({{\,\textrm{dist}\,}}(x^k,\Omega )\rightarrow 0\) as \(k\rightarrow +\infty \) by invoking Theorem 5.1. Assume without loss of generality that \((\forall k\in \mathbb {N})\) \(\delta _{k}>\varphi ^\star \), otherwise we would have \((\exists k_0\in \mathbb {N})\) \(x^{k_0}=x^{k_0+1}\) due to Theorem 5.1.(i), from which the desired result readily follows by simple induction. Thus, \((\exists k_0\in \mathbb {N})\) \((\forall k\ge k_0)\)
, \(\delta _{k}\rightarrow \varphi ^\star \) decreasingly and \({{\,\textrm{dist}\,}}(x^k,\Omega )\rightarrow 0\) as \(k\rightarrow +\infty \) by invoking Theorem 5.1. Assume without loss of generality that \((\forall k\in \mathbb {N})\) \(\delta _{k}>\varphi ^\star \), otherwise we would have \((\exists k_0\in \mathbb {N})\) \(x^{k_0}=x^{k_0+1}\) due to Theorem 5.1.(i), from which the desired result readily follows by simple induction. Thus, \((\exists k_0\in \mathbb {N})\) \((\forall k\ge k_0)\)  . Appealing to Theorem 5.1.(iii) and Lemma 4.2.(i) yields that
. Appealing to Theorem 5.1.(iii) and Lemma 4.2.(i) yields that  is constantly equal to \(\varphi ^\star \) on the compact set \(\Omega \). Note that
is constantly equal to \(\varphi ^\star \) on the compact set \(\Omega \). Note that  satisfies the KL property under Assumption 5.6.A3; see, e.g., [2, §4.3]. In turn, appealing to Assumption 5.6.A3 and a standard uniformizing technique of the KL property, see, e.g., [13, Lem. 6.2], implies that there exists a concave \(\psi \in \Psi _\eta \) such that for \(k\ge k_0\)
satisfies the KL property under Assumption 5.6.A3; see, e.g., [2, §4.3]. In turn, appealing to Assumption 5.6.A3 and a standard uniformizing technique of the KL property, see, e.g., [13, Lem. 6.2], implies that there exists a concave \(\psi \in \Psi _\eta \) such that for \(k\ge k_0\)

Define \((\forall k\in \mathbb {N})\)
Applying subdifferential calculus to  yields that
yields that

which together with Lemma 4.2.(iv) entails that  . In turn, Assumption 5.6.A2 implies that there exists \(M>0\) such that
. In turn, Assumption 5.6.A2 implies that there exists \(M>0\) such that

Finally, we show that \((x^k)_{k\in \mathbb {N}}\) is convergent. For simplicity, define \((\forall k,l\in \mathbb {N})\) \(\Delta _{k,l}=\psi \left( \delta _{k}-\varphi ^\star \right) -\psi \left( \delta _{l}-\varphi ^\star \right) \). Then, combining (B.1) and (B.2) yields

where the second inequality is implied by concavity of \(\psi \), the third one follows from (5.1), and the fourth one holds because \(\sigma >0\) is the strong convexity modulus of h on a convex compact set that contains all the iterates. Hence,

Summing (B.3) from \(k=k_0\) to an arbitrary \(l\ge k_0+1\) yields that

where the second inequality holds as \(\psi \ge 0\), from which one sees that \(\sum _{k=0}^\infty \Vert x^{k+1}-x^k\Vert \) is finite as l is arbitrary. A similar procedure shows that \((x^k)_{k\in \mathbb {N}}\) is Cauchy, which together with Theorem 5.1.(iii) entails the rest of the statement.
Proof of Theorem 5.9
Assume without loss of generality that  has desingularizing function \(\psi (t)=t^{1-\theta }/(1-\theta )\) and let \((\forall k\in \mathbb {N})\) \(\delta _{k}=\sum _{i=k}^\infty \Vert x^{i+1}-x^i\Vert \). We claim that
has desingularizing function \(\psi (t)=t^{1-\theta }/(1-\theta )\) and let \((\forall k\in \mathbb {N})\) \(\delta _{k}=\sum _{i=k}^\infty \Vert x^{i+1}-x^i\Vert \). We claim that
Indeed, summing (B.3) from every \(k\ge k_0\) to \(l\ge k+1\) and passing l to infinity give

from which the desired claim readily follows. It is routine to see that the desired sequential rate can be implied by those of \((e_k)_{k\in \mathbb {N}}\) through (C.1); see, e.g., [45, Thm. 5.3]; therefore, it suffices to prove convergence rate of \((e_k)_{k\in \mathbb {N}}\).
Recall from Theorem 5.1.(i) that \((e_k)_{k\in \mathbb {N}}\) is a decreasing sequence converging to 0. Then invoking the KL exponent assumption yields

where the first equality holds due to Lemma 4.5.(ii), which together with (B.2) implies that

Appealing again to Theorem 5.1.(i) gives

where the last inequality is implied by (C.2). Then [15, Lem. 10] justifies the desired rate of \((e_k)_{k\in \mathbb {N}}\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, Z., Themelis, A., Ou, H. et al. A Mirror Inertial Forward–Reflected–Backward Splitting: Convergence Analysis Beyond Convexity and Lipschitz Smoothness. J Optim Theory Appl (2024). https://doi.org/10.1007/s10957-024-02383-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10957-024-02383-9
Keywords
- Nonsmooth nonconvex optimization
- Forward–reflected–backward splitting
- Inertia
- Bregman distance
- Mordukhovich limiting subdifferential
- Relative smoothness


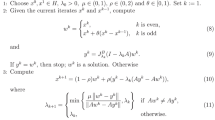


 is bounded for any
is bounded for any  compact.
compact.