Variable cross sections functionally grad beams on Pasternak foundations: An enhanced interaction theory for construction applications

Abstract

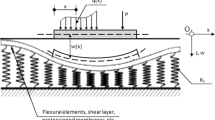
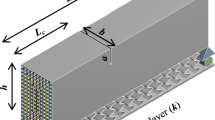
Functionally graded materials (FGMs) are commonly utilized in construction projects. They enhance the performance of functionally graded beams (FGBs) under various loading conditions. Therefore, the incorporation of variable-section FGBs theory into the analysis of structural and soil interactions is crucial for advancing engineering applications. Employing the variational principle and the transfer-matrix method, and considering the shear stiffness of the axially FGB structure itself, along with the continuity and shear strength of the soil, a semi-analytical solution for displacement and internal force of axially FGBs on Pasternak foundation (termed as P–T model) is derived in this paper. The semi-analytical solution is subsequently compared with finite difference solution results from prior studies, affirming the accuracy and precision of the proposed computational theory. The P–T model degenerates to the Winkler–Timoshenko model (W–T model) when the foundation’s shear layer stiffness is set to zero. Additional analysis is conducted on displacement and internal force variation when the beam stiffness follows different distribution along the axial direction. The results indicate that an asymmetrical distribution of stiffness on either side of the midpoint could increase the displacement at the middle section. Furthermore, when the beam stiffness adheres to a Gaussian distribution along the axial direction of the beam, a significant increase in displacement at the boundary position of the beam is observed. The proposed method is then integrated with the Mindlin stress solution to evaluate construction impact on an existing tunnel within a foundation pit project in Shenzhen. A comparative analysis of theoretical calculations, monitoring data, and numerical simulation results exhibits substantial concurrence across the three methods. The tunnel’s overall deflection adopts an “M” shape, and the computation using the variable-section FGB portrays the existing tunnel’s deformation trend with heightened accuracy, diminishing the calculation error from 35 to 8.3% compared to the conventional normal section beam.

Appendix

In Eq. (12), the detailed expression for $A_{i} (x),B_{i} (x),C_{i} (x),D_{i} (x)$ is as follows:

$$ \begin{aligned} A_{1} (x) = & {\text{ch}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \frac{{\beta^{2} \left[ {1 + \frac{D}{C}(\alpha^{2} + \beta^{2} )} \right] - \alpha^{2} \left[ {1 - \frac{D}{C}(\alpha^{2} + \beta^{2} )} \right]}}{2\alpha \beta }{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ B_{1} (x) = & \frac{C}{C + T}\left[ {\frac{{{\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\beta } + \frac{{{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha }} \right] \\ C_{1} (x) = & \frac{{\beta \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \alpha \left[ {1 - \frac{D}{C}(\alpha^{2} + \beta^{2} )} \right]{\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{{2\alpha \beta \left( {\alpha^{2} + \beta^{2} } \right)D\frac{C + T}{C}}} \\ D_{1} (x) = & - \frac{{{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{{2\alpha \beta D\frac{C + T}{C}}} \\ A_{2} (x) = & \frac{C + T}{C}\left\{ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right\} \cdot \frac{{\beta {\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \alpha {\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\alpha \beta } \\ \end{aligned} $$

$$ \begin{gathered} B_{2} (x) = {\text{ch}}(\alpha x)\cos (\beta x) + \frac{{\alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }{\text{sh}}(\alpha x)\sin (\beta x) \hfill \\ C_{2} \left( x \right) = - \frac{{\alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} }}{{2\alpha \beta \left( {\alpha^{2} + \beta^{2} } \right)D}} \cdot {\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \hfill \\ D_{2} \left( x \right) = - \frac{{\alpha \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]{\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) + \beta \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha \beta D} \hfill \\ A_{3} \left( x \right) = \frac{{D(C + T)(\alpha^{2} + \beta^{2} )}}{2\alpha C}\left\{ {\alpha^{2} \left[ {3 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\}{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{2\beta C} \hfill \\ B_{3} \left( x \right) = \frac{{DC\left( {\alpha^{2} + \beta^{2} } \right)^{2} }}{2\alpha \beta C} \cdot {\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \hfill \\ C_{3} \left( x \right) = {\text{ch}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \left[ {\frac{{\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }} \right]{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \hfill \\ D_{3} \left( x \right) = \left( {\alpha^{2} + \beta^{2} } \right)\left[ {\frac{{{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha } - \frac{{{\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\beta }} \right] \hfill \\ \end{gathered} $$

$$ \begin{aligned} B_{2} \left( x \right) = & {\text{ch}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \frac{{\alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ C_{2} \left( x \right) = & - \frac{{\alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} }}{{2\alpha \beta \left( {\alpha^{2} + \beta^{2} } \right)D}} \cdot {\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ D_{2} \left( x \right) = & - \frac{{\alpha \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]{\text{ch}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) + \beta \left[ {1 + \frac{D}{C}(\alpha^{2} + \beta^{2} )} \right]{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha \beta D} \\ A_{3} \left( x \right) = & \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{2\alpha C}\left\{ {\alpha^{2} \left[ {3 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\}{\text{sh}}(\alpha x)\cos \left( {\beta x} \right) + \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{2\beta C} \\ B_{3} \left( x \right) = & \frac{{DC\left( {\alpha^{2} + \beta^{2} } \right)^{2} }}{2\alpha \beta C} \cdot {\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ C_{3} \left( x \right) = & {\text{ch}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \left[ {\frac{{\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }} \right]{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ D_{3} \left( x \right) = & \left( {\alpha^{2} + \beta^{2} } \right)\left[ {\frac{{{\text{sh}}\left( {\alpha x} \right)\cos (\beta x)}}{2\alpha } - \frac{{{\text{ch}}\left( {\alpha x} \right)\sin (\beta x)}}{2\beta }} \right] \\ A_{4} \left( x \right) = & \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{2\alpha \beta C}\left\{ {\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right\} \cdot {\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ B_{4} \left( x \right) = & \left\{ {\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {3 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\} \cdot \frac{{{\text{ch}}(\alpha x)\cos \left( {\beta x} \right)D}}{2\alpha } \\ & \; + \left\{ {\beta^{2} \left[ {3 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right\} \cdot \frac{{{\text{ch}}(\alpha x)\sin \left( {\beta x} \right)D}}{2\beta } \\ C_{4} \left( x \right) = & \frac{C}{{C\left( {\alpha^{2} + \beta^{2} } \right)}}\left[ {\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right]\left[ {\frac{{{\text{sh}}\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha } + \frac{{{\text{ch}}\left( {\alpha x} \right)\sin (\beta x)}}{2\beta }\left( {\beta x} \right)} \right] \\ D_{4} \left( x \right) = & {\text{ch}}\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \frac{{\beta^{2} \left[ {1 + \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }{\text{sh}}\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ \end{aligned} $$