Elastoplastic peridynamic formulation for materials with isotropic and kinematic hardening

Abstract

We present an ordinary state-based peridynamic model in 2D and 3D consistent with rate-independent J2 plasticity with associated flow rule. The new contribution is the capability of the elastoplastic law to describe isotropic, kinematic and mixed hardening. The hardening formulations follow those available in the literature for classical elastoplasticity. The comparison between the results obtained with the peridynamic model and those obtained with a commercial FEM software shows that the two approaches are in good agreement. The extent of the plastic regions and von Mises stress computed with the new model for 2D and 3D examples match well those obtained with FEM-based solutions using ANSYS.

1 Introduction

Before crack initiation, most materials undergo elastoplastic deformation. The idea of plastic behavior appeared very early in the engineering literature to characterize the rheological behavior of materials under a wide range of circumstances of practical interest in which irreversible (or inelastic) deformations develop and, since the previous century, it has been extensively studied for a wide range of materials including metals, concrete, soils, ice, rocks, fiber composites and many other materials (see, e.g., [1, 2] for a review).

The most popular mathematical framework to describe irreversible deformations is the classical Plasticity Theory (the so-called elastoplasticity). The origin of elastoplasticity can be traced back to the middle of the nineteenth century and, following the substantial development that took place, particularly in the first half of the twentieth century, this theory is today well established on sound mathematical foundations. For a comprehensive treatment of the Theory of Plasticity, the reader is referred to [3,4,5,6,7].

According to elastoplasticity, a material behaves elastically in the initial stage of deformation, whereas plastic deformations develop, as the load increases, once a stress limit value is exceeded. The onset of plastic deformations is determined by a surface in the stress space, which is called the yield surface. The direction of plastic deformations is determined by another surface, the so-called plastic potential, whereas its magnitude can be determined from the consistency condition, which requires that a stress point remains on the yield surface when the material is loaded. Unloading occurs elastically.

Alternative to elastoplasticity, noteworthy are the Generalized Theory of Plasticity [8] and the Hypoplasticity [9]. These frameworks describe inelastic phenomena without using the notions yield surface, plastic potential, consistency condition and plastic multiplier, and are mainly applied to granular materials like soils.

In the case of metals, elastoplasticity is widely adopted. Experimental observations have revealed complex behavior in the plastic domain, inspiring models of isotropic and kinematic hardening to describe such complexities [10]. While such models have significantly improved predictions of elastoplastic deformations, the transition from plasticity to ductile fracture/failure has been more complicated.

In the last 20 years, peridynamics (PD) proposed by Silling [11] has attracted the attention of many researchers for its ability to handle discontinuities in materials, such as initiation and propagation of cracks. Unlike classical continuum mechanics models, PD does not use spatial derivatives and instead, an integral operator can easily handle discontinuities, including those present in the displacement field when cracks are involved.

The first peridynamic formulation developed by Silling is called bond-based peridynamics (BB-PD), in which the bond force (the interaction between two material points) only depends on the deformation of that bond. BB-PD-based models lead to a fixed Poisson’s ratio, 1/4 in 3D and 2D plane strain, and 1/3 in 2D plane stress [12]. To overcome this limitation the state-based version of the PD was proposed in [13]. Later, another approach, called extended bond-based peridynamic model (XBB-PD), was proposed in [14,15,16] to consider the bond rotation effect to handle the limitation of Poisson’s ratio present in bond-based PD.

In state-based peridynamics [13], the bond force depends on the deformation of the bond connecting the two material points and also on the overall deformation of all the other bonds connected to the two material points. The state-based PD formulation is divided into ordinary and non-ordinary versions. In ordinary state-based peridynamics (OSB-PD), the bond force is aligned with the bond whereas in non-ordinary state-based peridynamics (NOSB-PD), the bond force can be in a direction which is not aligned with that bond [13, 17]. It is worth mentioning that within the non-ordinary formulation, correspondence models have been introduced to allow a classical (local) material model to be used and adapted into the peridynamic framework [13]. Therefore, readers may wonder why bother with OSB-PD, which requires constructing the constitutive model, from the start, in the nonlocal PD setting. There are several reasons for pursuing “native” PD models, like the OSB-PD model discussed in this paper. Compared with NOSB-PD, OSB-PD models automatically satisfy the balance of angular momentum. Moreover, OSB-PD models do not exhibit zero-energy mode instabilities seen in correspondence models [18], and, therefore, do not require special treatment to reduce or eliminate them. Furthermore, correspondence models reintroduce deformation gradients in their formulation in order to map peridynamic states (forces and extensions, general nonlinear mappings) into stress and strain tensors (linear mappings) used in the existing, classically formulated constitutive laws. This is somewhat contrary to the PD philosophy of not using spatial gradients in the formulation with the aim of treating the evolution of damage in a mathematically consistent way. There is also a practical argument to be made for using OSB-PD models instead of correspondence models: reference [19] shows that correspondence models tend to be significantly more expensive to compute, due to the constant need of translating back-and-forth between force/extension states (the primary quantities that PD models operate with), and stress/strain tensors (the primary quantities in classical constitutive models).

Different PD models have been developed for the analysis of brittle fracture in elastic materials [11, 13, 20,21,22,23,24,25,26,27,28]. However, relatively few works have been dedicated to the development of PD models for the mechanical behavior of elastoplastic materials. In 2007, Silling et al. [13] developed an ordinary state-based peridynamic constitutive model for 3D elastoplastic materials with perfect plasticity. Then Mitchell [29] extended this 3D formulation to consider a non-local yield criterion based on J2 plasticity for perfectly-plastic materials. Madenci and Oterkus [30] developed an OSB-PD constitutive model for 2D elastoplastic materials with isotropic hardening. Later, their approach was extended to materials with kinematic hardening [31]. Liu et al. [32] developed another 2D and 3D OSB-PD elastoplastic constitutive model for materials with isotropic hardening but their numerical examples did not include 3D cases. Mousavi et al. [33] developed a similar formulation to [29] for 2D plane stress and plane strain cases, and they provided the solution of several examples.

Most of the PD literature for elastoplastic problems is in 2D. Our plasticity model is capable of solving 2D plane stress and plane strain cases, and 3D problems with small strains and large rotations considering isotropic and kinematic hardening. Although references [30, 31] developed elastoplastic models which solve materials with hardening, they do not address the solution of 3D problems and problems with large rotations. In addition, it is not clear whether their 2D formulation can model plane stress and plane strain conditions.

This paper presents an elastoplastic ordinary state-based peridynamic formulation for materials with isotropic and kinematic hardening. The J2 elastoplastic formulation, developed in [10, 34], is applied to the bond forces. After summarising previous formulations of perfect plasticity in 2D [33] and 3D [29], we equip them with isotropic and kinematic hardening.

The main contribution of this paper is an OSB-PD model for elastoplastic deformations (small strains but large rotations) in materials with isotropic and kinematic hardening, in 2D (plane stress and plane strain) and 3D.

The paper is organised as follows: in Sect. 2, the formulation is discussed; the numerical procedure is explained in Sect. 3, and then in Sect. 4, some numerical peridynamic results are compared with results obtained from the FEM using ANSYS for 2D and 3D examples to show the capabilities of the proposed approach.

The elastoplastic model introduced here is one step towards a future OSB-PD model for ductile fracture.

2 Elastoplastic peridynamic formulation for materials with isotropic and kinematic hardening

This section describes the proposed formulation to include the models of isotropic and kinematic hardening. In the text, underlined characters are used for PD states, bold characters refer to vectors and non-bold ones to scalars.

2.1 Ordinary state-based peridynamic formulation for elastic materials

The basic assumption of peridynamics is that a continuum is made of a set of material points, with infinitesimal volume and mass, which interact with each other via short-range potentials. In particular, each material point interacts with every point in its neighbourhood and the interaction is referred to as bond. For each material point, a neighbourhood with a constant radius, called horizon is considered. It is worth noting that, the neighbourhood and the horizon, are defined in the initial undeformed configuration of the body. The neighbourhood region is a line for 1D cases, a circular disk in 2D, and a sphere in 3D. These shapes can be, however, altered, when it is convenient to do so (see, e.g., [35]).

Fig. 1

Positions of two interacting material points in a peridynamic body: a initial and b deformed configuration

2.1.1 Displacement and force states

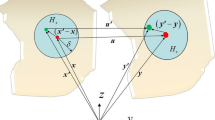
In state-based peridynamics, the following defines the extension in a bond:

$$\begin{aligned} \underline{e}=\underline{y}-\underline{x} \end{aligned}$$

(1)

where $\underline{y}=|\underline{\textrm{Y}}|=|{{\varvec{y}}}'-{{\varvec{y}}}|$ and $\underline{x}=|\underline{\textrm{X}}|=|{{\varvec{x}}}'-{{\varvec{x}}}|$. Here, ${{\varvec{x}}}$ is the reference position of a given material point, whereas ${{\varvec{x}}}'$ is the reference position of a generic point in its family. The family points are the material points located inside the neighbourhood of point ${{\varvec{x}}}$ (the points whose distance from ${{\varvec{x}}}$ is less than the horizon). Here, ${{\varvec{y}}}$ and ${{\varvec{y}}}'$ are the positions of the points ${{\varvec{x}}}$ and ${{\varvec{x}}}'$ in the deformed configuration of the body. Then, ${{\varvec{u}}}({{\varvec{x}}},t)$ is the displacement of point ${{\varvec{x}}}$ at time $t$, and the following holds: ${{\varvec{y}}}({{\varvec{x}}},t)={{\varvec{x}}}+{{\varvec{u}}}({{\varvec{x}}},t)$ (see Fig. 1). The extension of each bond can be decomposed into two parts, an isotropic and a deviatoric part, called $\underline{e}^{\textrm{iso}}$ and $\underline{e}^{\textrm{d}}$, respectively:

$$\begin{aligned} \underline{e}=\underline{e}^{\textrm{iso}}+\underline{e}^{\textrm{d}} \end{aligned}$$

(2)

Adopting for $\underline{e}^{\textrm{iso}}$ the expression developed in [13, 33], it follows that:

$$\begin{aligned} \underline{e}^{\textrm{d}}=\underline{e}-\underline{e}^{\textrm{iso}}= {\left\{ \begin{array}{ll} \underline{\textit{e}}-\frac{\theta \underline{\textit{x}}}{3} &{} \text{ for } \text{3D }, \\ \underline{\textit{e}}-\left( \frac{1}{3}+\frac{\kappa }{8\mu }\right) \theta \underline{\textit{x}} &{} \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ \underline{\textit{e}}-\frac{5}{12}\theta \underline{\textit{x}} &{} \text{ for } \text{2D } \text{ plane } \text{ strain }. \end{array}\right. } \end{aligned}$$

(3)

In this equation, $\kappa$ and $\mu$ are the bulk modulus and the shear modulus, respectively, whereas $\theta$ is the dilatation and is calculated by the following equation [13, 33]:

$$\begin{aligned} \theta ={\left\{ \begin{array}{ll} \frac{3}{m}\underline{\omega } \underline{\textit{x}}\cdot \underline{\textit{e}} &{} \quad \text{ for } \text{3D }, \\ \frac{2(2\nu -1)}{(\nu -1)m}\underline{\omega } \underline{\textit{x}}\cdot \underline{\textit{e}} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ \frac{2}{m}\underline{\omega } \underline{\textit{x}}\cdot \underline{\textit{e}} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ strain }, \end{array}\right. } \end{aligned}$$

(4)

where $\nu$ is the Poisson’s ratio. It is worth noting that, given two peridynamic states, $\underline{a}$ and $\underline{b}$, their dot product is defined by the following equation:

$$\begin{aligned} \underline{a} \cdot \underline{b}= \int _{\mathcal {H}}{\underline{\textit{a}}\langle {{\varvec{x}}}-{{\varvec{x}}}'\rangle \ \underline{\textit{b}}\langle {{\varvec{x}}}-{{\varvec{x}}}'\rangle \ dV_{{{\varvec{x}}}'} } \end{aligned}$$

(5)

where $\mathcal {H}$ is the neighbourhood of ${{\varvec{x}}}$, and $dV_{{{\varvec{x}}}'}$ refers to the volume associated with each family point in the neighbourhood. When a state operates on the vectors in $\mathcal {H}$, the vectors are written in angle brackets $\langle \cdots \rangle$. In Eq. 4, $m=\underline{\omega } \, \underline{\textit{x}}\cdot \underline{\textit{x}}$, where $\underline{\omega }$ is called influence function. In the present paper, it is assumed $\underline{\omega }=1$.

2.1.2 Equation of motion and force states

In state-based peridynamics, the equation of motion of each material point is given by [13]:

$$\begin{aligned}{} & {} \rho ({{\varvec{x}}}) \ddot{{{\varvec{u}}}}({{\varvec{x}}},t)\nonumber \\{} & {} \quad =\int _{\mathcal {H}}{(\underline{{{\varvec{T}}}}[{{\varvec{x}}},t]\langle {{\varvec{x}}}'-{{\varvec{x}}}\rangle -\underline{{{\varvec{T}}}}[{{\varvec{x}}}',t]\langle {{\varvec{x}}}-{{\varvec{x}}}'\rangle )\ dV_{{{\varvec{x}}}'} }+{{\varvec{b}}}({{\varvec{x}}},t), \end{aligned}$$

(6)

where ${{\varvec{b}}}({{\varvec{x}}},t)$ is the body force on the material point ${{\varvec{x}}}$ at time $t$ and $\rho ({{\varvec{x}}})$ represents the mass density of the point. $\underline{{{\varvec{T}}}}[{{\varvec{x}}},\textit{t}]$ is referred to as the force vector state on material point ${{\varvec{x}}}$ at time $\textit{t}$ corresponding to the bond vector ${{\varvec{x}}}'-{{\varvec{x}}}$. The force vector state $\underline{{{\varvec{T}}}}$ is found by the following equation:

$$\begin{aligned} \underline{{{\varvec{T}}}}=\underline{\textit{t}}\,\underline{{{\varvec{M}}}}. \end{aligned}$$

(7)

where t is the scalar force state. For ordinary state-based peridynamics, the force states produce bond forces which are aligned with the line connecting two material points:

$$\begin{aligned} \underline{{{\varvec{M}}}}({{\varvec{x}}},t)=\frac{{{\varvec{y}}}'-{{\varvec{y}}}}{|{{\varvec{y}}}'-{{\varvec{y}}}|}. \end{aligned}$$

(8)

Furthermore, t is given by the following equation [13, 33]:

$$\begin{aligned} \underline{t}={\left\{ \begin{array}{ll} \frac{3\kappa \theta }{m}\underline{\omega } \underline{\textit{x}}+\frac{15\mu }{m}\underline{\omega }\underline{e}^{\textrm{d}} &{} \quad \text{ for } \text{3D }, \\ \frac{2\kappa \theta }{m}\underline{\omega } \underline{\textit{x}}+\frac{8\mu }{m}\underline{\omega }\underline{e}^{\textrm{d}} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(9)

The scalar force state, $\underline{\textit{t}}$, is composed of an isotropic and a deviatoric part:

$$\begin{aligned} \underline{t}=\underline{t}^{\textrm{iso}}+\underline{t}^{\textrm{d}}. \end{aligned}$$

(10)

Based on [29, 33], $\underline{t}^{\textrm{iso}}$ is independent of the deviatoric part of the extension, $\underline{e}^{\textrm{d}}$, and $\underline{t}^{\textrm{d}}$ is independent of the dilatation, $\theta$. Thus, by separating these two parts of $\underline{\textit{t}}$, using Eq. 9, the following quantities are identified:

$$\begin{aligned}{} & {} \underline{t}^{\textrm{iso}}={\left\{ \begin{array}{ll} \frac{3\kappa \theta }{m}\underline{\omega } \underline{\textit{x}} &{} \quad \text{ for } \text{3D }, \\ \frac{2\kappa \theta }{m}\underline{\omega } \underline{\textit{x}} &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \underline{t}^{\textrm{d}}= {\left\{ \begin{array}{ll} \frac{15\mu }{m}\underline{\omega }\underline{e}^{\textrm{d}} &{} \quad \text{ for } \text{3D }, \\ \frac{8\mu }{m}\underline{\omega }\underline{e}^{\textrm{d}} &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(12)

Substituting Eq. 3 in Eq. 12, $\underline{t}^{\textrm{d}}$ is found as a function of $\underline{\textit{e}}$:

$$\begin{aligned} \underline{t}^{\textrm{d}}={\left\{ \begin{array}{ll} -5\mu \theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{15\mu }{m}\underline{\omega }\underline{\textit{e}} &{} \text{ for } \text{3D }, \\ (-\kappa -\frac{8\mu }{3})\theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }\underline{\textit{e}} &{} \text{ for } \text{2D } \text{ plane } \text{ stress },\\ -\frac{10\mu }{3}\theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }\underline{\textit{e}} &{} \text{ for } \text{2D } \text{ plane } \text{ strain }. \end{array}\right. } \end{aligned}$$

(13)

2.2 Elastoplastic formulation based on ordinary state-based peridynamics

In this section, the peridynamic formulation is extended to elastoplastic materials with isotropic and kinematic hardening. The elastoplastic theory proposed here is based on the standard rate independent J2 plasticity [10]. This approach was used in [29, 33] to develop the elastoplastic peridynamic formulations for materials with perfect plasticity.

2.2.1 Decomposition of displacement states into elastic and plastic parts, and force state relations

Based on J2 plasticity, the isotropic extension ($\underline{e}^{\textrm{iso}}$) can be only elastic. On the other hand, the deviatoric extension ($\underline{e}^{\textrm{d}}$) is the sum of an elastic ($\underline{e}^{\textrm{de}}$) and a plastic ($\underline{e}^{\textrm{dp}}$) component:

$$\begin{aligned} \underline{e}^{\textrm{d}}=\underline{e}^{\textrm{de}}+\underline{e}^{\textrm{dp}}. \end{aligned}$$

(14)

In the case of elastoplastic materials, Eq. 9 can be rewritten as in the following [29, 33]:

$$\begin{aligned} \underline{t}= {\left\{ \begin{array}{ll} \frac{3\kappa \theta }{m}\underline{\omega } \underline{\textit{x}}+\frac{15\mu }{m}\underline{\omega }(\underline{e}^{\textrm{d}}-\underline{e}^{\textrm{dp}}) &{} \text{ for } \text{3D }, \\ \frac{2\kappa \theta }{m}\underline{\omega } \underline{\textit{x}}+\frac{8\mu }{m}\underline{\omega }(\underline{e}^{\textrm{d}}-\underline{e}^{\textrm{dp}}) &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(15)

where $\theta$ is derived from Eq. 4:

$$\begin{aligned} \theta ={\left\{ \begin{array}{ll} \frac{3}{m}\underline{\omega } \underline{\textit{x}}\cdot (\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{} \quad \text{ for } \text{3D }, \\ \frac{2(2\nu -1)}{(\nu -1)m}\underline{\omega } \underline{\textit{x}}\cdot (\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ \frac{2}{m}\underline{\omega } \underline{\textit{x}}\cdot (\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ strain }. \end{array}\right. } \end{aligned}$$

(16)

The deviatoric part of the bond force for elastoplastic cases is found by Eq. 13:

$$\begin{aligned} \underline{t}^{\textrm{d}}={\left\{ \begin{array}{ll} -5\mu \theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{15\mu }{m}\underline{\omega }(\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{} \quad \text{ for } \text{3D }, \\ (-\kappa -\frac{8\mu }{3})\theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }(\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ -\frac{10\mu }{3}\theta \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }(\underline{\textit{e}}-\underline{e}^{\textrm{dp}}) &{}\quad \text{ for } \text{2D } \text{ plane } \text{ strain }. \end{array}\right. } \end{aligned}$$

(17)

2.2.2 Yield function based on deviatoric force state for materials with perfect plasticity

Based on the formulation developed in [29, 33], the following equation is used for the yield function for materials with perfect plasticity [13]:

$$\begin{aligned} f(\underline{t}^{\textrm{d}})= & {} \psi (\underline{t}^{\textrm{d}})-\psi _0\nonumber \\= & {} {\left\{ \begin{array}{ll} \frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}-\psi _0 &{} \quad \text{ for } \text{3D }, \\ \frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}+4\frac{(\underline{t}^{\textrm{d}}\cdot \underline{x})^2}{\pi \delta ^4h}-\psi _0 &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(18)

where $\Vert \underline{t}^{\textrm{d}}\Vert ^{2}=\int _{\mathcal {H}}{(\underline{t}^{\textrm{d}})^2\ dV_{{{\varvec{x}}}'} }$. $\delta$ is the size of the horizon and $h$ is the thickness of the body for 2D cases. The yield value in Eq. 18, $\psi _0$, is given by the following equation:

$$\begin{aligned} \psi _0={\left\{ \begin{array}{ll} \frac{25\sigma _{\textrm{y}}^2}{8\pi \delta ^5} &{} \quad \text{ for } \text{3D }, \\ \frac{8\sigma _{\textrm{y}}^2}{3\pi h \delta ^4} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(19)

In this equation, $\sigma _{\textrm{y}}$ is the 1D yield stress of the material. Finally, for future use, it is convenient to write the expression of the equivalent von Mises stress in PD as follows [33, 36]:

$$\begin{aligned} \sigma ^2_{\mathrm {vm(PD)}}={\left\{ \begin{array}{ll} \frac{8\pi \delta ^5}{25}\frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2} &{} \quad \text{ for } \text{3D }, \\ \frac{3\pi h \delta ^4}{8}\left( \frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}+4\frac{(\underline{t}^{\textrm{d}}\cdot \underline{x})^2}{\pi \delta ^4h}\right) &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(20)

Equation 20 expresses the von Mises stress in terms of the deviatoric force state.

2.2.3 Plastic flow rule, Kuhn–Tucker condition and consistency condition

In classical elastoplasticity, plastic strain rate is defined by the flow rule. In peridynamics, the plastic flow rule is written as [13, 29]:

$$\begin{aligned} \dot{\underline{e}}^{\textrm{dp}}=\lambda \nabla ^{\textrm{d}}\psi (\underline{t}^{\textrm{d}}), \end{aligned}$$

(21)

where $\psi (\underline{t}^{\textrm{d}})$ is implicitly defined in Eq. 18 and $\nabla ^{\textrm{d}}\psi (\underline{t}^{\textrm{d}})$ is its constrained Fréchet derivative. Here, $\lambda$ is the continuum consistency parameter [10]. $\lambda$ is also written as $\dot{\lambda }$ (e.g., [6]), which better reflects the meaning of this internal variable; however we use $\lambda$, which is more common in the peridynamics literature.

Based on classical plasticity theory, the loading–unloading conditions in Kuhn–Tucker form and the consistency condition should be satisfied in solving elastoplastic problems. The Kuhn–Tucker conditions are defined by the following expressions [29]:

$$\begin{aligned} \lambda \ge 0, \hspace{0.5em} f(\underline{t}^{\textrm{d}})\le 0, \hspace{0.5em} \lambda f(\underline{t}^{\textrm{d}})=0. \end{aligned}$$

(22)

We can rewrite Eq. 22 in the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} f(\underline{t}^{\textrm{d}})<0,\ \lambda =0 &{} \quad \text{ elastic } \text{ domain }, \\ f(\underline{t}^{\textrm{d}})=0,\ \lambda >0 &{} \quad \text{ elastoplastic } \text{ domain }. \end{array}\right. } \end{aligned}$$

(23)

Another condition, which should be satisfied, is the consistency condition:

$$\begin{aligned} \lambda \dot{f}(\underline{t}^{\textrm{d}})=0. \end{aligned}$$

(24)

For the elastoplastic domain ($\lambda >0$), the consistency condition leads to:

$$\begin{aligned} \dot{f}(\underline{t}^{\textrm{d}})=0. \end{aligned}$$

(25)

2.2.4 Yield function for materials with isotropic and kinematic hardening

In the classical 1D elastoplasticity theory, which is applied here to bond forces, the yield function for materials with isotropic and kinematic hardening is defined as [10]:

$$\begin{aligned} f=|\sigma _{\textrm{vm}}-q|-(\sigma _{\textrm{y}}+K\alpha ). \end{aligned}$$

(26)

In this equation, $\textit{K}$ is the isotropic hardening modulus, $\textit{q}$ is the amount of back stress resulting from the kinematic hardening, and $\alpha$ is the internal hardening variable [10]. Initially, $q=0$ and $\alpha =0$, whereas, in general, the evolution of $q$ and $\alpha$ is defined, respectively, according to:

$$\begin{aligned} \dot{q}= & {} \dot{\varepsilon }_{\textrm{p}} H, \end{aligned}$$

(27)

$$\begin{aligned} \dot{\alpha }= & {} \textrm{sign}(\sigma _{\textrm{vm}}-q)\dot{\varepsilon }_{\textrm{p}}, \end{aligned}$$

(28)

where $\textit{H}$ represents the kinematic hardening modulus, and $\varepsilon _{\textrm{p}}$ is the equivalent plastic strain [10]. To find the yield function, for materials with hardening, we can rewrite Eq. 26 as follows:

$$\begin{aligned} f={\left\{ \begin{array}{ll} \sigma _{\textrm{vm}}-(\sigma _{\textrm{y}}+K\alpha +q) &{} \quad \sigma _{\textrm{vm}}\ge q, \\ -\sigma _{\textrm{vm}}-(\sigma _{\textrm{y}}+K\alpha -q) &{}\quad \sigma _{\textrm{vm}}< q. \end{array}\right. } \end{aligned}$$

(29)

Summarizing Eq. 29, we have

$$\begin{aligned} f=\textrm{sign}(\sigma _{\textrm{vm}}-q)\sigma _{\textrm{vm}}-(\sigma _{\textrm{y}}+K\alpha +\textrm{sign}(\sigma _{\textrm{vm}}-q)q). \end{aligned}$$

(30)

As mentioned before, Eq. 18 is the PD equivalent to the CCM expression $\textit{f}=|\sigma _{\textrm{vm}}|-\sigma _{\textrm{y}}$ under perfect plasticity conditions. A similar idea is used for materials with isotropic and kinematic hardening. Hence, by considering Eq. 30, we can rewrite Eq. 18 for materials with hardening as in the following:

$$\begin{aligned} f(\underline{t}^{\textrm{d}})= & {} \psi (\underline{t}^{\textrm{d}})-\psi _0({{\varvec{x}}},t) \nonumber \\= & {} {\left\{ \begin{array}{ll} \frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}-\psi _0({{\varvec{x}}},t) &{} \quad \text{ for } \text{3D }, \\ \frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}+4\frac{(\underline{t}^{\textrm{d}}\cdot \underline{x})^2}{\pi \delta ^4 h}-\psi _0({{\varvec{x}}},t) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(31)

where Eq. 19 is modified as:

$$\begin{aligned} \psi _0({{\varvec{x}}},t)={\left\{ \begin{array}{ll} \frac{25[\sigma _{\textrm{y}}+K\alpha +\textrm{sign}(\sigma _{\textrm{vm}}-q)q]^2}{8\pi \delta ^5} &{} \quad \text{ for } \text{3D }, \\ \frac{8[\sigma _{\textrm{y}}+K\alpha +\textrm{sign}(\sigma _{\textrm{vm}}-q)q]^2}{3\pi h \delta ^4} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(32)

Here, $\psi _0({{\varvec{x}}},t)$ is not constant anymore, and it may vary with the step of loading for every material point in the plastic domain. Note that both $\psi _0({{\varvec{x}}},t)$ and $\psi (\underline{t}^{\textrm{d}})$ are positive scalar values. In Eq. 32, $q$ and $\alpha$ are found using Eqs. 27 and 28. Based on these two equations, $q$ and $\alpha$ depend on any change in $\varepsilon _{\textrm{p}}$. Consequently $\psi _0({{\varvec{x}}},t)$ is changed by any change in $\varepsilon _{\textrm{p}}$.

By considering peridynamic states, when we have a deviatoric plastic extension, $\underline{e}^{\textrm{dp}}$, we need to find its equivalent plastic strain in PD, $\underline{\varepsilon }^{\textrm{p}}$, to be used in Eqs. 27 and 28 [30,31,32]. To do this, we use the following equation [32]:

$$\begin{aligned} |\Delta \underline{\varepsilon }^{\textrm{p}}|={\left\{ \begin{array}{ll} \sqrt{\frac{5}{m}\Vert \Delta \underline{e}^{\textrm{dp}}\Vert ^{2}} &{} \quad \text{ for } \text{3D }, \\ \sqrt{\frac{2}{m}\Vert \Delta \underline{e}^{\textrm{dp}}\Vert ^{2}} &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(33)

where $\Vert \Delta \underline{e}^{\textrm{dp}}\Vert ^{2}= \int _{\mathcal {H}}{(\Delta \underline{e}^{\textrm{dp}})^2\ dV_{{{\varvec{x}}}'} }$ and

$$\begin{aligned} m={\left\{ \begin{array}{ll} \frac{4\pi \delta ^5}{5} &{} \quad \text{ for } \text{3D }, \\ \frac{\pi h \delta ^4}{2} &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(34)

It is worth noting that Eq. 33 is obtained by considering small displacements. In Eq. 33, $\Delta \underline{e}^{\textrm{dp}}$ is the amount of change in deviatoric plastic extension for each bond of the point ${{\varvec{x}}}$, and $\Delta \underline{\varepsilon }^{\textrm{p}}$ is the increment of the equivalent plastic strain in PD so that it reduced to uni-axial plastic strain in uni-axial tension. Equation 33 can be further rewritten as:

$$\begin{aligned} |\Delta \underline{\varepsilon }^{\textrm{p}}|= \sqrt{A_0 \Vert \Delta \underline{e}^{\textrm{dp}}\Vert ^{2}}, \end{aligned}$$

(35)

where $A_0$ is given by the following equation:

$$\begin{aligned} A_0= {\left\{ \begin{array}{ll} \frac{25}{4\pi \delta ^5} &{} \text{ for } \text{3D }, \\ \frac{4}{\pi h \delta ^4} &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(36)

The sign of $\Delta \underline{\varepsilon }^{\textrm{p}}$ depends on the sign of $(\sigma _{\textrm{vm}}-q)$ as follows: $\Delta \underline{\varepsilon }^{\textrm{p}}=\textrm{sign}({\sigma _{\textrm{vm}}}-q)|\Delta \underline{\varepsilon }^{\textrm{p}}|$.

3 Numerical discretization

This section describes the numerical implementation of the proposed elastoplastic model and the solution strategy adopted.

3.1 Solving peridynamic equation

The domain is discretized with a uniform square grid of nodes with grid spacing $\Delta x$. The spatial discretization of Eq. 6 for static problems is

$$\begin{aligned} \textbf{0}=\sum _{\textrm{j}}{(\underline{{{\varvec{T}}}}[{{\varvec{x}}}_{\textrm{i}}]\langle {{\varvec{x}}}_{\textrm{j}}-{{\varvec{x}}}_{\textrm{i}}\rangle -\underline{{{\varvec{T}}}}[{{\varvec{x}}}_{\textrm{j}}]\langle {{\varvec{x}}}_{\textrm{i}}-{{\varvec{x}}}_{\textrm{j}}\rangle )\ \Delta V_{\textrm{j}} }+{{\varvec{b}}}({{\varvec{x}}}_{\textrm{i}}), \end{aligned}$$

(37)

where subscripts $\textrm{i}$ and $\textrm{j}$ denote central node and family nodes, respectively and $\Delta V_{\textrm{j}}$ is the volume associated with the node $\textrm{j}$ within the neighborhood of node $\textrm{i}$ [37]. In this paper we solve non-linear static problems using an incremental loading approach. This involves dividing the load (in our case, an imposed displacement) into small steps and finding the equilibrium solution for each step using the dynamic relaxation method.

3.2 Return mapping algorithm

The key aspect for the numerical implementation of the elastoplastic behavior of materials is the definition of a return mapping algorithm that enables the evaluation of the plastic deformation dependent quantities for the load increment considered [10].

Having determined the position of the nodes at step $\textrm{n}$, it is possible to find the extension of each bond at step $\mathrm {n+1}$, using Eq. 37, assuming that this step is elastic (trial step), which means that there is no plastic extension at step $\mathrm {n+1}$, so that $\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}=\underline{e}^{\textrm{dp}}_{\textrm{n}}$ for every bond. Based on this assumption, the trial elastic extension ($\underline{e}_{\textrm{trial}}$) can be computed as

$$\begin{aligned} \underline{e}_{\textrm{trial}}=\underline{e}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_\textrm{n}. \end{aligned}$$

(38)

Since it is assumed $\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}=\underline{e}^{\textrm{dp}}_\textrm{n}$, (no change in plastic extension), the yield limit does not change. Therefore ${\psi _0}_{\textrm{trial}}({{\varvec{x}}})={\psi _0}_{\textrm{n}}({{\varvec{x}}})$; then from Eq. 32, we have:

$$\begin{aligned} {\psi _0}_{\textrm{trial}}({{\varvec{x}}})={\left\{ \begin{array}{ll} \frac{25[\sigma _\textrm{y}+K\alpha _\textrm{n}+\textrm{sign}({\sigma _{\textrm{vm}}}_\textrm{n}-q_\textrm{n})q_\textrm{n}]^2}{8\pi \delta ^5} &{} \text{ for } \text{3D }, \\ \frac{8[\sigma _\textrm{y}+K\alpha _\textrm{n}+\textrm{sign}({\sigma _{\textrm{vm}}}_\textrm{n}-q_\textrm{n})q_\textrm{n}]^2}{3\pi h \delta ^4} &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(39)

Using Eqs. 16 and 17 for step $\mathrm {n+1}$, $\underline{t}^{\textrm{d}}_{\textrm{trial}}$ is found as:

$$\begin{aligned} \underline{t}^\textrm{d}_{\textrm{trial}}={\left\{ \begin{array}{ll} -5\mu \theta (\underline{e}_{\textrm{trial}})\frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{15\mu }{m}\underline{\omega }\underline{\textit{e}}_{\textrm{trial}} &{} \text{ for } \text{3D }, \\ \left( -\kappa -\frac{8\mu }{3})\theta (\underline{e}_{\textrm{trial}}\right) \frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }\underline{\textit{e}}_{\textrm{trial}} &{} \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ -\frac{10\mu }{3}\theta (\underline{e}_{\textrm{trial}})\frac{\underline{\omega } \underline{\textit{x}}}{m}+\frac{8\mu }{m}\underline{\omega }\underline{\textit{e}}_{\textrm{trial}} &{} \text{ for } \text{2D } \text{ plane } \text{ strain }, \end{array}\right. } \end{aligned}$$

(40)

where $\theta (\underline{e}_{\textrm{trial}})$ is

$$\begin{aligned} \theta (\underline{e}_{\textrm{trial}})={\left\{ \begin{array}{ll} \frac{3}{m}\underline{\omega } \underline{\textit{x}}\cdot \underline{e}_{\textrm{trial}} &{} \text{ for } \text{3D }, \\ \frac{2(2\nu -1)}{(\nu -1)m}\underline{\omega } \underline{\textit{x}}\cdot \underline{e}_{\textrm{trial}} &{} \text{ for } \text{2D } \text{ plane } \text{ stress }, \\ \frac{2}{m}\underline{\omega } \underline{\textit{x}}\cdot \underline{e}_{\textrm{trial}} &{} \text{ for } \text{2D } \text{ plane } \text{ strain }. \end{array}\right. } \end{aligned}$$

(41)

In addition, the yield function is evaluated at the trial step from Eq. 31:

$$\begin{aligned} f(\underline{t}^{\textrm{d}}_{\textrm{trial}})={\left\{ \begin{array}{ll} \frac{\Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}}{2}-{\psi _0}_{\textrm{trial}}({{\varvec{x}}}) &{} \text{ for } \text{3D }, \\ \frac{\Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}}{2}+4\frac{(\underline{t}^{\textrm{d}}_{\textrm{trial}}\cdot \underline{x})^2}{\pi \delta ^4 h}-{\psi _0}_{\textrm{trial}}({{\varvec{x}}}) &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(42)

Based on the value of the yield function, it is possible to determine whether the trial step is elastic or elastoplastic.

$$\begin{aligned} {\left\{ \begin{array}{ll} \text{ if } \ \ f(\underline{t}^{\textrm{d}}_{\textrm{trial}})\le 0 &{} \quad \text{ elastic }, \\ \text{ if } \ \ f(\underline{t}^{\textrm{d}}_{\textrm{trial}}) >0 &{}\quad \text{ elastoplastic }. \end{array}\right. } \end{aligned}$$

(43)

If $f(\underline{t}^{\textrm{d}}_{\textrm{trial}})$ is less than zero, then the trial step is elastic, so $\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}=\underline{e}^{\textrm{dp}}_{\textrm{n}}$, $q_{\mathrm {n+1}}=q_{\textrm{n}}$, $\alpha _{\mathrm {n+1}}=\alpha _{\textrm{n}}$ and $\underline{t}^{\textrm{d}}_{\mathrm {n+1}}=\underline{t}^{\textrm{d}}_{\textrm{trial}}$. Otherwise, if $f(\underline{t}^{\textrm{d}}_{\textrm{trial}})$ is greater than zero, consequently the assumption of an elastic trial step is incorrect and we need to find $\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}$ satisfying the yield condition for step $\mathrm {n+1}$, using Eq. 31 and the Kuhn–Tucker conditions, Eq. 23, Eq. 31 becomes:

$$\begin{aligned} f(\underline{t}^{\textrm{d}}_{\mathrm {n+1}})={\left\{ \begin{array}{ll} \frac{\Vert \underline{t}^{\textrm{d}}_{\mathrm {n+1}}\Vert ^{2}}{2}-{\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{} \text{ for } \text{3D }, \\ \frac{\Vert \underline{t}^{\textrm{d}}_{\mathrm {n+1}}\Vert ^{2}}{2}+4\frac{(\underline{t}^{\textrm{d}}_{\mathrm {n+1}}\cdot \underline{x})^2}{\pi \delta ^4 h}-{\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(44)

where using Eq. 32,

$$\begin{aligned} {\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})= {\left\{ \begin{array}{ll} \frac{25({\sigma _\textrm{y}}_{\mathrm {n+1}})^2}{8\pi \delta ^5} &{} \quad \text{ for } \text{3D }, \\ \frac{8({\sigma _\textrm{y}}_{\mathrm {n+1}})^2}{3\pi h \delta ^4} &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(45)

and

$$\begin{aligned} {\sigma _\textrm{y}}_{(\mathrm {n+1})}={\sigma _\textrm{y}}_0+K\alpha _{\mathrm {n+1}}+\textrm{sign}({\sigma _{\textrm{vm}}}_\textrm{n}-q_\textrm{n})q_{\mathrm {n+1}}. \end{aligned}$$

(46)

In Eq. 44, $\underline{t}^{\textrm{d}}_{\mathrm {n+1}}$ is unknown. $\underline{t}^{\textrm{d}}_{\mathrm {n+1}}$ can be expressed as a function of $\underline{t}^{\textrm{d}}_{\textrm{trial}}$, by using the flow rule, from Eq. A6:

$$\begin{aligned} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}= \frac{\underline{t}^{\textrm{d}}_{\textrm{trial}}}{1-B\Delta \lambda }, \end{aligned}$$

(47)

where

$$\begin{aligned} B= {\left\{ \begin{array}{ll} -\frac{15\mu }{m}\underline{\omega } &{} \quad \text{ for } \text{3D }, \\ -\frac{8\mu }{m}\underline{\omega } &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(48)

and $\Delta \lambda$ is the unknown variation of the consistency parameter. Substituting Eq. 47 in Eq. 44, we obtain [29]:

$$\begin{aligned} f(\underline{t}^{\textrm{d}}_{\mathrm {n+1}})={\left\{ \begin{array}{ll} \frac{\Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}}{2(1-B\Delta \lambda )^2}-{\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{}\quad \text{ for } \text{3D }, \\ \frac{\Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}}{2(1-B\Delta \lambda )^2}+4\frac{(\underline{t}^{\textrm{d}}_{\textrm{trial}}\cdot \underline{x})^2}{\pi \delta ^4 h (1-B\Delta \lambda )^2}-{\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(49)

Equation 49 can be rewritten as

$$\begin{aligned}{} & {} f(\underline{t}^{\textrm{d}}_{\mathrm {n+1}})\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll} G^{2}P_1-2 {\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{} \quad \text{ for } \text{3D }, \\ G^{2}(P_1+2 A_0 P_2)-2 {\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})=0 &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }, \end{array}\right. } \end{aligned}$$

(50)

where $P_1=\Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}$, $P_2=(\underline{t}^{\textrm{d}}_{\textrm{trial}}\cdot \underline{x})^2$ and $G= \frac{1}{1-B\Delta \lambda }$. $A_0$ is found using Eq. 36. ${\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})$ and ${\sigma _{\textrm{y}}}_{(\mathrm {n+1})}$ (Eqs. 45 and 46) depend on $\alpha _{\mathrm {n+1}}$ and $q_{\mathrm {n+1}}$. These two parameters are a function of $\Delta \underline{\varepsilon }^{\textrm{p}}$.

From Eq. 35, $\Delta \underline{\varepsilon }^{\textrm{p}}$ is

$$\begin{aligned} |\Delta \underline{\varepsilon }^{\textrm{p}}|= \sqrt{A_0 \Vert \Delta \underline{e}^{\textrm{dp}}\Vert ^{2}}, \end{aligned}$$

(51)

with $\Delta \underline{e}^{\textrm{dp}}$ computed as:

$$\begin{aligned} \Delta \underline{e}^{\textrm{dp}}=\Delta \lambda \underline{t}^{\textrm{d}}_{\mathrm {n+1}} \end{aligned}$$

(52)

by Eq. A4 in which $\nabla ^{\textrm{d}}\psi _{\mathrm {n+1}}(\underline{t}^{\textrm{d}}_{\mathrm {n+1}})=\underline{t}^{\textrm{d}}_{\mathrm {n+1}}$.

Substituting Eq. 47 in Eq. 52, we obtain:

$$\begin{aligned} \Delta \underline{e}^{\textrm{dp}}=\Delta \lambda \frac{\underline{t}^{\textrm{d}}_{\textrm{trial}}}{1-B\Delta \lambda }. \end{aligned}$$

(53)

Then having Eq. 53 for every bond and substituting it in Eq. 51, since $\Delta \lambda$ is constant, we find:

$$\begin{aligned} |\Delta \underline{\varepsilon }^{\textrm{p}}|=\frac{\Delta \lambda }{1-B\Delta \lambda } \sqrt{A_0 \Vert \underline{t}^{\textrm{d}}_{\textrm{trial}}\Vert ^{2}}. \end{aligned}$$

(54)

In Eq. 54, $\Delta \lambda$ is the same for all bonds belonging to the same neighbourhood and $B$ is also constant (Eq. 48). Then we can rewrite Eq. 54 as

$$\begin{aligned} |\Delta \underline{\varepsilon }^{\textrm{p}}|=\Delta \lambda G \sqrt{A_0 P_1}. \end{aligned}$$

(55)

Equations 27 and 28 allow us to update $q_{\mathrm {n+1}}$ and $\alpha _{\mathrm {n+1}}$:

$$\begin{aligned}{} & {} q_{\mathrm {n+1}}=q_{\textrm{n}}+\Delta \underline{\varepsilon }^{\textrm{p}} H, \end{aligned}$$

(56)

$$\begin{aligned}{} & {} \alpha _{\mathrm {n+1}}=\alpha _{\textrm{n}}+\textrm{sign}(\sigma _{{\textrm{vm}}_{\textrm{n}}}-q_{\textrm{n}})\Delta \underline{\varepsilon }^{\textrm{p}}. \end{aligned}$$

(57)

Consequently, the parameters ${\psi _0}_{\mathrm {n+1}}({{\varvec{x}}})$ and ${\sigma _{\textrm{y}}}_{(\mathrm {n+1})}$, needed to define Eq. 50, can be obtained as a function of $\Delta \lambda$. Finally the unknown $\Delta \lambda$ is found by solving Eq. 50 with the Newton–Raphson method. Once $\Delta \lambda$ has been computed, we obtain $\underline{t}^{\textrm{d}}_{\mathrm {n+1}}$ and $\Delta \underline{e}^{\textrm{dp}}$, respectively from Eqs. 47 and 52. Therefore, the plastic component of the deviatoric extension is:

$$\begin{aligned} \underline{e}^{\textrm{dp}}_{\mathrm {n+1}}=\underline{e}^{\textrm{dp}}_{\textrm{n}}+\Delta \underline{e}^{\textrm{dp}}=\underline{e}^{\textrm{dp}}_{\textrm{n}}+\Delta \lambda \underline{t}^{\textrm{d}}_{\mathrm {n+1}}. \end{aligned}$$

(58)

The elastic extension is found using the following equation:

$$\begin{aligned} \underline{e}^{\textrm{e}}_{\mathrm {n+1}}=\underline{e}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}. \end{aligned}$$

(59)

The procedure is applied to all nodes of the model for each iteration of the dynamic relaxation method [38] until the static solution of the load increment under consideration is determined.

3.3 Summary of the procedure

The analysis procedure can be summarized in the following steps:

• 1. Read input data (material properties, initial node coordinates and boundary conditions)

• 2. Apply the external incremental load (in our examples, an imposed displacement condition is considered)

• 3. Find the equilibrium solution (displacement field) using the dynamic relaxation method. Note that in each iteration of the dynamic relaxation method, the return mapping algorithm is exploited to update the plastic values of extension and force states. The iterations continue until the equilibrium solution of Eq. 37 is reached.

• 4. If the applied load has reached its final value go to step 5, otherwise increase the applied load further (go to step 2)

• 5. End

Within an iteration of the Adaptive Dynamic Relaxation (ADR) procedure, for each node of the grid, the internal forces are computed as shown in the conceptual flow chart of Fig. 2.

Fig. 2

Flowchart for the calculation of internal forces at each node in each iteration of the Dynamic Relaxation procedure

4 Numerical results

In this section, three static cases are solved adopting the proposed elastoplastic PD model. In addition, the results are compared with the ones obtained with the FE simulation in ANSYS. In all the examples, $E=200\,\hbox {GPa}$, $\nu =0.3$, $\rho =8000\,\hbox {kg/m}^3$ and ${\sigma _{\textrm{y}}}_0=600\,\hbox {MPa}$. Where hardening is considered, the isotropic hardening modulus is $K=20\,\hbox {GPa}$, and the kinematic hardening modulus is $H=20\,\hbox {GPa}$.

In all numerical examples displacements are imposed to the models by using a fictitious layer of nodes [39], even in the case of zero imposed displacement. The surface effect [40] is not corrected where surfaces are free to move.

Fig. 3

a Geometry and boundary conditions, b fictitious boundary layers in the model

Fig. 4

Displacement loading in the ${\textrm{x}}$ direction ($u_{{\textrm{x}}}$)

4.1 2D plane stress case

A thin plate ($100\,{\hbox {mm}}\times 100\,{\hbox {mm}}\times 1\,{\hbox {mm}}$) with a central hole ($D=30\,{\hbox {mm}}$) in plane stress conditions is considered. Geometry and boundary conditions are shown in Fig. 3a. The loading “time history” is shown in Fig. 4. The load is applied to the structure in 120 steps of $0.0125\,{\hbox {mm}}$.

The PD model is discretized with a uniform grid ($\Delta {\textrm{x}}=\Delta \textrm{y}=0.25\,{\hbox {mm}}$) and is composed by 154336 nodes. The horizon size is $\delta =1.25\,{\hbox {mm}}$ and the $m$-ratio is $\frac{\delta }{\Delta {\textrm{x}}}=5$. The Dirichlet boundary conditions are applied on two fictitious layers added to the boundaries (Fig. 3b) with the width of $\delta$. The finite element model, prepared in ANSYS, is composed by 158150 2D 4-Node quadrilateral elements (plane182) and 159106 nodes.

In Fig. 5, the displacement in the ${\textrm{x}}$ and $\textrm{y}$ directions computed by PD and FE are compared at the last step of the first ramp of the loading ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$). Figure 6 shows the equivalent plastic strain at this load step. There is a good agreement between the FE and PD results. Figures 7, 8 and 9 compare the distribution of von Mises stress at load steps 10 ($u_{{\textrm{x}}}=0.125\,{\hbox {mm}}$), 20 ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$) and 60 ($u_{{\textrm{x}}}=-0.25\,{\hbox {mm}}$), respectively. Though there are some minor differences probably caused by surface effect in PD, the proposed PD approach accurately simulates the elastoplastic behavior of materials with isotropic hardening.

Fig. 5

Displacement in the ${\textrm{x}}$ direction ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$, at load step 20) solved by: a FE, b PD, displacement in the $\textrm{y}$ direction ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$, at load step 20) solved by: c FE, d PD

Fig. 6

Distribution of the equivalent plastic strain ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$, at load step 20) obtained by: a FE, b PD

Fig. 7

Distribution of von Mises stress ($u_{{\textrm{x}}}=0.125\,{\hbox {mm}}$, at load step 10) obtained by: a FE, b PD

Fig. 8

Distribution of von Mises stress ($u_{{\textrm{x}}}=0.25\,{\hbox {mm}}$, at load step 20) obtained by: a FE, b PD

Fig. 9

Distribution of von Mises stress during unloading ($u_{{\textrm{x}}}=-\,0.25\,{\hbox {mm}}$, at load step 60) obtained by: a FE, b PD

Figures 10, 11 and 12 compare the von Mises stress at point A (see Fig. 3a) for the entire load history for the three cases of isotropic, kinematic and mixed hardening, respectively. Furthermore, the reaction force in the $\mathrm{x}$ direction on the left boundary of the plate in the case of isotropic hardening is shown in Fig. 13. The agreement between PD and FEM results is good. Point A is in the region where plastic strains take place. Note that in these three figures, positive von Mises stress is associated with a tensile load, and negative von Mises stress with a compressive load [31].

Fig. 10

von Mises stress at point A versus displacement loading for material with isotropic hardening

Fig. 11

von Mises stress at point A versus displacement loading for material with kinematic hardening

Fig. 12

von Mises stress at point A versus displacement loading for material with mixed hardening

Fig. 13

Reaction force ($\textrm{F}_{{\textrm{x}}}$) versus displacement loading for material with isotropic hardening

4.2 3D cases

4.2.1 3D structure subjected to axial load

A three-dimensional structure is considered with the geometry shown in Fig. 14a. The structure is constrained ($u_{\textrm{y}}=0$) at the bottom, and is subjected to a displacement controlled load ($u_{\textrm{y}}$) at its top. As shown in Fig. 15, the load is applied in 120 steps of $0.0175\,{\hbox {mm}}$.

Fig. 14

a Geometry, cross sections and loading, b fictitious boundary layers in the PD model

Fig. 15

Cyclic displacement loading in the $\textrm{y}$ direction ($u_{\textrm{y}}$)

In the PD model a uniform grid is adopted with $\Delta {\textrm{x}}=\Delta \textrm{y}=\Delta \textrm{z}=0.625\,{\hbox {mm}}$ which results in 750776 nodes. The horizon is $\delta =1.875\,{\hbox {mm}}$ with $\frac{\delta }{\Delta {\textrm{x}}}=3$ (see “Appendix 2”). In the FE model the mesh is made of 500161 nodes and 2883749 4-Node tetrahedral elements (Solid285).

Figure 16 shows some PD results in 3D view. In the next figures, the PD results are compared with the FE results. Figures 17, 18, 19, 20 and 21 show some FE and PD results at the load step 20 ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$) considering the isotropic hardening behavior. Figure 17 compares the displacement in the ${\textrm{x}}$ direction in the front view of the structure obtained by PD and FE. The displacement in the $\textrm{y}$ direction in a vertical plane of symmetry of the structure (section C, see Fig. 14a) is shown in Fig. 18. The distribution of the equivalent plastic strain is shown in Fig. 19. The distribution of the von Mises stress on the front view of the structure is presented in Fig. 20. The von Mises stress distribution at the section C is shown in Fig. 21 for the load step 20, and Fig. 22 for the load step 60. In all cases the agreement between PD and FEM results is good despite the presence of the PD surface effect in the PD solution.

Fig. 16

a Displacement in the $\textrm{y}$ direction, b von Mises stress, obtained by PD at load step 20

Fig. 17

Displacement in the ${\textrm{x}}$ direction ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$, at load step 20) computed by: a FE, b PD

Fig. 18

Displacement in the $\textrm{y}$ direction (section C) ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$, at load step 20) computed by: a FE, b PD

Fig. 19

Distribution of the equivalent plastic strain ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$, at load step 20) obtained by: a FE, b PD

Fig. 20

Distribution of von Mises stress (front view) ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$, at load step 20) obtained by: a FE, b PD

Fig. 21

Distribution of von Mises stress (section C) ($u_{\textrm{y}}=0.35\,{\hbox {mm}}$, at load step 20) obtained by: a FE, b PD

Fig. 22

Distribution of von Mises stress during unloading ($u_{\textrm{y}}=-0.35\,{\hbox {mm}}$, at load step 60) obtained by: a FE, b PD

Finally, von Mises stress versus loading at node O (see Fig. 14a) is shown in Figs. 23, 24 and 25. Figure 23 illustrates the case with isotropic hardening, Fig. 24 with kinematic hardening, and Fig. 25 shows the case in which both hardenings are present (mixed hardening). Moreover, the reaction force in the $\mathrm{y}$ direction at the top boundary of the structure is presented in Figs. 26, 27 and 28 for isotropic, kinematic and mixed hardening, respectively. In all three cases there is a good agreement between the PD and FE results.

Fig. 23

von Mises stress at point O versus displacement loading for material with isotropic hardening

Fig. 24

von Mises stress at point O versus displacement loading for material with kinematic hardening

Fig. 25

von Mises stress at point O versus displacement loading for material with mixed hardening

Fig. 26

Reaction force ($\textrm{F}_{\textrm{y}}$) versus displacement loading for material with isotropic hardening

Fig. 27

Reaction force ($\textrm{F}_{\textrm{y}}$) versus displacement loading for material with kinematic hardening

Fig. 28

Reaction force ($\textrm{F}_{\textrm{y}}$) versus displacement loading for material with mixed hardening

4.2.2 3D beam with square section under transverse load

A three-dimensional beam with dimensions: 200 mm in the ${\textrm{x}}$ direction, 20 mm in the $\textrm{y}$ and $\textrm{z}$ directions is considered (Fig. 29a). A vertical displacement, $u_{\textrm{y}}$, is applied at the right end of the beam in 20 steps. This beam is fixed in three directions ($u_{{\textrm{x}}}=u_{\textrm{y}}=u_{\textrm{z}}=0$) at its left end. On the right end side of the beam, we apply the load on the top of the beam on a line along the $\textrm{z}$ direction.

In the PD simulation, a fictitious layer with the length of one horizon size is added to the left hand side of the beam as it is shown in Fig. 29b, and the boundary conditions are applied on this layer. The horizon size of $\delta =3 \Delta {\textrm{x}}=3\,{\hbox {mm}}$ is used in the PD model and the domain is discretized with $\Delta {\textrm{x}}=\Delta \textrm{y}=\Delta \textrm{z}=1\,{\hbox {mm}}$. In the PD model, we have 81200 nodes. The FE model is composed by 926424 nodes and 5358217 4-Node tetrahedral elements (Solid285). The problem involves large rotations; therefore, in ANSYS, the solution procedure “Large displacements” has been used, while the proposed PD approach is capable of solving problems with large rotations.

Assuming the material with isotropic hardening, several PD and FE results at $u_{\textrm{y}}=15\,{\hbox {mm}}$ are compared in Figs. 30, 31, 32 and 33. Displacement in the ${\textrm{x}}$ and $\textrm{y}$ directions are shown in Figs. 30 and 31. It is observed in these figures that displacements are in good agreement. In Figs. 32 and 33, the distributions of von Mises stress are compared at the load step 10 ($u_{\textrm{y}}=7.5\,{\hbox {mm}}$) and 20 ($u_{\textrm{y}}=15\,{\hbox {mm}}$). We can conclude that also in this case the agreement is acceptable.

Fig. 29

a Geometry, boundary conditions and loading, b fictitious boundary layer in PD

Fig. 30

Displacement in the $\textrm{y}$ direction when $u_{\textrm{y}}=15\,{\hbox {mm}}$ (at load step 20) obtained by: a FE, b PD

Fig. 31

Displacement in the ${\textrm{x}}$ direction when $u_{\textrm{y}}=15\,{\hbox {mm}}$ (at load step 20) obtained by: a FE, b PD

Fig. 32

Distribution of von Mises stress (3D view of the section on the vertical mid-plane of the beam) when $u_{\textrm{y}}=7.5\,{\hbox {mm}}$ (at load step 10) obtained by: a FE, b PD

Fig. 33

Distribution of von Mises stress (3D view of the section on the vertical mid-plane of the beam) when $u_{\textrm{y}}=15\,{\hbox {mm}}$ (at load step 20) obtained by: a FE, b PD

5 Conclusion

This paper proposes a rate-independent plasticity PD model to simulate the mechanical behavior of materials with isotropic, kinematic and mixed hardening in 2D and 3D cases. The approach is consistent with classical rate-independent J2 plasticity with associated flow rule. The presented method was applied to the simulation of several 2D and 3D cases whose results (displacement and stress fields) were compared with those obtained from the corresponding FEM models, showing good agreement between the model solutions in all cases. The accuracy of the solutions was further analysed by locally comparing the von Mises stress evolution during the load history obtained from the PD and FEM models, highlighting the capabilities of the proposed model and demonstrating good agreement between the results. The proposed formulation represents a first step towards the simulation of ductile fracture in solid materials with isotropic, kinematic and mixed hardening using an ordinary state-based peridynamic (OSB-PD) model.

Appendices

Appendix 1

We extend the procedure described in [29] to 2D plane stress and plane strain cases. What has been done is simpler than the approach proposed by [33].

Based on Eq. 12, $\underline{t}^{\textrm{d}}_{\mathrm {n+1}}$ can be found in terms of $\underline{t}^{\textrm{d}}_{\textrm{trial}}$. We rewrite Eq. 12 for elastoplastic materials (see also Eq. 15) at step $\mathrm {n+1}$:

$$\begin{aligned} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}={\left\{ \begin{array}{ll} \frac{15\mu }{m}\underline{\omega }(\underline{e}^{\textrm{d}}_{{\mathrm {n+1}}}-\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}) &{} \quad \text{ for } \text{3D }, \\ \frac{8\mu }{m}\underline{\omega }(\underline{e}^{\textrm{d}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(A1)

We can write this equation as follows:

$$\begin{aligned}{} & {} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}\nonumber \\{} & {} \quad ={\left\{ \begin{array}{ll} \frac{15\mu }{m}\underline{\omega }(\underline{e}^{\textrm{d}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}})-\frac{15\mu }{m}\underline{\omega }(\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}}) &{} \quad \text{ for } \text{3D }, \\ \frac{8\mu }{m}\underline{\omega }(\underline{\textit{e}}^{\textrm{d}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}})-\frac{8\mu }{m}\underline{\omega }(\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}}) &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(A2)

The first part of Eq. A2 is the $\underline{t}^{\textrm{d}}_{\textrm{trial}}$ based on our assumption for the trial step ($\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}=\underline{e}^{\textrm{dp}}_{\textrm{n}}$). Therefore

$$\begin{aligned} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}={\left\{ \begin{array}{ll} \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{15\mu }{m}\underline{\omega }(\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}}) &{} \quad \text{ for } \text{3D }, \\ \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{8\mu }{m}\underline{\omega }(\underline{e}^{\textrm{dp}}_{\mathrm {n+1}}-\underline{e}^{\textrm{dp}}_{\textrm{n}}) &{} \quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(A3)

Using plastic flow rule (Eq. 21) [29] for step $\mathrm {n+1}$, the following equation is obtained:

$$\begin{aligned} \Delta \underline{\textit{e}}^{\textrm{dp}}=\underline{\textit{e}}^{\textrm{dp}}_{\mathrm {n+1}}-\underline{\textit{e}}^{\textrm{dp}}_{\textrm{n}}=\Delta \lambda \nabla ^{\textrm{d}}\psi _{\mathrm {n+1}}. \end{aligned}$$

(A4)

By substituting Eq. A4 in Eq. A3, we derive:

$$\begin{aligned} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}={\left\{ \begin{array}{ll} \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{15\mu }{m}\underline{\omega }\Delta \lambda \nabla ^{\textrm{d}}\psi _{\mathrm {n+1}} &{} \text{ for } \text{3D }, \\ \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{8\mu }{m}\underline{\omega }\Delta \lambda \nabla ^{\textrm{d}}\psi _{\mathrm {n+1}} &{} \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(A5)

$\nabla ^{\textrm{d}}$ produces functions that have no dilatation [29]. As a consequence, when $\psi (\underline{t}^{\textrm{d}})=\frac{\Vert \underline{t}^{\textrm{d}}\Vert ^{2}}{2}$, then $\nabla ^{\textrm{d}}\psi (\underline{t}^{\textrm{d}})=\underline{t}^{\textrm{d}}$. Hence, for step $\mathrm {n+1}$ we have:

$$\begin{aligned} \underline{t}^{\textrm{d}}_{\mathrm {n+1}}= {\left\{ \begin{array}{ll} \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{15\mu }{m}\underline{\omega }\Delta \lambda \underline{t}^{\textrm{d}}_{\mathrm {n+1}} &{} \quad \text{ for } \text{3D }, \\ \underline{t}^{\textrm{d}}_{\textrm{trial}}-\frac{8\mu }{m}\underline{\omega }\Delta \lambda \underline{t}^{\textrm{d}}_{\mathrm {n+1}} &{}\quad \text{ for } \text{2D } \text{ plane } \text{ stress/strain }. \end{array}\right. } \end{aligned}$$

(A6)

Appendix 2: Convergence studies

A $\delta$-convergence study is performed for the example solved in 3D in Sect. 4.2.1. Four horizon sizes, $\delta =4.6875$, $3$, $1.875$, $1.5\,{\hbox {mm}}$, respectively, and corresponding discretizations resulting from using an m-ratio ($\frac{\delta }{\Delta {\textrm{x}}}$) of 3 are considered in the PD simulation. In Fig. 34, the distribution of PD von Mises stress due to the displacement loading $u_{\textrm{y}}=0.35\,{\hbox {mm}}$ is compared with the results obtained by FE. The figure shows that all the PD models provide very similar results. Since the difference between cases (c) and (d) is minor, the results presented in Sect. 4.2.1 are obtained using the horizon size (and corresponding discretization grid) of case (c).

Fig. 34

$\delta$-convergence study with $m=\frac{\delta }{\Delta {\textrm{x}}}=3$: distribution of von Mises stress when $u_{\textrm{y}}=0.35\,{\hbox {mm}}$ obtained by: PD a $\delta =4.6875\,{\hbox {mm}}$, b $\delta =3\,{\hbox {mm}}$, c $\delta =1.875\,{\hbox {mm}}$, d $\delta =1.5\,{\hbox {mm}}$, e FE

We also perform an $m$-convergence study for the 3D example solved in Sect. 4.2.1. Two $m$ values, $m=3$ and $m=4$, are considered with a fixed $\delta =1.875\,{\hbox {mm}}$ ($\frac{\delta }{\Delta {\textrm{x}}}=m$) in the PD simulation. In Fig. 35, the distribution of von Mises stress under the displacement loading $u_{\textrm{y}}=0.35\,{\hbox {mm}}$ is compared with the results obtained by FE. The figure confirms that there are no significant differences between case (a) and case (b). Hence, case (a), $m=3$, is used to find results in the example of Sect. 4.2.1.

Fig. 35

m-convergence study with $\delta =1.875\,{\hbox {mm}}$: distribution of von Mises stress when $u_{\textrm{y}}=0.35\,{\hbox {mm}}$ obtained by: PD a $m=3$, b $m=4$, c FE