1 Introduction

Let \( {\mathcal {S}}'({\mathbb {R}}^n)\) denote the space of tempered distributions on \( {\mathbb {R}}^n\). A fundamental solution of \(\text {Op}(p) = {\mathcal {F}}^{-1}p{\mathcal {F}}\) is a \(\mu _0 \in {\mathcal {S}}'({\mathbb {R}}^n)\) such that

$$\begin{aligned} \text {Op}(p)\mu _0 = \delta _0 \quad \text {in} \quad {\mathcal {S}}'({\mathbb {R}}^n), \end{aligned}$$

where \(\delta _0\) is the unit measure at 0, \({\mathcal {F}}\) is the Fourier transform, and p is the symbol. The study of these is classical, and most results are recorded in standard texts [7, 8]. The Hörmander–Lojasiewicz theorem [6, 9] ensures existence when p is a polynomial, and provides a way to construct a \(\mu _0\), at least in principle, explicitly from the symbol. But the situation becomes nebulous when p is not a polynomial or globally smooth. We address this problem when \(p^{-1}(0)\) is compact and p is real-analytic near \(p^{-1}(0)\), and obtain an integral representation that clearly shows the structure of \(\mu _0\).

In order to do so, we use a variant of Hironaka’s resolution of singularities [1]. Generally, the local charts that are supplied by Hironaka’s theorem are unknowable, but they allow us to build an integral representation out of the geometry of \(p^{-1}(0)\). Occasionally, a diffeomorphism that brings p into a resolved form can replace them, and such a diffeomorphism can often be constructed when there is global symmetry. Important examples with this property include any sum of powers of the Laplacian, or any sum of powers of certain elliptic self-adjoint second-order differential operators. However, the novel and most interesting case for us here is when p is not a polynomial, and p is not necessarily globally smooth, but with dimension \(n>1\) and order \(d>0\). We give examples showing the utility of this approach.

A lot of research has been devoted to the construction of explicit representations. See e.g. Ortner and Wagner [10] and Camus [3, 4] for a broad class of operators. Usually, it is very difficult to find explicit representations of fundamental solutions, and the study is often focused on a particular operator of fixed order and dimension. In the case of general homogeneous elliptic and some types of non-elliptic operators, Camus [3, 4] obtained explicit representations valid for any number of dimensions. Apart from the base practical value of constructing general solutions via convolution, an explicit form may find application in proofs of mapping properties of its operator. See e.g. Rabier [11], where the solution obtained in [3], implicit in [7], is used.

2 Notation

Let \(p\in C({\mathbb {R}}^n)\) be real-analytic in a neighbourhood of \(p^{-1}(0) \ne \emptyset \). It must be smooth outside an open ball B(0, R) centered at 0 of some radius \(R>0\). Putting \(\langle \xi \rangle = (1+ |\xi |^2)^\frac{1}{2}\) for \(\xi \in {\mathbb {R}}^n\), it must satisfy

$$\begin{aligned} \sup _{\xi \in {\mathbb {R}}^n\setminus B(0,R)} \langle \xi \rangle ^{-d} | \partial _\xi ^\alpha p(\xi ) | < \infty \quad \text {for all} \quad \alpha \in {\mathbb {N}}_0^n, \end{aligned}$$

and the ellipticity constraint

$$\begin{aligned} \inf _{\xi \in {\mathbb {R}}^n\setminus B(0,R)} \langle \xi \rangle ^{-d}|p(\xi )| > 0. \end{aligned}$$

Definition 2.1

(The Paley-Wiener spaces) Let \(K \subset {\mathbb {R}}^n\) be compact and convex. Define \(\text {PW}^d_K({\mathbb {R}}^n)\) to be the space of entire functions u satisfying

$$\begin{aligned} \sup _{x \in {\mathbb {C}}^n}\exp \Big (-\sup _{\xi \in K} \text {Im}(x) \cdot \xi \Big ) \langle x \rangle ^{-d}|u(x)| < \infty . \end{aligned}$$

If \(\{ K_j \}_{j=1}^\infty \) is an exhaustion of \({\mathbb {R}}^n\) by compact convex sets, we put

$$\begin{aligned} \text {PW}^d({\mathbb {R}}^n)&= \cup _{j=1}^\infty \text {PW}^d_{K_j}({\mathbb {R}}^n). \end{aligned}$$

Moreover, we put \(\text {PW}^{-\infty }({\mathbb {R}}^n) = \cap _{d\in {\mathbb {Z}}} \, \text {PW}^{d}({\mathbb {R}}^n)\) and \(\text {PW}^{+\infty }({\mathbb {R}}^n) = \cup _{d\in {\mathbb {Z}}} \, \text {PW}^{d}({\mathbb {R}}^n)\).

These spaces are related to \( {\mathcal {E}}'({\mathbb {R}}^n)\), the compactly supported distributions on \({\mathbb {R}}^n\). We write \(H^{t}_\text {loc}({\mathbb {R}}^n)\) for the Frechet space of distributions locally belonging to \(H^{t}({\mathbb {R}}^n)\), and \(H^{-t}_\text {comp}({\mathbb {R}}^n)\) for its dual space of compactly supported distributions in \(H^{-t}({\mathbb {R}}^n)\). Finally, \( {\mathcal {S}}({\mathbb {R}}^n)\) is the Schwartz space, \(u\in {\mathcal {S}}({\mathbb {R}}^n)\) decays faster than any polynomial, and we put \({\mathcal {F}}u(\xi ) = \int _{{\mathbb {R}}^n} e^{-ix\cdot \xi } u(x) \, dx\) and \({\mathcal {F}}^{-1}u(x) = \frac{1}{(2\pi )^n}{\mathcal {F}}u(-x)\) for \(x,\xi \in {\mathbb {R}}^n\).

3 Solution Operator

Our main tool is Hironaka’s resolution of singularities. Often it is stated abstractly [2], but we need a local embedded version.

Theorem 3.1

(Local embedded version of Hironaka’s theorem. From Atiyah [1]) Let \(U\subset {\mathbb {R}}^n \) be an open neighbourhood of 0, and let f be a function \(0 \not \equiv f \in C^\omega (U)\). Then there is an open \(0 \in V\subset U\), a real-analytic manifold M, and a map

$$\begin{aligned} \Psi : M \rightarrow V. \end{aligned}$$

It has the following properties:

  1. 1.

    \(\Psi : M \rightarrow V\) is proper and real-analytic.

  2. 2.

    \(\Psi : M {\setminus } (f\circ \Phi )^{-1}(0) \rightarrow V {\setminus } f^{-1}(0) \) is a real-analytic diffeomorphism.

  3. 3.

    \((f\circ \Psi )^{-1}(0)\) is a hypersurface in M with normal crossings.

As p is real-analytic near its zero-set, it is compact with Lebesgue measure zero. The resolution theorem implies that p can be written locally in normal crossing form. Fix an open cover \(\{V_j\}_{j=1}^N\) of \(p^{-1}(0)\) and open \(\{U_j\}_{j=1}^N\) such that

  1. 1.

    \(\Psi _j: U_j{\setminus } (p\circ \Psi _j)^{-1}(0) \rightarrow V_j{\setminus } p^{-1}(0)\) is a real-analytic diffeomorphism,

  2. 2.

    \((p\circ \Psi _j)(x) = c_j(x) x^{\alpha _j}\) for all \(x\in U_j\) for some \(\alpha _j \in {\mathbb {N}}_0^n\),

where each \(c_j\) is a complex-valued, but nowhere zero, real-analytic function on \(U_j\). Also, we put \(m=\max \{\alpha _j\}_{j=1}^N\).

Theorem 3.2

Let \(\{\chi _j \}_{j=1}^N\) be any partition of unity subordinate to \(\{V_j\}_{j=1}^N\). There is a fundamental solution \(\mu _0\), smooth away from \(x = 0\), of the form

$$\begin{aligned} \mu _0(x) = {\mathcal {F}}^{-1}\Big (\frac{\chi }{p}\Big )(x) +\sum _{j=1}^N\int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ e^{ix\cdot \Psi _j(z)} \frac{(\chi _j \circ \Psi _j)(z)}{c_j(z)} |\det d\Psi _j(z)| \Big ] \, dz, \end{aligned}$$

where \(\chi = 1-\sum _{j=1}^N \chi _j\), and the \(I_j\) are given a.e. by

$$\begin{aligned} I_j(z) = \frac{1}{(2\pi )^n} \prod _{\alpha _{j,k} \ne 0} \frac{-\ln |z_k| }{(\alpha _{j,k}-1)!}. \end{aligned}$$

It is weakly approximated in \(H^t_{\text {loc}}({\mathbb {R}}^n)\) for \(t< d- \frac{n}{2}\) by a sequence in \(\text {PW}^{m}({\mathbb {R}}^n)\). Finally, if \(p^{-1}(0)\) is embedded, any \(v \in \ker \text {Op}(p) \subset \text {PW}^\infty ({\mathbb {R}}^n)\) is of the form

$$\begin{aligned} v(x) =\sum _{j=1}^N \sum _{k\le k_j-1} \Big \langle (\Psi _j^*)^{-1} (u_{j,k} \otimes \partial _{z_n}^k \delta _0)(\xi ), e^{ix\cdot \xi } \Big \rangle , \end{aligned}$$

where \(u_{j,k} \in {\mathcal {E}}'(U_j^0)\) are supported in the \(z_n = 0\) slice \(U_j^0 = \{ z \in {\mathbb {R}}^{n-1} \, | \, (z,0) \in U_j \}\), and each \(\Psi _j\) is arranged so that

$$\begin{aligned} (p \circ \Psi _j) (x) = c_j(x) x^{k_j}_n. \end{aligned}$$

In this case, all other fundamental solutions differ from \(\mu _0\) by such a v.

The first step is to prove a lemma about principal value integrals with log kernel. It is used here in a way similar to Björk [2, Chapter 6, Theorem 1.5].

Lemma 3.3

Let \(\psi \in C^\infty ({\mathbb {R}})\) be either rapidly decaying or compactly supported. Then, for any \(k \in {\mathbb {N}}\), we have

$$\begin{aligned} \int _{-\infty }^\infty \psi (r) \, dr = \frac{-1}{(k-1)!} \int _{-\infty }^\infty \ln (|r|) \frac{d^k}{dr^k} \Big ( r^{k} \psi (r) \Big ) \, dr. \end{aligned}$$

Proof

The proof of this is a routine exercise in repeated integration by parts. Observe that we can write \(\psi (r) = r^{-k}r^k \psi (r)\), and

$$\begin{aligned} \int _{-\infty }^\infty \psi (r) \, dr&= \frac{-1}{k-1} r^1 \psi (r) \Big |_{-\infty }^\infty + \frac{1}{k-1} \int _{-\infty }^\infty r^{-k+1} \frac{d}{dr} \Big ( r^{k} \psi (r) \Big ) \, dr \\&\quad \cdots \\&=\frac{-1}{(k-1)!} r^{k-1}\psi (r) \Big |_{-\infty }^\infty + \frac{1}{(k-1)!} \int _{-\infty }^\infty r^{-1} \frac{d^{k-1}}{dr^{k-1}} \Big ( r^{k} \psi (r) \Big ) \, dr \\&= \frac{-1}{(k-1)!} \int _{-\infty }^\infty \ln (|r|) \frac{d^k}{dr^k} \Big ( r^{k} \psi (r) \Big ) \, dr, \end{aligned}$$

where all boundary terms at 0 in the final integration vanish, because

$$\begin{aligned} \lim _{r \rightarrow 0\pm } \ln (|r|) \frac{d^{k-1}}{dr^{k-1}} \Big ( r^{k} \psi (r) \Big ) = 0, \end{aligned}$$

and boundary terms at \(\pm \infty \) vanish by the hypothesis on \(\psi \). \(\square \)

Lemma 3.4

Define \(Q: {\mathcal {S}}({\mathbb {R}}^n) \rightarrow C^\infty ({\mathbb {R}}^n)\) by

$$\begin{aligned} Q v(x) = \sum _{j=1}^N\int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ e^{ix\cdot \Psi _j(z)} \frac{(\chi _j{\mathcal {F}}v) \circ \Psi _j (z)}{c_j(z)} |\det d\Psi _j(z)| \Big ] \, dz. \end{aligned}$$

Then \(P = \text {Op}(\frac{\chi }{p}) + Q \) satisfies both

$$\begin{aligned} \text {Op}(p)Pv = v \quad \text {and} \quad P\text {Op}(p)v = v \quad \text {for all} \quad v \in {\mathcal {S}}({\mathbb {R}}^n). \end{aligned}$$

Proof

The proof is an application of Lemma 3.3 and the Fubini–Tonelli theorem. Let \(\psi \in {\mathcal {S}}({\mathbb {R}}^n)\). Using Lemma 3.3 coordinate-wise, we compute

$$\begin{aligned} \langle \text {Op}(p)Q v, \psi \rangle&= \int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ \langle \text {Op}(p) e^{i(\cdot )\cdot \Psi _j(z)} , \psi \rangle \frac{(\chi _j{\mathcal {F}}v) \circ \Psi _j (z)}{c_j(z)} |\det d\Psi _j(z)| \Big ] \, dz \\&=\int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ z^{\alpha _j} \langle e^{i(\cdot )\cdot \Psi _j(z)} , \psi \rangle (\chi _j{\mathcal {F}}v) \circ \Psi _j (z) |\det d\Psi _j(z)| \Big ] \, dz \\&=\frac{1}{(2\pi )^n}\int _{{\mathbb {R}}^n \setminus (p\circ \Psi _j)^{-1}(0)} \langle e^{i(\cdot )\cdot \Psi _j(z)} , \psi \rangle (\chi _j{\mathcal {F}}v) \circ \Psi _j (z) |\det d\Psi _j(z)| \, dz \\&=\frac{1}{(2\pi )^n}\int _{{\mathbb {R}}^n \setminus p^{-1}(0)} \langle e^{i(\cdot )\cdot \xi } , \psi \rangle (\chi _j{\mathcal {F}}v) (\xi ) \, d\xi \\&= \langle \text {Op}(\chi _j)v, \psi \rangle , \end{aligned}$$

and we then get

$$\begin{aligned} \langle \text {Op}(p)Q v, \psi \rangle = \sum _{j=1}^N \langle \text {Op}(\chi _j)v, \psi \rangle = \langle v - \text {Op}(\chi )v, \psi \rangle . \end{aligned}$$

Point-wise in \(x\in {\mathbb {R}}^n\), we compute

$$\begin{aligned} Q\text {Op}(p)v(x)&=\int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ e^{i x \cdot \Psi _j(z)} \frac{(\chi _j{\mathcal {F}}\text {Op}(p)v) \circ \Psi _j (z)}{c_j(z)} |\det d\Psi _j(z)| \Big ] \, dz \\&=\int _{{\mathbb {R}}^n} I_j(z) \partial _z^{\alpha _j} \Big [ z^{\alpha _j} e^{ix\cdot \Psi _j(z)} (\chi _j{\mathcal {F}}v) \circ \Psi _j (z) |\det d\Psi _j(z)| \Big ] \, dz \\&=\frac{1}{(2\pi )^n}\int _{{\mathbb {R}}^n \setminus (p\circ \Psi _j)^{-1}(0)} e^{i x\cdot \Psi _j(z)} (\chi _j{\mathcal {F}}v) \circ \Psi _j (z) |\det d\Psi _j(z)| \, dz \\&=\frac{1}{(2\pi )^n}\int _{{\mathbb {R}}^n \setminus p^{-1}(0)} e^{ix\cdot \xi } (\chi _j{\mathcal {F}}v) (\xi ) \, d\xi \\&= \text {Op}(\chi _j)v(x), \end{aligned}$$

which shows that

$$\begin{aligned} Q\text {Op}(p)v = \sum _{j=1}^N \text {Op}(\chi _j)v = v - \text {Op}(\chi )v. \end{aligned}$$

Note that the properties of \(\Psi _j\) ensure that all the above integrals are well-defined. The determinant of \(d\Psi _j\) on each component of \(U_j {\setminus } (p\circ \Psi _j)^{-1}(0)\) never becomes zero. This completes the proof. \(\square \)

Lemma 3.5

\(P: {\mathcal {S}}({\mathbb {R}}^n) \rightarrow C^\infty ({\mathbb {R}}^n)\) is continuous.

Proof

The proof is just estimating \(C^\infty ({\mathbb {R}}^n)\) semi-norms of Q in those of \({\mathcal {S}}({\mathbb {R}}^n)\). By the chain rule, if \(v\in {\mathcal {S}}({\mathbb {R}}^n)\), we have

$$\begin{aligned} \partial _{z_k}({\mathcal {F}}v \circ \Psi _j) = -i({\mathcal {F}}(x_1 v)\circ \Psi _j, \ldots ,{\mathcal {F}}(x_n v)\circ \Psi _j) \cdot \partial _{z_k}\Psi _j. \end{aligned}$$

Using the Leibniz rule, we get for any \(\alpha \in {\mathbb {N}}^n_0\) some \(C_\alpha ',C_\alpha > 0\) such that

$$\begin{aligned} |\partial _{x}^\alpha Q v(x)|&\le C_\alpha ' \sum _{j=1}^N\int _{\text {supp}(\chi _j)} |I_j(z)| \sum _{\beta \le \alpha _j} \langle x\rangle ^{\alpha _j - \beta } |\partial _z^{\beta } ({\mathcal {F}}v \circ \Psi _j) (z)| \, dz\\&\le C_\alpha \sum _{j=1}^N \Big ( \int _{\text {supp}(\chi _j)} |I_j(z)| \, dz \Big ) \langle x \rangle ^{m} \max _{|\beta |\le m}\sup _{z\in {\mathbb {R}}^n} | {\mathcal {F}}(x^\beta v)(z) |, \end{aligned}$$

which by the continuity of \({\mathcal {F}}: {\mathcal {S}}({\mathbb {R}}^n) \rightarrow {\mathcal {S}}({\mathbb {R}}^n)\) implies the lemma. \(\square \)

Lemma 3.6

\(P: \text {PW}^{-\infty }({\mathbb {R}}^n) \rightarrow \text {PW}^m({\mathbb {R}}^n)\) is well-defined.

Proof

Because each map \(\Psi _j\) is proper, each \(( \chi _j {\mathcal {F}}v )\circ \Psi _j\) is compactly supported. By the well-known [7, Paley–Wiener–Schwartz Theorem 7.3.1], \(\text {Op}(\frac{\chi }{p})v \in \text {PW}^{-\infty }({\mathbb {R}}^n)\). A simple estimate gives \(C',C>0\) such that

$$\begin{aligned} |Qv(x)|&\le C' \sum _{j=1}^N\int _{\text {supp}(\chi _j)} |I_j(z)| \sum _{\beta \le \alpha _j} |\partial _z^{\beta } [ e^{ix\cdot \Psi _j(z)} ] | \, dz\\&\le C\sum _{j=1}^N \Big ( \int _{\text {supp}(\chi _j)} |I_j(z)| \, dz \Big ) \langle x \rangle ^{m} \exp \Big (\sup _{\xi \in K} \text {Im}(x)\cdot \xi \Big ), \end{aligned}$$

where K is a compact and convex set so large that

$$\begin{aligned} -\cup _{j=1}^N \text {supp}(\chi _j) \subset K, \end{aligned}$$

and so Qv is entire with \(Qv \in \text {PW}^{m}({\mathbb {R}}^n)\). \(\square \)

Define the reflection map A by \(A\psi (x) = \psi (-x)\) for all \(x\in {\mathbb {R}}^n\) on \(\psi \in C^\infty ({\mathbb {R}}^n)\). It takes \({\mathcal {S}}({\mathbb {R}}^n)\) and \(C^\infty _0({\mathbb {R}}^n)\) continuously to themselves. The transpose of Q is AQA. Using this fact and Lemma 3.5, we extend Q, hence P, by duality:

Definition 3.7

Define \(Q: u\mapsto Qu: {\mathcal {E}}'({\mathbb {R}}^n) \rightarrow {\mathcal {S}}'({\mathbb {R}}^n)\) by

$$\begin{aligned} \langle Qu, \psi \rangle = \langle u, A Q A\psi \rangle \quad \text {for all} \quad \psi \in {\mathcal {S}}({\mathbb {R}}^n). \end{aligned}$$

Lemma 3.8

\(\text {Op}(p)Ps = s\) holds for any \(s\in {\mathcal {E}}'({\mathbb {R}}^n)\).

Proof

By Lemma 3.4, if \(\psi \in {\mathcal {S}}({\mathbb {R}}^n)\), we have

$$\begin{aligned} \langle \text {Op}(p)P s , \psi \rangle&= \langle s, A P A \text {Op}(p)^* \psi \rangle \\&=\langle s, A P A {\mathcal {F}} (p {\mathcal {F}}^{-1}\psi ) \rangle \\&=\langle s, A P \text {Op}(p) A\psi \rangle \\&=\langle s, A^2\psi \rangle \\&=\langle s, \psi \rangle . \end{aligned}$$

\(\square \)

Applying Lemma 3.8, we get the fundamental solution \(\mu _0 = P\delta _0\) for the operator. Using e.g. [12, Theorems 5.2 and 7.1], or similar in [5], it is smooth in \(x \ne 0\), and

$$\begin{aligned} \mu _0 \in H^{t}_{\text {loc}}({\mathbb {R}}^n) \quad \text {if} \quad t < d-\frac{n}{2}. \end{aligned}$$

Lemma 3.9

\(\mu _0\) is weakly approximated in \(H^t_{\text {loc}}({\mathbb {R}}^n)\) by a \(\text {PW}^{m}({\mathbb {R}}^n)\) sequence.

Proof

Take a bump function \(\eta \in C^\infty _0({\mathbb {R}}^n)\) such that \(\eta (x) = 1\) holds for all \(|x|<1\). Put \(\eta _k(x) = \eta (\frac{x}{k})\) for all \(x \in {\mathbb {R}}^n\) and \(k\in {\mathbb {N}}\). By Lemma 3.6, \(P{\mathcal {F}}^{-1}\eta _k \in \text {PW}^{m}({\mathbb {R}}^n)\). Given any \(u\in H^{-t}_{\text {comp}}({\mathbb {R}}^n)\), then for k large enough, we get

$$\begin{aligned} |\langle \mu _0 - P{\mathcal {F}}^{-1}\eta _k, u \rangle |^2&= \Big |\Big \langle {\mathcal {F}}^{-1}\Big (\frac{\chi }{p}(1- \eta _k)\Big ) , u \Big \rangle \Big |^2 \\&=\Big |\Big \langle \frac{\chi }{p}(1- \eta _k) , {\mathcal {F}}^{-1}u \Big \rangle \Big |^2 \\&\le \Big ( \int _{{\mathbb {R}}^n} \langle \xi \rangle ^{2t} \Big |\frac{\chi }{p}(1- \eta _k)\Big |^2 \, d\xi \Big ) \Big ( \int _{{\mathbb {R}}^n} \langle \xi \rangle ^{-2t} |{\mathcal {F}}^{-1}u(\xi )|^2 \, d\xi \Big ) \end{aligned}$$

and so \(P{\mathcal {F}}^{-1}\eta _k \rightarrow \mu _0\) weakly in \(H^t_{\text {loc}}({\mathbb {R}}^n)\) as \(k\rightarrow \infty \). \(\square \)

Lemma 3.10

Suppose that \(p^{-1}(0)\) is embedded as a real-analytic submanifold. Then \(\ker \text {Op}(p)\) consists of functions \(v \in \text {PW}^{\infty }({\mathbb {R}}^n)\) of the form

$$\begin{aligned} v(x)= \sum _{j=1}^N \sum _{k\le k_j-1} \Big \langle (\Psi _j^*)^{-1} (u_{j,k} \otimes \partial _{z_n}^k \delta _0)(\xi ), e^{ix\cdot \xi } \Big \rangle , \end{aligned}$$

where \(u_{j,k} \in {\mathcal {E}}'(U_j^0)\) and \(\Psi _j\) are precisely as stated in Theorem 3.2.

Proof

Observe that \(p{\mathcal {F}}v = 0\) implies \(\text {supp}\, {\mathcal {F}}v \subset p^{-1}(0)\) so that \({\mathcal {F}}v\) is compact. Again by [7, Theorem 7.3.1], \(v \in \text {PW}^{\infty }({\mathbb {R}}^n)\). Observe then that

$$\begin{aligned} 0 = \Psi _j^* ( \chi _j p{\mathcal {F}}v ) = c_j z^{k_j}_n \Psi _j^* (\chi _j {\mathcal {F}}v), \end{aligned}$$

and since \(c_j\) is never zero, by [7, Theorem 2.3.5], we must have

$$\begin{aligned} \Psi _j^* ( \chi _j {\mathcal {F}}v ) = \sum _{k\le k_j-1} (2\pi )^n u_{j,k} \otimes \partial _{z_n}^k \delta _0, \end{aligned}$$

where \(u_{j,k} \in {\mathcal {E}}'({\mathbb {R}}^{n-1})\) are some distributions supported inside the \(z_n = 0\) slice of \(U_j\). It follows that

$$\begin{aligned} v(x)&= {\mathcal {F}}^{-1}\Big (\sum _{j=1}^N \chi _j {\mathcal {F}}v\Big )(x) \\&= \sum _{j=1}^N \sum _{k\le k_j-1} {\mathcal {F}}^{-1} (\Psi _j^{-1})^* \Big ((2\pi )^n u_{j,k} \otimes \partial _{z_n}^k \delta _0\Big )(x) \\&= \sum _{j=1}^N \sum _{k\le k_j-1} \Big \langle (\Psi _j^*)^{-1} (u_{j,k} \otimes \partial _{z_n}^k \delta _0)(\xi ), e^{ix\cdot \xi } \Big \rangle . \end{aligned}$$

\(\square \)

Fig. 1
figure 1

Deformation of a star-convex zero-set onto a circle

Full size image

The main Theorem 3.2 is finally obtained by combining the above partial results. Unfortunately, it is impossible to obtain \(\Psi _j\) explicitly for any given multiplier symbol. But if, for example, \(p^{-1}(0)\) is the real-analytic boundary of some star-convex domain, we can replace the charts by a single deformation \(\Psi \) of the boundary onto a sphere. Given p, we look for \(\Psi \) so that \(\Psi ^* p\) factorizes. Our main theorem gives

$$\begin{aligned} \mu _0(x) = {\mathcal {F}}^{-1}\Big (\frac{\chi }{p}\Big )(x) + Q\delta _0(x), \end{aligned}$$

where \(\chi \) appropriately suppresses a region surrounding \(p^{-1}(0)\) on which \(\Psi \) is defined (Fig. 1).

3.1 Sums of powers of \(\Delta _g\)

Let g be a positive-definite symmetric matrix. Consider for \(d\in {\mathbb {N}}\) and \(\{c_j\}_{j=0}^{d}\subset {\mathbb {C}}\) with \(c_d = 1\) and \(c_0 \ne 0\) the multiplier

$$\begin{aligned} \text {Op}(p) = \sum ^d_{j= 0} c_j \Delta _g^\frac{j}{2}. \end{aligned}$$

The symbol p is taken into a polynomial form by the map

$$\begin{aligned} \Psi : (0,\infty ) \times {\mathbb {S}}^{n-1} \rightarrow {\mathbb {R}}^{n}\setminus 0 : (r,\omega ) \mapsto r g^{-\frac{1}{2}} \omega . \end{aligned}$$

Pulling back, we find that

$$\begin{aligned} (p \circ \Psi )(r,\omega ) = c(r) \prod ^m_{j=1} (r-r_j)^{m_j}, \end{aligned}$$

where c is a polynomial with no root in \([0,\infty )\), and \(r_j>0\) are the positive real roots. Let \(C_{j,k}\) be the unique coefficients in \(\prod ^m_{j=1} (r-r_j)^{-m_j} = \sum _{j=1}^m \sum ^{m_j}_{k=1} C_{j,k} (r-r_j)^{-k}\). Pick \(\chi \in C^\infty ({\mathbb {R}}^n)\) so that \(1-\chi \circ \Psi \in C^\infty _0((0,\infty )\times {\mathbb {S}}^{n-1})\) is independent of \(\omega \in {\mathbb {S}}^{n-1}\), and equal to 1 in a neighbourhood of \(\cup _{j=1}^m \{r_j\} \times {\mathbb {S}}^{n-1}\), all of the spheres of radius \(r_j\). If the multiplicities satisfy \(m_j< n\), we have

$$\begin{aligned} Q\delta _0(x) = \sum _{j=1}^{m} \sum _{k=1}^{m_j} B_{j,k} \int ^\infty _0 \ln |r-r_j| \, \partial _r^k \Big [ (1-\chi \circ \Psi )(r) \frac{r^{\frac{n}{2}}}{c(r)}\frac{J_{\frac{n}{2}-1} (r|g^{-\frac{1}{2}}x|)}{|g^{-\frac{1}{2}}x|^{\frac{n}{2}-1}} \Big ] \, dr, \end{aligned}$$

where \(J_{\frac{n}{2}-1}\) is the cylindrical Bessel function of order \(\frac{n}{2}-1\), and

$$\begin{aligned} B_{j,k} = -\frac{\det \, g^{-\frac{1}{2}}}{(2\pi )^{\frac{n}{2}}(k-1)!} C_{j,k}. \end{aligned}$$
Fig. 2
figure 2

Covering the zero-set of p except for a point. Here \(a=\frac{1}{4}\) and \(n=12\)

Full size image

3.2 A perturbation of \(\Delta _g\)

Let \(\arg \xi \) be the multi-valued argument of \(\xi \in {\mathbb {R}}^2\). Consider instead the multiplier symbol

$$\begin{aligned} p : {\mathbb {R}}^2 \rightarrow {\mathbb {R}} : \xi \mapsto |\xi |_g^2 - \Big (1+a\cos (n \arg \xi ) \Big ), \end{aligned}$$

where \(n \in {\mathbb {N}}\) and \(a<\frac{1}{2}\). It is certainly real-analytic near its star-shaped zero-set. This p is taken into normal crossing form by the map

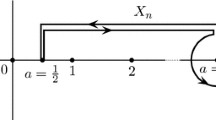
$$\begin{aligned} \Psi : (-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}}) \times (0, 2\pi ) \rightarrow {\mathbb {R}}^2 : (r,\theta ) \mapsto \Big (r + 1 + a\cos (n \theta ) \Big )^\frac{1}{2} g^{-\frac{1}{2}} (\cos \theta , \sin \theta ). \end{aligned}$$

It is clear that \(\Psi \) is a diffeomorphism onto its image, not covering the whole zero-set, as depicted in Fig. 2. But a representation using only \(\Psi \) is still possible, because it misses just a single point. Pulling back, we find that

$$\begin{aligned} ( p \circ \Psi )(r,\theta ) = r, \end{aligned}$$

and we compute

$$\begin{aligned} \det d\Psi (r, \theta ) = \frac{1}{2} \det g^{-\frac{1}{2}}. \end{aligned}$$

Pick \(\chi \) such that \(1-\chi \circ \Psi \in C^\infty ((-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}})\times (0,2\pi ))\) does not depend on \(\theta \in (0,2\pi )\), and is compactly supported in \((-{\textstyle \frac{1}{4}},{\textstyle \frac{1}{4}})\) and equal to 1 in a neighbourhood of \(r=0\). We tacitly extend \(\chi \) by one to all of \({\mathbb {R}}^2\). In that case, we have

$$\begin{aligned} Q\delta _0(x) = - \frac{\det g^{-\frac{1}{2}}}{8\pi ^2} \int _{-\frac{1}{2}}^{\frac{1}{2}}\ln |r|\, \partial _r \Big [ (1-\chi \circ \Psi )(r) \int _{0}^{2\pi }e^{ix\cdot \Psi (r,\theta )} \, d\theta \Big ] \, dr, \end{aligned}$$

and \(\ker \text {Op}(p)\) consists of v of the form

$$\begin{aligned} v(x) = \Big \langle u(\theta ), e^{ix\cdot \Psi (0,\theta )} \Big \rangle , \end{aligned}$$

where \(u \in {\mathcal {D}}'({\mathbb {R}}/2\pi {\mathbb {Z}})\) is a distribution on the space of \(2\pi \)-periodic smooth functions. We could replace \(|\xi |^2_g\) in p by any integer power of \(|\xi |^2_g\) and still get a similar result, provided that we adjust the fractional power \(\frac{1}{2}\) in \(\Psi \) in accordance with this change. A similar technique can be applied to sums of powers of such multipliers too.