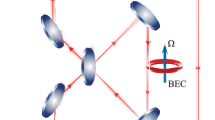
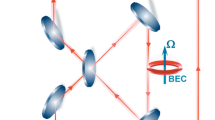
A perspective scheme of quantum gyroscope based on measurement of geometric phase emerging in atomic Bose–Einstein condensate (BEC) was developed. The main elements of the device are two ring-shaped BEC configurations intercepted by a pair of localized potentials—a barrier and a well. Their placement in each ring defines their orientation with respect to the angular velocity of rotation of the device’s frame. Proper variation of the parameters of the barriers and wells induces opposite-sign geometric phases in the BEC modes. Difference of these phases can be measured in interference experiment. We present results of geometric phase calculations for BEC of 87Rb atoms in ring potentials of 0.5 cm diameter and angular velocities comparable to that of the Earth’s rotation.
Similar content being viewed by others
INTRODUCTION
Modern experimental techniques of preparation and control of ultracold atomic ensembles find applications in high-sensitivity inertial sensors [1–3]. Investigations of perspective matter-wave devices using interference of coherent many-body states instead of interference of optical waves, as an alternative to optical devices, are highly topical. A typical example of such states (from theoretical point of view) is Bose–Einstein condensate (BEC). Classical optical gyroscopes are based on Sagnac effect. The detected Sagnac phase is given by [4, 5]
Here, \(\mathbf{\Omega} \) is angular velocity of rotation of the reference frame, \({\mathbf{S}}\) is an oriented area of interferometer, \(\omega \) is the radiation frequency. In atom interferometer, \(\omega \) should be replaced by \(m{{c}^{2}}{\text{/}}\hbar \), where m is the mass of the atom. This is a much greater value, which grants potential advantage to matter-wave devices over optical gyroscopes. However, direct replication of Sagnac interferometer with BEC is a non-trivial task. Different approaches to realizations of such schemes include building matter-wave analogues of waveguides [6–8], and also using BEC in specific quantum states [9].
In [10], an alternative approach to BEC-based gyroscopes was proposed. Instead of measuring Sagnac phase, measurement of specific geometric phase created by the rotation of the BEC reference frame was proposed. The concept of such gyroscopes can be imagined as follows, for a moment leaving aside the details of geometric phase generation. Consider BEC formed by two spatially separated modes 1 and 2, created by coherent splitting of initially uniform BEC. Configuration of both modes should grant sensitivity of BEC state to rotation of its reference frame. Orientations of modes’ configurations with respect to angular velocity \(\mathbf{\Omega} \) are such that rotation affects the states of the modes differently. In all other respects modes 1 and 2 are equivalent. It is assumed that the processes of geometric phase generation in both modes are also the same.Footnote 1 However, different susceptibility to rotation leads to emergence of different geometric phases: \({{\theta }_{1}} \ne {{\theta }_{2}}\). The BEC state is modified:
Here, N is the total number of atoms in BEC (we assume it to be fixed for simplicity), and fn are probability amplitudes of numbers of atoms in the modes. The difference of the modes’ relative phase is a physically meaningful quantity:
which modifies the interference pattern between the modes 1 and 2, and from it the information about the rotation rate \(\mathbf{\Omega} \) can be extracted.
In [10] ring-shaped spatial configurations of the modes interrupted by localized potentials—“defects” or “defect potentials” (Fig. 1) were considered. In absence of defects spatial configurations of the modes are identical. It is of utter importance that the forms of these defects set orientations of the rings (note that the modes in Fig. 1 are placed in such a way that additional potentials may be created with only two light beams propagating normally to the ring plane: one of them creates wells in both modes, while the other creates barriers, also in both modes). Geometric phase is generated by variation of parameters of additional potentials. In the scheme discussed in [10] the ring planes are normal to \(\mathbf{\Omega} \), with opposite orientations. Such conditions are optimal for rotation sensing: \({{\theta }_{1}} = - {{\theta }_{2}}\), and the difference \({{\theta }_{1}} - {{\theta }_{2}}\) is zero for \(\mathbf{\Omega} = 0\).
(Color online) Conceptual scheme of the main part of the gyroscope. Planes of both spatial configurations are normal to angular velocity vector \(\mathbf{\Omega} \) of the gyroscope reference frame. Symbolically labelled barrier and well define different orientation of the rings with respect to this vector.
The approach suggested in [10] was based on description of the defect in terms of transfer matrices. We relied on the main universal property of transfer matrices—that they belong to the \(\mathcal{S}\mathcal{U}(1,1)\) group. The orientations of the rings were defined by the order of multipliers in a product of two typical \(\mathcal{S}\mathcal{U}(1,1)\) matrices. Such approach was not limited to a specific structure of defect potential, which lead to a much simpler but somewhat artificial treatment. In particular, energy dependence of transfer matrix elements was completely ignored.
The purpose of this work is to construct a gyroscopic scheme in which the abstract transfer matrix is replaced by a rigorous derivation from the form of the defect potential that should grant orientation of the ring. The most obvious and simple variant of such potential is the combination of a barrier and a well. The next section is dedicated to construction of a scheme model with such potential. In the third section, the results of numerical calculations aimed for Earth’s rotation sensing are presented and discussed.
MODEL
We use the simplest model of non-interacting atomic BEC. For this reason, the single-particle wave function can be used for geometric phase evaluation. The wave functions describing modes’ spatial configurations thus do not depend on the numbers of atoms in them. However, the total number of atoms in BEC would matter during observation of interference between the modes (we will return to this question in the concluding section).
Consider the ring-shaped BEC modes’ reference frame rotating at angular velocity \(\mathbf{\Omega} \), oriented normally to the ring planes. The steady-state equation on a wave function of an atom in the ring is obtained from usual Schrödinger equation by introducing additional term related to rotation [11]:
Here, \(\varepsilon = m{{R}^{2}}E{\text{/}}{{\hbar }^{2}}\) is dimensionless energy (m is atom mass, R is ring radius), \(\xi = m{{R}^{2}}\Omega {\text{/}}\hbar \) is dimensionless parameter characterizing the rotation rate of the reference frame (note that it is equal to the Sagnac phase defined in (1), up to a \(4\pi \) factor), and derivatives with respect to the angular coordinate are denoted by primes. To give a figure of merit, for BEC of 87Rb atoms in a ring of \(R = 0.25\) cm radius (experimentally achievable in near-future experiments), and \(\Omega \) equal to the Earth’s axial rotation, \(\xi \) parameter is equal to 0.392. Note that for other alkali atoms and their isotopes in which Bose–Einstein condensation was observed (such as 7Li [12], 23Na [13], 39K [14], 40Ca [15], 133Cs [16] and others), the value of \(\xi \) would be of the same order. It is then reasonable to set the other parameters of the problem aimed at sensing the values \(\xi \simeq 0.1{-} 1\).
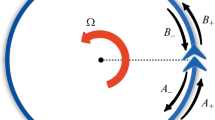
The right-hand side of (4) contains the terms describing the defect—a pair of singular potentials at \( \pm {{\varphi }_{0}}\); \({{a}_{ \pm }}\) are their characteristic values.Footnote 2 If \({{a}_{ + }} \ne {{a}_{ - }}\), then a pair of singular potentials obviously defines different orientations of the rings. The wave function is continuous, while its derivative suffers a jump at \( \pm {{\varphi }_{0}}\) [20]:
Outside the singular potentials atom movement is free and can be represented by a superposition of fundamental solutions:
The amplitudes \({{f}_{ \pm }}\) and \({{g}_{ \pm }}\) at \( \pm {{\varphi }_{0}}\) are related by conditions following from (5) and circular geometry:
It allows obtaining a system of equations directly on \({{g}_{ \pm }}\):
Transfer matrix \(\mathcal{M}\) appears to belong to \(\mathcal{S}\mathcal{U}(1,1)\), i.e., \({\text{|}}u{{{\text{|}}}^{2}} - \,{\text{|}}{v}{{{\text{|}}}^{2}} = 1\); the bar denotes complex conjugation. It thus possesses the main property mentioned in the Introduction.
In what follows, we will consider the case
i.e., we will assume that the height of the barrier and the depth of the well are the same. The transfer matrix elements become:Footnote 3
As one can see, the transfer matrix elements gain dependence on the energy of the atom—this effect could not be taken into account with abstract transfer matrix not related to a specific potential shape.
System (8) is consistent if
which can be regarded as equation on \(\kappa \). Amplitudes \({{g}_{ \pm }}\) also appear to be related:
If the parameters of the potential (the depth of the well and the height of the barrier) are changed, the spatial mode gains a phase \({{\theta }_{{{\text{total}}}}} = {{\theta }_{{{\text{dyn}}}}} + {{\theta }_{{{\text{geom}}}}}\) consisting of two parts—dynamical phase \({{\theta }_{{{\text{dyn}}}}}\) and geometric phase \({{\theta }_{{{\text{geom}}}}}\). To parameterize the variation of the potential, consider the following law:Footnote 4
With each chosen interval of variation of \(\alpha \) a definite geometric phase is associated:
Here, \({{\theta }_{{{\text{geom}}}}}\) is represented as a difference between \({{\theta }_{{{\text{total}}}}}\) (the first term in the right-hand side) and \({{\theta }_{{{\text{dyn}}}}}\). The dot above the symbol denotes derivative with respect to \(\alpha \). This expression is written in the form invariant not only under any gauge transformation
but also under transformations involving any smooth non-zero function \(F(\alpha )\) instead of exponential. The latter circumstance is convenient for calculations, since there is no need to normalize the wave function. The mentioned invariance of the geometric phase makes it true physically measurable quantity, unlike \({{\theta }_{{{\text{total}}}}}\) and \({{\theta }_{{{\text{dyn}}}}}\) [21]. In particular, by proper choice of \(\phi (\alpha )\) in (15) it is possible to compensate the dynamical phase (second term in (14)), which will reduce \({{\theta }_{{{\text{geom}}}}}\) to \({{\theta }_{{{\text{total}}}}}\).
As mentioned in the Introduction, the physical observable containing the information about angular velocity of rotation is the difference of phases gained by different spatial modes of the BEC. The latter differ by the orientation with respect to the angular velocity vector \(\mathbf{\Omega} \). The simplest way to change the orientation is to swap the positions of the well and the barrier, which in the considered case of the symmetric defect (9) is equivalent to changing the sign of \({{a}_{0}}\) in (13). The value of \(\kappa \) defined in (7) (and hence the energy \(\varepsilon \)) remains the same, since \(\kappa \) only depends on the absolute value of the potential, as follows from (13). Wave function, however, is sensitive to such change, because the amplitudes \({{f}_{ \pm }},{{g}_{ \pm }}\) depend on the first power of a (see (10), (12)). That said, it is of interest to calculate the value of
This quantity defines the shift of interference pattern in real experiment with the BEC modes. The necessary expressions for its calculation can be found in the Appendix.
RESULTS AND DISCUSSION
In [10], a scheme for compensation of dynamical phase was proposed. It was made possible by a suitable choice of the closed path for variation in the potential parameter space. For the potential of the form given in (13) this would be a cyclic variation \([{{\alpha }_{1}},{{\alpha }_{2}}] = [0,\pi ]\). However, the calculations according to (14), (16) show that \({{\theta }_{{{\text{geom}}}}}\) in this case is identically equal to zero.Footnote 5 Due to that, a two times smaller interval \([{{\alpha }_{1}},{{\alpha }_{2}}] = [0,\pi {\text{/}}2]\) was chosen. In this case, in the final point of the evolution the states of BEC modes become completely identical (because the rings have no orientation anymore), but the phase difference between them would be non-trivial.
The Fig. 2 shows how geometric phase difference \(\Delta {{\theta }_{{{\text{geom}}}}}\) defined in (16) depends on parameter \(\xi \) that characterizes the angular velocity, for different placements of the potential defects on a ring. A couple of features should be noted. First, the geometric phase difference depends weakly on the \({{a}_{0}}\). Second, the said difference is significantly affected by the mutual positions of the barrier and the well given by the angle \({{\varphi }_{0}}\). Its smaller values are of the most interest, as can be seen from Fig. 2. This follows from simple physical reasoning—the closer are the barrier and the well, the more pronounced are the orientations of the rings. For \({{\varphi }_{0}} = \pi {\text{/}}2\), the orientation vanishes, as well as the geometric phase difference. Near-zero values of \({{\varphi }_{0}}\) grant both maximal value of phase difference and maximal value of the slope for \(\xi \sim 0.4\). The latter circumstance allows for more precise measurements of angular velocities of the order of the Earth’s rotation (\(\xi = 0.392\)). On the other hand, the value of the angle between the barrier and the well only weakly affects the slope and hence the precision of the measurement for small values of \(\xi \sim 0.4\).
(Color online) The difference of geometric phases of the spatial modes for potential variation given by \(a = {{a}_{0}}{\text{co}}{{{\text{s}}}^{2}}\alpha \), \(\alpha \in [0,\pi {\text{/}}2]\), \({{a}_{0}} = 2\) as a function of dimensionless angular velocity \(\xi \) of reference frame rotation, for different placements of the well and the barrier.
The general form of the obtained curve is similar to the results of [10], from which one can conclude the correctness of the “abstract” transfer-matrix model.
In absence of information about the order of the angular velocity to be registered, it is desired to have the possibly widest interval of one-to-one correspondence between the measured phase difference and the angular velocity. This interval can be broadened by increasing the radius of the rings.
CONCLUSIONS
In this work, a model of quantum gyroscope based on geometric phase of atomic BEC was developed. The measured quantity containing information about the angular velocity of rotation is the relative phase of two ring-shaped spatial modes of a uniform condensate. Sensitivity to rotation is achieved by introducing localized potential configurations (“defects”) into each mode. By variation of the parameters of the defects, each mode gains a phase shift. Their difference can be detected as a shift of the interference pattern formed by the atoms from both modes, with respect to interference pattern in absence of geometric phase generation. Measurement precision for this shift will increase with the number of atoms involved into formation of the interference pattern. In this regard, the total number \(N\) of the atoms in the BEC becomes important. Realization of such an experiment would require a proper atom interferometer. Its detailed description falls outside the scope of the present work; however, with due caution it can be assumed that it should be based on the same principles as most of the matter-wave interferometric schemes—i.e., the initially separated spatial modes should be brought into overlap [22, 23].
As a model of defect, a combination of \(\delta \)-like barrier and well was used. Their relative placement on a ring sets its orientation and thus grants different sensitivity to rotation. Despite this being one of the simplest variants of the potential defect, it still can be applied to real experimental situation. In particular, in [24] it was shown that the problem with a single \(\delta \)-like potential on a ring is equivalent to the one with rectangular potential with certain height–width ratio.
Unlike the abstract description of defect by some transfer matrix, realistic barrier–well model requires open trajectories potential parameters variation. This is due to special “symmetric” way of its variation that was chosen—the depth of the well is at all times equal to the height of the barrier. It is the only parameter that is varied. Possibly one could choose a closed trajectory in a two-dimensional parameter space (barrier height–well depth) leading to non-zero geometric phase deference between the BEC modes. Taking into account atomic interactions is undoubtedly important. It could be done within well-known Ginzburg–Gross–Pitaevskii model or one-dimensional boson model with contact interaction.
The calculations support the claim that the proposed model possesses the necessary characteristics of a gyroscope, i.e., it allows to unambiguously (in a certain range) deduce the angular velocity of rotation of the reference frame from the measured phase shifts. The measurements should be done in pulse-like mode, because observation of interference between the modes would necessarily destroy the BEC. The values of the measured phase shifts are comparable to the Sagnac phase observed in traditional gyroscopic schemes based on atom interferometers.
Notes
By this we mean geometric phases of single-particle wave functions. We exclude interactions between the atoms for simplicity.
For \(a \ne 0\) the ring has definite orientation.
Since the defect only depends on one parameter, specific form of its variation is insignificant.
Different forms of variation lead to the same result, i.e., for any cyclic variation of the potential the geometric phase is identically equal to zero. This is due to the parameter space being one-dimensional.
REFERENCES
K. Bongs, M. Holynski, J. Vovrosh, P. Bouyer, G. Condon, E. Rasel, C. Schubert, W. P. Schleich, and A. Roura, Nat. Rev. Phys. 1, 731 (2019).
B. Barrett, R. Geiger, I. Dutta, M. Meunier, B. Canuel, A. Gauguet, P. Bouyer, and A. Landragin, C. R. Phys. 15, 875 (2014).
D. S. Durfee, Y. K. Shaham, and M. A. Kasevich, Phys. Rev. Lett. 97, 240801 (2006).
G. B. Malykin, Phys. Usp. 43, 1229 (2000).
P. Storey and C. Cohen-Tannoudji, J. Phys. II (Fr.) 4, 1999 (1994).
T. Muller, X. Wu, A. Mohan, A. Eyvazov, Y. Wu, and R. Dumke, New J. Phys. 10, 073006 (2008).
C. L. G. Alzar, AVS Quantum Sci. 1, 014702 (2019).
K. A. Krzyzanowska, J. Ferreras, C. Ryu, E. C. Samson, and M. G. Boshier, Phys. Rev. A 108, 043305 (2023).
L. Shao, W. Li, and X. Wang, arXiv: 2006.05794v1 [quant-ph] (2020).
A. M. Rostom, V. A. Tomilin, and L. V. Il’ichov, J. Exp. Theor. Phys. 135, 264 (2022).
A. J. Leggett, Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems (Oxford Univ. Press, Oxford, 2006).
C. C. Bradley, C. A. Sackett, J. J. Tollett, and R. G. Hulet, Phys. Rev. Lett. 75, 1687 (1995).
K. B. Davis, M.-O. Mewes, M. R. Andrews, N. J. van Druten, D. S. Durfee, D. M. Kurn, and W. Ketterle, Phys. Rev. Lett. 75, 3969 (1995).
M. Landini, S. Roy, G. Roati, A. Simoni, M. Inguscio, G. Modugno, and M. Fattori, Phys. Rev. A 86, 033421 (2012).
S. Kraft, F. Vogt, O. Appel, F. Riehle, and U. Sterr, Phys. Rev. Lett. 103, 130401 (2009).
T. Weber, J. Herbig, M. Mark, H. Nagerl, and R. Grimm, Science (Washington, DC, U. S.) 299, 232 (2003).
A. Ramanathan, K. C. Wright, S. R. Muniz, M. Zelan, W. T. Hill III, C. J. Lobb, K. Helmerson, W. D. Phillips, and G. K. Campbell, Phys. Rev. Lett. 106, 130401 (2011).
K. C. Wright, R. B. Blakestad, C. J. Lobb, W. D. Phillips, and G. K. Campbell, Phys. Rev. Lett. 110, 025302 (2013).
C. Ryu, P. W. Blackburn, A. A. Blinova, and M. G. Bo-shier, Phys. Rev. Lett. 111, 205301 (2013).
L. D. Landau and E. M. Lifshitz, Course of Theoretical Physics, Vol. 3: Quantum Mechanics: Non-Relativistic Theory (Fizmatlit, Moscow, 2004; Pergamon, New York, 1977).
N. Mukunda, Ann. Phys. 228, 205 (1993).
M. R. Andrews, C. G. Townsend, H.-J. Miesner, D. S. Durfee, D. M. Kurn, and W. Ketterle, Science (Washington, DC, U. S.) 275, 637 (1997).
Y. Shin, M. Saba, T. A. Pasquini, W. Ketterle, D. E. Pritchard, and A. E. Leanhardt, Phys. Rev. Lett. 92, 050405 (2004).
V. A. Tomilin and L. V. Il’ichov, JETP Lett. 113, 207 (2021).
Funding
This work was supported by the Russian Science Foundation, project no. 23-12-00182 (https://rscf.ru/project/23-12-00182/).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors of this work declare that they have no conflicts of interest.
Additional information
Publisher’s Note.
Pleiades Publishing remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
APPENDIX
APPENDIX
During variation of the potential, it is implicitly assumed that solution of (11) holds for all values of \(a\). Not all solution branches satisfy this restriction. These branches can be labeled, noting that at a = 0,
where \(n\) is an integer. Solution with \(n = 1\) was used during calculations, since it is this very solution that corresponds to BEC ground state. It is presented in Fig. 3.
Expression (14) for the geometric phase does not depend on the normalization of wave function \({\text{|}}\Psi \rangle \). Then, without loss of generality it can be assumed that
The scalar products can be evaluated as follows:
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tomilin, V.A., Rostom, A.M. & Il’ichov, L.V. Barrier–Well Potential Configuration for Quantum Gyroscope Based on Atomic BEC Geometric Phase. Jetp Lett. 119, 389–394 (2024). https://doi.org/10.1134/S0021364024600320
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021364024600320