“Teacher noticing, or the act of observing and interpreting classroom events (e.g., Sherin & van Es, 2009), influences the likelihood for desirable teacher actions” (Copur-Gencturk & Rodrigues, 2021, p. 1). Teachers must notice in order to learn and improve their practice, and the study of professional noticing in the field of mathematics education has become common in the last decade (Santagata et al., 2021; Schack et al., 2017; Sherin et al., 2011; van Es & Sherin, 2002, 2021). Definitions of teacher noticing vary slightly, but many encompass aspects of three practices: (a) who teachers make sense of in a situation, specifically the actor; (b) the stance of how noticing occurs, whether through the description, evaluation, interpretation, or some other means of conveying thinking; and (c) what is being noticed, (e.g., topic of focus or mathematics content) (van Es, 2011; van Es & Sherin, 2008). Other definitions focus on decisions about how to respond (i.e., Jacobs et al., 2010). Documenting teachers’ noticing practices provides important information about what teachers find noteworthy in the classroom and their response to student observations (Amador et al., 2022; Kilic, 2018). Furthermore, teacher noticing informs teaching and relates instructional quality and student learning (Friesen et al., 2021; Kersting et al., 2012; Schoenfeld, 2011).

Although many researchers have documented teacher noticing, they argue that noticing research has largely avoided specifying individual content areas (Friesen & Kuntze, 2021; Jacobs & Spangler, 2017; Thomas et al., 2017). Content-specific noticing is vital to a teachers’ practice because noticing students’ mathematics thinking is critical for effective mathematics teaching (Copur-Gencturk & Rodrigues, 2021; Jacobs et al., 2010; Walkoe et al., 2020). Many of the teacher noticing studies focusing on individual content areas (i.e., Choy & Dindyal, 2021; Friesen & Kuntze, 2021; Jong et al., 2021; Lee & Lee, 2022; Moreno et al., 2021; Schack et al., 2017; Stahnke et al., 2016) describe the mathematical content only as part of the setting, with teachers’ noticing being irrespective of the content they are teaching (Dindyal et al., 2021). One example of an exception is the work of Friesen and Kuntze (2016, 2018, 2021), who detailed the dearth of research on content-specific noticing and provided a contribution in visual representations of fractions and noticing. Specifically, these researchers leveraged a content-specific framework related to fractions to describe how mathematics teachers noticed. Teachers and students of other mathematical content areas may benefit from similar treatment as the result of examining how teachers notice using established content-specific frameworks because it could inform how teachers perceive and respond to students’ thinking within that content area (Amador et al., 2022; Friesen & Kuntze, 2021).

One mathematical content area ripe for study continues to be proportional reasoning. Proportional reasoning is a topic that children begin to learn early in life (Vanluydt et al., 2022) and is historically difficult to teach and learn (Lamon, 2007). Research on teachers’ noticing within a proportional reasoning setting has been conducted (Amador et al., 2022), but with a sole focus on analytic stance and without relating noticing to specific proportional reasoning content frameworks. Researchers have developed an analytic tool to describe teachers’ understanding of proportional reasoning through a tested and refined list of operationalized knowledge resources within Weiland et al.’s (2020) Framework for Teachers’ Robust Understanding of Proportional Reasoning for Teaching. This framework defines 19 knowledge resources, which are defined as types of knowledge associated with proportional reasoning that teachers can draw upon when responding to proportional reasoning tasks and settings. Knowledge resources are thus useful ways to categorize and describe teachers’ proportional reasoning in relation to classroom practices (Weiland et al., 2020), including noticing. Researchers recommend exploring teacher noticing specific to proportional reasoning to better understand how teachers interpret students' thinking in classroom settings (Amador et al., 2022).

This study was designed to address the research need to explore teacher noticing specific to proportional reasoning. We specifically wanted to examine teachers’ noticing practices (who, what, how) with respect to the content they noticed, that is, proportional reasoning. We engaged prospective teachers preparing to teach elementary, commonly termed primary, and those preparing to teach secondary students who were enrolled in mathematics methods courses at two different universities in an intensive three-part virtually delivered and video-mediated learning experience that was intentionally designed to develop the prospective teachers’ ability to notice through structured protocols, processes, and prompts. We intentionally focus on prospective teachers preparing to teach elementary and secondary students to illustrate how these two populations notice proportional reasoning—not to pit the two prospective teacher populations against each other for comparison purposes, but to provide a more holistic understanding of different ways of noticing for those focused on teaching different levels of students—because researchers have argued for the importance of tailoring support for prospective teachers specifically around proportionally (Ezaki & Copur-Gencturk, 2023), meaning the grade level of focus matters for teacher preparation and support.

In addition to focusing on the two population groups, we also examine ways participants respond to two different prompts, one that is teacher–student-interaction-focused and the other that is student-focused, as a way to also illuminate variation in how noticing occurs, particularly given work highlighting the importance of prompts in teacher education research (Estapa & Amador, 2022; Kaiser et al., 2015; Kenny et al., 2013; Schworm & Renkl, 2007). The inclusion of two populations with data coming from two different prompts based on video of middle grades teaching provides a deeper understanding of the participants’ proportional reasoning noticing.

To determine what kinds of proportional reasoning teachers notice when watching a video of students completing a proportional reasoning task, the Orange Juice Task (see Fig. 1, Lappan et al., 2009), we used Weiland et al.’s (2020) Framework for Teachers’ Robust Understanding of Proportional Reasoning for Teaching. The rationale for using this framework is that it aligns with the population and goals of this study, having been developed as an analytic tool to describe teachers’ understanding of proportional reasoning through a tested and refined list of operationalized knowledge resources. Additionally, the framework has been developed for use with mathematical tasks and refined with respect to the proportional reasoning task used in this study (i.e., the Orange Juice Task), meaning the analytic tool for describing the knowledge resources are even better suited to facilitate this study’s description of the teacher knowledge used in proportional situations and how teachers’ knowledge resources are organized (Glassmeyer et al., 2021; Weiland et al., 2020). We use this framework to describe teachers’ mathematical knowledge, specifically teachers’ proportional reasoning, in terms of what knowledge resources they draw upon when solving tasks and supporting students. Specifically, detailing how teachers draw upon the 19 knowledge resources when observing students solve a proportional reasoning problem indicates the content knowledge they notice.

Fig. 1
figure 1

Orange Juice Task (Lappan et al., 2009)

Full size image

Reporting the knowledge resources in relation to other noticing practices (who, what, how) provides a more complete picture of how teachers are interpreting an educational setting and how they might respond to students. Similar to prior work describing teachers’ noticing in relation to established coding schemes (van Driel et al., 2022), we use cooccurrences to describe the knowledge resources in relation to noticing practices. Therefore, our research question was:

  1. 1.

    What is the cooccurrence of proportional reasoning knowledge resources and noticing practices for elementary and secondary prospective teachers when watching a lesson on proportional reasoning and given one prompt about students and one prompt about teacher–student-interaction?

We focus on the interplay between: (a) noticing, and (b) proportional reasoning knowledge resources demonstrated through noticing. We make no claims about teachers’ proportional reasoning knowledge, but rather identify the knowledge resources they noticed when watching the videos of students completing a proportional reasoning task.

Theoretical frameworks

We theoretically frame this work with the notion of noticing, described as a core practice of effective teaching and a practice that is learnable (Jacobs & Spangler, 2017). In a recent review of literature on noticing, Dindyal et al. (2021) describe the variation in context for noticing studies and note that some researchers have focused on mathematical domains. For example, fractions (Lee & Lee, 2022), functions (Friesen & Kuntze, 2021), algebra (Jong et al., 2021), early arithmetic reasoning (Schack et al., 2013), measurement (Moreno et al., 2021) and calculus and statistics (Choy & Dindyal, 2021) have been studied, but Dindyal et al. (2021) argue that “the purpose of studying noticing within a particular domain of mathematics is often less explicit” (p. 9).

We explicitly focus our study on noticing and proportional reasoning to better understand what and how teachers (prospective in this case) notice as they view a middle grades lesson on proportional reasoning to understand how that noticing cooccurs with the knowledge resources upon which they draw (Weiland et al., 2020). The Framework for Teachers’ Robust Understanding of Proportional Reasoning for Teaching defined teachers’ knowledge in terms of the development of fine-grained, connected resources, called knowledge resources, that are drawn upon when solving tasks and supporting students (Weiland et al., 2020). The framework describes how teachers can draw upon the knowledge resources productively or counterproductively. Productively drawing upon knowledge resources is when the teacher moves forward in solving or understanding a proportional reasoning situation through use of the knowledge resources. Teachers counterproductively draw upon a knowledge resource when reliance does not move them forward in solving or understanding the proportional reasoning situation.

Weiland et al. (2020) defined the 19 knowledge resources based on proportional reasoning literature and extensive study on how teachers make sense of proportional reasoning tasks situated in the context of teaching. Other researchers (Glassmeyer et al., 2021) have further refined these knowledge resources based on examining teachers’ thinking about a comparison proportional reasoning problem, specifically the Orange Juice Task. Therefore, this framework affords this study a tested, operationalized list of knowledge resources specific for teachers working in a classroom context focused on proportional reasoning, which no other currently existing framework provides. This framework is situated outside of mathematical knowledge for teaching (i.e., Ball et al., 2008) and is not intended to make claims to differences between types of knowledge, such as specialized content knowledge or common content knowledge. Instead, the knowledge resources upon which prospective teachers draw illuminate fine-grained understandings which serve as resources for knowledge in particular situations (Weiland et al., 2020).

Glassmeyer et al. (2021) worked from Weiland et al.’s (2020) operationalized knowledge resources with the Robust Proportional Reasoning Framework and added code descriptions for each particular context. Both frameworks include 19 descriptors: Batches, Comparison of Quantities, Constant Ratio, Covariance, Distortion, Equivalence, Fluidity with Symbolic Representations, Horizon Knowledge, Multiplicative Comparison, Partitioning and Tiling, Proportional Situation, Ratios (P:P/P:W), Ratio as Measure, Ratios ≠ Fractions, Relative Thinking, Rules, Scaling Up/Down, Unit Rate, and Variable Parts (see Table 1). The knowledge resources were developed to investigate and organize teachers’ observable knowledge of proportional situations and serve as a code set (Weiland et al., 2020) to enable researchers with a method to characterize the thought process and actions of teachers as they consider proportion problems. The knowledge resources provide a way to describe the prospective teachers’ knowledge of proportion in a codable way that gives insight into the thinking of the participants.

Table 1 Operationalized knowledge resources within the Robust Proportional Reasoning Framework, based on Glassmeyer et al. (2021) and Weiland et al. (2020), taken from Glassmeyer et al. (2021, p. 6)
Full size table

Considerate of the work of Dindyal et al. (2021), we frame our work with cognizance of the work of Friesen and Kuntze (2021) who argue that noticing research has largely avoided specifying individual content areas. Their body of research has focused specifically on fractions and noticing (Friesen & Kuntze, 2016, 2018), with a recent paper highlighting both the dearth of research on content areas and noticing, while providing a contribution in visual representations of fractions and noticing. We consider this work to be the most closely related empirical study to our focus on proportional reasoning, primarily given the emphasis on fractions. Friesen and Kuntze (2021) assume the theoretical perspective that the teacher experience influences noticing (e.g., Schack et al., 2017; Stahnke et al., 2016) and argue that “context-aware measures for teacher noticing are still scarce” (p. 184). Therefore, although Friesen and Kuntze (2021) elevate content (i.e., fractions) with classroom situational contexts and noticing, we further explore content (i.e., proportional reasoning) with teachers’ knowledge resources for proportional reasoning (Weiland et al., 2020) and noticing. In full, we theoretically consider proportional reasoning knowledge resources by examining the interplay between who, what, and how prospective teachers notice.

Related literature

Proportional reasoning

“Of all the topics in the school curriculum, fractions, ratios, and proportions arguably hold the distinction of being the most protracted… the most difficult to teach, the most mathematically complex, the most cognitively challenging, the most essential to success in higher mathematics” (Lamon, 2007, p. 629). Lamon (1993, 2007) defines proportional reasoning as “detecting, expressing, analyzing, explaining, and providing evidence in support of assertions about proportional relationships” (2007, p. 647). Proportional reasoning has been traditionally assessed using comparison problems and missing-value problems. With comparison problems, two ratios (comprised of four quantities) are given, and the goal is to determine the relation between the ratios, while missing-value problems provide three of the four quantities in a proportion, and the goal is to find the missing value (Lamon, 2007). Researchers have documented how using comparison problems, specifically the Orange Juice Task, provides opportunities to reveal learners’ thinking about proportional reasoning (Brakoniecki et al., 2021; Lobato & Ellis, 2010). Despite much research, teacher professional development, and standards devoted to proportions and proportional reasoning, students often encounter challenges when reasoning about proportional relationships (Lamon, 2007; Nikula, 2010). Researchers also indicate teachers often encounter the same difficulties as their students and make calls for research on how teachers solve proportional reasoning problems (Arican, 2018). Video is one common tool being used for professional development and research purposes to support teacher understanding (Santagata et al., 2021).

Video for noticing

To better understand the cooccurrence of noticing and knowledge resources and given the emphasis on video in research (Santagata et al., 2021), classroom video was intentionally used as a representation of practice (Grossman et al., 2009) in this study. Santagata and colleagues (2021) completed a review of video-based studies designed to support teachers learning to notice. In an analysis of 35 articles, they found it was common for researchers and teacher educators to pair video clips with structured protocols. “The evidence is clear that engaging teachers in video-supported activities leads to meaningful changes and improvement in their noticing competencies” (p. 130). Similarly, in a review of video use, Gaudin and Chaliès (2015) found that video is an effective tool to support noticing. As mentioned in the introduction, there remains a need for examining the intersection of noticing practices within a context-specific setting.

Method

Prospective teachers at two different institutions participated in the same professional learning experience involving video and related tasks. The following describes the participants, the data collection process, and the analysis.

Participants

Participants included 33 prospective teachers. Twenty were prospective teachers taking a secondary content course at a private university in the northwestern USA and 13 were prospective teachers taking an elementary methods course at a public university in the western USA. Including both groups provides a greater understanding of the spectrum of the reliance on particular knowledge resources in cooccurrence with noticing, which in turn provides more holistic and broader findings about this understudied topic. The secondary prospective teachers were in a course focused on algebra and had previously taken multiple mathematics content courses, a majority having completed six three-credit university-level mathematics content courses beyond Calculus I. The elementary prospective teachers had taken a minimum of three mathematics courses, with one focused on algebra and the other two focused on mathematics content for elementary teachers. Both groups were approximately three-fourths of the way through a teacher preparation program; neither group had been explicitly taught to notice as a part of their teacher education program. However, the purpose of the learning experience in both contexts was to begin to support the awareness and development of noticing. Both participant groups were in programs that would certify them to teach middle grades mathematics; they had mathematics content coursework deemed necessary at their respective institutions for a middle grades teaching assignment. We purposely include both groups to better document how teachers at different levels noticed proportional reasoning.

Data collection context and related task

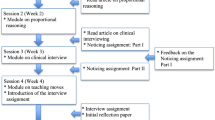
All participants took part in a three-part multi-week learning experience in a course in their teacher education program, which was intentionally designed to support understanding related to proportional reasoning. In Part One of the learning experience, prospective teachers solved the Orange Juice Task (see Fig. 1, Lappan et al., 2009) and were video recorded verbalizing and demonstrating how they solved the task. In Part Two of the learning experience, prospective teachers were asked to analyze four written middle school student responses to the Orange Juice Task and to compare each of the four student work samples. In Part Three of the learning experience, prospective teachers watched an edited video of a practicing teacher implementing the Orange Juice Task in a middle grades classroom. Participants watched the video in segments embedded in Qualtrics, a software for survey data collection and analysis, with intermittent periods of video clips and then embedded written prompts eliciting a prospective teacher response. For the purpose of this paper, we focus exclusively on data from Part Three of the learning experience project; prospective teachers’ written responses to prompts after watching the video segments that showed the implementation of a lesson.

Part three: prospective teachers’ noticing from a video of the orange juice task implementation

The task in Part Three of the learning experience was divided into four mini-segments. In the first segment, participants were given the content standards, key mathematics practice standards, and learning goals for the lesson. In the second segment, participants watched a five-minute video clip of the lesson launch (Van de Walle et al., 2016). The video features a classroom teacher introducing the Orange Juice Task to students. The teacher explains the idea of mixing orange juice from concentrate and how the flavor can be affected by the amount of concentrate and water used. Additionally, the teacher allows time for students to hypothesize about what mathematical questions could be asked about this situation and then provides students with a task and checks in with students about the goal of the written task. In the third segment, participants watched a seven-minute video clip of the same lesson. In this clip, the students are working in individual groups on the task. Different groups are highlighted at different times in the clip, and the teacher appears to work with groups at some points and leave them to continue their work at other times. When the teacher is present, he asks about strategy and asks for explanations. He also provides multiple representations for groups who are still trying to make sense of the problem. In the fourth segment, participants watched a final five-minute video clip and were given images of student work. In the video, students from each group come to the front of the classroom in turn and present the poster of the work their group has done on the problem. After each group presents, the teacher has students come up with questions and things they noticed about each presentation. As each new group presents, the already presented posters continue to be visible at the front of the board. The teacher draws attention to similarities and differences across the different methods. After watching the videos, participants were asked about what they noticed, teacher moves, and how the teacher moves may relate to students’ thinking—we refer to this as the student-focused prompt: “What did you notice about student thinking in this clip?” Participants were also asked about what they noticed, teacher moves, and how teacher moves related to lesson goals—we refer to this as the teacher–student-interaction-focused prompt: “What did you notice about how the teacher made connections between student strategies?” The coding unit was one participant’s entire response to a particular prompt.

Data analysis

Prospective teacher responses to the two focal questions were analyzed along similar dimensions to illuminate the productive and counterproductive proportional reasoning knowledge resources (Glassmeyer et al., 2021; Weiland et al., 2020) as well as prospective teacher noticing (van Es & Sherin, 2009). First all data were masked, so the authors did not know which responses were from elementary teachers and which were from secondary teachers. Responses to each prompt were analyzed independently, resulting in 66 total responses to be coded. Two authors then analyzed all responses for each of the two focal questions independently and assigned as many knowledge resources as were evident using the Robust Understanding of Proportional Reasoning for Teaching Framework (see Table 1). We also drew upon the nuances described by Glassmeyer et al., (2021) to differentiate between the 19 knowledge resources described in the framework (Table 1) to identify the productive and counterproductive ways prospective teachers drew upon the knowledge resources on each prompt. Counterproductive was defined using the framework’s definition of statements and mathematical work that did not move the prospective teachers forward in their thinking or understanding. Counterproductively drawing upon a knowledge resource can include unclear or imprecise statements interfering with communication of mathematical ideas, though not necessarily involving an incorrect computation or answer. After coding independently, the two authors agreed on nearly 90% of the codes. The two authors compared the knowledge resource codes for each participant, resolved disagreements, and compiled a summary count of the knowledge resources each prospective teacher drew upon for each of their two responses.

For example, elementary prospective teacher Mary (a pseudonym) gave the following response on the second prompt about students:

Each group had similar strategies, which involved creating ratios that had something in common. I found the last group’s strategy really interesting in that they created ratios that all had 1 as the numerator. This is something that I did not even consider doing when I solved this problem. I really liked how each student was able to explain their reasoning and compare their strategy to other groups.

Mary’s response was coded as productively drawing upon three knowledge resources: Proportional Situation because her prompt response recognized students explaining and making assertions about proportional relationships; Ratios (P:P/P:W) because her prompt response referenced ratios shown in the video (which were part-to-part); and Unit Rate because she referenced the students using sharing-like relationships such as amount-per-one indicated using a fraction with a one in the numerator and the amount in the denominator. An example of an elementary teacher counterproductively drawing upon a knowledge resource comes from Ethan, who stated in the second prompt about students that “I noticed that all the students went toward the big idea of multiplying to compare the fractions to each other.” However, Ethan was referring to student work that depicted part-to-part ratios, which differ according to Weiland et al.’s (2021) framework from fractions, which are part-to-whole representations. Therefore, Ethan’s response was coded as counterproductively drawing upon knowledge resource Ratios ≠ Fractions.

After the knowledge resource coding was complete, these data were hidden for the analysis of the noticing data. The van Es and Sherin (2009) coding categories for the analysis of noticing were used (see Table 2). Two authors each independently analyzed each prospective teacher response for the categories in Table 2 for each of the two different prompt responses per participant. Within each category (first column), a particular response was coded (second column) for as many codes as were present. As an example, a response could have been coded (Actor—Students, Teacher; Topic-Climate, Mathematical Thinking; Stance—Describe, Interpret, Evaluate; Specificity General). The exception was the Specificity code, in which all data were coded for one or the other code, but not both. After the individual analysis for each of the two responses for all the participants, agreement on codes was near 92%. The two authors who had coded the data met and reconciled any discrepancies, resulting in final codes for noticing for each of the prompts.

Table 2 Actor, Topic, Stance, Specificity Codebook for Noticing, based on van Es and Sherin (2009)
Full size table

Following the coding for the knowledge resources and noticing, we were interested in better understanding the cooccurrences of particular codes across the participant groups. To analyze these data, we conducted counts for each code type, meaning knowledge resources and noticing. We noted productive knowledge resources and counterproductive knowledge resources. We then extracted instances of cooccurrence, meaning instances where two codes occurred together for a given participant for a given response, to determine the context of codes in which other codes commonly were presented. We extracted cooccurrence when it occurred in 35% of the cases or more, as this cutoff represented the point where a recognizable number of prospective teachers had cooccurrence and it seemed significant to report. Cases below 35% were so infrequent that we were unable to draw any meaningful conclusions from those data. We followed this analysis process by analyzing the cooccurrence of three codes and four codes, considering aspects of noticing and the knowledge resources. The initial analysis of the knowledge resources and initial analysis of the noticing data were necessary in order to conduct the cooccurrence analysis and answer the research question about the cooccurrence of particular proportional reasoning knowledge resources and particular noticing practices. We note that we did not assess content knowledge independently; instead, we compared the knowledge resources (i.e., Weiland et al., 2020) the participants drew on and communicated in their noticing responses. Therefore, the claims made in the results section are based on the knowledge resources the participants included when responding to the prompts.

Results

Noticing: actor, topic, and stance

Considering both groups and both prompts, trends were identified with their noticing focus. When participants were prompted about what they noticed about how the teacher made connections between student strategies (teacher–student-interaction-focused prompt), the characterization of the responses was somewhat similar across the two participant groups. Figure 2 shows the percentages for each code for noticing, reporting the combined noticing percent. Note that all participants received either a specific or general code under the specificity part of the framework, and thus those columns total 100%. For the other areas of the framework (e.g., actor, topic, stance), codes are not mutually exclusive or automatic, and therefore column totals exceed 100%.

Fig. 2
figure 2

Percent of noticing codes for each participant group type for both prompts

Full size image

For actor, 48.5% of participants mentioned the Students, and 93.9% of participants mentioned the Teacher. For topic, 90.9% of participants focused on Mathematical Thinking and 93.9% on Pedagogy, with no focus on any other topic from any participant. In the stance category, 100% of participants Described, 12.1% were Evaluative, and 18.2% were Interpretative. The following is an example of a response from a secondary participant that included Interpretation (Interpretation italicized):

The teacher made connections between student strategies by asking students to think about the differences and/or similarities between each group’s strategy. For example, he had group 5 present their strategy first. By doing that, he pushed the students to think about why they used the common denominator of 18 and what it meant in this case. After revealing their reasoning, he then asked the other students to think about the displayed strategy and compared it with their own thinking/strategy. And then he had group 1 present their work. This group used the common denominator of 90 for each ratio. So in order for students to notice the difference and/or similarities between the previously presented strategy (i.e., the strategy of group 5), he asked students questions such as, “How is this strategy different from team 5’s strategy?” and “What is similar and what is completely different about their thinking?” Through this way the teacher encouraged students to make connections between each strategy that was presented.

In this example, the secondary participant interpreted the teacher’s action and came to conclusions about how the teacher’s action related to the learning opportunities in the lesson.

When prompted about what was noticed about students’ thinking (student-focused prompt), all participants focused on the Student as an actor, with 9.1% of participants focusing on the Teacher or Self when responding, with no notable differences between the two groups (see Fig. 2). With respect to topic, almost all prospective teachers focused on Mathematical Thinking (84.8%) and a fraction of both groups focused on Pedagogy (21.2%). With respect to stance, participants from both groups Described as they noticed. The following is an example from an elementary participant whose noticing was coded as Describe and Interpret (Interpretation italicized).

The majority of the students in the class, (at least groups one, two, and three) all had the idea to find a common denominator (or comparison) to compare their ratios to. Groups one and two compared concentrate to a common denominator of water, while group three compared water to a common “numerator” of concentrate. I noticed that all of the groups that shared were able to explain what each of the numbers in their ratios represented, although a few groups (like one and three) did struggle with coming up with ratios for each of the mixes. I noticed that during their turn and talk discussions, the students were able to pretty easily pick out similarities and differences between their work and their peers’ work, and I think that those moments where they were able to talk with one another helped some of those students to really solidify their understanding.

Knowledge resources

Considering both groups and both prompts, prospective teachers drew productively on eight knowledge resources and counterproductively on one knowledge resource (see Fig. 3).

Fig. 3
figure 3

Knowledge resources prospective teachers drew on for each video prompt, counterproductive code in orange font

Full size image

We note that the knowledge resources not shown in Fig. 3 were drawn on 0% for all instances.

In response to the teacher–student-interaction-focused prompt, elementary teachers drew heavily on three main knowledge resources (see Fig. 3), including Proportional Situation (84.6%), Ratios (P:P/P:W) (84.6%), and Unit Rate (84.6%). The next highest knowledge resource mentioned was Comparison of Quantities, with 53.8% of elementary prospective teachers drawing on that resource. Interestingly, when asked about the teacher, almost a third of the elementary participants (30.8%) drew on the counterproductive knowledge resource of Ratios ≠ Fractions. The secondary prospective teachers focused on similar knowledge resources as the elementary prospective teachers. When prompted about the teacher, 100% of the secondary participants drew on the knowledge resources of Proportional Situation and Unit Rate. Ninety-five percent drew on Ratios (P:P/P:W) and 75.0% drew on Comparison of Quantities. Only 10.0% drew on the counterproductive code of Ratios ≠ Fractions.

When prompted about what was noticed about students’ thinking (student-focused prompt), participants mainly drew on three main knowledge resources: Proportional Situation (78.8%), Ratios (P:P/P:W) (78.8%), and Unit Rate (69.7%). Figure 3 shows the percent for each participant group. Examining the particular knowledge resources more closely, when prompted about students, 92.3% of the elementary prospective teachers relied on the knowledge resource of Proportional Situation and 92.3% relied on Ratios (P:P/P:W). Interestingly, 15.4% of the elementary prospective teachers also included references to Ratios ≠ Fractions, which was lower than the 30.8% of them who drew on the counterproductive code for the teacher-focused prompt. Twenty percent of the secondary participants included reference to the counterproductive code with consideration of Ratios ≠ Fractions.

For this particular proportional reasoning task and classroom video, there were several knowledge resources that did not appear in the data that were collected for this study. For some resources, such as Horizon Knowledge, it seems reasonable that prospective teachers would draw upon this resource less frequently (if at all) for common proportional reasoning problems. But even excluding resources of that type, we would not expect work on one proportional reasoning problem to elicit all (or even a majority) of the knowledge resources from every beginning teacher. The knowledge resources of proportional reasoning pull from a spectrum of related content (Glassmeyer et al., 2021), and teachers and problem solvers each make judgment calls about how explicit they will be with more foundational content as compared with more sophisticated ideas when solving one problem. We can imagine that analyzing multiple problems or scenarios that require explicit attention to both foundational and explicit ideas would be more likely to showcase numerous knowledge resources.

Cooccurrence of knowledge resources and noticing

Figure 4 shows the cooccurrence of knowledge resources and noticing in instances when a minimum of 35% of participants in a particular population group drew on those resources and noticed those particular aspects for each of the two prompts. In Fig. 4, the colored columns indicate the cooccurrence for the elementary participants, and the gray columns refer to the secondary participants. Although the main purpose is not to compare these two groups, we report findings on both groups to illuminate the variance in the knowledge resources drawn on and the noticing between populations. We consider the inclusion of the two groups to provide a more holistic representation of the coordination of knowledge and noticing.

Fig. 4
figure 4

Cooccurrence of knowledge resource and noticing codes, elementary (n = 13 colored) and secondary (n = 20), gray

Full size image

Cooccurrence of knowledge resources and noticing for teacher–student-interaction-focused prompt

For the teacher–student-interaction-focused prompt, there were six noticing codes and six knowledge resource codes that had any cooccurrence of 35% of greater for either elementary or secondary participants in the data set. Most cooccurrence was between the noticing codes of Student, Teacher, Mathematical Thinking, Pedagogy, Describe, and Specific, and the knowledge resources of Proportional Situation, Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities, as evidenced in Fig. 4.

Actor

Both participant groups focused on Students nearly half the time and drew on the similar knowledge resources of Proportional Situation, Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities. What is striking is the extent to which the secondary participants focused on the Teacher (nearly 90%) for the cooccurrence for three of these codes, whereas the elementary participants focused on the Teacher in 69%. Therefore, when responding to the prompt about teacher–student-interaction, we found that secondary teachers noticed and commented about aspects related to the Teacher far more often than elementary participants, when considering cooccurrence of three codes. The following is an example of a response that focused on Proportional Situation and Students from a secondary participant, Nicole: “Additionally, students noticed that groups 1 and 5 got water to be common, while groups 2, 3, and 4 got concentrate to be common. The teacher made these observations explicit by writing on the board that in order to compare ratios, students need something to be common.” This quote includes explicit attention from the secondary participant to comment on what the students were doing in the video (in this case, commenting on what the students noticed). Additionally, the proportional situation knowledge resource appears as this secondary teacher identified how the teacher was recording an insight made in the class that to compare ratios in the problem, one of the quantities in the problem needed to be the same.

Topic of focus

Both participant groups had high levels of cooccurrence between Mathematical Thinking and Pedagogy and four knowledge resources: Proportional Situation, Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities. The two main topics of focus from the noticing codes were Mathematical Thinking and Pedagogy, with higher levels of cooccurrence occurring for the secondary participants. For Proportional Situation, nearly all secondary participants focused on Mathematical Thinking and Pedagogy, and numbers were similarly high for Ratios (P:P/P:W) and Unit Rate. For the elementary teachers, the three most common knowledge resource codes cooccurred 69% of the time. The following is an example of an elementary participant response, focused on Pedagogy and Ratios (P:P/P:W), among other codes. We select this example because it shows a particular pedagogical move this elementary participant identified, that is, the teacher asking students to look for connections across the examples by specifically asking them to identify what similarities existed across the work shown, and what differences. This example also highlights how this elementary participant drew upon their knowledge resource of Ratio (P:P/P:W), identifying the quantities in the problem, and signaling that some comparisons were ratios or fractions, and what equivalency meant in the context of the problem.

The teacher made connections by asking the students what was similar between certain groups and what was different. The teacher made connections between groups 1 and 5 because they made the water the equivalent number to compare. The other groups made the concentrate the equivalent number. He made connections by asking if two equivalent fractions or ratios would taste the same or not, and he also made connections by asking whether or not the student multiplied up or divided down like a unit rate. Group 2 is the only group to do the unit rate.” – Leanne

Stance

When responding to the prompt, the only Stance code with noteworthy cooccurrence numbers was Describe, meaning that as the participants drew on their knowledge resources to answer the prompt, they were Descriptive in their responses, without a high percentage Evaluating and/or making Inferences. Similar to prior trends in the noticing data, the secondary teachers more commonly Described and drew on particular knowledge resources simultaneously, with nearly all participants Describing as they drew on knowledge resources of Proportional Situation, Ratios (P:P/P:W), and Unit Rate. Elementary participants had cooccurrence of these codes in 77% of their responses. The above quote from Leanne is also a response coded as Describe and a knowledge resource of Unit Rate. As is evident in that quote, this elementary teacher also was describing many of the moves the teacher was making in describing the student group work. This participant also is explicit in identifying the particular student group that used unit rates in their work that they presented.

Specificity

On the whole, participants were Specific more than half the time when drawing on Proportional Situation, Ratios (P:P/P:W), and Unit Rate. The secondary participants were far more Specific than the elementary participants, with nearly all of them providing a Specific response when drawing on any one of the three aforementioned knowledge resources. However, both groups were detailed when drawing on the four most common knowledge resources, as evidenced in the following quote:

I saw how the teacher connected group 5 and group 1’s work, showing how they used different methods to create common denominators to compare the amount of concentrate, but that one group used a ratio table. The teacher then discussed group 4’s work, as they are similar to group 1 in their use of a ratio table, but they compared the amount of water by finding, as one student put it, the common numerator. This is where the teacher explains how you need to have “something” the same to be able to compare, and while these groups did not have the same “something,” they both used this idea to solve the problem. The teacher then briefly showed group 3’s work, showing how these students did not use a ratio table, similar to group 5, but did compare the concentrate by using “common numerators,” which was similar to group 4. Lastly, the teacher had group 2 explain their work and show how they too found a way to have the same “something,” in this case finding a unit rate and then comparing the decimals. He then used a student’s thought about how this group divided down, as opposed to all of the other groups multiplying up, to show how this group found a different method to compare their same something, but still had something that was the same.” – Mary

Here, it was very clear that Mary was being incredibly Specific in her response, detailing the moves the teacher was making, summarizing student work, and describing the mathematics of the problem. In this quote, this secondary participant drew upon the knowledge resources of: (a) Proportional Situation by identifying ratio tables that were used to compare the mixes, (b) Comparing Quantities by listing out the quantities of water and concentrate that are being compared, (c) Ratios (P:P/P:W) by describing the ratio table used to produce common quantities in each mixture, and (d) Unit Rate by talking about the unit rate group 2 used.

Overall, cooccurrence between the noticing codes and knowledge resource codes indicates that responses typically focused on the Teacher (with almost half also focused on the Students), included noticing coded as Mathematical Thinking and Pedagogy, were Descriptive, and were Specific, when cooccurring with the following knowledge resources: Proportional Situation Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities.

Cooccurrence of more than two codes

Analysis of the cooccurrence of three different codes for the teacher–student-interaction-focused prompt indicated that 92.3% of elementary prospective teachers’ prompts received the codes: Describe, Teacher, and Pedagogy. Of interest, 84.6% of the elementary prospective teachers described aspects related to Unit Rate and Pedagogy or Mathematical Thinking or Proportional Situation. All secondary prospective teachers were Specific and Described Proportional Situation, as well as Unit Rate. Additionally, there was a high occurrence (95.0%) of a focus on the Teacher, Pedagogy, and Proportional Situation or Unit Rate, in cases in which secondary elementary prospective teachers were Descriptive.

Cooccurrence of knowledge resources and noticing for student-focused prompt

For the student-focused prompt, there were six noticing codes and five knowledge resource codes that had any cooccurrence of 35% of greater for either elementary or secondary participants in the data set. Most cooccurrence was between the noticing codes of Student, Mathematical Thinking, Describe, Evaluate, Specific, and General, and the knowledge resources of Proportional Situation, Ratios (P:P/P:W), and Unit Rate, as evidenced in Fig. 4.

Actor

Both participant groups focused on Students and did not have high levels of cooccurrence with a focus on the Teacher. Cooccurrence between knowledge resources and a focus on Students was more common for elementary participants, with 92% focused on Student and Proportional Situation or Student and Ratios (P:P/P:W). The most common knowledge resources drawn on when focusing on Students include Proportional Situation, Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities. The following is an example focused on Students, drawing on the knowledge resources of Ratios (P:P/P:W).

The majority of the students in the class, (at least groups one, two, and three) all had the idea to find a common denominator (or comparison) to compare their ratios to. Groups one and two compared concentrate to a common denominator of water, while group three compared water to a common “numerator” of concentrate. I noticed that all of the groups that shared were able to explain what each of the numbers in their ratios represented, although a few groups (like one and three) did struggle with coming up with ratios for each of the mixes. – Eric

In this example, the elementary participant describes in detail the student work they were seeing present in the video clips. They also specifically describe the ratios that they were seeing, even talking about the quantities that parts of the ratio were representing.

Topic

The only topic with any noteworthy cooccurrence was Mathematical Thinking, with cooccurrence with five knowledge resources, including Proportional Situation, Ratios (P:P/P:W), Unit Rate, Comparison of Quantities, and Scaling Up/Down. Ninety-two percent of elementary participants focused on Mathematical Thinking and Proportional Situation. The following is an example:

Each group completed the task differently but with similar concepts. Some used ratios and some used fractions. Some groups made the concentrate the same to compare to the water and some made the water the same to compare to the concentrate. I did not see anyone compare part-to-whole. Also, one group divided down to find a unit rate while others multiplied up. – Loren

In this example, the elementary participant’s response specifically Describes the Mathematical Thinking that they observed in the video. They also drew upon the knowledge resource that this is a Proportional Situation by Describing the ratios and fractions that were used for Comparison of Quantities in the prompt and talking about a Unit Rate, and Ratios (P:P/P:W) for quantity comparison.

Stance

When responding on the prompt, there were two stance codes with cooccurrence, Describe and Evaluate. These stance codes cooccurred with Proportional Situation, Ratios (P:P/P:W), Unit Rate, and Comparison of Quantities. Both elementary and secondary participants had high levels of cooccurrence with Proportional Situation and Ratios (P:P/P:W), with 92% and 70% respectively. Of notable interest, 38% of elementary participants were Evaluative, drawing on knowledge resources of Proportional Situation, Ratios (P:P/P:W), and/or Unit Rate, with no notable cooccurrence occurring between knowledge resources and Evaluation for secondary participants. The following is an example of a response coded as Evaluative and Unit Rate:

Each group had similar strategies, which involved creating ratios that had something in common. I found the last group’s strategy really interesting in that they created ratios that all had 1 as the numerator. This is something that I did not even consider doing when I solved this problem. I really liked how each student was able to explain their reasoning and compare their strategy to other groups. – Mateo

In this example, the elementary participant’s comments are Evaluative as they Describe a particular strategy as an interesting strategy and discuss how they really liked something that occurred in the classroom. The knowledge resource of Unit Rate is also brought up explicitly with this response when the participant talks about particular sets all having had one as a numerator, allowing that ratio to have an amount of a quantity, to be compared to one unit of another quantity.

Specificity

Nearly half of both participant groups were Specific and drew on the knowledge resources of Proportional Situation, Ratios (P:P/P:W), and/or Unit Rate. The following is an example from Patty coded as Specific and Proportional Situation, “Students had similar concepts but different strategies. Some used common numerators, some used common denominators. Some multiplied. Some divided. All (if I remember correctly) were using part-part ratios rather than part-whole fractions.” With Patty’s response, she was Specific with her analysis of the video, talking about the mathematical ideas of finding common numerators or denominators in their different strategies. Additionally, with her specificity of identifying the part-part types of ratios that were being used by students in their comparisons, the secondary prospective teacher is drawing upon her knowledge resource of this being a Proportional Situation.

Overall, cooccurrence between the noticing codes and knowledge resource codes indicates that responses typically focused on the Student, Mathematical Thinking, were Descriptive, occasionally Evaluative, and were somewhat split between being Specific and General, when cooccurring with the following knowledge resources: Proportional Situation, Ratios (P:P/P:W), and Unit Rate.

Cooccurrence of more than two codes

When considering the coordination of three different codes, 92.3% of elementary prospective teachers noticed Students, Mathematical Thinking, and Describe. Similarly, 92.3% Described, focused on Students, Proportional Situation as well as Ratios (P:P/P:W). Overall, almost all the elementary prospective teachers (92.3%) had data coded as Describe about Students with a focus on Mathematical Thinking that foregrounded the content of Proportional Situation and Ratios (P:P/P:W). Secondary participants did not have similar notable patterns of three codes when given the student-focused prompt.

Comparison of cooccurrence across prompts

We compared the cooccurrences that happened for the teacher–student-interaction-focused prompt with those from the student-focused prompt and found that the cooccurrence of knowledge resources and noticing differed, based on the prompt asked, even with the same video. Considering participant responses for the two different prompts, there were notably more cooccurrences of codes for the teacher–student-interaction-focused prompt than the student-focused prompt, with 56 areas of notable cooccurrences compared to 34 instances, respectively (Fig. 4). The following describes differences in the knowledge resources and then noticing across prompts.

Knowledge resource difference across prompts

With two different prompts, there was a difference in the knowledge resources upon which participants drew that had cooccurrence with noticing codes, even though the video was the same. For both prompts, participants drew on Proportional Situation, Ratios (P:P/P:W), and Unit Rate. For the teacher–student-interaction-focused prompt, there was also heavy cooccurrence between noticing codes and Comparison of Quantities, which was not the case with the student-focused-prompt. Cooccurrence frequency for Scaling Up/Down was similar for both prompts; however, cooccurrence was evident for Equivalence with the teacher–student-interaction-focused prompt and was not for the student-focused prompt, indicating that different knowledge resources were drawn on for the two prompts.

Noticing difference across prompts

When the prompt changed, there were differences in the actor. The cooccurrence of Pedagogy on the teacher–student-interaction-focused prompt and not on the student-focused prompt would also be expected, with the variation in the prompt asked. However, there was an interesting difference in the stance codes, with cooccurrence happening with an Evaluative approach for the student-focused prompt and not the teacher–student-interaction-focused prompt. The Evaluative focus in response to the prompt about students indicates that participants evaluated students, but not necessarily the interactions with the teacher to similar levels. Also, participants were more Specific when responding about the teacher–student-interaction-focused prompt, as compared to the student-focused prompt, indicating that they were able to talk about specific moves or details related to the teacher interaction to a great extent than they were able to talk about specifics of students’ mathematical thinking.

Discussion

Findings revealed three significant contributions of this work. First, findings provided an increased understanding about how participants with varying backgrounds notice proportional reasoning, based on knowledge resources— highlighting the importance of gathering data on noticing and knowledge resources from a span of populations. Second, findings resulted in increased clarity about the challenges of noticing, particularly with certain analytic stances, while noticing proportional reasoning. Participants were primarily descriptive, highlighting the importance of supporting prospective teachers to make interpretations about students’ thinking and teacher pedagogical practice. Third, findings provided methodological contributions—the prompts used for research and supporting prospective teacher learning matter and using cooccurrence for analysis may be an approach for others to consider—highlighting the importance of gathering multiple sources of data if claims are going to be made about prospective teacher noticing and knowledge resources.

Various groups

Two population groups were included to illustrate variance in how noticing (van Es & Sherin, 2008) occurs and the knowledge resources (Weiland et al., 2020) that were noticed. Data indicate that the elementary and secondary prospective teachers drew on different knowledge resources and noticed differently as they responded about the proportional reasoning task, which would be expected given participants with varied backgrounds. These findings support the work of Ezaki and Copur-Gencturk, 2023 who argue that prospective teacher support should be tailored to those teaching different levels of students. Given our findings, we found a spectrum in the knowledge resources that were drawn on and how those knowledge resources cooccurred. As previously stated, in the USA context, while both elementary and secondary prospective teachers can be licensed to teach middle grades (the grade level of the video), findings about the interplay between their knowledge resources and noticing indicate that they may need different supports to teach middle grades effectively. For example, elementary participants may need additional specific support to develop content knowledge about equivalence (see Fig. 3). We encourage researchers and professional developers to become aware of the knowledge and noticing capacities of the populations with whom they work; we consider the data in this study to corroborate the need for targeted support for teachers as they learn and teach the challenging content of proportional reasoning (Lamon, 2007; Lobato & Ellis, 2010). Researchers should be context-aware (i.e., Friesen & Kuntze, 2021) and consider expanding their populations beyond one particular grade band of focus to gather a greater understanding of the various supports that are needed and the different perspectives of participants, as findings cannot be generalized across all prospective teacher groups. We also acknowledge that our findings are not generalizable beyond the participants in our study and are specific to proportional reasoning; however, the results illuminate how these particular participants noticed proportional reasoning.

Challenges in noticing

Another main implication of this work relates to the way the field of mathematics education supports the development of noticing, and how noticing is conceptualized, as a learnable set of skills (Jacobs et al., 2010). Findings indicated that cooccurrence of the noticing stance and drawing on particular knowledge resources specific to proportional reasoning (Weiland et al., 2020) resulted in descriptions (van Es & Sherin, 2009) of what was noticed, which can be attributed to attending to students’ thinking (Jacobs et al., 2010); prospective teachers rarely drew on knowledge resources of proportionality and interpreted students’ thinking in their responses, which is often considered a more advanced form of noticing (van Es, 2011). With the student-focused prompt, some of the elementary prospective teachers were evaluative as they drew on Proportional Situation, Ratio (P:P/P:W), and Unit Rate; however, this did not occur for the secondary prospective teachers or for either group with the teacher–student-interaction-focused prompt. Lobato and Ellis (2010) argued that proportionality is a challenging subject to teach and learn. Although we did not directly focus on the reason that higher levels of noticing did not occur for either group across either prompt with respect to certain knowledge resources, the findings raise questions about the relationship between the challenges of proportional reasoning as a content area and the challenges of interpretative noticing (Jacobs et al., 2010; van Es, 2011). We recognize that there may be a relationship between the manner in which drawing on noticing and knowledge resources for analytic purposes results in the occurrence of particular codes, when responding to particular prompts.

As a result, we build on the findings of Friesen and Kuntze (2016, 2018, 2021) and encourage other researchers to explore the intersection of knowledge and noticing across mathematics disciplines to further provide an understanding about the challenges of interpreting and how that relates to particular mathematics content (Friesen & Kuntze, 2021; Jacobs & Spangler, 2017; Thomas et al., 2017). We argue for the need for a focus on content-specific noticing within particular mathematics disciplines; our findings further support this call based on the nuances that were evident even with such a specific focus on proportional reasoning knowledge resources (Weiland et al., 2020) and noticing. Opportunities to study other content-specific mathematical areas and expand on current research in areas, such as geometry, algebra, measurement, and others, in relation to noticing is necessary. Additionally, we focused on knowledge resources, but contend that a direct assessment of knowledge (e.g., mathematical knowledge for teaching (Ball et al., 2008)) in comparison with noticing would be beneficial, as our data were limited to an analysis of noticed knowledge resources (Weiland et al., 2020) as directly reported in response to the prompt.

Methodological

The third contribution relates to methodological aspects of the project, specifically documenting the importance of prompts and the possible contribution of cooccurrence as an analytic approach. The analysis of the cooccurrence of knowledge resources (Weiland et al., 2010) and noticing (van Es & Sherin, 2009) illuminated differences in noticing when the prompt was different. The cooccurrence codes showed that noticing varied depending on the prompt for actor, topic, and stance, all areas of what and how noticing occurs (van Es et al., 2009), and there were subtle differences in the knowledge resources upon which prospective teachers drew (Weiland et al., 2020). When the focus of the prompt was on students, noticing cooccurred differently with knowledge resources as compared to when the prompt elicited a response about pedagogical thinking—some secondary prospective teachers had noticing codes cooccur with equivalence for the teacher–student-interaction-focused prompt and did not for the student-focused prompt. There were other differences in the extent to which particular noticing codes cooccurred with knowledge resources when comparing the two prompts. These findings illuminated a heightened awareness about the role of prompts to elicit noticing of various proportional reasoning knowledge resources.

Existing research (Kane & Saclarides, 2022; Lesseig et al., 2017; van Es & Sherin, 2008) has focused on the role of prompts to support teacher thinking in relation to their practice. Additional research has shown that the prompts given to prospective teachers matter (Estapa & Amador, 2022) with respect to noticing. We now know that what is being asked (the specific wording) matters for what knowledge resources are drawn on and the corresponding noticing. If, as a field, research is conducted where only one prompt is given (or likely one experience), results will only provide a glimpse into the findings from that one prompt or experience. Our findings, similar to the work of others (Estapa & Amador, 2022; Kaiser et al., 2015; Schworm & Renkl, 2007), show that prompts are consequential to the resulting data, so we encourage researchers to take a more holistic approach before drawing conclusions or labeling particular aspects related to noticing of proportional reasoning knowledge resources or other content-specific areas. Additionally, we encourage researchers and teacher educators to honor prospective teachers’ knowledge bases and abilities to notice, and to illuminate their comprehension by ensuring noticing of proportional reasoning is elicited in different ways—such as through different prompts.

Finally, the methodology used in this paper—analyzing knowledge resources in response to a prompt and noticing separately, and then the cooccurrence—provides a novel method to examine how teachers notice proportional reasoning. Schoenfeld (2011) called for means to better illuminate the role of content in teacher learning and Dindyal et al. (2021) called for increased studies on noticing and mathematics content. Researchers have argued that studies on noticing pertaining to particular content areas within mathematics are likely absent in the field (Friesen & Kuntze, 2021), illuminating the importance of considering how noticing occurs and what is noticed within the context of a proportional reasoning lesson. Considering the cooccurrence of the two provides a methodological approach for analysis and a window into data that may otherwise be overlooked. For example, questions are raised about the reasons that elementary participants were not Specific when it came to focusing on Students and Mathematical Thinking. Data indicate they drew on particular knowledge resources; however, the extent to which they were Specific was not near the level of Specificity for the secondary participants. The secondary participants were able to be Specific and have that cooccur with drawing on particular knowledge resources. These varied findings suggest that the analytic approach afforded opportunities for increased understanding in proportional reasoning, an area historically needing additional research emphasis (Weiland et al., 2020).

Limitations and considerations

We acknowledge limitations and considerations that should be made with respect to the research process and findings for this study. First, the proportional reasoning noticing, meaning the knowledge resources and the associated noticing, are limited by the content of the videos that the participants were shown. The participants were only able to notice aspects that actually existed in the videos. For example, no participants drew on the knowledge resources Multiplicative Comparison, Distortion, etc., likely resulting from the opportunities provided from the video representation of practice (Grossman et al., 2009). Additionally, participants were shown video in three different segments. The selection of using segments and choosing particular points and edited videos (for length) also contributed to the findings, as participants were only shown pieces of the larger video, limiting an understanding of everything that happened. Also related to the data collection, both prompts given closely refer to students’ thinking (e.g., mathematical thinking as topic) and the student(s)/teacher as the actor. It is possible that the given prompts influenced the occurrence of categories with regard to Codebook for Noticing (i.e., Table 2). This could imply that the cooccurrence of codes might be affected or even distorted by the given prompts. An additional acknowledgement is the different backgrounds, contexts, and coursework that participants within each group and the elementary and secondary participants had. Participants came to this project with different experiences and educational backgrounds, which contributed to a variety of different responses.

Conclusion

Over the last two decades, the research on teacher noticing in mathematics has expanded significantly (e.g., Rowland & Ruthven, 2011; Schack et al., 2017; Sherin et al., 2011). To fully encourage effective pedagogical practices, more needs to be known about the relationship between what teachers know and what they notice to make thoughtful decisions in the classroom. More could also be known about content-specific noticing in other mathematics disciplines (e.g., Dreher & Kuntze, 2015; Schoenfeld, 2011; Star & Strickland, 2008), and our focus on proportional reasoning knowledge resources and noticing is one example of work in this area. This study provided a glimpse into how individuals from two participant groups drew on knowledge resources related to proportional reasoning when noticing and how they responded to two different prompts. We encourage researchers to consider how they may further explore the coordination of teacher content-specific noticing to advance understanding in the field.