Abstract
The temperature increase of the system Earth-atmosphere can be described by means of a parallelism between the leaking bucket's dynamics and the energy balance between the incoming radiant power from the Sun and the outcoming net heat flow rate to outer space. The analogy is interesting from a didactical point of view, since the stable fixed point of the temperature can be related to the height of the water inside the leaking bucket in the presence of a fixed fluid flow rate. Qualitative predictions of global temperature increase for increasing concentration of greenhouse gases in the atmosphere can be obtained by reducing the outcoming net heat flow rate, using buckets with smaller orifices.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Environmental related issues are being carefully considered by young generations [1]. Teachers might thus be asked to answer to questions arising from the alarm-driven curiosity of their students. These questions might concern the influence on climate changes of an increase of the greenhouse gases in the atmosphere [2–4], the role played by renewable energies in mitigating the consequences of these changes [5], the temperature increase of the planet Earth [6, 7], and similar topics.
Teachers know that the properties of complex systems can be very difficult to describe mathematically and that simple answers can seldom be given. In 2021 the Nobel prize in physics was awarded to scientists who closely considered complex systems [8]. Nevertheless, it would not be useless to search for simple physics models to foster understanding of these large-scale phenomena. Therefore, studies dedicated to didactical approaches to global warming have been published in the recent [9–12].
In this work we focus our attention on the way temperature increase can be determined by an increase of greenhouse gases in the atmosphere. To develop a simple model, closely related to hydrodynamic concepts, we start from an illuminating sentence in [6] stating that the surface temperature 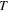 of the Earth resuming from greenhouse effect is similar to the depth
of the Earth resuming from greenhouse effect is similar to the depth  of water in a leaking bucket with a constant flow rate. These models, based on energy balance, are therefore implicitly described by Hansen et al in [6] and are known as zero-dimensional energy balance models (EBMs) [13]. Here we merely envision an elementary approach to the study of the salient properties of these types of models, by first analyzing the dynamics of water in a leaking bucket and by successively applying the same concepts to the prediction of temperature change of the planet Earth. The influence of the atmospheric convective effects will be neglected, for simplicity reasons, in our reconstruction process. These effects are considered in the so-called radiative and convective one-dimensional models [3]. Nevertheless, we shall consider only the simplest approach where the only variable is the absolute temperature
of water in a leaking bucket with a constant flow rate. These models, based on energy balance, are therefore implicitly described by Hansen et al in [6] and are known as zero-dimensional energy balance models (EBMs) [13]. Here we merely envision an elementary approach to the study of the salient properties of these types of models, by first analyzing the dynamics of water in a leaking bucket and by successively applying the same concepts to the prediction of temperature change of the planet Earth. The influence of the atmospheric convective effects will be neglected, for simplicity reasons, in our reconstruction process. These effects are considered in the so-called radiative and convective one-dimensional models [3]. Nevertheless, we shall consider only the simplest approach where the only variable is the absolute temperature 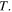 A very simple extension of the standard EBMs will be done, by assuming the atmosphere to be a single homogeneous static conducting layer around the Earth surface. This extension is only made to let student consider the relevance of some of the terms in the construction of the mathematical model of a real system.
A very simple extension of the standard EBMs will be done, by assuming the atmosphere to be a single homogeneous static conducting layer around the Earth surface. This extension is only made to let student consider the relevance of some of the terms in the construction of the mathematical model of a real system.
The present work is thus organized as follows. In the following section the leaking bucket problem is tackled from a purely hydrodynamic point of view. Following the hint given in [6], the application of this model to the energy balance problem characterizing the temperature variation of the planet Earth is introduced; a close parallelism with the hydrodynamic model is also made; differences between the two models are highlighted. The salient properties of the simple energy balance model of the Earth are investigated in the third section. By numerical analysis, in the fourth section some qualitative predictions based on this model are made. Some remarks about the present description of the global temperature increase are given in the last section.
2. The energy balance model
Let us first consider the hydrodynamic system consisting of a leaking bucket of cross section 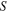 as in figure 1. In this figure
as in figure 1. In this figure 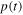 is the incoming water flux flow rate and
is the incoming water flux flow rate and 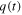 is the outcoming flux flow rate expressed by means of Torricelli's equation [14]
is the outcoming flux flow rate expressed by means of Torricelli's equation [14] 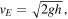 where
where 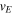 is the efflux velocity of the fluid from the bucket, so that
is the efflux velocity of the fluid from the bucket, so that  The water inside the bucket reaches a height
The water inside the bucket reaches a height  whose derivative with respect to time depends on the difference between the above two rates. In fact, by conservation of mass, we may write:
whose derivative with respect to time depends on the difference between the above two rates. In fact, by conservation of mass, we may write:

Figure 1. A leaking bucket of cross section 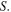 Water enters the bucket with a flux flow rate
Water enters the bucket with a flux flow rate 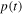 and exits from an orifice of cross section
and exits from an orifice of cross section 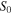 with a flux flow rate
with a flux flow rate 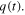 Part of the water accumulates inside the bucket and reaches a height
Part of the water accumulates inside the bucket and reaches a height 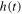 .
.
Download figure:
Standard image High-resolution imageThis rather simple model can be adopted to describe the energy balance problem of the system Earth-atmosphere [6]. In fact, being the hydrodynamic system easy to reproduce, the increase of the stationary level of water inside a transparent bucket can be clearly visualized when the incoming water flux flow rate 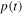 is constant and the flow rate
is constant and the flow rate 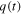 decreases by partially occluding the orifice. Students may notice that the stationary height is not instantaneously attained; i.e. after partial occlusion of the hole in the bucket, one needs to wait for a certain interval of time before the water level in the bucket stabilizes.
decreases by partially occluding the orifice. Students may notice that the stationary height is not instantaneously attained; i.e. after partial occlusion of the hole in the bucket, one needs to wait for a certain interval of time before the water level in the bucket stabilizes.
Let us then consider the schematic representation of the energy balance for the Earth represented in figure 2. In this scheme the term  is the net incoming irradiance from the Sun multiplied by the effective area
is the net incoming irradiance from the Sun multiplied by the effective area 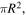 where
where 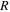 is the mean Earth's radius, so that:
is the mean Earth's radius, so that:

where 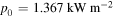 is the flux of solar radiation and
is the flux of solar radiation and 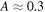 is the Earth's albedo. In this way,
is the Earth's albedo. In this way, 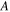 represents the percentage of reflected radiation by the atmosphere, oceans, and land surfaces. Variation of the solar intensity and of the solar wind might make the hypothesis that
represents the percentage of reflected radiation by the atmosphere, oceans, and land surfaces. Variation of the solar intensity and of the solar wind might make the hypothesis that 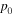 is constant rather weak. However, this simplifying hypothesis does not affect the validity of our analysis, since it is nowadays widely accepted that the global temperature increase is of anthropogenic origin [15] and not due to solar activity variations.
is constant rather weak. However, this simplifying hypothesis does not affect the validity of our analysis, since it is nowadays widely accepted that the global temperature increase is of anthropogenic origin [15] and not due to solar activity variations.
Figure 2. The term  can be related to the net incoming irradiance from the Sun; the term
can be related to the net incoming irradiance from the Sun; the term 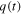 is given by the net radiation emitted by the Earth;
is given by the net radiation emitted by the Earth; 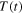 is the temperature of the Earth at time t and can be related to the height of water in the bucket.
is the temperature of the Earth at time t and can be related to the height of water in the bucket.
Download figure:
Standard image High-resolution imageThe term  can be related to the outcoming net heat flow rate. By assuming that the Earth is a black body, this term can be expressed in terms of the Stephan–Boltzmann law
can be related to the outcoming net heat flow rate. By assuming that the Earth is a black body, this term can be expressed in terms of the Stephan–Boltzmann law ![$\beta \left(t\right)=\sigma {\left[T\left(t\right)\right]}^{4},$](https://content.cld.iop.org/journals/0143-0807/45/2/025804/revision2/ejpad2429ieqn30.gif) where
where 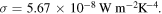 Here we also assume that a percentage
Here we also assume that a percentage 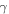 of the infrared radiation emitted by the Earth is trapped in the atmosphere in the vicinity of the Earth surface because of the so-called greenhouse effect [6]. The way the infrared radiation is absorbed by the atmosphere goes beyond the purpose of the present work. Here we shall only assume that a percentage
of the infrared radiation emitted by the Earth is trapped in the atmosphere in the vicinity of the Earth surface because of the so-called greenhouse effect [6]. The way the infrared radiation is absorbed by the atmosphere goes beyond the purpose of the present work. Here we shall only assume that a percentage  of the radiating power from the Earth is absorbed by the atmosphere, so that a first term of
of the radiating power from the Earth is absorbed by the atmosphere, so that a first term of 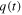 can be written as follows:
can be written as follows:

At the same time, the atmosphere can be seen as a thin layer of air extending from the surface of the Earth at temperature 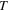 to the edge of space at temperature
to the edge of space at temperature 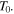 Therefore, neglecting convective effects in the atmosphere and only considering conduction of heat due to this thin layer of thickness
Therefore, neglecting convective effects in the atmosphere and only considering conduction of heat due to this thin layer of thickness 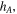 we may reason as follows. The conduction heat current
we may reason as follows. The conduction heat current  though an area
though an area 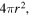 where
where 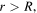 can be expressed, under steady conditions [16], as follows:
can be expressed, under steady conditions [16], as follows:

where 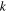 is an effective constant coefficient of thermal conductivity, which we may take comparable with that of air at standard temperature and pressure for an estimate of the relevance of this additional term
is an effective constant coefficient of thermal conductivity, which we may take comparable with that of air at standard temperature and pressure for an estimate of the relevance of this additional term 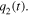 By separating variables, equation (4) can be written as follows:
By separating variables, equation (4) can be written as follows:

By integrating and solving for 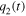 for
for 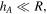 we have:
we have:

Therefore, we may write:
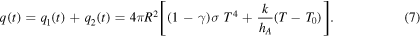
We shall see that the parameter 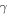 can be determined by knowledge of the temperature
can be determined by knowledge of the temperature 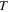 at a given instant of time. The term
at a given instant of time. The term  plays the role of the effective emissivity of the system Earth-atmosphere. Before proceeding further, let us see what the relative relevance of the terms
plays the role of the effective emissivity of the system Earth-atmosphere. Before proceeding further, let us see what the relative relevance of the terms 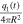 and
and 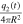 are. Therefore, by taking
are. Therefore, by taking 
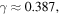
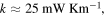 and
and  and by relying on the experimentally observed actual Earth's average temperature
and by relying on the experimentally observed actual Earth's average temperature 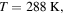 we find that
we find that 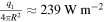 and
and  In this way, for any practical calculation, we may drop the second term, under these hypotheses, and write:
In this way, for any practical calculation, we may drop the second term, under these hypotheses, and write:

Having defined all relevant quantities in the model, we may now see that the time-dependent temperature 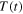 can be related to the height of water
can be related to the height of water 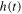 in the bucket. In fact, the heat
in the bucket. In fact, the heat 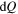 accumulated by the Earth in a brief time interval
accumulated by the Earth in a brief time interval 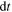 (infinitesimal on the scale of the characteristic time
(infinitesimal on the scale of the characteristic time 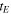 of the dynamical model we are going to describe) can be given by the following expression:
of the dynamical model we are going to describe) can be given by the following expression: 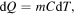 where
where 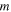 is the portion of the Earth's mass
is the portion of the Earth's mass  which contributes to the thermal exchange process,
which contributes to the thermal exchange process, 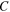 is an effective specific heat of the system Earth-atmosphere, and
is an effective specific heat of the system Earth-atmosphere, and 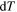 is the temperature change in the time interval
is the temperature change in the time interval 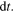 In this way, the rate of increase
In this way, the rate of increase  of heat content in the system 'Earth' can be written as follows:
of heat content in the system 'Earth' can be written as follows:

Therefore, from the above expression we see that the term 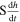 in equation (1) corresponds to the quantity
in equation (1) corresponds to the quantity 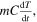 so that the Earth's temperature can be related to the depth of the water in the bucket. This analogy is very instructive from the didactical point of view, as we shall see.
so that the Earth's temperature can be related to the depth of the water in the bucket. This analogy is very instructive from the didactical point of view, as we shall see.
From the above, we may write the energy balance for the Earth-atmosphere system as follows:

By using equations (2) and (8), (10) can be written in the following way:
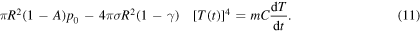
By now assuming that only a superficial spherical shell of height 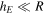 contributes to the heat exchange, we may set
contributes to the heat exchange, we may set  where
where 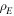 is the effective volume density of this superficial shell. In this way, equation (11) can be written as follows:
is the effective volume density of this superficial shell. In this way, equation (11) can be written as follows:
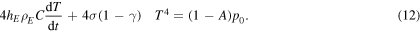
Since the atmosphere is seen as a single homogeneous static layer around the Earth surface in this simplified description, it would be more appropriate to speak about a compound Earth-atmosphere system. As for the difference with the hydrodynamic model, we notice that the efflux rate of the leaking bucket is given by Torricelli's law, so that it goes with the square root of the height 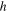 of the fluid in the bucket. In this case, however, the dependence is quartic on the temperature
of the fluid in the bucket. In this case, however, the dependence is quartic on the temperature 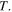
In equation (12) the effective thickness 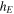 of the spherical shell is still to be determined. The nature of this shell will affect the values of its density
of the spherical shell is still to be determined. The nature of this shell will affect the values of its density 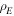 and the value of the effective specific heat
and the value of the effective specific heat 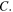 However, we shall notice that it is the product
However, we shall notice that it is the product  which determines the time scale of the dynamic system. We shall consider this quantity in detail in the following section.
which determines the time scale of the dynamic system. We shall consider this quantity in detail in the following section.
Even if the model described by equation (12) captures some of the main aspects of the dynamic of the temperature 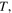 it still lacks many details as, for example, the angular dependence of the solar irradiance and the horizontal and vertical convective currents of moist air. Students should therefore be aware that more refined models may give more realistic predictions of the global temperature change. Furthermore, it is important to stress that this simple model can only be used for didactical purposes or for qualitative predictions. Nevertheless, the simplicity of the model makes it fit to accompany a first approach to the important topic of temperature increase of our planet, giving a rather concrete grasp of the main issues concerning this important issue, as we shall soon see.
it still lacks many details as, for example, the angular dependence of the solar irradiance and the horizontal and vertical convective currents of moist air. Students should therefore be aware that more refined models may give more realistic predictions of the global temperature change. Furthermore, it is important to stress that this simple model can only be used for didactical purposes or for qualitative predictions. Nevertheless, the simplicity of the model makes it fit to accompany a first approach to the important topic of temperature increase of our planet, giving a rather concrete grasp of the main issues concerning this important issue, as we shall soon see.
3. Salient properties of the dynamical model
Let us consider the energy balance equation as written in equation (12). The first important point to show is that, without the greenhouse effect (i.e. when 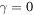 ), the average temperature of the Earth would be way too low with respect to the observed experimental value of
), the average temperature of the Earth would be way too low with respect to the observed experimental value of 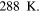 In fact, by the stationary solution of equation (12), we have:
In fact, by the stationary solution of equation (12), we have:

Setting 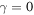 in the above equation, one can calculate the equilibrium temperature to be
in the above equation, one can calculate the equilibrium temperature to be ![${T}_{0}=\sqrt[4]{\frac{\left(1-A\right){p}_{0}}{4\sigma }}=255\,{\rm{K}}.$](https://content.cld.iop.org/journals/0143-0807/45/2/025804/revision2/ejpad2429ieqn84.gif) This would mean that, without the greenhouse effect, life on Earth would not be possible, because our planet would be way too cold. Instead, we know that the actual accepted value of
This would mean that, without the greenhouse effect, life on Earth would not be possible, because our planet would be way too cold. Instead, we know that the actual accepted value of 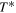 is
is 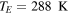 [7], which indeed allows life as we know on the planet. By setting
[7], which indeed allows life as we know on the planet. By setting 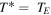 in equation (13) we may extract the value of the parameter
in equation (13) we may extract the value of the parameter 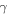 to be
to be 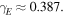
Therefore, we know that the temperature of the Earth is  and the greenhouse effect sustaining this level of temperature is characterized by a parameter
and the greenhouse effect sustaining this level of temperature is characterized by a parameter  Could equation (12) tell us where we would go in the future? In the limits of the simplicity of the model, the answer is affirmative. However, before we attempt any future prediction, let us discover more about the properties of the model. To do this, let us divide by
Could equation (12) tell us where we would go in the future? In the limits of the simplicity of the model, the answer is affirmative. However, before we attempt any future prediction, let us discover more about the properties of the model. To do this, let us divide by 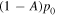 both members of equation (12), so that:
both members of equation (12), so that:
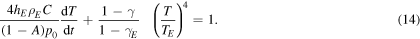
By looking at the above expression, the insurgence of a dimensionless variable  is evident. In this way, equation (14) can be written as follows:
is evident. In this way, equation (14) can be written as follows:
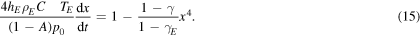
Being the right-hand side of equation (15) dimensionless, the left-hand side must be equally dimensionless, so that we may define a new dimensionless variable 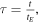 where:
where:

In this way, equation (15) can be finally cast in the following form:

The nonlinear ordinary differential equation (17) can now be interpreted as follows. The normalized temperature 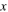 has a stable fixed point
has a stable fixed point 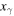 determined by setting to zero the derivative with respect to
determined by setting to zero the derivative with respect to 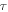 on the left-hand side of equation (17). This means that the planet Earth will always attain an equilibrium temperature
on the left-hand side of equation (17). This means that the planet Earth will always attain an equilibrium temperature 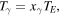 where:
where:

Therefore, any value the parameter 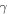 might attain, the Earth will always adjust, in due time, its temperature to
might attain, the Earth will always adjust, in due time, its temperature to 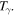 This is a first important conclusion we might drive also by means of a simple phase-plane analysis of the one-dimensional flow [17] in equation (17). This is done in figure 3, where the
This is a first important conclusion we might drive also by means of a simple phase-plane analysis of the one-dimensional flow [17] in equation (17). This is done in figure 3, where the 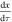 versus
versus 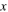 graph is shown for
graph is shown for 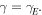 By setting
By setting  in equation (17), we notice that two fixed points are present:
in equation (17), we notice that two fixed points are present: 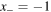 and
and 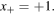 The first is unstable and not physically acceptable, since
The first is unstable and not physically acceptable, since 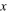 is always positive. The second is a stable fixed point. In fact, for
is always positive. The second is a stable fixed point. In fact, for 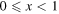 the derivative is positive and the function
the derivative is positive and the function 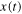 approaches the value
approaches the value 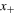 from the left. Similarly, for
from the left. Similarly, for 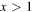 the derivative is negative and the function
the derivative is negative and the function 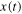 approaches the value
approaches the value  from the right. This behavior is described by the two arrows pointing toward the stable fixed point
from the right. This behavior is described by the two arrows pointing toward the stable fixed point 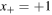 in figure 3.
in figure 3.
Figure 3. The properties of the differential equation describing the temperature dynamics as reported in equation (17) can be studied by means of the 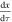 versus
versus 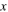 graph (phase-plane analysis) Here we consider γ = γE.
graph (phase-plane analysis) Here we consider γ = γE.
Download figure:
Standard image High-resolution imageThe same happens for 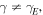 the only difference being that the stable fixed point is now given by
the only difference being that the stable fixed point is now given by 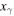 in equation (18). Therefore, because of the functional relation between
in equation (18). Therefore, because of the functional relation between  and
and 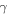 in equation (18), we have:
in equation (18), we have:

This derivative 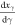 is therefore always positive, since
is therefore always positive, since 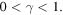 In this way, a small increment
In this way, a small increment 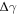 in the parameter
in the parameter  will cause, because of equation (19), an increment
will cause, because of equation (19), an increment 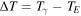 in the temperature, so that:
in the temperature, so that:

An analogous quantitative behavior can be found for the height of water in a leaking bucket. Even though the model in equation (17) does not enquire on the nature of the increment of the parameter 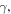 it is known that today's intense anthropic activities tend to give an increment of this parameter with respect to
it is known that today's intense anthropic activities tend to give an increment of this parameter with respect to 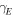 [7, 15], so that the value of
[7, 15], so that the value of 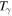 is expected to be higher than the actual average temperature
is expected to be higher than the actual average temperature  This is rather immediate qualitative prediction of the model. In the leaking bucket model, an increase in the value of
This is rather immediate qualitative prediction of the model. In the leaking bucket model, an increase in the value of 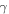 corresponds to a reduction of the cross section of the orifice which, on its turn, causes an increase of the level of water in the bucket. By this qualitative analogy, specifying that the efflux rate of the leaking bucket model is given by Torricelli's law, can well be used for a classroom demonstration of how—by keeping fixed the solar constant (the flux rate from the faucet)—the Earth temperature must rise, if the cross section of the orifice is made smaller.
corresponds to a reduction of the cross section of the orifice which, on its turn, causes an increase of the level of water in the bucket. By this qualitative analogy, specifying that the efflux rate of the leaking bucket model is given by Torricelli's law, can well be used for a classroom demonstration of how—by keeping fixed the solar constant (the flux rate from the faucet)—the Earth temperature must rise, if the cross section of the orifice is made smaller.
In the following section we shall investigate further on the time dependence of the temperature increase due to an increase of 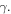 Before doing this, we preliminarily consider the time derivative, in the vicinity of the temperature
Before doing this, we preliminarily consider the time derivative, in the vicinity of the temperature 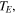 of both sides of equation (20), and write the following useful relation:
of both sides of equation (20), and write the following useful relation:
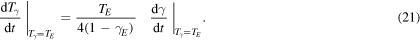
4. Time dependence
We would like to understand in what interval of time the changes in temperature occur and what could be future previsions as far as global temperature is concerned. This is not an easy task to accomplish, since it must rely on assumptions whose validity can be proven only within the specific framework of solar and terrestrial physics research. However, we may rely on simple reasoning to try to get some reasonable results. We then start by saying that, if the solid part of the Earth acts an insulator, only the oceans may act as heat reservoirs. This hypothesis is not too absurd, if we consider that horizontal convection currents tend to cool down the soil rather rapidly. Considering the following effective values 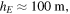
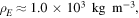 and
and 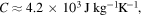 the quantity
the quantity 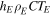 can be estimated to be approximately
can be estimated to be approximately 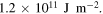 Therefore, the value of
Therefore, the value of 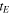 can be seen to be approximately
can be seen to be approximately 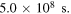 Converting this figure into years, we have:
Converting this figure into years, we have:

The quantity 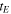 is only indicative of the characteristic time scale of the dynamics described in equation (17). This time scale thus represents the time interval in which a substantial change in the normalized temperature
is only indicative of the characteristic time scale of the dynamics described in equation (17). This time scale thus represents the time interval in which a substantial change in the normalized temperature 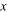 can be observed. The choice of
can be observed. The choice of 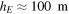 is because the upper part of the ocean is rapidly mixing, giving the main contribution to the heat capacitance [6]. Had we considered deep oceans (
is because the upper part of the ocean is rapidly mixing, giving the main contribution to the heat capacitance [6]. Had we considered deep oceans (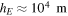 ) in this calculation, the value of
) in this calculation, the value of 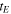 would be two orders of magnitude higher, meaning that the Earth can absorb, in the very long run and for millennia to come, the excess heat in the atmosphere, but at extremely slower rates.
would be two orders of magnitude higher, meaning that the Earth can absorb, in the very long run and for millennia to come, the excess heat in the atmosphere, but at extremely slower rates.
As reported in the Keeling curve [18], starting from year 1960, the average value of  concentration increases. Assuming now that this increase gives a linear change in the parameter
concentration increases. Assuming now that this increase gives a linear change in the parameter 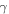 over the last few decades, we may write:
over the last few decades, we may write:

The rate 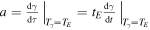 with which
with which 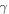 is increases can now be found by means of equation (21), so that:
is increases can now be found by means of equation (21), so that:

By considering 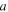 to be constant and by noticing that the global temperature has risen by
to be constant and by noticing that the global temperature has risen by 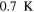 in the last century [7], we may estimate its value by equation (24) to be about
in the last century [7], we may estimate its value by equation (24) to be about  In this way equation (17) can be written as follows:
In this way equation (17) can be written as follows:

where 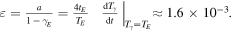 In the above equation the last addendum on the right-hand side can be considered as a perturbation term. A numerical solution of equation (25) is shown in figure 4, using the initial condition
In the above equation the last addendum on the right-hand side can be considered as a perturbation term. A numerical solution of equation (25) is shown in figure 4, using the initial condition  i.e.
i.e. 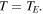 The initial time may be taken to be year 1950, before the almost linear increase of the global temperature
The initial time may be taken to be year 1950, before the almost linear increase of the global temperature 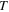 has been observed [7]. The
has been observed [7]. The 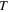 versus
versus 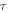 curve in figure 4 can also be obtained by a perturbation solution of equation (25) to first order in the parameter
curve in figure 4 can also be obtained by a perturbation solution of equation (25) to first order in the parameter 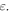 Notice that the initial slow growth of the temperature
Notice that the initial slow growth of the temperature 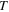 in this curve soon subsides to give rise to an asymptotic behavior with slope
in this curve soon subsides to give rise to an asymptotic behavior with slope 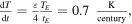 which is the same figure that we used in equation (24) to get the value of
which is the same figure that we used in equation (24) to get the value of 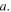
Figure 4. Solution of the dynamical equation (25). Assuming that 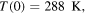 the global temperature
the global temperature 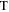 rises steadily, after a short transient. The normalized variable
rises steadily, after a short transient. The normalized variable  is used as the independent variable. In this time range (years 1950–2050) the first-order perturbation solution (red dotted-curve) and the numerical solution (blue curve) coincide.
is used as the independent variable. In this time range (years 1950–2050) the first-order perturbation solution (red dotted-curve) and the numerical solution (blue curve) coincide.
Download figure:
Standard image High-resolution imageTherefore, the qualitative result that we may extract form this analysis is that, if the coefficient 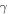 grows steadily as in equation (23), we may expect a steady increase of the global temperature over the years with a rate
grows steadily as in equation (23), we may expect a steady increase of the global temperature over the years with a rate 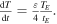 Of course, time dependences of the parameter
Of course, time dependences of the parameter 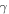 different from the linear one given in equation (23), will give different responses of the system.
different from the linear one given in equation (23), will give different responses of the system.
5. Conclusions
By considering the dynamics of the depth of water in a leaking bucket in the presence of a constant intake flux rate, it is noted that this hydrodynamic system is similar to the zero-dimensional energy balance model of the system Earth-atmosphere describing the dynamics of the global temperature. A qualitative similarity between these two models is attained, even though the efflux rate from the orifice depends, according to Torricelli's law, on the square root of the depth of water in the bucket, while the net heat flow rate from the Earth is given by the Stefan–Boltzmann law multiplied by the emissivity 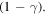 The qualitative similarity between the two models allows for a classroom or a video demonstration of the global temperature variation when greenhouse gases affect the emissivity
The qualitative similarity between the two models allows for a classroom or a video demonstration of the global temperature variation when greenhouse gases affect the emissivity  of the system Earth-atmosphere. In fact, an increase of the parameter
of the system Earth-atmosphere. In fact, an increase of the parameter 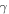 results in a reduced emissivity of infrared radiation from Earth to space. Consequently, a rise of the global temperature can be predicted. Similarly, a reduction of the size of the orifice in the leaking bucket will cause a decrease of the outflow flux rate and a rise in the water level at steady state. This analogy is possible because both dynamical systems arise from a conservation law and possess a similar analytic structure. However, the different expressions of the outflow term
results in a reduced emissivity of infrared radiation from Earth to space. Consequently, a rise of the global temperature can be predicted. Similarly, a reduction of the size of the orifice in the leaking bucket will cause a decrease of the outflow flux rate and a rise in the water level at steady state. This analogy is possible because both dynamical systems arise from a conservation law and possess a similar analytic structure. However, the different expressions of the outflow term 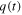 for the two systems only allows a qualitative comparison of the results.
for the two systems only allows a qualitative comparison of the results.
This analogy, however, should not lead students to think that the system Earth-atmosphere is simple to describe. In fact, mention of more complex one-dimensional EBMs should be made [3, 10, 11]. In this respect, one could explain to students that the convective flux of moist air plays an important role in determining the time evolution of the effective value of the emissivity  of the system Earth-atmosphere and, thus, of the global temperature
of the system Earth-atmosphere and, thus, of the global temperature 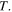 This additional complexity has not been considered in the present reduction process only to maintain the description of the dynamical model as simple as possible. Given this relative simplicity, in fact, the present work can be useful to advanced high-school or to first-year students. One hopes that by acquiring these notions, young students could gain awareness of how the greenhouse effect can allow life on Earth and how excessive emission of greenhouse gases in the atmosphere may cause an increase of the global temperature.
This additional complexity has not been considered in the present reduction process only to maintain the description of the dynamical model as simple as possible. Given this relative simplicity, in fact, the present work can be useful to advanced high-school or to first-year students. One hopes that by acquiring these notions, young students could gain awareness of how the greenhouse effect can allow life on Earth and how excessive emission of greenhouse gases in the atmosphere may cause an increase of the global temperature.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).





