Abstract
The classical Doppler effect has already been studied in many textbooks and papers. However, the formula currently used to describe the Doppler effect for a source and a receiver moving with constant velocities is not suitable for practical applications. Indeed, the formula makes use of two angles that depend on the state of the source-receiver system both at the emission instant and at the reception instant of sound, while in most real cases the state of the system is known only at one of the two instants. In this paper, two equivalent formulas are derived for the Doppler shift: one depending solely on the state of the system at the emission instant, and one depending solely on the state of the system at the reception instant. The paper also provides two more general expressions that describe the Doppler shift evolution over time. The expressions derived in this paper are compared with the existing ones in some special cases, obtaining consistent results.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The classical Doppler effect is a purely kinematic phenomenon caused by the finite propagation speed of waves in media. Since waves do not propagate instantly, any signal emitted by a source reaches the receiver with some delay. If the source and/or the receiver are in motion with respect to the medium, their distance in general varies over time, and the delay varies accordingly. The variation of the delay provokes a deformation of the received wave compared to the emitted one along the time axis. In the case of periodic waves, for which a frequency can be defined, it is observed that the frequency  perceived by the receiver differs from the frequency
perceived by the receiver differs from the frequency  emitted by the source. This phenomenon was first studied by Christian Andreas Doppler in 1842, and is therefore known as the Doppler effect, or Doppler shift [1].
emitted by the source. This phenomenon was first studied by Christian Andreas Doppler in 1842, and is therefore known as the Doppler effect, or Doppler shift [1].
The topic of this paper is the classical Doppler effect between a point-like source and a point-like receiver moving with constant velocities with respect to an inertial, non-dispersive medium. More precisely, we study what happens if the source emits a periodic, spherical wave, with the same intensity in all directions, propagating at a constant speed  An example of such wave is a musical note,
An example of such wave is a musical note, 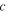 being the speed of sound in air. More generally, the classical Doppler effect concerns any kind of waves which can be described in terms of classical mechanics. However, we will always refer to sound waves for convenience. This way, we can avoid sentences such as ≪the receiver moves at a lower speed than the propagation speed of waves in the medium≫, stating, more briefly, ≪the receiver moves at subsonic speed≫.
being the speed of sound in air. More generally, the classical Doppler effect concerns any kind of waves which can be described in terms of classical mechanics. However, we will always refer to sound waves for convenience. This way, we can avoid sentences such as ≪the receiver moves at a lower speed than the propagation speed of waves in the medium≫, stating, more briefly, ≪the receiver moves at subsonic speed≫.
To begin with, let us define the main variables that describe the source-receiver system. We call 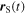 and
and 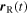 the positions of the source and receiver over time,
the positions of the source and receiver over time, 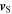 and
and 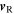 their respective velocities and
their respective velocities and 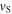 and
and 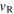 their speeds. We also call
their speeds. We also call  the position of the receiver with respect to the source: its norm,
the position of the receiver with respect to the source: its norm, 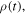 is the distance between the source and the receiver, while the unit vector
is the distance between the source and the receiver, while the unit vector 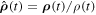 is the direction of the line linking the source to the receiver. We then define
is the direction of the line linking the source to the receiver. We then define 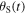 the angle between
the angle between  and
and 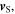
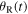 the angle between
the angle between  and
and 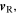 and
and 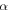 the constant angle between
the constant angle between 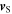 and
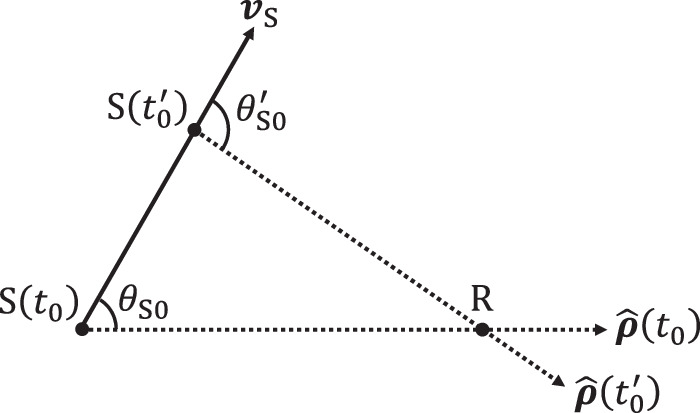
and 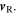 An example of a source-receiver system at a given instant
An example of a source-receiver system at a given instant  is shown in figure 1. Note that the vectors
is shown in figure 1. Note that the vectors 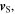
 and
and 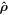 do not necessarily lay on the same plane.
do not necessarily lay on the same plane.
Figure 1. An example of a source-receiver system.
Download figure:
Standard image High-resolution imageA simple case of the Doppler effect is the longitudinal case, which occurs when the source and the receiver move along the same line, namely when the angles 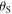 and
and  are equal to
are equal to 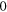 or
or 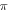 in the four possible combinations. In this case, it can be shown that
in the four possible combinations. In this case, it can be shown that

where the sign in the numerator is positive if the receiver moves towards the source (and negative otherwise), while the sign in the denominator is negative if the source moves towards the receiver (and positive otherwise). Equation (1) appears in several textbooks and papers [2–5], and it is known as the longitudinal Doppler effect formula.
The Doppler effect in three dimensions is more difficult to describe. Due to its complexity, it is often studied in some special cases, such as the case of a resting receiver with respect to the medium. Suppose that the source emits a maximum at the instant  and that the receiver hears that maximum at a later instant
and that the receiver hears that maximum at a later instant 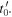 Since sound takes some time to reach the receiver, the source moves in the meantime. Therefore, at
Since sound takes some time to reach the receiver, the source moves in the meantime. Therefore, at 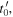 the direction
the direction 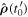 in which an observer holding the receiver sees the source does not coincide with the direction
in which an observer holding the receiver sees the source does not coincide with the direction 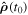 from which the observer hears the sound coming, as shown in figure 2.
from which the observer hears the sound coming, as shown in figure 2.
Figure 2. Doppler effect in the case of a resting receiver.
Download figure:
Standard image High-resolution imageWe will therefore call emission angle  namely the angle between
namely the angle between  and
and 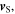 and reception angle
and reception angle 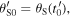 namely the angle between
namely the angle between 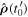 and
and 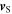 . The Doppler effect can be either expressed in terms of
. The Doppler effect can be either expressed in terms of 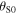 or
or 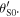 Textbooks usually report the formula in terms of
Textbooks usually report the formula in terms of 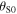 [6–8]:
[6–8]:

where 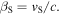
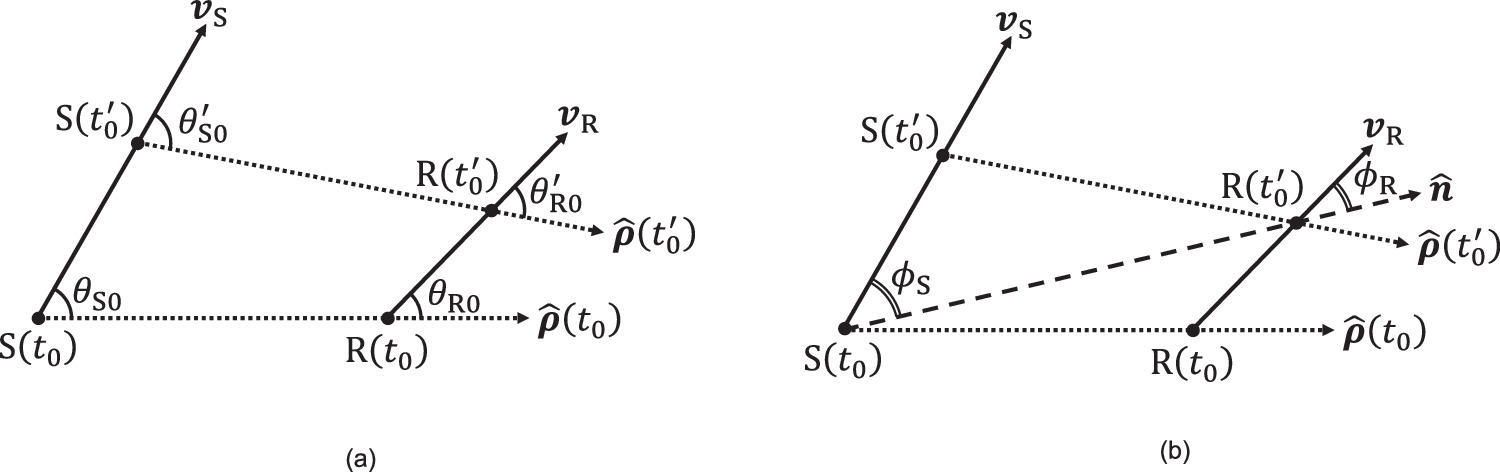
If both the source and the receiver move with respect to the medium, describing the Doppler effect is even more challenging. Since, in this case, both the source and the receiver are in motion, two emission angles and two reception angles can be defined, as shown in figure 3(a). More precisely, we call emission angles 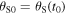 and
and  while we call reception angles
while we call reception angles 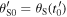 and
and 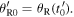
Figure 3. Emission and reception angles (a) versus hybrid angles (b).
Download figure:
Standard image High-resolution imageNote that an observer operating the source can easily measure the emission angles 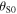 and
and 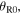 as they depend on
as they depend on  which is the direction where the observer sees the receiver while he is emitting the sound. Similarly, an observer holding the receiver can easily measure the reception angles
which is the direction where the observer sees the receiver while he is emitting the sound. Similarly, an observer holding the receiver can easily measure the reception angles  and
and  indeed, these angles depend on
indeed, these angles depend on 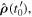 which is the direction where the observer sees the source while he is hearing the sound. Therefore, one would expect a Doppler effect formula in terms of the emission angles or the reception angles, but such a formula has yet to be found.
which is the direction where the observer sees the source while he is hearing the sound. Therefore, one would expect a Doppler effect formula in terms of the emission angles or the reception angles, but such a formula has yet to be found.
A few textbooks [9, 10] report as a general formula the expression

where 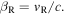 However, they fail to explain the meaning of
However, they fail to explain the meaning of 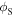 and
and  In fact,
In fact, 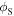 and
and 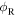 are neither the emission angles nor the reception angles, but the angles shown in figure 3(b), which we called hybrid angles. More precisely, if we call
are neither the emission angles nor the reception angles, but the angles shown in figure 3(b), which we called hybrid angles. More precisely, if we call 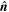 the unit vector linking the position of the source at the emission instant
the unit vector linking the position of the source at the emission instant 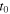 to the position of the receiver at the reception instant
to the position of the receiver at the reception instant 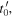
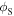 is the angle between
is the angle between 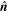 and
and 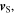 while
while 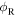 is the angle between
is the angle between 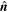 and
and 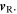 This is explained in two papers [11, 12], which also provide a derivation of equation (3).
This is explained in two papers [11, 12], which also provide a derivation of equation (3).
Of course, equation (3) continues to hold in the case of a resting receiver or in the case of a resting source. If the receiver is at rest, 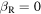 and
and 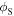 coincides with
coincides with 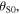 so we get once again equation (2). If the source is at rest,
so we get once again equation (2). If the source is at rest, 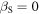 and
and 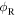 coincides with
coincides with 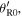 so we get a Doppler effect formula for a resting source in terms of the reception angle
so we get a Doppler effect formula for a resting source in terms of the reception angle 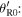

The problem with equation (3) is that it is hard to apply in practice. For instance, if an observer operating the source wants to use equation (3) to get the frequency perceived by the receiver, he needs to know the direction where the receiver will be at the reception instant, namely 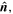 to establish the angles
to establish the angles 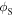 and
and 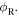 However, the direction where the receiver will be at the reception instant is unknown to the observer. So, equation (3) expresses the Doppler shift in terms of two unknown angles,
However, the direction where the receiver will be at the reception instant is unknown to the observer. So, equation (3) expresses the Doppler shift in terms of two unknown angles, 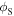 and
and 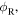 without explaining how to determine them. At this point, there are two possible ways to compute the Doppler shift: one can either find a mathematical way to establish the angles
without explaining how to determine them. At this point, there are two possible ways to compute the Doppler shift: one can either find a mathematical way to establish the angles 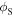 and
and 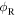 in terms of physical quantities that are known to the observer, or approach the problem in a completely new way. In this paper, we choose the second path.
in terms of physical quantities that are known to the observer, or approach the problem in a completely new way. In this paper, we choose the second path.
First, we set a rigorous definition of the Doppler shift, which offers a kinematical way to compute it. Then, we apply the definition to the case of a moving source and a moving receiver in 3D space. This way, we get two equivalent Doppler effect formulas: one in terms of the emission angles, which can be directly applied by an observer moving with the source, and one in terms of the reception angles, which can be directly applied by an observer moving with the receiver. We also obtain two more general expressions describing the Doppler shift evolution over time. Finally, to validate our results, we compare them with the known Doppler effect formulas in some special cases.
2. Definition of the doppler shift
The Doppler shift for a source-receiver system is usually defined as the ratio between the frequency 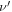 perceived by the receiver and the frequency
perceived by the receiver and the frequency 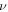 emitted by the source. However, such a definition can only work once the definition of
emitted by the source. However, such a definition can only work once the definition of 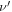 is set. Unfortunately, in most cases, even if the emitted wave is periodic, the received wave is not, so it is not possible to define its frequency in the classical sense of the term. In this paper, we define
is set. Unfortunately, in most cases, even if the emitted wave is periodic, the received wave is not, so it is not possible to define its frequency in the classical sense of the term. In this paper, we define 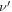 as follows. Suppose that the source emits a harmonic wave of period
as follows. Suppose that the source emits a harmonic wave of period 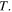 Suppose further that two consecutive maxima are emitted by the source at
Suppose further that two consecutive maxima are emitted by the source at 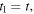
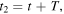 and received at
and received at 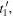
 We call perceived period,
We call perceived period, 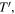 the time interval
the time interval 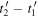 between the reception of the two maxima. We then define the perceived frequency,
between the reception of the two maxima. We then define the perceived frequency, 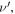 as
as 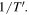
At this point, it would seem natural to define the Doppler shift as

with 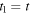 and
and  Equation (5) quantifies how shortened or stretched a single period of the emitted wave appears to the receiver. If we apply it to the longitudinal case, we get equation (1). Note that the right-hand side of equation (1) is constant. Thus,
Equation (5) quantifies how shortened or stretched a single period of the emitted wave appears to the receiver. If we apply it to the longitudinal case, we get equation (1). Note that the right-hand side of equation (1) is constant. Thus, 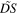 in the longitudinal case does not depend on the frequency of the source. This statement is by no means obvious. In fact, the problem with equation (5) is that
in the longitudinal case does not depend on the frequency of the source. This statement is by no means obvious. In fact, the problem with equation (5) is that  depends on
depends on 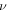 if the definition is applied to the 3D case. The reason is explained below.
if the definition is applied to the 3D case. The reason is explained below.
According to equation (5), to compute 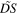 we first need to establish the reception instants
we first need to establish the reception instants 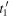 and
and 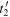 of the two maxima. The reception instant
of the two maxima. The reception instant 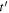 of a maximum can be established by knowing its corresponding emission instant
of a maximum can be established by knowing its corresponding emission instant 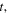 the state of the source-receiver system at
the state of the source-receiver system at 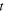 and the speed of sound. Let us assume that the state of the system at
and the speed of sound. Let us assume that the state of the system at 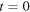 is known, as well as the speed of sound. The state of the system at
is known, as well as the speed of sound. The state of the system at 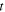 can be determined from the state at
can be determined from the state at 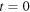 by simply knowing the elapsed time
by simply knowing the elapsed time 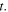 So, the reception instant of a maximum only depends on its emission instant:
So, the reception instant of a maximum only depends on its emission instant: 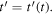 In our case, since the emission instants of the maxima are
In our case, since the emission instants of the maxima are 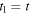 and
and 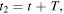 it follows that
it follows that  and
and 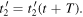 Thus, the perceived period,
Thus, the perceived period, 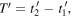 is a function of
is a function of 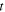 and
and  or simply
or simply 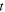 and
and 
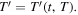 By consequence, the perceived frequency,
By consequence, the perceived frequency, 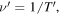 is also a function of
is also a function of 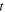 and
and 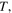 or else
or else 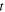 and
and 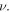 Finally, since
Finally, since 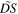 is equal to
is equal to 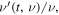 it depends in general on both
it depends in general on both 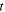 and
and 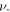 In some special cases, such as the longitudinal case,
In some special cases, such as the longitudinal case, 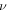 cancels out in computing the ratio. However, this does not happen in the 3D case.
cancels out in computing the ratio. However, this does not happen in the 3D case.
The dependence of 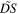 on
on 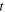 is simply a consequence of the time evolution of the system: as the configuration of the system evolves,
is simply a consequence of the time evolution of the system: as the configuration of the system evolves, 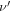 slowly changes over time, and
slowly changes over time, and 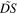 varies accordingly. The dependence on
varies accordingly. The dependence on  on the other hand, is more problematic. For example, by applying equation (5) in the case of a resting receiver, we do not get equation (2), but a more complex expression dependent on
on the other hand, is more problematic. For example, by applying equation (5) in the case of a resting receiver, we do not get equation (2), but a more complex expression dependent on  More precisely, for a sound emitted at
More precisely, for a sound emitted at  we get
we get
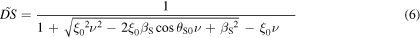
where 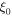 is the initial distance between the source and the receiver divided by the speed of sound.
is the initial distance between the source and the receiver divided by the speed of sound.
If we want the Doppler shift to be a physical quantity that does not depend on 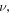 we need to choose the two emission instants
we need to choose the two emission instants 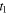 and
and 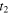 very close in time. More precisely, we need to compute the ratio
very close in time. More precisely, we need to compute the ratio 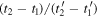 in the limit
in the limit  This way, we get a physical quantity that describes how an infinitely small portion of the emitted wave is perceived by the receiver. In short, we define the Doppler shift for a sound emitted at
This way, we get a physical quantity that describes how an infinitely small portion of the emitted wave is perceived by the receiver. In short, we define the Doppler shift for a sound emitted at 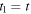 and received at
and received at 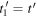 as
as

where the parenthesis  highlights the emission and the reception instants of sound.
highlights the emission and the reception instants of sound.
If the state of system at 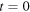 and the speed of sound are known, the reception instants
and the speed of sound are known, the reception instants 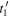 and
and 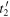 only depend on the emission instants
only depend on the emission instants 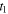 and
and 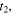 and so does the ratio
and so does the ratio 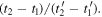 The limit
The limit 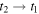 removes the dependence on
removes the dependence on 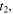 hence
hence 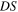 only depends on
only depends on 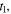 or else
or else 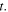
At this point, some may argue that  despite being well defined, does not represent what is normally meant by the Doppler effect, i.e. the ratio between the frequency perceived by the receiver and the frequency emitted by the source. So, let us show why this is not true. Suppose that the source emits a periodic wave of period
despite being well defined, does not represent what is normally meant by the Doppler effect, i.e. the ratio between the frequency perceived by the receiver and the frequency emitted by the source. So, let us show why this is not true. Suppose that the source emits a periodic wave of period  Computing the ratio
Computing the ratio 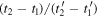 for
for  and
and 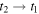 is equal to computing it for
is equal to computing it for 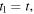
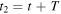 and
and 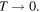 Therefore, equation (7) reads as
Therefore, equation (7) reads as

with  and
and 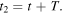 In other words, the Doppler shift is equal to the ratio
In other words, the Doppler shift is equal to the ratio 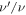 that one would observe over time if the source emitted a sound of a very high frequency. This means that, if the actual frequency emitted by the source is high enough,
that one would observe over time if the source emitted a sound of a very high frequency. This means that, if the actual frequency emitted by the source is high enough, 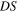 provides with good approximation the time deformation of the first period of the emitted wave, starting from time
provides with good approximation the time deformation of the first period of the emitted wave, starting from time 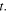
In the longitudinal case, the ratio  is constant, thus equation (7) becomes equivalent to equation (5). Equation (7) is also compatible with all the known Doppler effect formulas, including equation (3). Indeed, equation (3) was derived by assuming that the source emitted a first maximum at
is constant, thus equation (7) becomes equivalent to equation (5). Equation (7) is also compatible with all the known Doppler effect formulas, including equation (3). Indeed, equation (3) was derived by assuming that the source emitted a first maximum at 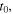 received at
received at 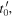 and a second maximum at
and a second maximum at 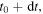 received at
received at  The Doppler shift was then computed as the ratio
The Doppler shift was then computed as the ratio  for
for 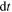 sufficiently small. If we set
sufficiently small. If we set 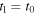 and
and 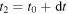 in equation (7), the ratio
in equation (7), the ratio 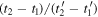 is clearly equal to
is clearly equal to 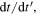 and assuming
and assuming 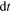 infinitely small is equivalent to computing the ratio in the limit
infinitely small is equivalent to computing the ratio in the limit 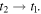
3. Doppler effect in terms of the emission instant
Having set a rigorous definition of the Doppler shift, we are now ready to compute it. As we have already explained in section 2, the Doppler shift can be expressed in terms of the emission instant of sound, of the speed of sound and of the initial state of the source-receiver system. The state of the system at a generic instant 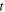 is given by the vectors
is given by the vectors 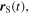
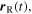
 and
and 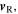 namely a set of twelve scalars. However, due to the homogeneity and the isotropy of space, we know that
namely a set of twelve scalars. However, due to the homogeneity and the isotropy of space, we know that 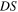 cannot depend on the orientation of the axes nor on the origin of the reference frame. We therefore define the useful state of the system as the equivalence class of all those states that only differ for a roto-translation of the reference frame. Only six scalars are required to describe the useful state of the system:
cannot depend on the orientation of the axes nor on the origin of the reference frame. We therefore define the useful state of the system as the equivalence class of all those states that only differ for a roto-translation of the reference frame. Only six scalars are required to describe the useful state of the system: 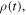
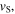
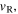
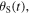
 and
and  which we will call essential variables. Thus, we expect
which we will call essential variables. Thus, we expect 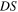 to depend on
to depend on 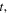
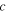 and on the initial values of the essential variables.
and on the initial values of the essential variables.
In order to compute the Doppler shift, we first need to establish the delay that occurs in the reception of a maximum. Suppose that the source emits a maximum at 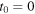 and a maximum at
and a maximum at 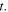 Since
Since 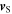 and
and  are constant,
are constant,


where 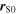 and
and 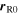 are the positions of the source and the receiver at the emission instant
are the positions of the source and the receiver at the emission instant 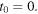 The position of the receiver with respect to the source at the instant
The position of the receiver with respect to the source at the instant  is therefore
is therefore
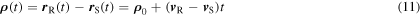
where 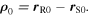 Now, let us call
Now, let us call 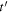 the reception instant of the maximum emitted at
the reception instant of the maximum emitted at 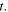 Since the maximum needs to travel from
Since the maximum needs to travel from 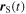 to
to  in order to reach the receiver, we can state that
in order to reach the receiver, we can state that

Equation (12) can also be written as
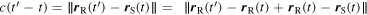
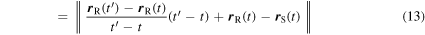
The fraction inside the norm is, by definition, the average velocity of the receiver in the time interval  which is clearly
which is clearly  The difference
The difference  is, by definition,
is, by definition, 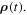 Finally, the time interval
Finally, the time interval  is the delay that occurs in the reception of the maximum, which we will call
is the delay that occurs in the reception of the maximum, which we will call  With these substitutions, equation (13) reads as
With these substitutions, equation (13) reads as

By taking the square of equation (14) and bringing everything to the left-hand side, we get
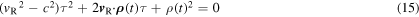
For convenience, we now introduce the dimensionless velocity 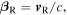 and we also define
and we also define 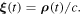 Equation (15) can be written in terms of
Equation (15) can be written in terms of 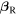 and
and 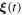 by dividing both sides for
by dividing both sides for 
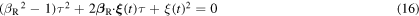
Equation (16) is a quadratic equation in 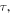 so it can have up to two solutions. However, since a maximum cannot be received before it is emitted, equation (16) needs to satisfy the causality condition
so it can have up to two solutions. However, since a maximum cannot be received before it is emitted, equation (16) needs to satisfy the causality condition 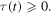 In the subsonic case (
In the subsonic case ( and
and  ) it is easy to show that equation (16) has only one acceptable solution:
) it is easy to show that equation (16) has only one acceptable solution:
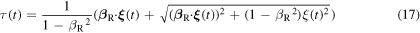
This means that a maximum emitted at a generic instant 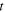 is always received at
is always received at

Let us express equation (17) in a more explicit form. Since 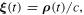 from equation (11) it follows immediately that
from equation (11) it follows immediately that

where 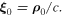 Thus, the terms
Thus, the terms  and
and 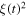 appearing in equation (17) can be expressed as
appearing in equation (17) can be expressed as

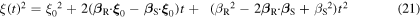
The dot products in equations (20) and (21) suggest introducing the angles 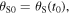
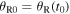 and
and 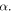 This way,
This way,
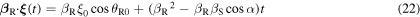
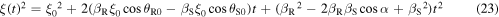
By substituting equations (22) and (23) into equation (17), and by adding the like terms, we get an explicit expression for 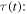
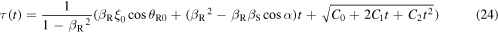
where we introduced the constants


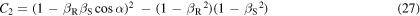
Now, suppose that the source emits a harmonic wave of period  If two consecutive maxima are emitted at
If two consecutive maxima are emitted at 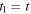 and
and 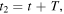 their reception instants are given by equation (18):
their reception instants are given by equation (18):


The ratio 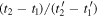 is then
is then
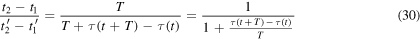
According to equation (8) the Doppler shift can be computed in the limit 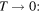
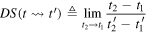
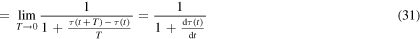
So, a general Doppler effect formula can be obtained by simply evaluating the derivative of 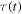 from equation (24) and substituting it into equation (31):
from equation (24) and substituting it into equation (31):
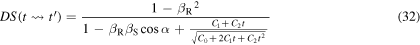
Equation (32) describes the Doppler shift for a sound emitted at 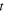 and received at
and received at  as a function of the emission instant
as a function of the emission instant 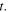 If we want to know the Doppler shift for a sound emitted at
If we want to know the Doppler shift for a sound emitted at 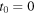 and received at
and received at  we just need to set
we just need to set  in equation (32). If we also substitute equations (25) and (26) into equation (32), we get the explicit expression:
in equation (32). If we also substitute equations (25) and (26) into equation (32), we get the explicit expression:
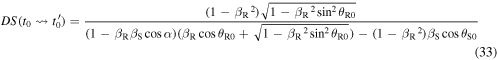
Equation (33) expresses the Doppler shift for a sound emitted at 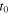 in terms of the essential variables of the system computed at
in terms of the essential variables of the system computed at 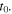 In particular, we note that
In particular, we note that 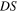 depends on the angles
depends on the angles 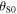 and
and 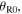 namely the emission angles. So, equation (33) can be directly applied to compute the Doppler shift by an observer operating the source.
namely the emission angles. So, equation (33) can be directly applied to compute the Doppler shift by an observer operating the source.
It is also important to point out that no assumptions were made on the state of the system at  which is simply what we chose as the origin of time. Due to the homogeneity of time, any instant can be chosen as the origin of time. Therefore, equation (33) holds for a sound emitted at any instant provided that the essential variables are computed at that precise instant.
which is simply what we chose as the origin of time. Due to the homogeneity of time, any instant can be chosen as the origin of time. Therefore, equation (33) holds for a sound emitted at any instant provided that the essential variables are computed at that precise instant.
The analysis that we have just conducted reveals two basic properties of the classical Doppler effect. First, we notice from equation (33) that, for 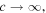
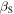 and
and 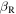 tend to
tend to 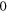 and
and 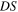 tends to
tends to 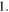 In other words, no Doppler effect is observed if the wave propagates instantly. This result supports the very first claim of the Introduction: the Doppler effect is due to the finite propagation speed of waves in media. Second, we notice from equation (31) that, if the delay is constant, the derivative of
In other words, no Doppler effect is observed if the wave propagates instantly. This result supports the very first claim of the Introduction: the Doppler effect is due to the finite propagation speed of waves in media. Second, we notice from equation (31) that, if the delay is constant, the derivative of 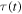 is zero and
is zero and 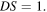 This result supports another important claim of the Introduction: the Doppler effect is due to the variation of the delay in the reception of signals.
This result supports another important claim of the Introduction: the Doppler effect is due to the variation of the delay in the reception of signals.
4. Example
To better understand the utility of equation (32), we now show how it can be applied in practice with an example. Suppose that the state of the system at the initial instant  is given by the vectors
is given by the vectors 
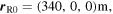
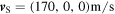 and
and 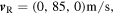 as shown in figure 4.
as shown in figure 4.
Figure 4. Initial state of the source-receiver system.
Download figure:
Standard image High-resolution imageSuppose further that the speed of sound is 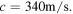 By definition, the essential variables of the system at
By definition, the essential variables of the system at 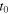 are
are 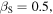
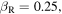
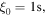
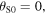
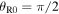 and
and 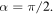 These can be used to compute the constants in equations (25), (26) and (27):
These can be used to compute the constants in equations (25), (26) and (27): 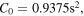
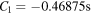 and
and 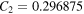 . Finally,
. Finally, 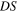 can be evaluated as a function of
can be evaluated as a function of 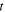 according to equation (32). The Doppler shift evolution over time is represented by the red curve in figure 5.
according to equation (32). The Doppler shift evolution over time is represented by the red curve in figure 5.
Figure 5. Doppler shift evolution over time.
Download figure:
Standard image High-resolution imageThe blue curve in figure 5 represents instead the Doppler effect 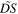 on the single periods, defined in equation (5). The values of
on the single periods, defined in equation (5). The values of 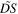 were obtained through a computer simulation. The reception instants of the maxima were established by evaluating the position of the corresponding wavefronts, the position of the source and the position of the receiver every microsecond.
were obtained through a computer simulation. The reception instants of the maxima were established by evaluating the position of the corresponding wavefronts, the position of the source and the position of the receiver every microsecond.
By definition, 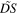 tends to
tends to 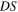 for
for 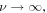 but, as we can see from figure 5, the two quantities are similar even at relatively low frequencies. More precisely, for the two quantities to be similar, the angles
but, as we can see from figure 5, the two quantities are similar even at relatively low frequencies. More precisely, for the two quantities to be similar, the angles 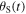 and
and  must not vary significantly in between the emission of two consecutive maxima. In the subsonic case, a sufficient condition to fulfill this requirement is
must not vary significantly in between the emission of two consecutive maxima. In the subsonic case, a sufficient condition to fulfill this requirement is 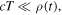 namely
namely 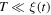 or
or 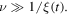 In our example,
In our example, 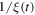 roughly stays around
roughly stays around 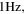 so an emitted frequency of
so an emitted frequency of 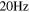 is already high enough to show the similarity between
is already high enough to show the similarity between 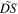 and
and 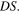 In most real cases, provided that the receiver stays far from the source, the condition
In most real cases, provided that the receiver stays far from the source, the condition  is largely satisfied.
is largely satisfied.
5. Doppler effect in terms of the reception instant
By following a similar procedure to the one shown in section 3, we can also derive a Doppler effect formula in terms of the reception instant of sound. Suppose that the source receives a maximum at  and a maximum at
and a maximum at 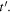 Since
Since 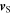 and
and 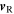 are constant,
are constant,


where 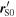 and
and 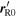 are the positions of the source and the receiver at the reception instant
are the positions of the source and the receiver at the reception instant  The position of the receiver with respect to the source at the instant
The position of the receiver with respect to the source at the instant 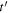 is therefore
is therefore

where 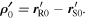 Now, let us call
Now, let us call 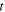 the emission instant of the maximum received at
the emission instant of the maximum received at 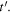 Since the maximum travelled from
Since the maximum travelled from 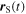 to
to 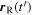 in order to reach the receiver, we can state that
in order to reach the receiver, we can state that

Equation (37) can also be written as
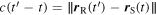
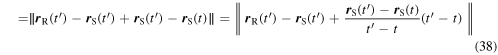
The fraction inside the norm is, by definition, the average velocity of the source in the time interval  which is clearly
which is clearly 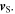 The difference
The difference 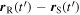 is, by definition,
is, by definition, 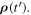 Finally, the time interval
Finally, the time interval  is the delay that occurs in the reception of the maximum, which we will still call
is the delay that occurs in the reception of the maximum, which we will still call 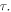 With these substitutions, equation (38) reads as
With these substitutions, equation (38) reads as

By taking the square of equation (39) and bringing everything to the left-hand side, we get
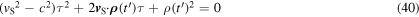
For convenience, we now introduce the dimensionless velocity 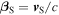 and set
and set 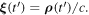 Equation (40) can be written in terms of
Equation (40) can be written in terms of 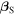 and
and 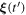 by dividing both sides for
by dividing both sides for 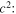
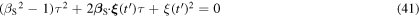
Equation (41) is a quadratic equation in 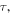 so it can have up to two solutions. However, since a maximum cannot be received before it is emitted, equation (41) needs to satisfy the causality condition
so it can have up to two solutions. However, since a maximum cannot be received before it is emitted, equation (41) needs to satisfy the causality condition 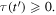 In the subsonic case (
In the subsonic case (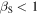 and
and 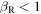 ) it is easy to show that equation (41) has only one acceptable solution:
) it is easy to show that equation (41) has only one acceptable solution:

This means that a maximum received at a generic instant 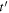 was emitted at
was emitted at

Let us express equation (42) in a more explicit form. Since  from equation (36) it follows immediately that
from equation (36) it follows immediately that

where 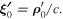 Thus, the terms
Thus, the terms 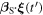 and
and 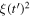 appearing in equation (42) can be expressed as
appearing in equation (42) can be expressed as

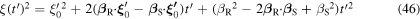
The dot products in equations (45) and (46) suggest introducing the angles 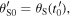
 and
and 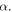 This way,
This way,
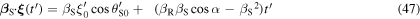
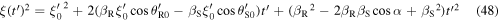
By substituting equations (47) and (48) into equation (42), and by adding the like terms, we get an explicit expression for 
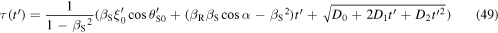
where we introduced the constants

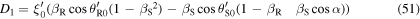
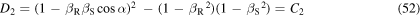
Now, suppose that source emits a harmonic wave of period 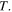 If two consecutive maxima are received at
If two consecutive maxima are received at 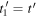 and
and 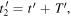 their emission instants are given by equation (43):
their emission instants are given by equation (43):


The ratio 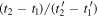 is then
is then

According to equation (8) the Doppler should be computed in the limit  However, in the subsonic case,
However, in the subsonic case,  if and only if
if and only if 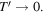 The two limits are therefore equivalent, and
The two limits are therefore equivalent, and

So, a general Doppler effect formula can be obtained by simply evaluating the derivative of  from equation (49) and substituting it into equation (56):
from equation (49) and substituting it into equation (56):
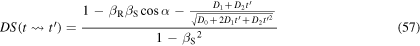
Equation (57) describes the Doppler shift for a sound emitted at  and received at
and received at 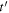 as a function of the reception instant
as a function of the reception instant 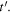 If we want to know the Doppler shift for a sound emitted at
If we want to know the Doppler shift for a sound emitted at  and received at
and received at 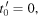 we just need to set
we just need to set  in equation (57). If we also substitute equations (50) and (51) into equation (57), we get the explicit expression:
in equation (57). If we also substitute equations (50) and (51) into equation (57), we get the explicit expression:
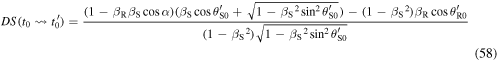
Equation (58) expresses the Doppler shift for a sound received at 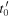 in terms of the essential variables of the system computed at
in terms of the essential variables of the system computed at 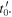 In particular, we note that
In particular, we note that 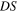 depends on the angles
depends on the angles 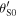 and
and  namely the reception angles. So, equation (58) can be directly applied to compute the Doppler shift by an observer holding the receiver.
namely the reception angles. So, equation (58) can be directly applied to compute the Doppler shift by an observer holding the receiver.
It is also important to point out that no assumptions were made on the state of the system at 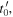 which is simply what we chose as the origin of time. Due to the homogeneity of time, any instant can be chosen as the origin of time. Therefore, equation (58) holds for a sound received at any instant provided that the essential variables are computed at that precise instant.
which is simply what we chose as the origin of time. Due to the homogeneity of time, any instant can be chosen as the origin of time. Therefore, equation (58) holds for a sound received at any instant provided that the essential variables are computed at that precise instant.
An interesting thing to observe is that equation (58) can be obtained from equation (33) by doing the following operations: replacing the emission angles 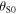 and
and 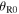 with the reception angles
with the reception angles 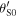 and
and 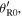 swapping everywhere the subscripts
swapping everywhere the subscripts 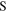 and
and 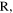 and inverting the fraction. This fact, which may appear to be a coincidence, has actually deep roots. Indeed, it can be shown that this property arises from the isotropy of time, but we will not delve into the topic in this paper.
and inverting the fraction. This fact, which may appear to be a coincidence, has actually deep roots. Indeed, it can be shown that this property arises from the isotropy of time, but we will not delve into the topic in this paper.
6. Special cases
Now that we have derived the general Doppler effect formulas, in this section we evaluate them in three special cases: the longitudinal case, the case of a resting source and the case of a resting receiver. The results will be compared, when possible, with the currently known Doppler effect formulas, providing further evidence that equations (32) and (57) are correct.
6.1. Doppler effect in the longitudinal case
First, let us show that equation (32) is consistent with the longitudinal Doppler effect formula. For simplicity, we only consider the case of a source and a receiver moving towards each other, as the three remaining cases can be treated in a similar way.
For a source and a receiver moving towards each other, 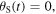
 and
and  The constants
The constants 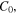
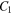 and
and 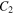 in equations (25), (26) and (27) therefore read as
in equations (25), (26) and (27) therefore read as



By substituting equations (59), (60) and (61) into equation (32), we get
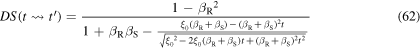
The term under root is a perfect square. We can therefore simplify the root, while in the numerator of the internal fraction we can collect 
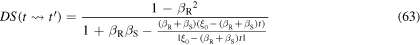
Note that, in order to simplify the internal fraction, we first need to establish the sign of the quantity 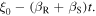 Assuming
Assuming  means considering only the emission instants
means considering only the emission instants 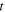 before the positions of the source and the receiver cross each other. For
before the positions of the source and the receiver cross each other. For 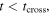 we get
we get
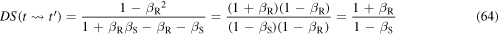
in agreement with equation (1). Equation (64) can also be derived in a similar way from equation (57).
6.2. Doppler effect for a resting receiver
Next, let us consider the case of a moving source and a resting receiver. Since this case is usually studied in terms of the emission instant, we will start from equation (32). For 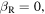 the constants
the constants 
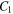 and
and 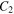 in equations (25), (26) and (27) read as
in equations (25), (26) and (27) read as



By substituting equations (65), (66) and (67) into (32), we get
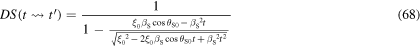
If we set 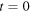 in equation (68), we obtain
in equation (68), we obtain

namely equation (2). Similarly, an equivalent formula in terms of the reception angle 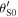 can be derived from equation (57) or equation (58). After some mathematical simplifications, one obtains
can be derived from equation (57) or equation (58). After some mathematical simplifications, one obtains
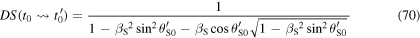
6.3. Doppler effect for a resting source
Finally, let us consider the case of a resting source and a moving receiver. Since this case is usually studied in terms of the reception instant, we will start from equation (57). For  the constants
the constants 
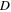 and
and 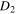 in equations (50), (51) and (52) read as
in equations (50), (51) and (52) read as



By substituting equations (71), (72) and (73) into (57), we get
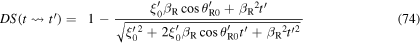
If we set  in equation (74), we obtain
in equation (74), we obtain

namely equation (4). Similarly, an equivalent formula in terms of the emission angle 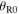 can be derived from equation (32) or equation (33). After some mathematical simplifications, one obtains
can be derived from equation (32) or equation (33). After some mathematical simplifications, one obtains
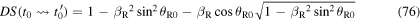
We also note that a formula in agreement with equation (74) was obtained in a paper in 2003 [12], where the reference frame and the origin of time were chosen so that 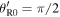 and
and 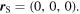 In this case, the cosine in equation (74) vanishes and
In this case, the cosine in equation (74) vanishes and 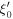 is simply equal to
is simply equal to 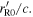
7. Conclusions
A rigorous definition of the Doppler shift has been set, which allows to compute it in a purely kinematic way. By applying the definition, two new formulas have been derived in the case of a source and a receiver moving with constant velocities: one expressing the Doppler shift in terms of the state of the system at the emission instant of sound, the other one expressing the Doppler shift in terms of the state of the system at the reception instant of sound. Contrarily to the existing formula, the new ones contain only directly measurable angles. A similarity between the two Doppler effect formulas has been noted: the second one can be obtained from the first one by replacing the emission angles with the reception angles, by swapping all the physical quantities relative to the source with the corresponding physical quantities relative to the receiver and by inverting the result. Two additional expressions have also been derived, describing the Doppler shift evolution over time.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Conflict of interest
The author declare that they have no conflicts of interest.