Reconstruction of Carrington Rotation Means of Open Solar Flux over the Past 154 Years

Abstract

We generate reconstructions of signed open solar flux (OSF) for the past 154 years using observations of geomagnetic activity. Previous reconstructions have been limited to annual resolution, but this is here increased by a factor of more than 13 by using averages over Carrington rotation (CR) intervals. We use two indices of geomagnetic activity, the homogeneous aa index, aa_H, and the IDV(1d) index; a combination of the two is fitted to OSF estimates from near-Earth interplanetary satellite data. For 1995 – 2022, these are corrected for excess flux (i.e. orthogardenhose flux and switchbacks) using strahl electrons. For 1970 – 2022, we also use the absolute values of the radial component of the near-Earth interplanetary magnetic field ${\langle }|{\langle }B_{r}{\rangle }_{\tau }|{\rangle }_{CR}$, where the excess flux is allowed for by adopting the optimum averaging interval ${\tau }$ of 20 h. However, in the interval 1970 – 1995, data gaps in the interplanetary data are a serious problem. The errors that these missing data cause in CR averages of OSF are evaluated by synthetically masking data for CRs that have a full complement, using the same number and time series of data gaps as for the CR in question. Given the potential for missing data to generate large errors, we use the near-continuous 1995 – 2022 data to derive the best-fit combination of the geomagnetic data and employ the 1970 – 1995 data for testing in which we can readily allow for the errors caused by data gaps. Errors caused by inaccuracies in the geomagnetic data are shown to be considerably smaller than the uncertainties due to the polynomial fitting. It is shown that the new reconstructions are consistent with the previous annual estimates and that there is considerable variability in the OSF values from one CR to the next; in particular, in high-activity solar cycles, there can be individual CRs in which the OSF exceeds that for adjacent CRs by a factor as large as two.

1 Introduction

1.1 Periodicities Caused by Solar Rotation

Sunspots around the solar equator have a sidereal rotation period (with respect to the fixed stars) of about 24.47 days, which gives an average synodic rotation period (as seen from Earth) of near 26.25 days, whereas for sunspots at heliographic latitude ${\Lambda}_{H} = {\pm}45^{\circ}$, the synodic period is roughly 28.9 days (Ruždjak et al., 2017; Permata and Herdiwijaya, 2019). The rotation periods of the solar corona are harder to measure accurately but also show differential rotation, but to a lesser degree than the photosphere (Mancuso et al., 2020; Morgan, 2011). In the lower corona, at heliocentric distances $r$ of $1.7R_{\odot}$ (where $R_{\odot} = 6.96{\times}10^{8}$ m is the mean radius of the photosphere), the synodic period is about 27.3 days at ${\Lambda}_{H} = 0^{\circ}$ and peaks at about 27.7 days at ${\pm}25^{\circ}$ before declining again at greater ${\Lambda}_{H}$ (Mancuso et al., 2020). In the higher corona, at $r=4R_{\odot}$, differential rotation is reduced compared to the lower corona, but variability and measurement uncertainty are high (Morgan, 2011).

The Carrington rotation (CR) system is based on assigning a sidereal rotation period of 25.38 days, which is the rotation period for sunspots near ${\Lambda}_{H} = {\pm}26^{\circ}$ and of the equatorial corona at $|{\Lambda}_{H}|$ below about $13^{\circ}$. The corresponding synodic period of a CR varies slightly during the year because of the changing speed of the Earth in its orbit, but averages 27.2753 days (654.6072 h). There is a subtle effect discussed in Section A.3 of the Appendix to the present article, which investigates the different periodicities introduced into parameters in near-Earth interplanetary space and into geomagnetic activity measures by the rotation of the Earth. The periodicity in interplanetary parameters related to the magnetic field sector structure, or to the longitudinal equatorial coronal hole distribution, are shown to be extremely close to (but very slightly shorter than) the synodic CR interval. However, it is shown that the Universal Time variation in solar wind-magnetosphere coupling (generated by the eccentric nature of Earth’s main dipole magnetic field and the rotation of the Earth) makes the peak periodicity of the geomagnetic data a whole number of days. This explains why Bartels, and subsequent geophysicists, have found 27-day intervals most useful for the study of geomagnetic activity whereas Carrington, and subsequent solar physicists, have found 27.2753-day intervals most useful to study solar effects. We here want to average out any longitudinal structure in the coronal and heliospheric magnetic fields and so need to average over integer numbers of whole CR intervals.

1.2 Open Solar Flux

The open solar flux (OSF) is the magnetic flux that threads the “coronal source surface” near the top of the corona, often taken to be a heliocentric sphere at $r = 2.5\mathrm{R}_{\odot}$ (Arge and Pizzo, 2000), and so the OSF is the flux that leaves the corona and enters the heliosphere. The OSF is often thought of as largely originating in coronal holes (e.g. Mackay and Yeates, 2012; Priest, 2014), which can be seen as regions of relatively low EUV and X-ray emission (Zirker, 1977; Cranmer, 2009). However, computation of the OSF from the integrated magnetic flux threading coronal holes detected this way (Lowder et al., 2014; Lowder, Qiu, and Leamon, 2017) leads to OSF estimates that are smaller than those derived from other methods by a factor close to 2 (Linker et al., 2017; Wallace et al., 2019), probably because of open flux embedded in the streamer belt that is not detected as dark in the EUV or X-ray emissions. Those other methods have included: potential field source surface (PFSS) modelling of coronal fields from photospheric field measurements (Altschuler and Newkirk, 1969; Schatten, Wilcox, and Ness, 1969; Wang and Sheeley, 1992); developments of the PFSS modelling such as current sheet source surface (CSSS) modelling (Koskela, Virtanen, and Mursula, 2019); non-potential modelling using magnetic flux transport and magneto-frictional simulations, which can also allow for currents below the coronal source surface (Yeates et al., 2010); MHD simulations based on photospheric field observations (Riley, Linker, and Mikić, 2001; Riley et al., 2011); interplanetary and geomagnetic observations (discussed below); and, at sunspot minimum (when polar coronal holes dominate), polar faculae and streamer belt width (Muñoz-Jaramillo et al., 2012; Lockwood et al., 2022b).

The OSF was first quantified from geomagnetic activity observations by Lockwood, Stamper, and Wild (1999) in a reconstruction of annual means that extended back to 1868. Subsequently, improvements have been made both to the historic geomagnetic data and to the reconstruction method (including allowance for the excess flux: see below) (Lockwood, 2003, 2013; Rouillard, Lockwood, and Finch, 2007; Lockwood and Owens, 2011, 2014; Lockwood, Rouillard, and Finch, 2009; Lockwood et al., 2014b; Lockwood, Owens, and Barnard, 2014; Lockwood et al., 2017a, 2022a). These improvements included expansion of the reconstructions to other interplanetary parameters such as the near-Earth solar wind speed, $V_{\normalfont{\mathrm{sw}}}$, the near-Earth heliospheric magnetic field (the interplanetary magnetic field, IMF, $B$), the latitudinal width of the streamer belt (Lockwood and Owens, 2014; Owens, Lockwood, and Riley, 2017), and the solar wind power input to the magnetosphere (Lockwood et al., 2017b). Other geomagnetic data were also employed to extend reconstructions back in time to 1844. However, all this work has used annual means to average out a variety of annual effects and to reduce observation and polynomial fitting noise. The present paper increases the time resolution by generating reconstructions of Carrington rotation resolution.

A key fact that allows these reconstructions is that the plasma $\beta$ is low close to the Sun. Hence the tangential plasma pressure is much smaller than the tangential magnetic pressure, $B_{r}^{2}/(2{\mu}_{o})$, where $B_{r}$ is the radial field. This means slight deviations from the radial flow of the solar wind plasma (and its frozen-in heliospheric magnetic field) in the innermost heliosphere equalise the tangential pressure and hence give $|B_{r}|$ that is close to being independent of heliographic latitude (Suess and Smith, 1996; Suess et al., 1996, 1998). The plasma $\beta$ increases with increasing radial distance, but this near-constant $|B_{r}|$ is “frozen-in” and carried out into the heliosphere. This was confirmed to be the case by the perihelion fast-latitude passes by the Ulysses spacecraft (Smith and Balogh, 1995; Smith et al., 2001, 2003; Lockwood et al., 2004; Lockwood and Owens, 2009). This means that we can compute the total signed (of “towards” or “away” polarity) heliospheric magnetic flux threading a spherical surface at heliocentric distance of an astronomical unit $r = R_{AU}$ from the formula

$$ F_{AU} = 2{\pi}R_{AU}^{2}{\times}{\langle}|B_{r}|{\rangle}_{CR}, $$

(1)

where the averaging interval is a whole number of Carrington rotations, which would average out any longitudinal structure, and $B_{r}$ is a high time-resolution measurement of the radial component of the IMF. Note the factor 2. This arises because $F_{AU}$ is here defined as the signed flux: this factor would be 4 for the unsigned flux (i.e. of either polarity). To compute the (signed) flux threading the solar source surface at the top of the solar corona, we need to subtract from $F_{AU}$ the “excess” signed flux ${\Delta}F$ (Lockwood, Owens, and Rouillard, 2009a,b; Lockwood and Owens, 2013; Owens et al., 2017):

$$ F_{s} = 2{\pi}R_{AU}^{2}{\times}{\langle}|B_{r}|{\rangle}_{CR} - { \Delta}F . $$

(2)

This excess flux ${\Delta}F$ arises because a magnetic flux tube the threads the solar source surface at $r=2.5R_{\odot}$ and then the spherical surface at $r=R_{AU}$ can bend back toward the Sun and thread the surface at $r=R_{AU}$ again, before bending back again to thread that surface for a third time. Hence such a flux tube of magnetic flux $f_{T}$ contributes a total of $3f_{T}$ to the unsigned flux at $r=R_{AU}$, but only $f_{T}$ to the unsigned flux at the source surface. Hence it contributes $2f_{T}$ to the unsigned excess flux and $f_{T}$ to the signed excess flux ${\Delta}F$. There are two main causes of this excess flux. The first is orthogardenhose heliospheric field where the large-scale structure in the heliosphere (for example, distortions to the Parker spiral configuration caused by draping of the field around coronal mass ejections (CMEs)) bends through of order 45^∘ – 135^∘ to re-thread the surface at $r= R_{AU}$ as orthogardenhose flux before threading it a third time to reach $r > R_{AU}$ (Lockwood, Owens, and Macneil, 2019). Secondly, there is what Lockwood, Owens, and Rouillard (2009b) termed “folded flux” and Owens, Crooker, and Lockwood (2013) termed “inverted flux”, and which since the advent of Parker Solar Probe observations is often called “switchbacks” (Bale et al., 2019; Jagarlamudi et al., 2023); in those the flux tube is bent back towards the Sun through of order 180^∘. Before the Parker Solar Probe mission, such structures were seen in data from several spacecraft, such as International Sun-Earth Explorer-3 (ISEE-3) (Kahler, Crooker, and Gosling, 1996), Ulysses (Neugebauer et al., 1995; Balogh et al., 1999), Advance Composition Explorer (ACE) and Wind (Borovsky, 2016) and Helios (Horbury, Matteini, and Stansby, 2018; Macneil et al., 2020, 2021). Using data from the Helios spacecraft, Macneil et al. (2020) showed that switchbacks were absent in the innermost heliosphere and increased in occurrence with increasing heliocentric distance, and so were generated in the heliosphere. Inverted flux can be generated by magnetic reconnection, in the corona or the heliosphere, or from other Alfvén wave sources.

In taking the modulus of the radial field $|B_{r}|$, we need to consider the effect of the averaging timescale of the data before the modulus is taken. This is because if this timescale is long, then we will average over switchbacks, or even orthogardenhose flux, and flux of opposing polarity will cancel. This can be useful in removing excess flux, because switchbacks and orthogardenhose flux are usually found in the heliosphere and are not a factor at the source surface and hence do not contribute to the coronal source flux (i.e. to the OSF). However, if the averaging timescale is long, then we will also average opposing polarity flux of the sector structure, which does map back to the source surface, and so this would lead to an underestimation of the source flux. Misunderstanding of the issue of the effect of averaging timescale led to the excess flux being labelled an “artefact” of taking the modulus of the field. Instead, Smith (2011) proposed that the field should be averaged over intervals of towards and away magnetic field sectors at the satellite. However, as pointed out by Lockwood and Owens (2013), the results of this depend critically on the choice of what constitutes a genuine sector boundary (i.e. a polarity reversal that maps back to the coronal source surface) and what is a switchback, or other, structure that originates in the heliosphere. Lockwood and Owens (2013) also pointed out that excess flux is a real physical phenomenon caused by switchbacks and orthogardenhose flux and not an artefact of the mathematical operation of taking the absolute value of a parameter.

Because the degree of field folding will increase with heliocentric distance (partly because the Parker spiral gardenhose angle increases with $r$), the excess flux also get larger farther way from the Sun. The survey of data from a great many heliospheric craft number by Owens et al. (2008) showed this to be the case, and the variation with radial distance $r$ observed was shown to be quantitatively consistent with expectations for excess flux by Lockwood, Owens, and Rouillard (2009b). The results of Owens et al. (2008) also showed that the latitudinal invariance of $|B_{r}|$ did not depend on $r$, and Lockwood and Owens (2009) used this survey to compute the uncertainties in quantifying $F_{AU}$ from a single point measurement at $r=R_{AU}$.

There are several ways in which we can account for the excess flux, ${\Delta}F$, and so use near-Earth heliospheric data to compute the OSF. Lockwood, Owens, and Rouillard (2009b) use the variation in the observed solar wind speed with frozen-in IMF and a kinetic (ballistic) model to make an estimate of ${\Delta}F$. This was based on observations that near-radial IMF resulted from the kinematic effect on frozen-in field in rarefaction regions where the solar wind velocity decayed (Jones, Balogh, and Forsyth, 1998; Riley and Gosling, 2007). Lockwood, Owens, and Rouillard (2009b) termed this method the “kinematic correction”. A more rigorous approach was developed by Owens et al. (2017) and employed by Frost et al. (2022). This method uses observations of strahl electrons to determine the magnetic connectivity of the observation point to the solar corona and so quantify the total inverted (folded) flux seen during a CR in switchbacks and orthogardenhose field regions. This gives the most accurate set of ${\Delta}F$ estimates to use in Equation 2. The main disadvantage of this method is that there is relatively limited availability of data with the required strahl observations. In addition, thus far, the method has only been applied to data from spacecraft in halo orbits around the L1 Lagrange point, for which the occurrence of folded flux is only detected close to the ecliptic plane; hence, flux that is folded in heliographic latitude and so folded out of the ecliptic is missed, but it is assumed that this is balanced by flux that was initially not in the ecliptic plane but is folded into it. Thirdly, we can use the averaging timescale ${\tau}$ applied before the modulus of the radial field is taken to give $|{\langle}B_{r}{\rangle}_{\tau}|$. If we could chose an ideal value of ${\tau}$, then this would cancel the folded flux but not cancel flux around the crossings of the heliospheric current sheet (HCS) that separate the sectors. If we achieve that, then we eliminate the ${\Delta}F$ term, and the equation for OSF becomes

$$ [F_{s}]_{IMF} = 2{\pi}R_{AU}^{2}{\times}{\langle}|{\langle}B_{r}{ \rangle}_{\tau}|{\rangle}_{CR}. $$

(3)

This is the most easily-implemented method, but it is also somewhat unsatisfactory. This is because, although there is always a value of ${\tau}$ that gives the correct $[F_{s}]_{IMF}$, this would almost certainly involve some incorrect cancellation of flux around HCS crossings but compensate for that by not fully cancelling all the folded flux that should be cancelled. Hence the required value of ${\tau}$ may vary.

Nevertheless, by comparison with the results from the strahl method, Frost et al. (2022) show that the averaging method accurately eliminates ${\Delta}F$ for a value of ${\tau}$ of 20 h for all CRs between 1995 and 2020. This is discussed further in Section 2 and in Section A.2 of the Appendix.

1.3 Structure of the Present Article

The present article uses CR means of geomagnetic activity data to reconstruct the OSF back to 1868 at CR resolution. This is done using the aa_H (Lockwood et al., 2018a,b) and IDV(1d) (Lockwood et al., 2013) geomagnetic indices, the derivation of which is discussed in Section 3. We employ a multiple regression with satellite observations of the OSF. The methods for making these OSF estimates from interplanetary observations were outlined in Section 1.2. The most satisfactory method is using strahl electrons with radial IMF observations, but these are available only after 1995. Sunspot numbers $R$ show that solar activity has been relatively quiet since 1995; the largest CR mean of $R$ in that interval is ${\langle}R{\rangle}_{CR}$ = 234.8, compared to the largest value since measurements began of 360.5 (in January 1958). Hence, it is useful to try to use radial IMF data from earlier intervals (the largest CR mean after 1970 is ${\langle}R{\rangle}_{CR}$ = 283.7, during the interval 1970 – 1995 there are 14 CRs for which ${\langle}R{\rangle}_{CR}$ exceeds 234.8, the largest value seen after 1995). Hence making use of the data from 1970 – 1995 extends the range of solar activity conditions contributing to the analysis. Section 2 compares the OSF generated with and without strahl data and quantifies the percent uncertainties ${\epsilon}$ in $[F_{s}]_{IMF}$ estimates made without strahl observations when there are gaps in the data series: this is done by synthetically introducing gaps into CRs with a full complement of observations. Unfortunately, in the data for 1970 – 1995 only 191 out of the 333 CRs contain enough data to give ${\epsilon} {\leq}20$%. As a result, we here use the strahl-derived data after 1995 to generate the multiple regression fit of the geomagnetic data and use the data from before 1995 for which ${\epsilon} {\leq}20$% as test data.

Section 2 and Appendix A.2 discuss the rationale for using a certain averaging interval ${\tau}$ with Equation 3 to allow for excess flux. They also give the details of the generation of the estimates of the uncertainty, ${\epsilon}$, caused by data gaps.

After describing the geomagnetic data in Section 3, Section 4 demonstrates why a combination of the aa_H and IDV(1d) geomagnetic indices can yield an OSF value and derives the algorithm for using these geomagnetic data to predict OSF on CR timescales. Section 5 presents the results and Section 6 evaluates the uncertainties caused by observation errors in the geomagnetic data. Section 7 compares with previous reconstructions.

Table 1 lists the all the datasets used in the present study and the intervals (and CR numbers) over which they are employed. This table also gives the percentages of CRs for which the data gaps are few enough and short enough to give percentage errors ${\epsilon}$ of less than 20%.

Table 1 Summary of the data used in this article to estimate CR means of signed open solar flux (OSF, $F_{s}$). The columns give the method used to compute the OSF, the derived parameter symbol, the number of the equation used, the dates and CR numbers of the start and end of the relevant periods for each method, the number of CRs, and the percent of CRs with sufficient data to give a percentage error in OSF, ${\epsilon}$, below 20%. ${\tau}$ is the averaging interval used to allow for excess flux if IMF data without strahl data are used. The bottom row is using the aa_H and IDV(1d) geomagnetic indices.

2 Near-Earth Interplanetary Magnetic Field Data

This section contrasts and compares the two methods for deriving CR averages of the OSF from in situ spacecraft observations of the radial IMF component. The errors introduced by data gaps are evaluated.

Equation 2 gives us a method for computing OSF when we have strahl electron data that allows us to determine the magnetic connectivity of field lines to the solar corona and hence to compute the excess flux, ${\Delta}F$ (Owens et al., 2017; Frost et al., 2022). This can be applied to interplanetary data obtained after 1995, but before then we have to use Equation 3 with the optimum averaging interval of ${\tau}$ of 20 h derived by Frost et al. (2022). This result is emphasised in Section A.2 of the Appendix, which confirms that 20 h is indeed the optimum averaging interval.

Figure 1 is a detailed look at the effects of averaging and then taking the modulus of one-minute or hourly Omni samples of the radial magnetic field in the near-Earth heliosphere, ${B_{r}}$. Data used are for 1981 – 2022 (inclusive), for which both one-minute and hourly resolution Omni interplanetary data are available.

Figure 1

Analysis of the effect of the averaging timescale (on which the absolute value of the radial IMF is taken) using “data density” plots (two-dimensional histograms) for 1981 – 2023, inclusive. In each panel the number of samples are colour coded (on a logarithmic scale) in bins of the two quantities shown along the axes. In (a), bins are 0.25 nT wide of both (horizontal axis) the modulus of hourly averages of the one-minute data $|{\langle}B_{r}{\rangle}_{1h}|$ and of (vertical axis) hourly averages of the modulus of the one-minute data ${\langle}|B_{r}|{\rangle}_{1h}$, where $B_{r}$ are one-minute samples of the radial IMF, as given by the Omni dataset. The bin widths in panels b and c is 0.25 nT, as in panel a. (b) is the same as (a) but for daily, rather than hourly values and compares $|{\langle}B_{r}{\rangle}_{1d}|$ and ${\langle}|B_{r}|{\rangle}_{1d}$. The vertical axis in (c) is the same as in (b), i.e. ${\langle}|B_{r}|{\rangle}_{1d}$, but for the $x$ axis, the modulus is taken on the hourly means, ${\langle}|{\langle}B_{r}{\rangle}_{1h^{\prime}}|{\rangle}_{1d}$, where the prime on the $h$ denotes that in this case the hourly means are as obtained from the Omni dataset; these values differ somewhat from the means derived from the one-minute data because of the variations in the satellite-to-Earth (to the bow shock) propagation lags applied to the data in the Omni dataset. (d) is the same as (c) but uses 655-h (Carrington rotation) running means of the data rather than one-day means, and the bin width is reduced to 0.025 nT. (e) and (f) are the same as (d), but the absolute value of $B_{r}$ is taken after averaging over 12 h and 1 day, respectively. In each panel, the dotted diagonal line is equality of the two values, and in panels (d), (e), and (f), the solid line is the best linear fit, the slope $s$ and intercept $c$ of which are given on the plot.

Figure 1a compares the modulus of hourly averages of the one-minute data, i.e. $|{\langle}B_{r}{\rangle}_{1h}|$, to hourly averages of the modulus of the one-minute data, ${\langle}|B_{r}|{\rangle}_{1h}$. The format is a “data density plot” (a two-dimensional histogram), in which the logarithm of the number of samples in bins of a given size are plotted as a function of the variables along the two axes. Because $B_{r}$ of opposite polarity in the averaging interval will cancel, $|{\langle}B_{r}{\rangle}_{1h}| {\leq} {\langle}|B_{r}|{\rangle}_{1h}$, as can be seen in the plot. Figure 1b is the same as Figure 1a, but for daily means; it shows the same behaviour as for the hourly means but to a greater extent, and the effect is clearly greatest at low values. Figure 1c shows another comparison of daily means. The vertical axis is again ${\langle}|B_{r}|{\rangle}_{1d}$, as in panel b. However, the horizontal axis is ${\langle}|{\langle}B_{r}{\rangle}_{1h^{\prime}}|{\rangle}_{1d}$, where the prime denotes that the hourly means provided by the Omni dataset are used. The same sort of behaviour as seen in panel b is observed, but there is spread in the data which, surprisingly, leads to some data points below the 45-degree line, i.e. ${ \langle}|{\langle}B_{r}{\rangle}_{1h^{\prime}}|{\rangle}_{1d} > { \langle}|B_{r}|{\rangle}_{1d}$, which at first sight should not be possible. This is an effect of the satellite-to-Earth propagation lags employed by the Omni dataset, which are different for hourly and minute data; the hourly Omni data are the averages of the up to 60 available one-minute samples in the same hour of the time of observation at the satellite, the average of which is then lagged allow for the satellite-to-Earth propagation. This is not the same as the averages of the 60 one-minute samples that fall in the same hour at the bow shock, after they have been individually lagged.

Panels d, e, and f look at CR averages. In each case the vertical axis is the mean of the modulus of the one-minute radial field samples in the CR interval. The horizontal axis uses the Omni-produced hourly means for which the modulus is taken after averaging over (panel d) 1 h, (panel e) 12 h, and (panel f) 1 day, respectively, i.e.${\langle}|{\langle}B_{r}{ \rangle}_{1h^{\prime}}|{\rangle}_{CR}$, ${\langle}|{\langle}B_{r}{\rangle}_{12h^{\prime}}|{\rangle}_{CR}$, and ${\langle}|{\langle}B_{r}{\rangle}_{1d^{\prime}}|{\rangle}_{CR}$. In these cases, the averaging over the CR has caused the shift to above the 45-degree line to be almost the same at all values and not just at low values, although the effect is still greater at lower values. The shift is greater the longer the averaging interval before the modulus is taken. This is because a longer averaging interval (greater ${\tau}$) causes more cancellation of opposite-polarity field within that interval, and so ${\langle}|{\langle}B_{r}{\rangle}_{\tau}|{\rangle}_{CR}$ is reduced.

Hereafter in this article, only the Omni hourly-averaged data are used, and so the prime symbol is no longer needed. These data give a sequence of continuous CR averages that extends back to 1970, although data gaps within the CRs are common before 1995.

Section A.2 of the Appendix looks at the effect of the averaging interval ${\tau}$ (before the absolute value of $B_{r}$ is taken) on the agreement between $[F_{s}]_{IMF}$, derived using Equation 3, and $[F_{s}]_{strahl}$, derived using Equation 2 with the excess flux calculated using strahl electrons (Frost et al., 2022). This confirms that ${\tau} = 20$ h is the optimum value, giving a maximum correlation coefficient $r$ and minimum r.m.s. difference between the two estimates, ${\Delta}_{rms}$. A scatter plot of the two OSF estimates for this optimum value of ${\tau}$ are shown in Figure 2. The polynomial fit to these data gives the regression

$$ [F_{s}]_{strahl} = 0.986[F_{s}]_{IMF} - 0.0081. $$

(4)

Figure 2

Scatter plot of CR means demonstrating that an averaging interval of ${\tau} = 20$ h gives OSF estimates $[F_{s}]_{IMF}$ from Equation 3 that closely match the estimates $[F_{s}]_{strahl}$ from Equation 2, with the excess flux ${\Delta}F$ computed using strahl observations. The r.m.s. deviation of $[F_{s}]_{IMF}$ and $[F_{s}]_{strahl}$ is ${\Delta}_{rms}$, and the linear correlation is $r$. The best fit is shown in mauve, and the band shown in grey is the $2\sigma$ fit uncertainty: 5% of observations do not overlap with this band, even allowing for the uncertainties in the $[F_{s}]_{strahl}$ estimates.

This equation has a very small intercept of 0.0081 (in units of $10^{14}$ Wb), but the slope of 0.986 is a bit smaller than the ideal value of unity. This is because, as shown in panels e and f, the effect of the averaging is slightly greater at low values than at high values. The very small value of the intercept means that $[F_{s}]_{IMF}$ is essentially proportional to $[F_{s}]_{strahl}$, and we here correct $[F_{s}]_{IMF}$ by multiplying the estimates by $1/0.986 = 1.0142$.

Before the advent of the ACE and Wind spacecraft in 1995, data gaps in the interplanetary record are a serious problem. Figure 3a shows the percentage availability of hourly samples of the radial IMF $B_{r}$, $d_{a}$ in CRs from 1970 to the present. The plot shows that after 1995, most CRs have a full complement of data ($d_{a}$ =100%) but that before 1995, $d_{a}$ is lower and even falls to 10% in one CR.

Figure 3

The effect of data gaps on the CR means of OSF values derived from the modulus of 20-hour averages of the hourly Omni values of $B_{r}$, ${\langle}[F_{s}]_{IMF}{\rangle}_{CR}$ where $[F_{s}]_{IMF} = (2{\pi}R_{AU}^{2}){\times}|{\langle}B_{r}{ \rangle}_{20h}|$ and $B_{r}$ is here (and in all subsequent) considerations the Omni hourly mean data. $R_{AU}$ is one Astronomical Unit. (a) Shows the percentage availability of the hourly samples in the CR intervals, and (b) shows the ${\langle}[F_{s}]_{IMF}{\rangle}_{CR}$ values with error bars in magenta, derived from the number and pattern of missing data in the CR in question (see text and Section A.1 of Appendix for details).

Section A.1 of the Appendix describes how the fractional r.m.s.e. (root mean square error) can be estimated by synthetically removing data from the 328 CRs that have a full complement of hourly means, using a mask that removes the same number of samples, and with the same pattern, as for the CR in question, and then comparing with the known value for the complete CR. For each of the 328 full-data CRs available, this is repeated 10 times (for phases between the mask and the data that are increased by 36^∘ with each repeat) and the mean error computed. It is shown that, because of the averaging over 20 h, errors are particularly large for CR means of $[F_{s}]_{IMF}$, compared to those for other parameters such as the IMF $B$, the solar wind speed $V_{sw}$, and the product $BV_{sw}^{1.76}$ (which has been used in the past to reconstruct annual means of OSF). Figure 3b shows the variation in the CR values of $[F_{s}]_{IMF}$ with uncertainty bars of plus and minus the $2{\sigma}$ error in mauve.

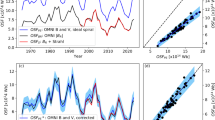
Figure 4 compares the values of $[F_{s}]_{IMF}$ and $[F_{s}]_{strahl}$ for averages over 1, 3, 5, and 13 CRs (i.e. 0.075yr, 0.225yr, 0.373 yr, and 0.971 yr). The 1970 – 2022 time-series in the left-hand panels show the $[F_{s}]_{strahl}$ data as black points with estimated error bars from the work of Frost et al. (2022), and the blue line is $[F_{s}]_{IMF}$ for the optimum ${\tau}$ of 20 h, with light blue error bars giving the uncertainty caused by missing data. The right-hand panels are the corresponding scatter plots for the post-1995 data. The plot demonstrates the reduction in the uncertainties and the increased agreement of the two estimates as the averaging interval in increased.

Figure 4

Comparison of open flux estimates from interplanetary data that allow for the excess flux ${\Delta}F$ using strahl observations (Equation 2), as generated by Frost et al. (2022), and using the optimum $B_{r}$ averaging timescale ${\tau}=20$ h (Equation 3). The rows, from top to bottom, are for averages over 1, 3, 5, and 13 CRs (i.e. 0.075 yr, 0.225 yr, 0.373 yr, and 0.971 yr). The right-hand plots are scatter plots with the strahl-corrected values in the vertical direction and the values using the ${\tau}=20$ h averaging timescale along the horizontal axis. The left-hand plots show the time series, with black points (with black error bars) the strahl-corrected values and the blue line (with blue error bars due to missing data) derived using the averaging timescale $\tau =20$ h.

3 Geomagnetic Data

Range geomagnetic indices were introduced by Bartels, Heck, and Johnston (1939). They are based on the range of variation of the background-subtracted horizontal magnetic field observed at a magnetometer station in 3-hour windows. Range indices from near-antipodal stations in southern England and Australia were used by Mayaud (1972, 1980) to generate the aa index, which could be constructed back to 1868. To obtain continuous sequences, data from three observatory sites were needed in both hemispheres. For the Northern Hemisphere, the sites used were Greenwich (IAGA station code GRW: 1868 – 1925), Abinger (ABN: 1926 – 1956), and Hartland (HAD: 1957 – present), and for the Southern Hemisphere, they were Melbourne (MEL: 1868 – 1918), Toolangi (TOO: 1919 – 1979), and Canberra (CNB: 1980 – present). The Northern and Southern Hemisphere data yield aa_N and aa_S, respectively, and aa is the arithmetic mean of the two. Mayaud intended aa to be used on annual timescales and showed that its annual means correlated exceptionally well with those of the Ap index, which is a range index compiled from 11 – 13 stations (at that time, all in the Northern Hemisphere) calibrated in terms of what would have been seen at Potsdam (see the review by Lockwood et al., 2019b, and references therein). An extension of aa back to 1846 was made by Nevanlinna and Kataja (1993) using the range index data from the Helsinki Observatory.

In constructing aa, Mayaud used the change in the stations to make a crude allowance for the secular change in the geomagnetic field. However, he made no change to the station calibration over the interval of the data from each station, meaning that the old and new stations did not necessarily agree at each of the joins between data series. It has often been assumed that Mayaud “daisy-chained” the data back in time, and so these discontinuities at the joins were thought to reveal errors. This is not the case, there are step-like changes between the stations that account for the secular variation of the intrinsic geomagnetic field. This issue was addressed by Lockwood et al. (2018a) and Lockwood et al. (2018b), who developed the “homogeneous aa index” aa_H from the same data. This index continuously adjusts the calibration of each station using the variation in geomagnetic latitude of the station due to the secular variation in the main field, computed using the International Geomagnetic Reference Field 12 (IGRF 12) main field model (Thébault et al., 2015) and extended back to before 1900 using the gufm1 model (Jackson, Jonkers, and Walker, 2000). This means inter-calibration of the stations at the joins is meaningful and was carried out for separate times of year and times of day rather than just using annual means. An indicator of the success of this is that whereas comparison of aa_N and aa_S showed considerable differences (Lockwood, 2003), comparison of aa_HN and aa_HS reveals only small differences, despite neither being used in the derivation of the other in any way.

The other geomagnetic index used is IDV(1d). This is based on the IDV (Inter-Diurnal Variation) index developed by Svalgaard and Cliver (2005). For a given station, IDV is the day-to-day difference in the hourly means of the observed horizontal field, taken at the hour closest to magnetic local midnight at the station. Because it uses a day-to-day difference, no background subtraction is required making the index both easier to generate and less prone to errors. In fact, the IDV index is based on the “u-index” of Bartels (1932), but where IDV uses the hourly mean closest to local magnetic midnight, the u-index used the mean of data taken over the whole day.

It is interesting to note why Bartels changed from the difference-based inter-diurnal index to the more difficult and complex range-based indices with his paper in 1939 (Bartels, Heck, and Johnston, 1939). The u-index was criticised because it did not clearly show the recurrent variations (every Carrington rotation) that were seen in geomagnetic data, but these were well captured by the range-based indices. As pointed out by Svalgaard and Cliver (2005), we now know that this was because the u-index responded mainly to changes in the near-Earth IMF $B$, whereas the range indices responded to a combination of both $B$ and the solar wind speed $V_{sw}$ (in fact, the product $BV_{sw}^{1.76}$ analysed in Figure 15). The recurrent disturbances are caused by corotating interaction regions (CIRs), where fast solar wind catches up with slow solar wind ahead of it, and their signature in $B$ is smaller than that in $V_{sw}$ and $BV_{sw}^{1.76}$. The IDV(1d) index was developed from the IDV concept by Lockwood et al. (2013), but these authors returned to Bartels’ original concept of using the means for the whole day rather than just the midnight value (the “(1d)” in the name stands for “1 day”). The reason for this was three-fold: (1) the averaging reduced the noise in the data; (2) the midnight values were more influenced by the substorm current wedge, which introduced a greater dependence on $V_{sw}$; and (3) the influence of the current wedge introduced a greater dependence on geomagnetic latitude into IDV. The difference in the responses of the aa_H and IDV(1d) indices is very valuable as it can be used to compute both $B$ and $V_{sw}$ (Svalgaard and Cliver, 2005; Rouillard, Lockwood, and Finch, 2007; Lockwood et al., 2014b); hence errors were reduced using IDV(1d) as it was more different in its optimum solar wind coupling function to the range indices than was IDV.

There was another major difference in the philosophy of construction of the IDV(1d) and IDV indices. The IDV index used all the available data from different stations, averaged together, which means there are many more stations contributing in recent years than contribute early in the data sequence. Although using more stations does reduce noise, the data sequence is not homogeneous, and so the data being compared with modern satellite data are not the same as the data used to reconstruct historic values. In particular, the value of IDV for one station depends critically on its geomagnetic latitude (Lockwood et al., 2013), and using the mean of all available stations introduces a long-term change because the mean latitude of the stations changes as we go back in time because the distribution of available stations changes. Hence in generating the IDV(1d) index, Lockwood et al. (2013) adopted the philosophy of making the modern day data as similar as possible to the historic data, and because there is only one station available at the start of the reconstruction, this means using only one station throughout. As for the aa index, there is no station that has operated throughout, and it was necessary to spline together the data from different stations at similar magnetic latitudes. The IDV(1d) index used the data from the Helsinki (HEL), Niemegk/Potsdam/Seddin (NGK/POT/SED), and Eskdalemuir (ESK) magnetometers, the main contributions being from HEL and ESK because they were at very similar latitudes. All three were normalised to the geomagnetic latitude of ESK in the year 2000 using the observed variation with geomagnetic latitude and the predictions of the geomagnetic latitude of the stations from the IGRF-12 main field model (Thébault et al., 2015), extended back from 1900 to the start of the HEL data using the gufm1 model (Jackson, Jonkers, and Walker, 2000). Data from HEL were used for 1845 – 1890 (inclusive) and 1893 – 1896 and from Eskdalemuir from 1911 to the present. The gaps are filled using latitude-normalised data from the Potsdam (POT, 1891 – 1892 and 1897 – 1907) and nearby Seddin (SED, 1908 – 1910) and Niemegk (NGK, after 1932) observatories and inter-calibration of the HEL and ESK data achieved using the POT/SED/NGK composite series.

Of course, the difficulty of this approach is that it is more subject to errors in the data from one station, errors that can be reduced (but for later data only) by averaging many stations. Martini and Mursula (2006) noted an error in the hourly means of the ESK data, and this was corrected by Macmillan and Clarke (2011). In addition, Svalgaard (2014) correctly noted that, compared to data from the vertical force variometer, the adopted scale value of the horizontal variometer at Helsinki was too low by $~30{\%}$ during the years 1866 – 1874.5, and the adopted scale value of the declination variometer appeared to be too low by a factor of about 2 during the interval 1885.8 – 1887.5. This was confirmed by Lockwood et al. (2014a) using the available data from nearby stations and the alternative variometer for the HEL data, and the required corrections to IDV(1d) were made.

The IDV(1d) composite has been checked against latitude-corrected data from several other stations Lockwood et al. (2014a, 2022a). One particularly useful station is Tucson, which started operation in 1910 and so covers the interval of the ESK data; it shows remarkably good agreement with the ESK data once allowance is made for the latitude difference. In addition, for before 1930, we have the u-index generated by Bartels (1932) from a number of stations, as well as some other short data sequences from other stations.

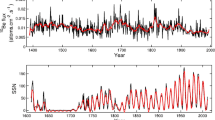
Figure 5 shows 1-CR and 13-CR averages of the aa_H and IDV(1d) geomagnetic data series, which are used here in the reconstruction of OSF. The plot also shows the international sunspot number $R$ in the same format (Clette et al., 2023).

Figure 5

(a) and (b) Show geomagnetic data used in this study, and (c) shows the international sunspot number $R$ for comparison. The grey lines are 1CR means and the mauve lines 13CR means. (a) Shows the homogeneous aa index, aa_H. (b) Shows the IDV(1d) index, which is the difference in daily means on successive days of the horizontal field at the Helsinki and Eskdalemuir stations, splined together using the Niemegk composite data. The derivation of these indices is described in the text. For comparison, (c) gives the sunspot numbers in the same format.

4 The Use of Geomagnetic Data to Compute the OSF

Section 3 has described the two geomagnetic indices used in this paper. This section demonstrates why the combination of the two gives information about the OSF and derives the optimum multivariate fit to the OSF observations.

Figure 6 shows three scatter plots that illustrate why the OSF can be calculated from these geomagnetic activity indices. In each case, the linear correlation coefficient is about 0.8. Panel a shows the correlation between the aa_H index and the product $BV_{sw}^{1.76}$, which was used by Lockwood et al. (2014b) and Lockwood et al. (2022a) in their reconstructions of $B$, $V_{sw}$, and $F_{s}$. Using an automated series of Nelder–Mead simplex searches (Nelder and Mead, 1965; Lagarias et al., 1998), it was found that the optimum linear correlation with $V_{sw}$ is using $[\mathrm{aa}_{\mathrm{H}}-\mathrm{IDV(1d)}]$, as shown in panel b. Hence panel b offers the potential to remove the dependence of aa_H on $V_{sw}$ but then we would need to convert the IMF $B$ derived into $F_{s}$, which could be done using the correlation shown in Figure 6c.

Figure 6

Three scatter plots of Carrington rotation means that demonstrate the relationships that make the OSF reconstruction using the geomagnetic data shown in Figure 5 possible (but which are not actually used in making the reconstructions in this paper). (a) Between the aa_H index and the product $BV_{sw}^{1.76}$, where $B$ is the IMF magnitude, and $V_{sw}$ is the solar wind speed. (b) Between the difference $[aa_{H}-IDV(1d)]$ and $V_{sw}$, and (c) is between $B$ and the OSF derived from $B_{r}$. Black points are for data for 1995 and after, grey (with computed error bars caused by data gaps) for before 1995.

However, implementing each relationship in this three-step procedure leads to a compounding of uncertainties that can be avoided. Instead, we here used a series of automated searches with the Nelder–Mead procedure to maximise the correlation between the prediction ($[F_{s}]_{G}$) and the value from interplanetary observations (we studied using both $[F_{s}]_{strahl}$ and $[F_{s}]_{IMF}$). The significance of each correlation was evaluated allowing for the number of free fit parameters, and the largest correlation and greatest significance was found for the formulation

$$ [F_{s}]_{G} = a + b\cdot \mathrm{aa}_{\mathrm{H}} + c[\mathrm{aa}_{\mathrm{H}}-\mathrm{IDV(1d)}] + d\cdot \mathrm{aa}_{\mathrm{H}} \cdot \mathrm{IDV(1d)}. $$

(5)

Figure 7 shows the results of one implementation of such fitting. This plot uses all $[F_{s}]_{IMF}$ values from the modulus of 20-h means of the radial field for which the fractional error due to data gaps is less than 20%. In the scatter plots on the right, the yellow points are for 1995 and after, whereas the blue points (with error bars) are for before 1995. The predicted linear least-squares fit and its $1{\sigma}$ uncertainties are shown by the mauve line and pink area, respectively. The plots to the left show the corresponding temporal variations of $[F_{s}]_{IMF}$ (in blue) and the best-fit from geomagnetic activity $[F_{s}]_{G}$ (in mauve). Rows, from top to bottom, are for averages over 1 CR, 3 CRs, 5 CRs, and 13 CRs.

Figure 7

The best-fit combination of the aa_H and IDV(1d) geomagnetic indices (using Equation 5, $[F_{s}]_{G}$) and the open flux derived from interplanetary observations of $B_{r}$ using Equation 3 for the optimum averaging interval of ${\tau}=20$ h ($[F_{s}]_{IMF}$). The data are for 1970 – 2022, inclusive. The scatter plots on the right show the values from the geomagnetic indices along the horizontal axis and from the interplanetary data along the vertical axis, with yellow points for data from or after 1995 and blue dots (with error bars due to missing data) for data for before 1995. Only data for which there are sufficient samples to keep the percentage OSF errors below 20% are shown. The mauve lines (with the surrounding $1\sigma$ uncertainty band in pink) are the optimum polynomial fits to these data. The left hand panels show the time series, with the optimum fit from the geomagnetic data in mauve and the interplanetary data in blue (with error bars due to data gaps). The rows, from top to bottom, are for averages over 1, 3, 5, and 13 CRs.

We do not further employ the fits shown in Figure 7 because it is not possible to evaluate the effects of data gaps on the derived fits. Overfitting, where the fit is influenced by noise in the data and loses predictive power as a result, is always a concern. Consequently, we use a simple two-fold procedure with a fitting data set and a separate testing data set. We use the near-continuous $[F_{s}]_{strahl}$ data for 1995 and after for fitting and test against the 1970 – 1995 $[F_{s}]_{IMF}$ data. This has the advantage that the uncertainties due to data gaps apply exclusively to the test data and the associated uncertainties are easier to allow for in the tests than in the fitting.

The results are shown in Figure 8. The fit data are shown in the scatter plots in the left-hand column, and the test data in the right-hand column. Rows, from top to bottom, are for averages over 1 CR, 3 CRs, 5 CRs, and 13 CRs, as before. The orange line is for equality of $[F_{s}]_{G}$ with the in situ data (i.e. for the left column $[F_{s}]_{strahl}$ and for the right column $[F_{s}]_{IMF}$). For the continuous fit data, the only error accounted for is in the $[F_{s}]_{G}$ data, and they are the estimated $1{\sigma}$ fit errors (vertical grey error bars). Note that there will, most likely, be errors in both the IMF OSF estimates arising from propagation uncertainties from the L1 satellite to Earth (both spatial and temporal) (Lockwood, 2022) and spacecraft measurement uncertainties. However, these uncertainties cannot be quantified. For the black points in Figure 8, $[F_{s}]_{G}$ and the in situ data agree to within the predicted $1{\sigma}$ uncertainties. For the red/blue points, $[F_{s}]_{G}$ is, respectively, greater/smaller than the in situ values by more than the predicted uncertainties. If those uncertainties were truly at the $1{\sigma}$ level, then we should expect 16% of points to be blue and 16% to be red. On each plot, the actual percentages are given, and they are, in most cases, considerably smaller than 16%, even considering the unquantified errors that will be present in the in situ values. The percentages are not, in the main, smaller than 2.5%, and so the uncertainty estimates are not at the $2{\sigma}$ level. However, we can say they are very conservative estimates of the $1{\sigma}$ errors. Note that for the test data in Figure 8, only data with estimated percentage error due to missing data of 20% or less are considered; however, including all data made only a small differences to the numbers in Table 2 or to the percentages disagreeing by more than estimated uncertainties given in the figure.

Figure 8

The fits used in the reconstructions. The fit data used are for 1995 – 2022, and scatter plots of the best-fit predicted OSF from geomagnetic activity ($[F_{s}]_{G}$, vertical axis) against the value from interplanetary observations using strahl data ($[F_{s}]_{strahl}$, horizontal axis) are shown in the left-hand column. The right-hand column is for the test $[F_{s}]_{IMF}$ data from 1970 – 1995; only data with estimated percentage error below 20% are shown, but nevertheless some data points have large error bars (in grey) because of limited data availability. For all data points, the vertical error bars are the $1{\sigma}$ fit uncertainties in $[F_{s}]_{G}$. The orange line is equality of the two OSF estimates, and points in red/blue show where $[F_{s}]_{G}$ is larger/smaller than the in situ interplanetary data estimate by the more than the predicted $1{\sigma}$ fit uncertainties. The percentages of data points in these two categories is given in each plot and should be 16% for $1{\sigma}$ uncertainties. That the percentages are lower than this shows that the uncertainties have been somewhat over-estimated. The rows, from top to bottom, are for averages over 1, 3, 5 and 13 CRs.

Table 2 The polynomial coefficients (Equation 5); linear correlation coefficients $r$; the probability of null correlation p; and r.m.s. differences between $[F_{s}]_{G}$ and the corresponding in situ interplanetary value, ${\Delta}_{rms}$. Values of $r$, p, and ${\Delta}_{rms}$ are given for both the fit and the test datasets. Units for the OSF estimates are $10^{14}$ Wb, and aa_H and IDV(1d) are in nT. The columns from left to right are for averages over 1 CR, 3 CRs, 5 CRs, and 13 CRs.

The right-hand plots are for the test data in the same format. For these data, there are often considerable errors in $[F_{s}]_{IMF}$ due to error gaps (horizontal grey bars). The red and blue dots are now for points that do not agree to within the combination of the two uncertainties. If anything, the percentages of red and blue points are lower than for the fit data, and, again, all are smaller than the 16% we would expect for $1{\sigma}$ uncertainties. This confirms that we can regard the uncertainties as conservative $1{\sigma}$ estimates.

Table 2 gives the coefficients in Equation 5 for each of the four CR averaging periods studied. Note that these are somewhat different for the four cases, indicating that the variation timescales influence the relationships between the OSF and the geomagnetic index. There is, however, a very small inconsistency in the reconstructions if we only apply the coefficients in Table 2. That is because, for example, if we take 13-point running means of the 1-CR reconstruction, then we do not get exactly the same variation as generated in the 13-CR reconstruction. The r.m.s. difference is less than 0.5%, but we here correct for it by adopting the 13-CR reconstruction and then multiplying the 1-CR reconstruction by the ratio of the 13-CR reconstruction and the 13-point soothed 1-CR reconstruction. This ensures that we have the near annual variation of the 13-CR variation in the 1-CR reconstruction, but we also maintain the higher frequency variations of the 1-CR reconstruction. Using the same procedure, we then correct the 3-CR and 5-CR reconstructions so that they match the 3- and 5-point running means of the corrected 1-CR variation; these corrections were extremely small (smaller than 0.1%). This procedure ensures that all four reconstructions are consistent. The correlations of $[F_{s}]_{G}$ and $[F_{s}]_{IMF}$ are always massively significant (the $p$-values of the null hypothesis are essentially zero), and correlations are always slightly higher for the fit dataset than the test dataset, which is expected because of the large errors in some of the test $[F_{s}]_{IMF}$ data due to the data gaps. The correlations increase and the r.m.s. deviations decrease with increased averaging interval, as we would expect and as can be seen from the scatter in Figure 8.

5 Reconstructed OSF Data Series

Figure 9 shows the reconstructed time series for the four averaging intervals as mauve lines with the grey lines bounding the uncertainty of plus and minus $1{\sigma}$ (which the tests in Figure 8 show are conservative estimates). The optimum reconstructions are superposed in Figure 10 on the same plot to show the effect of normalising the 13-point running means. A notable feature is that there are individual CRs in which there is a considerably increased OSF (up to a factor 2 larger than the value for surrounding CRs). These all occur around solar maximum and can also be seen as spikes in the IDV(1d) composite data series and are also found as similar spikes in the corresponding data from other stations. These events will be the subject of a later study.

Figure 9

Full time series of predicted OSF values (shown in mauve) with plus and minus estimated $1{\sigma}$ uncertainties shown by the grey area. Panels, from top to bottom, are for averages over 1, 3, 5, and 13 CRs.

Figure 10

(a) The optimum reconstructed OSF time series shown in mauve in Figure 9 is shown on the same plot to aid comparison: orange, mauve, cyan, and black lines are for over 1, 3, 5, and 13 CRs, respectively. (b) The same as (a) for the international sunspot number $R$.

6 Uncertainties Introduced by Errors in the Geomagnetic Data

The uncertainties shown in Figure 9 allow only for the uncertainties due to the polynomial fitting of modern data and do not account for any errors in the geomagnetic data that the reconstructions are based on. As discussed in Section 3, by comparisons with data from other stations, various errors have been detected and expunged. A problem is that there are increasingly fewer available stations to make comparisons with as we go back in time.

However, for both aa_H and IDV(1d), there are data that we can use to check the results. Rather than search for and quantify errors and then try to evaluate the propagation of that error through the procedure, we use a more direct approach: we substitute the alternative data into the reconstruction and analyse what difference it makes.

The aa_H index is the arithmetic mean of the Northern and Southern Hemisphere indices aa_HN and aa_HS. As discussed in Section 3, these are derived using observations and procedures that are completely independent of each other; in other words, aa_HN does not, in any way, influence the derivation of aa_HS, and vice versa. One of the important facets of the aa_H index, as compared to the classic aa index, is that the Northern and Southern Hemisphere indices agree to a considerable degree, despite this independence from each other. This is stressed in Figure 11. Panels a and b show the time series of aa_HN and aa_HS, with 1-CR means in grey and 13-CR means in mauve. The similarity of the two is stressed by the scatter plot of the 1-CR data in panel c.

Figure 11

Analysis of the effect of the geomagnetic data used. This figure analyses the uncertainty that could be caused by errors in the aa_H index. (a) and (b) Show, respectively, the time series of the fully independent Northern and Southern Hemisphere aa_H indices, aa_HN and aa_HS. The grey lines are 1-CR means, and the mauve lines are 13-CR means. (c) Shows a scatter plot of the 1-CR means of aa_HS as a function of the simultaneous means of aa_HN. (d) Shows the 1-CR OSF estimates derived by replacing aa_H with aa_HS (vertical axis) and by aa_HN (horizontal axis) in Equation 5. The grey lines are the estimated OSF fit uncertainties. The aa_H index is the arithmetic mean of aa_HS and aa_HN, and so the scatter in aa_H against aa_HS or aa_HN plots is half that in this plot.

Using aa_HN and aa_HS instead of aa_H in the polynomial Equation 5 generates two fully independent OSF reconstructions that are compared on panel d. The uncertainties are shown as grey error bars. On average, the two reconstructions differ by about a quarter of the estimated uncertainties. Because aa_H is the arithmetic mean of aa_HN and aa_HS, this means that the uncertainties in the aa_H geomagnetic data cause errors in the reconstructed OSF that are roughly an eighth of the estimated polynomial fit uncertainties.

Figure 12 shows a corresponding test of the effect of the uncertainties caused by errors in the IDV(1d) index. In this case, the IDV(1d) composite value is replaced by the value derived by the same procedure but using the inter-diurnal difference of the horizontal field measured by the Tucson magnetometer IDV(1d)_TUC, data that is available continuously from 1910 to the present day. These Tucson data are latitude-corrected, using the procedure described by Lockwood et al. (2013), but were not used in any way to derive the IDV(1d) composite, and so they provide an independent test of IDV(1d). Panel c shows the agreement of 1-CR means of IDV(1d) and IDV(1d)_TUC is not as close as that for the hemispheric aa_H indices shown in Figure 11c, but Figure 12d shows that this has very little effect on the OSF estimate. Only for the very largest OSF values we do see any scatter, and it is again much smaller that the polynomial fit uncertainties. This is because the fitted polynomial gives a much greater dependence on aa_H than IDV(1d).

Figure 12

Analysis of the effect of geomagnetic data employed in the same format as Figure 11. This figure analyses the uncertainty that could be caused by errors in the IDV(1d) index between 1910 and 2023. (a) and (b) Show, respectively, the time series of the fully independent IDV(1d)_TUC data series derived from the Tucson magnetometer and IDV(1d) (the latter from the Helsinki and Eskdalemuir magnetometers, splined together using data from Niemegk). The grey lines are 1-CR means, and the mauve lines are 13-CR means. (c) Shows a scatter plot of IDV(1d)_TUC as a function of IDV(1d)) for the years of data overlap (1910 – 2022). (d) Shows the effect of replacing IDV(1d) with IDV(1d)_TUC in the reconstruction of 1-CR means of OSF.

We do not have a single station that can be used to test the IDV(1d) composite before 1910, but Lockwood et al. (2013) did test this composite against a number of short data series from different, independent stations. However, Bartels (1932) gives monthly means of his u index for 1872 – 1930. This index is the same as IDV(1d) but was compiled from an evolving mix of stations, the weighted average of which was taken in any month. The stations used by Bartels were: Seddin (SED, 1905 – 1928); Potsdam (POT, 1891 – 1904); Greenwich (GRW, 1872 – 1890; Bartels notes errors in the later data and makes corrections but therefore gives them a lower weighting factor); a composite of stations near Bombay including Colaba (CLA, 1872 – 1927); Batavia (BTV, 1884 – 1926; various calibrations were needed to allow for instrument changes); Honolulu (HON, 1902 – 1930); Puerto Rico (SJG, 1902 – 1914); Tucson (TUC, 1917 – 1930); and Watheroo (WAT, 1919 – 1930). Many of these data, along with others from Wilhelmshaven (WLH, 1883 – 1895), St Petersburg (SPE, 1850 – 1862), Parc St Maur (PSM, 1883 – 1901), and Ekaterinburg (EKT, 1887 – 1929) were used by Lockwood and Owens (2013) to test the accuracy of IDV(1d).

Unfortunately, we have only monthly means of Bartels results, rather than Carrington rotation means. We here use linear interpolation of the the monthly values to the mid-points of the CR intervals. This is not ideal because sharp spikes in the u values will be reduced in amplitude unless the centres of the month and the CR intervals happen to coincide. In addition, the IDV(1d) values are scaled to the magnetic latitude of Eskdalemuir in the year 2000, whereas u is compiled from stations at a range of latitudes. To account for this, the interpolated u values are scaled in terms of IDV(1d) by linear regression, giving values we denote as u_c. These are compared to IDV(1d) for the period of overlapping data (1872 – 1930) in Figure 13.

Figure 13

Analysis of the effect of any errors in the early IDV(1d) geomagnetic data used (from the Helsinki magnetometer). The top two plots are the time series over 1872 – 1930 of (a) the scaled u-index data u_c from the monthly records given by Bartels (1932) (see text for details) and (b) for IDV(1d) index, both shown in the same format as Figure 12 (but note that the vertical scale is expanded). In the scatter plot (panel c) and the evaluation of the effect of replacing IDV(1d) with u_c (panel d), the same scales are used as in the corresponding panels in Figure 12.

The results in Figure 13 and very similar to those in Figure 12, other than OSF and geomagnetic activity values, were notably lower before 1930 than after.

7 Comparison with Previous Reconstructions

Lastly, we compare the present 13-CR reconstructions with previous reconstructions of annual means. The results are shown in Figure 14. The black line surrounded by the orange uncertainty band are the 13-CR (0.971 yr) OSF reconstructions presented in this paper. The blue line surrounded by the pale blue uncertainty band is the reconstruction of annual means by Lockwood et al. (2022a) from the same geomagnetic data (LEA22). Where the uncertainty bands for these two reconstructions overlap is shown in green; such overlap is always present. The uncertainties band is generally narrower for the present reconstruction and generally lies in the middle of the band for the previous reconstruction. Only in the first solar cycle of the period of overlap (Cycle 11), there is any consistent difference, but even here the two do still (just) agree to within estimated uncertainties.

Figure 14

Comparison of the 13-CR OSF reconstructions presented in this article (the black line surrounded by the orange uncertainty band) with some previous annual estimates. The blue line surrounded by the pale blue uncertainty band is the reconstruction of annual means by Lockwood et al. (2022a) from geomagnetic data (LEA22). Where the uncertainty bands for these two reconstructions overlap is shown in green. The black and yellow dotted line is the reconstruction by Lockwood, Owens, and Barnard (2014) from geomagnetic data (LEA14). The mauve line is the reconstruction from monthly sunspot number data by Krivova et al. (2021) (KEA21).

Also shown on the plot are the reconstructions by Lockwood, Owens, and Barnard (2014) from geomagnetic data (LEA14) and by Krivova et al. (2021) (KEA21). The LEA14 reconstruction does use the same pairing of aa_H and IDV(1d) as used here, but that is only one of four index pairings used, the results of which are averaged together. The KEA21 reconstruction is different; it is based on modelling and the monthly sunspot number $R$. There are some differences between these reconstructions, notably during Cycle 20. This is not a surprise as the modelled association between sunspot number and OSF has been unable to reproduce the observed OSF variation, indicating that another factor was important in this cycle, presumably because of the large and sudden decline in sunspot activity between Cycles 19 and 20. It is likely that resolving this difference in Cycle 20 would also improve the small disagreements found at other times. Nevertheless, the overall agreement is very good.

8 Conclusions

This article has presented Carrington rotation (CR) averages of open solar flux (OSF), derived from two geomagnetic activity indices for 1878 to the present day. The data are available for 1-CR, 3-CR, 5-CR, and 13-CR means (0.07 yr, 0.224 yr, 0.373 yr, and 0.971 yr, respectively) in the supplementary information file attached to this article. These values are all given with (conservative) $1{\sigma}$ uncertainty estimates. The OSF values are generated by polynomial fits of the geomagnetic indices to values from interplanetary satellite observations. These OSF data are generated in two ways. The fit data used are for 1995 – 2022 and use observations of strahl electrons to determine connectivity to the solar corona and thereby allow for the excess flux caused by orthogardenhose flux and switchbacks. It is shown that these data are closely matched by interplanetary observations that use the averaging interval ${\tau}$ to allow for excess flux. These are available for 1970 – 2022 and are used as tests of the polynomial fitting. However, before 1995, data gaps are a serious problem for some of the Carrington rotations, and the errors they cause have been quantified by synthetic removal of data from CRs with a full complement of observations.

We have tested for errors caused by inaccuracies in the geomagnetic data by substituting independent data into the polynomials and evaluating how much difference to the OSF estimates this causes. These errors are considerably smaller than the polynomial fitting uncertainties.

The OSF reconstructions on different averaging timescales have been normalised to make them consistent in their smoothed variations with the 13-CR means. The uncertainty band around the 13-CR means is narrower than that around previous annual reconstructions, and the former lies within the latter for almost all CRs. There is considerable variability from one CR to the next in the 1-CR reconstructions, and some CRs near solar maximum can show factor of 2 increases in OSF. These CRs are marked by particularly high values of the IDV(1d) index, which is seen in corresponding records from a great many magnetometer stations. These CRs may, for example, indicate bursts of high CME activity which raises questions about how isotopic or coincidentally Earth-directed such bursts may be. They will be the subject of further studies.

Appendix

1.1 A.1 Errors in CR Means Due to Data Gaps

The fractional errors due to missing interplanetary data were evaluated by using the number and pattern of data gaps in a given CR to make a mask, which was then used to remove data from the 328 CRs available that have valid means for all hours (i.e. $d_{a}$ = 100%). The resulting synthetic CR means were then compared to the known true value for the full-data CR and the fractional error caused by the data gaps evaluated for each of the full-data CRs. To increase numbers of fractional error samples, each full-data CR was masked 10 times using 10 different phasings of the CR mask, $36^{\circ}$ apart, relative to the data in the full-data CR. This gives 3280 estimates of the fractional uncertainty for a given CR, of which we take the root mean square (r.m.s.) value.

Figure 15 shows the results of the percentage error ${\xi}$ as a function of the percentage data availability $d_{a}$ in the CR. The panels are for the IMF $B$, the solar wind speed $V_{sw}$, the product $BV_{sw}^{1.76}$, and the open solar flux derived from the radial field using Equation 3, $[F_{s}]_{IMF}$ with the optimum averaging interval of ${\tau}$ of 20 h.

Figure 15

Percentage uncertainties in 1-CR data ${\xi}$ derived by masked removal of data from CRs with full data availability ($d_{a}=1$). (a) IMF field strength ${\langle}B{\rangle}_{CR}$, (b) the solar wind speed ${\langle}V_{sw}{\rangle}_{CR}$, (c) ${\langle}BV_{sw}^{1.76}{\rangle}_{CR}$, and (d) the OSF from IMF data ${\langle}[F_{s}]_{IMF}{\rangle}_{CR}$.

The full-data CRs ($d_{a}$ = 100%) obviously give ${\xi}=0$, and the errors ${\xi}$ increase with decreasing $d_{a}$. However, there is scatter because the pattern of the data gaps for a given $d_{a}$ has an effect.

Figure 15 demonstrates that the errors are smallest for a given $d_{a}$ for $V_{sw}$, as expected because of its greater persistence (Lockwood et al., 2019a; Lockwood, 2022). The errors for $B$ are larger, and for $BV_{sw}^{1.76}$, they are larger still. For any parameter, the variation of ${\xi}$ with decreasing $d_{a}$ will be hyperbolic, tending to infinity as $d_{a}$ approaches zero. Nevertheless, for the parameters shown in panels a, b, and c of Figure 15, the variation is approximately linear for $d_{a} {\geq}$ 25%. Hence, order-of-magnitude percentage errors in CR means can by estimated from $d_{a}$ ($d_{a} { \geq}$ 25%) using the equation

$$ {\xi} {\approx} s (100-d_{a}), $$

(6)

where ${\xi}$ and $d_{a}$ are in percent, and $s$ = 0.144 for $B$, $s$ = 0.089 for $V_{sw}$, and $s$ = 0.242 for $BV_{sw}^{1.76}$.

Panel d of Figure 15 shows that the error in $[F_{s}]_{IMF}$ is only quasi-linear with $d_{a}$ for $d_{a} {\geq}$ 50% and that $s$ is relatively large (0.440) even for that range of $d_{a}$.

In this paper, Equation 6 is not used because the value for the CR in question is always used. Nevertheless, this equation does provide a rapid away of computing an estimate of the error caused by missing data.

Panel d of Figure 15 is used in the present article to set a limit to the allowed errors in the OSF estimates. We only use data for which ${\xi} {\leq} 20{\%}$, which generally requires $d_{a}$ exceeding 50%.

1.2 A.2 Effect of Averaging Timescale on OSF Estimates from IMF Data

Figure 16 shows the effect of the averaging timescale ${\tau}$ (before the absolute value is taken) on the $[F_{s}]_{IMF}$ estimate from Equation 3. In each panel, the vertical grey band marks where the difference between $[F_{s}]_{IMF}$ and $[F_{s}]_{strahl}$ is not significantly different from the value for ${\tau}$ = 20 h at the $2{\sigma}$ level, computed using Welch’s t-test (Welch, 1947). Panel a shows that the correlation $r$ of $[F_{s}]_{IMF}$ with $[F_{s}]_{strahl}$ peaks at ${\tau}$ = 20 h, but it is a flat peak, and so values around 20 h do not give a significantly lower correlation. However, panel b shows it gives a better-defined minimum in the r.m.s. difference ${\Delta}_{rms}$ between the two. Panel c shows the slope $s$ of linear regressions of $[F_{s}]_{IMF}$ against $[F_{s}]_{strahl}$. It can be seen that ${\tau}$ = 20 h gives an $s$ of 0.986, slightly lower than the ideal value of unity, a value that is only achieved at ${\tau}$ = 38 h, for which $r$ is significantly lower and ${\Delta}_{rms}$ is significantly higher. However, the intercept of the regression $c$ is very close indeed to the ideal value of zero at ${\tau}$ = 20 h. Thus $[F_{s}]_{IMF}$ is proportional to $[F_{s}]_{strahl}$, and so $[F_{s}]_{IMF}$ for ${\tau}$ = 20 h can be corrected for the slightly low $s$ by multiplying by $1/0.968 = 1.014$.

Figure 16

The effect of averaging timescale ${\tau}$ on the $[F_{s}]_{IMF}$ estimate from Equation 3. (a) The correlation coefficient $r$ of CR means of $[F_{s}]_{IMF}$ and $[F_{s}]_{strahl}$ generated by Frost et al. (2022); (b) The r.m.s. deviation of CR means of $[F_{s}]_{IMF}$ from those of $[F_{s}]_{strahl}$, ${\Delta}_{rms}$; (c) and (d) the slope and intercept of the best linear fit of CR means of $[F_{s}]_{IMF}$ against $[F_{s}]_{strahl}$, $s$ and $c$, respectively. In all four panels the vertical grey band marks where the difference between $[F_{s}]_{IMF}$ and $[F_{s}]_{strahl}$ is not significantly different from the value for ${\tau}$ = 20 h at the $2{\sigma}$ level from Welch’s t-test.

1.3 A.3 Solar Rotation Periods Detected at 1AU in Interplanetary and Geomagnetic Data

The period of heliospheric rotation at $r = R_{AU}$ can be measured from the peak near 27 days in the autocorrelation functions (a.c.f.s) of interplanetary or geomagnetic parameters. Figure 17c shows that the peak of the a.c.f. of the radial IMF $B_{r}$ is at just 2.6 hours shorter than the nominal CR rotation interval. Given that $B_{r}$ is dominated by (and changes polarity with) the interplanetary sector structure, this gives a good estimate of how the low-latitude heliospheric sector structure rotates on average. The solar wind speed a.c.f. shown in Figure 17b peaks within 1 h of this estimate, indicating that the streamer belt and coronal holes that give fast and slow solar wind, respectively, also rotate with essentially the CR period on average.

Figure 17

Auto-correlation functions of (a) the aa_H index, (b) the solar wind speed $V_{sw}$, and (c) the radial IMF component $B_{r}$. The vertical black dashed lines are the Carrington rotation interval of 27.2753 days. The vertical dashed mauve lines mark the peaks of the a.c.f.s: for the aa_H index, the optimum recurrence interval is ${\delta}t$ = 6.6 h shorter than the CR duration; for $V_{sw}$, ${\delta}t$ is 3.6 h, and for $B_{r}$, ${\delta}t$ is 2.6 h. Note that for $B_{r}$, the a.c.f. turns negative because sectors have opposite polarity of $B_{r}$.

Panel a of Figure 17 shows the a.c.f. of the aa_H index. This a.c.f. reveals an additional diurnal variation, which, obviously, is not seen in interplanetary space. This could have arisen from a local time response of the stations, but that possibility is eliminated by the fact that the diurnal variations in the Northern and Southern Hemisphere sub-indices, aa_HN and aa_HS, are in phase, despite the stations being close to 180^∘ apart in longitude. Instead, this demonstrates the Universal Time variation in solar wind-magnetosphere coupling discussed by Lockwood, Owens, and Barnard (2023), Lockwood and Milan (2023), and Lockwood (2023). This diurnal variation contribution to the a.c.f. for aa_H peaks at whole numbers of days and so shifts the peak of the overall a.c.f.s for geomagnetic indices to the nearest whole number of days to the CR peak, which is 27 days. Hence the diurnal variation in solar wind-magnetosphere coupling (caused by the eccentric nature of the Earth’s main dipole field) is the reason why geomagnetic phenomena are organised by Bartels intervals of exactly 27 days, whereas the driving coronal and heliospheric phenomena are organised by the Carrington rotation intervals of 27.2753 days.