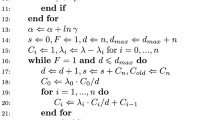1 Introduction

Regime-switching diffusion processes have wide-ranging applications in a variety of fields. One important area is financial economics in which a long legacy of contributions exists that study option pricing and other tasks in financial engineering for assets whose market price follows Brownian motion with two regimes (Naik 1993; di Masi et al. 1995; Guo 2001; Liu et al. 2006; Godin et al. 2019; Ramponi 2011; Zhou et al. 2021, among others). Other applications include diffusive media in material science (Aifantis and Hill 1980; Aggarwala and Nasim 1987; Polyanin 2008; Tsambali 2018) and movements of animals in biology (Yan et al. 2014; Pozdnyakov et al. 2019, 2020). Two monographs (Mao and Yuan 2006; Yin and Zhu 2010) provide summaries of extant knowledge on the existence of solutions, asymptotic properties and numerical approximation of switching diffusions. These monographs do, however, not cover the problem of parameter estimation for regime-switching diffusions. Overall, the literature on statistical inference for these processes seems to be extremely sparse and still in its infancy.

To the best of my knowledge, the following should be a nearly complete list of contributions that exist to date on parameter estimation of regime-switching diffusions. These contributions are almost exclusively confined to processes with two states only and they draw on theoretical results for the so-called telegraph process (Stadje and Zacks 2004; Pogorui et al. 2021). The telegraph process describes the trajectory of a particle on the real line whose direction changes at random times according to a Poisson arrival process. Known results on the occupation times of the two (positive and negative) regimes can be used to obtain analytical results for regime-switching diffusions with two states. While some earlier papers develop estimators for the parameters of the telegraph process itself (Yao 1985; Iacus and Yoshida 2009), the first attempt at estimating a two-state switching diffusion appears to be Yan et al. (2014). However, these authors consider the extreme case only in which the variance of one of the regimes is zero, and develop a composite likelihood approach for this case. Khasminskii and Kutoyants (2018) propose a one-step maximum likelihood estimator based on a moment estimator as starting point. Pozdnyakov et al. (2020) take advantage of the observation that regime-switching diffusions fall into the broad class of hidden Markov models, and that their conditional state probabilities in the two-state case can be derived from the well-known analytical results on the telegraph process, which allows them to formulate a full maximum likelihood estimator for the two-state case based on the analytical results for the telegraph process. Pozdnyakov et al. (2020) generalize their moving–resting model for animal motions by an intermediate state. With restrictive assumptions on the intensity matrix of the hidden three-state transition matrix, the telegraph solutions can be generalized for this special case and maximum likelihood estimation becomes again feasible. Another example of an analytical solution for a three-state regime-switching diffusion can be found in Fuh et al. (2012) in the context of option pricing (without estimation).

Higher-order switching diffusions of a very specific form are considered in Lux (2022). He compares different algorithms for sequential Monte Carlo estimation of so-called multifractal models in continuous time. The particular feature of these models is a hierarchical structure of the intensity matrix that is predefined and only leaves few parameters to be estimated. This design allows consideration of up to \(2^{15}\) regimes with only one parameter governing the hierarchical structure of the transition rates, and a second parameter governing the similarly hierarchical structure of the variances of the different regimes. This parsimonious structure even allows conducting Monte Carlo simulations to assess the quality of the estimators despite the fact that each estimation already is based upon a large number of particles itself in the sequential Monte Carlo scheme.

Our contribution in this paper will be the proposal of a generally applicable algorithm for maximum likelihood estimation of regime-switching diffusions beyond the case of only two states. The proposed approach is relatively straight forward although it seems not to have been proposed before in extant literature: The conditional state densities of any regime-switching diffusion are given by a system of linear partial differential equations, with their numbers being equal to the number of states (the so-called forward Kolmogorov or Fokker–Planck equations). A system of partial differential equations can, of course, be solved in closed-form only in rare cases (the two-state regime-switching diffusion being one example). One way to obtain a handle on partial differential equations that often proves useful is to perform a Fourier or Laplace transformation of the system (this actually provides one avenue to obtain the analytical solution in the two-state case). Because of the linear structure of the system of partial differential equations in the case of switching diffusions, a Fourier transformation will lead to a system of ordinary, linear differential equations. Solving these and transforming back to the original space domain, we obtain the summands of the log of the maximum likelihood function in its factorized form. Applicability of this approach is only constrained by the computational demands of solving the system of ordinary differential equations resulting from the Fourier transformation (i.e., computing its eigenvalues and eigenvectors) and the inverse Fourier transformation afterwards. This analytical approach provides an alternative to the emerging literature on stochastic approximations for the likelihood function of switching diffusions (Lux 2022, using sequential Monte Carlo, and Hibbah et al. 2020 and Blackwell et al. 2016, using Markov Chain Monte Carlo) that can be used in ‘plug-and-play’ form and for moderate numbers of states can be implemented with very modest computational costs.

The rest of this paper proceeds as follows: Sect. 2 presents the numerical algorithm, illustrated for the case of the two-state regime switching diffusion. Section 3 compares its performance with that of the well-known analytical solution in this case. Section 4 moves on to higher-order switching diffusions demonstrating the feasibility and efficiency of the algorithm for a selection of interesting models. Section 5 provides an empirical application to the three-state ‘moving–handling–resting’ model of animal motion with seven parameters. Section 6 concludes. Two appendices provide additional technical material: Appendix A sketches the analytical derivation of the solution for the two-state case using purely probabilistic arguments. Appendix B shows, how the present estimation algorithm can be adapted for bivariate switching diffusions (or multivariate switching diffusions in general).

2 The algorithm: illustration with two-state case

To illustrate the proposed approach and its efficiency, we first consider the case of a two-state switching diffusion. We define by \(s_t\), \(t \ge 0\), a continuous time Markov chain with two states \(\{0,1\}\), with transition rates \(\lambda _1\) and \(\lambda _2\) between states and by \(W_t\) a standard Brownian motion independent of \(s_t\). Assuming that the diffusion rate of \(W_t\) is governed by the Markov chain \(s_t\), the compound process is usually denoted a regime-switching or hybrid diffusion, and can also be interpreted as an instance of a hidden Markov model.

The so defined regime-switching process can then simply be described by a diffusion with two states \(s = 0\) and \(s=1\) with different variances \(\sigma _0^2\) and \(\sigma _1^2\): The state variable \(x_t\) of this diffusion will obey:

$$\begin{aligned} d x_t = \sigma _{s_t} d W_t \end{aligned}$$
(1)

with the hidden state process \(s_t\) being characterised by the intensity matrix:

$$\begin{aligned} {\varvec{Q}} = \begin{pmatrix} - \lambda _1 &{} \quad \lambda _1 \\ \lambda _2 &{} \quad - \lambda _2 \\ \end{pmatrix}_{\textstyle .} \end{aligned}$$
(2)

The two state process defined in this way also constitutes the main building block of the continuous-time multifractal model which we will consider below as an example for switching diffusions with a high number of states. In typical applications, \(x_t\) might be an asset price, the location of an animal, or the concentration of some liquid.

For elementary diffusion processes, the Feynman–Kac formula establishes a link between such stochastic processes and certain partial differential equations which can be used to derive the law of motion of the transient density of the process in the form of a forward Kolmogorov or Fokker–Planck equation. For Markov-switching diffusions, this connection is formally established by Baran et al. (2013).

Denoting the state-specific joint densities of \(x_t\) and \(s_t\) by \(u(x, t) = f(x, s=0; t)\) and \(w(x,t) = f(x, s=1;t)\), application of the Feynman–Kac formula to switching diffusions leads to the following system of partial differential equations:

$$\begin{aligned} \frac{\partial u}{\partial t}=&{} \frac{1}{2} \sigma _0^2 \frac{\partial ^2 u}{\partial x^2} - \lambda _1 u + \lambda _2 w,\nonumber \\ \frac{\partial w}{\partial t}=&{} \frac{1}{2} \sigma _1^2 \frac{\partial ^2 w}{\partial x^2} + \lambda _1 u - \lambda _2 w. \end{aligned}$$
(3)

Note that this system of Fokker–Planck- or forward Kolmogorov equations already appears in many of the references quoted in Sect. 1 where they have been derived in various more or less rigorous or heuristic ways. We now perform a Fourier transformation for the system (3) in the ‘space’ dimension:

$$\begin{aligned} \tilde{u} (\xi , t)= & {} \int _{- \infty }^{\infty } u(x, t) e^{- i \xi x } dx, \nonumber \\ \tilde{w} (\xi , t)= & {} \int _{- \infty }^{\infty } w(x, t) e^{- i \xi x} dx. \end{aligned}$$
(4)

One of the well-known properties of the Fourier transformation is that derivatives of the original function become powers of \(i \xi \) in the transformed equation. Hence, we arrive at the following system

$$\begin{aligned} \frac{\partial \tilde{u}}{\partial t}=&{} - \frac{\sigma _0^2}{2} \xi ^2 \tilde{u} - \lambda _1 \tilde{u} + \lambda _2 \tilde{w}, \nonumber \\ \frac{\partial \tilde{w}}{\partial t}=&{} - \frac{\sigma _1^2}{2} \xi ^2 \tilde{w} + \lambda _1 \tilde{u} - \lambda _2 \tilde{w}. \end{aligned}$$
(5)

For every frequency \(\xi \), system (5) can be easily solved admitting a representation:

$$\begin{aligned} \tilde{u}(\xi , t)= & {} A_1(\xi ) e^{\varLambda _1(\xi ) t} + A_2 (\xi )e^{\varLambda _2 (\xi )t},\nonumber \\ \tilde{w}(\xi , t)= & {} A_1(\xi ) \nu _1(\xi ) e^{\varLambda _1(\xi ) t} + A_2 (\xi ) \nu _2(\xi ) e^{\varLambda _2 (\xi )t} \end{aligned}$$
(6)

where \(\varLambda _1 (\xi )\) and \(\varLambda _2 (\xi )\) are the eigenvalues of the system, \(\nu _1 (\xi )\) and \(\nu _2 (\xi )\) are the second elements of the pertinent eigenvectors (their first elements having been normalized to unity) and \(A_1(\xi )\) and \(A_2(\xi )\) are the constants of integration which need two boundary conditions to be identified.

In principle, with \(\tilde{u}(\xi , t)\) and \(\tilde{w}(\xi , t)\) being solved for all values of \(\xi \), we can use the inverse Fourier transformation to arrive back at:

$$\begin{aligned} u(x,t)= & {} \frac{1}{2 \pi } \int _{- \infty }^{\infty }\tilde{u} (\xi , t) e^{i \xi x} d\xi , \nonumber \\ w(x,t)= & {} \frac{1}{2 \pi } \int _{- \infty }^{\infty }\tilde{w} (\xi , t) e^{i \xi x} d\xi . \end{aligned}$$
(7)

Solving Eq. (7) for all frequencies is, of course, impossible, so that it will be approximated by the inverse discrete Fourier transform:

$$\begin{aligned} f(x,t) = \frac{W}{2 \pi N} \sum _{n = - \frac{N}{2}+1}^{\frac{N}{2}+1} \tilde{f}\left( n \frac{W}{N}, t \right) e^{ix n \frac{W}{N}}, \end{aligned}$$
(8)

for both u(x, t) and w(x, t). Because of the symmetry of these functions in \(\xi \), and the periodicity of Eq. (8) we set \(W = 4 \pi \) and can actually restrict the numerical evaluation to the cosine terms in the Fourier series for \(n \in [0, \frac{N}{2}+1]\).

How is this solution entering the estimation algorithm? Note that we can interpret our variables \(x_t\) and \(s_t\) as the observed and hidden state of a Hidden Markov Model (HMM). It is well known that \(x_t\) is not Markov, but the joint process \((x_t,s_t)\) obeys the Markov property. One can, then, use the forward algorithm from the HMM literature that had already been applied in a similar context by Pozdnyakov et al. (2019). With a sample of equidistantly measured (in time) observations \(\{x_t\}\) \(t=1, \ldots ,T\), we define the so-called forward variables as:

$$\begin{aligned} \alpha (y_{t+1}, s_{t+1}, \theta ) = \sum _{s_t} f(y_{t+1}, s_{t+1} | s_t, \theta ) \alpha (y_t,s_t,\theta ) \end{aligned}$$
(9)

with \(y_{t+1} = x_{t+1} - x_t\) the increments of the observed variable and \(\theta \) the vector of parameters we wish to estimate.

Normalized forward variables are defined as:

$$\begin{aligned} {\hat{\alpha }}(y_t,s_t,\theta ) = \frac{\alpha (y_t,s_t,\theta )}{L(y_t,\theta )} \end{aligned}$$
(10)

with \(L(y_t,\theta ) = \sum _{s_t}\alpha (y_t,s_t,\theta )\).

If at time \(t=1\), no prior information is available, the updating would start with the ergodic probabilities of the hidden states, say \(P_0(s_0)\), and \(\alpha (y_1,s_1,\theta )\) would be formed as:

$$\begin{aligned} \alpha (y_1,s_1,\theta ) = \sum _{s_0} f(y_{1}, s_{1} | s_0, \theta ) P_0(s_0) \end{aligned}$$
(11)

Since the ergodic probabilities sum up to one, \(L(y_0,\theta )=L_0(\theta )=1\) so that \(\hat{\alpha }(y_1,s_1,\theta )=\alpha (y_1,s_1,\theta )\) holds.

Subsequent forward variables are determined following the recursion:

$$\begin{aligned}{} & {} {\hat{\alpha }}(y_{t+1},s_{t+1},\theta )\nonumber \\{} & {} \quad = \frac{L(y_t,\theta )}{L(y_{t+1},\theta )} \sum _{s_t} f(y_{t+1},s_{t+1} | s_t,\theta ) {\hat{\alpha }}(y_t,s_t,\theta ) \nonumber \\{} & {} \quad = \frac{\sum _{s_t} f(y_{t+1},s_{t+1} | s_t,\theta ) \hat{\alpha }(y_t,s_t,\theta )}{\sum _{s_{t+1}} \sum _{s_t} f(y_{t+1},s_{t+1} | s_t,\theta ) {\hat{\alpha }}(y_t,s_t,\theta )} \end{aligned}$$
(12)

Hence, we obtain a sequence of evaluations of the densities \(f(y_{t+1},s_{t+1}|s_t,\theta )\) which are subsequently standardized to be used as conditional probabilities for observing state \((y_{t+1},s_{t+1})\). The denominator of Eq. (12), i.e.

$$\begin{aligned} l (y_{t+1}, |y_t, \theta )= & {} \frac{L(y_{t+1},\theta )}{L(y_t,\theta )}\nonumber \\= & {} \sum _{s_{t+1}}\sum _{s_t} f(y_{t+1},s_{t+1}|s_t,\theta ) \hat{\alpha }(y_t,s_t,\theta )\nonumber \\ \end{aligned}$$
(13)

actually provides us with the density of \(y_{t+1}\) conditional on \(y_t\) which we need to evaluate the likelihood function in its factorized form. Pozdnyakov et al. (2019) derive the transition densities from the well-known results on the telegraph process while here the system of partial differential Eq. (3) and its Fourier transform is used for the same purpose. The advantage of the latter approach is that it can be generalized easily along various dimensions, i.e. for any number of states as well as for multivariate switching processes.

With equidistant observations, the time step can be normalized to unity, so that (7) would have to be evaluated at each iteration at the values \(u(y_t, 1)\) and \(w(y_t, 1)\). Note that the observation \(y_t\) enters as a constant only in Eq. (7) or its discrete implementation (namely, in place of x).

Lastly, the constants of integration of Eq. (6) are obtained from the initial values of the densities at \(t=0\), i.e. u(x, 0) and w(x, 0) which would be obtained from the iteration of the forward variables, i.e. Eq. (12) which are used as the initial values for the next iteration.

It is interesting to note that the eigenvalues of system (5) as well as all eigenvalues of any such system obtained from a switching diffusion with an arbitrary number of states are necessarily negative. This follows immediately from its property of a dominant negative diagonal (i.e. that the elements on the main diagonal are all negative and larger in absolute values than the sum of the other entries in the same row or column). Note also that the eigenvalues become the ‘more negative’, the higher \(\xi \) which guarantees convergence of the inverse Fourier transform. This is simply a consequence of the fact that the Fourier transform of the Gaussian also is an exponential function, and that the density of regime-switching diffusions is a mixture of Gaussians. This guarantees spectral convergence, i.e., exponential decay of the coefficients of the spectral frequencies and pointwise convergence of the discrete inverse Fourier transformation of the densities u(x, t) and w(x, t) (cf. for example Epstein 2005).

As with time, we also normalize ‘space’ in the factorized sequence of conditional densities by taking differences \(y_t = x_t - x_{t-1}\) which leads to \(u_0 = u(0,0)= {\hat{\alpha }}(y_{t-1},s_t = 0, \theta )\) and \(w_0 = w(0,0)= {\hat{\alpha }}(y_{t-1},s_t = 1, \theta )\) as initial conditions. The Fourier transform of these initial conditions is that of a Dirac delta function, e.g.,

$$\begin{aligned} \tilde{u}(\xi , 0) = \int _{- \infty }^{\infty } \delta (x)u(x,0)e^{-i \xi x} dx= u(x,0) \text { at } x=0\nonumber \\ \end{aligned}$$
(14)

and the same for \(\tilde{w}(\xi , 0)\). Hence, we obtain the constants of integration \(A_1\) and \(A_2\) in Eq. (6) as

$$\begin{aligned} A_1 = \frac{\nu _2 u_0 - w_0}{\nu _2 -\nu _1}, A_2 =\frac{w_0- \nu _1 u_0}{\nu _2 -\nu _1}. \end{aligned}$$

To summarize, the above algorithm obtains numerical solutions of the joint densities of \((x_t, s_t)\) or equivalently \((y_t, s_t)\) that are needed to implement the standard factorized likelihood function for state-space models within the framework of a regime-switching diffusion process. These conditional densities are obtained by solving the resulting system of ordinary differential equations obtained from the Fourier transformation of the ‘space’ variable and using the inverse Fourier transform to express this result again as a joint density of \((y_{t+1}, s_{t+1})\). It should be obvious that what has been presented for the sake of simplicity in a setting with two states only, can be generalized to any number of states without any conceptual changes to the algorithm. The scope of applicability would only be constrained by the increasing computational demands of multiple Fourier and inverse Fourier transforms, and the computation of eigenvalues and eigenvectors in higher-dimensional state spaces. One could alternatively also apply a Laplace transformation of the time dimension of Eq. (5). This would result in a linear system of equations for the state densities which would be even more straightforward to solve than the system of differential equations obtained from the Fourier transformation, but would then require a sequence of inverse Laplace and Fourier transformations to get back to the original space and time coordinates. It remains to be explored whether this alternative is computationally more efficient or not. Another variation would be to use symbolic computation for the solutions of Eq. (6) rather than evaluating this system numerically for each frequency \(\xi \).

3 Comparison of algorithms for two-state switching diffusion

While the numerical solution via Fourier and inverse Fourier transformations is universally applicable, a closed-form solution to the conditional density of regime-switching diffusion processes exists only in the simplest case of two states. This solution has also been obtained by a sequence of Fourier and Laplace transforms. It yields after some manipulations functions that upon application of the inverse transforms lead to the well-known form based on two modified Bessel functions. Slightly different versions of this derivation can be found in Pedler (1971), Aifantis and Hill (1980) and Aggarwala and Nasim (1987). It is, however, also possible to derive this solution on the base of purely probabilistic arguments without having to perform any transformation of the state variables. This proof is sketched in the Appendix. This alternative derivation provides intuition to the somewhat abstract representation of the transient densities by Bessel functions and elucidates that these transient densities indeed represent all possible trajectories between two time points.

To simplify, we assume that the transition rate \(\lambda = \lambda _1 = \lambda _2\) is the same between both states, denoted state 0 and state 1. Furthermore, the variances of both states are defined as \(m_0\) and \(m_1 = 2 - m_0\) so that the vector of parameters to be estimated consists of \(\theta = \{\lambda , m_0\}\). These restrictions can be relaxed without any conceptual efforts, but they allow us to conduct Monte Carlo experiments below for an estimation problem with two parameters only before moving to more complex settings.

Using the notation of the previous section, the analytical solution to the transient densities u(x, t) and w(x, t) with these assumptions reads:

$$\begin{aligned} u(x,t)= & {} u_0 e^{-\lambda t} h(x,m_0 t) + e^{-\lambda t} \int _{0}^{t}(u_0\left( \frac{\tau }{t-\tau } \right) ^{1/2}\nonumber \\{} & {} \lambda I_1(\eta ) + w_0 \lambda I_0 (\eta )) h(x,v(\tau ))d\tau , \nonumber \\ w(x,t)= & {} w_0 e^{-\lambda t} h(x,(2-m_0) t) + e^{-\lambda t} \int _{0}^{t}(u_0\lambda I_0(\eta ) \nonumber \\{} & {} + w_0 \lambda \left( \frac{t- \tau }{\tau } \right) ^{1/2} I_1(\eta )) h(x,v(\tau ))d\tau \end{aligned}$$
(15)

with \(\eta = 2\lambda (\tau (t-\tau ))^{1/2}\), \(h(x, v(\tau ))\) the density of the Normal distribution with mean zero and variance \(v(\tau )\) at x, \(v(\tau ) = m_0 \tau + (2-m_0)(t-\tau )\), and \(I_{n}(z)\) the modified Bessel functions:

$$\begin{aligned} I_n (z) = \sum _{k=0}^{\infty } \frac{1}{k! \varGamma (k+n+1)}\left( \frac{z}{2} \right) ^{2k+n}. \end{aligned}$$
(16)

In Eq. (15) the right-hand side is obtained as the product of the two densities of the regime-switching process times their respective expected occupation times within the interval [0, t]. The first entries are discrete ‘atoms’ of the distribution of the occupation times at t (i.e. no changes of the regime occur within the interval). The integrals of the Bessel functions identify expected occupation times for any number of regime switches from 1 to infinity and are multiplied by the resulting ‘averages’ of the Normal densities. It is curious how often Eq. (15) seems to have been rediscovered in the literature: While the first version appeared apparently in Pedler (1971), in the material sciences it has first been derived by Aifantis and Hill (1980) by which a long legacy of subsequent literature and applications has been set off. In finance, the first application of Eq. (15) for option pricing is Naik (1993). In 2001, Guo seemed to have rediscovered these results independently as he neither has any references to Pedler , Naik nor to Aifantis and Hill . Much of the subsequent literature in finance indeed then quotes Guo (2001) as the seemingly first contribution in this vein. Even more recently, Ratanov (2007) and Kolesnik and Ratanov (2013) have again, apparently independently, made the transition from the telegraph process (with its known solutions for occupation times of the two states) to the application of this result in option pricing.

Equations (15) can be used to compute directly the conditional densities of the two-state regime-switching process and to implement the iterative version of the likelihood function. The time 0 densities \(u_0\) and \(w_0\) are then set equal to the normalized joint densities of \((y_{t-1}, s_{t-1})\), i.e. \(u_0 (x=0,0) = {\hat{\alpha }} (y_{t-1}, s_t = 0,\theta )\), and \(w_0 (x=0,0) = {\hat{\alpha }} (y_{t-1}, s_{t}=1,\theta )\).

Table 1 Monte Carlo results for two-state switching diffusion
Full size table

Table 1 compares the performance of maximum likelihood estimation based on the telegraph solution of Eq. (15) with the one using the computational ‘detour’ of the Fourier and inverse Fourier transformations. In addition, to gauge the computational demand imposed by the Bessel functions, a functional approximation has been used in their place in the integrals of Eq. (15), cf. Martin et al. (2017). Table 1 reports the mean and standard deviations of the parameter estimates of \(m_0\) and \(\lambda \) for time series of length \(T=1000\), \(T=2000\) and \(T=5000\) across 200 Monte Carlo replications in each case. The number of Fourier frequencies used in the approximation developed in Sect. 2 was \(N=100\). The computations have been coded in GAUSS21 on a workstation with 32 AMD EPYC 7281 processors running on 2.10 GHz. While no explicit parallelization has been used in the code, GAUSS automatically runs many matrix operations in a multi-threaded mode.

Upon inspection, the parameter estimates from all three computational methods appear almost identical throughout. The correlation matrices on the right-hand side of Table 1 indeed indicate, that with larger sample sizes, the numerical results tend to become even more uniform. This suggests that slightly higher variation with smaller samples is more due to small occasional deviations between methods in the optimization algorithm (a standard BFGS algorithm has been used), than in the computation of the likelihood function itself. The results show nicely the \(T^{1/2}\) consistency of the maximum likelihood estimates (as it would be expected). The most interesting differences between the different methods are their computational demands: While the numerical approximation of the Bessel functions leads to a slight advantage against the built-in Bessel functions in GAUSS the detour through the frequency space comes at higher computational cost ranging from 20 s to about 1.5 min of average computing time for \(T=1000\) to \(T=5000\), roughly five times more compared to the solution based on Bessel functions.

However, this computational cost can be offset by outsourcing the Fourier approach to a tailor-made dynamic library that is then used as a single command line in the likelihood optimization loop in GAUSS. The fifth column of Table 1 shows that with a dynamic library in C the computational demands of the Fourier approach are only slightly higher than those of the closed-form solution based on Bessel functions (this comparison is, of course, ‘unfair’ as we still encode the latter approach fully in GAUSS). Note, however, that the dynamic library can be practically designed as a ‘plug-and-play’ module that could be applied to any regime-switching process with an arbitrary number of states and parameters.

4 State spaces of higher order

The solution algorithm illustrated in Sect. 2 for the case of a regime-switching diffusion with two states is generally applicable for any number of hidden states. The generalizations of Eqs. (5) to (8) are straightforward: With n the number of Markov states, the counterpart of Eq. (5) would consist of a system of n equations for the Fourier transforms of the regime-dependent densities. The counterpart of Eq. (6) would consist of the solutions of the densities which would all have n terms on their right-hand side made up of the eigenvalues and eigenvectors of the system of ordinary differential equations for the Fourier-transformed densities. Again, within the maximum likelihood loop, the initial conditions \(A_i(i=1, \ldots ,n)\) would be determined via the normalized densities obtained in the previous step, and the inverse Fourier transform would be used to obtain the new state densities in the original ‘space’ domain. Obviously, with increasing n the computational burden of these computations would become higher and higher. It is, therefore, interesting to explore the practical applicability of this algorithm by considering some selected examples with \(n>2\).

4.1 A four-state multifractal switching diffusion

The continuous-time multifractal model allows for an arbitrary number of hierarchical components in the variances of diffusion processes with a large number of states. In its Binomial form, each of these components might either assume a value of \(m_0\) or \(2-m_0\) as in the two-state example of Sect. 2.Footnote 1 With k such multipliers, this allows for a total of \(2^k\) Markov states. Since the hierarchical components enter multiplicatively, for \(k=2\), for instance, the state dependent variances would be: \(m_0m_0\), \((2-m_0)m_0\),\(m_0(2-m_0)\) and \((2-m_0)(2-m_0)\). Obviously, two of the four states share the same variance, but they need to be differentiated as they are governed by different transition rates (generally, for k multipliers, there would only be \(k+1\) different variances among the \(2^k\) states). More generally, with a number k of multipliers, the Binomial multifractal diffusion would be characterized by \(dx_t = \prod _{i = 1}^k M_t^{(i)}(s_t) dW_t\) with each \(M_t^{i}(s_t) \in \{m_0, 2 - m_0\}\).

The second defining characteristic of the multifractal diffusion is the hierarchy of transition rates with intensities \(\lambda _i,i=1, \ldots k\). In the simplest base-line model, the vectors of transition rates would just be described by a geometric degression, i.e. \(\frac{\lambda _{i+1}}{\lambda _i} = \beta < 1\). If switches at different hierarchical levels are independent, the intensity matrix becomes more and more sparse for higher k.

For example, for \(k=2\) with four states, denoting the states by \(s_t \in \{00,10,01,11\}\) according to whether level \(i=1\) or \(i=2\) assumes the realization \(m_0\) or \(m_1=2-m_0\), we would obtain the following system of four partial differential equations governing the joint densities \(u_{lm} = f(x, s = lm, t)\), \(l,m \in \{0,1\}\):

$$\begin{aligned} \frac{\partial u_{00}}{\partial t}= & {} \frac{1}{2} m_0^2 \frac{\partial ^2 u_{00}}{\partial x} - (\lambda _1+\lambda _2)u_{00} + \lambda _1 u_{10} + \lambda _2u_{01}\nonumber \\ \frac{\partial u_{10}}{\partial t}= & {} \frac{1}{2} m_0(2-m_0) \frac{\partial ^2 u_{10}}{\partial x} + \lambda _1 u_{00} - (\lambda _1+\lambda _2)u_{10} \nonumber \\{} & {} + \lambda _2u_{11}\nonumber \\ \frac{\partial u_{01}}{\partial t}= & {} \frac{1}{2} m_0(2-m_0) \frac{\partial ^2 u_{01}}{\partial x} + \lambda _2u_{00} - (\lambda _1+\lambda _2)u_{01} \nonumber \\{} & {} + \lambda _1 u_{11} \nonumber \\ \frac{\partial u_{11}}{\partial t}= & {} \frac{1}{2} (2-m_0)^2 \frac{\partial ^2 u_{11}}{\partial x} + \lambda _2u_{10} + \lambda _1 u_{01} \nonumber \\{} & {} - (\lambda _1+\lambda _2)u_{11} \end{aligned}$$
(17)

Despite its higher complexity, a designated plug-and-play code for the algorithm of Sect. 2 could also perform maximum likelihood estimation of the parameters \(m_0, \lambda _1, \lambda _2\) of this model without the need for any conceptual modifications.

Interestingly, due to the independence of the switches of the multipliers of both hierarchical levels, this case also has a closed form solution which follows directly from the well-known solution of the ‘telegraph’ diffusion above. Namely, each of the two components is characterized by the occupation times of its two states as used in Eq. (15) and derived in the Appendix. Since both levels are independent, the joint expected occupation times are just the product of both individual occupation times.

We can, therefore, express the densities \(u_{lm}(x,t)\) as:

$$\begin{aligned}{} & {} u_{l,m}(x,t)\nonumber \\{} & {} \quad = \int _{0}^{t}\int _{0}^{t} f_1^{(l)}(\tau _1,t)f_2^{(m)}(\tau _2,t)h(x,v(\tau _1,\tau _2))d\tau _1d\tau _2\nonumber \\ \end{aligned}$$
(18)

with \(l,m \in \{0,1\}\) and \(f_1^{(l)}(\cdot )\), \(f_2^{(m)}(\cdot )\) the occupation times of states l and m (0 and 1) at level i (1 or 2).

Just as in Eq. (15), the occupation times are:

$$\begin{aligned} f_i^{(0)}= & {} u_{0,i}e^{-\lambda _i t} \delta (t-\tau _i) + e^{-\lambda _i t} \{u_{0,i}\lambda _i \left( \frac{\tau _i}{t-\tau _i}\right) ^{1/2}\nonumber \\{} & {} \times I_1(\eta _i)+ u_{1,i} \lambda _i I_0 (\eta _i)\} \nonumber \\ f_i^{(1)}= & {} u_{1,i}e^{-\lambda _i t} \delta (t-\tau _i) + e^{-\lambda _i t} \{u_{0,i} \lambda _i I_0 (\eta _i) \nonumber \\{} & {} + u_{1,i}\lambda _i \left( \frac{t-\tau _i}{\tau _i} \right) ^{1/2} I_1(\eta _i)\} \end{aligned}$$
(19)

Here, \(\eta _i = 2\lambda _i(\tau _i(t-\tau _i))^{1/2}\), \(u_{0,i}= Prob(M^{(i)}_{t-1}=m_0\mid y_{t-1}, \theta )\) and \(u_{1,i}= Prob(M^{(i)}_{t-1}=m_1 = 2-m_0\mid y_{t-1}, \theta )\) which can be obtained from the forward variables defined in Sect. 2. Finally, \(h(x,v(\tau _1,\tau _2))\) is the density of the Normal distribution with mean zero and variance:

$$\begin{aligned} v(\tau _1,\tau _2)= & {} \tau _1\tau _2m_0^2 + (\tau _1+\tau _2 - 2\tau _1\tau _2)m_0(2-m_0) \nonumber \\{} & {} +(1-\tau _1)(1-\tau _2)(2-m_0)^2\text {.} \end{aligned}$$
(20)

We can now use either the Fourier transform algorithm of Sect. 2 or the double integrals of Eq. (18) to compute the state densities needed for maximum likelihood estimation. Prior to conducting estimation experiments, one may want to compare more directly the accuracy and computational demand of both alternatives. While both are based on exact solutions, the computational implementation involves necessarily some approximations: the discrete inverse Fourier transform in the first case, and the numerical approximation of the integrals of Eq. (18) in the second case. To gauge the influence of these factors, a series of evaluations of function values has been conducted. For all four densities \(u_{lm}\) the 60 function values between -3 and 2.9 with increments 0.1 have been evaluated at t=1. This exercise has been repeated for parameters \(m_0 = 1.3,1.5,1.7\) and \(\lambda _1 = \lambda =0.2\) and 0.4 (with \(\lambda _2 = 0.5\lambda _1\)), and for different settings in terms of the number of Fourier frequencies and the precision of the numerical integration.

As it turned out, the Fourier method showed no change in the function values at all for all numbers of frequencies N beyond a minimal number. More pronounced were the changes in the realizations of the integrals when varying the required precision. The integrals have been evaluated with an adaptive quadrature method which is available as a predefined function in GAUSS and takes as input a required level of absolute or relative accuracy.

Fig. 1
figure 1

The upper panel shows the average squared differences between density function evaluations based upon the Fourier transform and the direct solution of the integrals of Eq. (18). The lower panel shows the computation time of the evaluation of the integrals as a multiple of the computation time of the Fourier method

Full size image

Figure 1 shows the sum of squared deviations between both methods in dependency on the required precision in the integration together with the computation time of the evaluation of the integrals as a multiple of the time needed to implement the Fourier algorithm (implemented with \(N = 100\)). As one can see, one would need a prohibitive computation time to reach the same precision with the numerical evaluation of the integrals as with the Fourier algorithm. Admittedly, it has not been proven rigorously that the Fourier method gives a better approximation (since the ‘true’ numbers are not available) but the fact that the Fourier approximation shows fast convergence, and that the direct evaluation of the integrals also converges to the Fourier output with higher precision, suggests that the results of the Fourier approach should correspond closely to the ‘ground truth’. The differences are, indeed, not negligible: As Table 2 shows, the ML estimation on the base of the Fourier algorithm performs well in Monte Carlo simulations with clear indication of \(T^{1/2}\) consistency. In contrast, estimation based on the numerical integration and limited precision (\(10^{-3}\)) turned out to lead to less efficient estimates in Monte Carlo simulations (details not shown in the table). While this could certainly be ameliorated by imposing higher accuracy, this would come with an increase of computation time by two or three orders of magnitude. It, thus, appears that the relative advantage of what one might call a more ‘direct’ solution against the indirect way of the Fourier and inverse Fourier transform has turned into the opposite when moving from a two-state to a four-state switching diffusion.

Table 2 Monte Carlo results for more than two states
Full size table

4.2 Higher-order multifractal diffusions

When increasing the number of multipliers k in the multifractal framework, the number of states will increase by a factor 2. Hence, when moving from \(k=2\) to \(k=3\), we are proceeding from a four-state to an eight-state diffusion. The latter possesses only 4 distinct states (\(m_0^3, m_0^2(2-m_0), m_0(2-m_0)^2, (2-m_0)^3\)) but the full set of arrangements of \(M_t^{(1)} M_t^{(2)} M_t^{(3)}\), \(M_t^{(i)} \in \{m_0,2-m_0\}\), has to be taken into account since different arrangements of the same numbers of realizations \(m_0\) and \(2-m_0\) in the cascade come with different transition rates to other states.

How the system that results at increasing cascade levels is related to previous stages can easily be illustrated by the transition from \(k=2\) to \(k=3\): For \(k=2\) the counterpart of Eq. (5) in matrix form reads:

(21)

When adding a third hierarchical level, we might define the joint densities as \(u_{ijk}\) or \(\tilde{u}_{ijk}\) \((i,j,k = 0,1)\) depending on whether the pertinent multiplier is in state \(m_0\) or \(m_1 = 2-m_0\).

Keeping the ordering of Eq. (21) and adding a third multiplier \(M_t^{(3)}=m_0\) we obtain the first four entries to the \(2^3\) conditional densities at hierarchical level \(k=3\). Adding \(M_t^{(3)}=2-m_0\) to the sequence of the 4 multipliers at level 2 the second subset of states 5 through 8 is obtained. Denoting the vector of the eight densities by \({\textbf{u}}_{k=3}\) or \(\tilde{{\textbf{u}}}_{k=3}\), it is easy to see that the system of ordinary differential equations after Fourier transformation can be written as:

$$\begin{aligned} \frac{\partial \tilde{{\textbf{u}}}_{k=3}}{\partial t} = \begin{pmatrix} \varvec{A_0} &{} \varvec{B} \\ \varvec{B} &{} \varvec{A_1} \end{pmatrix} \tilde{{u}}_{k=3} \end{aligned}$$
(22)

where \(\varvec{A_0}\) and \(\varvec{A_1}\) are submatrices that both resemble closely the right-hand side of equation (21), and \(\varvec{B}\) is simply given by \(\varvec{B} = \lambda _3 \varvec{I_4}\), \(\varvec{I_4}\) the identity matrix of size 4.

Furthermore, \(\varvec{A_i}\) (\(i=0,1\)) can also be decomposed as:

$$\begin{aligned} \varvec{A_i} = \begin{pmatrix} \varvec{A_{i0}} &{} \lambda _2 \varvec{I_2} \\ \lambda _2 \varvec{I_2} &{} \varvec{A_{i1}} \end{pmatrix} \text {with } \varvec{A_{ij}} = \begin{pmatrix} A_{ij0} &{} \lambda _1 \\ \lambda _1 &{} A_{ij1} \end{pmatrix} \end{aligned}$$
(23)

and

$$\begin{aligned} A_{ijk} = -0.5 m_0^{3-i-j-k} (2-m_0)^{i+j+k} \xi ^2 - \sum _{m=1}^{3} \lambda _m. \end{aligned}$$
(24)

Hence, the systems of partial or ordinary differential equations governing the densities of a multifractal diffusion of any order can be easily constructed by adding new blocks of entries to those of previous stages.

One might wonder how our estimator performs for different specifications of the multifractal model. Table 2 shows results for \(k=2\) to \(k=4\) which can also be compared to the results depicted in Table 1 for the case of \(k=1\). To avoid very small transition rates, the highest rate \(\lambda _1\) has been chosen to be \(\lambda _1 = 0.2\) for \(k=2\) and \(\lambda _1 = 0.4\) for \(k=3\) and \(k=4\) keeping \(m_0 = 1.5\) throughout. The succession of transition rates is again geometric with a factor of 0.5. As a consequence, higher numbers of cascade levels allow for more variability of resulting time series but would not necessarily come with additional parameters to be estimated. While this parsimonious specification of multifractal models is seen as an advantage in applications, it could, of course, be modified if deemed useful: One could either dispense with any systematic progression altogether estimating all \(\lambda _i\) separately, or let the decay rate \(\beta \) be an unknown parameter.

Table 2 shows again satisfactory \(T^{1/2}\) convergence in all cases. As it transpires, the multipliers \(m_0\) can be estimated with higher precision for higher k and higher \(\lambda _1\) while the estimates of the transition rates show higher variability if this parameter is increased. The latter observation seems plausible as with a higher transition rate the states change more quickly and can be identified with less precision. Moving from \(k=1\) to \(k=2\) and from \(k=2\) over \(k= 3\) to \(k=4\) the computational demands increase by a factor 3 to 4 at each higher level.

Table 3 Monte Carlo results for three-state ‘moving–handling–resting’ process
Full size table

4.3 A three state moving–handling–resting model of animal motion

Pozdnyakov et al. (2020) have expanded the moving–resting model with two states of Yan et al. (2014) adding a third state for the handling of a prey by a predator, a state that might lead to smaller movements than the ‘moving’ state proper, but that is still different from the calm behavior during the resting phase. This model leads to a three-state diffusion with three different standard deviations \(\sigma _0,\sigma _1\) and \(\sigma _2\) and a transition rate matrix between states

$$\begin{aligned} \varvec{Q} = \begin{pmatrix} -\lambda _0 &{} \lambda _0p &{} \lambda _0(1-p) \\ \lambda _1 &{} -\lambda _1 &{} 0 \\ \lambda _2 &{} 0 &{} -\lambda _2 \end{pmatrix} \end{aligned}$$
(25)

where the order of the states is moving, handling, resting implying \(\sigma _0>\sigma _1 > \sigma _2\). The animal enters from the moving state to either the handling or resting states with transition rates \(\lambda _0p\) and \(\lambda _0(1-p)\), respectively, and from those back to moving with rates \(\lambda _1\) and \(\lambda _2\). No direct transition happens between the two latter states. In contrast to the multifractal diffusion this model comes with a total of seven parameters, \(\theta = \{\lambda _0, \lambda _1, \lambda _2, p, \sigma _0, \sigma _1, \sigma _2\}\) which allows us to explore the performance of the estimation in a more complex inferential problem in terms of the number of parameters.

Table 3 again shows that all parameters in a series of exemplary Monte Carlo simulations are well identified and obey \(T^{1/2}\) consistency with increasing sample size. Using the plug-and-play dynamic library, computational demands of this three-state model with several parameters are comparable to that of the \(k=3\)-multifractal model, i.e., a model with sixteen states but only two parameters. While the computational burden of the Fourier approach would be the same for any specification of a three-state regime switching diffusion, the higher number of parameters typically leads to a higher number of iterations until convergence in the numerical optimization of the likelihood function is reached.

5 An application: mountain lion movements

We conclude with an application of the model introduced in the previous subsection using sensor data of the movements of a mountain lion that has been recorded in the Gros Ventre Mountain Range in Wyoming, U.S.A, from 2009 to 2012. These data has also been used by Yan et al. (2014) and Pozdnyakov et al. (2019, 2020) to estimate two-state and three-state diffusion processes of the moving(–handling)–resting type. The data consist of 3917 time stamped spatial coordinates, and, thus, allows to compute the distance travelled by the lion in north/south and east/west directions during the time between adjacent recordings. The data can be downloaded from cran.r-project.org where also the code of the previous papers using this data is available. Since it had been observed that the behavior of these lions differs between seasons, I have followed previous authors in selecting only observations during the summer months, from 1 June to 31 August of each year, a total of 1136 remaining observations.

Fig. 2
figure 2

The upper panel shows the last 200 observations of the eastward motion of the mountain lion in the year 2012 (with 8-hour intervals as the unit time step), the bottom panel exhibits the posterior probabilities of the three states in cumulative fashion

Full size image

Figure 2 provides an impression of the movement in the east/west direction in terms of differences between adjacent recordings which clearly conveys the impression of switches between periods with relatively large movement in space (the units are in 1000 ms) and much more calm periods.

In contrast to Pozdnyakov et al. (2020) and Yan et al. (2014) we allow for non-zero diffusion coefficients in all three (or two) states. If locations are estimated precisely, handling might go along with some movements over smaller distances, and even resting might not lead to a completely stationary location (in the data, only 11 observations in the northward and 6 in the eastward direction show exactly zero changes of position which, however, still includes a rounding of the coordinates). With this assumption, the empirical application of the two-state and three-state models falls into the general framework as presented in the last subsection and no adjustment for off-states is needed.

In implementing the estimation algorithm of the previous sections, the measured time differences between recordings have been used instead of the uniform time step that has been assumed in the simulations. This only requires to adjust the counterpart of Eq. (6) in a way that the measured time that has elapsed between recordings enters and, the value used for t, thus, varies between observations. As the base time unit, I have chosen 8 h as this has been the targeted frequency for the transmission by the sensor. Hence, all estimates reported below have to be interpreted as transition rates and diffusion coefficients per 8 h interval.

For the estimation of the competing models, the north/south and east/west movements have been interpreted as a bivariate diffusion with three states, identical diffusion coefficients in both directions in each state and uncorrelated increments. Appendix B provides details on how the maximum likelihood estimation via Fourier transforms can be adapted to the case of a bivariate regime-switching diffusion (or, more generally, any multivariate regime-switching diffusion).

Table 4 displays the resulting parameter estimates together with the maximized likelihood, AIC and BIC criteria for both the three-state and the simpler two-state model. Both criteria favour the three-state model over the simpler alternative. The unconditional probabilities of the three (two) states on the bottom of the table indicate that the two states of the simpler model each absorb part of the probability of the intermediate handling state of the richer one. The information criteria and the significant parameter estimates, however, indicate that an intermediate state adds explanatory power. One also notes that the diffusion coefficient of the moving states in the two-state model also lies between those of moving and handling in the three-state scenario.

Table 4 Parameter estimates for two-state and three-state ‘moving-(handling-) resting’ process
Full size table

Although the estimation algorithm did not impose any restrictions on the diffusion coefficients besides positivity, the parameter for \(\sigma _2\) turned out to be extremely close to zero. The pertinent value for the two-state model is slightly higher as it counts a number of the handling episodes among the states of rest.

In comparison to the estimates reported in Pozdnyakov et al. (2020), one striking difference is that their model assigns 90 percent of the lion’s activity as ’handling’ while in the present approach only 10 percent of the time is on average spent in the intermediate state. Similarly, our moving state applies during roughly 28 percent of the time, while Pozdnyakov et al. find ’movement’ proper in only 1.3 percent of the time. Finally, ’resting’ comes with a stationary probability of about 9 percent in their model, while here we obtain 62 percent. It is, of course, possible that the present model identifies a new regime with slow speed rather than the original ’handling’ regime. However, the estimated standard deviation of 0.345 agrees well with the reported hovering within a distance of about 250 m of a kill side which motivated the introduction fo the handling regime. Besides that, the samples are not the same: only summer of 2012 is used by Pozdnyakov et al. , while here also data of the summers from 2009 to 2012 have been combined.

The lower panel of Fig. 2 shows the posterior probabilities for the three states for the last 200 observations in the year 2012. The three probabilities are displayed in cumulative fashion. One observes that the posterior identifies particularly sharply whether the lion is resting or not (not difficult actually given that the diffusion rate for the resting state is minuscule), but it sometimes has problems distinguishing between moving and handling. However, there are also periods (e.g., two times during the last four observations) when a probability of close to 1 is assigned to the intermediate ‘handling’ state (e.g., around time step 90 in Fig. 2)

6 Conclusion

This paper has proposed a universally applicable algorithm for implementation of the maximum likelihood estimator for regime-switching diffusions with an arbitrary number of states and parameters. While computational constraints will eventually impose limitations on the applicability for very large models, the selected examples have shown that various interesting models with moderate numbers of states and parameters can be effectively handled by this approach. As illustrated in Sect. 5, the algorithm can also be easily adapted to multivariate regime-switching diffusions. The proposed algorithm also comes with the advantage that it can be applied in any regime-switching model of interest in a ‘plug-and-play’ mode without any specific adjustments. Further efforts at parallelization of the main body of the algorithm would also increase the possible range of models it can be applied to. While this paper has concentrated on pure diffusion processes, the proposed estimation methodology can also be generalized to regime-switching processes with state-dependent drift and state-dependent jump components (cf. Lux 2023 for the details of the adapted algorithm).