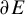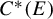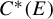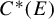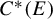1 Introduction
There is an abundance of C
![]() $^{*}$
-algebras which can be realised as the C
$^{*}$
-algebras which can be realised as the C
![]() $^{*}$
-algebras of topological graphs. To name a few examples, C
$^{*}$
-algebras of topological graphs. To name a few examples, C
![]() $^{*}$
-algebras arising from crossed products of
$^{*}$
-algebras arising from crossed products of
![]() $\mathbb {Z}$
by homeomorphisms, C
$\mathbb {Z}$
by homeomorphisms, C
![]() $^{*}$
-algebras arising from directed graphs, Kirchberg algebras satisfying the UCT and AF-algebras [Reference KatsuraKat06a]. Since C
$^{*}$
-algebras arising from directed graphs, Kirchberg algebras satisfying the UCT and AF-algebras [Reference KatsuraKat06a]. Since C
![]() $^{*}$
-algebras of topological graphs provide a rich class of examples, it is natural to study concepts like traces on such algebras.
$^{*}$
-algebras of topological graphs provide a rich class of examples, it is natural to study concepts like traces on such algebras.
The study of tracial states on topological graph C
![]() $^{*}$
-algebras was initiated by Schaufhauser in [Reference RenaultSch18]. Schaufhauser proved that the gauge-invariant tracial states are affinely homeomorphic to a set of probability measures on the vertex set
$^{*}$
-algebras was initiated by Schaufhauser in [Reference RenaultSch18]. Schaufhauser proved that the gauge-invariant tracial states are affinely homeomorphic to a set of probability measures on the vertex set
![]() $E^{0}$
, which we in this paper call the vertex-invariant measures. This generalises similar known results from the cases of directed graphs and crossed products by homeomorphisms, and it is known from these cases that this simplification of the problem of describing gauge-invariant tracial states is very useful for providing concrete descriptions of traces. For directed graphs and crossed products, it is also known that under the right assumptions, namely condition (K) for directed graphs and freeness of the action for crossed products, all tracial states are gauge-invariant. The notion of freeness of topological graphs generalises both of these conditions, which motivated Schaufhauser to make the following conjecture in [Reference RenaultSch18].
$E^{0}$
, which we in this paper call the vertex-invariant measures. This generalises similar known results from the cases of directed graphs and crossed products by homeomorphisms, and it is known from these cases that this simplification of the problem of describing gauge-invariant tracial states is very useful for providing concrete descriptions of traces. For directed graphs and crossed products, it is also known that under the right assumptions, namely condition (K) for directed graphs and freeness of the action for crossed products, all tracial states are gauge-invariant. The notion of freeness of topological graphs generalises both of these conditions, which motivated Schaufhauser to make the following conjecture in [Reference RenaultSch18].
Conjecture. All tracial states on the C
![]() $^{*}$
-algebra of a free topological graph are gauge-invariant.
$^{*}$
-algebra of a free topological graph are gauge-invariant.
If the C
![]() $^{*}$
-algebra of a topological graph is simple, the graph has to be free, so a positive answer to this conjecture in particular implies that all tracial states on simple topological graph C
$^{*}$
-algebra of a topological graph is simple, the graph has to be free, so a positive answer to this conjecture in particular implies that all tracial states on simple topological graph C
![]() $^{*}$
-algebras can be described by vertex-invariant measures. This is a strong motivation for answering this conjecture, since it means that one can greatly simplify the problem of describing traces for simple topological graph C
$^{*}$
-algebras can be described by vertex-invariant measures. This is a strong motivation for answering this conjecture, since it means that one can greatly simplify the problem of describing traces for simple topological graph C
![]() $^{*}$
-algebras. The last part of [Reference RenaultSch18] additionally argues that for many topological graphs, the gauge-invariant tracial states are affinely homeomorphic with the states on the
$^{*}$
-algebras. The last part of [Reference RenaultSch18] additionally argues that for many topological graphs, the gauge-invariant tracial states are affinely homeomorphic with the states on the
![]() $K_{0}$
-group of the graph C
$K_{0}$
-group of the graph C
![]() $^{*}$
-algebra, which further stresses the importance of characterising which states are gauge-invariant.
$^{*}$
-algebra, which further stresses the importance of characterising which states are gauge-invariant.
The purpose of this paper is to continue the analysis of tracial states on topological graph C
![]() $^{*}$
-algebras initiated in [Reference RenaultSch18]. In particular, we will provide an affirmative answer to the above conjecture for separable C
$^{*}$
-algebras initiated in [Reference RenaultSch18]. In particular, we will provide an affirmative answer to the above conjecture for separable C
![]() $^{*}$
-algebras. In fact, we provide a graph-theoretical condition which we prove is equivalent to the existence of a non-gauge-invariant tracial state, cf. Theorem 7.3 and Definition 5.1, and we then prove that a free graph cannot satisfy this condition.
$^{*}$
-algebras. In fact, we provide a graph-theoretical condition which we prove is equivalent to the existence of a non-gauge-invariant tracial state, cf. Theorem 7.3 and Definition 5.1, and we then prove that a free graph cannot satisfy this condition.
Instead of considering tracial states, we extend the scope of [Reference RenaultSch18] by considering tracial weights. After establishing the preliminaries, we therefore commence the paper by generalising the result of [Reference RenaultSch18] by establishing in Proposition 3.6 a bijection between the following three sets:
-
• the regular vertex-invariant measures on the vertex space
 $E^{0}$
;
$E^{0}$
; -
• the regular shift-invariant measures on the boundary path space
 $\partial E$
of E;
$\partial E$
of E; -
• the gauge-invariant tracial weights on the graph C
 $^{*}$
-algebra
$^{*}$
-algebra
 $C^{*}(E)$
.
$C^{*}(E)$
.
We then focus on two kinds of regular invariant measures on
![]() $\partial E$
. First, we analyse the extremal measures concentrated on the set of finite paths in
$\partial E$
. First, we analyse the extremal measures concentrated on the set of finite paths in
![]() $\partial E$
, and in Theorem 4.2, we give a complete description of such measures. Second, we analyse the extremal invariant measures which are concentrated on paths in
$\partial E$
, and in Theorem 4.2, we give a complete description of such measures. Second, we analyse the extremal invariant measures which are concentrated on paths in
![]() $\partial E$
which are eventually cyclic, and we completely describe these measures in Theorem 6.2. Using this description, we provide both a necessary and sufficient condition for the existence of a non-gauge-invariant tracial state on
$\partial E$
which are eventually cyclic, and we completely describe these measures in Theorem 6.2. Using this description, we provide both a necessary and sufficient condition for the existence of a non-gauge-invariant tracial state on
![]() $C^{*}(E)$
, and a necessary and sufficient condition for the existence of a non-gauge-invariant tracial weight. Both of these conditions are graph-theoretical, which allows us to prove that on a second countable free topological graph, all tracial weights are gauge-invariant, proving that Schaufhauser conjecture is also true for tracial weights on separable
$C^{*}(E)$
, and a necessary and sufficient condition for the existence of a non-gauge-invariant tracial weight. Both of these conditions are graph-theoretical, which allows us to prove that on a second countable free topological graph, all tracial weights are gauge-invariant, proving that Schaufhauser conjecture is also true for tracial weights on separable
![]() $C^{*}$
-algebras arising from topological graphs.
$C^{*}$
-algebras arising from topological graphs.
2 Preliminaries
We let
![]() $\mathbb {N}_{0}$
denote the natural numbers including zero.
$\mathbb {N}_{0}$
denote the natural numbers including zero.
2.1 Topological graphs
We will in the following introduce our terminology on topological graphs. We refer the reader to Katsura’s original paper for more background [Reference KatsuraKat04].
A topological graph
![]() $E=(E^{0}, E^{1}, r,s)$
consists of two locally compact Hausdorff spaces
$E=(E^{0}, E^{1}, r,s)$
consists of two locally compact Hausdorff spaces
![]() $E^{0}$
and
$E^{0}$
and
![]() $E^{1}$
, a local homeomorphism
$E^{1}$
, a local homeomorphism
![]() $s: E^{1}\to E^{0}$
and a continuous map
$s: E^{1}\to E^{0}$
and a continuous map
![]() $r: E^{1} \to E^{0}$
. We call s the source map and r the range map. Following the terminology for directed graphs, we refer to elements in
$r: E^{1} \to E^{0}$
. We call s the source map and r the range map. Following the terminology for directed graphs, we refer to elements in
![]() $E^{0}$
as vertices and elements in
$E^{0}$
as vertices and elements in
![]() $E^{1}$
as edges. We call the topological graph E second countable when the two spaces
$E^{1}$
as edges. We call the topological graph E second countable when the two spaces
![]() $E^{0}$
and
$E^{0}$
and
![]() $E^{1}$
are second countable topological spaces.
$E^{1}$
are second countable topological spaces.
We follow the convention for traversing paths which is used in [Reference KatsuraKat04, Reference RenaultSch18], that is, a path
![]() $\alpha _{1}\alpha _{2} \cdots \alpha _{n}$
is a concatenation of edges
$\alpha _{1}\alpha _{2} \cdots \alpha _{n}$
is a concatenation of edges
![]() $\alpha _{1}, \dots , \alpha _{n} \in E^{1}$
satisfying that
$\alpha _{1}, \dots , \alpha _{n} \in E^{1}$
satisfying that
![]() $s(\alpha _{i})=r(\alpha _{i+1})$
for
$s(\alpha _{i})=r(\alpha _{i+1})$
for
![]() $i=1, \dots , n-1$
. We say a path
$i=1, \dots , n-1$
. We say a path
![]() $\alpha :=\alpha _{1}\alpha _{2} \cdots \alpha _{n}$
has length n and we write this
$\alpha :=\alpha _{1}\alpha _{2} \cdots \alpha _{n}$
has length n and we write this
![]() $|\alpha |=n$
. We interpret the vertices
$|\alpha |=n$
. We interpret the vertices
![]() $E^{0}$
as paths of length zero. For any
$E^{0}$
as paths of length zero. For any
![]() $n\in \mathbb {N}_{0}$
, we denote by
$n\in \mathbb {N}_{0}$
, we denote by
![]() $E^{n}$
the paths of length n, which is then in keeping with the definition of vertices
$E^{n}$
the paths of length n, which is then in keeping with the definition of vertices
![]() $E^{0}$
and edges
$E^{0}$
and edges
![]() $E^{1}$
for
$E^{1}$
for
![]() $n=0,1$
. The space
$n=0,1$
. The space
![]() $E^{n}$
with
$E^{n}$
with
![]() $n\in \mathbb {N}$
inherits a locally compact Hausdorff topology by considering it as a subspace of the product space
$n\in \mathbb {N}$
inherits a locally compact Hausdorff topology by considering it as a subspace of the product space
![]() $\prod _{i=1}^{n} E^{1}$
with the product topology. Endowing
$\prod _{i=1}^{n} E^{1}$
with the product topology. Endowing
![]() $E^{n}$
with this topology for all
$E^{n}$
with this topology for all
![]() $n\in \mathbb {N}$
, we define the finite path space
$n\in \mathbb {N}$
, we define the finite path space
![]() $E^{*}$
as the set
$E^{*}$
as the set
 $$ \begin{align*} E^{*}:= \bigsqcup_{n=0}^{\infty} E^{n} \end{align*} $$
$$ \begin{align*} E^{*}:= \bigsqcup_{n=0}^{\infty} E^{n} \end{align*} $$
with the topology generated by the topologies on the spaces
![]() $E^{n}$
. We define the infinite path space
$E^{n}$
. We define the infinite path space
![]() $E^{\infty }$
as the set of infinite concatenations
$E^{\infty }$
as the set of infinite concatenations
![]() $\alpha _{1}\alpha _{2}\cdots $
with
$\alpha _{1}\alpha _{2}\cdots $
with
![]() $s(\alpha _{i})=r(\alpha _{i+1})$
for all
$s(\alpha _{i})=r(\alpha _{i+1})$
for all
![]() $i\in \mathbb {N}$
, and we write
$i\in \mathbb {N}$
, and we write
![]() $|\alpha | =\infty $
for such a path
$|\alpha | =\infty $
for such a path
![]() $\alpha :=\alpha _{1} \alpha _{2} \cdots $
. We can naturally extend the range map r to a map on all paths in
$\alpha :=\alpha _{1} \alpha _{2} \cdots $
. We can naturally extend the range map r to a map on all paths in
![]() $E^{*}$
and
$E^{*}$
and
![]() $E^{\infty }$
by setting
$E^{\infty }$
by setting
![]() $r(\alpha )=r(\alpha _{1})$
when
$r(\alpha )=r(\alpha _{1})$
when
![]() $|\alpha |\geq 1$
and
$|\alpha |\geq 1$
and
![]() $r(v)=v$
when
$r(v)=v$
when
![]() $v\in E^{0}$
. Likewise, we can extend the source map to
$v\in E^{0}$
. Likewise, we can extend the source map to
![]() $E^{*}$
by setting
$E^{*}$
by setting
![]() $s(\alpha )=s(\alpha _{|\alpha |})$
. The extensions of r and s to
$s(\alpha )=s(\alpha _{|\alpha |})$
. The extensions of r and s to
![]() $E^{*}$
are then respectively also a continuous map and a local homeomorphism. We follow the standard convention of writing e.g.
$E^{*}$
are then respectively also a continuous map and a local homeomorphism. We follow the standard convention of writing e.g.
![]() $AE^{*}B$
for paths
$AE^{*}B$
for paths
![]() $\alpha \in E^{*}$
with
$\alpha \in E^{*}$
with
![]() $r(\alpha ) \in A$
and
$r(\alpha ) \in A$
and
![]() $s(\alpha ) \in B$
when
$s(\alpha ) \in B$
when
![]() $A,B \subseteq E^{0}$
.
$A,B \subseteq E^{0}$
.
There exists a maximal open subset
![]() $E_{\mathrm {reg}}^{0}$
of
$E_{\mathrm {reg}}^{0}$
of
![]() $E^{0}$
satisfying that r restricts to a proper surjection
$E^{0}$
satisfying that r restricts to a proper surjection
![]() $r^{-1}(E_{\mathrm {reg}}^{0}) \to E_{\mathrm {reg}}^{0}$
. More concretely
$r^{-1}(E_{\mathrm {reg}}^{0}) \to E_{\mathrm {reg}}^{0}$
. More concretely
![]() $E_{\mathrm {reg}}^{0}$
can be described as the set of vertices
$E_{\mathrm {reg}}^{0}$
can be described as the set of vertices
![]() $v\in E^{0}$
satisfying that there exists an open neighbourhood W of v with
$v\in E^{0}$
satisfying that there exists an open neighbourhood W of v with
![]() $\overline {W}$
compact,
$\overline {W}$
compact,
![]() $r^{-1}(\overline {W}) \subseteq E^{1}$
compact and
$r^{-1}(\overline {W}) \subseteq E^{1}$
compact and
![]() $r(r^{-1}(W))=W$
. We call
$r(r^{-1}(W))=W$
. We call
![]() $E^{0}_{\mathrm {reg}}$
the set of regular vertices, and we define
$E^{0}_{\mathrm {reg}}$
the set of regular vertices, and we define
![]() $E^{0}_{\mathrm {sng}}=E^{0} \setminus E^{0}_{\mathrm {reg}}$
to be the set of singular vertices. We set
$E^{0}_{\mathrm {sng}}=E^{0} \setminus E^{0}_{\mathrm {reg}}$
to be the set of singular vertices. We set
2.2 The boundary path space of a topological graph
We will in the following introduce the boundary path space
![]() $\partial E$
of a topological graph E. We refer the reader to [Reference TomfordeYee07] and [Reference RenaultSch18, §3] for a more rigorous introduction.
$\partial E$
of a topological graph E. We refer the reader to [Reference TomfordeYee07] and [Reference RenaultSch18, §3] for a more rigorous introduction.
As a set, we define the boundary path space
![]() $\partial E$
to be
$\partial E$
to be
For any subset
![]() $S\subseteq E^{*}$
, we define
$S\subseteq E^{*}$
, we define
Sets on the form
![]() $Z(U) \setminus Z(K)$
, where
$Z(U) \setminus Z(K)$
, where
![]() $U\subseteq E^{*}$
is open and
$U\subseteq E^{*}$
is open and
![]() $K\subseteq E^{*}$
is compact, form a basis for a locally compact Hausdorff topology on
$K\subseteq E^{*}$
is compact, form a basis for a locally compact Hausdorff topology on
![]() $\partial E$
. With this, topology sets on the form
$\partial E$
. With this, topology sets on the form
![]() $Z(K)$
are compact in
$Z(K)$
are compact in
![]() $\partial E$
whenever
$\partial E$
whenever
![]() $K\subseteq E^{*}$
is a compact set.
$K\subseteq E^{*}$
is a compact set.
We define a map
![]() $\sigma :\partial E\setminus E^{0} \to \partial E$
by setting
$\sigma :\partial E\setminus E^{0} \to \partial E$
by setting
and
![]() $\sigma (\alpha )=s(\alpha _{1})$
when
$\sigma (\alpha )=s(\alpha _{1})$
when
![]() $\alpha =\alpha _{1}\in \partial E$
satisfies
$\alpha =\alpha _{1}\in \partial E$
satisfies
![]() $|\alpha |=1$
. This map is a local homeomorphism which we call the backwards shift map, cf. [Reference RenaultSch18, Proposition 3.5]. The observation in the following Lemma 2.1 is implicitly used in the proof of [Reference RenaultSch18, Proposition 3.5]. Since it will be vital for us at a later point, we will provide a proof for clarity. The statement of the lemma also uses
$|\alpha |=1$
. This map is a local homeomorphism which we call the backwards shift map, cf. [Reference RenaultSch18, Proposition 3.5]. The observation in the following Lemma 2.1 is implicitly used in the proof of [Reference RenaultSch18, Proposition 3.5]. Since it will be vital for us at a later point, we will provide a proof for clarity. The statement of the lemma also uses
![]() $\sigma $
to denote the map
$\sigma $
to denote the map
![]() $E^{*} \setminus E^{0} \to E^{*}$
which is defined completely analogous to above. We also use the notation
$E^{*} \setminus E^{0} \to E^{*}$
which is defined completely analogous to above. We also use the notation
for subsets
![]() $U\subseteq E^{k}$
and
$U\subseteq E^{k}$
and
![]() $V \subseteq E^{l}$
. Notice that
$V \subseteq E^{l}$
. Notice that
![]() $UV$
is open if
$UV$
is open if
![]() $U,V$
are open,
$U,V$
are open,
![]() $UV$
is closed if
$UV$
is closed if
![]() $U,V$
are closed and
$U,V$
are closed and
![]() $UV$
is compact if
$UV$
is compact if
![]() $U,V$
are compact.
$U,V$
are compact.
Lemma 2.1. The set
![]() $\partial E \setminus E^{0}$
is open and has a basis of sets on the form
$\partial E \setminus E^{0}$
is open and has a basis of sets on the form
![]() $Z(U) \setminus Z(K)$
satisfying:
$Z(U) \setminus Z(K)$
satisfying:
-
(1)
 $U\subseteq E^{*}$
is open and
$U\subseteq E^{*}$
is open and
 $K\subseteq E^{*}$
is compact;
$K\subseteq E^{*}$
is compact; -
(2)
 $U\subseteq E^{l}$
for some
$U\subseteq E^{l}$
for some
 $l\geq 1$
and
$l\geq 1$
and
 $K\cap E^{0}=\emptyset $
;
$K\cap E^{0}=\emptyset $
; -
(3) there exists
 $W\subseteq E^{1}$
with s injective on W and
$W\subseteq E^{1}$
with s injective on W and
 $x_{1}\in W$
for all
$x_{1}\in W$
for all
 $x\in K\cup U$
; and
$x\in K\cup U$
; and -
(4)
 $\sigma (Z(U) \setminus Z(K)) = Z(\sigma (U)) \setminus Z(\sigma (K))$
.
$\sigma (Z(U) \setminus Z(K)) = Z(\sigma (U)) \setminus Z(\sigma (K))$
.
Proof. Remark first that
![]() $\partial E \setminus E^{0}= Z(E^{1})$
is an open set and that item (3) implies item (4), because when s is injective on W, then
$\partial E \setminus E^{0}= Z(E^{1})$
is an open set and that item (3) implies item (4), because when s is injective on W, then
![]() $\sigma $
is injective on
$\sigma $
is injective on
![]() $Z(W)$
, and item (4) then follows since
$Z(W)$
, and item (4) then follows since
![]() $Z(U), Z(K) \subseteq Z(W)$
.
$Z(U), Z(K) \subseteq Z(W)$
.
Now consider a compact set
![]() $K \subseteq E^{*}$
, an open set
$K \subseteq E^{*}$
, an open set
![]() $U\subseteq E^{*}$
and an element
$U\subseteq E^{*}$
and an element
![]() $x\in (\partial E \setminus E^{0} ) \cap (Z(U)\setminus Z(K))$
. Since
$x\in (\partial E \setminus E^{0} ) \cap (Z(U)\setminus Z(K))$
. Since
![]() $K\subseteq E^{*}$
is compact, there exists a
$K\subseteq E^{*}$
is compact, there exists a
![]() $n\in \mathbb {N}$
such that all paths in K have length less than or equal to n. We can assume without loss of generality that there exists a
$n\in \mathbb {N}$
such that all paths in K have length less than or equal to n. We can assume without loss of generality that there exists a
![]() $l\in \mathbb {N}_{0}$
with
$l\in \mathbb {N}_{0}$
with
![]() $U \subseteq E^{l}$
. If
$U \subseteq E^{l}$
. If
![]() $U\subseteq E^{0}$
, we can replace it by
$U\subseteq E^{0}$
, we can replace it by
![]() $r^{-1}(U)\subseteq E^{1}$
, so we can also assume that
$r^{-1}(U)\subseteq E^{1}$
, so we can also assume that
![]() $l\geq 1$
. Since
$l\geq 1$
. Since
![]() $Z(U E^{k}) \subseteq Z(U)$
, we can also assume that either
$Z(U E^{k}) \subseteq Z(U)$
, we can also assume that either
![]() $ n \leq l \leq |x|$
or
$ n \leq l \leq |x|$
or
![]() $l=|x|$
, depending on whether
$l=|x|$
, depending on whether
![]() $|x|\geq n$
or
$|x|\geq n$
or
![]() $|x| <n$
.
$|x| <n$
.
Assume first that
![]() $l \geq n$
. For each
$l \geq n$
. For each
![]() $1\leq k \leq l$
, we choose an open neighbourhood
$1\leq k \leq l$
, we choose an open neighbourhood
![]() $V_{k} \subseteq E^{1}$
of
$V_{k} \subseteq E^{1}$
of
![]() $x_{k}$
such that
$x_{k}$
such that
![]() $\overline {V_{k}}$
is compact and
$\overline {V_{k}}$
is compact and
![]() $\overline {V_{k}} \subseteq W_{k}$
, where
$\overline {V_{k}} \subseteq W_{k}$
, where
![]() $W_{k} \subseteq E^{1}$
is open and
$W_{k} \subseteq E^{1}$
is open and
![]() $s:W_{k} \to E^{0}$
is injective. Set
$s:W_{k} \to E^{0}$
is injective. Set
Since
![]() $K\cap E^{0}$
is closed and
$K\cap E^{0}$
is closed and
![]() $r|_{E^{l}}:E^{l}\to E^{0}$
is continuous, then
$r|_{E^{l}}:E^{l}\to E^{0}$
is continuous, then
![]() $U'$
is open. Clearly,
$U'$
is open. Clearly,
![]() $x_{1} \cdots x_{l}\in U'$
. Now set
$x_{1} \cdots x_{l}\in U'$
. Now set
 $$ \begin{align*}K'= (K\setminus E^{0}) \cap \bigg( \bigcup_{i=1}^{l} \overline{V_{1}} \cdots \overline{V_{i}} \bigg), \end{align*} $$
$$ \begin{align*}K'= (K\setminus E^{0}) \cap \bigg( \bigcup_{i=1}^{l} \overline{V_{1}} \cdots \overline{V_{i}} \bigg), \end{align*} $$
then
![]() $U'$
and
$U'$
and
![]() $K'$
satisfy items (1), (2) and (3) with
$K'$
satisfy items (1), (2) and (3) with
![]() $W=W_{1}$
. An element
$W=W_{1}$
. An element
![]() $y\in Z(U')\cap Z(K)$
can be written
$y\in Z(U')\cap Z(K)$
can be written
![]() $y=uy'$
with
$y=uy'$
with
![]() $u\in U'$
and since
$u\in U'$
and since
![]() $l\geq n$
, then
$l\geq n$
, then
![]() $u=\kappa u'$
with
$u=\kappa u'$
with
![]() $\kappa \in K$
. Since
$\kappa \in K$
. Since
![]() $r(u)\notin K\cap E^{0}$
, then
$r(u)\notin K\cap E^{0}$
, then
![]() $|\kappa |>0$
and hence
$|\kappa |>0$
and hence
![]() $\kappa \in K'$
. This implies that
$\kappa \in K'$
. This implies that
![]() $y\in Z(K')$
. Hence,
$y\in Z(K')$
. Hence,
which proves the lemma in this case.
Assume then that
![]() $l=|x|$
and define
$l=|x|$
and define
![]() $U'$
as before. For each
$U'$
as before. For each
![]() $1\leq k\leq l$
, define
$1\leq k\leq l$
, define
If
![]() $k>l$
, let
$k>l$
, let
![]() $K_{i}$
be the projection of
$K_{i}$
be the projection of
![]() $K\cap E^{k}$
onto the ith coordinate of
$K\cap E^{k}$
onto the ith coordinate of
![]() $E^{k}$
for
$E^{k}$
for
![]() $i\leq k$
. Then
$i\leq k$
. Then
![]() $K_{i}$
is compact, and we set
$K_{i}$
is compact, and we set
and we define
![]() $K'= N_{1} \cup \cdots \cup N_{n}$
. It is straightforward to check that
$K'= N_{1} \cup \cdots \cup N_{n}$
. It is straightforward to check that
![]() $U'$
and
$U'$
and
![]() $K'$
satisfy items (1)–(3), and that
$K'$
satisfy items (1)–(3), and that
![]() $x\in Z(U') \setminus Z(K')$
. To see that
$x\in Z(U') \setminus Z(K')$
. To see that
take an arbitrary element
![]() $y\in Z(U')\cap Z(K)$
, and write
$y\in Z(U')\cap Z(K)$
, and write
![]() $y=\kappa y'$
with
$y=\kappa y'$
with
![]() $\kappa \in K$
and
$\kappa \in K$
and
![]() $y= uy"$
with
$y= uy"$
with
![]() $u\in U'$
. If
$u\in U'$
. If
![]() $|\kappa | \leq l$
, then
$|\kappa | \leq l$
, then
![]() $u=\kappa u'$
and hence
$u=\kappa u'$
and hence
![]() $\kappa \in V_{1} \cdots V_{|\kappa |}$
, implying that
$\kappa \in V_{1} \cdots V_{|\kappa |}$
, implying that
![]() $\kappa \in N_{|\kappa |} \subseteq K'$
. If
$\kappa \in N_{|\kappa |} \subseteq K'$
. If
![]() $|\kappa |>l$
, then
$|\kappa |>l$
, then
![]() $\kappa =u\kappa '$
, so since
$\kappa =u\kappa '$
, so since
![]() $\kappa \in K$
, we get
$\kappa \in K$
, we get
![]() $\kappa \in N_{|\kappa |} \subseteq K'$
. In conclusion,
$\kappa \in N_{|\kappa |} \subseteq K'$
. In conclusion,
![]() $Z(U')\cap Z(K) \subseteq Z(K')$
which proves equation (2.1).
$Z(U')\cap Z(K) \subseteq Z(K')$
which proves equation (2.1).
We call a subset
![]() $M \subseteq \partial E$
invariant under
$M \subseteq \partial E$
invariant under
![]() $\sigma $
, or just invariant, if it satisfies
$\sigma $
, or just invariant, if it satisfies
We will need the following result on the Borel sets of
![]() $\partial E$
, which in particular implies that
$\partial E$
, which in particular implies that
![]() $E^{*}_{\mathrm {sng}}$
is an invariant Borel set of
$E^{*}_{\mathrm {sng}}$
is an invariant Borel set of
![]() $\partial E$
.
$\partial E$
.
Lemma 2.2. Let
![]() $S\subseteq E^{0}$
be a Borel set. Then the set
$S\subseteq E^{0}$
be a Borel set. Then the set
is an invariant Borel subset of
![]() $\partial E$
.
$\partial E$
.
Proof. The set
![]() $E^{n}$
is open in
$E^{n}$
is open in
![]() $E^{*}$
for any
$E^{*}$
for any
![]() $n\in \mathbb {N}_{0}$
, from which it follows that
$n\in \mathbb {N}_{0}$
, from which it follows that
![]() $ E_{\mathrm {sng}}^{n}= Z(E^{n})\setminus Z(E^{n+1})$
is a Borel set in
$ E_{\mathrm {sng}}^{n}= Z(E^{n})\setminus Z(E^{n+1})$
is a Borel set in
![]() $\partial E$
. If
$\partial E$
. If
![]() $V\subseteq E^{0}$
is open, then
$V\subseteq E^{0}$
is open, then
and hence
![]() $\{ \alpha \in E^{n}_{\mathrm {sng}} \mid s(\alpha ) \in S \}$
is Borel for all
$\{ \alpha \in E^{n}_{\mathrm {sng}} \mid s(\alpha ) \in S \}$
is Borel for all
![]() $n\in \mathbb {N}_{0}$
, proving that
$n\in \mathbb {N}_{0}$
, proving that
![]() $E_{\mathrm {sng}}^{*} S$
is Borel.
$E_{\mathrm {sng}}^{*} S$
is Borel.
To see that the set is invariant, notice that if
![]() $\alpha \in E_{\mathrm {sng}}^{*}S$
with
$\alpha \in E_{\mathrm {sng}}^{*}S$
with
![]() $|\alpha |\geq 1$
, then
$|\alpha |\geq 1$
, then
![]() $s(\sigma (\alpha ))=s(\alpha )\in S\cap E_{\mathrm {sng}}^{0}$
, implying that
$s(\sigma (\alpha ))=s(\alpha )\in S\cap E_{\mathrm {sng}}^{0}$
, implying that
![]() $\sigma (\alpha ) \in E_{\mathrm {sng}}^{*} S$
. If
$\sigma (\alpha ) \in E_{\mathrm {sng}}^{*} S$
. If
![]() $|\alpha |\geq 1$
and
$|\alpha |\geq 1$
and
![]() $\sigma (\alpha )\in E^{*}_{\mathrm {sng}}S$
, then
$\sigma (\alpha )\in E^{*}_{\mathrm {sng}}S$
, then
![]() $s(\alpha )=s(\sigma (\alpha ))\in S\cap E_{\mathrm {sng}}^{0}$
. Hence,
$s(\alpha )=s(\sigma (\alpha ))\in S\cap E_{\mathrm {sng}}^{0}$
. Hence,
![]() $\alpha \in E^{*}_{\mathrm {sng}} S$
which proves equation (2.2) with
$\alpha \in E^{*}_{\mathrm {sng}} S$
which proves equation (2.2) with
![]() $M=E_{\mathrm {sng}}^{*} S$
.
$M=E_{\mathrm {sng}}^{*} S$
.
2.3 Graph C
 $^{*}$
-algebras and their groupoid picture
$^{*}$
-algebras and their groupoid picture
If E is a topological graph, we can define a left and right action of
![]() $C_{0}(E^{0})$
on
$C_{0}(E^{0})$
on
![]() $C_{c}(E^{1} )$
by
$C_{c}(E^{1} )$
by
![]() $a\cdot \xi = (a \circ r) \xi $
and
$a\cdot \xi = (a \circ r) \xi $
and
![]() $\xi \cdot a = \xi (a\circ s)$
for
$\xi \cdot a = \xi (a\circ s)$
for
![]() $a\in C_{0}(E^{0})$
and
$a\in C_{0}(E^{0})$
and
![]() $\xi \in C_{c}(E^{1})$
. This makes
$\xi \in C_{c}(E^{1})$
. This makes
![]() $C_{c}(E^{1} )$
into a bimodule. For
$C_{c}(E^{1} )$
into a bimodule. For
![]() $\xi , \eta \in C_{c}(E^{1})$
, then
$\xi , \eta \in C_{c}(E^{1})$
, then
 $$ \begin{align*} E^{0}\ni v\mapsto \langle \xi, \eta\rangle(v) = \sum_{e\in s^{-1}(v)} \overline{\xi(e)}\eta(e) \end{align*} $$
$$ \begin{align*} E^{0}\ni v\mapsto \langle \xi, \eta\rangle(v) = \sum_{e\in s^{-1}(v)} \overline{\xi(e)}\eta(e) \end{align*} $$
defines a
![]() $C_{0}(E^{0})$
valued inner product on
$C_{0}(E^{0})$
valued inner product on
![]() $C_{c} (E^{1})$
. One obtains a C
$C_{c} (E^{1})$
. One obtains a C
![]() $^{*}$
-correspondence
$^{*}$
-correspondence
![]() $H(E)$
by completing
$H(E)$
by completing
![]() $C_{c}(E^{1})$
with respect to this inner product. The graph C
$C_{c}(E^{1})$
with respect to this inner product. The graph C
![]() $^{*}$
-algebra
$^{*}$
-algebra
![]() $C^{*}(E)$
associated to the graph E is then the Cuntz–Pimsner algebra of the C
$C^{*}(E)$
associated to the graph E is then the Cuntz–Pimsner algebra of the C
![]() $^{*}$
-correspondence
$^{*}$
-correspondence
![]() $(H(E), C_{0}(E^{0}) )$
. We remind the reader that our assumption of
$(H(E), C_{0}(E^{0}) )$
. We remind the reader that our assumption of
![]() $E^{0}$
and
$E^{0}$
and
![]() $E^{1}$
being second countable is equivalent with
$E^{1}$
being second countable is equivalent with
![]() $C^{*}(E)$
being separable, cf. [Reference KatsuraKat04, Proposition 6.3].
$C^{*}(E)$
being separable, cf. [Reference KatsuraKat04, Proposition 6.3].
For the analysis we will carry out in this paper, it is crucial that any separable topological graph C
![]() $^{*}$
-algebra
$^{*}$
-algebra
![]() $C^{*}(E)$
can be realised as the groupoid C
$C^{*}(E)$
can be realised as the groupoid C
![]() $^{*}$
-algebra
$^{*}$
-algebra
![]() $C^{*}(\mathcal {G}_{E})$
of a second countable locally compact Hausdorff étale groupoid
$C^{*}(\mathcal {G}_{E})$
of a second countable locally compact Hausdorff étale groupoid
![]() $\mathcal {G}_{E}$
. Following [Reference TomfordeYee07], we construct a groupoid
$\mathcal {G}_{E}$
. Following [Reference TomfordeYee07], we construct a groupoid
![]() $\mathcal {G}_{E}$
which as a set is defined as
$\mathcal {G}_{E}$
which as a set is defined as
The groupoid
![]() $\mathcal {G}_{E}$
is a locally compact Hausdorff étale groupoid when we equip it with the topology generated by sets
$\mathcal {G}_{E}$
is a locally compact Hausdorff étale groupoid when we equip it with the topology generated by sets
where
![]() $m, n \in \mathbb {N}_{0}$
, and
$m, n \in \mathbb {N}_{0}$
, and
![]() $U\subseteq \sigma ^{-m}(\partial E)$
and
$U\subseteq \sigma ^{-m}(\partial E)$
and
![]() $V\subseteq \sigma ^{-n}(\partial E)$
are open sets satisfying that respectively
$V\subseteq \sigma ^{-n}(\partial E)$
are open sets satisfying that respectively
![]() $\sigma ^{m}$
and
$\sigma ^{m}$
and
![]() $\sigma ^{n}$
are homeomorphisms on them. Endowed with this topology, we can identify the topological space
$\sigma ^{n}$
are homeomorphisms on them. Endowed with this topology, we can identify the topological space
![]() $\partial E$
with the unit space
$\partial E$
with the unit space
![]() $\mathcal {G}_{E}^{(0)}$
via the map
$\mathcal {G}_{E}^{(0)}$
via the map
![]() $\partial E \ni \alpha \mapsto (\alpha , 0, \alpha ) \in \mathcal {G}_{E}^{(0)}$
, and the gauge-action
$\partial E \ni \alpha \mapsto (\alpha , 0, \alpha ) \in \mathcal {G}_{E}^{(0)}$
, and the gauge-action
![]() $\{\gamma _{z} \}_{z\in \mathbb {T}}$
on
$\{\gamma _{z} \}_{z\in \mathbb {T}}$
on
![]() $C^{*}(E)$
can be described as the dual action of the homomorphism
$C^{*}(E)$
can be described as the dual action of the homomorphism
![]() $\Phi : \mathcal {G}_{E} \to \mathbb {Z}$
given by
$\Phi : \mathcal {G}_{E} \to \mathbb {Z}$
given by
![]() $\Phi (\alpha , k, \beta )=k$
. This groupoid becomes amenable [Reference Okada and OkazakiYW17] and
$\Phi (\alpha , k, \beta )=k$
. This groupoid becomes amenable [Reference Okada and OkazakiYW17] and
![]() $C^{*}(\mathcal {G}_{E}) \simeq C^{*}(E)$
.
$C^{*}(\mathcal {G}_{E}) \simeq C^{*}(E)$
.
2.4 Tracial weights
We will apply results that were developed for describing KMS states for C
![]() $^{*}$
-dynamical systems arising from continuous
$^{*}$
-dynamical systems arising from continuous
![]() $1$
-cocycles on étale groupoids. These were first developed by Renault for principal groupoids [Reference Yeend and WilliamsRen80] and later generalised by Neshveyev to non-principal groupoids [Reference YeendNes13]. These results in particular apply to tracial states. We will in the following give a recap of these result for tracial weights, see [Reference ChristensenChr23] for the generalisation from states to weights.
$1$
-cocycles on étale groupoids. These were first developed by Renault for principal groupoids [Reference Yeend and WilliamsRen80] and later generalised by Neshveyev to non-principal groupoids [Reference YeendNes13]. These results in particular apply to tracial states. We will in the following give a recap of these result for tracial weights, see [Reference ChristensenChr23] for the generalisation from states to weights.
Recall that a weight
![]() $\psi $
on a C
$\psi $
on a C
![]() $^{*}$
-algebra
$^{*}$
-algebra
![]() $\mathcal {A}$
is a map
$\mathcal {A}$
is a map
![]() $\psi : \mathcal {A}_{+} \to [0, \infty ]$
with
$\psi : \mathcal {A}_{+} \to [0, \infty ]$
with
![]() $\psi (a+b)=\psi (a)+\psi (b)$
and
$\psi (a+b)=\psi (a)+\psi (b)$
and
![]() $\psi (\unicode{x3bb} a) = \unicode{x3bb} \psi (a)$
for all
$\psi (\unicode{x3bb} a) = \unicode{x3bb} \psi (a)$
for all
![]() $\unicode{x3bb} \geq 0$
. We call
$\unicode{x3bb} \geq 0$
. We call
![]() $\psi $
a tracial weight if it is densely defined, lower semi-continuous and
$\psi $
a tracial weight if it is densely defined, lower semi-continuous and
![]() $\psi (a^{*}a)=\psi (aa^{*})$
for all
$\psi (a^{*}a)=\psi (aa^{*})$
for all
![]() $a\in \mathcal {A}$
. A tracial weight
$a\in \mathcal {A}$
. A tracial weight
![]() $\psi $
is extremal when any decomposition
$\psi $
is extremal when any decomposition
![]() $\psi =\psi _{1}+\psi _{2}$
into tracial weights satisfies
$\psi =\psi _{1}+\psi _{2}$
into tracial weights satisfies
![]() $\psi _{1}, \psi _{2} \in \{ \unicode{x3bb} \psi \mid \unicode{x3bb} \geq 0 \}$
.
$\psi _{1}, \psi _{2} \in \{ \unicode{x3bb} \psi \mid \unicode{x3bb} \geq 0 \}$
.
Let us in the following elucidate the close connection between tracial weights on groupoid C
![]() $^{*}$
-algebras and so-called invariant measures on the unit space of the groupoid. Let
$^{*}$
-algebras and so-called invariant measures on the unit space of the groupoid. Let
![]() $\mathcal {G}$
be a locally compact second countable Hausdorff étale groupoid with unit space
$\mathcal {G}$
be a locally compact second countable Hausdorff étale groupoid with unit space
![]() $\mathcal {G}^{(0)}$
, and denote the range map by
$\mathcal {G}^{(0)}$
, and denote the range map by
![]() $r: {\mathcal {G}}\to {\mathcal {G}^{(0)}}$
and the source map by
$r: {\mathcal {G}}\to {\mathcal {G}^{(0)}}$
and the source map by
![]() $s: {\mathcal {G}} \to {\mathcal {G}^{(0)}}$
. Recall that a bisection
$s: {\mathcal {G}} \to {\mathcal {G}^{(0)}}$
. Recall that a bisection
![]() $W \subseteq \mathcal {G}$
is an open set such that
$W \subseteq \mathcal {G}$
is an open set such that
![]() $r(W)$
and
$r(W)$
and
![]() $s(W)$
are open sets, and
$s(W)$
are open sets, and
![]() $r|_{W}:W\to r(W)$
and
$r|_{W}:W\to r(W)$
and
![]() $s|_{W} : W \to s(W)$
are homeomorphisms. We call a measure
$s|_{W} : W \to s(W)$
are homeomorphisms. We call a measure
![]() $\nu $
on
$\nu $
on
![]() ${\mathcal {G}^{(0)}}$
an invariant measure if it is a regular Borel measure on
${\mathcal {G}^{(0)}}$
an invariant measure if it is a regular Borel measure on
![]() $\mathcal {G}^{(0)}$
which satisfies
$\mathcal {G}^{(0)}$
which satisfies
for all open bisection
![]() $W \subseteq \mathcal {G}$
. (We refer to [Reference CohnCoh13] for the definition of a regular measure. We will only consider locally compact second countable Hausdorff spaces, so our measures are regular if and only if they are finite on compact sets.) For any tracial weight
$W \subseteq \mathcal {G}$
. (We refer to [Reference CohnCoh13] for the definition of a regular measure. We will only consider locally compact second countable Hausdorff spaces, so our measures are regular if and only if they are finite on compact sets.) For any tracial weight
![]() $\psi $
on
$\psi $
on
![]() $C^{*}({\mathcal {G}})$
, the restriction of
$C^{*}({\mathcal {G}})$
, the restriction of
![]() $\psi $
to
$\psi $
to
![]() $C_{0}({\mathcal {G}^{(0)}})$
gives rise to an invariant measure
$C_{0}({\mathcal {G}^{(0)}})$
gives rise to an invariant measure
![]() $\nu _{\psi }$
on
$\nu _{\psi }$
on
![]() $\mathcal {G}^{(0)}$
, and any invariant measure
$\mathcal {G}^{(0)}$
, and any invariant measure
![]() $\nu $
on
$\nu $
on
![]() ${\mathcal {G}^{(0)}}$
gives rise to a tracial weight via the formula
${\mathcal {G}^{(0)}}$
gives rise to a tracial weight via the formula
where
![]() $P: C^{*}({\mathcal {G}}) \to C_{0}({\mathcal {G}^{(0)}})$
is the conditional expectation, cf. [Reference ChristensenChr23, Theorem 6.3]. We call an invariant measure
$P: C^{*}({\mathcal {G}}) \to C_{0}({\mathcal {G}^{(0)}})$
is the conditional expectation, cf. [Reference ChristensenChr23, Theorem 6.3]. We call an invariant measure
![]() $\nu $
extremal if any decomposition
$\nu $
extremal if any decomposition
![]() $\nu =\nu _{1}+\nu _{2}$
into invariant measures satisfies that
$\nu =\nu _{1}+\nu _{2}$
into invariant measures satisfies that
![]() $\nu _{1}, \nu _{2} \in \{\unicode{x3bb} \nu \mid \unicode{x3bb} \geq 0 \}$
. We call it ergodic if any invariant Borel set B of
$\nu _{1}, \nu _{2} \in \{\unicode{x3bb} \nu \mid \unicode{x3bb} \geq 0 \}$
. We call it ergodic if any invariant Borel set B of
![]() $\mathcal {G}^{(0)}$
, that is a set with
$\mathcal {G}^{(0)}$
, that is a set with
![]() $s(r^{-1}(B))=B$
, satisfies either
$s(r^{-1}(B))=B$
, satisfies either
![]() $\nu (B)=0$
or
$\nu (B)=0$
or
![]() $\nu (B^{C})=0$
. It then follows from e.g. [Reference ChristensenChr23, Theorem 5.5] that for an invariant measure
$\nu (B^{C})=0$
. It then follows from e.g. [Reference ChristensenChr23, Theorem 5.5] that for an invariant measure
![]() $\nu $
, then
$\nu $
, then
Let us now consider the case of the second countable locally compact Hausdorff étale groupoid
![]() $\mathcal {G}_{E}$
arising from a second countable topological graph E. For this groupoid, it is straightforward to check that
$\mathcal {G}_{E}$
arising from a second countable topological graph E. For this groupoid, it is straightforward to check that
![]() $B\subseteq \mathcal {G}_{E}^{(0)} \cong \partial E$
is invariant in the sense that
$B\subseteq \mathcal {G}_{E}^{(0)} \cong \partial E$
is invariant in the sense that
![]() $s(r^{-1}(B))=B$
if and only if it is invariant under
$s(r^{-1}(B))=B$
if and only if it is invariant under
![]() $\sigma $
as in equation (2.2). If we let
$\sigma $
as in equation (2.2). If we let
![]() $\nu _{\psi }$
be the invariant measure on
$\nu _{\psi }$
be the invariant measure on
![]() ${\mathcal {G}^{(0)}}$
corresponding to a tracial weight
${\mathcal {G}^{(0)}}$
corresponding to a tracial weight
![]() $\psi $
, then the map
$\psi $
, then the map
![]() $\psi \mapsto \nu _{\psi }$
is a surjection from the set of extremal tracial weights on
$\psi \mapsto \nu _{\psi }$
is a surjection from the set of extremal tracial weights on
![]() $C^{*}({\mathcal {G}}_{E})$
to the set of ergodic invariant measures on
$C^{*}({\mathcal {G}}_{E})$
to the set of ergodic invariant measures on
![]() $\partial E$
, cf. [Reference ChristensenChr23, Corollary 7.5]. Furthermore, a regular Borel measure
$\partial E$
, cf. [Reference ChristensenChr23, Corollary 7.5]. Furthermore, a regular Borel measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
satisfies equation (2.3) for
$\partial E$
satisfies equation (2.3) for
![]() $\mathcal {G}_{E}$
if and only if it satisfies the following condition:
$\mathcal {G}_{E}$
if and only if it satisfies the following condition:
see e.g. [Reference ThomsenTho14, (the proof of) Lemma 3.2].
For the groupoid
![]() $\mathcal {G}_{E}$
, we can use [Reference ChristensenChr23, Theorem 7.4] with the groupoid homomorphism
$\mathcal {G}_{E}$
, we can use [Reference ChristensenChr23, Theorem 7.4] with the groupoid homomorphism
![]() $c=0$
and
$c=0$
and
![]() $\Phi : \mathcal {G}_{E} \to \mathbb {Z}$
given by
$\Phi : \mathcal {G}_{E} \to \mathbb {Z}$
given by
![]() $(x,k,y)\mapsto k$
to get the following description of the tracial weights on
$(x,k,y)\mapsto k$
to get the following description of the tracial weights on
![]() $C^{*}(E)$
.
$C^{*}(E)$
.
Theorem 2.3. Let E be a second countable topological graph. Define for all
![]() $\alpha \in \partial E$
the set
$\alpha \in \partial E$
the set
Let
![]() $\nu $
be an extremal non-zero invariant measure on
$\nu $
be an extremal non-zero invariant measure on
![]() $\partial E$
. There exists a unique subgroup H of
$\partial E$
. There exists a unique subgroup H of
![]() $\mathbb {Z}$
with
$\mathbb {Z}$
with
and there is an affine bijection between the state space of
![]() $C^{*}(H)$
and the set of tracial weights
$C^{*}(H)$
and the set of tracial weights
![]() $\psi $
on
$\psi $
on
![]() $C^{*}(\mathcal {G}_{E})$
satisfying that
$C^{*}(\mathcal {G}_{E})$
satisfying that
![]() $\nu _{\psi }=\nu $
. A state
$\nu _{\psi }=\nu $
. A state
![]() $\phi $
on
$\phi $
on
![]() $C^{*}(H)$
maps to a tracial weight
$C^{*}(H)$
maps to a tracial weight
![]() $\psi _{\nu , \phi }$
satisfying
$\psi _{\nu , \phi }$
satisfying
 $$ \begin{align*} \psi_{\nu, \phi}(f) := \int_{\partial E} \sum_{(\alpha, k-l, \alpha) \in \mathcal{G}_{E}} f((\alpha, k-l, \alpha)) \phi(u_{k-l})\,{d} \nu(\alpha) \quad \text{for all}\ f\in C_{c}(\mathcal{G}_{E}), \end{align*} $$
$$ \begin{align*} \psi_{\nu, \phi}(f) := \int_{\partial E} \sum_{(\alpha, k-l, \alpha) \in \mathcal{G}_{E}} f((\alpha, k-l, \alpha)) \phi(u_{k-l})\,{d} \nu(\alpha) \quad \text{for all}\ f\in C_{c}(\mathcal{G}_{E}), \end{align*} $$
where
![]() $\{u_{g}\}_{g\in H}$
are the canonical unitary generators of
$\{u_{g}\}_{g\in H}$
are the canonical unitary generators of
![]() $C^{*}(H)$
.
$C^{*}(H)$
.
3 Invariant measures and their Riesz decomposition
Having established the necessary preliminaries, we will now study the invariant measures on the boundary path space
![]() $\partial E$
.
$\partial E$
.
Assume
![]() $\varphi :X\to Y$
is a local homeomorphism between two locally compact Hausdorff spaces X and Y. For
$\varphi :X\to Y$
is a local homeomorphism between two locally compact Hausdorff spaces X and Y. For
![]() $f\in C_{c}(X)$
, the function
$f\in C_{c}(X)$
, the function
![]() $Y\ni y\mapsto \sum _{x\in \varphi ^{-1}(y)} f(x)$
is an element of
$Y\ni y\mapsto \sum _{x\in \varphi ^{-1}(y)} f(x)$
is an element of
![]() $C_{c}(Y)$
, cf. [Reference RenaultSch18, Lemma 2.5]. It follows that any regular measure
$C_{c}(Y)$
, cf. [Reference RenaultSch18, Lemma 2.5]. It follows that any regular measure
![]() $\mu $
on Y gives rise to a regular measure
$\mu $
on Y gives rise to a regular measure
![]() $\varphi ^{*}\mu $
on X via this map.
$\varphi ^{*}\mu $
on X via this map.
Let
![]() $E=(E^{0}, E^{1}, r,s)$
be a topological graph. Since
$E=(E^{0}, E^{1}, r,s)$
be a topological graph. Since
![]() $s:E^{1} \to E^{0}$
is a local homeomorphism, any regular Borel measure
$s:E^{1} \to E^{0}$
is a local homeomorphism, any regular Borel measure
![]() $\mu $
on
$\mu $
on
![]() $E^{0}$
gives rise to a regular Borel measure
$E^{0}$
gives rise to a regular Borel measure
![]() $s^{*}\mu $
on
$s^{*}\mu $
on
![]() $E^{1}$
satisfying that
$E^{1}$
satisfying that
 $$ \begin{align*} \int_{E^{1}} h\,{d} s^{*} \mu = \int_{E^{0}} \sum_{e\in s^{-1}(v)} h(e)\,{d} \mu(v) \quad\text{for all } h\in C_{c}(E^{1}). \end{align*} $$
$$ \begin{align*} \int_{E^{1}} h\,{d} s^{*} \mu = \int_{E^{0}} \sum_{e\in s^{-1}(v)} h(e)\,{d} \mu(v) \quad\text{for all } h\in C_{c}(E^{1}). \end{align*} $$
Definition 3.1. Let
![]() $\mu $
be a regular Borel measure on
$\mu $
be a regular Borel measure on
![]() $E^{0}$
. We call
$E^{0}$
. We call
![]() $\mu $
a vertex-invariant measure if it satisfies
$\mu $
a vertex-invariant measure if it satisfies
for all positive functions
![]() $f\in C_{c}(E^{0})$
, and with equality when
$f\in C_{c}(E^{0})$
, and with equality when
![]() $\text {supp}(f) \subseteq E_{\mathrm {reg}}^{0}$
.
$\text {supp}(f) \subseteq E_{\mathrm {reg}}^{0}$
.
Notice that our vertex-invariant measures were introduced as invariant measure in [Reference RenaultSch18, Definition 4.1], except that we consider regular measures where [Reference RenaultSch18] requires that the measures are probability measures. Since we also use the term invariant measure for the
![]() $\sigma $
-invariant measures on the boundary path space
$\sigma $
-invariant measures on the boundary path space
![]() $\partial E$
, cf. equation (2.5), we will use the terminology vertex-invariant measure for a measure satisfying Definition 3.1. It was established in [Reference RenaultSch18, Proposition 4.4] that a vertex-invariant probability measure gives rise to an invariant probability measure on the boundary path space
$\partial E$
, cf. equation (2.5), we will use the terminology vertex-invariant measure for a measure satisfying Definition 3.1. It was established in [Reference RenaultSch18, Proposition 4.4] that a vertex-invariant probability measure gives rise to an invariant probability measure on the boundary path space
![]() $\partial E$
. In the following, we will generalise this result to all regular measures.
$\partial E$
. In the following, we will generalise this result to all regular measures.
Proposition 3.2. [Reference RenaultSch18]
Let E be a second countable topological graph and let
![]() $\mu $
be a vertex-invariant measure on
$\mu $
be a vertex-invariant measure on
![]() $E^{0}$
. There exists a regular invariant measure
$E^{0}$
. There exists a regular invariant measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
such that
$\partial E$
such that
We will provide a new proof of this result, in part to handle the more general case of regular measures and in part because our new proof will provide a better understanding of regular invariant measures, which will be important in our later analysis. The first step in this new proof is to decompose the vertex-invariant measures. For the statement of the next theorem, we remind the reader that the notation
![]() $\varphi _{*}\mu $
denotes the push-forward measures of
$\varphi _{*}\mu $
denotes the push-forward measures of
![]() $\mu $
under the map
$\mu $
under the map
![]() $\varphi $
.
$\varphi $
.
Theorem 3.3. Let E be a second countable topological graph and let T denote the map
![]() $\mu \mapsto r_{*}(s^{*}(\mu ))$
which maps regular Borel measures on
$\mu \mapsto r_{*}(s^{*}(\mu ))$
which maps regular Borel measures on
![]() $E^{0}$
to Borel measures on
$E^{0}$
to Borel measures on
![]() $E^{0}$
.
$E^{0}$
.
Let
![]() $\mu $
be a vertex-invariant measure on
$\mu $
be a vertex-invariant measure on
![]() $E^{0}$
. Then
$E^{0}$
. Then
![]() $\mu $
has a unique decomposition
$\mu $
has a unique decomposition
![]() $\mu =\mu _{1}+\mu _{2}$
into two vertex-invariant measures
$\mu =\mu _{1}+\mu _{2}$
into two vertex-invariant measures
![]() $\mu _{1}$
and
$\mu _{1}$
and
![]() $\mu _{2}$
, where
$\mu _{2}$
, where
Proof. Assume that
![]() $f\in C_{c}(E^{0})$
is positive and
$f\in C_{c}(E^{0})$
is positive and
![]() $\mu $
is vertex-invariant. We then claim that
$\mu $
is vertex-invariant. We then claim that
for all
![]() $n\in \mathbb {N}$
. By assumption, it is true for
$n\in \mathbb {N}$
. By assumption, it is true for
![]() $n=1$
. Assume that it holds true for all
$n=1$
. Assume that it holds true for all
![]() $k\leq n$
for some
$k\leq n$
for some
![]() $n\in \mathbb {N}$
. Then
$n\in \mathbb {N}$
. Then
![]() $T^{n} \mu $
and
$T^{n} \mu $
and
![]() $T^{n-1} \mu $
are regular and
$T^{n-1} \mu $
are regular and
![]() $T^{n} \mu \leq T^{n-1} \mu $
, so
$T^{n} \mu \leq T^{n-1} \mu $
, so
 $$ \begin{align*} \int_{E^{0}} f\,{d} (T^{n+1}\mu) &= \int_{E^{0}} \sum_{e\in s^{-1}(v)} f\circ r(e)\,{d} (T^{n}\mu)(v) \leq \int_{E^{0}} \sum_{e\in s^{-1}(v)} f\circ r(e)\,{d} (T^{n-1}\mu) (v)\\ &= \int_{E^{0}} f\,{d} (T^{n}\mu), \end{align*} $$
$$ \begin{align*} \int_{E^{0}} f\,{d} (T^{n+1}\mu) &= \int_{E^{0}} \sum_{e\in s^{-1}(v)} f\circ r(e)\,{d} (T^{n}\mu)(v) \leq \int_{E^{0}} \sum_{e\in s^{-1}(v)} f\circ r(e)\,{d} (T^{n-1}\mu) (v)\\ &= \int_{E^{0}} f\,{d} (T^{n}\mu), \end{align*} $$
proving the claim. It follows that
![]() $T^{n} \mu $
is a regular measure for all
$T^{n} \mu $
is a regular measure for all
![]() $n\in \mathbb {N}_{0}$
when
$n\in \mathbb {N}_{0}$
when
![]() $\mu $
is a vertex-invariant measure. As a consequence, we can define a regular measure
$\mu $
is a vertex-invariant measure. As a consequence, we can define a regular measure
![]() $\mu _{1}$
with
$\mu _{1}$
with
![]() $\mu _{1} \leq \mu $
by setting
$\mu _{1} \leq \mu $
by setting
Since
![]() $\mu _{1} \leq \mu $
and
$\mu _{1} \leq \mu $
and
 $$ \begin{align*} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e)\,{d} \mu <\infty \end{align*} $$
$$ \begin{align*} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e)\,{d} \mu <\infty \end{align*} $$
for
![]() $f\in C_{c}(E^{0})$
, one can use dominated convergence to prove
$f\in C_{c}(E^{0})$
, one can use dominated convergence to prove
 $$ \begin{align*} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e) \,{d}\mu_{1} = \lim_{n\to \infty} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e) \,{d}(T^{n}\mu) \end{align*} $$
$$ \begin{align*} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e) \,{d}\mu_{1} = \lim_{n\to \infty} \int_{E^{0}} \sum_{e\in s^{-1}(v)} f \circ r(e) \,{d}(T^{n}\mu) \end{align*} $$
for
![]() $f\in C_{c}(E^{0})$
. This implies that
$f\in C_{c}(E^{0})$
. This implies that
![]() $T\mu _{1} = \mu _{1}$
. Set
$T\mu _{1} = \mu _{1}$
. Set
![]() $\mu _{2}=\mu -\mu _{1}$
, it is then straightforward to check that
$\mu _{2}=\mu -\mu _{1}$
, it is then straightforward to check that
![]() $\mu _{1}$
and
$\mu _{1}$
and
![]() $\mu _{2}$
are vertex-invariant. For any function
$\mu _{2}$
are vertex-invariant. For any function
![]() $f\in C_{c}(E^{0})$
and
$f\in C_{c}(E^{0})$
and
![]() $\varepsilon>0$
, there then exists an
$\varepsilon>0$
, there then exists an
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
 $$ \begin{align*} \bigg|{\int_{E^{0}}}\, f \,{d}(T^{n}\mu_{2}) \bigg |= \bigg |{\int_{E^{0}}}\, f \,{d}(T^{n}\mu) - \int_{E^{0}} f \,{d}\mu_{1} \bigg | \leq \varepsilon \quad \text{for all } n\geq N. \end{align*} $$
$$ \begin{align*} \bigg|{\int_{E^{0}}}\, f \,{d}(T^{n}\mu_{2}) \bigg |= \bigg |{\int_{E^{0}}}\, f \,{d}(T^{n}\mu) - \int_{E^{0}} f \,{d}\mu_{1} \bigg | \leq \varepsilon \quad \text{for all } n\geq N. \end{align*} $$
This proves that the decomposition exists. We leave it to the reader to check that the decomposition is unique.
Using Theorem 3.3, we can now provide a new proof of Proposition 3.2.
Proof of Proposition 3.2
Assume first that
![]() $\mu $
is a vertex-invariant measure satisfying that
$\mu $
is a vertex-invariant measure satisfying that
We define a regular positive measure
![]() $\eta $
on
$\eta $
on
![]() $E^{0}$
by
$E^{0}$
by
It is straightforward to check that
![]() $E_{\mathrm {sng}}^{n}$
with the subspace topology from
$E_{\mathrm {sng}}^{n}$
with the subspace topology from
![]() $E^{n}$
is homeomorphic with the Borel subset
$E^{n}$
is homeomorphic with the Borel subset
![]() $E_{\mathrm {sng}}^{n}$
of
$E_{\mathrm {sng}}^{n}$
of
![]() $\partial E$
. Let
$\partial E$
. Let
![]() $s_{n}: E^{n} \to E^{0}$
be the source map, since it is a local homeomorphism, we can therefore consider
$s_{n}: E^{n} \to E^{0}$
be the source map, since it is a local homeomorphism, we can therefore consider
![]() $s_{n}^{*} \eta $
as a Borel measure on
$s_{n}^{*} \eta $
as a Borel measure on
![]() $\partial E$
supported on
$\partial E$
supported on
![]() $E^{n}_{\mathrm {sng}}$
. We now claim that
$E^{n}_{\mathrm {sng}}$
. We now claim that
 $$ \begin{align*} \nu:=\sum_{n=0}^{\infty} s_{n}^{*} \eta \end{align*} $$
$$ \begin{align*} \nu:=\sum_{n=0}^{\infty} s_{n}^{*} \eta \end{align*} $$
is a regular invariant measure on
![]() $\partial E$
such that
$\partial E$
such that
![]() $r_{*}\nu = \mu $
. Let
$r_{*}\nu = \mu $
. Let
![]() $f\in C_{c}(E^{0})$
be positive. The map
$f\in C_{c}(E^{0})$
be positive. The map
![]() $f\circ r$
is not necessarily compactly supported, but by approximating it by compactly supported functions from below and using monotone convergence, we get for any
$f\circ r$
is not necessarily compactly supported, but by approximating it by compactly supported functions from below and using monotone convergence, we get for any
![]() $i\in \mathbb {N}_{0}$
that
$i\in \mathbb {N}_{0}$
that
 $$ \begin{align*} \int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha)\,{d} T\mu(v)&= \int_{E^{0}} \sum_{e\in s^{-1}(v)}\sum_{\alpha \in s_{i}^{-1}(r(e)) } f\circ r(\alpha) \,{d} \mu(v)\\ &=\int_{E^{0}} \sum_{\beta \in s_{i+1}^{-1}(v) } f\circ r(\beta)\,{d} \mu(v) , \end{align*} $$
$$ \begin{align*} \int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha)\,{d} T\mu(v)&= \int_{E^{0}} \sum_{e\in s^{-1}(v)}\sum_{\alpha \in s_{i}^{-1}(r(e)) } f\circ r(\alpha) \,{d} \mu(v)\\ &=\int_{E^{0}} \sum_{\beta \in s_{i+1}^{-1}(v) } f\circ r(\beta)\,{d} \mu(v) , \end{align*} $$
from which it follows that
 $$ \begin{align*} \int_{\partial E} f\circ r\,{d} s_{i}^{*} \eta &=\int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} \eta(v) \\ &= \int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} \mu(v) -\int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} T\mu(v) \\ &= \int_{E^{0}} f \, {d} T^{i}\mu - \int_{E^{0}} f \,{d} T^{i+1}\mu. \end{align*} $$
$$ \begin{align*} \int_{\partial E} f\circ r\,{d} s_{i}^{*} \eta &=\int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} \eta(v) \\ &= \int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} \mu(v) -\int_{E^{0}} \sum_{\alpha \in s_{i}^{-1}(v) } f\circ r(\alpha) \,{d} T\mu(v) \\ &= \int_{E^{0}} f \, {d} T^{i}\mu - \int_{E^{0}} f \,{d} T^{i+1}\mu. \end{align*} $$
By assumption, this implies that
If
![]() $S\subseteq E^{0}$
, it is easy to check that
$S\subseteq E^{0}$
, it is easy to check that
![]() $1_{S} \circ r = 1_{Z(S)}$
, and since
$1_{S} \circ r = 1_{Z(S)}$
, and since
![]() $\partial E$
can be covered by open sets
$\partial E$
can be covered by open sets
![]() $Z(U)$
with
$Z(U)$
with
![]() $U\subseteq E^{0}$
open and
$U\subseteq E^{0}$
open and
![]() $\mu (U)<\infty $
, this equality implies that
$\mu (U)<\infty $
, this equality implies that
![]() $\nu $
is a regular measure. Since
$\nu $
is a regular measure. Since
![]() $s_{i}^{*} \eta $
is concentrated on
$s_{i}^{*} \eta $
is concentrated on
![]() $E^{i}_{\mathrm {sng}}$
, we first see that if
$E^{i}_{\mathrm {sng}}$
, we first see that if
![]() $A\subseteq E^{\infty }$
is Borel, then
$A\subseteq E^{\infty }$
is Borel, then
![]() $\nu (A)=0=\nu (\sigma (A))$
. By second countability, it therefore suffices to check that
$\nu (A)=0=\nu (\sigma (A))$
. By second countability, it therefore suffices to check that
![]() $\nu (A)=\nu (\sigma (A))$
for a Borel set
$\nu (A)=\nu (\sigma (A))$
for a Borel set
![]() $A \subseteq E^{i}_{\mathrm {sng}}$
with
$A \subseteq E^{i}_{\mathrm {sng}}$
with
![]() $s_{i}$
and
$s_{i}$
and
![]() $\sigma $
injective on A, yet for such a set, we have that
$\sigma $
injective on A, yet for such a set, we have that
which proves the proposition for measures
![]() $\mu $
satisfying equation (3.1).
$\mu $
satisfying equation (3.1).
Assume now that
![]() $\mu $
satisfies that
$\mu $
satisfies that
![]() $T\mu = \mu $
. Following [Reference RenaultSch18, §3], we define
$T\mu = \mu $
. Following [Reference RenaultSch18, §3], we define
![]() $\partial E_{n} := E_{\mathrm {sng}}^{0} \cup \cdots \cup E_{\mathrm {sng}}^{n-1}\cup E^{n}$
and set
$\partial E_{n} := E_{\mathrm {sng}}^{0} \cup \cdots \cup E_{\mathrm {sng}}^{n-1}\cup E^{n}$
and set
where
![]() $S \subseteq E^{*}$
. Then,
$S \subseteq E^{*}$
. Then,
![]() $\partial E_{n}$
equipped with the topology generated by the basis
$\partial E_{n}$
equipped with the topology generated by the basis
![]() $Z_{n}(U)\setminus Z_{n}(K)$
with
$Z_{n}(U)\setminus Z_{n}(K)$
with
![]() $U\subseteq E^{*}$
open and
$U\subseteq E^{*}$
open and
![]() $K \subseteq E^{*}$
compact satisfies that
$K \subseteq E^{*}$
compact satisfies that
![]() $\rho _{n}:\partial E_{n} \to \partial E_{n-1}$
, defined by
$\rho _{n}:\partial E_{n} \to \partial E_{n-1}$
, defined by
 $$ \begin{align*} \rho_{n}(\alpha_{1} \cdots \alpha_{k})= \begin{cases} \alpha_{1} \cdots \alpha_{n-1} & \text{if } k=n , \\ \alpha_{1} \cdots \alpha_{k} & \text{if } k<n, \end{cases} \end{align*} $$
$$ \begin{align*} \rho_{n}(\alpha_{1} \cdots \alpha_{k})= \begin{cases} \alpha_{1} \cdots \alpha_{n-1} & \text{if } k=n , \\ \alpha_{1} \cdots \alpha_{k} & \text{if } k<n, \end{cases} \end{align*} $$
is a proper, continuous and surjective map, and that we get a homeomorphism
cf. [Reference RenaultSch18, Proposition 3.3]. Since
![]() $\sigma ^{n}:\partial E_{n} \cap E^{n} \to E^{0}$
is a local homeomorphism by [Reference RenaultSch18, Proposition 3.5], we can define a Borel measure
$\sigma ^{n}:\partial E_{n} \cap E^{n} \to E^{0}$
is a local homeomorphism by [Reference RenaultSch18, Proposition 3.5], we can define a Borel measure
![]() $(\sigma ^{n})^{*}(\mu )$
on
$(\sigma ^{n})^{*}(\mu )$
on
![]() $\partial E_{n}$
which is concentrated on
$\partial E_{n}$
which is concentrated on
![]() $E^{n}$
.
$E^{n}$
.
Claim:
![]() $r_{*}(\sigma ^{n})^{*} \mu = \mu $
for all
$r_{*}(\sigma ^{n})^{*} \mu = \mu $
for all
![]() $n\in \mathbb {N}$
. Assume that
$n\in \mathbb {N}$
. Assume that
![]() $f\in C_{c}(E^{0})$
is positive and
$f\in C_{c}(E^{0})$
is positive and
![]() $n\in \mathbb {N}$
. Then
$n\in \mathbb {N}$
. Then
 $$ \begin{align*} \int_{E^{0}} f\,{d} r_{*}(\sigma^{n+1})^{*} \mu &= \int_{\partial E_{n+1}} f\circ r \,{d} (\sigma^{n+1})^{*} \mu = \int_{E^{0}} \sum_{\alpha\in (\sigma^{n+1})^{-1} (v) } f\circ r(\alpha) \,{d} \mu (v) \\ &= \int_{E^{0}} \sum_{e \in s^{-1}(v)} \sum_{\alpha\in (\sigma^{n})^{-1} (r(e)) } f\circ r(\alpha e) \,{d} \mu (v)\\ &= \int_{E^{0}} \sum_{\alpha\in (\sigma^{n})^{-1} (v) } f\circ r(\alpha) \,{d} T\mu (v) \\ &= \int_{E^{0}} f \,{d} r_{*}(\sigma^{n})^{*} \mu, \end{align*} $$
$$ \begin{align*} \int_{E^{0}} f\,{d} r_{*}(\sigma^{n+1})^{*} \mu &= \int_{\partial E_{n+1}} f\circ r \,{d} (\sigma^{n+1})^{*} \mu = \int_{E^{0}} \sum_{\alpha\in (\sigma^{n+1})^{-1} (v) } f\circ r(\alpha) \,{d} \mu (v) \\ &= \int_{E^{0}} \sum_{e \in s^{-1}(v)} \sum_{\alpha\in (\sigma^{n})^{-1} (r(e)) } f\circ r(\alpha e) \,{d} \mu (v)\\ &= \int_{E^{0}} \sum_{\alpha\in (\sigma^{n})^{-1} (v) } f\circ r(\alpha) \,{d} T\mu (v) \\ &= \int_{E^{0}} f \,{d} r_{*}(\sigma^{n})^{*} \mu, \end{align*} $$
since
![]() $T\mu = \mu $
. This proves the claim.
$T\mu = \mu $
. This proves the claim.
Using the claim, we can now see that for
![]() $U\subseteq E^{0}$
open with compact closure, then
$U\subseteq E^{0}$
open with compact closure, then
and hence
![]() $(\sigma ^{n})^{*}(\mu )$
is a regular measure on
$(\sigma ^{n})^{*}(\mu )$
is a regular measure on
![]() $\partial E_{n}$
. For
$\partial E_{n}$
. For
![]() $f\in C_{c}(\partial E_{n-1})$
, we get
$f\in C_{c}(\partial E_{n-1})$
, we get
 $$ \begin{align*} \int_{\partial E_{n}} f\circ \rho_{n} \,{d} (\sigma^{n})^{*} \mu &= \int_{E^{0}} \sum_{\alpha \in (\sigma^{n})^{-1}(v)} f\circ \rho_{n}(\alpha) \,{d} \mu(v)\\ &= \int_{E^{0}} \sum_{e\in s^{-1}( v)} \sum_{\beta \in (\sigma^{n-1})^{-1}(r(e))} f(\beta) \,{d} \mu(v)\\ &=\int_{E^{0}} \sum_{\beta \in (\sigma^{n-1})^{-1}(v)} f(\beta) \,{d} T\mu(v) = \int_{\partial E_{n-1}} f \,{d} (\sigma^{n-1})^{*}\mu , \end{align*} $$
$$ \begin{align*} \int_{\partial E_{n}} f\circ \rho_{n} \,{d} (\sigma^{n})^{*} \mu &= \int_{E^{0}} \sum_{\alpha \in (\sigma^{n})^{-1}(v)} f\circ \rho_{n}(\alpha) \,{d} \mu(v)\\ &= \int_{E^{0}} \sum_{e\in s^{-1}( v)} \sum_{\beta \in (\sigma^{n-1})^{-1}(r(e))} f(\beta) \,{d} \mu(v)\\ &=\int_{E^{0}} \sum_{\beta \in (\sigma^{n-1})^{-1}(v)} f(\beta) \,{d} T\mu(v) = \int_{\partial E_{n-1}} f \,{d} (\sigma^{n-1})^{*}\mu , \end{align*} $$
which proves that
![]() $(\rho _{n})_{*} (\sigma ^{n})^{*} \mu = (\sigma ^{n-1})^{*} \mu $
. By [Reference NeshveyevOO78, Theorem 1], there therefore exists a unique regular measure
$(\rho _{n})_{*} (\sigma ^{n})^{*} \mu = (\sigma ^{n-1})^{*} \mu $
. By [Reference NeshveyevOO78, Theorem 1], there therefore exists a unique regular measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
such that
$\partial E$
such that
![]() $\nu \circ p_{n}^{-1} = (\sigma ^{n})^{*} \mu $
, where
$\nu \circ p_{n}^{-1} = (\sigma ^{n})^{*} \mu $
, where
![]() $p_{n}$
is the projection from
$p_{n}$
is the projection from
![]() $\partial E$
to
$\partial E$
to
![]() $\partial E_{n}$
.
$\partial E_{n}$
.
To see that
![]() $\nu $
is invariant, let
$\nu $
is invariant, let
![]() $O \subseteq E^{*}$
be an open set such that
$O \subseteq E^{*}$
be an open set such that
![]() $\sigma $
is injective on
$\sigma $
is injective on
![]() $Z(O) \subseteq \partial E \setminus E^{0}$
. Pick a
$Z(O) \subseteq \partial E \setminus E^{0}$
. Pick a
![]() $k\in \mathbb {N}$
and open subsets
$k\in \mathbb {N}$
and open subsets
![]() $Z(U_{i}) \setminus Z(K_{i}) \subseteq Z(O)$
for
$Z(U_{i}) \setminus Z(K_{i}) \subseteq Z(O)$
for
![]() $i=1, \dots , k$
as in Lemma 2.1. For sufficiently big n, then
$i=1, \dots , k$
as in Lemma 2.1. For sufficiently big n, then
![]() $p_{n}^{-1}(Z_{n}(U_{i}) \setminus Z_{n}(K_{i})) = Z(U_{i}) \setminus Z(K_{i})$
for all
$p_{n}^{-1}(Z_{n}(U_{i}) \setminus Z_{n}(K_{i})) = Z(U_{i}) \setminus Z(K_{i})$
for all
![]() $1\leq i \leq k$
, so we have that
$1\leq i \leq k$
, so we have that
 $$ \begin{align*} \nu\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i}) \bigg) = (\sigma^{n})^{*} \mu \bigg(\bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) \end{align*} $$
$$ \begin{align*} \nu\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i}) \bigg) = (\sigma^{n})^{*} \mu \bigg(\bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) \end{align*} $$
and using that
![]() $\sigma $
is injective on
$\sigma $
is injective on
![]() $Z(O)$
and item (3) in Lemma 2.1, we get that
$Z(O)$
and item (3) in Lemma 2.1, we get that
 $$ \begin{align} \nonumber \nu\bigg[\sigma\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg)\bigg] &=\nu\bigg[\bigcap_{i=1}^{k} Z(\sigma(U_{i})) \setminus Z(\sigma(K_{i}))\bigg] \\ &=(\sigma^{n-1})^{*} \mu \bigg(\bigcap_{i=1}^{k} Z_{n-1}(\sigma(U_{i})) \setminus Z_{n-1}(\sigma(K_{i}))\bigg)\nonumber\\ &= (\sigma^{n-1})^{*} \mu \bigg( \sigma\bigg(\bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) \bigg). \end{align} $$
$$ \begin{align} \nonumber \nu\bigg[\sigma\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg)\bigg] &=\nu\bigg[\bigcap_{i=1}^{k} Z(\sigma(U_{i})) \setminus Z(\sigma(K_{i}))\bigg] \\ &=(\sigma^{n-1})^{*} \mu \bigg(\bigcap_{i=1}^{k} Z_{n-1}(\sigma(U_{i})) \setminus Z_{n-1}(\sigma(K_{i}))\bigg)\nonumber\\ &= (\sigma^{n-1})^{*} \mu \bigg( \sigma\bigg(\bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) \bigg). \end{align} $$
If
![]() $\sigma $
is injective on a set
$\sigma $
is injective on a set
![]() $A \subseteq \partial E_{n} \setminus E^{0}$
, then by second countability, we can write
$A \subseteq \partial E_{n} \setminus E^{0}$
, then by second countability, we can write
such that
![]() $\sigma ^{n}$
is injective on
$\sigma ^{n}$
is injective on
![]() $A_{k}$
for
$A_{k}$
for
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $A_{0} \cap E^{n}=\emptyset $
, and hence
$A_{0} \cap E^{n}=\emptyset $
, and hence
Using this observation and equation (3.2), we see that
 $$ \begin{align*} \nu\bigg[\sigma\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg)\bigg] = (\sigma^{n})^{*} \mu \bigg( \bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) =\nu\bigg[\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg] , \end{align*} $$
$$ \begin{align*} \nu\bigg[\sigma\bigg(\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg)\bigg] = (\sigma^{n})^{*} \mu \bigg( \bigcap_{i=1}^{k} Z_{n}(U_{i}) \setminus Z_{n}(K_{i})\bigg) =\nu\bigg[\bigcap_{i=1}^{k} Z(U_{i}) \setminus Z(K_{i})\bigg] , \end{align*} $$
and since intersections of such sets from Lemma 2.1 are a
![]() $\pi $
-system, we have that
$\pi $
-system, we have that
![]() $\nu $
is
$\nu $
is
![]() $\sigma $
-invariant, cf. [Reference CohnCoh13, Corollary 1.6.4].
$\sigma $
-invariant, cf. [Reference CohnCoh13, Corollary 1.6.4].
By linearity and Theorem 3.3, we have now proven Proposition 3.2.
Remark 3.4. Notice that the invariant measure associated to a vertex-invariant measure
![]() $\mu $
with
$\mu $
with
![]() $T\mu =\mu $
is concentrated on
$T\mu =\mu $
is concentrated on
![]() $E^{\infty }$
, while an invariant measure associated to a vertex-invariant measure
$E^{\infty }$
, while an invariant measure associated to a vertex-invariant measure
![]() $\mu $
with
$\mu $
with
is concentrated on
![]() $E^{*}_{\mathrm {sng}}$
.
$E^{*}_{\mathrm {sng}}$
.
Remark 3.5. The motivation for providing a new proof is mainly to deduce Remark 3.4, but there is also a minor detail in the original proof in [Reference RenaultSch18] that is unclear. In [Reference RenaultSch18, equation (6) of Proposition 4.4], a function
![]() $f\in C_{c}(\partial E_{n+1})$
is integrated over
$f\in C_{c}(\partial E_{n+1})$
is integrated over
![]() $\partial E_{n+1}\setminus E^{0}$
for a regular measure on
$\partial E_{n+1}\setminus E^{0}$
for a regular measure on
![]() $\partial E_{n+1}\setminus E^{0}$
. A priori, this is not necessarily finite: if m is a regular measure on U and U is an open set in a space X, then m might not be a regular measure on X. As an example, consider the topological graph E with
$\partial E_{n+1}\setminus E^{0}$
. A priori, this is not necessarily finite: if m is a regular measure on U and U is an open set in a space X, then m might not be a regular measure on X. As an example, consider the topological graph E with
![]() $E^{0}=[0,1]$
,
$E^{0}=[0,1]$
,
![]() $E^{1}=(0,1)$
, and r and s the inclusion maps. It is then clear that
$E^{1}=(0,1)$
, and r and s the inclusion maps. It is then clear that
![]() $\partial E_{1}=[0,1]$
with its normal topology and that
$\partial E_{1}=[0,1]$
with its normal topology and that
![]() $\partial E_{1}\setminus E_{0}=(0,1)$
. Consider the measure
$\partial E_{1}\setminus E_{0}=(0,1)$
. Consider the measure
on
![]() $(0,1)$
, where
$(0,1)$
, where
![]() $\delta _{1/n}$
is the Dirac-measure at
$\delta _{1/n}$
is the Dirac-measure at
![]() $1/n$
. Then m is a regular measure on
$1/n$
. Then m is a regular measure on
![]() $(0,1)$
since it is finite on compact sets, yet it is not a regular measure on
$(0,1)$
since it is finite on compact sets, yet it is not a regular measure on
![]() $[0,1]$
. In the proof of [Reference RenaultSch18, Proposition 4.4], one can remedy this fact by including a regularity statement in the inductive proof of equation (7).
$[0,1]$
. In the proof of [Reference RenaultSch18, Proposition 4.4], one can remedy this fact by including a regularity statement in the inductive proof of equation (7).
It is proven in [Reference RenaultSch18, Theorem 6.3] that there exists an affine homeomorphisms between the vertex-invariant probability measures and the gauge-invariant tracial states on
![]() $C^{*}(E)$
. Since a tracial state
$C^{*}(E)$
. Since a tracial state
![]() $\omega $
is gauge-invariant if and only if
$\omega $
is gauge-invariant if and only if
![]() $\omega =\omega \circ P$
with
$\omega =\omega \circ P$
with
![]() $P:C^{*}(E)\to C_{0}(\partial E)$
the canonical conditional expectation, one gets an affine bijection between the vertex-invariant probability measures and the invariant probability measures. For regular invariant measures, we provide a direct proof of this fact for second countable graphs.
$P:C^{*}(E)\to C_{0}(\partial E)$
the canonical conditional expectation, one gets an affine bijection between the vertex-invariant probability measures and the invariant probability measures. For regular invariant measures, we provide a direct proof of this fact for second countable graphs.
Proposition 3.6. Let
![]() $E=(E^{0}, E^{1}, r, s)$
be a second countable topological graph. The map
$E=(E^{0}, E^{1}, r, s)$
be a second countable topological graph. The map
![]() $\nu \mapsto r_{*} \nu $
defines an affine bijection between the set of invariant measures on
$\nu \mapsto r_{*} \nu $
defines an affine bijection between the set of invariant measures on
![]() $\partial E$
and the set of vertex-invariant measures on
$\partial E$
and the set of vertex-invariant measures on
![]() $E^{0}$
.
$E^{0}$
.
Proof. Let us first check that the map is well defined, that is, that
![]() $r_{*} \nu $
satisfies Definition 3.1. Let therefore
$r_{*} \nu $
satisfies Definition 3.1. Let therefore
![]() $\nu $
be a regular measure on
$\nu $
be a regular measure on
![]() $\partial E$
. If
$\partial E$
. If
![]() $K\subseteq E^{0}$
is compact, then
$K\subseteq E^{0}$
is compact, then
![]() $Z(K)$
is compact in
$Z(K)$
is compact in
![]() $\partial E$
and hence
$\partial E$
and hence
![]() $\nu (r^{-1}(K))=\nu (Z(K))<\infty $
. So
$\nu (r^{-1}(K))=\nu (Z(K))<\infty $
. So
![]() $r_{*}\nu $
is a regular measure. Let
$r_{*}\nu $
is a regular measure. Let
![]() $f\in C_{c}(E^{0})$
be positive, then we get
$f\in C_{c}(E^{0})$
be positive, then we get
 $$ \begin{align} \int_{E^{1}} f \circ r \,{d} s^{*}(r_{*}\nu) &= \int_{E^{0}} \sum_{e\in s^{-1}(v) } f \circ r (e)\,{d} r_{*}\nu (v) = \int_{\partial E} \sum_{e\in s^{-1}(r(\alpha)) } f \circ r (e)\,{d} \nu (\alpha) \nonumber\\ &= \int_{\partial E} \sum_{\beta\in \sigma^{-1}(\alpha) } f \circ r (\beta)\,{d} \nu (\alpha). \end{align} $$
$$ \begin{align} \int_{E^{1}} f \circ r \,{d} s^{*}(r_{*}\nu) &= \int_{E^{0}} \sum_{e\in s^{-1}(v) } f \circ r (e)\,{d} r_{*}\nu (v) = \int_{\partial E} \sum_{e\in s^{-1}(r(\alpha)) } f \circ r (e)\,{d} \nu (\alpha) \nonumber\\ &= \int_{\partial E} \sum_{\beta\in \sigma^{-1}(\alpha) } f \circ r (\beta)\,{d} \nu (\alpha). \end{align} $$
When
![]() $\nu $
is invariant on
$\nu $
is invariant on
![]() $\partial E$
, we know from equation (2.5) that
$\partial E$
, we know from equation (2.5) that
![]() $\sigma ^{*}\nu (A)=\nu (\sigma (A))=\nu (A)$
whenever
$\sigma ^{*}\nu (A)=\nu (\sigma (A))=\nu (A)$
whenever
![]() $\sigma $
is injective on A, and hence it is true for all
$\sigma $
is injective on A, and hence it is true for all
![]() $A\subseteq \partial E\setminus E^{0}$
. Since
$A\subseteq \partial E\setminus E^{0}$
. Since
![]() $f\circ r$
might not be zero on
$f\circ r$
might not be zero on
![]() $E^{0}$
, we get that
$E^{0}$
, we get that
 $$ \begin{align*} \int_{\partial E} \sum_{\beta\in \sigma^{-1}(\alpha) } f \circ r (\beta)\,{d} \nu (\alpha)= \int_{\partial E\setminus E^{0}} f \circ r \,{d} \sigma^{*}\nu \leq \int_{\partial E } f \circ r \,{d} \nu = \int_{E^{0} } f \,{d} (r_{*}\nu) , \end{align*} $$
$$ \begin{align*} \int_{\partial E} \sum_{\beta\in \sigma^{-1}(\alpha) } f \circ r (\beta)\,{d} \nu (\alpha)= \int_{\partial E\setminus E^{0}} f \circ r \,{d} \sigma^{*}\nu \leq \int_{\partial E } f \circ r \,{d} \nu = \int_{E^{0} } f \,{d} (r_{*}\nu) , \end{align*} $$
with equality if
![]() $f\circ r$
is zero on
$f\circ r$
is zero on
![]() $E^{0}_{\mathrm {sng}}$
. If
$E^{0}_{\mathrm {sng}}$
. If
![]() $\text {supp}(f) \subseteq E_{\mathrm {reg}}^{0}$
, then
$\text {supp}(f) \subseteq E_{\mathrm {reg}}^{0}$
, then
![]() $f\circ r$
is zero on
$f\circ r$
is zero on
![]() $E^{0}_{\mathrm {sng}}$
, which proves that the map
$E^{0}_{\mathrm {sng}}$
, which proves that the map
![]() $\nu \mapsto r_{*} \nu $
is well defined. That it is surjective follows from Proposition 3.2. To check injectivity, assume that
$\nu \mapsto r_{*} \nu $
is well defined. That it is surjective follows from Proposition 3.2. To check injectivity, assume that
![]() $r_{*}\nu _{1} = r_{*}\nu _{2}$
for two invariant measures
$r_{*}\nu _{1} = r_{*}\nu _{2}$
for two invariant measures
![]() $\nu _{1}$
and
$\nu _{1}$
and
![]() $\nu _{2}$
. If
$\nu _{2}$
. If
![]() $U \subseteq E^{0}$
is Borel, we have by definition of
$U \subseteq E^{0}$
is Borel, we have by definition of
![]() $Z(U)$
that
$Z(U)$
that
For a given
![]() $n\in \mathbb {N}$
and a Borel set
$n\in \mathbb {N}$
and a Borel set
![]() $V \subseteq E^{n}$
satisfying that
$V \subseteq E^{n}$
satisfying that
![]() $\sigma ^{n} : V \to \sigma ^{n}(V) \subseteq E^{0}$
is injective, we have by invariance of the two measures that
$\sigma ^{n} : V \to \sigma ^{n}(V) \subseteq E^{0}$
is injective, we have by invariance of the two measures that
If
![]() $V_{n} \subseteq E^{n}$
and
$V_{n} \subseteq E^{n}$
and
![]() $V_{m} \subseteq E^{m}$
are two such sets with
$V_{m} \subseteq E^{m}$
are two such sets with
![]() $m\geq n$
, then the set
$m\geq n$
, then the set
is open, and since
such sets are a
![]() $\pi $
-system that generates the Borel
$\pi $
-system that generates the Borel
![]() $\sigma $
-algebra. It follows that
$\sigma $
-algebra. It follows that
![]() $\nu _{1} = \nu _{2}$
, which finishes the proof.
$\nu _{1} = \nu _{2}$
, which finishes the proof.
Example 3.7. Assume that E is a second countable discrete topological graph, that is, that it is a countable directed graph. A measure
![]() $\mu $
on
$\mu $
on
![]() $E^{0}$
is then vertex-invariant if and only if it satisfies Definition 3.1 for all functions on the form
$E^{0}$
is then vertex-invariant if and only if it satisfies Definition 3.1 for all functions on the form
![]() $f=1_{\{v\}}$
with
$f=1_{\{v\}}$
with
![]() $v\in E^{0}$
, which is true if and only if
$v\in E^{0}$
, which is true if and only if
 $$ \begin{align*} \mu(\{v\}) &\geq \int_{E^{1}} 1_{v} \circ r \,{d} s^{*}\mu = \int_{E^{0}} \sum_{e\in s^{-1}(w)} 1_{v} \circ r(e) \,{d} \mu(w)\\ &= \sum_{w\in E^{0}} \mu(\{ w \}) \sum_{e\in s^{-1}(w)} 1_{v} \circ r(e) \\ &= \sum_{w\in E^{0}} \mu(\{ w \}) |v E^{1} w| , \end{align*} $$
$$ \begin{align*} \mu(\{v\}) &\geq \int_{E^{1}} 1_{v} \circ r \,{d} s^{*}\mu = \int_{E^{0}} \sum_{e\in s^{-1}(w)} 1_{v} \circ r(e) \,{d} \mu(w)\\ &= \sum_{w\in E^{0}} \mu(\{ w \}) \sum_{e\in s^{-1}(w)} 1_{v} \circ r(e) \\ &= \sum_{w\in E^{0}} \mu(\{ w \}) |v E^{1} w| , \end{align*} $$
with equality when v is a regular vertex, that is, when
![]() $0<|r^{-1}(v)| < \infty $
. If we interpret
$0<|r^{-1}(v)| < \infty $
. If we interpret
![]() $\mu $
as a vector
$\mu $
as a vector
![]() $\mu : E^{0} \to [0, \infty [$
and A is the vertex matrix
$\mu : E^{0} \to [0, \infty [$
and A is the vertex matrix
![]() $A(v,w)=|vE^{1}w|$
for
$A(v,w)=|vE^{1}w|$
for
![]() $v,w\in E^{0}$
, we get that
$v,w\in E^{0}$
, we get that
![]() $\mu $
is vertex-invariant if and only if
$\mu $
is vertex-invariant if and only if
![]() $(A\mu )_{v} \leq \mu _{v}$
with equality when v is regular. It is a well-established fact that invariant measures for directed graphs are in a bijective correspondence with exactly that class of vectors, see e.g. [Reference ThomsenTho17, Theorem 2.7] and [Reference SchafhauserTom03, §3]. So in the discrete case, Proposition 3.6 is well known.
$(A\mu )_{v} \leq \mu _{v}$
with equality when v is regular. It is a well-established fact that invariant measures for directed graphs are in a bijective correspondence with exactly that class of vectors, see e.g. [Reference ThomsenTho17, Theorem 2.7] and [Reference SchafhauserTom03, §3]. So in the discrete case, Proposition 3.6 is well known.
For discrete graphs, it is customary to use the Riesz decomposition of the these vectors to analyse them, cf. e.g. [Reference ThomsenTho17]. This approach provides the motivation behind Theorem 3.3 and the new proof of Proposition 3.2.
Using our new proof of Proposition 3.2, we obtain a decomposition of invariant measures corresponding to the decomposition in Theorem 3.3.
Proposition 3.8. Let E be a second countable topological graph. Let
![]() $\nu $
be an invariant measure on
$\nu $
be an invariant measure on
![]() $\partial E$
and let
$\partial E$
and let
![]() $\mu = r_{*}\nu $
be the associated vertex-invariant measure. Then:
$\mu = r_{*}\nu $
be the associated vertex-invariant measure. Then:
-
(1)
 $\nu $
is concentrated on
$\nu $
is concentrated on
 $E^{\infty }$
if and only if
$E^{\infty }$
if and only if
 $T\mu = \mu $
; and
$T\mu = \mu $
; and -
(2)
 $\nu $
is concentrated on
$\nu $
is concentrated on
 $E^{*}_{\mathrm {sng}}$
if and only if
$E^{*}_{\mathrm {sng}}$
if and only if
 $\lim _{n} \int _{E^{0}} f \,{d} T^{n}\mu =0$
for all
$\lim _{n} \int _{E^{0}} f \,{d} T^{n}\mu =0$
for all
 $f\in C_{c}(E^{0})$
.
$f\in C_{c}(E^{0})$
.
Proof. Remark 3.4 implies the if implication in both statements. For the only if implication in item (1), assume that
![]() $\nu $
is concentrated on
$\nu $
is concentrated on
![]() $E^{\infty }$
and decompose
$E^{\infty }$
and decompose
![]() $r_{*}\nu =\mu _{1}+\mu _{2}$
as in Theorem 3.3. Let
$r_{*}\nu =\mu _{1}+\mu _{2}$
as in Theorem 3.3. Let
![]() $\nu _{i}$
be the invariant measure with
$\nu _{i}$
be the invariant measure with
![]() $r_{*}\nu _{i}=\mu _{i}$
for
$r_{*}\nu _{i}=\mu _{i}$
for
![]() $i=1,2$
. It follows that
$i=1,2$
. It follows that
![]() $\nu =\nu _{1}+\nu _{2}$
and that
$\nu =\nu _{1}+\nu _{2}$
and that
![]() $\nu _{2}$
is concentrated on
$\nu _{2}$
is concentrated on
![]() $E^{*}_{\mathrm {sng}}$
, and hence
$E^{*}_{\mathrm {sng}}$
, and hence
![]() $\nu _{2}=0$
since
$\nu _{2}=0$
since
![]() $\nu (E^{*}_{\mathrm {sng}})=0$
. This implies that
$\nu (E^{*}_{\mathrm {sng}})=0$
. This implies that
![]() $\mu _{2}=0$
and proves the only if implication. The only if implication in item (2) follows similarly.
$\mu _{2}=0$
and proves the only if implication. The only if implication in item (2) follows similarly.
It follows from Theorem 3.3 that we have a very natural decomposition of vertex-invariant measures, which corresponds to a very natural decomposition of invariant measures by Proposition 3.8. The following terminology is inspired by the properties of paths in
![]() $\partial E$
on which the invariant measures are concentrated, and is in line with the terminology for directed graphs [Reference ThomsenTho17].
$\partial E$
on which the invariant measures are concentrated, and is in line with the terminology for directed graphs [Reference ThomsenTho17].
Definition 3.9. We call a vertex-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $E^{0}$
a boundary measure if
$E^{0}$
a boundary measure if
In accordance with this, we call an invariant measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
a boundary measure if it is concentrated on
$\partial E$
a boundary measure if it is concentrated on
![]() $E_{\mathrm {sng}}^{*}$
.
$E_{\mathrm {sng}}^{*}$
.
We call a vertex-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $E^{0}$
harmonic if
$E^{0}$
harmonic if
![]() $T\mu =\mu $
. In accordance with this, we call an invariant measure
$T\mu =\mu $
. In accordance with this, we call an invariant measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
harmonic if it is concentrated on
$\partial E$
harmonic if it is concentrated on
![]() $E^{\infty }$
.
$E^{\infty }$
.
It follows from equation (2.4) that any extremal invariant measure is either a boundary measure or a harmonic measure. We will therefore in the following investigate the boundary measures and the harmonic measures separately.
4 Boundary measures
We will in the following give a complete description of the extremal boundary measures.
Proposition 4.1. Let E be a second countable topological graph. If
![]() $\nu $
is an extremal non-zero boundary measure on
$\nu $
is an extremal non-zero boundary measure on
![]() $\partial E$
, there exists a vertex
$\partial E$
, there exists a vertex
![]() $v\in E^{0}_{\mathrm {sng}}$
such that for any
$v\in E^{0}_{\mathrm {sng}}$
such that for any
![]() $w\in E^{0}$
, there is an open neighbourhood
$w\in E^{0}$
, there is an open neighbourhood
![]() $V_{w}$
of w in
$V_{w}$
of w in
![]() $E^{0}$
with
$E^{0}$
with
![]() $|V_{w} E^{*} v|<\infty $
and such that
$|V_{w} E^{*} v|<\infty $
and such that
![]() $\nu $
is concentrated on the countable set
$\nu $
is concentrated on the countable set
![]() $E^{*} v$
.
$E^{*} v$
.
In particular, this implies that there exists an
![]() $r> 0$
such that
$r> 0$
such that
![]() $\nu $
is on the form
$\nu $
is on the form
Proof. Let for each
![]() $i \in \mathbb {N}$
the set
$i \in \mathbb {N}$
the set
![]() $U_{i} \subseteq E^{0}$
satisfy that
$U_{i} \subseteq E^{0}$
satisfy that
![]() $\overline {U_{i}}$
is compact,
$\overline {U_{i}}$
is compact,
![]() $U_{i}$
is open and
$U_{i}$
is open and
![]() $E^{0} = \bigcup _{i\in \mathbb {N}} U_{i}$
. Define
$E^{0} = \bigcup _{i\in \mathbb {N}} U_{i}$
. Define
![]() $V_{1}=U_{1}$
and for each
$V_{1}=U_{1}$
and for each
![]() $n>1$
, define
$n>1$
, define
The sets
![]() $\{V_{n}\}_{n\in \mathbb {N}}$
are disjoint with union
$\{V_{n}\}_{n\in \mathbb {N}}$
are disjoint with union
![]() $E^{0}$
, so we get
$E^{0}$
, so we get
Since
![]() $\nu $
is extremal and hence ergodic, it follows from Lemma 2.2 that there exists a unique
$\nu $
is extremal and hence ergodic, it follows from Lemma 2.2 that there exists a unique
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $\nu ((E^{*}_{\mathrm {sng}} V_{m} )^{C}) =0$
. The relative topology on
$\nu ((E^{*}_{\mathrm {sng}} V_{m} )^{C}) =0$
. The relative topology on
![]() $\overline {U_{m}}$
makes it a compact second countable Hausdorff space, and hence a metrisable space. Using standard arguments, we can therefore find a sequence
$\overline {U_{m}}$
makes it a compact second countable Hausdorff space, and hence a metrisable space. Using standard arguments, we can therefore find a sequence
![]() $\{W_{i}\}_{i=1}^{\infty }$
of Borel subsets of
$\{W_{i}\}_{i=1}^{\infty }$
of Borel subsets of
![]() $\overline {U_{m}}$
with
$\overline {U_{m}}$
with
![]() $W_{i+1} \subseteq W_{i}$
such that the diameter of
$W_{i+1} \subseteq W_{i}$
such that the diameter of
![]() $W_{i}$
is at most
$W_{i}$
is at most
![]() $1/i$
, and such that
$1/i$
, and such that
![]() $\nu ( (E^{*}_{\mathrm {sng}} W_{i} )^{C}) =0$
for all i. We now have that
$\nu ( (E^{*}_{\mathrm {sng}} W_{i} )^{C}) =0$
for all i. We now have that
 $$ \begin{align*} 0= \nu \bigg( \bigcup_{i\in \mathbb{N} }(E^{*}_{\mathrm{sng}} W_{i})^{C} \bigg) =\nu \bigg(\bigg(\bigcap_{i\in \mathbb{N} } E^{*}_{\mathrm{sng}} W_{i} \bigg )^{C} \bigg) = \nu \bigg(\bigg(E^{*}_{\mathrm{sng}} \bigg(\bigcap_{i\in \mathbb{N} } W_{i} \bigg) \bigg)^{C}\bigg). \end{align*} $$
$$ \begin{align*} 0= \nu \bigg( \bigcup_{i\in \mathbb{N} }(E^{*}_{\mathrm{sng}} W_{i})^{C} \bigg) =\nu \bigg(\bigg(\bigcap_{i\in \mathbb{N} } E^{*}_{\mathrm{sng}} W_{i} \bigg )^{C} \bigg) = \nu \bigg(\bigg(E^{*}_{\mathrm{sng}} \bigg(\bigcap_{i\in \mathbb{N} } W_{i} \bigg) \bigg)^{C}\bigg). \end{align*} $$
Since
![]() $\nu \neq 0$
, it follows that
$\nu \neq 0$
, it follows that
![]() $\bigcap _{i\in \mathbb {N} } W_{i}= \{v \}$
for some
$\bigcap _{i\in \mathbb {N} } W_{i}= \{v \}$
for some
![]() $v\in E^{0}$
. Hence, we have that
$v\in E^{0}$
. Hence, we have that
![]() $0=\nu ((E^{*}_{\mathrm {sng}} v)^{C})$
, so
$0=\nu ((E^{*}_{\mathrm {sng}} v)^{C})$
, so
![]() $v\in E^{0}_{\mathrm {sng}}$
. Since the topology is second countable and s is a local homeomorphism, the set
$v\in E^{0}_{\mathrm {sng}}$
. Since the topology is second countable and s is a local homeomorphism, the set
![]() $E^{*}_{\mathrm {sng}} v=E^{*}v$
contains at most countably many elements. Now take a path
$E^{*}_{\mathrm {sng}} v=E^{*}v$
contains at most countably many elements. Now take a path
![]() $\alpha \in E^{*} v$
, we then have by equation (2.5) that
$\alpha \in E^{*} v$
, we then have by equation (2.5) that
![]() $\nu (\{v\})=\nu (\sigma ^{|\alpha |}(\{\alpha \}) )=\nu (\{\alpha \})$
. This implies that
$\nu (\{v\})=\nu (\sigma ^{|\alpha |}(\{\alpha \}) )=\nu (\{\alpha \})$
. This implies that
where
![]() $\nu (\{v\})>0$
by assumption. Since
$\nu (\{v\})>0$
by assumption. Since
![]() $\nu $
is regular and
$\nu $
is regular and
![]() $Z(K)$
is a compact set for any compact
$Z(K)$
is a compact set for any compact
![]() $K\subseteq E^{0}$
, we can for any
$K\subseteq E^{0}$
, we can for any
![]() $w\in E^{0}$
find an open neighbourhood
$w\in E^{0}$
find an open neighbourhood
![]() $V_{w}$
of w in
$V_{w}$
of w in
![]() $E^{0}$
with
$E^{0}$
with
![]() $\nu (Z(V_{w})) <\infty $
. Since
$\nu (Z(V_{w})) <\infty $
. Since
this finishes the proof.
Recall for the following theorem that a ray of measures is a set on the form
![]() $\{ r\nu \mid r> 0\}$
, where
$\{ r\nu \mid r> 0\}$
, where
![]() $\nu $
is measure.
$\nu $
is measure.
Theorem 4.2. Let E be a second countable topological graph. There is a bijection between the set of rays of non-zero extremal invariant boundary measures on
![]() $\partial E$
and the set of vertices
$\partial E$
and the set of vertices
![]() $v\in E^{0}_{\mathrm {sng}}$
satisfying the following condition: for any
$v\in E^{0}_{\mathrm {sng}}$
satisfying the following condition: for any
![]() $w\in E^{0}$
, there exists an open neighbourhood
$w\in E^{0}$
, there exists an open neighbourhood
![]() $V_{w} \subseteq E^{0} $
of w satisfying
$V_{w} \subseteq E^{0} $
of w satisfying
![]() $|V_{w}E^{*}v|< \infty $
.
$|V_{w}E^{*}v|< \infty $
.
The ray of extremal invariant boundary measures corresponding to such a
![]() $v\in E_{\mathrm {sng}}^{0}$
is on the form
$v\in E_{\mathrm {sng}}^{0}$
is on the form
![]() $\{ r \cdot \nu \; |\; r>0\}$
, where
$\{ r \cdot \nu \; |\; r>0\}$
, where
Proof. Assume that
![]() $v\in E^{0}_{\mathrm {sng}}$
satisfies that for any
$v\in E^{0}_{\mathrm {sng}}$
satisfies that for any
![]() $w\in E^{0}$
, there exists an open neighbourhood
$w\in E^{0}$
, there exists an open neighbourhood
![]() $V_{w} \subseteq E^{0}$
of w satisfying
$V_{w} \subseteq E^{0}$
of w satisfying
![]() $|V_{w}E^{*}v|< \infty $
, and define
$|V_{w}E^{*}v|< \infty $
, and define
![]() $\nu :=\sum _{\alpha \in E^{*}v} \delta _{\alpha }$
. If
$\nu :=\sum _{\alpha \in E^{*}v} \delta _{\alpha }$
. If
![]() $V\subseteq E^{0}$
is an open set, then
$V\subseteq E^{0}$
is an open set, then
Since the set
![]() $Z(V_{w})$
with
$Z(V_{w})$
with
![]() $w\in E^{0}$
is an open cover of
$w\in E^{0}$
is an open cover of
![]() $\partial E$
, it follows that
$\partial E$
, it follows that
![]() $\nu $
is a regular measure. Now assume that
$\nu $
is a regular measure. Now assume that
![]() $A \subseteq \partial E \setminus E^{0}$
with
$A \subseteq \partial E \setminus E^{0}$
with
![]() $\sigma $
injective on A. Since
$\sigma $
injective on A. Since
![]() $\sigma (\alpha ) \in E^{*}v$
if and only if
$\sigma (\alpha ) \in E^{*}v$
if and only if
![]() $\alpha \in E^{*}v$
for all
$\alpha \in E^{*}v$
for all
![]() $\alpha \in A$
, we get that
$\alpha \in A$
, we get that
which by equation (2.5) proves that
![]() $\nu $
is an invariant boundary measure. The measure is clearly extremal, because any invariant set A either contains
$\nu $
is an invariant boundary measure. The measure is clearly extremal, because any invariant set A either contains
![]() $E^{*}v$
or is disjoint from it, depending on whether it contains v. It follows that the map which maps such a vertex v to the extremal ray of boundary measures
$E^{*}v$
or is disjoint from it, depending on whether it contains v. It follows that the map which maps such a vertex v to the extremal ray of boundary measures
![]() $\{ r \cdot \nu \mid r>0\}$
is well defined, and by Proposition 4.1, it is also surjective. To see that it is injective, notice that
$\{ r \cdot \nu \mid r>0\}$
is well defined, and by Proposition 4.1, it is also surjective. To see that it is injective, notice that
![]() $\nu (\{w\})>0$
for a
$\nu (\{w\})>0$
for a
![]() $w\in E^{0}$
if and only if
$w\in E^{0}$
if and only if
![]() $w=v$
, which proves that the map is a bijection.
$w=v$
, which proves that the map is a bijection.
Remark 4.3. If
![]() $E^{0}$
is compact, we can exchange the condition: for any
$E^{0}$
is compact, we can exchange the condition: for any
![]() $w\in E^{0}$
, there exists an open neighbourhood
$w\in E^{0}$
, there exists an open neighbourhood
![]() $V_{w} \subseteq E^{0}$
of w satisfying
$V_{w} \subseteq E^{0}$
of w satisfying
![]() $|V_{w}E^{*}v|< \infty $
, with the condition that
$|V_{w}E^{*}v|< \infty $
, with the condition that
![]() $|E^{*}v| < \infty $
.
$|E^{*}v| < \infty $
.
It follows from Theorem 4.2 that the rays of non-zero extremal finite invariant boundary measures map bijectively onto the vertices satisfying the extra condition
![]() $|E^{*}v|<\infty $
. This gives the corollary below.
$|E^{*}v|<\infty $
. This gives the corollary below.
Corollary 4.4. Let E be a second countable topological graph. There is a bijection between the set of extremal invariant boundary probability measures on
![]() $\partial E$
and the set of vertices
$\partial E$
and the set of vertices
![]() $v\in E^{0}_{\mathrm {sng}}$
with
$v\in E^{0}_{\mathrm {sng}}$
with
![]() $|E^{*}v|< \infty $
. The extremal invariant boundary probability measures corresponding to such a vertex are on the form
$|E^{*}v|< \infty $
. The extremal invariant boundary probability measures corresponding to such a vertex are on the form
 $$ \begin{align*} \nu = \frac{1}{|E^{*}v|}\sum_{\alpha \in E^{*}v} \delta_{\alpha}. \end{align*} $$
$$ \begin{align*} \nu = \frac{1}{|E^{*}v|}\sum_{\alpha \in E^{*}v} \delta_{\alpha}. \end{align*} $$
The upshot of Theorem 4.2 is that the extremal boundary measures are easy to describe. To support this statement, let us argue that for simple C
![]() $^{*}$
-algebras of topological graphs, boundary measures only occurs in the very special cases where the
$^{*}$
-algebras of topological graphs, boundary measures only occurs in the very special cases where the
![]() $C^{*}$
-algebra of the graph is (isomorphic to) the compact operators
$C^{*}$
-algebra of the graph is (isomorphic to) the compact operators
![]() $\mathcal {K}(H)$
on a Hilbert space H.
$\mathcal {K}(H)$
on a Hilbert space H.
Corollary 4.5. Assume that E is a second countable topological graph and that
![]() $C^{*}(E)$
is simple. If there exists an invariant boundary measure
$C^{*}(E)$
is simple. If there exists an invariant boundary measure
![]() $\nu $
on
$\nu $
on
![]() $\partial E$
, then there exists a
$\partial E$
, then there exists a
![]() $v\in E^{0}_{\mathrm {sng}}$
with
$v\in E^{0}_{\mathrm {sng}}$
with
![]() $E^{*}v$
countable such that
$E^{*}v$
countable such that
Proof. Let us first argue that there will also exist an extremal invariant boundary measure. Set
![]() $\eta = \int _{\partial E} P(\cdot )\,{d} \nu $
which is a tracial weight on
$\eta = \int _{\partial E} P(\cdot )\,{d} \nu $
which is a tracial weight on
![]() $C^{*}(E)$
. Take an
$C^{*}(E)$
. Take an
![]() $f\in C_{c}(E^{0})_{+}$
with
$f\in C_{c}(E^{0})_{+}$
with
which we can rewrite using equation (3.3) to get
 $$ \begin{align} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu(\alpha) < \int_{\partial E} f\circ r \,{d} \nu. \end{align} $$
$$ \begin{align} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu(\alpha) < \int_{\partial E} f\circ r \,{d} \nu. \end{align} $$
Since
![]() $r^{-1}(\text {supp}(f))=Z(\text {supp}(f))$
, then
$r^{-1}(\text {supp}(f))=Z(\text {supp}(f))$
, then
![]() $f\circ r \in C_{c}(\partial E)_{+}$
. We now want to use Choquet theory to find an extremal measure satisfying equation (4.1), but since
$f\circ r \in C_{c}(\partial E)_{+}$
. We now want to use Choquet theory to find an extremal measure satisfying equation (4.1), but since
![]() $f\circ r$
does not a priori lie in
$f\circ r$
does not a priori lie in
![]() $C_{c}(\partial E \setminus E^{0})$
, we take increasing sequence
$C_{c}(\partial E \setminus E^{0})$
, we take increasing sequence
![]() $\{ g_{n} \}_{n\in \mathbb {N}} \subseteq C_{c}(\partial E \setminus E^{0} )$
of positive functions with
$\{ g_{n} \}_{n\in \mathbb {N}} \subseteq C_{c}(\partial E \setminus E^{0} )$
of positive functions with
![]() $\lim _{n\to \infty } g_{n} = f\circ r|_{\partial E \setminus E^{0}}$
. Using that
$\lim _{n\to \infty } g_{n} = f\circ r|_{\partial E \setminus E^{0}}$
. Using that
![]() $\mathcal {G}_{E}$
is a minimal groupoid, [Reference ChristensenChr23, Proposition 6.10] implies that the tracial weights
$\mathcal {G}_{E}$
is a minimal groupoid, [Reference ChristensenChr23, Proposition 6.10] implies that the tracial weights
![]() $\psi $
satisfying
$\psi $
satisfying
![]() $\psi (f\circ r)=\eta (f\circ r)$
is a simplex. Since
$\psi (f\circ r)=\eta (f\circ r)$
is a simplex. Since
 $$ \begin{align*} \lim_{n\to \infty} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} g_{n}(\beta)\,{d} \nu(\alpha) = \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta) \,{d} \nu(\alpha) < \int_{\partial E} f\circ r \,{d} \nu \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} g_{n}(\beta)\,{d} \nu(\alpha) = \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta) \,{d} \nu(\alpha) < \int_{\partial E} f\circ r \,{d} \nu \end{align*} $$
and
![]() $\alpha \mapsto \sum _{\beta \in \sigma ^{-1}(\alpha )} g_{n}(\beta )$
lies in
$\alpha \mapsto \sum _{\beta \in \sigma ^{-1}(\alpha )} g_{n}(\beta )$
lies in
![]() $C_{c}(\partial E)$
, then Choquet theory implies that there is an extremal tracial weight
$C_{c}(\partial E)$
, then Choquet theory implies that there is an extremal tracial weight
![]() $\psi $
with
$\psi $
with
![]() $\psi (f\circ r)=\eta (f\circ r)$
and
$\psi (f\circ r)=\eta (f\circ r)$
and
 $$ \begin{align*} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu_{\psi}(\alpha) =\lim_{n\to \infty} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} g_{n}(\beta) \,{d} \nu_{\psi}(\alpha) < \int_{\partial E} f\circ r \,{d} \nu_{\psi} , \end{align*} $$
$$ \begin{align*} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu_{\psi}(\alpha) =\lim_{n\to \infty} \int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} g_{n}(\beta) \,{d} \nu_{\psi}(\alpha) < \int_{\partial E} f\circ r \,{d} \nu_{\psi} , \end{align*} $$
where
![]() $\nu _{\psi }$
is the measures associated to
$\nu _{\psi }$
is the measures associated to
![]() $\psi $
. This implies that
$\psi $
. This implies that
 $$ \begin{align*} \int_{E^{0}} f\,{d} T(r_{*}\nu_{\psi}) =\int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu_{\psi}(\alpha) < \psi(f\circ r)=\int_{E^{0}}f\,{d} (r_{*}\nu_{\psi}), \end{align*} $$
$$ \begin{align*} \int_{E^{0}} f\,{d} T(r_{*}\nu_{\psi}) =\int_{\partial E} \sum_{\beta \in \sigma^{-1}(\alpha)} f\circ r(\beta)\,{d} \nu_{\psi}(\alpha) < \psi(f\circ r)=\int_{E^{0}}f\,{d} (r_{*}\nu_{\psi}), \end{align*} $$
from which it follows that
![]() $\nu _{\psi }$
is an extremal boundary measure.
$\nu _{\psi }$
is an extremal boundary measure.
So we can assume without loss of generality that
![]() $\nu $
is an extremal invariant boundary measure. It follows that there exists a
$\nu $
is an extremal invariant boundary measure. It follows that there exists a
![]() $v \in E_{\mathrm {sng}}^{0}$
such that
$v \in E_{\mathrm {sng}}^{0}$
such that
![]() $\nu $
is concentrated on the countable set
$\nu $
is concentrated on the countable set
![]() $E^{*}v$
. If we can prove that
$E^{*}v$
. If we can prove that
![]() $\partial E = E^{*}v$
, this will prove the corollary, because then
$\partial E = E^{*}v$
, this will prove the corollary, because then
![]() $Z(V_{w})=V_{w}E^{*}v$
and hence
$Z(V_{w})=V_{w}E^{*}v$
and hence
![]() $\partial E$
is discrete, and the groupoid corresponding to the graph will be isomorphic to the equivalence relation
$\partial E$
is discrete, and the groupoid corresponding to the graph will be isomorphic to the equivalence relation
![]() $E^{*}v \times E^{*}v$
, which exactly gives rise to the C
$E^{*}v \times E^{*}v$
, which exactly gives rise to the C
![]() $^{*}$
-algebra
$^{*}$
-algebra
![]() $\mathcal {K}(l^{2}(E^{*}v))$
. Since
$\mathcal {K}(l^{2}(E^{*}v))$
. Since
![]() $E^{*}v$
is invariant and
$E^{*}v$
is invariant and
![]() $C^{*}(E)$
is simple, it suffices to prove that
$C^{*}(E)$
is simple, it suffices to prove that
![]() $E^{*}v$
is a closed set to see that
$E^{*}v$
is a closed set to see that
![]() $\partial E = E^{*} v$
, because a non-trivial closed invariant set in the unit space of a groupoid gives rise to a non-trivial ideal.
$\partial E = E^{*} v$
, because a non-trivial closed invariant set in the unit space of a groupoid gives rise to a non-trivial ideal.
Assume now that
![]() $\alpha \in \partial E$
with
$\alpha \in \partial E$
with
![]() $\alpha \notin E^{*}v$
. By existence of
$\alpha \notin E^{*}v$
. By existence of
![]() $\nu $
, there is an open set
$\nu $
, there is an open set
![]() $U \subseteq E^{0}$
such that
$U \subseteq E^{0}$
such that
![]() $r(\alpha ) \in U$
yet
$r(\alpha ) \in U$
yet
![]() $|U E^{*} v| < \infty $
. Write
$|U E^{*} v| < \infty $
. Write
![]() $U E^{*} v = \{ \beta ^{1}, \dots , \beta ^{n} \}$
. We consider two cases. First, assume that
$U E^{*} v = \{ \beta ^{1}, \dots , \beta ^{n} \}$
. We consider two cases. First, assume that
![]() $r(\alpha _{j})\neq v$
for all
$r(\alpha _{j})\neq v$
for all
![]() $1\leq j \leq |\alpha |$
. By definition, each
$1\leq j \leq |\alpha |$
. By definition, each
![]() $\beta ^{i}$
has
$\beta ^{i}$
has
![]() $s(\beta ^{i}) = v$
, so it follows that
$s(\beta ^{i}) = v$
, so it follows that
![]() $\alpha \notin Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
. Since
$\alpha \notin Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
. Since
![]() $\{\beta ^{1}, \dots , \beta ^{n} \}$
is compact, the set
$\{\beta ^{1}, \dots , \beta ^{n} \}$
is compact, the set
![]() $Z(U)\setminus Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
is an open set containing
$Z(U)\setminus Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
is an open set containing
![]() $\alpha $
, yet a
$\alpha $
, yet a
![]() $\gamma \in E^{*}v \cap Z(U)$
has to be an element of
$\gamma \in E^{*}v \cap Z(U)$
has to be an element of
![]() $U E^{*} v$
, proving that
$U E^{*} v$
, proving that
![]() $Z(U)\setminus Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
is disjoint from
$Z(U)\setminus Z(\{\beta ^{1}, \dots , \beta ^{n} \})$
is disjoint from
![]() $E^{*} v$
.
$E^{*} v$
.
Assume for the other case that
![]() $r(\alpha _{i})=v$
for some
$r(\alpha _{i})=v$
for some
![]() $i\in \mathbb {N}$
. If this was true for more than one i, we would have
$i\in \mathbb {N}$
. If this was true for more than one i, we would have
![]() $|U E^{*} v|=\infty $
. So this i is unique. It follows that there exists a unique
$|U E^{*} v|=\infty $
. So this i is unique. It follows that there exists a unique
![]() $\beta ^{k}\in U E^{*} v$
with
$\beta ^{k}\in U E^{*} v$
with
![]() $\alpha =\beta ^{k}\alpha '$
. Since
$\alpha =\beta ^{k}\alpha '$
. Since
![]() $\alpha \notin E^{*}v$
, we have
$\alpha \notin E^{*}v$
, we have
![]() $|\alpha |>|\beta ^{k}|$
. Now let
$|\alpha |>|\beta ^{k}|$
. Now let
![]() $W\subseteq E^{|\beta ^{k}|+1}$
be an open set containing the path
$W\subseteq E^{|\beta ^{k}|+1}$
be an open set containing the path
![]() $\alpha _{1}\dots \alpha _{|\beta ^{k}|+1}$
such that
$\alpha _{1}\dots \alpha _{|\beta ^{k}|+1}$
such that
![]() $r(W)\subseteq U$
, which can be arranged since
$r(W)\subseteq U$
, which can be arranged since
![]() $r:E^{*} \to E^{0}$
is continuous. The set
$r:E^{*} \to E^{0}$
is continuous. The set
is an open set in
![]() $\partial E$
containing
$\partial E$
containing
![]() $\alpha $
. Assume for a contradiction that
$\alpha $
. Assume for a contradiction that
![]() $\gamma $
lies in this open set and
$\gamma $
lies in this open set and
![]() $E^{*}v$
. By choice of W, then
$E^{*}v$
. By choice of W, then
![]() $r(\gamma )\in r(W)\subseteq U$
, proving that
$r(\gamma )\in r(W)\subseteq U$
, proving that
![]() $\gamma =\beta ^{i}$
for some
$\gamma =\beta ^{i}$
for some
![]() $1\leq i \leq n$
. Since
$1\leq i \leq n$
. Since
![]() $\gamma \notin Z(\{ \beta ^{1}, \dots , \beta ^{k-1}, \beta ^{k+1}, \dots , \beta ^{n} \})$
, then
$\gamma \notin Z(\{ \beta ^{1}, \dots , \beta ^{k-1}, \beta ^{k+1}, \dots , \beta ^{n} \})$
, then
![]() $\gamma =\beta ^{k}$
. Since
$\gamma =\beta ^{k}$
. Since
![]() $W\subseteq E^{|\beta ^{k}|+1}$
, then
$W\subseteq E^{|\beta ^{k}|+1}$
, then
![]() $\gamma \notin Z(W)$
, and hence the intersection is empty. In conclusion,
$\gamma \notin Z(W)$
, and hence the intersection is empty. In conclusion,
![]() $E^{*}v$
is a closed set.
$E^{*}v$
is a closed set.
Remark 4.6. If there exists an invariant boundary probability measure in Corollary 4.5, then
![]() $E^{*}v$
is finite and
$E^{*}v$
is finite and
![]() $C^{*}(E)\simeq M_{|E^{*}v|}(\mathbb {C} )$
.
$C^{*}(E)\simeq M_{|E^{*}v|}(\mathbb {C} )$
.
While the extremal boundary measures are easy to describe in general, describing all harmonic measures is much more complicated, as illustrated in the following example.
Example 4.7. Let X be a second countable locally compact Hausdorff space and let
![]() $\varphi $
be a homeomorphism on X. Define a topological graph
$\varphi $
be a homeomorphism on X. Define a topological graph
![]() $E_{X}$
by setting
$E_{X}$
by setting
![]() $E_{X}^{0}=E_{X}^{1}=X$
,
$E_{X}^{0}=E_{X}^{1}=X$
,
![]() $s=id_{X}$
and
$s=id_{X}$
and
![]() $r=\varphi $
. It then follows from [Reference KatsuraKat04, Example 2] that
$r=\varphi $
. It then follows from [Reference KatsuraKat04, Example 2] that
![]() $C^{*}(E_{X}) \simeq C(X)\rtimes _{\varphi } \mathbb {Z}$
. Since
$C^{*}(E_{X}) \simeq C(X)\rtimes _{\varphi } \mathbb {Z}$
. Since
![]() $s^{*}\mu = \mu $
for any regular measure on X, it follows from Definition 3.1 that a regular measure
$s^{*}\mu = \mu $
for any regular measure on X, it follows from Definition 3.1 that a regular measure
![]() $\mu $
on X is vertex-invariant and harmonic if and only if it satisfies that
$\mu $
on X is vertex-invariant and harmonic if and only if it satisfies that
![]() $\int _{X} f\circ \varphi \,{d} \mu =\int _{X} f\,{d} \mu $
for all
$\int _{X} f\circ \varphi \,{d} \mu =\int _{X} f\,{d} \mu $
for all
![]() $f\in C_{c}(X)$
, that is, that
$f\in C_{c}(X)$
, that is, that
![]() $\mu $
is a
$\mu $
is a
![]() $\varphi $
-invariant measure on X. It follows that describing the extremal harmonic vertex-invariant measures in this case is equivalent to describing the ergodic
$\varphi $
-invariant measure on X. It follows that describing the extremal harmonic vertex-invariant measures in this case is equivalent to describing the ergodic
![]() $\varphi $
-invariant measures on X. It is known from ergodic theory that it is a very difficult problem to provide a concrete description of all such ergodic invariant measures in general.
$\varphi $
-invariant measures on X. It is known from ergodic theory that it is a very difficult problem to provide a concrete description of all such ergodic invariant measures in general.
5 Loops in topological graphs
As illustrated in Example 4.7, it is not feasible to obtain formulae for all extremal harmonic measures in a similar manner as was done for boundary measures. It however turns out that we can describe the extremal harmonic measures which gives rise to non-gauge-invariant tracial weights much more concretely by analysing loops in the graph. Before turning to this analysis of harmonic measures, we will need some preliminary results on loops in topological graphs.
We call a finite path
![]() $\alpha \in E^{*}$
a loop if it satisfies that
$\alpha \in E^{*}$
a loop if it satisfies that
![]() $|\alpha |\geq 1$
and
$|\alpha |\geq 1$
and
![]() $s(\alpha )=r(\alpha )$
. Any loop
$s(\alpha )=r(\alpha )$
. Any loop
![]() $\alpha \in E^{*}$
gives rise to a well-defined infinite path
$\alpha \in E^{*}$
gives rise to a well-defined infinite path
![]() $\alpha ^{\infty } \in E^{\infty }$
given by
$\alpha ^{\infty } \in E^{\infty }$
given by
For a loop
![]() $\alpha $
in E, we introduce the notation
$\alpha $
in E, we introduce the notation
Similar to our conventions for
![]() $E^{*}$
, we write
$E^{*}$
, we write
![]() $AE_{\alpha }^{*}$
for the paths
$AE_{\alpha }^{*}$
for the paths
![]() $\beta \in E_{\alpha }^{*}$
with
$\beta \in E_{\alpha }^{*}$
with
![]() $r(\beta )\in A$
, where
$r(\beta )\in A$
, where
![]() $A \subseteq E^{0}$
. We call a loop
$A \subseteq E^{0}$
. We call a loop
![]() $\alpha $
simple if
$\alpha $
simple if
![]() $r(\alpha _{i})\neq r(\alpha _{j})$
for all
$r(\alpha _{i})\neq r(\alpha _{j})$
for all
![]() $i\neq j$
, cf. [Reference KatsuraKat06b, Definition 6.5]. We will furthermore work with the following two kinds of loops.
$i\neq j$
, cf. [Reference KatsuraKat06b, Definition 6.5]. We will furthermore work with the following two kinds of loops.
Definition 5.1. Let E be a topological graph. We call a loop
![]() $\alpha \in E^{*}$
an isolated loop if it satisfies the following two conditions:
$\alpha \in E^{*}$
an isolated loop if it satisfies the following two conditions:
-
(a)
 $\alpha \neq \gamma ^{n}$
for any loop
$\alpha \neq \gamma ^{n}$
for any loop
 $\gamma \in E^{*}$
and any
$\gamma \in E^{*}$
and any
 $n\geq 2$
; and
$n\geq 2$
; and -
(b) there exists an open neighbourhood
 $V_{r(\alpha )} \subseteq E^{0}$
of
$V_{r(\alpha )} \subseteq E^{0}$
of
 $r(\alpha )$
with
$r(\alpha )$
with
 $| V_{r(\alpha )} E_{\alpha }^{*} | < \infty $
.
$| V_{r(\alpha )} E_{\alpha }^{*} | < \infty $
.
We call a loop
![]() $\alpha $
a summable loop if it satisfies conditions (a) and (b
$\alpha $
a summable loop if it satisfies conditions (a) and (b
![]() $'$
):
$'$
):
-
(b′) for any
 $w\in E^{0}$
, there exists an open neighbourhood
$w\in E^{0}$
, there exists an open neighbourhood
 $V_{w} \subseteq E^{0}$
of w with
$V_{w} \subseteq E^{0}$
of w with
 $| V_{w} E_{\alpha }^{*} | < \infty $
.
$| V_{w} E_{\alpha }^{*} | < \infty $
.
Clearly, a summable loop is isolated. We will prove that an isolated loop is a simple loop.
Lemma 5.2. Let E be a topological graph. If
![]() $\alpha $
is an isolated loop, then there cannot exist a loop
$\alpha $
is an isolated loop, then there cannot exist a loop
![]() $\gamma \in r(\alpha )E^{*}$
such that
$\gamma \in r(\alpha )E^{*}$
such that
![]() $\gamma \notin \{ \alpha ^{n} \}_{n\in \mathbb {N}}$
. In particular, an isolated loop is simple.
$\gamma \notin \{ \alpha ^{n} \}_{n\in \mathbb {N}}$
. In particular, an isolated loop is simple.
Proof. Assume for a contradiction that
![]() $\gamma \in r(\alpha )E^{*}$
is a loop such that
$\gamma \in r(\alpha )E^{*}$
is a loop such that
![]() $\gamma \notin \{ \alpha ^{n} \}_{n\in \mathbb {N}}$
. Write
$\gamma \notin \{ \alpha ^{n} \}_{n\in \mathbb {N}}$
. Write
![]() $\gamma = \gamma '\alpha ^{n}$
with
$\gamma = \gamma '\alpha ^{n}$
with
![]() $n\geq 0$
as big as possible. It follows that
$n\geq 0$
as big as possible. It follows that
![]() $|\gamma '|>0$
and that
$|\gamma '|>0$
and that
![]() $\gamma '$
is a loop. We can also decompose
$\gamma '$
is a loop. We can also decompose
![]() $\gamma '= \gamma " \delta $
, where
$\gamma '= \gamma " \delta $
, where
![]() $\delta \in r(\alpha ) E^{*}$
is a loop and
$\delta \in r(\alpha ) E^{*}$
is a loop and
![]() $r(\delta _{i})\neq r(\alpha )$
for
$r(\delta _{i})\neq r(\alpha )$
for
![]() $2\leq i\leq |\delta |$
. Since n was chosen as big as possible, we have that
$2\leq i\leq |\delta |$
. Since n was chosen as big as possible, we have that
![]() $\delta \in E_{\alpha }^{*} $
.
$\delta \in E_{\alpha }^{*} $
.
We now claim that
![]() $\delta ^{m} \in E_{\alpha }^{*}$
for all
$\delta ^{m} \in E_{\alpha }^{*}$
for all
![]() $m\geq 2$
. If
$m\geq 2$
. If
![]() $|\delta | \geq |\alpha |$
, this follows directly from the fact that
$|\delta | \geq |\alpha |$
, this follows directly from the fact that
![]() $\delta \in E_{\alpha }^{*} $
. If
$\delta \in E_{\alpha }^{*} $
. If
![]() $|\delta |<|\alpha |$
and
$|\delta |<|\alpha |$
and
![]() $\delta ^{m}=\beta \alpha $
, then we can assume (by possibly picking a smaller m) that
$\delta ^{m}=\beta \alpha $
, then we can assume (by possibly picking a smaller m) that
![]() $|\beta | < |\delta |$
. By assumption (a), then
$|\beta | < |\delta |$
. By assumption (a), then
![]() $|\beta |\neq 0$
, which means that
$|\beta |\neq 0$
, which means that
![]() $\delta =\beta \gamma $
with
$\delta =\beta \gamma $
with
![]() $\gamma $
and
$\gamma $
and
![]() $\beta $
loops, which can not be the case since
$\beta $
loops, which can not be the case since
![]() $r(\delta _{i})\neq r(\alpha )$
for
$r(\delta _{i})\neq r(\alpha )$
for
![]() $2\leq i\leq |\delta |$
. So
$2\leq i\leq |\delta |$
. So
![]() $\{ \delta ^{m}\}_{m\in \mathbb {N}} \subseteq V_{r(\alpha )}E_{\alpha }^{*}$
, which contradicts assumption (b).
$\{ \delta ^{m}\}_{m\in \mathbb {N}} \subseteq V_{r(\alpha )}E_{\alpha }^{*}$
, which contradicts assumption (b).
If
![]() $\alpha $
is not simple, then there exists an
$\alpha $
is not simple, then there exists an
![]() $i<j$
such that
$i<j$
such that
![]() $r(\alpha _{i})=r(\alpha _{j})$
, but then
$r(\alpha _{i})=r(\alpha _{j})$
, but then
![]() $\gamma :=\alpha _{1}\cdots \alpha _{i-1}\alpha _{j}\cdots \alpha _{|\alpha |} \in r(\alpha )E^{*}$
is a loop such that
$\gamma :=\alpha _{1}\cdots \alpha _{i-1}\alpha _{j}\cdots \alpha _{|\alpha |} \in r(\alpha )E^{*}$
is a loop such that
![]() $\gamma \notin \{ \alpha ^{n}\}_{n\in \mathbb {N}}$
.
$\gamma \notin \{ \alpha ^{n}\}_{n\in \mathbb {N}}$
.
Definition 5.3. [Reference KatsuraKat06b]
A free topological graph is a graph E such that there does not exist an element
![]() $v\in E^{0}$
satisfying all of the following three conditions.
$v\in E^{0}$
satisfying all of the following three conditions.
-
(F1) There exists a simple loop
 $l_{1}\cdots l_{n}$
in E with
$l_{1}\cdots l_{n}$
in E with
 $r(l_{1})=v$
.
$r(l_{1})=v$
. -
(F2) If
 $e\in E^{1}$
with
$e\in E^{1}$
with
 $s(e)\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
$s(e)\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
 $r(e)=r(l_{k})$
for some k, then
$r(e)=r(l_{k})$
for some k, then
 $e=l_{k}$
.
$e=l_{k}$
. -
(F3) v is isolated in
 $\{r(\beta ) \mid \beta \in E^{*}v\}$
.
$\{r(\beta ) \mid \beta \in E^{*}v\}$
.
This notion of freeness introduced by Katsura is a simultaneous generalisation of the notion of condition
![]() $(K)$
for directed graphs and the notion of freeness for crossed products by homeomorphisms.
$(K)$
for directed graphs and the notion of freeness for crossed products by homeomorphisms.
Lemma 5.4. Let E be a second countable topological graph. Then E is free if and only if there does not exist an isolated loop.
Proof. Assume that E is not a free graph and let
![]() $\alpha \in vE^{*}$
be the simple loop from
$\alpha \in vE^{*}$
be the simple loop from
![]() $(\text {F}1)$
. Since
$(\text {F}1)$
. Since
![]() $\alpha $
is simple, it clearly satisfies condition (a) in Definition 5.1. By
$\alpha $
is simple, it clearly satisfies condition (a) in Definition 5.1. By
![]() $(\text {F}3)$
, we can find an open set
$(\text {F}3)$
, we can find an open set
![]() $V_{v} \subseteq E^{0}$
such that
$V_{v} \subseteq E^{0}$
such that
![]() $r(\beta )\in V_{v}$
and
$r(\beta )\in V_{v}$
and
![]() $\beta \in E^{*}v$
implies that
$\beta \in E^{*}v$
implies that
![]() $r(\beta )=v$
. Now assume for a contradiction that
$r(\beta )=v$
. Now assume for a contradiction that
![]() $\gamma \in V_{v} E_{\alpha }^{*}$
with
$\gamma \in V_{v} E_{\alpha }^{*}$
with
![]() $|\gamma | \neq 0$
. Then
$|\gamma | \neq 0$
. Then
![]() $r(\gamma )\in V_{v}$
and
$r(\gamma )\in V_{v}$
and
![]() $\gamma \in E^{*}v$
, and hence
$\gamma \in E^{*}v$
, and hence
![]() $\gamma $
is a loop in
$\gamma $
is a loop in
![]() $vE^{*}$
. Then
$vE^{*}$
. Then
![]() $s(\gamma _{1})\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
$s(\gamma _{1})\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
![]() $r(\gamma _{1})=r(\alpha _{1})$
, so by
$r(\gamma _{1})=r(\alpha _{1})$
, so by
![]() $(\text {F}2)$
, then
$(\text {F}2)$
, then
![]() $\gamma _{1}=\alpha _{1}$
. If
$\gamma _{1}=\alpha _{1}$
. If
![]() $|\gamma |\geq 2$
, then
$|\gamma |\geq 2$
, then
![]() $s(\gamma _{2})\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
$s(\gamma _{2})\in \{r(\beta ) \mid \beta \in E^{*}v\}$
and
![]() $r(\gamma _{2})=s(\gamma _{1})=s(\alpha _{1})=r(\alpha _{2})$
, so
$r(\gamma _{2})=s(\gamma _{1})=s(\alpha _{1})=r(\alpha _{2})$
, so
![]() $\gamma _{2}=\alpha _{2}$
. We can continue like this to write
$\gamma _{2}=\alpha _{2}$
. We can continue like this to write
![]() $\gamma =\alpha ^{n}\alpha _{1}\cdots \alpha _{k}$
for some
$\gamma =\alpha ^{n}\alpha _{1}\cdots \alpha _{k}$
for some
![]() $0\leq k <|\alpha |$
. However,
$0\leq k <|\alpha |$
. However,
![]() $s(\gamma )=r(\alpha )$
, so since
$s(\gamma )=r(\alpha )$
, so since
![]() $\alpha $
is simple, we get that
$\alpha $
is simple, we get that
![]() $k=0$
. Since
$k=0$
. Since
![]() $|\gamma |\neq 0$
and
$|\gamma |\neq 0$
and
![]() $\gamma \in E_{\alpha }^{*}$
, we reach a contradiction. So
$\gamma \in E_{\alpha }^{*}$
, we reach a contradiction. So
![]() $V_{v} E_{\alpha }^{*} = \{v\}$
, and hence
$V_{v} E_{\alpha }^{*} = \{v\}$
, and hence
![]() $\alpha $
also satisfies condition (b) in Definition 5.1 which makes it an isolated loop.
$\alpha $
also satisfies condition (b) in Definition 5.1 which makes it an isolated loop.
Assume now that there exists an isolated loop
![]() $\alpha $
in
$\alpha $
in
![]() $E^{*}$
. Set
$E^{*}$
. Set
![]() $v=r(\alpha )$
. By Lemma 5.2,
$v=r(\alpha )$
. By Lemma 5.2,
![]() $\alpha $
is simple. Let now
$\alpha $
is simple. Let now
![]() $e\in E^{1}$
satisfy that
$e\in E^{1}$
satisfy that
![]() $s(e)=r(\beta )$
with
$s(e)=r(\beta )$
with
![]() $\beta \in E^{*}v$
and
$\beta \in E^{*}v$
and
![]() $r(e)=r(\alpha _{k})$
for some k. It follows that we have a loop
$r(e)=r(\alpha _{k})$
for some k. It follows that we have a loop
![]() $\alpha _{1}\cdots \alpha _{k-1}e\beta \in r(\alpha )E^{*}$
. By Lemma 5.2, then
$\alpha _{1}\cdots \alpha _{k-1}e\beta \in r(\alpha )E^{*}$
. By Lemma 5.2, then
![]() $\alpha _{1}\cdots \alpha _{k-1}e\beta =\alpha ^{n}$
. So
$\alpha _{1}\cdots \alpha _{k-1}e\beta =\alpha ^{n}$
. So
![]() $e=\alpha _{k}$
, which proves
$e=\alpha _{k}$
, which proves
![]() $(\text {F}2)$
. Lastly, let us prove that v is isolated in
$(\text {F}2)$
. Lastly, let us prove that v is isolated in
![]() $\{r(\beta ) \mid \beta \in E^{*}v\}$
. By assumption, there exists an open neighbourhood
$\{r(\beta ) \mid \beta \in E^{*}v\}$
. By assumption, there exists an open neighbourhood
![]() $V_{v}$
of v in
$V_{v}$
of v in
![]() $E^{0}$
with
$E^{0}$
with
![]() $|V_{v} E^{*}_{\alpha } |< \infty $
. It follows that
$|V_{v} E^{*}_{\alpha } |< \infty $
. It follows that
is a finite set in
![]() $E^{0}$
, and hence the set
$E^{0}$
, and hence the set
![]() $V_{v} \setminus N$
is an open set in
$V_{v} \setminus N$
is an open set in
![]() $E^{0}$
containing v yet which does not contain any other elements of
$E^{0}$
containing v yet which does not contain any other elements of
![]() $\{r(\beta ) \mid \beta \in E^{*}v\}$
. In conclusion, the vertex v ensures that E is not a free graph which proves the lemma.
$\{r(\beta ) \mid \beta \in E^{*}v\}$
. In conclusion, the vertex v ensures that E is not a free graph which proves the lemma.
We say that two loops
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are equivalent if there exists a k such that
$\beta $
are equivalent if there exists a k such that
This condition is equivalent to having
![]() $|\alpha |=|\beta |$
and
$|\alpha |=|\beta |$
and
![]() $\sigma ^{k}(\alpha ^{\infty } )=\beta ^{\infty }$
for some k. The following observation will become vital later.
$\sigma ^{k}(\alpha ^{\infty } )=\beta ^{\infty }$
for some k. The following observation will become vital later.
Lemma 5.5. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two equivalent loops. If
$\beta $
be two equivalent loops. If
![]() $|VE_{\beta }^{*}|<\infty $
, then
$|VE_{\beta }^{*}|<\infty $
, then
![]() $|VE_{\alpha }^{*}|<\infty $
for
$|VE_{\alpha }^{*}|<\infty $
for
![]() $V\subseteq E^{0}$
. In particular, then
$V\subseteq E^{0}$
. In particular, then
![]() $\alpha $
is summable if and only if
$\alpha $
is summable if and only if
![]() $\beta $
is summable.
$\beta $
is summable.
Proof. Assume that
![]() $|\alpha |=|\beta |=n$
and
$|\alpha |=|\beta |=n$
and
![]() $\beta =\alpha _{k+1}\cdots \alpha _{n}\alpha _{1} \cdots \alpha _{k}$
. If
$\beta =\alpha _{k+1}\cdots \alpha _{n}\alpha _{1} \cdots \alpha _{k}$
. If
![]() $\gamma \in VE_{\alpha }^{*}$
, then
$\gamma \in VE_{\alpha }^{*}$
, then
![]() $\gamma \alpha _{1}\cdots \alpha _{k} \in VE^{*}r(\beta )$
. If
$\gamma \alpha _{1}\cdots \alpha _{k} \in VE^{*}r(\beta )$
. If
![]() $\gamma \alpha _{1}\cdots \alpha _{k}=\delta \beta ^{2}$
for some
$\gamma \alpha _{1}\cdots \alpha _{k}=\delta \beta ^{2}$
for some
![]() $\delta $
, then we have that
$\delta $
, then we have that
which contradicts that
![]() $\gamma \in E_{\alpha }^{*}$
. Hence, we have an injective map
$\gamma \in E_{\alpha }^{*}$
. Hence, we have an injective map
and hence
![]() $|VE_{\alpha }^{*}|<\infty $
if
$|VE_{\alpha }^{*}|<\infty $
if
![]() $|VE_{\beta }^{*}|<\infty $
. By symmetry, it follows that
$|VE_{\beta }^{*}|<\infty $
. By symmetry, it follows that
![]() $\alpha $
satisfies condition (b
$\alpha $
satisfies condition (b
![]() $'$
) if and only if
$'$
) if and only if
![]() $\beta $
does. If
$\beta $
does. If
![]() $\alpha =\gamma ^{l}$
with
$\alpha =\gamma ^{l}$
with
![]() $l\geq 2$
and
$l\geq 2$
and
![]() $\sigma ^{k}(\alpha ^{\infty } )=\beta ^{\infty }$
, then
$\sigma ^{k}(\alpha ^{\infty } )=\beta ^{\infty }$
, then
which implies that
![]() $\beta $
also does not satisfy condition (a) in Definition 5.1. This proves the lemma.
$\beta $
also does not satisfy condition (a) in Definition 5.1. This proves the lemma.
To analyse the harmonic measures, we will need to work with the eventually cyclic paths, which are paths on the form
![]() $\beta \alpha ^{\infty }\in E^{\infty }$
where
$\beta \alpha ^{\infty }\in E^{\infty }$
where
![]() $\alpha $
is a loop and
$\alpha $
is a loop and
![]() $\beta \in E^{*}$
satisfies that
$\beta \in E^{*}$
satisfies that
![]() $s(\beta )=r(\alpha )$
. We set
$s(\beta )=r(\alpha )$
. We set
![]() $\mathcal {C}$
to be the set of eventually cyclic paths, that is,
$\mathcal {C}$
to be the set of eventually cyclic paths, that is,
and we define for any subset
![]() $S \subseteq E^{0}$
the set
$S \subseteq E^{0}$
the set
![]() $\mathcal {C}S$
as
$\mathcal {C}S$
as
 $$ \begin{align*} \mathcal{C}S:&= \{ x\in \mathcal{C} \mid s(x_{i}) \in S \text{ for infinitely many}\ i\in \mathbb{N} \} \\ &= \{ x\in \mathcal{C} \mid x=\beta \alpha^{\infty} \text{ with}\ \alpha\ \text{a loop}, \beta \in E^{*}r(\alpha)\ \text{and}\ s(\alpha_{i}) \in S\ \text{for some}\ 1\leq i \leq |\alpha| \}. \end{align*} $$
$$ \begin{align*} \mathcal{C}S:&= \{ x\in \mathcal{C} \mid s(x_{i}) \in S \text{ for infinitely many}\ i\in \mathbb{N} \} \\ &= \{ x\in \mathcal{C} \mid x=\beta \alpha^{\infty} \text{ with}\ \alpha\ \text{a loop}, \beta \in E^{*}r(\alpha)\ \text{and}\ s(\alpha_{i}) \in S\ \text{for some}\ 1\leq i \leq |\alpha| \}. \end{align*} $$
Lemma 5.6. If
![]() $S \subseteq E^{0}$
is a Borel set, then the set
$S \subseteq E^{0}$
is a Borel set, then the set
![]() $\mathcal {C}S$
is an invariant Borel subset of
$\mathcal {C}S$
is an invariant Borel subset of
![]() $\partial E$
.
$\partial E$
.
Proof. It is straightforward to check that
![]() $\mathcal {C}S$
is invariant under
$\mathcal {C}S$
is invariant under
![]() $\sigma $
. Take an
$\sigma $
. Take an
![]() $n\in \mathbb {N}$
. The map
$n\in \mathbb {N}$
. The map
![]() $r\circ \sigma ^{i}: E^{\infty } \to E^{0}$
is continuous for any
$r\circ \sigma ^{i}: E^{\infty } \to E^{0}$
is continuous for any
![]() $i\in \mathbb {N}$
, so the set
$i\in \mathbb {N}$
, so the set
 $$ \begin{align*} M_{n}:=\{x\in E^{\infty} \mid \sigma^{n}(x)=x \} \cap \bigcup_{i=0}^{n-1} \{ x\in E^{\infty} \mid r\circ \sigma^{i}(x) \in S \} \end{align*} $$
$$ \begin{align*} M_{n}:=\{x\in E^{\infty} \mid \sigma^{n}(x)=x \} \cap \bigcup_{i=0}^{n-1} \{ x\in E^{\infty} \mid r\circ \sigma^{i}(x) \in S \} \end{align*} $$
is Borel in
![]() $E^{\infty }$
and hence in
$E^{\infty }$
and hence in
![]() $\partial E$
by Lemma 2.2. Since
$\partial E$
by Lemma 2.2. Since
 $$ \begin{align*} \mathcal{C} S = \bigcup_{n=1}^{\infty} \bigcup_{m=0}^{\infty} \sigma^{-m}(M_{n}) \;, \end{align*} $$
$$ \begin{align*} \mathcal{C} S = \bigcup_{n=1}^{\infty} \bigcup_{m=0}^{\infty} \sigma^{-m}(M_{n}) \;, \end{align*} $$
then
![]() $\mathcal {C}S$
is a Borel subset of
$\mathcal {C}S$
is a Borel subset of
![]() $\partial E$
, proving the lemma.
$\partial E$
, proving the lemma.
6 Harmonic measures on eventually cyclic paths
We will now turn to the analysis of harmonic measures. We will not achieve a complete description of all the extremal harmonic measures, as was the case for boundary measures, but we will describe all extremal harmonic measures concentrated on the eventually cyclic paths. It turns out that the existence of non-gauge-invariant tracial weights is closely relate to the existence of such measures.
Proposition 6.1. Let E be a second countable topological graph. Assume that
![]() $\nu $
is a non-zero extremal harmonic measure on
$\nu $
is a non-zero extremal harmonic measure on
![]() $\partial E$
satisfying that
$\partial E$
satisfying that
![]() $\nu (\mathcal {C}^{C})=0$
. Then there exists a summable loop
$\nu (\mathcal {C}^{C})=0$
. Then there exists a summable loop
![]() $\alpha $
in E such that
$\alpha $
in E such that
![]() $\nu $
is concentrated on the countable set
$\nu $
is concentrated on the countable set
This implies that there exists an
![]() $r> 0$
such that
$r> 0$
such that
 $$ \begin{align*} \nu = r \cdot \sum_{\beta \in E_{\alpha}^{*} } \delta_{\beta \alpha^{\infty}}. \end{align*} $$
$$ \begin{align*} \nu = r \cdot \sum_{\beta \in E_{\alpha}^{*} } \delta_{\beta \alpha^{\infty}}. \end{align*} $$
Proof. Let
![]() $\{V_{i} \}_{i\in \mathbb {N}}$
be a countable basis of
$\{V_{i} \}_{i\in \mathbb {N}}$
be a countable basis of
![]() $E^{0}$
of open sets with compact closures. Then
$E^{0}$
of open sets with compact closures. Then
 $$ \begin{align*} \mathcal{C} = \bigcup_{i=1}^{\infty} \mathcal{C} V_{i}. \end{align*} $$
$$ \begin{align*} \mathcal{C} = \bigcup_{i=1}^{\infty} \mathcal{C} V_{i}. \end{align*} $$
Since
![]() $\nu $
is extremal and
$\nu $
is extremal and
![]() $\mathcal {C} V_{i} $
is an invariant Borel set by Lemma 5.6, there exists some j with
$\mathcal {C} V_{i} $
is an invariant Borel set by Lemma 5.6, there exists some j with
![]() $\nu ( (\mathcal {C} \overline {V_{j}})^{C} )=0$
. Since
$\nu ( (\mathcal {C} \overline {V_{j}})^{C} )=0$
. Since
![]() $\overline {V_{j}}$
is a second countable compact Hausdorff space in the relative topology, we can view the topology on it as generated by a metric. We can therefore find a sequence
$\overline {V_{j}}$
is a second countable compact Hausdorff space in the relative topology, we can view the topology on it as generated by a metric. We can therefore find a sequence
![]() $\{W_{i} \}_{i=1}^{\infty }$
of Borel sets in
$\{W_{i} \}_{i=1}^{\infty }$
of Borel sets in
![]() $\overline {V_{j}}$
such that
$\overline {V_{j}}$
such that
![]() $\nu ((\mathcal {C} W_{i})^{C})=0$
for all i, such that
$\nu ((\mathcal {C} W_{i})^{C})=0$
for all i, such that
![]() $W_{i+1} \subseteq W_{i}$
for all i and such that the diameter of
$W_{i+1} \subseteq W_{i}$
for all i and such that the diameter of
![]() $W_{i}$
is less than
$W_{i}$
is less than
![]() $1/i$
. It follows that
$1/i$
. It follows that
 $$ \begin{align*} 0= \nu\bigg( \bigcup_{i\in \mathbb{N}} (\mathcal{C} W_{i})^{C} \bigg) = \nu \bigg ( \bigg( \bigcap_{i\in \mathbb{N}} \mathcal{C} W_{i} \bigg)^{C} \bigg) = \nu \bigg ( \bigg( \mathcal{C} \bigcap_{i\in \mathbb{N}} W_{i} \bigg)^{C} \bigg) , \end{align*} $$
$$ \begin{align*} 0= \nu\bigg( \bigcup_{i\in \mathbb{N}} (\mathcal{C} W_{i})^{C} \bigg) = \nu \bigg ( \bigg( \bigcap_{i\in \mathbb{N}} \mathcal{C} W_{i} \bigg)^{C} \bigg) = \nu \bigg ( \bigg( \mathcal{C} \bigcap_{i\in \mathbb{N}} W_{i} \bigg)^{C} \bigg) , \end{align*} $$
but since
![]() $W_{i}$
has diameter less than
$W_{i}$
has diameter less than
![]() $1/i$
and
$1/i$
and
![]() $\nu \neq 0$
, this implies that
$\nu \neq 0$
, this implies that
![]() $\bigcap _{i\in \mathbb {N}} W_{i}=\{v\}$
for some
$\bigcap _{i\in \mathbb {N}} W_{i}=\{v\}$
for some
![]() $v\in E^{0}$
. We now have that
$v\in E^{0}$
. We now have that
This implies in particular that
![]() $\mathcal {C} \{v\} \neq \emptyset $
. Since s is a local homeomorphism and E is second countable, there exists an at most countable collection
$\mathcal {C} \{v\} \neq \emptyset $
. Since s is a local homeomorphism and E is second countable, there exists an at most countable collection
![]() $\{\alpha ^{i}\}_{i\in I}$
of loops satisfying that
$\{\alpha ^{i}\}_{i\in I}$
of loops satisfying that
![]() $s(\alpha ^{i})=v$
. It follows by definition of
$s(\alpha ^{i})=v$
. It follows by definition of
![]() $\mathcal {C}$
that we can write
$\mathcal {C}$
that we can write
and since each of these sets is invariant, there is a loop
![]() $\alpha $
such that
$\alpha $
such that
![]() $r(\alpha )=s(\alpha )=v$
and
$r(\alpha )=s(\alpha )=v$
and
It follows that
![]() $\nu $
is concentrated on
$\nu $
is concentrated on
![]() $\{ \beta \alpha ^{\infty } \mid \beta \in E^{*}r(\alpha ) \}$
. Let
$\{ \beta \alpha ^{\infty } \mid \beta \in E^{*}r(\alpha ) \}$
. Let
![]() $n\in \mathbb {N}$
be the smallest number such that
$n\in \mathbb {N}$
be the smallest number such that
![]() $\sigma ^{n}(\alpha ^{\infty })=\alpha ^{\infty }$
. By possible substituting
$\sigma ^{n}(\alpha ^{\infty })=\alpha ^{\infty }$
. By possible substituting
![]() $\alpha $
, we can assume that
$\alpha $
, we can assume that
![]() $|\alpha |=n$
. We claim that the surjective map
$|\alpha |=n$
. We claim that the surjective map
is also injective. If
![]() $\beta \alpha ^{\infty }=\delta \alpha ^{\infty }$
with
$\beta \alpha ^{\infty }=\delta \alpha ^{\infty }$
with
![]() $|\delta |<|\beta |$
, then
$|\delta |<|\beta |$
, then
![]() $\beta = \delta \beta '$
, and hence using
$\beta = \delta \beta '$
, and hence using
![]() $\sigma ^{|\delta |}$
on
$\sigma ^{|\delta |}$
on
![]() $\beta \alpha ^{\infty }=\delta \alpha ^{\infty }$
, we get that
$\beta \alpha ^{\infty }=\delta \alpha ^{\infty }$
, we get that
![]() $\beta '\alpha ^{\infty }=\alpha ^{\infty }$
. Since
$\beta '\alpha ^{\infty }=\alpha ^{\infty }$
. Since
![]() $\beta '\in E_{\alpha }^{*}$
, we can write
$\beta '\in E_{\alpha }^{*}$
, we can write
![]() $\beta '=\alpha ^{k} \zeta $
with
$\beta '=\alpha ^{k} \zeta $
with
![]() $0<|\zeta |< |\alpha |$
, which implies that
$0<|\zeta |< |\alpha |$
, which implies that
![]() $\zeta \alpha ^{\infty }=\alpha ^{\infty }$
. Iterating this equality, we see that
$\zeta \alpha ^{\infty }=\alpha ^{\infty }$
. Iterating this equality, we see that
![]() $\zeta ^{\infty }=\alpha ^{\infty }$
, which contradicts our choice of
$\zeta ^{\infty }=\alpha ^{\infty }$
, which contradicts our choice of
![]() $\alpha $
. Hence, the map is surjective, and since
$\alpha $
. Hence, the map is surjective, and since
![]() $\nu (\{ \beta \alpha ^{\infty }\})=\nu (\{ \alpha ^{\infty }\})$
, we get that
$\nu (\{ \beta \alpha ^{\infty }\})=\nu (\{ \alpha ^{\infty }\})$
, we get that
 $$ \begin{align*} \nu= \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}} \; \nu(\{ \beta \alpha^{\infty}\}) = \nu(\{ \alpha^{\infty}\}) \cdot \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}. \end{align*} $$
$$ \begin{align*} \nu= \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}} \; \nu(\{ \beta \alpha^{\infty}\}) = \nu(\{ \alpha^{\infty}\}) \cdot \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}. \end{align*} $$
We now only have to prove that
![]() $\alpha $
is a summable loop. Fix therefore a
$\alpha $
is a summable loop. Fix therefore a
![]() $w\in E^{0}$
. Since
$w\in E^{0}$
. Since
![]() $\nu $
is regular on
$\nu $
is regular on
![]() $\partial E$
, there exists an open neighbourhood
$\partial E$
, there exists an open neighbourhood
![]() $V_{w}$
of w in
$V_{w}$
of w in
![]() $E^{0}$
with
$E^{0}$
with
![]() $\overline {V_{w}}$
compact, and hence
$\overline {V_{w}}$
compact, and hence
![]() $\nu (Z(V_{w}))<\infty $
. Since
$\nu (Z(V_{w}))<\infty $
. Since
 $$ \begin{align*} \nu(Z(V_{w})) = r\cdot \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}(Z(V_{w})) = r \cdot | V_{w} E_{\alpha}^{*} | , \end{align*} $$
$$ \begin{align*} \nu(Z(V_{w})) = r\cdot \sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}(Z(V_{w})) = r \cdot | V_{w} E_{\alpha}^{*} | , \end{align*} $$
then
![]() $\alpha $
is in fact a summable loop.
$\alpha $
is in fact a summable loop.
Similarly to the case of boundary measures, we can now prove that equivalence classes of summable loops in the graph are bijective corresponding to the rays of extremal harmonic measures concentrated on eventually cyclic paths.
Theorem 6.2. Let E be a second countable topological graph. There is a bijection between the rays of non-zero extremal harmonic measures concentrated on
![]() $\mathcal {C}$
and equivalence classes of summable loops
$\mathcal {C}$
and equivalence classes of summable loops
![]() $\alpha $
in E. The ray corresponding to such a loop
$\alpha $
in E. The ray corresponding to such a loop
![]() $\alpha $
is on the form
$\alpha $
is on the form
![]() $\{ r \cdot \nu \mid r\geq 0 \}$
, where
$\{ r \cdot \nu \mid r\geq 0 \}$
, where
 $$ \begin{align} \nu = \sum_{\beta \in E_{\alpha}^{*} } \delta_{\beta \alpha^{\infty}}. \end{align} $$
$$ \begin{align} \nu = \sum_{\beta \in E_{\alpha}^{*} } \delta_{\beta \alpha^{\infty}}. \end{align} $$
Proof. Let
![]() $\alpha \in E^{*}$
be a summable loop. The set
$\alpha \in E^{*}$
be a summable loop. The set
![]() $E_{\alpha }^{*} $
is countable by second countability of E. We define the measure
$E_{\alpha }^{*} $
is countable by second countability of E. We define the measure
![]() $\nu $
as in equation (6.1). It follows as in the proof of Theorem 4.2 that
$\nu $
as in equation (6.1). It follows as in the proof of Theorem 4.2 that
![]() $\nu $
is non-zero, regular, extremal, invariant and satisfies that
$\nu $
is non-zero, regular, extremal, invariant and satisfies that
![]() $\nu (\mathcal {C}^{C})=0$
. If two loops
$\nu (\mathcal {C}^{C})=0$
. If two loops
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are equivalent, they clearly give rise to the same measure. Hence, the map which sends an equivalence class of a summable loop
$\beta $
are equivalent, they clearly give rise to the same measure. Hence, the map which sends an equivalence class of a summable loop
![]() $\alpha $
to a measure
$\alpha $
to a measure
![]() $\nu $
is well defined, and it is surjective by Proposition 6.1. To see that it is injective, let
$\nu $
is well defined, and it is surjective by Proposition 6.1. To see that it is injective, let
![]() $\nu _{i}$
be defined by the loop
$\nu _{i}$
be defined by the loop
![]() $\alpha ^{i}$
for
$\alpha ^{i}$
for
![]() $i=1,2$
and assume
$i=1,2$
and assume
![]() $\nu _{1}=\nu _{2}$
. Then
$\nu _{1}=\nu _{2}$
. Then
![]() $\nu _{2}((\alpha ^{1})^{\infty })>0$
, and hence
$\nu _{2}((\alpha ^{1})^{\infty })>0$
, and hence
![]() $(\alpha ^{1})^{\infty }=\beta (\alpha ^{2})^{\infty }$
for some
$(\alpha ^{1})^{\infty }=\beta (\alpha ^{2})^{\infty }$
for some
![]() $\beta \in E_{\alpha _{2}}^{*}$
. This implies that
$\beta \in E_{\alpha _{2}}^{*}$
. This implies that
![]() $\alpha _{1}$
and
$\alpha _{1}$
and
![]() $\alpha _{2}$
are equivalent because
$\alpha _{2}$
are equivalent because
![]() $\sigma ^{|\beta |}((\alpha ^{1})^{\infty })=(\alpha ^{2})^{\infty }$
. Hence, our map is a bijection which proves the theorem.
$\sigma ^{|\beta |}((\alpha ^{1})^{\infty })=(\alpha ^{2})^{\infty }$
. Hence, our map is a bijection which proves the theorem.
Remark 6.3. If
![]() $E^{0}$
is compact, we can exchange the condition: for any
$E^{0}$
is compact, we can exchange the condition: for any
![]() $w\in E^{0}$
, there exists an open neighbourhood
$w\in E^{0}$
, there exists an open neighbourhood
![]() $V_{w}$
of w in
$V_{w}$
of w in
![]() $E^{0}$
satisfying
$E^{0}$
satisfying
![]() $|V_{w}E_{\alpha }^{*}|< \infty $
, with the condition that
$|V_{w}E_{\alpha }^{*}|< \infty $
, with the condition that
![]() $|E_{\alpha }^{*}| < \infty $
.
$|E_{\alpha }^{*}| < \infty $
.
By Lemma 5.5, then
![]() $|E_{\alpha }^{*}|<\infty $
if and only if
$|E_{\alpha }^{*}|<\infty $
if and only if
![]() $|E_{\beta }^{*}|<\infty $
for two equivalent loops
$|E_{\beta }^{*}|<\infty $
for two equivalent loops
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. It follows from Theorem 6.2 that the extremal rays of finite harmonic measures concentrated on
$\beta $
. It follows from Theorem 6.2 that the extremal rays of finite harmonic measures concentrated on
![]() $\mathcal {C}$
maps bijectively onto the equivalence classes of summable loops
$\mathcal {C}$
maps bijectively onto the equivalence classes of summable loops
![]() $\alpha $
satisfying the extra condition
$\alpha $
satisfying the extra condition
![]() $|E_{\alpha }^{*}|<\infty $
. This observation gives the corollary below.
$|E_{\alpha }^{*}|<\infty $
. This observation gives the corollary below.
Corollary 6.4. Let E be a second countable topological graph. There is a bijection between the set of extremal harmonic probability measures concentrated on
![]() $\mathcal {C}$
and the set of equivalence classes of summable loops
$\mathcal {C}$
and the set of equivalence classes of summable loops
![]() $\alpha $
with
$\alpha $
with
![]() $|E_{\alpha }^{*}|< \infty $
. The extremal harmonic probability measures corresponding to such a loop is on the form
$|E_{\alpha }^{*}|< \infty $
. The extremal harmonic probability measures corresponding to such a loop is on the form
 $$ \begin{align*} \nu = \frac{1}{|E_{\alpha}^{*}|}\sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}. \end{align*} $$
$$ \begin{align*} \nu = \frac{1}{|E_{\alpha}^{*}|}\sum_{\beta \in E_{\alpha}^{*}} \delta_{\beta \alpha^{\infty}}. \end{align*} $$
7 Gauge-invariant tracial weights
With the analysis of measures concentrated on eventually cyclic paths from §6, we can now give criteria for when there exists non-gauge-invariant tracial weights.
Proposition 7.1. Assume that E is a second countable topological graph. If there exists a tracial weight on
![]() $C^{*}(E)$
which is not gauge-invariant, then there exists a summable loop in E.
$C^{*}(E)$
which is not gauge-invariant, then there exists a summable loop in E.
If there exists a tracial state on
![]() $C^{*}(E)$
which is not gauge-invariant, then there exists a summable loop
$C^{*}(E)$
which is not gauge-invariant, then there exists a summable loop
![]() $\alpha $
in E with
$\alpha $
in E with
![]() $|E_{\alpha }^{*}|<\infty $
.
$|E_{\alpha }^{*}|<\infty $
.
Proof. Let
![]() $\omega $
be a tracial weight on
$\omega $
be a tracial weight on
![]() $C^{*}(E)$
which is not gauge-invariant. Since
$C^{*}(E)$
which is not gauge-invariant. Since
![]() $\partial E$
is second countable, we can find a strictly positive function
$\partial E$
is second countable, we can find a strictly positive function
![]() $h\in C_{0}(\partial E)$
such that
$h\in C_{0}(\partial E)$
such that
Letting
![]() $\mathcal {W}(C^{*}(E))$
denote the tracial weights on
$\mathcal {W}(C^{*}(E))$
denote the tracial weights on
![]() $C^{*}(E)$
, we make the following claim.
$C^{*}(E)$
, we make the following claim.
Claim. The set
![]() $\mathcal {N}:=\{\psi \in \mathcal {W}(C^{*}(E)) \mid \psi (h)\leq 1\}$
is compact.
$\mathcal {N}:=\{\psi \in \mathcal {W}(C^{*}(E)) \mid \psi (h)\leq 1\}$
is compact.
Let
![]() $\{E_{n}\}_{n\in \mathbb {N}} \subseteq C_{c}(\partial E)_{+}$
be an approximate identity as chosen in [Reference ChristensenChr23, §4]. To see that
$\{E_{n}\}_{n\in \mathbb {N}} \subseteq C_{c}(\partial E)_{+}$
be an approximate identity as chosen in [Reference ChristensenChr23, §4]. To see that
![]() $\mathcal {N}$
is a closed set notice, by e.g. [Reference ChristensenChr23, Corollary 4.8], that
$\mathcal {N}$
is a closed set notice, by e.g. [Reference ChristensenChr23, Corollary 4.8], that
Since h is strictly positive, there exists an
![]() $\varepsilon _{n}>0$
for each
$\varepsilon _{n}>0$
for each
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $h(x) \geq \varepsilon _{n}$
for
$h(x) \geq \varepsilon _{n}$
for
![]() $x\in \text {supp}(E_{n})$
. If
$x\in \text {supp}(E_{n})$
. If
![]() $\psi \in \mathcal {N}$
, it follows that
$\psi \in \mathcal {N}$
, it follows that
and hence
![]() $\psi (E_{n}^{2}) \leq \varepsilon _{n}^{-1}$
. It follows that the elements of
$\psi (E_{n}^{2}) \leq \varepsilon _{n}^{-1}$
. It follows that the elements of
![]() $\mathcal {N}$
restricted to
$\mathcal {N}$
restricted to
![]() $\mathcal {A}_{n}:=\overline {E_{n} C^{*}(E)E_{n} }$
are contained in the ball in
$\mathcal {A}_{n}:=\overline {E_{n} C^{*}(E)E_{n} }$
are contained in the ball in
![]() $\mathcal {A}_{n}^{*}$
of radius
$\mathcal {A}_{n}^{*}$
of radius
![]() $\varepsilon _{n}^{-1}$
. The topological space we embed
$\varepsilon _{n}^{-1}$
. The topological space we embed
![]() $\mathcal {W}(C^{*}(E))$
in is
$\mathcal {W}(C^{*}(E))$
in is
![]() $\varprojlim _{n} \mathcal {A}_{n}^{*}$
, cf. [Reference ChristensenChr23, §4], and hence
$\varprojlim _{n} \mathcal {A}_{n}^{*}$
, cf. [Reference ChristensenChr23, §4], and hence
![]() $\mathcal {N}$
is compact in this space. This proves the claim.
$\mathcal {N}$
is compact in this space. This proves the claim.
Let now
![]() $f\in C_{c}(\mathcal {G}_{E})$
be supported in
$f\in C_{c}(\mathcal {G}_{E})$
be supported in
![]() $\Phi ^{-1}(\{k\})$
for some
$\Phi ^{-1}(\{k\})$
for some
![]() $k\in \mathbb {Z} \setminus \{0\}$
satisfying that
$k\in \mathbb {Z} \setminus \{0\}$
satisfying that
![]() $\omega (f)\neq 0$
. Since the
$\omega (f)\neq 0$
. Since the
![]() $\psi \in \mathcal {N}$
with
$\psi \in \mathcal {N}$
with
![]() $\psi (f) \neq 0$
is an open set by definition of the topology on
$\psi (f) \neq 0$
is an open set by definition of the topology on
![]() $\varprojlim _{n} \mathcal {A}_{n}^{*}$
, we have by the Krein–Milman theorem that there exists an element
$\varprojlim _{n} \mathcal {A}_{n}^{*}$
, we have by the Krein–Milman theorem that there exists an element
![]() $\psi ' \in \mathcal {N}$
which is a finite convex combination of extremal elements in
$\psi ' \in \mathcal {N}$
which is a finite convex combination of extremal elements in
![]() $\mathcal {N}$
with
$\mathcal {N}$
with
![]() $\psi '(f) \neq 0$
. In particular, there exists an extremal element
$\psi '(f) \neq 0$
. In particular, there exists an extremal element
![]() $\psi \in \mathcal {N}$
with
$\psi \in \mathcal {N}$
with
![]() $\psi (f)\neq 0$
. It follows that
$\psi (f)\neq 0$
. It follows that
![]() $\psi \neq 0$
, so since
$\psi \neq 0$
, so since
![]() $h>0$
on
$h>0$
on
![]() $\partial E$
, then
$\partial E$
, then
![]() $\psi (h)>0$
. Since
$\psi (h)>0$
. Since
![]() $\psi $
is extremal in
$\psi $
is extremal in
![]() $\mathcal {N}$
, we must have
$\mathcal {N}$
, we must have
![]() $\psi (h)=1$
.
$\psi (h)=1$
.
To see that
![]() $\psi $
also has to be an extremal tracial weight on
$\psi $
also has to be an extremal tracial weight on
![]() $C^{*}(E)$
, write
$C^{*}(E)$
, write
![]() $\psi =\psi _{1}+\psi _{2}$
for two non-zero tracial weights
$\psi =\psi _{1}+\psi _{2}$
for two non-zero tracial weights
![]() $\psi _{1}$
and
$\psi _{1}$
and
![]() $\psi _{2}$
on
$\psi _{2}$
on
![]() $C^{*}(E)$
. Since
$C^{*}(E)$
. Since
![]() $\psi (h)=1$
, then
$\psi (h)=1$
, then
![]() $\psi _{i}(h)<\infty $
for
$\psi _{i}(h)<\infty $
for
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $h>0$
, then
$h>0$
, then
![]() $\psi _{i}(h)=0$
would imply that the associated measure
$\psi _{i}(h)=0$
would imply that the associated measure
![]() $\nu _{\psi _{i}}=0$
which would contradict that
$\nu _{\psi _{i}}=0$
which would contradict that
![]() $\psi _{i}\neq 0$
. Hence, we can write
$\psi _{i}\neq 0$
. Hence, we can write
which implies that
![]() $\psi _{1} =\psi \cdot \psi _{1}(h)$
since
$\psi _{1} =\psi \cdot \psi _{1}(h)$
since
![]() $\psi $
is extremal in
$\psi $
is extremal in
![]() $\mathcal {N}$
. In conclusion, we have an extremal tracial weight
$\mathcal {N}$
. In conclusion, we have an extremal tracial weight
![]() $\psi $
with
$\psi $
with
![]() $\psi (f)\neq 0$
. Since
$\psi (f)\neq 0$
. Since
![]() $\text {supp}(f) \subseteq \Phi ^{-1}(\{k\})$
, then
$\text {supp}(f) \subseteq \Phi ^{-1}(\{k\})$
, then
![]() $\gamma _{z}(f)=z^{k} f$
, so
$\gamma _{z}(f)=z^{k} f$
, so
![]() $\psi $
is not gauge-invariant.
$\psi $
is not gauge-invariant.
By Theorem 2.3, it follows that the subgroup
![]() $H\subseteq \mathbb {Z}$
with
$H\subseteq \mathbb {Z}$
with
is not
![]() $\{0\}$
. If
$\{0\}$
. If
![]() $\text {Per}(x)\neq \{0\}$
, then there exists
$\text {Per}(x)\neq \{0\}$
, then there exists
![]() $k>l$
such that
$k>l$
such that
![]() $\sigma ^{k}(x)=\sigma ^{l}(x)$
. Then
$\sigma ^{k}(x)=\sigma ^{l}(x)$
. Then
![]() $\sigma ^{k-l}(\sigma ^{l}(x)) = \sigma ^{l}(x)$
and it follows that
$\sigma ^{k-l}(\sigma ^{l}(x)) = \sigma ^{l}(x)$
and it follows that
![]() $x\in \mathcal {C}$
. In conclusion,
$x\in \mathcal {C}$
. In conclusion,
![]() $\nu _{\psi }(\mathcal {C}^{C})=0$
, and by Proposition 6.1, there exists a summable loop in E.
$\nu _{\psi }(\mathcal {C}^{C})=0$
, and by Proposition 6.1, there exists a summable loop in E.
Assume now that
![]() $\omega $
is a tracial state and let
$\omega $
is a tracial state and let
![]() $f\in C_{c}(\mathcal {G}_{E})$
be supported in
$f\in C_{c}(\mathcal {G}_{E})$
be supported in
![]() $\Phi ^{-1}(\{k\})$
for some
$\Phi ^{-1}(\{k\})$
for some
![]() $k\in \mathbb {Z} \setminus \{0\}$
satisfying that
$k\in \mathbb {Z} \setminus \{0\}$
satisfying that
![]() $\omega (f)\neq 0$
. The set
$\omega (f)\neq 0$
. The set
is a weak
![]() $^{*}$
compact subset of the dual for all
$^{*}$
compact subset of the dual for all
![]() $r\geq 0$
. Since
$r\geq 0$
. Since
![]() $M_{r_{2}} \subseteq M_{r_{1}}$
for
$M_{r_{2}} \subseteq M_{r_{1}}$
for
![]() $r_{2} \geq r_{1}$
, there exists a unique
$r_{2} \geq r_{1}$
, there exists a unique
![]() $r_{0}>0$
such that
$r_{0}>0$
such that
![]() $M_{r_{0}}\neq \emptyset $
and
$M_{r_{0}}\neq \emptyset $
and
![]() $M_{r} = \emptyset $
for
$M_{r} = \emptyset $
for
![]() $r>r_{0}$
. Assume that
$r>r_{0}$
. Assume that
![]() $\psi $
is an extremal element in
$\psi $
is an extremal element in
![]() $M_{r_{0}}$
, and that
$M_{r_{0}}$
, and that
![]() $\psi =\psi _{1}'+\psi _{2}'$
for two non-zero tracial weights
$\psi =\psi _{1}'+\psi _{2}'$
for two non-zero tracial weights
![]() $\psi _{1}'$
and
$\psi _{1}'$
and
![]() $\psi _{2}'$
. Set
$\psi _{2}'$
. Set
![]() $\unicode{x3bb} = \nu _{\psi _{1}'}(\partial E)$
. Since
$\unicode{x3bb} = \nu _{\psi _{1}'}(\partial E)$
. Since
![]() $\nu _{\psi }(\partial E)=1$
, defining
$\nu _{\psi }(\partial E)=1$
, defining
![]() $\psi _{1}=\unicode{x3bb} ^{-1} \psi _{1}'$
and
$\psi _{1}=\unicode{x3bb} ^{-1} \psi _{1}'$
and
![]() $\psi _{2}=(1-\unicode{x3bb} )^{-1} \psi _{2}'$
gives
$\psi _{2}=(1-\unicode{x3bb} )^{-1} \psi _{2}'$
gives
This implies that
by definition of
![]() $r_{0}$
. Hence, we have equality throughout, and
$r_{0}$
. Hence, we have equality throughout, and
![]() $\psi _{i} \in M_{r_{0}}$
for
$\psi _{i} \in M_{r_{0}}$
for
![]() $i=1,2$
. This proves that
$i=1,2$
. This proves that
![]() $\psi $
is a tracial state which is extreme in the set of tracial weights and which satisfies
$\psi $
is a tracial state which is extreme in the set of tracial weights and which satisfies
![]() $\psi (f)\neq 0$
. The rest of the proof follows as in the tracial weight case and by invoking Corollary 6.4.
$\psi (f)\neq 0$
. The rest of the proof follows as in the tracial weight case and by invoking Corollary 6.4.
Proposition 7.2. Assume that E is a second countable topological graph. If there exists a summable loop
![]() $\alpha $
in E, then there exists a non-gauge-invariant tracial weight on
$\alpha $
in E, then there exists a non-gauge-invariant tracial weight on
![]() $C^{*}(E)$
. If there exists a summable loop
$C^{*}(E)$
. If there exists a summable loop
![]() $\alpha $
in E with
$\alpha $
in E with
![]() $|E_{\alpha }^{*}|<\infty $
, then there exists a non-gauge invariant tracial state on
$|E_{\alpha }^{*}|<\infty $
, then there exists a non-gauge invariant tracial state on
![]() $C^{*}(E)$
.
$C^{*}(E)$
.
Proof. If there exists a summable loop
![]() $\alpha $
in E, then the measure
$\alpha $
in E, then the measure
![]() $\nu =\sum _{\beta \in E_{\alpha }^{*}} \delta _{\beta \alpha ^{\infty }}$
is an extremal harmonic measure by Theorem 6.2. The unique subgroup H corresponding to
$\nu =\sum _{\beta \in E_{\alpha }^{*}} \delta _{\beta \alpha ^{\infty }}$
is an extremal harmonic measure by Theorem 6.2. The unique subgroup H corresponding to
![]() $\nu $
in Theorem 2.3 is
$\nu $
in Theorem 2.3 is
![]() $|\alpha | \mathbb {Z}$
. Let the state
$|\alpha | \mathbb {Z}$
. Let the state
![]() $\phi $
on
$\phi $
on
![]() $C^{*}(|\alpha | \mathbb {Z})$
satisfy that
$C^{*}(|\alpha | \mathbb {Z})$
satisfy that
![]() $\phi (u_{g})=1$
for all
$\phi (u_{g})=1$
for all
![]() $g\in |\alpha | \mathbb {Z}$
. Recall that the map
$g\in |\alpha | \mathbb {Z}$
. Recall that the map
![]() $\Phi $
on
$\Phi $
on
![]() $\mathcal {G}_{E}$
given by
$\mathcal {G}_{E}$
given by
![]() $(x, k, y)\mapsto k$
gives rise to the gauge-action
$(x, k, y)\mapsto k$
gives rise to the gauge-action
![]() $\{\gamma _{z}\}_{z\in \mathbb {T}}$
on
$\{\gamma _{z}\}_{z\in \mathbb {T}}$
on
![]() $C^{*}(\mathcal {G}_{E})$
. If
$C^{*}(\mathcal {G}_{E})$
. If
![]() $f\in C_{c}(\mathcal {G}_{E})$
is a positive function which is supported on a bisection inside
$f\in C_{c}(\mathcal {G}_{E})$
is a positive function which is supported on a bisection inside
![]() $\Phi ^{-1}(|\alpha |)$
and satisfies
$\Phi ^{-1}(|\alpha |)$
and satisfies
![]() $f(\alpha ^{\infty }, |\alpha |, \alpha ^{\infty })=1$
, then
$f(\alpha ^{\infty }, |\alpha |, \alpha ^{\infty })=1$
, then
![]() $\psi _{\nu , \phi }(f)>0$
. Hence,
$\psi _{\nu , \phi }(f)>0$
. Hence,
![]() $\psi _{\nu , \phi }(\gamma _{z}(f))=z^{|\alpha |}\psi _{\nu , \phi }(f)$
and there exists a tracial weight which is not gauge-invariant. If
$\psi _{\nu , \phi }(\gamma _{z}(f))=z^{|\alpha |}\psi _{\nu , \phi }(f)$
and there exists a tracial weight which is not gauge-invariant. If
![]() $|E_{\alpha }^{*} |<\infty $
, then
$|E_{\alpha }^{*} |<\infty $
, then
![]() $\nu $
is finite, and the weight
$\nu $
is finite, and the weight
![]() $\psi _{\nu , \phi }$
can be normalised to a tracial state.
$\psi _{\nu , \phi }$
can be normalised to a tracial state.
Combining Propositions 7.2 and 7.1, we obtain the following two theorems.
Theorem 7.3. Let E be a second countable topological graph. All tracial states on
![]() $C^{*}(E)$
are gauge-invariant if and only if there does not exist a summable loop
$C^{*}(E)$
are gauge-invariant if and only if there does not exist a summable loop
![]() $\alpha $
in E with
$\alpha $
in E with
![]() $|E_{\alpha }^{*} | < \infty $
.
$|E_{\alpha }^{*} | < \infty $
.
Theorem 7.4. Let E be a second countable topological graph. All tracial weights on
![]() $C^{*}(E)$
are gauge-invariant if and only if there does not exist a summable loop
$C^{*}(E)$
are gauge-invariant if and only if there does not exist a summable loop
![]() $\alpha $
in E.
$\alpha $
in E.
We will now use Proposition 7.1 to provide an affirmative answer to a conjecture of Schaufhauser for second countable graphs.
Theorem 7.5. If E is a free second countable topological graph, then every tracial weight on
![]() $C^{*}(E)$
is gauge-invariant. This implies that there is a bijection between:
$C^{*}(E)$
is gauge-invariant. This implies that there is a bijection between:
-
(1) the set of invariant measures on
 $\partial E$
;
$\partial E$
; -
(2) the set of vertex-invariant measures on
 $E^{0}$
; and
$E^{0}$
; and -
(3) the set of tracial weights on
 $C^{*}(E)$
.
$C^{*}(E)$
.
The bijection between items (1) and (2) is given by
![]() $\nu \mapsto r_{*} \nu $
. The bijection between items (1) and (3) is given by
$\nu \mapsto r_{*} \nu $
. The bijection between items (1) and (3) is given by
![]() $\nu \mapsto \omega _{\nu }$
, where
$\nu \mapsto \omega _{\nu }$
, where
![]() $\omega _{\nu }$
is the weight
$\omega _{\nu }$
is the weight
Since Theorem 7.5 in particular implies that every tracial state on a second countable free topological graph is gauge-invariant, it gives an affirmative answer to [Reference RenaultSch18, Conjecture 6.5] for second countable graphs E, that is, for graphs E with
![]() $C^{*}(E)$
a separable C
$C^{*}(E)$
a separable C
![]() $^{*}$
-algebra. Before turning to the proof of the theorem, let us write out the following corollary, which follows from the observation that E is a free topological graph if
$^{*}$
-algebra. Before turning to the proof of the theorem, let us write out the following corollary, which follows from the observation that E is a free topological graph if
![]() $C^{*}(E)$
is simple, cf. [Reference KatsuraKat06b, Theorem 8.12].
$C^{*}(E)$
is simple, cf. [Reference KatsuraKat06b, Theorem 8.12].
Corollary 7.6. If
![]() $C^{*}(E)$
is simple and separable, then every tracial weight on
$C^{*}(E)$
is simple and separable, then every tracial weight on
![]() $C^{*}(E)$
is gauge-invariant. This implies that there is a bijection between:
$C^{*}(E)$
is gauge-invariant. This implies that there is a bijection between:
-
(1) the set of invariant measures on
 $\partial E$
;
$\partial E$
; -
(2) the set of vertex-invariant measures on
 $E^{0}$
; and
$E^{0}$
; and -
(3) the set of tracial weights on
 $C^{*}(E)$
.
$C^{*}(E)$
.
The bijection between items (1) and (2) is given by
![]() $\nu \mapsto r_{*} \nu $
. The bijection between items (1) and (3) is given by
$\nu \mapsto r_{*} \nu $
. The bijection between items (1) and (3) is given by
![]() $\nu \mapsto \omega _{\nu }$
, where
$\nu \mapsto \omega _{\nu }$
, where
![]() $\omega _{\nu }$
is the weight
$\omega _{\nu }$
is the weight
Proof of Theorem 7.5
We will prove that if there exists a non-gauge-invariant tracial weight, then the graph is not free. If there exists a non-gauge-invariant tracial weight, it follows from Proposition 7.1 that there exists a summable loop
![]() $\alpha $
in
$\alpha $
in
![]() $E^{*}$
. We have already noted that summable loops are isolated, so by Lemma 5.4, the graph is not free.
$E^{*}$
. We have already noted that summable loops are isolated, so by Lemma 5.4, the graph is not free.
Acknowledgement
This work was supported by a DFF-International Postdoctoral Grant.