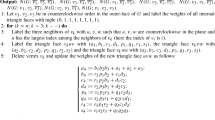Abstract
In 2015, Haviv introduced the Remote set problem (RSP) and studied the complexity of the covering radius problem (CRP), which is a classical problem in lattices. The RSP aims to identify a set containing a point that is sufficiently distant from a given lattice \(\pmb {\mathcal {L}}\). It introduced a new method for analyzing the complexity of CRP. An open question in RSP is whether we can obtain the approximation factor \(\gamma =1/2\). This paper investigates this question and proposes a probabilistic polynomial-time algorithm for RSP with an approximation factor of \(1/2-1/(c\lambda ^{(p)}_n)\), where \(c\in \mathbb {Z}^{+}\) and \(\lambda ^{(p)}_n\) is the n-th successive minima in lattice under \(l_p\)-norm. For a given lattice \(\pmb {\mathcal {L}}\) with rank n and positive integer d, our algorithm outputs a set S of size d in polynomial time. This set S includes a point at least \((\frac{1}{2}-\frac{1}{c\lambda ^{(p)}_n}){{\rho }^{(p)}}(\pmb {\mathcal {L}})\) from lattice \(\pmb {\mathcal {L}}\) with a probability greater than \(1-1/2^d\). Here, c is a positive integer and \(\rho ^{(p)}(\pmb {\mathcal {L}})\) denotes the covering radius of \(\pmb {\mathcal {L}}\) in \(l_p\)-norm(\(1\le p\le \infty \)). Based on this, we obtain that \(\text {GAPCRP}_{2+1/2^{O(n)}}\) belongs to the complexity class coRP, and we provide new reductions from GAPCRP to GAPCVP.


Similar content being viewed by others
References
Alon, N., Panigrahy, R., Yekhanin, S.: Deterministic approximation algorithms for the nearest codeword problem. In: Dinur, I., Jansen, K., Naor, J., Rolim, J.D.P. (eds.) Algorithms and Techniques, 12th International Workshop, APPROX 2009, and 13th International Workshop, vol. 5687, pp. 339–351. Springer, Berkeley, CA, USA (2009). https://doi.org/10.1007/978-3-642-03685-9_26
Guruswami, V., Micciancio, D., Regev, O.: The complexity of the covering radius problem. Comput. Complex. 14(2), 90–121 (2005)
Haviv, I., Lyubashevsky, V., Regev, O.: A note on the distribution of the distance from a lattice. Discret. Comput. Geom. 41(1), 162–176 (2009)
Haviv, I., Regev, O.: Hardness of the covering radius problem on lattices. Chic. J. Theor. Comput. Sci. 2012 (2012)
Micciancio, D.: Almost perfect lattices, the covering radius problem, and applications to ajtai’s connection factor. SIAM J. Comput. 34(1), 118–169 (2004)
Haviv, I.: The remote set problem on lattices. Comput. Complex. 24(1), 103–131 (2015)
Wang, W., Lv, K., Liu, J.: The variant of remote set problem on lattices. In: Lam, K., Chi, C., Qing, S. (eds.) Information and Communications Security, vol. 9977, pp. 124–133. Springer, Singapore (2016). https://doi.org/10.1007/978-3-319-50011-9_10
Zeidler, E.: Applied Functional Analysis, 1st edn. Springer, New York (1995)
Micciancio, D., Goldwasser, S.: Complexity of Lattice Problems - a Cryptographic Perspective, vol. 671. Springer, Boston (2002)
Aggarwal, D., Dadush, D., Stephens-Davidowitz, N.: Solving the closest vector problem in 2 \(\hat{}\) n the discrete gaussian strikes again! In: Guruswami, V. (ed.) IEEE 56th Annual Symposium on Foundations of Computer Science, pp. 563–582. IEEE Computer Society, Berkeley, CA, USA (2015). https://doi.org/10.1109/FOCS.2015.41
Ajtai, M., Kumar, R., Sivakumar, D.: A sieve algorithm for the shortest lattice vector problem. In: Vitter, J.S., Spirakis, P.G., Yannakakis, M. (eds.) Proceedings on 33rd Annual ACM Symposium on Theory of Computing, pp. 601–610. ACM, Heraklion, Crete, Greece (2001). https://doi.org/10.1145/380752.380857
Becker, A., Ducas, L., Gama, N., Laarhoven, T.: New directions in nearest neighbor searching with applications to lattice sieving. In: Krauthgamer, R. (ed.) Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 10–24. SIAM, Arlington, VA, USA (2016). https://doi.org/10.1137/1.9781611974331.ch2
Micciancio, D., Voulgaris, P.: Faster exponential time algorithms for the shortest vector problem. In: Charikar, M. (ed.) Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1468–1480. SIAM, Austin, Texas, USA (2010). https://doi.org/10.1137/1.9781611973075.119
Doulgerakis, E., Laarhoven, T., Weger, B.: Finding closest lattice vectors using approximate voronoi cells. In: Ding, J., Steinwandt, R. (eds.) Post-Quantum Cryptography - 10th International Conference, vol. 11505, pp. 3–22. Springer, Chongqing, China (2019). https://doi.org/10.1007/978-3-030-25510-7_1
Laarhoven, T., Mariano, A.: Progressive lattice sieving. In: Lange, T., Steinwandt, R. (eds.) Post-Quantum Cryptography - 9th International Conference, PQCrypto, vol. 10786, pp. 292–311. Springer, Fort Lauderdale, FL, USA (2018). https://doi.org/10.1007/978-3-319-79063-3_14
Laarhoven, T.: Sieving for shortest vectors in lattices using angular localitysensitive hashing. In: Gennaro, R., Robshaw, M. (eds.) Advances in Cryptology - CRYPTO 2015 - 35th Annual Cryptology Conference, vol. 9215, pp. 3–22. Springer, Santa Barbara, CA, USA (2015). https://doi.org/10.1007/978-3-662-47989-6_1
Author information
Authors and Affiliations
Contributions
Yijie Chen wrote the main manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Experiment Data
Appendix A: Experiment Data
In Section 3.3, the lattice basis used is orthogonal. Without loss of generality, each basic vector of lattice basis \(B=[\varvec{b}_1,\ldots ,\varvec{b}_n]\) takes value in the i-th element, the other elements are 0. For instance, \(\varvec{b}_i=(0,\ldots ,0,\alpha ,0,\ldots ,0),\alpha \in \mathbb {Z}^{+}\). We show the experiment data below. Since each basic vector takes value in the i-th element and the other elements are 0, we only present the value of the i-th element.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chen, Y., Lv, K. New Results on the Remote Set Problem and Its Applications in Complexity Study. Theory Comput Syst 68, 283–298 (2024). https://doi.org/10.1007/s00224-024-10162-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-024-10162-2