Abstract
Given a fixed finite metric space \((V,\mu )\), the minimum 0-extension problem, denoted as \(\mathtt{0\hbox {-}Ext}[{\mu }]\), is equivalent to the following optimization problem: minimize function of the form \(\min \nolimits _{x\in V^n} \sum _i f_i(x_i) + \sum _{ij} c_{ij}\hspace{0.5pt}\mu (x_i,x_j)\) where \(f_i:V\rightarrow \mathbb {R}\) are functions given by \(f_i(x_i)=\sum _{v\in V} c_{vi}\hspace{0.5pt}\mu (x_i,v)\) and \(c_{ij},c_{vi}\) are given nonnegative costs. The computational complexity of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) has been recently established by Karzanov and by Hirai: if metric \(\mu \) is orientable modular then \(\mathtt{0\hbox {-}Ext}[{\mu }]\) can be solved in polynomial time, otherwise \(\mathtt{0\hbox {-}Ext}[{\mu }]\) is NP-hard. To prove the tractability part, Hirai developed a theory of discrete convex functions on orientable modular graphs generalizing several known classes of functions in discrete convex analysis, such as \(L^\natural \)-convex functions. We consider a more general version of the problem in which unary functions \(f_i(x_i)\) can additionally have terms of the form \(c_{uv;i}\hspace{0.5pt}\mu (x_i,\{u,v\})\) for \(\{u,\!\hspace{0.5pt}\hspace{0.5pt}v\}\in F\), where set \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \) is fixed. We extend the complexity classification above by providing an explicit condition on \((\mu ,F)\) for the problem to be tractable. In order to prove the tractability part, we generalize Hirai’s theory and define a larger class of discrete convex functions. It covers, in particular, another well-known class of functions, namely submodular functions on an integer lattice. Finally, we improve the complexity of Hirai’s algorithm for solving \(\mathtt{0\hbox {-}Ext}[{\mu }]\) on orientable modular graphs.
Similar content being viewed by others
1 Introduction
Consider a metric space \((V,\mu )\) where V is a finite set and \(\mu \) is a nonnegative function \(V\times V\rightarrow \mathbb R\) satisfying the axioms of a metric: \(\mu (x,y)=0\) \(\Leftrightarrow \) \(x=y\), \(\hspace{0.5pt}\mu (x,y)=\mu (y,x)\), \(\hspace{0.5pt}\mu (x,y)+\mu (y,z)\ge \mu (x,z)\) for all \(x,y,z\in V\). We study optimization problems of the following form:
where weights \(c_{ij}\) are nonnegative. If unary terms \(f_i:V\rightarrow \mathbb R\) are allowed to be arbitrary nonnegative functions then this is a well-studied Metric Labeling Problem [22]. Another important special case is when the unary terms are given by
with nonnegative weights \(c_{vi}\). This is a classical facility location problem, known as multifacility location problem [33]. It can be interpreted as follows: we are going to locate n new facilities in V, where the facilities communicate with each other and communicate with existing facilities in V. The cost of the communication is propositional to the distance. The goal is to find a location of minimum total communication cost. The multifacility location problem is also equivalent to the minimum 0-extension problem formulated by Karzanov [20]. We denote \(\mathtt{0\hbox {-}Ext}[{\mu }]\) to be class of problems of the form (1), (2).
Optimization problems of the form above have applications in computer vision and related clustering problems in machine learning [4, 11, 14, 22]. \(\mathtt{0\hbox {-}Ext}[{\mu }]\) also includes a number of basic combinatorial optimization problems. For example, the multiway cut problem on k vertices can be obtained by setting \((V,\mu )\) to be the uniform metric on \(|V|=k\) elements; it can be solved in polynomial time (via a maximum flow algorithm) if \(k=2\), and is NP-hard for \(k\ge 3\).
We explore a generalization of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) in which the unary terms are given by
Here F is a fixed set of subsets of V, \(c_{vi},c_{Ui}\) are nonnegative weights, and \(\mu (x_i,U)=\min _{v\in U}\mu (x_i,v)\). We refer to this generalization as \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\). In the facility location interpretation, allowing terms of the form \(c_{Ui} \mu (x_i,U)\) means that the i-th facility can be “served” by any of the facilities in U, and it can choose to communicate with the closest facility to minimize the communication cost.
Note that \(\mathtt{0\hbox {-}Ext}[{\mu }]=\mathtt{0\hbox {-}Ext}[{\mu ,\varnothing }]\). Furthermore, \(\mathtt{0\hbox {-}Ext}[{\mu ,2^V}]\), where \(2^V=\{U\,|\,U\subseteq V\}\) is the set of all subsets of V, is the restricted Metric Labeling Problem [8], which is equivalent to the Metric Labeling Problem [6, Section 5.2].
1.1 Complexity classifications
The computational complexity of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) has been established in [15, 20]. The tractability criterion is based on the properties of graph \(H_\mu =(V,E,w)\) defined as the minimal undirected weighted graph whose path metric equals \(\mu \). Clearly, we have
and w is the restriction of \(\mu \) to E. For brevity, we usually denote the elements of \(\left( {\begin{array}{c}V\\ 2\end{array}}\right) \) as xy instead of \(\{x,y\}\).
In order to state the classification of \(\mathtt{0\hbox {-}Ext}[{\mu }]\), we need to introduce a few definitions.
Orientable modular graphs Let us fix metric \(\mu \). For nodes \(x,y\in V\) let \(I(x,y)=I_\mu (x,y)\) be the metric interval of x, y, i.e. the set of points \(z\in V\) satisfying \(\mu (x,z)+\mu (z,y)=\mu (x,y)\). Metric \(\mu \) is called modular if for every triplet \(x,y,z\in V\) the intersection \(I(x,y)\cap I(y,z) \cap I(x,z)\) is non-empty. (Points in this intersection are called medians of x, y, z.) We say that graph H is modular if \(H=H_\mu \) for a modular metric \(\mu \).
Let o be an edge-orientation of graph H with the relation \(\rightarrow _o\) on \(V\times V\). This orientation is called admissible for H if, for every 4-cycle \((x_1,x_2,x_3,x_4)\), condition \(x_1\rightarrow _o x_2\) implies \(x_4\rightarrow _o x_3\). H is called orientable if it has an admissible orientation.
Theorem 1
([20]) If \(H_\mu \) is not orientable or not modular then \(\mathtt{0\hbox {-}Ext}[{\mu }]\) is NP-hard.
Theorem 2
([15]) If \(H_\mu \) is orientable modular then \(\mathtt{0\hbox {-}Ext}[{\mu }]\) can be solved in polynomial time.Footnote 1
Our results We extend the classification above to problems \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) in which all subsets \(U\in F\) have cardinality 2, i.e. \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \). To formulate the tractability criterion, we need to introduce some definitions. Let o be an orientation of (H, F), i.e. each edge of H is assigned an orientation, and each element of F is assigned an orientation. We say that o is admissible for (H, F) if it is admissible for H and, for every \(\{x,y\}\in F\) with \(x\rightarrow _o y\), the following holds: if P is a shortest x-y path in H then all edges of P are oriented according to o. We say that H is F-orientable modular if it is orientable modular and (H, F) admits an admissible orientation o. We can now formulate the main result of this paper.
Theorem 3
If \(H_\mu \) is F-orientable modular then \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) can be solved in polynomial time. Otherwise \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) is NP-hard.
To prove the tractability part, we define L-convex functions on extended modular complexes, and show that they can be minimized in polynomial time. This generalizes L-convex functions on modular complexes introduced by Hirai in [15, 16].
1.2 Discrete convex analysis
As Hirai remarks, the approach in [15, 16] had been inspired by discrete convex analysis developed in particular in [13, 27, 28, 30, 32] and [12, Chapter VII]. This is a theory of convex functions on integer lattice \(\mathbb Z^n\), with the goal of providing a unified framework for polynomially solvable combinatorial optimization problems including network flows, matroids, and submodular functions. Hirai’s work extends this theory to more general graph structures, in particular to orientable modular graphs, and provides a unified framework for polynomially solvable minimum 0-extension problems and related multiflow problems.
We develop a yet another generalization. To illustrate the relation to previous work, consider two fundamental classes of functions on the integer lattice \(V=[k]=\{1,2,\ldots ,k\}\): submodular functions and \(L^\natural \)-convex functions. These are functions \(f:[k]^n \rightarrow \overline{\mathbb R}\) satisfying conditions (4) and (5), respectivelyFootnote 2


where all operations are applied componentwise.
If, for example, \(f(x)=\sum _i f_i(x_i) + \sum _{ij} f_{ij}(x_j-x_i)\), then f is submodular if all functions \(f_{ij}\) are convex, and f is \(L^\natural \)-convex if all functions \(f_i\) and \(f_{ij}\) are convex. The class of submodular functions on [k] is strictly larger than the class of \(L^\natural \)-functions. However, \(L^\natural \)-convex functions possess additional properties that allow more efficient minimization algorithms, such as the Steepest Descent Algorithm [24, 29, 31].
The theory developed in [15, 16] covers \(L^\natural \)-convex functions and several other function classes, such as bisubmodular functions, k-submodular functions [18], skew-bisubmodular functions [19], and strongly-tree submodular functions [23]. However, it excludes submodular functions on [k] for \(k\ge 3\), which is a fundamental class of functions in discrete convex analysis. This paper fills this gap by introducing a unified framework that includes all classes of functions mentioned above.
Algorithms for solving \(\mathtt{0\hbox {-}Ext}[{\mu }]\) and \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) The tractability of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) for orientable modular \(\mu \) was proven in [16] as follows. Given an instance \(f:V^n\rightarrow {{\overline{{\mathbb R}}}}\), Hirai defines a different instance \(f^*_\times :(V^*)^n\rightarrow {{\overline{{\mathbb R}}}}\) with the same minimum, where \(|V^*|=O(|V|^2)\). Function \(f^*_\times \) is then minimized using the Steepest Descent Algorithm (SDA). This is an iterative technique that at each step computes a minimizer of \(f^*_\times \) in a certain local neighborhood of the current iterate (by solving a linear programming relaxation). We refer to this technique as the SDA\(^*\) approach.
We present an alternative algorithm (for tractable classes of \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\)) that minimizes function f directly via a version of SDA that we call  -SDA (“diamond-SDA”). Both approaches terminate after O(|V|) steps. However, one step of SDA\(^*\) is more expensive than one step of SDA: the LP problem involves up to \(O(|V^*|)=O(|V|^2)\) labels per node in the former approach compared to O(|V|) labels in the latter approach. Thus, we improve the complexity of solving \(\mathtt{0\hbox {-}Ext}[{\mu }]\).
-SDA (“diamond-SDA”). Both approaches terminate after O(|V|) steps. However, one step of SDA\(^*\) is more expensive than one step of SDA: the LP problem involves up to \(O(|V^*|)=O(|V|^2)\) labels per node in the former approach compared to O(|V|) labels in the latter approach. Thus, we improve the complexity of solving \(\mathtt{0\hbox {-}Ext}[{\mu }]\).
Orthogonal generalizations of the minimum 0-extension problem In [16] Hirai considered the minimum 0-extension problem on swm-graphs (that generalize orientable modular graphs), and defined L-extendable functions on swm-graphs. Minimizing L-extendable functions on swm-graphs is an NP-hard problem (unless the graph is orientable modular); however, these functions admit a discrete relaxation on an orientable modular graph (which is an L-convex function). The relaxation can be minimized in polynomial time and yields a partial optimal solution for the original function. Based on this, Chalopin, Chepoi, Hirai and Osajda [5] obtained a 2-approximation algorithm for the minimum 0-extension problem on swm-graphs. They also developed the theory of swm-graphs.
In [17] Hirai and Mizutani considered minimum 0-extension problem for directed metrics, and provided some partial results (including a dichotomy for directed metrics of a star graph).
1.3 Valued Constraint Satisfaction Problems (VCSPs)
Results of this paper can be naturally stated in the framework of Valued Constraint Satisfaction Problems (VCSPs). This framework is defined below.
Let us fix a finite set D called a domain. A cost function over D of arity n is a function of the form \(f:D^n\rightarrow \overline{\mathbb R}\). It is called finite-valued if \(f(x)<\infty \) for all \(x\in D^n\). We denote \({{\,\mathrm{{\texttt {dom}}}\,}}f=\{x\in D^n\,|\,f(x)<\infty \}\). A (VCSP) language over D is a (possibly infinite) set \(\Phi \) of cost functions over D. Language \(\Phi \) is called finite-valued if all functions \(f\in \Phi \) are finite-valued.
A VCSP instance \(\mathcal{I}\) is a function \(D^n\rightarrow {{\overline{{\mathbb R}}}}\) given by
It is specified by a finite set of variables [n], finite set of terms T, cost functions \(f_t: D^{n_t}\rightarrow {{\overline{{\mathbb R}}}}\) of arity \(n_t\) and indices \(v(t, k)\in [n]\) for \(t\in T, k =1,\ldots , n_t\). A solution to \(\mathcal{I}\) is a labeling \(x\in [n]^V\) that minimizes \(f_\mathcal{I}(x)\). Instance \(\mathcal{I}\) is called a \(\Phi \)-instance if all terms \(f_t\) belong to \(\Phi \). The set of all \(\Phi \)-instances is denoted as \({\text {VCSP}}(\Phi )\). Language \(\Phi \) with finite \(|\Phi |\) is called tractable if instances in \({\text {VCSP}}(\Phi )\) can be solved in polynomial time, and NP-hard if \({\text {VCSP}}(\Phi )\) is NP-hard. If \(|\Phi |\) is infinite then \(\Phi \) is called tractable if every finite \(\Phi '\subseteq \Phi \) is tractable, and NP-hard if there exists finite \(\Phi '\subseteq \Phi \) which is NP-hard.
A key algorithmic tool in the VCSP theory is the Basic Linear Programming (BLP) relaxation of instance \(\mathcal{I}\). We refer to [25] for the description of this relaxation. We say that BLP solves instance \(\mathcal{I}\) if this relaxation is tight, i.e. its optimal value equals \(\min _{x\in D^n}f_\mathcal{I}(x)\).
The following results are known; we refer to Sect. 6 for the definition of a “binary symmetric fractional polymorphism”.
Theorem 4
([25]) Let \(\Phi \) be a finite-valued language. Then BLP solves \(\Phi \) if and only if \(\Phi \) admits a binary symmetric fractional polymorphism. If the condition holds, then an optimal solution of an \(\Phi \)-instance can be computed in polynomial time.
Theorem 5
([34]) If a finite-valued language \(\Phi \) does not satisfy the condition in Theorem 4 then \(\Phi \) is NP-hard.
Application to the minimum 0-extension problem Consider again a metric space \((V,\mu )\) and subset \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \). For a set \(U\subseteq V\) let \(\delta _U:V\rightarrow \{0,\infty \}\) be the indicator function of set U, with \(\delta _U(v)=0\) iff \(v\in U\). For brevity, we write \(\delta _{\{u_1,\ldots , u_k\}}\) as \(\delta _{u_1\ldots u_k}\). Clearly, the minimum 0-extension problems introduced earlier can be equivalently defined by the following languages over domain \(D=V\):
Note that the existence of the dichotomy given in Theorem 3 follows from Theorems 4 and 5 (but not the specific criterion for tractability).Footnote 3
1.4 Summary of contributions
As described in earlier sections, our first contribution is complexity classification of \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) for subsets \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \) with an explicit criterion for tractability, which is achieved by generalizing Hirai’s theory of modular complexes to extended modular complexes. While some of the proofs are relatively straightforward extensions of the corresponding proofs in [15, 16], there are also a number of proofs where we use novel techniques. We already mentioned a new  -SDA algorithm that improves the complexity of solving the standard 0-minimum extension problem. In order to analyze this algorithm, we introduce new binary operations
-SDA algorithm that improves the complexity of solving the standard 0-minimum extension problem. In order to analyze this algorithm, we introduce new binary operations  for (extended) modular complexes and establish their properties. Another key technical component that we use is the notion of f-extremality that we introduce. We believe that these concepts deepen our understanding of orientable modular graphs.
for (extended) modular complexes and establish their properties. Another key technical component that we use is the notion of f-extremality that we introduce. We believe that these concepts deepen our understanding of orientable modular graphs.
As our last contribution, we prove that the BLP relaxation directly solves L-convex functions on extended modular complexes. Previously, this was shown to hold (for standard modular complexes) only assuming that \(\texttt {P}\ne \texttt {NP}\) (see Section 6 in [15]).
The rest of the paper is organized as follows. Section 2 reviews Hirai’s theory and defines L-convex functions on modular complexes and the SDA algorithm for minimizing them. Section 3 generalizes this to L-convex functions on extended modular complexes and presents  -SDA algorithm. Both sections use the notion of submodular functions on valuated modular semilattices, which are formally defined in Sect. 4. All proofs missing in Sect. 3 are given in Sects. 5 and 6.1; this completes the proof of the tractability direction of Theorem 3. The NP-hardness direction of Theorem 3 is proven in Sect. 6.2. Section 7 concludes the paper with a list of open problems.
-SDA algorithm. Both sections use the notion of submodular functions on valuated modular semilattices, which are formally defined in Sect. 4. All proofs missing in Sect. 3 are given in Sects. 5 and 6.1; this completes the proof of the tractability direction of Theorem 3. The NP-hardness direction of Theorem 3 is proven in Sect. 6.2. Section 7 concludes the paper with a list of open problems.
2 Background on orientable modular graphs
Notation for graphs If H is a simple undirected graph and o its edge orientation, then the pair (H, o) can be viewed as a simple directed graph. We will usually denote this graph as \(\Gamma =(V_\Gamma ,E_\Gamma ,w_\Gamma )\). \(\Gamma \) is called oriented modular, or a modular complex, if it is an admissible orientation of an orientable modular graph [15, 21].
We let \(\rightarrow _\Gamma \) be the edge relation of \(\Gamma \), i.e. condition \(u\rightarrow _\Gamma v\) means that there is an edge from u to v in \(\Gamma \). When \(\Gamma \) is clear from the context, we may omit subscript \(\Gamma \) and write \(V,E,w,\rightarrow \), etc. A path \((u_0,u_1,\ldots ,u_k)\) in a directed graph \(\Gamma \) is defined as a path in the undirected version of \(\Gamma \), i.e. for each i we must have either \(u_i\rightarrow u_{i+1}\) or \(u_{i+1}\rightarrow u_{i}\). An x-y path in \(\Gamma \) is a path from \(x\in V\) to \(y\in V\). With some abuse of notation we sometimes view \(\Gamma \) as a set of its nodes, and write e.g. \(v\in \Gamma \) to mean \(v\in V\).
Orbits For an undirected graph \(H=(V,E,w)\) edges \(e,e'\in E\) are called projective if there is a sequence of edges \((e_0,e_1,\ldots ,e_m)\) with \((e_0,e_m)=(e,e')\) such that \(e_i,e_{i+1}\) are vertex-disjoint and belong to a common 4-cycle of H. Clearly, projectivity is an equivalence relation on E. An equivalence class of this relation in called an orbit [21]. Edge weights \(w:E\rightarrow \mathbb R_{>0}\) are called orbit-invariant if \(w(e)=w(e')\) for any pair of edges \(e,e'\) in the same orbit (equivalently, for vertex-disjoint edges \(e,e'\) belonging to a common 4-cycle).
Theorem 6
([1, 21]) Consider undirected graph \(H=H_\mu =(V,E,w)\).
- (a):
-
If \(\mu \) is modular then w is orbit-invariant, and path P is shortest in H if and only if it is shortest in (V, E, 1).
- (b):
-
The following conditions are equivalent: (i) H is (orientable) modular; (ii) w is orbit-invariant and (V, E, 1) is (orientable) modular.
Metric spaces For a weighted directed or undirected graph \(G=(V,E,w)\) let \(\mu _G\) and \(d_G\) (or simply \(\mu \) and d, when G is clear) be its path metrics w.r.t. edge lengths w and 1, respectively. If graph G is directed then edge orientations are again ignored.
For a metric space \((V,\mu )\), subset \(U\subseteq V\) is called convex if \(I(x,y)\subseteq U\) for every \(x,y\in U\). Note, if G is an orientable (or oriented) modular graph then the definitions of the metric interval I(x, y) and of convex sets coincide for metric spaces \((V_G,\mu _G)\) and \((V_G,d_G)\) (by Theorem 6).
Posets A modular complex \(\Gamma \) known to be an acyclic graph [15, Lemma 2.3], and thus induces a partial order \(\preceq \) on V. Partially ordered sets (posets) play a key role in the study of oriented modular graphs. Below we describe basic facts about posets and terminology that we use, mainly following [15, 16].
Consider poset \(\mathcal{L}\) with relation \(\preceq \). For elements p, q with \(p\preceq q\), the interval [p, q] is the set \(\{x\in \mathcal{L}\,|\,p\preceq x\preceq q\}\). A chain from p to q of length k is a sequence \(u_0\prec u_1\prec \ldots \prec u_k\) with \((u_0,u_k)=(p,q)\), where notation \(a\prec b\) means that \(a\preceq b\) and \(a\ne b\). The length r[p, q] of interval [p, q] is defined as the maximum length of a chain from p to q. If \(\mathcal{L}\) has the lowest element (denoted as 0) then the rank r(a) of element \(a\in \mathcal{L}\) is defined by \(r(a)=r[0,a]\), and elements of rank 1 are called atoms.
Element q covers p if \(p\prec q\) and there is no element u with \(p\prec u\prec q\). The Hasse diagram of \(\mathcal{L}\) is a directed graph on \(\mathcal{L}\) with the set of edges \(\{p\rightarrow q\,|\,q\hbox { covers }p\}\), and the covering graph of \(\mathcal{L}\) is the corresponding undirected graph.
A pair \(x,y\in \mathcal{L}\) is said to be upper-bounded (resp. lower-bounded) if x, y have a common upper bound (resp. common lower bound). The lowest common upper bound, if exists, is denoted by \(x\vee y\) (the “join” of x, y), and the greatest common lower bound, if exists, is denoted by \(x\wedge y\) (the “meet” of x, y). \(\mathcal{L}\) is called a (meet-)semilattice if every pair \(x,y\in \mathcal{L}\) has a meet, and it is called a lattice if every pair \(x,y\in \mathcal{L}\) has both a join and a meet. If \(\mathcal{L}\) is a semilattice and \(x,y\in \mathcal{L}\) are upper-bounded then \(x\vee y\) is known to exist.
A (positive) valuation of a semilattice \(\mathcal{L}\) is a function \(v:\mathcal{L}\rightarrow \mathbb R\) satisfying
In particular, if \(\mathcal{L}\) is a lattice then (7b) should hold for all \(p,q\in \mathcal{L}\). A semilattice with valuation v will be called a valuated semilattice. We will view the Hasse diagram of a valuated semilattice \(\mathcal{L}\) (and the corresponding covering graph) as weighted graphs, where the weight of \(p\rightarrow q\) is given by \(v(q)-v(p)>0\).
A lattice \(\mathcal{L}\) is called modular if for every \(x,y,z \in \mathcal{L}\) with \(x \preceq z\) there holds \(x \vee (y \wedge z) = (x \vee y) \wedge z\). A semilattice \(\mathcal{L}\) is called modular [2] if for every \(p\in \mathcal{L}\) poset \((\{x\in \mathcal{L}\,|\,x\preceq p\},\preceq )\) is a modular lattice, and for every \(x,y,z \in \mathcal{L}\) the join \(x \vee y \vee z\) exists provided that \(x \vee y\), \(y \vee z\), \(z \vee x\) exist. It is known that a lattice \(\mathcal{L}\) is modular if and only if its rank function \(r(\cdot )\) is a valuation [3, Chapter III, Corollary 1]. Furthermore, a (semi)lattice is modular if and only if its covering graph is modular, see [35, Proposition 6.2.1]; [2, Theorem 5.4]. The Hasse diagram of a (valuated) modular semilattice is known to be oriented modular [15, page 13].
Boolean pairs From now on we fix a modular complex \(\Gamma =(V,E,w)\). Graph B is called a cube graph if it is isomorphic to the Hasse diagram of the Boolean lattice \(\{0,1\}^k\) for some \(k\ge 0\). A pair of vertices (p, q) of \(\Gamma \) is called a Boolean pair if \(\Gamma \) contains cube graph B as a subgraph so that p and q are respectively the source and the sink of B. Let \(\sqsubseteq \) be the following relation on V: \(p\sqsubseteq q\) iff (p, q) is a Boolean pair in \(\Gamma \). We have \(p\sqsubseteq p\) for any \(p\in V\), and condition \(p\sqsubseteq q\) implies that \(p\preceq q\). Graph \(\Gamma \) is called well-oriented if the opposite implication holds, i.e. if relations \(\preceq \) and \(\sqsubseteq \) are the same. Note that relation \(\sqsubseteq \) is not necessarily transitive. We write \(p\sqsubset q\) to mean \(p\sqsubseteq q\) and \(p\ne q\). Let  be the graph with nodes V and edges \(\{p\rightarrow q\,|\,p,q\in V,p\sqsubset q\}\). Clearly, \(\Gamma \) is a subgraph of
be the graph with nodes V and edges \(\{p\rightarrow q\,|\,p,q\in V,p\sqsubset q\}\). Clearly, \(\Gamma \) is a subgraph of  (ignoring edge weights).
(ignoring edge weights).
For a vertex \(p\in V\) define the following subsets of V:
When \(\Gamma \) is clear from the context, we will omit it for brevity (and if \(\Gamma \) is not clear, we may write \(\preceq _\Gamma \) and \(\sqsubseteq _\Gamma \) instead of \(\preceq \) and \(\sqsubseteq \)). We view \(\mathcal{L}^\uparrow _p,\mathcal{L}^+_p\) as posets with relation \(\preceq \), and \(\mathcal{L}^\downarrow _p,\mathcal{L}^-_p\) as posets with the reverse of relation \(\preceq \). Note, if \(\Gamma \) is well-oriented then \(\mathcal{L}_p^+=\mathcal{L}^\uparrow _p\) and \(\mathcal{L}_p^-=\mathcal{L}^\downarrow _p\) for every node p of \(\Gamma \).
Lemma 7
[[15, Proposition 4.1, Theorem 4.2, Lemma 4.14]] Let \(\Gamma \) be a modular complex.
- (a):
-
If elements a, b are upper-bounded then \(a\vee b\) exists. Similarly, if a, b are lower-bounded then \(a\wedge b\) exists.
- (b):
-
Consider elements p, q with \(p\preceq q\). Then \(\mathcal{L}^\uparrow _p\), \(\mathcal{L}^\downarrow _p\), \(\mathcal{L}^+_p\), \(\mathcal{L}^-_p\) are modular semilattices, and \([p,q]=\mathcal{L}^\uparrow _p\cap \mathcal{L}^\downarrow _p\) is a modular lattice. Furthermore, these (semi)lattices are convex in \(\Gamma \), and function \(v(\cdot )\) defined via \(v(a)=\mu _\Gamma (p,a)\) is a valid valuation of these (semi)lattices.
We will always view \(\mathcal{L}^\uparrow _p\), \(\mathcal{L}^\downarrow _p\), \(\mathcal{L}^+_p\), \(\mathcal{L}^-_p\) as valuated semilattices, where the valuation is defined as in the lemma.
L-convex functions Next, we review the notion of an L-convex function on a modular complex \(\Gamma \) introduced by Hirai in [15, 16]. The definition involves the following steps.
-
First, Hirai defines the notion of a submodular function on a valuated modular semilattice \(\mathcal{L}\). These are functions \(f:\mathcal{L}\rightarrow \overline{\mathbb R}\) satisfying certain linear inequalities. Formulating these inequalities is rather lengthy, and we defer it to Sect. 4.
-
Second, Hirai defines 2-subdivision of \(\Gamma \) as the directed weighted graph \(\Gamma ^*=(V^*,E^*,w^*)\) constructed as follows:
-
(i)
set \(V^*=\{[p,q]\,|\,p\sqsubseteq q\}\);
-
(ii)
for each \([p,q],[p,q']\in V^*\) with \(q\rightarrow _\Gamma q'\) add edge \([p,q]\rightarrow [p,q']\) to \(\Gamma ^*\) with weight \( w(qq')\);
-
(iii)
for each \([p',q],[p,q]\in V^*\) with \(p'\rightarrow _\Gamma p\) add edge \([p,q]\rightarrow [p',q]\) to \(\Gamma ^*\) with weight \( w(p'p)\).
It can be seen that graph \((V^*,E^*)\) is the Hasse diagram of the poset \((V^*,\subseteq )\) (which is the definition used in [16]).Footnote 4 Hirai proves that graph \(\Gamma ^*\) is oriented modular ([15, Theorem 4.3]) and well-oriented ([15, Lemma 2.14]). Consequently, poset \(\mathcal{L}_{[p,p]}^+(\Gamma ^*)=\mathcal{L}_{[p,p]}^\uparrow (\Gamma ^*)\) is a valuated modular semilattice for each \(p\in V\). For brevity, this poset will be denoted as \(\mathcal{L}_{p}^*(\Gamma )\), or simply as \(\mathcal{L}_{p}^*\).
-
(i)
-
Each function \(f:V\rightarrow \overline{\mathbb R}\) is extended to a function \(f^*:V^*\rightarrow \overline{\mathbb R}\) via \(f^*([p,q])=f(p)+f(q)\).
-
Function \(f:V\rightarrow \overline{\mathbb R}\) is now called L-convex on \(\Gamma \) if (i) subset \({{\,\mathrm{{\texttt {dom}}}\,}}f\subseteq V\) is connected in
 , and (ii) for every \(p\in V\), the restriction of \(f^*\) to \(\mathcal{L}^*_{p}\) is submodular on valuated modular semilattice \(\mathcal{L}^*_{p}\).
, and (ii) for every \(p\in V\), the restriction of \(f^*\) to \(\mathcal{L}^*_{p}\) is submodular on valuated modular semilattice \(\mathcal{L}^*_{p}\).
Minimum 0-extension problem and L-convex functions Next, we describe the relation between problem \(\mathtt{0\hbox {-}Ext}[{\mu }]\) and L-convex functions on \(\Gamma \) (where \(\mu \) is an orientable modular metric and \(\Gamma \) is an admissible orientation of \(H_\mu \)).
If \(\Gamma ,\Gamma '\) are two modular complexes, then their Cartesian product \(\Gamma \times \Gamma '\) is defined as the directed graph with the vertex set \(V_\Gamma \times V_{\Gamma '}\) and the following edge set: there is an edge \((p,p')\rightarrow (q,q')\) iff either (i) \(p=q\) and \(p'\rightarrow _{\Gamma '} q'\), or (ii) \(p'=q'\) and \(p\rightarrow _\Gamma q\). The weight of the edge is \(w_{\Gamma '}(p'q')\) in the first case and \(w_{\Gamma }(pq)\) in the second case. The n-fold Cartesian product \(\Gamma \times \ldots \times \Gamma \) is denoted as \(\Gamma ^n\).
A Cartesian product \(\mathcal{L}\times \mathcal{L}'\) of two posets \(\mathcal{L},\mathcal{L}'\) is defined in a natural way (with \((p,p')\preceq (q,q')\) iff \(p\preceq p\) and \(q\preceq q'\)). It is straightforward to verify from definitions that if \(\mathcal{L},\mathcal{L}'\) are modular semilattices then so is \(\mathcal{L}\times \mathcal{L}'\). If \(\mathcal{L},\mathcal{L}'\) are valuated modular semilattices with valuations \(v_{\mathcal{L}},v_{\mathcal{L}'}\) then \(\mathcal{L}\times \mathcal{L}'\) is also assumed to be valuated with the valuation \(v_{\mathcal{L}\times \mathcal{L}'}(p,p')=v_{\mathcal{L}}(p)+v_{\mathcal{L}'}(p')\).
Lemma 8
([15, Lemma 4.7]) Consider modular complexes \(\Gamma ,\Gamma '\) and element \((p,p')\in \Gamma \times \Gamma '\).
- (a):
-
Graph \(\Gamma \times \Gamma '\) is a modular complex (i.e. oriented modular).
- (b):
-
\(\mathcal{L}^\sigma _{(p,p')}(\Gamma \times \Gamma ')=\mathcal{L}^\sigma _{p}(\Gamma )\times \mathcal{L}^\sigma _{p'}(\Gamma ')\) for \(\sigma \in \{-,+\}\).
Theorem 9
([15, Theorem 4.8 and Lemma 4.9]; [16, Lemmas 4.1, 4.2 and Proposition 4.4]) Consider modular complexes \(\Gamma ,\Gamma '\) and functions \(f,f':\Gamma \rightarrow \overline{\mathbb R}\) and \(\tilde{f}:\Gamma \times \Gamma '\rightarrow \overline{\mathbb R}\).
- (a):
-
If \(f,f'\) are L-convex on \(\Gamma \) then \(f+f'\) and \(c\cdot f\) for \(c\in \mathbb R_+\) are also L-convex on \(\Gamma \).
- (b):
-
If f is L-convex on \(\Gamma \) and \({\tilde{f}}(p,p')=f(p)\) for \((p,p')\in \Gamma \times \Gamma '\) then \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\).
- (c):
-
If \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\) and \(f(p)={\tilde{f}}(p,p')\) for fixed \(p'\in \Gamma '\) then f is L-convex on \(\Gamma \).
- (d):
-
The indicator function \(\delta _U:V\rightarrow \{0,\infty \}\) of a \(d_\Gamma \)-convex set U is L-convex on \(\Gamma \).
- (e):
-
Function \(\mu _\Gamma :\Gamma \times \Gamma \rightarrow \mathbb R_+\) is L-convex on \(\Gamma \times \Gamma \).
- (f):
-
If f is L-convex on \(\Gamma \) then the restriction of f to \(\mathcal{L}^\sigma _p(\Gamma )\) is submodular on \(\mathcal{L}^\sigma _p(\Gamma )\) for every \(p\in \Gamma \) and \(\sigma \in \{-,+\}\).
It follows that an instance of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) can be reduced to the problem of minimizing function \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\), \(n\ge 1\) such that (i) f is L-convex on \(\Gamma ^n\), and (ii) \(f(x_1,\ldots ,x_n)\) can be written as a sum of unary and pairwise terms that are L-convex on \(\Gamma \) and \(\Gamma \times \Gamma \), respectively. This minimization problem is considered next.
Minimizing L-convex functions A key property of L-convex functions is that local optimality implies global optimality.
Theorem 10
[[15, Lemma 2.3]] Let \(f:V\rightarrow \overline{\mathbb R}\) be an L-convex function on a modular complex \(\Gamma \). If p is a local minimizer of f on \(\mathcal{L}^\pm _p(\Gamma )\), i.e. \(f(p)=\min _{q\in \mathcal{L}^\pm _p(\Gamma )}f(q)\), then it is also a global minimizer of f, i.e. \(f(p)=\min _{q\in V}f(q)\).
This theorem implies that the Steepest Descent Algorithm (SDA) given below is guaranteed to produce a global minimizer of f after a finite number of steps.
By Lemma 8, for \(x=(x_1,\ldots ,x_n)\) we have \(\mathcal{L}^\sigma _x(\Gamma ^n)=\mathcal{L}^\sigma _{x_1}(\Gamma )\times \ldots \times \mathcal{L}^\sigma _{x_n}(\Gamma )\) for \(\sigma \in \{-,+\}\). By Theorem 9(f), function f is submodular on \(\mathcal{L}^\sigma _x(\Gamma ^n)\). The result below thus implies that the two minimization problems in line 3 can be solved in polynomial time assuming that f is an instance of \(\mathtt{0\hbox {-}Ext}[{\mu }]\).
Theorem 11
[15, Theorem 3.9] Consider VCSP instance \(f:\mathcal{L}_1\times \ldots \times \mathcal{L}_n\rightarrow \overline{\mathbb R}\). Suppose that \(\mathcal{L}_1,\ldots ,\mathcal{L}_n\) are valuated modular semilattices and function f is submodular on \(\mathcal{L}=\mathcal{L}_1\times \ldots \times \mathcal{L}_n\). Then BLP relaxation solves f.
To show that \(\mathtt{0\hbox {-}Ext}[{\mu }]\) can be solved in polynomial time, a few additional definitions and results are needed. Elements p, q of a modular complex \(\Gamma \) are said to be  -neighbors if \(p,q\in [a,b]\) for some a, b with \(a\sqsubseteq b\). Equivalently, p, q are
-neighbors if \(p,q\in [a,b]\) for some a, b with \(a\sqsubseteq b\). Equivalently, p, q are  -neighbors if \(p\wedge q,p\vee q\) exist and \(p\wedge q\sqsubseteq p\vee q\). Let
-neighbors if \(p\wedge q,p\vee q\) exist and \(p\wedge q\sqsubseteq p\vee q\). Let  be an undirected unweighted graph on nodes \(V_\Gamma \) such that p, q are connected by an edge in
be an undirected unweighted graph on nodes \(V_\Gamma \) such that p, q are connected by an edge in  if and only if p, q are
if and only if p, q are  -neighbors. This graph is called a thickening of \(\Gamma \). The distance from p to q in
-neighbors. This graph is called a thickening of \(\Gamma \). The distance from p to q in  will be denoted as
will be denoted as  , or simply as
, or simply as  . These distances will give a bound on the number of steps of SDA.
. These distances will give a bound on the number of steps of SDA.
Theorem 12
[16, Theorem 4.7, Lemma 2.18] Suppose that modular complex \(\Gamma \) is well-oriented, and function \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\) is L-convex on \(\Gamma ^n\). SDA terminates after at most  iterations where x is the initial vertex and \(\texttt{opt}_i(f)=\{x^*_i\,|\,x^*\in \mathop {\mathrm {arg\,min}}\limits f\}\subseteq V_\Gamma \) is the set of minimizers of f projected to the i-th component.
iterations where x is the initial vertex and \(\texttt{opt}_i(f)=\{x^*_i\,|\,x^*\in \mathop {\mathrm {arg\,min}}\limits f\}\subseteq V_\Gamma \) is the set of minimizers of f projected to the i-th component.
Theorem 13
[5, Proposition 6.10], [16, Lemma 2.14] If \(\Gamma \) is a modular complex then graph \(\Gamma ^*\) is well-oriented.
Theorem 14
[16, Proposition 4.9], [15, Lemma 4.7] If \(\Gamma \) is a modular complex and function \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\) is L-convex on \(\Gamma ^n\) then function \(f^*_\times :(\Gamma ^*)^n\rightarrow \overline{\mathbb R}\) defined via \(f^*_\times ([x_1,y_1],\ldots ,[x_n,y_n])=f(x)+f(y)\) is L-convex on \((\Gamma ^*)^n\).
From the results above one can now conclude that any instance \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\) of \(\mathtt{0\hbox {-}Ext}[{\mu }]\) for an oriented modular metric \(\mu \) can be solved in polynomial time. Indeed, apply SDA to minimize function \(f^*_\times :(\Gamma ^*)^n\rightarrow \overline{\mathbb R}\). It will produce a minimizer \(([x_1,y_1],\ldots ,[x_n,y_n])\) after at most  iterations; both x and y are minimizers of f. Hirai gives the bound
iterations; both x and y are minimizers of f. Hirai gives the bound  in [16, Theorem 5.7]. As pointed out by an anonymous reviewer, this bound can be improved to
in [16, Theorem 5.7]. As pointed out by an anonymous reviewer, this bound can be improved to  .
.
Note that in the earlier paper [15] Hirai proved that \(\mathtt{0\hbox {-}Ext}[{\mu }]\) can be solved in weakly polynomial time via a different algorithm, namely the Steepest Descent Algorithm (applied to \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\)) but combined with a cost-scaling approach.
Remark 1
Our terminology is slightly different from that of [16]. In particular,  -neighbors were called \(\Delta \)-neighbors in [16], and a path in
-neighbors were called \(\Delta \)-neighbors in [16], and a path in  was called a \(\Delta '\)-path.
was called a \(\Delta '\)-path.
3 Extended modular complexes
To prove our main tractability result from Theorem 3, we will introduce the following definition.
Definition 15
Let \(\Gamma \) be a modular complex. Binary relation \(\sqsubseteq \) on \(V=V_\Gamma \) is called admissible if it coarsens \(\preceq \) (i.e. \(p\sqsubseteq q\) implies \(p\preceq q\)), \(p\sqsubseteq p\) for every \(p\in V\), \(p\sqsubseteq q\) for every edge \(p\rightarrow q\), and the following conditions hold.
- (15a):
-
Suppose that \(p\sqsubseteq q\), \(a\preceq b\) and \(a,b\in [p,q]\). Then \(a\sqsubseteq b\).
- (15b):
-
Suppose that \(p\sqsubseteq q_1\), \(p\sqsubseteq q_2\) and \(q_1\vee q_2\) exists. Then \(p\sqsubseteq q_1\vee q_2\).
- (15c):
-
Suppose that \(p_1\sqsubseteq q\), \(p_2\sqsubseteq q\) and \(p_1\wedge p_2\) exists. Then \(p_1\wedge p_2\sqsubseteq q\).
A pair \((\Gamma ,\sqsubseteq )\) where \(\Gamma \) is a modular complex and \(\sqsubseteq \) is admissible will be called an extended modular complex. With some abuse of notation, we will use letter \(\Gamma \) for an extended modular complex, and treat it as an oriented modular graph when needed. Note that previously we used notation \(\sqsubseteq \) for Boolean pairs in \(\Gamma \). From now on we will write \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, q\) if (p, q) is a Boolean pair in \(\Gamma \), and reserve notation \(\sqsubseteq \) (or \(\sqsubseteq _\Gamma \)) for the binary relation that comes with an extended modular complex \(\Gamma \). As before, we write \(p \sqsubset q\) to mean \(p \sqsubseteq q\) and \(p\ne q\).
Proposition 16
Let \(\Gamma \) be a modular complex. (a) Relations \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) and \(\preceq \) are admissible for \(\Gamma \). (b) If relation \(\sqsubseteq \) is admissible for \(\Gamma \) then \(p\, {{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, q\) implies \(p \sqsubseteq q\).
This proposition shows that a modular complex is a special case of an extended modular complex (obtained by setting \(\sqsubseteq \) to be \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\)). Also, \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) and \(\preceq \) are respectively the coarsest and the finest admissible relations. Next, we will show that many of the results in Sect. 2 still hold if relation \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) is replaced with an arbitrary admissible relation \(\sqsubseteq \).
From now on we fix an extended modular complex \(\Gamma \). We define graphs  and
and  as in Sect. 2, and for \(p\in V\) define posets \((\mathcal{L}^+_p,\mathcal{L}^-_p,\mathcal{L}^\pm _p)=(\mathcal{L}^+_p(\Gamma ),\mathcal{L}^-_p(\Gamma ),\mathcal{L}^\pm _p(\Gamma ))\) as in Eq. (8). Note, in all cases \(\sqsubseteq \) now has the new meaning (it is the relation that comes with \(\Gamma \)).
as in Sect. 2, and for \(p\in V\) define posets \((\mathcal{L}^+_p,\mathcal{L}^-_p,\mathcal{L}^\pm _p)=(\mathcal{L}^+_p(\Gamma ),\mathcal{L}^-_p(\Gamma ),\mathcal{L}^\pm _p(\Gamma ))\) as in Eq. (8). Note, in all cases \(\sqsubseteq \) now has the new meaning (it is the relation that comes with \(\Gamma \)).
Lemma 17
Let \(\Gamma \) be an extended modular complex, and p be its element. Then \(\mathcal{L}^+_p,\mathcal{L}^-_p\) are modular semilattices that are convex in \(\Gamma \). Furthermore, function \(v(\cdot )\) defined via \(v(a)=\mu _\Gamma (p,a)\) is a valid valuation of these (semi)lattices.
We define a 2-subdivision of \(\Gamma \) exactly as in Sect. 2; it is the graph \(\Gamma ^*=(V^*,E^*,w^*)\) where \(V^*=\{[p,q]\,{:}\,p,q\in \Gamma ,p\sqsubseteq _\Gamma q\}\). Using condition (15a), it is straightforward to verify that \((V^*,E^*)\) is the Hasse diagram of the poset \((V^*,\subseteq )\). We will show the following result.
Theorem 18
If \(\Gamma \) is an extended modular complex then \((V^*,E^*,w^*)\) is a modular complex (i.e. an oriented modular graph).
Recall that if \(\Gamma \) is a modular complex (equivalently, an extended modular complex with the relation \(\sqsubseteq _\Gamma ={{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}_\Gamma \)) then \(\Gamma ^*\) is well-oriented, i.e. \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}_{\Gamma ^*}=\,\preceq _{\Gamma ^*}\). For extended modular complexes this is not necessarily the case, as e.g. for the example in Fig. 1c. We will treat \(\Gamma ^*\) as an extended modular complex with the relation \(\sqsubseteq _{\Gamma ^*}\,=\,\preceq _{\Gamma ^*}\), so that we have \(\mathcal{L}_{[p,p]}^+(\Gamma ^*)=\mathcal{L}_{[p,p]}^\uparrow (\Gamma ^*)\) by construction. Let us set \(\mathcal{L}^*_p=\mathcal{L}^*_p(\Gamma )=\mathcal{L}_{[p,p]}^+(\Gamma ^*)=\mathcal{L}_{[p,p]}^\uparrow (\Gamma ^*)\). We can now define L-convex functions exactly as in the previous section:
-
Function \(f:V\rightarrow \overline{\mathbb R}\) is called L-convex on extended modular complex \(\Gamma \) if (i) subset \({{\,\mathrm{{\texttt {dom}}}\,}}f\subseteq V\) is connected in
 , and (ii) for every \(p\in V\), the restriction of \(f^*\) to \(\mathcal{L}^*_{p}=\mathcal{L}^\uparrow _{[p,p]}(\Gamma ^*)\) is submodular on valuated modular semilattice \(\mathcal{L}^*_{p}\).
, and (ii) for every \(p\in V\), the restriction of \(f^*\) to \(\mathcal{L}^*_{p}=\mathcal{L}^\uparrow _{[p,p]}(\Gamma ^*)\) is submodular on valuated modular semilattice \(\mathcal{L}^*_{p}\).
Cartesian products If \((\Gamma ,\sqsubseteq ),(\Gamma ',\sqsubseteq ')\) are two extended modular complexes, then their Cartesian product \((\Gamma ,\sqsubseteq )\times (\Gamma ',\sqsubseteq ')\) is defined as the pair \((\Gamma \times \Gamma ',\sqsubseteq _{\times })\) where \((p,p') \sqsubseteq _{\times } (q,q')\) iff \(p \sqsubseteq q\) and \(p' \sqsubseteq ' q'\).
Lemma 19
Consider extended modular complexes \(\Gamma ,\Gamma '\) and element \((p,p')\in \Gamma \times \Gamma '\).
- (a):
-
\(\Gamma \times \Gamma '\) is an extended modular complex.
- (b):
-
\(\mathcal{L}^\sigma _{(p,p')}(\Gamma \times \Gamma ')=\mathcal{L}^\sigma _{p}(\Gamma )\times \mathcal{L}^\sigma _{p'}(\Gamma ')\) for \(\sigma \in \{-,+\}\).
Theorem 20
Consider extended modular complexes \(\Gamma ,\Gamma '\) and functions \(f,f':\Gamma \rightarrow \overline{\mathbb R}\) and \(\tilde{f}:\Gamma \times \Gamma '\rightarrow \overline{\mathbb R}\).
- (a):
-
If \(f,f'\) are L-convex on \(\Gamma \) then \(f+f'\) and \(c\cdot f\) for \(c\in \mathbb R_+\) are also L-convex on \(\Gamma \).
- (b):
-
If f is L-convex on \(\Gamma \) and \({\tilde{f}}(p,p')=f(p)\) for \((p,p')\in \Gamma \times \Gamma '\) then \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\).
- (c):
-
If \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\) and \(f(p)={\tilde{f}}(p,p')\) for fixed \(p'\in \Gamma '\) then f is L-convex on \(\Gamma \).
- (d):
-
The indicator function \(\delta _U:V\rightarrow \{0,\infty \}\) is L-convex on \(\Gamma \) in the following cases: (i) U is a \(d_\Gamma \)-convex set; (ii) \(U=\{p,q\}\) for elements p, q with \(p\sqsubseteq q\).
- (e):
-
Function \(\mu _\Gamma :\Gamma \times \Gamma \rightarrow \mathbb R_+\) is L-convex on \(\Gamma \times \Gamma \).
- (f):
-
If f is L-convex on \(\Gamma \) then the restriction of f to \(\mathcal{L}^\sigma _p(\Gamma )\) is submodular on \(\mathcal{L}^\sigma _p(\Gamma )\) for every \(p\in \Gamma \) and \(\sigma \in \{-,+\}\).
Theorem 21
Let \(f:V\rightarrow \overline{\mathbb R}\) be an L-convex function on an extended modular complex \(\Gamma \). If p is a local minimizer of f on \(\mathcal{L}^\pm _p(\Gamma )\), i.e. \(f(p)=\min _{q\in \mathcal{L}^\pm _p(\Gamma )}f(q)\), then it is also a global minimizer of f, i.e. \(f(p)=\min _{q\in V}f(q)\).
For extended modular complex \(\Gamma \) let \(\Phi _\Gamma \) be the language over domain \(D=V_\Gamma \) that consists of all functions \(f:D^n\rightarrow \overline{\mathbb R}\) such that f is L-convex on \(\Gamma ^n\). The results above imply that any instance \(\mathcal{I}\) of \(\Phi _\Gamma \) can be solved by the Steepest Descent Algorithm (Algorithm 1), and each subproblem in line 2 can be solved in polynomial time. However, we do not know whether the number of steps would be polynomially bounded. To get a polynomial bound, we introduce an alternative algorithm, which we denote  -SDA.
-SDA.
From Theorems 11 and 20(f) we can conclude that points  in lines 3 and 4 can be computed in polynomial time via the BLP relaxation. To see this for
in lines 3 and 4 can be computed in polynomial time via the BLP relaxation. To see this for  , observe that function \(f+\delta _U\) for convex set \(U=\mathcal{L}^+_{x^-}\cap \mathcal{L}^-_{x^+}\) is L-convex on \(\Gamma \) by Theorem 20(a,d), and thus its restriction to \(\mathcal{L}^+_{x^-}\) is submodular on \(\mathcal{L}^+_{x^-}\) by Theorem 20(f). (Alternatively, the claim can be deduced from Theorem 23 given later.)
, observe that function \(f+\delta _U\) for convex set \(U=\mathcal{L}^+_{x^-}\cap \mathcal{L}^-_{x^+}\) is L-convex on \(\Gamma \) by Theorem 20(a,d), and thus its restriction to \(\mathcal{L}^+_{x^-}\) is submodular on \(\mathcal{L}^+_{x^-}\) by Theorem 20(f). (Alternatively, the claim can be deduced from Theorem 23 given later.)
Theorem 22
Let \(\Gamma \) be an extended modular complex and \(f:\Gamma ^n\rightarrow {{\overline{{\mathbb R}}}}\) be an L-convex function on \(\Gamma ^n\).  -SDA algorithm applied to function f terminates after generating exactly
-SDA algorithm applied to function f terminates after generating exactly  distinct points, where x is the initial vertex and \(\texttt {opt}_i(f)\) is as defined in Theorem 12.
distinct points, where x is the initial vertex and \(\texttt {opt}_i(f)\) is as defined in Theorem 12.
Remark 2
Suppose that \(\sqsubset _\Gamma \,=\,\preceq _\Gamma \), and the initial vertex x in  -SDA is computed as follows: pick some \(x_0\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and then set either \(x\in \mathop {\mathrm {arg\,min}}\limits \{f(y)\,|\,y\in \mathcal{L}^-_{x_0}\}\) or \(x\in \mathop {\mathrm {arg\,min}}\limits \{f(y)\,|\,y\in \mathcal{L}^+_{x_0}\}\). It can be seen that in that case
-SDA is computed as follows: pick some \(x_0\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and then set either \(x\in \mathop {\mathrm {arg\,min}}\limits \{f(y)\,|\,y\in \mathcal{L}^-_{x_0}\}\) or \(x\in \mathop {\mathrm {arg\,min}}\limits \{f(y)\,|\,y\in \mathcal{L}^+_{x_0}\}\). It can be seen that in that case  -SDA becomes equivalent to SDA: we will have
-SDA becomes equivalent to SDA: we will have  at even steps and
at even steps and  at odd steps, or vice versa. Thus, Theorem 22 generalizes Theorem 12 in two ways: from modular complexes to extended modular complexes, and by allowing relations \(\sqsubseteq _\Gamma \) and \(\preceq _\Gamma \) to be distinct.
at odd steps, or vice versa. Thus, Theorem 22 generalizes Theorem 12 in two ways: from modular complexes to extended modular complexes, and by allowing relations \(\sqsubseteq _\Gamma \) and \(\preceq _\Gamma \) to be distinct.
Note that the algorithm for \(\mathtt{0\hbox {-}Ext}[{\mu }]\) described in the previous section required applying SDA on 2-subdivision \(\Gamma ^*\). This blows up the size of the graph and the size of LPs that need to be solved at each iteration by an up to a quadratic factor.  -SDA provides an alternative that avoids such blow-up.
-SDA provides an alternative that avoids such blow-up.
Remark 3
Algorithm 2 can also be specialized for minimizing \(L^\natural \)-convex functions (i.e. when \(\Gamma \) a directed path on consecutive integers and \(a\sqsubset b\) iff \(b=a+1\)). In this case \(\mathcal{L}^-_x(\Gamma ^n)=[x-\textbf{1},x]\), \(\mathcal{L}^+_x(\Gamma ^n)=[x,x+\textbf{1}]\) and \(\mathcal{L}^+_{x^-}(\Gamma ^n)\cap \mathcal{L}^-_{x^+}(\Gamma ^n)=U_1\times \ldots \times U_n\) where
Note that the resulting algorithm is different from previously proposed versions of SDA [24, 29, 31]. Thus,  -SDA adds to the toolbox for \(L^\natural \)-convex minimization.
-SDA adds to the toolbox for \(L^\natural \)-convex minimization.
We can now show the tractability part of Theorem 3. Suppose that graph \(H_\mu \) is F-orientable modular for a metric space \((V,\mu )\) and subset \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \). Choose an admissible orientation of \((H_\mu ,F)\), and let \(\Gamma \) be the corresponding extended modular complex with the relation \(\sqsubseteq \;=\;\preceq \). Clearly, for any \(\{x,y\}\in F\) we have either \(x\preceq y\) or \(y\preceq x\). From Theorem 20 we conclude that \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\subseteq \Phi _\Gamma \), and so \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) can be solved in polynomial time by the  -SDA algorithm.
-SDA algorithm.
More generally, this shows tractability of \({\text {VCSP}}(\Phi _\Gamma )\) for an extended modular complex \(\Gamma \) assuming that a feasible solution of any \(\Phi _\Gamma \)-instance can be computed in polynomial time. Our last result shows that \({\text {VCSP}}(\Phi _\Gamma )\) is tractable even without this assumption.
Theorem 23
If \(\Gamma \) is an extended modular complex then BLP relaxation solves \(\Phi _\Gamma \), and an optimal solution of any \(\Phi _\Gamma \)-instance can be computed in polynomial time.
Note that previously Hirai remarked that BLP directly solves \(\mathtt{0\hbox {-}Ext}[{\mu }]\) for orientable modular metrics only assuming that \(\texttt {P}\ne \texttt {NP}\), as a consequence of VCSP dichotomy for finite-valued languages (see Section 6 in [15]). Theorem 23 now establishes this fact unconditionally.
All proofs are given in Sects. 5 and 6. For Lemmas 17, 19 and Theorems 18, 20, 21 we mostly follow the proofs of the corresponding claims in [5, 15, 16] (replacing properties of relation \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) with the properties of an admissible relation \(\sqsubseteq \)). To analyze  -SDA (Theorem 22), we introduce new concepts, such as binary operations
-SDA (Theorem 22), we introduce new concepts, such as binary operations  and the notion of f-extremality (see Sects. 5.6 and 5.9). Theorem 23 does not have an analogue in [5, 15, 16].
and the notion of f-extremality (see Sects. 5.6 and 5.9). Theorem 23 does not have an analogue in [5, 15, 16].
4 Submodular functions on a valuated modular semilattice
Let \(\mathcal{L}\) be a valuated modular semilattice with valuation v. This section gives the definition of a submodular function on \(\mathcal{L}\), and thus completes the definition of L-convex functions.
Let \(\Gamma =(V,E,w)\) be the Hasse diagram of \(\mathcal{L}\) where edge \(p\rightarrow q\) is assigned weight \(v(q)-v(p)>0\). As discussed in Sect. 2, graph \(\Gamma \) is oriented modular. Denote \(\mu =\mu _\Gamma \) and \(d=d_\Gamma \). Recall that \(\mathcal{L}\) is viewed as a metric space with the metric \(\mu \), and the definitions of the metric interval I(p, q), convex sets, etc would be the same for \((\mathcal{L},\mu )\) and \((\mathcal{L},d)\).
For \(p\preceq q\) let us denote \(v[p,q]=v(q)-v(p)\). The following facts are known.
Lemma 24
[15, Lemma 2.15] The following holds for each \(p,q\in \mathcal{L}\) with \(s=p\wedge q\).
- (a):
-
\(\mu (p,q)=\mu (s,p)+\mu (s,q)=v[s,p]+v[s,q]\).
- (b):
-
The metric interval I(p, q) is equal to the set of elements u that is represented as \(u = a \vee b\) for some \((a,b) \in [s,p] \times [s,q]\), where such a representation is unique, and (a, b) equals \((u \wedge p, u \wedge q)\).
- (c):
-
For \(u,u'\in I(p,q)\) there holds \(u\wedge u'=(u\wedge u'\wedge p)\vee (u\wedge u'\wedge q)\); in particular \(u\wedge u'\in I(p,q)\).
The construction in [15] can be described as follows (see Fig. 2a for a conceptual diagram).
a Each point in I(p, q) is assigned a coordinate in \(\mathbb R^2\). The convex hull of these coordinates (\(\mathop \textrm{Conv} I(p,q)\)) is in gray. Distinct points may have the same coordinates (as some of the points shown in the interior of the gray region), but the coordinates of points in \(\mathcal{E}(p,q)=\{u_0,u_1,\ldots ,u_k\}\) are guaranteed to be unique. b Definition of \(\{\theta _i\}_i\) and \(p\vee _\theta q\). First, define points \(\alpha _{-1},\alpha _0,\ldots ,\alpha _k\) in \(\mathbb R^2\) as follows: set \(\alpha _{-1}=(\sqrt{2}/2,0)\), \(\alpha _{k}=(0,\sqrt{2}/2)\) (so that \(||\alpha _k-\alpha _{-1}||=1\)), and for \(i\in [k-1]\) let \(\alpha _i\) be the intersection of segment \([\alpha _{-1},\alpha _k]\) and the line that goes through the origin and is perpendicular to the line passing through points \(v_{pq}(u_{k})\) and \(v_{pq}(u_{k+1})\). Then \(\theta _i=||\alpha _i-\alpha _{-1}||\) and \(p\wedge _\theta q=u_i\) for each \(i\in [0,k]\) and \(\theta \in (\theta _{i-1},\theta _i)\). c Bounded pair (p, q). d Antipodal pair (p, q)
- (i):
-
For \(u \in I(p,q)\), let \(v_{pq}(u)\) be the vector in \(\mathbb R^2_+\) defined by
$$\begin{aligned} v_{pq}(u) = (v[s,u \wedge p], v[s,u \wedge q])\qquad \hbox {where~~~~} s=p\wedge q \end{aligned}$$(9) - (ii):
-
Let \(\mathop \textrm{Conv} I(p,q)\) denote the convex hull of vectors \(v_{pq}(u)\) for all \(u \in I(p,q)\).
- (iii):
-
Let \(\mathcal{E}(p,q)\) be the set of elements u in I(p, q) such that \(v_{pq}(u)\) is a maximal extreme point of \(\mathop \textrm{Conv} I(p,q)\). (This set is called “(p, q)-envelope”). Note that \(p,q\in \mathcal{E}(p,q)\). Hirai proves that elements of \(\mathcal{E}(p,q)\) receive unique coordinates [15, Lemma 3.1]:
$$\begin{aligned} v_{pq}(u)\ne v_{pq}(u') \qquad \forall u\in \mathcal{E}(p,q),u'\in I(p,q)-\{u\} \end{aligned}$$(10) - (iv):
-
For \(\theta \in [0,1]\) define vector \(c_\theta =(1-\theta ,\theta )\). For points \(p,q\in \mathcal{L}\) let \(p\vee _\theta q\) be the point \(u\in I(p,q)\) that maximizes \(\langle c_\theta ,v_{pq}(u)\rangle \), assuming that the maximizer is unique. If a maximizer is not unique then instead set \(p\vee _\theta q=\perp \) (“undefined”).
- (v):
-
By the property in Eq. (10), there are only a finite number of values \(\theta \in [0,1]\) such that \(p\vee _\theta q=\perp \) for some \(p,q\in \mathcal{L}\). Let \(\Theta \) be the set of values \(\theta \in [0,1]\) such that \(p\vee _\theta q\ne \perp \) for all \(p,q\in \mathcal{L}\), then \(\Theta \subseteq [0,1]\) has measure 1.
We are now ready to define submodular functions on \(\mathcal{L}\). A function \(f:\mathcal{L}\rightarrow \overline{\mathbb R}\) is called submodular if every \(p,q\in \mathcal{L}\) satisfies
This is equivalent to the inequality
where \(u_0,\ldots ,u_k\) are the sorted elements of \(\mathcal{E}(p,q)\) with \((u_0,u_k)=(p,q)\) and \((\theta _{-1},\theta _k)=(0,1)\),
for \(i\in [0,k-1]\). (See Fig. 2b for a geometric interpretation of values \(\theta _i\)).
Hirai also gives a simplified characterization of submodularity. Pair (p, q) is called bounded if \(p\vee q\) exists, implying \(\mathcal{E}(p,q)=\{p,q,p\vee q\}\) (Fig. 2c). Pair (p, q) is called antipodal if \(\mathcal{E}(p,q)=\{p,q\}\) (Fig. 2d). Equivalently, (p, q) is antipodal if and only if
We say that (p, q) is special if it is either bounded or antipodal. For special pairs inequality (11) reduces to
These inequalities are called respectively submodularity and \(\wedge \)-convexity inequalities for (p, q).
Theorem 25
[15, Theorem 3.5] Function \(f:\mathcal{L}\rightarrow \overline{\mathbb R}\) is submodular if and only if it satisfies
- (1):
-
\(\mathcal{E}(p,q) \subseteq {{\,\mathrm{{\texttt {dom}}}\,}}f\) for \(p,q \in {{\,\mathrm{{\texttt {dom}}}\,}}f\);
- (2):
-
the submodularity inequality for every bounded pair (p, q);
- (3):
-
the \(\wedge \)-convexity inequality for every antipodal pair (p, q).
We observe that condition (1) can be strengthened further (though we will not use this observation). For elements \(p,q,u,u'\in \mathcal{L}\) we write \((p,q)\lhd (u,u')\) if \(u,u'\in I(p,q)-\{p,q\}\) and point \(\frac{1}{2}(v_{pq}(u)+v_{pq}(u'))\) lies strictly above the segment \([v_{pq}(p),v_{pq}(q)]\) in \(\mathbb R^2\). Note that all elements \(u\in \mathcal{E}(p,q)-\{p,q\}\) satisfy \((p,q)\lhd (u,u)\), and pair (p, q) is antipodal if and only if there is no \(u\in \mathcal{L}\) with \((p,q)\lhd (u,u)\). The following theorem is proven in [10, Appendix A].
Theorem 26
Function \(f:\mathcal{L}\rightarrow \overline{\mathbb R}\) satisfies condition (1) of Theorem 25 if and only if it satisfies the following condition:
- (1\('\)):
-
Suppose that \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and \(\mathcal{E}(p,q)\ne \{p,q\}\). Let \(u^-\) and \(u^+\) be the elements in \(\mathcal{E}(p,q)-\{p,q\}\) that are closest to p and to q, respectively. Then there exists \(t\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) such that either \((p,q)\lhd (u^-,t)\) or \((p,q)\lhd (u^+,t)\).
5 Proofs
Throughout the proofs we usually denote \(d,\mu \) to be the distance functions in an extended modular complex \(\Gamma \), and  and
and  to be the distance functions in
to be the distance functions in  and in
and in  respectively. We write
respectively. We write  to indicate that nodes x, y are neighbors in
to indicate that nodes x, y are neighbors in  (equivalently, that either \(x\sqsubset y\) or \(y\sqsubset x\)). Note that
(equivalently, that either \(x\sqsubset y\) or \(y\sqsubset x\)). Note that  if and only if
if and only if  .
.
A sequence \((u_0,u_1,\ldots ,u_k)\) of nodes in \(\Gamma \) is called a shortest subpath if \(\mu (u_0,u_k)=\mu (u_0,u_1)+\mu (u_1,u_2)+\ldots +\mu (u_{k-1},u_k)\). Recall that for a modular graph \(\Gamma \) this is equivalent to the condition \(d(u_0,u_k)=d(u_0,u_1)+d(u_1,u_2)+\ldots +d(u_{k-1},u_k)\). We will often implicitly use the following fact.
Proposition 27
Consider elements p, q in a modular complex \(\Gamma \). (a) If \(p\wedge q\) exists then \((p,p\wedge q,q)\) is a shortest subpath. Conversely, if \(p\succeq x\preceq q\) and (p, x, q) is a shortest subpath then \(x=p\wedge q\). (b) If \(p\vee q\) exists then \((p,p\vee q,q)\) is a shortest subpath. Conversely, if \(p\preceq x\succeq q\) and (p, x, q) is a shortest subpath then \(x=p\vee q\).
Proof
To see the claim, combine Lemma 7 and Lemma 24(a). \(\square \)
We say that sequence \((x_1,x_2,x_3,x_4)\) is an isometric rectangle if \((x_{i-1},x_i,x_{i+1})\) are shortest subpaths for all \(i\in [4]\), where \(x_j=x_{j\!\!\mod 4}\). Isometric rectangles have the following properties.
Proposition 28
If \((x_1,x_2,x_3,x_4)\) is an isometric rectangle in graph \(\Gamma \) in then \(d(x_1,x_2)=d(x_3,x_4)\) and \(d(x_1,x_4)=d(x_2,x_3)\). Furthermore, if graph \(\Gamma \) is modular then for any \(y_1\in I(x_1,x_4)\) there exists \(y_2=I(x_2,x_3)\) (namely, a median of \(y_1,x_2,x_3\)) such that sequences \((x_1,x_2,y_2,y_1)\) and \((y_1,y_2,x_3,x_4)\) are isometric rectangles.
Proof
The definition of an isometric rectangle implies that \(d(x_1,x_2)+d(x_2,x_3)=d(x_4,x_1)+d(x_3,x_4)\) and \(d(x_2,x_3)+d(x_3,x_4)=d(x_1,x_2)+d(x_4,x_1)\), which in turns implies that \(d(x_1,x_2)=d(x_3,x_4)\) and \(d(x_1,x_4)=d(x_2,x_3)\). Now suppose that \(y_1\in I(x_1,x_4)\) and \(y_2\) is a median of \(y_1,x_2,x_3\). \((x_1,y_1,x_4,x_3)\) and \((y_1,y_2,x_3)\) are shortest subpaths, and thus so is \((x_1,y_1,y_2,x_3)\). By a symmetric argument, \((x_4,y_1,y_2,x_2)\) is also a shortest subpaths. This implies the claim. \(\square \)
5.1 Preliminaries
First, we state some known facts about orientable modular graphs that will be needed later in the proofs.
Lemma 29
([2, Proposition 1.7], see [35, Proposition 6.2.6, Chapter I]) A connected graph \(\Gamma \) with distances \(d=d_\Gamma \) is modular if and only if
- (1):
-
\(\Gamma \) is bipartite, and
- (2):
-
for vertices p, q and neighbors \(p_1,p_2\) of p with \(d(p_1,q)=d(p_2,q)=d(p,q)-1\), there exists a common neighbor \(p^*\) of \(p_1,p_2\) with \(d(p^*, q)=d(p,q)-2\).
Convex sets and gated sets Consider metric space \((V,\mu )\). Recall that subset \(U\subseteq V\) is called convex if \(I(x,y)\subseteq U\) for every \(x,y\in U\). It is called gated if for every \(p\in V\) there exists unique \(p^*\in U\), called the gate of p at U, such that \(\mu (p,q)=\mu (p,p^*)+\mu (p^*,q)\) holds for every \(q\in U\). The gate \(p^*\) will be denoted as \(\Pr _U(p)\) (“projection of p onto U”). Thus, \(\Pr _U\) is a map \(V\rightarrow U\).
Theorem 30
[9] Let A and \(A'\) be gated subsets of \((V,\mu )\) and let \(B:= \Pr _{A}(A')\) and \(B':= \Pr _{A'}(A)\).
- (a):
-
\(\Pr _{A}\) and \(\Pr _{A'}\) induce isometries, inverse to each other, between \(B'\) and B.
- (b):
-
For \(p \in A\) and \(p' \in A'\), the following conditions are equivalent:
- (i):
-
\(\mu (p,p') = \mu (A,A')\).
- (ii):
-
\(p = \Pr _{A}(p')\) and \(p' = \Pr _{A'}(p)\).
- (c):
-
B and \(B'\) are gated, and \(\Pr _{B} = \Pr _{A} \circ \Pr _{A'}\) and \(\Pr _{B'} = \Pr _{A'} \circ \Pr _{A}\).
Now let us consider a modular graph \(\Gamma =(V,E,w)\). Such graph induces two natural metrics on V, namely \(\mu =\mu _\Gamma \) and \(d=d_\Gamma \) (shortest path metrics w.r.t. edge lengths w and 1, respectively). In the light of Theorem 6, the definitions of convex sets, gated sets, gates and maps \(\Pr _U\) would be the same for both metric spaces (\((V,\mu )\) and (V, d)). In addition, convex and gated sets for such metrics coincide.
Lemma 31
([7], see [15, Lemma 2.9]) Let \(\Gamma \) be a modular graph. For \(U\subseteq V\), the following conditions are equivalent:
- (1):
-
U is convex.
- (2):
-
U is gated.
- (3):
-
\(\Gamma [U]\) is connected and \(I(x,y)\subseteq U\) holds for every \(p,q\in U\) with \(d_\Gamma (p,q)=2\).
Next, we review properties of modular complexes. A path \((p_0,p_1,p_2,\ldots ,p_k)\) in a directed acyclic graph \(\Gamma =(V,E,w)\) is said to be ascending if \(p_0 \prec p_1\prec \ldots \prec p_k\).
Lemma 32
[15, Lemma 4.13] Let \(\Gamma \) be a modular complex. For \(p,q \in V\) with \(p \preceq q\), a (p, q)-path P is shortest if and only if P is an ascending path from p to q. In particular, \(I(p,q) = [p,q]\), any maximal chain in [p, q] has the same length, and the rank r of [p, q] is given by \(r(a) = d(a,p)\).
Since set [p, q] is convex in \(\Gamma \) by Lemma 7, one can define projection \(\Pr _{[p,q]}: V \rightarrow [p,q]\). The lemma below describes some properties of this projection.
Lemma 33
[15, Lemma 4.15] Let \(\Gamma \) be a modular complex. For elements \(p,q,p',q'\) with \(p \preceq q\) and \(p' \preceq q'\) define
Then we have:
- (1):
-
\(u \preceq v\), \(u' \preceq v'\), \(\Pr _{[p',q']}([p,q]) = [u', v']\), and \(\Pr _{[p,q]}([p',q']) = [u, v]\).
- (2):
-
[u, v] is isomorphic to \([u',v']\) by map \(w \mapsto \Pr _{[p',q']}(w)\).
5.2 Properties of extended modular complexes
In this section \(\Gamma \) is always assumed to be an extended modular complex on nodes V with relation \(\sqsubseteq \).
Lemma 34
Suppose that \(p\sqsubseteq q_1\), \(p\sqsubseteq q_2\), \(q_1\ne q_2\) and q is a common neighbor of \(q_1,q_2\) (implying that \(d(q_1,q_2)=2\)). Then \(p\sqsubseteq q\).
Proof
Modulo symmetry, three cases are possible.
-
\(q_1\rightarrow q\rightarrow q_2\). Since \(p\sqsubseteq q_2\), condition (15a) gives \(p\sqsubseteq q\).
-
\(q_1\rightarrow q\leftarrow q_2\). Then \(q=q_1\vee q_2\) by Lemma 7(a), and condition (15b) gives \(p\sqsubseteq q\).
-
\(q_1\leftarrow q\rightarrow q_2\). Then \(q=q_1\wedge q_2\) by Lemma 7(a), implying \(p\preceq q\) (since p lower-bounds \(q_1,q_2\)). Condition (15a) gives \(p\sqsubseteq q\).
\(\square \)
Lemma 35
Consider elements p, q, a, b such that (p, a, b) and (a, b, q) are shortest subpaths and \(p\sqsubseteq q\). Then \(a\sqsubseteq b\).
Proof
We use induction on \(d(p,q)+d(p,a)+d(q,b)\). First, assume that (a, p, q) is not a shortest subpath. Let \(p'\) be a median of a, p, q, then \(p'\in [p,q]-\{p\}\) and so \(p'\sqsubseteq q\). The induction hypothesis for \(p',q,a,b\) gives the claim. We can thus assume that (a, p, q) is a shortest subpath. By a symmetric argument we can also assume that (b, q, p) is a shortest subpath. Sequence (p, q, b, a) is thus an isometric rectangle, and so \(d(p,q)=d(a,b)\) and \(d(p,a)=d(q,b)\). We now consider 5 possible cases.
-
\(d(p,a)=d(q,b)=0\). The claim then holds trivially.
-
\(d(p,a)=d(q,b)=1\), \(q\rightarrow b\). Then \(p\preceq b\) and (p, a, b) is a shortest subpath, and so \(p\rightarrow a\preceq b\) by Lemma 32. We have \(a\vee q\preceq b\) and (a, b, q) is a shortest subpath; this implies that \(a\vee q=b\). Since \(p\sqsubseteq a\) and \(p\sqsubseteq q\), we obtain \(p\sqsubseteq a\vee q=b\) by condition (15b), and thus \(a\sqsubseteq b\) since \(a\in [p,b]\).
-
\(d(p,a)=d(q,b)=1\), \(p\leftarrow a\). This case is symmetric to the previous one.
-
\(d(p,a)=d(q,b)=1\), \(p\rightarrow a\), \(b\rightarrow q\). We will show that \(a\preceq b\); this will imply that (p, a, b, q) is a shortest subpath by Lemma 32, contradicting condition \(d(p,q)=d(a,b)\). If \(d(p,q)=d(a,b)=0\) then the claim is trivial. If \(d(p,q)=d(a,b)=1\) then (p, q, b, a) is a 4-cycle, and so \(p\rightarrow q\) implies that \(a\rightarrow b\). Suppose that \(d(p,q)=d(a,b)\ge 2\). By Proposition 28, there exist \(x\in I(p,q)-\{p,q\}\) and \(y\in I(a,b)\) such that (p, x, y, a) and (q, x, y, b) are isometric rectangles. We have \(p\sqsubseteq x\sqsubseteq q\), so by the induction hypothesis \(a\sqsubseteq y\sqsubseteq b\), implying the claim.
-
\(d(p,a)=d(q,b)\ge 2\). By Proposition 28, there exist \(p'\in I(p,a)\) and \(q'\in I(q,b)\) such that \((p,q,q',p')\) and \((p',q',b,a)\) are isometric rectangles. The induction hypothesis for elements \(p,q,p',q'\) gives \(p'\sqsubseteq q'\). The induction hypothesis for elements \(p',q',a,b\) gives \(a\sqsubseteq b\). \(\square \)
Corollary 36
Suppose that \(p\sqsubseteq q\) and \(A'\subseteq V\) is a convex set in \(\Gamma \). Let \(p'=\Pr _{A'}(p)\) and \(q'=\Pr _{A'}(q)\). Then \(p'\sqsubseteq q'\).
Lemma 17
(restated). Let \(\Gamma \) be an extended modular complex, and p be its element. Then \(\mathcal{L}^+_p,\mathcal{L}^-_p\) are modular semilattices that are convex in \(\Gamma \). Furthermore, function \(v(\cdot )\) defined via \(v(a)=\mu _\Gamma (p,a)\) is a valid valuation of these (semi)lattices.
Proof
By symmetry, it suffices to consider only \(\mathcal{L}^+_p\). Note that \(\mathcal{L}^+_p\) is a subset of \(\mathcal{L}^\uparrow _p\) such that for any \(a,b\in \mathcal{L}_p^+\) we have (i) \(a\wedge b\in \mathcal{L}_p^+\) and (ii) \(a\vee b\in \mathcal{L}_p^+\) assuming that \(a\vee b\) exists (by Definition 15). Thus, all claims except convexity follow from the corresponding properties of \(\mathcal{L}^\uparrow _p\) (see Lemma 7). Let us show the convexity. In view of Lemma 31, it suffices to show that for any \(a,b\in \mathcal{L}_p^+\) with \(d(a,b)=2\) we have \(I(a,b)\subseteq \mathcal{L}^+_p\). This claim follows directly from Lemma 34. \(\square \)
In the next two results we use the same notation d for \(d_\Gamma \) and \(d_{\Gamma ^*}\) (since they can be distinguished by the arguments). Similarly, we use \(\mu \) for both \(\mu _\Gamma \) and \(\mu _{\Gamma ^*}\).
Lemma 37
Let \(\Gamma ^*\) be the 2-subdivision of \(\Gamma \) on nodes \(V^*\). Then
Proof
If \(P=([p_0,q_0],\ldots ,[p_k,q_k])\) is a path in \(\Gamma ^*\) from \([p_0,q_0]=[p,q]\) to \([p_k,q_k]=[p',q']\) then the length of P in \(\Gamma ^*\) equals \(\sum _{i=0}^{k-1}(d(p_i,p_{i+1})+d(q_i,q_{i+1}))\ge d(p,p')+d(q,q')\); hence \((\ge )\) holds.
To show equality, we use induction on \(D=d(p,p')+d(q,q')\). The base case \(D=0\) is trivial; suppose that \(D\ge 1\). It suffices to show that one of the following holds:
- (i):
-
p has neighbor a in \(\Gamma \) such that \(a\sqsubseteq q\) and \(d(a,p')=d(p,p')-1\).
- (ii):
-
q has neighbor b in \(\Gamma \) such that \(p\sqsubseteq b\) and \(d(b,q')=d(q,q')-1\).
Indeed, if (i) holds then \(d([a,q],[p',q'])=d(a,p')+d(q,q')=D-1\) by induction, and hence \(d([p,q],[p',q'])\le (D-1)+1=D\), as required. Case (ii) is similar. Alternatively, it would also suffice to show symmetrical cases when \(p'\) or \(q'\) have appropriate neighbors.
Define \(u,v,u',v'\) by (14). Note that \(p\preceq u\preceq v\preceq q\) and \(p'\preceq u'\preceq v'\preceq q'\). Modulo symmetry, two cases are possible.
-
\(p\ne u\), implying \(p\prec u\). Let \(a\in [p,u]\subseteq [p,q]\) be an out-neighbor of p in \(\Gamma \) (i.e. \(p\rightarrow a\preceq u\)), then \(a\sqsubseteq q\) by condition (15a), and \((p,a,p')\) is a shortest subpath since (p, a, u) and \((p,u,p')\) are shortest subpaths. Thus, case (i) holds.
-
\((p,q,p',q')=(u,v,u',v')\). Then \((p,q,q',p')\) is an isometric rectangle. By Proposition 28 there exist \(a\in I(p,p')\) and \(b\in I(q,q')\) such that (p, q, b, a) and \((p',q',b,a)\) are isometric rectangles and \(d(q,b)=d(p,a)=1\). We have \(a\sqsubseteq b\) by Lemma 35. If \(a\rightarrow p\) then Lemma 32 for elements \(a\preceq q\) gives \(a\preceq b\rightarrow q\). By Lemma 7(a), \(p\wedge b\) exists. Since (p, q, b) is a shortest subpath, we have \(b\notin I(p,q)=[p,q]\), therefore \(p\not \preceq b\) and \(p\wedge b=a\). Condition (15c) gives \(a\sqsubseteq q\), and so case (i) holds. If \(q\rightarrow b\) then by a symmetric argument we conclude that case (ii) holds. The last remaining case \(p\rightarrow a,b\rightarrow q\) is impossible by Lemma 32 for elements \(p\preceq q\). \(\square \)
Theorem 18
(restated). If \(\Gamma \) is an extended modular complex then \((V^*,E^*,w^*)\) is a modular complex (i.e. an oriented modular graph).
Proof
Any 4-cycle in \(\Gamma ^*\) is represented as \(([p,q], [p,q'], [p',q'], [p',q])\) or \(([p',q], [p',q'], [p,q'], [p,q])\) for some edges \(p\rightarrow p',q\rightarrow q'\) in \(\Gamma \), or ([p, x], [p, y], [p, z], [p, w]) or ([x, p], [y, p], [z, p], [w, p]) for 4-cycle (x, y, z, w) and vertex p in \(\Gamma \). This immediately implies that the orientation of \(\Gamma ^*\) is admissible and orientation and \(w^*\) is orbit-invariant.
To show that \(\Gamma ^*\) is modular, we are going to verify that \(\Gamma ^*\) satisfies the two conditions of Lemma 29. If [p, q] and \([p',q']\) are joined by an edge, then \(d_{\Gamma }(p,q)\) and \(d_{\Gamma }(p',q')\) have different parity. This implies that \(\Gamma ^*\) is bipartite.
We next verify condition (2) of Lemma 29. Take intervals \([p,q],[p',q']\in V^*\), and denote \(D_p=d(p,p')\), \(D_q=d(q,q')\), \(D=d([p,q],[p',q'])=D_p+D_q\). Suppose further that we are given two distinct neighbors \([p_1,q_1],[p_2,q_2]\) of [p, q] with \(d([p_1,q_1],[p',q'])=d([p_2,q_2],[p',q'])=D-1\). Our goal is to show the existence of a common neighbor \([p^*,q^*]\) of \([p_1,q_1],[p_2,q_2]\) with \(d([p^*,q^*],[p',q'])=D-2\).
Modulo symmetry, two cases are possible.
-
\(p_1=p=p_2\). Condition \(d([p_i,q_i],[p',q'])=D-1\) implies that \(d(q_i,q')=D_q-1\) for \(i=1,2\). By Lemma 29(2) for \(\Gamma \), there is a common neighbor \(q^*\) of \(q_1,q_2\) with \(d(q^*,q')=D_q-2\). By Lemma 34, \(p\sqsubseteq q^*\). Thus, \([p,q^*]\) is a desired common neighbor of \([p,q_1],[p,q_2]\).
-
\(p_1=p\), \(q_2=q\). For better readability let us denote \(s=p_2\), \(t=q_1\). To summarize, we know that \((p,s,p')\) and \((q,t,q')\) are shortest subpaths, \(d(p,s)=d(q,t)=1\), \(s\sqsubseteq q\), \(p\sqsubseteq t\), \(p\sqsubseteq q\), \(p'\sqsubseteq q'\). It suffices to show \(s\sqsubseteq t\); this will imply that [s, t] is a desired common neighbor of \([p_1,q_1],[p_2,q_2]\). Modulo symmetry, three subcases are possible. Case 1: \(s\rightarrow p\), \(t\rightarrow q\). Then \(s\sqsubseteq q\) and \(s\preceq p\preceq t\preceq q\), so condition (15a) gives \(s\sqsubseteq t\). Case 2: \(p\rightarrow s\), \(t\rightarrow q\). By Lemma 33, \(\Pr _{[p,q]}([p',q'])\) is equal to interval [a, b] for \(a=\Pr _{[p,q]}(p')\) and \(b=\Pr _{[p,q]}(q')\). Note that \(s,t,a,b\in [p,q]\). Since \((p,s,p')\) and \((s,a,p')\) are shortest subpaths, so is \((p,s,a,p')\) and thus \(s\preceq a\). Similarly \(b\preceq t\). Thus \(p\preceq s \preceq a\preceq b\preceq t\preceq q\) and \(p\sqsubseteq q\) imply \(s\sqsubseteq t\) (by condition (15a)), as desired. Case 3: \(s\rightarrow p\), \(q\rightarrow t\). Observe that \(x\vee y\), \(x\wedge y\) are defined and belong to [s, t] for all \(x,y\in [s,t]\) by Lemma 7. Consider set \(\Pr _{[s,t]}([p',q'])\), which is equal to [u, v] for \(u=\Pr _{[s,t]}(p')\) and \(v=\Pr _{[s,t]}(q')\) (Lemma 33). We must have \(p\not \preceq u\) (implying \(p\wedge u=s\)); otherwise (s, p, u), \((s,u,p')\) and thus \((s,p,u,p')\), \((s,p,p')\) would be shortest subpaths, contradicting the assumption that \((p,s,p')\) is a shortest subpath and \(p\ne s\). Similarly, \(v\vee q=t\). Note that \(u\sqsubseteq v\) by Corollary 36. Define \(a=u\wedge q\). We claim that \(a\sqsubseteq t\). Indeed, we have \(a\sqsubseteq q\) since \(s\preceq a\preceq q\) and \(s\sqsubseteq q\). It now suffices to show that there exists b such that \(a \sqsubseteq b\) and \(b\vee q=t\); the claim will then follow by condition (15b). If \(a=u\) then we can take \(b=v\). Otherwise, if \(a\prec u\), take b to be an out-neighbor of a in [a, u] (i.e. \(a\rightarrow b\preceq u\)); we have \(b\notin [a,q]\) since \(a=u\wedge q\), and hence \(b\vee q=t\). We have \(p\sqsubseteq t\), \(a\sqsubseteq t\) and \(p\wedge a=p\wedge u \wedge q=s\wedge q=s\), so condition (15c) gives \(s\sqsubseteq t\).
\(\square \)
By combining Lemma 37, Theorem 18 and Theorem 6(a) we obtain:
Corollary 38
Let \(\Gamma ^*\) be the 2-subdivision of \(\Gamma \) on nodes \(V^*\). Then
Lemma 39
Let \(f:\Gamma \rightarrow \overline{\mathbb R}\) be an L-convex function on an extended modular complex \(\Gamma \). Then for every \(p\in \Gamma \) the restrictions of f to \(\mathcal{L}^-_p\) and to \(\mathcal{L}^+_p\) are submodular functions.
Proof
Let us define \(\mathcal{L}_p^{*+}=\{[p,q]\,{:}\,p\sqsubseteq q\}\subseteq \mathcal{L}_p^*\). By Lemma 37, any vertex in any shortest path between [p, q] and \([p,q']\) is of the form [p, u]. Hence \(\mathcal{L}_p^{*+}\) is convex in \(\Gamma \) and in \(\mathcal{L}_p^{*}\). Therefore, submodularity of \(f^*\) on \(\mathcal{L}_p^*\) implies \(f^*\) is submodular on \(\mathcal{L}_p^{*+}\) (by [15, Lemma 3.7(4)]). Obviously \(\mathcal{L}_p^{*+}\) is isomorphic to \(\mathcal{L}_p^+\) by \([p,q] \mapsto q\). By using relation \(f(q) = f^*([p,q]) - f(p)\) \((q \in \mathcal{L}^+_p)\), we see the submodularity of f on \(\mathcal{L}^+_p\). The proof of submodularity of f on \(\mathcal{L}^-_p\) is symmetric. \(\square \)
5.3 Proof of Proposition 16
Proposition 16
(restated). Let \(\Gamma \) be a modular complex. (a) Relations \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) and \(\preceq \) are admissible for \(\Gamma \). (b) If relation \(\sqsubseteq \) is admissible for \(\Gamma \) then \(p\, {{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, q\) implies \(p \sqsubseteq q\).
To prove this proposition, we will need the following result. A modular lattice \(\mathcal{L}\) is called complemented if the maximal element \(1_\mathcal{L}\) is a join of atoms. (This is one possible characterization of complemented modular lattices, see [3, Chapter IV, Theorem 4.1]).
Proposition 40
[5, Proposition 6.5] Consider elements p, q in a modular complex \(\Gamma \) with \(p\preceq q\). Then \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, q\) if and only if [p, q] is a complemented modular lattice.
We now proceed with the proof of Proposition 16.
(a) Checking admissibility of \(\preceq \) is straightforward. Clearly, if B is a cube graph and p, q are elements of B with \(p\preceq q\) then the subgraph of B induced by [p, q] is also a cube graph; this implies that \({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\) satisfies condition (15a). Let us show that condition (15b) holds (condition (15c) is symmetric). Suppose that \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, a\), \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, b\) and \(a\vee b\) exists. Let \(a_1,\ldots ,a_k\) be the atoms of a and \(b_1,\ldots ,b_\ell \) be the atoms of b, then \(a=a_1\vee \ldots \vee a_k\) and \(b=b_1\vee \ldots \vee b_\ell \) by Proposition 40. Thus, \(a\vee b=a_1\vee \ldots \vee a_k\vee b=b_1\vee \ldots \vee b_\ell \), and so \(a\vee b\) is a join of atoms of \([p,a\vee b]\). Proposition 40 gives that \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, a\vee b\).
(b) We use induction on d(p, q). Consider elements p, q with \(p\, {{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, q\), \(d(p,q)\ge 2\). Using Proposition 40, we conclude that \(q=a\vee b\) for some \(a,b\in [p,q]-\{q\}\). We have \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, a\) and \(p\,{{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\, b\) by part (a), and so \(p\sqsubseteq a\) and \(p\sqsubseteq b\) by the induction hypothesis. Condition (15b) gives \(p\sqsubseteq q\).
5.4 Properties of the Cartesian product and L-convexity of the metric function
In this section we prove several properties related to the Cartesian product of extended modular complexes \(\Gamma \times \Gamma '\). We denote \((V_\Gamma ,V_{\Gamma '},V_{\Gamma \times \Gamma '})=(V,V',V_\times )\) for brevity, and use similar notation for other objects (e.g. relations \(\preceq ,\sqsubseteq ,\rightarrow \), distances \(d,\mu \), etc). Recall that \((p,p') \sqsubseteq _\times (q,q')\) iff \(p \sqsubseteq q\) and \(p' \sqsubseteq ' q'\).
Lemma 19
(restated). Consider extended modular complexes \(\Gamma ,\Gamma '\) and element \((p,p')\in \Gamma \times \Gamma '\).
- (a):
-
\(\Gamma \times \Gamma '\) is an extended modular complex.
- (b):
-
\(\mathcal{L}^\sigma _{(p,p')}(\Gamma \times \Gamma ')=\mathcal{L}^\sigma _{p}(\Gamma )\times \mathcal{L}^\sigma _{p'}(\Gamma ')\) for \(\sigma \in \{-,+\}\).
Proof
(a) In the light of Lemma 8(a), it suffices to verify that relation \(\sqsubseteq _{\times }\) is admissible, i.e. satisfies the properties in Definition 15. We need to show the following:
-
\((p,p')\sqsubseteq _\times (q,q')\) implies \((p,p')\preceq _\times (q,q')\).
-
\((p,p')\sqsubseteq _\times (p,p')\) for every \((p,p')\in V_\Gamma \times V_{\Gamma '}\).
-
\((p,p')\sqsubseteq _\times (q,q')\) for every edge \((p,p')\rightarrow _\times (q,q')\).
-
If \((p,p')\sqsubseteq _\times (q,q')\), \((a,a')\preceq _\times (b,b')\) and \((a,a'),(b,b')\in [(p,p'),(q,q')]\), then \((a,a')\sqsubseteq _\times (b,b')\).
-
If \((p,p')\sqsubseteq (q_1,q'_1)\), \((p,p')\sqsubseteq (q_2,q'_2)\) and \((q_1,q'_1)\vee (q_2,q'_2)\) exists, then \((p,p')\sqsubseteq _\times (q_1,q'_1)\vee (q_2, q'_2)\).
Checking each property is mechanical, and is omitted.
(b) From definitions, \(\mathcal{L}^+_{(p,p')}(\Gamma \times \Gamma ')=\{(q,q')\,{:}\,p\sqsubseteq q,p'\sqsubseteq ' q'\}=\mathcal{L}^+_{p}(\Gamma )\times \mathcal{L}^+_{p'}(\Gamma ')\) as sets. Furthermore, the partial order is the same in both cases, and so \(\mathcal{L}^+_{(p,p')}(\Gamma \times \Gamma ')\) and \(\mathcal{L}^+_{p}(\Gamma )\times \mathcal{L}^+_{p'}(\Gamma ')\) also equal as posets (which are modular semilattices by Lemma 17). Finally, both semilattices are assigned the same valuation, namely \(v_\times (q,q')=\mu _\times ((p,p'),(q,q'))=\mu (p,q)+\mu '(p',q')\). The case \(\sigma =-\) is symmetric. \(\square \)
Lemma 41
Consider extended modular complexes \(\Gamma ,\Gamma '\). Graphs \((\Gamma \times \Gamma ')^*\) and \(\Gamma ^*\times {\Gamma '}^*\) are isomorphic with the isomorphism given by \([(p,p'),(q,q')]\mapsto ([p,q],[p',q'])\) for \(p,q\in \Gamma ,p',q'\in \Gamma '\) with \(p\sqsubseteq q,p'\sqsubseteq ' q'\). Consequently, \(\mathcal{L}^*_{(p,p')}(\Gamma \times \Gamma ')\) and \(\mathcal{L}^*_p(\Gamma )\times \mathcal{L}^*_{p'}(\Gamma ')\) are isomorphic valuated modular semilattices for any \((p,p')\in \Gamma \times \Gamma '\).
Proof
Clearly, the mapping defined in the lemma is a bijection between the nodes of \((\Gamma \times \Gamma ')^*\) and the nodes of \(\Gamma ^*\times {\Gamma '}^*\). Checking that this bijection preserves edges and edge weights is mechanical. \(\square \)
Lemma 42
Consider extended modular complexes \(\Gamma ,\Gamma '\) and functions \(f,f':\Gamma \rightarrow \overline{\mathbb R}\) and \(\tilde{f}:\Gamma \times \Gamma '\rightarrow \overline{\mathbb R}\) such that \({{\,\mathrm{{\texttt {dom}}}\,}}f\) is connected in  .
.
- (a):
-
If f is L-convex on \(\Gamma \) and \({\tilde{f}}(p,p')=f(p)\) for \((p,p')\in \Gamma \times \Gamma '\) then \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\).
- (b):
-
If \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\) and \(f(p)={\tilde{f}}(p,p')\) for fixed \(p'\in \Gamma '\) then f is L-convex on \(\Gamma \).
Proof
Since \((\Gamma \times \Gamma ')^*\) and \(\Gamma ^*\times {\Gamma '}^*\) are isomorphic, for a function \({{\tilde{f}}}^{\,*}:(\Gamma \times \Gamma ')^*\rightarrow {{\overline{{\mathbb R}}}}\) we can define function \({{\tilde{f}}}^{\,*}_\times :\Gamma ^*\times {\Gamma '}^*\rightarrow {{\overline{{\mathbb R}}}}\) via \({{\tilde{f}}}^{\,*}_\times ([p,q],[p',q'])={{\tilde{f}}}^{\,*}([(p,p'),(q,q')])\). Clearly, \({{\tilde{f}}}^{\,*}\) is submodular on \(\mathcal{L}^*_{(x,x')}(\Gamma \times \Gamma ')\) if and only if \({{{\tilde{f}}}}^{\,*}_\times \) is submodular on \(\mathcal{L}^*_x(\Gamma )\times \mathcal{L}^*_{x'}(\Gamma ')\).
(a) Checking connectivity of \({{\,\mathrm{{\texttt {dom}}}\,}}{\tilde{f}}\) in  is straightforward. We can write \({{{\tilde{f}}}}^{\,*}_\times ([p,q],[p',q'])=\tilde{f}(p,p')+{\tilde{f}}(q,q')=f(p)+f(q)= f^*([p,q])\). L-convexity of f means that \(f^*\) is submodular on \(\mathcal{L}^*_x\) for any \(x\in \Gamma \). Therefore, by [15, Lemma 3.7(2)], function \({{{\tilde{f}}}}^{\,*}_\times \) is submodular on \(\mathcal{L}^*_x(\Gamma )\times \mathcal{L}^*_{x'}(\Gamma ')\) for any \((x,x')\in \Gamma \times \Gamma '\), and thus \({{\tilde{f}}}^{\,*}\) is submodular on \(\mathcal{L}^*_{(x,x')}(\Gamma \times \Gamma ')\).
is straightforward. We can write \({{{\tilde{f}}}}^{\,*}_\times ([p,q],[p',q'])=\tilde{f}(p,p')+{\tilde{f}}(q,q')=f(p)+f(q)= f^*([p,q])\). L-convexity of f means that \(f^*\) is submodular on \(\mathcal{L}^*_x\) for any \(x\in \Gamma \). Therefore, by [15, Lemma 3.7(2)], function \({{{\tilde{f}}}}^{\,*}_\times \) is submodular on \(\mathcal{L}^*_x(\Gamma )\times \mathcal{L}^*_{x'}(\Gamma ')\) for any \((x,x')\in \Gamma \times \Gamma '\), and thus \({{\tilde{f}}}^{\,*}\) is submodular on \(\mathcal{L}^*_{(x,x')}(\Gamma \times \Gamma ')\).
(b) \(f^*([p,q])=f(p)+f(q)={\tilde{f}}(p,p')+\tilde{f}(q,p')={{{\tilde{f}}}}^{\,*}([(p,p'),(q,p')])={{\tilde{f}}}^{\,*}_\times ([p,q],[p',p'])\). \(L\hbox {-convexity}\) of \({\tilde{f}}\) means that \({{{\tilde{f}}}}^{\,*}_\times \) is submodular on \(\mathcal{L}^*_x(\Gamma )\times \mathcal{L}^*_{p'}(\Gamma ')\). Therefore, by [15, Lemma 3.7(3)], function \(f^*\) is submodular on \(\mathcal{L}^*_{x}(\Gamma )\) for any \(x\in \Gamma \). \(\square \)
Lemma 43
[15, Lemma 4.18] Let \(\Lambda \) be a modular complex. The distance function \(\mu _\Lambda \) is submodular on \(\mathcal{L}_{(a,b)}^\uparrow (\Lambda \times \Lambda )=\mathcal{L}_{a}^\uparrow (\Lambda )\times \mathcal{L}_{b}^\uparrow (\Lambda )\) for every \((a,b)\in \Lambda \times \Lambda \).
Lemma 44
Let \(\Gamma \) be an extended modular complex. (a) Function \(\mu _\Gamma :\Gamma \times \Gamma \rightarrow \mathbb R_+\) is L-convex on \(\Gamma \times \Gamma \). (b) For each \(p\in \Gamma \), function \(\mu _{\Gamma ,p}:\Gamma \rightarrow \mathbb R_+\) defined via \(\mu _{\Gamma ,p}(x)=\mu (x,p)\) is L-convex on \(\Gamma \).
Proof
It suffices to prove (a); claim (b) will then follow by Lemma 42(b). To be consistent with the notation in Lemma 42, denote \(\Gamma '=\Gamma \) and \(\tilde{f}=\mu _\Gamma \). By Corollary 38, for each \([p,q],[p',q']\in V^*\) we have \({{\tilde{f}}}^{\,*}_\times ([p,q],[p',q'])={{\tilde{f}}}^{\,*}([(p,p'),(q,q')])= \mu _\Gamma (p,p')+\mu _\Gamma (q,q')=\mu _{\Gamma ^*}([p,q],[p',q'])\), i.e. \({{{\tilde{f}}}}^{\,*}_\times =\mu _{\Gamma ^*}\). Consider \((x,y)\in \Gamma \times \Gamma \). Lemma 43 for \(\Lambda =\Gamma ^*\) and \(a=[x,x]\), \(b=[y,y]\) gives that \({{\tilde{f}}}^{\,*}_\times =\mu _{\Gamma ^*}\) is submodular on \(\mathcal{L}^\uparrow _{[x,x]}(\Gamma ^*)\times \mathcal{L}^\uparrow _{[y,y]}(\Gamma ^*)=\mathcal{L}^*_x(\Gamma )\times \mathcal{L}^*_y(\Gamma )\), and therefore \({{{\tilde{f}}}}^{\,*}\) is submodular on \(\mathcal{L}^*_{(x,y)}(\Gamma \times \Gamma )\). \(\square \)
5.5 Proof of Theorem 21: Local optimality implies global optimality
In this section we prove the following result.
Theorem 21
(equivalent formulation). Let \(f:V\rightarrow \overline{\mathbb R}\) be an L-convex function on an extended modular complex \(\Gamma \). Consider element p with \(\min _{q\in \Gamma }f(q)<f(p)<\infty \). There exists element u with  .
.
We use the same argument as in [15] (slightly rearranged).
Lemma 45
[15, Lemma 4.20] Let f be a submodular function on a modular semilattice \(\mathcal{L}\). For \(p,q\in \mathcal{L}\) and \(\alpha \in \mathbb R\) with \(f(p)\le \alpha \), \(f(q)<\alpha \), there exists sequence \((u_0,u_1,\ldots ,u_k)\) with \((u_0,u_k)=(p,q)\) such that for each \(i\in [k]\) we have \(f(u_i)<\alpha \) and elements \(u_{i-1},u_i\) are comparable.
Lemma 46
Let f be an L-convex function on an extended modular complex \(\Gamma \). Consider triplet (x, y, z) and \(\alpha \in \mathbb R\) with \(x\sqsubseteq y\sqsubseteq z\), \(x\not \sqsubseteq z\), \(f(x)\le \alpha \), \(f(y)<\infty \), \(f(z)< \alpha \). There exists sequence \((u_0,u_1,\ldots ,u_k)\) with \((u_0,u_k)=(x,z)\) such that for each \(i\in [k]\) we have \(f(u_i)<\alpha \) and \(u_{i-1}\sqsubseteq u_i\).
Proof
We denote the desired sequence as P(x, y, z), if exists. We prove that P(x, y, z) exists using induction on \(d(x,z)+d(x,y)\). We know that function \(f^*\) is submodular on \(\mathcal{L}^*_y\). Let us apply inequality (11b) to elements \(p=[x,y]\) and \(q=[y,z]\) (with \(p\wedge q=[y,y]\)). Since \(f^*(p) + f^*(q)=f(x)+f^*(p\wedge q)+f(z)\), there must exist \([a,b]\in \mathcal{E}(p,q)-\{p,q\}\) with \(f(a)+f(b)=f^*([a,b])\le f(x)+f(z)\). Since \([a,b]\in I(p,q)\), we must have \(a\in [x,y]\), \(b\in [y,z]\) by Lemma 37 (and also \(a\sqsubseteq b\)). Condition \(x\not \sqsubseteq z\) implies that \((a,b)\ne (x,z)\). Therefore, three cases are possible.
-
\(a=x\), \(y\prec b\prec z\). Then we have \(f(b)\le f(z)< \alpha \) and \(x\sqsubseteq b\sqsubseteq z\). Thus, we can set \(P(x,y,z)=(x,b,z)\).
-
\(x\prec a\prec y\), \(b=z\). Then we have \(f(a)\le f(x)\le \alpha \) and \(x\sqsubseteq a\sqsubseteq z\). Thus, we can set \(P(x,y,z)=P(x,a,z)\), where we used the induction hypothesis (note that \(d(x,a)<d(x,y)\)).
-
\(x\prec a\preceq b\prec z\). Since \(f(a)+f(b)\le f(x)+f(z)<2\alpha \), one of the following must hold: \(\underline{f(a)<\alpha .}\) Then we set \(P(x,y,z)=(x,a,z)\) if \(a\sqsubseteq z\), and \(P(x,y,z)=(x,P(a,y,z))\) otherwise. \(\underline{f(b)<\alpha .}\) Then we set \(P(x,y,z)=(x,b,z)\) if \(x\sqsubseteq b\), and \(P(x,y,z)=(P(x,y,b),z)\) otherwise.
\(\square \)
Corollary 47
Consider elements x, y, z in an extended modular complex \(\Gamma \) such that  ,
,  , \(f(x)\le \alpha \), \(f(y)<\infty \), \(f(z)<\alpha \). Then there exists path \((u_0,u_1,\ldots ,u_k)\) in
, \(f(x)\le \alpha \), \(f(y)<\infty \), \(f(z)<\alpha \). Then there exists path \((u_0,u_1,\ldots ,u_k)\) in  with \((u_0,u_k)=(x,z)\) such that \(f(u_i)<\alpha \) for all \(i\in [k]\).
with \((u_0,u_k)=(x,z)\) such that \(f(u_i)<\alpha \) for all \(i\in [k]\).
Proof
Modulo symmetry, two cases are possible:
-
\(x\sqsupset y\sqsubset z\). The claim then follows from Lemma 45, since function f is submodular on \(\mathcal{L}_y^+\) by Lemma 39.
-
\(x\sqsubset y\sqsubset z\). The claim then follows from Lemma 46.
\(\square \)
We now proceed with the proof of Theorem 21. For value \(\alpha \in \mathbb R\) let  and
and  be the subgraphs of
be the subgraphs of  induced by nodes p with \(f(p)\le \alpha \) and with \(f(p)< \alpha \), respectively.
induced by nodes p with \(f(p)\le \alpha \) and with \(f(p)< \alpha \), respectively.
Lemma 48
 is connected for any \(\alpha \ge \alpha ^*{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}\min _{p\in \Gamma } f(p)\).
is connected for any \(\alpha \ge \alpha ^*{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}\min _{p\in \Gamma } f(p)\).
Proof
Suppose the claim is false. For a sufficiently large \(\alpha \) graph  is connected, since \({{\,\mathrm{{\texttt {dom}}}\,}}f\) is connected in
is connected, since \({{\,\mathrm{{\texttt {dom}}}\,}}f\) is connected in  . Thus, there must exist \(\alpha > \alpha ^*\) such that
. Thus, there must exist \(\alpha > \alpha ^*\) such that  is connected but
is connected but  is disconnected. There must exist a pair of vertices \(p,p'\) belonging to different components of
is disconnected. There must exist a pair of vertices \(p,p'\) belonging to different components of  ; in particular, \(f(p)<\alpha \) and \(f(p')<\alpha \), and there exists path \(P=(p_0,p_1,\ldots ,p_k)\) in
; in particular, \(f(p)<\alpha \) and \(f(p')<\alpha \), and there exists path \(P=(p_0,p_1,\ldots ,p_k)\) in  with \((p_0,p_k)=(p,p')\), \(k\ge 2\) and \(f(p_i)\le \alpha \) for all \(i\in [k-1]\). Pick such \(p,p',P\) so that \(k\ge 2\) is minimum. The minimality of k implies that
with \((p_0,p_k)=(p,p')\), \(k\ge 2\) and \(f(p_i)\le \alpha \) for all \(i\in [k-1]\). Pick such \(p,p',P\) so that \(k\ge 2\) is minimum. The minimality of k implies that  . Apply Corollary 47 to elements \((x,y,z)=(p_{k-2},p_{k-1},p_k)\). We obtain a path \((u_0,\ldots ,u_\ell )\) in
. Apply Corollary 47 to elements \((x,y,z)=(p_{k-2},p_{k-1},p_k)\). We obtain a path \((u_0,\ldots ,u_\ell )\) in  between \(u_0=p_{k-2}\) and \(u_\ell =p_k\) with \(f(u_i)<\alpha \) for all \(i\in [\ell ]\). Note that \(u_1,p'\) are in the same connected component of
between \(u_0=p_{k-2}\) and \(u_\ell =p_k\) with \(f(u_i)<\alpha \) for all \(i\in [\ell ]\). Note that \(u_1,p'\) are in the same connected component of  (which is different from that of p), and path \((p_0,\ldots ,p_{k-2},u_1)\) has shorter length compared to P. This contradicts the minimality of k. \(\square \)
(which is different from that of p), and path \((p_0,\ldots ,p_{k-2},u_1)\) has shorter length compared to P. This contradicts the minimality of k. \(\square \)
Now consider element \(p\in \Gamma \) which is not a global minimum, i.e. \(f(p)>\alpha ^*\). Connectivity of  for \(\alpha =f(p)\) implies that there exists path \(P=(p_0,p_1,\ldots ,p_k)\) in
for \(\alpha =f(p)\) implies that there exists path \(P=(p_0,p_1,\ldots ,p_k)\) in  with \(p_0=p\), \(f(p_i)\le \alpha \) for \(i\in [k]\), and \(f(p_k)<\alpha \). Let us pick such P so that k is minimum. It suffices to show that \(k=1\); clearly, this would imply Theorem 21. Suppose not, i.e. \(k\ge 2\). The minimality of k implies that
with \(p_0=p\), \(f(p_i)\le \alpha \) for \(i\in [k]\), and \(f(p_k)<\alpha \). Let us pick such P so that k is minimum. It suffices to show that \(k=1\); clearly, this would imply Theorem 21. Suppose not, i.e. \(k\ge 2\). The minimality of k implies that  . Applying Corollary 47 to elements \((x,y,z)=(p_{k-2},p_{k-1},p_k)\) gives element \(u_1\) so that \(f(u_1)<\alpha \) and
. Applying Corollary 47 to elements \((x,y,z)=(p_{k-2},p_{k-1},p_k)\) gives element \(u_1\) so that \(f(u_1)<\alpha \) and  . This contradicts the minimality of k.
. This contradicts the minimality of k.
We can strengthen Theorem 21 as follows.
Lemma 49
Let \(f:V\rightarrow \overline{\mathbb R}\) be an L-convex function on an extended modular complex \(\Gamma \) and p, q be distinct elements in \({{\,\mathrm{{\texttt {dom}}}\,}}f\). (a) If \(f(p)\ge f(q)\) then there exists element \(u\in I(p,q)\) such that \(f(u)\le f(p)\) and  . Additionally, if \(f(p)> f(q)\) then \(f(u)<f(p)\). (b) There exists element \(u\in I(p,q)\cap {{\,\mathrm{{\texttt {dom}}}\,}}f\) such that
. Additionally, if \(f(p)> f(q)\) then \(f(u)<f(p)\). (b) There exists element \(u\in I(p,q)\cap {{\,\mathrm{{\texttt {dom}}}\,}}f\) such that  .
.
Proof
(a) For element \(x\in \Gamma \) define function \(\mu _x:\Gamma \rightarrow \mathbb R\) via \(\mu _x(u)=\mu (x,u)\). By Lemma 44, function \(\mu _x\) is L-convex on \(\Gamma \). Now for value \(C\ge 0\) define function \(f_C:\Gamma \rightarrow \overline{\mathbb R}\) via \(f_C(u)=f(u)+C(\mu _p(u)+\mu _q(u)-\mu (p,q))\). It is straightforward to check that \(f_C\) is L-convex on \(\Gamma \). (Note that \({{\,\mathrm{{\texttt {dom}}}\,}}f_C={{\,\mathrm{{\texttt {dom}}}\,}}f\), since functions \(\mu _p,\mu _q\) are finite-valued). We have the following properties: (i) \(f_C(u)=f(u)\) for all \(u\in I(p,q)\); (ii) if C is sufficiently large then \(f_C(u)>f(p)\) for all \(u\in V_\Gamma -I(p,q)\). Applying Lemma 48 to function \(f_C\) gives the first claim, while applying Theorem 21 to function \(f_C\) gives the second claim.
(b) We can assume w.l.o.g. that \(f(p)>f(q)\), since adding function of the form \(C\mu _q\), \(C\ge 0\) to f preserves L-convexity of f and does not affect the statement. The claim now follows from part (a). \(\square \)
5.6 Graph thickening and operations 
Let us recall some definitions from Sects. 2, 3. Elements p, q of an extended modular complex \(\Gamma \) are said to be  -neighbors if \(p,q\in [a,b]\) for some a, b with \(a\sqsubseteq b\). Equivalently, p, q are
-neighbors if \(p,q\in [a,b]\) for some a, b with \(a\sqsubseteq b\). Equivalently, p, q are  -neighbors if \(a\wedge b,a\vee b\) exist and \(a\wedge b\sqsubseteq a\vee b\). Let
-neighbors if \(a\wedge b,a\vee b\) exist and \(a\wedge b\sqsubseteq a\vee b\). Let  be an undirected unweighted graph on nodes \(V_\Gamma \) such that p, q are connected by an edge in
be an undirected unweighted graph on nodes \(V_\Gamma \) such that p, q are connected by an edge in  if and only if p, q are \(\Delta \)-neighbors. This graph is called a thickening of \(\Gamma \). A path in
if and only if p, q are \(\Delta \)-neighbors. This graph is called a thickening of \(\Gamma \). A path in  is called a
is called a  -path. The shortest path distance between p and q in
-path. The shortest path distance between p and q in  will be denoted as
will be denoted as  . These concepts were introduced in [5] in the case when \(\sqsubseteq \,={{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\); we now use them for an arbitrary admissible relation \(\sqsubseteq \). In order to work with
. These concepts were introduced in [5] in the case when \(\sqsubseteq \,={{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\); we now use them for an arbitrary admissible relation \(\sqsubseteq \). In order to work with  , in this section we introduce binary operations
, in this section we introduce binary operations  on an extended modular complex \(\Gamma \) and establish some of their properties. They will be used, in particular, for proving Theorem 22 (bound on the number of steps of
on an extended modular complex \(\Gamma \) and establish some of their properties. They will be used, in particular, for proving Theorem 22 (bound on the number of steps of  -SDA), and for proving that the sum of L-convex functions is L-convex.
-SDA), and for proving that the sum of L-convex functions is L-convex.
For vertices \(p,q\in \Gamma \) let \(\preceq _{pq}\) be a partial order on I(p, q) defined as follows: \(x\preceq _{pq} y\) iff (p, x, y, q) is a shortest subpath. For vertices \(x,y\in I(p,q)\) this is equivalent to the condition \(x\in I(p,y)\), or to the condition \(y\in I(x,q)\). Clearly, \((I(p,q),\preceq _{pq})\) is a poset with the minimal element p and the maximal element q. We will need the following result.
Theorem 50
([5, Theorem 6.1]) Let \(\Gamma \) be a modular complex. For every \(p,q\in \Gamma \) poset \({(I(p,q),\preceq _{pq})}\) is a modular lattice.
We denote the meet and join operations in this poset as \(\wedge _{pq}\) and \(\vee _{pq}\), respectively. Clearly, for each \(x,y\in I(p,q)\) the meet \(x \wedge _{pq}y\) is a median of p, x, y, and in fact it is the unique median (since every median m of p, x, y belongs to I(p, q) and satisfies \(m\preceq _{pq}x\) and \(m\preceq _{pq}y\)). Similarly, \(x \vee _{pq}y\) is the unique median of x, y, q.
For elements \(p,q\in \Gamma \) we define  to be the gate of q at \(\mathcal{L}^+_p\) (which is a convex subset of \(\Gamma \) by Lemma 17):
to be the gate of q at \(\mathcal{L}^+_p\) (which is a convex subset of \(\Gamma \) by Lemma 17):  . Similarly, we let
. Similarly, we let  . Clearly, by the definition of the gate and by Lemma 32 we have
. Clearly, by the definition of the gate and by Lemma 32 we have


We also define  .
.
Lemma 51
Consider elements p, q of an extended modular complex \(\Gamma \). There holds  (and consequently \(p,p\diamond q\) are
(and consequently \(p,p\diamond q\) are  -neighbors). If \(p\ne q\) then \(p\ne p\diamond q\).
-neighbors). If \(p\ne q\) then \(p\ne p\diamond q\).
Proof
Denote  . We know that \(a\sqsubseteq p\sqsubseteq b\) and (p, a, c), (p, b, c), (a, c, b) are shortest subpaths (since c is a median of a, b, q and \(a,b\in I(p,q)\)). From Lemma 35 we conclude that \(a\sqsubseteq c\sqsubseteq b\). Since \(p\succeq a \preceq c\) and (p, a, c) is a shortest subpath, we must have \(a=p\wedge c\). Similarly, \(b=p\vee c\). Condition (15b) gives \(a\sqsubseteq b\). Now suppose that \(p\ne q\), and consider shortest p-q path \((p,u,\ldots ,q)\). If \(p\rightarrow u\) then
. We know that \(a\sqsubseteq p\sqsubseteq b\) and (p, a, c), (p, b, c), (a, c, b) are shortest subpaths (since c is a median of a, b, q and \(a,b\in I(p,q)\)). From Lemma 35 we conclude that \(a\sqsubseteq c\sqsubseteq b\). Since \(p\succeq a \preceq c\) and (p, a, c) is a shortest subpath, we must have \(a=p\wedge c\). Similarly, \(b=p\vee c\). Condition (15b) gives \(a\sqsubseteq b\). Now suppose that \(p\ne q\), and consider shortest p-q path \((p,u,\ldots ,q)\). If \(p\rightarrow u\) then  and \(p\diamond q\ne p\), and if \(p\leftarrow u\) then
and \(p\diamond q\ne p\), and if \(p\leftarrow u\) then  and \(p\diamond q\ne p\). \(\square \)
and \(p\diamond q\ne p\). \(\square \)
For elements p, q an integer \(k\ge 0\) define \(p\diamond ^k q\) as follows: \(p\diamond ^0 q=p\), and \(p\diamond ^{k+1}q=(p\diamond ^k q)\diamond q\) for \(k\ge 0\). Clearly, \(p\diamond ^k q=q\) for some index \(k\ge 0\). If k is the minimum such index then the sequence \((p\diamond ^0 q,p\diamond ^1 q,\ldots ,p\diamond ^k q)\) will be called the normal p-q path. By the previous lemma, it is a  -path (i.e. a path in
-path (i.e. a path in  ).
).
For node \(p\in \Gamma \) and integer \(k\ge 0\) denote  (a ball of radius k in
(a ball of radius k in  ). We will show later that
). We will show later that  is convex in \(\Gamma \) for any p and k. First, we establish this for \(k=1\).
is convex in \(\Gamma \) for any p and k. First, we establish this for \(k=1\).
Lemma 52
For each \(p\in \Gamma \), set  is convex in \(\Gamma \).
is convex in \(\Gamma \).
Proof
By Lemma 31, it suffices to show the following: if \(x,x'\) are distinct  -neighbors of p and y is a common neighbor of \(x,x'\) in \(\Gamma \) then p, y are
-neighbors of p and y is a common neighbor of \(x,x'\) in \(\Gamma \) then p, y are  -neighbors. Denote \((a,b)=(p\wedge x,p\vee x)\) and \((a',b')=(p\wedge x',p\vee x')\), then \(a\sqsubseteq b\) and \(a'\sqsubseteq b'\). Recall that sets [a, b] and \([a',b']\) are convex in \(\Gamma \) by Lemma 7. If \(d(p,y)=d(p,x)-1\) then \(y\in I(p,x)\), and so by convexity of [a, b] we have \(y\in [a,b]\), implying that p, y are
-neighbors. Denote \((a,b)=(p\wedge x,p\vee x)\) and \((a',b')=(p\wedge x',p\vee x')\), then \(a\sqsubseteq b\) and \(a'\sqsubseteq b'\). Recall that sets [a, b] and \([a',b']\) are convex in \(\Gamma \) by Lemma 7. If \(d(p,y)=d(p,x)-1\) then \(y\in I(p,x)\), and so by convexity of [a, b] we have \(y\in [a,b]\), implying that p, y are  -neighbors. We can thus assume that \(d(p,y)=d(p,x)+1\), and also that \(d(p,y)=d(p,x')+1\) (by a symmetric argument). Modulo symmetry, two cases are possible.
-neighbors. We can thus assume that \(d(p,y)=d(p,x)+1\), and also that \(d(p,y)=d(p,x')+1\) (by a symmetric argument). Modulo symmetry, two cases are possible.
-
\(x\rightarrow y\rightarrow x'\). Since (p, a, x) and (p, x, y) are shortest subpaths, so is (p, a, y). Since \((p,b',x')\) and \((p,x',y')\) are shortest subpaths, so is \((p,b',y)\). \((a,p,b')\) and \((a,y,b')\) are also shortest subpaths (since \(a\preceq p\prec b'\) and \(a\preceq y\prec b'\)). Thus, we have \((a,b')=(p\wedge y,p\vee y)\) and \(a\sqsubseteq y\sqsubseteq b'\) (by Lemma 35). Condition (15b) for pairs \(a\sqsubseteq p\) and \(a\sqsubseteq y\) gives \(a\sqsubseteq p\vee y=b'\), and so p, y are
 -neighbors.
-neighbors. -
\(x\rightarrow y\leftarrow x'\). By Lemma 29, nodes \(x,x'\) have a common neighbor z with \(d(p,z)=d(p,x)-1=d(p,x')-1\). Since \(z\in I(p,x)\), we must have \(z\in [a,b]\) by convexity of [a, b]. Similarly, \(z\in [a',b']\). Since \((x,y,x',z)\) is a 4-cycle, we must have \(x\leftarrow z\rightarrow x'\). Since \(a=p\wedge x\) and \(z\in [a,x]\), we must have \(a=p\wedge z\). By a symmetric argument, \(a'=p\wedge z\), and so \(a=a'\). We know that \(p,x,x',b,b'\in \mathcal{L}^+_a\). By Lemma 17, \(\mathcal{L}^+_a\) is a modular semilattice which is convex in \(\Gamma \). Since \(y\in I(x,x')\), we must have \(y=x\vee x'\in \mathcal{L}^+_a\) by convexity. Since joins \(p\vee x=b\), \(p\vee x'=b'\), \(x\vee x'=y\) exist, the join \({\hat{b}}=p\vee x\vee x'\) must also exist in \(\mathcal{L}^+_a\) by definition of modular semilattices. We obtain \(a\sqsubseteq {\hat{b}}\) and \(p,y\in [a,{\hat{b}}]\), and so p, y are
 -neighbors.
-neighbors.
\(\square \)
Lemma 53
If p, x are  -neighbors then \((x,p\diamond q,q)\) is a shortest subpath.
-neighbors then \((x,p\diamond q,q)\) is a shortest subpath.
Proof
We use induction on \(d(x,p\diamond q)\). Let \(x'\) be a median of \(x,p\diamond q,q\). First, assume that \(x'\ne x\). By Lemma 52, \(p,x'\) are  -neighbors (since \(x'\in I(x,p\diamond q)\)). By the induction hypothesis, \((x',p\diamond q,q)\) is a shortest subpath. \((x,x',q)\) is also a shortest subpath, and thus so is \((x,x',p\diamond q,q)\). Now assume that \(x'=x\), i.e. \((p\diamond q, x, q)\) is a shortest subpath. \((p,p\diamond q,q)\) is a shortest subpath, and thus so is \((p,p\diamond q,x,q)\). Let \((a,b)=(p\wedge x,p\vee x)\). (p, a, x) and (p, b, x) are shortest subpaths, and thus so are (p, a, x, q) and (p, b, x, q), implying \(a,b\in I(p,q)\). (a, x, b) is a shortest subpath since \(a\preceq x\preceq b\), and so x is a median of a, b, q. Thus, we must have \(x=a \vee _{pq} b\). We also have \(a\sqsubseteq b\), and thus
-neighbors (since \(x'\in I(x,p\diamond q)\)). By the induction hypothesis, \((x',p\diamond q,q)\) is a shortest subpath. \((x,x',q)\) is also a shortest subpath, and thus so is \((x,x',p\diamond q,q)\). Now assume that \(x'=x\), i.e. \((p\diamond q, x, q)\) is a shortest subpath. \((p,p\diamond q,q)\) is a shortest subpath, and thus so is \((p,p\diamond q,x,q)\). Let \((a,b)=(p\wedge x,p\vee x)\). (p, a, x) and (p, b, x) are shortest subpaths, and thus so are (p, a, x, q) and (p, b, x, q), implying \(a,b\in I(p,q)\). (a, x, b) is a shortest subpath since \(a\preceq x\preceq b\), and so x is a median of a, b, q. Thus, we must have \(x=a \vee _{pq} b\). We also have \(a\sqsubseteq b\), and thus  by Eq. (15). By a similar argument,
by Eq. (15). By a similar argument,  . We have
. We have  and
and  , and so
, and so  . This implies that \((x,p\diamond q,q)\) is a shortest subpath. \(\square \)
. This implies that \((x,p\diamond q,q)\) is a shortest subpath. \(\square \)
Lemma 54
If (p, u, q) is a shortest subpath then the following sequences are also shortest subpaths:
- (i):
-
 ;
; - (ii):
-
 ;
; - (iii):
-
 .
.
Proof
First, let us show (i). For brevity, denote  . Define \(z=b\vee _{pq} u\). (b, z, u) is a shortest subpath (since z is the median of b, u, q). Also, \(u \preceq _{pq} z\), meaning that (p, u, z, q) is a shortest subpath. Lemma 35 for elements p, b, u, z gives that \(u\sqsubseteq z\). This shows that \(z\in \mathcal{L}^+_u\cap I(u,q)\), and thus
. Define \(z=b\vee _{pq} u\). (b, z, u) is a shortest subpath (since z is the median of b, u, q). Also, \(u \preceq _{pq} z\), meaning that (p, u, z, q) is a shortest subpath. Lemma 35 for elements p, b, u, z gives that \(u\sqsubseteq z\). This shows that \(z\in \mathcal{L}^+_u\cap I(u,q)\), and thus  is a shortest subpath by Eq. (15). Since
is a shortest subpath by Eq. (15). Since  and (p, b, z, q) are shortest subpaths, so is
and (p, b, z, q) are shortest subpaths, so is  .
.
A symmetric argument gives (ii). We can now show (iii) as follows:  . \(\square \)
. \(\square \)
Theorem 55
If \((p_0,p_1,\ldots ,p_k)\) is a  -path with \(p_0=p\) then \((p_i,p\diamond ^i q,q)\) is a shortest subpath for any \(i\in [0,k]\).
-path with \(p_0=p\) then \((p_i,p\diamond ^i q,q)\) is a shortest subpath for any \(i\in [0,k]\).
Proof
We use induction on i. For \(i=0\) the claim holds by Lemma 53. Let us show it for \(i\in [k]\). Denote \({\bar{p}}=p_{i-1}\), \(x=p_i\), \(u=p\diamond ^{i-1} q\). By the induction hypothesis, \((p_{i-1},p\diamond ^{i-1} q,q)=({\bar{p}},u,q)\) is a shortest subpath. By Lemma 53, \((x,{\bar{p}}\diamond q,q)\) is a shortest subpath. By Lemma 54, \(({\bar{p}} \diamond q,u\diamond q,q)\) is a shortest subpath. Thus, \((x,{\bar{p}}\diamond q,u\diamond q,q)\) and so \((x,u\diamond q,q)=(p_i,p\diamond ^i q,q)\) are shortest subpaths. \(\square \)
Corollary 56
The normal p-q path \((p,p\diamond ^1 q,p\diamond ^2 q,\ldots , q)\) is a shortest  -path from p to q.
-path from p to q.
Proof
Let \((p_0,p_1,\ldots ,p_k)\) be a shortest  -path with \((p_0,p_k)=(p,q)\). By Theorem 55 with \(q=p_k\), \((p_k,p\diamond ^k q,q)=(q,p\diamond ^k q,q)\) is a shortest subpath, therefore \(p\diamond ^k q=q\). This means that the length of the normal p-q path is at most k. \(\square \)
-path with \((p_0,p_k)=(p,q)\). By Theorem 55 with \(q=p_k\), \((p_k,p\diamond ^k q,q)=(q,p\diamond ^k q,q)\) is a shortest subpath, therefore \(p\diamond ^k q=q\). This means that the length of the normal p-q path is at most k. \(\square \)
Our next goal is to prove that set  is convex in \(\Gamma \) for any p and k. For that we will first need a technical result.
is convex in \(\Gamma \) for any p and k. For that we will first need a technical result.
Lemma 57
Suppose that \((p,p',q',q)\) is an isometric rectangle in an extended modular complex \(\Gamma \) and p, q are  -neighbors. Then \(p',q'\) are also
-neighbors. Then \(p',q'\) are also  -neighbors.
-neighbors.
Proof
Note that \(I(p,q)\cup I(p',q')\subseteq I(p,q')\cap I(p',q)\). For a node \(x\in I(p,q)\) let \(x'\in I(p',q')\) be the median of \(x,p',q'\). (This median is unique and equals \(x\vee _{pq'} p'\), since \(x,p'\in I(p,q')\). Furthermore, \(p'\) is a median of \(p,p',q'\) and \(q'\) is a median of \(q,p',q'\), so this notation is consistent). Since \((p,x,q,q')\) and \((x,x',q')\) are shortest subpaths, so is \((p,x,x',q')\). Analogously, since \((p',p,x,q)\) and \((p',x',x)\) are shortest subpaths, so is \((p',x',x,q)\). We can now conclude that \((p,p',x',x)\) and \((q,q',x',x)\) are isometric rectangles.
Denote \((a,b)=(p\wedge q,p\vee q)\), then \(a\sqsubseteq b\) and \(a,b\in I(p,q)\). Since \((p,p',a',a)\) is an isometric rectangle and \(a\sqsubseteq p\), we get \(a'\sqsubseteq p'\) by Lemma 35. By similar arguments we get \(p'\sqsupseteq a'\sqsubseteq q'\) and \(p'\sqsubseteq b'\sqsupseteq q'\). \((p',a',q')\) and \((p',b',q')\) are shortest subpaths, and thus \((a',b')=(p'\wedge q',p'\vee q')\). We have \(a'\sqsubseteq b'\) by condition (15b), and so \(p',q'\) are  -neighbors. \(\square \)
-neighbors. \(\square \)
Theorem 58
For each \(p\in \Gamma \) and \(k\ge 0\), set  is convex in \(\Gamma \).
is convex in \(\Gamma \).
Proof
We use induction on k. Consider \(k\ge 1\). By Lemma 29, it suffices to show that for distinct nodes  and a common neighbor \(q'\) of \(q_1,q_2\) we have
and a common neighbor \(q'\) of \(q_1,q_2\) we have  . Denote \(p_1=p\diamond ^{k-1} q_1\) and \(p_2=p\diamond ^{k-1} q_2\). By Theorem 55, \((p_1,p_2,q_2)\) and \((p_2,p_1,q_1)\) are shortest subpaths. Let \(p'\) be a median of \(p_1,p_2,q'\). Since \(p'\in I(p_1,p_2)\), we have
. Denote \(p_1=p\diamond ^{k-1} q_1\) and \(p_2=p\diamond ^{k-1} q_2\). By Theorem 55, \((p_1,p_2,q_2)\) and \((p_2,p_1,q_1)\) are shortest subpaths. Let \(p'\) be a median of \(p_1,p_2,q'\). Since \(p'\in I(p_1,p_2)\), we have  by the induction hypothesis. It thus suffices to show that \(p',q'\) are
by the induction hypothesis. It thus suffices to show that \(p',q'\) are  -neighbors. We can assume that \(p_1\ne p_2\) (otherwise \(p_1=p_2=p'\) and the claim holds by Lemma 52). By symmetry, we can assume that \(p_1\ne p'\). We know that \((p_2,p',p_1,q_1)\) and \((p_1,p',q')\) are shortest subpaths. We also have \(D{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}d(p_1,p') \ge 1\), \(d(p',q')+D\le d(p_1,q_1)+1\) and \(d(p_1,q_1)+D\le d(p',q')+1\). This implies that \(D=1\), \(d(p_1,q_1)=d(p',q')\) and \((p_1,p',q',q_1)\) is an isometric rectangle. Lemma 57 now gives that \(p',q'\) are
-neighbors. We can assume that \(p_1\ne p_2\) (otherwise \(p_1=p_2=p'\) and the claim holds by Lemma 52). By symmetry, we can assume that \(p_1\ne p'\). We know that \((p_2,p',p_1,q_1)\) and \((p_1,p',q')\) are shortest subpaths. We also have \(D{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}d(p_1,p') \ge 1\), \(d(p',q')+D\le d(p_1,q_1)+1\) and \(d(p_1,q_1)+D\le d(p',q')+1\). This implies that \(D=1\), \(d(p_1,q_1)=d(p',q')\) and \((p_1,p',q',q_1)\) is an isometric rectangle. Lemma 57 now gives that \(p',q'\) are  -neighbors, as desired. \(\square \)
-neighbors, as desired. \(\square \)
To conclude this section, we state one property of operations  that will be needed later.
that will be needed later.
Lemma 59
Consider elements p, u, q and operation  such that \((p,p\circ q,u,q)\) is a shortest subpath. Then \(p\circ u=p\circ q\).
such that \((p,p\circ q,u,q)\) is a shortest subpath. Then \(p\circ u=p\circ q\).
Proof
To see the claim for  , observe that for every \(x\in \mathcal{L}^+_p\) sequence
, observe that for every \(x\in \mathcal{L}^+_p\) sequence  is a shortest subpath and thus there exists a shortest x-u path going through
is a shortest subpath and thus there exists a shortest x-u path going through  . This means that
. This means that  is the gate of u at \(\mathcal{L}^+_p\), i.e.
is the gate of u at \(\mathcal{L}^+_p\), i.e.  . A symmetric argument gives the claim for
. A symmetric argument gives the claim for  . Now suppose that \((p,p\diamond q,u,q)\) is a shortest subpath. We know that
. Now suppose that \((p,p\diamond q,u,q)\) is a shortest subpath. We know that  and thus
and thus  are shortest subpaths, so the previous result gives
are shortest subpaths, so the previous result gives  . Similarly, we have
. Similarly, we have  . By definition, \(m=p\diamond u\) is the unique median of a, b, u. It can be seen that m is also a median of a, b, q. (Note that (a, u, q), (a, m, u) and thus (a, m, u, q) are shortest subpaths). Therefore, \(m=p\diamond q\). \(\square \)
. By definition, \(m=p\diamond u\) is the unique median of a, b, u. It can be seen that m is also a median of a, b, q. (Note that (a, u, q), (a, m, u) and thus (a, m, u, q) are shortest subpaths). Therefore, \(m=p\diamond q\). \(\square \)
Remark 4
For nodes p, q with  let us define
let us define  . It can be deduced from Theorem 55 that
. It can be deduced from Theorem 55 that  is the gate of q at the convex set
is the gate of q at the convex set  where
where  . This operation was introduced in [5] under the name “\(\Delta \)-gate of p at q” (in the case when \(\sqsubseteq \,={{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\)). The normal p-q path \((p_0,p_1,\ldots ,p_k)\) was also used in [5] (and was shown to be a shortest
. This operation was introduced in [5] under the name “\(\Delta \)-gate of p at q” (in the case when \(\sqsubseteq \,={{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}}\)). The normal p-q path \((p_0,p_1,\ldots ,p_k)\) was also used in [5] (and was shown to be a shortest  -path from p to q). However, it was defined by a different construction, namely via a recursion
-path from p to q). However, it was defined by a different construction, namely via a recursion  for \(i=k,k-1,\ldots ,1\). To our knowledge, operations
for \(i=k,k-1,\ldots ,1\). To our knowledge, operations  and Theorem 55 have not appeared in [5]; instead, the proof techniques in [5] relied on the notion of “Helly graphs” and on the operation \(\langle \langle x,y\rangle \rangle \) (the minimal convex set containing x, y), which we do not use.
and Theorem 55 have not appeared in [5]; instead, the proof techniques in [5] relied on the notion of “Helly graphs” and on the operation \(\langle \langle x,y\rangle \rangle \) (the minimal convex set containing x, y), which we do not use.
5.7 Connectivity of \({{\,\mathrm{{\texttt {dom}}}\,}}f\)
In this section we will show that following.
Theorem 60
If \(f:\Gamma \rightarrow \overline{\mathbb R}\) is an L-convex function on an extended modular complex \(\Gamma \) and \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) then  .
.
Corollary 61
For any \(p,q\in \Gamma \) there exists a p-q path \((p_0,p_1,\ldots ,p_k)\) in  with \((p_0,p_k)=(p,q)\) which is a shortest subpath and has the following property: for any L-convex function f on \(\Gamma \) with \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) one has \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) for all \(i\in [0,k]\). (This path is obtained by setting either
with \((p_0,p_k)=(p,q)\) which is a shortest subpath and has the following property: for any L-convex function f on \(\Gamma \) with \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) one has \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) for all \(i\in [0,k]\). (This path is obtained by setting either  or
or  ; one of these two elements is distinct from \(p_i\) if \(p_i\ne q\)).
; one of these two elements is distinct from \(p_i\) if \(p_i\ne q\)).
To prove Theorem 60, we start with technical observations.
Lemma 62
Consider elements \(p,q,u\in {{\,\mathrm{{\texttt {dom}}}\,}}f\).
- (a):
-
If \(p\sqsupseteq u \sqsubseteq q\) then
 . Similarly, if \(p\sqsubseteq u \sqsupseteq q\) and \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) then
. Similarly, if \(p\sqsubseteq u \sqsupseteq q\) and \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) then 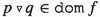 .
. - (b):
-
If \(p\sqsubseteq u \sqsubseteq q\) then
 . Similarly, if \(p\sqsupseteq u \sqsupseteq q\) then
. Similarly, if \(p\sqsupseteq u \sqsupseteq q\) then  .
.
Proof
By symmetry, it suffices to prove only the first claim in (a) and in (b). In both cases we denote  .
.
(a) Denote \(s=p\wedge q\), then \(p\sqsupseteq s \sqsubseteq q\). We know that f is submodular on \(\mathcal{L}^+_s\). It suffices to show that \(a\in \mathcal{E}(p,q)\); this would imply that \(a\in {{\,\mathrm{{\texttt {dom}}}\,}}f\).
Point p has coordinates \(v_{pq}(p)=(X,0)\) where \(X=\mu (s,p)\). We have \(a\in I(p,q)\), \(p\sqsubseteq a\) and \(a\wedge p=p\), therefore a has coordinates \(v_{pq}(a)=(X,\ldots )\). Suppose that \(a\notin \mathcal{E}(p,q)\), then there exists \(a' \in I(p,q)\) with \(v_{pq}(a')=(X,\ldots )\) and \(\mu (p,a')>\mu (p,a)\). We have \(a'\wedge p\in [s,p]\) and \(\mu (s,a'\wedge p)=X=\mu (s,p)\), thus \(a'\wedge p=p\) or equivalently \(p\preceq a'\). For any \(x\in I(p,q)\) we have \(s\sqsubseteq x\) (this follows from condition \(p\sqsupseteq s \sqsubseteq q\), Lemma 24(b) and properties (15a,b)). Thus, we have \(s\sqsubseteq a'\) and hence \(p\sqsubseteq a'\) (since \(s\preceq p\preceq a'\)). Equation (15) gives  , contradicting condition \(\mu (p,a')>\mu (p,a)\).
, contradicting condition \(\mu (p,a')>\mu (p,a)\).
(b) We know that \(f^*\) is submodular on \(\mathcal{L}^*_u\). Note that \([x,y]\in I([p,u],[u,q])\) if and only if \(x\sqsubseteq y\), \(x\in [p,u]\), \(y\in [u,q]\) (by Lemma 37). For such [x, y] we have \(v_{[p,u], [u,q]}([x,y])=(\mu (x,u),\mu (u,y))\). It suffices to show that \([p,a]\in \mathcal{E}([p,u],[u,q])\); this would imply that \([p,a]\in {{\,\mathrm{{\texttt {dom}}}\,}}f^*\) and \(a\in {{\,\mathrm{{\texttt {dom}}}\,}}f\).
From the lemma’s assumption and Eq. (15) we conclude that \(p\sqsubseteq u\sqsubseteq a\sqsubseteq q\) and \(p\sqsubseteq a\), and hence \([p,a]\in \mathcal{L}^*_u\cap I([p,u],[u,q])\). Elements [p, u] and [p, a] have coordinates respectively (X, 0) and (X, Y) where \(X=\mu (p,u)\) and \(Y=\mu (u,a)\). If \([p,a]\notin \mathcal{E}([p,u],[u,q])\) then there exists element \([p,a']\in \mathcal{L}^*_u\cap I([p,u],[u,q])\) whose second coordinate is \(Y'=\mu (u,a')>\mu (u,a)=Y\). This contradicts Eq. (15). \(\square \)
Lemma 63
Consider elements \(p,q,u\in \Gamma \) such that  . Define
. Define  and
and  . Then
. Then  and
and  .
.
Proof
Clearly, we have  , and sequence
, and sequence  is a shortest subpath. Thus, we have
is a shortest subpath. Thus, we have  , and so
, and so  by Eq. (15). Sequence
by Eq. (15). Sequence  is thus a shortest subpath, so Lemma 59 gives the first claim:
is thus a shortest subpath, so Lemma 59 gives the first claim:  .
.
To show the second claim, let  be the median of
be the median of  . We have \(x\sqsubseteq u\) (by the same argument as in the proof of Lemma 51) and \(x\in I(u,q)\), therefore
. We have \(x\sqsubseteq u\) (by the same argument as in the proof of Lemma 51) and \(x\in I(u,q)\), therefore  by Eq. (15). Sequence \((u,x,u^-,q)\) is a thus shortest subpath.
by Eq. (15). Sequence \((u,x,u^-,q)\) is a thus shortest subpath.  is also a shortest subpath, and hence so is
is also a shortest subpath, and hence so is  . Lemma 59 now gives
. Lemma 59 now gives  . \(\square \)
. \(\square \)
Lemma 64
If \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) then  .
.
Proof
We use induction on d(p, q). Suppose that \(d(p,q)>0\). By Lemma 49, there exists \(u\in I(p,q)\cap {{\,\mathrm{{\texttt {dom}}}\,}}f\) such that  . By symmetry, we can assume that \(p\sqsubset u\). We then have
. By symmetry, we can assume that \(p\sqsubset u\). We then have  . Denote
. Denote  and
and  , then we have \(u^+,u^-\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) by the induction hypothesis.
, then we have \(u^+,u^-\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) by the induction hypothesis.
Let us show that  . We have
. We have  by Lemma 63. If \(u^-\ne q\) then the claim holds by the induction hypothesis. If \(u^-=q\) then \(u\sqsupseteq q\), and the claim follows from Lemma 62(a).
by Lemma 63. If \(u^-\ne q\) then the claim holds by the induction hypothesis. If \(u^-=q\) then \(u\sqsupseteq q\), and the claim follows from Lemma 62(a).
Let us show that  . We have
. We have  by Lemma 63. If \(u^+\ne q\) then the claim holds by the induction hypothesis. If \(u^+=q\) then \(u\sqsubseteq q\), and the claim follows from Lemma 62(b). \(\square \)
by Lemma 63. If \(u^+\ne q\) then the claim holds by the induction hypothesis. If \(u^+=q\) then \(u\sqsubseteq q\), and the claim follows from Lemma 62(b). \(\square \)
5.8 Proof of Theorem 20
Theorem 20
(restated). Consider extended modular complexes \(\Gamma ,\Gamma '\) and functions \(f,f':\Gamma \rightarrow \overline{\mathbb R}\) and \(\tilde{f}:\Gamma \times \Gamma '\rightarrow \overline{\mathbb R}\).
- (a):
-
If \(f,f'\) are L-convex on \(\Gamma \) then \(f+f'\) and \(c\cdot f\) for \(c\in \mathbb R_+\) are also L-convex on \(\Gamma \).
- (b):
-
If f is L-convex on \(\Gamma \) and \({\tilde{f}}(p,p')=f(p)\) for \((p,p')\in \Gamma \times \Gamma '\) then \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\).
- (c):
-
If \({\tilde{f}}\) is L-convex on \(\Gamma \times \Gamma '\) and \(f(p)={\tilde{f}}(p,p')\) for fixed \(p'\in \Gamma '\) then f is L-convex on \(\Gamma \).
- (d):
-
The indicator function \(\delta _U:V\rightarrow \{0,\infty \}\) is L-convex on \(\Gamma \) in the following cases: (i) U is a \(d_\Gamma \)-convex set; (ii) \(U=\{p,q\}\) for elements p, q with \(p\sqsubseteq q\).
- (e):
-
Function \(\mu _\Gamma :V\times V\rightarrow \mathbb R_+\) is L-convex on \(\Gamma \times \Gamma \).
- (f):
-
If f is L-convex on \(\Gamma \) then the restriction of f to \(\mathcal{L}^\sigma _p(\Gamma )\) is submodular on \(\mathcal{L}^\sigma _p(\Gamma )\) for every \(p\in \Gamma \) and \(\sigma \in \{-,+\}\).
(a) We need to show that \({{\,\mathrm{{\texttt {dom}}}\,}}(f+f')=({{\,\mathrm{{\texttt {dom}}}\,}}f)\cap ({{\,\mathrm{{\texttt {dom}}}\,}}f')\) is connected in  ; checking other conditions of L-convexity is straightforward. Consider \(p,q\in ({{\,\mathrm{{\texttt {dom}}}\,}}f)\cap ({{\,\mathrm{{\texttt {dom}}}\,}}f')\), and let \((p_0,p_1,\ldots ,p_k)\) be the path in
; checking other conditions of L-convexity is straightforward. Consider \(p,q\in ({{\,\mathrm{{\texttt {dom}}}\,}}f)\cap ({{\,\mathrm{{\texttt {dom}}}\,}}f')\), and let \((p_0,p_1,\ldots ,p_k)\) be the path in  constructed in Corollary 61. By the corollary, for each \(i\in [0,k]\) we have \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f'\), which implies the claim.
constructed in Corollary 61. By the corollary, for each \(i\in [0,k]\) we have \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f'\), which implies the claim.
(b) The claim holds by Lemma 42(a).
(c) It suffices to prove that \({{\,\mathrm{{\texttt {dom}}}\,}}f\) is connected in  , the claim will then follow from Lemma 42(b). Consider \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). We know that \((p,p'),(q,p')\in {{\,\mathrm{{\texttt {dom}}}\,}}{\tilde{f}}\), and thus there exists path \(({\tilde{p}}_0,{\tilde{p}}_1,\ldots ,{\tilde{p}}_k)\) in
, the claim will then follow from Lemma 42(b). Consider \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). We know that \((p,p'),(q,p')\in {{\,\mathrm{{\texttt {dom}}}\,}}{\tilde{f}}\), and thus there exists path \(({\tilde{p}}_0,{\tilde{p}}_1,\ldots ,{\tilde{p}}_k)\) in  with \((\tilde{p}_0,{\tilde{p}}_k)=((p,p'),(q,p'))\) and \({\tilde{p}}_i\in {{\,\mathrm{{\texttt {dom}}}\,}}{\tilde{f}}\) for all i. By Corollary 61, such path can be chosen so that \({\tilde{p}}_i\in I((p,p'),(q,p'))\) for all i. Thus, we have \({\tilde{p}}_i=(p_i,p')\) for all i. Sequence \((p_0,p_1,\ldots ,p_k)\) is now a path in
with \((\tilde{p}_0,{\tilde{p}}_k)=((p,p'),(q,p'))\) and \({\tilde{p}}_i\in {{\,\mathrm{{\texttt {dom}}}\,}}{\tilde{f}}\) for all i. By Corollary 61, such path can be chosen so that \({\tilde{p}}_i\in I((p,p'),(q,p'))\) for all i. Thus, we have \({\tilde{p}}_i=(p_i,p')\) for all i. Sequence \((p_0,p_1,\ldots ,p_k)\) is now a path in  satisfying \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) for all i.
satisfying \(p_i\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) for all i.
(d) Clearly, in both cases U is connected in  ; in the case (i) this holds since U is connected in \(\Gamma \), and in the case (ii) the claim is trivial.
; in the case (i) this holds since U is connected in \(\Gamma \), and in the case (ii) the claim is trivial.
Let \(U^*\) be the set of vertices [p, q] in \(\Gamma ^*\) with \(p,q\in U\), and for \(x\in \Gamma \) denote \(U^*_x=U^*\cap \mathcal{L}^*_x\). Note that \(\delta _U^*=\delta _{U^*}\), and the restriction of \(\delta _{U^*}\) to \(\mathcal{L}^*_x\) equals \(\delta _{U^*_x}\). It suffices to show that \(U^*_x\) is convex in \(\mathcal{L}^*_x\); the submodularity of \(\delta _{U^*_x}\) on \(\mathcal{L}^*_x\) will then follow from [15, Lemma 3.7(4)].
If \(U=\{p,q\}\) where \(p\sqsubseteq q\) then \(U^*_x=\{[p,q]\}\) if \(x\in [p,q]\), and \(U^*_x=\varnothing \) otherwise; in both cases \(U^*_x\) is clearly convex. Suppose that U is a convex set in \(\Gamma \). It suffices to show that \(U^*\) is convex in \(\Gamma ^*\). (Since \(\mathcal{L}^*_x\) is convex in \(\Gamma ^*\) by Lemma 17, the intersection \(U^*\cap \mathcal{L}^*_x\) would then be convex in \(\Gamma ^*\) and thus also in \(\mathcal{L}^*_x\)).
We use Lemma 31 to show that \(U^*\) is convex in \(\Gamma ^*\). Let \([u,v]\in \Gamma ^*\) be common neighbor of distinct \([p,q],[p',q']\in U^*\); we need to show that \([u,v]\in U^*\). Modulo symmetry, 4 cases are possible:
-
\(p=u=p'\) and \(q\rightarrow v\rightarrow q'\).
-
\(p=u=p'\) and \(q\rightarrow v\leftarrow q'\).
-
\(p=u=p'\) and \(q\leftarrow v\rightarrow q'\).
-
\(p\rightarrow u=p'\) and \(q\rightarrow v=q'\).
In each of these cases conditions \(p,q,p',q'\in U\) and convexity of U implies that \(u,v\in U\), and so \([u,v]\in U^*\).
(e) The claim holds by Lemma 44(a).
(f) The claim holds by Lemma 39.
Corollary 65
If function f is an L-convex on \(\Gamma \) and U is convex in \(\Gamma \) then function \(f+\delta _U\) is L-convex on \(\Gamma \). In particular,  is L-convex for any \(x\in \Gamma \) and \(k\ge 0\).
is L-convex for any \(x\in \Gamma \) and \(k\ge 0\).
5.9 f-extremality
Given an L-convex function \(f:\Gamma \rightarrow {{\overline{{\mathbb R}}}}\), we say that pair (p, q) is f-extremal if \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and \(f(p)=\min \{f(x)\,{:}\,x\in I(p,q)\}\). We say that it is strictly f-extremal if \(p,q\in {{\,\mathrm{{\texttt {dom}}}\,}}f\) and \(\mathop {\mathrm {arg\,min}}\limits \{f(x)\,{:}\,x\in I(p,q)\}=\{p\}\). In this section we establish some key facts about f-extremal pairs that will be used in the analysis of the  -SDA algorithm.
-SDA algorithm.
Lemma 66
Suppose that (p, q) is f-extremal,  and
and  . Then (s, q) is f-extremal.
. Then (s, q) is f-extremal.
Proof
Note that  by Theorem 60, and thus \(s\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). Suppose the claim is false, then there exists \(q'\in I(s,q)-\{s\}\) with \(f(q')<f(s)\). By Lemma 49, there exists \(u\in I(s,q')\subseteq I(p,q)\) with
by Theorem 60, and thus \(s\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). Suppose the claim is false, then there exists \(q'\in I(s,q)-\{s\}\) with \(f(q')<f(s)\). By Lemma 49, there exists \(u\in I(s,q')\subseteq I(p,q)\) with  and \(f(u)<f(s)\). First, suppose that \(u\sqsubset s\). Note that \(u\preceq s\preceq p\) and \(f(u)\ge f(p)\). We claim that there exists \(x\in I(u,p)=[u,p]\) with \(x\sqsubset p\) and \(f(x)\le f(u)\). Indeed, define sequence \(u_0\sqsubset u_1 \sqsubset \ldots \sqsubset u_k\sqsubset p\) with \(u_0=u\) and \(f(u_0)\ge f(u_1)\ge \ldots f(u_k)\ge f(p)\) via the following rule: if \(u_i\sqsubset p\) then set \(k=i\) and stop, otherwise let \(u_{i+1}\) be an element in \([u_i,p]\) with \(u_i\sqsubset u_{i+1}\) and \(f(u_i)\ge f(u_{i+1})\), which exists by Lemma 49. Taking \(x=u_k\) now proves the claim.
and \(f(u)<f(s)\). First, suppose that \(u\sqsubset s\). Note that \(u\preceq s\preceq p\) and \(f(u)\ge f(p)\). We claim that there exists \(x\in I(u,p)=[u,p]\) with \(x\sqsubset p\) and \(f(x)\le f(u)\). Indeed, define sequence \(u_0\sqsubset u_1 \sqsubset \ldots \sqsubset u_k\sqsubset p\) with \(u_0=u\) and \(f(u_0)\ge f(u_1)\ge \ldots f(u_k)\ge f(p)\) via the following rule: if \(u_i\sqsubset p\) then set \(k=i\) and stop, otherwise let \(u_{i+1}\) be an element in \([u_i,p]\) with \(u_i\sqsubset u_{i+1}\) and \(f(u_i)\ge f(u_{i+1})\), which exists by Lemma 49. Taking \(x=u_k\) now proves the claim.
Clearly, \(x\in I(p,q)\), and thus  and \(f(x)\le f(u)<f(s)\), which contradicts the choice of s. Thus, we must have \(u\sqsupset s\). Note that \(p\wedge u=s\) since \(p\succeq s\preceq u\) and (p, s, u) is a shortest subpath. We know that f is submodular on a modular semilattice \(\mathcal{L}_s^+\), and \(p,u\in \mathcal{L}_s^+\). Thus, \(f(p)+f(u)\ge f(s)+\sum _{a\in \mathcal{E}(p,u)}\lambda _a f(a)\) where \(\lambda _a\) are nonnegative numbers with \(\sum _{a\in \mathcal{E}(p,u)}\lambda _a =1\). This gives a contradiction since \(f(u)<f(s)\) and \(f(p)\le f(a)\) for all \(a\in \mathcal{E}(p,u)\subseteq I(p,q)\). \(\square \)
and \(f(x)\le f(u)<f(s)\), which contradicts the choice of s. Thus, we must have \(u\sqsupset s\). Note that \(p\wedge u=s\) since \(p\succeq s\preceq u\) and (p, s, u) is a shortest subpath. We know that f is submodular on a modular semilattice \(\mathcal{L}_s^+\), and \(p,u\in \mathcal{L}_s^+\). Thus, \(f(p)+f(u)\ge f(s)+\sum _{a\in \mathcal{E}(p,u)}\lambda _a f(a)\) where \(\lambda _a\) are nonnegative numbers with \(\sum _{a\in \mathcal{E}(p,u)}\lambda _a =1\). This gives a contradiction since \(f(u)<f(s)\) and \(f(p)\le f(a)\) for all \(a\in \mathcal{E}(p,u)\subseteq I(p,q)\). \(\square \)
Corollary 67
If (p, q) is f-extremal and \(p\wedge q\) exists then \((p\wedge q,q)\) is f-extremal.
Proof
The claim follows by repeatedly applying Lemma 66 (with an induction argument). \(\square \)
Lemma 68
If (p, q) is f-extremal then \(f(p\diamond q)\le f(q)\).
Proof
We use induction on d(p, q). We can assume that \(p\diamond q\ne q\), otherwise the claim is trivial. It would suffice to show the following:
- (\(\star \)):
-
There exists \(y\ne q\) such that \(f(y)\le f(q)\) and \((p\diamond q,y,q)\) is a shortest subpath.
Indeed, by Lemma 59 we would then have \(p\diamond q=p\diamond y\), and so the induction hypothesis for (p, y) would give \(f(p\diamond q)=f(p\diamond y)\le f(y)\le f(q)\).
One of  must be different from p. By symmetry, we can assume that
must be different from p. By symmetry, we can assume that  . We can further assume the following: if
. We can further assume the following: if  and
and  then condition \(p\sqsupseteq p\wedge q \sqsubseteq q\) does not hold, where the existence of \(p\wedge q\) is a part of the condition. Indeed, conditions \(p\sqsupseteq p\wedge q \sqsubseteq q\) and \(p\sqsubseteq p\vee q \sqsupseteq q\) cannot hold simultaneuosly (otherwise we would have \(p\diamond q= q\)), so we can pick the condition that does not hold and then change the orientation if necessary.
then condition \(p\sqsupseteq p\wedge q \sqsubseteq q\) does not hold, where the existence of \(p\wedge q\) is a part of the condition. Indeed, conditions \(p\sqsupseteq p\wedge q \sqsubseteq q\) and \(p\sqsubseteq p\vee q \sqsupseteq q\) cannot hold simultaneuosly (otherwise we would have \(p\diamond q= q\)), so we can pick the condition that does not hold and then change the orientation if necessary.
Denote  , and pick \(s\in \mathop {\mathrm {arg\,min}}\limits \{f(s)\,{:}\,s\in [x,p]-\{p\}\}\). By Lemma 66, (s, q) is f-extremal. Four cases are possible.
, and pick \(s\in \mathop {\mathrm {arg\,min}}\limits \{f(s)\,{:}\,s\in [x,p]-\{p\}\}\). By Lemma 66, (s, q) is f-extremal. Four cases are possible.
 Denote \(y=s\diamond q\), then \(y\ne q\). By Lemma 54, \((p\diamond q,y,q)\) is a shortest subpath. By the induction hypothesis for (s, q) we have \(f(y)\le f(q)\). Thus, \((\star )\) holds.
Denote \(y=s\diamond q\), then \(y\ne q\). By Lemma 54, \((p\diamond q,y,q)\) is a shortest subpath. By the induction hypothesis for (s, q) we have \(f(y)\le f(q)\). Thus, \((\star )\) holds.
In the remaining cases we have  . We will denote \(a=s\wedge q=p\wedge q\). Note that \(p\sqsupseteq s\sqsupseteq a\sqsubseteq q\). Furthermore, \(x\in [a,s]\). Indeed, (p, s, x, q) and thus (s, x, q) are shortest subpaths and \(s\sqsupseteq x\), so
. We will denote \(a=s\wedge q=p\wedge q\). Note that \(p\sqsupseteq s\sqsupseteq a\sqsubseteq q\). Furthermore, \(x\in [a,s]\). Indeed, (p, s, x, q) and thus (s, x, q) are shortest subpaths and \(s\sqsupseteq x\), so  by Eq. (15). One can check that (p, s, x, a, q) is a shortest subpath (since (p, s, q), (s, a, q), (s, x, a) are shortest subpaths). Furthermore, \((p\wedge q,q)=(a,q)\) is f-extremal by Corollary 67.
by Eq. (15). One can check that (p, s, x, a, q) is a shortest subpath (since (p, s, q), (s, a, q), (s, x, a) are shortest subpaths). Furthermore, \((p\wedge q,q)=(a,q)\) is f-extremal by Corollary 67.
 We have \(p\sqsupseteq a\sqsubseteq q\), which implies that
We have \(p\sqsupseteq a\sqsubseteq q\), which implies that  and thus
and thus  . f-extremality of (a, q) gives \(f(a)\le f(q)\). We have \(a\ne q\) since we assumed that \(p\diamond q\ne q\). Thus, element \(y=a\) satisfies condition (\(\star \)).
. f-extremality of (a, q) gives \(f(a)\le f(q)\). We have \(a\ne q\) since we assumed that \(p\diamond q\ne q\). Thus, element \(y=a\) satisfies condition (\(\star \)).
 We have
We have  where the first two equalities hold since \(p\succeq a\) and by Lemma 59, respectively. Since (a, q) is f-extremal, we get \(a\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). Since \(a\ne q\), we can apply the induction hypothesis for (p, a) and get \(f(x)=f(p\diamond a)\le f(a)\).
where the first two equalities hold since \(p\succeq a\) and by Lemma 59, respectively. Since (a, q) is f-extremal, we get \(a\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). Since \(a\ne q\), we can apply the induction hypothesis for (p, a) and get \(f(x)=f(p\diamond a)\le f(a)\).
Conditions  and \(x\in [a,s]\) imply that \(y{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}x\vee q\) exists and \(a\sqsubseteq x\). Note that \(x\wedge q=a\). By submodularity inequality for x, q in modular semilattice \(\mathcal{L}_a^+\) we get \(f(x)+f(q)\ge f(a)+f(y)\), and so \(f(y)\le f(q)\). Clearly, (p, x, y, q) is a shortest subpath. By applyng Lemma 24 to modular semilattice \(\mathcal{L}_a^\uparrow \) we obtain that
and \(x\in [a,s]\) imply that \(y{{\mathop {=}\limits ^{{\tiny \mathtt ~def~}}}}x\vee q\) exists and \(a\sqsubseteq x\). Note that \(x\wedge q=a\). By submodularity inequality for x, q in modular semilattice \(\mathcal{L}_a^+\) we get \(f(x)+f(q)\ge f(a)+f(y)\), and so \(f(y)\le f(q)\). Clearly, (p, x, y, q) is a shortest subpath. By applyng Lemma 24 to modular semilattice \(\mathcal{L}_a^\uparrow \) we obtain that  is a shortest subpath (since \(y\in I(p,q)\) and \(y\succeq q\)). Since
is a shortest subpath (since \(y\in I(p,q)\) and \(y\succeq q\)). Since  and
and  , we get
, we get  , i.e. \((p,p\diamond q,y,q)\) is a shortest subpath. We have \(x\ne a\) (since \(p\sqsupseteq x\) and \(p\not \sqsupseteq a\)) and thus \(y\ne q\). Therefore, \((\star )\) holds.
, i.e. \((p,p\diamond q,y,q)\) is a shortest subpath. We have \(x\ne a\) (since \(p\sqsupseteq x\) and \(p\not \sqsupseteq a\)) and thus \(y\ne q\). Therefore, \((\star )\) holds.
 We have \(q\preceq x\preceq s\preceq p\), \(q\sqsubseteq s\) (since
We have \(q\preceq x\preceq s\preceq p\), \(q\sqsubseteq s\) (since  ) and \(x\sqsubseteq p\). Note that
) and \(x\sqsubseteq p\). Note that  . Also, \(q\ne x\) (since \(q\not \sqsubseteq p\) and \(x\sqsubseteq p\)). By Theorem 60 we have \(x\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). We claim that \((\star )\) holds. Indeed, suppose this is false, then \(f(y)>f(q)\) for all \(y\in [q,x]-\{q\}\). Denote \(\alpha =[q,s]\), \(\beta =[x,s]\), \(\gamma =[x,p]\), then \(\alpha ,\beta ,\gamma \in \mathcal{L}^*_s\) and \(\alpha \wedge \gamma =\alpha \cap \gamma =\beta \). We know that function \(f^*:\mathcal{L}^*_s\rightarrow {{\overline{{\mathbb R}}}}\) is submodular on \(\mathcal{L}^*_s\). Condition \(f(q)<f(x)\) implies that \(f^*(\alpha )<f^*(\beta )\). Condition \(f(p)\le f(s)\) implies that \(f^*(\gamma )\le f^*(\beta )\).
. Also, \(q\ne x\) (since \(q\not \sqsubseteq p\) and \(x\sqsubseteq p\)). By Theorem 60 we have \(x\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). We claim that \((\star )\) holds. Indeed, suppose this is false, then \(f(y)>f(q)\) for all \(y\in [q,x]-\{q\}\). Denote \(\alpha =[q,s]\), \(\beta =[x,s]\), \(\gamma =[x,p]\), then \(\alpha ,\beta ,\gamma \in \mathcal{L}^*_s\) and \(\alpha \wedge \gamma =\alpha \cap \gamma =\beta \). We know that function \(f^*:\mathcal{L}^*_s\rightarrow {{\overline{{\mathbb R}}}}\) is submodular on \(\mathcal{L}^*_s\). Condition \(f(q)<f(x)\) implies that \(f^*(\alpha )<f^*(\beta )\). Condition \(f(p)\le f(s)\) implies that \(f^*(\gamma )\le f^*(\beta )\).
Consider \(\delta =[u,v]\in \mathcal{E}(\alpha ,\gamma )-\{\gamma \}\). By Lemma 37 we must have \(u\in [q,x]\) and \(v\in [s,p]\). We must have \(v\ne p\) (otherwise condition \(\delta \ne \gamma \) would imply that \(u\in [q,x]-\{x\}\); we would also have \(u\sqsubseteq v=p\) which is impossible since  ). Conditions \(u\in [q,x]\) and \(v\in [s,p]-\{p\}\) have two implications: (i) the second coordinate of \(v_{\alpha \gamma }(\delta )\) is strictly smaller than the second coordinate of \(v_{\alpha \gamma }(\gamma )\); (ii) \(f(u)\ge f(q)\), \(f(v)\ge f(s)\) and hence \(f^*(\delta )\ge f^*(\alpha )\).
). Conditions \(u\in [q,x]\) and \(v\in [s,p]-\{p\}\) have two implications: (i) the second coordinate of \(v_{\alpha \gamma }(\delta )\) is strictly smaller than the second coordinate of \(v_{\alpha \gamma }(\gamma )\); (ii) \(f(u)\ge f(q)\), \(f(v)\ge f(s)\) and hence \(f^*(\delta )\ge f^*(\alpha )\).
By submodularity, \(f^*(\alpha )+f^*(\gamma )\ge f^*(\beta )+\sum _{\delta \in \mathcal{E}(\alpha ,\gamma )}\lambda _\delta f^*(\delta )\) where \(\lambda _\delta \) are nonnegative numbers with \(\sum _{\delta \in \mathcal{E}(\alpha ,\gamma )}\lambda _\delta =1\). By implication (i), we have \(\lambda _\gamma >0\). The submodularity inequality can be rewritten as
All numbers in square brackets are non-positive, thus they must all be 0. This implies that \(f^*(\gamma )=f^*(\beta )\) and \(f^*(\alpha )=f^*(\gamma )\), which contradicts condition \(f^*(\alpha )<f^*(\beta )\).
\(\square \)
We conclude this section with a couple of results that will help to deal with cases when values of f are not unique.
Lemma 69
If (p, q) is strictly f-extremal and \(p\diamond q\ne q\) then \(f(p\diamond q)<f(q)\).
Proof
For \(\varepsilon >0\) define function \(f_\varepsilon :\Gamma \rightarrow {{\overline{{\mathbb R}}}}\) via \(f_\varepsilon (x)=f(x)+\varepsilon \mu (x,q)\). Note that \(f_\varepsilon \) is L-convex on \(\Gamma \). Clearly, there exists \(\varepsilon >0\) such that (p, q) is \(f_\varepsilon \)-extremal. Using Lemma 68, we obtain \(f(p\diamond q)=f_\varepsilon (p\diamond q)-\varepsilon \mu (p\diamond q,q)<f_\varepsilon (p\diamond q)\le f_\varepsilon (q)=f(q)\). \(\square \)
Lemma 70
Suppose that (p, q) is f-extremal, \(p\preceq q\), \(p\not \sqsubseteq q\), \(q\diamond p\preceq p\diamond q\) and \(f(q')\ge f(q)\) for all \(q'\in [p\diamond q,q]\). Then there exists \(p'\in [p,q\diamond p]-\{p\}\) with \(f(p')=f(p)\).
Proof
Denote \((a,b)=(q\diamond p,p\diamond q)\), then \(p\preceq a\preceq b\preceq q\), \(p\sqsubseteq b\), \(a\sqsubseteq q\) and hence \(a\sqsubseteq b\). By Theorem 60, we have \(a,b\in {{\,\mathrm{{\texttt {dom}}}\,}}f\). Denote \(\alpha =[p,b]\), \(\beta =[a,b]\), \(\gamma =[a,q]\), then \(\alpha ,\beta ,\gamma \in \mathcal{L}^*_a\) and \(\alpha \wedge \gamma =\beta \). Note that \(f^*(\alpha )+f^*(\gamma )=f^*(\beta )+f(p)+f(q)\). By submodularity, \(f^*(\alpha )+f^*(\gamma )\ge f^*(\beta )+\sum _{\delta \in \mathcal{E}(\alpha ,\gamma )}\lambda _\delta f^*(\delta )\), or equivalently \(f(p)+f(q)\ge \sum _{\delta \in \mathcal{E}(\alpha ,\gamma )}\lambda _\delta f^*(\delta )\) where \(\lambda _\delta \) are nonnegative numbers with \(\sum _{\delta \in \mathcal{E}(\alpha ,\gamma )}\lambda _\delta =1\). For every \(\delta =[u,v]\in \mathcal{E}(\alpha ,\gamma )\) we have \(u\in [p,a]\), \(v\in [b,q]\) by Lemma 37. Furthermore, \(f(u)\ge f(p)\) and \(f(v)\ge f(q)\) by the lemma’s assumption, and so \(f^*(\delta )\ge f(p)+f(q)\). This implies that \(f(u)=f(p)\), \(f(v)=f(q)\) for every \(\delta =[u,v]\in \mathcal{E}(\alpha ,\gamma )\) with \(\lambda _\delta >0\). Note that \([p,q]\notin \mathcal{L}^*_a\) since \(p\not \sqsubseteq q\), and so \(\alpha \vee \gamma \) does not exist in \(\mathcal{L}^*_a\). This implies that \(\alpha \ne \beta \ne \gamma \). Therefore, there exists \(\delta =[u,v]\in \mathcal{E}(\alpha ,\gamma )-\{\alpha \}\) with \(\lambda _\delta >0\) (and hence with \(f(u)=f(p)\)). We claim that \(u\ne p\) (and so \(u\in [p,a]-\{p\}\), implying the lemma). Indeed, if \(u=p\) then condition \(\delta \ne \alpha \) gives that \(v\ne b\), and hence \(v\in [b,q]-\{b\}\). This is impossible since \(p=u\sqsubseteq v\) and  . \(\square \)
. \(\square \)
5.10 Proof of Theorem 22: analysis of the  -SDA algorithm
-SDA algorithm
Theorem 22
(restated). Let \(\Gamma \) be an extended modular complex and \(f:\Gamma ^n\rightarrow {{\overline{{\mathbb R}}}}\) be an L-convex function on \(\Gamma ^n\).  -SDA algorithm applied to function f terminates after generating exactly
-SDA algorithm applied to function f terminates after generating exactly  distinct points, where x is the initial vertex and \(\texttt {opt}_i(f)\) is as defined in Theorem 12.
distinct points, where x is the initial vertex and \(\texttt {opt}_i(f)\) is as defined in Theorem 12.
First, we show the following fact.
Lemma 71
Suppose that \(\Gamma \) is a Cartesian product of extended modular complexes: \(\Gamma =\Gamma _1\times \ldots \times \Gamma _n\). Then  .
.
Proof
It suffices to show the following fact for extended modular complexes \(\Gamma ,\Gamma '\).
- (\(*\)):
-
The following conditions are equivalent for elements \(x,y\in \Gamma \) and \(x',y'\in \Gamma '\):
(a) \((x,x'),(y,y')\) are  -neighbors;
-neighbors;
(b) x, y are  -neighbors and \(x',y'\) are
-neighbors and \(x',y'\) are  -neighbors.
-neighbors.
Let us define \((a,b)=(x\wedge y,x\vee y)\) and \((a',b')=(x'\wedge y',x'\vee y')\). (These expressions are defined if either (a) or (b) holds). By the definition of the Cartesian product \(\Gamma \times \Gamma '\), we have the following implications:
\(\square \)
In the light of this lemma, it suffices to prove Theorem 22 in the case when \(n=1\). Accordingly, from on we assume that  -SDA is applied to minimize function \(f:\Gamma \rightarrow {{\overline{{\mathbb R}}}}\) which is L-convex on an extended modular complex \(\Gamma \).
-SDA is applied to minimize function \(f:\Gamma \rightarrow {{\overline{{\mathbb R}}}}\) which is L-convex on an extended modular complex \(\Gamma \).
Let \({\bar{x}}\) be the initial vertex of the  -SDA algorithm, and for \(k\ge 0\) define function
-SDA algorithm, and for \(k\ge 0\) define function  . By Corollary 65, \(f_k\) is L-convex on \(\Gamma \) for any \(k\ge 0\).
. By Corollary 65, \(f_k\) is L-convex on \(\Gamma \) for any \(k\ge 0\).
Lemma 72
For any \(q\in \mathop {\mathrm {arg\,min}}\limits f_{k-1}\) there exists \(p\in \mathop {\mathrm {arg\,min}}\limits f_{k}\) with  .
.
Proof
Let p be an element of \(\mathop {\mathrm {arg\,min}}\limits f_{k}\) which is closest to q. Clearly, (p, q) is \(f_k\)-extremal, and in fact strictly \(f_{k}\)-extremal. (If there exists \(p'\in I(p,q)-\{p\}\) with \(f_k(p')=f_k(p)\) then \(p'\) also belongs to \(\mathop {\mathrm {arg\,min}}\limits f_{k}\) and is closer to q than p, contradicting the choice of p). Since  , there exists
, there exists  with
with  . \((u,p\diamond q,q)\) is a shortest subpath by Theorem 55. We have
. \((u,p\diamond q,q)\) is a shortest subpath by Theorem 55. We have  and thus
and thus  by convexity of
by convexity of  (Theorem 58). If \(p\diamond q\ne q\) then \(f_k(p\diamond q)<f_k(q)\) by Lemma 69, which contradicts the choice of q. Thus, we must have \(p\diamond q=q\) and so
(Theorem 58). If \(p\diamond q\ne q\) then \(f_k(p\diamond q)<f_k(q)\) by Lemma 69, which contradicts the choice of q. Thus, we must have \(p\diamond q=q\) and so  . \(\square \)
. \(\square \)
Lemma 73
Consider \(x\in {{\,\mathrm{{\texttt {dom}}}\,}}f\), and let p be an element of  which is closest to x. Let \(x^-\in \mathop {\mathrm {arg\,min}}\limits \,\{f(y)\,|\,y\in \mathcal{L}^-_x(\Gamma )\} \) and \(x^+\in \mathop {\mathrm {arg\,min}}\limits \,\{f(y)\,|\,y\in \mathcal{L}^+_x(\Gamma )\} \). Then \(x^-\sqsubseteq p \sqsubseteq x^+\).
which is closest to x. Let \(x^-\in \mathop {\mathrm {arg\,min}}\limits \,\{f(y)\,|\,y\in \mathcal{L}^-_x(\Gamma )\} \) and \(x^+\in \mathop {\mathrm {arg\,min}}\limits \,\{f(y)\,|\,y\in \mathcal{L}^+_x(\Gamma )\} \). Then \(x^-\sqsubseteq p \sqsubseteq x^+\).
Proof
By symmetry, it suffices to prove that \(p\sqsubseteq q\) where we denoted \(q=x^+\). Define \((a,b)=(p\wedge x,p\vee x)\). Note that [a, b] is a modular lattice. Since \(q\succeq x\), the meet \(s=p\wedge q\) exists and satisfies \(s\in [a,p]\). Define \(y=s\vee x\), then \(y\in [s,q]\) and \(p\vee y=b\). Since \(p\sqsupseteq a\sqsubseteq x\), we get \(p\sqsupseteq s\sqsubseteq y\) (using, in particular, Lemma 35). This means that  ,
,  and \(p\diamond q\in [y,q]\subseteq [x,q]\).
and \(p\diamond q\in [y,q]\subseteq [x,q]\).
Note that  and thus
and thus  by convexity of
by convexity of  . The choice of p thus implies that (p, q) is f-extremal. We claim that \(f(p)=f(s)\). Indeed, suppose that \(f(p)<f(s)\). Pair (s, q) is f-extremal by Corollary 67, and thus \(f(p)<f(s)\le f(q)\). Let \(p'\) be an element of I(p, q) with \(f(p')=f(p)\) which is closest element to q. By construction, \(p'\ne q\) and \((p',q)\) is strictly f-extremal. If \(p'\diamond q\ne q\) then \(f(p'\diamond q)<f(q)\) by Lemma 69, and \((p,p\diamond q,p'\diamond q,q)\) is a shortest subpath by Lemma 54. Condition \(p\diamond q\in [x,q]\) thus implies that \(x\preceq p\diamond q\preceq p'\diamond q\preceq q\). Condition \(x\sqsubseteq q\) now gives \(x\sqsubseteq p'\diamond q\), contradicting the choice of q. Thus, we must have \(p'\diamond q=q\). By the choice of \(p'\) we have \(f(p')<f(p'\wedge q)\), so the submodularity inequality for \((p',q)\) gives that \(f(p'\vee q)<f(q)\) where \(p'\vee q\) exists since \(p'\diamond q=q\). Note that \(x\preceq q\preceq p'\vee q\) and
. The choice of p thus implies that (p, q) is f-extremal. We claim that \(f(p)=f(s)\). Indeed, suppose that \(f(p)<f(s)\). Pair (s, q) is f-extremal by Corollary 67, and thus \(f(p)<f(s)\le f(q)\). Let \(p'\) be an element of I(p, q) with \(f(p')=f(p)\) which is closest element to q. By construction, \(p'\ne q\) and \((p',q)\) is strictly f-extremal. If \(p'\diamond q\ne q\) then \(f(p'\diamond q)<f(q)\) by Lemma 69, and \((p,p\diamond q,p'\diamond q,q)\) is a shortest subpath by Lemma 54. Condition \(p\diamond q\in [x,q]\) thus implies that \(x\preceq p\diamond q\preceq p'\diamond q\preceq q\). Condition \(x\sqsubseteq q\) now gives \(x\sqsubseteq p'\diamond q\), contradicting the choice of q. Thus, we must have \(p'\diamond q=q\). By the choice of \(p'\) we have \(f(p')<f(p'\wedge q)\), so the submodularity inequality for \((p',q)\) gives that \(f(p'\vee q)<f(q)\) where \(p'\vee q\) exists since \(p'\diamond q=q\). Note that \(x\preceq q\preceq p'\vee q\) and  . This implies that \(x\sqsubseteq p'\vee q\), contradicting the choice of q. We proved that \(f(p)=f(s)\), and thus \(p=s\) by the choice of p, since (p, s, x) is a shortest subpath.
. This implies that \(x\sqsubseteq p'\vee q\), contradicting the choice of q. We proved that \(f(p)=f(s)\), and thus \(p=s\) by the choice of p, since (p, s, x) is a shortest subpath.
We now know that \(p\sqsubseteq y\sqsubseteq q\) where \(y=b=x\vee p\). Suppose that \(p\not \sqsubseteq q\). Clearly, we have \(p\diamond q\in [y,q]\), \(q\diamond p\in [p,y]\) and \(q\diamond p\preceq y\preceq p\diamond q\). By choice of q we must have \(f(q')\ge f(q)\) for any \(q'\in [p\diamond q,q]\subseteq [y,q]\subseteq [x,q]\). By Lemma 70, there exists \(p'\in [p,q\diamond p]-\{p\}\subseteq [p,y]-\{p\}\) with \(f(p')=f(p)\). This contradicts the choice of p, since \((p,p',y,x)\) is a shortest subpath. \(\square \)
Corollary 74
Element  computed in line 4 of Algorithm 2 satisfies
computed in line 4 of Algorithm 2 satisfies  .
.
Proof
Clearly, any \(y\in \mathcal{L}^+_{x^-}(\Gamma )\cap \mathcal{L}^-_{x^+}(\Gamma )\) satisfies  . The claim now follows directly from Lemma 73. \(\square \)
. The claim now follows directly from Lemma 73. \(\square \)
Lemma 72 and Corollary 74 imply that after k iterations point x in  -SDA satisfies \(x\in \mathop {\mathrm {arg\,min}}\limits f_k\) (via an induction argument). This yields Theorem 22.
-SDA satisfies \(x\in \mathop {\mathrm {arg\,min}}\limits f_k\) (via an induction argument). This yields Theorem 22.
6 VCSP proofs
In this section we prove two results: Theorem 23 (BLP relaxation solves language \(\Phi _\Gamma \) for an extended modular complex \(\Gamma \)) and the hardness direction of Theorem 3. Below we give some background on Valued Constraint Satisfaction Problems (VCSPs) which will be needed for these proofs.
Let us fix finite set D. Let \(\mathcal{O}^{(m)}\) be the set of operations \(g:D^m\rightarrow D\). Operation \(g\in \mathcal{O}^{(m)}\) is called symmetric if \(g(x_1,\ldots ,x_m)=g(x_{\pi (1)},\ldots ,x_{\pi (m)})\) for any tuple \((x_1,\ldots ,x_m)\in D^m\) and any permutation \(\pi :[m]\rightarrow [m]\). A fractional operation of arity m is a probability distribution over \(\mathcal{O}^{(m)}\), i.e. vector \(\omega \in [0,1]^{\mathcal{O}^{(m)}}\) with \(\sum _g \omega (g)=1\). Fractional operation \(\omega \) is called symmetric if all operations in \({{\,\textrm{supp}\,}}(\omega )=\{g\in \mathcal{O}^{(m)}\,|\,\omega (g)>0\}\) are symmetric.
A cost function \(f:D^n\rightarrow {{\overline{{\mathbb R}}}}\) is said to admit \(\omega \) (or \(\omega \) is a fractional polymorphism of f) if
where operation \(g(\cdot )\) is applied componentwise, i.e.
Language \(\Phi \) over D is said to admit \(\omega \) if all functions \(f\in \Phi \) admit \(\omega \). In this case \(\omega \) is called a fractional polymorphism of \(\Phi \).
The expressive power \(\langle \Phi \rangle \) of language \(\Phi \) is defined as the set of all cost functions \(f:D^n\rightarrow {{\overline{{\mathbb R}}}}\) of the form \( f(x)=\min _{y\in D^k} f_\mathcal{I}(x,y) \) where \(\mathcal{I}\) is a \(\Phi \)-instance with \(n+k\) variables. It is known that if \(\Phi \) admits a fractional polymorphism \(\omega \) then \(\langle \Phi \rangle \) also admits \(\omega \).
Definition 75
Language \(\Phi \) on domain D is said to satisfy condition (MC) if there exist distinct \(a,b\in D\) and binary function \(f\in \langle \Phi \rangle \) such that \(\mathop {\mathrm {arg\,min}}\limits f=\{(a,b),(b,a)\}\).
Theorem 76
([34, Theorem 3.4], [25, Theorem 5]) Let \(\Phi \) be a finite-valued language on domain D such that for every \(a\in D\) there exists a unary cost function \(g_a\in \langle \Phi \rangle \) with \(\mathop {\mathrm {arg\,min}}\limits g_a=\{a\}\). If \(\Phi \) does not satisfy (MC) then \(\Phi \) admits a symmetric fractional polymorphism of every arity \(m\ge 2\).
Theorem 77
([25, Theorem 1, Proposition 8]) Let \(\Phi \) be a general-valued language. BLP solves \(\Phi \) if and only if \(\Phi \) admits a symmetric fractional polymorphism of every arity \(m\ge 2\). If this condition holds then an optimal solution of any \(\Phi \)-instance can be computed in polynomial time.
6.1 Proof of Theorem 23
Recall that \(\Phi _\Gamma \) is the language over domain \(D=V_\Gamma \) that consists of all functions \(f:D^n\rightarrow \overline{\mathbb R}\) such that f is L-convex on \(\Gamma ^n\).
Theorem 78
If \(\Gamma \) is an extended modular complex then \(\Phi _\Gamma \) does not satisfy (MC).
Proof
Suppose the claim is false, then there exists an instance \(f:\Gamma \times \Gamma \times \Gamma ^n\rightarrow \overline{\mathbb R}\) of \(\Phi _\Gamma \) with \(n+2\ge 2\) variables such that function \(g:\Gamma \times \Gamma \rightarrow \overline{\mathbb R}\) defined via \(g(x,y)=\min _{z\in \Gamma ^{n}} f(x,y,z)\) satisfies \(\mathop {\mathrm {arg\,min}}\limits g=\{(a,b),(b,a)\}\) for some distinct \(a,b\in \Gamma \). Denote \(A=\mathop {\mathrm {arg\,min}}\limits f\subseteq \Gamma \times \Gamma \times \Gamma ^n\), \(A_{ab}=\{(a,b,z)\,|\,z\in \Gamma ^n\}\) and \(A_{ba}=\{(b,a,z)\,|\,z\in \Gamma ^n\}\). By construction, \(A\subseteq A_{ab}\cup A_{ba}\), \(A\cap A_{ab}\ne \varnothing \) and \(A\cap A_{ba}\ne \varnothing \). By Lemma 48, the subgraph of  induced by set A is connected. Thus, there must exist \(p\in A_{ab}\), \(q\in A_{ba}\) such that
induced by set A is connected. Thus, there must exist \(p\in A_{ab}\), \(q\in A_{ba}\) such that  . By symmetry, we can assume that \(p\sqsubset q\). We have \(p=(a,b,x)\) and \(q=(b,a,y)\) for some \(x,y\in \Gamma ^n\). Condition \(p\sqsubset q\) thus implies that \(a\sqsubset b\) and \(b\sqsubset a\), which is impossible. \(\square \)
. By symmetry, we can assume that \(p\sqsubset q\). We have \(p=(a,b,x)\) and \(q=(b,a,y)\) for some \(x,y\in \Gamma ^n\). Condition \(p\sqsubset q\) thus implies that \(a\sqsubset b\) and \(b\sqsubset a\), which is impossible. \(\square \)
We can finally prove that BLP solves \(\Phi _\Gamma \).
Theorem 79
Let \(\Gamma \) be an extended modular complex. Language \(\Phi _\Gamma \) admits a symmetric fractional polymorphism of every arity \({m\ge 2}\). Consequently, BLP relaxation solves \(\Phi _\Gamma \), and an optimal solution of any \(\Phi _\Gamma \)-instance can be computed in polynomial time.
Proof
If language \(\Phi _\Gamma \) were finite-valued then the claim would immediately follow from Theorems 78 and 76. The main concern will thus be dealing with non finite-valued languages.
Let us define \(\Phi ^\circ _\Gamma =\{f\in \langle \Phi _\Gamma \rangle \,|\,f\hbox { is finite-valued}\,\}\). Since language \(\Phi _\Gamma \) does not satisfy (MC), languages \(\langle \Phi _\Gamma \rangle \) and \(\Phi ^\circ _\Gamma \) also do not satisfy (MC). Clearly, for each \(a\in \Gamma \) language \(\Phi ^\circ _\Gamma \) contains unary function \(g_a\) with \(\mathop {\mathrm {arg\,min}}\limits g_a=\{a\}\), namely \(g_a(x)=\mu (a,x)\). By Theorem 76, \(\Phi ^\circ _\Gamma \) admits a symmetric fractional polymorphism of every arity \(m\ge 2\). Let \(\omega _m\) be such fractional polymorphism. We claim that \(\Phi _\Gamma \) also admits \(\omega _m\). Indeed, consider function \(f:\Gamma ^n\rightarrow \overline{\mathbb R}\) in \(\Phi _\Gamma \). We can assume w.l.o.g. that \(f(x)\ge 0\) for all \(x\in {{\,\mathrm{{\texttt {dom}}}\,}}f\), and \(\mu (x,y)\ge 1\) for distinct \(x,y\in \Gamma \). Define function \(\mu _{n}:\Gamma ^n\times \Gamma ^n\rightarrow \mathbb R\) via \(\mu _n(x,y)=\mu _{\Gamma ^n}(x,y)\). By Theorem 44, \(\mu _n\) is L-convex on \(\Gamma ^n\times \Gamma ^n\), and thus \(\mu _n\in \Phi _\Gamma \). For value \(C>0\) define function \(f_C:\Gamma ^n\rightarrow \mathbb R\) via \(f_C(x)=\min _{y\in \Gamma ^n} (f(y)+C\mu _n(x,y))\), then \(f_C\in \Phi ^\circ _\Gamma \) and thus \(f_C\) admits \(\omega _m\). Clearly, for any \(C>\max _{x\in {{\,\mathrm{{\texttt {dom}}}\,}}f}f(x)\) the following holds: \(f_C(x)=f(x)\) if \(x\in {{\,\mathrm{{\texttt {dom}}}\,}}f\), and \(f_C(x)\ge C\) if \(f(x)=\infty \). By taking the limit \(C\rightarrow \infty \) we conclude that f also admits \(\omega _m\). \(\square \)
6.2 Proof of the hardness direction of Theorem 3
We will use a technique from [26].
Consider language \(\Phi \) on domain D. A pair of elements \((a,b)\in D\times D\) is called conservative if there exists a unary function \(g_{ab}\in \langle \Phi \rangle \) with \(\mathop {\mathrm {arg\,min}}\limits g_{ab}=\{a,b\}\). Let \(\mathcal{S}(\Phi )\subseteq D\times D\) be the set of conservative pairs in \(\Phi \). For a tuple \(p=(a,b)\in \mathcal{S}(\Phi )\), we denote \({\bar{p}}=(b,a)\); clearly, \({\bar{p}}\in \mathcal{S}(\Phi )\). Now consider two tuples \(p=(a,b)\) and \(q=(c,d)\). We say that pair (p, q) is strictly submodular if there exists binary cost function \(f\in \langle \Phi \rangle \) such that
Clearly, if (p, q) is strictly submodular, then (q, p) is also strictly submodular, since function \(f'\) defined via \(f'(x,y)=f(y,x)\) also belongs to \(\langle \Phi \rangle \). We thus say that \(\{p,q\}\) is strictly submodular if (p, q) is strictly submodular (or equivalently, if (q, p) is strictly submodular). Let \(\mathcal{E}(\Phi )\subseteq \left( {\begin{array}{c}\mathcal{S}(\Phi )\\ 2\end{array}}\right) \) be the set of strictly submodular pairs \(\{p,q\}\), and define undirected graph \(\mathcal{G}(\Phi )=(\mathcal{S}(\Phi ),\mathcal{E}(\Phi ))\).
Theorem 80
[26, Theorem 3.2(a) and Lemma 5.1(b)] Suppose that language \(\Phi \) is finite-valued and that, for each \(a\in D\), there exists unary cost function \(g_a\in \langle \Phi \rangle \) with \(\mathop {\mathrm {arg\,min}}\limits g_a=\{a\}\).
- (a):
-
If \(\{p,q\},\{q,r\}\in \mathcal{E}(\Phi )\), then \(\{p,r\}\in \mathcal{E}(\Phi )\).
- (b):
-
If \(\{p,{\bar{p}}\}\in \mathcal{E}(\Phi )\) for some \(p\in \mathcal{S}(\Phi )\), then \(\Phi \) is NP-hard.
Remark 5
In [26] Kolmogorov and Živný formulated Theorem 80 only in the case when \(\Phi \) contains all possible \(\{0,1\}\)-valued unary functions (and thus \(\mathcal{S}(\Phi )=D\times D\)). However, the proofs of the results above use only weaker preconditions stated in Theorem 80.
Note that the graph defined in [26] had an edge \(\{p,q\}\) if and only if our graph \(\mathcal{G}(\Phi )\) has an edge \(\{p,{\bar{q}}\}\). We translated the results from [26] accordingly.
We now apply these results to the generalized minimum 0-extension problem for metric space \((V,\mu )\) and subset \(F\subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \). Let us define the following language over domain \(D=V\):
where unary function \(\mu _a\), \(\mu _{ab}\) are defined via \(\mu _a(x)=\mu (x,a)\) and \(\mu _{ab}(x)=\min \{\mu (x,a),\mu (x,b)\}\). Clearly, we have \(\Phi \subseteq \langle \mathtt{0\hbox {-}Ext}[{\mu ,F}]\rangle \).
Let \(H=H_\mu =(V,E,w)\) be the graph corresponding to \(\mu \). Suppose that H is not F-orientable; our goal is to show that \(\Phi \) is NP-hard. We can assume w.l.o.g. that H is modular, otherwise \(\Phi \) is NP-hard by Theorem 1. Define
Let us introduce relations \(\parallel \), \(\lhd \), \(\approx \) for tuples \(p=(a,b)\) and \(q=(c,d)\) as follows:
-
\(p\parallel q\) if \(p,q\in \vec {E}\) and (a, b, d, c) is a 4-cycle in H;
-
\(p\lhd q\) if \(p\in \vec {E}\), \(q\in \vec {F}\), \(p\ne q\), and (c, a, b, d) is a shortest subpath in H;
-
\(p\approx q\) if at least one of the following holds: (i) \(p\parallel q\); (ii) \(p\lhd q\); (iii) \(q\lhd p\).
Note that relation \(\approx \) is symmetric, and accordingly, \((\vec {E}\cup \vec {F},\,\approx )\) is an undirected graph.
Lemma 81
Let \(p,q \in \mathcal{S}(\Phi )\).
- (a):
-
\(\vec {E}\cup \vec {F}\subseteq \mathcal{S}(\Phi )\).
- (b):
-
If \(p\parallel q\), then \(\{p,q\}\in \mathcal{E}(\Phi )\).
- (c):
-
If \(p\lhd q\), then \(\{p,q\}\in \mathcal{E}(\Phi )\).
- (d):
-
If \(p\approx q\), then \(\{p,q\}\in \mathcal{E}(\Phi )\).
Proof
(a) First, \(\vec {F}\subseteq \mathcal{S}(\Phi )\) holds by the definition of \(\Phi \).
As for \(\vec {E}\), for each \(\{a,b\}\in E\), we construct a function \(g_{ab} \in \langle \Phi \rangle \) by \(g_{ab}(x):= \mu _a(x)+\mu _b(x)\). From the minimality of H, we have \(I(a,b) = \{a,b\}\). We therefore see that \(\mathop {\mathrm {arg\,min}}\limits g_{ab}=\{a,b\}\), and thus, we obtain \((a,b)\in \mathcal{S}(\Phi )\).
(b) Suppose that \(p=(a,b)\in \vec {E}\), \(q=(c,d)\in \vec {E}\), and (a, b, d, c) is a 4-cycle in H. The modularity of H implies that \(\{a,d\}\notin E\); otherwise a, b, d would not have a median. Similarly, \(\{b,c\}\notin E\); otherwise b, d, c would not have a median. By Theorem 6(a), sequences (a, b, d) and (b, d, c) are shortest subpaths in H. This implies that \( \mu (a, c)+\mu (b, d) < \mu (a, d)+\mu (b, c) \). We thereby obtain \(\{p,q\}\in \mathcal{E}(\Phi )\).
(c) Suppose that \(p=(a,b)\in \vec {E}\), \(q=(c,d)\in \vec {F}\), and (c, a, b, d) is a shortest subpath in H. Then \(\mu (a, c)+\mu (b, d) < (\mu (a, c)+\mu (a,b)) + (\mu (a,b)+\mu (b, d))= \mu (b,c) + \mu (a, d)\), and so, we again obtain \(\{p,q\}\in \mathcal{E}(\Phi )\).
(d) We decompose \(p\approx q\) into cases. If \(p\parallel q\), we apply (b). If \(p\lhd q\), we apply (c). If \(q\lhd p\), we utilize \(\{p,q\} = \{q,p\}\) and apply (c) again. We conclude that \(\{p,q\}\in \mathcal{E}(\Phi )\). \(\square \)
We can finally finish the proof of Theorem 3.
We claim that there exists an element \(p\in \vec {E}\cup \vec {F}\) such that \(p,{\bar{p}}\) are connected by a path in \((\vec {E}\cup \vec {F},\,\approx )\). Indeed, if no such p exists, then there exists a mapping \(\sigma :\vec {E}\cup \vec {F}\rightarrow \{-1,+1\}\) with the following properties: (i) if \(q\approx r\), then \(\sigma (q)=\sigma (r)\); (ii) \(\sigma (q)=-\sigma ({\bar{q}})\) for each \(q\in \vec {E}\cup \vec {F}\). Such mapping can be constructed by greedily assigning connected components of graph \((\vec {E}\cup \vec {F},\hspace{0.5pt}\approx )\); the assumption ensures that no conflicts arise. Using the mapping \(\sigma \), we can define an orientation of (H, F) by orienting \(\{a,b\} \in E \cup F\) as \(\hspace{0.5pt}a \!\hspace{0.5pt}\rightarrow \hspace{0.5pt}\! b\hspace{0.5pt}\) if \(\sigma (a,b)=+1\) and as \(\hspace{0.5pt}a \!\hspace{0.5pt}\leftarrow \hspace{0.5pt}\! b\hspace{0.5pt}\) if \(\sigma (a,b)=-1\). Clearly, this orientation is admissible, which contradicts the assumption that H is not F-orientable.
From Theorem 80(a) and Lemma 81, we conclude that \(\{p,\bar{p}\}\in \mathcal{E}(\Phi )\). Theorem 80(b) now gives that \(\Phi \) is NP-hard.
7 Open questions
In this section we state some open problems that we find interesting.
One of the motivations for this work was trying to find the “structure” of tractable finite-valued languages. This leads to the following question.
-
Can it be case that for every tractable finite-valued language \(\Phi \) there exists an extended modular complex \(\Gamma \) such all functions \(f\in \Phi \) are L-convex on \(\Gamma \)? A negative answer could yield new interesting classes of functions that are not yet known in the area of Discrete Convex Analysis.
To simplify the problem, one may a consider a restricted class of languages.
-
Resolve the question above for (a) languages of the form \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\) where \(\mu \) is a metric on V and F is a subset of \(2^V\); (b) languages corresponding to directed metrics, as in [17]. Note that [17] characterized tractable directed metrics on a star, with some complicated fractional polymorphisms. As a special case, it would be interesting to verify whether these tractable classes are captured by the theory developed in this paper. (This question was suggested by an anonymous reviewer).
There are also some open problems concerning L-convex functions on extended modular complexes.
-
Is it possible to show that the normal SDA algorithm terminates after a polynomial number of iterations?
-
As shown in [15, 16], if f an an L-convex function on a modular complex \(\Gamma \) then \(f^*\) is L-convex on \(\Gamma ^*\). Is this also true for extended modular complexes?
-
Let \(\sqsubseteq ,\sqsubseteq '\) be admissible relations for modular complex \(\Gamma \) such that \(\sqsubseteq \) coarsens \(\sqsubseteq '\). Is it true that if function f is L-convex on \((\Gamma ,\sqsubseteq )\) then it is also L-convex on \((\Gamma ,\sqsubseteq ')\)? This is known to hold when \(\Gamma \) is an oriented path and \((\sqsubseteq ,\sqsubseteq ')=({{\mathop {\sqsubseteq }\limits ^{{\tiny \mathtt ~Bp}}}},\preceq )\): any \(L^\natural \)-convex function is submodular on an integer lattice. However, we were unable to prove or disprove it in the general case.
-
Theorem 23 shows that L-convex functions on extended modular complexes admit a binary symmetric fractional polymorphism, however the proof of this fact is non-constructive. Is there a more explicit construction of this polymorphism? As remarked in Section 6 of [15], answering this question might require a further thorough investigation of orientable modular graphs.
Notes
In this result \(\mu \) is implicitly assumed to be rational-valued, since \(\mu \) is treated as part of the input. The same remark applies to later results on VCSPs.
We use a common notation \({\overline{{\mathbb R}}}={\mathbb R}\cup \{\infty \}\), \({\overline{{\mathbb Q}}}={\mathbb Q}\cup \{\infty \}\), \({\overline{{\mathbb Z}}:}={\mathbb Z}\cup \{\infty \}\) where \(\infty \) is an infinity element treated as follows: \(\infty \cdot 0 = 0\), \(x < \infty \) \((x \in {\mathbb R})\), \(\infty + x = \infty (x \in {\overline{{\mathbb R}}})\), \(x \cdot \infty = \infty (a \in {\mathbb R}: a > 0)\). We also denote \({\mathbb R}_+,{\mathbb Q}_+,{\mathbb Z}_+\) to be the sets of nonnegative elements of \({\mathbb R},{\mathbb Q},{\mathbb Z}\), respectively.
Theorems 4 and 5 are not directly applicable to \(\mathtt{0\hbox {-}Ext}[{\mu }]\) since \(\mathtt{0\hbox {-}Ext}[{\mu }]\) is not finite-valued. However, we can get a finite-valued language by replacing functions \(\delta _u:V\rightarrow \{0,\infty \}\) with functions \(\mu _u:V\rightarrow {\mathbb R}\) defined via \(\mu _u(x)=\mu (x,u)\). It is not difficult to show that such transformation does not affect the complexity of \(\mathtt{0\hbox {-}Ext}[{\mu }]\). A similar remark applies to \(\mathtt{0\hbox {-}Ext}[{\mu ,F}]\).
References
Bandelt, H.-J.: Networks with condorcet solutions. Eur. J. Oper. Res. 20, 314–326 (1985)
Bandelt, H.-J., van de Vel, M., Verheul, E.: Modular interval spaces. Math. Nachr. 163, 177–201 (1993)
Birkhoff, G.: Lattice Theory, 3rd edn. American Mathematical Society, (1967)
Blake, A., Kohli, P., Rother, C.: Markov Random Fields for Vision and Image Processing, MIT Press, (2011)
Chalopin, J., Chepoi, V., Hirai, H., Osajda, D.: Weakly modular graphs and nonpositive curvature. Memoirs AMS, 268(1309), (2020)
Chekuri, C., Khanna, S., Naor, J., Zosin, L.: A linear programming formulation and approximation algorithms for the metric labeling problem. SIAM J. Dis. Math. 18(3), 608–625 (2004)
Chepoi, V.: Classification of graphs by means of metric triangles (in Russian). Metody Diskretnogo Analiza 49, 75–93 (1989)
Chuzhoy, J., Naor, J.: The hardness of metric labeling. SIAM J. Comput. 36(2), 498–515 (2006)
Dress, A.W.M., Scharlau, R.: Gated sets in metric spaces. Aequationes Math. 34, 112–120 (1987)
Dvorak, M., Kolmogorov, V.: Generalized minimum 0-extension problem and discrete convexity. arXiv:2109.10203v3, October (2021)
Felzenszwalb, P., Pap, G., Tardos, E., Zabih, R.: Globally optimal pixel labeling algorithms for tree metrics. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2010)
Fujishige, S.: Submodular Funct. Optimiz., 2nd edn. Elsevier, Amsterdam (2005)
Fujishige, S., Murota, K.: Notes on L-/M-convex functions and the separation theorems. Math. Progr. Ser. A 88, 129–146 (2000)
Gridchyn, I., Kolmogorov, V.: Potts model, parametric maxflow and k-submodular functions. In: Proceedings of the 14th IEEE International Conference on Computer Vision (ICCV’13), pp. 2320–2327. IEEE, (2013)
Hirai, H.: Discrete convexity and polynomial solvability in minimum 0-extension problems. Math. Progr. Ser. A 155, 1–55 (2016)
Hirai, H.: L-convexity on graph structures. J. Oper. Res. Soc. Japan 61, 71–109 (2018)
Hirai, H., Mizutani, R.: Minimum 0-extension problems on directed metrics. Discret. Optim. 40, (2021)
Huber, A., Kolmogorov, V.: Towards Minimizing \(k\)-Submodular Functions. In: Proceedings of the 2nd International Symposium on Combinatorial Optimization (ISCO’12), volume 7422 of Lecture Notes in Computer Science, pp. 451–462. Springer, (2012)
Huber, A., Krokhin, A., Powell, R.: Skew bisubmodularity and valued CSPs. SIAM J. Comput. 43(3), 1064–1084 (2014)
Karzanov, A.V.: Minimum 0-extensions of graph metrics. Eur. J. Comb. 19, 71–101 (1998)
Karzanov, A.V.: One more well-solved case of the multifacility location problem. Discret. Optim. 1(1), 51–66 (2004)
Kleinberg, J., Tardos, É.: Approximation algorithms for classification problems with pairwise relationships: metric labeling and markov random fields. J. ACM 49, 616–639 (2002)
Kolmogorov, V.: Submodularity on a tree: Unifying \(l^{\sharp }\)-convex and bisubmodular functions. In: Proceedings of the 36th International Symposium on Mathematical Foundations of Computer Science (MFCS’11), volume 6907 of Lecture Notes in Computer Science, pp. 400–411. Springer, (2011)
Kolmogorov, V., Shioura, A.: New algorithms for convex cost tension problem with application to computer vision. Discret. Optim. 6, 378–393 (2009)
Kolmogorov, V., Thapper, J., Živný, S.: The power of linear programming for general-valued CSPs. SIAM J. Comput. 44(1), 1–36 (2015)
Kolmogorov, V., Živný, S.: The complexity of conservative valued CSPs. J. ACM, 60(2), Article 10 (2013)
Murota, K.: Discrete convex analysis. Math. Progr. 83, 313–371 (1998)
Murota, K.: Discret. Convex Anal. SIAM, Philadelphia (2003)
Murota, K.: On steepest descent algorithms for discrete convex functions. SIAM J. Optim. 14, 699–707 (2003)
Murota, K., Shioura, A.: M-convex function on generalized polymatroid. Math. Oper. Res. 24, 95–105 (1999)
Murota, K., Shioura, A.: Exact bounds for steepest descent algorithms of L-convex function minimization. Oper. Res. Lett. 42, 361–366 (2014)
Murota, K., Tamura, A.: Proximity theorems of discrete convex functions. Math. Progr. Ser. A 99, 539–562 (2004)
Tansel, B.C., Francis, R.L., Lowe, T.J.: Location on networks I II. Manag. Sci. 29, 498–511 (1983)
Thapper, J., Živný, S.: The complexity of finite-valued CSPs. J. ACM (JACM), 63(4), (2016)
van de Vel, M.L.J.: Theory Convex Struct. North-Holland, Amsterdam (1993)
Acknowledgements
We thank the anonymous reviewers for their careful reading of our manuscript and their many insightful comments and suggestions.
Funding
Open access funding provided by Institute of Science and Technology (IST Austria).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors do not have any conflicting interests related to this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dvorak, M., Kolmogorov, V. Generalized minimum 0-extension problem and discrete convexity. Math. Program. (2024). https://doi.org/10.1007/s10107-024-02064-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10107-024-02064-5



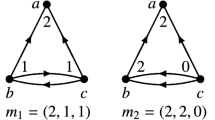
 , and (ii) for every
, and (ii) for every 

 , and (ii) for every
, and (ii) for every 


 -neighbors.
-neighbors. -neighbors.
-neighbors. ;
; ;
; .
. . Similarly, if
. Similarly, if 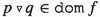 .
. . Similarly, if
. Similarly, if  .
. -SDA algorithm
-SDA algorithm