Abstract
We study finite-time performance of a recently proposed distributed dual subgradient (DDSG) method for convex-constrained multi-agent optimization problems. The algorithm enjoys performance guarantees on the last primal iterate, as opposed to those derived for ergodic means for standard DDSG algorithms. Our work improves the recently published convergence rate of \({{\mathcal {O}}}(\log T/\sqrt{T})\) with decaying step-sizes to \({{\mathcal {O}}}(1/\sqrt{T})\) with constant step-size on a metric that combines sub-optimality and constraint violation. We then numerically evaluate the algorithm on three grid optimization problems. Namely, these are tie-line scheduling in multi-area power systems, coordination of distributed energy resources in radial distribution networks, and joint dispatch of transmission and distribution assets. The DDSG algorithm applies to each problem with various relaxations and linearizations of the power flow equations. The numerical experiments illustrate various properties of the DDSG algorithm–comparison with standard DDSG, impact of the number of agents, and why Nesterov-style acceleration can fail in DDSG settings.












Similar content being viewed by others
References
Ahmadi-Khatir, A., Conejo, A.J., Cherkaoui, R.: Multi-area energy and reserve dispatch under wind uncertainty and equipment failures. IEEE Trans. Power Syst. 28(4), 4373–4383 (2013)
Arnold, M., Knopfli, S., Andersson, G.: Improvement of OPF decomposition methods applied to multi-area power systems. In: 2007 IEEE Lausanne Power Tech, pp. 1308–1313. IEEE, Lausanne, Switzerland (2007)
Bakirtzis, A.G., Biskas, P.N.: A decentralized solution to the DC-OPF of interconnected power systems. IEEE Trans. Power Syst. 18(3), 1007–1013 (2003)
Baldick, R., Chatterjee, D.: Coordinated dispatch of regional transmission organizations: theory and example. Comput. Oper. Res. 41, 319–332 (2014)
Baran, M.E., Felix, F.W.: Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 4(1), 725–734 (1989)
Bazaraa, M.S., Sherali, H.D., Shetty, C.M.: Nonlinear Programming: Theory and Algorithms, 3rd edn. Wiley, New York (2006)
Bertsekas, D.P., Tsitsiklis, J.N.: Parallel and Distributed Computation: Numerical Methods. Athena Scientific, Belmont, MA (1997)
Bhattarai, B.P., de Cerio Mendaza, I.D., Myers, K.S., Bak-Jensen, B., Paudyal, S.: Optimum aggregation and control of spatially distributed flexible resources in smart grid. IEEE Trans. Smart Grid 9(5), 5311–5322 (2018)
Bose, S., Gayme, D.F., Mani Chandy, K., Steven, H.: Low quadratically constrained quadratic programs on acyclic graphs with application to power flow. IEEE Trans. Control Netw. Syst. 2(3), 278–287 (2015)
Boyd, S., Xiao, L., Mutapcic, A., Mattingley, J.: Notes on Decomposition Methods EE364B. Stanford University, Stanford (2015)
Bubeck, S.: Convex optimization: algorithms and complexity. Found. Trends Mach. Learn. 8(3–4), 231–357 (2015)
Cain, M.B., O’Neill, R.P., Castillo, A.: History of optimal power flow and formulations. Federal Energy Regul. Comm. 1, 1–36 (2012)
Cherukuri, A., Cortés, J.: Distributed coordination of DERs with storage for dynamic economic dispatch. IEEE Trans. Autom. Control 63(3), 835–842 (2018)
Dall’Anese, E., Guggilam, S.S., Andrea Simonetto, Yu., Chen, C., Dhople, S.V.: Optimal regulation of virtual power plants. IEEE Trans. Power Syst. 33(2), 1868–1881 (2018)
de Oliveira, W., Sagastizábal, C., Lemaréchal, C.: Convex proximal bundle methods in depth: a unified analysis for inexact oracles. Math. Program. 148(1–2), 241–277 (2014)
Di, W., Lian, J., Sun, Y., Yang, T., Hansen, J.: Hierarchical control framework for integrated coordination between distributed energy resources and demand response. Electr. Power Syst. Res. 150, 45–54 (2017)
Doan, T.T., Bose, S., Nguyen, H.D., Beck, C.L.: Convergence of the iterates in mirror descent methods. IEEE Control Syst. Lett. 3(1), 114–119 (2019)
Dominguez-Garcia, A.D., Hadjicostis, C.N.: Coordination and control of distributed energy resources for provision of ancillary services. In: 2010 1st IEEE International Conference on Smart Grid Communications, pp. 537–542. IEEE, Gaithersburg, MD, USA (2010)
Doostizadeh, M., Aminifar, F., Lesani, H., Ghasemi, H.: Multi-area market clearing in wind-integrated interconnected power systems: a fast parallel decentralized method. Energy Convers. Manag. 113, 131–142 (2016)
Duchi, J.C., Agarwal, A., Wainwright, M.J.: Dual averaging for distributed optimization: convergence analysis and network scaling. IEEE Trans. Autom. Control 57(3), 592–606 (2012)
Erseghe, T.: A distributed approach to the OPF problem. EURASIP J. Adv. Signal Process. 2015(1), 45 (2015)
Falsone, A., Margellos, K., Garatti, S., Prandini, M.: Dual decomposition for multi-agent distributed optimization with coupling constraints. Automatica 84, 149–158 (2017)
Farivar, M., Low, S.H.: Branch flow model: relaxations and convexification—Part I & II. IEEE Trans. Power Syst. 28(3), 2554–2572 (2013)
Frédéric Bonnans, J., Shapiro, A.: Perturbation Analysis of Optimization Problems. Springer, New York (2000)
Gan, L., Li, N., Topcu, U., Low, S.H.: Exact convex relaxation of optimal power flow in radial networks. IEEE Trans. Autom. Control 60(1), 72–87 (2015)
Gharesifard, B., Basar, T., Dominguez-Garcia, A.D.: Price-based coordinated aggregation of networked distributed energy resources. IEEE Trans. Autom. Control 61(10), 2936–2946 (2016)
Grangereau, M., van Ackooij, W., Gaubert, S.: Multi-stage stochastic alternating current optimal power flow with storage: bounding the relaxation gap. Electri. Power Syst. Res. 206, 107774 (2022)
Guannan, Q., Li, N.: Accelerated distributed nesterov gradient descent. IEEE Trans. Autom. Control 65(6), 2566–2581 (2020)
Guo, J., Hug, G., Tonguz, O.: Enabling distributed optimization in large-scale power systems (2016). arXiv:1605.09785
Guo, Y., Bose, S., Tong, L.: On robust tie-line scheduling in multi-area power systems. IEEE Trans. Power Syst. 33(4), 4144–4154 (2018)
Gustavsson, E., Patriksson, M., Strömberg, A.-B.: Primal convergence from dual subgradient methods for convex optimization. Math. Program. 150(2), 365–390 (2015)
Halilbasic, L., Chatzivasileiadis, S., Pinson, P.: Coordinating flexibility under uncertainty in multi-area AC and DC grids. In: 2017 IEEE Manchester Power Tech, pp. 1–6. IEEE, Manchester, UK (2017)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1985)
Huang, Y., Meng, Z., Sun, J., Ren, W.: A unified distributed method for constrained networked optimization via saddle-point dynamics. IEEE Trans. Autom. Control (2023). https://doi.org/10.1109/TAC.2023.3327940
Ji, Y., Tong, L.: Multi-area interchange scheduling under uncertainty. IEEE Trans. Power Syst. 33(2), 1659–1669 (2018)
Ji, Y., Zheng, T., Tong, L.: Stochastic interchange scheduling in the real-time electricity market. IEEE Trans. Power Syst. 32(3), 2017–2027 (2017)
Jinming, X., Tian, Y., Sun, Y., Scutari, G.: Distributed algorithms for composite optimization: unified framework and convergence analysis. IEEE Trans. Signal Process. 69, 3555–3570 (2021)
Kao, H., Subramania, V.: Convergence rate analysis for distributed optimization with localization. In: 2019 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 384–390. IEEE (2019)
Kim, B.H., Baldick, R.: Coarse-grained distributed optimal power flow. IEEE Trans. Power Syst. 12(2), 932–939 (1997)
Lai, X., Xia, Q., Xie, L.: Inter-area power exchange preserving multi-area economic dispatch. In: 2014 IEEE Power & Energy Society General Meeting (PESGM), pp. 1–5. IEEE, National Harbor, MD, USA (2014)
Lai, X., Xie, L., Xia, Q., Zhong, H., Kang, C.: Decentralized multi-area economic dispatch via dynamic multiplier-based lagrangian relaxation. IEEE Trans. Power Syst. 30(6), 3225–3233 (2015)
Larsson, T., Patriksson, M., Strömberg, A.-B.: Ergodic, primal convergence in dual subgradient schemes for convex programming. Math. Program. 86(2), 283–312 (1999)
Lavaei, J., Low, S.H.: Zero duality gap in optimal power flow problem. IEEE Trans. Power Syst. 27(1), 92–107 (2012)
Li, Z., Zeng, B., Zhang, B., Zheng, W.: Decentralized multiarea robust generation unit and tie-line scheduling under wind power uncertainty. IEEE Trans. Sustain. Energy 6(4), 1377–1388 (2015)
Li, Z., Wenchuan, W., Shahidehpour, M., Zhang, B.: Adaptive robust tie-line scheduling considering wind power uncertainty for interconnected power systems. IEEE Trans. Power Syst. 31(4), 2701–2713 (2016)
Li, Z., Wenchuan, W., Zeng, B., Shahidehpour, M., Zhang, B.: Decentralized contingency-constrained tie-line scheduling for multi-area power grids. IEEE Trans. Power Syst. 32(1), 354–367 (2017)
Liang, S., Wang, L.Y., Yin, G.: Distributed smooth convex optimization with coupled constraints. IEEE Trans. Autom. Control 65(1), 347–353 (2020)
Liang, S., Wang, L.Y., Yin, G.: Distributed dual subgradient algorithms with iterate-averaging feedback for convex optimization with coupled constraints. IEEE Trans. Cybern. 51(5), 2529–2539 (2021)
Low, S.H.: Convex relaxation of optimal power flow—part II: exactness. IEEE Trans. Control Netw. Syst. 1(2), 177–189 (2014)
Ma, J.: Recovery of Primal Solution in Dual Subgradient Schemes. Massachusetts Institute of Technology, Cambridge, MA (2007)
Madavan, A.N., Bose, S.: A stochastic primal-dual method for optimization with conditional value at risk constraints. J. Optim. Theory Appl. 190(2), 428–460 (2021)
Mateos-Nunez, D., Cortes, J.: Distributed saddle-point subgradient algorithms with laplacian averaging. IEEE Transactions on Automatic Control 62(6), 2720–2735 (2017)
Necoara, I., Nedelcu, V.: On linear convergence of a distributed dual gradient algorithm for linearly constrained separable convex problems. Automatica 55, 209–216 (2015)
Nedić, A., Ozdaglar, A.: Approximate primal solutions and rate analysis for dual subgradient methods. SIAM J. Optim. 19(4), 1757–1780 (2009)
Nedić, A., Ozdaglar, A.: Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control 54(1), 48–61 (2009)
Nesterov, Y.: Introductory Lectures on Convex Optimization: a Basic Course. In: Applied Optimization, vol. 87. Springer, Boston, MA (2004)
Nesterov, Y., Shikhman, V.: Dual subgradient method with averaging for optimal resource allocation. Eur. J. Oper. Res. 270(3), 907–916 (2018)
Notarnicola, I., Notarstefano, G.: Constraint-coupled distributed optimization: a relaxation and duality approach. IEEE Trans. Control Netw. Syst. 7(1), 483–492 (2020)
Notarstefano, G., Notarnicola, I., Camisa, A.: Distributed optimization for smart cyber-physical networks. Found. Trends Syst. Control 7(3), 253–383 (2020)
Papadaskalopoulos, D., Pudjianto, D., Strbac, G.: Decentralized coordination of microgrids with flexible demand and energy storage. IEEE Trans. Sustain. Energy 5(4), 1406–1414 (2014)
Polyak, B.T.: Introduction to Optimization. Translations Series in Mathematics and Engineering. Optimization Software Publications Division, New York (1987)
Sherson, T., Heusdens, R., Bastiaan Kleijn, W.: On the distributed method of multipliers for separable convex optimization problems. IEEE Trans. Signal Inf. Process. Netw. 5(3), 495–510 (2019)
Simonetto, A., Jamali-Rad, H.: Primal recovery from consensus-based dual decomposition for distributed convex optimization. J. Optim. Theory Appl. 168(1), 172–197 (2016)
Stott, B., Jardim, J., Alsac, O.: DC power flow revisited. IEEE Trans. Power Syst. 24(3), 1290–1300 (2009)
van Ackooij, W., Frangioni, A.: Incremental bundle methods using upper models. SIAM J. Optim. 28(1), 379–410 (2018)
Wang, J., Zhong, H., Lai, X., Xia, Q., Shu, C., Kang, C.: Distributed real-time demand response based on lagrangian multiplier optimal selection approach. Appl. Energy 190, 949–959 (2017)
Wentian, L., Liu, M., Lin, S., Li, L.: Fully decentralized optimal power flow of multi-area interconnected power systems based on distributed interior point method. IEEE Trans. Power Syst. 33(1), 901–910 (2018)
Zhang, B., Tse, D.: Geometry of injection regions of power networks. IEEE Trans. Power Syst. 28(2), 788–797 (2013)
Zhao Yuan and Mohammad Reza Hesamzadeh: Hierarchical coordination of TSO-DSO economic dispatch considering large-scale integration of distributed energy resources. Appl. Energy 195, 600–615 (2017)
Zhao, F., Litvinov, E., Zheng, T.: A marginal equivalent decomposition method and its application to multi-area optimal power flow problems. IEEE Trans. Power Syst. 29(1), 53–61 (2014)
Zhou, X., Dall’Anese, E., Chen, L., Simonetto, A.: An incentive-based online optimization framework for distribution grids. IEEE Trans. Autom. Control 63(7), 2019–2031 (2018)
Acknowledgements
This project was partially supported by grants from the Power Systems Engineering Research Center (PSERC), the US National Science Foundation CPS grant 2038775, JSPS Kakenhi Grant Number JP23K03906, and the National Science Foundation of China under grant 51977115.
Funding
Power Systems Engineering Research Center Grant no. (2038775), Japan Society for the Promotion of Science Grant no. JP23K03906, National Natural Science Foundation of China Grant no. (51977115).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Wim van Ackooij.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Dual Subgradient Methods Cannot Generally be Accelerated
Nesterov-type acceleration relies on smoothness of the objective function. Here, we illustrate why such acceleration is generally untenable in dual subgradient settings. We first present examples where the dual function for constrained optimization problems are nonsmooth. Then, we illustrate through examples how nonsmoothness of the objective function impairs acceleration. Consider an optimization problem of the form

with \({\varvec{\Xi }}\) being positive semidefinite (but not positive definite) and \(\mathbb {X}\) being a convex polyhedral set. This is a quadratic program (QP) that simplifies to a linear program (LP) when \({\varvec{\Xi }}=0\). Associate multipliers \({\varvec{z}} \ge 0\) with \({\varvec{A}}\varvec{x} \le \varvec{b}\). Then, the dual function for the problem in (51) is given by

With parameter choices

we plot \({{\mathcal {D}}}({\varvec{z}})\) with \({\varvec{\Xi }} = 0\) and \({\varvec{\Xi }} = \mathop {\text {diag}}\left( 24, 26, 0 \right) \), respectively, in the left and right of Fig. 10. The primal and dual optimum is \({{\mathcal {P}}}^\star = {{\mathcal {P}}}^\star _{D} = 2.43\) for the QP and 2.30 for the LP.
Illustrations of nonsmooth \({{\mathcal {D}}}({\varvec{z}})\) on top and a slice \({{\mathcal {D}}}(\cdot , z_2^\star )\) on the bottom for (51) with parameters in (53). The plots on the left are obtained with \({\varvec{\Xi }} = 0\) and on the right with \({\varvec{\Xi }} = \mathop {\text {diag}}\left( 24, 26, 0 \right) \)
\({{\mathcal {D}}}\) in Fig. 10 is nonsmooth. One might expect that for QP with \({\varvec{\Xi }} \ne 0\), \({{\mathcal {D}}}\) might be smooth. Indeed with positive definite \({\varvec{\Xi }}\), \({{\mathcal {D}}}\) becomes smooth, per [53, Lemma 2.2] or [6, Theorem 6.3.3]. Smoothness can no longer be guaranteed, when \({\varvec{\Xi }}\) is only positive semidefinite, as evidenced by Fig. 10.
To demonstrate the impact of nonsmoothness on acceleration, consider the problem
With \({\varvec{x}_{\text {C}}}= 0\), f is minimized at the origin. If \(\lambda =0\), then f is smooth. For \(\lambda >0\), f is nonsmooth at the origin. With \({\varvec{x}_{\text {C}}}\ne 0\), f is again smooth with \(\lambda = 0\). However, with \(\lambda > 0\), f is nonsmooth at the origin, but not at the optimum of f.
We compare (sub)gradient descent, i.e., \(\varvec{x}(t+1) = \varvec{x}(t) - \eta \nabla f(\varvec{x}(t))\), with an accelerated variant described in Algorithm 4 on (54).
Accelerated Gradient Descent adopted from [71], Sect. 3.7.2
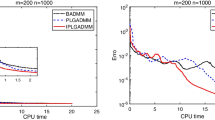
We start both algorithms at (0.05, 0.05) with \(\eta = 0.003\). For accelerated (sub)gradient descent (AGD), we also set \(\alpha (1) = 0\). The plot on the left side of Fig. 11 shows the progress of subgradient descent (SGD) and AGD on (54) with \({\varvec{x}_{\text {C}}}= 0\). Note that when \(\lambda = 0\), i.e., when f is smooth, AGD outperforms SGD. However, when \(\lambda = 0.01\) and f is nonsmooth at the optimum, AGD performs better initially, but both algorithms oscillate around the optimum with similar errors, eventually.
In the right subgraph of Fig. 11, we compare SGD and AGD under the same settings, but with \({\varvec{x}_{\text {C}}}= (0.1,0.1)\). Note that AGD now performs better than SGD with zero and nonzero \(\lambda \). That is, when the nonsmoothness is away from the optimum, AGD can accelerate convergence to the optimum locally, as long as the iterates remain within a region around the optimum where the function is locally smooth.
Comparison of SGD and AGD on (54) with \({\varvec{x}_{\text {C}}}=0\) on the left and with \({\varvec{x}_{\text {C}}}=(0.1, 0.1)\) on the right
Appendix B: Simulation Details for Sections 4, 5 and 6
Network data were obtained from MATPOWER 7.1.
1.1 Appendix B1: Data for Solving \({{\mathcal {P}}}_1\)
The multi-area power system considered in Section 4 is illustrated in Figure 1. The 118-bus networks were modified as follows. Tie-line capacities were set to 100MW and their reactances were set to 0.25p.u. Capacities of transmission lines internal to each area were set to 100MW. All loads and generators at boundary buses were removed. Quadratic cost coefficients were neglected and the linear cost coefficients \({\varvec{c}}_j\) of the generators were perturbed to \(\widetilde{{\varvec{c}}}_j := {\varvec{c}}_j \circ \left( 0.99 + 0.02 {\varvec{\xi }}_j \right) \), for \(j = 1,\ldots ,N\), where entries of \({\varvec{\xi }}_j\) are independent \({{\mathcal {N}}}(0,1)\) (standard normal) variables. All phase angles were restricted to \([-\frac{\pi }{6}, \frac{\pi }{6}]\).
1.2 Appendix B2: Data for Solving \({{\mathcal {P}}}_2\)
The 4-bus network considered in Section 5, shown in Figure 6, is modified from the IEEE 4-bus network as follows. The branch joining buses 1 and 4 was altered to connect buses 3 and 4. We enforced squared current flows as \(\ell _{j,k} \in [0, 200]\) Amp\(^2\), real and reactive branch power flows as \(P_{j,k} \in [-1, 1]\) MW and \(Q_{j,k} \in [-1, 1]\) MVAR, respectively. DER generators were added at buses 2, 3 and 4. Bus 1 defined the T &D interface. Generation capacities were fixed to [0, 1] MW and \([-1, 1]\) MVAR. Generation costs were \(\alpha _{pj} (p^G_j)^2 + \beta _{pj} p^G_j + \alpha _{qj} (q^G_j)^2\) with coefficients in Table 2.
For the IEEE 15-bus system shown in Figure 5, we modified the branch flow limits to mirror those for the 4-bus system. We added 7 distributed generators at buses 5, 7, 8, 10, 13, 14, 15, where bus 1 is the T &D interface, all with capacities [0, 0.2] MW and \([-0.2, 0.2]\) MVAR. Generation costs were similar to the 4-bus network with coefficients in Table 3.
We randomized the real and reactive power demands at each change point by scaling each (real/reactive) load by \(\left[ \omega + (\omega ' - \omega ) \xi \right] \), where \(\xi \sim {{\mathcal {N}}}(0,1)\). Parameters \((\omega , \omega ')\) were varied at the change points in the sequence (0.70, 1.30), (0.80, 1.20), (0.85, 1.15), (0.75, 1.20), (0.95, 1.05). The experiment was initialized with default loads from MATPOWER.
1.3 Appendix B3: Data for Solving \({{\mathcal {P}}}_3\)
In Section 6, for the 204-bus system in Figure 7, the 6-bus transmission network was modified as follows. All branch capacities are set to 5MW. All real and reactive generation capacities were set to [0, 5]MW and \([-5, 5]\) MVAR, respectively. We considered \({P}_\ell ^D + j Q_\ell ^D = (4 + j 4) \text {[MVA]}\) at each bus \(\ell = 1,\ldots ,6\). Generation costs were similar to the 4-bus network with coefficients in Table 4.
For all 33-bus distribution networks, all branch capacities were set to 4 MW. Four DER generators were added at buses 18, 22, 25 and 33. Bus 1 is the T &D interface. Again, we considered generation costs as for \({{\mathcal {P}}}_2\) but with coefficients \({\varvec{\alpha }}_{p\ell } = 5 \circ \left( 0.9 + 0.1 {\varvec{\xi }}_\ell \right) \), \({\varvec{\beta }}_{p\ell } = 20 \circ \left( 0.9 + 0.1 {\varvec{\xi }}'_\ell \right) \) and \({\varvec{\alpha }}_{q\ell } = 3 \circ \left( 0.9 + 0.1 {\varvec{\xi }}''_\ell \right) \) for \(\ell = 1,\ldots ,n^{\text {tran}}\), where all entries of \({\varvec{\xi }}_\ell \), \({\varvec{\xi }}'_\ell \), \({\varvec{\xi }}''_\ell \) are drawn from \({{\mathcal {N}}}(0,1)\). Real and reactive power demands in the distribution networks were randomized similarly to that for \({{\mathcal {P}}}_2\) with \(\omega =0.9\) and \(\omega '=1.1\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, H., Bose, S., Nguyen, H.D. et al. Distributed Dual Subgradient Methods with Averaging and Applications to Grid Optimization. J Optim Theory Appl (2024). https://doi.org/10.1007/s10957-024-02385-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10957-024-02385-7