Vegetation effects on radiation-induced natural convection in sloping water bodies

Abstract

In this work, vegetation effects on the characteristics of radiation-induced natural convection (isotherms, circulation patterns, exchange flow rate) in sloping water bodies are investigated numerically. The water body consists of (a) a sloping vegetated region (with a bottom slope equal to 0.1) and (b) a deep region with a horizontal bottom. The vegetation of porosity 0.85 (typical of aquatic plants found in lakes) has a length equal to the length of the sloping region. It can block (totally or partially) the radiation and as a result a non-uniform (differential) heating is developed along the free surface of the water body. The Volume-Averaged Navier–Stokes equations together with the Volume-Averaged Energy equation are solved numerically in the vegetated region. The radiation-induced natural convection in a water body with only a sloping region (with no vegetation) is also considered for validation purposes since numerical and scaling analysis results are available in literature. The results indicate significant vegetation effects on the thermal and flow patterns especially for vegetation which blocks completely surface heating.

1 Introduction

Natural convection in sloping water bodies (lakes, reservoirs, wetlands) can occur when surface waters are heated or cooled with the same rate [1,2,3,4]. The uniform cooling or heating along the free surface and the increasing water depth of the sloping water body, result in a more rapid cooling or heating of the shallow waters than that of the deep waters [5,6,7,8,9,10,11]. When cooling occurs, the generated horizontal temperature density gradient can drive an offshore-onshore exchange flow (large-scale overturning circulation), also known as “thermal siphon” [12]. The latter increases the water exchange between nearshore and offshore waters, which in turn affects the ecological characteristics of the water body [13]. In contrast, the more rapid warming of the shallow waters than that of the deep waters, due to surface heating, results in an onshore-offshore exchange flow with a large-scale circulation of opposite rotation in comparison with that of cooling. Natural convection in a triangular enclosure, induced by absorption of radiation, was studied by Lei and Patterson [5, 14] and Mao et al. [9] using numerical modeling and scaling analysis. The scaling analysis separates the entire flow domain into different sub-regions with distinct flow and thermal features. Four possible flow scenarios are identified depending on the bottom slope and the maximum water depth (i) shallow waters with relatively large bottom slope, (ii) deep waters with relatively large bottom slope, (iii) shallow waters with relatively small bottom slope and (iv) deep waters with relatively small bottom slope. For each flow scenario the flow domain may be composed of multiple sub regions with distinct thermal and flow features depending on the Rayleigh number [9].

Vegetation effects on natural convection, induced by surface heating due to radiation, have been studied for waterbodies of constant water depth with emphasis on the development of the horizontal convective currents, near the free surface, due to the non-uniform surface heating of the vegetated and non-vegetated regions of the waterbody [15,16,17,18,19]. The vegetation can block (totally or partially) the heating and as a result a non-uniform (differential) heating is developed along the free surface of the waterbody. Horizontal convective currents are developed [2], which are affected by the vegetation porosity φ and permeability k_p.

Coates and Patterson [15] studied the unsteady natural convection in a rectangular water body which was heated by radiation entering through the half free surface. The other half was opaque, simulating thick floating vegetation mats, with no radiation entering the water body. The differential heating induces a convective exchange flow with substantial velocities which may affect the ecology and water quality of waterbodies. Coates and Ferris [16] showed experimentally that shading from floating vegetation of limited thickness can generate an exchange flow. However, the flow was displaced downward, beneath the vegetation due to its low porosity. Lövstedt and Bengston [17] measured in the field the density-driven currents between reed belts and open water in the shallow Lake Krakesjon. Such currents, due to the differential heating of surface waters, have maximum velocities up to 1.5 cm/s for a net radiation at the free surface being 85% lower within the region with Phragmites australis than that in the open non-vegetated area. Zhang and Nepf [18] experimentally examined the impact of rooted emergent vegetation for which the vegetation (solid cylinders) extends over the full depth of the half waterbody and blocks completely the radiation at its top surface. Also, a scaling analysis revealed the expected flow regimes and the associated velocity scales. Papaioannou and Prinos [19] numerically investigated the exchange flow produced experimentally by Zhang and Nepf [18] using one-waveband and three-waveband radiation absorption models. They extended the calculations for vegetation porosity less than that used in the experiments covering a range of porosities from 0.75 to 0.97. They found that the three-waveband radiation model performs better in predicting the temperature increase due to the motion of the horizontal convective currents.

The vegetation presence in the shallow nearshore region of a sloping water body and its effect on natural convection induced by absorption of radiation has been investigated numerically by Lin and Wu [20]. The sloping water body had a triangular shape with a very small slope (equal to 10⁻⁵) while a periodic radiation flux at the water surface was used, assuming that was uniformly distributed over the local water depth. Using asymptotic solutions, they determined the effect of vegetation shading (blockage), during surface heating, on the exchange flow rates and the general circulation in a sloping water body. The asymptotic solutions were able to provide reasonable estimates of horizontal velocity and exchange flowrates, however they ignored the non-linear terms of the governing equations, excluded the flow instabilities, and limited the vegetation density.

In this work a two-dimensional water body model, of composite shape, is considered. It consists of (a) a region with a slope S_o and length L_s and (b) another region with horizontal bottom (deep region) and length L_h. The vegetation is present in the sloping region and its effect on natural convection, induced by radiation, is investigated numerically, without major simplifications as in [20], for the first time. Also, the slope S_o, equal to 0.1, is relatively large, found in alpine and peri-alpine lakes [21], in contrast with small slopes used previously [20]. The unsteady Volume-Averaged Navier–Stokes (VANS) equations are solved in conjunction with the unsteady Volume-Averaged equation in the vegetated region, using the Boussinesq approach [11]. The averaging of the Navier–Stokes (NS) equations and the energy equation is based on the method of Volume Averaging [22]. In the non-vegetated region these equations are simplified to the classical NS and Energy equations.

Initially, the natural convection, induced by absorption of radiation, in a water body with only the sloping region (triangular shape) is investigated for validation purposes. Numerical and scaling analysis results of Lei and Patterson [5, 14] and Mao et al. [9] are available for comparison purposes.

The water body with the two regions, as described previously, with and without vegetation in the sloping region is considered next. The water body with no vegetation is heated from the top free surface with a uniform flux I_o. With a vegetated sloping region, a thermal flux I_o is applied at the top free surface of the deep region while a reduced flux I_v, equal to φI_o, is applied in the region with vegetation (the upper part of the emergent vegetation blocks 15% of the incoming radiation). Finally, a water body with vegetation in the sloping region which completely blocks the incoming radiation is considered. In this case, a strong differential heating is applied at the top surface, the deep region is heated faster than the sloping region shaded by the vegetation and the large-scale circulation in the quasi-steady regime is of opposite rotation to that in water body with no vegetation.

2 Conceptual model and numerical procedure

2.1 Conceptual model

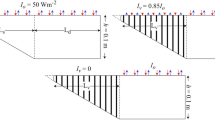
A two-dimensional model of a water body with two regions, as presented before, is considered (Fig. 1). In the same figure the water body with one sloping region is shown which is used for validation purposes against numerical results of Mao et al. [9]. Previous studies [1] have shown that a two-dimensional simulation can adequately reproduce the three-dimensional nature of the flow. The slope S_o is equal to 0.1 while L_s and L_d have the same values (= 1.0 m). The deep region has a water depth h = 0.1 m. The vegetation, with porosity φ = 0.85, is present in the sloping region with length L_v equal to L_h. The Rayleigh number Ra, based on radiation flux I_o equal to 5.8 Wm⁻² and h, is set equal to 1.4 × 10⁷ ($Ra = \frac{{g\beta I_{o} h^{4} }}{{vk^{2} \rho_{o} C_{p} }}$, g = acceleration due to gravity, β = thermal expansion coefficient, ρ_ο = initial water density, C_P = specific heat of water, v = kinematic viscosity, k = thermal diffusivity). The Prandtl number Pr (= ν/k) is equal to 7.0. The values 5.8 (Fig. 1a–c) and 0.58 Wm⁻² (Fig. 1d) for I_o are relatively low, however they were used for having the same values of Ra number as those of [9] for comparison purposes.

Fig. 1

Water body geometry with and without vegetation

The adopted Cartesian coordinate system starts at the left bottom point of the model. The (a) geometry is a non-vegetated case with radiation intensity I_o equal to 5.8 W/m² and Ra number equal to 1.4 × 10⁷. The absorption coefficient η is set equal to 6.2 m⁻¹. The maximum water depth h is less that the penetration depth of the solar radiation (h < η⁻¹) and hence the water body is considered shallow. The vegetated region, with porosity φ = 0.85 and length L_v = L_s, is heated with intensity I_v equal to 0.85 I_o and 0.0 for the (b) and (c) configurations respectively.

For the above-mentioned values of S_o, h, η and Ra, the following inequalities are valid $S_{o} > {\text{Ra}}_{c}^{ - 0.5} , \, h\eta \, < \,4.0{\text{ and Ra}}\, > \,{\text{Ra}}_{c}^{3} S_{o}^{4} e^{\eta h} \,$(Ra_c = critical Ra number, equal to 1106.5, [23]) and hence, in the quasi–steady regime, the sloping region, with no vegetation, is expected to have three sub-regions (1) Region I-indistinct, conductive, (2) Region II-distinct, stable conductive and (3) unstable conductive [9]. Although these regions are for a water body of triangular shape, they are also found in the sloping region of a composite water body since the second region (flat basin) does not affect the circulation patterns.

2.2 Governing equations

For the numerical simulation, the unsteady VANS equations are solved (Eqs. 1 and 2 in conjunction with the unsteady VAE equation (Eq. 3) in the vegetated region, using the Boussinesq approach. The derivation of these equations is based on the method of volume averaging [22] and is presented in detail by [24,25,26,27]. In the non-vegetated region these equations are simplified to the classical NS and Energy equations. These equations are shown below:

$$ \frac{{\partial \left\langle {U_{i} } \right\rangle^{f} }}{{\partial x_{i} }} = 0 $$

(1)

$$ \frac{{\partial \left\langle {U_{i} } \right\rangle^{f} }}{\partial t} + \left\langle {U_{j} } \right\rangle^{f} \frac{{\partial \left\langle {U_{i} } \right\rangle }}{{\partial x_{j} }}^{f} = - \frac{1}{{\rho_{o} }}\frac{\partial \left\langle P \right\rangle }{{\partial x_{i} }}^{f} + \frac{\partial }{{\partial x_{j} }}\left[ {v\left( {\frac{{\partial \left\langle {U_{i} } \right\rangle^{f} }}{{\partial x_{j} }} + \frac{{\partial \left\langle {U_{j} } \right\rangle }}{{\partial x_{i} }}^{f} } \right)} \right] + g\beta \left( {\left\langle T \right\rangle^{f} - \left\langle {T_{o} } \right\rangle^{f} } \right) + F_{i} $$

(2)

$$ \frac{\partial \left\langle T \right\rangle }{{\partial t}}^{f} + \left\langle {U_{j} } \right\rangle^{f} \frac{\partial \left\langle T \right\rangle }{{\partial x_{j} }}^{f} = \frac{\partial }{{\partial x_{j} }}\left[ {k\left( {\frac{\partial \left\langle T \right\rangle }{{\partial x_{j} }}^{f} } \right)} \right] + < S_{h} >^{f} $$

(3)

where U_i = velocity in the direction i, P = pressure, T, T_o = fluid temperature and initial temperature respectively, F_i = resistance term due to vegetation and S_h = heat source term determining the absorption of the solar radiation by the water body.

The symbols <  > and <  > ^f indicate the superficial and the intrinsic volume average of a parameter A (scalar, vector, or tensor) respectively which are defined as:

$$ \left\langle A \right\rangle = \frac{1}{V}\int\limits_{{V^{f} }} {AdV} {\text{ and }}\left\langle A \right\rangle^{f} = \frac{1}{{V_{f} }}\int\limits_{{V^{f} }} {AdV} $$

(4)

where V_f is the fluid volume contained in a volume V. The latter consists of a horizontal slab, extensive enough to eliminate plant-to-plant variations, but thin enough to preserve the characteristic variation of properties in the vertical dimension.

The term F_i, due to vegetation, is given by the Darcy–Forchheimer equation which includes linear and non-linear forces using porous media characteristics (e.g., vegetation permeability k_p):

$$ F_{i} = - \varphi \frac{v}{{k_{p} }}\left\langle {U_{i} } \right\rangle - \varphi^{2} \frac{{C_{f} }}{{\sqrt {k_{p} } }}\left\langle {U_{i} } \right\rangle \left| {\left\langle {U_{i} } \right\rangle } \right| $$

(5)

where φ = vegetation porosity, k_p = vegetation permeability (m²) and C_f = dimensionless empirical coefficient. The permeability k_p and the dimensionless coefficient C_f are determined by the following Eqs. (6) and (7) given by [28, 29]:

$$ k_{p} = \frac{{d_{50}^{2} \varphi^{3} }}{{a_{1} (1 - \varphi )^{2} }} $$

(6)

$$ C_{f} = b_{1} \frac{1 - \varphi }{\varphi }\frac{{\sqrt {k_{p} } }}{{d_{50} }} $$

(7)

where d₅₀ is the grain diameter, a₁ and b₁ are empirical coefficients. When the porous medium consists of cylinders then d₅₀ is equal to 1.5 d (d is the diameter of the cylinders [28]). The empirical coefficients a₁ and b₁ take different values, depending on the type and the length scale of the porous medium [26]. For φ = 0.85, d₅₀ = 9.0 mm, α₁ = 1000 and b₁ = 1.1 the values for C_f and k_p are calculated as: C_f = 0.484, k_p = 5.04 × 10⁻⁶ m².

The term S_h is given by the following:

$$ S_{h} = I\eta e^{ - \eta (h - y)} $$

(8)

where I = I_o or I_v, η = attenuation coefficient (= 6.2 m⁻¹).

The boundary conditions are defined as follows: (a) The left tip on Fig. 1 is cut off at x = 1.6 cm for avoiding a singularity and a side wall is assumed there which has a height 1.6 mm and is rigid, non-slip and adiabatic. (b) The side wall in the deep region is also assumed to be rigid non-slip and adiabatic. (c) The bottom of the sloping and the horizontal region is also rigid, non-slip and the following thermal flux is applied, assuming that the radiation absorbed by the boundary is conducted back into the fluid [5]:

$$ \frac{{\partial {\rm T}}}{\partial n} = - \frac{I}{{k\rho_{o} C_{p} }}e^{ - \eta (h - y)} \, $$

(9)

where n direction normal to the bottom boundary. (d) The water surface is assumed to act as a symmetry axis $\left( {\frac{\partial u}{{\partial y}} = 0,{\text{ v}}\,{ = }\,{0}} \right)$ and the applied thermal boundary condition is $\frac{\partial T}{{\partial y}} = 0$. Initially, the water body has a temperature T_o = 293.15 K and is motionless.

2.3 Numerical procedure and mesh dependency tests

The Fluent 15.0.7 CFD code is applied for numerical computations using a control volume technique. The extra source term F_i is introduced to the initial equations using User Defined Functions (UDF) based on C++ code. The computational domain is divided into finite control volumes on which the governing equations are integrated. The Gambit program is used for mesh generation. The segregated solution method is used, and the velocity–pressure coupling is achieved with the SIMPLE algorithm. The PRESTO scheme is used for discretizing the pressure equation (continuity equation), while the QUICK scheme is used for the momentum and the energy equations [30]. The time step is sufficiently small such that the Courant–Friedrichs–Lewy condition for numerical stability is satisfied.

For the triangular water body, three different meshes of 1000 × 100, 2000 × 200 and 4000 × 400 were tested for examining the solution dependence on the grid spacing. The time step is set equal to 0.1 s based on the smallest nearshore cell. The total simulation time is up to 16,000 s which is sufficient for establishing quasi-steady flow for the cases considered. The grid size in the y direction was smaller in the vicinity of the top and bottom boundaries while it was uniform in the x direction. The smallest nearshore cell, adjacent to the top and bottom boundary, was 1.0 mm × 0.16 mm, 0.5 mm × 0.08 mm and 0.25 mm × 0.04 mm for the three meshes while the biggest one, in the deep section of h = 0.1 m, was 1.0 mm × 1.4 mm, 0.5 mm × 0.7 mm and 0.25 mm × 0.35 mm. The grid resolution (Δx, Δy) for the three meshes was compared with the Batchelor microscale, $\eta_{b} = \Pr^{ - 1/2} (\nu^{3} /\varepsilon )^{1/4}$(ε = local rate of kinetic energy dissipation) which was calculated after the end of the simulations and its minimum value was found equal to 0.485 mm. The last two meshes have $\Delta x_{\max } /\eta_{b} \le 0.59{\text{ and }}\Delta y_{\max } /\eta_{b} \le 0.82 \,$ which satisfy the criterion $\left[ {\Delta x,\Delta y} \right]_{\max } /\eta_{b} \le \pi$ proposed by [31] and used by [32].

Figures 2 and 3 show the effect of grid size on the contours of ΔΤ/(I_oh/κ) and ψ/(ρ_οhk) in the quasi-steady regime for the triangular water body (Ra = 1.4 × 10⁶). All contours are quite similar with the two finer meshes to give closer results for both temperature and stream function. The three sub-regions, as predicted by scaling analysis of [9], are shown clearly. In the nearshore region (x/h < 0.8) the isotherms are almost vertical indicating that conduction is dominant, and the thermal boundary layer is indistinct and stable, in the middle region (0.8 < x/h < 5.0 the heat transfer is dominated by stable convection and the thermal boundary layer is distinct and stable and for x/h > 5.0 unstable convection is dominant. The scaling analysis [9] indicates that the lines at x_o/h = 0.924 and x₁/h = 5.75 separate the three regions while the computed results by the two finer grids show that these two lines are at shorter distances from the shore (x_o/h = 0.8 and x₁/h = 5.0).

Fig. 2

Effect of grid size on the isotherms (ΔΤ//(I_oh/κ)) in the quasi-steady regime (Ra = 1.4 × 10⁶)

Fig. 3

Effect of grid size on the streamlines (ψ/ρ_οhk) in the quasi-steady regime (Ra = 1.4 × 10⁶)

The dashed and solid lines show clockwise and anticlockwise rotation respectively.

For the composite water body, the previously used meshes for the triangular water body were increased to 2000 × 100, 4000 × 200, and 8000 × 400 respectively due to the attached deep region of horizontal bottom with length equal to that of the sloping region. For these three meshes the effect of the grid size on the isotherms and the streamlines was investigated as before. For the sake of brevity this effect on velocity distribution at three verticals along the sloping region of the water body is shown in Fig. 4. A quasi-steady regime has been established in the water body for Ra = 1.4 × 10⁷. The velocity distribution is the same for the three meshes at x/h = 2.0 and 6.0 while there is a small difference between the coarser mesh and the other two meshes at x/h = 10.0.

Fig. 4

Effect of grid size on velocity distribution at three verticals along the inclined region of the water body (Ra = 1.4 × 10⁷)

Also, for the temperature distribution (not shown here) there is a small difference between the 2000 × 100 mesh and the other two meshes at x/h = 10.0. Based on the above the second mesh was used for both the triangular and the composite water body.

2.4 Model validation

Initially, results are presented and analysed for the sloping water body without the flat region and with no vegetation for validation purposes. They are compared with respective numerical and scaling analysis results of [3].

The variation of dimensionless horizontal heat transfer rate, Η(x)/(I_o/ρ_oC_p), by conduction and convection, averaged over the local water depth, with time t/(h²/k) is shown in Fig. 5 at two locations x/h = 1.5 and 4.0 together with the numerical results of [9]. The heat transfer rate H(x) is determined from the following Eq. (10):

$$ H(x) = \frac{1}{{S_{o} x}}\int\limits_{{S_{o} x}}^{{h - S_{o} x}} {\left( {U_{x} (T - T_{avg} ) - k\frac{{\partial (T - T_{avg} }}{\partial x}} \right)dy} $$

(10)

where U_x is the velocity component in the x-direction and T_avg is the average temperature of the water body. The results indicate good agreement for both the conductive and convective heat transfer rates between the present numerical results and those of [9].

Fig. 5

Variation of heat transfer rate with time in the triangular water body a x/h = 1.5, b x/h = 4.0

Figure 6 shows the temperature difference ΔΤ (= T − T_o), made dimensionless with I_oh/κ, at five characteristic times t* (= t/(h²/k)) 0.143 × 10⁻² (100 s), 1.43 × 10⁻² (1000 s), 7.14 × 10⁻² (5000 s) 14.28 × 10⁻² (10,000 s) and 21.42 × 10⁻² (15,000 s). At the first two time instants (t* = 1.43 × 10⁻³ and 1.43 × 10⁻²) the developing thermal boundary layer near the inclined bottom is stable everywhere while instabilities start to develop at a specific location when the time needed for the thermal flow to become unstable, t_B ($t_{B} = ({{Ra_{c} } \mathord{\left/ {\vphantom {{Ra_{c} } {Ra}}} \right. \kern-0pt} {Ra}})^{0.5} (h^{2} /k)e^{{S_{o} \eta x/2}}$) is less than the time scale for the steady state of the thermal boundary layer t_c ($t_{C} = x^{2/3} e^{{S_{o} \eta x/3}} Ra^{ - 1/3} (h^{4/3} /k)$).

Fig. 6

Contours of (T − T_o/(I_oh/κ)) for surface heating due to radiation (Ra = 1.4 × 10⁶)

Based on these two scales the thermal boundary layer becomes initially unstable at x/h = 5.75 where t_B < t_C (2379.1 s < 2384 s) and finally at x/h = 10.0 where t_B < t_C (2680.7 s < 3570.0 s). Hence, at t* equal to 3.83 × 10^–2 (2680.7 s) instabilities occur from 5.75 to 10.0.. The isotherms, after some time, indicate a quasi-steady regime with three sub-regions (a) an indistinct conductive nearshore region, (b) a distinct, stable convective middle region and (c) an unstable convective deep region. The length of each sub-region is calculated based on the scaling analysis of [9] and is compared with the numerical results of Figs. 2 and 6 (t* = 0.2145).

As stated before, the comparison indicates slightly longer unstable convective region in comparison with that of the scaling analysis. It should be noted that the time scale t_c estimated along the sloping region is everywhere less than (kη²)⁻¹ which is the time scale for the switch of the dominant heating mode due to bottom flux to direct absorption of radiation. Hence, during the whole phenomenon the bottom heating dominates.

The streamlines in Fig. 7 indicate a clockwise large circulation for the whole time with smooth streamlines initially and bulged streamlines with hot plumes appearing in the unstable convective region and convective cells developing in the middle of this region.

Fig. 7

Streamlines (ψ/ρ_οhk) for surface heating due to radiation (Ra = 1.4 × 10⁶). The dashed and solid lines show clockwise and anticlockwise rotation respectively

3 Analysis of results

In this section numerical results (temperatures, streamlines, exchange flow rates) for the water body with the flat deep section are presented and analysed. The Ra number is equal to 1.4 × 10⁷.

Figure 8 shows the temperature difference ΔΤ (= T − T_o), made dimensionless with I_oh/κ, at five characteristic times t* (= t/(h²/k)) 0.0143 (1000 s), 0.0428 (3000 s), 0.0714 (5000 s), 0.2142 (15,000 s) and 0.4283 (30,000 s) for the composite water body with no vegetation.

Fig. 8

Contours of (T − T_o/(I_oh/κ)) for Ra = 1.4 × 10⁷ (water body with no vegetation)

At the first three time instants (t* = 0.0143, 0.0428 and 0.0714) the isotherms and the streamlines (ψ/ρ_οhk) (Figs. 8 and 10 respectively) show the development of a thermal boundary layer at the waterbody bottom, due to the thermal flux boundary condition imposed and the transformation of opposing rolls, appearing initially in the sloping region, to a large scale circulation pattern which is extended from the very shallow part of the sloping region up to the side wall of the deep, flat region.

Subsequently (t* = 0.2142 (15,000 s) and 0.4283 (30,000 s)) a quasi-steady regime has been established with three distinct sub-regions in the sloping region, as predicted by scaling analysis of [9]. For Ra equal to 1.4 × 10⁷, greater than Ra_c³S_o⁴e^ηh, a nearshore conductive region (x < x_o), a middle stable convective region (x_o < x < x₁) and an unstable convective region (x > x₁) are shown clearly. The first is characterized by vertical isotherms while the second one by V-shaped isotherms and the third one by wavy lines (uprising plumes). The enlarged view of the nearshore section (Fig. 9) shows more clearly the above three sub-regions. For the Ra considered, scaling analysis [9] indicates that x_o/h = 0.52 and x₁/h = 3.19 which are in close agreement with the numerical results. Also, in this case, the steady–state time scale t_c is everywhere less than (kη²)⁻¹ which is the time scale for the switch of the dominant heating mode due to bottom flux to direct absorption of radiation. Hence, also in this case the phenomenon is dominated by bottom heating.

Fig. 9

Enlarged view of the isotherms in the nearshore region during the quasi-steady regime

Streamlines are shown in Fig. 10 at the same time instants which indicate a large-scale circulation, which extends in the whole length of the water body, with the same intensity for both time instants. Small rolls near the horizontal bottom indicate the effect of the hot rising plumes on the general circulation pattern, developed in the quasi-steady regime.

Fig. 10

Streamlines (ψ/ρ_οhk) for Ra = 1.4 × 10⁷ (water body with no vegetation). The dashed and solid lines show clockwise and anticlockwise rotation respectively

The temporal evolution of the exchange flow rate Q/k from the initial to the transitional and finally to the quasi-steady regime is shown in Fig. 11. The exchange flow rate Q is determined by integrating the flow rate Q(x), at a given x location, along the horizontal direction x. Hence,

$$ Q = \frac{1}{L}\int\limits_{0}^{L} {Q(x)} dx\;{\text{where}}\;Q(x) = \frac{1}{2}\int\limits_{0}^{h} {\left| {U_{x} } \right|} dy $$

(11)

Fig. 11

Variation of Q/k with time for a water body with and without vegetation (Ra = 1.4 × 10⁷)

The two vertical dotted lines indicate the times for the onset of instabilities (t_b) and for the onset of a quasi-steady regime for a water body with no vegetation. The former is calculated equal to approximately 685 s. In the same figure the variation of Q/k with time is presented for the other two cases with the vegetation present.

For I_v = 0.85 I_o, the quasi-steady regime is not reached even at a such very large time (t* = 0.4283). This has to do with the lower heating of the sloping region and the isotropic convective cells in the deep region which are present for a long time.

For I_v = 0.0 quasi –steady regime is established for t* between 0.3 and 0.4. The mean value of Q/k is slightly lower than that of the water body with no vegetation, however the mechanisms for establishing quasi-steady state as well as the circulation patterns developed are different in these two cases. This is better explained later when the isotherms and the streamlines are presented for this case.

In the following paragraphs the vegetation effects on isotherms and streamlines are analysed. Figures 12 and 13 show the isotherms and the streamlines respectively for the water body with a vegetated sloping region and I_v = 0.85I_o (the vegetation structure is such that the sloping region absorbs 85% of the radiation).

Fig. 12

Contours of (ΔΤ/(I_oh/κ)) due to surface radiation (water body with vegetation, I_v = φΙ_ο)

Fig. 13

Streamlines (ψ/ρ_οhk) due to surface radiation (water body with vegetation, I_v = φΙ_ο). The dashed and solid lines show clockwise and anticlockwise rotation respectively

Figure 12 shows the development of isotherms in the whole waterbody which continues up to t* = 0.4283 (30,000 s) indicating that the flow has not reached a quasi-steady flow regime. The latter is also clear from the streamlines (Fig. 13) which show that the cell formed at the middle of the water body, near the vegetated/non vegetated interface, due to the horizontal temperature gradient develops continuously up to t* = 0.2142. In the sloping vegetated region, a large-scale recirculation of clockwise rotation is developed due to the faster heating of the shallow part of the vegetated region than that of the deeper part. At very large time (t* = 0.4283) the circulation pattern, originated in the sloping vegetated region, has been extended up to the right-side wall, however, the flow has not reached yet the quasi-steady regime.

Finally, the case for which there is no heating of the vegetated sloping region is analysed. For I_v = 0.0, Figs. 14 and 15 show the isotherms and the streamlines respectively at various times. In this case, the non-uniform heating at the water surface initiates a horizontal temperature gradient near the middle of the water body (interface between vegetated and non-vegetated areas) while a thermal boundary layer, due to the bottom heat flux, develops only at the horizontal bottom of the water body which becomes unstable later.

Fig. 14

Contours of (ΔT/(I_oh/κ)) due to surface radiation (water body with vegetation, I_v = 0.0)

Fig. 15

Streamlines (ψ/ρ_οhk) due to surface radiation (water body with vegetation, I_v = 0.0). The dashed and solid lines show clockwise and anticlockwise rotation respectively

The streamlines (Fig. 15) indicate the development of cells with opposite rotation in the area close to the interface which is due to the non-uniform heating of this area together with the different topography. Two cells, adjacent to the vegetated region, start to develop with opposing rotation. The first one, due to the horizontal temperature gradient at the middle of the water body, has an anticlockwise rotation since the non-vegetated area is heated faster that the vegetated one in which heating is blocked by the vegetation. Gravity currents start to develop along the inclined bottom, which move towards the horizontal bed. The second one has a clockwise rotation due to the rising plumes, developed in the non-vegetated deep region, near the interface, where the bottom thermal boundary layer becomes unstable. At late times (t* = 0.2142 and 0.4238) the first one has covered the whole part of the deep section since the gravity currents have reached the side wall of the deep basin. A large-scale recirculation is developed in the quasi-steady regime with an anticlockwise rotation which is opposite to that developed in the water body with no vegetation. While this recirculation is anticlockwise and the one for the water body with no vegetation is clockwise the magnitude of the generated flow exchange is similar for both cases (Fig. 11). The streamlines of both cases indicate similar strength, although of opposite rotation, which result in similar values of Q/k. This is shown more clearly in Fig. 16 where the variation of Q(x)/k along x/h is indicated. For x/h < 14 the flow exchange is higher in the water body with no-vegetation than that with no vegetation and I_v = 0.0. The opposite occurs for x/h > 14 where Q(x)/k is lower for the no vegetation case.

Fig. 16

Variation of Q(x)/k with x/h

4 Conclusions

The present work considers the surface heating, due to solar radiation, of sloping water bodies and the effects of aquatic vegetation, present in the sloping region of the water body, on the flow regimes, the recirculation patterns, and the exchange flow rates. The following conclusions can be derived:

• (a) Numerical results for a triangular water body, with a sloping region of 0.1 slope and no vegetation, are in satisfactory agreement with those presented by [9] for a Ra number equal to 1.46 × 10⁶. The thermal boundary layer near the inclined bottom becomes unstable in the deeper part of the water body (from x/L_s = 0.5 up to x/L_s = 1.0) at a certain time while later a quasi-steady regime with three sub-regions is established. The whole phenomenon is dominated by bottom heating rather than direct radiation absorption from the top since the time scale for the steady state of the thermal boundary layer everywhere less than that for the switch of the dominant heat mode.

• (b) When vegetation (φ = 0.85) blocks partially the incoming solar radiation (I_v = 0.85 I_o), due to the vegetation cover, a quasi-steady regime is not established even at very large time since the faster heating of the shallow part of the vegetated region than that of the deeper part has as a result the development of a recirculation pattern with opposite rotation than that developed in the region of the water body with the horizontal bottom. The former pattern extends slowly towards the side wall of the deep region, however, the quasi-steady regime would be reached if the simulation had been run longer.

• (c) When the vegetation blocks completely the incident solar radiation into the water body (I_v = 0.0), there is a significant differential heating at the free surface (horizontal convection). Also, a thermal boundary layer, due to the bottom heat flux, develops only at the horizontal bottom of the water body which becomes unstable near the change of the bottom slope. Gravity currents develop along the inclined bottom of the vegetated region and a large-scale recirculation is finally established in the quasi-steady regime which is of opposite rotation than that of the water body with no vegetation.

• (d) The present investigation considers natural convection, due to solar radiation, in vegetated and non-vegetated sloping water bodies. The characteristic Rayleigh number is in the order of 10⁷ while in natural systems this number is much higher (in the order of 10¹²). The validity of the present results for such high Ra numbers is questionable and hence, field and numerical experiments are required for high Ra numbers. The radiation flux is assumed steady while, in natural systems, the flux varies during the day. The latter is easily accomplished in numerical experiments and is the subject of future work. Finally, rigid vegetation is considered in this work as a porous medium with isotropic permeability. In natural systems the vegetation may be flexible with anisotropic permeability. Such vegetation characteristics may not affect the main circulation patterns significantly, however, their effects on the initial flow development may be important.