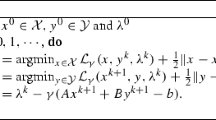The Inexact Cyclic Block Proximal Gradient Method and Properties of Inexact Proximal Maps

Abstract

This paper expands the cyclic block proximal gradient method for block separable composite minimization by allowing for inexactly computed gradients and pre-conditioned proximal maps. The resultant algorithm, the inexact cyclic block proximal gradient (I-CBPG) method, shares the same convergence rate as its exactly computed analogue provided the allowable errors decrease sufficiently quickly or are pre-selected to be sufficiently small. We provide numerical experiments that showcase the practical computational advantage of I-CBPG for certain fixed tolerances of approximation error and for a dynamically decreasing error tolerance regime in particular. Our experimental results indicate that cyclic methods with dynamically decreasing error tolerance regimes can actually outpace their randomized siblings with fixed error tolerance regimes. We establish a tight relationship between inexact pre-conditioned proximal map evaluations and $\delta$-subgradients in our $(\delta ,B)$-Second Prox theorem. This theorem forms the foundation of our convergence analysis and enables us to show that inexact gradient computations can be subsumed within a single unifying framework.

Proof of Lemma 3.3

Proof

Fix $k\ge 2$. We begin by dividing both sides of (27) by $A_\ell A_{\ell +1}$,

$$\begin{aligned} \frac{1}{\gamma }\frac{A_{\ell +1}}{A_\ell } \le \frac{1}{A_{\ell +1}}-\frac{1}{A_\ell }+\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}, \end{aligned}$$

then rearrange and use monotonicity of $\{A_\ell \}_{\ell \ge 0}$ to simplify this to

$$\begin{aligned} \frac{1}{A_{\ell +1}}-\frac{1}{A_\ell } \ge \frac{1}{\gamma }\frac{A_{\ell +1}}{A_\ell } -\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}. \end{aligned}$$

This rearrangement foreshadows the important roles of $A_{\ell +1}/A_\ell$ and $\Delta _{\ell +1}/(A_\ell A_{\ell +1})$. We consider two cases, divided according to the typical size of the ratio $A_{\ell +1}/A_\ell$ for $\ell + 1 \le k$. In the second case, when the values of $A_\ell$ fall at what one may consider a relatively slow rate over this range, we consider three subcases based on the behavior of $\{\Delta _\ell \}_{\ell \ge 1}$ and the typical values of $\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}$.

• (i) For at least $\lfloor k/2\rfloor$ values of $0\le \ell \le k-1$, we have $A_{\ell +1}/A_\ell \le 1/2$.

• (ii) For at least $\lfloor k/2\rfloor$ values of $0\le \ell \le k-1$, we have $1/2 < A_{\ell +1}/A_\ell \le 1$. In this case, we consider three subcases based on the values of $\Delta _{\ell +1}/(A_\ell A_{\ell +1})$ and the sequence $\{\Delta _\ell \}_{\ell \ge 1}$.

Case 1: For at least $\lfloor k/2\rfloor$ values of $0\le \ell \le k-1$, $\frac{A_{\ell +1}}{A_\ell }\le \frac{1}{2}$.

This is the easy case. First, assume that k is even. Then, we have that $A_{\ell +1}\le \frac{1}{2}A_\ell$ for at least k/2 values of $0\le \ell \le k-1$ so

$$\begin{aligned} A_k\le \left( \frac{1}{2}\right) ^{k/2}A_0, \end{aligned}$$

since the $A_\ell$ terms are decreasing. If $k>2$ is odd, then $k-1$ is even, so by the same logic

$$\begin{aligned} A_k\le \left( \frac{1}{2}\right) ^{(k-1)/2}A_0. \end{aligned}$$

Case 2: For at least $\lfloor k/2\rfloor$ values of $0\le \ell \le k-1$, $\frac{1}{2} < \frac{A_{\ell +1}}{A_\ell } \le 1$.

We examine the following three subcases in turn:

• (i) $\Delta _{\ell } = \Delta \ge 0$ for all $\ell$.

• (ii) The sequence $\{\Delta _\ell \}_{\ell \ge 1}$ shrinks at the sublinear rate ${\mathcal {O}}(1/\ell ^2)$ and for at least $\lfloor k/4\rfloor$ of the values for which $\frac{1}{2}< \frac{A_{\ell +1}}{A_\ell }\le 1$ it also holds that $\frac{1}{4\gamma }>\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}$.

• (iii) The sequence $\{\Delta _\ell \}_{\ell \ge 1}$ shrinks at the sublinear rate ${\mathcal {O}}(1/\ell ^2)$ and for at least $\lfloor k/4\rfloor$ of the values for which $\frac{1}{2}<\frac{A_{\ell +1}}{A_\ell }\le 1$ it also holds that $\frac{1}{4\gamma } \le \frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}$.

Case 2, Subcase i: $\Delta _\ell = \Delta \ge 0$ for all $\ell$.

Assume for now that k is even. Define $u=\sqrt{\Delta \gamma }$, and let $\tilde{A}_{\ell }=A_{\ell }-u$. Then, the recurrence (27) implies that $\frac{1}{\gamma }A_{\ell +1}^2\le A_\ell -A_{\ell +1}+\Delta _{\ell +1}$, which we may express as

$$\begin{aligned} \frac{1}{\gamma }(\tilde{A}_{\ell +1}+u)^2=\frac{1}{\gamma }A_{\ell +1}^2\le A_\ell -A_{\ell +1}+\Delta =\tilde{A}_\ell -\tilde{A}_{\ell +1}+\Delta . \end{aligned}$$

Expanding the square on the left, using the definition of u, and rearranging we see

$$\begin{aligned} \frac{1}{\gamma }\tilde{A}_{\ell +1}^2\le \tilde{A}_\ell -\left( 1+\frac{2u}{\gamma }\right) \tilde{A}_{\ell +1}. \end{aligned}$$

If $\tilde{A}_{k} \le 0$, the result is immediate, so suppose that $\tilde{A}_{k} > 0$, from which it follows that the earlier $\tilde{A}_{\ell }$ terms are also positive. Then, for any $\ell$ with $0 \le \ell \le k-1$, we may divide the recurrence inequality by the product $\tilde{A}_{\ell +1}\tilde{A}_\ell$ to obtain

$$\begin{aligned} \frac{1}{\tilde{A}_{\ell +1}} - \left( 1 + \frac{2u}{\gamma }\right) \frac{1}{\tilde{A}_\ell } \ge \frac{1}{\gamma }\frac{\tilde{A}_{\ell +1}}{\tilde{A}_\ell }. \end{aligned}$$

Now, by hypothesis, for at least k/2 indices in the range $0 \le \ell \le k -1$

$$\begin{aligned} \frac{1}{\tilde{A}_{\ell +1}} - \frac{1}{\tilde{A}_\ell } \ge \frac{1}{\gamma }\frac{\tilde{A}_{\ell +1}}{\tilde{A}_\ell } + \frac{2u}{\gamma } \frac{1}{\tilde{A}_\ell } \ge \frac{1}{\gamma }\frac{1 }{2} + \frac{2u}{\gamma } \frac{1}{\tilde{A}_0}. \end{aligned}$$

Iterating backward, one obtains

$$\begin{aligned} \frac{1}{\tilde{A}_k} \ge \frac{1}{\tilde{A}_{k}} - \frac{1}{\tilde{A}_0} \ge \frac{k}{2} \left( \frac{1}{2\gamma } + \frac{2u}{\gamma } \frac{1}{\tilde{A}_0} \right) {,} \end{aligned}$$

which gives $\tilde{A}_k \le 4\gamma \tilde{A}_0/[k (\tilde{A}_0+4u)]$. The result follows from noting that $k-1$ is even if k is odd, so we may replace k with $k-1$ above to obtain a generic bound.

Case 2, Subcase ii: The sequence $\{\Delta _\ell \}_{\ell \ge 1}$ shrinks at the sublinear rate ${\mathcal {O}}(1/\ell ^2)$ and for at least $\lfloor k/4\rfloor$ of the values for which $\frac{1}{2} < \frac{A_{\ell +1}}{A_\ell } \le 1$, it also holds that$\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}< \frac{1}{4\gamma }$.

Our reasoning follows the same idea as when $\Delta _\ell =\Delta \ge 0$ for all $\ell \ge 1$ (Case 2, Subcase i). First, assume that k is divisible by 4. We have for k/4 values of $0\le \ell \le k-1$ that

$$\begin{aligned} \frac{1}{A_{\ell +1}}-\frac{1}{A_\ell }\ge \frac{1}{2\gamma }-\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}\ge \frac{1}{2\gamma }-\frac{1}{4\gamma }=\frac{1}{4\gamma }. \end{aligned}$$

This inequality iterated backward, plus monotonicity and non-negativity of the sequence $\{A_\ell \}_{\ell \ge 0}$, implies that

$$\begin{aligned} \frac{1}{A_k}\ge \frac{1}{A_k}-\frac{1}{A_0}\ge \frac{k}{4}\left[ \frac{1}{4\gamma }\right] =\frac{k}{16\gamma }. \end{aligned}$$

Rearranging, we have that $A_k \le 16\gamma / k$. If $k > 4$ is not divisible by 4, then $k-1$, $k-2$, or $k-3$ must be, so in the worst case $A_k \le 16\gamma /(k-3)$.

Case 2, Subcase iii: The sequence $\{\Delta _\ell \}_{\ell \ge 1}$ shrinks at the sublinear rate ${\mathcal {O}}(1/\ell ^2)$ and for at least $\lfloor k/4\rfloor$ of the values for which $\frac{1}{2} < \frac{A_{\ell +1}}{A_\ell } \le 1$, it also holds that $\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}\ge \frac{1}{4\gamma }$.

First, suppose k is divisible by 4. Let $\ell ^*$ denote the largest $\ell \in \{0,\ldots ,k-1\}$ for which $\frac{\Delta _{\ell +1}}{A_\ell A_{\ell +1}}\ge \frac{1}{4\gamma }$ holds. By hypothesis, $\ell ^*$ must be at least as big as $\frac{k}{4} - 1$, and $\Delta ^2_\ell \le D/\ell ^2$, so

$$\begin{aligned} \frac{1}{4\gamma }\cdot A_k^2\le \frac{1}{4\gamma }\cdot A_k A_{k-1}\le \frac{1}{4\gamma }\cdot A_{\ell ^*+1} A_{\ell ^*}\le \Delta _{\ell ^*+1}\le \Delta _{k/4}\le \frac{D}{(k/4)^2}. \end{aligned}$$

Dividing by $1/4\gamma$ and taking square roots, we have $A_{k}\le \frac{8\sqrt{\gamma D}}{k}$. If $k>4$ is not divisible by 4, then one of $k-1$, $k-2$, or $k-3$ are, so at worst $A_k\le \frac{8\sqrt{\gamma D}}{k-3}$.

Having completed our analysis, we may now combine the results from Case 1 with the appropriate Subcase(s) of Case 2 to establish the results in Lemma 3.3.

$\square$