Abstract
Answering a question of Mitchell (Trans Am Math Soc 329(2):507–530, 1992) we show that a limit of accumulation points can be singular in \({\mathcal {K}}\). Some additional constructions are presented.
Similar content being viewed by others
1 Introduction
Mitchell [10] stated the following problem (2.12 there):
Suppose that \(\mathbf {\kappa }={\langle }\kappa _i \mid i<\omega {\rangle }\) is an increasing sequence of measurable cardinals in the core model such that \(o(\kappa _{i+1})=\kappa _i\). Is there a larger model M in which each \(\kappa _i\) is still measurable and such that if \(\mathbf {\gamma }\) and \(\mathbf {\beta }\) are any sequences such that \(\gamma _i<\kappa _i\) and \(\beta _i<o(\kappa _i)\), for all \(i<\omega \), then there is a sequence \(\textbf{c}\) which is a sequence of indiscernibles for \((\mathbf {\kappa },\mathbf {\beta })\) such that \(\gamma _i<c_i\) for all \(i<\omega \)?
The problem is tightly related to the problem of existence of accumulation points. Such points are one of the basic components of the Mitchell Covering Lemma (see, for example, [11]). Mitchell showed that if accumulation points exist then there is a cardinal \(\alpha \) such that \(\{o(\beta ) \mid \beta <\alpha \}\) is unbounded in \(\alpha \). On the other hand in [5], starting with such measurable \(\alpha \), a model with accumulation points was constructed.
It remained open whether a measurability of \(\alpha \) can be removed and if a limit of accumulation points can be singular in the core model. Mitchell noted in [10] that an affirmative answer to the problem above would answer both of these questions affirmatively.
The main purpose of the paper is to give an affirmative answer to the Mitchell problem.
This is done in Sect. 2. A new variation of short extenders forcing, based on names in order to compensate for incompleteness of the extenders, is used for this. It may be of an interest by its own.
In Sect. 3, we address a question of maximality of sequences of indiscernibles. By results of Jensen-Dodd and Mitchell (see for example [11]), if \(o(\kappa )<\kappa \), \(\kappa \) changes its cofinality, then there is such a sequence. We will show that this not true anymore if \(o(\kappa )=\kappa \).
2 A variation of short extenders forcing
We would like now to present the extender based Prikry forcing using very short extenders. This will allow to give an affirmative answer to a problem of Mitchell.
Assume GCH. Let \(\kappa =\bigcup _{n<\omega }\kappa _n\) with \({\langle }\kappa _n\mid n<\omega {\rangle }\) increasing.
Assume that each \(\kappa _n\) is measurable and there exists a coherent sequence \(\textbf{U}^n={\langle }U(\alpha ,\beta ) \mid \kappa _{n-1}<\alpha \le \kappa _n, \beta <o^{\textbf{U}^n}(\alpha ) {\rangle }\) with \(o^{\textbf{U}^n}(\kappa _n)=\kappa _{n-1}\), where \(\kappa _{-1}=1\).
Force first with the forcing of [4] and turn the Mitchell order into the Rudin-Keisler order. Basically this forcing changes cofinality of cardinals and replaces the connection of the ultrafilters on the coherent sequence via projections to elements of sequences which witness singularity.
Denote the extension by \(V_1\). For each \(n<\omega \), the \(\triangleleft -\)increasing sequence \({\langle }U(\kappa _n, \beta ) \mid \beta <\kappa _{n-1}{\rangle }\) is turned into a \(\le _{R-K}-\)sequence \({\langle }U^{*}(\kappa _n, \beta ) \mid \beta <\kappa _{n-1}{\rangle }\) in \(V_1\).
Let \(j_n:V_1 \rightarrow M_n\) be the corresponding direct limit embedding.
Then \({}^{\kappa _{n-1}>}M_n\subseteq M_n\).
Note that \(M_0\) will be just the ultrapower by \(U^*(\kappa _0,0)\), and so it is closed under \(\kappa _0-\)sequences of its elements.
We view \({\langle }U^{*}(\kappa _n, \beta ) \mid \beta <\kappa _{n-1}{\rangle }\) as an extender over \(\kappa _n\).
Namely, define a \((\kappa _n,j_n(\kappa _n))-\)extender \(E_n\) by setting
Our next task will be to force, using \({\langle }E_n \mid n<\omega {\rangle }\), \(\kappa ^+-\)many \(\omega -\)sequences in \(\prod _{n<\omega }\kappa _n\).
We will use a variation of a forcing of [6] and [1] for this purpose.
A slight complication here is that the extenders \(E_n\) are only \(<\kappa _{n-1}-\)closed.
We are now ready to define our first forcing notion. It will resemble the one element Prikry forcing and will be built from two pieces.
Fix \(n<\omega \).
Definition 2.1
Let
We order \(Q_{n1}\) by inclusion. Denote this order by \(\le _1\).
Thus \(Q_{n1}\) is basically the usual Cohen forcing for adding a function from \(\kappa ^+\) to \(\kappa _n\).
Definition 2.2
Let \(Q_{n0}\) be the set of triples \(p={\langle }a,A,f{\rangle }\) so that
-
(1)
\(f\in Q_{n1}\),
-
(2)
a is an order preserving partial function from \(\kappa ^+\) to \(j_n(\kappa _n)\) such that
-
(2)(i)
\(|a| <\kappa _{n-1}\), if \(n>0\), and \(|a|<\kappa _0\), if \(n=0\),
-
(2)(ii)
\(\textrm{dom}(a)\ \cap \ \textrm{dom}(f)=\emptyset \),
-
(2)(iii)
\(\textrm{rng}(a)\) has a \(\le _{E_n}\)-maximal element, i.e. an element \(\alpha \in \textrm{rng}(a)\) such that \({\alpha }\ge _{E_n}\beta \) for every \(\beta \in \textrm{rng}(a)\).
-
(3)
\(A\in U_{n\max (\textrm{rng}(a))}\),
-
(4)
for every \({\alpha },\beta ,\gamma \in \textrm{rng}(a)\), if \({\alpha }\ge _{E_n}\beta \ge _{E_n}\gamma \), then \(\pi _{{\alpha }\gamma }(\rho )=\pi _{\beta \gamma }(\pi _{{\alpha }\beta } (\rho ))\) for every \(\rho \in \pi _{max(\textrm{rng}(a)),{\alpha }}\mathrm{``} A\),
-
(5)
for every \({\alpha }>\beta \) in a and every \(\nu \in A\)
$$\begin{aligned} \pi _{\max (\textrm{rng}(a)),{\alpha }}(\nu )>\pi _{\max (\textrm{rng}(a)),\beta }(\nu )\ . \end{aligned}$$
Further we will often denote a by a(p), A by A(p) and f by f(p).
Definition 2.3
Let \({\langle }a,A,f{\rangle }, {\langle }b,B,g{\rangle }\in Q_{n0}\). Then
(\({\langle }a,A,f{\rangle }\) is stronger than \({\langle }b,B,g{\rangle }\)) iff
-
(1)
\(f\supseteq g\)
-
(2)
\(a\supseteq b\)
-
(3)
\(\pi _{\max (a), \max (b)}\mathrm{``}A\subseteq B\)
We now define a forcing notion \(Q_n\):
Definition 2.4
\(Q_n=Q_{n0}\cup Q_{n1}\).
Definition 2.5
The direct extension ordering \(\le ^*\) on \(Q_n\) is defined to be \(\le _0\cup \le _1\).
Definition 2.6
(One step extension) Let \(p={\langle }a,A,f{\rangle }\in Q_{n0}\) and \(\nu \in A\). Define \(p^\frown \nu \) to be an element \(g \in Q_{n 1}\) such that
-
1.
\(\textrm{dom}(g)=\textrm{dom}(a)\cup \textrm{dom}(f)\),
-
2.
for every \(\alpha \in \textrm{dom}(f)\), \(g(\alpha )=f(\alpha )\),
-
3.
\(g(\max (\textrm{dom}(a))= \nu \),
-
4.
for every \(\beta \in \textrm{dom}(a),\ \ g(\beta )=\pi _{\max (\textrm{rng}(a)),a(\beta )}(\nu )\).
Definition 2.7
Let \(p,q\in Q_n\).
Then \(p\le q\) iff either
-
(1)
\(p\le ^*q\) or
-
(2)
\(p={\langle }a,A,f{\rangle }\in Q_{n0}, q\in Q_{n1}\) and the following holds for some \(\nu \in A\), \(q\ge _1 p^\frown \nu \).
Clearly, the forcing \({\langle }Q_n,\le {\rangle }\) is equivalent to \({\langle }Q_{n1},\le _1{\rangle }\), i.e. the Cohen forcing. However, the following basic facts relate it to the Prikry type forcing notion.
The next two lemmas are standard.
Lemma 2.8
\({\langle }Q_n,\le ^*{\rangle }\) is \(\kappa _{n-1}\)-closed.
Lemma 2.9
\({\langle }Q_n,\le ,\le ^*{\rangle }\) satisfies the Prikry condition, i.e. for every \(p\in Q_n\) and every statement \(\sigma \) of the forcing language there is \(q\ge ^* p\) deciding \(\sigma \).
Now let us put the blocks \(Q_n,n<\omega \) together. A difference from the usual short extenders forcings is that \(Q_n\)’s are not complete enough (only \(\kappa _{n-1}-\)complete, due to incompleteness of the extender \(E_n\)). In order to overcome this names (but rather simple ones) will be used.
Let us deal first with two - \(Q_0,Q_1\).
Definition 2.10
The set \({\mathcal {P}}_{\le 1}\) consists of sequences \(p={\langle }p_0,p_1{\rangle }\) so that either
-
1.
\(p_0\in Q_{01}\) and \(p_1\in Q_{11}\), i.e. \(p \in Q_{01}\times Q_{11}\).
Or
-
2.
\(p_0\in Q_{01}\) and \(p_1\in Q_{10}\), i.e. \(p \in Q_{01}\times Q_{10}\).
Or
-
3.
\(p_0\in Q_{00}\) and
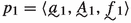 ,
,where
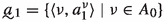 ,
, 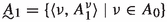 and
and 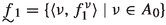 are such that
are such that -
(a)
for every \(\nu \in A_0\), \({\langle }a^\nu _1, A^\nu _1, f^\nu _1{\rangle }\in Q_{1 0}\),
-
(b)
for every \(\nu \in A_0\), \(\textrm{dom}(a_1^\nu )\supseteq \textrm{dom}(a(p_0))\).Footnote 1
The intuitive meaning is that a choice of an element in \(A_0\) determines the function \(a_1\), the set of measure one \(A_1\) for \(E_{1 \max (\textrm{rng}(a_1))}\) and the Cohen function \(f_1\).
-
(a)
Define now orders \(\le ^*\) and \(\le \) on \({\mathcal {P}}_{\le 1}\). Start with \(\le ^*\).
Definition 2.11
Let \(p={\langle }p_0,p_1{\rangle }\) and \(q={\langle }q_0,q_1{\rangle }\) be in \({\mathcal {P}}_{\le 1}\). Set \(p\ge ^* q\) iff either
-
1.
\(p,q \in Q_{01}\times Q_{11}\) and \(p\ge _{Q_{01}\times Q_{11}} q\),
or
-
2.
\(p,q \in Q_{01}\times Q_{10}\) and \(p\ge _{Q_{01}\times Q_{10}} q\),
or
-
3.
\(p_0={\langle }a(p)_0,A(p)_0,f(p)_0{\rangle }, q_0={\langle }a(p)_0,A(p)_0,f(p)_0{\rangle }\in Q_{00}\),
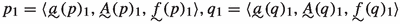 ,
,and then the following hold:
-
(a)
\(q_0\le _{Q_{00}} p_0\),
-
(b)
for every \(\nu \in A(p)_0\),
\({\langle }{a}(q)_1^\rho , {A}(q)_1^\rho , f(q)_1^\rho {\rangle }\le _{Q_{10}} {\langle }{a}(p)_1^\nu , {A}(p)_1^\nu , f(p)_1^\nu {\rangle }\),
where \(\rho =\pi _{\max (\textrm{rng}(a(p)_0)), \max (\textrm{rng}(a(q)_0))}(\nu )\).
-
(a)
Let now \(p={\langle }p_0,p_1{\rangle }\in {\mathcal {P}}_{\le 1}\),  and \(\nu \in A(p)_0\).
and \(\nu \in A(p)_0\).
We set \(p^\frown \nu = {\langle }p_0{}^\frown \nu , {\langle }{a}(p)_1^\nu , {A}(p)_1^\nu , f(p)_1^\nu {\rangle }\).
If \(\nu _1 \in {A}(p)_1^\nu \), then set \(p^\frown {\langle }\nu ,\nu _1{\rangle }= {\langle }p_0{}^\frown \nu , p_1^\nu {}^\frown \nu _1{\rangle }\), where \(p_1^\nu ={\langle }{a}(p)_1^\nu , {A}(p)_1^\nu , f(p)_1^\nu {\rangle }\).
Definition 2.12
Let \(p={\langle }p_0,p_1{\rangle }\) and \(q={\langle }q_0,q_1{\rangle }\) be in \({\mathcal {P}}_{\le 1}\). Set \(p\ge q\) iff either
-
1.
\(p\ge ^* q\),
or
-
2.
for some \(\nu \), \(q^\frown \nu \) is defined and \(p\ge ^* q^\frown \nu \),
or
-
3.
for some \({\langle }\nu _0, \nu _1 {\rangle }\), \(q^\frown {\langle }\nu _0, \nu _1 {\rangle }\) is defined and \(p\ge ^* q^\frown {\langle }\nu _0, \nu _1 {\rangle }\).
Define for every \(n<\omega \), \({\mathcal {P}}_{\le n}\) in a similar fashion.
Definition 2.13
The set \({\mathcal {P}}_{\le n}\) consists of sequences \(p={\langle }p_0,p_1,\ldots ,p_n{\rangle }\) so that either
-
1.
for every \(m\le n\), \(p_m\in Q_{m1}\), i.e. \(p \in Q_{01}\times Q_{11}\times ...\times Q_{n 1}\).
Or
-
2.
there is \(\ell (p)<n\) such that
-
(a)
for every \(m<\ell (p)\), \(p_m\in Q_{m 1}\),
-
(b)
\(p_{\ell (p)}\in Q_{\ell (p) 0}\),
-
(c)
for every \(m, \ell (p)< m\le n\),
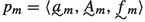 , where
, where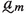 consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, a^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\)
consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, a^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\)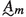 consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, A^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\)
consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, A^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\)and
 consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, f^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\), such that
consists of pairs \({\langle }{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }, f^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\), such that\(\nu _{\ell (p)} \in A_{\ell (p)}\), \(\nu _{\ell (p)+1}\in A^{\nu _{\ell (p)}}_{{\ell (p)+1}}\),..., \(\nu _k \in A^{\nu _{\ell (p)},\ldots , \nu _{k-1}}_{{k}}\),..., \(\nu _{m-1} \in A^{\nu _{\ell (p)},\ldots , \nu _{m-2}}_{{m-1}}\).
Further let us call such sequences \({\langle }\nu _k \mid \ell (p)\le k\le m{\rangle }\)- suitable extension sequences for p.
We require that \({\langle }a^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m, A^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m, f^{{\langle }\nu _k \mid \ell (p)\le k<m{\rangle }}_m{\rangle }\in Q_{m 0}\).
Moreover, if \({\langle }\nu _k \mid \ell (p)\le k<m_1{\rangle }\) and \({\langle }\mu _k \mid \ell (p)\le k<m_2{\rangle }\), are two suitable extension sequences, \(m_1<m_2\) and \({\langle }\nu _k \mid \ell (p)\le k<m_1{\rangle }\) is an initial segment of \({\langle }\mu _k \mid \ell (p)\le k<m_2{\rangle }\) then \(\textrm{dom}(a^{{\langle }\nu _k \mid \ell (p)\le k<m_1{\rangle }}_{m_1})\subseteq \textrm{dom}(a^{{\langle }\nu _k \mid \ell (p)\le k<m_2{\rangle }}_{m_2})\).Footnote 2
-
(a)
Definition 2.14
Let \({\langle }\nu _k \mid \ell (p)\le k\le m{\rangle }\) be a suitable extension sequence for p. Define \(p^\frown {\langle }\nu _k \mid \ell (p)\le k\le m{\rangle }\) to be \(q={\langle }q_0,\ldots ,q_n{\rangle }\) such that
-
1.
for every \(k<\ell (p)\), \(q_k=p_k\),
-
2.
\(q_{\ell (p)}=p_{\ell (p)}{}^\frown \nu _{\ell (p)}\),
-
3.
\(q_k={\langle }a^{{\langle }\nu _s \mid \ell (p)\le s<k{\rangle }}_k, A^{{\langle }\nu _s \mid \ell (p)\le s<k{\rangle }}_k, f^{{\langle }\nu _s \mid \ell (p)\le s<k{\rangle }}_k{\rangle }{}^\frown \nu _k\), for every \(k, \ell (p)<k\le m\),
-
4.
for every \(k, m<k\le n\),
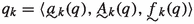 , where
, where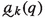 consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, a^{{\langle }\mu _i \mid m<i<k{\rangle }}_k{\rangle }\),
consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, a^{{\langle }\mu _i \mid m<i<k{\rangle }}_k{\rangle }\),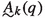 consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, A^{{\langle }\mu _i \mid m< i<k{\rangle }}_k{\rangle }\)
consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, A^{{\langle }\mu _i \mid m< i<k{\rangle }}_k{\rangle }\)and
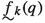 consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, f^{{\langle }\mu _i \mid m< i<k{\rangle }}_k{\rangle }\), such that
consists of pairs \({\langle }{\langle }\mu _i \mid m< i<k{\rangle }, f^{{\langle }\mu _i \mid m< i<k{\rangle }}_k{\rangle }\), such that\({\langle }\nu _k \mid \ell (p)\le k\le m{\rangle }^\frown {\langle }\mu _i \mid m< i<k{\rangle }\) is suitable extension sequence for p.
The orders \(\le ^*\) and \(\le \) are defined on \({\mathcal {P}}_{\le n}\) similarly to those on \({\mathcal {P}}_{\le 1}\).
Definition 2.15
The set \({\mathcal {P}}\) consists of sequences \(p={\langle }p_n\mid n<\omega {\rangle }\) so that
-
(1)
for every \(n<\omega ,\ p\upharpoonright n+1\in {\mathcal {P}}_{\le n}\).
-
(2)
there is an \(\ell (p) <\omega \) so that for every \(n<\ell (p),\ p_n\in Q_{n1}\),
and for every
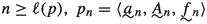 ,
, -
(3)
if for some suitable extension sequence \(\mathbf {\nu }={\langle }\nu _k \mid \ell (p)\le k<m{\rangle }\), an ordinal \(\alpha \) is in \(\textrm{dom}(f_m^{\mathbf {\nu }})\cup \textrm{dom}(a_m^{\mathbf {\nu }})\), then there is \(m(\alpha ), m\le m(\alpha )<\omega \), for every \(r, m(\alpha )\le r<\omega \), we have \(\alpha \in \textrm{dom}(a_r^{\mathbf {\rho }})\), for every suitable extension sequence \(\mathbf {\rho }\) of the length r.
Note that the total number of ordinals which appear in \(\textrm{dom}(f_m^{\mathbf {\nu }})\), for any \(m<\omega \) and any suitable extension sequence \(\mathbf {\nu }\), is at most \(\kappa \). Recall that \(\kappa =\bigcup _{n<\omega }\kappa _n\). So, we can spread such ordinals among the domains of \(a_n\)’s.
Condition 3 will allow to show that for any \(\alpha<\beta <\kappa ^+\), a generic \(\omega -\)sequences produced by the forcing \({\mathcal {P}}\) for \(\alpha \) is dominated (mod finite) by a generic \(\omega -\)sequences for \(\beta \).
-
(4)
There is \(\eta <\kappa ^+\) which is the maximal element of p in the following sense:
-
for some suitable extension sequence \(\mathbf {\nu }={\langle }\nu _k \mid \ell (p)\le k<m{\rangle }\), \(\eta \in \textrm{dom}(a_m^{\mathbf {\nu }})\),
-
for every ordinal \(\alpha \), if \(\alpha \in \textrm{dom}(f_{m_1}^{\mathbf {\nu }})\cup \textrm{dom}(a_{m_1}^{\mathbf {\nu }})\), for some suitable extension sequence \(\mathbf {\nu }={\langle }\nu _k \mid \ell (p)\le k<{m_1}{\rangle }\), then \(\alpha \le \eta \),
-
for every ordinal \(\alpha \le \eta \), there is a suitable sequence \(\mathbf {\nu }={\langle }\nu _k \mid \ell (p)\le k<{m_2}{\rangle }\) such that \(\alpha \in \textrm{dom}(a_{m_2}^{\mathbf {\nu }})\).
This condition allows to avoid situations of the following type:
For some \(\alpha +1<\beta <\kappa ^+\), \(\alpha , \beta \in \textrm{dom}(a_n)\) and \(a_n(\beta )=a_n(\alpha )+1\), for every \(n<\omega \).
Here no room is left in order to add \(\alpha +1\) to domain \(a_n\), for any n, since \(a_n\)’s are order preserving.
Let us argue that this cannot happen, if we have \(\eta \), as above. Thus let \(\alpha +1<\beta \le \eta \). Then for some suitable sequences \(\mathbf {\nu }={\langle }\nu _k \mid \ell (p)\le k<i{\rangle }\), \(\mathbf {\zeta }={\langle }\zeta _k \mid \ell (p)\le k<{i'}{\rangle }\), \(\alpha +1\in \textrm{dom}(a_{i}^{\mathbf {\nu }})\) and \(\beta \in \textrm{dom}(a_{i'}^{\mathbf {\zeta }})\). Let \(m^*=\max (m(\alpha +1), m(\beta ))\). Then the condition (3) above implies that \(\alpha +1,\beta \in \textrm{dom}(a_r^{\mathbf {\rho }})\), for every suitable extension sequence \(\mathbf {\rho }\) of the length \(r\ge m^*\). Hence, by order preservation, \(a_r^{\mathbf {\rho }}(\beta )>a_r^{\mathbf {\rho }}(\alpha +1)\).
Let us denote such \(\eta \) by md(p).
-
Definition 2.16
Let \(p,q\in {\mathcal {P}}\). We set \(p\ge q\) \((p\ge ^*q)\) iff for every \(n<\omega \), \(p\upharpoonright n+1\ge _{{\mathcal {P}}_{\le n}}q\upharpoonright n+1\) \((p\upharpoonright n+1\ge ^*_{{\mathcal {P}}_{\le n}}q\upharpoonright n+1)\).
The forcing \({\langle }{\mathcal {P}},\le {\rangle }\) does not satisfy the \(\kappa ^+\)-c.c., however its cardinality is \(\kappa ^+\), and so, there is no issue of preserving cardinals above \(\kappa ^+\).
Then the following lemmas are obvious:
Lemma 2.17
\({\langle }{\mathcal {P}}_{\le n}, \le {\rangle }\) has a dense subset equivalent to the Cohen forcing for \(\kappa ^+\), for every \(n<\omega \).
Lemma 2.18
\({\mathcal {P}}\simeq {\mathcal {P}}_{\le n}*{\mathcal {P}}_{>n}\) for every \(n<\omega \).
Lemma 2.19
\({\langle }{\mathcal {P}}_{>n},\le ^*{\rangle }\) is \(\kappa _n\)-closed in \(V_1^{{\mathcal {P}}_{\le n}}\). Moreover if \({\langle }p^{\alpha }\mid {\alpha }<\delta {\rangle }\) is a \(\le ^*-\)increasing sequence of elements of \({\mathcal {P}}_{>n}\) with \(\delta <\kappa _{\ell (p^0)-1}\), then there is \(p\ge ^*p^{\alpha }\) for every \({\alpha }<\delta \).
Proof
Let \({\langle }p^{\alpha }\mid {\alpha }<\delta {\rangle }\) is a \(\le ^*-\)increasing sequence of elements of \({\mathcal {P}}_{>n}\) with \(\delta <\kappa _{\ell (p^0)-1}\). Denote \(md(p^\alpha )\) by \(\eta ^\alpha \), for every \(\alpha <\delta \). Then the sequence \({\langle }\eta _\alpha \mid \alpha <\delta {\rangle }\) is non-decreasing. Set \(\eta =\bigcup _{ \alpha <\delta } \eta _\alpha \).
Let \(p^\alpha ={\langle }p_m^\alpha \mid n<m<\omega {\rangle }\), and  , for every \(m, \ell (p^\alpha )\le m<\omega \), for every \({\alpha }<\delta \).
, for every \(m, \ell (p^\alpha )\le m<\omega \), for every \({\alpha }<\delta \).
By usual means, using completeness, we can find \(q={\langle }q_m \mid n<m<\omega {\rangle }\), with \(\ell (q)=\ell (p^0)\), \(q_m=\bigcup _{\alpha <\delta } p^\alpha _m\), \(n<m<\ell (p^0)\) and  stronger than \(p^\alpha _m\), for every \(m, \ell (p^0)\le m<\omega \), \({\alpha }<\delta \).
stronger than \(p^\alpha _m\), for every \(m, \ell (p^0)\le m<\omega \), \({\alpha }<\delta \).
Let us turn q into an element \(p={\langle }p_m \mid n<m<\omega {\rangle }\) of \({\mathcal {P}}_{>n}\) by adding \(\eta \), which is needed in order to satisfy (4) of Definition 2.15. Proceed as follows:
set \(p_m=q_m\), for every \(m, n<m<\ell (p^0)\). Let us add \(\eta \) to \(\textrm{dom}(b_{\ell (p^0)})\) and map it into order preserving fashion to some \(\eta ^{\ell (p^0)}\) below \(j_{{\ell (p^0)}}(\kappa _{\ell (p^0)})\) which is above in the order \(\le _{E_{\ell (p^0)}}\) every element of \(\textrm{rng}(b_{\ell (p^0)})\). Now, we move \(B_{\ell (p^0)}\) to \(\eta ^{\ell (p^0)}\). \(A_{\ell (p^0)}\) be the corresponding large set.
Set \(p_{\ell (p^0)}\) to be \({\langle }b_{\ell (p^0)}\cup \{(\eta , \eta ^{\ell (p^0)})\}, A_{\ell (p^0)}, h_{\ell (p^0)}{\rangle }\).
Then for every \(\nu \in A_{\ell (p^0)}\) we repeat the process of adding \(\eta \) to \(b_{\ell (p^0)+1}^\nu \).
Continue in the same fashion for every \(m>\ell (p^0)+1\). The resulting p will be as desired.
Note that such p will satisfy the condition (4) of Definition 2.15, since each of \(p^\alpha \)’s satisfies 2.15(3). \(\square \)
We will turn now to the Prikry condition.
Let us introduce first some notation. For \(p={\langle }p_n\mid n<\omega {\rangle }\in {\mathcal {P}}\) and m with \(\ell (p)\le m<\omega \), let  . Denote
. Denote  by
by  ,
,  by
by  and
and  by
by  .
.
Lemma 2.20
Let \(q \in {\mathcal {P}}\) and \(\alpha <\kappa ^+\). Then there is \(p\ge ^* q\) with \(\alpha \le md(p)\).
Proof
If \(\alpha \le md(q)\), then just take \(p=q\). Suppose that \(\alpha > md(q)\). Consider \(\alpha +1\setminus md(q)\). It is a set of cardinality at most \(\kappa \). So we can present it as a non-decreasing union \(\bigcup _{i<\omega }x_i\) with \(|x_i|<\kappa \). For every \(i<\omega \), let \(n(i)<\omega \) be the least with \(|x_i|<\kappa _{n(i)-1}\). Now, for every \(n, n(i)\le n<\omega \), we extend \(a_n\) by adding \(x_i\) to its domain and mapping it to \(j_n(\kappa _{n})\) in an order preserving fashion. Definition 2.15(4) insures that this can be done and no collisions with functions part (i.e., \(f_n\)’s) occur.
This will easily define a desired condition p with \(md(p)=\alpha \). \(\square \)
Lemma 2.21
Let \(p\in {\mathcal {P}}\) and D be a dense open subset of \({\langle }{\mathcal {P}},\le {\rangle }\) above p. Then there are \(p^*\ge ^* p\) and \(n^*<\omega \) such that for every suitable extension sequence \({\langle }\nu _0,\ldots ,\nu _{n^*}{\rangle }\) for \(p^*\),
Proof
If there is a direct extension of p inside D, then we are done. Suppose otherwise.
Assume for simplicity that \(\ell (p)=0\).
Proceed by induction on \(\nu \in A_0\). Let \(\nu =\textrm{min}(A_0)\).
Consider \(p^\frown \nu \). If there is a direct extension of \(p^\frown \nu \) which is in D, then let r be such extension.
Set \(p(0)={\langle }p_n(0) \mid n<\omega {\rangle }\) to be a direct extension of p defined as follows:
-
1.
\(p_0(0)=p_0\),
-
2.
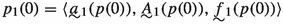 , where
, where -
1.
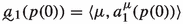 , where \(a^\mu _1(p(0))=a^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \),
, where \(a^\mu _1(p(0))=a^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \),then \(a^\mu _1(p(0))=a^\mu _1(r)\),
-
2.
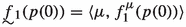 , where \(f^\mu _1(p(0))=f^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \),
, where \(f^\mu _1(p(0))=f^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \),then \(f^\mu _1(p(0))=f^\mu _1(r)\),
-
3.
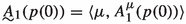 , where \(A^\mu _1(p(0))=A^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \), then \(A^\mu _1(p(0))=A^\mu _1(r)\).
, where \(A^\mu _1(p(0))=A^\mu _1(p)\), unless \(\mu =\nu \), and if \(\mu =\nu \), then \(A^\mu _1(p(0))=A^\mu _1(r)\).
-
1.
-
4.
for every \(m, 1<m<\omega \),
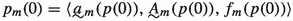 , where
, where -
1.
 ,
,where \(\mathbf {\mu }={\langle }\mu _0,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for p and \(a^{\mathbf {\mu }}_m(p(0))=a^{\mathbf {\mu }}_m(p)\),
unless \(\mu _0=\nu \) and if \(\mu _0=\nu \), then \({\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for r and \(a^{\mathbf {\mu }}_m(p(0))=a^{{\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }}_m(r)\),
-
2.
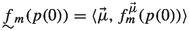 ,
,where \(\mathbf {\mu }={\langle }\mu _0,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for p and \(f^{\mathbf {\mu }}_m(p(0))=f^{\mathbf {\mu }}_m(p)\),
unless \(\mu _0=\nu \) and if \(\mu _0=\nu \), then \({\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for r and \(f^{\mathbf {\mu }}_m(p(0))=f^{{\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }}_m(r)\),
-
3.
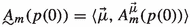 ,
,where \(\mathbf {\mu }={\langle }\mu _0,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for p and \(A^{\mathbf {\mu }}_m(p(0))=A^{\mathbf {\mu }}_m(p)\),
unless \(\mu _0=\nu \) and if \(\mu _0=\nu \), then \({\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }\) is a suitable extension sequence for r and \(A^{\mathbf {\mu }}_m(p(0))=A^{{\langle }\mu _1,\ldots ,\mu _{m-1}{\rangle }}_m(r)\).
-
1.
If there is no direct extension of \(p^\frown \nu \) in D then set \(p(0)=p\).
Turn next to the second element \(\nu (1)\) of \(A_0\). If there is no direct extension of \(p(0)^\frown \nu (1)\) in D, then set \(p(1)=p(0)\). Otherwise, pick such a direct extension \(r\ge ^* p(0)\) in D and define p(1) as above replacing p by p(0) and \(\nu \) by \(\nu (1)\).
Continue by induction. We have enough completeness at coordinates 2 and above, at coordinate 1 the lack of completeness (recall that there we have only \(\kappa _0-\)completeness) is compensated by taking names.
Denote by \(p^*(0)\) the resulting direct extension of p, i.e. the one obtained after passing through all \(\nu \)’s in \(A_0\) and finally using the argument of Lemmas 2.19, 2.20 in order to satisfy Definitions 2.13, 2.15.
Then, for every \(\nu \in A_0\), if there is a direct extension of \(p^*(0)^\frown \nu \) in D, then already \(p^*(0)^\frown \nu \in D\).
Shrink now \(A_0\) to \(A_0^*\in E_{0 \max (\textrm{rng}(a_0))}\) such that for every \(\nu ,\nu ' \in A_0^*\),
Let \(p^{**}(0)\) be obtained from \(p^*(0)\) by replacing \(A_0\) with \(A_0^*\).
If for some (every) \(\nu \in A_0^*\), \(p^*(0)^\frown \nu \in D\), then \(p^*(0)\) is as required and we are done.
Suppose otherwise. Proceed to the next level and repeat the process.
This way \(p^{**}(n)\)’s will be constructed, for \(n<\omega \).
The process should stop at some stage \(n^*<\omega \) and the resulting \(p^{**}(n^*)\) will be as desired. \(\square \)
By standard arguments it follows now:
Proposition 2.22
The forcing \({\langle }{\mathcal {P}},\le {\rangle }\) does not add new bounded subsets to \(\kappa \) and preserves all the cardinals.
In particular, each \(\kappa _n (n<\omega )\) remains measurable.
Let us show that this forcing adds \(\kappa ^+\) \(\omega \)-sequences to \(\kappa \). Thus, let \(G\subseteq {\mathcal {P}}\) be generic. For every \(n<\omega \) define a function \(F_n:\kappa ^+\rightarrow \kappa _n\) as follows:
\(F_n({\alpha })=\nu \) if for some \(p={\langle }p_m\mid m<\omega {\rangle }\in G\) with \(\ell (p) >n\), \(p_n({\alpha })=\nu \).
Now for every \({\alpha }<\kappa ^+\) set \(t_{\alpha }={\langle }F_n({\alpha })\mid n<\omega {\rangle }\). Let us show that the set \(\{ t_{\alpha }\mid {\alpha }<\kappa ^+\}\) has cardinality \(\kappa ^+\).
Lemma 2.23
For every \(\beta<\alpha <\kappa ^+\), \(t_\beta (n)<t_\alpha (n)\), for all but finitely many \(n<\omega \).
Proof
Work in \(V_1\). Let \(q\in {\mathcal {P}}\). By Lemma 2.20 there is a direct extension p of q such that \(\alpha ,\beta \le md(p)\). Use Definition 2.15(3,4). Let \(m^*=\max (m(\alpha ),m(\beta ))\). Then for every \(r, m^*\le r<\omega \), we have \(\alpha , \beta \in \textrm{dom}(a_r^{\mathbf {\rho }}(p))\), for every suitable extension sequence \(\mathbf {\rho }\) of the length r.
Now, the order preservation implies

\(\square \)
Let us argue that \({\langle }t_\alpha \mid \alpha <\kappa ^+ {\rangle }\) is actually a scale in \(\prod _{n<\omega } \kappa _n\) mod finite, i.e., for every \(t \in \prod _{n<\omega } \kappa _n\), there is \(\alpha <\kappa ^+ \) such that for all but finitely many \(n<\omega \), \(t(n)<t_\alpha (n)\).
We will show a bit stronger statement which will insure that unboundedly many \(\alpha \)’s, \(t_\alpha \) is a sequence of indiscernibles.
Definition 2.24
A sequence \({\langle }c_n \mid n<\omega {\rangle }\in \prod _{n<\omega } \kappa _n\) is called a principle sequence iff
-
1.
for some \(\alpha <\kappa ^+\), for all but finitely many \(n<\omega \), \(c_n=t_\alpha (n)\),
-
2.
there is \(p \in G\) such that
-
(a)
\(\alpha \in \textrm{dom}(a_{\ell (p)}(p))\).
It follows, by 2.13((2)b,c), that for every \(n, \ell (p)< n <\omega \), for every suitable extension sequence \({\langle }\nu _{\ell (p)},\ldots ,\nu _{n-1}{\rangle }\) for p, \(\alpha \in \textrm{dom}(a_n(p)^{{\langle }\nu _{\ell (p)},\ldots ,\nu _{n-1}{\rangle }})\).
-
(b)
\(a_{\ell (p)}(p)(\alpha )\) is a generator of \(E_{\ell (p)},\)Footnote 3
-
(c)
for every \(k, \ell (p)<k<\omega \), for every suitable extension sequence \({\langle }\nu _{\ell (p)},\ldots ,\nu _{k-1}{\rangle }\) for p, \(a_{k}(p)^{{\langle }\nu _{\ell (p)},\ldots ,\nu _{k-1}{\rangle }}(\alpha )\) is a generator of \(E_{k}\).
-
(a)
Lemma 2.25
Let \(t\in \prod _{n<\omega }\kappa _n\) in \(V_1[G]\). Then there is \({\alpha }<\kappa ^+\) such that for all but finitely many \(n<\omega \), \(t_{\alpha }(n) >t(n)\).
Moreover, such \(t_\alpha \) can be picked to be a principle sequence.
Proof
Work in \(V_1\). Let  Suppose for simplicity that \(\ell (p)=0\). Let
Suppose for simplicity that \(\ell (p)=0\). Let  be a name of the ordinal \(t(n)<\kappa _n\).
be a name of the ordinal \(t(n)<\kappa _n\).
Start with  .
.
Set  .
.
Clearly, \(D_0\) is a dense open subset of \({\mathcal {P}}\).
Apply Lemma 2.21 to p and \(D_0\).
Let \(n_0<\omega \) be the least possible which satisfies the conclusion of Lemma 2.21.
Let \(p^*(0)\) be a witnessing direct extension of p.
Claim 1
\(n_0=0\).
Proof
First note that due to degrees of completeness \(n_0\le 1\).
Suppose that \(n_0=1\).
Let \(\nu \in A_0(p^*(0))\). Consider \(A_1^\nu (p^*(0))\).
It is a set in \(\kappa _1-\)complete ultrafilter \(E_{1 \max (\textrm{rng}(a_1^\nu (p^*(0))))}\).
For every \(\rho \in A_1^\nu (p^*(0))\), \( p^*(0)^\frown {\langle }\nu ,\rho {\rangle }\in D_0\), hence there is \(\eta (\nu ,\rho )<\kappa _0\) such that

Now, using \(\kappa _1-\)completeness of \(E_{1 \max (\textrm{rng}(a_1^\nu (p^*(0))))}\), we can shrink \(A_1^\nu (p^*(0))\) to a set \(A_1^\nu \in E_{1 \max (\textrm{rng}(a_1^\nu (p^*(0))))}\) such that for every \(\rho \in A_1^\nu \)

where \(\eta (\nu )<\kappa _0\) does not depend on \(\rho \).
Preform the above for every \(\nu \in A_0(p^*(0))\). Then replace in \(p^*(0)\) the sets \(A_1^\nu (p^*(0))\)’s by \(A_1^\nu \).
This will reduce \(n_0\), which is impossible by its minimality.
Contradiction.
\(\square \) of the claim.
Proceed by induction on \(k<\omega \) and define \(D_k\),\(n_k, p^*(k)\ge ^*p^*(k-1)\) as above.
As in the claim, we will have \(n_k=k\).
Let finally, \(p^*\) be a common direct extension of all \( p^*(k)\)’s.
Then for every \(k<\omega \), for every suitable extension sequence \({\langle }\nu _0,\ldots ,\nu _k{\rangle }\) for \(p^*\),

Denote the decided values by \({\langle }\eta _0(\nu _0,\ldots ,\nu _k),\ldots ,\eta _k(\nu _0,\ldots ,\nu _k){\rangle }\).
Pick now \(\alpha <\kappa ^+\) above everything that appears in \(p^*\). Let us define a direct extension \(p^{**}\) of \(p^*\) by adding \(\alpha \) to domains of \(a_n(p^*)\)’s and insuring that \(p^{**}\) will force  for every \(n<\omega \).
for every \(n<\omega \).
Start with \(n=0\). Consider \(\max (\textrm{rng}(a_0(p^*)))\). It is an ordinal \(<j_0(\kappa _0)\).
Actually, we are here in a special case - \(E_0\) is just equivalent to the normal ultrafilter \(U^*(\kappa _0,0)\), i.e. it has a single generator \(\kappa _0\). Consider the function \(\nu \mapsto \eta _0(\nu )\) on \(A_0(p^*)\). It represents an ordinal \(\gamma _0<j_0(\kappa _0)\). Pick \(\alpha _0<j_0(\kappa _0)\) to be above both \(\gamma _0\) and \(\max (\textrm{rng}(a_0(p^*)))\).
Extend \(a_0(p^*)\) by adding \(\alpha \) to its domain and setting its value to be \(\alpha _0\).
Turn to the next step - \(n=1\).
Fix \(\nu \in A_0(p^*)\). Consider a function \(\rho \mapsto \eta (\nu ,\rho )\) defined on \(A_1^\nu (p^*)\).
We have \(A_1^\nu (p^*)\in E_{1 \max (\textrm{rng}(a_1^\nu (p^*)))}\). Recall that \(E_1\) is a \((\kappa _1, j_1(\kappa _1))-\)extender generated by taking a direct limit of a Rudin-Keisler increasing sequence \({\langle }U^*(\kappa _1, \gamma ) \mid \gamma <\kappa _0{\rangle }\) of ultrafilters over \(\kappa _1\).
Note that for every \(\gamma <\kappa _0\), \(j_{U(\kappa _1,\gamma )}(\kappa _1)=j_{U^*(\kappa _1,\gamma )}(\kappa _1)\), by arguments of [4]. This is due to the fact that an Easton support iteration was used in [4]. This forcing satisfies \(\kappa _1-\)c.c., and so, every function from \(\kappa _1\) to \(\kappa _1\) is dominated by a function from \(\kappa _1\) to \(\kappa _1\) in the ground model. We refer a reader unfamiliar with such arguments to the appendix of the paper which provides details related to the structure of ultrafilters after the forcing of [4].
So, \(j_1(\kappa _1)=\bigcup _{\gamma <\kappa _0}j_{U(\kappa _1,\gamma )}(\kappa _1)\) and every \(j_{U(\kappa _1,\gamma )}(\kappa _1)\) is a generator of \(E_1\).
Pick \(\gamma _\nu <\kappa _0\) such that \(\max (\textrm{rng}(a_1^\nu (p^*)))<j_{U(\kappa _1,\gamma _\nu )}(\kappa _1)\). Set \(\alpha _1^\nu =j_{U(\kappa _1,\gamma _\nu )}(\kappa _1)\). Extend \(a^\nu _1\) by adding \(\alpha \) to its domain and setting its value to be \(\alpha _1^\nu \).
Do the above for every \(\nu \in A_0(p^*)\) (separately).
Continue up to \(n=2\) etc. We will construct a desired direct extension of \(p^*\). \(\square \)
Let us show that our construction provides an affirmative answer to the problem of W. Mitchell [10] stated the introduction.
Lemma 2.26
Suppose that \(\textbf{c}={\langle }c_n \mid n<\omega {\rangle }\in \prod _{n<\omega }\kappa _n\) is a principle sequence. Then it is a sequence of indiscernibles for \(\mathbf {\kappa }={\langle }\kappa _n \mid n<\omega {\rangle }\)Footnote 4.
Proof
Let N be a covering model (we refer to Mitchell [11] for definitions) with \(\textbf{c}\in N\). Then \(N\cap {\mathcal {K}}_\kappa =h^N(\rho ;{\mathbb {C}}^N)\), for some \(\rho <\kappa \), sequence of indiscernibles \({\mathbb {C}}^N\) and a Skolem function \(h^N \in {\mathcal {K}}\).
Suppose that infinitely many of \(c_n\)’s are not indiscernibles for N.
Assume for simplicity that none of \(c_n\)’s is an indiscernible.
Then for every \(n<\omega \) there is a finite sequence of ordinals \(\textbf{d}_n\) below \(c_n\) such that \(h^N(\textbf{d}_n)=c_n\). Define in \({\mathcal {K}}\) a function \(\tilde{h} \in \prod _{n<\omega }\kappa _n\) as follows:
Let \(\nu <\kappa \), pick the least \(n<\omega \) such that \(\nu <\kappa _n\).
Set
Define \(\tilde{h}_n=\tilde{h}\upharpoonright \kappa _n\). Clearly, \(\tilde{h}_n:\kappa _n \rightarrow \kappa _n\).
Then, \(c_n\le \tilde{h}(\max (\mathbf {d_n}))=\tilde{h}_n(\max (\mathbf {d_n}))<\kappa _n\) and \(\max (\mathbf {d_n})<c_n\), for every \(n<\omega \). It is impossible to have this type of situation, since by the definition of a principal sequence, \(c_n\) corresponds to a generator of extender \(E_n\) for all but finitely many \(n<\omega \). \(\square \)
Now, Lemma 2.25 and Lemma 2.26 imply the following:
Lemma 2.27
For every \(\mathbf {\gamma }={\langle }\gamma _n \mid n<\omega {\rangle }\in \prod _{n<\omega }\kappa _n\) there is \(\alpha <\kappa ^+\) such that
-
1.
\(t_\alpha \) is a principal sequence,
-
2.
\(t_\alpha (n)>\gamma _n\), for all but finitely many \(n<\omega \).
The next lemma completes the proof:
Lemma 2.28
Let \(\mathbf {\beta }={\langle }\beta _n \mid n<\omega {\rangle }\in \prod _{n<\omega }\kappa _{n-1}\) in \(V_1[G]\). Then there are arbitrary large \(\alpha <\kappa ^+\) such that
-
1.
\(t_\alpha \) is a principal sequence,
-
2.
\(o^{{\mathcal {K}}}(t_\alpha (n))=\beta _n\), for all but finitely many \(n<\omega \).
Proof
We repeat the proof of Lemma 2.25 with \(t=\mathbf {\beta }\). Find \(p^*\) which suitable extensions of the length \(n-1\) decide  for all n’s. Next, \(\alpha <\kappa ^+\) above everything in \(p^*\) is picked and added to domains of \(a_n(p^*)\)’s. The final stage was to specify images of \(\alpha \). Generators of \(E_n\)’s were picked for this purpose.
for all n’s. Next, \(\alpha <\kappa ^+\) above everything in \(p^*\) is picked and added to domains of \(a_n(p^*)\)’s. The final stage was to specify images of \(\alpha \). Generators of \(E_n\)’s were picked for this purpose.
Note that for given \(n, 0<n<\omega \), there are arbitrary large generators \(\zeta \) of \(E_n\) with \(o^{{\mathcal {K}}^{M_n}}(\zeta )=\beta _n\). One can take, for example, \(\xi \)’s which generate \(U(\kappa _n, \beta _n)\), i.e. \(U(\kappa _n, \beta _n)\subseteq \{X\subseteq \kappa _n \mid \xi \in j_{E_n}(X)\}\). So we are free to choose one of them to be the image of \(\alpha \).
This process will produce the desired \(t_\alpha \). \(\square \)
3 No maximal sequence of indiscernibles for a measurable
Let \(o(\kappa )=\delta \le \kappa \) as witnessed by \(\textbf{U}={\langle }U(\kappa ,\beta ) \mid \beta <\delta {\rangle }\).
Suppose that the Prikry or Magidor or Radin forcing with \(\textbf{U}\) is used. Let \(C_{\textbf{U}}\) be a generic club.
Then in \(V[C_{\textbf{U}}]\), we have
-
(A)
for every \(A\in \bigcap _{\beta <\delta } U(\kappa ,\beta )\) there is \(\eta <\kappa \) such that \(C_{\textbf{U}}{\setminus } \eta \subseteq A\).
-
(B)
(Maximality) If \(C'\subseteq \kappa \) is so that for every \(A\in \bigcap _{\beta <\delta } U(\kappa ,\beta )\) there is \(\eta <\kappa \) such that \(C\setminus \eta \subseteq A\), then a final segment of \(C'\) is subset of \(C_{\textbf{U}}\).
By results of Jensen-Dodd and Mitchell, if \(o(\kappa )<\kappa \), \(\kappa \) changes its cofinality, then there is a club \(C\subseteq \kappa \) which satisfies both items above.
We would like to show here that this not true anymore if \(o(\kappa )=\kappa \).
Namely, we will construct a generic extension V[G] which satisfies the following:
-
1.
\({{\,\textrm{cof}\,}}(\kappa )=\omega \),
-
2.
there is no \(C\subseteq \kappa \) which satisfies Items (A) and (B) above.
The final extension V[G] will be built in three steps. The first one will be a tree Prikry forcing extracted from the Radin forcing with \(\textbf{U}\) which will change the cofinality of \(\kappa \) to \(\omega \). Let \({\langle }\kappa ^n \mid n<\omega {\rangle }\) be such Prikry sequence. The next forcing will be an Easton support iteration of Prikry, Magidor forcings for changing cofinality of each measurable \(\nu \in \kappa {\setminus } \{\kappa ^n \mid n<\omega \}\) according to \(o(\nu )\). Then the final one will a variant of short extenders forcing similar to those of [1]. Also the forcing of the previous section can be used, but this will make the matters more complicated due to use of names.
Let us describe the first one - P\({}_{\textbf{U}}\) a tree Prikry forcing with \(\textbf{U}\).
Definition 3.1
P\({}_{\textbf{U}}\) consists of pairs \({\langle }t, T{\rangle }\) such that
-
1.
t is a finite increasing sequence of ordinals \(<\kappa \),
-
2.
T is a tree of finite increasing sequences of ordinals \(<\kappa \) with trunk t,
-
3.
if t is the empty sequence, then \(Suc_T(t) \in U(\kappa , 0)\),
-
4.
if \(s \in T\) and s extends t, then \(Suc_T(s)\in U(\kappa , \max (s))\).
The orders \(\le \) and \(\le ^*\) are defined on P\({}_{\textbf{U}}\) in the standard fashion.
Let \({\langle }\kappa _n \mid n<\omega {\rangle }\) be a generic Prikry sequence.
By removing an initial segment if necessary, we can assume that for every \(n<\omega \), \(o(\kappa _{n+1})>(\kappa _n)^+\) is an inaccessible cardinal \(<\kappa _{n+1}\).
The second stage is to force further with Easton support iteration of Prikry, Magidor forcings for changing cofinality of each measurable \(\nu \in \kappa \setminus \{\kappa _n \mid n<\omega \}\) according to \(o(\nu )\). We refer to [3, 4] for details.
Let \(n<\omega \). The sequence \({\langle }U(\kappa _n, \beta ) \mid \beta <o(\kappa _n) {\rangle }\), which is increasing in the Mitchell order, is turned into a sequence \({\langle }U^*(\kappa _n, \beta ) \mid \beta <o(\kappa _n) {\rangle }\) which still increasing, but in the Rudin-Keisler order. We view this sequence as an extender \(E_n\) over \(\kappa _n\).
The final stage will be to force with a short extenders forcing \({\mathcal {P}}\) with \({\langle }E_n \mid n<\omega {\rangle }\).
We just use the forcing of the previous section, but without names anymore.
Note that here we assumed that \(o(\kappa _{n+1})>(\kappa _n)^+\) is an inaccessible cardinal \(<\kappa _{n+1}\). This will guarantee enough completeness at the final stage, and so, will eliminate the need of using names.Footnote 5
Let us argue that there is no maximal set of indiscernibles. An analysis of subsets of \(\kappa \) will be needed for this.
Denote \(V[{\langle }\kappa _n \mid n<\omega {\rangle }]\) by \(V_0\), the second extension by \(V_1\) and the final third by \(V_2\).
Suppose that in \(V_2\) there is a club \(C\subseteq \kappa \) which satisfies Items (A) and (B) above.
Note that for every \(n<\omega \), \(C_n=C\cap \kappa _n \in V_1\), since the forcing with \({\mathcal {P}}\) does not add new bounded subsets to \(\kappa \).
We have \(2^{\kappa _n}=\kappa _n^+\), so \(C_n\) can be coded (in \(V_1\)) by an ordinal \(\xi _n<\kappa _n^+\).
Work in \(V_1\). Let  be a name of such C,
be a name of such C,  and
and  names for \({\langle }C_n \mid n<\omega {\rangle }\) and for \({\langle }\xi _n \mid n<\omega {\rangle }\).
names for \({\langle }C_n \mid n<\omega {\rangle }\) and for \({\langle }\xi _n \mid n<\omega {\rangle }\).
Let \(p\in {\mathcal {P}}\) be a condition forcing this.
Assume for simplicity that \(\ell (p)=0\).
Proceed as in the previous section and find a direct extension \(p^*\) of p such that for every \(m<\omega \), \({\langle }\nu _0,\ldots ,\nu _m{\rangle }\in \prod _{i\le m}A_i(p^*),\)

and so decides  as well.
as well.
Note that there is no need here in suitable extension sequences due to degree of completeness of extenders \(E_n\)’s.
Split now into two cases.
Case 1. For infinitely many \(n<\omega \) there are \(A_m \subseteq A_m(p^*), A_m\in E_{m \max (\textrm{rng}(a_m(p^*)))},\) \( m\le n\) such that for every \({\langle }\nu _0,\ldots ,\nu _n{\rangle }\in \prod _{m\le n}A_m,\) the value of  decided by \( p^*{}^\frown {\langle }\nu _0,\ldots ,\nu _n{\rangle }\) is bounded in \(\kappa _n\).
decided by \( p^*{}^\frown {\langle }\nu _0,\ldots ,\nu _n{\rangle }\) is bounded in \(\kappa _n\).
Then, as in Lemma 2.27, in \(V_2\) there will be \(\alpha <\kappa ^+\) with \(t_\alpha \) being a sequence of indiscernibles such that \(t_\alpha (n) \not \in C\) for infinitely many \(n<\omega \).
Contradiction to the maximality of C, i.e. to Item (B).
Case 2. For all but finitely many \(n<\omega \), for every \({\langle }\nu _0,\ldots ,\nu _n{\rangle }\in \prod _{m\le n}A_m(p^*),\) the value of  decided by \( p^*{}^\frown {\langle }\nu _0,\ldots ,\nu _n{\rangle }\) is unbounded in \(\kappa _n\).
decided by \( p^*{}^\frown {\langle }\nu _0,\ldots ,\nu _n{\rangle }\) is unbounded in \(\kappa _n\).
Let show that then Item (A) breaks down.
Suppose for simplicity that the above holds for every \(n<\omega \).
Fix \(n<\omega \).
Denote the value decided by \( p^*{}^\frown {\langle }\nu _0,\ldots ,\nu _n{\rangle }\) value of  by \(C_n(\nu _0,\ldots ,\nu _n)\).
by \(C_n(\nu _0,\ldots ,\nu _n)\).
By the assumption, it is an unbounded subset of \(\kappa _n\).
Define a function \(h_n\!:\!\prod _{m\le n} \kappa _m \!\rightarrow \! \kappa _n\) by setting \(h_n( \nu _0,\ldots ,\nu _n )\!=\!\textrm{min}(C_n(\nu _0,\ldots ,\nu _n){\setminus } \nu _n+1)\), whenever the right side is defined and 0 otherwise.
Such \({\langle }h_n \mid n<\omega {\rangle }\) naturally defines, in \(V_2\), an unbounded sequence \({\langle }\eta _n \mid n<\omega {\rangle }\in \prod _{n<\omega } \kappa _n\) such that \(\eta _n \in C_n\subseteq C,\) for every \(n<\omega \).
Let us argue that it cannot be a sequence of indiscernibles in some (every) covering model over V. This easily implies a failure of Item (A).
Fix \(n<\omega \). Work in \(V_0\). Recall that the forcing below \(\kappa _n\) used over \(V_0\) in order to get \(V_1\) satisfies \(\kappa _n-\)c.c., nothing is done at \(\kappa _n\) and no new subsets are added to \(\kappa _n\) by iteration above it.
Apply \(\kappa _n-\)c.c.. So, there is a function \(g_n:\prod _{m\le n} \kappa _m \rightarrow \kappa _n\) in \(V_0\) which dominates \(h_n\) everywhere.
Now consider \({\langle }g_n \mid n<\omega {\rangle }\in V_0\).
Recall that \(V_0\) is an extension of V obtained by adding a generic Prikry sequence \({\langle }\kappa _n \mid n<\omega {\rangle }\) for the forcing P\({}_{\textbf{U}}\). No new bounded subsets are added to \(\kappa \) by such extension. In particular, each \(g_n\) is in V.
Work in V. Let  be the sequence of names of \({\langle }g_n \mid n<\omega {\rangle }\). Suppose that a condition \({\langle }{\langle }{\rangle }, T{\rangle }\in \)P\({}_{\textbf{U}}\) forces this.
be the sequence of names of \({\langle }g_n \mid n<\omega {\rangle }\). Suppose that a condition \({\langle }{\langle }{\rangle }, T{\rangle }\in \)P\({}_{\textbf{U}}\) forces this.
Use the normality of the ultrafilters involved and define \({\langle }{\langle }{\rangle }, T^*{\rangle }\ge ^* {\langle }{\langle }{\rangle }, T{\rangle }\) and \({\langle }R_t \mid t \in T^*{\rangle }\) such that for every \(t \in T^*\),
-
1.
\(R_t: [\kappa ]^{<\omega } \rightarrow \kappa \),
-
2.
for every \(\nu \in Suc_{T^*}(t)\),
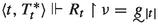 .
.
In particular, for every \(\nu \in Suc_{T^*}({\langle }{\rangle })\),

and, for every \(\nu \in Suc_{T^*}({\langle }\kappa _0 {\rangle })\),

Now, for every \(t \in T^*\) let
Clearly it is a club, and so, is inside every \(U(\kappa ,\beta ), \beta <\kappa \).
Set
Clearly, A is a club. Then \(A \in U(\kappa ,\beta ), \beta <\kappa \), due to normality.
Now, let us argue that in \(V_2\), \(C{\setminus } A\) will be unbounded in \(\kappa \), as witnessed by \({\langle }\eta _n \mid n<\omega {\rangle }\). This will contradict Item (A).
Namely, assume that \(\eta _n \in A\), for some \(n<\omega \). Then
We have \(R_{{\langle }\kappa _0,\ldots ,\kappa _{n-1}{\rangle }}\upharpoonright \kappa _n=g_n\).
Hence, \(R_{{\langle }\kappa _0,\ldots ,\kappa _{n-1}{\rangle }}(\nu _0,\ldots ,\nu _n)=g_n(\nu _0,\ldots ,\nu _n)>\eta _n\), and so, \(\eta _n \not \in A_{{\langle }\kappa _0,\ldots ,\kappa _{n-1}{\rangle }}\).
But \(\eta _n>\kappa _{n-1}=\max ({{\langle }\kappa _0,\ldots ,\kappa _{n-1}{\rangle }})\) and \(\eta _n\in A\), hence \(\eta _n \in A_{{\langle }\kappa _0,\ldots ,\kappa _{n-1}{\rangle }}\). Which is impossible. Contradiction.
Notes
It is possible to simplify the names in the definition further by putting additional requirements on agreements between Cohen functions involved and using \(\kappa -\)completeness of this forcing.
It is possible to define this type forcing using "simpler names". For example, we can require that
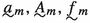 depend only on the previous coordinate \(m-1\). The degree of completeness of the forcing at the level m is \(\kappa _{m-1}\). This can be used in order to eliminate dependence on levels below \(m-1\).
depend only on the previous coordinate \(m-1\). The degree of completeness of the forcing at the level m is \(\kappa _{m-1}\). This can be used in order to eliminate dependence on levels below \(m-1\).Recall that an ordinal \(\eta \) is called a generator of an extender F over \(\lambda \), if for every \(n<\omega \) and \(h:[\lambda ]^n\rightarrow \lambda \), \(\eta \not =j_F(h)(a)\), for any \(a\in [\eta ]^{n}\), where \(j_F\) denotes the corresponding elementary embedding.
Note that \(o(\kappa _n)=\kappa _{n-1}\) implies that the measure over \(\kappa _n \) to which \(c_n\) corresponds is \(U(\kappa _n, o(c_n))\).
In the previous section, the assumption \(o(\kappa _{n+1})=\kappa _n\) was used, as required by Mitchell in his problem, see the introduction.
We think that it is possible to proceed without the assumptions on \(V={\mathcal {K}}\) and to use the arguments of [8] instead, however this seems to be lengthy and likely to require another paper.
References
Ben-Neria, O., Gitik, M., Neeman, I., Unger, S.: On the powersets of singular cardinals in HOD. Proc. Am. Math. Soc. 148(4), 1777–1789 (2020)
Cummings, J.: Iterated forcing and elementary embeddings. In: Foreman, K. (ed.) Handbook of Set Theory, vol. 2, pp. 776–879. Springer, Berlin (2010)
Gitik, M.: Prikry type forcings. In: Foreman, K. (ed.) Handbook of Set Theory, vol. 2, pp. 1351–1447. Springer, Berlin (2010)
Gitik, M.: Changing cofinality and the nonstationary ideal. Israel J. Math. 56(3), 280–314 (1986)
Gitik, M.: The strength of the failure of the Singular Cardinal Hypothesis. Ann. Pure Appl. Logic 51, 215–240 (1991)
Gitik, M.: Blowing up the power of a singular cardinal. Ann. Pure Appl. Logic 80, 17–33 (1996)
Gitik, M., Kaplan, E.: On restrictions of ultrafilter from generic extensions to ground models. J. Symb. Logic 88(1), 169–190 (2023)
Gitik, M., Kaplan, E.: On Easton support iteration of Prikry type forcing notions. J. Symb. Logic (2023). https://doi.org/10.48550/arXiv.2301.12421
Mitchell, W.: The core model for sequences of measures I. Math. Proc. Camb. Philos. Soc. 95, 1449–1495 (1984)
Mitchell, W.: On the singular cardinal hypothesis. Trans. Am. Math. Soc. 329(2), 507–530 (1992)
Mitchell, W.: The covering Lemma. In: Foreman, K. (ed.) Handbook of Set Theory, vol. 3, pp. 1497–1594. Springer, Berlin (2010)
Schindler, R.: Iterates of the core model. J. Symb. Logic 71(1), 241–251 (2006)
Funding
Open access funding provided by Tel Aviv University. We are grateful to the referee of the paper for his remarks and corrections. The work was partially supported by ISF Grants No. 1216/18, 882/22.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix on the ultrafilters structure after the forcing of [4]
Appendix on the ultrafilters structure after the forcing of [4]
Our purpose here will be to show that for every \(\gamma <\kappa _0\), \(j_{U(\kappa _1,\gamma )}(\kappa _1)=j_{U^*(\kappa _1,\gamma )}(\kappa _1)\), building on the arguments of [4].
Recall the basic settings of [4], Sects. 2, 3 with adaptations to our present context.
So, we have an Easton support iteration  of Prikry type forcing notions. Let \(G(P_{\kappa _1})\) denotes a generic subset of \(P_{\kappa _1}\). We have \(V_1=V[G(P_{\kappa _1})]\).
of Prikry type forcing notions. Let \(G(P_{\kappa _1})\) denotes a generic subset of \(P_{\kappa _1}\). We have \(V_1=V[G(P_{\kappa _1})]\).
Let \(\gamma <\kappa _1\). Then \(U^*(\kappa _1,\gamma )\) is defined as follows:
\(X\in U^*(\kappa _1,\gamma )\) iff \(X\subseteq \kappa \), for some \(r \in G(P_{\kappa _1})\), \(\xi <\kappa _1^+\), names  of X,
of X,  , in \(M_{U(\kappa _1,\gamma )}\), the following holds:
, in \(M_{U(\kappa _1,\gamma )}\), the following holds:

where \(p_\xi \) is from the master condition sequence above \(\kappa _1\).
By Sects. 2, 3 of [4], \(U^*(\kappa _1,\gamma )\) extends \(U(\kappa _1,\gamma )\) and \(Cub_{\kappa _1}\). However, it is not normal, unless \(\gamma =0\).
For each \(\beta <\gamma \), \(U^*(\kappa _1,\gamma )\ge _{R-K} U^*(\kappa _1,\beta )\). Moreover, the function that maps a typical \(\nu <\kappa _1\) to the \(\omega ^\beta -\)th member of a generic Prikry or Magidor sequence of \(\nu \) projects \(U^*(\kappa _1,\gamma )\) onto \(U^*(\kappa _1,\beta )\). Denote by \(k_{\beta \gamma }: M_{U^*(\kappa _1,\beta )} \rightarrow M_{U^*(\kappa _1,\gamma )}\) the corresponding embedding.
Lemma 4.1
Let \(\gamma <\kappa _0\) and \(\alpha \) be an ordinal in the interval \(( [id]_{U^*(\kappa _1,\gamma )}, j_{U^*(\kappa _1,\gamma )}(\kappa _1))\). Set \(U^*(\kappa _1,\gamma )_\alpha =\{X\subseteq \kappa _1\mid \alpha \in j_{U^*(\kappa _1,\gamma )}(X)\}\). Then, for some club C of \(\kappa _1\) in V, \(C\not \in U^*(\kappa _1,\gamma )_\alpha \).
Proof
Let \(\gamma <\kappa _0\) and \(\alpha \) be an ordinal in the interval \(( [id]_{U^*(\kappa _1,\gamma )}, j_{U^*(\kappa _1,\gamma )}(\kappa _1))\). Pick a function \(f:\kappa _1\rightarrow \kappa _1\) such that \(j_{U^*(\kappa _1,\gamma )}(f)([id]_{U^*(\kappa _1,\gamma )})=\alpha \). The forcing \(P_{\kappa _1}\) satisfies \(\kappa _1-\)c.c., so there will be \(g:\kappa _1\rightarrow \kappa _1\) in V, which dominates f mod bounded. Then \(\alpha <[g]_{U^*(\kappa _1,\gamma )}\). Define
Then C is a club in V and \(C\not \in U^*(\kappa _1,\gamma )_\alpha \). \(\square \)
Fix \(\gamma <\kappa _0\).
Let us deal with functions below the identity function. If \(\gamma =0\), then they are just constant, since \(U^*(\kappa _1,0)\) is a normal ultrafilter. So assume that \(\gamma >0\) and let \(f:\kappa \rightarrow \kappa \) such that \([f]_{U^*(\kappa _1,\gamma )}<[id]_{U^*(\kappa _1,\gamma )}\).
Then, by the Prikry (or what is now called a strong Prikry) property of the forcing  , there will be \(\beta <\gamma \) and a function \(h:\kappa \rightarrow \kappa \) (or may be a function \(h:[\kappa ]^n\rightarrow \kappa \), for some \(n, 1<n<\omega \)) such that f is equal to h mod \(U^*(\kappa _1,\beta )\) (or in the later case mod finite product of such type of ultrafilters). Let us assume for simplicity we deal with a single ultrafilter \(U^*(\kappa _1,\beta )\). Such \(\beta \) can be taken to be the least such that \([f]_{U^*(\kappa _1,\gamma )}\) is below the \(\beta +1-\)th member of the generic Prikry or Magidor sequence for \([id]_{U^*(\kappa _1,\gamma )}\) in \(M_{U^*(\kappa _1,\gamma )}\). Note that the length of the ultrafilters sequence is \(\kappa _0<\kappa _1\), and hence the statements of this type can be decided by taking a direct extension.
, there will be \(\beta <\gamma \) and a function \(h:\kappa \rightarrow \kappa \) (or may be a function \(h:[\kappa ]^n\rightarrow \kappa \), for some \(n, 1<n<\omega \)) such that f is equal to h mod \(U^*(\kappa _1,\beta )\) (or in the later case mod finite product of such type of ultrafilters). Let us assume for simplicity we deal with a single ultrafilter \(U^*(\kappa _1,\beta )\). Such \(\beta \) can be taken to be the least such that \([f]_{U^*(\kappa _1,\gamma )}\) is below the \(\beta +1-\)th member of the generic Prikry or Magidor sequence for \([id]_{U^*(\kappa _1,\gamma )}\) in \(M_{U^*(\kappa _1,\gamma )}\). Note that the length of the ultrafilters sequence is \(\kappa _0<\kappa _1\), and hence the statements of this type can be decided by taking a direct extension.
So, \(k_{\beta \gamma }\upharpoonright j_{U^*(\kappa _1,\beta )}(\kappa _1) \) is the identity. Then, the critical point of \(k_{\beta \gamma }\) is \(j_{U^*(\kappa _1,\beta )}\) and, in \(M_{U^*(\kappa _1,\gamma )}\), it is the \(\beta +1-\)th member of the generic sequence of \([id]_{U^*(\kappa _1,\gamma )}\).
Let us assume that there is no inner model which satisfies \(\exists \alpha \quad o(\alpha )=\alpha ^{++}\) and V is the core model \({\mathcal {K}}\).Footnote 6 Consider \(j:=j_{U^*(\kappa _1,\gamma )}\upharpoonright {\mathcal {K}}:{\mathcal {K}}\rightarrow {\mathcal {K}}_1\), where \({\mathcal {K}}_1\) denotes the core model of \(M_{U^*(\kappa _1,\gamma )}\). By W. Mitchell [9] (or by R. Schindler [12] in a wider context) it is a normal (i.e., a measure with a smaller index is used before the one with a bigger index) iteration of \({\mathcal {K}}\) by its measures. We have here \({}^{\kappa _1}M_{U^*(\kappa _1,\gamma )}\subseteq M_{U^*(\kappa _1,\gamma )}\) which implies by [9] that measures can be used in the iteration at most \(\omega -\)many times.
Recall that \(U(\kappa _1,\gamma )\subseteq U^*(\kappa _1,\gamma )\), \(M_{U^*(\kappa _1,\gamma )}\) is an ultrapower by \(U^*(\kappa _1,\gamma )\) and \(\gamma <\kappa _0\). This implies that \(U(\kappa _1,\gamma )\) (or its images) were used in the iterated ultrapower j. Let \(\tilde{j}:{\mathcal {K}}\rightarrow {\tilde{{\mathcal {K}}}}\) be the part of j up to the first step of the iteration j when \(U(\kappa _1,\gamma )\) was used, i.e. the next step is the ultrapower by \(\tilde{j}(U(\kappa _1,\gamma ))\), and then the iteration continues to \({\mathcal {K}}_1\). Denote the rest of the iteration by k. So, \(j=k\circ j_{\tilde{j}(U(\kappa _1,\gamma ))}\circ \tilde{j}\). Denote \(j_{\tilde{j}(U(\kappa _1,\gamma ))}\circ \tilde{j}\) by \(j'\)
Let us argue that \(j_{\tilde{j}(U(\kappa _1,\gamma ))}(\tilde{j}(\kappa _1))=j_{U(\kappa _1,\gamma )}(\kappa _1)\) and k does not move it further.
Deal with \(j':{\mathcal {K}}\rightarrow {\mathcal {K}}'\). Change the order of the iteration \(j'\) by applying \(U(\kappa _1,\gamma )\) first and then all the rest. Then \(j'=k'\circ j_{U(\kappa _1,\gamma )}\), for some \(k':M_{U(\kappa _1,\gamma )}\rightarrow {\mathcal {K}}'\). Note that \(j_{U(\kappa _1,\gamma )}(\kappa _1)\) will not be moved by \(k'\) due to its inaccessibility in \(M_{U(\kappa _1,\gamma )}\) and the anti-large cardinals assumptions made. Hence, \(j_{U(\kappa _1,\gamma )}(\kappa _1)=k'(j_{U(\kappa _1,\gamma )}(\kappa _1))=j'(\kappa _1).\) Suppose for a moment that the further iteration k is not the identity. Then its critical point is \(j'(\kappa _1)\), by the choice of \(j'\). However, if \([id]_{U^*(\kappa _1,\gamma )}<j'(\kappa _1)<j_{U^*(\kappa _1,\gamma )}(\kappa _1)\), then Lemma 4.1 will imply the contradiction.
So it remains to show that \([id]_{U^*(\kappa _1,\gamma )}<j'(\kappa _1)\). Suppose otherwise. Then
Consider the ultrafilter \(W=\{X\subseteq \kappa _1 \mid k'(\kappa _1)\in j_{U^*(\kappa _1,\gamma )}(X)\}\), in \(V_1\). It extends \(U(\kappa _1,\gamma )\). However, by the previous observations, each \(\delta <[id]_{U^*(\kappa _1,\gamma )}\) can be located already in the ultrapower by \(U^*(\kappa ,\beta )\), for some \(\beta <\gamma \) (or using a finite product of such ultrafilters). In particular, pick such \(\beta <\gamma \) for \(\delta =k'(\kappa _1)\). This will mean that \(U^*(\kappa ,\beta )\) (or a finite product) will be above, in the Rudin-Kiesler order, of the ultrafilter W which extends \(U(\kappa _1,\gamma )\). We can use the induction and assume that \(j_{U^*(\kappa ,\alpha )}(\kappa )=j_{U(\kappa ,\alpha )}(\kappa )\), for every \(\alpha <\gamma \). In particular, \(j_{U^*(\kappa ,\beta )}(\kappa )=j_{U(\kappa ,\beta )}(\kappa )\). However, \(j_{U(\kappa ,\beta )}(\kappa ) <j_{U(\kappa ,\gamma )}(\kappa )\), since \(U(\kappa ,\beta )\lhd U(\kappa ,\gamma )\), which rules out the possibility of existence of such W.
Contradiction.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gitik, M. Around accumulation points and maximal sequences of indiscernibles. Arch. Math. Logic (2024). https://doi.org/10.1007/s00153-024-00913-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00153-024-00913-w



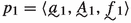 ,
,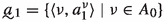 ,
, 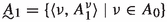 and
and 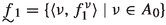 are such that
are such that 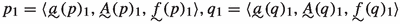 ,
,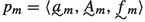 , where
, where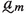 consists of pairs
consists of pairs 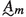 consists of pairs
consists of pairs  consists of pairs
consists of pairs 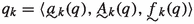 , where
, where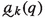 consists of pairs
consists of pairs 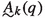 consists of pairs
consists of pairs 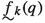 consists of pairs
consists of pairs 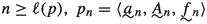 ,
,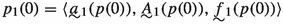 , where
, where 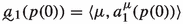 , where
, where 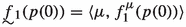 , where
, where 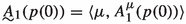 , where
, where 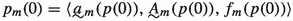 , where
, where  ,
,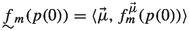 ,
,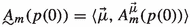 ,
,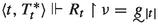 .
.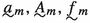 depend only on the previous coordinate
depend only on the previous coordinate