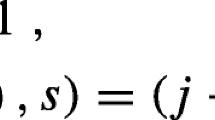Imperative Process Algebra and Models of Parallel Computation

Abstract

Studies of issues related to computability and computational complexity involve the use of a model of computation. Central in such a model are computational processes. Processes of this kind can be described using an imperative process algebra based on ACP (Algebra of Communicating Processes). In this paper, it is investigated whether the imperative process algebra concerned can play a role in the field of models of computation. It is demonstrated that the process algebra is suitable to describe in a mathematically precise way models of computation corresponding to existing models based on sequential, asynchronous parallel, and synchronous parallel random access machines as well as time and work complexity measures for those models.

1 Introduction

Central in a model of computation are computational processes, i.e. processes that solve a computational problem. A computational process is applied to a data environment that consists of data organized and accessible in a specific way. Well-known examples of data environments are the tapes found in Turing machines and the memories found in random access machines. The application of a computational process to a data environment yields another data environment. The data environment to which the process is applied represents an instance of the computational problem that is solved by the process and the data environment yielded by the application represents the solution of that instance. A computational process is divided into simple steps, each of which depends on and has an impact on only a small portion of the data environment to which the process is applied.

A basic assumption in this paper is that a model of computation is fully characterized by: (a) a set of possible computational processes, (b) for each possible computational process, a set of possible data environments, and (c) the effect of applying such processes to such environments. The set of possible computational processes is usually given indirectly, mostly by means of abstract machines that have a built-in program that belongs to a set of possible programs which is such that the possible computational processes are exactly the processes that are produced by those machines when they execute their built-in program. The abstract machines with their built-in programs emphasize the mechanical nature of the possible computational processes. However, in this way, details of how possible computational processes are produced become part of the model of computation. To the best of my knowledge, all definitions that have been given with respect to a model of computation and all results that have been proved with respect to a model of computation can do without reference to such details.

In [29], an extension of ACP (Algebra of Communicating Processes) [5] is presented whose additional features include assignment actions to change data in the course of a process, guarded commands to proceed at certain stages of a process in a way that depends on changing data, and data parameterized actions to communicate data between processes. The extension concerned is called $\text {ACP}_{\epsilon }^{\tau }$-I.

The term imperative process algebra was coined in [13] for process algebras like $\text {ACP}_{\epsilon }^{\tau }$-I. Some examples of other imperative process algebras are VPLA [22], IPAL [13], CSP$_\sigma$ [11], AWN [15], and the nameless process algebra proposed in [9]. In [29], it is discussed what qualities of $\text {ACP}_{\epsilon }^{\tau }$-I distinguish it from imperative process algebras such as the above-mentioned ones, how its distinguishing qualities are achieved, and what its relevance is to the verification of properties of processes carried out by contemporary computer-based systems. Moreover, that paper goes into one of the application areas of $\text {ACP}_{\epsilon }^{\tau }$-I, namely the area of information-flow security analysis.

The current paper studies whether $\text {ACP}_{\epsilon }^{\tau }$-I can play a role in the field of models of computation. The idea of this study originates from the experience that definitions of models of computation and results about them in the scientific literature tend to lack preciseness, in particular if it concerns models of parallel computation. The study takes for granted the basic assumption about the characterization of models of computation mentioned above. Moreover, it focuses on models of computation that are intended for investigation of issues related to computability and computational complexity. It does not consider models of computation geared to computation as it takes place on concrete computers or computer networks of a certain kind. Such models are left for follow-up studies. Outcomes of this study are among other things mathematically precise definitions of models of computation corresponding to models based on sequential random access machines, asynchronous parallel random access machines, and synchronous parallel random access machines.

This paper is organized as follows. First, a survey of the imperative process algebra $\text {ACP}_{\epsilon }^{\tau }$-I and its extension with recursion is given (Section 2). Next, it is explained in this process algebra what it means that a given process computes a given function (Section 3). After that, a version of the sequential random access machine model of computation is described in the setting introduced in the previous two sections (Section 4). Following that, an asynchronous parallel random access machine model of computation and a synchronous parallel random access machine model of computation are described in that setting as well (Sections 5 and 6, respectively). Then, complexity measures for the models of computation presented in the previous three sections are introduced (Section 7). Thereafter, the question whether the presented synchronous parallel random access machine model of computation is a reasonable model of computation is treated (Section 8). Finally, some concluding remarks are made (Section 9).

Section 2 is an abridged version of [29]. Portions of Sections 2-4 of that paper have been copied verbatim or slightly modified.

2 The Imperative Process Algebra ACP$_{\epsilon }^{\tau }$-I

The imperative process algebra $\text {ACP}_{\epsilon }^{\tau }$-I is an extension of $\text {ACP}_{\epsilon }^{\tau }$, the version of $\text {ACP}$ with empty process and silent step constants that was first presented in [4, Section 5.3]. In this section, first a survey of $\text {ACP}_{\epsilon }^{\tau }$ is given and then $\text {ACP}_{\epsilon }^{\tau }$-I is introduced as an extension of $\text {ACP}_{\epsilon }^{\tau }$. Moreover, recursion in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I is treated and some relevant results about $\text {ACP}_{\epsilon }^{\tau }$-I with recursion are presented.

2.1 $\text {ACP}$ with Empty Process and Silent Step

The survey of $\text {ACP}_{\epsilon }^{\tau }$ given in this section is kept brief. A more comprehensive treatment of this process algebra can be found in [4, Section 5.3].

In $\text {ACP}_{\epsilon }^{\tau }$, it is assumed that a fixed but arbitrary finite set $\textsf{A}$ of basic actions, with $\tau ,\delta ,\epsilon \not \in \textsf{A}$, and a fixed but arbitrary commutative and associative communication function ${\gamma } \, {:}\, (\textsf{A}\cup \{ \tau ,\delta \}) \times (\textsf{A}\cup \{ \tau ,\delta \}) \rightarrow (\textsf{A}\cup \{ \tau ,\delta \})$, such that $\gamma (\tau ,a) = \delta$ and $\gamma (\delta ,a) = \delta$ for all $a \in \textsf{A}\cup \{ \tau ,\delta \}$, have been given. Basic actions are taken as atomic processes. The function $\gamma$ is regarded to give the result of simultaneously performing any two basic actions for which this is possible, and to be $\delta$ otherwise. Henceforth, we write ${\textsf{A}_\tau }$ for $\textsf{A}\cup \{ \tau \}$ and ${\textsf{A}_{\tau \delta }}$ for $\textsf{A}\cup \{ \tau ,\delta \}$.

The algebraic theory $\text {ACP}_{\epsilon }^{\tau }$ has one sort: the sort $\textbf{P}$ of processes. This sort is made explicit to anticipate the need for many-sortedness later on. The algebraic theory $\text {ACP}_{\epsilon }^{\tau }$ has the following constants and operators to build terms of sort $\textbf{P}$:

• a basic action constant ${a} \, {:}\, \textbf{P}$ for each $a \in \textsf{A}$;

• a silent step constant ${\tau } \, {:}\, \textbf{P}$;

• an inaction constant ${\delta } \, {:}\, \textbf{P}$;

• an empty process constant ${\epsilon } \, {:}\, \textbf{P}$;

• a binary alternative composition or choice operator ${\,{+}\,} \, {:}\, \textbf{P}\times \textbf{P} \rightarrow \textbf{P}$;

• a binary sequential composition operator ${\cdot } \, {:}\, \textbf{P}\times \textbf{P} \rightarrow \textbf{P}$;

• a binary parallel composition or merge operator ${\, {\parallel }\,} \, {:}\, \textbf{P}\times \textbf{P} \rightarrow \textbf{P}$;

• a binary left merge operator ${\lfloor \kern-.25em\lfloor } \, {:}\, \textbf{P}\times \textbf{P} \rightarrow \textbf{P}$;

• a binary communication merge operator ${\mid } \, {:}\, \textbf{P}\times \textbf{P} \rightarrow \textbf{P}$;

• a unary encapsulation operator ${{\partial _{H}}} \, {:}\, \textbf{P} \rightarrow \textbf{P}$ for each $H \subseteq \textsf{A}$ and for $H = {\textsf{A}_\tau }$;

• a unary abstraction operator ${{\tau _{I}}} \, {:}\, \textbf{P} \rightarrow \textbf{P}$ for each $I \subseteq \textsf{A}$.

It is assumed that there is a countably infinite set $\mathcal {X}$ of variables of sort $\textbf{P}$, which contains x, y and z. Terms are built as usual. Infix notation is used for the binary operators. The following precedence conventions are used to reduce the need for parentheses: the operator ${} \cdot {}$ binds stronger than all other binary operators and the operator ${} \,{+}\,{}$ binds weaker than all other binary operators.

The constants a ($a \in \textsf{A}$), $\tau$, $\epsilon$, and $\delta$ can be explained as follows:

• a denotes the process that first performs the observable action a and then terminates successfully;

• $\tau$ denotes the process that first performs the unobservable action $\tau$ and then terminates successfully;

• $\epsilon$ denotes the process that terminates successfully without performing any action;

• $\delta$ denotes the process that cannot do anything, it cannot even terminate successfully.

Let t and $t'$ be closed $\text {ACP}_{\epsilon }^{\tau }$ terms denoting processes p and $p'$, respectively. Then the operators $\,{+}\,$, $\cdot$, $\, {\parallel }\,$, ${\partial _{H}}$ ($H \subseteq \textsf{A}$ or $H = {\textsf{A}_\tau }$), and ${\tau _{I}}$ ($I \subseteq \textsf{A}$) can be explained as follows:

• $t \,{+}\,t'$ denotes the process that behaves as either p or $p'$;

• $t \cdot t'$  denotes the process that behaves as p and $p'$ in sequence;

• $t \, {\parallel }\,t'$ denotes the process that behaves as p and $p'$ in parallel;

• ${\partial _{H}}(t)$ denotes the process that behaves as p, except that actions from H are blocked from being performed;

• ${\tau _{I}}(t)$  denotes the process that behaves as p, except that actions from I are turned into the unobservable action $\tau$.

Here “behaves as p and $p'$ in parallel” means that (a) each time an action is performed, either a next action of p is performed or a next action of $p'$ is performed or a next action of p and a next action of $p'$ are performed synchronously and (b) successful termination may take place at any time that both p and $p'$ can terminate successfully.

The operators ${\lfloor \kern-.25em\lfloor }$ and ${\mid }$ are of an auxiliary nature. They make a finite axiomatization of $\text {ACP}_{\epsilon }^{\tau }$ possible.

Table 1 Axioms of ACP$_{\epsilon }^{\tau }$

The axioms of $\text {ACP}_{\epsilon }^{\tau }$ are presented in Table 1. In this table, a, b, and $\alpha$ stand for arbitrary members of ${\textsf{A}_{\tau \delta }}$,  H stands for an arbitrary subset of $\textsf{A}$ or the set ${\textsf{A}_\tau }$, and I stands for an arbitrary subset of $\textsf{A}$. So, CM3, CM7, D0–D4, T0–T4, and BE are actually axiom schemas. In this paper, axiom schemas are usually referred to as axioms.

The term ${\partial _{{\textsf{A}_\tau }}}\!(x) \cdot {\partial _{{\textsf{A}_\tau }}}\!(y)$ occurring in axiom CM1E is needed to handle successful termination in the presence of $\epsilon$: it stands for the process that behaves the same as $\epsilon$ if both x and y stand for a process that has the option to behave the same as $\epsilon$ and it stands for the process that behaves the same as $\delta$ otherwise. In [4, Section 5.3], the symbol $\surd$ is used instead of ${\partial _{{\textsf{A}_\tau }}}$.

Notice that the equation $\alpha \cdot \delta = \alpha$ would be derivable from the axioms of $\text {ACP}_{\epsilon }^{\tau }$ if operators ${\partial _{H}}$ where $H \ne {\textsf{A}_\tau }$ and $\tau \in H$ were added to $\text {ACP}_{\epsilon }^{\tau }$.

The notation $\sum _{i=1}^{n} t_i$, where $n \ge 1$, is used for right-nested alternative compositions. For each $n \in \mathbb {N}^+$,¹ the term $\sum _{i = 1}^{n} t_i$ is defined by induction on n as follows: $\sum _{i = 1}^{1} t_i = t_1$ and $\sum _{i = 1}^{n + 1} t_i = t_1 \,{+}\,\sum _{i = 1}^{n} t_{i+1}$. In addition, the convention is used that $\sum _{i = 1}^{0} t_i = \delta$. Moreover, we write ${\partial _{a}}$ and ${\tau _{a}}$, where $a \in \textsf{A}$, for ${\partial _{\{ a \}}}$ and ${\tau _{\{ a \}}}$, respectively.

2.2 Imperative ACP$_{\epsilon }^{\tau }$-I

This section concerns $\text {ACP}_{\epsilon }^{\tau }$-I, imperative $\text {ACP}_{\epsilon }^{\tau }$. $\text {ACP}_{\epsilon }^{\tau }$-I extends $\text {ACP}_{\epsilon }^{\tau }$ with features to communicate data between processes, to change data involved in a process in the course of the process, and to proceed at certain stages of a process in a way that depends on the changing data. A more comprehensive treatment of this imperative process algebra than that given in this section can be found in [29], the paper in which $\text {ACP}_{\epsilon }^{\tau }$-I was first presented.

In $\text {ACP}_{\epsilon }^{\tau }$-I, it is assumed that the following has been given with respect to data:

• a many-sorted signature $\Sigma _{\mathfrak {D}}$ that includes:

  • a sort ${\textbf{D}}$ of data and a sort ${\textbf{B}}$ of bits;

  • constants of sort ${\textbf{D}}$ and/or operators with result sort ${\textbf{D}}$;

  • constants $0$ and $1$ of sort ${\textbf{B}}$ and operators with result sort ${\textbf{B}}$;

• a minimal algebra ${\mathfrak {D}}$ of the signature $\Sigma _{\mathfrak {D}}$ in which the carrier of sort ${\textbf{B}}$ has cardinality 2 and the equation $0= 1$ does not hold.

The sort ${\textbf{B}}$ is assumed to be given in order to make it possible for operations to serve as predicates.

In $\text {ACP}_{\epsilon }^{\tau }$-I, it is moreover assumed that a finite or countably infinite set $\mathcal {V}$ of flexible variables has been given. A flexible variable is a variable whose value may change in the course of a process. The term flexible variable is used for this kind of variables in e.g. [26, 35].

We write $\mathbb {D}$ for the set of all closed terms over the signature $\Sigma _{\mathfrak {D}}$ that are of sort ${\textbf{D}}$.

A flexible variable valuation is a function from $\mathcal {V}$ to $\mathbb {D}$. We write $\mathcal{V}\mathcal{V}\kern-.1em al$ for the set of all flexible variable valuations.

Flexible variable valuations are intended to provide the data values — which are members of ${\mathfrak {D}}$’s carrier of sort ${\textbf{D}}$ — assigned to flexible variables when an $\text {ACP}_{\epsilon }^{\tau }$-I term of sort ${\textbf{D}}$ is evaluated. To fit better in an algebraic setting, they provide closed terms from $\mathbb {D}$ that denote those data values instead.

Because ${\mathfrak {D}}$ is a minimal algebra, for each sort S that is included in $\Sigma _{\mathfrak {D}}$, each member of ${\mathfrak {D}}$’s carrier of sort S can be represented by a closed term over $\Sigma _{\mathfrak {D}}$ that is of sort S.

In the rest of this paper, for each sort S that is included in $\Sigma _{\mathfrak {D}}$, let $ct _S$ be a function from ${\mathfrak {D}}$’s carrier of sort S to the set of all closed terms over $\Sigma _{\mathfrak {D}}$ that are of sort S such that, for each member d of ${\mathfrak {D}}$’s carrier of sort S, the term $ct _S(d)$ represents d. We write d, where d is a member of ${\mathfrak {D}}$’s carrier of sort S, for $ct _S(d)$ if it is clear from the context that d stands for a closed term of sort S representing d.

Flexible variable valuations are used in Sections 4–6 to represent the data enviroments referred to in Section 1.

Let $V \subseteq \mathcal {V}$. Then a V-indexed data environment is a function from V to ${\mathfrak {D}}$’s carrier of sort ${\textbf{D}}$. Let $\mu$ be a V-indexed data environment and $\rho$ be a flexible variable valuation. Then $\rho$ represents $\mu$ if $\rho (v) = ct _{\textbf{D}}(\mu (v))$ for all $v \in V$.

Below, the sorts, constants and operators of $\text {ACP}_{\epsilon }^{\tau }$-I are introduced. The operators of $\text {ACP}_{\epsilon }^{\tau }$-I include two variable-binding operators. The formation rules for $\text {ACP}_{\epsilon }^{\tau }$-I terms are the usual ones for the many-sorted case (see e.g. [34, 38]) and in addition the following rule:

• if O is a variable-binding operator ${O} \, {:}\, S_1 \times \ldots \times S_n \rightarrow S$ that binds a variable of sort $S'$, $t_1,\ldots ,t_n$ are terms of sorts $S_1,\ldots ,S_n$, respectively, and X is a variable of sort $S'$, then $O X (t_1,\ldots ,t_n)$ is a term of sort S.

An extensive formal treatment of the phenomenon of variable-binding operators can be found in [33].

$\text {ACP}_{\epsilon }^{\tau }$-I has the following sorts: the sorts included in $\Sigma _{\mathfrak {D}}$, the sort ${\textbf{C}}$ of conditions, and the sort $\textbf{P}$ of processes.

For each sort S included in $\Sigma _{\mathfrak {D}}$ other than ${\textbf{D}}$, $\text {ACP}_{\epsilon }^{\tau }$-I has only the constants and operators included in $\Sigma _{\mathfrak {D}}$ to build terms of sort S.

$\text {ACP}_{\epsilon }^{\tau }$-I has, in addition to the constants and operators included in $\Sigma _{\mathfrak {D}}$ to build terms of sorts ${\textbf{D}}$, the following constants to build terms of sort ${\textbf{D}}$:

• for each $v \in \mathcal {V}$, the flexible variable constant ${v} \, {:}\, {\textbf{D}}$.

We write $\mathcal {D}$ for the set of all closed $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort ${\textbf{D}}$.

$\text {ACP}_{\epsilon }^{\tau }$-I has the following constants and operators to build terms of sort ${\textbf{C}}$:

• a binary equality operator ${=} \, {:}\, {\textbf{B}}\times {\textbf{B}} \rightarrow {\textbf{C}}$;

• a binary equality operator ${=} \, {:}\, {\textbf{D}}\times {\textbf{D}} \rightarrow {\textbf{C}}$;²

• a truth constant ${{\textsf{t}}} \, {:}\, {\textbf{C}}$;

• a falsity constant ${{\textsf{f}}} \, {:}\, {\textbf{C}}$;

• a unary negation operator ${\lnot } \, {:}\, {\textbf{C}} \rightarrow {\textbf{C}}$;

• a binary conjunction operator ${\wedge } \, {:}\, {\textbf{C}}\times {\textbf{C}} \rightarrow {\textbf{C}}$;

• a binary disjunction operator ${\vee } \, {:}\, {\textbf{C}}\times {\textbf{C}} \rightarrow {\textbf{C}}$;

• a binary implication operator ${ {\Rightarrow }} \, {:}\, {\textbf{C}}\times {\textbf{C}} \rightarrow {\textbf{C}}$;

• a unary variable-binding universal quantification operator ${\forall } \, {:}\, {\textbf{C}} \rightarrow {\textbf{C}}$ that binds a variable of sort ${\textbf{D}}$;

• a unary variable-binding existential quantification operator ${\exists } \, {:}\, {\textbf{C}} \rightarrow {\textbf{C}}$ that binds a variable of sort ${\textbf{D}}$.

We write $\mathcal {C}$ for the set of all closed $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort ${\textbf{C}}$.

$\text {ACP}_{\epsilon }^{\tau }$-I has, in addition to the constants and operators of $\text {ACP}_{\epsilon }^{\tau }$, the following operators to build terms of sort $\textbf{P}$:

• an n-ary data parameterized action operator ${a} \, {:}\, {\textbf{D}}^n \rightarrow \textbf{P}$ for each $a \in \textsf{A}$, for each $n \in \mathbb {N}$;

• a unary assignment action operator ${v \, {{:}{=}}\,} \, {:}\, {\textbf{D}} \rightarrow \textbf{P}$ for each $v \in \mathcal {V}$;

• a binary guarded command operator ${{:\rightarrow }\,} \, {:}\, {\textbf{C}}\times \textbf{P} \rightarrow \textbf{P}$;

• a unary evaluation operator ${{\textsf{V}_{\rho }}} \, {:}\, \textbf{P} \rightarrow \textbf{P}$ for each $\rho \in \mathcal{V}\mathcal{V}\kern-.1em al$.

We write $\mathcal {P}$ for the set of all closed $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort $\textbf{P}$.

It is assumed that there are countably infinite sets of variables of sort ${\textbf{D}}$ and ${\textbf{C}}$ and that the sets of variables of sort ${\textbf{D}}$, ${\textbf{C}}$, and $\textbf{P}$ are mutually disjoint and disjoint from $\mathcal {V}$.

The same notational conventions are used as before. Infix notation is also used for the additional binary operators. Moreover, the notation $[v \, {{:}{=}} e]$, where $v \in \mathcal {V}$ and e is a $\text {ACP}_{\epsilon }^{\tau }$-I term of sort ${\textbf{D}}$, is used for the term $v \, {{:}{=}}\,(e)$.

Each term from $\mathcal {C}$ can be taken as a formula of a first-order language with equality of ${\mathfrak {D}}$ by taking the flexible variable constants as variables of sort ${\textbf{D}}$. The flexible variable constants are implicitly taken as variables of sort ${\textbf{D}}$ wherever the context asks for a formula. In this way, each term from $\mathcal {C}$ can be interpreted in ${\mathfrak {D}}$ as a formula.

The notation $\phi \, {\Leftrightarrow}\,\psi$, where $\phi$ and $\psi$ are $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort ${\textbf{C}}$, is used for the term $(\phi \, {\Rightarrow}\,\psi ) \wedge (\psi \, {\Rightarrow}\,\phi )$. The axioms of $\text {ACP}_{\epsilon }^{\tau }$-I (given below) include an equation $\phi = \psi$ for each two terms $\phi$ and $\psi$ from $\mathcal {C}$ for which the formula $\phi \, {\Leftrightarrow}\,\psi$ holds in ${\mathfrak {D}}$.

Let a be a basic action from $\textsf{A}$, $e_1$, ..., $e_n$, and e be terms from $\mathcal {D}$, $\phi$ be a term from $\mathcal {C}$, and t be a term from $\mathcal {P}$ denoting a process p. Then the additional operators to build terms of sort $\textbf{P}$ can be explained as follows:

• the term $a(e_1,\ldots ,e_n)$ denotes the process that first performs the data parameterized action $a(e_1,\ldots ,e_n)$ and then terminates successfully;

• the term $[v \, {{:}{=}}\, e]$ denotes the process that first performs the assignment action $[v \, {{:}{=}}\, e]$, whose intended effect is the assignment of the result of evaluating e to flexible variable v, and then terminates successfully;

• the term $\phi \, {:\rightarrow }\,t$ denotes the process that behaves as p if condition $\phi$ holds and as $\delta$ otherwise;

• the term ${\textsf{V}_{\rho }}(t)$ denotes the process that behaves as p, except that each subterm of t that belongs to $\mathcal {D}$ is evaluated using flexible variable valuation $\rho$ updated according to the assignment actions that have taken place at the point where the subterm is encountered.

Evaluation operators are a variant of state operators (see e.g. [3]).

The following closed $\text {ACP}_{\epsilon }^{\tau }$-I term is reminiscent of a program that computes the difference d between two integers i and j by subtracting the smaller one from the larger one ($i, j, d \in \mathcal {V}$):³

$$\begin{aligned}{}[d \, {{:}{=}}\, i] \cdot ((d \ge j = 1) \, {:\rightarrow}\,[d \, {{:}{=}}\, d - j] \,{+}\,(d \ge j = 0) \, {:\rightarrow}\,[d \, {{:}{=}}\, j - d])\;. \end{aligned}$$

That is, the final value of d is the absolute value of the result of subtracting the initial value of i from the initial value of j. Let $\rho$ be a flexible variable valuation such that $\rho (i) = 11$ and $\rho (j) = 3$. Then the following equation can be derived from the axioms of $\text {ACP}_{\epsilon }^{\tau }$-I given below:

$$\begin{aligned} {\textsf{V}_{\rho }} ([d \, {{:}{=}}\, i] \cdot ((d \ge j = 1) \, {:\rightarrow}\,[d \, {{:}{=}}\, d - j] \,{+}\,(d \ge j = 0) \, {:\rightarrow}\,[d \, {{:}{=}}\, j - d])) {} = [d \, {{:}{=}}\, 11] \cdot [d \, {{:}{=}}\, 8]\;. \end{aligned}$$

This equation shows that in the case where the initial values of i and j are 11 and 3 the final value of d is 8, which is the absolute value of the result of subtracting 11 from 3.

A flexible variable valuation $\rho$ can be extended homomorphically from flexible variables to $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort ${\textbf{D}}$ and $\text {ACP}_{\epsilon }^{\tau }$-I terms of sort ${\textbf{C}}$. Below, these extensions are denoted by $\rho$ as well. Moreover, we write $\rho [v \mapsto e]$ for the flexible variable valuation $\rho '$ defined by $\rho '(v') = \rho (v')$ if $v' \ne v$ and $\rho '(v) = e$.

The subsets $\mathcal {A}^{\textsf{par}}$, $\mathcal {A}^{\textsf{ass}}$, and $\mathcal {A}$ of $\mathcal {P}$ referred to below are defined as follows:

$$\begin{aligned} \mathcal {A}^{\textsf{par}}= & {} {} \bigcup _{n \in \mathbb {N}^+} \{ a(e_1,\dots ,e_n) \, {\mid}\,a \in \textsf{A}\wedge e_1,\dots ,e_n \in \mathcal {D} \}\;, \\ \mathcal {A}^{\textsf{ass}}= & {} \{ [v \, {{:}{=}}\, e] \, {\mid}\,v \in \mathcal {V}\wedge e \in \mathcal {D} \}\;, \\ \mathcal {A}= & {} \textsf{A}\cup \mathcal {A}^{\textsf{par}}\cup \mathcal {A}^{\textsf{ass}}\;. \end{aligned}$$

The elements of $\mathcal {A}$ are the terms from $\mathcal {P}$ that denote the processes that are considered to be atomic. Henceforth, we write $\mathcal {A}_{\tau }$ for $\mathcal {A}\cup \{ \tau \}$, $\mathcal {A}_{\delta }$ for $\mathcal {A}\cup \{ \delta \}$, and $\mathcal {A}_{\tau \delta }$ for $\mathcal {A}\cup \{ \tau ,\delta \}$.

Table 2 Additional axioms of ACP$_{\epsilon }^{\tau }$-I

The axioms of $\text {ACP}_{\epsilon }^{\tau }$-I are the axioms presented in Tables 1 and 2, where $\alpha$ stands for an arbitrary term from $\mathcal {A}_{\tau \delta }$,  H stands for an arbitrary subset of $\mathcal {A}$ or the set $\mathcal {A}_{\tau }$,  I stands for an arbitrary subset of $\mathcal {A}$,  e, $e_1,e_2,\ldots$ and $e'$, $e'_1,e'_2,\ldots$ stand for arbitrary terms from $\mathcal {D}$,  $\phi$ and $\psi$ stand for arbitrary terms from $\mathcal {C}$, v stands for an arbitrary flexible variable from $\mathcal {V}$, and $\rho$ stands for an arbitrary flexible variable valuation from $\mathcal{V}\mathcal{V}\kern-.1em al$. Moreover,  a, b, and c stand for arbitrary members of ${\textsf{A}_{\tau \delta }}$ in Table 1 and for arbitrary members of $\textsf{A}$ in Table 2.

2.3 ACP$_{\epsilon }^{\tau }$-I with Recursion

In this section, recursion in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I is treated. A closed $\text {ACP}_{\epsilon }^{\tau }$-I term of sort $\textbf{P}$ denotes a process with a finite upper bound to the number of actions that it can perform. Recursion allows the description of processes without a finite upper bound to the number of actions that it can perform.

A recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I is a set $\{ X_i = t_i \, {\mid}\,i \in I \}$, where I is a set, each $X_i$ is a variable from $\mathcal {X}$, each $t_i$ is a $\text {ACP}_{\epsilon }^{\tau }$-I term of sort $\textbf{P}$ in which only variables from $\{ X_i \, {\mid}\,i \in I \}$ occur, and $X_i \ne X_j$ for all $i,j \in I$ with $i \ne j$. We write $\textrm{vars}(E)$, where E is a recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I, for the set of all variables that occur in E. Let E be a recursive specification and let $X \in \textrm{vars}(E)$. Then there exists a unique equation in E whose left-hand side is X. This equation is called the recursion equation for X in E.

Below, guarded linear recursive specifications over $\text {ACP}_{\epsilon }^{\tau }$-I are introduced. The set $\mathcal {L}$ of linear $\text {ACP}_{\epsilon }^{\tau }$-I terms is inductively defined by the following rules:

• 1. $\delta \in \mathcal {L}$;

• 2. if $\phi \in \mathcal {C}$, then $\phi \, {:\rightarrow}\,\epsilon \in \mathcal {L}$;

• 3. if $\phi \in \mathcal {C}$, $\alpha \in \mathcal {A}_{\tau }$, and $X \in \mathcal {X}$, then $\phi \, {:\rightarrow}\,\alpha \cdot X \in \mathcal {L}$;

• 4. if $t,t' \in \mathcal {L}\setminus \{ \delta \}$, then $t \,{+}\,t' \in \mathcal {L}$.

Let $t \in \mathcal {L}$. Then we refer to the subterms of t that have the form $\phi \, {:\rightarrow}\,\epsilon$ or the form $\phi \, {:\rightarrow}\,\alpha \cdot X$ as the summands of t.

Let X be a variable from $\mathcal {X}$ and let t be an $\text {ACP}_{\epsilon }^{\tau }$-I term in which X occurs. Then an occurrence of X in t is guarded if t has a subterm of the form $\alpha \cdot t'$ where $\alpha \in \mathcal {A}$ and $t'$ contains this occurrence of X.

An occurrence of a variable X in a linear $\text {ACP}_{\epsilon }^{\tau }$-I term may be not guarded because a linear $\text {ACP}_{\epsilon }^{\tau }$-I term may have summands of the form $\phi \, {:\rightarrow}\,\tau \cdot X$.

A guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I is a recursive specification $\{ X_i = t_i \, {\mid}\,i \in I \}$ over $\text {ACP}_{\epsilon }^{\tau }$-I where each $t_i$ is a linear $\text {ACP}_{\epsilon }^{\tau }$-I term and there does not exist an infinite sequence $i_0\;i_1\;\ldots \,$ over I such that, for each $k \in \mathbb {N}$, there is an occurrence of $X_{i_{k+1}}$ in $t_{i_k}$ that is not guarded.

A solution of a guarded linear recursive specification E over $\text {ACP}_{\epsilon }^{\tau }$-I in some model of $\text {ACP}_{\epsilon }^{\tau }$-I is a set $\{ p_X \, {\mid}\,X \in \textrm{vars}(E) \}$ of elements of the carrier of sort $\textbf{P}$ in that model such that each equation in E holds if, for all $X \in \textrm{vars}(E)$, X is assigned $p_X$. A guarded linear recursive specification has a unique solution under the equivalence defined in [29] for $\text {ACP}_{\epsilon }^{\tau }$-I extended with guarded linear recursion. If $\{ p_X \, {\mid}\,X \in \textrm{vars}(E) \}$ is the unique solution of a guarded linear recursive specification E, then, for each $X \in \textrm{vars}(E)$, $p_X$ is called the X-component of the unique solution of E.

$\text {ACP}_{\epsilon }^{\tau }$-I is extended with guarded linear recursion by adding constants for solutions of guarded linear recursive specifications over $\text {ACP}_{\epsilon }^{\tau }$-I and axioms concerning these additional constants. For each guarded linear recursive specification E over $\text {ACP}_{\epsilon }^{\tau }$-I and each $X \in \textrm{vars}(E)$, a constant $\langle X \vert E \rangle$ of sort $\textbf{P}$, that stands for the X-component of the unique solution of E, is added to the constants of $\text {ACP}_{\epsilon }^{\tau }$-I. The equation RDP and the conditional equation RSP given in Table 3 are added to the axioms of $\text {ACP}_{\epsilon }^{\tau }$-I. In this table, X stands for an arbitrary variable from $\mathcal {X}$, t stands for an arbitrary $\text {ACP}_{\epsilon }^{\tau }$-I term of sort $\textbf{P}$,  E stands for an arbitrary guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I, and the notation $\langle t \vert E \rangle$ is used for t with, for all $X \in \textrm{vars}(E)$, all occurrences of X in t replaced by $\langle X \vert E \rangle$. Side conditions restrict what X, t and E stand for.

Table 3 Axioms for guarded linear recursion

We write $\text {ACP}_{\epsilon }^{\tau }$-I +REC for the resulting theory. Furthermore, we write $\mathcal {P}_{\textsf{rec}}$ for the set of all closed $\text{ACP}_{\epsilon }^{\tau }-\text {I} +\text{REC}$ terms of sort $\textbf{P}$.

RDP and RSP together postulate that guarded linear recursive specifications over $\text {ACP}_{\epsilon }^{\tau }$-I have unique solutions.

Because RSP introduces conditional equations in $\text {ACP}_{\epsilon }^{\tau }$-I +REC, it is understood that conditional equational logic is used in deriving equations from the axioms of $\text {ACP}_{\epsilon }^{\tau }$-I +REC. A complete inference system for conditional equational logic can for example be found in [4, 18].

The following closed $\text {ACP}_{\epsilon }^{\tau }$-I +REC term is reminiscent of a program that computes by repeated subtraction the quotient q and remainder r of dividing a non-negative integer i by a positive integer j ($i, j, q, r \in \mathcal {V}$):

$$\begin{aligned}{}[q \, {{:}{=}}\, 0] \cdot [r \, {{:}{=}}\, i] \cdot \langle Q \vert E \rangle \;, \end{aligned}$$

where E is the guarded linear recursive specification that consists of the following two equations ($Q,R \in \mathcal {X}$):

$$\begin{aligned}{} & {} Q = (r \ge j = 1) \, {:\rightarrow}\,[q \, {{:}{=}}\, q + 1] \cdot R \,{+}\,(r \ge j = 0) \, {:\rightarrow}\,\epsilon \;, \\{} & {} R = {\textsf{t}}\, {:\rightarrow}\,[r \, {{:}{=}}\, r - j] \cdot Q\;. \end{aligned}$$

Let $\rho$ be a flexible variable valuation such that $\rho (i) = 11$ and $\rho (j) = 3$. Then the following equation can be derived from the axioms of $\text {ACP}_{\epsilon }^{\tau }$-I +REC:

$$\begin{aligned}{} & {} {\textsf{V}_{\rho }} ([q \, {{:}{=}}\, 0] \cdot [r \, {{:}{=}}\, i] \cdot \langle Q \vert E \rangle ) \\{} & {} \; = [q \, {{:}{=}}\, 0] \cdot [r \, {{:}{=}}\, 11] \cdot [q \, {{:}{=}}\, 1] \cdot [r \, {{:}{=}}\, 8] \cdot [q \, {{:}{=}}\, 2] \cdot [r \, {{:}{=}}\, 5] \cdot [q \, {{:}{=}}\, 3] \cdot [r \, {{:}{=}}\, 2]\;. \end{aligned}$$

This equation shows that in the case where the initial values of i and j are 11 and 3 the final values of q and r are 3 and 2, which are the quotient and remainder of dividing 11 by 3.

In [29], an equational axiom schema CFAR (Cluster Fair Abstraction Rule) is added to $\text {ACP}_{\epsilon }^{\tau }$-I +REC. CFAR expresses that every cluster of $\tau$ actions will be exited sooner or later. This is a fairness assumption made in the verification of many properties concerning the external behaviour of systems. We write $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR for the theory $\text {ACP}_{\epsilon }^{\tau }$-I +REC extended with CFAR.

We write $T \vdash t = t'$, where T is $\text {ACP}_{\epsilon }^{\tau }$-I +REC or $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR, to indicate that the equation $t = t'$ is derivable from the axioms of T using a complete inference system for conditional equational logic.

2.4 Results about ACP$_{\epsilon }^{\tau }$-I with Recursion

In [29], a structural operational semantics of $\text {ACP}_{\epsilon }^{\tau }$-I +REC is presented and an equivalence relation $\underline{\leftrightarrow }_{\textsf{rb}}$ on $\mathcal {P}_{\textsf{rec}}$ based on this structural operational semantics is defined. This equivalence relation reflects the idea that two processes are equivalent if they can simulate each other insofar as their observable potentials to make transitions by performing actions and to terminate successfully are concerned, taking into account the assignments of data values to flexible variables under which the potentials are available.

Soundness and semi-completeness results for the axiom system of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR with respect to $\underline{\leftrightarrow }_{\textsf{rb}}$ are proved in [29]. The axiom system of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR is incomplete with respect to $\underline{\leftrightarrow }_{\textsf{rb}}$ for equations between terms from $\mathcal {P}_{\textsf{rec}}$ and there is no straightforward way to rectify this. However, the axiom system of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR is complete with respect to $\underline{\leftrightarrow }_{\textsf{rb}}$ for equations between abstraction-free terms from $\mathcal {P}_{\textsf{rec}}$ and for equations between bool-conditional terms from $\mathcal {P}_{\textsf{rec}}$.

A term $t \in \mathcal {P}_{\textsf{rec}}$ is called abstraction-free if no abstraction operator occurs in t. A term $t \in \mathcal {P}_{\textsf{rec}}$ is called bool-conditional if, for each $\phi \in \mathcal {C}$ that occurs in t, ${\mathfrak {D}} \, {\,\models \,}\, \phi \, {\Leftrightarrow}\,{\textsf{t}}$ or ${\mathfrak {D}} \, {\,\models \,}\, \phi \, {\Leftrightarrow}\,{\textsf{f}}$.

The following auxiliary results about abstraction-free terms and bool-conditional terms are proved in [29]:

• for all abstraction-free $t \in \mathcal {P}_{\textsf{rec}}$, there exists a guarded linear recursive specification E and $X \in \textrm{vars}(E)$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}\vdash t = \langle X \vert E \rangle$;

• for all bool-conditional $t \in \mathcal {P}_{\textsf{rec}}$, there exists a guarded linear recursive specification E and $X \in \textrm{vars}(E)$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash t = \langle X \vert E \rangle$.

The soundness and semi-completeness results referred to above are as follows:

• for all terms $t,t' \in \mathcal {P}_{\textsf{rec}}$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash t = t'$ only if $t \underline{\leftrightarrow }_{\textsf{rb}}t'$;

• for all abstraction-free $t,t' \in \mathcal {P}_{\textsf{rec}}$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}\vdash t = t'$ if $t \underline{\leftrightarrow }_{\textsf{rb}}t'$;

• for all bool-conditional $t,t' \in \mathcal {P}_{\textsf{rec}}$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash t = t'$ if $t \underline{\leftrightarrow }_{\textsf{rb}}t'$.

For a better understanding of the evaluation operators, some results about these rather unfamiliar operators are given below.

The following lemma tells us that a closed term of the form ${\textsf{V}_{\rho }}(t)$ equals a bool-conditional closed term.

Lemma 1

For all $t \in \mathcal {P}_{\textsf{rec}}$ and $\rho \in \mathcal{V}\mathcal{V}\kern-.1em al$, there exists a bool-conditional $t' \in \mathcal {P}_{\textsf{rec}}$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash {\textsf{V}_{\rho }}(t) = t'$.

Proof

This is straightforwardly proved by induction on the length of t, case distinction on the structure of t, and in the case of the constants for solutions of guarded linear recursive specifications additionally by induction on the structure of the right-hand side of a recursion equation. $\square$

As a corollary of Lemma 1 and the soundness and completeness result mention above, we have:

• for all $t,t' \in \mathcal {P}_{\textsf{rec}}$ and $\rho \in \mathcal{V}\mathcal{V}\kern-.1em al$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash {\textsf{V}_{\rho }}(t) = {\textsf{V}_{\rho }}(t')$ iff ${\textsf{V}_{\rho }}(t) \underline{\leftrightarrow }_{\textsf{rb}}{\textsf{V}_{\rho }}(t')$.

Below, an elimination theorem for closed terms of the form ${\textsf{V}_{\rho }}(t)$ is presented. In preparation, the subsets $\mathcal {B}$ and $\mathcal {B}_{\textsf{cf}}$ of $\mathcal {P}$ are introduced.

The set $\mathcal {B}$ of basic $\text {ACP}_{\epsilon }^{\tau }$-I terms is inductively defined by the following rules:

• 1. $\delta \in \mathcal {B}$;

• 2. if $\phi \in \mathcal {C}$, then $\phi \, {:\rightarrow}\,\epsilon \in \mathcal {B}$;

• 3. if $\phi \in \mathcal {C}$, $\alpha \in \mathcal {A}_{\tau }$, and $t \in \mathcal {B}$, then $\phi \, {:\rightarrow}\,\alpha \cdot t \in \mathcal {B}$;

• 4. if $t,t' \in \mathcal {B}\setminus \{ \delta \}$, then $t \,{+}\,t' \in \mathcal {B}$.

The set $\mathcal {B}_{\textsf{cf}}$ of condition-free basic $\text {ACP}_{\epsilon }^{\tau }$-I terms is inductively defined by the following rules:

• 1. $\delta \in \mathcal {B}_{\textsf{cf}}$;

• 2. $\epsilon \in \mathcal {B}_{\textsf{cf}}$;

• 3. if $\alpha \in \mathcal {A}_{\tau }$, and $t \in \mathcal {B}_{\textsf{cf}}$, then $\alpha \cdot t \in \mathcal {B}_{\textsf{cf}}$;

• 4. if $t,t' \in \mathcal {B}_{\textsf{cf}}\setminus \{ \delta \}$, then $t \,{+}\,t' \in \mathcal {B}_{\textsf{cf}}$.

Lemma 2

For all bool-conditional $t \in \mathcal {P}$, there exists a bool-conditional $t' \in \mathcal {B}$ such that $\text {ACP}_{\epsilon }^{\tau }\text {-I}\vdash t = t'$.

Proof

This is straightforwardly proved by induction on the length of t and case distinction on the structure of t. $\square$

Lemma 3

For all bool-conditional $t \in \mathcal {B}$, there exists a $t' \in \mathcal {B}_{\textsf{cf}}$ such that $\text {ACP}_{\epsilon }^{\tau }\text {-I}\vdash t = t'$.

Proof

This is easily proved by induction on the structure of t. $\square$

A term $t \in \mathcal {P}_{\textsf{rec}}$ is called a finite-process term if there exists a term $t' \in \mathcal {P}$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash t = t'$.

The following theorem tells us that a finite-process term of the form ${\textsf{V}_{\rho }}(t)$ equals a condition-free basic term.

Theorem 1

For all $t \in \mathcal {P}_{\textsf{rec}}$ and $\rho \in \mathcal{V}\mathcal{V}\kern-.1em al$ for which ${\textsf{V}_{\rho }}(t)$ is a finite-process term, there exists a $t' \in \mathcal {B}_{\textsf{cf}}$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash {\textsf{V}_{\rho }}(t) = t'$.

Proof

This follows immediately from Lemmas 1, 2, and 3. $\square$

The terms from $\mathcal {B}_{\textsf{cf}}$ are reminiscent of computation trees. In Section 3, use is made of the fact that each finite-process term of the form ${\textsf{V}_{\rho }}(t)$ equals such a term.

Not every term from $\mathcal {B}_{\textsf{cf}}$ corresponds to a computation tree of which each path represents a computation that eventually halts, not even when it concerns a computation tree with a single path.

A term $t \in \mathcal {P}_{\textsf{rec}}$ is called a terminating-process term if there exists a term $t' \in \mathcal {B}_{\textsf{cf}}$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash t = t'$ and $t'$ can be formed by applying only the formation rules 2, 3, and 4 of $\mathcal {B}_{\textsf{cf}}$.

2.5 Extensions

This section concerns two extensions of $\text {ACP}_{\epsilon }^{\tau }$-I that are relevant to this paper, namely an extension with projection and an extension with action renaming. It is not unusual to come across these extensions in applications of $\text {ACP}$-style process algebras. The first extension is treated here because projections can be used to determine the maximum number of actions that a finite process can perform. The second extension is treated here because action renaming enables to easily define the synchronous variant of the parallel composition operator of $\text {ACP}_{\epsilon }^{\tau }$-I needed later in this paper.

Table 4 Axioms for the projection operators

$\text {ACP}_{\epsilon }^{\tau }$-I, $\text {ACP}_{\epsilon }^{\tau }$-I +REC, and $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR can be extended with projection by adding, for each $n \in \mathbb {N}$, a unary projection operator ${\pi _{n}} \, {:}\, \textbf{P} \rightarrow \textbf{P}$ to the operators of T and adding the axioms given in Table 4 to the axioms of T. In this table, n stands for an arbitrary natural number, $\alpha$ stands for an arbitrary term from $\mathcal {A}_{\delta }$, and $\phi$ stands for an arbitrary term from $\mathcal {C}$.

Let t be a closed term of the extended theory. Then the projection operator $\pi _{n}$ can be explained as follows: $\pi _{n}(t)$ denotes the process that behaves the same as the process denoted by t except that it terminates successfully after n actions have been performed.

Let T be $\text {ACP}_{\epsilon }^{\tau }$-I, $\text {ACP}_{\epsilon }^{\tau }$-I +REC or $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR. Then we write T+$PR$ for T extended with the projection operators $\pi _{n}$ and the axioms PR1–PR6 from Table 4.

Table 5 Axioms for the action renaming operators

$\text {ACP}_{\epsilon }^{\tau }$-I, $\text {ACP}_{\epsilon }^{\tau }$-I +REC, and $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR can be extended with action renaming by adding, for each function ${f} \, {:}\, \mathcal {A} \rightarrow \mathcal {A}$ such that $f(\alpha ) = \alpha$ for all $\alpha \in \mathcal {A}^{\textsf{ass}}$, a unary action renaming operator ${\rho _{f}} \, {:}\, \textbf{P} \rightarrow \textbf{P}$ to the operators of T and adding the axioms given in Table 5 to the axioms of T. In this table, f stands for an arbitrary function ${f} \, {:}\, \mathcal {A} \rightarrow \mathcal {A}$ such that $f(\alpha ) = \alpha$ for all $\alpha \in \mathcal {A}^{\textsf{ass}}$, $\alpha$ stands for an arbitrary term from $\mathcal {A}$, and $\phi$ stands for an arbitrary term from $\mathcal {C}$.

Let t be a closed term of the extended theory. Then the action renaming operator $\rho _{f}$ can be explained as follows: $\rho _{f}(t)$ denotes the process that behaves the same as the process denoted by t except that, where the latter process performs an action $\alpha$, the former process performs the action $f(\alpha )$.

Let T be $\text {ACP}_{\epsilon }^{\tau }$-I, $\text {ACP}_{\epsilon }^{\tau }$-I +REC, $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR or $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR+$PR$. Then we write T+$RN$ for T extended with the action renaming operators $\rho _{f}$ and the axioms RN1–RN7 from Table 5.

3 Computation and the RAM Conditions

In order to investigate whether $\text {ACP}_{\epsilon }^{\tau }$-I +REC can play a role in the field of models of computation, it has to be explained in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I +REC what it means that a given process computes a given function. This requires that assumptions about ${\mathfrak {D}}$ have to be made. The assumptions concerned are given in this section. They are based on the idea that the data environment of a computational process consists of one or more RAM (Random Access Machine) memories. Because the assumptions amount to conditions to be satisfied by ${\mathfrak {D}}$, they are called the RAM conditions on ${\mathfrak {D}}$. It is also made precise in this section what it means, in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I +REC where ${\mathfrak {D}}$ satisfies the RAM conditions, that a given process computes a given partial function from ${(\{ 0,1 \}^*)}^n$ to $\{ 0,1 \}^*$ ($n \in \mathbb {N}$).

3.1 The RAM Conditions

The memory of a RAM consists of a countably infinite number of registers which are numbered by natural numbers. Each register is capable of containing a bit string of arbitrary length. The contents of the registers constitute the state of the memory of the RAM. The execution of an instruction by the RAM amounts to carrying out an operation on its memory state that changes the content of at most one register or to testing a property of its memory state. The RAM conditions are presented in this section using the notions of a RAM memory state, a RAM operation, and a RAM property.

A RAM memory state is a function ${\sigma } \, {:}\, \mathbb {N} \rightarrow \{ 0,1 \}^*$ that satisfies the condition that there exists an $i \in \mathbb {N}$ such that, for all $j \in \mathbb {N}$, $\sigma (i + j) = \lambda$.⁴ We write $\Sigma _{\textsf{ram}}$ for the set of all RAM memory states.

Let $\sigma$ be a RAM memory state. Then, for all $i \in \mathbb {N}$, $\sigma (i)$ is the content of the register with number i in memory state $\sigma$. The condition on $\sigma$ expresses that the part of the memory that is actually in use remains finite.

The input region and output region of a function ${o} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \Sigma _{\textsf{ram}}$, written ${IR}(o)$ and ${OR}(o)$, respectively, are the subsets of $\mathbb {N}$ defined as follows:

$$\begin{aligned} {OR}(o)= & {} \{ i \in \mathbb {N}\, {\mid}\,\exists \sigma \in \Sigma _{\textsf{ram}} \, {\scriptstyle \bullet}\, \sigma (i) \ne o(\sigma )(i) \}\;,\\ {IR}(o)= & {} \{ i \in \mathbb {N}\, {\mid}\,\exists \sigma _1,\sigma _2 \in \Sigma _{\textsf{ram}} \,{\scriptstyle \bullet}\, {} (\forall j \in \mathbb {N}\setminus \{ i \} \, {\scriptstyle \bullet}\, \sigma _1(j) = \sigma _2(j) \wedge {} \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \exists j \in {OR}(o) \, {\scriptstyle \bullet}\, o(\sigma _1)(j) \ne o(\sigma _2)(j)) \}\;. \end{aligned}$$

Let ${o} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \Sigma _{\textsf{ram}}$. Then ${OR}(o)$ consists of the numbers of all registers that can be affected by o; and ${IR}(o)$ consists of the numbers of all registers that can affect the registers whose numbers are in ${OR}(o)$ under o.

A basic RAM operation is a function ${o} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \Sigma _{\textsf{ram}}$ that satisfies the condition that ${IR}(o)$ is finite and ${OR}(o)$ has cardinality 0 or 1. We write $O_{\textsf{ram}}$ for the set of all basic RAM operations.

Let o be a basic RAM operation and $\sigma$ be a RAM memory state. Then carrying out o on a RAM memory in state $\sigma$ changes the state of the RAM memory into $o(\sigma )$. The condition on o expresses that the content of at most one register can be affected and that, if there is such a register, only a finite number of registers can affect it.

The following theorem states that each basic RAM operation transforms states of a RAM memory that coincide on its input region to states that coincide on its output region.

Theorem 2

Let $\sigma _1,\sigma _2 \in \Sigma _{\textsf{ram}}$ and $o \in O_{\textsf{ram}}$. Then $\sigma _1 \, {\upharpoonright}\,{IR}(o) = \sigma _2 \, {\upharpoonright}\,{IR}(o)$ implies $o(\sigma _1) \, {\upharpoonright}\,{OR}(o) = o(\sigma _2) \, {\upharpoonright}\,{OR}(o)$.⁵

Proof

It is easy to see that the 4-tuple $(\mathbb {N},\{ 0,1 \}^*,\Sigma _{\textsf{ram}},O_{\textsf{ram}})$ is a computer according to Definition 3.1 from [28]. From this and Theorem 3.1 from [28], the theorem follows immediately. $\square$

The input region of a function ${p} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \{ 0,1 \}$, written ${IR}(p)$ is the subset of $\mathbb {N}$ defined as follows:

$$\begin{aligned}{} & {} {IR}(p) = \{ i \in \mathbb {N}\, {\mid}\,\exists \sigma _1,\sigma _2 \in \Sigma _{\textsf{ram}} \, {\scriptstyle \bullet}\, {} (\forall j \in \mathbb {N}\setminus \{ i \} \, {\scriptstyle \bullet}\, \sigma _1(j) = \sigma _2(j) \wedge {} \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad p(\sigma _1) \ne p(\sigma _2) \}\;. \end{aligned}$$

Let ${p} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \{ 0,1 \}$. Then ${IR}(p)$ consists of the numbers of all registers that can affect what the value of p is.

A basic RAM property is a function ${p} \, {:}\, \Sigma _{\textsf{ram}} \rightarrow \{ 0,1 \}$ that satisfies the condition that ${IR}(p)$ is finite. We write $P_{\textsf{ram}}$ for the set of all basic RAM properties.

Let p be a basic RAM property and $\sigma$ be a RAM memory state. Then testing the property p on a RAM memory in state $\sigma$ yields the value $p(\sigma )$ and does not change the state of the RAM memory. The condition on p expresses that only a finite number of registers can affect what this value is. We say that p holds in $\sigma$ if $p(\sigma ) = 1$.

The following theorem states that each basic RAM property holds in some state of a RAM memory if and only if it holds in all states of the RAM memory that coincide with that state on its input region.

Theorem 3

Let $\sigma _1,\sigma _2 \in \Sigma _{\textsf{ram}}$ and $p \in P_{\textsf{ram}}$. Then $\sigma _1 \, {\upharpoonright}\,{IR}(p) = \sigma _2 \, {\upharpoonright}\,{IR}(p)$ implies $p(\sigma _1) = p(\sigma _2)$.

Proof

Let $\Sigma _{\textsf{ram}}'$ be the set of all functions ${\sigma } \, {:}\, \mathbb {N}\cup \{ -1 \} \rightarrow \{ 0,1 \}^*$ that satisfy the condition that there exists an $i \in \mathbb {N}$ such that, for all $j \in \mathbb {N}$, $\sigma (i + j) = \lambda$, let $O_{\textsf{ram}}'$ be the set of all functions ${o} \, {:}\, \Sigma _{\textsf{ram}}' \rightarrow \Sigma _{\textsf{ram}}'$, let $\sigma '_1,\sigma '_2 \in \Sigma _{\textsf{ram}}'$ be such that $\sigma '_1 \, {\upharpoonright}\,\mathbb {N}= \sigma _1$ and $\sigma '_2 \, {\upharpoonright}\,\mathbb {N}= \sigma _2$, and let $o \in O_{\textsf{ram}}'$ be such that, for all $\sigma \in \Sigma _{\textsf{ram}}'$, $o(\sigma ) \, {\upharpoonright}\,\mathbb {N}= \sigma \, {\upharpoonright}\,\mathbb {N}$ and $o(\sigma )(-1) = p(\sigma )$. Then $\sigma _1 \, {\upharpoonright}\,{IR}(p) = \sigma _2 \, {\upharpoonright}\,{IR}(p)$ implies $p(\sigma _1) = p(\sigma _2)$ iff $\sigma '_1 \, {\upharpoonright}\,{IR}(o) = \sigma '_2 \, {\upharpoonright}\,{IR}(o)$ implies $o(\sigma '_1) = o(\sigma '_2)$. Because of this and the fact that $(\mathbb {N}\cup \{ -1 \},\{ 0,1 \}^*,\Sigma _{\textsf{ram}}',O_{\textsf{ram}}')$ is also a computer according to Definition 3.1 from [28], this theorem now follows immediately from Theorem 3.1 from [28]. $\square$

With basic RAM operations only computational processes can be considered whose data environment consists of one RAM memory. Below, n-RAM operations are introduced to remove this restriction. They are defined such that the basic RAM operations are exactly the 1-RAM operations.

An n-RAM operation ($n \in \mathbb {N}^+$) is a function ${o} \, {:}\, {\Sigma _{\textsf{ram}}}^n \rightarrow \Sigma _{\textsf{ram}}$ that satisfies the condition that there exist a basic RAM operation $o'$ and a $k \in \mathbb {N}$ with $1 \le k \le n$ such that, for all $\sigma _1,\ldots ,\sigma _n \in \Sigma _{\textsf{ram}}$, $o'(\beta (\sigma _1,\ldots ,\sigma _n)) = \beta (\sigma _1,\ldots ,\sigma _{k-1},o(\sigma _1,\ldots ,\sigma _n), \sigma _{k+1},\ldots ,\sigma _n)$, where ${\beta } \, {:}\, {\Sigma _{\textsf{ram}}}^n \rightarrow \Sigma _{\textsf{ram}}$ is the unique function such that $\beta (\sigma _1,\ldots ,\sigma _n)(n \cdot i + k - 1) = \sigma _k(i)$ for all $i \in \mathbb {N}$ and $k \in \mathbb {N}$ with $1 \le k \le n$. We write $O_{n\text {-}\textsf{ram}}$, where $n \in \mathbb {N}^+$, for the set of all n-RAM operations.

The function ${\zeta } \, {:}\, \{ k \in \mathbb {N}^+\, {\mid}\,k \le n \} \times \mathbb {N} \rightarrow \mathbb {N}$ defined by $\zeta (k,i) = n \cdot i + k - 1$ is a bijection. From this it follows that the basic RAM operation $o'$ and the $k \in \mathbb {N}$ referred to in the above definition are unique if they exist.

The operations from $\bigcup _{n \ge 1} O_{n\text {-}\textsf{ram}}$ are referred to as RAM operations.

In a similar way as n-RAM operations, n-RAM properties are defined. The basic RAM properties are exactly the 1-RAM properties.

An n-RAM property ($n \in \mathbb {N}^+$) is a function ${p} \, {:}\, {\Sigma _{\textsf{ram}}}^n \rightarrow \{ 0,1 \}$ that satisfies the condition that there exists a basic RAM property $p'$ such that, for all $\sigma _1,\ldots ,\sigma _n \in \Sigma _{\textsf{ram}}$, $p'(\beta (\sigma _1,\ldots ,\sigma _n)) = p(\sigma _1,\ldots ,\sigma _n)$, where ${\beta } \, {:}\, {\Sigma _{\textsf{ram}}}^n \rightarrow \Sigma _{\textsf{ram}}$ is defined as above. We write $P_{n\text {-}\textsf{ram}}$, where $n \in \mathbb {N}^+$, for the set of all n-RAM properties.

The properties from $\bigcup _{n \ge 1} P_{n\text {-}\textsf{ram}}$ are referred to as RAM properties.

The RAM conditions on ${\mathfrak {D}}$ are:

• 1. the signature $\Sigma _{\mathfrak {D}}$ of ${\mathfrak {D}}$ includes (in addition to what is stated in Section 2.2):

  • a sort ${\textbf{BS}}$ of bit strings and a sort ${\textbf{N}}$ of natural numbers;

  • constants ${\lambda ,0,1} \, {:}\, {\textbf{BS}}$ and a binary operator ${\curvearrowright } : {{\textbf {BS}}}\times {{\textbf {BS}}} \rightarrow {{\textbf {BS}}}$;

  • constants ${0,1} \, {:}\, {\textbf{N}}$ and a binary operator ${+} \, {:}\, {\textbf{N}}\times {\textbf{N}} \rightarrow {\textbf{N}}$;

  • a constant ${\sigma _\lambda } \, {:}\, {\textbf{D}}$ and a ternary operator ${\oplus } \, {:}\, {\textbf{D}}\times {\textbf{N}}\times {\textbf{BS}} \rightarrow {\textbf{D}}$;

• 2. the sorts, constants, and operators mentioned under 1 are interpreted in ${\mathfrak {D}}$ as follows:

  • the sort ${\textbf{BS}}$ is interpreted as the set $\{ 0,1 \}^*$, the sort ${\textbf{N}}$ is interpreted as the set $\mathbb {N}$, and the sort ${\textbf{D}}$ is interpreted as the set $\Sigma _{\textsf{ram}}$;

  • the constant ${\lambda } \, {:}\, {\textbf{BS}}$ is interpreted as the empty bit string, the constants ${0,1} \, {:}\, {\textbf{BS}}$ are interpreted as the bit strings with the bit 0 and 1, respectively, as sole element, and the operator ${\curvearrowright } : {{\textbf {BS}}}\times {{\textbf {BS}}} \rightarrow {{\textbf {BS}}}$ is interpreted as the concatenation operation on $\{ 0,1 \}^*$;

  • the constants ${0,1} \, {:}\, {\textbf{N}}$ are interpreted as the natural numbers 0 and 1, respectively, and the operator ${+} \, {:}\, {\textbf{N}}\times {\textbf{N}} \rightarrow {\textbf{N}}$ is interpreted as the addition operation on $\mathbb {N}$;

  • the constant ${\sigma _\lambda } \, {:}\, {\textbf{D}}$ is interpreted as the unique $\sigma \in \Sigma _{\textsf{ram}}$ such that $\sigma (i) = \lambda$ for all $i \in \mathbb {N}$ and the operator ${\oplus } \, {:}\, {\textbf{D}}\times {\textbf{N}}\times {\textbf{BS}} \rightarrow {\textbf{D}}$ is interpreted as the override operation defined by $\oplus (\sigma ,i,w)(i) = w$ and, for all $j \in \mathbb {N}$ with $i \ne j$, $\oplus (\sigma ,i,w)(j) = \sigma (j)$;

• 3. the signature $\Sigma _{\mathfrak {D}}$ of ${\mathfrak {D}}$ is restricted as follows:

  • for each operator from $\Sigma _{\mathfrak {D}}$, the sort of its result is ${\textbf{D}}$ only if the sort of each of its arguments is ${\textbf{D}}$ or the operator is $\oplus$;

  • for each operator from $\Sigma _{\mathfrak {D}}$, the sort of its result is ${\textbf{B}}$ only if the sort of each of its arguments is ${\textbf{D}}$;

• 4. the interpretation of the operators mentioned under 3 is restricted as follows:

  • each operator with result sort ${\textbf{D}}$ other than $\oplus$ is interpreted as a RAM operation;

  • each operator with result sort ${\textbf{B}}$ is interpreted as a RAM property.

The notation $\sigma \{i \mapsto w\}$, where $\sigma \in \Sigma _{\textsf{ram}}$, $i \in \mathbb {N}$, and $w \in \{ 0,1 \}^*$, is used for the term $\oplus (\sigma ,i,w)$.

The RAM conditions make it possible to explain what it means that a given process computes a given partial function from ${(\{ 0,1 \}^*)}^n$ to $\{ 0,1 \}^*$ ($n \in \mathbb {N}$). Moreover, the RAM conditions are nonrestrictive: presumably they allow to deal with all proposed versions of the RAM model of computation as well as all proposed models of parallel computation that are based on a version of the RAM model and the idea that the data environment of a computational process consists of one or more RAM memories.

3.2 Computing Partial Functions from $(\{ 0,1 \}^*)^n$ to $\{ 0,1 \}^*$

Below, we make precise in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR, where ${\mathfrak {D}}$ is assumed to satisfy the RAM conditions, what it means that a given process computes a given partial function from $(\{ 0,1 \}^*)^n$ to $\{ 0,1 \}^*$ ($n \in \mathbb {N}$).

In the rest of this paper, ${\mathfrak {D}}$ is assumed to satisfy the RAM conditions. Moreover, it is assumed that $\textsf{m}\in \mathcal {V}$.

Henceforth, the notation $\rho _{w_1,\ldots ,w_n}$, where $w_1,\ldots ,w_n \in \{ 0,1 \}^*$, is used for the unique $\rho \in \mathcal{V}\mathcal{V}\kern-.1em al$ such that $\rho (\textsf{m}) = \sigma _\lambda \{1 \mapsto w_1\} \ldots \{n \mapsto w_n\}$ and $\rho (v) = \sigma _\lambda$ for all $v \in \mathcal {V}\setminus \{ \textsf{m} \}$.

If $t \in \mathcal {P}_{\textsf{rec}}$ is a finite-process term, then there is a finite upper bound to the number of actions that the process denoted by t can perform.

The depth of a finite-process term $t \in \mathcal {P}_{\textsf{rec}}$, written $depth (t)$, is defined as follows: $depth (t) = \min \{ n \in \mathbb {N}\, {\mid}\,\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}{+}PR \vdash \pi _{n}(t) = t \}$. This means that $depth (t)$ is the maximum number of actions other than $\tau$ that the process denoted by t can perform.

Let $n \in \mathbb {N}$, let $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$,⁶ and let ${W} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$. Then, roughly speaking, a process p computes F in W steps if:

• for all $w_1,\ldots ,w_n \in \{ 0,1 \}^*$ such that $F(w_1,\ldots ,w_n)$ is defined: if p is started in a RAM memory state $\sigma$ in which $\sigma (1) = w_1$, ..., $\sigma (n) = w_n$, then:

  • it terminates successfully in a state $\sigma '$ in which $\sigma '(0) = F(w_1,\ldots ,w_n)$;

  • the total number of actions that it performs is not greater than W(l), where l is the sum of the lengths of $w_1,\ldots ,w_n$;

• for all $w_1,\ldots ,w_n \in \{ 0,1 \}^*$ such that $F(w_1,\ldots ,w_n)$ is undefined: if p is started in a RAM memory state $\sigma$ in which $\sigma (1) = w_1$, ..., $\sigma (n) = w_n$, then:

  • it does not terminate successfully.

Below a precise definition in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR is given. In that definition, the equation ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t) = {\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t \cdot (\textsf{m}= \sigma ' \, {:\rightarrow}\,\epsilon ))$ expresses that the RAM memory state at successful termination satisfies $\sigma '(0) = F(w_1,\ldots ,w_n)$. This is the case because $\textsf{m}= \sigma ' \, {:\rightarrow}\,\epsilon$ equals $\epsilon$ if the latter equation is satisfied and $\delta$ otherwise.

Let $t \in \mathcal {P}_{\textsf{rec}}$, let $n \in \mathbb {N}$, let $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$, and let ${W} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$. Then t computes F in W steps if:

• for all $w_1,\ldots ,w_n \in \{ 0,1 \}^*$ such that $F(w_1,\ldots ,w_n)$ is defined, there exists a $\sigma ' \in \Sigma _{\textsf{ram}}$ with $\sigma '(0) = F(w_1,\ldots ,w_n)$ such that:⁷

  $$\begin{aligned}{} & {} {\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)\; \text {is\; a\; terminating-process\; term}\;,\\{} & {} \text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}\vdash {\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t) = {\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t \cdot (\textsf{m}= \sigma ' \, {:\rightarrow}\,\epsilon ))\;,\\{} & {} depth ({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)) \le W(\ell (w_1) + \ldots + \ell (w_n))\;;\end{aligned}$$

• for all $w_1,\ldots ,w_n \in \{ 0,1 \}^*$ such that $F(w_1,\ldots ,w_n)$ is undefined:

  $$\begin{aligned} {\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)\; \text {is\; not\; a\; terminating-process\; term}\;. \end{aligned}$$

We say that t computes F if there exists a ${W} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$ such that t computes F in W steps, we say that F is a computable function if there exists a $t \in \mathcal {P}$ such that t computes F, and we say that t is a computational process if there exists a $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$ such that t computes F.

We write $\mathcal{C}\mathcal{P}_{\textsf{rec}}$ for the set $\{ t \in \mathcal {P}_{\textsf{rec}}\, {\mid}\,t \mathrm {\;is\; a\; computational\; process} \}$.

With the above definition, we can establish whether a process of the kind considered in the current setting computes a given partial function from ${(\{ 0,1 \}^*)}^n$ to $\{ 0,1 \}^*$ ($n \in \mathbb {N}$) by equational reasoning using the axioms of $\text {ACP}_{\epsilon }^{\tau }$-I +REC+CFAR. This setting is more general than the setting provided by any known version of the RAM model of computation. It is not suitable as a model of computation itself. However, various known models of computation can be defined by fixing which RAM operations and which RAM properties belong to ${\mathfrak {D}}$ and by restricting the computational processes to the ones of a certain form. To the best of my knowledge, the models of computation that can be dealt with in this way include all proposed versions of the RAM model as well as all proposed models of parallel computation that are based on a version of the RAM model and the idea that the data environment of a computational process consists of one or more RAM memories.

Whatever model of computation is obtained by fixing the RAM operations and the RAM properties and by restricting the computational processes to the ones of a certain form, it is an idealization of a real computer because it offers an unbounded number of registers that can contain a bit string of arbitrary length instead of a bounded number of registers that can only contain a bit string of a fixed length.

4 The RAMP Model of Computation

The setting introduced in the previous sections is used in this section to describe a version of the RAM model of computation. Because it focuses on the processes that are produced by RAMs when they execute their built-in program, the version of the RAM model of computation described in this section is called the RAMP (Random Access Machine Process) model of computation.

First, the operators are introduced that represent the RAM operations and the RAM properties that belong to ${\mathfrak {D}}$ in the case of the RAMP model of computation. Next, the interpretation of those operators as a RAM operation or a RAM property is given. Finally, the RAMP model of computation is described.

4.1 Operators for the RAMP Model

In this section, the operators that are relevant to the RAMP model of computation are introduced.

In the case of the RAMP model of computation, the set of operators from $\Sigma _{\mathfrak {D}}$ that are interpreted in ${\mathfrak {D}}$ as RAM operations or RAM properties is the set $\mathcal {O}_\textsf{RAMP}$ defined as follows:

where

$$\begin{aligned} Binop= & {} \{ \textsf{add},\textsf{sub},\textsf {and},\textsf{or} \}\;, \\ Unop= & {} \{ \textsf{not},\textsf{shl},\textsf{shr},\textsf{mov} \}\;, \\ Cmpop= & {} \{ \textsf{eq},\textsf{gt},\textsf{beq} \}\; \end{aligned}$$

and

$$\begin{aligned} Src= & {} \{ \# i \, {\mid}\,i \in \mathbb {N} \} \cup \mathbb {N}\cup \{ @ i \, {\mid}\,i \in \mathbb {N} \}\;, \\ Dst= & {} \mathbb {N}\cup \{ @ i \, {\mid}\,i \in \mathbb {N} \}\;. \end{aligned}$$

We write $\mathcal {O}^\textrm{p}_\textsf{RAMP}$ for the set $\{ cmpop {:} s _1{:} s _2 \, {\mid}\, cmpop \in Cmpop \wedge s _1, s _2 \in Src \}$ and $\mathcal {O}^\textrm{o}_\textsf{RAMP}$ for the set $\mathcal {O}_\textsf{RAMP}\setminus \mathcal {O}^\textrm{p}_\textsf{RAMP}$.

The operators from $\mathcal {O}^\textrm{o}_\textsf{RAMP}$ are the operators that are interpreted in ${\mathfrak {D}}$ as basic RAM operations and the operators from $\mathcal {O}^\textrm{p}_\textsf{RAMP}$ are the operators that are interpreted in ${\mathfrak {D}}$ as basic RAM properties.

The following is a preliminary explanation of the operators from $\mathcal {O}_\textsf{RAMP}$:

• carrying out the operation denoted by an operator of the form $binop {:} s _1{:} s _2{:} d$ on a RAM memory in some state boils down to carrying out the binary operation named $binop$ on the values that $s _1$ and $s _2$ stand for in that state and then changing the content of the register that $d$ stands for into the result of this;

• carrying out the operation denoted by an operator of the form $unop {:} s _1{:} d$ on a RAM memory in some state boils down to carrying out the unary operation named $unop$ on the value that $s$ stands for in that state and then changing the content of the register that $d$ stands for into the result of this;

• carrying out the operation denoted by an operator of the form $cmpop {:} s _1{:} s _2$ on a RAM memory in some state boils down to carrying out the binary operation named $cmpop$ on the values that $s _1$ and $s _2$ stand for in that state.

The value that $s _i$ ($i = 1,2$) stands for is as follows:

• immediate: it stands for the shortest bit string representing the natural number i if it is of the form $\# i$;

• direct addressing: it stands for the content of the register with number i if it is of the form i;

• indirect addressing: it stands for the content of the register whose number is represented by the content of the register with number i if it is of the form @i;

and the register that $d$ stands for is as follows:

• direct addressing: it stands for the register with number i if it is of the form i;

• indirect addressing: it stands for the register whose number is represented by the content of the register with number i if it is of the form @i.

The following kinds of operations and relations on bit strings are covered by the operators from $\mathcal {O}_\textsf{RAMP}$: arithmetic operations ($\textsf{add},\textsf{sub}$), logical operations (and,or,not), bit-shift operations ($\textsf{shl},\textsf{shr}$), data-transfer operations ($\textsf{mov}$), arithmetic relations ($\textsf{eq},\textsf{gt}$), and the bit-wise equality relation ($\textsf{beq}$). The arithmetic operations on bit strings are operations that model arithmetic operations on natural numbers with respect to their binary representation by bit strings, the logical operations on bit strings are bitwise logical operations, and the data transfer operation on bit strings is the identity operation on bit strings (which is carried out when copying bit strings). The arithmetic relations on bit strings are relations that model arithmetic relations on natural numbers with respect to their binary representation by bit strings.

4.2 Interpretation of the Operators for the RAMP Model

The interpretation of the operators from $\mathcal {O}_\textsf{RAMP}$ in ${\mathfrak {D}}$ is defined in this section.

We start with defining auxiliary functions for conversion between natural numbers and bit strings and evaluation of the elements of $Src$ and $Dst$.

We write ${\mathop {-}\limits ^{\varvec{\cdot }}}$ for proper subtraction of natural numbers. We write $\div$ for zero-totalized Euclidean division of natural numbers, i.e. Euclidean division made total by imposing that division by zero yields zero (like in meadows, see e.g. [6, 7]). We use juxtaposition for concatenation of bit strings.

The natural to bit string function ${\textsf{b}} \, {:}\, \mathbb {N} \rightarrow \{ 0,1 \}^*$ is recursively defined as follows:

• $\textsf{b}(n) = n$ if $n \le 1 \quad$ and $\quad \textsf{b}(n) = (n \bmod 2) \kern.1em\textsf{b}(n \div 2)$ if $n > 1$

and the bit string to natural function ${\textsf{n}} \, {:}\, \{ 0,1 \}^* \rightarrow \mathbb {N}$ is recursively defined as follows:

• $\textsf{n}(\lambda ) = 0 \quad$ and $\quad \textsf{n}(b \kern.1emw) = b + 2 \cdot \textsf{n}(w)$.

These definitions tell us that, when viewed as the binary representation of a natural number, the first bit of a bit string is considered the least significant bit. Results of applying $\textsf{b}$ have no leading zeros, but the operand of $\textsf{n}$ may have leading zeros.

Thus, we have that $\textsf{n}(\textsf{b}(n)) = n$ and $\textsf{b}(\textsf{n}(w)) = w'$, where $w'$ is w without leading zeros, if $w \ne \lambda$.

For each $\sigma \in \Sigma _{\textsf{ram}}$, the src-valuation in $\sigma$ function ${\textsf{v}_{\sigma }} \, {:}\, Src \rightarrow \{ 0,1 \}^*$ is defined as follows:

• $\textsf{v}_{\sigma }(\# i) = \textsf{b}(i)$, $\textsf{v}_{\sigma }(i) = \sigma (i)$, and $\textsf{v}_{\sigma }(@ i) = \sigma (\textsf{n}(\sigma (i)))$

and, for each $\sigma \in \Sigma _{\textsf{ram}}$, the dst-valuation in $\sigma$ function ${\textsf{r}_{\sigma }} \, {:}\, Dst \rightarrow \mathbb {N}$ is defined as follows:

• $\textsf{r}_{\sigma }(i) = i$ and $\textsf{r}_{\sigma }(@ i) = \textsf{n}(\sigma (i))$.

We continue with defining the operations on bit strings that the operation names from $Binop \cup Unop$ refer to.

We define the operations on bit strings that the operation names $\textsf{add}$ and $\textsf{sub}$ refer to as follows:

$$\begin{aligned} {+} \, {:}\, \{ 0,1 \}^*\times \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:&\,\, w_1 + w_2 = \textsf{b}(\textsf{n}(w_1) + \textsf{n}(w_2)); \\ {{\mathop {-}\limits ^{\varvec{\cdot }}}} \, {:}\, \{ 0,1 \}^*\times \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:&\,\, w_1 {\mathop {-}\limits ^{\varvec{\cdot }}}w_2 = \textsf{b}(\textsf{n}(w_1) {\mathop {-}\limits ^{\varvec{\cdot }}}\textsf{n}(w_2)). \end{aligned}$$

These definitions tell us that, although the operands of the operations $+$ and ${\mathop {-}\limits ^{\varvec{\cdot }}}$ may have leading zeros, results of applying these operations have no leading zeros.

We define the operations on bit strings that the operation names and, $\textsf{or}$, and $\textsf{not}$ refer to recursively as follows:

$$\begin{aligned}&{\wedge } \, {:}\, \{ 0,1 \}^*\times \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:\, \lambda \wedge \lambda = \lambda , \lambda \wedge (b \kern.1emw) = 0\kern.1em(\lambda \wedge w), \\&\quad \,\,(b \kern.1emw) \wedge \lambda = 0\kern.1em(w \wedge \lambda ), (b_1 \kern.1emw_1) \wedge (b_2 \kern.1emw_2) = (b_1 \wedge b_2) \kern.1em(w_1 \wedge w_2);\\&{\vee } \, {:}\, \{ 0,1 \}^*\times \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:\, \, \lambda \vee \lambda = \lambda , \lambda \vee (b \kern.1emw) = b \kern.1em(\lambda \vee w), \\&\quad \,\,(b \kern.1emw) \vee \lambda = b \kern.1em(w \vee \lambda ), (b_1 \kern.1emw_1) \vee (b_2 \kern.1emw_2) = (b_1 \vee b_2) \kern.1em(w_1 \vee w_2);\\&{\lnot } \, {:}\, \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:\, \, \lnot \lambda = \lambda ,\, \lnot (b \kern.1emw) = (\lnot b) \kern.1em(\lnot w). \end{aligned}$$

These definitions tell us that, if the operands of the operations $\wedge$ and $\vee$ do not have the same length, sufficient leading zeros are assumed to exist. Moreover, results of applying these operations and results of applying $\lnot$ can have leading zeros.

We define the operations on bit strings that the operation names $\textsf{shl}$ and $\textsf{shr}$ refer to as follows:

$$\begin{aligned} {{\ll }\kern.1em} \, {:}\, \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:&\,\, {\ll }\kern.1em\lambda = \lambda ,\, {\ll }\kern.1em(b \kern.1emw) = 0\kern.1emb \kern.1emw; \\ {{\gg }\kern.1em} \, {:}\, \{ 0,1 \}^* \rightarrow \{ 0,1 \}^*:&\,\, {\gg }\kern.1em\lambda = \lambda , \, {\gg }\kern.1em(b \kern.1emw) = w. \end{aligned}$$

These definitions tell us that results of applying the operations ${\ll }\kern.1em$ and ${\gg }\kern.1em$ can have leading zeros. We have that $\textsf{n}({\ll }\kern.1emw) = \textsf{n}(w) \cdot 2$ and $\textsf{n}({\gg }\kern.1emw) = \textsf{n}(w) \div 2$.

Now, we are ready to define the interpretation of the operators from $\mathcal {O}_\textsf{RAMP}$ in ${\mathfrak {D}}$. For each $o \in \mathcal {O}_\textsf{RAMP}$, the interpretation of o in ${\mathfrak {D}}$, written $[\![ o ]\!]$, is defined as follows:

$$\begin{aligned}{}[\![ \textsf{add}{:}s_1{:}s_2{:}d ]\!](\sigma )= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \textsf{v}_{\sigma }(s_1) + \textsf{v}_{\sigma }(s_2)\};\\ [\![ \textsf{sub}{:}s_1{:}s_2{:}d ]\!](\sigma )= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \textsf{v}_{\sigma }(s_1) {\mathop {-}\limits ^{\varvec{\cdot }}}\textsf{v}_{\sigma }(s_2)\};\\ [\![ \textsf {and}{:}s_1{:}s_2{:}d ]\!](\sigma )= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \textsf{v}_{\sigma }(s_1) \wedge \textsf{v}_{\sigma }(s_2)\};\\ [\![ \textsf{or}{:}s_1{:}s_2{:}d ]\!](\sigma )\quad= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \textsf{v}_{\sigma }(s_1) \vee \textsf{v}_{\sigma }(s_2)\};\\ [\![ \textsf{not}{:}s_1{:}d ]\!](\sigma )\quad \,\,\,= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \lnot \textsf{v}_{\sigma }(s_1)\};\\ [\![ \textsf{shl}{:}s_1{:}d ]\!](\sigma )\quad \,\,\,\,= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto {\ll }\kern.1em\textsf{v}_{\sigma }(s_1)\};\\ [\![ \textsf{shr}{:}s_1{:}d ]\!](\sigma )\quad \,\,\,\,= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto {\gg }\kern.1em\textsf{v}_{\sigma }(s_1)\};\\ [\![ \textsf{mov}{:}s_1{:}d ]\!](\sigma )\quad= & {} \sigma \{\textsf{r}_{\sigma }(d) \mapsto \textsf{v}_{\sigma }(s_1)\};\\ [\![ \textsf{eq}{:}s_1{:}s_2 ]\!](\sigma )\quad \,\,\,= & {} \left\{ \begin{array}{l} 1 \;\textrm{if}\; \textsf{n}(\textsf{v}_{\sigma }(s_1)) = \textsf{n}(\textsf{v}_{\sigma }(s_2)), \\ 0 \;\textrm{otherwise}; \end{array} \right. \\ [\![ \textsf{gt}{:}s_1{:}s_2 ]\!](\sigma )\quad \,\,\,= & {} \left\{ \begin{array}{l} 1 \;\textrm{if}\; \textsf{n}(\textsf{v}_{\sigma }(s_1)) > \textsf{n}(\textsf{v}_{\sigma }(s_2)),\\ 0 \;\textrm{otherwise}; \end{array}\right. \\ [\![ \textsf{beq}{:}s_1{:}s_2 ]\!](\sigma )\quad= & {} \left\{ \begin{array}{l} 1 \;\textrm{if}\; \textsf{v}_{\sigma }(s_1) = \textsf{v}_{\sigma }(s_2), \\ 0 \;\textrm{otherwise}. \end{array} \right. \end{aligned}$$

Clearly, the interpretation of each operator from $\mathcal {O}^\textrm{o}_\textsf{RAMP}$ is a basic RAM operation and the interpretation of each operator from $\mathcal {O}^\textrm{p}_\textsf{RAMP}$ is a basic RAM property.

4.3 RAMP Terms and the RAMP Model

Below, the RAMP model of computation is characterized in the setting introduced in Sections 2 and 3. However, first the notion of a RAMP term is defined. This notion is introduced to make precise what the set of possible computational processes is in the case of the RAMP model of computation.

In this section, ${\mathfrak {D}}$ is fixed as follows:

• $\Sigma _{\mathfrak {D}}$ is the smallest signature including (a) all sorts, constants, and operators required by the assumptions made about ${\mathfrak {D}}$ in $\text {ACP}_{\epsilon }^{\tau }$-I or the RAM conditions on ${\mathfrak {D}}$ and (b) all operators from $\mathcal {O}_\textsf{RAMP}$;

• all sorts, constants, and operators mentioned under (a) are interpreted in ${\mathfrak {D}}$ as required by the assumptions made about ${\mathfrak {D}}$ in $\text {ACP}_{\epsilon }^{\tau }$-I or the RAM conditions on ${\mathfrak {D}}$;

• all operators mentioned under (b) are interpreted in ${\mathfrak {D}}$ as defined at the end of Section 4.2.

Moreover, it is assumed that $\textsf{m}\in \mathcal {V}$.

A RAM process term, called a RAMP term for short, is a term from $\mathcal {P}_{\textsf{rec}}$ that is of the form $\langle X \vert E \rangle$, where, for each $Y \in \textrm{vars}(E)$, the recursion equation for Y in E has one of the following forms:

$$\begin{aligned}&Y&= {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, o(\textsf{m})] \cdot Z, \\&Y&= (p(\textsf{m}) = 1) \, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{m}] \cdot Z \,{+}\,(p(\textsf{m}) = 0) \, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{m}] \cdot Z', \\&Y&= {\textsf{t}}\, {:\rightarrow}\,\epsilon , \end{aligned}$$

where $o \in \mathcal {O}^\textrm{o}_\textsf{RAMP}$, $p \in \mathcal {O}^\textrm{p}_\textsf{RAMP}$, and $Z,Z' \in \textrm{vars}(E)$. We write $\mathcal {P}_\textsf{RAMP}$ for the set of all RAMP terms, and we write $\mathcal{C}\mathcal{P}_\textsf{RAMP}$ for $\mathcal {P}_\textsf{RAMP}\cap \mathcal{C}\mathcal{P}_{\textsf{rec}}$.

In the definition of a RAMP term above, E would not be a guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I if the (ineffective) assignment action $[\textsf{m} \, {{:}{=}}\, \textsf{m}]$ had been omitted from the summands of recursion equations of the second form. Because we regard both performing a RAM operation and testing a RAM property as a step of a computational process, the presence of this action has the technical advantage that counting of steps becomes counting of actions.

A process that can be denoted by a RAMP term is called a RAM process or a RAMP for short. So, a RAMP is a process that is definable by a guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I of the kind described above.

As mentioned in Section 1, a basic assumption in this paper is that a model of computation is fully characterized by: (a) a set of possible computational processes, (b) for each possible computational process, a set of possible data environments, and (c) the effect of applying such processes to such environments.

${\mathfrak {D}}$ as fixed above and $\mathcal{C}\mathcal{P}_\textsf{RAMP}$ induce the RAMP model of computation:

• the set of possible computational processes is the set of all processes that can be denoted by a term from $\mathcal{C}\mathcal{P}_\textsf{RAMP}$;

• for each possible computational process, the set of possible data environments is the set of all $\{ \textsf{m} \}$-indexed data environments;

• the effect of applying the process denoted by a $t \in \mathcal{C}\mathcal{P}_\textsf{RAMP}$ to a $\{ \textsf{m} \}$-indexed data environment $\mu$ is ${\textsf{V}_{\rho }}(t)$, where $\rho$ is a flexible variable valuation that represents $\mu$.

The RAMP model of computation described above is intended to be essentially the same as the standard RAM model of computation extended with logical instructions and bit-shift instructions. The RAMs from that model are referred to as the BBRAMs (Basic Binary RAMs). There is a strong resemblance between $\mathcal {O}_\textsf{RAMP}$ and the set ${\mathcal {I}_\textsf{BBRAM}}$ of instructions from which the built-in programs of the BBRAMs can be constructed. Because the concrete syntax of the instructions does not matter, ${\mathcal {I}_\textsf{BBRAM}}$ can be defined as follows:

$$\begin{aligned} {\mathcal {I}_\textsf{BBRAM}}= (\mathcal {O}^\textrm{o}_\textsf{RAMP}) \cup \{ \textsf{jmp}{:}p{:}i \, {\mid}\,p \in \mathcal {O}^\textrm{p}_\textsf{RAMP}\wedge i \in \mathbb {N}^+ \} \cup \{ \textsf{halt} \}\;. \end{aligned}$$

A BBRAM program is a non-empty sequence C from ${\mathcal {I}_\textsf{BBRAM}}^*$ in which instructions of the form $\textsf{jmp}{:}p{:}i$ with $i > \ell (C)$ do not occur. We write ${\mathcal{I}\mathcal{S}_\textsf{BBRAM}}$ for the set of all BBRAM programs.

The execution of an instruction o from $\mathcal {O}^\textrm{o}_\textsf{RAMP}$ by a BBRAM causes the state of its memory to change according to $[\![ o ]\!]$. The execution of an instruction of the form $\textsf{jmp}{:}p{:}i$ or the instruction $\textsf{halt}$ by a BBRAM has no effect on the state of its memory. After execution of an instruction by a BBRAM, the BBRAM proceeds to the execution of the next instruction from its built-in program except when the instruction is of the form $\textsf{jmp}{:}p{:}i$ and $[\![ p ]\!] = 1$ or when the instruction is $\textsf{halt}$. In the case that the instruction is of the form $\textsf{jmp}{:}p{:}i$ and $[\![ p ]\!] = 1$, the execution proceeds to the ith instruction of the program. In the case that the instruction is $\textsf{halt}$, the execution terminates successfully.

The processes that are produced by the BBRAMs when they execute their built-in program are given by a function ${\mathcal {M}} \, {:}\, {\mathcal{I}\mathcal{S}_\textsf{BBRAM}} \rightarrow \mathcal {P}_\textsf{RAMP}$ that is defined up to consistent renaming of variables as follows: $\mathcal {M}(c_1\, \ldots \, c_n) = \langle X_1 \vert E \rangle$, where E consists of, for each $i \in \mathbb {N}$ with $1 \le i \le n$, an equation

$$\begin{aligned} X_i= & {} {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, c_i(\textsf{m})] \cdot X_{i+1}\qquad \qquad \qquad \qquad \qquad \qquad \,\,\,\, \text {if}\, c_i \in \mathcal {O}^\textrm{o}_\textsf{RAMP}, \\ X_i= & {} (p(\textsf{m}) = 1) \, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{m}] \cdot X_j\,{+}\,(p(\textsf{m}) = 0) \, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{m}] \cdot X_{i+1} \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text {if}\, c_i \equiv \textsf{jmp}{:}p{:}j, \\ X_i= & {} {\textsf{t}}\, {:\rightarrow}\,\epsilon \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\,\, \text {if}\, c_i \equiv \textsf{halt}, \end{aligned}$$

where $X_1,\ldots ,X_n$ are different variable from $\mathcal {X}$.

Let $C \in {\mathcal{I}\mathcal{S}_\textsf{BBRAM}}$. Then $\mathcal {M}(C)$ denotes the process that is produced by the BBRAM whose built-in program is C when it executes its built-in program.

The definition of $\mathcal {M}$ is in accordance with the descriptions of various versions of the RAM model of computation in the literature on this subject (see e.g. [1, 12, 21, 32]). However, to the best of my knowledge, none of these descriptions is precise and complete enough to allow of a proof of this.

The RAMPs are exactly the processes that can be produced by the BBRAMs when they execute their built-in program.

Theorem 4

For each constant $\langle X \vert E \rangle \in \mathcal {P}_{\textsf{rec}}$, $\langle X \vert E \rangle \in \mathcal {P}_\textsf{RAMP}$ iff there exists a $C \in {\mathcal{I}\mathcal{S}_\textsf{BBRAM}}$ such that $\langle X \vert E \rangle$ and $\mathcal {M}(C)$ are identical up to consistent renaming of variables.

Proof

It is easy to see that (a) for all $C \in {\mathcal{I}\mathcal{S}_\textsf{BBRAM}}$, $\mathcal {M}(C) \in \mathcal {P}_\textsf{RAMP}$ and (b) $\mathcal {M}$ is an bijection up to consistent renaming of variables. From this, the theorem follows immediately. $\square$

Notice that, if $\langle X \vert E \rangle$ and $\langle X' \vert E' \rangle$ are identical up to consistent renaming of variables, then the equation $\langle X \vert E \rangle = \langle X' \vert E' \rangle$ is derivable from RDP and RSP.

The following theorem is a result concerning the computational power of RAMPs.

Theorem 5

For each $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$, there exists a $t \in \mathcal {P}_\textsf{RAMP}$ such that t computes F iff F is Turing-computable.

Proof

By Theorem 4, it is sufficient to show that each BBRAM is Turing equivalent to a Turing machine. The BBRAM model of computation is essentially the same as the BRAM model of computation from [14] extended with bit-shift instructions. It follows directly from simulation results mentioned in [14] (part (3) of Theorem 2.4, part (3) of Theorem 2.5, and part (2) of Theorem 2.6) that each BRAM can be simulated by a Turing machine and vice versa. Because each Turing machine can be simulated by a BRAM, we immediately have that each Turing machine can be simulated by a BBRAM. It is easy to see that the bit-shift instructions can be simulated by a Turing machine. From this and the fact that each BRAM can be simulated by a Turing machine, it follows that each BBRAM can be simulated by a Turing machine as well. Hence, each BBRAM is Turing equivalent to a Turing machine.$\square$

Henceforth, we write $POLY$ for $\{ f \, {\mid}\,{f} \, {:}\, \mathbb {N} \rightarrow \mathbb {N} \wedge f \mathrm {\,is\,a\,polynomial\,function} \}$. The following theorem tells us that the decision problems that belong to the complexity class $\varvec{P}$ are exactly the decision problems that can be solved by means of a RAMP in polynomially many steps.

Theorem 6

For each ${F} \, {:}\, \{ 0,1 \}^* \rightarrow \{ 0,1 \}$, there exist a $t \in \mathcal {P}_\textsf{RAMP}$ and a $W \in POLY$ such that t computes F in W steps iff $F \in \varvec{P}$.

Proof

By Theorem 4, it is sufficient to show that time complexity on BBRAMs under the uniform time measure, i.e. the number of steps, and time complexity on multi-tape Turing machines are polynomially related. The BBRAM is essentially the same as the BRAM model of computation from [14] extended with bit-shift instructions. It follows directly from simulation results mentioned in [14] (part (3) of Theorem 2.4, part (3) of Theorem 2.5, and part (2) of Theorem 2.6) that time complexity on BRAMs under the uniform time measure and time complexity on multi-tape Turing machines are polynomially related. It is easy to see that the bit-shift instructions can be simulated by a multi-tape Turing machine in linear time. Hence, the time complexities remain polynomially related if the BRAM model is extended with the bit-shift instructions.

$\square$

5 The APRAMP Model of Computation

The setting introduced in Sections 2 and 3 is used in this section to describe an asynchronous parallel RAM model of computation. Because it focuses on the processes that are produces by asynchronous parallel RAMs when they execute their built-in programs, the parallel RAM model of computation described in this section is called the APRAMP (Asynchronous Parallel Random Access Machine Process) model of computation. In this model of computation, a computational process is the parallel composition of a number of processes that each has its own private RAM memory. However, together they also have a shared RAM memory for synchronization and communication.

First, the operators are introduced that represent the RAM operations and the RAM properties that belong to ${\mathfrak {D}}$ in the case of the APRAMP model of computation. Next, the interpretation of those operators as a RAM operation or a RAM property is given. Finally, the APRAMP model of computation is described.

In the case of the APRAMP model of computation, the set of operators from $\Sigma _{\mathfrak {D}}$ that are interpreted in ${\mathfrak {D}}$ as RAM operations or RAM properties is the set $\mathcal {O}_\textsf{PRAMP}$ defined as follows:

$$\begin{aligned} \mathcal {O}_\textsf{PRAMP}= & {} \mathcal {O}_\textsf{RAMP}\cup \{ \textsf{ini}{:}\# i \, {\mid}\,i \in \mathbb {N}^+ \} \\&\cup&\{ \textsf{loa}{:}@ i{:} d \, {\mid}\,i \in \mathbb {N}\wedge d \in Dst \} \cup \{ \textsf{sto}{:} s {:}@ i \, {\mid}\, s \in Src \wedge i \in \mathbb {N} \}\;, \end{aligned}$$

where $Src$ and $Dst$ are as defined in Section 4.1.

In operators of the forms $binop {:} s _1{:} s _2{:} d$, $unop {:} s _1{:} d$, and $cmpop {:} s _1{:} s _2$ from $\mathcal {O}_\textsf{RAMP}$, $s _1$, $s _2$, and $d$ refer to the private RAM memory. In operators of the form $\textsf{loa}{:}@ i{:} d$ and $\textsf{sto}{:} s {:}@ i$ from $\mathcal {O}_\textsf{PRAMP}\setminus \mathcal {O}_\textsf{RAMP}$, $s$ and $d$ refer to the private RAM memory too. The operators of the form $\textsf{loa}{:}@ i{:} d$ differ from the operators of the form $\textsf{mov}{:}@ i{:} d$ in that @i stands for the content of the register from the shared RAM memory whose number is represented by the content of the register with number i from the private memory. The operators of the form $\textsf{sto}{:} s {:}@ i$ differ from the operators of the form $\textsf{mov}{:} s {:}@ i$ in that @i stands for the register from the shared RAM memory whose number is represented by the content of the register with number i from the private memory. The operators of the form $\textsf{ini}{:}\# i$ initialize the registers from the private memory as follows: the content of the register with number 0 becomes the shortest bit string that represents the natural number i and the content of all other registers becomes the empty bit string.

Now, we are ready to define the interpretation of the operators from $\mathcal {O}_\textsf{PRAMP}$ in ${\mathfrak {D}}$. For each $o \in \mathcal {O}_\textsf{PRAMP}$, the interpretation of o in ${\mathfrak {D}}$, written $[\![ o ]\!]$, is as defined in Section 4.2 for operators from $\mathcal {O}_\textsf{RAMP}$ and as defined below for the additional operators:

$$\begin{aligned}{}[\![ \textsf{ini}{:}\# i ]\!](\sigma _p)\quad \quad \quad \,\,\,= & {} \sigma _\lambda \{0 \mapsto \textsf{b}(i)\}; \\ [\![ \textsf{loa}{:}@ i{:}d ]\!](\sigma _p,\sigma _s)= & {} \sigma _p\{\textsf{r}_{\sigma _p}(d) \mapsto \sigma _s(\textsf{n}(\sigma _p(i)))\}; \\ [\![ \textsf{sto}{:}s{:}@ i ]\!](\sigma _p,\sigma _s)= & {} \sigma _s\{\textsf{n}(\sigma _p(i)) \mapsto \textsf{v}_{\sigma _p}(s)\}. \end{aligned}$$

Here, $\sigma _p$ should be thought of as a private-memory state and $\sigma _s$ should be thought of as a shared-memory state.

Clearly, the interpretation of each operator of the form $\textsf{ini}{:}\# i$ is a 1-RAM operation and the interpretation of each operator of the form $\textsf{loa}{:}@ i{:}d$ or $\textsf{sto}{:}s{:}@ i$ is a 2-RAM operation.

Below, the APRAMP model of computation is characterized in the setting introduced in Sections 2 and 3. However, first the notion of an APRAMP term is defined. This notion is introduced to make precise what the set of possible computational processes is in the case of the APRAMP model of computation.

In this section, ${\mathfrak {D}}$ is fixed as follows:

• $\Sigma _{\mathfrak {D}}$ is the smallest signature including (a) all sorts, constants, and operators required by the assumptions made about ${\mathfrak {D}}$ in $\text {ACP}_{\epsilon }^{\tau }$-I or the RAM conditions on ${\mathfrak {D}}$ and (b) all operators from $\mathcal {O}_\textsf{PRAMP}$;

• all sorts, constants, and operators mentioned under (a) are interpreted in ${\mathfrak {D}}$ as required by the assumptions made about ${\mathfrak {D}}$ in $\text {ACP}_{\epsilon }^{\tau }$-I or the RAM conditions on ${\mathfrak {D}}$;

• all operators mentioned under (b) are interpreted in ${\mathfrak {D}}$ as defined above.

Moreover, it is assumed that $\textsf{m}\in \mathcal {V}$ and, for all $i \in \mathbb {N}^+$, $\textsf{m}_i \in \mathcal {V}$. We write $\mathcal {V}^\textsf{m}_n$, where $n \in \mathbb {N}^+$, for the set $\{ \textsf{m} \} \cup \{ \textsf{m}_i \, {\mid}\,i \in \mathbb {N}^+\wedge i \le n \}$.

An n-APRAM process term ($n \in \mathbb {N}^+$), called an n-APRAMP term for short, is a term from $\mathcal {P}_{\textsf{rec}}$ that is of the form $\langle X_1 \vert E_1 \rangle \, {\parallel }\,\ldots \, {\parallel }\,\langle X_n \vert E_n \rangle$, where, for each $i \in \mathbb {N}^+$ with $i \le n$:

• for each $X \in \textrm{vars}(E_i)$, the recursion equation for X in $E_i$ has one of the following forms:

  • (1) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{ini}{:}\# i\,(\textsf{m}_i)] \cdot Y$,

  • (2) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{loa}{:}@ j{:}d\,(\textsf{m}_i,\textsf{m})] \cdot Y$,

  • (3) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{sto}{:}s{:}@ j\,(\textsf{m}_i,\textsf{m})] \cdot Y$,

  • (4) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, o(\textsf{m}_i)] \cdot Y$,

  • (5) $X = (p(\textsf{m}_i) = 1) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y \,{+}\,(p(\textsf{m}_i) = 0) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y'$,

  • (6) $X = {\textsf{t}}\, {:\rightarrow}\,\epsilon$,

  where $o \in \mathcal {O}^\textrm{o}_\textsf{RAMP}$, $p \in \mathcal {O}^\textrm{p}_\textsf{RAMP}$, and $Y,Y' \in \textrm{vars}(E_i)$;

• for each $X \in \textrm{vars}(E_i)$, the recursion equation for X in $E_i$ is of the form (1) iff $X \equiv X_i$.

We write $\mathcal {P}_\textsf{APRAMP}$ for the set of all terms $t \in \mathcal {P}_{\textsf{rec}}$ such that t is an n-APRAMP term for some $n \in \mathbb {N}^+$, and we write $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$ for $\mathcal {P}_\textsf{APRAMP}\cap \mathcal{C}\mathcal{P}_{\textsf{rec}}$. Moreover, we write $deg (t)$, where $t \in \mathcal {P}_\textsf{APRAMP}$, for the unique $n \in \mathbb {N}^+$ such that t is an n-APRAMP term.

The terms from $\mathcal {P}_\textsf{APRAMP}$ are referred to as APRAMP terms.

A process that can be denoted by an APRAMP term is called an APRAM process or an APRAMP for short. So, an APRAMP is a parallel composition of processes that are definable by a guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I of the kind described above. Each of those parallel processes starts with an initialization step in which the number of its private memory is made available in the register with number 0 from its private memory.

It follows from the auxiliary result about abstraction-free terms mentioned in Section 2.4 that, for all $t \in \mathcal {P}_\textsf{APRAMP}$, there exists a guarded linear recursive specification E and $X \in \textrm{vars}(E)$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}\vdash t = \langle X \vert E \rangle$.

As mentioned before, a basic assumption in this paper is that a model of computation is fully characterized by: (a) a set of possible computational processes, (b) for each possible computational process, a set of possible data environments, and (c) the effect of applying such processes to such environments.

${\mathfrak {D}}$ as fixed above and $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$ induce the APRAMP model of computation:

• the set of possible computational processes is the set of all processes that can be denoted by a term from $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$;

• for each possible computational process p, the set of possible data environments is the set of all $\mathcal {V}^\textsf{m}_{ deg (t)}$-indexed data environments, where t is a term from $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$ denoting p;

• the effect of applying the process denoted by a $t \in \mathcal{C}\mathcal{P}_\textsf{APRAMP}$ to a $\mathcal {V}^\textsf{m}_{ deg (t)}$-indexed data environment $\mu$ is ${\textsf{V}_{\rho }}(t)$, where $\rho$ is a flexible variable valuation that represents $\mu$.

The APRAMP model of computation described above is intended to be close to the asynchronous parallel RAM model of computation sketched in [10, 25, 30]. However, the time complexity measure for this model that will be introduced in Section 7 is quite different from the ones proposed in those papers. The APRAMP model described above is considered less close to the asynchronous parallel RAM model sketched in [17] because the latter provides special instructions for synchronization.

The APRAMPs can be looked upon as the processes that can be produced by a collection of BBRAMs with an extended instruction set when they execute their built-in program asynchronously in parallel.

The BBRAMs with the extended instruction set are referred to as the SMBRAMs (Shared Memory Binary RAMs). There is a strong resemblance between $\mathcal {O}_\textsf{PRAMP}$ and the set ${\mathcal {I}_\textsf{SMBRAM}}$ of instructions from which the built-in programs of the SMBRAMs can be constructed. Because the concrete syntax of the instructions does not matter, ${\mathcal {I}_\textsf{SMBRAM}}$ can be defined as follows:

$$\begin{aligned} {\mathcal {I}_\textsf{SMBRAM}}= (\mathcal {O}_\textsf{PRAMP}\setminus \mathcal {O}^\textrm{p}_\textsf{RAMP}) \cup \{ \textsf{jmp}{:}p{:}i \, {\mid}\,p \in \mathcal {O}^\textrm{p}_\textsf{RAMP}\wedge i \in \mathbb {N}^+ \} \cup \{ \textsf{halt} \}\;. \end{aligned}$$

An SMBRAM program is a non-empty sequence C from ${\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}^*$ in which instructions of the form $\textsf{jmp}{:}p{:}i$ with $i > \ell (C)$ do not occur. We write ${\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$ for the set of all SMBRAM programs.

For the SMBRAMs whose private memory has number i ($i \in \mathbb {N}^+$), the processes that are produced when they execute their built-in program are given by a function ${\mathcal {M}_i} \, {:}\, {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}} \rightarrow \mathcal {P}_\textsf{APRAMP}$ that is defined up to consistent renaming of variables as follows: $\mathcal {M}_i(c_1\, \ldots \, c_n) = \langle X_i \vert E_i \rangle$, where $E_i$ consists of the equation

$$\begin{aligned} X_i = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{ini}{:}\# i\,(\textsf{m}_i)] \cdot Y_1 \end{aligned}$$

and, for each $j \in \mathbb {N}$ with $1 \le j \le n$, an equation

$$\begin{aligned} Y_j= & {} {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, c_j(\textsf{m}_i,\textsf{m})] \cdot Y_{j+1} \qquad \qquad \qquad \qquad \qquad \qquad \text {if}\, c_j \in Load , \\ Y_j= & {} {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, c_j(\textsf{m}_i,\textsf{m})] \cdot Y_{j+1} \qquad \qquad \qquad \qquad \qquad \qquad \,\, \text {if}\, c_j \in Store , \\ Y_j= & {} {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, c_j(\textsf{m}_i)] \cdot Y_{j+1} \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\, \text {if}\, c_j \in \mathcal {O}^\textrm{o}_\textsf{RAMP}, \\ Y_j= & {} (p(\textsf{m}_i) = 1) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y_{j'}\,{+}\,(p(\textsf{m}_i) = 0) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y_{j+1} \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\,\, \text {if}\, c_j \equiv \textsf{jmp}{:}p{:}j', \\ Y_j= & {} {\textsf{t}}\, {:\rightarrow}\,\epsilon \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\, \text {if}\, c_j \equiv \textsf{halt}, \end{aligned}$$

where $Load = \{ \textsf{loa}{:}@ i{:} d \, {\mid}\,i \in \mathbb {N}\wedge d \in Dst \}$, $Store = \{ \textsf{sto}{:} s {:}@ i \, {\mid}\, s \in Src \wedge i \in \mathbb {N} \}$, and $Y_1,\ldots ,Y_n$ are different variables from $\mathcal {X}\setminus \{ X_i \}$.

The APRAMPs are exactly the processes that can be produced by a collection of SMBRAMs when they execute their built-in program asynchronously in parallel.

Theorem 7

Let $n \in \mathbb {N}^+$. For all constants $\langle X_1 \vert E_1 \rangle , \ldots , \langle X_n \vert E_n \rangle \in \mathcal {P}_{\textsf{rec}}$, $\langle X_1 \vert E_1 \rangle \, {\parallel }\,\ldots \, {\parallel }\,\langle X_n \vert E_n \rangle \in \mathcal {P}_\textsf{APRAMP}$ iff there exist $C_1, \ldots , C_n \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$ such that $\langle X_1 \vert E_1 \rangle \, {\parallel }\,\ldots \, {\parallel }\,\langle X_n \vert E_n \rangle$ and $\mathcal {M}_1(C_1) \, {\parallel }\,\ldots \, {\parallel }\,\mathcal {M}_n(C_n)$ are identical up to consistent renaming of variables.

Proof

Let $i \in \mathbb {N}^+$ be such that $i \le n$. It is easy to see that (a) for all $C \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$, $\mathcal {M}_i(C) \in \mathcal {P}_\textsf{APRAMP}$ and (b) $\mathcal {M}_i$ is an bijection up to consistent renaming of variables. From this, it follows immediately that there exists a $C \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$ such that $\langle X_i \vert E_i \rangle$ and $\mathcal {M}_i(C)$ are identical up to consistent renaming of variables. From this, the theorem follows immediately. $\square$

6 The SPRAMP Model of Computation

In the asynchronous parallel RAM model of computation presented in Section 5, the parallel processes that make up a computational process do not automatically synchronize after each computational step. In this section, we describe a parallel RAM model of computation where the parallel processes that make up a computational process automatically synchronize after each computational step.

6.1 Synchronization of Parallel Processes

For the purpose of synchronizing parallel processes, a special instance of the synchronization merge operator of CSP [23] is defined in terms of the operators of $\text {ACP}_{\epsilon }^{\tau }$-I+$RN$. It is assumed that $\textsf{sync},\widetilde{\textsf{sync}}\in \textsf{A}$ and $\gamma$ is such that $\gamma (\textsf{sync},\textsf{sync}) = \widetilde{\textsf{sync}}$, $\gamma (\textsf{sync},a) = \delta$ for all $a \in \textsf{A}\setminus \{ \textsf{sync} \}$, and $\gamma (\widetilde{\textsf{sync}},a) = \delta$ for all $a \in \textsf{A}$. The special instance of the synchronization merge operator, $\, {\parallel }\,_\textsf{sync}$, is defined as follows:

$$\begin{aligned} t \, {\parallel }\,_\textsf{sync}t' = \rho _{f}({\partial _{\{ \textsf{sync} \}}}(\rho _{f}(t) \, {\parallel }\,\rho _{f}(t')))\;, \end{aligned}$$

where the renaming function f is defined by $f(\widetilde{\textsf{sync}}) = \textsf{sync}$ and $f(\alpha ) = \alpha$ if $\alpha \in \mathcal {A}\setminus \{ \widetilde{\textsf{sync}} \}$.

The process denoted by $t_1 \, {\parallel }\,_\textsf{sync}\ldots \, {\parallel }\,_\textsf{sync}t_n$ behaves as the n processes denoted by $t_1,\ldots ,t_n$ in parallel, but with the restriction that the special synchronization action $\textsf{sync}$ can only be performed simultaneously by all n processes.

Because of the use of an action renaming operator in the definition of $\, {\parallel }\,_\textsf{sync}$, it is assumed in Sections 6.2 and 7.3 that:

• from Section 2.4, $\mathcal {P}_{\textsf{rec}}$ stands for the set of all closed $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}{+}RN$ terms of sort $\textbf{P}$;

• from Section 2.4, all occurrences of $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}$, and $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}{+}PR$ have been replaced by $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}{+}RN$, $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}{+}RN$, and $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}+\text {CFAR}{+}PR {+}RN$, respectively.

What is defined by the definitions given from Section 3 is the same before and after these changes. Moreover, all results given from Section 2.4, including the soundness and semi-completeness results, go through after these changes.

6.2 SPRAMP Terms and the SPRAMP Model

The parallel RAM model of computation described in this section is called the SPRAMP (Synchronous Parallel Random Access Machine Process) model of computation.

The operators that represent the RAM operations and the RAM properties that belong to ${\mathfrak {D}}$ in the case of the SPRAMP model of computation are the same as in the case of the APRAMP model of computation. The interpretation of those operators as a RAM operation or a RAM property is also the same as in the case of the APRAMP model of computation. Moreover, ${\mathfrak {D}}$ is fixed as in Section 5.

Below, the SPRAMP model of computation is characterized. However, first the notion of an n-SPRAMP term is defined.

Like in Section 5, it is assumed that $\textsf{m}\in \mathcal {V}$ and, for all $i \in \mathbb {N}^+$, $\textsf{m}_i \in \mathcal {V}$. Again, we write $\mathcal {V}^\textsf{m}_n$, where $n \in \mathbb {N}^+$, for the set $\{ \textsf{m} \} \cup \{ \textsf{m}_i \, {\mid}\,i \in \mathbb {N}^+\wedge i \le n \}$.

An n-SPRAM process term ($n \in \mathbb {N}^+$), called an n-SPRAMP term for short, is a term from $\mathcal {P}_{\textsf{rec}}$ that is of the form $\langle X_1 \vert E_1 \rangle \, {\parallel }\,_\textsf{sync}\ldots \, {\parallel }\,_\textsf{sync}\langle X_n \vert E_n \rangle$, where, for each $i \in \mathbb {N}^+$ with $i \le n$:

• for each $X \in \textrm{vars}(E_i)$, the recursion equation for X in $E_i$ has one of the following forms:

  • (1) $X = {\textsf{t}}\, {:\rightarrow}\,\textsf{sync}\cdot Y$,

  • (2) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{ini}{:}\# i\,(\textsf{m}_i)] \cdot Y$,

  • (3) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{loa}{:}@j{:}d\,(\textsf{m}_i,\textsf{m})] \cdot Y$,

  • (4) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, \textsf{sto}{:}s{:}@j\,(\textsf{m}_i,\textsf{m})] \cdot Y$,

  • (5) $X = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, o(\textsf{m}_i)] \cdot Y$,

  • (6) $X = (p(\textsf{m}_i) = 1) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y \,{+}\,(p(\textsf{m}_i) = 0) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y'$,

  • (7) $X = {\textsf{t}}\, {:\rightarrow}\,\epsilon$,

  where $o \in \mathcal {O}^\textrm{o}_\textsf{RAMP}$, $p \in \mathcal {O}^\textrm{p}_\textsf{RAMP}$, and $Y,Y' \in \textrm{vars}(E_i)$;

• for each $X,Y \in \textrm{vars}(E_i)$ with Y occurring in the right-hand side of the recursion equation for X in $E_i$, the recursion equation for X in $E_i$ is of the form (1) iff the recursion equation for Y in $E_i$ is not of the form (1);

• for each $X \in \textrm{vars}(E_i)$, the recursion equation for X in $E_i$ is of the form (2) iff $X \equiv X_i$.

We write $\mathcal {P}_\textsf{SPRAMP}$ for the set of all terms $t \in \mathcal {P}_{\textsf{rec}}$ such that t is an n-SPRAMP term for some $n \in \mathbb {N}^+$, and we write $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ for $\mathcal {P}_\textsf{SPRAMP}\cap \mathcal{C}\mathcal{P}_{\textsf{rec}}$. Moreover, we write $deg (t)$, where $t \in \mathcal {P}_\textsf{SPRAMP}$, for the unique $n \in \mathbb {N}^+$ such that t is an n-SPRAMP term.

The terms from $\mathcal {P}_\textsf{SPRAMP}$ are referred to as SPRAMP terms.

A process that can be denoted by an SPRAMP term is called an SPRAM process or an SPRAMP for short. So, an SPRAMP is a synchronous parallel composition of processes that are definable by a guarded linear recursive specification over $\text {ACP}_{\epsilon }^{\tau }$-I of the kind described above. Each of those parallel processes starts with an initialization step in which the number of its private memory is made available in the register with number 0 from its private memory.

It follows from the auxiliary result about abstraction-free terms mentioned in Section 2.4 that, for all $t \in \mathcal {P}_\textsf{APRAMP}$, there exists a guarded linear recursive specification E and $X \in \textrm{vars}(E)$ such that $\text {ACP}_{\epsilon }^{\tau }-\text {I} +\text {REC}{+}RN \vdash t = \langle X \vert E \rangle$.

${\mathfrak {D}}$ as fixed above and $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ induce the SPRAMP model of computation:

• the set of possible computational processes is the set of all processes that can be denoted by a term from $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$;

• for each possible computational process p, the set of possible data environments is the set of all $\mathcal {V}^\textsf{m}_{ deg (t)}$-indexed data environments, where t is a term from $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ denoting p;

• the effect of applying the process denoted by a $t \in \mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ to a $\mathcal {V}^\textsf{m}_{ deg (t)}$-indexed data environment $\mu$ is ${\textsf{V}_{\rho }}(t)$, where $\rho$ is a flexible variable valuation that represents $\mu$.

The SPRAMP model of computation described above is intended to be close to the synchronous parallel RAM model of computation sketched in [36].⁸ However, that model is a PRIORITY CRCW model whereas the SPRAMP model is essentially an ARBITRARY CRCW model. Roughly speaking, this means that, in the case that two or more parallel processes attempt to change the content of the same register at the same time, there is a difference in how the process that succeeds in its attempt is chosen (see also Section 8). Moreover, in the model sketched in [36], the built-in programs of the RAMs that make up a PRAM must be the same whereas the parallel processes that make up an SPRAMP may be different.

The SPRAMPs can be looked upon as the processes that can be produced by a collection of SMBRAMs when they execute their built-in program synchronously in parallel.

For the SMBRAMs whose private memory has number i ($i \in \mathbb {N}^+$), the processes that are produced when they execute their built-in program are now given by a function ${\mathcal {M}^\textsf{sync}_i} \, {:}\, {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}} \rightarrow \mathcal {P}_\textsf{SPRAMP}$ that is defined up to consistent renaming of variables as follows: $\mathcal {M}^\textsf{sync}_i(c_1\, \ldots \, c_n) = \langle X_i \vert E_i \rangle$, where $E_i$ consists of the equation

$$\begin{aligned} X_i = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{ini}{:}\# i\,(\textsf{m}_i)] \cdot Y_1 \end{aligned}$$

and, for each $j \in \mathbb {N}$ with $1 \le j \le n$, an equation

$$\begin{aligned}{} & {} Y_{2j-1}= {\textsf{t}}\, {:\rightarrow}\,\textsf{sync}\cdot Y_{2j}\\{} & {} Y_{2j} = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, c_j(\textsf{m}_i,\textsf{m})] \cdot Y_{2j+1} \qquad \qquad \qquad \qquad \qquad \qquad \quad \, \text {if}\, c_j \in Load , \\{} & {} Y_{2j} = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m} \, {{:}{=}}\, c_j(\textsf{m}_i,\textsf{m})] \cdot Y_{2j+1} \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\, \text {if}\, c_j \in Store , \\{} & {} Y_{2j} = {\textsf{t}}\, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, c_j(\textsf{m}_i)] \cdot Y_{2j+1} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\,\,\, \text {if}\, c_j \in \mathcal {O}^\textrm{o}_\textsf{RAMP}, \\{} & {} Y_{2j}= (p(\textsf{m}_i) = 1) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y_{2j'-1}\,{+}\,(p(\textsf{m}_i) = 0) \, {:\rightarrow}\,[\textsf{m}_i \, {{:}{=}}\, \textsf{m}_i] \cdot Y_{2j+1} \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\, \text {if}\, c_j \equiv \textsf{jmp}{:}p{:}j', \\{} & {} Y_{2j} = {\textsf{t}}\, {:\rightarrow}\,\epsilon \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, \text {if}\, c_j \equiv \textsf{halt}, \end{aligned}$$

where $Load = \{ \textsf{loa}{:}@ i{:} d \, {\mid}\,i \in \mathbb {N}\wedge d \in Dst \}$, $Store = \{ \textsf{sto}{:} s {:}@ i \, {\mid}\, s \in Src \wedge i \in \mathbb {N} \}$, and $Y_1,\ldots ,Y_{2n}$ are different variables from $\mathcal {X}\setminus \{ X_i \}$.

The SPRAMPs are exactly the processes that can be produced by a collection of SMBRAMs when they execute their built-in program synchronously in parallel.

Theorem 8

Let $n \in \mathbb {N}^+$. For all constants $\langle X_1 \vert E_1 \rangle , \ldots ,\! \langle X_n \vert E_n \rangle \in \mathcal {P}_{\textsf{rec}}$, $\langle X_1 \vert E_1 \rangle \, {\parallel }\,_\textsf{sync}\ldots \, {\parallel }\,_\textsf{sync}\langle X_n \vert E_n \rangle \in \mathcal {P}_\textsf{SPRAMP}$ iff there exist $C_1, \ldots , C_n \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$ such that $\langle X_1 \vert E_1 \rangle \, {\parallel }\,_\textsf{sync}\ldots \, {\parallel }\,_\textsf{sync}\langle X_n \vert E_n \rangle$ and $\mathcal {M}^\textsf{sync}_1(C_1) \, {\parallel }\,_\textsf{sync}\ldots \, {\parallel }\,_\textsf{sync}\mathcal {M}^\textsf{sync}_n(C_n)$ are identical up to consistent renaming of variables.

Proof

Let $i \in \mathbb {N}^+$ be such that $i \le n$. It is easy to see that (a) for all $C \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$, $\mathcal {M}^\textsf{sync}_i(C) \in \mathcal {P}_\textsf{SPRAMP}$ and (b) $\mathcal {M}^\textsf{sync}_i$ is an bijection up to consistent renaming of variables. From this, it follows immediately that there exists a $C \in {\mathcal{I}\mathcal{S}_\textsf{SMBRAM}}$ such that $\langle X_i \vert E_i \rangle$ and $\mathcal {M}^\textsf{sync}_i(C)$ are identical up to consistent renaming of variables. From this, the theorem follows immediately. $\square$

The first synchronous parallel RAM models of computation, e.g. the models proposed in [16, 19, 36], are older than the first asynchronous parallel RAM models of computation, e.g. the models proposed in [10, 25, 30]. It appears that the synchronous parallel RAM models have been primarily devised to be used in the area of computational complexity and that the asynchronous parallel RAM models have been primarily devised because the synchronous models were considered of restricted value in the area of algorithm efficiency.

7 Time and Work Complexity Measures

This section concerns complexity measures for the models of computation presented in Sections 4–6. Before the complexity measures in question are introduced, it is made precise in the current setting what a complexity measure is and what the complexity of a computable function from ${(\{ 0,1 \}^*)}^n$ to $\{ 0,1 \}^*$ under a given complexity measure is.

Let $CP\subseteq \mathcal{C}\mathcal{P}_{\textsf{rec}}$. Then a complexity measure for $CP$ is a partial function $M : CP\times \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m \ \shortmid {\kern-13.0pt}\rightarrow \mathbb {N}$ such that, for all $t \in CP$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$, $M(t,(w_1,\ldots ,w_n))$ is defined iff ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

This notion of a complexity measure bears little resemblance to Blum’s notion of a complexity measure [8], but it is in accordance with Blum’s notion.

Let $CP\subseteq \mathcal{C}\mathcal{P}_{\textsf{rec}}$ and let M be a complexity measure for $CP$. Let $n \in \mathbb {N}$ and let $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$ be a computable function. Let ${V} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$. Then F is of complexity V under the complexity measure M if there exists a $t \in CP$ such that:

• t computes F;

• for all $w_1,\ldots ,w_n \in \{ 0,1 \}^*$ such that $F(w_1,\ldots ,w_n)$ is defined:

  $$\begin{aligned} M(t,(w_1,\ldots ,w_n)) \le V(\ell (w_1) + \ldots + \ell (w_n))\;. \end{aligned}$$

7.1 The RAMP Model of Computation

Below, a time complexity measure and a work complexity measure for the RAMP model of computation are introduced.

The sequential uniform time measure yields, for a given RAMP and a given data environment, the maximum number of steps that can be performed by the given RAMP before eventually halting in the case where the initial data environment is the given data environment.

The sequential uniform time measure is the complexity measure $\textrm{M}_\textsf{SUT}$ for $\mathcal{C}\mathcal{P}_\textsf{RAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{SUT} (t,(w_1,\ldots ,w_n)) = depth ({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)) \end{aligned}$$

for all $t \in \mathcal{C}\mathcal{P}_\textsf{RAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

The sequential uniform time measure is essentially the same as the uniform time complexity measure for the standard RAM model of computation (see e.g [1]).

It is an idealized time measure: the simplifying assumption is made that a RAMP performs one step per time unit.

The maximum number of steps that can be performed by a given RAMP can also be looked upon as the maximum amount of work. This makes the sequential uniform time measure a very plausible work measure as well.

The sequential work measure is the complexity measure $\textrm{M}_\textsf{SW}$ for $\mathcal{C}\mathcal{P}_\textsf{RAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{SW} (t,(w_1,\ldots ,w_n)) = \textrm{M}_\textsf{SUT} (t,(w_1,\ldots ,w_n)) \end{aligned}$$

for all $t \in \mathcal{C}\mathcal{P}_\textsf{RAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

In the sequential case, it is in accordance with our intuition that the uniform time complexity measure coincides with the work complexity measure. In the parallel case, this is not in accordance with our intuition: it is to be expected that the introduction of parallelism results in a reduction of the amount of time needed but not in a reduction of the amount of work needed.

The following connection between the complexity measure $\textrm{M}_\textsf{SUT}$ and the notion of “computability in W steps” from Section 3.2 is a corollary of the definitions involved.

Corollary 1

For each computable function $F:(\{0,1\}^{*})^{n}\ \shortmid {\kern-13.0pt}\rightarrow \{0, 1\}^{*}$ and function ${V} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$, F is of complexity V under the complexity measure $\textrm{M}_\textsf{SUT}$ iff there exists a $t \in \mathcal {P}_\textsf{RAMP}$ such that t computes F in V steps.

7.2 The APRAMP Model of Computation

Below, a time complexity measure and a work complexity measure for the APRAMP model of computation are introduced.

The asynchronous parallel uniform time measure yields, for a given APRAMP and a given data environment, the maximum over all parallel processes that make up the given APRAMP of the maximum number of steps that can be performed before eventually halting in the case where the initial data environment is the given data environment.

The asynchronous parallel uniform time measure is the complexity measure $\textrm{M}_\textsf{APUT}$ for $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{APUT} (t,(w_1,\ldots ,w_n)) = \max \{ depth ({\tau _{\overline{\!H_i\!}}}({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t))) \, {\mid}\,1 \le i \le deg (t) \}\;, \end{aligned}$$

where $\overline{\!H_i\!}$ is the set of all $\alpha \in \mathcal {A}$ in which $\textsf{m}_i$ does not occur, for all $t \in \mathcal{C}\mathcal{P}_\textsf{APRAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

In this definition, ${\tau _{\overline{\!H_i\!}}}$ turns steps of the process denoted by ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ that are not performed by the parallel process whose private memory is referred to by $\textsf{m}_i$ into silent steps. Because $depth$ does not count silent steps, $depth ({\tau _{\overline{\!H_i\!}}}({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)))$ is the maximum number of steps that the parallel process whose private memory is referred to by $\textsf{m}_i$ can perform.

Because it yields the maximum number of steps that can be performed by one of the parallel processes that make up a given APRAMP, the asynchronous parallel uniform time measure differs from the asynchronous parallel work measure.

The asynchronous parallel work measure is the complexity measure $\textrm{M}_\textsf{APW}$ for $\mathcal{C}\mathcal{P}_\textsf{APRAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{APW} (t,(w_1,\ldots ,w_n)) = depth ({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)) \end{aligned}$$

for all $t \in \mathcal{C}\mathcal{P}_\textsf{APRAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

The sequential work measure and the asynchronous parallel work measure are such that comparison of complexities under these measures have some meaning: both concern the maximum number of steps that can be performed by a computational process.

Like all complexity measures introduced in this section, the asynchronous parallel uniform time measure introduced above is a worst-case complexity measure. It is quite different from the parallel time complexity measures that have been proposed for the asynchronous parallel RAM model of computation sketched in [10, 25, 30]. The round complexity measure is proposed as parallel time complexity measure in [10, 25] and an expected time complexity measure is proposed as parallel time complexity measure in [30]. Neither of those measures is a worst-case complexity measure: the round complexity measure removes certain cases from consideration and the expected time complexity measure is an average-case complexity measure.

It appears that the round complexity measure and the expected time complexity measure are more important to analysis of the efficiency of parallel algorithms whereas the asynchronous parallel time complexity measure introduced above is more important to analysis of the complexity of computational problems that are amenable to solution by a parallel algorithm. After all, the area of computational complexity is mostly concerned with worst-case complexity.

In [30], the asynchronous parallel uniform time measure introduced above is explicitly rejected. Consider the case where there exists an interleaving of the parallel processes that make up an APRAMP that is close to performing all steps of each of the processes uninterrupted by steps of the others. Then the interleaving concerned is not ruled out by synchronization (through the shared memory) and may even be enforced by synchronization. So it may be likely or unlikely to occur. Seen in that light, it is surprising why it is stated in [30] that such an interleaving has “very low probability, yielding a sequential measure”.

7.3 The SPRAMP Model of Computation

Below, a time complexity measure and a work complexity measure for the SPRAMP model of computation are introduced.

The time complexity measure introduced below is essentially the same as the uniform time complexity measure that goes with the synchronous parallel RAM model of computation sketched in [36] and similar models.

The synchronous parallel uniform time measure yields, for a given SPRAMP and a given data environment, the maximum number of synchronization steps that can be performed by the given SPRAMP before eventually halting in the case where the initial data environment is the given data environment.

The synchronous parallel uniform time measure is the complexity measure $\textrm{M}_\textsf{SPUT}$ for $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{SPUT}(t,(w_1,\ldots ,w_n)) = depth ({\tau _{\overline{\textsf{sync}}}}({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)))\;, \end{aligned}$$

where $\overline{\textsf{sync}} = \mathcal {A}\setminus \{ \textsf{sync} \}$, for all $t \in \mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

In this definition, ${\tau _{\overline{\textsf{sync}}}}$ turns all steps of the process denoted by ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ other than synchronization steps, i.e. all computational steps, into silent steps. Because $depth$ does not count silent steps, $depth ({\tau _{\overline{\textsf{sync}}}}({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)))$ is the maximum number of synchronization steps that can be performed by the process denoted by ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ before eventually halting.

Because the parallel processes that make up a given SPRAMP synchronize after each computational step, the time between two consecutive synchronization steps can be considered one time unit. Therefore, the synchronous parallel uniform time measure is a plausible time measure. Clearly, the maximum number of synchronization steps that can be performed by the given SPRAMP and the maximum number of computational steps that can be performed by the given SPRAMP are separate numbers. So the synchronous parallel uniform time measure differs from the synchronous parallel work measure.

The synchronous parallel work measure is the complexity measure $\textrm{M}_\textsf{SPW}$ for $\mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ defined by

$$\begin{aligned} \textrm{M}_\textsf{SPW} (t,(w_1,\ldots ,w_n)) = depth ({\tau _{\textsf{sync}}}({\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t))) \end{aligned}$$

for all $t \in \mathcal{C}\mathcal{P}_\textsf{SPRAMP}$ and $(w_1,\ldots ,w_n) \in \bigcup _{m \in \mathbb {N}} (\{ 0,1 \}^*)^m$ such that ${\textsf{V}_{\rho _{w_1,\ldots ,w_n}}}(t)$ is a terminating-process term.

The sequential work measure and the synchronous parallel work measure are such that comparison of complexities under these measures have some meaning: both concern the maximum number of computational steps that can be performed by a computational process.

Take an SPRAMP and the APRAMP which is the SPRAMP without the automatic synchronization after each computational step. Assume that at any stage the next step to be taken by any of the parallel processes that make up the APRAMP does not depend on the steps that have been taken by the other parallel processes. Then the synchronous parallel time measure $\textrm{M}_\textsf{SPUT}$ yields for the SPRAMP the same result as the asynchronous parallel time measure $\textrm{M}_\textsf{APUT}$ yields for the APRAMP.

8 SPRAMPs and the Parallel Computation Thesis

The SPRAMP model of computation is a simple model based on an idealization of existing shared memory parallel machines that abstracts from synchronization overhead. The synchronous parallel uniform time measure introduced for this model is a simple, hardware independent, and worst-case complexity measure.

The question is whether the SPRAMP model of computation is a reasonable model of parallel computation. A model of parallel computation is generally considered reasonable if the parallel computation thesis holds. In the current setting, this thesis can be phrased as follows: the parallel computation thesis holds for a model of computation if, for each computable partial function from ${(\{ 0,1 \}^*)}^n$ to $\{ 0,1 \}^*$ ($n \in \mathbb {N}$), its complexity under the time complexity measure for that model is polynomially related to its complexity under the space complexity measure for the multi-tape Turing machine model of computation.

Before we answer the question whether the SPRAMP model of computation is a reasonable model of parallel computation, we go into a classification of synchronous parallel RAMs. This classification is used later on in answering the question. Following [24], PRAM is used as a common name for a synchronous parallel RAM regardless of its classification.

First of all, there are PRAMs whose constituent RAMs may execute different programs and PRAMs whose constituent RAMs must execute the same program. The former PRAMs are classified as MIMD (Multiple Instruction, Multiple Data) and the latter PRAMs are classified as SIMD (Single Instruction, Multiple Data).

In [24, Section 2.1], PRAMs are classified according to their restrictions on shared memory access as EREW (Exclusive-Read Exclusive-Write), CREW (Concurrent-Read Exclusive-Write) or CRCW (Concurrent-Read Concurrent-Write). CRCW PRAMs are further classified according to their way of resolving write conflicts as COMMON, where all values attempted to be written concurrently into the same shared register must be identical, ARBITRARY, where one of the values attempted to be written concurrently into the same shared register is chosen arbitrarily, or PRIORITY, where the RAMs making up the PRAM are numbered and, from all values attempted to be written concurrently into the same shared register, the one attempted to be written by the RAM with the lowest number is chosen.

An SPRAMP is a process that can be produced by a MIMD ARBITRARY CRCW PRAM with SMBRAMs (see Section 5) as constituent RAMs.

Below, the next two lemmas about the above classifications of PRAMs will be used to show that the parallel computation thesis holds for the SPRAMP model of computation.

Lemma 4

Assuming a fixed instruction set:

• 1. MIMD PRIORITY CRCW PRAMs can be simulated by MIMD ARBITRARY CRCW PRAMs with the same number of RAMs and with the parallel time increased by a factor of $O(\log (p))$, where p is the number of RAMs;

• 2. MIMD ARBITRARY CRCW PRAMs can be simulated by MIMD PRIORITY CRCW PRAMs with the same number of RAMs and the same parallel time.

Proof

Assume a fixed instruction set.

Part 1.  It is shown in [24, Section 3.1] that MIMD PRIORITY CRCW PRAMs can be simulated by MIMD EREW PRAMs with the same number of RAMs and with the parallel time increased by only a factor of $O(\log (p))$, where p is the number of RAMs. It follows directly from the definitions concerned that MIMD EREW PRAMs can be simulated by MIMD ARBITRARY CRCW PRAMs with the same number of RAMs and the same parallel time (the programs involved can be executed directly). Hence, MIMD PRIORITY CRCW PRAMs can be simulated by MIMD ARBITRARY CRCW PRAMs with the same number of RAMs and with the parallel time increased by a factor of $O(\log (p))$, where p is the number of RAMs.

Part 2.  It follows directly from the definitions concerned that MIMD ARBITRARY CRCW PRAMs can be simulated by MIMD PRIORITY CRCW PRAMs with the same number of RAMs and the same parallel time (the programs involved can be executed directly). $\square$

Lemma 5

Assuming a fixed instruction set:

• 1. SIMD PRIORITY CRCW PRAMs can be simulated by MIMD PRIORITY CRCW PRAMs with the same number of RAMs and with the same parallel time;

• 2. MIMD PRIORITY CRCW PRAMs can be simulated by SIMD PRIORITY CRCW PRAMs with the same number of RAMs and with the parallel time increased by a constant factor.

Proof

Assume a fixed instruction set.

Part 1.  This follows directly from the definitions concerned (the programs involved can be executed directly).

Part 2.  This is a special case of Theorem 3 from [39]. $\square$

The next theorem expresses that the parallel computation thesis holds for the SPRAMP model of computation.

Theorem 9

Let $F : {(\{ 0,1 \}^*)}^m \ \shortmid {\kern-13.0pt}\rightarrow \{ 0,1 \}^*$ for some $m \in \mathbb {N}$ be a computable function and let ${T,S} \, {:}\, \mathbb {N} \rightarrow \mathbb {N}$. Then:

• if F is of complexity T(n) under the synchronous parallel time complexity measure $\textrm{M}_\textsf{SPUT}$ for the SPRAMP model of computation, then there exists a $k \in \mathbb {N}$ such that F is of complexity $O({T(n)}^k)$ under the space complexity measure for the multi-tape Turing machine model of computation;

• if F is of complexity S(n) under the space complexity measure for the multi-tape Turing machine model of computation, then there exists a $k \in \mathbb {N}$ such that F is of complexity $O({S(n)}^k)$ under the synchronous parallel time complexity measure $\textrm{M}_\textsf{SPUT}$ for the SPRAMP model of computation provided that $S(n) \ge \log (n)$ for all $n \in \mathbb {N}$.

Proof

In [19], SIMDAGs are introduced. SIMDAGs are SIMD PRIORITY CRCW PRAMs with a subset of the instruction set of SMBRAMs as instruction set. Because $\textrm{DSPACE}(S(n)) \subseteq \textrm{NSPACE}(S(n)) \subseteq \textrm{DSPACE}({S(n)}^2)$, the variant of the current theorem for the SIMDAG model of computation follows immediately from Theorems 2.1 and 2.2 from [19] under a constructibility assumption for S(n). However, the proofs of those theorems go through with the instruction set of SMBRAMs because none of the SMBRAM instructions builds bit strings that are more than O(T(n)) bits long in T(n) time. Moreover, if we take forking variants of SIMDAGs with the instruction set of SMBRAMs (resembling the P-RAMs from [16]), the constructibility assumption for S(n) is not needed. This can be shown in the same way as in the proof of Lemma 1a from [16].

In the rest of this proof, we write E-SIMDAG for a SIMDAG with the instruction set of SMBRAMs and forking E-SIMDAG for a forking variant of an E-SIMDAG.

The variant of the current theorem for the forking E-SIMDAG model of computation follows directly from the above-mentioned facts.

Now forking E-SIMDAGs can be simulated by E-SIMDAGs with O(p) number of SMBRAMs and with the parallel time increased by a factor of $O(\log (p))$, where p is the number of SMBRAMs used by the forking E-SIMDAG concerned. This is proved as in the proof of Lemma 2.1 from [20]. The other way round, E-SIMDAGs can be simulated by forking E-SIMDAGs with eventually the same number of SMBRAMs and with the parallel time increased by $O(\log (p))$, where p is the number of SMBRAMs of the E-SIMDAG concerned. This is easy to see: before the programs of the p SMBRAMs involved can be executed directly, the p SMBRAMs must be created by forking and this can be done in $O(\log (p))$ time. It follows immediately from these simulation results that time complexities on forking E-SIMDAGs are polynomially related to time complexities on E-SIMDAGs.

The variant of the current theorem for the E-SIMDAG model of computation follows directly from the variant of the current theorem for the forking E-SIMDAG model of computation and the above-mentioned polynomial relationship. From this, the fact that E-SIMDAGs are actually SIMD PRIORITY CRCW PRAMs that are composed of SMBRAMs, Lemmas 5, 4, and Theorem 8, the current theorem now follows directly. $\square$

9 Concluding Remarks

In this paper, it has been studied whether the imperative process algebra $\text {ACP}_{\epsilon }^{\tau }$-I can play a role in the field of models of computation.

Models of computation corresponding to models based on sequential random access machines, asynchronous parallel random access machines, synchronous parallel random access machines, and complexity measures for those models have been described in a direct and mathematically precise way in the setting of $\text {ACP}_{\epsilon }^{\tau }$-I.Central in the models described are the computational processes considered instead of the abstract machines that produce those processes when they execute their built-in program.

The work presented in this paper pertains to formalizing models of computation. Little work has been done in this area. Three notable exceptions are [2, 31, 40]. Those papers are concerned with formalization in a theorem prover (HOL4, Isabelle/HOL, Matita) and focusses on some version of the Turing machine model of computation. This makes it impracticable to compare the work presented in those papers with the work presented in this paper.

Whereas it is usual in versions of the RAM model of computation that bit strings are represented by natural numbers, here natural numbers are represented by bit strings. Moreover, the choice has been made to represent the natural number 0 by the bit string 0 and to adopt the empty bit string as the register content that indicates that a register is (as yet) unused.