Introduction

The subject of high-temperature superconductivity in the cuprates is by now a mature field with a diverse array of candidate theories. This applies as well to theories of the mysterious pseudogap which has captured the attention of the community. It is notable that there is still no consensus about the nature of the machinery and the mechanism behind this phenomenon. This should be clear from the large number of review articles1,2,3,4, which represent a range of different perspectives and viewpoints. It can be plausibly argued that, as the field is so mature, what is most needed now is for candidate cuprate theories to formulate testable, preferably falsifiable predictions.

This is the goal of the present paper for one particular theory, called ‘BCS-BEC crossover theory’. Here we address the question of whether high-temperature superconductors have anything in common with BCS-BEC crossover theory. We understand this to be a highly controversial issue, but note that this subject has received recent attention in the literature5,6. For this purpose, we focus on the Ginzburg-Landau (GL) coherence length, \({\xi }_{0}^{{{{\rm{coh}}}}}\), appropriate to near or slightly above Tc. In this paper we provide direct predictions for its behavior as a function of hole doping. We argue that these predictions can be used to directly assess the appropriateness of BCS-BEC crossover theory for the cuprate family, when \({\xi }_{0}^{{{{\rm{coh}}}}}\) is measured systematically across the Tc dome in the phase diagram and for the different cuprate families.

This crossover theory has the advantage over many other cuprate theory candidates of potentially being applicable to a wide collection of strongly correlated superconductors. This broad range of applicability is exploited in the present work. Over the years we have acquired a knowledge base which has shown how to connect different types of experimental findings with ‘crossover physics’. BCS-BEC crossover candidate materials include iron-based superconductors7,8,9,10,11,12,13,14, organic superconductors15,16,17,18,19, magic-angle twisted bilayer (MATBG)20,21 and trilayer graphene (MATTG)22,23, gate-controlled two-dimensional devices24,25,26, interfacial superconductivity27,28,29, and magneto excitonic condensates in graphene heterostructures30.

The theory of BCS-BEC crossover2,31,32,33,34,35,36 belongs to a class of preformed-pair theories associated with relatively strong ‘pairing glue’. As a result, fermion pairs form at a higher temperature before they Bose condense at the superfluid transition temperature Tc, as found in the BEC phase of a Bose superfluid. Importantly, there is a continuous evolution between the two endpoints of a crossover theory: the conventional, weak-pairing BCS limit and the strong-pairing BEC limit. We emphasize that this theory pertains only to the machinery of superconductivity. It calls for a revision of the more familiar BCS approach, while still contemplating a charge 2e pairing-based scheme. It does not address the specific microscopic pairing mechanism.

Whether crossover theory is applicable to the cuprates or not is the question we wish to help address in the course of future experiments. That the transition temperature is high and there are indications that the GL coherence length (in comparison to traditional superconductors) is small are argued37 to be suggestive of strong pairing ‘glue’. But it is clearly of interest to find more definitive and quantitative evidence for or against this scenario.

Here and in the vast literature on ultracold atomic Fermi gases2,34,35, a superconductor/superfluid in the ‘crossover’ regime is conventionally viewed as belonging somewhere intermediate between BCS and BEC. There should be little doubt that the cuprates are not in the BEC limit. In this regime, all signs of fermionic physics have disappeared, which is clearly not the case for the cuprate superconductors; this point has been made recently by Sous et al.6 in their analysis of the behavior of the fermionic chemical potential. The more relevant issue is whether the high-temperature superconductors can be described as belonging to an intermediate regime, somewhere between BCS and BEC and, if so, where in this spectrum a given cuprate might lie.

Indeed, even when a superconductor is on the fermionic side of the crossover, it can behave in a rather anomalous fashion both above and below Tc. We list here three necessary conditions for this crossover scenario to apply. (i) It is associated with the presence of a fermionic excitation gap or ‘pseudogap’ which has a temperature onset, T*, substantially above Tc (say, T*/Tc ≳ 1.2). (ii) It is also associated with sizable ratios of the zero-temperature gap to Fermi energy, Δ0/EF, (say, Δ0/EF ≳ 0.1) and finally (iii) it has an anomalously small GL coherence length (say, \({k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}\lesssim 30\), where kF represents the ideal-gas measure of the carrier density).

In this context, it should be noted that large T*/Tc is a necessary but not sufficient criterion for a pairing pseudogap, as there are alternative reasons why this ratio might be large38. On the other hand, a moderately large Δ0/EF may be more indicative of BCS-BEC crossover, but this ratio can be rather complicated to assess. This is because EF is usually hard to quantify in a typical superconductor, as it is related to complex band structures. And for the cuprates one would presumably have to quantify this ratio over the entire Tc dome as a function of hole doping.

This leaves the GL coherence length as arguably the most useful parameter for characterizing BCS-BEC crossover. This length scale, which essentially reflects normal-state pairing correlations, should not be confused with other length scales such as the London penetration depth, which characterizes the superconducting components of the system. To be specific, the zero-temperature London penetration depth is related to the density-to-mass ratio of the constituent fermions, which is independent of pairing correlations (here, for simplicity, we consider a 3D superconductor in free space). We also emphasize here that in the crossover regime, this coherence length deviates from its BCS-limit expression and that it is similarly distinct from a measure of the size of the Cooper pairs.

Results

Coherence length in BCS-BEC crossover

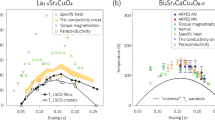
A recent paper19 on a candidate organic superconductor has provided a template of the coherence length for us to use here in presenting predictions for the cuprates. This is shown in Fig. 1a where the dimensionless coherence length \({k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}\) is plotted across the entire Tc dome. Here the nominal Fermi momentum kF simply reflects the carrier density. For this particular organic superconductor, pressure is used as a tuning parameter to effect the crossover between the weak-coupling and strong-pairing limit.

Fig. 1: Comparison between experiment and theory for the in-plane coherence length and the Tc dome.
figure 1

a Pressure dependence of the measured in-plane coherence length \({k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}\) near Tc, and superconducting transition temperatures in κ-(BEDT-TTF)4Hg2.89Br8, taken from ref. 19. Here kF is determined from the carrier density measured by the Hall coefficient. The Tc dome with overlain coherence length provides a rather ideal prototype for BCS-BEC crossover physics. b Calculated in-plane Ginzburg-Landau coherence length, based on fits to the cuprate phase diagram in Fig. 3. This coherence length should be associated with measurements at very low magnetic fields and near T ≈ Tc. The red circles indicate the selected hole concentrations on the Tc ~ p dome where both T* and Tc were simultaneously fitted to yield the computed coherence lengths (blue diamonds).

Full size image

A central result of the present paper is establishing the counterpart behavior of Fig. 1a for the cuprates, particularly for the entire range of hole doping over the Tc dome. This is shown in Fig. 1b. Indeed, the GL coherence length has become a preferred quantity to measure for many of the newer BCS-BEC candidate systems22,24.

The coherence length that we are interested in here can be obtained in several different ways. In principle, it enters into the slope of the upper critical magnetic field, Hc2, very near Tc:

$${\left.\frac{d{H}_{{{{\rm{c2}}}}}}{dT}\right| }_{T = {T}_{{{{\rm{c}}}}}}=-\frac{{\Phi }_{0}}{2\pi {T}_{{{{\rm{c}}}}}{({\xi }_{0}^{{{{\rm{coh}}}}})}^{2}}\quad {{{\rm{with}}}}\quad {\Phi }_{0}=\frac{hc}{| 2e| }.$$

This is based on using the temperature-dependent coherence length \({\xi }_{0}^{{{{\rm{coh}}}}}(T)\), which is defined in terms of the quantity of interest, \({\xi }_{0}^{{{{\rm{coh}}}}}\), as \({\xi }_{0}^{{{{\rm{coh}}}}}(T)={\xi }_{0}^{{{{\rm{coh}}}}}/\sqrt{({T}_{{{{\rm{c}}}}}-T)/{T}_{{{{\rm{c}}}}}}\) as in conventional superconducting fluctuation theories. As discussed in the context of MATTG22, extracting \({\xi }_{0}^{{{{\rm{coh}}}}}\) experimentally from dHc2/dT is not entirely straightforward as it involves determining Tc(H) in the presence of a substantial field-induced broadening of the transition.

Alternatively, in line with the philosophy in this paper, one can avoid some of these complications by determining the GL coherence length through studies of the fluctuation magnetotransport39 in the normal state above Tc. Such experiments are generally performed in combination with theoretical analyses based on the Aslamazov-Larkin (AL) pairing fluctuations40,41.

Theory overview

We next evaluate the GL coherence length within BCS-BEC crossover theory. In the presence of a vector potential, the effects from non-condensed pairs (and the associated pseudogap) are inhomogeneous, and thus directly evaluating Hc2(T) to extract \({\xi }_{0}^{{{{\rm{coh}}}}}\) poses a great challenge to theory. By contrast, here we deduce the coherence length alternatively based on (normal-state) fluctuation theory42,43. Superconducting fluctuations are generally associated with AL contributions40 which reflect bosonic or pairing degrees of freedom. Their contributions40 to transport and thermodynamics generally scale as powers of ϵ ≡ (T − Tc)/Tc or the effective chemical potential of the pairs.

There is a rather direct association between the AL treatment of conventional weak-pairing fluctuations and that deriving from the strong-pairing regime. The conventional fluctuation propagator40 depends on two parameters, ϵ and \({\xi }_{0}^{{{{\rm{coh}}}}}\). Similarly, for strong pairing the pair propagator, called the t-matrix, depends on an analogous pair of parameters, the pair chemical potential μpair and the inverse pair mass \({M}_{{{{\rm{pair}}}}}^{-1}\). While conventional fluctuation transport calculations are complex40, the central parameters ϵ and \({\xi }_{0}^{{{{\rm{coh}}}}}\) are essentially all that is needed to arrive at the entire collection of transport coefficients. Importantly, those calculations serve as a template for doing transport in the strong-pairing regime44,45, provided one makes the association ϵ → ∣μpair∣/Tc and similarly relates the pair mass Mpair to the coherence length \({\xi }_{0}^{{{{\rm{coh}}}}}\) within the strong-pairing theory via

$${\hslash }^{2}/\left[2{M}_{{{{\rm{pair}}}}}({T}_{{{{\rm{c}}}}}){\left({\xi }_{0}^{{{{\rm{coh}}}}}\right)}^{2}\right]={k}_{{{{\rm{B}}}}}{T}_{{{{\rm{c}}}}}.$$
(1)

It should not be surprising then that (because BCS theory and its BCS-BEC crossover extension treat the Cooper pair degrees of freedom as quasi-ideal bosons interacting indirectly only via the constituent fermions), the expression for the transition temperature Tc essentially follows that of an ideal Bose gas (see Methods). For three dimensions (3D), this is given by

$${T}_{{{{\rm{c}}}}}=\left(\frac{2\pi }{{{{\mathcal{C}}}}}\right)\left[\frac{{\hslash }^{2}}{{k}_{{{{\rm{B}}}}}}\frac{{n}_{{{{\rm{pair}}}}}^{2/3}({T}_{{{{\rm{c}}}}})}{{M}_{{{{\rm{pair}}}}}({T}_{{{{\rm{c}}}}})}\right],$$
(2)

where \({{{\mathcal{C}}}}={\left[\zeta (3/2)\right]}^{2/3}\) with ζ(s) the Riemann zeta function. In this equation, npair and Mpair represent the respective number density and mass of the preformed Cooper pairs, which will condense at the transition. These parameters must be determined self consistently (see Methods).

It then follows from Eqs. (1) and (2) that \({\xi }_{0}^{{{{\rm{coh}}}}}\) assumes a very simple form; it depends only on the non-condensed or normal-state pair density npair presumed at the onset of the transition:

$${k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}=1.2{(n/{n}_{{{{\rm{pair}}}}})}^{1/3},$$
(3)

where \({k}_{{{{\rm{F}}}}}^{3}\) reflects the total particle density n.

It should be noted that the above discussion can be extended to 2D as well, leading to a similar conclusion for the GL coherence length36:

$${k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}=1.6{(n/{n}_{{{{\rm{pair}}}}})}^{1/2}.$$
(4)

For the quasi-2D cuprates, both Mpair and \({\xi }_{0}^{{{{\rm{coh}}}}}\) in Eq. (1) are naturally anisotropic, but here we are interested in the in-plane coherence length so that, as in experiment, only the in-plane parameters will be used throughout.

We note that the above equations are easy to understand physically. The GL coherence length is a length representing the effective separation between preformed pairs. It relates to the density of pairs at Tc as distinct from the pair size. In BCS theory there are almost no pairs present at Tc and the length which represents their average separation is necessarily very long. As pairing becomes stronger more pairs form and their separation becomes shorter. On a lattice, in the BEC regime their separation is bounded from below by the characteristic lattice spacing and \({\xi }_{0}^{{{{\rm{coh}}}}}\) approaches an asymptote set by the inter-particle distance as the system varies from BCS to BEC.

More importantly, the rather natural expressions for \({k}_{{{{\rm{F}}}}}{\xi }_{0}^{{{{\rm{coh}}}}}\) in Eqs. (3) and (4) also reveal the location of a given system within the BCS-BEC crossover. Since the number of pairs at Tc varies from approximately 0 in the BCS limit to n/2 in the BEC case, the GL coherence length provides a quantitative measure of where a given superconductor is within the BCS-BEC spectrum.

Application to the cuprates

In application to the cuprates it is useful first to present a Tc versus attraction strength ∣U∣ phase diagram for the case of d-wave pairing symmetry. This is deduced2,36,46 based on Eq. (2) for Tc [see Methods]. Here, for the pseudogap onset temperature T* we use a straightforward mean-field theory. The results are shown in Fig. 2. What is notable here is the fact that, in contrast to the s-wave pairing in BCS-BEC crossover36, for the case of a d-wave superconducting order parameter, the BEC regime is not generally accessible except when the underlying conduction band has an extremely low filling. Although not relevant to the cuprates which are near half-filling, there may be other BCS-BEC crossover candidate systems which exhibit a d-wave BEC phase.

Fig. 2: BCS-BEC crossover phase diagram for a d-wave superconductor with constant carrier density.
figure 2

This diagram47 shows that the system (with a single electronic conduction band nearly half-filled) has vanishing Tc before the onset of the BEC regime, where the zero-temperature fermionic chemical potential drops below the band bottom. This can be compared with the low-density s-wave case in which the BEC regime is in principle accessible.

Full size image

Heuristically, we understand the above contrast between s − and d − wave pairing as a consequence of the fact that d-wave pairs are more extended in size, so that multiple lattice sites are involved in the pairing. Consequently, repulsion between pairs is enhanced due to a stronger Pauli exclusion effect experienced by these extended pairs, and as a result their hopping is greatly impeded. Adding to this is the well known33 observation that hopping of pairs on a lattice becomes more problematic in the strong-attraction regime, since the paired fermions have to unbind in the process. While in a low carrier density, s-wave pairing superconductor, Tc consequently approaches zero asymptotically in the BEC regime, generally for d-wave superconductors, Tc will vanish before the BEC limit is reached.

The above discussion brings us to the central topic of this paper: how one should determine whether the cuprates are associated with a BCS-BEC scenario and, if so, where a given cuprate precisely lies in the spectrum of BCS to BEC. Our proposal to quantitatively address this question is to focus on the calculated GL coherence length, with the goal of providing a counterpart plot like that in Fig. 1a, but now for the cuprates.

To that end, the first immediate task is to connect the d-wave crossover phase diagram in Fig. 2 with the experimental cuprate phase diagram in Fig. 3, where the horizontal axis is hole doping p, instead of ∣U∣. To establish the connection, we fit the calculated T* and Tc at a number of hole concentrations in the theory phase diagram to their corresponding experimental values, and deduce the associated properties of the GL coherence length. What is subtle but important here is that the phase diagram of Fig. 2 was obtained for a fixed carrier density. For application to the cuprates we need to readjust the density at each point in the Tc ~ p dome.

Fig. 3: Experimental phase diagram for hole-doped cuprates, taken from ref. 57.
figure 3

T* and Tc shown in (a) are quantitatively plotted in (b). The error bars in (b) represent the standard deviation.

Full size image

To be specific, by taking the experimental T*, Tc, and the corresponding density as input fitting parameters from Fig. 3, we can establish from T*/Tc the magnitude of the attractive interaction ratio ∣U∣/t, using the theoretical phase diagram in Fig. 2. Here t is the effective hopping parameter. Then fitting the numerical value of T* yields the value of t, which determines the bandwidth and Fermi energy for each cuprate with a different hole concentration. From the fitted parameters {U, t} and the hole concentration, we can compute (see Methods) npair and Mpair, using our t-matrix theory46,47, and then extract the coherence length.

For definiteness, we adopt a quasi-2D band structure considered to be appropriate for the cuprates: \({\epsilon }_{{{{\bf{k}}}}}=(4t+4{t}^{{\prime} }+2{t}_{z})-2t(\cos {k}_{x}+\cos {k}_{y})-4{t}^{{\prime} }\cos {k}_{x}\cos {k}_{y}-2{t}_{z}\cos {k}_{z}\) with \({t}^{{\prime} }/t=-0.3\). We presume a very small tz/t = 0.01 is also present, but it should be stressed that Tc has only a very weak logarithmic dependence on tz47. This band structure has a van Hove singularity which is prominent for the band fillings we address.

The predicted results for the GL coherence length based on our fitting procedure and BCS-BEC crossover theory are presented in Fig. 1b. These results show that, not unexpectedly, the coherence length is predicted to decrease monotonically with increased underdoping of holes, reflecting that the pairing strength is strongest in the most underdoped systems. Note that for the cuprates, the predicted minimum value of the coherence length is not particularly short. This more moderate value for \({\xi }_{0}^{{{{\rm{coh}}}}}\) in the underdoped regime is associated with the d-wave symmetry of the cuprates. In this doping regime, npair, the number of pairs at the transition temperature Tc, remains far below its maximum possible value of n/2; stated alternatively, the corresponding ∣U∣/t at these hole concentrations is smaller than the value of ∣U∣/t where Tc vanishes (see Fig. 2). This implies that the underdoped cuprates are still well within the fermionic side of the crossover ‘transition’, which is defined as where μ = 0 at Tc.

On the experimental side, in the earlier literature there is a prototypical set of experiments39 which address \({\xi }_{0}^{{{{\rm{coh}}}}}\) in the immediate vicinity of the transition. Importantly, this analysis is based on a normal-state fluctuation analysis; as in a similar spirit to the theoretical calculation of \({\xi }_{0}^{{{{\rm{coh}}}}}\), this avoids difficulties associated with evaluating \(d{H}_{{{{\rm{c2}}}}}/dT{| }_{T = {T}_{{{{\rm{c}}}}}}\) more directly. As seen in Fig. 14a of ref. 39, this analysis finds that in La2−xSrxCuO4 single-crystal films, there is a rather weak decrease of \({\xi }_{0}^{{{{\rm{coh}}}}}\) observed with increased underdoping. However, in the overdoped regime the measured coherence length is not as large as suggested in our Fig. 1b.

This and related research have emphasized that experiments based on standard fluctuation analyses below Tc are more problematic than above Tc. It is the shortness of the coherence length itself which is causing the difficulty. More specifically, the short coherence length results in a small characteristic energy associated with vortex pinning centers. This allows their motion to be more readily thermally activated. As a result, this enhanced vortex depinning significantly increases the width of the resistivity transition, making it difficult to determine the precise value of Tc(H) and, similarly, \({\xi }_{0}^{{{{\rm{coh}}}}}\).

These T ≈ Tc studies which we focus on here should be contrasted with coherence-length measurements at low temperatures where use is made of the vortex core size48,49. Interestingly, here and in related transport experiments50 there are similar challenges in measuring the coherence length which were attributed to the presence of a vortex liquid rather than vortex solid phase.

There are also other potential complications stemming from Fermi-surface reconstruction51, which can be viewed as deriving from ordering in the particle-hole channel, seen at high magnetic fields H. If this reconstruction persists in the very low H limit, those regions of the T-p phase diagram where reconstruction appears will complicate the interpretation of Tc(H) and, in turn, affect the inferred \({\xi }_{0}^{{{{\rm{coh}}}}}\). Indeed, it is now understood that three cuprate families (YBa2Cu3O6+δ, La2−xSrxCuO4, and HgBa2CuO4+δ) each show significant Fermi-surface reconstruction in magnetic fields. These lead to non-monotonicity in the inferred51,52,53Hc2(T = 0) and related T = 0 coherence length49, as a function of hole doping. We note that for the Bi2Sr2CaCu2O8+δ family, by contrast, it appears from Nernst measurements that Hc2(T) may not have these dramatic non-monotonicities in hole doping54,55, from which one might presume that this family is not subject to Fermi surface reconstruction. Thus, these cuprates might be more suitable candidates for future experiments.

Fluctuation temperature scale in cuprates

There is another temperature scale besides T* and Tc apparent in the phase diagram of Fig. 3 which, for completeness, needs to be addressed within the crossover scenario. We interpret this additional temperature scale in Fig. 3 as36 the onset temperature for superconducting fluctuations which, as a function of hole doping in the cuprates, is observed to follow Tc, although remaining well separated.

It should be clear that within the crossover scheme the cuprates cannot be described by conventional fluctuation theory owing to the existence of a pairing gap onset temperature, T*, significantly higher than Tc. That is, in the presence of a pseudogap associated with preformed pairs, the pairs are present over a much wider temperature range than in conventional fluctuation theory.

More specifically, as in fluctuation theories40,41, fluctuation contributions in the crossover scenario derive from bosonic or pair degrees of freedom; they have an onset temperature which we define as Tfluc = Tc + δTc. This is expected to be significantly below the pseudogap onset T*. At this latter temperature, a gap in the fermionic excitation spectrum first starts to appear, reflecting the onset of pair formation. That Tfluc and T* are distinct temperatures is a consequence of the fact that there must be an appreciable number of pairs before they are clearly observable in thermodynamical properties and transport.

For the case of conventional fluctuations, Tfluc can be associated with the characteristic size of the critical region, which can be related to Gi, the Ginzburg-Levanyuk number. This is, of course, extremely small in 3D although somewhat larger in 2D. (For conventional fluctuation theory40, in 3D, \(\delta {T}_{{{{\rm{c}}}}}/{T}_{c0}\approx \sqrt{{G}_{i}}\), with \({G}_{i} \sim 80{({T}_{{{{\rm{c}}}}}/{E}_{{{{\rm{F}}}}})}^{4}\). In 2D, \(\delta {T}_{{{{\rm{c}}}}}/{T}_{c0}\approx {G}_{i}\ln 1/{G}_{i}\), with Gi ≈ Tc/EF. Here, Tc0 is the mean-field transition temperature.)

In the crossover scenario one can address this somewhat different fluctuation picture in a more quantitative fashion. The onset temperature (Tfluc) for pair-fluctuation effects on thermodynamics and transport requires sufficiently small but non-vanishing56 values for the pair chemical potential, ∣μpair∣. In this way, δTc represents the temperature range over which non-condensed pairs are present in moderate quantity. Our discussion in this section has thus emphasized that the onset temperature for fluctuations is necessarily distinct, not only from Tc, but also from T*.

Discussion

This paper is motivated by the observation that, because there are so many disparate approaches to understanding high-temperature cuprate superconductivity with as yet no consensus, for future progress it is important to subject candidate theories to falsifiability tests as much as is possible. Here we address one particular scenario: the BCS-BEC crossover picture. This has an added advantage among cuprate theories of being experimentally realized both in Fermi gas superfluids2,34,35 and in a broader class of strongly correlated superconductors36, which include some organic superconductors, twisted graphene families, interfacial superconductors and gated superconducting devices. These systems provide an instructive knowledge base for what to expect with different experimental probes. Importantly, with this knowledge base we have learned how to address the applicability of crossover theory36.

In this paper, we have argued that the GL coherence length \({\xi }_{0}^{{{{\rm{coh}}}}}\) is a preferred parameter for assessing the appropriateness of BCS-BEC crossover theory for the cuprate family, when it is measured systematically across the Tc dome in the phase diagram and for the different cuprate families. We emphasize that this coherence length corresponds to temperatures around and slightly above Tc as it is associated with normal-state pairs. This is necessarily different from the size of Cooper pairs and also from the BCS expression for the zero-temperature coherence length: \({\xi }_{0}^{{{{\rm{BCS}}}}}=\hslash {v}_{{{{\rm{F}}}}}/\left(\pi {\Delta }_{0}\right)\) where vF is the Fermi velocity and Δ0 = ΔBCS(T = 0). That the behavior is different from BCS theory should be obvious as BCS theory does not contain preformed pairs. Note also that the coherence length extracted at T ≳ Tc in the cuprates should also not be confused with a counterpart measured in the ground state which has very different properties, relating to the superconducting condensate.

This same GL coherence length has been extensively studied in other BCS-BEC crossover candidate systems. Indeed, one can see by comparing the behavior for the organic superconductor in Fig. 1a with the prediction in Fig. 1b for the cuprates that these plots are rather similar, although the horizontal axes represent different variables. For the cuprates, one sees that the GL coherence length is predicted to monotonically decrease with increased underdoping, which reflects the fact that the pairing strength is strongest in the most underdoped systems. Also predicted in Fig. 1b is that the minimum value of the coherence length will not be as short as for the organic family, which seems to suggest these latter systems are closer to the BEC regime.

It is important to note that for assessing the appropriateness of a BEC scenario where fermions are absent, there are more direct experiments. Rather than focusing on the coherence length, one can study the chemical potential to determine whether, as would be expected, all signs of a Fermi surface have disappeared. Using this approach, recent work6 has demonstrated that the cuprates are nowhere near the BEC endpoint of the crossover, where the chemical potential approaches the band bottom. Notably, however, the failure to observe BEC signatures does not constitute evidence for the ‘the absence of BCS-BEC crossover’.

That in the cuprates we are lacking a systematic characterization of the GL coherence length \({\xi }_{0}^{{{{\rm{coh}}}}}\), over the entire class of cuprate superconductors, is perhaps surprising, as it is one of the most fundamental properties of any superconductor. Moreover, with very few exceptions, detailed measurements of \({\xi }_{0}^{{{{\rm{coh}}}}}\) have been used to provide support for or against a BCS-BEC crossover scenario in nearly all other candidate superconductors that have been studied36. This serves to emphasize how central a role \({\xi }_{0}^{{{{\rm{coh}}}}}\) has played, and the importance of further experiments on cuprates. In the process, these types of experiments will clarify the relevance (or lack thereof) of the BCS-BEC crossover scenario for the high-transition temperature copper-oxide superconductors.

Methods

Theory underlying BCS-BEC crossover

To determine the GL coherence length within BCS-BEC crossover theory, it is useful to summarize a few simple equations. We adopt the particular version of BCS-BEC crossover theory which builds on the T = 0 BCS ground state,

$${\Psi }^{{{{\rm{BCS}}}}}={\Pi }_{{{{\bf{k}}}}}\left({u}_{{{{\bf{k}}}}}+{v}_{{{{\bf{k}}}}}{a}_{{{{\bf{k}}}},\uparrow }^{{\dagger} }{a}_{-{{{\bf{k}}}},\downarrow }^{{\dagger} }\right)\left\vert 0\right\rangle .$$
(5)

This state, originally devised for weak-coupling, can be readily generalized31 to incorporate stronger pairing glue through a self-consistent calculation of the parameters uk and vk, which can be determined in conjunction with the fermionic chemical potential μ as the pairing interaction is varied.

The coherence length, which appears in Eq. (1), depends on the pair density npair and pair mass Mpair. These two quantities are important for arriving at the plots in Fig. 1b and Fig. 2. They must be determined self consistently and we do so here using a particular theory2,36, designed to be consistent with Eq. (5) and its finite-temperature extension, as established by Kadanoff and Martin46. Within this theory one can show that Eq. (2) is equivalent to a generalized Thouless condition, which dictates that the bosonic chemical potential of preformed pairs, μpair, which enters into their propagator (called the t-matrix) must vanish at T = Tc. This generalized Thouless condition will, in turn, lead to a BCS-like gap equation (for T at Tc),

$$1=(-U)\mathop{\sum}\limits_{{{{\bf{k}}}}}{\left.\frac{1-2f({E}_{{{{\bf{k}}}}})}{2{E}_{{{{\bf{k}}}}}}{\varphi }_{{{{\bf{k}}}}}^{2}\right\vert }_{T = {T}_{{{{\rm{c}}}}}},$$
(6)

where \(f(x)={\left[\exp \left(x/({k}_{{{{\rm{B}}}}}T)\right)+1\right]}^{-1}\) is the Fermi-Dirac distribution function, \({E}_{{{{\bf{k}}}}}=\sqrt{{\xi }_{{{{\bf{k}}}}}^{2}+| \Delta ({T}_{{{{\rm{c}}}}}){\varphi }_{{{{\bf{k}}}}}{| }^{2}}\) with ξk = ϵk − μ, and \({\varphi }_{{{{\bf{k}}}}}=\cos {k}_{x}-\cos {k}_{y}\) is the d-wave pairing symmetry form factor. Here, − U > 0 represents the strength of the attractive interaction. Note that the central change from strict BCS theory (aside from a self-consistent readjustment of the fermionic chemical potential) is that Tc is determined in the presence of a nonzero excitation gap, Δ(Tc), reflecting the non-condensed pairs.

The process of establishing Eq. (6) provides values for npair and Mpair associated with our extended form of BCS theory having a ground state of the form Eq. (5). While Thouless has argued that a divergence of a sum of ‘ladder’ diagrams (within a pair propagator) is to be associated with the BCS transition temperature, Kadanoff and Martin established that this Thouless condition can be extended to characterize the full BCS temperature-dependent gap equation for all T≤Tc, provided one adopts a particular form for the pair propagator or t-matrix

$$\frac{1}{t(i{\Omega }_{m},{{{\bf{q}}}})}=T\mathop{\sum}\limits_{n}\mathop{\sum}\limits_{{{{\bf{k}}}}}G(i{\omega }_{n},{{{\bf{k}}}}){G}_{0}(i{\Omega }_{m}-i{\omega }_{n},{{{\bf{q}}}}-{{{\bf{k}}}})+\frac{1}{U},$$
(7)

The bare and dressed fermionic Green’s functions in the above equation are respectively \({G}_{0}(i{\omega }_{n},{{{\bf{k}}}})={\left(i{\omega }_{n}-{\xi }_{{{{\bf{k}}}}}\right)}^{-1}\) and \(G(i{\omega }_{n},{{{\bf{k}}}})\equiv {\left[{G}_{0}^{-1}(i{\omega }_{n},{{{\bf{k}}}})-\Sigma (i{\omega }_{n},{{{\bf{k}}}})\right]}^{-1}\), with Σ(iωn, k) = − Δ2G0( − iωn, − k). ℏωn = (2n + 1)πkBT and ℏΩm = 2mπkBT are fermionic and bosonic Matsubara frequencies (times ℏ), respectively.

Calculation of pair mass and number density

We are now in a position to compute the pair mass and number density from t(iΩm, q). After analytical continuation, iΩm → Ω + i0+, we expand the (inverse) t-matrix for small argument Ω and q to find

$$t(\Omega ,{{{\bf{q}}}})\,\approx\, \frac{{Z}^{-1}}{\Omega -{\Omega }_{{{{\bf{q}}}}}+{\mu }_{{{{\rm{pair}}}}}},$$
(8)

where the pair mass can be calculated from the pair dispersion Ωq = ℏ2q2/(2Mpair). In this equation Z is a constant independent of Ω and q. {Mpair, μpair, Z} are all functions of the fermionic gap Δ and chemical potential μ, which are in turn functions of ∣U∣ and temperature T for given total carrier density n. Finally, one can obtain the density of non-condensed pairs by treating them as stable and independent bosons, for which we have

$${n}_{{{{\rm{pair}}}}}=\mathop{\sum}\limits_{{{{\bf{q}}}}}b({\Omega }_{{{{\bf{q}}}}}-{\mu }_{{{{\rm{pair}}}}})=Z{\Delta }^{2}.$$
(9)

Here, \(b(x)={[\exp \left(x/({k}_{{{{\rm{B}}}}}T)\right)-1]}^{-1}\) is the Bose-Einstein distribution function. To derive the last equality in Eq. (9), we have used Δ2 = − T ∑m ∑qt(iΩm, q). Equation (9) is valid for T ≥ Tc, while for T < Tc, where μpair ≡ 0, the q = 0 component, which represents condensed pairs, needs to be treated separately.

Right at T = Tc and for given {∣U∣, n}, we solve the gap equation Eq. (6) and Eq. (9) with μpair = 0, together with the total electron density constraint

$$n=\mathop{\sum}\limits_{{{{\bf{k}}}}}\left[1-\frac{{\xi }_{{{{\bf{k}}}}}}{{E}_{{{{\bf{k}}}}}}\tanh \left(\frac{{E}_{{{{\bf{k}}}}}}{2{k}_{{{{\rm{B}}}}}T}\right)\right],$$
(10)

to determine {Tc, Δ(Tc), μ(Tc)}. In this way we can map out the Tc − ∣U∣ phase diagram for a given density n. The result is schematically shown in Fig. 2, where the pseudogap onset temperature T* is obtained by solving the mean-field BCS Tc equation in the absence of non-condensed pairs. Furthermore, from the calculated μ and Δ we can compute {Mpair, μpair} using Eq. (8). Then substituting the results into Eq. (1) gives us \({\xi }_{0}^{{{{\rm{coh}}}}}\) as a function of ∣U∣ and n. In application to cuprate superconductors, we use the calculated T*/Tc ratio to determine ∣U∣ for given hole doping p = 1 − n, by following the fitting procedure outlined in the Section ‘Application to the cuprates’. This allows us to determine \({\xi }_{0}^{{{{\rm{coh}}}}}\) as a function of hole doping p for the entire Tc dome as shown in Fig. 1b.