About the onset of the Hopf bifurcation for convective flows in horizontal annuli

Abstract

Experimental and numerical results cannot yet settle whether, between horizontal coaxial cylinders, if the curvature is large, the first transition for convection is an exchange of stability or rather an Hopf bifurcation. We directly show that if the curvature tends to infinity, no periodic linear perturbation exists when the Rayleigh number is equal to the critical one for nonlinear stability.

1 Introduction

We can expect convective flows in any nonisothermal setting where a fluid moves in a gravitational field. In actual facts, in Bénard’s problem the rest state can occur, in spite of the buoyancy force, with a downward temperature gradient. However, this happens just because the steady conductive temperature gradient has exactly the same direction of the weight, pointwise in the layer. On the other hand, if a fluid lies between two horizontal coaxial cylindrical surfaces, with the inner one kept at a higher temperature with respect to the outer one, conduction would be in the radial direction so that no rest state is possible [1, 2].

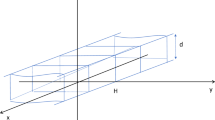
Just to fix the ideas, let us denote by $\textbf{e}_3$ the vertical ascendant direction of the z-axis, so that $\textbf{g}$ as the opposite orientation, let us denote with $\varphi \in [0,2\pi )$ the angle between the horizontal x-axis and the position vector, while $R_o$ is the outer radius and $R_i$ is the inner one, then the boundary condition for the temperature field T is

$$\begin{aligned} T(R_o,\varphi ,t)=T_o\,\, ,\qquad T(R_i,\varphi ,t)=T_i\,\, , \end{aligned}$$

(1.1)

for all time t and for all $\varphi$. We have to assume positive $T_i-T_o:=\delta T>0$ in order to have convective motions, which are observed, 2-D and steady below a threshold for all positive $\delta T$, no matter how small (see [3] both for experimental and numerical results). Precisely, with 2-D we mean bi-dimensional flows characterized by velocity fields with no components in the horizontal y-direction of the cylinder axis and which, as vector functions, do not depend on the variable y, as well as the scalar function T.

Fig. 1

Flow region

Fig. 2

The line represents the critical Rayleigh number above which dual steady solutions exist for Pr = 0.7. Below the dashed line experiments show prevailing steady 2D flow. From [2]

Conversely, in the flat layer a critical value for $\delta T$ exists, under which the null velocity field $\textbf{v}$ is observed. It corresponds to the basic solution for the full set of balance laws which exists also for large $\delta T$, though in such a case it cannot be observed because it becomes an unstable solution.

Let us consider the Oberbeck–Boussinesq approximation of the full set of balance laws, from which the O–B system, the most studied model for convection, rigorously follows under suitable smallness conditions on nondimensional quantities (see, for instance, [4]). As we are going to see, a basic steady solution of the system exists in the annulus for all values of the relevant physical quantities, possibly unstable for large $\delta T$. Such steady flows are nonzero because the system of partial differential equations is not homogeneous in the annulus.

To be more precise, in the present physical setting, there are dimensionless parameters which are analogous to the usual ones for convection in a layer, i.e., the Prandtl and Rayleigh numbers:

$$\begin{aligned} \textrm{Pr}:=\frac{\nu }{D}\, \qquad \textrm{Ra}:=\frac{\alpha g \delta T}{\nu D}(R_o-R_i)^3\, \,, \end{aligned}$$

where $\nu$, D, $\alpha$ and g, respectively, denote kinematic viscosity, thermal diffusivity, thermal expansion coefficient and gravity acceleration. But now, a further independent dimensionless parameter, besides the two above mentioned, is necessary to study the dynamical system. It is the inverse relative gap

$$\begin{aligned} {\mathcal {A}}:=\frac{2R_i}{R_o-R_i}\, \,. \end{aligned}$$

As $\textrm{Pr}$ depends only on the chosen fluid, ${\mathcal {A}}$ depends only on the chosen geometry and increases as the curvature decreases. On the other hand, most of the experimental results deal with air ($\textrm{Pr}=0.7$) and consist in qualitative studies of the flows as $\textrm{Ra}$ increases. In fact, by definition $\textrm{Ra}$ proves to be the relevant parameter for the convective transitions, since thermal expansion and difference of temperature make the convective transport increase. On the opposite, viscosity and heat diffusion work against the buoyancy force.

The physical consistency of the O–B system of equations is not discussed here, but we want to point out that although the isochoric motion condition is in the system, it can hold true also for compressible fluids, such as perfect gases, as recently shown in [5]. Compared to the classical O–B system, the system rigorously derived in [5] is different only for an extra independent nondimensional parameter. Such parameter involves the compressibility factor and lies in front of the convective term of the energy equation. In fact, for the sake of thermodynamical consistency, several convective models including compressibility were recently analyzed, see, for instance, [6] and also [7,8,9,10]. The model in [5] is specific for gases and includes the constraint of divergence free flow into a rigorous derivation through a perturbation theory.

Thus, let us define the family of nondimensional domains

$$\begin{aligned} \Omega =\left\{ (r,\varphi )\in {\mathbb {R}}^2:\, \frac{{\mathcal {A}}}{2}<r<\frac{{\mathcal {A}}}{2}+1\right\} \,; \end{aligned}$$

then, the nondimensional system we study is

$$\begin{aligned}&\nabla \cdot {\textbf{v}}=0\nonumber \\&\frac{1}{\textrm{Pr}}\bigg (\frac{\partial {\textbf{v}}}{\partial {t}}+{\textbf{v}}\cdot \nabla {\textbf{v}}\bigg )-\Delta {\textbf{v}}+\nabla p=\frac{\textrm{Ra}}{b}\sin {\varphi }\mathbf {{e}_r}+\textrm{Ra}\tau \mathbf {e_3}\nonumber \\&\frac{\partial {\tau }}{\partial {t}}+{\textbf{v}}\cdot \nabla {\tau }-\Delta {\tau }=\frac{1}{b}\frac{v_r}{r }. \end{aligned}$$

(1.2)

By the Helmholtz–Weyl decomposition, the equation for the pressure field p decouples from the system, so that one can consider as unknown $(\textbf{v},\tau )$ with Dirichlet conditions at the boundary of $\Omega$ for both the fields. As a matter of fact, $\tau :=T-T^*$ is such that the solution of $\Delta T^*=0$ absorbs boundary conditions (1.1) for T. By replacing the explicit expression of $T^*$, one gets

$$\begin{aligned} \tau =\frac{T-T_i}{T_i-T_o}+\frac{\ln r-\ln R_i}{\ln R_o-\ln R_i}\,. \end{aligned}$$

Moreover, the parameter b is a function of ${\mathcal {A}}$. Precisely,

$$\begin{aligned} b=\ln \left( 1+\frac{2}{{\mathcal {A}}}\right) \end{aligned}$$

(1.3)

diverges as ${\mathcal {A}}$ tends to zero.

By looking at the first term on the right-hand side of the second equation in (1.2), one sees that it is not gradient-like. That is why the system is not homogeneous when projected in the space of divergence free vector fields, so that the rest state is not a solution.

The region of the parameter space we are going to investigate is approximately ${\mathcal {A}}<2$, because the outcome of the observations and numerical experiments (see, for instance, [3, 11, 12]) says that there could be 2-D oscillating solutions if $\textrm{Ra}$ is large. More, the critical value of Ra corresponding to the first transition could be unbounded as ${\mathcal {A}}$ tends to zero but, on the other hand, we theoretically proved, in [2], that the basic solution tends to zero as ${\mathcal {A}}$ tends to zero. So, a further motivation comes from the possibility to overcome, in the limit for small ${\mathcal {A}}$, the mathematical difficulties related to the lack of an analytic expression for the basic solution.

The organization of the paper is the following: In Sect. 2, estimates for the gradient of the basic solution in $L^2(\Omega )$ are given, as well as a linear homogeneous version of system (1.2). Such system proves to be the Stokes limit as ${\mathcal {A}}$ tends to zero of the system whose unknown is the perturbation to the steady solutions of (1.2). Finally, the result for nonlinear stability is recalled and the critical value $\textrm{Ra}_c$ is defined as a function of ${\mathcal {A}}$, since it is a maximum taken over an $L^2$-space whose domain depends on ${\mathcal {A}}$. Moreover, $\textrm{Ra}_c$ is bounded from below in the given region.

In Sect. 3, we prove that the solutions of the Euler–Lagrange equations arising from the definition of $\textrm{Ra}_c$ are a complete basis for the Hilbert space of the steady solutions of system (1.2). Next, we project on that basis the system for the linear perturbation of the steady solution and write the Galerkin ordinary differential equation system. Finally, by simple linear algebra tools, we show that no time periodic solution exists for the system if $\textrm{Ra}\le \textrm{Ra}_c$.

In conclusion, for our problem we define a critical value $\textrm{Ra}_c$ identifying nonlinear stability in the limit as ${\mathcal {A}}$ tends to zero, so that the steady basic solution is stable for lower $\textrm{Ra}$. In Bénard’s problem, such a critical value coincides with the one for linear instability, i.e., for $\textrm{Ra}=\textrm{Ra}_c$, a new steady solution arises, and for $\textrm{Ra}>\textrm{Ra}_c$, there exists at least one linear perturbation whose norm grows in time. In the present situation, by taking the limit as ${\mathcal {A}}$ tends to zero, we do not know whether for $\textrm{Ra}=\textrm{Ra}_c$ a new stable solution arises but, in case, it would not be an oscillating solution, although it could be a further steady solution, as suggested by numerical results in [11].

2 Notation and preliminary results

For $q>1$, we use Lebesgue and Sobolev spaces $L^q(\Omega )$ and $W^{m,q}(\Omega )$, with $L^q$-norm defined as

$$\begin{aligned} \Vert u\Vert _q=\left( \int \limits _\Omega |u|^q\textrm{d}x\right) ^\frac{1}{q}<\infty \,, \end{aligned}$$

for scalar- and vector-valued functions, as well as for their distributional derivatives up to order $m\in {\mathbb {N}}$, but for $q=\infty$ the norm is obtained by taking the supremum. Next, we denote with $L^2(\Omega )$ and $(L^2(\Omega ))^2$ the Hilbert spaces of scalar and vector functions, which are, respectively, endowed with the inner products

$$\begin{aligned} \langle u|v\rangle :=\int \limits _{\Omega }uv\ \textrm{d}x\qquad \langle \textbf{u}|\textbf{v}\rangle :=\int \limits _{\Omega }\textbf{u}\cdot \textbf{v}\ \textrm{d}x\, . \end{aligned}$$

For the sake of simplicity, we are going to use both for vector and scalar function a single symbol for the Poincaré constant in inequality

$$\begin{aligned} \Vert u\Vert _2\le c_p\Vert \nabla u\Vert _2\,, \end{aligned}$$

which holds true in $\Omega$ with $c_p$ estimated by (see [13])

$$\begin{aligned} c_p\le k_p({\mathcal {A}}):=\min \bigg \{ \frac{1}{2}\sqrt{1+\frac{2}{{\mathcal {A}}}};\frac{\sqrt{2}}{\pi }\bigg (1+\frac{{\mathcal {A}}}{2}\bigg )\bigg \}. \end{aligned}$$

When dealing with a Cartesian product of Hilbert spaces, the inner product is the sum of the inner products, and so are the norms.

In order to find the solutions of the O–B system, we describe the velocity field by defining ${\mathcal {H}}(\Omega )$ and ${\mathcal {W}}_0^{m,2}(\Omega )$ as the closure of all solenoidal vector fields $\textbf{u}$ (i.e., $\nabla \cdot \textbf{u}=0$) belonging to $({\mathcal {C}}_0^\infty (\Omega ))^2$, respectively, in the norm of $(L^2(\Omega ))^2$ and $(W^{m,2}(\Omega ))^2$; of course, for the temperature field we simply consider $L^2(\Omega )$ and $W_0^{m,2}(\Omega )$, which are the closure of ${\mathcal {C}}_0^\infty (\Omega )$ in the norm of $W^{m,2}(\Omega )$ (here $m=0,1,2$). For the solutions of the unsteady problem and the related Bochner spaces, we use the notation $L^q(0,T;{\mathcal {W}}_0^{m,2}(\Omega ))$ or $L^q(0,T;W_0^{m,2}(\Omega ))$, but for $m=0$ we write ${\mathcal {H}}(\Omega )$ in place of ${\mathcal {W}}_0^{0,2}(\Omega )$ and $L^2(\Omega )$ in place of $W_0^{0,2}(\Omega )$.

The global existence of steady solutions of (1.2) is proved in [2]. Here, with global existence we mean that existence is proved in any point of the 3D parameter space. Steady solutions are expected to be symmetric with respect to the z-axis, not only because of experimental outcomes but also because the body force and the domain possess such mirror symmetry. Actually, if one could prove that steady solutions are unique they would enjoy the symmetry property as a consequence of uniqueness. But from the experiments they are not unique, neither uniqueness was ever proved for large $\textrm{Ra}$. Therefore, in [2] the expression of $(\textbf{v},\tau )$ is constructed by the Galerkin method with two bases of symmetric 2-D divergence free vector and scalar fields, respectively.

Theorem 2.1

For arbitrary Ra, ${\mathcal {A}}$ and Pr, there exists a weak steady solution

$$\begin{aligned} (\textbf{v}_s,\tau _s)\in {\mathcal {W}}_0^{1,2}(\Omega )\times W^{1,2}(\Omega ) \end{aligned}$$

of system (1.2) verifying

$$\begin{aligned} \Vert \nabla \textbf{v}_s\Vert _2\le c\, \textrm{Ra}\, b^{-1}\qquad \Vert \nabla \tau _s\Vert _2\le c\, \textrm{Ra}\, b^{^{-\frac{3}{2}}} \end{aligned}$$

(2.1)

where $c=c(\textrm{Ra},{\mathcal {A}})$ is a uniformly continuous function.

For the existence and the regularity of time-dependent solutions, one can recall the results in [1], starting with the definition of weak solution

Definition 2.1

A couple

$$\begin{aligned} (\textbf{v},\tau )\in [L^{\infty }(0,T;{\mathcal {H}}(\Omega ))\cap L^2(0,T;{\mathcal {W}}_0^{1,2}(\Omega ))]\times [L^{\infty }(0,T;L^2(\Omega ))\cap L^2(0,T;W_0^{1,2}(\Omega ))] \end{aligned}$$

is a weak solution for system (1.2) in [0, T], if a.e. for $t\in (0,T)$

$$\begin{aligned}&\langle \nabla \textbf{v},\nabla \mathbf {\varphi }\rangle +\langle \frac{1}{\textrm{Pr}}\left( \frac{\partial {\textbf{v}}}{\partial {t}}+{\textbf{v}}\cdot \nabla {\textbf{v}}\right) -\frac{\textrm{Ra}}{b}\sin {\varphi }\textbf{e}_r-\textrm{Ra}\tau \mathbf {e_3}\, ,\, \mathbf {\varphi }\, \rangle =0\\&\langle \nabla \tau ,\nabla \phi \rangle +\langle \frac{\partial {\tau }}{\partial {t}}+{\textbf{v}}\cdot \nabla {\tau }-\frac{1}{b}\frac{v_r}{r }\, ,\, \phi \, \rangle =0 \end{aligned}$$

for all $\mathbf {\varphi }\in L^2(0,T;{\mathcal {W}}_0^{1,2}(\Omega ))$ and $\phi \in L^2(0,T;W_0^{1,2}(\Omega ))$.

The existence and regularity result in [1] are the following.

Theorem 2.2

By prescribing initial conditions $(\textbf{v}_0,\tau _0)\in {\mathcal {H}}(\Omega )\times L^2(\Omega )$, for any Ra, ${\mathcal {A}}$ and Pr system (1.2) has got a unique weak solution $\forall \, T>0$; if moreover $(\textbf{v}_0,\tau _0)\in {\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )$, then the solution is even more regular, i.e.,

$$\begin{aligned} (\textbf{v},\tau )\in [L^{\infty }(0,T;{\mathcal {W}}_0^{1,2}(\Omega ))\cap L^2(0,T;{\mathcal {W}}_0^{2,2}(\Omega ))]\times [L^{\infty }(0,T;W_0^{1,2}(\Omega ))\cap L^2(0,T;W_0^{2,2}(\Omega ))]. \end{aligned}$$

Let us write the solution of the unsteady problem as the sum of a steady solution plus an unknown time-dependent couple of fields:

$$\begin{aligned} \textbf{v}=\textbf{v}_s+\frac{1}{b}\textbf{u}\qquad \tau =\tau _s+\frac{\theta }{\sqrt{b^3\textrm{Ra}}}\, . \end{aligned}$$

Then, by substituting these equations in (1.2), by taking into account that $(\textbf{v}_s,\tau _s)$ actually verifies (1.2), by multiplying the second equation by b and the third by $\sqrt{b^3\, \textrm{Ra}}$, the perturbation $(\textbf{u},\theta )$ verifies the homogeneous system:

$$\begin{aligned}&\nabla \cdot {\textbf{u}}=0\nonumber \\&\frac{1}{\textrm{Pr}}\bigg (\frac{\partial {\textbf{u}}}{\partial {t}}+{\textbf{u}}\cdot \nabla {\textbf{v}_s}+{\textbf{v}_s}\cdot \nabla {\textbf{u}}+\frac{1}{b}{\textbf{u}}\cdot \nabla {\textbf{u}}\bigg )-\Delta {\textbf{u}}+\nabla P=\sqrt{\frac{\textrm{Ra}}{b}}\, \theta \mathbf {e_3}\nonumber \\&\frac{\partial {\theta }}{\partial {t}}+\sqrt{b\, \textrm{Ra}}\, {\textbf{u}} \cdot \nabla {\tau _s}+ {\textbf{v}_s}\cdot \nabla {\theta }+\frac{1}{b}{\textbf{u}}\cdot \nabla {\theta }-\Delta {\theta }=\sqrt{\frac{\textrm{Ra}}{b}}\, \frac{u_r}{r}. \end{aligned}$$

(2.2)

Remark 2.1

Notice that system (1.2) has got a constant in time body force term leading to the finiteness of the existence interval (0, T). This can be seen in the derivation of the estimates involved in the quoted Theorem 2.2. However, once the existence of steady solutions, obviously global in time, is proved then one is left with system (2.2). Since this system is homogeneous, it can easily be seen that now T can go to $\infty$.

Let us examine estimates (2.1): They suggest to assume that $\textbf{v}_s$ is of order $\textrm{Ra}\, \cdot b^{-1}$ and $\tau _s$ of order $\textrm{Ra}\, \cdot b^{-\frac{3}{2}}$. These assumptions are reasonable, not simply in the $L^2$-norm but also pointwise. As a matter of fact, they could be proved through a standard regularization procedure, which is allowed because the boundary is regular.

Under such hypotheses, we get

$$\begin{aligned} {\textbf{u}}\cdot \nabla {\textbf{v}_s}\!=\!O\left( \frac{\textrm{Ra}}{b}\right) \qquad {\textbf{v}_s}\cdot \nabla {\textbf{u}}\!=\!O\left( \frac{\textrm{Ra}}{b}\right) \qquad {\textbf{u}} \cdot \nabla {\tau _s}\!=\!O\left( \frac{\textrm{Ra}}{\sqrt{b^3}}\right) \qquad {\textbf{v}_s}\cdot \nabla {\theta }\!=\!O\left( \frac{\textrm{Ra}}{b}\right) . \end{aligned}$$

(2.3)

Then, as usually done to get Stokes problem as limit for Navier–Stokes, we set $\epsilon :=\frac{1}{\sqrt{b}}$ and neglect the terms of order $\epsilon ^2$. By inserting estimates (2.3) in system (2.2), we see that all such terms are of order $\epsilon ^2$. Next, one should not forget that $\Omega$ itself depends on $\frac{1}{b}$ through ${\mathcal {A}}$. By the definition

$$\begin{aligned} {\mathcal {A}}=\frac{1}{e^b-1}\Rightarrow {\mathcal {A}}\le \frac{2}{b}\,, \end{aligned}$$

so if we neglect terms of order $\frac{1}{b}$, then ${\mathcal {A}}$ has to be extremely small. Finally, in the limit as ${\mathcal {A}}\rightarrow 0$ one obtains the system:

$$\begin{aligned}&\nabla \cdot {\textbf{u}}=0\nonumber \\&\frac{1}{\textrm{Pr}}\frac{\partial {\textbf{u}}}{\partial {t}}-\Delta {\textbf{u}}+\nabla P=\sqrt{\frac{\textrm{Ra}}{b}}\, \theta \mathbf {e_3}\nonumber \\&\frac{\partial {\theta }}{\partial {t}}-\Delta {\theta }=\sqrt{\frac{\textrm{Ra}}{b}}\, \frac{u_r}{r}\, , \end{aligned}$$

(2.4)

in the circle

$$\begin{aligned} \Omega _0=\left\{ (r,\varphi )\in {\mathbb {R}}^2:\, 0<r<1\right\} \,, \end{aligned}$$

with homogeneous boundary conditions.

Nevertheless, instead of simply studying the limit problem, one could study the approximation problem obtained by neglecting the small terms in the equations and keep a domain $\Omega$ different from $\Omega _0$, though very close to it as close as required by the value of $\epsilon$ which identifies the approximation.

As a matter of fact, an analogous of system (2.4) is also studied in [2] for arbitrary domains $\Omega ({\mathcal {A}})$. By implicitly defining $\textrm{Ra}_c({\mathcal {A}})$ as

$$\begin{aligned} \qquad {\sqrt{\frac{b}{\textrm{Ra}_c}}}:=\sup _{{\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )} \frac{\langle \textbf{u}\cdot \nabla S|\theta \rangle }{\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2}\,,\quad \, \end{aligned}$$

(2.5)

where

$$\begin{aligned} S=\ln {r}+r\sin {\varphi }\rightarrow \nabla S=\frac{\textbf{e}_r}{r}+\textbf{e}_3\,, \end{aligned}$$

(2.6)

the result in [2] can be rewritten as follows.

Theorem 2.3

Let Ra, ${\mathcal {A}}$ and Pr be arbitrary. Then for any $(\textbf{u}_0,\theta _0)\in {\mathcal {H}}(\Omega )\times L^2(\Omega )$ there exists a unique weak solution

$$\begin{aligned} (\textbf{u},\theta )\in [L^{\infty }(0,\infty ;{\mathcal {H}}(\Omega ))\cap L^2(0,\infty ;{\mathcal {W}}_0^{1,2}(\Omega ))]\times [L^{\infty }(0,\infty ;L^2(\Omega ))\cap L^2(0,\infty ;W_0^{1,2}(\Omega ))] \end{aligned}$$

of (2.4). If $\textrm{Ra}<\textrm{Ra}_c({\mathcal {A}})$, such a solution is globally exponentially stable; i.e., there exists $\alpha >0$ such that for almost every $t\in (0,\infty )$

$$\begin{aligned} d_1(\Vert \textbf{u}(t)\Vert _2^2+\Vert \theta (t)\Vert _2^2)\le d_2(\Vert \textbf{u}_0\Vert _2^2+\Vert \theta _0\Vert _2^2)e^{-\alpha t} \end{aligned}$$

(2.7)

where $d_1=\min \big \{\frac{1}{\textrm{Pr}},1\big \}$ and $d_2=\max \big \{\frac{1}{\textrm{Pr}},1\big \}$.

Proof

We just recall the energy method as sufficient condition for stability and thus define

$$\begin{aligned} E(\textbf{u},\theta ):=\frac{1}{2}\bigg (\frac{1}{\textrm{Pr}}\Vert \textbf{u}\Vert _2^2+\Vert \theta \Vert _2^2\bigg ). \end{aligned}$$

Next, we perform the $L^2$-inner product of the second equation in (2.4) by $\textbf{u}$ and of the third one with $\theta$ to find

$$\begin{aligned} \frac{1}{2{\textrm{Pr}}}\frac{\textrm{d} \Vert \textbf{u}\Vert _2^2}{\textrm{d} t}+\Vert \nabla \textbf{u}\Vert _2^2&=\sqrt{\frac{\textrm{Ra}}{b}}\, \langle \theta e_3|\textbf{w}\rangle \\ \frac{1}{2{\textrm{Pr}}}\frac{\textrm{d} \Vert \theta \Vert _2^2}{\textrm{d} t}+\Vert \nabla \theta \Vert _2^2&=\sqrt{\frac{\textrm{Ra}}{b}}\, \left\langle \frac{u_r}{r}|\theta \right\rangle \, . \end{aligned}$$

By summing the two equations, one gets

$$\begin{aligned} \frac{\textrm{d} E}{\textrm{d}t}=-\Vert \nabla \textbf{u}\Vert _2^2-\Vert \nabla \theta \Vert _2^2+\sqrt{\frac{\textrm{Ra}}{b}}\langle \textbf{u}\cdot \nabla S|\theta \rangle . \end{aligned}$$

By uniqueness, which is still proved in [2]), we know that the sum of the norms of the gradients never vanishes for initial conditions different from zero. So, by (2.5) we can write

$$\begin{aligned} \frac{\textrm{d} E}{\textrm{d}t}&=-(\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2)+\sqrt{\frac{\textrm{Ra}}{b}}\frac{\langle \textbf{u}\cdot \nabla S|\theta \rangle }{\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2}(\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2)\le \nonumber \\&\le -\sqrt{\frac{\textrm{Ra}}{b}}(\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2)\bigg (\sqrt{\frac{b}{\textrm{Ra}}}-\sqrt{\frac{b}{\textrm{Ra}_c}}\bigg ). \end{aligned}$$

(2.8)

Then, the sufficient condition for stability is $\sqrt{\textrm{Ra}_c}>\sqrt{\textrm{Ra}}$.

Finally, the Poincaré inequality ensures that the stability is asymptotic, since E is equivalent to the $L^2$-norm in the Cartesian product space,¹ we can write

$$\begin{aligned} -(\Vert \nabla \textbf{u}\Vert _2^2+\Vert \nabla \theta \Vert _2^2)\le -\frac{1}{c_p^2}\bigg (\Vert \textbf{u}\Vert _2^2+\Vert \theta \Vert _2^2\bigg ) \le - \frac{\min \{\textrm{Pr};1\}}{c_p^2}\bigg (\frac{\Vert \textbf{u}\Vert _2^2}{\textrm{Pr}}+\Vert \theta \Vert _2^2\bigg )=-\frac{2}{d_2c_p^2}E \end{aligned}$$

and insert this inequality in (2.8), so getting exponential decay for $\textrm{Ra}<\textrm{Ra}_c$. $\square$

For the full system (1.2), it is easily shown that steady solutions are stable for sufficiently small Ra, with arbitrary ${\mathcal {A}}$ and Pr. However, in [2] a more relevant achievement is obtained: for sufficiently small ${\mathcal {A}}$, then Ra does not need to be extremely small for steady solutions to be stable (and unique). As a matter of fact, with the present scaling of the perturbation, one still gets that $\textrm{Ra}_c$ is bounded from below (as in [2]), at least for ${\mathcal {A}}<2$. The choice of the number 2 is only related to the regions of the parameter space which are usually identified in the literature [3, 11, 12]. By the same techniques as in [2], one shows:

Lemma 2.1

The critical value $\textrm{Ra}_c({\mathcal {A}})$ defined in (2.5) is bounded from below for ${\mathcal {A}}<2$, i.e., $\textrm{Ra}_c>c({\mathcal {A}})$ with $c({\mathcal {A}})$ bounded from below.

This follows by the boundedness of the functional at the right-hand side of (2.5): Due to the Poincaré and Hölder inequalities, it is in fact bounded from above by a continuous function of ${\mathcal {A}}$, and the inverse of such function is bounded from below (see Lemma 4.2 in [2]) also in the present case.

Then, the stability result in [2], which can be found in Theorem 4.4, states

Theorem 2.4

For all Pr and $\mu \in (0,1)$, one can find ${\mathcal {A}}^*(\textrm{Pr},\mu )$ such that $\forall {\mathcal {A}}\in (0,{\mathcal {A}}^*)$ one has asymptotic stability of the steady solution $(\textbf{v}_s,\tau _s)$ provided $\textrm{Ra}<(1-\mu )\textrm{Ra}_c({\mathcal {A}})$.

Proof

A sketch of the proof consists in writing an energy inequality for system (2.2):

$$\begin{aligned} \!\frac{\textrm{d}E}{\textrm{d}t}\!+\!\Vert \nabla {\textbf{u}}\Vert _2^2+\!\Vert \nabla {\theta }\Vert _2^2\!\le \!\!\sqrt{\frac{\textrm{Ra}}{b}}\!\left( \langle \theta \mathbf {e_3}|\textbf{u}\rangle \!+\!\langle \frac{u_r}{r}|\theta \rangle \right) \!+\!{\frac{1}{\textrm{Pr}}|\!\langle {\textbf{u}}\!\cdot \!\nabla {\textbf{v}_s}|\textbf{u}\rangle \!|}\!+\!{\sqrt{bRa}|\!\langle {\textbf{u}}\!\cdot \!\nabla {\tau _s}|\theta \rangle \!|}. \end{aligned}$$

Next, we use (see, for instance, [14]) Hölder, Ladyzhenskaya and Poincaré inequalities, together with estimates (2.3), to bound the trilinear terms at the right-hand side

$$\begin{aligned} |\!\langle {\textbf{u}}\!\cdot \!\nabla {\textbf{v}_s}|\textbf{u}\rangle \!|&\le \Vert \textbf{u}\Vert _4^2\Vert \nabla \textbf{v}_s\Vert _2\le \textrm{Ra}\frac{c}{b}\Vert \textbf{u}\Vert _2\Vert \nabla \textbf{u}\Vert _2\le \textrm{Ra}\ k_p\frac{c}{b}\Vert \nabla \textbf{u}\Vert _2^2\\ |\!\langle {\textbf{u}}\!\cdot \!\nabla {\tau _s}|\theta \rangle \!|&\le \Vert \textbf{u}\Vert _4\Vert \theta \Vert _4\Vert \nabla \tau _s\Vert _2\le \textrm{Ra}\frac{c}{b^{\frac{3}{2}}}\sqrt{\Vert \textbf{u}\Vert _2\Vert \nabla \textbf{u}\Vert _2}\sqrt{\Vert \theta \Vert _2\Vert \nabla \theta \Vert _2}\le \\ {}&\le \textrm{Ra}\ k_p\frac{c}{b^{\frac{3}{2}}}\Vert \nabla \theta \Vert _2\Vert \nabla \textbf{u}\Vert _2\le \textrm{Ra}\ k_p\frac{c}{2b^{\frac{3}{2}}}(\Vert \nabla \theta \Vert _2^2+\Vert \nabla \textbf{u}\Vert _2^2)\, , \end{aligned}$$

and we immediately see they are higher order small as ${\mathcal {A}}$ tends to zero, so that inequality (2.8) can be obtained, but the coefficient of the gradients at the left-hand side, which is slightly smaller than 1. $\square$

For these reasons, in the next section of the present paper we study system (2.4) in $\Omega ({\mathcal {A}})$ for small ${\mathcal {A}}$, as a linear approximation of system (2.2) in the same domain, so facing the onset of linear instability.

3 Solutions of the linear problem at the criticality point

In the present section, we look for solutions to the linear approximation system (2.4) by means of a special orthonormal basis for the Hilbert space of the weak steady solutions. We start considering what happens in flat geometry: For Bénard’s problem, the solutions of the Euler–Lagrange equations obtained from looking for the optimal nonlinear stability Ra are precisely the same basis functions used for finding the growth of instability in the linear system. They were used by Rayleigh more than one century ago, simply because their use splits the linear system in normal modes, without any insight that such functions were solutions of the E–L equations. Thus, also in the present case we try to solve the linear system by means of a basis of solutions to the E–L equations, with the hope to get particular geometric features possibly simplifying the calculus. The first part of this section is devoted to prove that among the E–L solutions there is in fact a complete basis.

In [15], studying the flows and the heat transfer in the vertical annulus, the Euler–Lagrange equations whose solution maximizes the functional in (2.5) were formally written by means of a usual procedure in calculus of variations: It is assumed that a maximum (or a minimum) exists at the point $(\textbf{w},\sigma )$, and then, one writes the functional about this point by adding to the argument an arbitrary variation, belonging to the same Hilbert space. The variation is multiplied by a real parameter, say $\epsilon$. Finally, the derivative with respect to $\epsilon$ is calculated and forced to vanish in $\epsilon =0$ for arbitrary variations.

In this way, the equations can be written without proving neither that their solutions are actually a complete basis, nor that the maximum exists. Nevertheless, even the orthogonality properties have already been derived, so that we can recall the results in [15]. In order to find where the functional has possibly an unknown maximum $\lambda \in {\mathbb {R}}$, the E–L equations are

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot \textbf{w}=0\\ \sigma \nabla S+2\lambda \Delta \textbf{w}=\nabla f\\ \textbf{w}\cdot \nabla S +2\lambda \Delta \sigma =0 \end{array}\right. } \end{aligned}$$

(3.1)

with $(\textbf{w},\sigma )\in {\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )$ and S the function defined in (2.6). Then, if a maximum positive $\lambda$, allowing (3.1) to be solvable, existed it would be by definition equal to $\sqrt{\frac{b}{\textrm{Ra}_c}}$.

Since $(\textbf{w},\sigma )$ vanishes on the boundary, the linear operator in system (3.1) is symmetric: In order to see this, it is sufficient to write the system in the weak form and integrate by parts. Therefore, in [15] one can find the derivation of the orthogonality relations for the (possibly existing) eigenfunctions: Given any $\lambda _j\in {\mathbb {R}}$, for which (3.1) can be solved by a couple $(\textbf{w}_j,\sigma _j)$ one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} \langle \textbf{w}_j\cdot \nabla S|\sigma _k\rangle -2\lambda _j \langle \nabla \sigma _k|\nabla \sigma _j\rangle =0\, ,\\ \langle \sigma _k\nabla S|\textbf{w}_j\rangle -2\lambda _k \langle \nabla \textbf{w}_k|\nabla \textbf{w}_j\rangle =0\, . \end{array}\right. } \end{aligned}$$

Thus, by subtracting the above equations one obtains

$$\begin{aligned} (\lambda _k-\lambda _j)(\langle \nabla \sigma _k|\nabla \sigma _j\rangle +\langle \nabla \textbf{w}_k|\nabla \textbf{w}_j\rangle )=0\,, \end{aligned}$$

and for $\lambda _j\ne \lambda _k$,

$$\begin{aligned} \langle \nabla \sigma _j|\nabla \sigma _k\rangle + \langle \nabla \textbf{w}_j|\nabla \textbf{w}_k\rangle =0\,, \end{aligned}$$

(3.2)

so that now by summing the same equations, one gets

$$\begin{aligned} \langle \sigma _k\nabla S|\textbf{w}_j\rangle = \langle \textbf{w}_j\cdot \nabla S|\sigma _k\rangle =0\,. \end{aligned}$$

(3.3)

Further, for $j=k$, a normalization can be chosen

$$\begin{aligned} \Vert \nabla \textbf{w}_j\Vert =\Vert \nabla \sigma _j\Vert =1\qquad \lambda _j=\frac{1}{2}\langle \sigma _j\nabla S|\textbf{w}_j\rangle . \end{aligned}$$

(3.4)

As a matter of fact, showing the existence of the maximum for the functional is not as hard, since it is at least bounded, as remarked in Lemma 2.1. Thus, by using that in definition (2.5) the supremum can be taken over $\Vert \nabla \textbf{u}\Vert +\Vert \nabla \theta \Vert =2$ and, moreover, since by Rellich’s theorem ${\mathcal {W}}_0^{1,2}(\Omega )$ is compactly embedded in ${\mathcal {H}}(\Omega )$ as well as $W_0^{1,2}(\Omega )$ is compactly embedded in $L^2(\Omega )$, then what we are looking for is the supremum in a compact subset of ${\mathcal {H}}(\Omega )\times L^2(\Omega )$, and this means that the supremum is actually a maximum.

Now, we prove that the solutions of (3.1) exist and are a numerable set and a complete basis in ${\mathcal {H}}(\Omega )\times L^2(\Omega )$ for fields in ${\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )$. In particular, use will be made of the spectral decomposition theorem, saying that if, in an Hilbert space, a self-adjoint (symmetric) linear operator is compact and invertible, then there exists a set of numerable eigenfunctions of the operator which is a complete basis. Moreover, the eigenvalues $\mu _j$ are infinitely many and

$$\begin{aligned} \lim _{j\rightarrow \infty }\mu _j=0\,. \end{aligned}$$

(3.5)

Thus, let us notice that E–L equations can be thought as the eigenvalue problem for the operator ${\mathbb {A}}$ defined as follows:

$$\begin{aligned} {\mathbb {A}}:{\mathcal {H}}(\Omega )\!\!\times \!\! L^{2}(\Omega )\rightarrow&H\\ H:=\overline{\{\textbf{u}\!\in \![{\mathcal {C}}_0^{\infty }(\Omega )]^2:\nabla \!\cdot \!\textbf{u}=0\}}^{\Vert \nabla \cdot \Vert _2}&\!\times \!\overline{{{\mathcal {C}}_0^{\infty }(\Omega )}}^{\Vert \nabla \cdot \Vert _2} \end{aligned}$$

and the image of $(\textbf{w},\sigma )$ through ${\mathbb {A}}$

$$\begin{aligned} {\mathbb {A}}(\textbf{w},\sigma )=(\textbf{u},\theta ) \end{aligned}$$

is implicitly defined as the solution of the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot \textbf{u}=0\\ \Delta \textbf{u}=-\sigma \nabla S+\nabla f\\ \Delta \theta =-\textbf{w}\cdot \nabla S\, . \end{array}\right. } \end{aligned}$$

(3.6)

Thus, by replacing $(\textbf{u},\theta )=(2\lambda \textbf{w},2\lambda \sigma )$ in (3.6) one obtains system (3.1) and verifies that its solution would be also eigenfunction of ${\mathbb {A}}$ related to the eigenvalue $\mu =2\lambda$:

$$\begin{aligned} {\mathbb {A}}(\textbf{w},\sigma )=2\lambda (\textbf{w},\sigma )\,. \end{aligned}$$

Let us prove first that ${\mathbb {A}}$ is invertible.

Lemma 3.1

System (3.1) does not allow for nontrivial solutions $(\textbf{w},\sigma )$ if $\lambda =0$.

Proof

Write the second equation in (3.1) for $\lambda =0$, then

$$\begin{aligned} \sigma \nabla S=\nabla f\, . \end{aligned}$$

More, by taking the curl of this equation one obtains

$$\begin{aligned} \nabla \sigma \times \nabla S =0. \end{aligned}$$

So, the two gradients must be parallel, that is to say $g(r, \varphi )$ should exist such that

$$\begin{aligned} \nabla \sigma =g\, \nabla S\,. \end{aligned}$$

In polar coordinates:

$$\begin{aligned}{} & {} \frac{\partial \sigma }{\partial r}=g(r, \varphi )\left( \frac{1}{r}+\sin \varphi \right) \\{} & {} \frac{\partial \sigma }{\partial \varphi }=r\, g(r, \varphi )\left( \frac{1}{r}+\sin \varphi \right) \,. \end{aligned}$$

By asking

$$\begin{aligned} \frac{\partial ^2 \sigma }{\partial \varphi \partial r}=\frac{\partial ^2 \sigma }{\partial r\partial \varphi }\,, \end{aligned}$$

after a little calculation one derives also the necessary condition $\nabla g\times \nabla S=0\,.$

Hence, since the gradients are parallel we deduce that for all $\eta \in {\mathbb {R}}$ the possible nonzero $\sigma$ must be constant on the curves

$$\begin{aligned} \ln r+r\sin \varphi =\eta \,. \end{aligned}$$

Such curves are the leaves of a foliation in the plane, they intersect the boundaries of $\Omega$, and $\sigma$ can be thought as defined on the quotient. Then, $\sigma$ explicitly depends on $\varphi$. However, no $\sigma$ of this kind can verify Dirichlet boundary conditions: $\sigma =0$ on the two circles would imply that its derivative with respect to $\varphi$ vanishes pointwise there, which is impossible. $\square$

Now, in order to show the existence of a complete basis of eigenfunctions, we are going to proof that ${\mathbb {A}}$ is self-adjoint and compact. The symmetry of ${\mathbb {A}}$ is obvious, because the weak form of (3.6) is symmetric, as one can immediately see by performing the inner product with test functions in the dual space, integrating by parts and using the homogeneous boundary conditions.

Concerning the prove of the compactness, let us describe the action of ${\mathbb {A}}$ on the couple $(\textbf{w},\sigma )$: It takes $\textbf{w}$ makes the inner product with $-\nabla S$ and applies the inverse of the Laplacian to the result; then, it takes $\sigma$ multiplies by $-\nabla S$ and applies the inverse of the Stokes operator. At this point, we notice that both such inverse operators are compact. This is well known, since in bounded regular domains and with homogeneous boundary conditions, the solutions of both the corresponding direct problems are bounded in $W^{1,2}$ by the norm of the data in $L^2$. Thus, still by Rellich’s theorem, from a bounded sequence of data one can extract a subsequence of the corresponding solutions which is strongly convergent in the $L^2$-norm. By remarking that the composition of a compact operator with a bounded one is still compact, the compactness of ${\mathbb {A}}$ follows from the boundedness of the operator ${\mathbb {E}}$ so defined:

$$\begin{aligned} {\mathbb {E}}:\, (\textbf{w},\sigma )\, \rightarrow \, (-\sigma \, \nabla S, -\textbf{w}\cdot \nabla S)\,. \end{aligned}$$

On the other hand, ${\mathbb {E}}$ is bounded because of the two inequalities:

$$\begin{aligned} \Vert \sigma \nabla S\Vert _2\le \Vert \nabla S\Vert _{\infty }\Vert \sigma \Vert _2\qquad \Vert \textbf{w}\cdot \nabla S\Vert _2\le \Vert \nabla S\Vert _{\infty }\Vert \textbf{w}\Vert _2\, . \end{aligned}$$

A further feature of (3.1) is that if $\lambda$ is an eigenvalue then $-\lambda$ is an eigenvalue too. To show this, let us assume that

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma \nabla S+2\lambda \Delta \textbf{w}=\nabla f\\ \textbf{w}\cdot \nabla S+2\lambda \Delta \sigma =0. \end{array}\right. } \end{aligned}$$

Then, if we rewrite $\textbf{w}$ as $-(-\textbf{w})$ we get:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma \nabla S-2\lambda \Delta (-\textbf{w})=\nabla f\\ -(-\textbf{w})\cdot \nabla S+2\lambda \Delta \sigma =0\, . \end{array}\right. } \end{aligned}$$

By multiplying the second equation by $-1$, we finally obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma \nabla S-2\lambda \Delta (-\textbf{w})=\nabla f\\ (-\textbf{w})\cdot \nabla S-2\lambda \Delta \sigma =0\, , \end{array}\right. } \end{aligned}$$

which is the E–L equation solved for $-\lambda$ by $(-\textbf{w},\sigma )$. This new solution is independent from the solution for $\lambda$, i.e., $(\textbf{w},\sigma )$.

All the above results are summarized by the following theorem.

Theorem 3.1

System (3.1) admits a numerable set of solutions $(\textbf{w}_j,\sigma _j)\in {\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )$ whose gradients are orthogonal by the Hilbert space inner product. Such solutions are a complete basis in ${\mathcal {H}}(\Omega )\times L^2(\Omega )$ for arbitrary elements in ${\mathcal {W}}_0^{1,2}(\Omega )\times W_0^{1,2}(\Omega )$. The corresponding $\lambda _j$’s are pairs of real numbers of opposite sign, different from zero and enjoying the last property in (3.4):

$$\begin{aligned} \lambda _j=\frac{1}{2}\langle \sigma _j\nabla S|\textbf{w}_j\rangle \end{aligned}$$

Moreover, $\{|\lambda _j|\}_{j\in {\mathbb {N}}}$ is a decreasing sequence and tends to zero as $j\rightarrow \infty$. On the opposite, the largest $|\lambda _j|$ is

$$\begin{aligned} \lambda _1=\frac{1}{2}{\sqrt{\frac{b}{\textrm{Ra}_c}}} \end{aligned}$$

where b is defined in (1.3) and $\textrm{Ra}_c$ in (2.5), as the largest Rayleigh number under which the rest state solution of (2.4) is certainly stable.

Now, let us rewrite system (2.4) and look for particular solutions different from the rest state

$$\begin{aligned} {\left\{ \begin{array}{ll} \nabla \cdot \textbf{u}=0\\ \frac{1}{\textrm{Pr}}\frac{\partial \textbf{u}}{\partial t}-\Delta \textbf{u}+\nabla p=\sqrt{\frac{\textrm{Ra}}{b}}\theta \textbf{e}_3\\ \frac{\partial \theta }{\partial t}-\Delta \theta =\sqrt{\frac{\textrm{Ra}}{b}}\frac{u_r}{r}. \end{array}\right. } \end{aligned}$$

The onset of an Hopf bifurcation is characterized by a solution of the kind

$$\begin{aligned} \textbf{u}(t,r,\varphi )=e^{i\gamma t}\textbf{u}(r,\varphi )\qquad \theta (t,r,\varphi )=e^{i\gamma t}\theta (r,\varphi ). \end{aligned}$$

We can rename $\lambda _{-j}=-\lambda _j$ and write series with $j\in {\mathbb {Z}}$. Then, we can try to see whether an oscillating solution exists by writing it in the form

$$\begin{aligned} \begin{pmatrix} \textbf{u}\\ \theta \end{pmatrix} = e^{i\gamma t}\sum _{j\in {\mathbb {Z}}} c_j \begin{pmatrix} \mathbf {w_j}\\ \sigma _j \end{pmatrix} \end{aligned}$$

(3.7)

with $c_j\in {\mathbb {C}}$. We can replace (3.7) in the system and perform the inner product (in the sense of the Cartesian product) with $(\mathbf {w_k}, \sigma _k)$. Since by (3.2) the gradients of the eigenfunctions are orthogonal, we obtain for any $k\in {\mathbb {Z}}$

$$\begin{aligned} i\gamma \sum _{j\in {\mathbb {Z}}} c_j\left( \frac{1}{\textrm{Pr}}\langle \textbf{w}_j|\textbf{w}_k\rangle +\langle \sigma _j|\sigma _k\rangle \right) +2c_k=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}c_j\left( \langle \sigma _j\mathbf {e_3}|\textbf{w}_k\rangle +\left\langle \frac{w_j^r}{r}\, |\, \sigma _k\right\rangle \right) . \end{aligned}$$

(3.8)

In Eq. (3.8), the basis properties, (3.4) in particular, allow us to simplify the products at the right-hand side. From

$$\begin{aligned} \langle \sigma _j\mathbf {e_3}|\textbf{w}_k\rangle =\left\langle \left( \nabla S-\frac{\textbf{e}_r}{r}\right) \sigma _j\, |\, \textbf{w}_k\right\rangle =\langle \sigma _j\nabla S|\textbf{w}_k\rangle -\left\langle \sigma _j\frac{\textbf{e}_r}{r}\, |\, \textbf{w}_k\right\rangle \, , \end{aligned}$$

it follows that if $\lambda _j\ne \lambda _k$, then the first product on the right-hand side vanish; otherwise, the result is $\lambda _k$ for $j=k$:

$$\begin{aligned} {i\gamma }\sum _{j\in {\mathbb {Z}}}c_j\left( \frac{1}{\textrm{Pr}}\!\langle \textbf{w}_j|\textbf{w}_k\rangle \!+\!\langle \sigma _j|\sigma _k\rangle \right) \!+\!2c_k\!=\!\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}\!c_j\!\left( 2\lambda _j\delta _{jk}\!+\!\left\langle {\frac{w_j^r}{r}}\, |\, \sigma _k\right\rangle \!-\!\left\langle \frac{w_k^r}{r}\, |\, \sigma _j\right\rangle \right) . \end{aligned}$$

(3.9)

Let us define some operator to simplify the notation. First, we denote the metric tensor in complex $\ell ^2$, whose entries are real and which is positive defined since it corresponds to the metric of ${\mathcal {H}}(\Omega )\times L^2(\Omega )$

$$\begin{aligned} G_{jk}:= \frac{1}{\textrm{Pr}}\langle \textbf{w}_j|\textbf{w}_k\rangle +\langle \sigma _j|\sigma _k\rangle . \end{aligned}$$

(3.10)

Next, at the right-hand side of Eq. (3.9) there is a skew-symmetric operator with entries

$$\begin{aligned} \Omega _{jk}:= \left\langle \sigma _k\, |\, \frac{w_j^r}{r}\right\rangle -\left\langle \sigma _j\, |\, \frac{w_k^r}{r}\right\rangle . \end{aligned}$$

(3.11)

Finally, it is convenient define also the diagonal matrix

$$\begin{aligned} \Lambda _{jk}:=2\left( 1-\lambda _k\sqrt{\frac{\textrm{Ra}}{b}}\right) \delta _{jk}\,. \end{aligned}$$

(3.12)

In terms of these operators, Eq. (3.9) becomes

$$\begin{aligned} \sum _{j\in {\mathbb {Z}}} c_j(i\gamma G_{jk}+\Lambda _{jk})=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}c_j\Omega _{jk}. \end{aligned}$$

(3.13)

Here, although the coefficients are real, the unknowns are complex. Since $c_j\in {\mathbb {C}}$, the complex conjugate of Eq. (3.13) is independent:

$$\begin{aligned} \sum _{j\in {\mathbb {Z}}} \bar{c}_j(-i\gamma G_{jk}+\Lambda _{jk})=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}\bar{c}_j\Omega _{jk}. \end{aligned}$$

(3.14)

In order to bring back the problem to real unknowns, we have to extract the real and imaginary part of the equations. Thus, we sum equations (3.13) and (3.14) and divide by 2 the result; then, we subtract them and divide by 2i:

$$\begin{aligned}&\sum _{j\in {\mathbb {Z}}}(-\gamma Im({c}_j)G_{jk}+Re({c}_j)\Lambda _{jk})&=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}Re({c}_j)\Omega _{jk} \end{aligned}$$

(3.15)

$$\begin{aligned}&\sum _{j\in {\mathbb {Z}}}(\gamma Re({c}_j)G_{jk}+Im({c}_j)\Lambda _{jk})&=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}Im({c}_j)\Omega _{jk}. \end{aligned}$$

(3.16)

Just for simplicity, we set $a_j:=Re(c_j)\in {\mathbb {R}}$ and $b_j:=Im(c_j)\in {\mathbb {R}}$, as they were entries of vectors. So, we reversed the complexification of the space, by writing in place of (3.15) and (3.16)

$$\begin{aligned}&-\gamma \sum _{j\in {\mathbb {Z}}} b_jG_{jk}+2\left( 1-\lambda _k\sqrt{\frac{\textrm{Ra}}{b}}\right) a_k&=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}a_j\Omega _{jk} \end{aligned}$$

(3.17)

$$\begin{aligned}&\gamma \sum _{j\in {\mathbb {Z}}} a_jG_{jk}+2\left( 1-\lambda _k\sqrt{\frac{\textrm{Ra}}{b}}\right) b_k&=\sqrt{\frac{\textrm{Ra}}{b}}\sum _{j\in {\mathbb {Z}}}b_j\Omega _{jk}\, . \end{aligned}$$

(3.18)

As a matter of fact, in (3.17) and (3.18) the unknown is the kernel of a linear operator in $\ell ^2\times \ell ^2$.

For $\textrm{Ra}<\textrm{Ra}_c$, the results in Theorem 2.3 holds true: The null solution is asymptotically stable and we have not to expect the onset of an oscillating solution, which corresponds to a nontrivial kernel. On the other hand, by showing that there is no kernel also for $\textrm{Ra}=\textrm{Ra}_c$ we would prove that there is no Hopf bifurcation, since the existence of an oscillatory solution at the criticality is necessary condition for it, see [16].

Theorem 3.2

Let us define in $\ell ^2\times \ell ^2$ the linear operator

$$\begin{aligned} L_{_{\textrm{Ra}}}\begin{pmatrix} \textbf{a}\\ \textbf{b} \end{pmatrix}:=\begin{pmatrix} \Lambda -\sqrt{\frac{\textrm{Ra}}{b}}\Omega &{}\quad -\gamma G\\ \gamma G &{}\quad \Lambda -\sqrt{\frac{\textrm{Ra}}{b}}\Omega \end{pmatrix} \begin{pmatrix} \textbf{a}\\ \textbf{b} \end{pmatrix}, \end{aligned}$$

(3.19)

where G, $\Lambda$ and $\Omega$ are the operators, acting on $\ell ^2$, defined in (3.10), (3.11) and (3.12) while $\gamma \in {\mathbb {R}}$. Then, for $\textrm{Ra}\le \textrm{Ra}_c$

$$\begin{aligned} L_{_{\textrm{Ra}}}(\textbf{a},\textbf{b})=(\textbf{0},\textbf{0})\quad \Rightarrow \quad (\textbf{a},\textbf{b})=(\textbf{0},\textbf{0})\,, \end{aligned}$$

i.e., the kernel of the operator is trivial.

Proof

Since $\Omega$ is skew-symmetric,

$$\begin{aligned}<\textbf{a}|\Omega \, \textbf{b}>_{\ell ^2}=-<\textbf{b}|\Omega \, \textbf{a}>_{\ell ^2}\, , \end{aligned}$$

while G is symmetric, as well as the diagonal matrix $\Lambda$, so that

$$\begin{aligned}<\textbf{a}|G\, \textbf{b}>_{\ell ^2}=<\textbf{b}|G\, \textbf{a}>_{\ell ^2}\, ,\\<\textbf{a}|\Lambda \, \textbf{b}>_{\ell ^2}=<\textbf{b}|\Lambda \, \textbf{a}>_{\ell ^2} \, . \end{aligned}$$

It is important to notice that if the strict inequality $\textrm{Ra}<\textrm{Ra}_c$ holds true, not only the metric tensor G but also $\Lambda$ is positive defined, as one can see by the definition (3.12). Indeed, on the one hand the negative $\lambda _j$’s induce positive values on the diagonal, while the smallest value corresponds to the largest positive $\lambda$ which, by Theorem3.1, can be replaced in (3.12) getting

$$\begin{aligned} \Lambda _{11}=2\left( 1-\sqrt{\frac{\textrm{Ra}}{\textrm{Ra}_c}}\right) >0\,. \end{aligned}$$

Conversely, for $\textrm{Ra}=\textrm{Ra}_c$, one has $\Lambda _{11}=0$ .

With this in mind, from definition (3.19) we can derive some necessary conditions for the pair $(\textbf{a},\textbf{b})$ to verify $L_{_{\textrm{Ra}}}(\textbf{a},\textbf{b})=(\textbf{0},\textbf{0})$. If so, then for arbitrary $(\textbf{x},\textbf{y})$ it must hold $<(\textbf{x},\textbf{y})|L_{_{\textrm{Ra}}}(\textbf{a},\textbf{b})>=0$. Thus, we try with the pairs $(\textbf{x},\textbf{y})=(\textbf{a},\textbf{b})$ and $(\textbf{x},\textbf{y})=(\textbf{b},-\textbf{a})$ and impose

$$\begin{aligned} 0=<(\textbf{a},\textbf{b})|L_{_{\textrm{Ra}}}(\textbf{a},\textbf{b})>_{\ell ^2\times \ell ^2}= \end{aligned}$$

(3.20)

$$\begin{aligned}= & {} lt;\textbf{a}|\Lambda \, \textbf{a}>_{\ell ^2}-\gamma<\textbf{a}|G\, \textbf{b}>_{\ell ^2}+\gamma<\textbf{b}|G\, \textbf{a}>_{\ell ^2}+<\textbf{b}|\Lambda \, \textbf{b}>_{\ell ^2}=\\= & {} lt;\textbf{a}|\Lambda \, \textbf{a}>_{\ell ^2}+ <\textbf{b}|\Lambda \, \textbf{b}>_{\ell ^2}\, . \end{aligned}$$

Also the next condition has to hold true:

$$\begin{aligned} 0=<(\textbf{b},-\textbf{a})|L_{_{\textrm{Ra}}}(\textbf{a},\textbf{b})>_{\ell ^2\times \ell ^2}= \end{aligned}$$

(3.21)

$$\begin{aligned}&= -\sqrt{\frac{\textrm{Ra}}{b}}\!<\textbf{b}|\Omega \, \textbf{a}>_{\ell ^2}-\gamma<\textbf{b}|G\, \textbf{b}>_{\ell ^2}+\sqrt{\frac{\textrm{Ra}}{b}}\!<\textbf{a}|\Omega \, \textbf{b}>_{\ell ^2}-\gamma<\textbf{a}|G\, \textbf{a}>_{\ell ^2}=\\&=-\gamma (<\textbf{a}|G\, \textbf{a}>_{\ell ^2}+<\textbf{b}|G\, \textbf{b}>_{\ell ^2})+2\sqrt{\frac{\textrm{Ra}}{b}}\!<\textbf{a}|\Omega \, \textbf{b}>_{\ell ^2}\, . \end{aligned}$$

By varying $\textrm{Ra}\in (0,\textrm{Ra}_c)$, condition (3.20) is sufficient to obtain the implication in the thesis. It is verified if and only if $\textbf{a}=\textbf{b}=0$, because $\Lambda$ is positive defined.

However, for $\textrm{Ra}=\textrm{Ra}_c$ the element $\Lambda _{11}$ vanishes and (3.20) could be verified without any change in the calculus for $\textbf{a}$ and $\textbf{b}$ so defined

$$\begin{aligned} a_j=a_1\delta _{1j}\, \qquad b_j=b_1\delta _{1j}\,, \end{aligned}$$

with arbitrary real $a_1$ and $b_1$. Nevertheless, this possible new choice should verify also condition (3.21). Here, the last term in the last line disappears, because $\textbf{a}$ and $\textbf{b}$ are parallel and $\Omega$ is skew-symmetric, but, since G is positive defined, the other two terms cannot vanish, unless $a_1=b_1=0$. $\square$

Remark 3.1

The result holds true also for steady solutions as a particular case of the oscillating ones for $\textrm{Ra}<\textrm{Ra}_c$. But for $\textrm{Ra}=\textrm{Ra}_c$, since steady solutions have got $\gamma =0$, the second part of the previous proof does not work because the implication $a_1=b_1=0$ falls.