1 Introduction

Fractional differential equations (FDEs) are differential equations that have derivatives of arbitrary (fractional) order. Fractional derivatives offer a fantastic tool for describing diverse materials and processes’ memory and inherited characteristics. A more comprehensive range of behaviours can be modelled by switching from integer order to fractional derivatives. It has been discovered that the fractional-order system theory may accurately describe the behaviour of many physical systems. Partial differential equations (PDEs), which are the mathematical depiction of physical, chemical, and biological issues encountered in real-world situations, are used to describe a variety of physical events in nature. PDE has evolved in recent years into a common language for several disciplines, including general relativity, electrostatics, thermodynamics, quantum physics, elasticity, sound, and heat. Nonlinear models are a common source of real-world issues in many branches of research and engineering, particularly in chemical physics, plasma physics, solid-state physics, fluid mechanics, and plasma waves. Due to their extensive use in science and engineering, fractional differential equations are gaining a lot of study attention. Therefore, it is essential to study fractional-order differentiation.

fractional partial differential equations are frequently used to represent equations in a variety of study domains, including continuous-time random walks, chaos, mechanical schemes, anomalous diffusive, control, chaos synchronisation, etc. Many fundamental problems are modelled using fractional partial differential equations. The fractional-order technique has the advantage of allowing the problem to have more substantial degrees of freedom. The term “local operator” refers to a differential operator with integer order. In contrast, a fractional-order differential operator is a nonlocal operator since it takes into account that a possible state depends on all of its preceding instances’ past and present. i.e. The integer-order derivative is useful for studying a point’s immediate environment, whereas the fractional derivative is useful for studying the entire interval [1, 38,39,40,41]. Developing precise and effective techniques for solving fractional differential equations has been a focus of active study. The numerical solution of differential equations of integer order has been a central idea in numerical and computational mathematics for a very long time.

However, despite many newly framed applied problems, the state of the art is far less advanced for generalised order equations, and only a few techniques have been proposed for numerically solving these equations. The majority of these numerical methods deal with linear single-term problems of orders lower than unity. Little efforts have been made to address nonlinear problems. Due to their ability to imitate complicated processes, they have attracted much interest. The fractional derivative was initially formulated by Liouville and Riemann near the close of the nineteenth century. Riemann invented the Riemann–Liouville derivative concept in 1876. Since then, a wide range of scientific and technological sectors have shown how these Riemann–Liouville fractional derivatives and integrals can be used. The essential role and basic properties of the fractional differential equations are briefly explained in [2,3,4,5]. In applied mathematics and mathematical analysis, the fractional derivative is a derivative of any arbitrary order, real or complex. Even though the term “fractional” is a misnomer, it has been widely accepted for such a derivative for a long time. The concept of a fractional derivative was coined by the famous mathematician Leibnitz in 1695 in his letter to L’Hôpital. In recent years, fractional calculus has drawn increasing attention due to its applications in many fields. We use the Caputo derivative with fractional order that was proposed by Italian Caputo in 1967. Its physical meaning, advantages, and disadvantages are explained in [48].

Many mathematicians and physicists have exploited diverse techniques for the investigation of fractional partial differential equations such as the Laplace transform method [6], Legendre functions matrix method [7], an efficient approach for fractional Rosenau–Hyman equation [8], Hermite wavelets approach for the multi-term fractional differential equations [9], wavelet technique for the fractional telegraph equation [10], Legendre polynomials method for fractional Sobolev equation [11], fractional model of Fokker–Planck equations [12], numerical solution for nonlinear KG equation [13], an efficient numerical approach for space FPDEs [14], a new approach for KG equation [15], generalised Mellin transform method [44], Haar wavelet method [51, 52], and modified decomposition method [16].

Let’s consider the fractional partial differential equation of the form:

$$\begin{aligned} \frac{{\partial }^{2\delta }\mathrm {y(x,t)}}{{{\partial \textrm{t}}}^{\textrm{2}\delta }} =\frac{{\partial }^{\textrm{2}\alpha }\mathrm {y(x,t)}}{{{\partial \textrm{x}}}^{\textrm{2}\alpha }}\mathrm {+F}\left[ \textrm{x,t,y}\left( \textrm{x,t} \right) ,\frac{{\partial \textrm{y}}\left( \textrm{x,t} \right) }{{\partial \textrm{x}}}{,\ldots ,}\frac{{\partial }^{{\beta -1}}\textrm{y}\left( \textrm{x,t} \right) }{{{\partial \textrm{x}}}^{{\beta -1}}} \right] , \end{aligned}$$
(1.1)

with the primary condition,

$$\begin{aligned} y\left( x,0 \right) =h(x) \end{aligned}$$

boundary condition

$$\begin{aligned} y\left( 0,t \right) =i\left( t \right) ,\quad y\left( \beta _{1},t \right) =j\left( t \right) . \end{aligned}$$

where \(\delta \) and \({\alpha }\) are fractional or integer values, \(\delta ,\, {\alpha \in (0,\,1]}\) and \(h\left( x \right) ,\, i\left( t \right) ,\) and \(j\left( t \right) \) are real functions, \(\beta _{1}\) is a positive real constant.

Wavelet is a function, more precisely, a mathematical function used to separate a specified function signal into different scale components. Wavelets comprise a family of functions created by the translation and dilation of a single function known as the mother wavelet. Wavelets are built on Joseph Fourier’s fundamental theory of superpositioning, which states that a collection of self-similar functions can express a complex function. The mathematical analysis of Morlet, Meyer, Stromberg, Daubechies, and Grossmann has greatly advanced wavelet theory. This wavelet-based representation of differential operations can be precise and stable even in areas with significant gradients or oscillations. Many scholars are drawn to it because of its distinctive characteristics, such as orthogonality, compactly supported, and multiresolution analysis. Numerous dynamical system problems have extensively used approximate solutions using an orthogonal family of functions. Using truncated orthogonal functions to approximate the various signals in the equation, one can approximate the underlying differential equation using orthogonal functions. For some of the common mathematical problems, different wavelet collocation methods have been used, such as the Chebyshev wavelet collocation method [17], the collocation method based on Bernoulli and Gegenbauer wavelets [18], and Laguerre wavelet collocation method [19]. Several wavelet collocation techniques are typically employed to solve fractional differential equations, which include Haar wavelets [20], Chelyshkov wavelets [21], Fibonacci wavelets [22], Cubic B spline [23], Chebyshev wavelets [24], Genocchi wavelets [25], Bernoulli wavelets [26,27,28], Legendre wavelet tau method [29], Legendre wavelets [45] and Gegenbauer wavelets [30]. Wavelets are being used widely in the field of numerical analysis by mathematicians, and as a result, many novel strategies for solving differential equations have recently been developed. One such technique is a study using Hermite wavelets for the fractional Jaulent–Miodek equation [31], HWM for fractional differential equations [32, 46, 47], HWM for solving nonlinear Rosenau–Hyman equation [33], high mass transfer via wavelet frames [34], integrodifferential equations via Hermite wavelet [35] and so on [36, 37, 49, 50].

The major goal of this article is to present a novel wavelet-based method for solving a system of fractional partial differential equations. According to our review of the literature, there are no studies on fractional partial differential equations using Hermite wavelets. Here, we implemented a creative strategy using a functional integration matrix and solved a few fractional partial differential equations. The suggested method is clear, does not require any alterations for the situations given, and is easy to apply numerically. As a result, we are forced to suggest the HWM for the higher-order fractional partial differential equations and the effectiveness of the current approach is demonstrated using tables and graph simulation.

This article is organised as follows: Section 2 is devoted to the properties of the Hermite wavelets and convergence analysis. Section 3 is devoted to the functional integration of the matrix. Section 4 is about the Hermite wavelet method. Section 5 is concerned with the numerical experiment, results, and error analysis of the illustrative problems. Finally, the conclusion of the proposed work is discussed in section 6.

2 Results on Hermite wavelets and fractional derivatives

Definition 1

The Riemann–Liouville’s fractional integral of \(f\,\epsilon \,C_{\mu }\) of the order \(\delta \ge 0\) defined as [42, 43],

$$\begin{aligned} J_{s}^{\delta }f\left( s \right) =\left\{ {\begin{array}{*{20}c} f(s) &{} if\,\delta =0\\ \frac{1}{\varGamma (\delta )}\int \limits _0^s {\left( s-t \right) ^{\delta -1}f\left( t \right) \textrm{d}t} &{} if\,\delta >0.\\ \end{array} } \right. \end{aligned}$$

The gamma function is indicated here by the symbol \(\varGamma \), where \(C_{\mu }\) is continuous linear space.

Definition 2

The Caputo fractional derivative of \(f\left( s \right) \,\epsilon \,C_{\mu }\) is defined as [42, 43]:

$$\begin{aligned} \frac{\partial ^{\delta }f\left( s \right) }{\partial s^{\delta }}=\frac{1}{\varGamma (m-\delta )}\int \limits _0^s {\left( s-t \right) ^{m-\delta -1}f^{\left( m \right) }\left( t \right) \,\textrm{d}t} \end{aligned}$$

for \(m-1<\delta \le m\), m is any positive integer, \(s>0,\quad f\left( s \right) \,\epsilon \, C_{\mu }^{m},\,\mu \ge -1.\) where \(C_{\mu }^{m}\) is continuous linear space containing \(f^{m}(s)\).

Definition 3

The Hermite wavelets are defined as [36]:

$$\begin{aligned} \phi _{n,m}\left( x \right) =\left\{ {\begin{array}{ll} \frac{2^{\frac{k+\,1}{2}}}{\sqrt{\pi }}{H}_{m}\left( 2^{k}x-2n+1 \right) , &{} \frac{n-1}{{ 2}^{k-1}}\le x<\frac{n}{2^{k-1}} \\ 0,&{} \textrm{Otherwise} \\ \end{array}} \right. \end{aligned}$$

where \(m=0,1,2,\ldots ,M-1,n=1,2,\ldots ,2^{k-1}\). Here \(H_{m}\left( x \right) \) is Hermite polynomials of degree m concerning weight function \(W\left( x \right) =\sqrt{1-x^{2}} \) on the real line R and satisfies the following recurrence formula \(H_{0}\left( x \right) =1,H_{1}\left( x \right) =2x\),

$$\begin{aligned} H_{m+2}\left( x \right) =2x\,H_{m+1}\left( x \right) -2\left( m+1 \right) H_{m}\left( x \right) ,\quad m=0,1,2,\ldots . \end{aligned}$$

Theorem 1

If \(\{\phi _{i,j}(t)\}\) be the sequence of continuous functions on \(\left[ a,b \right] \) converges to the function \(\phi \left( t \right) \) uniformly on \(\left[ a,b \right] \). Then \(\phi \left( t \right) \) is continuous on \(\left[ a,b \right] \).

Proof

By data \(\phi _{i,j}\left( t \right) \) uniformly converges to    \(\phi \left( t \right) \). Let \(\varepsilon >0\) be an arbitrary real number, then,

$$\begin{aligned} \left\| \phi _{i,j}\left( t \right) -\phi (t) \right\| <\frac{\varepsilon }{3},\forall t\in \left[ a,b \right] \end{aligned}$$

Since each \(\phi _{i,j}\left( t \right) \) is continuous in [a, b]. Then, there exists \(\delta >0\) such that

\(\left\| \phi _{i,j}\left( t \right) -\phi (t) \right\| <\frac{\varepsilon }{3}\), whenever \(\left\| t_{0}-t \right\| <\varepsilon ,\forall t_{0},t\in [a,b]\).

By Minkowski’s inequality, we have

$$\begin{aligned} \left\| \phi (t_{0})-\phi (t) \right\|= & {} \left\| \phi \left( t_{0} \right) -\phi _{i,j}\left( t_{0} \right) +\phi _{i,j}\left( t_{0} \right) +\phi _{i,j}\left( t \right) -\phi _{i,j}\left( t \right) -\phi (t) \right\| \\ \left\| \phi (t_{0})-\phi (t) \right\|\le & {} \left\| \phi \left( t_{0} \right) -\phi _{i,j}\left( t_{0} \right) \right\| +\left\| \phi _{i,j}\left( t \right) -\phi \left( t \right) \right\| +\left\| \phi _{i,j}\left( t_{0} \right) -\phi _{i,j}\left( t \right) \right\| \\ \left\| \phi (t_{0})-\phi (t) \right\|< & {} \frac{\varepsilon }{3}+\frac{\varepsilon }{3}+\frac{\varepsilon }{3}=\varepsilon .where\left| t_{0}-t \right| <\delta \,\textrm{with}\,t_{0},t\in [a,b]. \end{aligned}$$

Hence, \(\phi \left( t \right) \) is continuous on \(\left[ a,b \right] \).

Theorem 2

Let \(y\left( x,t \right) \in L^{2}\left( R\times R \right) \) be bounded continuous function defined on \(\left[ 0.1 \right) \times \left[ 0.1 \right) ,\) then the Hermite wavelet expansion of \(y\left( x,t \right) \) is uniformly converged to it [19].

Proof

Consider \(y\left( x,t \right) \) to be a continuous function defined on \(\left[ \textrm{0,1} \right) {\times }\left[ \textrm{0,1} \right) \) and \(\left| y\left( x,t \right) \right| {\le }M\), where M is a positive real number. Then, we define \(y\left( x,t \right) \) in the form

$$\begin{aligned} y\left( x,t \right) =\sum \limits _{i\mathrm {=1}}^{\infty } {} \sum \limits _{j=0}^{\infty } {} C_{i,j}\phi _{i,j}\left( x \right) \phi _{i,j}\left( t \right) , \end{aligned}$$

where \(C_{i,j}=<y\left( x,t \right) ,\phi _{i,j}\left( x \right) \phi _{i,j}\left( t \right)>\) and \({<},>\) denotes inner product. Then, Hermite wavelet coefficients of continuous functions \(y\left( x,t \right) \) are defined as:

$$\begin{aligned} C_{i,j}= & {} \int \limits _\textrm{0}^\textrm{1} {} \int \limits _\textrm{0}^\textrm{1} {} y\left( x,t \right) \phi _{i,j}\left( x \right) \phi _{i,j}\left( t \right) \textrm{d}x\textrm{d}t,\\ C_{i,j}= & {} \int \limits _\textrm{0}^\textrm{1} {} \int \limits _I {} y\left( x,t \right) \frac{\textrm{2}^{\frac{k+1}{\textrm{2}}}}{\sqrt{\pi }}h_{m}\left( \textrm{2}^{k}x\mathrm {-2}n\mathrm {+1} \right) \phi _{i,j}\left( t \right) \textrm{d}x\textrm{d}t{,}\,where\,I=\left[ \frac{n\mathrm {-1}}{\textrm{2}^{k\mathrm {-1}}},\frac{n}{\textrm{2}^{k\mathrm {-1}}} \right) \end{aligned}$$

Now, by changing the variable \(\textrm{2}^{k}x\mathrm {-2}n\mathrm {+1=}p,\) we obtain

$$\begin{aligned} C_{i,j}=\frac{\textrm{2}^{\frac{k+1}{\textrm{2}}}}{\sqrt{\pi }}\int \limits _\textrm{0}^\textrm{1} {} \left[ \int \limits _{\mathrm {-1}}^\textrm{1} {} y\left( \frac{p\mathrm {-1+2}n}{\textrm{2}^{k}},t \right) h_{m}\left( p \right) \frac{dp}{\textrm{2}^{k}} \right] \phi _{i,j}\left( t \right) \textrm{d}t, \end{aligned}$$
$$\begin{aligned} C_{i,j}=\frac{\textrm{2}^{\frac{\mathrm {1-}k}{\textrm{2}}}}{\sqrt{\pi }}\int \limits _\textrm{0}^\textrm{1} {} \left[ \int \limits _{\mathrm {-1}}^\textrm{1} {} y\left( \frac{p\mathrm {-1+2}n}{\textrm{2}^{k}},t \right) h_{m}\left( p \right) dp \right] \phi _{i,j}\left( t \right) \textrm{d}t, \end{aligned}$$

Using the generalised mean value theorem for integrals, we obtain the following equation

$$\begin{aligned} C_{i,j}=\frac{\textrm{2}^{\frac{\mathrm {1-}k}{\textrm{2}}}}{\sqrt{\pi }}\int \limits _\textrm{0}^\textrm{1} {} y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},t \right) \phi _{i,j}\left( t \right) \textrm{d}t\left[ \int \limits _{\mathrm {-1}}^\textrm{1} {} \textrm{h}_{m}\left( p \right) dp \right] {,} \end{aligned}$$

where \(\zeta {\in }\left( \mathrm {-1,1} \right) \). Since \(h_{m}\left( x \right) \) is continuous and integrable on \(\left( \mathrm {-1,1} \right) \), we choose\(\int \limits _{\mathrm {-1}}^\textrm{1} {} L_{m}\left( p \right) dp=A\) such that,

$$\begin{aligned} C_{i,j}= & {} A\frac{\textrm{2}^{\frac{\mathrm {1-}k}{\textrm{2}}}}{\sqrt{\pi }}\int \limits _\textrm{0}^\textrm{1} {} y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},t \right) \phi _{i,j}\left( t \right) \textrm{d}t,\\ C_{i,j}= & {} A\frac{\textrm{2}^{\frac{\mathrm {1-}k}{\textrm{2}}}}{\sqrt{\pi }}\int \limits _\frac{n\mathrm {-1}}{\textrm{2}^{k\mathrm {-1}}}^\frac{n}{\textrm{2}^{k\mathrm {-1}}} {} y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},t \right) \frac{\textrm{2}^{\frac{k+1}{\textrm{2}}}}{\sqrt{\pi }}h_{m}\left( \textrm{2}^{k}t\mathrm {-2}n\mathrm {+1} \right) \textrm{d}t, \end{aligned}$$

Now, by repeating the above procedure and by changing the variable \(\textrm{2}^{k}t\mathrm {-2}n\mathrm {+1=}q,\) we obtain,

$$\begin{aligned} C_{i,j}= & {} \frac{2A}{\mathrm {(}\sqrt{\pi }\mathrm {)}^{\textrm{2}}}\int \limits _{\mathrm {-1}}^\textrm{1} {} y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},\frac{q\mathrm {-1+2}n}{\textrm{2}^{k}} \right) h_{m}\left( q \right) \frac{dq}{\textrm{2}^{k}},\\ C_{i,j}= & {} \frac{A\textrm{2}^{\mathrm {1-}k}}{\mathrm {(}\sqrt{\pi }\mathrm {)}^{\textrm{2}}}\int \limits _{\mathrm {-1}}^\textrm{1} {} y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},\frac{q\mathrm {-1+2}n}{\textrm{2}^{k}} \right) h_{m}\left( q \right) dq, \end{aligned}$$

Also, using the generalised mean value theorem for integrals,

$$\begin{aligned} C_{i,j}=\frac{A\textrm{2}^{\mathrm {1-}k}}{\mathrm {(}\sqrt{\pi }\mathrm {)}^{\textrm{2}}}y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},\frac{\eta \mathrm {-1+2}n}{\textrm{2}^{k}} \right) \int \limits _{\mathrm {-1}}^\textrm{1} {} h_{m}\left( q \right) dq{,}\,where\,\eta {\in }\left( \mathrm {-1,1} \right) , \end{aligned}$$

Since \(h_{m}\left( x \right) \) is continuous and integrable on \(\left( \mathrm {-1,1} \right) \), we choose \(\int \limits _{\mathrm {-1}}^\textrm{1} {} L_{m}\left( q \right) dq=B\), and this gives the following,

$$\begin{aligned} C_{i,j}=\frac{A{\textrm{B2}}^{\mathrm {1-}k}}{\mathrm {(}\sqrt{\pi }\mathrm {)}^{\textrm{2}}}y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},\frac{\eta \mathrm {-1+2}n}{\textrm{2}^{k}} \right) {,}where{}\eta ,\zeta {\in }\left( \mathrm {-1,1} \right) , \end{aligned}$$

Therefore,

$$\begin{aligned} \left| C_{i,j} \right| =\left| \frac{A{\textrm{B2}}^{\mathrm {1-}k}}{{\pi }} \right| \left| y\left( \frac{\zeta \mathrm {-1+2}n}{\textrm{2}^{k}},\frac{\eta \mathrm {-1+2}n}{\textrm{2}^{k}} \right) \right| \textrm{,}\,where\,\eta ,\zeta {\in }\left( \mathrm {-1,1} \right) , \end{aligned}$$

Since \(y\left( x,t \right) \) is bounded. That is, \(\left| y\left( x,t \right) \right| {\le }M\), where M is the real constant.

$$\begin{aligned} \left| C_{i,j} \right| =\left| \frac{A{\textrm{B2}}^{\mathrm {1-}k}}{{\pi }} \right| M=\frac{\left| A \right| \left| B \right| \textrm{2}M}{{\pi }\textrm{2}^{k}}\textrm{,} \end{aligned}$$

where M is any positive integer. Therefore, \(\sum \nolimits _{i=0}^{\infty } {} \sum \nolimits _{j=0}^{\infty } {} c_{i,j}\) is convergent. Hence, the Hermite wavelet expansion of \(y\left( x,t \right) \) is converged uniformly. \(\square \)

3 Functional integration matrix

The Hermite wavelet is a compactly supported, continuous, and orthogonal basis studied in [22]. At k \(=\) 1, the following Hermite wavelet bases were extracted:

$$\begin{aligned} \phi _{1,0} (x)= & {} \frac{2}{\sqrt{\pi }} \\ \phi _{1,1} (x)= & {} \frac{1}{\sqrt{\pi }}(8x-4) \\ \phi _{1,2} (x)= & {} \frac{1}{\sqrt{\pi }}(32x^{2}-32x+4) \\ \phi _{1,3} (x)= & {} \frac{1}{\sqrt{\pi }}(128x^{3}-192x^{2}+48x+8) \\ \phi _{1,4} (x)= & {} \frac{1}{\sqrt{\pi }}(512x^{4}-1024x^{3}+384x^{2}+128x-40) \\ \phi _{1,5} (x)= & {} \frac{1}{\sqrt{\pi }}(2048x^{5}-5120x^{4}+2560x^{3}+1280x^{2}-800x+16)\\ \phi _{1,6} (x)= & {} \frac{1}{\sqrt{\pi }}(8192x^{6}-24576x^{5}+15360x^{4}+10240x^{3}-9600x^{2}+384x+368)\\ \phi _{1,7} (x)= & {} \frac{1}{\sqrt{\pi }}(32768x^{7}-114688x^{6}+86016x^{5}\\{} & {} +71680x^{4}-89600x^{3}+5376x^{2}+10304x-928)\\ \phi _{1,8} (x)= & {} \frac{1}{\sqrt{\pi }}(131072x^{8}-524288x^{7}+458752x^{6}+458752x^{5}-716800x^{4} \\{} & {} +57344x^{3}+164864x^{2}-29696x-3296)\\ \phi _{1,9} (x)= & {} \frac{1}{\sqrt{\pi }}(524288x^{9}-2359296x^{8}+2359296x^{7}+2752512x^{6}-5160960x^{5}+516096x^{4}\\{} & {} +1978368x^{3}-534528x^{2}-118656x+21440)\\ \phi _{1,10} (x)= & {} \frac{1}{\sqrt{\pi }}(2097152x^{10}-10485760x^{9}+11796480x^{8}+15728640x^{7}-34406400x^{6} \\{} & {} +4128768x^{5}+19783680x^{4}-7127040x^{3}\\{} & {} -2373120x^{2}+857600x+16448)\\ \phi _{1,11} (x)= & {} \frac{1}{\sqrt{\pi }}(8388608x^{11}-46137344x^{10}+57671680x^{9}+86507520x^{8}-216268800x^{7}\\{} & {} +30277632x^{6}+174096384x^{5}-78397440x^{4}\\{} & {} -34805760x^{3}+18867200x^{2}+723712x-461696)\\ \phi _{1,12} (x)= & {} \frac{1}{\sqrt{\pi }}(33554432x^{12}-201326592x^{11}+276824064x^{10}\\{} & {} +461373440x^{9}-1297612800x^{8}+207618048x^{7}\\{} & {} +1392771072x^{6}-752615424x^{5}-417669120x^{4}\\{} & {} +301875200x^{3}+17369088x^{2}-22161408x+561536) \end{aligned}$$

where \(\phi _{9} (x)=[\phi _{1,0} (x),\phi _{1,1} (x),\phi _{1,2} (x),\,\phi _{1,3} (x),\,\phi _{1,4} (x),\,\phi _{1,5} (x),\,\phi _{1,6} (x),\phi _{1,7} (x),\phi _{1,8} (x)]^{T}\).

Integrate the aforementioned first nine basis concerning the x limit between 0 and x, and then express as a linear combination of Hermite wavelet basis as

$$\begin{aligned} \int \limits _0^x {\varphi _{1,0}\left( x \right) \textrm{d}x}= & {} \left[ {\begin{array}{*{20}c} \frac{1}{2} &{} \frac{1}{4} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,1}\left( x \right) \textrm{d}x}= & {} \left[ {\begin{array}{*{20}c} \frac{-1}{4} &{} 0 &{} \frac{1}{8} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,2}(x)} \textrm{d}x= & {} \left[ {\begin{array}{*{20}c} \frac{-1}{3} &{} 0 &{} 0 &{} \frac{1}{12} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,3}(x)} \textrm{d}x= & {} \left[ {\begin{array}{*{20}c} \frac{5}{4} &{} 0 &{} 0 &{} 0 &{} \frac{1}{16} &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,4}(x)} \textrm{d}= & {} \left[ {\begin{array}{*{20}c} \frac{-2}{5} &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{20} &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,5}\left( x \right) \textrm{d}x}= & {} \left[ {\begin{array}{*{20}c} \frac{-23}{3} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{24} &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,6}(x)} \textrm{d}x= & {} \left[ {\begin{array}{*{20}c} \frac{116}{7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{28} &{} 0\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,7}(x)} \textrm{d}x= & {} \left[ {\begin{array}{*{20}c} \frac{103}{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{32}\\ \end{array} } \right] \varphi _{9}(x)\\ \int \limits _0^x {\varphi _{1,8}\left( x \right) \textrm{d}x}= & {} \left[ {\begin{array}{*{20}c} \frac{-2680}{9} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{array} } \right] \varphi _{9}(x)+\frac{1}{36}\varphi _{1,9}(x). \end{aligned}$$

Hence,

$$\begin{aligned} \int \limits _0^x {\,\phi (x)} \,\textrm{d}x=H_{9\times 9} \,\,\phi _{9} (x)+\,\,\bar{{\phi }}_{9} (x) \end{aligned}$$

where

$$\begin{aligned} H_{9\times 9}= & {} \left[ {{\begin{array}{*{20}c} {{1 \over 2}} &{} {{1 \over 4}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-1} \over 4}} &{} 0 &{} {{1 \over 8}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-1} \over 3}} &{} 0 &{} 0 &{} {{1 \over {12}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{5 \over 4}} &{} 0 &{} 0 &{} 0 &{} {{1 \over {16}}} &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-2} \over 5}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {20}}} &{} 0 &{} 0 &{} 0 \\ {{{-23} \over 3}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {24}}} &{} 0 &{} 0 \\ {{{116} \over 7}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {28}}} &{} 0 \\ {{{103} \over 2}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {32}}} \\ {{{-2680} \over 9}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\,\overline{\phi _{9} } (x)=\left[ {{\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\frac{1}{36}\phi _{1,9} (x)} \\ \end{array} }} \right] _{{.}} \end{aligned}$$

Then, the above-mentioned nine basis are twice integrated as shown below.

$$\begin{aligned} \int \limits _0^x {\int \limits _0^x {\phi _{1,0} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{3}{16}} &{} {\frac{1}{8}} &{} {\frac{1}{32}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,1} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{-1}{6}} &{} {\frac{-1}{16}} &{} 0 &{} {\frac{1}{96}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,2} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{-1}{16}} &{} {\frac{-1}{12}} &{} 0 &{} 0 &{} {\frac{1}{192}} &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,3} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{3}{5}} &{} {\frac{5}{16}} &{} 0 &{} 0 &{} 0 &{} {\frac{1}{320}} &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,4} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{-7}{12}} &{} {\frac{-1}{10}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {\frac{1}{480}} &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,5} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{-22}{7}} &{} {\frac{-23}{12}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {\frac{1}{672}} &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,6} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{81}{8}} &{} {\frac{29}{7}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {\frac{1}{896}} \\ \end{array} }} \right] \,\phi _{9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,7} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{148}{9}} &{} {\frac{103}{8}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)+\frac{1}{1152}\phi _{1,9} (x)\\ \int \limits _0^x {\int \limits _0^x {\phi _{1,8} (x)} \,\textrm{d}x\textrm{d}x}= & {} \left[ {{\begin{array}{*{20}c} {\frac{-773}{5}} &{} {\frac{-670}{9}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] \,\phi _{9} (x)+\frac{1}{1440}\phi _{1,10} (x). \end{aligned}$$

Hence,

$$\begin{aligned} \int \limits _0^x {\int \limits _0^x {\,\phi (x)} \,\textrm{d}x} \textrm{d}x={H}'_{9\times 9} \,\,\phi _{9} (x)+\,\,{\bar{{\phi }}}'_{9} (x) \end{aligned}$$

where,

$$\begin{aligned} {H}'_{9\times 9} =\left[ {{\begin{array}{*{20}c} {{3 \over {16}}} &{} {{1 \over 8}} &{} {{1 \over {32}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-1} \over 6}} &{} {{{-1} \over {16}}} &{} 0 &{} {{1 \over {96}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-1} \over {16}}} &{} {{{-1} \over {12}}} &{} 0 &{} 0 &{} {{1 \over {192}}} &{} 0 &{} 0 &{} 0 &{} 0 \\ {{3 \over 5}} &{} {{5 \over {16}}} &{} 0 &{} 0 &{} 0 &{} {{1 \over {320}}} &{} 0 &{} 0 &{} 0 \\ {{{-7} \over {12}}} &{} {{{-1} \over {10}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {480}}} &{} 0 &{} 0 \\ {{{-22} \over 7}} &{} {{{-23} \over {12}}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {672}}} &{} 0 \\ {{{81} \over 8}} &{} {{{29} \over 7}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {{1 \over {896}}} \\ {{{148} \over 9}} &{} {{{103} \over 8}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ {{{-773} \over 5}} &{} {{{-670} \over 9}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} }} \right] ,\,\,\overline{{\phi }'_{9} } (x)=\left[ {{\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {\frac{1}{1152}\phi _{1,9} (x)} \\ {\frac{1}{1440}\phi _{1,10} (x)} \\ \end{array} }} \right] . \end{aligned}$$

Similarly, we can generate matrices for our suitability.

4 Method of Solution

The collocation approach is used in this section along with the wavelet’s functional matrix to solve the fractional partial differential equations defined in Eq. (1.1).

Assume that,

$$\begin{aligned} \frac{\partial ^{3}y(x,t)}{{\partial x}^{2}\partial t}={\phi (t)}^{T}K\phi (x) \end{aligned}$$
(4.1)

where

$$\begin{aligned} \phi ^{T}\left( t \right)= & {} \left[ \phi _{1,0}\left( t \right) ,\ldots ,\phi _{1,M-1}\left( t \right) ,\phi _{2,0}\left( t \right) ,\ldots ,\phi _{2,M-1}\left( t \right) ,{\ldots ,\phi }_{2^{k-1},M-1}\left( t \right) \right] ,\\ \phi \left( x \right)= & {} \left[ \phi _{1,0}\left( x \right) ,\ldots ,\phi _{1,M-1}\left( x \right) ,\phi _{2,0}\left( x \right) ,\ldots ,\phi _{2,M-1}\left( x \right) ,{\ldots ,\phi }_{2^{k-1},M-1}\left( x \right) \right] ^{T}, \end{aligned}$$

\(K=\left[ a_{pq} \right] _{n\times n}\), where \(a_{pq}\) stands for undetermined coefficients that need to be determined and \({n=2}^{k-1}M.\)

Integrating Eq. (4.1) concerning t from 0 to t now yields

$$\begin{aligned} \frac{\partial ^{2}y(x,t)}{{\partial x}^{2}}= & {} \frac{\partial ^{2}y(x,0)}{{\partial x}^{2}}+\int \limits _0^t {{\phi (t)}^{T}K\phi (x)} \textrm{d}t,\nonumber \\ \frac{\partial ^{2}y(x,t)}{{\partial x}^{2}}= & {} \frac{\partial ^{2}y(x,0)}{{\partial x}^{2}}+\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\phi \left( x \right) . \end{aligned}$$
(4.2)

Integrating Eq. (4.2) concerning x from 0 to x,

$$\begin{aligned} \frac{\partial y(x,t)}{\partial x}= & {} \frac{\partial y(0,t)}{\partial x}+\frac{\partial y(x,0)}{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x}+\int \limits _0^x {\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\phi \left( x \right) } \textrm{d}x\nonumber \\ \frac{\partial y(x,t)}{\partial x}= & {} \frac{\partial y(0,t)}{\partial x}+\frac{\partial y(x,0)}{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x}+\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H_{n\times n}\phi \left( x \right) +\bar{\phi }(x) \right] . \end{aligned}$$
(4.3)

Integrating Eq. (4.3) concerning x from 0 to x,

$$\begin{aligned} y\left( x,t \right)= & {} y\left( 0,t \right) +y\left( x,0 \right) -y\left( 0,0 \right) +x\left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right] \nonumber \\{} & {} +\int \limits _0^x \left[ \left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H_{n\times n}\phi \left( x \right) +\bar{\phi }(x) \right] \right] \textrm{d}x\nonumber \\ y\left( x,t \right)= & {} y\left( 0,t \right) +y\left( x,0 \right) -y\left( 0,0 \right) +x\left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right] \nonumber \\{} & {} +\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(4.4)

Put \(x=\beta \) in the above equation,

$$\begin{aligned} y\left( \beta ,t \right)= & {} y\left( 0,t \right) +y\left( \beta ,0 \right) -y\left( 0,0 \right) +\beta \left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right] \nonumber \\{} & {} +\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }.\nonumber \\ \left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right]= & {} \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) -y\left( \beta ,0 \right) +y\left( 0,0 \right) \right] \nonumber \\{} & {} -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \end{aligned}$$
(4.5)

Substituting Eq. (4.5) in (4.4), we get,

$$\begin{aligned} y\left( x,t \right)= & {} y\left( 0,t \right) +y\left( x,0 \right) -y\left( 0,0 \right) \nonumber \\{} & {} +x\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) -y\left( \beta ,0 \right) +y\left( 0,0 \right) \right] \right. \nonumber \\{} & {} \left. -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \nonumber \\{} & {} +\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(4.6)

By twice differentiating Eq. (4.6) concerning t, we obtain

$$\begin{aligned} \frac{\partial y(x,t)}{\partial t}= & {} \frac{\partial y(0,t)}{\partial t}+x\frac{\textrm{d}}{\textrm{d}t}\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) \right] -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }\left( t \right) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \nonumber \\{} & {} +\frac{\textrm{d}}{\textrm{d}t}\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] .\end{aligned}$$
(4.7)
$$\begin{aligned} \frac{\partial ^{2}y(x,t)}{{\partial t}^{2}}= & {} \frac{\partial ^{2}y(0,t)}{{\partial t}^{2}}+x\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) \right] -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }\left( t \right) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \nonumber \\{} & {} +\frac{\textrm{d}{2}}{\textrm{d}t^{2}}\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(4.8)

Substituting Eqs. (4.8), (4.6), and (4.2) in Eq. (1.1) assuming \(\delta =2=\alpha ,\) we get,

$$\begin{aligned}{} & {} \left[ \frac{\partial ^{2}y\left( 0,t \right) }{{\partial t}^{2}}+x\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) \right] -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \right. \\{} & {} \quad \left. +\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \right] \\{} & {} \quad =\left[ \frac{\partial ^{2}y(x,0)}{{\partial x}^{2}}+\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\phi \left( x \right) \right] \\{} & {} \qquad \quad +F\left[ t,x,\left( y\left( 0,t \right) +y\left( x,0 \right) -y\left( 0,0 \right) +x\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) -y\left( \beta ,0 \right) +y\left( 0,0 \right) \right] \right. \right. \right. \\{} & {} \quad \qquad \left. \left. \left. -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \right. \right. \\{} & {} \quad \qquad \left. \left. +\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \right) ,\right. \\{} & {} \quad \qquad \left. \left( \frac{\partial y(0,t)}{\partial t}+x\frac{d}{\textrm{d}t}\left[ \frac{1}{\beta }\left[ y\left( \beta ,t \right) -y\left( 0,t \right) \right] \right. \right. \right. \\{} & {} \quad \left. \left. \left. -\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }\left( t \right) \right] ^{T}K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \right. \right. \\{} & {} \qquad \quad \left. \left. +\frac{\textrm{d}}{\textrm{d}t}\left[ H_{n\times n}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T} \right. \right. \\{} & {} \qquad \quad \left. \left. K\left[ H^{'}_{n\times n}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \right) \right] \end{aligned}$$

Collocate the aforementioned equation by the collocation points \(x_{i}=t_{i}=\frac{2i-1}{2n^{2}},i=1,2,\ldots ,n^{2}\) and then use suitable solvers to resolve this system to provide Hermite wavelet coefficients. By substituting these coefficients in (4.6), we get a numerical solution of (1.1).

For the fractional order: differentiate Eq. (4.6) concerning t and x of order \(\delta \in (0,1)\) and \(\alpha \in (0,1)\), respectively. Then substitute \(\frac{{\partial }^{2\delta }\mathrm {y(x,t)}}{{{\partial \textrm{t}}}^{\textrm{2}\delta }},\frac{{\partial }^{\textrm{2}\alpha }\mathrm {y(x,t)}}{{{\partial \textrm{x}}} ^{\textrm{2}\alpha }}\), \(y\left( x,t \right) \) and \(\frac{\partial y(x,t)}{\partial x}\) in Eq. (1.1) and collocate the obtained equation using the following collocation points \(x_{i}=t_{i}=\frac{2i-1}{2n^{2}},i=1,2,\ldots ,n^{2}\). Then consider this obtained system of algebraic equations by Newton’s Raphson method to get the Hermite wavelet coefficients. By substituting these coefficients in (4.6), we get a numerical solution of (1.1) for the fractional order.

5 Applications

Example 1

Consider the Telegraph FPDEs [6]:

$$\begin{aligned} \frac{\partial ^{2\delta }y}{{\partial x}^{2\delta }}-\frac{\partial ^{2\alpha }y}{{\partial t}^{2\alpha }}-\frac{\partial ^{\alpha }y}{{\partial t}^{\alpha }}-y+\left( \frac{x^{\delta }}{\delta } \right) ^{2}+\left( \frac{t^{\alpha }}{\alpha } \right) =1, \end{aligned}$$
(5.0)

With conditions,

$$\begin{aligned} y\left( x,0 \right) =x^{2},y\left( 0,t \right) =t,\,and\,y\left( 1,t \right) =1+t. \end{aligned}$$

For this problem \(y\left( x,t \right) =x^{2}+t\) is the exact solution at \(\delta =\alpha =1\). Using the proposed method described in Section 4 at \(n=3\), we were able to solve this problem and obtained a Hermite wavelet numerical solution that is the same as the exact solution. A visual representation of the solution obtained by the HWM is drawn in Fig. 1. HWM solution at distinct values of \(\delta \) and \(\alpha \) is shown in Fig. 2. Figures 3 and 4 represent the HWM solution for various fractional values at \(x=1\,and\,t=1\), respectively. Table 1 represents the absolute error of the ND solver and HWM with the exact solution. Table 1 shows the accuracy of HWM, and it is better than the ND solver solution in Mathematica.

Fig. 1
figure 1

Geometrical interpretation of HWM solution and its AE

Full size image
Fig. 2
figure 2

Plot of HWM solution at \(\delta =1,\,\alpha =0.2,0.4,0.6\) and \(\alpha =1,\,\delta =0.2,0.4,0.6.\)

Full size image
Fig. 3
figure 3

Plot of HWM solution at \(\delta =1,\, x=1,\) and various values of \(\alpha \)

Full size image
Fig. 4
figure 4

Plot of HWM at \(\alpha =1,\, t=1,\) and distinct values of \(\delta \)

Full size image

Numerical implementation:

Assume that,

$$\begin{aligned} \frac{\partial ^{3}y(x,t)}{{\partial x}^{2}\partial t}={\phi (t)}^{T}K\phi (x) \end{aligned}$$
(5.1)

where

$$\begin{aligned} \phi ^{T}\left( t \right) =\left[ \phi _{1,0}\left( t \right) {,\phi }_{1,1}(t),\phi _{1,2}\left( t \right) \right] , \phi \left( x \right) =\left[ \phi _{1,0}\left( x \right) {,\phi }_{1,1}(x),\phi _{1,2}\left( x \right) \right] ^{T}, \text {and}\, K=\left[ a_{pq} \right] _{3\times 3}, \end{aligned}$$

Using Eq. (5.1) to integrate the data for t from 0 to t, we obtain

$$\begin{aligned} \frac{\partial ^{2}y(x,t)}{{\partial x}^{2}}=\frac{\partial ^{2}y(x,0)}{{\partial x}^{2}}+\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\phi \left( x \right) . \end{aligned}$$
(5.2)

Integrating Eq. (5.2) concerning x from 0 to x,

$$\begin{aligned} \frac{\partial y(x,t)}{\partial x}=\frac{\partial y(0,t)}{\partial x}+\frac{\partial y(x,0)}{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x}+\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H_{3\times 3}\phi \left( x \right) +\bar{\phi }(x) \right] . \end{aligned}$$
(5.3)

Integrating Eq. (5.3) concerning x from 0 to x,

$$\begin{aligned} y\left( x,t \right)= & {} y\left( 0,t \right) +y\left( x,0 \right) -y\left( 0,0 \right) +x\left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right] \nonumber \\{} & {} +\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(5.4)

Put \(x=1\) in the above equation,

$$\begin{aligned} \left[ \frac{\partial y\left( 0,t \right) }{\partial x}-\frac{\partial y\left( 0,0 \right) }{\partial x} \right]= & {} \left[ y\left( 1,t \right) -y\left( 0,t \right) -y\left( 1,0 \right) +y\left( 0,0 \right) \right] \nonumber \\{} & {} -\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=1}. \end{aligned}$$
(5.5)
Table 1 The AE of the HWM at n = 3 and ND solver with the exact solution
Full size table

Substituting Eq. (5.5) in (5.4), we get,

$$\begin{aligned} y\left( x,t \right)= & {} t+x^{2}+x\left[ -\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=1} \right] \nonumber \\{} & {} +\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(5.6)

Differentiating Eq. (5.6) twice concerning t, we get

$$\begin{aligned} \frac{\partial y\left( x,t \right) }{\partial t}= & {} 1+x\frac{\textrm{d}}{\textrm{d}t}\left[ -\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }\left( t \right) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \nonumber \\{} & {} +\frac{\textrm{d}}{\textrm{d}t}\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(5.7)
$$\begin{aligned} \frac{\partial ^{2}y\left( x,t \right) }{{\partial t}^{2}}= & {} x\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}\left[ -\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }\left( t \right) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] \vert _{x=\beta }. \right] \nonumber \\{} & {} +\frac{\textrm{d}^{2}}{\textrm{d}t^{2}}\left[ H_{3\times 3}\phi \left( t \right) +\bar{\phi }(t) \right] ^{T}K\left[ H^{'}_{3\times 3}\phi \left( x \right) +\bar{\phi ^{'}}\left( x \right) \right] . \end{aligned}$$
(5.8)

Substituting Eqs. (5.8), (5.7), (5.6), and (5.2) in Eq. (5.0) and collocating with the grid points mentioned below,

$$\begin{aligned} x_{i}=t_{i}=\frac{2i-1}{18},i=1,2,\ldots ,9, \end{aligned}$$
Fig. 5
figure 5

Visual representation of HWM solution with its AE

Full size image
Fig. 6
figure 6

HWM solution at \(\delta =1,\,\alpha =0.2,0.4,0.6\) and \({\alpha =1,\,\delta =0.2,0.4,0.6.}\)

Full size image
Fig. 7
figure 7

HWM solution at \({\alpha =1,\,t=1,}\) and different values of \({\delta }\)

Full size image
Fig. 8
figure 8

Numerical solution by HWM at \({\delta =1,\, x=1,}\) and different values of \( {\alpha }\)

Full size image

then we get the following system,

$$\begin{aligned}{} & {} \mathrm {0.0686}\textrm{a}_{\textrm{11}}\mathrm {-0.1377}\textrm{a}_{\textrm{12}} \mathrm {-0.1379}\textrm{a}_{\textrm{13}}\mathrm {-0.1217}\textrm{a}_{\textrm{21}} \mathrm {+0.2455}\textrm{a}_{\textrm{22}}\\{} & {} \quad \mathrm {+0.2402}\textrm{a}_{\textrm{23}} \mathrm {-0.1961}\textrm{a}_{\textrm{31}}\mathrm {+0.3889}\textrm{a}_{\textrm{32}} \mathrm {+0.4103}\textrm{a}_{\textrm{33}}=0\\{} & {} 0.1915\textrm{a}_{\textrm{11}} -0.3959\textrm{a}_{\textrm{12}}-0.4032 \textrm{a}_{\textrm{13}}-0.2462\textrm{a}_{\textrm{21}} +0.5466\textrm{a}_{\textrm{22}}+0.4164\textrm{a}_{\textrm{23}}\\{} & {} \quad -0.8379\textrm{a}_{\textrm{31}} +1.6122\textrm{a}_{\textrm{32}}+2.0863\textrm{a}_{\textrm{33}}=0\\{} & {} 0.2909\textrm{a}_{\textrm{11}}-0.6439\textrm{a}_{\textrm{12}} -0.6905\textrm{a}_{\textrm{13}}-0.2120\textrm{a}_{\textrm{21}}\\{} & {} \quad +0.6710\textrm{a}_{\textrm{22}}+0.1269\textrm{a}_{\textrm{23}} -1.6370\textrm{a}_{\textrm{31}}+3.0976\textrm{a}_{\textrm{32}} +4.8687\textrm{a}_{\textrm{33}}=0\\{} & {} 0.3614\textrm{a}_{\textrm{11}}-0.9017\textrm{a}_{\textrm{12}} -1.0692\textrm{a}_{\textrm{13}}-0.0219\textrm{a}_{\textrm{21}} +0.7083\textrm{a}_{\textrm{22}}\\{} & {} \quad -0.6262\textrm{a}_{\textrm{23}} -2.3822\textrm{a}_{\textrm{31}}+4.6001\textrm{a}_{\textrm{32}} +8.4683\textrm{a}_{\textrm{33}}=0\\{} & {} 0.3978\textrm{a}_{\textrm{11}}-1.1936\textrm{a}_{\textrm{12}} -1.6446\textrm{a}_{\textrm{13}}+0.3183\textrm{a}_{\textrm{21}} +0.7427\textrm{a}_{\textrm{22}}\\{} & {} \quad -1.7683\textrm{a}_{\textrm{23}} -2.8647\textrm{a}_{\textrm{31}}+6.0478\textrm{a}_{\textrm{32}} +12.5201\textrm{a}_{\textrm{33}}=0\\{} & {} 0.3950\textrm{a}_{\textrm{11}}-1.5488\textrm{a}_{\textrm{12}} -2.5646\textrm{a}_{\textrm{13}}+0.7997\textrm{a}_{\textrm{21}} +0.8494\textrm{a}_{\textrm{22}}\\{} & {} \quad -3.1699\textrm{a}_{\textrm{23}} -2.8817\textrm{a}_{\textrm{31}}+7.5347\textrm{a}_{\textrm{32}} +16.7988\textrm{a}_{\textrm{33}}=0\\{} & {} 0.3476\textrm{a}_{\textrm{11}}-2.0010\textrm{a}_{\textrm{12}} -4.0272\textrm{a}_{\textrm{13}}+1.4104\textrm{a}_{\textrm{21}} +1.0912\textrm{a}_{\textrm{22}}\\{} & {} \quad -4.6713\textrm{a}_{\textrm{23}} -2.2396\textrm{a}_{\textrm{31}}+9.3091\textrm{a}_{\textrm{32}} +21.4058\textrm{a}_{\textrm{33}}=0\\{} & {} 0.2505\textrm{a}_{\textrm{11}}-2.5887\textrm{a}_{\textrm{12}} -6.2865\textrm{a}_{\textrm{13}}+2.1351\textrm{a}_{\textrm{21}} +1.5151\textrm{a}_{\textrm{22}}\\{} & {} \quad -6.1139\textrm{a}_{\textrm{23}} -0.7575\textrm{a}_{\textrm{31}}+11.7579\textrm{a}_{\textrm{32}} +26.9210\textrm{a}_{\textrm{33}}=0\\{} & {} 0.0983\textrm{a}_{\textrm{11}}-3.3549\textrm{a}_{\textrm{12}}-9.6603 \textrm{a}_{\textrm{13}}+2.9556\textrm{a}_{\textrm{21}} +2.1486\textrm{a}_{\textrm{22}}\\{} & {} \quad -7.3761\textrm{a}_{\textrm{23}} +1.7290\textrm{a}_{\textrm{31}}+15.3856\textrm{a}_{\textrm{32}} +34.5067\textrm{a}_{\textrm{33}}=0 \end{aligned}$$

The following are the Hermite wavelet coefficients obtained after solving the aforementioned system using Newton’s Raphson method:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} a_{11}=0\\ a_{12}=0\\ a_{13}=0\\ \end{array} }\\ {\begin{array}{*{20}c} a_{21}=0\\ a_{22}=0\\ a_{23}=0\\ \end{array} }\\ {\begin{array}{*{20}c} a_{31}=0\\ a_{32}=0\\ a_{33}=0\\ \end{array} }\\ \end{array} } \right] \end{aligned}$$

then substitute these values in Eq. (5.6), we get a numerical solution of Eq. (5.0) as \(y\left( x,t \right) =x^{2}+t.\)

Table 2 The AE of the HWM at n=3 with the exact solution
Full size table
Table 3 The AE of the HWM solution at n=3 with the exact solution
Full size table
Table 4 The AE of the ND solver with the exact solution
Full size table
Table 5 The AE of the ND solver with the exact solution
Full size table

Example 2

Consider the Telegraph FPDEs [6]:

$$\begin{aligned} \frac{\partial ^{2\alpha }y}{{\partial t}^{2\alpha }}-\frac{\partial ^{2\delta }y}{{\partial x}^{2\delta }}-2t\frac{\partial ^{\alpha }y}{{\partial t}^{\alpha }}+y=0, \end{aligned}$$

With conditions,

$$\begin{aligned} y\left( x,0 \right) =0,y\left( 0,t \right) =t^{2},\,and\,y\left( 1,t \right) =e^{1}t^{2}. \end{aligned}$$
Fig. 9
figure 9

HWM solution represented graphically together with its absolute error

Full size image
Fig. 10
figure 10

Visual representation of solution by HWM at \(\delta =1,\,\alpha =0.2,0.4,0.6\) and \({\alpha =1,\, \delta =0.2,0.4,0.6.}\)

Full size image
Fig. 11
figure 11

Numerical solution by HWM at \({\delta =1,\, x=1/2,}\) and different values of \({\alpha .}\)

Full size image
Fig. 12
figure 12

Plot of the solution by HWM at \({\alpha =1,\, t=1,}\) at different values of \({\delta .}\)

Full size image
Table 6 The AE of the HWM at n=3 with the exact solution
Full size table
Table 7 The AE of the HWM solution at n=3 with the exact solution
Full size table
Table 8 The AE of the ND solver with the exact solution
Full size table
Table 9 The AE of the ND solver with the exact solution
Full size table

For this problem \(y\left( x,t \right) =e^{x}t^{2}\) is the exact solution at \(\delta =\alpha =1\). Using the method described in Section 4 at \(n=3\), we were able to solve this problem and obtained a Hermite wavelet numerical solution tabulated in the tables and graphs. A visual representation of the solution obtained by the HWM is drawn in Fig. 5. HWM solution at distinct values of \(\delta \) and \(\alpha \) is shown in Fig. 6. Figures 7 and 8 represent the HWM solution for numerous fractional values at \(x=1\,and\,t=1\), respectively. Tables 2 and 3 show the absolute error of the HWM solution with the exact solution for different values of x and t. Tables 4 and 5 show the absolute error of the ND solver solution obtained by Mathematica with the exact solution for different values of x and t. From Tables 2, 3, 4 and 5, we can see that HWM is better than ND solver in terms of accuracy in the solution.

Example 3

The fractional PDE is of the form [6]:

$$\begin{aligned} \frac{\partial ^{2\delta }y}{{\partial x}^{2\delta }}-\frac{\partial ^{2\alpha }y}{{\partial t}^{2\alpha }}=sin\left( \frac{\pi x^{\delta }}{\delta } \right) ,\end{aligned}$$

With the following constraints,

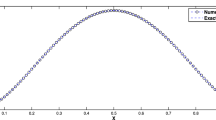
$$\begin{aligned} y\left( x,0 \right) =0,y\left( 0,t \right) =0,\,and\,y\left( 1,t \right) =0. \end{aligned}$$

The exact solution is \(y\left( x,t \right) =\frac{sin\left( \pi x \right) }{\pi ^{2}}\left[ cos\left( \pi t \right) -1 \right] \) at \(\delta =\alpha =1\). We solved this problem by the current approach at \(n=3,9,\) and obtained an HMT numerical solution. Figure 9 illustrates the geometrical interpretation of the HWM solution and its absolute error in comparison with the actual solution for various values of n. The numerical solution by HWM for various values of \(\delta \) and \(\alpha \) is shown in Fig. 10. Figures 11 and 12 represent the HWM solution for various fractional values at \(x=\frac{1}{2}\) and \(t=1\), respectively.

6 Conclusion

This article established an innovative technique for FPDEs through the functional matrix of Hermite wavelets. By using discrete grid points, this method converts a given FPDE into a set of algebraic equations. We solved three examples by HWM. Tables and graphs are used to discuss the results, together with the exact solution. This study shows that HWM is easy to use, produces superior results, and takes considerably less time. As the matrix size rises, the accuracy of the solution likewise improves, as seen in Fig. 9. From the figures and tables above, we infer that the numerical solutions achieved by the developed methodology are closer to the exact solution and require less CPU time than the current methods. It is important to note that the developed strategy minimises the amount of computational work compared to the existing techniques while upholding excellent accuracy of numerical results. Therefore, the suggested scheme (HWM) effectively solves FPDEs. Some theorems are discussed with proof of convergence analysis. Tables 1–9 reveal that the proposed technique is better than the ND solver in Mathematica.