Stabilization of Semi-Markovian Jumping Uncertain Complex-Valued Networks with Time-Varying Delay: A Sliding-Mode Control Approach

Abstract

This paper pays close attention to the stabilization issue for delayed uncertain semi-Markovian jumping complex-valued networks via sliding mode control. The concerned corresponding transition rates depend on a positive constant, i.e., sojourn-time, which is not required to obey the general exponential distribution. Combine the generalized Dynkin’s formula with Lyapunov stability theory as well as the characteristics of cumulative distribution functions, a few sufficient criteria are proposed to ascertain the stochastic stability of the obtained sliding mode dynamical system. In addition, design a novel sliding mode controller to ensure all state trajectories of the potential closed-loop system can reach the synthesized sliding mode switching surface in a finite time and maintain there in the subsequent time. In the end of paper, one simple example is presented to verify superiority and feasibility of the provided controller design scheme.

1 Introduction

Over the last couple of years, complex-valued networks (CVNs) have drawn extensive attention devoted to their widespread and potential applications which mainly include image processing, quantum waves, radar acquisition, associative memory, ultrasonic and combinatorial optimization [1,2,3,4]. In particular, most of the existed works focus on the dynamical performances of CVNs, most of all, the stability should be considered [5, 6]. It is well known that stability is one of the most important and interesting phenomenon mostly because it can preferably explain many natural phenomena [7]. Therefore, in general it is urgent, both theoretically and practically to investigate the issue of stability/stabilization for the considered CVNs.

It is worth noticing that, in hardware implementation, time delay inevitably occurs when neuron transmits information [8] and always arises quite naturally in propagation phenomena, population dynamics or engineering systems such as chemical processes, long transmission lines in pneumatic systems, etc. On another front, in the hardware implementation of the neural networks and the multiagent systems, due to the communication times and the limited speed of the the amplifiers, time delays are ubiquitous/unavoidable in the transmission process of the neuron information. Existence of the time delays may result in poor performances such as instability, oscillation, divergence or other undesired dynamic behaviours such as bifurcation and chaos. On the other hand, the time delay can also improve convergence speed and shorten stability time of delayed systems. Sometimes, the involved delay may induce an unstable system to be stable. Based on this visual angle, it is practical to take time delay account into CVNs. In terms of this view, the stability and control problems of delayed neural networks and multiagent systems have been significant themes. Up to now, a good deal of relevant and significative results have been proposed in this area. With the aid of delay decomposition technology, for stochastic neural networks with finite/infinite distributed delays, the issue of global asymptotic stability has been discussed in [9]. For the uncertain Markov-type sensor networks with mode-dependent distributed delays the issue of distributed state estimation has been studied in [10]. For second-order multi-agent systems with intentionally induced delay, it can draw a conclusion that the intentional delay can sometimes benefit and promote the consensus of the considered system in [11]. For the second-order multiagent systems under network topologies with time delay, the consensus issue has also been considered in [12]. For the first-order multiagent systems under the network topology with a directed spanning tree, design a distributed PID controller with time delay to analyze the consensus issue in [13].

In the real world, signals transmitted between subsystem of CVNs are unavoidably subject to stochastic perturbations and parameter uncertainty due mainly to the environment changes, that is to say, they can been regarded as stochastic systems to depict practical situations. Recently, a great many of researchers model this phenomenon by a Markovian switching mechanism, which means that the networks switch from one mode to another one at different time. Up to now, all kinds of related results on stability and synchronization have stirred research interests [14,15,16]. It is worth pointing out that all of above-listed references assume the concerned sojourn-time is governed by the general exponential distribution. In other words, the transition rates are usually constants, which means that the jump speed is independent of the past information of the Markov process. Furthermore, network mode always keeps the memoryless restriction, which is independent on the called sojourn-time. Meanwhile, Markovian switching systems have been widely applied in engineering fields, such as The Multiple-Mode Vertical Take-Off Landing Helicopter [17] and The Automotive Electronic Throttle Body [18]. The class of multiple-mode vertical take-off landing helicopters are representative Markovian switching systems. At each time instant, the variation of the airspeed is switched according to four velocities of operations: the horizontal velocity, the vertical velocity, the pitch rate, and the pitch angle. These four operation modes are characterized by a Markov chain. In addition, for the automotive electronic throttle body, the power amplifier module is adapted to produce power failures, and consequently, the voltage fluctuations commonly exit. At each time instant, a power failure is activated (or deactivated) according to four distinct modes of operations: normal, soft failure, intermediate failure, and hard failure. These four operation modes are driven by a Markov chain. As a result, this kind of constraint is unsuitable to describe realistic applications. Such as, for fault-tolerant control systems, the bathtub curve is generally utilized to characterize this kind transition rate function, which includes decreasing part, constant part, and increasing part [19]. Such situation cannot be directly modeled by general Markovian switching systems. Faced with this situation, many scholars have adopted the semi-Markovian switching systems to characterize that. For semi-Markovian switching systems, the considered transition rate is usually time-varying instead of a constant. It should be pointed out that the involved sojourn-time is usually a random variable, which is governed by a more general non-exponential distribution, such as Weibull distribution, Laplace distribution, Phase distribution. Not only can it significantly reflect the sojourn-time dependent property of transition rate matrix, but also widely expands the scope of its application. Meanwhile, for semi-Markovian switching systems, the practical engineering example can be The Operational Amplifier Circuit [20]. For the operational amplifier circuit with a switching positive temperature coefficient thermistor, which includes two operation modes: low resistance and high resistance, these two operation modes are modeled by a finite-mode semi-Markov chain. In view of this point, the Markovian switching system is a special case of semi-Markovian switching system, compared with general Markovian switching systems, it possesses much extensive significance [21,22,23,24]. So far, the relevant achievements on dynamical analysis of semi-Markovian switching neural networks are relatively not enough [25,26,27,28]. Considering the issue of the stabilization for delayed uncertain semi-Markovian switching CVNs, it still remains as a research issue worthy of exploring. Such a situation motivates our present research.

On another research forefront, sliding mode control is usually regarded as an effective robust control scheme in the control field because of it owns various advantages, such as eliminating external disturbances, modeling uncertainties satisfying the given conditions and reducing of the order of the state equation [29, 30]. In terms of sliding mode control, the main procedure is to determine a switching surface accord with the pre-designed specifications. Then, with the aid of the designed controller, the state trajectories of considered systems can effectively reach on the proposed sliding mode surface. Meanwhile, the obtained sliding mode amics will lose sensitivity to parameter variations [31, 32]. Recently, a lot of related achievement have been carried out [33,34,35]. Moreover, it should be pointed out that, for most practical switching systems, they are not limited by the memoryless restriction, which means that the dynamical behaviors of these kinds of systems depend on the past information. With that in mind, it is urgent to exploit the dynamical potentialities for semi-Markovian switching systems, which greatly relaxes the memoryless characteristic of the Markovian switching systems. According to the authors’ knowledge, few relevant achievements to report this kind problem [37, 38]. Unfortunately, the results they have proposed are not perfect. For such reasons, under the proposed sliding mode control scheme, this paper shortens such a gap and addresses the issue of stabilization for delayed uncertain semi-Markovian switching CVNs.

Through the above analysis and motivations, this paper will tackle the issue of stabilization for delayed uncertain semi-Markovian switching CVNs by a sliding mode approach. To achieve preconcerted performance, an integral sliding surface is firstly designed. Next, combine with semi-Markovian Lyapunov function, some stability criteria are firstly achieved for the sliding mode dynamical CVNs. Finally, construct a novel control law to let the state trajectories of considered systems reach on the pre-specified sliding mode surface and maintain there in the subsequent time. In comparing with existing literatures, the main highlights can be presented as the following four points: (1): This paper effectually extends and modifies the existed works on the stabilization problem for delayed uncertain semi-Markovian switching CVNs by resorting to the sliding-mode control. (2): Design a more general sliding motion control law to let state trajectories reach the given pre-specified sliding mode surface in finite time and maintain there in the subsequent time. (3): By resorting to the stochastic analysis, Lyapunov stability theory and matrix inequality technology, sufficient delay/mode dependent criteria will be shown to assure the considered system is stochastically stable. (4): Propose an appropriate integral sliding mode surface to facilitate analysis, which owns feature that the order of the sliding-mode dynamics is equal to the order of the original state space.

All parts are arranged as follows. The considered model and some useful preliminaries are given in Sect. 2. Meanwhile, an novel integral sliding-mode surface is established. In Sect. 3, the stochastic stabilization criteria of the considered system are established by utilizing the Lyapunov functional theory, Dynkin’s formula and matrix inequality technology. In Sect. 4, design an appropriate sliding mode controller to let the state trajectories reach the predetermined sliding surface in finite time and maintain there in the subsequent time. One simulation example is presented in Sect. 5 to show the validity of corresponding theoretical results. The final conclusion is drawn in Sect. 6.

Notations. $I_n$ denotes the $n\times n$ identity matrix. ${\mathbb {C}}^n$ and $\mathbb {R}^n$ stand for the sets of n-dimensional complex and real vectors, respectively. ${\mathbb {C}}^{m\times n}$ and ${\mathbb {R}}^{m\times n}$ mean, respectively, the sets of $m\times n$ complex and real matrices. ‘$\otimes$’ means the Kronecker product and the superscript ‘T’ stands for matrix transposition. $\textrm{col}(A_i)_{i=1}^n$ is $(A_1^T,A_2^T,\ldots ,A_n^T)^T$ and $\textrm{diag}\{A_i\}_{i=1}^n$ denotes $\textrm{diag}\{A_1,A_2,\ldots ,A_n\}$. $\textbf{i}$ represents the imaginary unit. $\Vert Q\Vert$ is the spectral norm of matrix Q, i.e. $\Vert Q\Vert =[\lambda _{\textrm{max}}(Q^TQ)]^{\frac{1}{2}}$. $(\Omega , \mathscr {F}, \{\mathscr {F}_t\}_{t\ge 0}, \mathcal {P})$ is a complete probability space, in which filtration $\mathscr {F}_t$ is monotonically right continuous for all $t\ge 0$ and all $\mathcal {P}$-null sets are included in the filtration $\mathscr {F}_0$. $\mathbb {E}\{\cdot \}$ denotes the mathematical expectation.

2 Model Description

Consider the semi-Markovian jumping delayed uncertain CVNs as follows:

$$\begin{aligned} \mathop w \limits ^\centerdot (t)=&-(E(r(t))+\Delta E(r(t),t))w(t)+A(r(t))f(w(t))+B(r(t))g(w(t-\tau (t)))\nonumber \\&+D(r(t))\tilde{u}(t),~~t\ge 0 \end{aligned}$$

(1)

where $w(t)=\textrm{col}(w_\iota (t))_{\iota =1}^n\in {\mathbb {C}}^n$, which denotes the network state vector at time t. E(r(t)) is the self-feedback connection weight matrix, which is defined as $\textrm{diag}\{e_\iota (r(t))\}_{\iota =1}^n\in {\mathbb {R}}^{n\times n}$ with $e_\iota (r(t)) > 0$, the connection weight matrices $A(r(t)) = (a_{\iota \kappa }(r(t)))_{n\times n}$ and $B(r(t))=(b_{\iota \kappa }(r(t)))_{n\times n}$ owning appropriate dimensions. $D(r(t))=(d_{\iota \kappa }(r(t)))_{n\times m} \in {\mathbb {R}}^{n\times m}~(m<n)$ is a known mode-dependent constant matrix with appropriate dimension. $g(w(t))=\textrm{col}(g_\iota (w_\iota (t)))_{\iota =1}^n$ and $f(w(t))=\textrm{col}(f_\iota (w_\iota (t)))_{\iota =1}^n$ are nonlinear functions. $\tilde{u}(t) \in \mathbb {C}^m$ stands for the external control input vector. $\tau (t)$ means the common time-varying transmission delay, and it satisfies $0\le \tau (t)\le \bar{\tau }$. Moreover, $\dot{\tau }(t)\le \varpi <1$. $\{r(t):t\ge 0 \}$ is a stochastic process, which is defined on the probability space $(\Omega , \mathscr {F}, \{\mathscr {F}_t\}_{t\ge 0}, \mathcal {P})$ and the mode value takes from a finite set $\mathcal {S}\triangleq \{1,2,\ldots ,N\}$. Moreover, $\Delta E(r(t),t)$ denotes the mode-dependent parameter uncertainty satisfying the following norm-bounded constraint:

$$\begin{aligned} \Delta E(r(t),t)=\mathcal {M}(r(t))\mathcal {F}(t)\mathcal {N}(r(t)) \end{aligned}$$

(2)

where $\mathcal {M}(r(t))$ and $\mathcal {N}(r(t))$ are known real matrices, and $\mathcal {F}(t)$ is an unknown real matrix subject to

$$\begin{aligned} \mathcal {F}^T(t)\mathcal {F}(t)\le I. \end{aligned}$$

(3)

To clearly characterize the semi-Markovian process $r(t):t\ge 0$, we need to introduce the following three stochastic processes:

• $\{t_n:n\in \mathbb {N}\}$, where $t_n$ is a non-negative real number standing for the n-th transition instant of the process $\{r(t):t\ge 0\}$ with $t_0=0$ and $\lim _{n\rightarrow \infty } t_n=+\infty$.

• $\{h_n:n\in \mathbb {N}\}$, where $h_n$ is a non-negative real number representing the sojourn time of the $(n-1)$-th switching, i.e., $h_n=t_n-t_{n-1}$. Moreover, $h_0$ is set as 0.

• $\{r_n:n\in \mathbb {N}\}$, where $r_n$ stands for the mode index at the n-th transition, which takes value in $\mathcal {S}$.

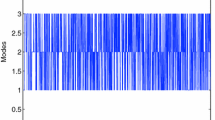
Figure 1 is given to portray the conceivable variation of the above three stochastic processes. For more details, one can refer to [39, 40] and the references cited therein. It is supposed that the random sequence $\{r_n:n\in \mathbb {N} \}$ owns the following transition probabilities:

$$\begin{aligned} q_{ij}=\mathcal {P}\{r_{n+1}=j|r_n=i\},~~~~~\forall i,j\in \mathcal {S}. \end{aligned}$$

(4)

Fig. 1

Illustration of the stochastic processes $\{t_n\}$, $\{h_n\}$, and $\{r_n\}$ for $N=3$

Moreover, the cumulative distribution function is known as [40]

$$\begin{aligned} W_{ij}(t)&\triangleq \mathcal {P}\{h_{n+1}\le t|r_n=i,r_{n+1}=j\}\nonumber \\&= \mathcal {P}\{h_{n+1}\le t|r_n=i\}=W_{i}(t)=\int _0^t \hbar _i(s)\textrm{d}s,~~~~~\forall i,j\in \mathcal {S},~\forall t\ge 0 \end{aligned}$$

(5)

in which $\hbar _i(\cdot )$ denotes the foreknown probability density function.

Based on the above analysis, for arbitrary $t\ge 0$, we set $h\triangleq h(t)=t-\sup \{t_k:t_k\le t\}=t-t_n$ for certain $n\in \mathbb {N}$ as the sojourn time. Combining (4) with (5), for all $i\ne j\in \mathcal {S}$, the transition rate $\lambda _{ij}(h)$ can be obtained as

$$\begin{aligned} \lambda _{ij}(h)\triangleq&\lim \limits _{\delta \rightarrow 0^{+}} \frac{\mathcal {P}\{r(t+\delta )=j|r(t)=i\}}{\delta }\nonumber \\ =&\lim _{\delta \rightarrow 0^+}\bigg \{\frac{\mathcal {P}\{h<t_{n+1} -t_n\le h+\delta , r(t_{n+1})=j, r(t_n)=i\}}{\delta \mathcal {P}\{r(t_{n+1})=j,r(t_n)=i\}}\nonumber \\&\times \frac{\mathcal {P}\{ r(t_{n+1})=j,r(t_n)=i\}}{\mathcal {P}\{r(t_n)=i\}\mathcal {P}\{t_{n+1}-t_n> h|r(t_n)=i\}}\bigg \}\nonumber \\ =&\lim _{\delta \rightarrow 0^+}\bigg \{\frac{\mathcal {P}\{h<t_{n+1} -t_n\le h+\delta |r(t_n)=i\}}{\delta }\times \frac{1}{\mathcal {P}\{t_{n+1}-t_n> h|r(t_n)=i\}}\nonumber \\&\times \frac{\mathcal {P}\{r(t_{n+1})=j,r(t_n)=i \}}{\mathcal {P}\{r(t_n)=i\}}\bigg \}\nonumber \\ =&\lim _{\delta \rightarrow 0^+}\bigg \{\frac{W_i(h+\delta )-W_i(h)}{\delta }\times \frac{1}{1-W_i(h)}\times q_{ij}\bigg \}\nonumber \\ =&q_{ij}\frac{\hbar _i(h)}{1-W_i(h)} \end{aligned}$$

(6)

where $\delta$ is a positive infinitesimal quantity. Further define $\lambda _{ii}(h)\triangleq -\sum _{j=1,j\ne i}^N\lambda _{ij}(h)$, and denote the infinitesimal generator matrix of $\{r(t): t\ge 0\}$ as $\Lambda (h)=(\lambda _{ij}(h))_{N\times N}$. Obviously, one has

$$\begin{aligned} \mathcal {P}\{r(t+\delta )=j|r(t)=i\}= {\left\{ \begin{array}{ll} \lambda _{ij}(h)\delta +o(\delta ),~~~~~~~~i\ne j\\ 1+\lambda _{ii}(h)\delta +o(\delta ),~~~i=j. \end{array}\right. } \end{aligned}$$

(7)

Remark 1

It should be pointed out that, for continuous-time Markovian jumping systems, the sojourn time is closely related to the probability distribution function, which obeys the exponential distribution, and this means that the transition rate is time-invariant, i.e., $\lambda _{ij}(h)=\lambda _{ij}$. In this case, the switching speed is independent of the history, and it straightforwardly brings a lot of constraints. In this paper, the considered sojourn time concerned could obey the non-exponential distribution, and the transition rate $\lambda _{ij}(h)$ is in fact time-varying, which might better characterize the practical situations and thus expand the application range.

The considered nonlinear functions, for further discussion, are assumed to satisfy the following conditions, which play the vital role in the proof of the theoretical results.

Assumption 1

Let $\alpha =\alpha _1+\textbf{i}\alpha _2$ with $\alpha _1$, $\alpha _2\in {\mathbb R}$. $f_\iota (\alpha )$ and $g_\iota (\alpha )$ are displayed as

$$\begin{aligned} f_\iota (\alpha )=f_\iota ^R(\alpha _1,\alpha _2)+\textbf{i}f_\iota ^I(\delta _1,\alpha _2),~~~~ g_\iota (\alpha )=g_\iota ^R(\alpha _1,\alpha _2)+\textbf{i}g_\iota ^I(\alpha _1,\alpha _2) \end{aligned}$$

where $\iota =1,2,\ldots ,n$, and $f_\iota ^R(\cdot )$, $f_\iota ^I(\cdot )$, $g_\iota ^R(\cdot )$, $g_\iota ^I(\cdot ): {\mathbb R}^2\rightarrow {\mathbb R}$ satisfy

$$\begin{aligned}&|f_\iota ^R(\alpha _1,\alpha _2)|\le \gamma ^{RR}_\iota |\alpha _1|+\gamma ^{RI}_\iota |\alpha _2|,~~~|f_\iota ^I(\alpha _1,\alpha _2)|\le \gamma ^{IR}_\iota |\alpha _1|+\gamma ^{II}_\iota |\alpha _2|,\\&|g_\iota ^R(\alpha _1,\alpha _2)|\le \zeta ^{RR}_\iota |\alpha _1|+\zeta ^{RI}_\iota |\alpha _2|,~~~|g_\iota ^I(\alpha _1,\alpha _2)|\le \zeta ^{IR}_\iota |\alpha _1|+\zeta ^{II}_\iota |\alpha _2| \end{aligned}$$

in which $\gamma ^{RR}_\iota$, $\gamma ^{RI}_\iota$, $\gamma ^{IR}_\iota$, $\gamma ^{II}_\iota$, $\zeta ^{RR}_\iota$, $\zeta ^{RI}_\iota$, $\zeta ^{IR}_\iota$, and $\zeta ^{II}_\iota$ are foreknown positive constants. Moreover, $f_{\iota }(0)=g_{\iota }(0)=0$.

Denote $w(t)=x(t)+\textbf{i}y(t)$. Here, states x(t) and y(t) both belong to $\mathbb {R}^n$. When $r(t)=i\in \mathcal {S}$, A(r(t)) is written as $A_i$ for simplicity, and $A_i^R$ and $A_i^I$ represent, respectively, the real and the imaginary parts of $A_i$. Other symbols not mentioned have the similar meaning, which are omitted for briefly if no confusion arises. To facilitate the research, when $r(t)=i\in \mathcal {S}$, we present the following compact form of network (1):

$$\begin{aligned} \dot{\beta }(t)=&-(E_{1i}+\Delta E_{1i}(t))\beta (t)+A_{2i} f_2(\beta (t))+A_{1i} f_1(\beta (t))+B_{1i} g_1(\beta (t-\tau (t)))\nonumber \\&+B_{2i}g_2(\beta (t-\tau (t)))+D_{1i}u(t) \end{aligned}$$

(8)

where $\beta (t)=(x^T(t),y^T(t))^T$, $E_{1i}=I_2\otimes E_i$, $\Delta E_{1i}(t)=I_2\otimes \Delta E_i(t)$, $D_{1i}=I_2\otimes D_i$, $A_{1i}=\textrm{diag}\{A_i^R, A_i^I\}$, $A_{2i}=\textrm{diag}\{-A_i^I, A_i^R\}$, $u(t)=((\tilde{u}^R(t))^T,(\tilde{u}^I(t))^T)^T$, $B_{1i}=\textrm{diag}\{B_i^R, B_i^I\}$, $B_{2i}=\textrm{diag}\{-B_i^I, B_i^R\}$, $f_1(\beta (t))=I_2\otimes f^R(x(t),y(t))$, $f_2(\beta (t))=I_2\otimes f^I(x(t),y(t))$, $g_1(\beta (t))=I_2\otimes g^R(x(t),y(t))$, $g_2(\beta (t))=I_2\otimes g^I(x(t),y(t))$ in which $I_2$ is the 2-dimensional vector with all elements being 1.

For system (8), its initial value is set as

$$\begin{aligned} \beta (s)= \vartheta (s),~~~s\in [-\bar{\tau },0] \end{aligned}$$

(9)

in which $\vartheta (s)=(\vartheta _1(s),\vartheta _2(s),\ldots ,\vartheta _{2n}(s))^T\in \mathbb {R}^{2n}$ belongs to $L_{\mathscr {F}_0}^2([-\bar{\tau },0],\mathbb {R}^{2n})$, and $L_{\mathscr {F}_0}^2([-\bar{\tau },0],\mathbb {R}^{2n})$ stands for the family of $\mathscr {F}_0$-measurable ${\textbf{C}}^1([-\bar{\tau },0],\mathbb {R}^{2n})$-valued random variables with $\sup _{-\bar{\tau }\le s\le 0}\mathbb {E}\{\Vert \vartheta (s)\Vert ^2\}<\infty$, where $\textbf{C}^1([-\bar{\tau },0],\mathbb {R}^{2n})$ denotes the first-order continuously differentiable function space that maps interval $[-\bar{\tau },0]$ to $\mathbb {R}^{2n}$.

Definition 1

System (6) with semi-Markovian jumping parameters is called to be stochastically stable if there is an effective positive constant $T(\vartheta (\cdot ),r_0)$ such that the inequality given below is valid in the context of the given initial condition $\vartheta (\cdot )$ and the given initial jumping mode $r_0\in \mathcal {S}$:

$$\begin{aligned} \mathbb {E}\bigg \{\int _0^{\infty }\Vert \beta (t)\Vert ^2\textrm{d}t\Big |\vartheta (\cdot ),r_0\bigg \}\le T(\vartheta (\cdot ),r_0). \end{aligned}$$

(10)

Lemma 1

[36] Let M, N, $\Omega$ be any matrices with $\Omega ^T\Omega \le I$. For any given positive scalar $\varphi$, the following inequality holds:

$$\begin{aligned} M\Omega N +(M\Omega N)^T \le \varphi ^{-1}MM^T+\varphi N^TN. \end{aligned}$$

This paper aims to propose a mode-dependent sliding surface to assure the stochastic stability of the considered system (8) in virtue of the sliding mode control scheme. In addition, it is necessary to design an appropriate sliding mode controller, which makes the state trajectory of system (8) reach the satisfied sliding mode surface within finite time.

According to system (8), construct the switching integral sliding mode surface/function S(i, t) given below:

$$\begin{aligned} S(i,t)= V_i \beta (t)-V_i\int _0^t(-E_{1i}-D_{1i}K_i)\beta (s)\textrm{d}s \end{aligned}$$

(11)

where $V_i$ and $K_i$ are cofficient matrices with appropriate dimensions to be designed, and $V_i$ is taken to ensure $V_iD_{1i}$ non-singular. Based on the idea of the switching sliding mode surface, it is a necessary condition that $\dot{S}(i,t)=0$ so as to make the state trajectory slide on the designed surface $S(i,t)=0$. Based on this, we can obtain

$$\begin{aligned} 0=&-V_i\Delta E_{1i}(t)\beta (t)+V_iA_{1i}f_1(\beta (t))+V_iA_{2i}f_2(\beta (t))\nonumber \\&+V_iB_{1i}g_1(\beta (t-\tau (t)))+V_iD_{1i}K_i\beta (t)\nonumber \\&+V_iD_{1i}u(t)+V_iB_{2i}g_2(\beta (t-\tau (t))). \end{aligned}$$

(12)

Solving (12) and the isovalent control law $u_{eq}(i,t)$ is derived as

$$\begin{aligned} u_{eq}(i,t)=&-K_i\beta (t)+\bar{V}_i\Delta E_{1i}\beta (t)-\bar{V}_iA_{1i}f_1(\beta (t))-\bar{V}_iB_{1i}g_1(\beta (t-\tau (t)))\nonumber \\&-\bar{V}_iA_{2i}f_2(\beta (t))-\bar{V}_iB_{2i}g_2(\beta (t-\tau (t))) \end{aligned}$$

(13)

where $\bar{V}_i=(V_iD_{1i})^{-1}V_i$. Subtituting (13) into (8), the holonomic sliding mode dynamical system can be immediately acquired:

$$\begin{aligned} \dot{\beta }(t)=&\,(-E_{1i}-D_{1i}K_i-\Delta E_{1i}(t)+D_{1i}\bar{V}_i\Delta E_{1i}(t))\beta (t)+(A_{1i}-D_{1i}\bar{V}_iA_{1i})f_1(\beta (t))\nonumber \\&+(A_{2i}-D_{1i}\bar{V}_iA_{2i})f_2(\beta (t)) +(B_{1i}-D_{1i}\bar{V}_iB_{1i})g_1(\beta (t-\tau (t)))\nonumber \\&+(B_{2i}-D_{1i}\bar{V}_iB_{2i})g_2(\beta (t-\tau (t))). \end{aligned}$$

(14)

In addition, system (14) is also regarded as sliding mode dynamics. Obviously, the sliding mode dynamics (14) is established under the necessary condition $\dot{S}(i,t)=0$.

Remark 2

As is well-known, on account of the sliding mode control owns the strong robustness against external disturbances, model uncertainties and structural mode changes, it has been widely adopted in a mass of fields. Furthermore, the sliding mode control strategy has also been applied to Markovian jumping systems, where the jump speed is a stochastic process and independent of the past case. However, in fact, when the mode switch to another one, the process of going through may be more complex and ruleless in modern life. In a view of this point, we adopt the sliding mode control to further discuss the stabilization issue of semi-Markovian jumping CVNs in the paper. In addition, the proposed integral sliding surface improves the reaching phase bottleneck, although system has not yet reached on this surface in the initial period.

With the aid of the full-blown sliding mode control theory, the essential problem is to show an effective sliding mode controller u(t) for semi-Markovian system (8), which can present the sufficient stochastic stability criteria for the proposed sliding mode dynamical system (14) with any mode $i\in \mathcal {S}$. Moreover, the designed sliding mode controller can insure the effective reachability, which means the state trajectories of system (8) can get on the satisfied sliding surface within the finite time.

3 Stability Analysis

Some sufficient theoretical results are presented to ensure the stochastic stability of the proposed network (8). For this aim, the authoritative theorem is given below.

Theorem 1

Let matrices $V_i$, $K_i$ be given with $\mathrm {\det }(V_iD_{1i})\ne 0$. Based on Assumption 1, the network (8) is stochastically stable in the switching sliding mode surface $S(i,t)=0$ under the designed control law (13) if there are real symmetric positive definite matrices $P_i$, Q, positive diagonal matrices $M_\rho =\textrm{diag}\{\mu _{\rho \iota }\}_{\iota =1}^n~(\rho =1,2,3,4)$, positive matrices $L_\rho$, positive scalars $\vartheta _\rho$ and $\varphi$ such that the matrix inequalities given below are valid for all $i\in \mathcal {S}$:

$$\begin{aligned}&\Upsilon _i= \begin{bmatrix} \Upsilon _{11}&{}0&{}\Upsilon _{13}&{}\Upsilon _{14}&{}\Upsilon _{15}&{}\Upsilon _{16}&{}\Upsilon _{17}&{}\Upsilon _{18}\\ *&{}\Upsilon _{22}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}\Upsilon _{33}&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}\Upsilon _{44}&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}\Upsilon _{55}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}\Upsilon _{66}&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}-\varphi I&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}-\varphi I \end{bmatrix}<0, \end{aligned}$$

(15)

$$\begin{aligned}&\Phi _\rho \le L_\rho \end{aligned}$$

(16)

where $\Upsilon _{11}=\sum _{j=1}^N\bar{\lambda }_{ij}P_j+Q+P_i(-E_{1i}-D_{1i}K_i) +(-E_{1i}-D_{1i}K_i)^TP_i+2(\vartheta _1L_1+\vartheta _2L_2)$, $\Upsilon _{22}=-(1-\varpi )Q+2(\vartheta _3L_3+\vartheta _4L_4)$, $\Upsilon _{33}=-\vartheta _1(I_2\otimes M_1)$, $\Upsilon _{44}=-\vartheta _2(I_2\otimes M_2)$, $\Upsilon _{55}=-\vartheta _3(I_2\otimes M_3)$, $\Upsilon _{66}=-\vartheta _4(I_2\otimes M_4)$, $\Upsilon _{13}=P_i(A_{1i}-D_{1i}\bar{V}_iA_{1i})$, $\Upsilon _{14}=P_i(A_{2i}-D_{1i}\bar{V}_iA_{2i})$, $\Upsilon _{15}=P_i(B_{1i}-D_{1i}\bar{V}_iB_{1i})$, $\Upsilon _{16}=P_i(B_{2i}-D_{1i}\bar{V}_iB_{2i})$, $\Upsilon _{17}=\varphi P_i(D_{1i}\bar{V}_i I)\widetilde{\mathcal {M}}_i$, $\Upsilon _{18}= \widetilde{\mathcal {N}}_i^T$, $\bar{\lambda }_{ij}=\int _0^{\infty }\lambda _{ij}\hbar _i(h)\textrm{d}h$,

$$\begin{aligned}&\Phi _1= \begin{pmatrix} M_1(\Theta ^{RR})^2 &{} M_1\Theta ^{RR}\Theta ^{RI}\\ M_1\Theta ^{RR}\Theta ^{RI} &{} M_1(\Theta ^{RI})^2 \end{pmatrix},~~~ \Phi _2= \begin{pmatrix} M_2(\Theta ^{IR})^2 &{} M_2\Theta ^{IR}\Theta ^{II}\\ M_2\Theta ^{IR}\Theta ^{II} &{} M_2(\Theta ^{II})^2 \end{pmatrix},\\&\Phi _3= \begin{pmatrix} M_3(\Delta ^{RR})^2 &{} M_3\Delta ^{RR}\Delta ^{RI}\\ M_3\Delta ^{RR}\Delta ^{RI} &{} M_3(\Delta ^{RI})^2 \end{pmatrix},~~ \Phi _4= \begin{pmatrix} M_4(\Delta ^{IR})^2 &{} M_4\Delta ^{IR}\Delta ^{II}\\ M_4\Delta ^{IR}\Delta ^{II} &{} M_4(\Delta ^{II})^2 \end{pmatrix} \end{aligned}$$

with $\widetilde{\mathcal {M}}_i=I_2\otimes \mathcal {M}_i$, $\widetilde{\mathcal {N}}_i=I_2\otimes \mathcal {N}_i$, $\Theta ^{RR}=\textrm{diag}\{\gamma _{\iota }^{RR}\}_{\iota =1}^{n}$, $\Theta ^{RI}=\textrm{diag}\{\gamma _{\iota }^{RI}\}_{\iota =1}^{n}$, $\Theta ^{IR}=\textrm{diag}\{\gamma _{\iota }^{IR}\}_{\iota =1}^{n}$, $\Theta ^{II}=\textrm{diag}\{\gamma _{\iota }^{II}\}_{\iota =1}^{n}$, and $\Delta ^{RR}=\textrm{diag}\{\zeta _{\iota }^{RR}\}_{\iota =1}^{n}$, $\Delta ^{RI}=\textrm{diag}\{\zeta _{\iota }^{RI}\}_{\iota =1}^{n}$, $\Delta ^{IR}=\textrm{diag}\{\zeta _{\iota }^{IR}\}_{\iota =1}^{n}$, $\Delta ^{II}=\textrm{diag}\{\zeta _{\iota }^{II}\}_{\iota =1}^{n}$.

Proof

Choose a Lyapunov functional candidate given below for network (14) as

$$\begin{aligned} \textbf{V}(i,t,\beta _t(s))\triangleq \sum \limits _{\kappa =1}^2\textbf{V}_\kappa (i,t,\beta _t(s)),~~~~~~~s\in [-\bar{\tau },0] \end{aligned}$$

(17)

where $t\ge 0$, $\beta _t(s)=\beta (t+s)$ and

$$\begin{aligned} \textbf{V}_1(i,t,\beta _t(s))&=\beta ^T(t)P_i\beta (t),\\ \textbf{V}_2(i,t,\beta _t(s))&=\int _{t-\tau (t)}^{t} \beta ^T(s)Q\beta (s)\textrm{d}s \end{aligned}$$

where $P_i$ and Q are matrices to be determined. When the system is at the point $\{r(t)=i,t,\beta _t(s)\}$, define the weak infinitesimal generator as $\mathscr {L}$. With aid of the definition of $\mathscr {L}$ [39, 40], one has

$$\begin{aligned} \mathscr {L}\textbf{V}(i,t,\beta _t(s))=\lim _{\delta \rightarrow 0^+}\frac{\mathbb {E}\{\textbf{V}(r(t+\delta ),t+\delta ,\beta _{t+\delta }(s)) |r(t),\beta _t(s)\} -\textbf{V}(r(t)=i,t,\beta _t(s))}{\delta }. \end{aligned}$$

For simplicity, denote $\mathcal {V}_\kappa \triangleq \mathscr {L} \textbf{V}_\kappa (r(t)=i,t,\beta _t(s))$. Combining the inherent performance of the conditional expectation with the law of total probability, along the similar discussions in [41], it infers

$$\begin{aligned} \mathcal {V}_1=&\lim _{\delta \rightarrow 0^+}\frac{1}{\delta }\Bigg \{\bigg [\sum _{j=1,j\ne i}^N\mathcal {P}\{r_{n+1}=j,h_{n+1}\le h+\delta |h_{n+1}>h,r_n=i\}\mathbb {E}\{\beta ^T(t+\delta )\nonumber \\&\times P_j\beta (t+\delta )|\beta _t(s)\}+\mathcal {P}\{r_{n+1}=i,h_{n+1}> h+\delta |h_{n+1}>h,r_n=i\}\mathbb {E}\{\beta ^T(t+\delta )\nonumber \\&\times P_i\beta (t+\delta )|\beta _t(s)\}+\mathcal {P}\{r_{n+1}=i,h_{n+1}\le h+\delta |h_{n+1}>h,r_n=i\}\mathbb {E}\{\beta ^T(t+\delta )\nonumber \\&\times P_i\beta (t+\delta )|\beta _t(s)\}\bigg ]-\beta ^T(t)P_i\beta (t)\Bigg \}\nonumber \\ =&\lim _{\delta \rightarrow 0^+}\frac{1}{\delta }\Bigg \{\bigg [\sum _{j=1,j\ne i}^N\frac{\mathcal {P}\{r_{n+1}=j,r_n=i\}}{\mathcal {P}\{r_n=i\}}\times \frac{\mathcal {P}\{h<h_{n+1}\le h+\delta |r_{n+1}=j,r_n=i\}}{\mathcal {P}\{h_{n+1}>h|r_n=i\}}\nonumber \\&\times \mathbb {E}\{\beta ^T(t+\delta )P_j\beta (t+\delta )|\beta _t(s)\}+\frac{\mathcal {P}\{h_{n+1}> h+\delta ,r_{n+1}=i|r_n=i\}}{\mathcal {P}\{h_{n+1}> h|r_n=i\}}\nonumber \\&\times \mathbb {E}\{\beta ^T(t+\delta )P_i\beta (t+\delta )|\beta _t(s)\}+\frac{\mathcal {P}\{h<h_{n+1}\le h+\delta ,r_{n+1}=i|r_n=i\}}{\mathcal {P}\{h_{n+1}> h|r_n=i\}} \nonumber \\ {}&\times \mathbb {E}\{\beta ^T(t+\delta )P_i\beta (t+\delta )|\beta _t(s)\}\bigg ]-\beta ^T(t)P_i\beta _t(s)\Bigg \}\nonumber \\ =&\lim _{\delta \rightarrow 0^+}\frac{1}{\delta }\Bigg \{\bigg [\sum _{j=1,j\ne i}^N\frac{q_{ij}(W_i(h+\delta )-W_i(\delta ))}{1-W_i(h)}\times \mathbb {E}\{ \beta ^T(t+\delta )P_j\beta (t+\delta )|\beta _t(s))\}\nonumber \\&{+q_{ii}\frac{W_i(h+\delta )-W_i(h)}{1-W_i(h)}\times \mathbb {E}\{\beta ^T(t+\delta )P_i\beta (t+\delta )|\beta _t(s)}\}\nonumber \\&+\frac{1-W_i(h+\delta )}{1-W_i(h)}\times \mathbb {E}\{\beta ^T(t+\delta )P_i\beta (t+\delta )|\beta _t(s)\}\big ]-\beta ^T(t)P_i\beta (t)\Bigg \}. \end{aligned}$$

(18)

Furthermore, for a small positive number $\delta$, it easily obtains that

$$\begin{aligned} \beta (t+\delta )=\beta (t)+\delta \dot{\beta }(t)+o(\delta ). \end{aligned}$$

(19)

This combining with (18) assures that

$$\begin{aligned} \mathcal {V}_1=&\lim _{\delta \rightarrow 0^+}\frac{1}{\delta }\mathbb {E}\Bigg \{\sum _{j=1,j\ne i}^N\frac{ q_{ij}(W_i(h+\delta )-W_i(h))}{1-W_i(h)}(\delta \dot{\beta }(t)+\beta (t)+o(\delta ))^TP_j(\delta \dot{\beta }(t)+\beta (t)\nonumber \\&+o(\delta ))+\frac{1-W_i(h+\delta )}{1-W_i(h)}(\delta \dot{\beta }(t)+\beta (t)+o(\delta ))^TP_i(\delta \dot{\beta }(t)+\beta (t)+o(\delta ))\nonumber \\&+\frac{q_{ii}(W_i(h+\delta )-W_i(h)}{1-W_i(h)}(\delta \dot{\beta }(t)+\beta (t)+o(\delta ))^TP_i(\delta \dot{\beta }(t)+\beta (t)+o(\delta ))\Big \}\nonumber \\&-\beta ^T(t)P_i\beta (t)\big |\beta _t(s)\Bigg \}. \end{aligned}$$

(20)

Based on the facts $\lim \limits _{\delta \rightarrow 0^+}\frac{1-W_i(h+\delta )}{1-W_i(h)}=1$ and $\lim \limits _{\delta \rightarrow 0^+}\frac{W_i(h+\delta )-W_i(h)}{1-W_i(h)}=0$, it yields

$$\begin{aligned} \mathcal {V}_1=\lim _{\delta \rightarrow 0^+}\mathbb {E}\bigg \{\frac{1-W_i(h+\delta )}{1-W_i(h)}\big [\beta ^T(t)P_i\dot{\beta }(t) +\dot{\beta }^T(t)P_i\beta (t)\big ]+\beta ^T(t)\mathscr {P}_i\beta (t)\big |\beta _t(s)\Bigg \} \end{aligned}$$

(21)

where

$$\begin{aligned}&\mathscr {P}_i=\sum _{j=1,j\ne i}^N\frac{ q_{ij}(W_i(h+\delta )-W_i(h))}{\delta (1-W_i(h))}P_j +\frac{W_i(h)-W_i(h+\delta )}{\delta (1-W_i(h))}P_i\\&\quad +\frac{q_{ii}(W_i(h +\delta )-W_i(h))}{\delta (1-W_i(h))}P_i. \end{aligned}$$

By using the property that the row sum of the transition rate matrix is zero, it infers

$$\begin{aligned} \mathcal {V}_1=\mathbb {E}\Bigg \{\beta ^T(t)\sum _{j=1}^N\bar{\lambda }_{ij}P_j\beta (t)+\dot{\beta }^T(t)P_i\beta (t)+\beta ^T(t)P_i\dot{\beta }(t)\big |\beta _t(s)\Bigg \}. \end{aligned}$$

(22)

Simultaneously, we also get

$$\begin{aligned} \mathcal {V}_2&= \mathbb {E}\Big \{ \beta ^T(t)Q\beta (t)-(1-\dot{\tau }(t))\beta ^T(t-\tau (t))Q\beta (t-\tau (t))\big |\beta _t(s)\Big \}\nonumber \\&\le \mathbb {E}\Big \{\beta ^T(t)Q\beta (t)-(1-\varpi )\beta ^T(t-\tau (t))Q\beta (t-\tau (t))\big |\beta _t(s)\Big \}. \end{aligned}$$

(23)

By virtue of Assumption 1, it can be obtained that

$$\begin{aligned} \begin{aligned}&f_1^T(\beta (t))(I_2\otimes M_1) f_1(\beta (t))\\&\quad =2\sum _{\iota =1}^n \mu _{1\iota }(f_\iota ^R(x_\iota (t),y_\iota (t)))^2\\&\quad \le 2 \sum _{\iota =1}^n \begin{pmatrix} |x_\iota (t)|\\ |y_\iota (t)| \end{pmatrix}^T \begin{pmatrix} \mu _{1\iota }(\gamma _\iota ^{RR})^2 &{} \mu _{1\iota }\gamma _\iota ^{RR}\gamma _\iota ^{RI}\\ \mu _{1\iota }\gamma _\iota ^{RR}\gamma _\iota ^{RI} &{}\mu _{1\iota }(\gamma _\iota ^{RI})^2 \end{pmatrix} \begin{pmatrix} |x_\iota (t)|\\ |y_\iota (t)| \end{pmatrix}\\&\quad = 2 \begin{pmatrix} |x(t)|\\ |y(t)| \end{pmatrix}^T \begin{pmatrix} M_1(\Theta ^{RR})^2 &{} M_1\Theta ^{RR}\Theta ^{RI}\\ M_1\Theta ^{RR}\Theta ^{RI} &{} M_1(\Theta ^{RI})^2 \end{pmatrix} \begin{pmatrix} |x(t)|\\ |y(t)| \end{pmatrix}\le 2\beta ^T(t)L_1\beta (t). \end{aligned} \end{aligned}$$

(24)

In a similar way as shown in (24), one also gets

$$\begin{aligned}&f_2^T(\beta (t))(I_2\otimes M_2) f_2(\beta (t))\le 2 \beta ^T(t)L_2 \beta (t), \end{aligned}$$

(25a)

$$\begin{aligned}&g_1^T(\beta (t-\tau (t)))(I_2\otimes M_3)g_1(\beta (t-\tau (t)))\le 2 \beta ^T(t-\tau (t))L_3 \beta (t-\tau (t)), \end{aligned}$$

(25b)

$$\begin{aligned}&g_2^T(\beta (t-\tau (t)))(I_2\otimes M_4)g_2(\beta (t-\tau (t)))\le 2 \beta ^T(t-\tau (t))L_4 \beta (t-\tau (t)). \end{aligned}$$

(25c)

Therefore, for any $\vartheta _\rho >0~(\rho =1,2,3,4)$, it is straightforward to obtain that the inequalities given below hold:

$$\begin{aligned} 0\le&\vartheta _1[ 2 \beta ^T(t)L_1 \beta (t) - f_1^T(\beta (t))(I_2\otimes M_1)f_1(\beta (t))], \end{aligned}$$

(26a)

$$\begin{aligned} 0\le&\vartheta _2[ 2 \beta ^T(t)L_2\beta (t) - f_2^T(\beta (t))(I_2\otimes M_2)f_2(\beta (t))], \end{aligned}$$

(26b)

$$\begin{aligned} 0\le&\vartheta _3[ 2 \beta ^T(t-\tau (t))L_3 \beta (t-\tau (t))-g_1^T(\beta (t-\tau (t)))(I_2\otimes M_3) g_1(\beta (t-\tau (t)))], \end{aligned}$$

(26c)

$$\begin{aligned} 0\le&\vartheta _4[ 2 \beta ^T(t-\tau (t))L_4 \beta (t-\tau (t))-g_2^T(\beta (t-\tau (t)))(I_2\otimes M_4) g_2(\beta (t-\tau (t)))]. \end{aligned}$$

(26d)

Combining (14), (22)–(23) with (26a)–(26d), one gets

$$\begin{aligned} \mathscr {L}\textbf{V}(i,t,\beta _t(s))\le \mathbb {E}\{\xi ^T(t)\Upsilon _i(t)\xi (t)|\beta _t(s)\} \end{aligned}$$

(27)

where $\xi (t)=(\beta ^T(t), \beta ^T(t-\tau (t)), f_1^T(\beta (t)), f_2^T(\beta (t)), g_1^T(\beta (t-\tau (t))), g_2^T(\beta (t-\tau (t))))^T$, and $\Upsilon _i(t)$ is defined as follows:

$$\begin{aligned}&\Upsilon _i(t)\triangleq \begin{bmatrix} \tilde{\Upsilon }_{11}(t)&{}0&{}\Upsilon _{13}&{}\Upsilon _{14}&{}\Upsilon _{15}&{}\Upsilon _{16}\\ *&{}\Upsilon _{22}&{}0&{}0&{}0&{}0\\ *&{}*&{}\Upsilon _{33}&{}0&{}0&{}0\\ *&{}*&{}*&{}\Upsilon _{44}&{}0&{}0\\ *&{}*&{}*&{}*&{}\Upsilon _{55}&{}0\\ *&{}*&{}*&{}*&{}*&{}\Upsilon _{66} \end{bmatrix} \end{aligned}$$

in which $\tilde{\Upsilon }_{11}(t)=\sum _{j=1}^N\bar{\lambda }_{ij}P_j+Q+P_i(-E_{1i}-D_{1i}K_i)+\Delta E_{1i}^T(t)(D_{1i}\bar{V}_i-I)^TP_i+P_i(D_{1i}\bar{V}_i-I)\Delta E_{1i}(t)+(-E_{1i}-D_{1i}K_i)^TP_i+2(\vartheta _1L_1+\vartheta _2L_2)$, and other symbols are taken as the ones in (15).

Obviously, $\Upsilon _i(t)=\Upsilon _i+\Delta \Upsilon _i(t)$, in which

$$\begin{aligned} \Upsilon _i\triangleq \begin{bmatrix} \Upsilon _{11}&{}0&{}\Upsilon _{13}&{}\Upsilon _{14}&{}\Upsilon _{15}&{}\Upsilon _{16}\\ *&{}\Upsilon _{22}&{}0&{}0&{}0&{}0\\ *&{}*&{}\Upsilon _{33}&{}0&{}0&{}0\\ *&{}*&{}*&{}\Upsilon _{44}&{}0&{}0\\ *&{}*&{}*&{}*&{}\Upsilon _{55}&{}0\\ *&{}*&{}*&{}*&{}*&{}\Upsilon _{66} \end{bmatrix},~~~ \Delta \Upsilon _i(t)\triangleq \begin{bmatrix} \Delta \Upsilon _{11}(t)&{}0&{}0&{}0&{}0&{}0\\ *&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}0 \end{bmatrix}, \end{aligned}$$

with $\Delta \Upsilon _{11}(t)=\Delta E_{1i}^T(t)(D_{1i}\bar{V}_i-I)^TP_i+P_i(D_{1i}\bar{V}_i-I)\Delta E_{1i}(t)$, and $\Upsilon _i(t)$ can be found in (15). Next, it follows from Lemma 1 that there exists a scalar $\varphi >0$ satisfying

$$\begin{aligned} \Delta \Upsilon _i(t)=\widehat{\mathcal {M}}_i\widehat{\mathcal {F}}(t)\widehat{\mathcal {N}}_i +\widehat{\mathcal {N}}_i^T\widehat{\mathcal {F}}^T(t)\widehat{\mathcal {M}}_i^T\le \varphi \widehat{\mathcal {M}}_i \widehat{\mathcal {M}}_i^T+\varphi ^{-1}\widehat{\mathcal {N}}_i^T\widehat{\mathcal {N}}_i \end{aligned}$$

(28)

where $\widehat{\mathcal {M}}_i^T=[\widetilde{\mathcal {M}}_i^T(D_{1i}\bar{V}_i-I)^TP_i~0~0~0~0~0~0]$, $\widehat{\mathcal {N}}_i=[\widetilde{\mathcal {N}}_i~0~0~0~0~0~0]$, and $\widehat{\mathcal {F}}(t)=I_2\otimes \mathcal {F}(t)$. By resorting to the common Schur!‘-s complementary lemma, it is known that

$$\begin{aligned} \mathscr {L}\textbf{V}(i,t,\beta _t(s))\le \mathrm {\max }_{i\in \mathcal {S}}\{\lambda _\mathrm {\max }(\mathbf {\Upsilon }_i)\}\mathbb {E}\{\beta ^T(t)\beta (t)|\beta _t(s)\}. \end{aligned}$$

(29)

According to the generalized Dynkin’s formula, one yields

$$\begin{aligned} \mathbb {E}\{\textbf{V}(i,t,\beta _t(s))\}-\textbf{V}(r_0,0,\vartheta (s))\}\le \mathrm {\max }_{i\in \mathcal {S}}\{\lambda _\mathrm {\max }(\mathbf {\Upsilon }_i)\} \mathbb {E}\bigg \{\int _0^t\beta ^T(s)\beta (s)\textrm{d}s\bigg \}. \end{aligned}$$

(30)

Furthermore, the condition (15) indicates $\mathrm {\max }_{i\in \mathcal {S}}\{\lambda _\mathrm {\max }(\mathbf {\Upsilon }_i)\}<0$, then it is obtained that

$$\begin{aligned} \mathbb {E}\bigg \{\int _0^t\beta ^T(s)\beta (s)\textrm{d}s\bigg \}\le -\frac{\mathbb {E}\{\textbf{V}(r_0,0,\vartheta (s))\}}{\mathrm {\max }_{i\in \mathcal {S}}\{\lambda _\mathrm {\max }(\mathbf {\Upsilon }_i)\}}. \end{aligned}$$

(31)

Next, let t approach to infinity, it is easy to get

$$\begin{aligned} \mathbb {E}\bigg \{\int _0^\infty \beta ^T(s)\beta (s)\textrm{d}s\bigg \}\le -\frac{\mathbb {E}\{\textbf{V}(r_0,0,\vartheta (s))\}}{\mathrm {\max }_{i\in \mathcal {S}}\{\lambda _\mathrm {\max }(\mathbf {\Upsilon }_i)\}}\triangleq T(\vartheta (s),r_0). \end{aligned}$$

(32)

From the above discussion and Definition 1, the stochastic stability of system (8) on the sliding mode surface can be derived. The proof is now completed. $\square$

To above end, some sufficient stability criteria of system (8) have been proposed. It’s worth noting that some unknown parameter matrices are nonlinear, we cannot solve them by the LMI toolbox of MATLAB. Therefore, it is urgent and necessary to present the proper deformation. This issue will be addressed in the Theorem 2 below.

Theorem 2

Based on Assumption 1, system (8) is stochastically stable on the sliding mode surface $S(i,t)=0$ under the control law (13) if there are symmetric positive definite matrices $\bar{P}_i$, $\tilde{Q}$, and any matrices $\bar{K}_i$, $\bar{V}_i$, positive diagonal matrices $\tilde{M}_\rho =\textrm{diag}\{\tilde{\mu }_{\rho \iota }\}_{\iota =1}^n$, positive matrices $\tilde{L}_\rho$, positive scalars $\vartheta _\rho$ and $\varphi$ such that the matrix inequalities given below are valid for all $i\in \mathcal {S}$:

$$\begin{aligned}&\Pi _i= \begin{bmatrix} \Pi _{11}&{}0&{}\Pi _{13}&{}\Pi _{14}&{}\Pi _{15}&{}\Pi _{16}&{}\Pi _{17}&{}\Pi _{18}&{}\Pi _{19}\\ *&{}\Pi _{22}&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}\Pi _{33}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}\Pi _{44}&{}0&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}\Pi _{55}&{}0&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}\Pi _{66}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}-\varphi I&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}-\varphi I&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}*&{}\Pi _{99} \end{bmatrix}<0, \end{aligned}$$

(33)

$$\begin{aligned}&\tilde{\Phi }_\rho \le \tilde{L}_\rho \end{aligned}$$

(34)

$$\begin{aligned}&\bar{V}_iD_{1i}=I \end{aligned}$$

(35)

where $\Pi _{11}=\bar{\lambda }_{ii}\bar{P}_i+\tilde{Q}+(-E_{1i}\bar{P}_i-D_{1i}\bar{K}_i)+(-E_{1i}\bar{P}_i-D_{1i}\bar{K}_i)^T+2(\vartheta _1\tilde{L}_1+\vartheta _2\tilde{L}_2)$, $\Pi _{13}=A_{1i}-D_{1i}\bar{V}_iA_{1i}$, $\Pi _{14}=A_{2i}-D_{1i}\bar{V}_iA_{2i}$, $\Pi _{22}=-(1-\varpi )Q+2(\vartheta _3\tilde{L}_3+\vartheta _4\tilde{L}_4)$, $\Pi _{33}=-\vartheta _1(I_2\otimes \tilde{M}_1)$, $\Pi _{44}=-\vartheta _2(I_2\otimes \tilde{M}_2)$, $\Pi _{55}=-\vartheta _3(I_2\otimes \tilde{M}_3)$, $\Pi _{66}=-\vartheta _4(I_2\otimes \tilde{M}_4)$, $\Pi _{15}=B_{1i}-D_{1i}\bar{V}_iB_{1i}$, $\Pi _{16}=B_{2i}-D_{1i}\bar{V}_iB_{2i}$, $\Pi _{17}=\varphi (D_{1i}\bar{V}_i-I)\widetilde{\mathcal {M}}_i$, $\Pi _{18}=\bar{P}_i\widetilde{\mathcal {N}}_i^T$, $\Pi _{19}=[\sqrt{\bar{\lambda }_{i1}}\bar{P}_i\ldots \sqrt{\bar{\lambda }_{ii-1}}\bar{P}_i~\sqrt{\bar{\lambda }_{ii+1}}\bar{P}_i\ldots \sqrt{\bar{\lambda }_{iN}}\bar{P}_i]$, $\Pi _{99}=\textrm{diag}\{-\bar{P}_1,\ldots ,-\bar{P}_{i-1},-\bar{P}_{i+1},\ldots ,-\bar{P}_N\}$,

$$\begin{aligned}&\tilde{\Phi }_1= \begin{pmatrix} \tilde{M}_1(\Theta ^{RR})^2 &{} \tilde{M}_1\Theta ^{RR}\Theta ^{RI}\\ \tilde{M}_1\Theta ^{RR}\Theta ^{RI} &{} \tilde{M}_1(\Theta ^{RI})^2 \end{pmatrix},~~~ \tilde{\Phi }_2= \begin{pmatrix} \tilde{M}_2(\Theta ^{IR})^2 &{} \tilde{M}_2\Theta ^{IR}\Theta ^{II}\\ \tilde{M}_2\Theta ^{IR}\Theta ^{II} &{} \tilde{M}_2(\Theta ^{II})^2 \end{pmatrix},\\&\tilde{\Phi }_3= \begin{pmatrix} \tilde{M}_3(\Delta ^{RR})^2 &{} \tilde{M}_3\Delta ^{RR}\Delta ^{RI}\\ \tilde{M}_3\Delta ^{RR}\Delta ^{RI} &{} \tilde{M}_3(\Delta ^{RI})^2 \end{pmatrix},~~ \tilde{\Phi }_4= \begin{pmatrix} \tilde{M}_4(\Delta ^{IR})^2 &{} \tilde{M}_4\Delta ^{IR}\Delta ^{II}\\ \tilde{M}_4\Delta ^{IR}\Delta ^{II} &{} \tilde{M}_4(\Delta ^{II})^2 \end{pmatrix}, \end{aligned}$$

the other symbols note mentioned have the same meaning as defined in Theorem 1. Moreover, the matrices $K_i$ and $V_i$ in the integral sliding mode surface could be designed as

$$\begin{aligned} K_i=\bar{K}_i\bar{P}_i^{-1},~~~~~~V_i=D_{1i}^T. \end{aligned}$$

(36)

Proof

Denote the following block diagonal matrix:

$$\begin{aligned} \Psi _i=\textrm{diag}\{\bar{P}_i,\bar{P}_i,I,I,I,I,I,I\}. \end{aligned}$$

Set $P_i=\bar{P}_i^{-1}$, then pre-multiplying and post-multiplying (15) by $\Psi _i$ and its transpose respectively, by noticing the fact $K_i\bar{P}_i=\bar{K}_i$ and $V_i=D_{1i}^T$, we can easily obtain (33) by resorting to Schur complement lemma. In addition, based on the same techniques used in Theorem 1, another conditions (34) and (35) can be readily obtained. Here, the proof is omitted. $\square$

Remark 3

With the help of designed sliding mode controller, Theorem 2 presents some sufficient criterion to insure the stochastic stability of network (8). It should be pointed out that there is little research achievement on the dynamic analysis of semi-Markovian switching CVNs via sliding-mode controller. In addition, it is also observed that the obtained matrix inequality (33) is linear when positive scalars $\vartheta _\rho ~(\rho =1,2,3,4)$ are given, which means they can be easily calculated by the common MATLAB toolbox. Besides, the high dimension and plenty of variables can be effectively handled through a higher performance computer. Therefore, it vastly expands many engineering applications.

4 Sliding Mode Control Design

Through the above analysis, we will show a theorem to demonstrate the sliding mode controller synthesis procedure. A novel control law will be constructed, which can drive the system state trajectories onto the purpose-designed sliding mode surface $S(i,t)=0$ within the finite time and maintain them on the surface afterwards.

Theorem 3

Based on Assumption 1, it is supposed that the sliding mode switching surface is proposed as (11) where $K_i$, $V_i$ can be achieved by Theorem 2. The significative sliding motion controller is designed as follows:

$$\begin{aligned} u(t)=&-K_i \beta (t)-\big [V_i(D_{1i}V_i)^{-1}({\pi _i}+\Vert A_{1i}f_1(\beta (t))\Vert +\Vert B_{1i}g_1(\beta (t-\tau (t)))\Vert \nonumber \\&+\Vert A_{2i}f_2(\beta (t))\Vert \nonumber \\&+\Vert B_{2i}g_2(\beta (t-\tau (t)))\Vert +\Vert \widetilde{\mathcal {M}}_i\Vert \Vert \widetilde{\mathcal {N}}_i\beta (t)\Vert )\big ]\textrm{sign}(V_i^TS(i,t)) \end{aligned}$$

(37)

in which ${\pi _i}$ is a positive constant. Then, for the network (8), the state trajectories will be driven onto the purpose-designed sliding mode switching surface $S(i,t)=0$ within the finite time and maintained there in the subsequent time.

Proof

Choose the following Lyapunov function:

$$\begin{aligned} W(S(i,t))=\frac{1}{2}S^T(i,t)S(i,t). \end{aligned}$$

(38)

Combine (2), (3) with (38), by considering the time derivative of the sliding mode surface S(i, t), it is easy to get

$$\begin{aligned} \dot{W}(S(i,t))&=S^T(i,t)\dot{S}(i,t)\nonumber \\&=S^T(i,t)(V_i\dot{\beta }(t)+V_iE_{1i}\beta (t)+V_iD_{1i}K_i\beta (t))\nonumber \\&=S^T(i,t)\{V_i[-(E_{1i}+\Delta E_{1i})\beta (t)+A_{1i}f_1(\beta (t))\nonumber \\&\quad +A_{2i}f_2(\beta (t))+B_{1i}g_1(\beta (t-\tau (t)))\nonumber \\&\quad +B_{2i}g_2(\beta (t-\tau (t)))+D_{1i}u(t)] +V_iE_{1i}\beta (t)+V_iD_{1i}K_i\beta (t)\}\nonumber \\&=S^T(i,t)\Big \{V_i\big [-(E_{1i}+\widetilde{\mathcal {M}}_i\widehat{\mathcal {F}}(t) \widetilde{\mathcal {N}}_i)\beta (t)+A_{1i}f_1(\beta (t))+B_{1i}g_1(\beta (t-\tau (t)))\nonumber \\&\quad +A_{2i}f_2(\beta (t))\nonumber \\&\quad +B_{2i}g_2(\beta (t-\tau (t)))+D_{1i}[-K_i \beta (t)-({\pi _i}+V_i(D_{1i}V_i)^{-1}(\Vert A_{1i}f_1(\beta (t))\Vert \nonumber \\&\quad +\Vert A_{2i}f_2(\beta (t))\Vert +\Vert B_{1i}g_1(\beta (t-\tau (t)))\Vert +\Vert B_{2i}g_2(\beta (t-\tau (t)))\nonumber \\&\quad +\Vert \widetilde{\mathcal {M}}_i\Vert \Vert \widetilde{\mathcal {N}}_i\beta (t)\Vert ))\textrm{sign}(V_i^TS(i,t)))]\big ] +V_iE_{1i}\beta (t)+V_iD_{1i}K_i\beta (t)\Big \}\nonumber \\&\le \Vert S^T(i,t)V_i\Vert \Vert \widetilde{\mathcal {M}}_i\Vert \Vert \widetilde{\mathcal {N}}_i\beta (t)\Vert -\Vert \widetilde{\mathcal {M}}_i\Vert \Vert \widetilde{\mathcal {N}}_i\beta (t)\Vert \Vert V_i^TS(i,t)\Vert -{\pi _i}\Vert V_i^TS(i,t)\Vert \nonumber \\&=-{\pi _i}\Vert V_i^TS(i,t)\Vert =-\sqrt{2}{\pi _i}\Vert V_i\Vert W^{\frac{1}{2}}(S(i,t)). \end{aligned}$$

(39)

Next, set $S(r(0),0)=S_0$ and integrate both sides of the inequality (39) from 0 to t, one has

$$\begin{aligned} \mathbb {E}\{W(S(i,t))|S_0,r_0\}\le -\frac{\sqrt{2}}{2}{\pi _i} \Vert V_i\Vert t+W^{\frac{1}{2}}(S_0,r_0). \end{aligned}$$

(40)

Considering the fact that the left-hand of (40) is nonnegative, based on this, it can determine that W(t, i) will go to zero within the finite time regardless of $i\in \mathcal {S}$. Moreover, the finite time $t^{*}$ can be estimated by

$$\begin{aligned} t^{*}\le \frac{\sqrt{2W(S_0,r_0)}}{{\pi _i} \Vert V_i\Vert }. \end{aligned}$$

(41)

Therefore, it is obvious that the state trajectories of network (8) can be derived on to the designed surface $S(i,t)=0$ in virtue of the sliding motion control law (37) in finite time. That is to say, the sliding mode surface S(i, t) is reachable. The proof is completed. $\square$

Remark 4

For the existing relevant results on sliding mode control for semi-Markovian switching systems [37, 38], by resorting to the law of total probability, it can be found that the term $q_{ii}\times (W_i(h+\delta )-W_i(h)/(1-W_i(h))\times \mathbb {E}\{\beta ^T(t+\delta )P_i\beta (t+\delta )|\beta _t(s)\}$ has been lost. Although the achieved results are correct, the derivation process is not perfect. To solve this problem, this paper attempts to investigate the stabilization issue for delayed uncertain semi-Markovian switching CVNs via the proposed sliding mode control scheme, which further facilitates to understand the so-called “semi-Markovian switching model”.

Remark 5

It is imperative to point out that due to the stochastic perturbations in the practical environment, in this paper, the parameter uncertainties and the semi-Markovian switching mechanisms are taken into account when exploring the stabilization issue of the considered delayed CVNs via sliding mode control, which extends the related works [42, 43]. Moreover, the achieved results also mean that the parameter uncertainties have a great influence on the designed sliding mode controller.

Remark 6

It should be mentioned that, compare with the literature [44], in this paper, the designed sliding mode controller is more general because of the proposed sliding mode controller requires the involved matrix $D_{li}$ must be square matrix, while mine not. Moreover, the designed sliding mode controller also contains the matrices $\widetilde{\mathcal {M}}_i$ and $\widetilde{\mathcal {N}}_i$, which further illustrates the system parameter uncertainties have a great impact on the the designed sliding mode controller.

Remark 7

As is well-known that for the obtained the linear matrix inequalities, the computational complexity depends on the maximum number of decision variables, which sometimes brings time complexity in the process of solving. It is noteworthy that there are two common types of methods in the existing literature: the free variable method [44] and the Lyapunov-Krasovskii functionals [45], which will lead to the number of decision variables becomes large. At the same time, the corresponding computational burden will increase. In order to overcome this problem, we choose an appropriate Lyapunov-Krasovskii functionals without using the delay-decomposition technology and the free variable method. Some sufficient and less conservative results can be proposed compared with those in [44, 45]. When the considered systems are transformed into the general complex networks, the number of decision various in our results is $7 n^2+9n+2mn$. However, for the existing literatures [44, 45] without external disturbance and Markovian switching, the number of decision various is $12.5n^2+14.5n+3mn$ and $7 n^2+9.5n+2.5mn$, respectively. From this point of view, it was obvious that our results are less conservative in terms of computational complexity.

5 Numerical Example

In this section, an illustrative example is given to testify effectiveness of the achieved results. Consider a three-mode continuous-time semi-Markovian switching CVN (1), in which $E_1=\textrm{diag}\{0.14,0.15\}$, $E_2=\textrm{diag}\{0.12,0.12\}$, $E_3=\textrm{diag}\{0.10,0.10\}$, the remaining parameters are as follows:

$$\begin{aligned}&A_1= \begin{bmatrix} 1.11 + 1.23\textbf{i} &{} 0.96 - 0.83\textbf{i}\\ 1.12 - 1.31\textbf{i} &{}1.42 + 1.48\textbf{i} \end{bmatrix},~~~ B_1= \begin{bmatrix} 0.82 + 1.17\textbf{i}&{} 1.21 - 1.23\textbf{i}\\ 0.85 - 0.82\textbf{i}&{} 1.02 - 1.52\textbf{i} \end{bmatrix},~~~ D_1= \begin{bmatrix} 0.14\\ 1.43 \end{bmatrix},\\&A_2= \begin{bmatrix} 1.32 - 1.65\textbf{i} &{} 0.72 + 0.63\textbf{i} \\ 0.82 + 0.92\textbf{i} &{} 0.61+ 0.83\textbf{i} \end{bmatrix},~~~ B_2= \begin{bmatrix} 0.94 + 1.23\textbf{i} &{}0.81 - 1.25\textbf{i}\\ 0.82 + 0.93\textbf{i} &{} 0.74 - 0.72\textbf{i} \end{bmatrix},~~~ D_2= \begin{bmatrix} 0.21\\ 1.32 \end{bmatrix},\\&A_3= \begin{bmatrix} 0.42 - 1.34\textbf{i}&{} 0.68 + 1.13\textbf{i} \\ 1.34 + 0.12\textbf{i}&{} 0.82 + 0.78\textbf{i} \end{bmatrix},~~~ B_3= \begin{bmatrix} 0.78 + 1.21\textbf{i}&{} 0.71 - 1.12\textbf{i}\\ 0.81 + 1.28\textbf{i}&{} 0.77 - 0.86\textbf{i} \end{bmatrix},~~~ D_3= \begin{bmatrix} 0.16 \\ 1.28 \end{bmatrix}, \end{aligned}$$

and the activation functions are chosen as

$$\begin{aligned} f_{\iota }(w_{\iota })=g_{\iota }(w_{\iota })=\frac{1-A_\iota }{1+A_\iota } +\textbf{i}\frac{1-B_\iota }{1+B_\iota }. \end{aligned}$$

where $A_\iota =\exp (-x_{\iota })$ and $B=\exp (-y_{\iota })$. Therefore, it verifies that Assumption 1 holds with $\gamma _{\iota }^{RR}=\gamma _{\iota }^{II}=\zeta _{\iota }^{RR}=\zeta _{\iota }^{II}=0.5$, $\gamma _{\iota }^{RI}=\gamma _{\iota }^{IR}=\zeta _{\iota }^{RI}=\zeta _{\iota }^{IR}=0$. In addition, the time-varying delays $\tau (t)=0.4+0.1\sin (t)$. Furthermore, it also directly infers $\bar{\tau }=0.5$, $\varpi =0.1$.

In addition, the considered uncertain system parameters are obedient to the condition (2):

$$\begin{aligned}&\mathcal {M}_1= \begin{bmatrix} 0.21 &{} 0.13\\ 0.34 &{} 0.42 \end{bmatrix},~~~~~~ \mathcal {M}_2= \begin{bmatrix} 0.43 &{} 0.26\\ 0.31 &{} 0.45 \end{bmatrix},~~~~~~ \mathcal {M}_3= \begin{bmatrix} 0.43 &{} 0.26\\ 0.31 &{} 0.45 \end{bmatrix},\\&\mathcal {N}_1= \begin{bmatrix} 0.52 &{} 0.23\\ 0.25 &{} 0.39 \end{bmatrix},~~~~~~~~ \mathcal {N}_2= \begin{bmatrix} 0.17 &{} 0.23\\ 0.25 &{} 0.36 \end{bmatrix},~~~~~~~ \mathcal {N}_3= \begin{bmatrix} 0.17 &{} 0.21 \\ 0.25 &{} 0.54 \end{bmatrix} \end{aligned}$$

and the unknown real matrix $\mathcal {F}(t)$ is set as a random $2\times 2$ matrix, which satisfies the constraint (3).

The semi-Markovian switching trajectory is shown in Fig. 2. Suppose sojourn-time obeys a Weibull distribution, and the corresponding probability density function $\hbar (h)=(\tilde{\beta }/{\tilde{\alpha }^{\tilde{\beta }}})h^{\tilde{\beta }-1}\exp [-(h/\tilde{\alpha })^{\tilde{\beta }}]$, where $\tilde{\alpha }$ is the scale parameter and $\tilde{\beta }$ denotes the shape parameter. When mode $i=1$, set $\tilde{\alpha }=1$ and $\tilde{\beta }=2$, it infers the transition rate function is 2h, then $\hbar _1(h)=2he^{-h^2}$; When mode $i=2$, set $\tilde{\alpha }=2$ and $\tilde{\beta }=2$, it means the transition rate function is 0.5h, then $\hbar _2(h)=0.5he^{-0.25h^2}$; When mode $i=3$, let $\tilde{\alpha }=1$ and $\tilde{\beta }=3$, it gets the transition rate function is 3h, then $\hbar _3(h)=3h^2e^{-h^2}$. Therefore, the transition rate matrix is readily concluded as follows

$$\begin{aligned} \Lambda (h)= \begin{bmatrix} -4h &{} 2h&{}2h \\ 0.5h &{} -h&{}0.5h \\ 3h^2 &{} 3h^2&{}-6h^2 \end{bmatrix}. \end{aligned}$$

Fig. 2

Illustration of the trajectory for semi-Markovian chain r(t)

Based on the above analysis, combine with the principle of calculating mathematical expectations, for the transition rate $\lambda _{12}(h)$, we can obtain $\mathbb {E}\{\lambda _{12}(h)\}=\int _0^{\infty }2\,h \hbar _1(h)\textrm{d}h= \int _0^{\infty }4\,h^2 e^{-h^2} \textrm{d}h=1.7725$. In a same way, for the given transition rate matrix, its mathematical expectation can be computed as

$$\begin{aligned} \mathbb {E}\{\Lambda (h)\}= \begin{bmatrix} -3.5450 &{} 1.7725&{}1.7725 \\ 0.8862&{} -1.7724&{}0.8862\\ 2.4372 &{} 2.4372&{}-4.8744 \end{bmatrix}. \end{aligned}$$

Based on the above system parameters, feasible solution to inequalities (33)–(35) in Theorem 2 can be derived by utilizing the Matlab Toolbox. In consideration of the space limitation, only partial solutions are listed as $\vartheta _\iota =1~(\iota =1,2,3,4)$, $\varphi =1024.6$, $\tilde{M}_2 =\textrm{diag}\{1.7958, 1.6746\}$, $\tilde{M}_3 =\textrm{diag}\{12.1368,14.9074\}$, $\tilde{M}_4 =\textrm{diag}\{12.1417,14.9074\}$, and

$$\begin{aligned}&\bar{P}_1=1.0e+03* \begin{bmatrix} 2.4353 &{} 2.9785 &{} 0 &{} 0\\ 2.9785 &{} 3.6757 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.9089 &{} 1.0868\\ 0 &{} 0 &{} 1.0868 &{} 1.3161 \end{bmatrix},\\&\tilde{L}_1= \begin{bmatrix} 35.6666 &{} 39.0480 &{} 0 &{} 0\\ 39.0480 &{} 43.7975 &{} 0 &{} 0\\ 0 &{} 0 &{} 42.6983 &{} 47.3194\\ 0 &{} 0 &{} 47.3194 &{} 52.6494 \end{bmatrix},\\&\bar{P}_3=1.0e+03* \begin{bmatrix} 1.8454 &{} 2.1263 &{} 0 &{} 0\\ 2.1263 &{} 2.4798 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.7860 &{} 0.8834\\ 0 &{} 0 &{} 0.8834 &{} 1.0063 \end{bmatrix},\\&\tilde{L}_2= \begin{bmatrix} 35.7036 &{} 39.0429 &{} 0 &{} 0\\ 39.0429 &{} 43.7908 &{} 0 &{} 0\\ 0 &{} 0 &{} 42.6983 &{} 47.3194\\ 0 &{} 0 &{} 47.3194 &{} 52.6494 \end{bmatrix},\\&\bar{K}_3= \begin{bmatrix} 274.8230 &{} 148.7940&{} 0 &{} 0\\ 0 &{} 0 &{} 310.1467 &{} 273.9653\\ \end{bmatrix}, \end{aligned}$$

and the other matrices are omitted for space consideration. Then, the desired gain matrices $K_i~(i=1,2,3)$ can be obtained by simple calculation as follows:

$$\begin{aligned}&K_1=\bar{K}_1\bar{P}_1^{-1}= \begin{bmatrix} -21.4415 &{} 18.6954 &{} 0 &{} 0\\ 0 &{} 0 &{}-15.9144 &{} 14.2719 \end{bmatrix}, \\&K_2=\bar{K}_2\bar{P}_2^{-1}= \begin{bmatrix} 4.7800 &{} -3.7596 &{} 0 &{} 0\\ 0 &{} 0 &{} 3.9535 &{} -2.8977 \end{bmatrix}, \\&K_3=\bar{K}_3\bar{P}_3^{-1}= \begin{bmatrix} 6.6017 &{} -5.6005 &{} 0 &{} 0\\ 0 &{} 0 &{} 6.7351 &{} -5.6409 \end{bmatrix}. \end{aligned}$$

In addition, setting $V_i=\bar{V}_i~(i=1,2,3)$, we can obtain the following mode-dependent switching surfaces:

$$\begin{aligned}&S(1,t)= V_1 \beta (t)-V_1\int _0^t(-E_{11}-D_{11}K_1)\beta (s)\textrm{d}s,~~~~\text {for} ~i=1,\\&S(2,t)= V_2 \beta (t)-V_2\int _0^t(-E_{12}-D_{12}K_2)\beta (s)\textrm{d}s,~~~~\text {for} ~i=2,\\&S(3,t)= V_3 \beta (t)-V_3\int _0^t(-E_{13}-D_{13}K_3)\beta (s)\textrm{d}s,~~~~\text {for} ~i=3. \end{aligned}$$

On the other hand, when the considered systems are transformed into the same networks and address the same stabilization problem, it can be effectively varied that the achieved theoretical results in [44] have no feasible solutions, while our criteria have. In other words, the achieved theoretical criteria in this paper own less conservative performance than the existing results in [44].

The simulation results of this paper are showed in the following Figs. 3, 4, 5 and 6, and the numerical simulation is performed from the initial conditions $w_1(t)=2.5+3.2\textbf{i}$, $w_2(t)=-3-4.6\textbf{i}$ for $t\in [-0.5,0]$. When $u(t)=0$, the time responses of the real part and imaginary part of the states w(t) for the open-loop system (8) are shown in Fig. 3. Obviously, the open-loop system (8) is unstable. Choose ${\pi _i}=0.1$, according to the proposed sliding mode control law u(t) in (37), the the time responses of the real and imaginary parts for the closed-loop system (8) is shown in Fig. 4. Figure 5 depicts the trajectories of the sliding mode surface function. Besides, the external control input u(t) is shown in Fig. 6. Based on this visual angle, it can draw a conclusion that the designed sliding mode control scheme is effective and feasible.

Fig. 3

The trajectories of practical real and imaginary parts of the state w(t) for network (1)

Fig. 4

The trajectories of practical real and imaginary parts of the state w(t) for network (1)

Fig. 5

The trajectories of the sliding mode switching surface S(t, r(t))

Fig. 6

The trajectories of the sliding mode control input u(t) with three modes

6 Conclusions

This is the first time to propose a more general design scheme on sliding mode controller for delayed uncertain semi-Markovian switching CVNs. Combining the original system and switching surface, a holonomic sliding mode dynamical system has been obtained to explore the dynamical properties. By utilizing Dynkin’s formula, Lyapunov stability theory as well as the characteristics of cumulative distribution functions, several sufficient criteria are achieved to insure the issue of stochastic stability for sliding mode dynamic system. Furthermore, for the underlying closed-loop system, design a proper sliding mode controller to guarantee the state trajectories can let the given presupposed sliding mode surface within the finite time and maintain there in the subsequent time. Finally, effectiveness of the derived theoretical results is illustrated by one simulation example. In the future, some attentions will be investigated for for the stabilization issue of semi-Markovian switching uncertain CVNs with generally uncertain transition rates by means of the mode-dependent integral sliding mode controller [46, 47], where the considered transition rates information the semi-Markovian process is assumed to be two cases: completely unknown and unknown but with known bounds, which may more reflect some certain practical systems.