Skip to main content
SpringerLink
Log in

Finite element formulation for higher-order shear deformation beams using two-phase local/nonlocal integral model

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

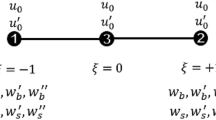
In this paper, the static and dynamic analysis of the higher-order shear deformation nanobeam is investigated within the framework of the two-phase local/nonlocal integral model, in which, the stress is described as the integral convolution form between the strain field and a decay kernel function to address the long-range force interactions in the domain. Based on the principle of minimum potential energy, the finite element formulation of the nonlocal higher-order shear deformation theory nanobeams is derived in a general sense through finite element method (FEM). The explicit expressions of the stiffness, geometric stiffness and mass stiffness matrix of the higher-order shear deformation theory nanobeams are derived directly. The efficiency and accuracy of the developed finite element model of higher-order shear deformation nanobeam are validated by conducting a comparation with the existing analysis results in the researches. Furthermore, under different loading and supported conditions, the effect of nonlocal parameter, nonlocal phase parameter and slenderness ratio on the bending, buckling and free vibration responses of higher-order shear deformation theory nanobeams is investigated in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Touratier, M.: An efficient standard plate theory. Int. J. Eng. Sci. 29, 901–916 (1991)

    Article  Google Scholar 

  2. Reddy, J.N.: A simple higher-order theory for laminated composite plates. Transactions of the ASME. J. Appl. Mech. 51, 745–752 (1984)

    Article  ADS  Google Scholar 

  3. Yesilce, Y., Catal, S.: Free vibration of axially loaded Reddy-Bickford beam on elastic soil using the differential transform method. Struct. Eng. Mech. 31, 453–475 (2009)

    Article  Google Scholar 

  4. Yesilce, Y., Catal, H.H.: Solution of free vibration equations of semi-rigid connected Reddy–Bickford beams resting on elastic soil using the differential transform method. Arch. Appl. Mech. 81, 199–213 (2011)

    Article  ADS  Google Scholar 

  5. Yesilce, Y.: Effect of axial force on the free vibration of Reddy–Bickford multi-span beam carrying multiple spring-mass systems. J. Vib. Control 16, 11–32 (2010)

    Article  MathSciNet  Google Scholar 

  6. Lee, C.W.J.R.K.: Shear deformable beams and plates relationships with classical solutions. Eng. Struct. 23, 873–874 (2001)

    Article  Google Scholar 

  7. Soldatos, K.P.: A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 94, 195–220 (1992)

    Article  MathSciNet  Google Scholar 

  8. Aydogdu, M., Taskin, V.: Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 28, 1651–1656 (2007)

    Article  Google Scholar 

  9. Ben-Oumrane, S., Abedlouahed, T., Ismail, M., Mohamed, B.B., Mustapha, M., El Abbas, A.B.: A theoretical analysis of flexional bending of Al/Al2O3 S-FGM thick beams. Comput. Mater. Sci. 44, 1344–1350 (2009)

    Article  CAS  Google Scholar 

  10. Şimşek, M.: Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nucl. Eng. Des. 240, 697–705 (2010)

    Article  Google Scholar 

  11. Li, X.-F., Wang, B.-L., Han, J.-C.: A higher-order theory for static and dynamic analyses of functionally graded beams. Arch. Appl. Mech. 80, 1197–1212 (2010)

    Article  ADS  Google Scholar 

  12. Wattanasakulpong, N., Prusty, B.G., Kelly, D.W.: Thermal buckling and elastic vibration of third-order shear deformable functionally graded beams. Int. J. Mech. Sci. 53, 734–743 (2011)

    Article  Google Scholar 

  13. Imek, M.J.I.J.E.A.: Static analysis of a functionally graded beam under a uniformly distributed load by Ritz method. Int. J. Eng. Appl. Sci. 1(3), 1–11 (2009)

    Google Scholar 

  14. Wang, B., Zhou, S., Zhao, J., Chen, X.: Size-dependent pull-in instability of electrostatically actuated microbeam-based MEMS. J. Micromech. Microeng. 21(2), 027001 (2011)

    Article  ADS  Google Scholar 

  15. Witvrouw, A., Mehta, A.: The use of functionally graded poly-SiGe layers for MEMS applications. In: VanderBiest, O., Gasik, M., Vleugels, J. (eds.) Functionally Graded Materials, pp. 255–260. Trans Tech Publications Ltd (2005)

    Google Scholar 

  16. Lee, Z., Ophus, C., Fischer, L.M., Nelson-Fitzpatrick, N., Westra, K.L., Evoy, S., et al.: Metallic NEMS components fabricated from nanocomposite Al-Mo films. Nanotechnology 17, 3063–3070 (2006)

    Article  CAS  Google Scholar 

  17. Eringen, A.C.: On nonlocal elasticity. Int. J. Eng. Sci. 10, 233–248 (1972)

    Article  MathSciNet  Google Scholar 

  18. Eringen, A.C.: On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54, 4703–4710 (1983)

    Article  ADS  Google Scholar 

  19. Lam, D.C.C., Yang, F., Chong, A.C.M., Wang, J., Tong, P.: Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 51, 1477–1508 (2003)

    Article  ADS  Google Scholar 

  20. Yang, F., Chong, A.C.M., Lam, D.C.C., Tong, P.: Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 39, 2731–2743 (2002)

    Article  Google Scholar 

  21. Kröner, E.: Elasticity theory of materials with long range cohesive forces. Int. J. Solids Struct. 3, 731–742 (1967)

    Article  Google Scholar 

  22. Eringen, A.C.: Theory of nonlocal elasticity and some applications. Res Mechanica. 21, 313–342 (1987)

    Google Scholar 

  23. Eringen, A.C.: Nonlocal continuum mechanics based on distributions. Int. J. Eng. Sci. 44, 141–147 (2006)

    Article  MathSciNet  Google Scholar 

  24. Wang, C.M., Xiang, Y., Kitipornchai, S.: Postbuckling of nano rods/tubes based on nonlocal beam theory. Int. J. Appl. Mech. 1, 259–266 (2009)

    Article  Google Scholar 

  25. Nejad, M.Z., Hadi, A., Rastgoo, A.: Buckling analysis of arbitrary two-directional functionally graded Euler–Bernoulli nano-beams based on nonlocal elasticity theory. Int. J. Eng. Sci. 103, 1–10 (2016)

    Article  MathSciNet  Google Scholar 

  26. Elmeichea, N., Abbadb, H., Mechabc, I., Bernard, F.: Free vibration analysis of functionally graded beams with variable cross-section by the differential quadrature method based on the nonlocal theory. Struct. Eng. Mech. 75, 737–746 (2020)

    Google Scholar 

  27. Sayyad, A.S., Ghugal, Y.M.: Bending, buckling and free vibration analysis of size-dependent nanoscale FG beams using refined models and Eringen’s nonlocal theory. Int. J. Appl. Mech. 12(1), 2050007 (2020)

    Article  Google Scholar 

  28. Jena, S.K., Chakraverty, S., Malikan, M., Mohammad-Sedighi, H.: Hygro-magnetic vibration of the single-walled carbon nanotube with nonlinear temperature distribution based on a modified beam theory and nonlocal strain gradient model. Int. J. Appl. Mech. 12(05), 2050054 (2020)

    Article  Google Scholar 

  29. Refaeinejad, V., Rahmani, O., Hosseini, S.A.H.: Evaluation of nonlocal higher order shear deformation models for the vibrational analysis of functionally graded nanostructures. Mech. Adv. Mater. Struct. 24, 1116–1123 (2017)

    Article  Google Scholar 

  30. Huu-Tai, T., Vo, T.P.: Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 62, 57–66 (2012)

    Article  Google Scholar 

  31. Ebrahimi, F., Barati, M.R.: A nonlocal higher-order shear deformation beam theory for vibration analysis of size-dependent functionally graded nanobeams. Arab. J. Sci. Eng. 41, 1679–1690 (2015)

    Article  MathSciNet  Google Scholar 

  32. Challamel, N., Wang, C.M.: The small length scale effect for a non-local cantilever beam: a paradox solved. Nanotechnology 19(34), 345703 (2008)

    Article  CAS  PubMed  Google Scholar 

  33. Li, C., Yao, L., Chen, W., Li, S.: Comments on nonlocal effects in nano-cantilever beams. Int. J. Eng. Sci. 87, 47–57 (2015)

    Article  Google Scholar 

  34. Fernandez-Saez, J., Zaera, R., Loya, J.A., Reddy, J.N.: Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 99, 107–116 (2016)

    Article  MathSciNet  Google Scholar 

  35. Lu, P., Lee, H.P., Lu, C., Zhang, P.Q.: Dynamic properties of flexural beams using a nonlocal elasticity model. J. Appl. Phys. 99, 073510 (2006)

    Article  ADS  Google Scholar 

  36. Wang, C.M., Zhang, Y.Y., He, X.Q.: Vibration of nonlocal Timoshenko beams. Nanotechnology 18(10), 105401 (2007)

    Article  ADS  Google Scholar 

  37. Tuna, M., Kirca, M.: Exact solution of Eringen’s nonlocal integral model for bending of Euler–Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 105, 80–92 (2016)

    Article  MathSciNet  Google Scholar 

  38. Tuna, M., Kirca, M.: Exact solution of Eringen’s nonlocal integral model for vibration and buckling of Euler–Bernoulli beam. Int. J. Eng. Sci. 107, 54–67 (2016)

    Article  Google Scholar 

  39. Alotta, G., Failla, G., Zingales, M.: Finite element method for a nonlocal Timoshenko beam model. Finite Elem. Anal. Des. 89, 77–92 (2014)

    Article  Google Scholar 

  40. Norouzzadeh, A., Ansari, R.: Finite element analysis of nano-scale Timoshenko beams using the integral model of nonlocal elasticity. Phys. E-Low-Dimens. Syst. Nanostruct. 88, 194–200 (2017)

    Article  ADS  Google Scholar 

  41. Eptaimeros, K.G., Koutsoumaris, C.C., Tsamasphyros, G.J.: Nonlocal integral approach to the dynamical response of nanobeams. Int. J. Mech. Sci. 115, 68–80 (2016)

    Article  Google Scholar 

  42. Rajasekaran, S., Khaniki, H.B.: Finite element static and dynamic analysis of axially functionally graded nonuniform small-scale beams based on nonlocal strain gradient theory. Mech. Adv. Mater. Struct. 26, 1245–1259 (2019)

    Article  Google Scholar 

  43. Taghizadeh, M., Ovesy, H.R., Ghannadpour, S.A.M. Beam Buckling Analysis by Nonlocal Integral Elasticity Finite Element Method. International Journal of Structural Stability and Dynamics. 2016, 16.

  44. Romano, G., Barretta, R.: Comment on the paper “Exact solution of Eringen’s nonlocal integral model for bending of Euler Bernoulli and Timoshenko beams” by Meral Tuna & Mesut Itirca. Int. J. Eng. Sci. 109, 240–242 (2016)

    Article  Google Scholar 

  45. Barretta, R., de Sciarra, F.M.: Constitutive boundary conditions for nonlocal strain gradient elastic nano-beams. Int. J. Eng. Sci. 130, 187–198 (2018)

    Article  MathSciNet  Google Scholar 

  46. Eringen, A.C.: Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 10, 425–435 (1975)

    Article  Google Scholar 

  47. Fakher, M., Behdad, S., Naderi, A., Hosseini-Hashemi, S.: Thermal vibration and buckling analysis of two-phase nanobeams embedded in size dependent elastic medium. Int. J. Mech. Sci. 171, 105381 (2020)

    Article  Google Scholar 

  48. Fakher, M., Hosseini-Hashemi, S.: Vibration of two-phase local/nonlocal Timoshenko nanobeams with an efficient shear-locking-free finite-element model and exact solution. Eng. Comput. 38, 231–245 (2022)

    Article  Google Scholar 

  49. Danesh, H., Javanbakht, M.: Free vibration analysis of nonlocal nanobeams: a comparison of the one-dimensional nonlocal integral Timoshenko beam theory with the two-dimensional nonlocal integral elasticity theory. Math. Mech. Solids 27, 557–577 (2022)

    Article  MathSciNet  Google Scholar 

  50. Khodabakhshi, P., Reddy, J.N.: A unified integro-differential nonlocal model. Int. J. Eng. Sci. 95, 60–75 (2015)

    Article  MathSciNet  Google Scholar 

  51. Naghinejad, M., Ovesy, H.R.: Nonlinear post-buckling analysis of viscoelastic nano-scaled beams by nonlocal integral finite element method. Zamm-Zeitschrift Fur Angewandte Mathematik Und Mechanik. 102(7), e202100148 (2022)

    Article  MathSciNet  Google Scholar 

  52. Pinnola, F.P., Vaccaro, M.S., Barretta, R., de Sciarra, F.M.: Finite element method for stress-driven nonlocal beams. Eng. Anal. Boundary Elem. 134, 22–34 (2021)

    Article  MathSciNet  Google Scholar 

  53. Reddy, J.N.: A simple higher-order theory for laminated composite plates. J. Appl. Mech. 51(4), 745–752 (1985)

    Article  Google Scholar 

  54. Touratier, M.: An efficient standard plate-theory. Int. J. Eng. Sci. 29, 901–916 (1991)

    Article  Google Scholar 

  55. Soldatos, K.P.: A transverse-shear deformation-theory for homogeneous monoclinic plates. Acta Mech. 94, 195–220 (1992)

    Article  MathSciNet  Google Scholar 

  56. Eringen, A.C.: Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 10, 425–435 (1972)

    Article  Google Scholar 

  57. Wang, Y.B., Zhu, X.W., Dai, H.H.: Exact solutions for the static bending of Euler-Bernoulli beams using Eringen’s two-phase local/nonlocal model. AIP Adv. 6, 085114 (2016)

    Article  ADS  Google Scholar 

  58. Zhu, X., Wang, Y., Dai, H.-H.: Buckling analysis of Euler-Bernoulli beams using Eringen’s two-phase nonlocal model. Int. J. Eng. Sci. 116, 130–140 (2017)

    Article  MathSciNet  Google Scholar 

  59. Zhang, P., Schiavone, P., Qing, H.: Local/nonlocal mixture integral models with bi-Helmholtz kernel for free vibration of Euler-Bernoulli beams under thermal effect. J. Sound Vibr. 525, 116798 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

The work is supported by the National Natural Science Foundation of China(No. 12172169) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Author information

Authors and Affiliations

  1. State Key Laboratory of Mechanics and Control for Aerospace Structures, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Yuan Tang & Hai Qing

Authors
  1. Yuan Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai Qing
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Y.T. and H.Q. wrote the main manuscript text and prepared all figures. H.Q. reviewed the manuscript.

Corresponding author

Correspondence to Hai Qing.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, Y., Qing, H. Finite element formulation for higher-order shear deformation beams using two-phase local/nonlocal integral model. Arch Appl Mech (2024). https://doi.org/10.1007/s00419-024-02571-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00419-024-02571-z

Keywords

Search

Navigation