Solving Maxmin Optimization Problems via Population Games

Abstract

Population games are games with a finite set of available strategies and an infinite number of players, in which the reward for choosing a given strategy is a function of the distribution of players over strategies. The paper shows that, in a certain class of maxmin optimization problems, it is possible to associate a population game to a given maxmin problem in such a way that solutions to the optimization problem are found from Nash equilibria of the associated game. Iterative solution methods for maxmin optimization problems can then be derived from systems of differential equations whose trajectories are known to converge to Nash equilibria. In particular, we use a discrete-time version of the celebrated replicator equation of evolutionary game theory, also known in machine learning as the exponential multiplicative weights algorithm. The resulting algorithm can be viewed as a generalization of the Iteratively Reweighted Least Squares (IRLS) method, which is well known in numerical analysis as a useful technique for solving Chebyshev function approximation problems on a finite grid. Examples are provided to show the use of the generalized IRLS method in collective investment and in decision making under model uncertainty.

1 Introduction

In a maxmin problem, the objective is to find a point in a given set at which the minimum of a given collection of functions defined on that set is maximized. Problems of this nature can be viewed from the perspective of social planning. The given set is then interpreted as a space of possible decisions that may be taken by a social planner. The given functions defined on this set represent the benefits that are experienced by different members of a collective as a consequence of the planner’s decision. The use of the maxmin criterion indicates that the planner follows the ethical guideline of Rawls [52]: among all possible ways of organizing society, choose the one that maximizes the happiness of those who are least advantaged.

Within the mindset of social planning, one can think also of using the weighted-utilitarian guideline: maximize the weighted sum of the welfares of all members of the collective. The optimization problem that arises from this rule may well be easier to solve than the nonsmooth maxmin problem. One may then imagine the following iterative scheme to solve the maxmin problem, using the assumption that the planner has an effective way of parametrizing decisions in terms of weights. Starting with an arbitrary set of weights, the planner computes the corresponding decision, and subsequently notes which participants in the collective would be worst off if this decision would be implemented. In the second round of the iteration, the weights of those participants are increased, and the planner determines a new tentative decision on the basis of the updated weights. In the next round, the weights of those who are found to be worst off under this decision are increased, and so on. The iteration stops when a set of weights is found that is concentrated on a group of participants who are equally affected by the corresponding decision, while all others, even though they have zero weights, are in fact better off, or at least not worse off. If the parametrization of decisions in terms of weights satisfies certain conditions (see Definition 2.4 below), we have arrived at a maxmin solution (Lemma 2.2).

The success of this iterative method depends crucially, of course, on the update rule that is used for the weights. The innovative approach that we propose in this paper is to make use of update rules that have been designed in the field of population games. Population games are rooted in biology [42] and have been successfully applied to traffic networks and to other fields of study; see for instance [58]. They have, however, not been leveraged to solve maxmin problems before.

To specify a (single-)population game, one begins with a finite set of pure strategies that may be chosen by agents. The number of agents is thought of as large enough to be treated as infinite, and agents are only distinguished by the strategy that they choose. The population state is defined as the vector whose i-th entry gives the population fraction of agents who follow strategy i. The payoffs of strategies are given by reward functions that depend on the population state. In a Nash equilibrium, all strategies that are used by a positive fraction of agents have equal payoffs, whereas strategies that are not used have worse payoffs, or at least not better payoffs. Such an equilibrium may be reached by gradual evolution in time, when agents adapt their strategies in response to differences in payoffs. To a large extent, the literature on population games revolves around different evolutionary dynamics (adaptation rules) that may lead to Nash equilibrium.

In this paper, conditions are given under which the solution of a given maxmin problem can be found from a Nash equilibrium in a corresponding population game. From the perspective of maxmin problems, the connection gives access to a rich array of potential iterative solution algorithms, obtained by discretization of the continuous-time dynamical systems studied in the theory of population games. From the perspective of game theory, these applications provide a motivation to study the special properties of population games that arise from maxmin problems; we call them “tester games”, for reasons that will be explained later. While there is of course a traditional link between game theory and maxmin problems via two-person zero-sum games, the connection established in this paper is of an entirely different nature.

Relations to the literature. The work that we have found to be most closely related to the approach of this paper is concerned with approximation of a function by a linear combination of preset basis functions in such a way that the maximal error on a given finite set of grid points is minimized (approximation in $\ell _\infty$ norm, also called Chebyshev approximation). More than sixty years ago, Charles L. Lawson proposed in his PhD thesis¹ [37] an iterative method based on adapting weights in a weighted-sum problem using transformed objectives: he replaced the absolute values of errors at grid points by their squares. Lawson called this the Iteratively Reweighted Least Squares (IRLS) method. The IRLS method is still in use as a tool for function approximation; see [44] for a modern implementation. The main generalizations of Lawson’s method in the literature have been to function approximation in other than the max ($\ell _\infty$) norm. In particular, the use of the $\ell _1$ norm has attracted much interest, in statistics because of its robustness properties and in signal processing because of its sparsity features [20, 60, 61]. Approximation in $\ell _p$ norm with $2< p < \infty$ has found application in the design of finite impulse response (FIR) filters [17].² These generalizations to approximations in alternative norms are achieved by appropriate modifications of the multiplicative update rule for weights that was used by Lawson. In this paper, we undertake a different generalization. We allow for more general transformations of the individual objectives; in particular, different transformations may be applied to different objectives. Going even further, we identify the crucial properties of the parametrization in terms of weights, and allow any mapping that satisfies these properties. Connections to population games were not noted by Lawson or in the subsequent literature in numerical analysis.

The present paper also relates to the large body of literature on learning in games. The notion that a Nash equilibrium in mixed strategies can be found from a differential equation (or, in discrete time, by an iteration) goes back to the early days of game theory [15, 16, 54]. Updating rules for strategies have ever since remained a topic of interest; see for instance [25] for an extensive treatment, and [27, 39, 43] for a sample of recent contributions. Among the many learning rules that have been proposed, the Multiplicative Weights Algorithm (MWA) stands out as the one that is perhaps most prominent. Generally speaking, multiplicative weights algorithms are iterations defined on a simplex or on a finite product of simplices, in which in each step the current point in the simplex or product of simplices is multiplied componentwise by a vector whose entries typically represent rewards or costs, or by a componentwise monotonic transformation of such a vector; the monotonic transformation may contain an adjustable parameter that is called the “step size” or the “learning rate”. The update rule used in [37] is a multiplicative weights rule (without adjustable parameter). An early reference in the literature on machine learning is the winnow algorithm of [40]. The term “multiplicative weights” as such may have been used first in [24]; they may also have been the first to use the exponential form of the MWA that we employ in this paper as well. A survey of the use of the MWA in game theory and machine learning is given in [1]. The cited paper collects many examples of applications of the MWA, with a focus on learning in games and machine learning. Lawson’s method is not mentioned, however; it seems that the connection between learning in games and maxmin problems as discussed in this paper has not been noticed in the literature before. From another (engineering) perspective, the tester games that we consider in this paper are evolutionary games designed to achieve a particular goal, and hence are examples of evolutionary mechanism design; see, for instance, [49].

Contributions. The main contribution of the paper is the introduction of the notion of “tester games” and the proof (see Theorem 3.1) that Nash equilibria in these games provide solutions to certain types of maxmin problems. As a practical result, this leads to the generalized IRLS method for solving maxmin problems (Algorithm 5.1). We also give necessary conditions for a population game to be a tester game (Proposition 3.1).

Outline. Following the present introduction, the class of maxmin problems to which the method of this paper applies is defined in Sect. 2. We then introduce tester games in Sect. 3 and show how Nash equilibria of these games produce maxmin solutions. Section 4 considers the special case in which a tester game is constructed from the given objective functions directly, without transformations; in this case, it turns out that (under smoothness assumptions) the tester game is in fact a contractive potential game. To derive a computational method, Sect. 5 brings in the exponential version of the MWA. Applications to collective investment and to decision making under model uncertainty are given in Sect. 6. Section 7 concludes. An example illustrating a theoretical point is worked out in the “Appendix”.

Notation and conventions. We use ${\mathbb {R}}_+$ to denote the set of nonnegative real numbers, and ${\mathbb {R}}_{++}$ to denote the set of positive real numbers. When z is a function from a set N to ${\mathbb {R}}$ (i.e., z is a vector in ${\mathbb {R}}^N$) and K is a nonempty subset of N, the restriction of z to K is denoted by $z_K$. The vector $z_K$ belongs to ${\mathbb {R}}^K$. Conversely, if a vector $z \in {\mathbb {R}}^K$ is given, we can associate to it a vector in ${\mathbb {R}}^N$, still denoted by z, by defining $z_i = 0$ for $i \in N \setminus K$. This defines a natural embedding of ${\mathbb {R}}^K$ into ${\mathbb {R}}^N$. Since we do not distinguish notationally between $z \in {\mathbb {R}}^K$ and its embedding into ${\mathbb {R}}^N$, the symbol ${\mathbb {R}}^K$ can refer to a linear space by itself, or to the subset of ${\mathbb {R}}^N$ of vectors whose entries with indices outside K are 0. The unit simplex associated to a nonempty finite set N is defined by

$$\begin{aligned} \varDelta _N = \{ w \in {\mathbb {R}}^N \mid w_i \ge 0 \text { for all } i \in N, \;\; \sum _{i\in N} w_i = 1 \}. \end{aligned}$$

In analogy with the conventions above, when K is a nonempty subset of N, the simplex $\varDelta _K$ is identified with the face of the simplex N consisting of vectors w such that $w_i=0$ for $i \in N {\setminus } K$. When K is a singleton, say $K = \{k\}$, the corresponding face contains only one point; this point is denoted by $e_k$. The function from N to ${\mathbb {R}}$ that takes the value 1 for all $i \in N$ (the “all-one vector”) is denoted by $\mathbbm {1}_N$. The tangent space $T\varDelta _N$ of the simplex is the set $\{ z \in {\mathbb {R}}^N \mid \mathbbm {1}_N^{\tiny \top }z = 0 \}$. The set of vectors that can be written as the product of a vector in $\varDelta _N$ and a positive scalar (i.e., “unnormalized weight vectors”) is written as

$$\begin{aligned} \varDelta _N^+= \{ w \in {\mathbb {R}}^N \mid w_i \ge 0 \text { for all } i \in N, \;\; \sum _{i\in N} w_i > 0 \} = {\mathbb {R}}^N_+ \setminus \{0\}. \end{aligned}$$

A vector-valued function F defined on $\varDelta _N^+$ is said to be homogeneous of degree m if $F(aw)=a^mF(w)$ for all $a>0$ and $w \in \varDelta _N^+$.

Following [2], we use the term “Pareto optimal” for what in part of the literature is called “weakly Pareto optimal”; see Definition 2.1.³ Correspondingly, we use “Pareto improvement” for what is often called “strict Pareto improvement”.

2 Simplicial Social Decision Problems

Throughout the paper, our goal is to characterize and compute maxmin points for a class of problems we call simplicial social decision problems. In this section, we introduce this class of problems and collect some basic properties. Most results in this section are elementary and have been stated before, e.g., in the decision theory literature or—with a different terminology—in the statistics literature. The main innovation is the concept of a “Pareto map”, a certain smooth parametrization of the Pareto surface which will play a key role in later sections.

Definition 2.1

A social decision problem is a triple $(N,{\mathcal {X}},V)$ where N is a finite set called the collective, ${\mathcal {X}}$ is a topological space called the decision space, and $V\,{:}\;{\mathcal {X}}\rightarrow {\mathbb {R}}^N$ is a continuous mapping called the evaluation map. A point $x \in {\mathcal {X}}$ is said to be

• equalizing if $V_i(x) = V_j(x)$ for all $i,j \in N$

• Pareto optimal if there does not exist ${\tilde{x}}\in {\mathcal {X}}$ such that $V_i({\tilde{x}}) > V_i(x)$ for all $i \in N$

• strongly Pareto optimal if there does not exist ${\tilde{x}}\in {\mathcal {X}}$ such that $V_i({\tilde{x}}) \ge V_i(x)$ for all $i \in N$ and $V_j({\tilde{x}}) > V_j(x)$ for some $j \in N$

• maxmin if there does not exist ${\tilde{x}}\in {\mathcal {X}}$ such that $\min _{i\in N} V_i({\tilde{x}}) > \min _{i\in N} V_i(x)$, or, equivalently, if $\min _{i\in N} V_i(x) = \max _{{\tilde{x}}\in {\mathcal {X}}} \min _{i\in N} V_i({\tilde{x}})$.

The collective N can take different forms in different application areas; without referring to a specific application, its members (i.e., the points in the set N) are called participants. The decision x affects all participants and is made on their behalf by a social planner. The vector-valued function V generates for every participant $i\in N$ the agent’s utility (or evaluation) $V_i(x)$ of decision x. The components of the vector-valued function $V\,{:}\;{\mathcal {X}}\rightarrow {\mathbb {R}}^n$ are also referred to as individual objective functions.⁴

It is easily seen that every maxmin point is Pareto optimal.⁵ A maxmin point is not necessarily equalizing, and an equalizing point is not necessarily Pareto optimal. However, we do have the following.⁶

Lemma 2.1

Let a social decision problem $(N,{\mathcal {X}},V)$ be given. If $x \in {\mathcal {X}}$ is both equalizing and Pareto optimal, then x is a maxmin solution.

Proof

Suppose that $x \in {\mathcal {X}}$ is both equalizing and Pareto optimal, but not a maxmin solution. Then there exists ${\tilde{x}}\in {\mathcal {X}}$ such that

$$\begin{aligned} \min _{j\in N} V_j({\tilde{x}}) > \min _{j\in N} V_j(x). \end{aligned}$$

(1)

Because x is equalizing, we have $\min _{j\in N} V_j(x) = V_i(x)$ for all $i \in N$. It then follows from (1) that, for all $i \in N$,

$$\begin{aligned} V_i({\tilde{x}}) \ge \min _{j\in N} V_j({\tilde{x}}) > V_i(x). \end{aligned}$$

In other words, ${\tilde{x}}$ is a Pareto improvement of x, so that we have a contradiction. $\square$

The lemma as such is not always useful as a criterion to verify whether a proposed decision is maxmin, because there are many maxmin problems in which one cannot expect to be able to find an equalizing solution. A more generally applicable result can be formulated when Pareto efficiency with respect to subgroups is introduced. Generally speaking, given a social decision problem $(N,{\mathcal {X}},V)$ and a nonempty subset K of N, one can define the subproblem $(K,{\mathcal {X}},V_K)$, where $V_K \,{:}\;{\mathcal {X}}\rightarrow {\mathbb {R}}^K$ is defined by $(V_K)_i(x) = V_i(x)$ for $x \in {\mathcal {X}}$ and $i \in K$. Any Pareto optimal point for $(K,{\mathcal {X}},V_K)$ is also Pareto optimal for $(N,{\mathcal {X}},V)$, but the converse is not true in general. Consequently, Pareto optimality with respect to a subgroup is a stronger property than Pareto optimality with respect to the collective as a whole. We can therefore expect that stronger statements can be made, as is indeed shown in the following lemma.

Lemma 2.2

(“verification lemma”) Let a social decision problem $(N,{\mathcal {X}},V)$ be given, and take $x \in {\mathcal {X}}$. If there exists a nonempty subgroup $K \subset N$ such that

• (i) $V_i(x) \le V_j(x)$ for all $i \in K$ and $j \in N$, and

• (ii) the decision x is Pareto optimal for the subproblem $(K,{\mathcal {X}},V_K)$,

then x is a maxmin point for the problem $(N,{\mathcal {X}},V)$.

Proof

Condition (i) implies that $V_i(x)=V_j(x)$ for all $i,j \in K$; in other words, x is an equalizing solution for the subproblem $(K,{\mathcal {X}},V)$. Using also (ii), it follows from Lemma 2.1 that x is a maxmin solution for $(K,{\mathcal {X}},V_K)$. Suppose now that x is not a maxmin solution for $(N,{\mathcal {X}},V)$. Then there exists ${\tilde{x}}\in {\mathcal {X}}$ such that $\min _{i\in N} V_i({\tilde{x}}) > \min _{i \in N} V_i(x)$. But then

$$\begin{aligned} \min _{i\in K} V_i({\tilde{x}}) \ge \min _{i\in N} V_i({\tilde{x}}) > \min _{i \in N} V_i(x) = \min _{i \in K} V_i(x), \end{aligned}$$

where the equality in the final step follows from (i). Since x is a maxmin point for the subproblem $(K,{\mathcal {X}},V_K)$, we arrive at a contradiction. $\square$

A standard way to arrive at Pareto optimal solutions is weighted-sum optimization (see for instance [23, Ch. 3] or [34, Section 11.2.1]): given $w \in \varDelta _N$, solve

$$\begin{aligned} \sum _{i\in N} w_i V_i(x) \; \rightarrow \; \max \qquad \qquad (x \in {\mathcal {X}}). \end{aligned}$$

(2)

If there is a maximizer x for this problem, then it easily follows that x is Pareto optimal; indeed, if there would be a Pareto improvement ${\tilde{x}}$, then we would have $\sum _{i\in N} w_i V_i({\tilde{x}}) > \sum _{i\in N} w_i V_i(x)$, so that x would not be optimal. The weighted-sum problem (2) can be cast as a parametric optimization problem, with the unit simplex $\varDelta _N$ as its parameter space.

Definition 2.2

A solution map for the parametric optimization problem (2) is a map $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ such that

$$\begin{aligned} w^{\tiny \top }V(\xi (w)) = \max _{x \in {\mathcal {X}}} w^{\tiny \top }V(x) \qquad \text {for all } w \in \varDelta _N. \end{aligned}$$

(3)

If $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ is a solution map for (2), then, for all $w \in \varDelta _N$, $\xi (w)$ is Pareto optimal for the problem $(N,{\mathcal {X}},V)$. In view of Lemma 2.2 above, it is important to note that the same argument that was given for this fact can also be applied to subgroups. To state this formally, we first introduce a term for the relevant property.

Definition 2.3

A mapping $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ is said to be subgroup efficient for the social decision problem $(N,{\mathcal {X}},V)$ if, for every nonempty subset $K \subset N$ and every $w \in \varDelta _K$, the decision $\xi (w)$ is Pareto optimal for the subproblem $(K,{\mathcal {X}},V_K)$.

Proposition 2.1

Every solution map for the weighted-sum parametric optimization problem (2) is subgroup efficient.

The following definition introduces a concept that is central to this paper.

Definition 2.4

A Pareto map for the social decision problem $(N,{\mathcal {X}},V)$ is a map $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ that is subgroup efficient and continuous. A social decision problem is said to be simplicial if it admits a Pareto map.

Remark 2.1

Not all social decision problems are simplicial. For instance, if the decision space is discrete, the continuity requirement implies that a Pareto map must in fact be constant. The requirement of subgroup efficiency then means that there is a decision that is optimal from the points of view of all participants. Therefore, a Pareto map typically does not exist when participants have different preferences and the decision space is discrete. But also when the decision space is continuous, a Pareto map may not exist; an example of such a case is worked out in the “Appendix”.

The following proposition is an immediate consequence of Proposition 2.1; we state it for ease of reference. The proposition shows that every continuous solution map is a Pareto map. However, Pareto maps do not necessarily need to be constructed in this way.

Proposition 2.2

Let a social decision problem $(N,{\mathcal {X}},V)$ be given. If the parametric optimization problem (2) admits a continuous solution map $\xi \,{:}\;\varDelta _N\rightarrow {\mathcal {X}}$, then the problem $(N,{\mathcal {X}},V)$ is simplicial, with Pareto map $\xi$.

A sufficient condition for existence of a continuous solution map for the parametric optimization problem (2) is given in the following lemma, which, under a compactness condition, shows that uniqueness implies continuity. The lemma can be viewed as a special case of Thm. 1 in [55], which in turn relies on results from [10]. For the convenience of the reader, we provide a direct proof.

Lemma 2.3

Let $(N,{\mathcal {X}},V)$ be a social decision problem. If, for each $w \in \varDelta _N$, the weighted-sum optimization problem (2) has a unique maximizer $\xi (w)$, and the set $\{ \xi (w) \mid w \in \varDelta _N \}$ is contained within a compact subset ${\mathcal {X}}_c \subset {\mathcal {X}}$, then the solution map $\xi$ is continuous.

Proof

Take ${\bar{w}}\in \varDelta _N$, and let $(w^j)_{j=1,2,\dots }$ be a sequence of points in $\varDelta _N$ converging to ${\bar{w}}$. Since the set ${\mathcal {X}}_c$ is compact, the proof will be complete if we can show that the set of accumulation points of the sequence $(\xi (w^j))_{j=1,2,\dots }$ has only one element, namely $\xi ({\bar{w}})$. Let ${\bar{x}}$ be an accumulation point of the sequence $\xi (w^j)$. By considering a subsequence and re-indexing if necessary, we can assume that the sequence $\xi (w^j)$ converges to ${\bar{x}}$. We claim that ${\bar{x}}$ is a maximizer of the weighted-sum optimization problem with weights ${\bar{w}}$. Indeed, suppose it is not, and let ${\tilde{x}}\in {\mathcal {X}}$ be such that $\sum _{i\in N} {\bar{w}}_i V_i({\tilde{x}}) > \sum _{i\in N} {\bar{w}}_i V_i({\bar{x}})$. From the relations

$$\begin{aligned} \lim _{j \rightarrow \infty } \sum _{i\in N} w^j_i V_i({\tilde{x}}) = \sum _{i\in N} {\bar{w}}_i V_i({\tilde{x}}) > \sum _{i\in N} {\bar{w}}_i V_i({\bar{x}}) = \lim _{j \rightarrow \infty } \sum _{i\in N} w^j_i V_i(\xi (w^j)) \end{aligned}$$

it then follows that $\sum _{i\in N} w^j_i V_i({\tilde{x}}) > \sum _{i\in N} w^j_i V_i(\xi (w^j))$ for all sufficiently large j, contradicting the assumed optimality of $\xi (w^j)$. By the assumed uniqueness of the maximizer, it now follows that ${\bar{x}}= \xi ({\bar{w}})$. $\square$

A typical case in which the uniqueness of the maximum can be guaranteed occurs when the decision space ${\mathcal {X}}$ is convex and the evaluation functions $V_i$ are strictly concave. When the individual evaluation functions are unimodal but not strictly concave, weighted-sum optimization may fail to produce a Pareto map, as shown in the following example.

Example 2.1

Let ${\mathcal {X}}={\mathbb {R}}$, $\mu \in {\mathbb {R}}^N$, and $V_i(x)=\exp (-(x-\mu _i)^2)$ for $i\in N$. In this case, the weighted sum $\sum _{i\in N} w_i V_i(x)$ is basically a mixture of Gaussian kernels which, depending on $\mu$ and w, can be multimodal and possess multiple global maxima. Moreover, small changes in the weights can lead to discontinuous changes in the solution of weighted-sum optimization. For a concrete example, let $N=\{1,2\}$, $\mu =\{-1,1\}$ and consider w in a neighborhood of $(\frac{1}{2},\frac{1}{2})$.

While direct weighted-sum optimization in the above example fails to produce a Pareto map, we shall see that it is possible to find a Pareto map for the social decision problem in the example, and hence the problem is simplicial. This is in contrast to the problem in Example A.1, for which it can be shown that no Pareto map exists.

The following definition and lemma significantly extend the range of applications of Lemma 2.3 and Proposition 2.2.

Definition 2.5

Two social decision problems $(N,{\mathcal {X}},V)$ and $(N,{\mathcal {X}},U)$, with the same set of agents and the same decision space, are said to be monotonically related if there exist strictly increasing functions $g_i\,{:}\;{\mathbb {R}}\rightarrow {\mathbb {R}}$ ($i \in N$) such that $V_i(x) = g_i(U_i(x))$ for all $x \in {\mathcal {X}}$ and $i\in N$.

Lemma 2.4

(“modulation lemma”) A social decision problem that is monotonically related to a simplicial social decision problem with Pareto map $\xi$ is itself simplicial with Pareto map $\xi$.

Proof

Let $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ be a Pareto map for the problem $(N,{\mathcal {X}},U)$, and let $(N,{\mathcal {X}},V)$ be monotonically related to $(N,{\mathcal {X}},U)$. For $i \in N$, let $g_i$ be a strictly increasing function such that $V_i(x)=g_i(U_i(x))$ for all $x \in {\mathcal {X}}$. To show that the mapping $\xi$ is a Pareto map for the problem $(N,{\mathcal {X}},V)$, take a nonempty subset K of N, and take $w \in \varDelta _K$. Suppose that $\xi (w)$ is not Pareto optimal for the subproblem $(K,{\mathcal {X}},V_K)$; then there exists a Pareto improvement, say ${\tilde{x}}$. For each $i\in K$, we have $g_i(U_i({\tilde{x}}))=V_i({\tilde{x}}) > V_i(\xi (w)) = g_i(U_i(\xi (w)))$, which implies that $U_i({\tilde{x}}) > U_i(\xi (w))$ and hence that ${\tilde{x}}$ is also a Pareto improvement of $\xi (w)$ in the problem $(K,{\mathcal {X}},U_K)$. By definition of a Pareto map, this is not possible. It follows that $\xi$ is subgroup efficient in $(N,{\mathcal {X}},V)$, and hence that $\xi$ is a Pareto map for $(N,{\mathcal {X}},V)$. $\square$

The technique of applying different monotonic transformations to evaluation functions of different participants will be called modulation, whence the name of the lemma. The idea of modulation is that, while construction of a Pareto map on the basis of weighted-sum optimization directly with respect to the evaluation mapping V may be computationally unattractive or even completely infeasible, there might be a monotonically related evaluation map U that does support such a construction. In the algorithmic implementation that will be discussed below (Sect. 5), this means that, to solve the problem of maximizing $\min _{i \in N} V_i(x)$, one solves a sequence of problems of the form

$$\begin{aligned} \sum _{i\in N} w_i U_i(x) \; \rightarrow \; \max \qquad \qquad (x \in {\mathcal {X}}), \end{aligned}$$

(4)

where U is monotonically related to V. This may be much easier than using (2).

Example 2.1(continued). It is easy to verify existence of a unique solution to weighted-sum optimization for the modulated problem $U_i(x)=\log (V_i(x))=-(x-\mu _i)^2$, since $\sum _{i\in N } w_i U_i(x)$ is a strictly concave quadratic polynomial in x for any $w\in \varDelta _N$. By Lemma 2.4, the resulting Pareto map $\xi (w)$ applies equally in the modulated problem $(N,{\mathcal {X}},U)$ and in the original problem $(N,{\mathcal {X}},V)$. Consequently, both problems are simplicial.

More generally than in the example above, we allow for different transformations to be applied to different individual objectives. In some applications, this is essential; see for instance Sect. 6.1. While weighted-sum optimization with respect to possibly modulated individual objective functions is a typical way to construct a Pareto map, sometimes one can easily construct a Pareto map without invoking optimization at all. For an instance of this, see Example 3.1 below.

3 Tester Games

In this section, we connect social decision problems to population games. Generally speaking, a (single-)population game is a pair (N, F) where N is a finite set (usually interpreted as a set of pure strategies, rather than as a set of agents), and F is a continuous mapping from the simplex $\varDelta _N$ to ${\mathbb {R}}^N$ called the fitness function or reward function. The entries of $w \in \varDelta _N$ are interpreted as the relative frequencies or probabilities of occurrence of the strategies in N within a large population. The number $F_i(w)$ represents the reward of strategy i in a situation in which the strategies in N occur with frequencies given by the vector w. For given $y \in \varDelta _N$, one may also think of the quantity $y^{\tiny \top }F(w)$ within the framework of symmetric two-player games as the expected reward for the player who chooses the mixed strategy y, when the other player chooses w. Within this setting, a symmetric Nash equilibrium is a vector $w^* \in \varDelta _N$ such that the condition

$$\begin{aligned} w^{*{\tiny \top }} F(w^*) = \max _{w\in \varDelta _N} w^{\tiny \top }F(w^*) \end{aligned}$$

(5)

holds, which expresses that “$w^*$ is a best reply to itself”. In the context of population games, such a point is usually simply called a Nash equilibrium, without mention of the symmetry property. Equivalently, one can define a Nash equilibrium of the population game (N, F) as any point $w^* \in \varDelta _N$ such that $F_i(w^*) \ge F_j(w^*)$ for all $i,j \in N$ with $w_i^{{*}}> 0$. A fundamental result is that every population game has at least one Nash equilibrium (see for instance [58, Thm. 2.1.1]).

Fig. 1

Coupling between Pareto map and tester game; see Definitions 2.1, 2.4, and  3.1

We now propose to relate simplicial social decision problems to population games in the following way.

Definition 3.1

The tester game associated to a social decision problem $(N,{\mathcal {X}},V)$ with Pareto map $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ is the population game (N, F) with reward mapping $F\,{:}\;\varDelta _N \rightarrow {\mathbb {R}}^N$ defined by

$$\begin{aligned} F(w) = -V(\xi (w)) \end{aligned}$$

(6)

for $w \in \varDelta _N$.

The minus sign in (6) implements the reversal of order that was already discussed in the Introduction. By choosing the rewards in this way, testers are incentivized to bring out the cases in which a proposed decision works out badly; the term “tester” is derived by analogy with beta testers in software design. Continuity of the reward function, as required in the definition of population games, follows from continuity of the evaluation map V and the Pareto map $\xi$. The main theoretical result of this paper is the following; it shows how the maxmin problem is connected to the tester game.

Theorem 3.1

Let a social decision problem $(N,{\mathcal {X}},V)$ be given, and assume that $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ is a Pareto map for the problem. Let $x^*$ be given by $x^*=\xi (w^*)$, where $w^*$ is a Nash equilibrium of the tester game (N, F) associated to the problem $(N,{\mathcal {X}},V)$ with Pareto map $\xi$. Then $x^*$ is a maxmin point for $(N,{\mathcal {X}},V)$.

Proof

Let the subset $K \subset N$ be defined by

$$\begin{aligned} K = \{ i \in {N} \mid w^*_i > 0 \}. \end{aligned}$$

(7)

We then have $w^* \in \varDelta _K$. By definition of a Pareto map, the point $x^* = \xi (w^*)$ is Pareto optimal for the subproblem $(K,{\mathcal {X}},V_K)$. By definition of a Nash equilibrium, we have

$$\begin{aligned} F_i(w^*) \ge F_j(w^*) \quad \hbox {for all}\ i \in K \hbox {,}\ j \in N. \end{aligned}$$

In particular, $F_i(w^*) = F_j(w^*)$ for all $i,j \in K$. From (6), it therefore follows that

$$\begin{aligned} V_i(x^*) \le V_j(x^*) \quad \text {for all}\ i \in K, j \in N \end{aligned}$$

(8)

and in particular $V_i(x^*) = V_j(x^*)$ for all $i,j \in K$. Hence, Lemma 2.1 implies that $x^*$ is a maxmin point for $(K,{\mathcal {X}},V_K)$. Now, suppose that $x^*$ is not a maxmin point for $(N,{\mathcal {X}},V)$. Under this assumption, there exists ${\tilde{x}}\in {\mathcal {X}}$ such that $\min _{j\in N} V_j({\tilde{x}}) > \min _{j\in N} V_j(x^*)$. We then have, using (8),

$$\begin{aligned} \min _{j\in K} V_j({\tilde{x}}) \ge \min _{j\in N} V_j({\tilde{x}}) > \min _{j\in N} V_j(x^*) = \min _{j\in K} V_j(x^*). \end{aligned}$$

This is a contradiction, since $x^*$ is a maxmin point for $(K,{\mathcal {X}},V_K)$. $\square$

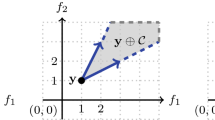
The way in which the population game is related to the maxmin optimization problem is illustrated graphically in Fig. 1.

Remark 3.1

If continuity would be dropped from the definition of a Pareto map, the theorem would be still valid but less useful, since the existence of a Nash equilibrium is then not guaranteed. The fact that the proof does not require continuity may motivate a study of population games in which the reward function is discontinuous or multivalued.

Although tester games are not intended as models of biological or economic situations, there are cases in which a tester game can be readily interpreted as such. The following is an example.

Example 3.1

Consider the problem of dividing one unit of an infinitely divisible good (such as a cake) among n members of a collective, who evaluate the planner’s decision simply by the size of the allotments they receive. Formally, this problem is given by $(N,\varDelta _N,I)$ where $N=\{1,\ldots ,n\}$ and $I\,{:}\;{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ denotes the identity mapping. The mapping I also serves as a Pareto map for this problem. The associated population game is then given $(N,-I)$. This game can be interpreted as a very simple congestion game. The reward function in a congestion game is defined in general as a function of resources that are used by a particular strategy (out of a given set of resources, for instance links in a network) and the extent to which these resources are used by the population as a whole. The game $(N,-I)$ arises when each population member uses exactly one of the resources in the set N, and the reward for each of these options is the negative of the fraction of the population that choose the same option. From experience in daily life, this congestion game can be described as Pick-a-Queue—the problem that arises when you have to choose one from a number of parallel server queues, such as checkout lanes in a (pre-self-checkout) supermarket. It is readily verified that there is only one Nash equilibrium for the population game $(N,-I)$, namely $w = \big (\frac{1}{n}, \dots , \frac{1}{n}\big )$. The same vector is indeed also a maxmin vector for the Divide-the-Cake problem of dividing one unit among n participants. Hence, we can say that (the maxmin version of) Divide-the-Cake is solved by Pick-a-Queue.

Definition 3.1 describes tester games in terms of a particular construction. A natural question is whether it is is possible to give a characterization of tester games as a subclass of population games having certain properties. We leave this as an open question. However, we can prove at least that not all population games are tester games. We do this by introducing the following concepts. Take a population game (N, F), and suppose it is in population state $w \in \varDelta _N$. Imagine a new agent who is joining the population and who is aware of the population state. If this incoming agent is free to choose a strategy from the set of strategies N, then the agent is able to secure the reward $\max _{i \in N} F_i(w)$. This might be called the incoming agent value of the population state w. Let us say that a population state is least favorable when its incoming agent value is minimal among all population states. We can then introduce a class of population games as follows.

Definition 3.2

A population game (N, F) is adverse if each of its Nash equilibria is least favorable.

The definition implies in particular that the incoming agent value of each Nash equilibrium is the same. We can now state the following.

Proposition 3.1

Tester games are adverse.

Proof

Let $(N,{\mathcal {X}},V)$ be a social decision problem with Pareto map $\xi$, let (N, F) be the associated tester game, and let $w^*$ be a Nash equilibrium of (N, F). We have

$$\begin{aligned} \min _{i \in N} V_i(\xi (w^*)) \le \max _{w \in \varDelta _N} \min _{i \in N} V_i(\xi (w)) \le \max _{x \in {\mathcal {X}}} \min _{i \in N} V_i(x) = \min _{i \in N} V_i(\xi (w^*)), \end{aligned}$$

where the second inequality follows since $\xi (w) \in {\mathcal {X}}$ for all $w \in \varDelta _N$, and the equality in the final step is implied by Theorem 3.1. It follows that equality holds in all steps. Consequently,

$$\begin{aligned} \max _{i \in N} F_i(w^*) = - \min _{i \in N} V_i(\xi (w^*)) = - \max _{w \in \varDelta _N} \min _{i \in N} V_i(\xi (w)) = \min _{w \in \varDelta _N} \max _{i \in N} F_i(w). \end{aligned}$$

This shows the adversity of (N, F). $\square$

An example of a population game that is not adverse is the game (N, I), in which N can be any collective (of size larger than one), and the reward function is given by $F_i(w)=w_i$ for all $i \in N$. This might be called the Meet-your-Friends game; the set N then refers to a number of different places where people can go to hang out, and the reward associated to choosing a given place is proportional to the number of people who choose the same location.⁷ Every population state of the form $(1/k)\mathbbm {1}_K$, where K is a nonempty subset of N and k is the number of elements of K, is a Nash equilibrium. The incoming agent values of these equilibria are not the same, and hence the Meet-your-Friends game is not adverse.

4 Special Case: Tester Potential Games

Theorem 3.1 imposes no restrictions on the way in which the Pareto map is constructed. When we do introduce such restrictions, it may be expected that more can be said about the associated tester game. In this section, we consider the situation in which the Pareto map is constructed from direct weighted-sum optimization of the individual objective functions, rather than via modulation or by another method, and moreover the resulting map satisfies additional smoothness conditions. It will be seen that, in this case, the related tester game indeed acquires special properties. The definitions below describe subclasses of population games that play a major role in the literature; see for instance [58, Ch. 3].

Definition 4.1

A population game (N, F), in which F is defined on $\varDelta _N^+$, is a (full) potential game if there exists a continuously differentiable function $f: {\mathbb {R}}^N_+ \rightarrow {\mathbb {R}}$ such that $F(w) = \nabla f(w)$ for all $w \in \varDelta _N^+$. Any function f that satisfies this condition is called a potential function for the game.

In potential games, Nash equilibria can be found from an optimization problem as stated in the following lemma.

Lemma 4.1

Let (N, F) be a full potential game, with potential function f. Then any maximizer of f on $\varDelta _N$ is a Nash equilibrium of (N, F).

This follows because the Karush-Kuhn-Tucker (KKT) conditions for optimality imply the conditions for a Nash equilibrium, and moreover the KKT conditions are necessary since the simplex satisfies the linear independence qualification constraint; see for instance [58, Thm. 3.1.3] or [59, Thm. 13.5].

If the reward function F is continuously differentiable, then the game (N, F) is a potential game if and only if the Jacobian JF of F is symmetric [58, Observation 3.1.1]. The class of population games in the definition below includes potential games for which the Jacobian is negative semidefinite on the tangent space of the simplex, i.e., the Jacobian satisfies $z^{\tiny \top }JF(x) z \le 0$ for $x\in \varDelta _N$ and $z \in T\varDelta _N$.

Definition 4.2

A population game (N, F) is a contractive game⁸ if

$$\begin{aligned} (w^1-w^2)^{\tiny \top }(F(w^1)-F(w^2)) \le 0 \end{aligned}$$

(9)

for all $w^1, w^2 \in \varDelta _N$.

Now, consider a social decision problem $(N,{\mathcal {X}},{V})$. We shall use the following smoothness assumptions.

Assumption 4.1

The following conditions hold.

• (i) The decision space ${\mathcal {X}}$ is an open subset of a finite-dimensional real linear space.

• (ii) The evaluation functions $V_i$ ($i \in N$) are continuously differentiable.

• (iii) The parametric optimization problem (2) admits a continuously differentiable solution map.

By allowing unnormalized weights rather than only normalized ones, the domain of the solution map $\xi$ can be extended to $\varDelta _N^+$ in a natural way; the extension is homogeneous of degree 0. The function F defined in (6) then likewise becomes a function on $\varDelta _N^+$ that is homogeneous of degree 0. The function f defined by $f(w) = w^{\tiny \top }F(w)$ is homogeneous of degree 1, and can be defined on all of ${\mathbb {R}}_+^N$ by setting $f(0)=0$. The pair (N, F) with the extended version of F will be called the extended tester game associated to the problem $(N,{\mathcal {X}},V)$ with Pareto map $\xi$.

Proposition 4.1

Consider a social decision problem $(N,{\mathcal {X}},V)$ that satisfies Assumption 4.1, and let $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ be a continuously differentiable solution map. The extended tester game (N, F) associated to $(N,{\mathcal {X}},V)$ with Pareto map $\xi$ is a full potential game with potential function given by $f(w) = w^{\tiny \top }F(w)$.

Proof

The gradient of the function $f\,{:}\;w \mapsto w^{\tiny \top }F(w)$ can be calculated by means of the chain rule:

$$\begin{aligned} \nabla f(w) = F(w) - \Big [ \frac{\partial (w^{\tiny \top }V)}{\partial x}(\xi (w)) \, \frac{\partial \xi }{\partial w}(w) \Big ]^{\tiny \top }= F(w), \end{aligned}$$

(10)

where the final equality holds because the gradient of the function $x \mapsto w^{\tiny \top }V(x)$ vanishes at $x = \xi (w)$. This shows that f is a potential function for F. $\square$

In the special situation of this section, the tester game is not only a potential game, but also a contractive game. The proof of this fact does not require smoothness assumptions apart from continuity of the solution map for the parametric problem (2).

Proposition 4.2

Let a social decision problem $(N,{\mathcal {X}},V)$ be given. If $\xi \,{:}\;\varDelta _N \rightarrow {\mathcal {X}}$ is a continuous solution map, then the tester game (N, F) associated to $(N,{\mathcal {X}},V)$ with Pareto map $\xi$ is contractive.

Proof

Take $w^1, w^2 \in \varDelta _N$. Since $\xi (w^1)$ and $\xi (w^2)$ are maximizers of $w^{1{\tiny \top }}V(x)$ and $w^{2{\tiny \top }}V(x)$ respectively, we have

$$\begin{aligned} w^{1{\tiny \top }}V(\xi (w^1)) \ge w^{1{\tiny \top }}V(\xi (w^2)), \qquad w^{2{\tiny \top }}V(\xi (w^2)) \ge w^{2{\tiny \top }}V(\xi (w^1)) \end{aligned}$$

and hence

$$\begin{aligned}&(w^1-w^2)^{\tiny \top }\big ( V(\xi (w^1)) - V(\xi (w^2)) \big ) \\&\quad = w^{1{\tiny \top }} \big ( V(\xi (w^1)) - V(\xi (w^2)) \big ) + w^{2{\tiny \top }} \big ( V(\xi (w^2)) - V(\xi (w^1)) \big ) \ge 0. \end{aligned}$$

Since $F(w) = -V(\xi (w))$, the relation (9) holds. $\square$

Fig. 2

Classical case: coupling between social planner and potential game. See Definition 3.1 and Eqn. (3)

The structure used in Propositions 4.1 and  4.2 is illustrated graphically in Fig. 2. The term “classical” is used here because the social planner acts in what might be called a classical way [29],⁹ namely on the basis of optimization of a social welfare function that is constructed as a weighted sum of individual utilities. In this situation, we can compare Theorem 3.1 to arguments based on duality. It follows from Proposition 4.1 and Lemma 4.1 together with Theorem 3.1 that maximizers of the function $f(w) = w^{\tiny \top }F(w)$ give rise to maxmin points for the underlying social decision problem when F is defined by (6), and the Pareto mapping $\xi$ satisfies (3). The same conclusion can also be reached without appealing to Theorem 3.1 if it is assumed that strong duality holds, so that the minmax property

$$\begin{aligned} \max _{x \in {\mathcal {X}}} \min _{w \in \varDelta _N} w^{\tiny \top }V(x) = \min _{w \in \varDelta _N} \max _{x \in {\mathcal {X}}} w^{\tiny \top }V(x) \end{aligned}$$

(11)

is satisfied. Indeed, let $w^*$ be a maximizer of the potential function $w^{\tiny \top }F(w)$, so that (see Lemma 4.1) it is a best reply to itself in the game (N, F). We can then write, using the best reply property in the first step,

$$\begin{aligned}{} & {} \min _{i \in N} V_i(\xi (w^*)) = \min _{w\in \varDelta _N} w^{\tiny \top }V(\xi (w^*)) = w^{*{\tiny \top }} V(\xi (w^*)) = \min _{w\in \varDelta _N} w^{\tiny \top }V(\xi (w))\nonumber \\{} & {} \quad = \min _{w\in \varDelta _N} \max _{x\in {\mathcal {X}}} w^{\tiny \top }V(x) = \max _{x\in {\mathcal {X}}} \min _{w\in \varDelta _N} w^{\tiny \top }V(x) = \max _{x \in {\mathcal {X}}} \min _{i \in N} V_i(x) {.} \end{aligned}$$

(12)

Equation (12) shows directly that $\xi (w^*)$ is a maximizer of $\min _{i\in N} V_i(x)$. The use of the minmax theorem in this argument is replaced in Theorem 3.1 by the assumption of simpliciality. It should also be noted that the situation of Fig. 1 is significantly more general than the situation of Fig. 2, since in the latter it is assumed that the weighted-sum optimality property (3) is satisfied in terms of the given (unmodulated) objective functions, whereas the former allows modulation or any other way of constructing a Pareto map.

5 Iterative Algorithm

The design of dynamical systems whose stationary points are Nash equilibria has been an active research topic since the early stages of game theory. Traditionally, these dynamical systems are interpreted as representing a process of actual learning and revision of behavior by agents, or in the biological setting as an evolutionary process. The process may lead to an equilibrium in the sense of dynamical systems that turns out to be an equilibrium in the sense of game theory as well. Alternatively, the dynamics can be viewed as representing computational processes, serving as numerical methods to find game-theoretic equilibria. The latter point of view is taken here. Our interest is therefore focused less on studying a range of alternative dynamics that can all be viewed as plausible representations of learning or evolution, and more on finding a particular process that leads quickly and reliably to game-theoretic equilibrium. Moreover, since computation must take place in discrete steps, we consider dynamics in discrete time.

We may take the IRLS algorithm developed in [37] as a starting point. The optimization problem addressed by Lawson is

$$\begin{aligned} \max _i \Big (\,\Big | \sum _{j=1}^n \alpha _j f_j(z_i) - \varphi (z_i) \Big |\,\Big ) \;\; \rightarrow \;\; \text {min} \qquad (\alpha \in {\mathbb {R}}^m), \end{aligned}$$

(13)

where $\varphi$ and $f_j$ ($j=1,\dots ,m$) are given functions defined on an interval [a, b], and $a \le z_1< z_2< \cdots < z_n \le b$. In other words, the problem is to find the best approximation of the function $\varphi$ by a linear combination of the functions $f_j$, in the sense that the maximum of the absolute errors on given gridpoints $z_i$ is minimized. The problem can be phrased in the terminology of this paper as follows. Define $N = \{1,\dots ,n\}$, ${\mathcal {X}}= {\mathbb {R}}^m$, and $V_i(\alpha ) = -|\sum _{j=1}^n \alpha _j f_j(z_i) - \varphi (z_i)|$. The problem (13) is then to find a maxmin point for the social decision problem $(N,{\mathcal {X}},V)$. A monotonically related problem is obtained by defining $U_i(\alpha ) = -V_i(\alpha )^2$ for $\alpha \in {\mathcal {X}}$ and $i \in N$. To a given set of weights $w \in \varDelta _N$, one can associate the uniquely defined solution $\xi (w)$ of the weighted least-squares problem

$$\begin{aligned} -\sum _{i=1}^n w_i U_i(\alpha ) = \sum _{i=1}^n w_i \Big ( \sum _{j=1}^n \alpha _j f_j(z_i) - \varphi (z_i) \Big )^2 \;\; \rightarrow \;\; \text {min}. \end{aligned}$$

(14)

The map $\xi$ is a Pareto map for $(N,{\mathcal {X}},U)$ and hence also for $(N,{\mathcal {X}},V)$ by Lemma 2.4. The population game associated to $(N,{\mathcal {X}},V)$ via the map $\xi$ is (N, F), where $F\,{:}\;\varDelta _N \rightarrow {\mathbb {R}}^N$ is defined by

$$\begin{aligned} F_i(w) = -V_i(\xi (w)) = \Big |\sum _{j=1}^n \xi _j(w) f_j(z_i) - \varphi (z_i)\Big |. \end{aligned}$$

Lawson proves (in a different but equivalent formulation) that the solution to (13) is given by $\xi (w^*)$, where $w^* \in \varDelta _N$ is the limit of the sequence $(w^k)_{k=1,2,\dots }$ obtained recursively by taking (for instance) $w^0 = (\frac{1}{n},\dots ,\frac{1}{n})$ and defining

$$\begin{aligned} w_i^{k+1} = \frac{w_i^k F_i(w^k)}{\sum _{j\in N} w_j^k F_j(w^k)} \qquad \qquad (i \in N{; \; k=0,1,2,\dots }). \end{aligned}$$

(15)

The update rule (15) can be used only when the components $F_i(w)$ of the rewards function are guaranteed to be nonnegative, as is indeed the case in the application investigated by Lawson. To make the update rule applicable in situations where rewards might be negative, a simple solution is to apply a transformation to the rewards that renders them positive while maintaining the ordering; this does not affect the maxmin solution.¹⁰ The natural candidate is the exponential transformation. When this is used, the rule (15) is modified to

$$\begin{aligned} w_i^{k+1} \;{=}\; \frac{w_i^k \exp (hF_i(w^k))}{\sum _{j\in N}w_j^k \exp (hF_j(w^k))} \qquad \qquad (i \in N{; \; k=0,1,2,\dots }), \end{aligned}$$

(16)

where $h > 0$ is a parameter that can be used to tune the behavior of the iteration.

The iteration (16) is by no means new to the field of population games. In fact, as detailed below in Remark 5.1, it can be viewed as a discrete-time version of the famous replicator equation of evolutionary game theory [62], which is given by

$$\begin{aligned} \frac{dw_i}{dt}(t) = w_i(t) \Big ( F_i(w(t)) - \sum _{j\in N} w_j(t)F_j(w(t)) \Big ), \qquad i \in N. \end{aligned}$$

(17)

Many alternative dynamical systems have been proposed which likewise can be thought of as representing actual evolutionary behavior of populations both in biological and economic applications; see for instance [19, 32, 33], and [58]. These systems include the replicator equation (17) as well as the projection, best response, logit, Smith, and BNN (Brown/von Neumann/Nash) dynamics, all formulated in continuous time [58, Ch. 5]. The attention spent on the convergence analysis of discrete-time counterparts appears relatively small in comparison, although there are for instance the contributions of [56, 47], and [50]. Standard results for the continuous-time replicator equation (see for instance [14, Thm. 25, Thm. 26], [58, Thm. 8.1.1]) suggest that dynamically stable fixed points of (17) are Nash equilibria, so that fixed points that are found by iteration are expected to give rise to maxmin solutions via the Pareto map. The observation that the discrete-time replicator equation (16) can be used to solve maxmin problems appears to be new. A detailed investigation of the convergence behavior of (16) in tester games is undertaken in [4].

In the literature on machine learning and learning in games, the iteration (16) is called the multiplicative weights algorithm (MWA). A survey of its use in these fields is given in [1].¹¹ Several versions exist, which are distinguished by the way in which rewards (or costs) are transformed. An exponential transformation is used in (16), for reasons already explained. The untransformed version, as in [37], is used in [8]. The authors of [62], in the paper that introduces the continuous-time replicator equation, employ $1+F_i$ instead of $F_i$; in [47], $1+hF_i$ is used, where $h > 0$ is a parameter. In the derivation as shown in Remark 5.1, the parameter h appears naturally as a step size. The same parameter h, or a rescaling of it, is also referred to in the machine learning literature as a learning rate or as an intensity of choice.

Remark 5.1

To see the relation between (16) and (17),¹² note that the trajectories of (17) can be obtained by normalization from trajectories of the vector differential equation

$$\begin{aligned} \frac{dz_i}{dt}(t) = z_i(t) F_i(z(t)) \qquad i\in N, \end{aligned}$$

(18)

where the mapping F is extended to the set of unnormalized weight vectors $\varDelta _N^+$ in the way already discussed above. Indeed it can be verified by direct computation that, if $z(\cdot )$ satisfies (18), then the function $w(\,\cdot \,)\,{:}\;[0,\infty ) \rightarrow \varDelta _N$ defined by $w(t) = z(t)/(\mathbbm {1}^{\tiny \top }z(t))$ satisfies the replicator equation (17). In other words, the system (18) is an “unnormalized” version of (17). By rewriting the equations (18) as $(d/dt) \log z_i(t) = F_i(z(t))$ and applying a simple Euler discretization scheme to this equation, one obtains the recursion $\log z_i(t+h) = \log z_i(t) + h F_i(z(t))$, where h is a chosen time step. This in turn can be rewritten as $z_i(t+h) = \exp (hF_i(z(t)))z_i(t)$, which, finally, produces the recursion (16) after normalization.¹³

The generalized IRLS method for finding maxmin points of a given social decision problem $(N,{\mathcal {X}},V)$ can now be described as follows.

Algorithm 5.1

(GIRLS)¹⁴

• 1. Find, if possible, a Pareto map $\xi$ for the problem $(N,{\mathcal {X}},V)$.

• 2. Define $F\,{:}\;\varDelta _N \rightarrow {\mathbb {R}}^N$ by $F_i(w) = -V_i(\xi (w))$.

• 3. Choose an initial point $w^0$ in the interior of the simplex (for instance $w^0 = (\frac{1}{n}, \cdots , \frac{1}{n})$), choose a step size h, and run the iteration (16) until convergence takes place. If convergence fails, reduce the step size.

• 4. Define $x^* = \xi (w^*)$, where $w^*$ is the limit obtained in step 3.

• 5. Verify that $V_j(x^*) \ge V_i(x^*)$ for $i \in K:=\{ i \in N \mid w^*_i > 0\}$ and $j \in N$. If so, conclude that $x^*$ is a maxmin point.

The success of the algorithm hinges on whether or not a Pareto map is available that can be computed efficiently, since this mapping is used in every step of the iteration. To obtain such a map, one possibility is to look for monotonic transformations of the individual objective functions represented by the entries of the vector V(x) (possibly different transformations for different entries) such that the weighted-sum problem for the transformed objectives can be computed quickly. For example, in the linear approximation problem of minimizing $\Vert Ax-b\Vert _\infty$ where $A \in {\mathbb {R}}^{n\times m}$ and $b \in {\mathbb {R}}^m$ are given, with $n > m$, the “individual objectives” $|(Ax-b)_i|$ can be monotonically transformed to $(Ax-b)_i^2$, which is successful since the weighted-sum problem in terms of these objectives is just a weighted least-squares problem, for which an explicit solution formula can be given. This is essentially the application in the original work of [37]. Other applications are shown below in Sects. 6.1 and 6.2. For further situations in which efficient Pareto maps can be constructed, one may think for instance of collective investment under disagreement in probabilities [5], minmax estimation in statistics ([38, Ch. 5], [41]), and facility location problems [36].

As discussed above, there are alternative differential equations that may be used instead of the replicator equation (17), and each of these could be discretized in various ways. The resulting iterations could be used instead of (16) in step 3. The conclusion in step 5 is justified by Lemma 2.2 and by the subgroup efficiency property of Pareto maps. The inequalities that are to be checked in this step imply that $V_i(x^*) = V_j(x^*)$ for all i, j in the active set K. This property is already ensured when $w^*$ is a fixed point of the iteration (16) (the same holds for alternatives), so that it suffices to verify that $V_j(x^*) \ge V_i(x^*)$ for $i \in K$ and $j \in N {\setminus } K$. It can be shown [4] that the method will be successful under mild conditions, for sufficiently small step size.

With respect to the original IRLS method, Algorithm 5.1 is a three-way generalization: (i) the uniform quadratic transformation used by Lawson is replaced by a transformation $U_i(x)=g_i(V_i(x))$ where $g_i$ can be any increasing function, and can depend on i; (ii) Pareto maps do not necessarily come from weighted-sum parametrization; (iii) the iteration (15) is replaced by (16) (or an alternative) which includes a step size / learning rate parameter that can be manipulated to adjust the convergence behavior. Applications in the following section illustrate the extension of the scope that is reached with the GIRLS method.

6 Applications

In this section, we discuss two applications. The first concerns a collective investment problem in which agents have different preferences. Certainty equivalents are used to achieve a form of interpersonal comparability of evaluations. The setting can be compared to the “random preferences” model of Desmettre and Steffensen [22]. In that paper, however, the objective is an average of certainty equivalents with respect to a prior on a one-dimensional parameter space, whereas we solve a maxmin problem and allow for heterogeneity of preferences described by multiple parameters. Desmettre and Steffensen focus mainly on time consistency issues; we do not discuss these here. The second application is a simple example of a situation in which heterogeneity is due to disagreement on model parameters. The use of the maxmin criterion in situations of model uncertainty is quite standard; see for instance [9]. The problem discussed below is convex by nature; the purpose of the subsection is just to show that, even in this case, there is something to be said for the use of the GIRLS method.

6.1 Investment Under Preference Heterogeneity

Here we consider an optimal investment problem within a discrete setting. The formulation of the problem is standard, except for the fact that we consider the investment decision to be taken on behalf of the members of a heterogeneous collective. The criterion used by the decision maker (social planner, which could be a board of trustees) is assumed to be of minmax regret form, where regret is defined as the ratio of individually optimal certainty equivalent with respect to the individual certainty equivalent derived from the planner’s decision. In the example that we work out, heterogeneity exists along multiple dimensions.

To describe the problem formally, let $\varOmega = \{ \omega _1,\dots , \omega _m \}$ be a finite sample space representing possible future states. The probability of state $\omega _j$ is $p_j$. The price of the Arrow-Debreu security that pays 1 if state $\omega _j$ is realized and 0 otherwise is $q_j$. It is assumed that $p_j > 0$ and $q_j > 0$ for all $j = 1,\dots ,m$. Suppose that u(x) is an increasing, differentiable, and strictly concave function defined on $(0,\infty )$, satisfying the Inada conditions

$$\begin{aligned} \lim _{x \downarrow 0} u'(x) = \infty , \qquad \qquad \lim _{x \rightarrow \infty } u'(x) = 0. \end{aligned}$$

Let an initial capital $W_0 > 0$ be given. It is shown for instance in [21, Thm. 3.1.3] that the solution $x^*$ of the optimization problem

$$\begin{aligned} \text {maximize} \quad E[u(X)] = \sum _{j=1}^m p_j u(x_j) \qquad \text {s.t.} \quad x \in {\mathbb {R}}^m_{++}, \quad \sum _{j=1}^m q_j x_j \le W_0 \end{aligned}$$

(19)

is determined uniquely by the requirements

$$\begin{aligned} \exists \lambda > 0: \; u'(x_j^*) = \lambda \,\frac{q_j}{p_j} \quad (j=1,\dots ,m), \qquad \sum _{j=1}^m q_jx_j^* = W_0. \end{aligned}$$

(20)

Suppose now that there is a collective N consisting of individuals who agree on the model parameters $p_j$ and $q_j$ ($j = 1,\dots ,m$), but who rank portfolio decisions using different utility functions $u_i$, $i \in N$. Assume that all utility functions $u_i(x)$ satisfy the same conditions as above. The expected utility of a portfolio decision $x \in {\mathbb {R}}^m_{++}$ to participant i is given by

$$\begin{aligned} E[u_i(x)] = \sum _{j=1}^m p_j u_i(x_j). \end{aligned}$$

The corresponding certainty equivalent is defined as the number $\textrm{CE}_i(x)$ that is uniquely defined by

$$\begin{aligned} u_i(\textrm{CE}_i(x)) = E[u_i(x)]. \end{aligned}$$

Let an initial capital $W_0$ be fixed. It follows from the results mentioned above that, corresponding to this initial capital, there is for each participant an optimal portfolio decision $x_i^*$. Since certainty equivalents are always positive, the regret of participant $i \in N$ resulting from decision $x \in {\mathbb {R}}^m$ can be defined as the ratio

$$\begin{aligned} \textrm{Rgr}_i(x) = \frac{\textrm{CE}_i(x_i^*)}{\textrm{CE}_i(x)}. \end{aligned}$$

(21)

The quantity so obtained is dimensionless, and is always at least equal to 1. To rephrase the problem in a maxmin framework, define satisfaction by

$$\begin{aligned} \textrm{Sat}_i(x) = 1/\textrm{Rgr}_i(x) = \frac{\textrm{CE}_i(x)}{\textrm{CE}_i(x_i^*)} \in (0,1]. \end{aligned}$$

A social decision problem $(N,{\mathcal {X}},V)$ is then specified by

$$\begin{aligned} {\mathcal {X}}= \big \{ x \in {\mathbb {R}}^m_{++} \;\big |\; \sum _{j=1}^m q_j x_j \le W_0 \big \}, \qquad V_i(x) = \textrm{Sat}_i(x) \quad (x \in {\mathcal {X}}, \; i \in N). \end{aligned}$$

(22)

It is readily verified that the mapping $V\,{:}\;{\mathcal {X}}\rightarrow {\mathbb {R}}^N$ is indeed continuous with respect to the usual topology of ${\mathcal {X}}$ as a subset of ${\mathbb {R}}^m$. The maxmin problem associated to (22) is

$$\begin{aligned} \text {maximize} \;\; \min _{i \in N} \textrm{Sat}_i(x) \qquad \text {subject to} \;\;\; x \in {\mathbb {R}}^m_{++}, \quad \sum _{j=1}^m q_j x_j \le W_0. \end{aligned}$$

(23)

A direct attack on this nonsmooth problem does not seem promising. However, satisfaction is for each individual participant monotonically related to expected utility. Let $\xi (w)$ denote the solution of the weighted-sum expected utility optimization problem with weights w. Continuity of the mapping $\xi$ can be shown following the argument in the proof of Lemma 2.3, by extending the decision space to ${\overline{{\mathcal {X}}}}:= \{ x \in {\mathbb {R}}^m_+ \mid \sum _{j=1}^m q_j x_j \le W_0 \}$, and allowing the evaluation mapping to take the value $-\infty$ in case $\lim _{x \downarrow 0} u(x) = -\infty$. The Inada condition at 0 guarantees that solutions $x \in {\mathbb {R}}^m_+$ with $x_j=0$ for some $j \in \{1,\dots ,m\}$ are not optimal for any set of weights. Using also Proposition 2.1, we conclude that $\xi$ is a Pareto map. From the modulation lemma (Lemma 2.4), it follows that the maxmin satisfaction problem is of simplicial type with Pareto map $\xi$. Hence, the algorithm of Sect. 5 can be applied. For the practical feasibility of the algorithm, a key factor is that the Pareto map can be computed efficiently. Indeed, a weighted sum of the utility functions $u_i(x)$ satisfies the same qualitative conditions as the functions $u_i$ themselves, so that, for any given set of weights, it is a simple numerical exercise to solve the weighted-sum expected utility optimization problem. Here, we make essential use of Lemma 2.4, since it would not be as easy to optimize a weighted sum of satisfactions.

To show the results of the algorithm in a specific case, we take a collective consisting of  20 participants whose preferences are given by power utility with saturation.¹⁵ Their utility functions are

$$\begin{aligned} u_i(x) = \frac{(\min (x,\alpha _i e^{rT}W_0))^{1-\gamma _i}}{1-\gamma _i}, \end{aligned}$$

where $\alpha _i$ is the ratio of the saturation level relative to the level that would be obtained by investing all capital in riskless assets. The coefficients of risk aversion $\gamma _i$ and the saturation levels $\alpha _i$ are jointly drawn randomly in the ranges $2 \le \gamma \le 5$ and $1 \le \alpha \le 1.5$. A stochastic model is constructed in a 1201-point sample space to represent a discretized Black-Scholes economy with the following parameters: interest rate 2%, expected return of risky asset 8%, volatility of risky asset 20%, investment horizon 5 years. The left panel of Fig. 3 shows the convergence of the MWA iteration to a point on a six-dimensional face of the simplex. The preferences of the corresponding group members, parametrized by coefficient of risk aversion $\gamma$ and saturation level $\alpha$, are shown as squares in the right panel of Fig. 3 and are given in tabular form below.

weight	46.6%	29.5%	14.8%	3.72%	3.68%	1.70%
$\gamma$	3.04	2.28	2.08	3.26	2.00	2.42
$\alpha$	1.02	1.45	1.35	1.05	1.16	1.01

These members all attain the same level of satisfaction, namely $97.85\%$.¹⁶ It is easily verified that the levels of satisfaction of other group members are higher, and hence the solution found is a maxmin point by the verification lemma (Lemma 2.2).

Fig. 3

The left panel shows convergence of the algorithm to a point on a six-dimensional face of the simplex. The preferences of the corresponding six group members are indicated as squares in the right panel; the boxed squares correspond to members with weights exceeding 10%. Other members (represented by dots) have zero weights

The maxmin solution itself is shown in Fig. 4. For ease of interpretation, the wealth at time T is indicated not as a nonincreasing function of the pricing kernel $q_j/p_j$ but rather as a nondecreasing function of its reciprocal, which is the return on the growth optimal portfolio [3].¹⁷ This return has been annualized for use as a readily interpretable scale on the horizontal axis. In addition to the maxmin solution, the individually optimal policies of the six critical members are shown as well in Fig. 4. Computation of these results in Matlab is completed in a few seconds on a standard laptop computer.

To interpret the graphs in terms of a portfolio strategy within the Black-Scholes model, one should take into account that replication by the delta hedge calls for a position in risky assets that is higher when the payoff graph at the current point is steeper, and that the payoff graph at times before the terminal time is a diffused and somewhat shifted version of the payoff graph at the terminal time; see for instance [48, Ch. 7]. The plateaus that are seen in Fig. 4 therefore correspond to situations in which little risk is taken. The impact of the saturation levels of the critical members on the maxmin decision can be seen clearly.

Fig. 4

The bold curve represents the minmax regret decision for the group with preferences indicated in the right panel of Fig. 3. Portfolio value at time T is shown as a function of the annualized return on the optimal growth portfolio (the fixed-mix portfolio that is optimal under log utility). The individual preferences of group members with nonzero weights are indicated as grey lines; dark grey lines correspond to group members with weights exceeding 10%. The dashed line indicates the level $e^{rT}W_0$, which is the final wealth that is achieved by the strategy of investing all capital into riskless assets

6.2 Disagreement on Models

Even when members of a collective have identical preferences, they may still disagree on actions to be taken in a given situation because they hold different views on the dynamics of the process they are facing and the impact that actions will have. As is well known for instance in climate policy research, different models of climate dynamics may lead to radically different conclusions, even when the objective function is fixed. In an alternative interpretation, finding a compromise decision in the face of different opinions on models can be viewed as a way of addressing model uncertainty.

For a very simple example, suppose that member $i \in N$ believes that the state $x_1$ that will be reached at time 1 from an initial state $x_0$ under the action $v_0$ is given by

$$\begin{aligned} x_1 = a_i x_0 + b_i v_0. \end{aligned}$$

(24)

Also, assume that all members aim to minimize the quantity given by

$$\begin{aligned} J(x_1,v_0) = x_1^2 + v_0^2. \end{aligned}$$

(25)

In the interpretation of a two-period climate model, all members therefore agree that the ideal state of climate corresponds to the situation in which the state variable takes the value 0. They disagree, however, when it comes to the question how the situation will evolve if nothing is done (as captured by $a_i$) and the question how large the effect of action will be per unit expense (as captured by $b_i$).

We take the action relative to the current state as the decision variable, so that the decision space is ${\mathbb {R}}$. The cost of decision $k \in {\mathbb {R}}$ from the perspective of participant i is

$$\begin{aligned} C_i(k) = (a_i x_0 + b_i k x_0)^2 + (k x_0)^2 = \big ((a_i+b_ik)^2 + k^2\big ) x_0^2. \end{aligned}$$

The decision that would be preferred by participant i is obtained by minimizing the expression above, which leads to

$$\begin{aligned} k_i^* = - \frac{a_i b_i}{1 + b_i^2} . \end{aligned}$$

(26)

As an evaluation function of social decisions, we may use the regret of participant i (which we define here additively rather than multiplicatively) given by

$$\begin{aligned} \textrm{Rgr}_i(k) = C_i(k) - C_i(k_i^*) \in (-\infty , 0]. \end{aligned}$$

The social decision problem that is obtained in this way is specified by

$$\begin{aligned} {\mathcal {X}}= {\mathbb {R}}, \qquad V_i(k) = -\textrm{Rgr}_i(k) \quad (k \in {\mathcal {X}}, \; i \in N). \end{aligned}$$

(27)

The continuity of the mapping $V\,{:}\;{\mathcal {X}}\rightarrow {\mathbb {R}}^N$ is trivially verified. The maxmin problem associated to (27) is a convex optimization problem, since the functions $V_i$ are concave, and the pointwise minimum of a set of a concave functions is again concave. While therefore in this case the maxmin problem could be solved by standard (gradient ascent) methods, still it can be said that the weighted-sum problem is simpler, because it can be solved analytically. Indeed, the parametric optimization problem

$$\begin{aligned} \text {minimize} \;\; \sum _{i\in N} w_i \textrm{Rgr}_i(k) \quad \text {subject to} \;\; k \in {\mathbb {R}}\end{aligned}$$

with parameter $w \in \varDelta _N$ is solved by $k = \kappa (w)$, where $\kappa \,{:}\;\varDelta _N \rightarrow {\mathbb {R}}$ is defined by

$$\begin{aligned} \kappa (w) = \frac{\sum _{i\in N} w_i a_i b_i }{ 1 + \sum _{i\in N} w_i b_i^2 }. \end{aligned}$$

(28)

As is readily verified, the mapping $\kappa$ defined by (28) is a Pareto map for the social decision problem (27). In this case, the Pareto map is constructed by optimization of a weighted sum of the evaluation functions themselves, and so we are in the “classical” case of Fig. 2.

The result of applying the generalized IRLS method in a particular case is shown in Fig. 5. A collective consisting of 50 members was formed with beliefs described by parameters $a_i$ and $b_i$, drawn randomly from the intervals $[0.7, \, 1.2]$ and $[0.1, \, 0.3]$ respectively. The compromise decision according to the minmax regret rule is found to be determined by two group members. One of these attaches a high value to both coefficients a and b, which means that this participant believes that the state will move dangerously far from the optimal value 0 when no action is taken, and also thinks that action will have a big impact on the state. The other participant holds opposite views: the state will return to 0 even if no action is undertaken, and moreover action is not very cost-effective. The optimal choice of action for the first participant is given by $k = -0.31$, whereas for the second participant it is given by $k = -0.08$. The compromise under the minmax regret rule is $k = -0.20$.

Fig. 5

The left panel shows convergence of the algorithm to a point on a two-dimensional face of the simplex. The preferences of the corresponding two group members are indicated as boxed squares in the right panel. Other members (represented by dots) have zero weights

7 Conclusions

Maxmin or minmax problems arise in many different fields, from operations research to statistics and from numerical analysis to finance. When phrased in the language of welfare theory as we have chosen to do in this paper, these problems can be described in terms of a social planner who takes a decision on behalf of a heterogeneous collective, and who wants to do this in such a way that the minimum utility across the members of the collective is maximized. We have proposed a solution method that is a generalization of the iteratively reweighted least-squares (IRLS) method originally devised by [37] in the context of function approximation. We have also shown that there is a close connection between social decision problems on the one hand and associated population games on the other hand. The connection involves a change of sign, as well as a re-interpretation of decision weights as population fractions. Nash equilibria of the associated population game (the tester game) give rise to maxmin points of the original social decision problem. The connection is of interest both from a conceptual perspective and from an algorithmic point of view. Conceptually, it is remarkable that social decision problems, which are optimization problems with a single decision maker (the social planner), are related under certain conditions to population games, which involve many decision makers who just pursue their own interests. From the algorithmic perspective, the theorem invites the application of algorithms that have been developed for finding Nash equilibria in population games to computational methods for solving social decision problems.

With the idea of relating maxmin problems to population games in place, many followup questions can be asked. We mention just a few. In several applications, for instance in statistics, it is natural to work with continuous collectives, i.e., collectives that are modeled as a continuum, rather than as a finite set. It would be of interest to extend the computational method of this paper to cover such cases, perhaps using as inspiration the Remez algorithm (see for instance [46]) that is used for the same purpose in the specialized context of Chebyshev approximation. Instead of the MWA iteration on which we have focused in this paper, one might also use discretized versions of alternative dynamical systems that have been proposed as descriptions of evolutionary dynamics of population games. This would lead to alternative numerical schemes which could be compared in terms of efficiency, scalability and so on. We have only discussed single-stage problems. It would be natural to consider multi-stage problems as well, and to investigate how the connection between maxmin problems and population games interacts with the methods of dynamic programming. While the solution of maxmin problems using methods taken from evolutionary games is important in applications, one may also reverse the perspective and ask what new insights about population games can be obtained. For instance, it would be of interest to extend Proposition 3.1 to a full characterization of tester games.

Appendix

We demonstrate here a social decision problem with a continuous decision space that is not simplicial, which means that there exists no continuous map from the simplex to the decision space that is subgroup efficient.

Example A.1

Take a group consisting of three members who live at points A, B, and C along a circular road, at equal distances from each other. The planner needs to place a facility at some point x along the road. The decision space ${\mathcal {X}}$ is therefore a circle. All members of the group evaluate the decision by a function $V_i(x)$ that is the negative of the length of the arc from the location i to x. With respect to the group as a whole, all points on the circle are Pareto optimal. For the subgroup consisting of members A and B, the set of Pareto optimal points is the arc from A to B, and so on. It is not possible to construct a Pareto map via weighted-sum optimization, even when nonuniqueness of the weighted-sum optimal solution would be resolved by a tiebreak rule. The reason is that, as is easily verified, only the three points A, B, and C can arise as solutions of a weighted-sum optimization problem when all weights are nonzero. A continuous map from the interior of the simplex to the discrete set $\{\text {A,B,C}\}$ has to be constant, and hence such a map cannot coincide with the weighted-sum solution.

The fact that weighted-sum optimization fails to provide a Pareto map does not by itself imply that a Pareto map could not be constructed in some other way. However, we now show that this is not possible. For a proof by contradiction, suppose there exists a Pareto map $\xi$ for the given problem. For $t\in [0,1]$ and $\eta \in [0,1]$, define the parametrized set of curves $t \mapsto w(t;\eta )$ by

$$\begin{aligned} w(t;\eta ) = (1-\eta ,\eta (1-t),\eta t). \end{aligned}$$

(weights on A, B, and C respectively). The decision space can be described as the interval $[-\pi ,\pi ]$ where the two end points are identified, and where the locations of the points A, B, and C are given by 0, $-\frac{2}{3}\pi$, and $\frac{2}{3}\pi$ respectively. For $\eta =0$, we have $\xi (w(t;0))=0$ for all t. As $\eta$ increases from 0 to 1, the point $\xi (w(0;\eta ))$ moves continuously from 0 to $-\frac{2}{3}\pi$, in such a way that $\xi (w(0;\eta )) \in [-\frac{2}{3}\pi ,0]$ for all $\eta$. Likewise, the point $\xi (w(1;\eta ))$ moves continuously from 0 to $\frac{2}{3}\pi$, in such a way that $\xi (w(1;\eta )) \in [0,\frac{2}{3}\pi ]$ for all $\eta$. Consequently, for all $\eta \in [0,1]$, there exists $t \in [0,1]$ such that $\xi (w(t;\eta )) = 0$. In particular, this holds for $\eta =1$. We have a contradiction, since the point 0, which corresponds to location A, is not efficient for the subgroup consisting of participants B and C.

For an alternative proof, one may use the fact that there is no continuous mapping from the unit disk to the unit circle that leaves the circle invariant; see for instance [26, Prop. 4.3].