Efficient bead-on-plate weld model for parameter estimation towards effective wire arc additive manufacturing simulation

Abstract

Despite the advances in hardware and software techniques, standard numerical methods fail in providing real-time simulations, especially for complex processes such as additive manufacturing applications. A real-time simulation enables process control through the combination of process monitoring and automated feedback, which increases the flexibility and quality of a process. Typically, before producing a whole additive manufacturing structure, a simplified experiment in the form of a bead-on-plate experiment is performed to get a first insight into the process and to set parameters suitably. In this work, a reduced order model for the transient thermal problem of the bead-on-plate weld simulation is developed, allowing an efficient model calibration and control of the process. The proposed approach applies the proper generalized decomposition (PGD) method, a popular model order reduction technique, to decrease the computational effort of each model evaluation required multiple times in parameter estimation, control, and optimization. The welding torch is modeled by a moving heat source, which leads to difficulties separating space and time, a key ingredient in PGD simulations. A novel approach for separating space and time is applied and extended to 3D problems allowing the derivation of an efficient separated representation of the temperature. The results are verified against a standard finite element model showing excellent agreement. The reduced order model is also leveraged in a Bayesian model parameter estimation setup, speeding up calibrations and ultimately leading to an optimized real-time simulation approach for welding experiment using synthetic as well as real measurement data.

1 Introduction

In industrial settings, the driving factor to use a specific process is often the achievable benefit. Thus, with the rise of additive manufacturing in industry, the race for cost reduction started. Typically, numerical simulations (such as finite element simulations) are used in the design stage to avoid an in-series production of real, physical prototypes, which are nothing but test cases [1]. Such simulations also provide more flexibility in optimization with the drawback of heavy computation times as well as a complex implementation. For the calibration of the simulation (through parameter estimation) and optimization of the results using real data, in the context of setting-up a digital twin, additional methods are required. These methods are often based on sampling approaches like Markov chain Monte Carlo (MCMC). Such approaches require a huge number of evaluations of the numerical model, with varying parameter sets, resulting in tremendous computational costs. Therefore, new approaches are required with the aim of providing real-time simulations and calibration. A popular concept to decrease the computational effort is model order reduction, where the evaluation of the model is faster than classically used approaches, even for complex processes.

Fig. 1

Experimental setup (left) and the derived parametric problem (right)

On the other hand, computational weld mechanics [2] has become a powerful tool to analyze the heat effects during welding and gaining a deeper understanding of the underlying physics, especially in arc welding processes [3,4,5,6,7,8]. However, due to the necessary simplifications in modelling, a validation against experimental reference data is compulsory [9]. A calibration of numerical models, through parameter estimation, is generally performed using deterministic model calibration such as least square [10]. An alternative to deterministic modelling is a Bayesian approach, which aims to approximate the posterior probability density function of the model parameters, allowing a full characterization of the uncertainties, as discussed in detail in [11]. However, in all cases, the computational cost of the direct simulations is still a limiting factor. These computational costs can be decreased by applying reduced order modelling (ROM). Its goal is to find a lower dimensional representation, which is able to capture the dominant behavior of the investigated system. A large variety of different approaches have been developed in the last decades. One of them is the “a priori” proper generalized decomposition [12,13,14], which has been used in several applications, for example surgery simulations [15, 16], data-driven applications [17, 18], contact problems [19, 20], and parameter estimation [21, 22]. Based on an a priori approximation of the solution field by a separated representation given by a number of proper generalized decomposition (PGD) modes, for all possible model parameters, a solution is generated giving all solution fields in a fixed parameter space. In general, each PGD mode is defined in a one-dimensional space, but a grouping of parameters, such as a mode defined in a 3D space, is possible, too. These additional PGD parameters could be besides the physical space, the time, and each model parameter. If the problem is hardly separable, a separation of the PGD weak form into the chosen PGD parameters is not possible. Novel methods are published to handle these cases; Ghnatios et al. [23] derived a method to operate such problems.

In the present paper, a hardly separable problem is addressed in the context of wire arc additive manufacturing, developing an efficient reduced order model of the temperature evolution using the PGD method. Since the welding torch is modeled by a moving heat source as a function of time, a standard PGD application will reach its limits [24]. In [23, 25, 26], a mapping approach is developed with a key idea to map those hardly separable parametric problem through the use of a coordinate transformation to a space where the separation is possible. The PGD calculation is typically computationally more complex than a standard finite element calculation, which considers a single set of parameters, but afterwards, the evaluation of the solution field for specific parameter sets can be done efficiently without solving any equation system. Thus, PGD is an appealing tool in cases where the same problem must be evaluated multiple times while varying its parameters, like model calibration or optimization tasks. Recently, the PGD approach has also been applied to thermal problems in the context of welding simulations. In Rubio et al. [22], a PGD model considering the width of a moving heat source as PGD parameter is discussed. It was also used as a forward model within a Bayesian model updating framework, by calling the PGD model in each sample of the underlying Markov chain sampling approach. In that case, the moving heat source was handled by a movement of the global coordinate system instead of a direct movement of the torch as well as an approximation by an asymptotic series. Furthermore, Favaretto et al. [27] considered temperature-dependent material parameters in their PGD model and Lu et al. [28] a coupling to the mechanical problem.

Fig. 2

Experiment’s substrate plate with thermocouples before (left) and after (right) the welding process

Fig. 3

Measurement of the weld pool length (left) and weld pool width (right) by counting pixels

The aim of this paper is to develop a fast to evaluate digital numerical reduced order model for arc welding simulations allowing for an efficient and reliable parameter estimation and control of the underlying process. Usually, the first step on the way to implement a wire arc additive manufacturing production is the bead-on-plate experiment. For that reason, the paper focuses on this experiment, but the proposed procedure can be extended to more complex problems. In such more complex problems, the geometry of the weld penetration changes completely due to the different heat conduction in a beat-on-plate seam and a build-up welds in higher layers, which means that an adapted heat source must be used [29]. Furthermore, in the bead-on-plate weld experiment, conventional technology with thermocouples and a camera is used to monitor the welding process. In Richter et al. [30], a new possibility of weld pool monitoring is described.

The related bead-on-plate weld experiment is first described before a general thermal transient model for its temperature evolution is derived with a finite element reference model and the PGD reduced order model. This reduced order model is coupled to a mapping approach, which handles the hardly separable parametric problem caused by the moving heat source. Moreover, this work extends the mapping approach by Ghnatios et al. [23] to a real 3D bead-on-plate weld problem. Furthermore, the derived reduced order model is used in a Bayesian inference setup for a stochastic parameter estimation. Several convergence studies as well as an efficient parameter estimation leveraging the reduced order model are performed, showing an excellent performance of the reduced order model.

2 Bead-on-plate experiment

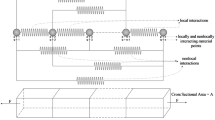
The investigated bead-on-plate weld experiment shown in Fig. 1 (left) is an automated pulsed-MIG process with a M12 (Ar+2.5% CO$_2$) as shielding gas. In the investigated setup, a 6-axis industrial robot moves the welding torch over the x-y-plane of a plate with dimensions $(L_x,L_y,L_z)$. The welding torch starts at the point $(x_0,y_0,z_0)$, moves in x-direction with a prescribed speed v in 1 G welding position, and is turned on at the time $t_\textrm{on}$ with average thermal power P, which can be determined by measurement of the transient arc voltage and power. During the movement, the welding torch passes four type K thermocouples T01, T02, T03, and T04, which measure the process temperature (see Fig. 2). The thermocouple T01 is on the bottom of the plate, whereas the other three are on top of the plate. Furthermore, the thermocouple T04 is inserted directly into the weld pool behind the welding torch during the welding process. Additionally, the whole process is captured by several cameras. Alternatively, the welding process can also be monitored using other approaches as in [30]. The used power source is a Fronius TPS 500i. Before the welding process starts, the plate has fully adapted to the ambient temperature $T_\infty$. At the bottom of the plate, normal convection occurs, since the plate is slightly elevated. At the time $t_\textrm{off}$, the welding torch is turned off and the plate cools down. The plate as well as the deposition material is 1.4404 (AISI 316 L) — an austenitic stainless steel, which is often used in the chemical industry, due to its lack of a solid phase transformation as well as its excellent corrosion resistance. The material properties that are considered are the density $\varrho$, the specific heat capacity $c_p$ and the thermal conductivity k. For the numerical analysis these material parameters are assumed to be temperature independent and given. The setup is shown in Fig. 2 before (left) and after (right) the welding process. Furthermore, Fig. 3 shows the weld pool size recorded during the experiment. The corresponding process parameter values are listed in Table 1. The effective heat input into the workpiece and the convection’s heat transfer coefficient are process parameters that are estimated using the measurement data. For that reason, they are added as additional variables in the reduced order model to efficiently solve the forward problem (thermal field as a function of these parameters) within the inverse parameter estimation problem. The number of forward model evaluations in the solution of the inverse problem depends on the methodology and ranges from less than a hundred for deterministic gradient based models up to more than a million for Bayesian inference procedures.

Table 1 Bead-on-plate experiment’s process parameters

3 Models and methods

3.1 Thermal transient model

WAAM is often used to produce thick–walled structures; thus, the heat accumulation is a main issue in the process [31, 32]. A parametric problem for simulating temperature evolution of the bead-on-plate experiment described in Section 2 is sketched in Fig. 1 (right). The simulation focuses on the thermal problem as it is one of the most important phenomena and consists a required input to find other relevant information, such as the solid phase distribution. The energy input of the welding torch is modeled by a moving heat source. Hence, the thermal transient problem with a moving heat source can be described by the classical heat equation

$$\begin{aligned} \varrho c_p \frac{\partial {T}}{\partial {t}} -k \Delta T = q = {\left\{ \begin{array}{ll} q_\textrm{G}, &{} t \in [t_\textrm{on},t_\textrm{off}] \\ 0, &{} \textrm{else}, \end{array}\right. } \end{aligned}$$

(1)

where T(x, y, z, t) is the temperature field and q(x, y, z, t) is the heat source in the 3D-domain $\Omega = [0,L_x] \times [0,L_y] \times [0,L_z]$ over a time interval $I=[0, t_\textrm{end}]$. The heat source is simulated by the commonly used mathematical model proposed by Goldak et al. [33]. Different heat source models are analyzed in [34, 35]. The Goldak heat source approximates the energy distribution by a double-ellipsoid Gaussian distribution. Thus, the moving heat source taking the movement in x-direction with velocity v into account is defined as

$$\begin{aligned} q_\textrm{G}(\varvec{x},t) = {\left\{ \begin{array}{ll} q_\textrm{f}(\varvec{x},t) = \frac{6\sqrt{3}\eta P}{(a_\textrm{f}+a_\textrm{r})bc\pi ^{\frac{3}{2}}} \exp ^{-3\left( \frac{x-(x_0+vt)}{a_\textrm{f}}\right) ^2} \\ \qquad \qquad \qquad \exp ^{-3\left( \frac{y-y_0}{b}\right) ^2} \exp ^{-3\left( \frac{z-z_0}{c}\right) ^2}, &{} x \ge x_0+vt \\ q_\textrm{r}(\varvec{x},t) = \frac{6\sqrt{3}\eta P}{(a_\textrm{f}+a_\textrm{r})bc\pi ^{\frac{3}{2}}} \exp ^{-3\left( \frac{x-(x_0+vt)}{a_\textrm{r}}\right) ^2} \\ \qquad \qquad \qquad \exp ^{-3\left( \frac{y-y_0}{b}\right) ^2} \exp ^{-3\left( \frac{z-z_0}{c}\right) ^2}, &{} x < x_0+vt, \\ \end{array}\right. } \end{aligned}$$

(2)

with $q_\textrm{f}$ the energy input in the heat source’s front part; $q_\textrm{r}$ the energy input in the heat source’s rear part; $\eta$ the arc efficiency; P the thermal power; $a_\textrm{f}$, $a_\textrm{r}$, b, and c the spatial distribution parameters as depicted in Fig. 4 measured via camera pictures during the experiment of Fig. 3; and $\varvec{x} = \begin{bmatrix} x&y&z \end{bmatrix}^\intercal$ a vector containing the global spatial coordinates. For the computation of multiple layers, an adjustment coefficient for the heat source as in [29] would be necessary, since the weld penetration changes in higher layers. The coordinate system’s origin is located in the lower corner of the plate shown in Fig. 1 (right). By definition, the energy input of the heat source reaches 5% intensity at its boundary given by $a_\textrm{f}$, $a_\textrm{r}$, b, and c. Thereafter, it is assumed that the heat source vanishes. Figure 5 shows a simplified representation of the heat source’s movement across the plate. There, the heat source is active for $t \in [t_\textrm{on},t_\textrm{off}]$, that is in the heating phase, and its path is marked by a solid line. Afterwards, the heat source is turned off and the plate cools down in the cooling phase.

Fig. 4

Goldak heat source model with moving local coordinate system $\varvec{x}' = \begin{bmatrix} x'&y'&z' \end{bmatrix}^\intercal$

Fig. 5

Values of the moving heat source in the heating and cooling phase. The movement of the active heat source across the plate is marked by a solid line

The plate starts at ambient temperature $T_\infty$. Thus, the initial condition is given by

$$\begin{aligned} T(x,y,z,t=0) = T_\infty . \end{aligned}$$

(3)

Heat loss is undergone through convective heat transfer as boundary condition over $\partial \Omega$ writes:

$$\begin{aligned} -k\nabla T_{\textrm{s}} \cdot \textbf{n} = h (T_\textrm{s} - T_\infty ), \end{aligned}$$

(4)

with $T_\textrm{s}$ the surface temperature and h the heat transfer coefficient. In this work, the radiation boundary condition is not directly considered; instead, it is combined with the convection boundary condition by linearization of the radiation through

$$\begin{aligned} \dot{Q}_\textrm{total}&= \dot{Q}_\textrm{conv} + \dot{Q}_\textrm{rad} = h (T_\textrm{s}-T_\infty ) + \varepsilon \sigma (T^4_\textrm{s}-T^4_\infty ) \nonumber \\&= h_\textrm{combined} (T_\textrm{s}-T_\infty ), \end{aligned}$$

(5)

with $\varepsilon$ the emissivity, $\sigma$ the Stefan-Boltzmann constant, and

$$\begin{aligned} h_\textrm{combined} = h + \varepsilon \sigma (T_\textrm{s}+T_\infty )(T^2_\textrm{s}+T^2_\infty ). \end{aligned}$$

(6)

3.2 Full order FE model

Applying the standard procedure to derive the weak form of Eq. (1) with the boundary conditions given in Eqs. (3) and (4), where in the following $h=h_\textrm{combined}=\textrm{const}$ is assumed, that is multiplying with a test function $T^*$, integrating and applying Green’s first identity, yields the weak form of Eq. (1)

$$\begin{aligned} \int _{\Omega } \varrho c_p T^*\frac{\partial {T}}{\partial {t}} + k \nabla T^*\cdot \nabla T \text {d}{V} + \int _{\partial \Omega } h T^*(T-T_\infty ) \text {d}{A} = \int _{\Omega } T^*q \text {d}{V}. \end{aligned}$$

(7)

Furthermore, to increase the stability of numerical methods solving Eq. (7), the space, time, and temperature in dimensionless form are considered. Thus, defining

$$\begin{aligned} \xi _x:= \frac{x}{L_\textrm{ref}}, \quad \xi _y:= \frac{y}{L_\textrm{ref}}, \quad \xi _z:= \frac{z}{L_\textrm{ref}}, \quad \tau := \frac{t}{t_\textrm{ref}} \quad \textrm{and} \quad \Theta := \frac{T}{T_\textrm{ref}}, \end{aligned}$$

(8)

with arbitrary but fixed $L_\textrm{ref}, t_\textrm{ref}, T_\textrm{ref} \in \mathbb {R}^+$ yields the dimensionless weak form

$$\begin{aligned} \int _{\mathfrak {Q}} T^*\frac{\partial \Theta }{\partial \tau } + \mathrm {Fo\,} \nabla T^*\cdot \nabla \Theta \text {d}{V} + \mathrm {Bi\,Fo} \int _{\partial \mathfrak {Q}} T^*\Theta \text {d}{A}\nonumber \\ = \mathfrak {k} \int _{\mathfrak {Q}} T^*q \text {d}{V} + \mathrm {Bi\,Fo} \int _{\partial \mathfrak {Q}} T^*T_\infty \text {d}{A}, \end{aligned}$$

(9)

with the dimensionless spaces $\mathfrak {Q} = \Omega / L_\textrm{ref}$ and $\mathfrak {I} = I / t_\textrm{ref}$,

$$\begin{aligned} \textrm{Fourier number} \quad&\textrm{Fo} = \frac{k t_\textrm{ref}}{\varrho c_p L^2_\textrm{ref}}, \nonumber \\ \textrm{Biot number} \quad&\textrm{Bi} = \frac{h L_\textrm{ref}}{k} \nonumber \\ \textrm{and} \quad&\mathfrak {k} = \frac{t_\textrm{ref}}{\varrho c_p T_\textrm{ref}}. \end{aligned}$$

(10)

As a reference full order model, the dimensionless weak form given in Eq. (9) is solved by applying the finite element method. A backward Euler approach is used for the time integration

$$\begin{aligned} \frac{\partial \Theta ^{m+1}}{\partial \tau } = \frac{\Theta ^{m+1}-\Theta ^m}{\Delta \tau }. \end{aligned}$$

(11)

Hence, the discrete system of the full order model for each time step m is given as

$$\begin{aligned} (\varvec{M}+ & {} \Delta \tau \, \varvec{K}) \Theta ^{m+1} \nonumber \\= & {} \Delta \tau \, \left( \mathfrak {k} \int _{\mathfrak {Q}} \varvec{N}^\intercal q^{m+1} \text {d}{V} + \mathrm {Bi\,Fo} \int _{\partial \mathfrak {Q}} \varvec{N}^\intercal T_\infty \text {d}{A} \right) \nonumber \\+ & {} \varvec{M} \, \Theta ^m, \end{aligned}$$

(12)

with the mass matrix $\varvec{M}$ and stiffness matrix $\varvec{K}$. Here, $\varvec{M} = \int _{\mathfrak {Q}} \varvec{N}^\intercal \varvec{N} \text {d}{V}$ and $\varvec{K} = \textrm{Fo} \int _{\mathfrak {Q}} \varvec{B}^\intercal \varvec{B} \text {d}{V} + \mathrm {Bi\,Fo} \int _{\partial \mathfrak {Q}} \varvec{N}^\intercal \varvec{N} \text {d}{A}$, with $\varvec{N} = \begin{bmatrix}\phi _1&\phi _2&\dots \end{bmatrix}$ a vector containing the linear, second-order finite element shape functions and $\varvec{B} = \begin{bmatrix}\varvec{\nabla } \phi _1&\varvec{\nabla } \phi _2&\dots \end{bmatrix}$ its space derivatives. The heat source $q^{m+1}$ is split as in Eq. (1) into

$$\begin{aligned} q^{m+1} = {\left\{ \begin{array}{ll} q_\textrm{G}^{m+1}, \quad &{} \mathrm {heating\; phase} \\ 0, &{} \mathrm {cooling\; phase.} \end{array}\right. } \end{aligned}$$

(13)

Fig. 6

Mapping from the actual space T(x, t) (left) to the mapped space T(s, r) (right)

3.3 PGD reduced model with mapping

Examples for deriving a PGD model for various transient thermal problems can be found in [27, 36]. First, a separate representation of the unknown temperature field has to be chosen. Since the arc efficiency $\eta$ and the heat transfer coefficient h are to be identified based on real measurements, both parameters $\eta$ and h are defined as additional PGD coordinates in intervals $\mathfrak {N}:= [\eta _\textrm{min},\eta _\textrm{max}]$ and $E:= [h_\textrm{min},h_\textrm{max}]$ in addition to the dimensionless space $\xi _x,\xi _y,\xi _z$ and time $\tau$. The interval boundaries of $\mathfrak {N}$ and E represent the minimum and maximum possible inputs into the PGD model. In order to increase the stability of the PGD model, the heat transfer coefficient h in dimensionless form is used, that is $h=h_\textrm{0}\mathfrak {h}$, $\mathfrak {h} \in \mathfrak {H}:= E/h_\textrm{0}$ with a fixed value $h_\textrm{0} \in \mathbb {R}^+$ based on prior knowledge. Thus, the temperature field will be approximated as

$$\begin{aligned} \Theta \approx \Theta ^n(\xi _x,\xi _y,\xi _z,\tau ,\eta ,\mathfrak {h})&= \sum _{i=1}^{n-1} F_1^i(\xi _x) F_2^i(\xi _y) F_3^i(\xi _z) F_4^i(\tau ) F_5^i(\eta ) F_6^i(\mathfrak {h}) \nonumber \\&\quad + X(\xi _x) Y(\xi _y) Z(\xi _z) K(\tau ) M(\eta ) H(\mathfrak {h}) \nonumber \\&\quad + G_x(\xi _x) G_y(\xi _y) G_z(\xi _z) G_t(\tau ) G_{\eta }(\eta ) G_h(\mathfrak {h}) \nonumber \\&= \Theta ^{n-1} + X Y Z K M H + G_x G_y G_z G_t G_{\eta } G_h, \end{aligned}$$

(14)

with the PGD modes (old set $F_j$ and new set X, Y, Z, K, M, H), homogeneous boundary condition $F_4(\tau =0)=0$ and the given inhomogeneous initial condition G separated for each system parameter. Hence, G holds

$$\begin{aligned} G_x(\xi _x)&= G_y(\xi _y) = G_z(\xi _z) = G_{\eta }(\eta ) = G_h(\mathfrak {h}) \equiv 1,\nonumber \\&\textrm{and} \quad G_t(\tau ) \equiv T_\infty . \end{aligned}$$

(15)

More details of this splitting into homogeneous and inhomogeneous part can be found in [36]. Inserting the PGD approach of Eq. (14) into the dimensionless weak form given in Eq. (9) yields a nonlinear problem for the PGD modes $F_j^i, j=1,\dots ,6, i=1,\dots ,n$. This nonlinear problem is solved iteratively for each new mode set X, Y, Z, K, M, H assuming the old $\Theta ^{n-1}$ is already known. Furthermore, the resulting nonlinear problem

$$\begin{aligned}{} & {} \int _{\mathfrak {Q \times \mathfrak {F}}} T^*\frac{\partial \Theta ^n}{\partial \tau } + \mathrm {Fo\,} \nabla T^*\cdot \nabla \Theta ^n \text {d}{V}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}}\nonumber \\{} & {} \qquad \qquad + \int _{\partial \mathfrak {Q \times \mathfrak {F}}} \mathrm {Bi\,Fo\,} T^*\Theta ^{n} \text {d}{A}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}}\nonumber \\{} & {} \quad = \mathfrak {k} \int _{\mathfrak {Q \times \mathfrak {F}}} T^*q \text {d}{V}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}} + \int _{\partial \mathfrak {Q \times \mathfrak {F}}} \mathrm {Bi\,Fo\,} T^*T_\infty \text {d}{A}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}}, \end{aligned}$$

(16)

with $\mathfrak {F}:= \mathfrak {I} \times \mathfrak {N} \times \mathfrak {H}$ is solved by an iterative scheme. An alternated directions fixed-point algorithm is used, as proposed in [37]. In this approach, each iteration consists of a number of steps equal to the number of PGD variables, which are repeated until reaching the fixed point. In the first step, the first PGD variable is updated; thus, $T^*$ reduces to

$$\begin{aligned} T^*= X^*Y Z K M H, \end{aligned}$$

(17)

while assuming all modes independent from the current variable as known. Next, the integral is separated into each variable, leading to a multiparameter solution without solving a huge multiparameter problem, but rather many small dimensional problems. These problems can be solved by standard approaches like finite elements, finite differences, or similar. The procedure for the first PGD variable’s mode is then repeated successively for each variable, leading to the new mode values after convergence. The used algorithm for that can be found in [38]. In this work, the problem regarding the time t is solved using finite differences, whereas the other problems are solved using finite elements.

However, the function describing the moving heat source given in Eq. (2) is not separable in space and time affine to the proposed separation in Eq. (14). Therefore, another approach for the separation is required allowing an efficient computation of the PGD modes as described above. Ghnatios et al. [23] developed a method for such hardly separable parametric problems. Details related to the derivation of the weak form are given in Appendix 1. The main idea of that approach is to map a hardly separable problem into a separable one by a coordinate transformation. Hence, the time t is transformed to the position of the heat source r. Additionally, the domain, where the heat source is moving, is separated into three parts s, as shown in Fig. 6 (right). The first part $s \in [0,1)$ comprises everything behind the heat source, the second part $s \in [1,2]$ depicts the heat source, and the last part $s \in (2,3]$ comprises everything in front of the heat source. Hence, this domain splitting is dependent on the heat source’s current position. When the heat source is turned off, in other words in the cooling phase, the right-hand side term vanishes and thus, the mapping is no longer needed.

Making use of this approach for the heating phase with $q=q_\textrm{G}$ leads to the definition of the first mapping parameter r

$$\begin{aligned} r:= x_0 + vt_\textrm{ref}\tau \quad \Leftrightarrow \quad&\tau = \frac{r-x_0}{vt_\textrm{ref}}, \qquad r \in [r_\textrm{on}, r_\textrm{off}]=:\mathfrak {R}, \end{aligned}$$

(18)

where $r_\textrm{on}$ and $r_\textrm{off}$ are restrictions, which are necessary to have a well-posed problem. These restrictions represent a spatial offset at the plate edges, since a weld that protrudes beyond it cannot be computed with the mapping approach. The load’s position is described by two functions $h_1(r)$, $h_2(r)$ and the constant width $h_\textrm{g}$, as shown in Fig. 6 (left). Here, the width $h_\textrm{g}$ is set to $h_\textrm{g} = a_\textrm{f} + a_\textrm{r}$, since this is the size of the Goldak heat source in x-direction as shown in Fig. 4, whereas the functions $h_1(r)$ and $h_2(r)$ are defined as

$$\begin{aligned} h_1(r) = r-a_\textrm{r}, \qquad&h_2(r) = L_x-a_\textrm{f}-r, \nonumber \\ \frac{\partial h_1(r)}{\partial r} = 1, \qquad&\frac{\partial h_2(r)}{\partial r} = -1. \end{aligned}$$

(19)

The second mapping parameter s, which separates the domain into three parts, is then defined as

$$\begin{aligned} s \in [0,1):&s:= \frac{L_\textrm{ref}\xi _x}{h_1(r)}\Leftrightarrow & {} \xi _x = \frac{sh_1(r)}{L_\textrm{ref}}, \nonumber \\ s \in [1,2]:&s:= \frac{L_\textrm{ref}\xi _x-h_1(r)}{h_\textrm{g}}+1\Leftrightarrow & {} \xi _x = \frac{(s-1)h_\textrm{g}+h_1(r)}{L_\textrm{ref}}, \nonumber \\ s \in (2,3]:&s:= \frac{L_\textrm{ref}\xi _x-h_\textrm{g}-h_1(r)}{h_2(r)}+2\Leftrightarrow & {} \xi _x = \frac{(s-2)h_2(r)+h_\textrm{g}+h_1(r)}{L_\textrm{ref}}. \end{aligned}$$

(20)

Since it is not allowed to divide by zero, the restrictions $r_\textrm{on}$ and $r_\textrm{off}$ need to hold $h_1(r_\textrm{on}) > 0$ and $h_2(r_\textrm{off}) > 0$ and thus $r_\textrm{on} > a_\textrm{r}$ and $L_x - r_\textrm{off} > a_\textrm{f}$. However, if the heat source is switched on at time $t_\textrm{on}$, such that the whole weld pool is on the plate, then $r_\textrm{on} = x_0 + v t_\textrm{on} > a_\textrm{r}$ is a suitable choice. Correspondingly, if the source is switched off before the plate edge at time $t_\textrm{off}$, $r_\textrm{off} = x_0 + v t_\textrm{off} < L_x - a_\textrm{f}$ is a suitable choice. These choices also fit the performed experiment.

Transforming the $\Theta (\xi _x,\xi _y,\xi _z,\tau ,\eta ,\mathfrak {h})$ problem to the mapped $\Theta (s,\xi _y,\xi _z,r,\eta ,\mathfrak {h})$ problem is given by coordinate transformation

$$\begin{aligned} \text {d}{\xi _x}\text {d}{\xi _y}\text {d}{\xi _z}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}} = \det (\varvec{J})\text {d}{s}\text {d}{\xi _y}\text {d}{\xi _z}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}}. \end{aligned}$$

Details of that transformation, as well as the definition of the simplifications $\nabla _{\varvec{\xi }r}\Theta$ and $\varvec{B}_{\tau } \nabla _{sr}\Theta$ can be found in Appendix 2.

Applying the mapped PGD approach

$$\begin{aligned} \Theta \approx \Theta ^n(s,\xi _y,\xi _z,r,\eta ,\mathfrak {h})&= \sum _{i=1}^{n-1} F_1^i(s) F_2^i(\xi _y) F_3^i(\xi _z) F_4^i(r) F_5^i(\eta ) F_6^i(\mathfrak {h}) \nonumber \\&\quad + S(s) Y(\xi _y) Z(\xi _z) R(r) M(\eta ) H(\mathfrak {h}) \nonumber \\&\quad + G_s(s) G_y(\xi _y) G_z(\xi _z) G_r(r) G_{\eta }(\eta ) G_h(\mathfrak {h}) \nonumber \\&= \Theta ^{n-1} + S Y Z R M H + G_s G_y G_z G_r G_{\eta } G_h \end{aligned}$$

(21)

to the dimensionless weak form given in Eq. (16) yields the mapped weak form

$$\begin{aligned}{} & {} \int _{\mathfrak {O}\times \mathfrak {A}} T^*\varvec{B}_{\tau } \nabla _{sr} \Theta ^n \,\det (\varvec{J}) + \mathrm {Fo\,} \nabla _{\varvec{\xi }r}T^*\cdot \nabla _{\varvec{\xi }r}\Theta ^n \,\det (\varvec{J}) \text {d}{V}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}}\nonumber \\{} & {} \quad + \int _{\partial \mathfrak {O}\times \mathfrak {A}} \mathrm {Bi\,Fo\,} T^*\Theta ^{n} \,\det (\varvec{J}) \nonumber \text {d}{A}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}} \nonumber \\{} & {} = \mathfrak {k} \int _{\mathfrak {O}\times \mathfrak {A}} T^*q \,\det (\varvec{J}) \text {d}{V}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}}\nonumber \\{} & {} \quad + \int _{\partial \mathfrak {O}\times \mathfrak {A}} \mathrm {Bi\,Fo\,} T^*T_\infty \,\det (\varvec{J}) \text {d}{A}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}}, \end{aligned}$$

(22)

with $\mathfrak {O}:= [0,3]\times [0,L_y/L_\textrm{ref}]\times [0,L_z/L_\textrm{ref}]$ and $\mathfrak {A}:= \mathfrak {R}\times \mathfrak {N}\times \mathfrak {H}$. The calculation of the required Jacobian and derivatives can be found in Appendix 2. On the weak form’s right-hand side of Eq. (22), the heat source q must be mapped accordingly. Therefore, applying the mapping for $s \in [1,2]$, that is

$$\begin{aligned} \tau = \frac{r-x_0}{vt_\textrm{ref}} \quad \textrm{and} \quad \xi _x = \frac{(s-1)h_\textrm{g}+h_1(r)}{L_\textrm{ref}} = \frac{(s-1)h_\textrm{g}+r-a_\textrm{r}}{L_\textrm{ref}} \end{aligned}$$

(23)

to the Goldak heat source given in Eq. (2) leads to

$$\begin{aligned} \bar{q}_\textrm{G}(s,\xi _y,\xi _z,r,\eta ,\mathfrak {h}) = {\left\{ \begin{array}{ll} \bar{q}_\textrm{f} = \underbrace{\frac{6\sqrt{3}P}{(a_\textrm{f}+a_\textrm{r})bc\pi ^{\frac{3}{2}}}} _{=: \bar{q}_4(r) \bar{q}_6(\mathfrak {h})} \underbrace{\eta }_{=: \bar{q}_5(\eta )} \\ \qquad \qquad \underbrace{\exp ^{-3\left( \frac{(s-1)h_\textrm{g}-a_\textrm{r}}{a_\textrm{f}}\right) ^2}} _{=: \bar{q}_1(s)} \\ \qquad \qquad \qquad \underbrace{\exp ^{-3\left( \frac{L_\textrm{ref}\xi _y-y_0}{b}\right) ^2}} _{=: \bar{q}_2(\xi _y)} \\ \qquad \qquad \qquad \qquad \underbrace{\exp ^{-3\left( \frac{L_\textrm{ref}\xi _z-z_0}{c}\right) ^2}} _{=: \bar{q}_3(\xi _z)}, &{} s \ge \frac{a_\textrm{r}}{h_\textrm{g}}+1 \\ \bar{q}_\textrm{r} = \underbrace{\frac{6\sqrt{3}P}{(a_\textrm{f}+a_\textrm{r})bc\pi ^{\frac{3}{2}}}} _{=: \bar{q}_4(r) \bar{q}_6(\mathfrak {h})} \underbrace{\eta }_{=: \bar{q}_5(\eta )} \\ \qquad \qquad \underbrace{\exp ^{-3\left( \frac{(s-1)h_\textrm{g}-a_\textrm{r}}{a_\textrm{r}}\right) ^2}} _{=: \bar{q}_1(s)} \\ \qquad \qquad \qquad \underbrace{\exp ^{-3\left( \frac{L_\textrm{ref}\xi _y-y_0}{b}\right) ^2}} _{=: \bar{q}_2(\xi _y)} \\ \qquad \qquad \qquad \qquad \underbrace{\exp ^{-3\left( \frac{L_\textrm{ref}\xi _z-z_0}{c}\right) ^2}} _{=: \bar{q}_3(\xi _z)}, &{} s < \frac{a_\textrm{r}}{h_\textrm{g}}+1, \end{array}\right. } \end{aligned}$$

(24)

with $s\in [1,2]$. The mapping is not required for the right-hand side, since $q=0$ is assumed for $s \in [0,1)\bigcup (2,3]$. This transformed equation can easily be separated for each parameter into $\prod _{i=1}^6 \bar{q}_i$ — the reason why the mapping approach was introduced — and is furthermore independent of r.

The model including the mapping cannot be extended to take the cooling phase into account, due to its restriction in r. Thus, a second PGD model is added for the cooling phase given Eq. (16) with $q=0, t\in (t_\textrm{off},t_\textrm{end}]$ and as initial condition the temperature at the last time point of the heating phase.

In summary, two coupled PGD models are introduced. On the one hand, a model ($\Theta _1$) with the mapping for the heating phase and, on the other hand, a model ($\Theta _2$) without the mapping for the cooling phase. These problems are summarized as:

Heating phase

$$ \frac{\partial \Theta ^n_1}{\partial \tau } - \mathrm {Fo\,} \Delta \Theta ^n_1 = \mathfrak {k} \bar{q}_\textrm{G} $$

$$ \Theta ^n_1(s,\xi _y,\xi _z,r=r_\textrm{on}, \eta , \mathfrak {h}) = T_\infty $$

$$\begin{aligned} \Theta ^n_1(s,\xi _y,\xi _z,r,\eta ,\mathfrak {h}) =&\sum _{i=1}^{n} F_1^i(s) F_2^i(\xi _y) F_3^i(\xi _z) F_4^i(r) F_5^i(\eta ) F_6^i(\mathfrak {h})\\&+ G_s(s) G_y(\xi _y) G_z(\xi _z) G_r(r) G_{\eta }(\eta ) G_h(\mathfrak {h}), \nonumber \end{aligned}$$

(25)

Cooling phase

$$ \frac{\partial \Theta ^n_2}{\partial \tau } - \mathrm {Fo\,} \Delta \Theta ^n_2 = 0 $$

$$ \Theta ^n_2(\xi _x,\xi _y,\xi _z,\tau =\frac{t_\textrm{off}}{t_\textrm{ref}}, \eta , \mathfrak {h}) = \Theta ^n_1(s,\xi _y,\xi _z,r=r_\textrm{off}, \eta , \mathfrak {h}) $$

$$\begin{aligned} \Theta ^n_2(\xi _x,\xi _y,\xi _z,\tau ,\eta ,\mathfrak {h}) =&\sum _{i=1}^{n} F_1^i(\xi _x) F_2^i(\xi _y) F_3^i(\xi _z) F_4^i(\tau ) F_5^i(\eta ) F_6^i(\mathfrak {h})\\&+ G_x(\xi _x) G_y(\xi _y) G_z(\xi _z) G_t(\tau ) G_{\eta }(\eta ) G_h(\mathfrak {h}). \nonumber \end{aligned}$$

(26)

3.4 Bayesian model calibration

A frequently applied method to estimate a simulation model’s parameters while accounting for the associated uncertainties is Bayesian parameter estimation. In this approach, based on some prior knowledge with respect to the model’s parameters in combination with given observations, the parameter’s joint posterior probability distribution is computed using Bayes’ rule via

$$\begin{aligned} p(\varvec{\theta }\,|\,\mathcal {D}) = \frac{p(\mathcal {D}\,|\,\varvec{\theta })\,p(\varvec{\theta })}{\int p(\mathcal {D}\,|\,\varvec{\theta })\,p(\varvec{\theta })\,\textrm{d}\varvec{\theta }}. \end{aligned}$$

(27)

In this equation, $\varvec{\theta }\in \mathbb {R}^n$, $n\in \mathbb {N}$ represents the vector of model parameters, $p(\varvec{\theta })$ the corresponding prior distribution, $p(\varvec{\theta }\,|\,\mathcal {D})$ the parameter’s posterior distribution and $p(\mathcal {D}\,|\,\varvec{\theta })$ the likelihood function, in other words the probability that the model has generated the data given the model parameters. Note that the computed posterior distribution may be seen as an update of the prior distribution given the provided observations $\mathcal {D}$. More details on the mathematical background can be found for example in [39].

In order to evaluate Eq. (27), several approaches are available, for example direct computation, approximations [40], or sampling-based methods [41]. Note that the main effort in this evaluation is associated with the possibly high-dimensional integral over the parameter space in the denominator of the right-hand-side expression. In this work, a sampling-based approach in the form of Markov chain Monte Carlo (MCMC) sampling [42, 43] is applied. The corresponding computations are conducted using probeye [44], a Python package developed at the corresponding author’s department for defining and solving parameter estimation problems.

Those calibration approaches are usually very time-consuming, since a huge number of problem evaluations often in the order of $10^4$–$10^6$ with different parameter values are required. Here, the derived PGD reduced model is used, which allows real-time evaluation for all parameter values in a prescribed range leading to a very efficient parameter estimation setup.

Fig. 7

The real measurement data over the whole time domain. The beginning of the cooling phase is marked by the dashed line

3.5 Error measurement

Ensuring that a model creates trustworthy data is mandatory. This can be achieved with convergence analysis and error measurement. For this purpose, a mesh convergence analysis should be carried out for the FEM model, which ensures that the generated data no longer changes. Here, the error between different solutions is given as the local relative error integrated in time:

$$\begin{aligned} \epsilon (x,y,z,\eta ,h) = \frac{\Vert {T_\textrm{M1}(x,y,z,t,\eta ,h) - T_\textrm{M2}(x,y,z,t,\eta ,h)}\Vert _{L^2(I)}}{\Vert {T_\textrm{M2}(x,y,z,t,\eta ,h)}\Vert _{L^2(I)}}. \end{aligned}$$

(28)

This error should decrease in each step of a mesh convergence study with M1 the FE model at iteration $l-1$ and M2 the FE model at iteration l. As soon as this difference is below a user-defined threshold, the solution is assumed to be converged. Furthermore, checking the accuracy of a model against another model, for example with M1 the PGD model and M2 the reference FE model, the smaller the error defined in Eq. (28) is, the better the models fit to each other.

Table 2 Bead-on-plate model parameters

Fig. 8

Reduced order model’s temperature field at $t={25}$s

4 Results and discussion

4.1 Experimental results

During the experiment described in Section 2, the temperature evolution was measured by several thermocouples. Figure 7 shows measured temperature data at three thermocouples for this experiment, where the heating and cooling phase is separated by a dashed line. In the heating phase, the thermocouple T04 is inserted directly into the weld pool behind the welding torch during the welding process. Hence, for this thermocouple, the relevant data starts after the breakdown of all thermocouples, since this breakdown of all the thermocouples is a consequence of the insertion of the thermocouple T04 into the molten steel. For the other thermocouples, the temperature peak is reached when the arc is as close as possible to them. Furthermore, it can be observed that in the heating phase, after the temperature peak has been reached, the temperature drops much faster at the thermocouples which are on the top of the plate than for the thermocouple at the bottom of the plate.

Fig. 9

Mean over all four sensor positions of the relative error $\epsilon$ of the space mesh (left) and time mesh (right) analysis with $\eta = 0.8$ and $h={15}{\text {W}/(\text {m}^{2}\text {K})}$

Fig. 10

Mean relative local error integrated in time over a data set (six parameter combinations) in the heating (left) and in the cooling (right) phase. T01 to T04 are the available measurement sensors

4.2 Numerical results

The validation of the proposed PGD model, which extends the mapping approach by Ghnatios et al. [23] to a real 3D bead-on-plate weld problem, is first performed by a comparison with the FEM solution without taking the experimental data into account. The goal is to analyze the quality of the reduced order model with a sensitivity analysis related to the numerical parameters such as the number of modes or the mesh discretization. For this validation, the model parameters are set according to Table 2. Even though the arc efficiency $\eta$ (PGD variable) is in general less than 1, the model should be able to notice untypical cases with $\eta \ge 1$, where most likely inaccuracies in the experimental setup occurred. Thus, $\eta _\textrm{max}$ is chosen larger than 1, such that the PGD model is able to handle these cases. Additionally, the heat transfer is represented by convection and linearized radiation with a combined and constant heat transfer coefficient $\mathfrak {h}$ (PGD variable). For illustration purposes, a snapshot of the PGD model solution is plotted in Fig. 8. It shows the reduced order model’s temperature field at a specific time point (25s) in the heating phase. Here, the extreme local temperature changes typical of the experiment can be observed.

The numerical accuracy of a PGD model depends on the discretization of each PGD parameter space as well as on the number of PGD modes. A typical approach for a PGD convergence analysis is to compare the PGD solution with a full order model solution with parameters in the PGD space to show that the PGD solution can adapt to different settings correctly. To obtain such a reference FEM solution, a mesh convergence study is required. Figure 9 shows the averaged error according to Eq. (28) over the refinement steps with fixed parameters $\eta = 0.8$ and $h={15}{\text {W}/(\text {m}^{2}\text {K})}$. Here, the initial spatial discretization has 40 elements in x-direction, 20 in y-direction, and 2 in z-direction. In each refinement step, the number of elements is doubled. The error in the time mesh analysis converges after 8 refinement steps with an error of $10^{-3}$. The same magnitude of the error in the space mesh analysis is reached after 6 refinement steps. For both meshes, the last but one refinement is used as mesh discretization for the FEM reference solution, respectively.

Fig. 11

Comparison of FEM and PGD solution at thermocouples T02 and T04 with $\eta = 0.8$, $h={15}{\text {W}/(\text {m}^{2}\text {K})}$ and 60 modes in the heating (left) and 30 modes in the cooling (right) phase

Fig. 12

Pair plot of the predicted posteriori (left) and calibrated PGD approximation with 1.0 standard deviations of the mean at thermocouple T02 (right) of the reference FE model value calibration

Based on the FEM mesh convergence analysis, the number of elements of the corresponding PGD meshes is chosen as $s:3945, \; \xi _y:640, \; \xi _z:44, \; r:1280, \; \eta :200, \; and \mathfrak {h}:140$. Figure 10 shows the decrease of the mean local error according to Eq. (28) integrated in time for six sets of chosen parameters $(\eta , h)$ at the four thermocouples, as the number of PGD modes in the heating as well as in the cooling phase increases. In the heating phase, within the first 60 modes, a typical non-monotonic convergence to around $3\%$ accuracy can be observed. The PGD modes in the cooling phase converge in the first 30 modes to the FEM reference solution up to an accuracy of around $4\%$. The different behavior in terms of a more monotonic decrease of the error in the cooling phase results from the absence of the large temperature gradients in the heating phase.

In Fig. 11, the temperature evolution over time computed with the PGD model compared with the reference FEM simulation at thermocouples T02 and T04 is plotted for a specific parameter set $(\eta =0.8, h={15}{\text {W}/(\text {m}^{2}\text {K})}$. An excellent agreement of the solutions can be observed.

Fig. 13

Pair plot of the predicted posteriori of the PGD model calibration using real measurement data

4.3 Bead-on-plate calibration

The performed calibration of the proposed bead-on-plate experiment aims to identify the heat transfer coefficient h as well as the arc efficiency $\eta$ from the experiment’s temperature data described in Section 4.1. The calibration is independent of the temperature measurement method, in other words independent of whether a conventional approach with thermocouples or a newer approach with a pyrometer as in [30] is used to measure the temperature. The calibration of the heat transfer coefficient h needs an understanding of the welding process itself. Even though the convection has an effect all the time, it is marginal as long as the heat source is still active. This behavior is reflected in the PGD modes in $\mathfrak {h}$, which are almost constant in the heating phase. Thus, the convection is marginal in this phase and a calibration of h would be inaccurate. Hence, to identify the heat transfer coefficient h, the cooling phase needs to be considered as also done in [45].

First, a calibration with synthetic measurement data is performed. Thus, the temperature values of the reference FE model (cooling phase) at all thermocouples, with $\eta =0.8$ and $h={15}{\text {W}/(\text {m}^{2}\text {K})}$, are used as measured data by adding a normal distributed measurement noise with zero mean and standard deviation $\sigma ={15}^{\circ }$C. The usage of virtual data allows to validate the developed model as well as to do some parametric studies, for example an investigation of the influence on the number of data points. The calibration is performed using MCMC with 20 chains, 1000 samples in the burn in phase, and 10,000 samples afterwards using

$$\begin{aligned} \eta&\sim \mathcal{T}\mathcal{N}(1,\, 0.3,\, \eta _\textrm{min},\, \eta _\textrm{max}), \end{aligned}$$

(29)

$$\begin{aligned} h&\sim \mathcal{T}\mathcal{N}(12,\, 4.5,\, h_\textrm{min},\, h_\textrm{max}) \quad \textrm{and} \end{aligned}$$

(30)

$$\begin{aligned} \sigma&\sim \mathcal {U}(0,\, 30) \end{aligned}$$

(31)

as prior distributions. The definition of the used likelihood function can be found in Appendix 3, where $\textbf{y}_e$ denotes the measurement data at all thermocouples. The identified posteriori is depicted in Fig. 12 (left). Due to the applied probabilistic approach, the result is again a probability distribution instead of a single set on parameter values resulting from the usual deterministic approaches as in [45, 46]. Furthermore, the used measured data is compared to the PGD model evaluated at the identified mean parameter values, which is shown in Fig. 12 (right) for the thermocouple T02. There, an excellent accuracy can be observed. Additionally, due to the properties of the MCMC method, the added noise is identified as well.

Fig. 14

Calibrated PGD model approximation using real measurement data at thermocouple T01 for the heating (left) and cooling (right) phase, with 1.0 and 2.0 standard deviations of the mean

Second, a calibration with real measurement data given in Fig. 7 splitted in training and testing is performed. The training is performed at the thermocouples T03 and T04, using the same settings as before, in other words the same priors and the same number of chains and samples. In the likelihood, the vector $\textbf{y}_e$ is filled with temperature values measured by the thermocouples T03 and T04, considering only the cooling phase. The testing is then done at the thermocouple T01. In the process, the inference estimates the posteriori parameter distribution for the reduced model to fit the real data. In Fig. 13, the identified posteriori is depicted. The identified means of the parameters are

$$\begin{aligned} \bar{\eta } = 0.995 \quad \textrm{and} \quad \bar{h} = {6,694}{\text {W}/(\text {m}^{2}\text {K})}. \end{aligned}$$

Figure 14 shows the validation of the calibrated PGD model at thermocouple T01, which is not included in the parameter estimation. The predictive posterior is computed by the samples of the MCMC algorithm. Since the parameter distributions are narrow, which is favored by a time correlation through a large number of data points, the uncertainty of the parameters is low. Thus, the standard deviation of the predictive posterior is dominated by the identified measurement noise with mean $\bar{\sigma } = {12.32}^{\circ }$C. Several things can be observed. First, on the left is the heating phase, which is not included in the calibration procedure. The error of the model to the measurement data is expected, since the model contains temperature independent material parameters as well as no further weld pool analysis and a welding process is a complex procedure, for example with an influence of the temperature dependency of the material parameters, especially in the heating phase. The focus here lies on the cooling phase, which is depicted on the right. There, a good agreement with the real cooling temperature decrease can be observed. Thus, even though the investigated models only use temperature independent material parameters as well as no further weld pool analysis, the approximation of real temperature data in the cooling phase of such a wire arc welding process is possible.

The great advantage lies in the computational time saving. A full order model like a FE model, which is the usual model for a welding simulation as in [34, 35, 47, 48], needs several hours for a single computation, whereas the reduced model only takes milliseconds for one evaluation, for example a computation of the temperature for the full time domain takes around 3.7 ms per thermocouple for the presented PGD model, and thus the complete calibration lasts minutes. Such high-speed parameter estimations were done using analytical models as in [49, 50], which come with a big trade-off in the amount of assumptions needed to set them up. Thus, the usage of the reduced order model combines the advantages of the accuracy of a FEM model with the speed of an analytical model. With that, the proposed methodology using the reduced order model enables an efficient model parameter estimation and builds the basis for the usage of a future digital twin in process control, where real-time measurement data is fed into a numerical model that augments the sensor data by computing additional indicators that can then be used for direct process control. However, the heat source has to be adjusted for a multi-layer simulation, since the geometry of the weld penetration changes due to the different heat conduction. A fitting approach for this is discussed in [29], where an adjustment term is added in the heat source model, which could be treated as an additional PGD variable.

5 Conclusion

In the present paper, a PGD forward model with a mapping capturing the hardly separable moving heat source for the temperature field of the wire arc additive manufacturing bead-on-plate weld problem is introduced and combined with a model calibration process. The hardly separable moving heat source term is handled by a mapping approach, which is extended to a 3D problem allowing the derivation of an efficient separated representation of the temperature. The proposed methods form the basis for a future digital twin regarding the real-time wire arc additive manufacturing process control.

Convergence studies are performed for the presented models showing good agreement of the PGD and FE model. A comparison of the PGD model to real measurement data shows an expected error in the heating phase due to the assumption of temperature independent material parameters as well as no further weld pool analysis, but also shows a good approximation in the cooling phase.

Furthermore, an efficient Bayesian model calibration by using the PGD forward model is performed. This enables a calibration procedure with several thousand samplings evaluated in some minutes. Here, the PGD model calibration process with reference FE model data shows an excellent accuracy of the estimated parameters heat power $\eta$ and heat transfer coefficient h. Finally, the calibration process with real measurement data is performed leading to a good approximation of the cooling phase. Due to the superb operational time of the reduced model, the model calibration process is fast as well. The reduction of the computational effort through reduced order models yields an excellent calibration possibility, inspiring the use of reduced order models as a tool for future digital twins as defined in [51].

Appendices

Appendix 1. Extended PGD formulation

Solving Eq. (16) (no mapping applied) requires a choice for the test function $T^*$. A possibility is

$$\begin{aligned} T^*= X^*Y Z K M H + X Y^*Z K M H + \dots + X Y Z K M H^*. \end{aligned}$$

(32)

To solve the resulting nonlinear problem, an alternated directions fixed-point algorithm is applied. Therefore, the test function considering x as variable reduces to

$$\begin{aligned} T^*= X^*Y Z K M H, \end{aligned}$$

(33)

while assuming all modes independent from the current variable as known. Inserting this approach in the homogeneous form of Eq. (16), that is with $q=0$, and separate it for each model parameter, yields (for the sake of simplicity, the integral limits are not given)

$$\begin{aligned}&\sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} \int YF_2^i(\xi _y) \text {d}{\xi _y} \int ZF_3^i(\xi _z)\text {d}{\xi _z} \int K\frac{\partial F_4^i(\partial \tau )}{\tau } \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*X \text {d}{\xi _x} \int YY \text {d}{\xi _y} \int ZZ \text {d}{\xi _z} \int K\frac{\partial K}{\partial \tau } \text {d}{\tau } \int MM \text {d}{\eta } \int HH \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*G_x\text {d}{\xi _x} \int YG_y \text {d}{\xi _y} \int ZG_z \text {d}{\xi _z} \int K\frac{\partial G_t}{\partial \tau } \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\mathrm {Fo\,} \sum _{i=1}^{n-1} \int \frac{\partial X^*}{\partial \xi _x}\frac{\partial F_1^i(\partial \xi _x)}{\xi _x} \text {d}{\xi _x} \int YF_2^i(\xi _y) \text {d}{\xi _y} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int \frac{\partial X^*}{\partial \xi _x}\frac{\partial X}{\partial \xi _x} \text {d}{\xi _x} \int YY \text {d}{\xi _y} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int HH \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int \frac{\partial X^*}{\partial \xi _x}\frac{\partial G_x}{\partial \xi _x} \text {d}{\xi _x} \int YG_y \text {d}{\xi _y} \int ZG_z \text {d}{z\hat{}} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\mathrm {Fo\,} \sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} \int \frac{\partial Y}{\partial \xi _y}\frac{\partial F_2^i(\partial \xi _y)}{\xi _y} \text {d}{\xi _y} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int X^*X \text {d}{\xi _x} \int \frac{\partial Y}{\partial \xi _y}\frac{\partial Y}{\partial \xi _y} \text {d}{\xi _y} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int HH \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int X^*G_x \text {d}{\xi _x} \int \frac{\partial Y}{\partial \xi _y}\frac{\partial G_y}{\partial \xi _y} \text {d}{\xi _y} \int ZG_z \text {d}{z\hat{}} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\mathrm {Fo\,} \sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} \int Y F_2^i(\xi _y) \text {d}{\xi _y} \int \frac{\partial Z}{\partial \xi _z}\frac{\partial F_3^i(\partial \xi _z)}{\xi _z} \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int X^*X \text {d}{\xi _x} \int YY \text {d}{\xi _y} \int \frac{\partial Z}{\partial \xi _z}\frac{\partial Z}{\partial \xi _z} \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int HH \text {d}{\mathfrak {h}} \nonumber \\ +&\textrm{Fo} \int X^*G_x \text {d}{\xi _x} \int YG_y \text {d}{\xi _y} \int \frac{\partial Z}{\partial \xi _z}\frac{\partial G_z}{\partial \xi _z} \text {d}{z\hat{}} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int HG_h \text {d}{\mathfrak {h}} \nonumber \\ \end{aligned}$$

$$\begin{aligned} +&\sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} \int YF_2^i(\xi _y) \text {d}{\xi _y} [ZF_3^i(\xi _z)]_{\xi _z=\xi _{z_\textrm{max}}} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*X \text {d}{\xi _x} \int YY \text {d}{\xi _y} [ZZ]_{\xi _z=\xi _{z_\textrm{max}}} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*G_x \text {d}{\xi _x} \int YG_y \text {d}{\xi _y} [ZG_z]_{\xi _z=\xi _{z_\textrm{max}}} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} \int YF_2^i(\xi _y) \text {d}{\xi _y} [ZF_3^i(\xi _z)]_{\xi _z=\xi _{z_\textrm{min}}} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*X \text {d}{\xi _x} \int YY \text {d}{\xi _y} [ZZ]_{\xi _z=\xi _{z_\textrm{min}}} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*G_x \text {d}{\xi _x} \int YG_y \text {d}{\xi _y} [ZG_z]_{\xi _z=\xi _{z_\textrm{min}}} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} [YF_2^i(\xi _y)]_{\xi _y=\xi _{y_\textrm{max}}} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*X \text {d}{\xi _x} [YY]_{\xi _y=\xi _{y_\textrm{max}}} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*G_x \text {d}{\xi _x} [YG_y]_{\xi _y=\xi _{y_\textrm{max}}} \int ZG_z \text {d}{\xi _z} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\sum _{i=1}^{n-1} \int X^*F_1^i(\xi _x) \text {d}{\xi _x} [YF_2^i(\xi _y)]_{\xi _y=\xi _{y_\textrm{min}}} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*X \text {d}{\xi _x} [YY]_{\xi _y=\xi _{y_\textrm{min}}} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&\int X^*G_x \text {d}{\xi _x} [YG_y]_{\xi _y=\xi _{y_\textrm{min}}} \int ZG_z \text {d}{\xi _z} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\sum _{i=1}^{n-1} [X^*F_1^i(\xi _x)]_{\xi _x=\xi _{x_\textrm{max}}} \int YF_2^i(\xi _y) \text {d}{\xi _y} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&[X^*X]_{\xi _x=\xi _{x_\textrm{max}}} \int YY \text {d}{\xi _y} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&[X^*G_x]_{\xi _x=\xi _{x_\textrm{max}}} \int YG_y \text {d}{\xi _y} \int ZG_z \text {d}{\xi _z} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ +&\sum _{i=1}^{n-1} [X^*F_1^i(\xi _x)]_{\xi _x=\xi _{x_\textrm{min}}} \int YF_2^i(\xi _y) \text {d}{\xi _y} \int ZF_3^i(\xi _z) \text {d}{\xi _z} \int KF_4^i(\tau ) \text {d}{\tau } \nonumber \\&\qquad \quad \int MF_5^i(\eta ) \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HF_6^i(\mathfrak {h}) \text {d}{\mathfrak {h}} \nonumber \\ +&[X^*X]_{\xi _x=\xi _{x_\textrm{min}}} \int YY \text {d}{\xi _y} \int ZZ \text {d}{\xi _z} \int KK \text {d}{\tau } \int MM \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HH \text {d}{\mathfrak {h}} \nonumber \\ +&[X^*G_x]_{\xi _x=\xi _{x_\textrm{min}}} \int YG_y \text {d}{\xi _y} \int ZG_z \text {d}{\xi _z} \int KG_t \text {d}{\tau } \int MG_{\eta } \text {d}{\eta } \int \mathrm {Bi\,Fo\,}HG_h \text {d}{\mathfrak {h}} \nonumber \\ =&T_\infty \int X^*\text {d}{\xi _x} \int Y \text {d}{\xi _y} [Z]_{\xi _z=\xi _{z_\textrm{max}}} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}} \nonumber \\ +&T_\infty \int X^*\text {d}{\xi _x} \int Y \text {d}{\xi _y} [Z]_{\xi _z=\xi _{z_\textrm{min}}} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}} \nonumber \\ +&T_\infty \int X^*\text {d}{\xi _x} [Y]_{\xi _y=\xi _{y_\textrm{max}}} \int Z \text {d}{\xi _z} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}} \nonumber \\ +&T_\infty \int X^*\text {d}{\xi _x} [Y]_{\xi _y=\xi _{y_\textrm{min}}} \int Z \text {d}{\xi _z} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}} \nonumber \\ +&T_\infty [X^*]_{\xi _x=\xi _{x_\textrm{max}}} \int Y \text {d}{\xi _y} \int Z \text {d}{\xi _z} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}} \nonumber \\ +&T_\infty [X^*]_{\xi _x=\xi _{x_\textrm{min}}} \int Y \text {d}{\xi _y} \int Z \text {d}{\xi _z} \int K \text {d}{\tau } \int M \text {d}{\eta } \int \mathrm {Bi\,Fo\,}H \text {d}{\mathfrak {h}}, \end{aligned}$$

(34)

which can be solved for $X^*$. The procedure for the first PGD variable’s mode is then repeated successively for each variable, leading to the new mode values after convergence.

Appendix 2. Coordinate transformation

Transforming the dimensionless $\Theta (\xi _x,\xi _y,\xi _z,\tau ,\eta ,\mathfrak {h})$ problem to the mapped $\Theta (s,\xi _y,\xi _z,r,\eta ,\mathfrak {h})$ problem is given by coordinate transformation

$$\begin{aligned} \text {d}{\xi _x}\text {d}{\xi _y}\text {d}{\xi _z}\text {d}{\tau }\text {d}{\eta }\text {d}{\mathfrak {h}} = \det (\varvec{J})\text {d}{s}\text {d}{\xi _y}\text {d}{\xi _z}\text {d}{r}\text {d}{\eta }\text {d}{\mathfrak {h}}, \quad \textrm{with} \end{aligned}$$

$$\begin{aligned} \varvec{J}&= \begin{bmatrix} \frac{\partial \xi _x}{\partial s} &{} \frac{\partial \xi _x}{\partial \xi _y} &{} \frac{\partial \xi _x}{\partial \xi _z} &{} \frac{\partial \xi _x}{\partial r} &{} \frac{\partial \xi _x}{\partial \eta } &{} \frac{\partial \xi _x}{\partial \mathfrak {h}} \\ \frac{\partial \xi _y}{\partial s} &{} \frac{\partial \xi _y}{\partial \xi _y} &{} \frac{\partial \xi _y}{\partial \xi _z} &{} \frac{\partial \xi _y}{\partial r} &{} \frac{\partial \xi _y}{\partial \eta } &{} \frac{\partial \xi _y}{\partial \mathfrak {h}} \\ \frac{\partial \xi _z}{\partial s} &{} \frac{\partial \xi _z}{\partial \xi _y} &{} \frac{\partial \xi _z}{\partial \xi _z} &{} \frac{\partial \xi _z}{\partial r} &{} \frac{\partial \xi _z}{\partial \eta } &{} \frac{\partial \xi _z}{\partial \mathfrak {h}} \\ \frac{\partial \tau }{\partial s} &{} \frac{\partial \tau }{\partial \xi _y} &{} \frac{\partial \tau }{\partial \xi _z} &{} \frac{\partial \tau }{\partial r} &{} \frac{\partial \tau }{\partial \eta } &{} \frac{\partial \tau }{\partial \mathfrak {h}} \\ \frac{\partial \eta }{\partial s} &{} \frac{\partial \eta }{\partial \xi _y} &{} \frac{\partial \eta }{\partial \xi _z} &{} \frac{\partial \eta }{\partial r} &{} \frac{\partial \eta }{\partial \eta } &{} \frac{\partial \eta }{\partial \mathfrak {h}} \\ \frac{\partial \mathfrak {h}}{\partial s} &{} \frac{\partial \mathfrak {h}}{\partial \xi _y} &{} \frac{\partial \mathfrak {h}}{\partial \xi _z} &{} \frac{\partial \mathfrak {h}}{\partial r} &{} \frac{\partial \mathfrak {h}}{\partial \eta } &{} \frac{\partial \mathfrak {h}}{\partial \mathfrak {h}} \end{bmatrix} = \begin{bmatrix} \frac{\partial \xi _x}{\partial s} &{} 0 &{} 0 &{} \frac{\partial \xi _x}{\partial r} &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \frac{\partial \tau }{\partial r} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial \Theta }{\partial \xi _x}&= \frac{\partial \Theta }{\partial s}\frac{\partial s}{\partial \xi _x} + \frac{\partial \Theta }{\partial \xi _y}\frac{\partial \xi _y}{\partial \xi _x} + \frac{\partial \Theta }{\partial \xi _z}\frac{\partial \xi _z}{\partial \xi _x} + \frac{\partial \Theta }{\partial r}\frac{\partial r}{\partial \xi _x}\nonumber \\&= \underbrace{\begin{bmatrix}\frac{\partial s}{\partial \xi _x}&\frac{\partial r}{\partial \xi _x}\end{bmatrix}}_{=: \varvec{B}_{\xi _x}} \underbrace{\begin{bmatrix}\frac{\partial \Theta }{\partial s}\\ \frac{\partial \Theta }{\partial r}\end{bmatrix}}_{=: \nabla _{sr}\Theta } = \varvec{B}_{\xi _x} \nabla _{sr}\Theta , \nonumber \\ \frac{\partial \Theta }{\partial \xi _y}&= \frac{\partial \Theta }{\partial s}\frac{\partial s}{\partial \xi _y} + \frac{\partial \Theta }{\partial \xi _y}\frac{\partial \xi _y}{\partial \xi _y} + \frac{\partial \Theta }{\partial \xi _z}\frac{\partial \xi _z}{\partial \xi _y} + \frac{\partial \Theta }{\partial r}\frac{\partial r}{\partial \xi _y} = \frac{\partial \Theta }{\partial \xi _y}, \nonumber \\ \frac{\partial \Theta }{\partial \xi _z}&= \frac{\partial \Theta }{\partial s}\frac{\partial s}{\partial \xi _z} + \frac{\partial \Theta }{\partial \xi _y}\frac{\partial \xi _y}{\partial \xi _z} + \frac{\partial \Theta }{\partial \xi _z}\frac{\partial \xi _z}{\partial \xi _z} + \frac{\partial \Theta }{\partial r}\frac{\partial r}{\partial \xi _z} = \frac{\partial \Theta }{\partial \xi _z}, \nonumber \\ \frac{\partial \Theta }{\partial \tau }&= \frac{\partial \Theta }{\partial s}\frac{\partial s}{\partial \tau } + \frac{\partial \Theta }{\partial \xi _y}\frac{\partial \xi _y}{\partial \tau } + \frac{\partial \Theta }{\partial \xi _z}\frac{\partial \xi _z}{\partial \tau } + \frac{\partial \Theta }{\partial r}\frac{\partial r}{\partial \tau }\nonumber \\&= \underbrace{\begin{bmatrix}\frac{\partial s}{\partial \tau }&\frac{\partial r}{\partial \tau }\end{bmatrix}}_{=: \varvec{B}_{\tau }} \begin{bmatrix}\frac{\partial \Theta }{\partial s}\\ \frac{\partial \Theta }{\partial r}\end{bmatrix} = \varvec{B}_{\tau } \nabla _{sr}\Theta . \end{aligned}$$

(36)

Thus, it holds

$$\begin{aligned} \nabla \Theta = \begin{bmatrix} \frac{\partial \Theta }{\partial \xi _x} \\ \frac{\partial \Theta }{\partial \xi _y} \\ \frac{\partial \Theta }{\partial \xi _z} \end{bmatrix} = \underbrace{\begin{bmatrix} \varvec{B}_{\xi _x} \nabla _{sr}\Theta \\ \frac{\partial \Theta }{\partial \xi _y} \\ \frac{\partial \Theta }{\partial \xi _z} \end{bmatrix}}_{=: \nabla _{\varvec{\xi }r}\Theta }. \end{aligned}$$

(37)

All these derivatives occurred in the weak form given in Eq. (22) and need to be calculated in each of the three s-parts, but are trivial with one exception, the first entry of $\varvec{B}_{\tau }$:

$$\begin{aligned} s \in [0,1):&\quad \frac{\partial s}{\partial \tau } = \frac{\partial }{\partial \tau }\left( \frac{L_\textrm{ref}\xi _x}{h_1}\right) = -\frac{L_\textrm{ref}\xi _x}{h_1^2} \frac{\partial h_1}{\partial \tau } = -\frac{L_\textrm{ref}\xi _x}{h_1^2} \underbrace{\frac{\partial h_1}{\partial r}}_{=1} \frac{\partial r}{\partial \tau }\nonumber \\&\hspace{.8cm} = -\frac{vt_\textrm{ref} L_\textrm{ref}\xi _x}{h_1^2} = -\frac{vt_\textrm{ref}s}{h_1} \nonumber \\ \quad&\quad \nonumber \\ s \in [1,2]:&\quad \frac{\partial s}{\partial \tau } = \frac{\partial }{\partial \tau } \left( \frac{L_\textrm{ref}\xi _x-h_1}{h_\textrm{g}}+1\right) = -\frac{1}{h_\textrm{g}} \underbrace{\frac{\partial h_1}{\partial r}}_{=1} \frac{\partial r}{\partial \tau } = -\frac{vt_\textrm{ref}}{h_\textrm{g}} \nonumber \\ \quad&\quad \nonumber \\ s \in (2,3]:&\quad \frac{\partial s}{\partial \tau } = \frac{\partial }{\partial \tau } \left( \frac{L_\textrm{ref}\xi _x-h_\textrm{g}-h_1}{h_2}+2\right) \nonumber \\&\hspace{.8cm} = -\frac{L_\textrm{ref}\xi _x-h_\textrm{g}-h_1}{h_2^2} \underbrace{\frac{\partial h_2}{\partial r}}_{=-1} \frac{\partial r}{\partial \tau } - \frac{1}{h_2} \underbrace{\frac{\partial h_1}{\partial r}}_{=1} \frac{\partial r}{\partial \tau } \nonumber \\&\hspace{.8cm} = \frac{vt_\textrm{ref}}{h_2} \frac{L_\textrm{ref}\xi _x-h_\textrm{g}-h_1}{h_2} - \frac{vt_\textrm{ref}}{h_2} = \frac{vt_\textrm{ref}(s-3)}{h_2} \end{aligned}$$

(38)

Considering the above computation yields

$$\begin{aligned} s \in [0,1):&\quad \det (\varvec{J}) = \frac{h_1}{L_\textrm{ref}vt_\textrm{ref}}, \quad \varvec{B}_{\xi _x} = L_\textrm{ref}\begin{bmatrix} \frac{1}{h_1}&0 \end{bmatrix}, \quad \varvec{B}_{\tau } = t_\textrm{ref}\begin{bmatrix} -\frac{vs}{h_1}&v \end{bmatrix}, \nonumber \\ \quad&\quad \nonumber \\ s \in [1,2]:&\quad \det (\varvec{J}) = \frac{h_\textrm{g}}{L_\textrm{ref}vt_\textrm{ref}}, \quad \varvec{B}_{\xi _x} = L_\textrm{ref}\begin{bmatrix} \frac{1}{h_\textrm{g}}&0 \end{bmatrix}, \quad \varvec{B}_{\tau } = t_\textrm{ref}\begin{bmatrix} -\frac{v}{h_\textrm{g}}&v \end{bmatrix}, \nonumber \\ \quad&\quad \nonumber \\ s \in (2,3]:&\quad \det (\varvec{J}) = \frac{h_2}{L_\textrm{ref}vt_\textrm{ref}}, \quad \varvec{B}_{\xi _x} \!=\! L_\textrm{ref}\begin{bmatrix} \frac{1}{h_2}&0 \end{bmatrix}, \quad \varvec{B}_{\tau } \!=\! t_\textrm{ref}\begin{bmatrix} \frac{v(s-3)}{h_2}&v \end{bmatrix}. \end{aligned}$$

(39)

Appendix 3. Likelihood function

Let $\textbf{y}_e\in \mathbb {R}^d,\, d\in \mathbb {N}$ denote the measurement data that depends on a set of input data $\textbf{x}_e = (x,y,z,t)$, where (x, y, z) describe the position of all thermocouples and t the time interval. Furthermore, the output of the PGD forward model $\textbf{y}$ at any sensor and at any time is defined as

$$\begin{aligned} \mathbf {\mu }(\textbf{x}_e) = \textbf{y}(\textbf{x}_e, \eta , h), \end{aligned}$$

(40)

and the additive covariance matrix as

$$\begin{aligned} \mathbf {\Sigma }(\textbf{x}_e) = \mathbf {\Sigma }_\textrm{model}(\textbf{x}_e,\eta ,h) + \mathop {\textrm{diag}}(\sigma ^2). \end{aligned}$$

(41)

With these definitions, the likelihood function is defined as

$$\begin{aligned} \mathcal {L}(\textbf{x}_e,\eta ,h) = \frac{\exp \left( -\frac{1}{2} (\textbf{y}_e-\mathbf {\mu }(\textbf{x}_e))^\intercal \mathbf {\Sigma }(\textbf{x}_e)^{-1}(\textbf{y}_e-\mathbf {\mu }(\textbf{x}_e))\right) }{\sqrt{(2\pi )^d \det \mathbf {\Sigma }(\textbf{x}_e)}}. \end{aligned}$$

(42)

These definitions are based on the more general case noted down in the probeye documentation https://probeye.readthedocs.io/en/latest/mathematics.html, last checked on 16.12.2022.