1 Introduction

The measurement of strain change in the Earth’s crust is fundamental to improve our understanding of long-term tectonic deformation, tidal and atmospheric variations and hydrological perturbations (Braitenberg, 1999; Zadro & Braitenberg, 1999). Developed during the 1970s to complement existing geodetic techniques (e.g., tilt and leveling measurements) and designed to operate in deep boreholes to reduce measurement noise, the Gladwin Tensor Strain Monitor (GTSM) belongs to the class of multi-component (tensor) sensors. GTSM sensors are designed to measure relative strain variations with a resolution greater than \(10^{-11}\) strain at periods of minutes to months (Gladwin, 1984; Gladwin & Hart, 1985) (for comparison, Global Positioning System sub-diurnal accuracy is \(\sim 10^{-7}\) strain (Reuveni et al., 2012)). Since their first deployment in California in the early 1980s (Gladwin et al., 1987), GTSMs have been deployed in numerous active regions around the world. They represent a major component of the Network of the Americas (NOTA) (Barbour et al., 2015; Langbein, 2015), and sensors have also been installed in Australia, Japan, South Korea and recently in Turkey, along the North Anatolian fault (Martinez-Garzon et al., 2019). Beginning in 2021, six GTSMs were deployed in Central Italy, as part of a multidisciplinary geophysical monitoring of the Alto Tiberina fault system (Chiaraluce et al., 2020). In the last decades, GTSMs have contributed to the detection and analysis of possible precursory strain anomalies (Gladwin et al., 1991), episodic tremor and slow slip events (Hawthorne & Rubin, 2010; Durand et al., 2022), aseismic creep episodes (e.g., Gladwin et al., 1994), coseismic and postseismic deformation (Langbein, 2015; Hawthorne et al., 2016), seismic wave propagation (Cao et al., 2018; Barbour et al., 2021) and hydrological processes (Barbour & Wyatt, 2014; Lu & Wen, 2018).

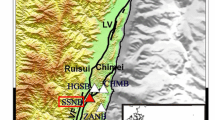
In the framework of an island-wide project to intensify the earthquake monitoring system following the devastating 1999 moment magnitude (\(M_w\)) 7.7 Chi-Chi earthquake (Shyn & Teng, 2001), 13 GTSMs were deployed in Taiwan by the Central Geological Survey between 2003 and 2010 (Chen et al., 2021). The first sensors were installed on the opposite ends of the Tsengwen reservoir in southwest Taiwan, where topographic effects are particularly significant. Two and three years later, additional networks were deployed in Hsinchu and Nantou counties, respectively, which are regions with steep topography and frequent landslides. The last instruments were installed in the Taipei county on a flat terrain but in an highly anthropized area (Fig. 1).

Fig. 1
figure 1

GTSM sensors deployed by the Central Geological Survey in north and central Taiwan (dark blue triangles) considered for tidal calibration (11 stations). Purple rectangles outline the different arrays. Red lines mark the traces of the main faults in Taiwan (Shyu et al., 2005). Colored circles show \(M_w \ge 5\) earthquakes from 1980 to 2023 from USGS catalog sized by magnitude. The yellow star marks the epicenter of the 1999 \(M_w\) 7.7 Chi-Chi earthquake. The inset shows Taiwan island location

Full size image

2 Instrumentation and Data

The GTSM sensor analyzed consists of a vertical stack of four extensometers (usually referred to as “gauges”), each of them enclosed in a \(\sim 9\) cm diameter by \(\sim 37\) cm long cylinder. The azimuths of three gauges (\(CH_0\), \(CH_1\), \(CH_2\)) are equally spaced by 60\(^\circ \) from each other, and \(CH_3\) is oriented 90\(^\circ \) from \(CH_1\) (Fig. 2). Having four gauges provides measurement redundancy as well as a back-up channel in case of a gauge malfunction. Each gauge hosts a Stacey-type differential capacitance bridge (Stacey et al., 1969) designed to measure the change in the instrument diameter under stress. The transducer consists of two parallel plate capacitors, one with fixed plates (used as reference), while a third plate is free to move in response to external forcing (Gladwin, 1984). The differential capacitance is directly related to the horizontal deformation of the instrument, namely the uniaxial strain in the azimuth of the gauge. GTSM is designed to perform optimally in contractional environments, condition assured by both the expansive grout used to cement the sensor into the borehole (Gladwin, 1984), and the borehole itself. Anthropogenic noise (e.g., highways, railroads, water pumped in wells), local effects (e.g., complex topography, cavities) (Harrison, 1976; Zadro & Braitenberg, 1999) and highly fractured and porous medium (Canitano et al., 2014) represent perturbations that likely impact the deployment and alter the data quality. Figure 3 illustrates the diversity of the sensor long-term relaxation patterns that deviate from the expected contraction, which possibly reflects the complex environment surrounding the sensors.

Fig. 2
figure 2

a Schematic view of a GTSM sensor, b orientation of the gauges in a North-East referential, and c cross-section of a Stacey-type differential transducer

Full size image
Fig. 3
figure 3

Example of strain data complexity revealed by the variability of long-term relaxation, with gauges showing long-term expansion (\(> 0\)) or contraction (\(< 0\)) for each GTSM sensor

Full size image

Based on the redundancy of GTSM measures due to the relative orientation of the strain gauges, tensor strain signals can be estimated in two ways (Roeloffs, 2010). Areal strain sensed by the strainmeter (indicated by superscript I) can be stated as:

$$\begin{aligned} \epsilon _A^I= & {} \dfrac{2}{3}\times (g_0e_0 + g_1e_1 + g_2e_2) \end{aligned}$$
(1)
$$\begin{aligned} \epsilon _{A0}^I= & {} \quad g_1e_1 + g_3 e_3 \end{aligned}$$
(2)

where \(e_i\) and \(g_i\) represent the elongation and the mechanical gain of gauge \(CH_i\), respectively. In the reference system defined by \(CH_1\) and \(CH_3\) (i.e. with the EW axis rotated parallel to CH1 azimuth) (Fig. 2(b)), differential extension can be expressed as:

$$\begin{aligned} \gamma _1^I= & {} \dfrac{2}{3}\times (2g_1e_1 - g_0e_0 - g_2e_2) \end{aligned}$$
(3)
$$\begin{aligned} \gamma _{10}^I= & {} \quad g_1e_1 - g_3 e_3 \end{aligned}$$
(4)

On the other hand, only one gauge combination provides engineering shear:

$$\begin{aligned} \gamma _2^I = \dfrac{2}{\sqrt{3}}\times (g_2e_2 - g_0 e_0) \quad \end{aligned}$$
(5)

In this study, we calibrate the tensor strain components for eleven sensors deployed in four arrays (Table 1), since two sensors were damaged shortly after deployment due to lightning strike, by comparing the tidally induced strain measured by the GTSMs with the synthetic tides modeled through Gotic2 software (Matsumoto et al., 2001). To separate solid Earth and ocean tidal signals from other signals present in the strain time-series, we perform a tidal analysis for each gauge using Baytap08 software (Tamura et al., 1991) and then compute the related tidal waveforms (thereafter referred to as “tidal extractions”). We select a large range of semi-diurnal (\(M_2\), \(S_2\), \(N_2\), \(K_2\)) and diurnal (\(O_1\), \(Q_1\), \(K_1\), \(P_1\)) tidal constituents to allow an accurate waveform extraction. To optimize the calibration process, we correct strain signals for long-term borehole relaxation and atmospheric pressure-induced strain (Canitano et al., 2018) using admittances estimated during the Baytap08 process. To verify the power reduction at 12 h and 24 h tidal periods, we compare the power spectrum before and after the removal of the extracted tides (Fig. 4), and we observe a large reduction of the energy content at such frequencies.

Table 1 Detailed informations of the GTSM stations calibrated in this study
Full size table
Fig. 4
figure 4

(Top) Example of Baytap08 analysis for the four gauges of station DARB. From top to bottom: estimated long-term trend, Earth and ocean tidal strain (“tidal extractions”) and residual strain signal. The residual strain is obtained after correcting the observed time-series for the long-term trend and the tidal signals. (Bottom) Power spectrum for semidiurnal and diurnal tidal periods showing tidal energy before (blue curve) and after the removal of the extracted tides (red curve) for each \(CH_i\) (respectively panels a–d)

Full size image

As we mentioned above, we utilize Gotic2 software to compute synthetic Earth and ocean tidal strain which are used as reference for calibration. The software provides a global tide model (NAO.99b) with a resolution of 0.5\(^\circ \) and also a regional ocean tide model (NAO.99Jb) with a resolution of 1/12\(^\circ \) which includes Taiwan (Matsumoto et al., 2000). In this work, we make use of this latter to compute the ocean loading. Reference strain tensor \(\epsilon ^F\) (i. e., in the rock formation) is computed in the E-N reference system (Fig. 2b):

$$\begin{aligned} \epsilon ^F = \begin{pmatrix} \epsilon _{EW} &{} \epsilon _{EN} \\ \epsilon _{EN} &{} \epsilon _{NS}\\ \end{pmatrix} \end{aligned}$$
(6)

where \(\epsilon _{EW}\) and \(\epsilon _{NS}\) are the EW and NS horizontal strain components, respectively, and \(\epsilon _{EN}\) is the EN shear component. Reference tensor strain components (areal strain \(\epsilon _A^F\), differential extension \(\gamma _1^F\), engineering shear \(\gamma _2^F\)) are computed using the following relations:

$$\begin{aligned} \epsilon _A^F&= \epsilon _{EW} + \epsilon _{NS}\nonumber \\ \gamma _1^F&= \epsilon _{EW} - \epsilon _{NS}\nonumber \\ \gamma _2^F&= 2\epsilon _{EN} \end{aligned}$$
(7)

Hereinafter, to estimate the sensor orientation and calibration factors, we will rotate the strain tensor by an angle \(\theta \) applying the rotation matrix \(R_M\):

$$\begin{aligned} R_M = \begin{pmatrix} cos(\theta ) &{} -sin(\theta ) \\ sin(\theta ) &{} cos(\theta )\\ \end{pmatrix} \end{aligned}$$
(8)

In the \(x'-y'\) referential, the strain tensor \(\epsilon ^{F'}\) resulting from the rotation by the angle \(\theta \) counterclockwise from the E-N reference system, is expressed as:

$$\begin{aligned} \epsilon ^{F'} = R_M^T \epsilon ^F R_M = \begin{pmatrix} \epsilon _{x'x'} &{} \epsilon _{x'y'} \\ \epsilon _{x'y'} &{} \epsilon _{y'y'}\\ \end{pmatrix} \end{aligned}$$
(9)

where \(\epsilon _{x'x'}\) and \(\epsilon _{y'y'}\) are the horizontal strain components along x\('\) and y\('\) axis, respectively, and \(\epsilon _{x'y'}\) is the x\('\)-y\('\) shear component. Finally, tensor strain components in the x\('\)-y\('\) referential are computed as follows:

$$\begin{aligned} \epsilon _A^{F'}&= \epsilon _{x'x'} + \epsilon _{y'y'}\nonumber \\ \gamma _1^{F'}&= \epsilon _{x'x'} - \epsilon _{y'y'}\nonumber \\ \gamma _2^{F'}&= 2\epsilon _{x'y'} \end{aligned}$$
(10)

3 Calibration Workflow for GTSM Sensors

The measurement of strain in a borehole differs from the strain applied in the rock formation (i.e., far enough from the borehole so that the strain field is in an unperturbed state) because of the perturbations induced by the borehole, the grout that cements the strainmeter in the borehole and the sensor itself, as well as due to the difference between the instrument’s and the rock formation’s mechanical properties. To transform the recordings of multi-component borehole strainmeter to formation strain requires a calibration matrix. In the most simplistic case (isotropic coupling case), one can link the relative elongation \(e_i\) and azimuth \(\theta _i\) of gauge \(CH_i\) to the reference strain tensor components through the equation (Hart et al., 1996; Roeloffs, 2010):

$$\begin{aligned} g_i e_i = \frac{1}{2} \bigl [ \tilde{C}\epsilon _A^F + \tilde{D}\gamma _1^F cos(2 \theta _i) + \tilde{D}\gamma _2^F sin(2 \theta _i) \bigl ] \end{aligned}$$
(11)

in which, \(\tilde{C}\) and \(\tilde{D}\) (in count/n\(\epsilon \)) are the areal and shear coupling coefficients, respectively, relating strain observations to formation strain. The isotropic case assumes a common areal strain coupling for the four gauges but also a common shear coupling factor between differential extension and engineering shear. However, this protocol proved to be unsuitable for all our sensors, and a common shear coupling coefficient \(\tilde{D}\) could not be found. In general, isotropic calibration fails to reconcile observed and synthetic tides (Langbein, 2015), which points toward the need to add further complexity in the calibration protocol (Hodgkinson et al., 2013; Canitano et al., 2018).

The second calibration approach (quasi-isotropic case) relaxes the condition of a fully isotropic medium and thus allows for a certain degree of anisotropy. We assume that a common factor \(\tilde{C}\) for areal strain still exists for the four gauges but that shear coupling factors may differ. The calibration equation for gauge \(CH_i\) becomes:

$$\begin{aligned} g_ie_i = \frac{1}{2} \bigl [\tilde{C}\epsilon _A^F + \tilde{D}_{dif}\gamma _1^F cos(2 \theta _i) + \tilde{D}_{eng}\gamma _2^F sin(2 \theta _i) \bigl ] \end{aligned}$$
(12)

where \(\tilde{D}_{dif}\) and \(\tilde{D}_{eng}\) are the differential extension and engineering shear coupling factors, respectively. Finally, if a strong deviation from the isotropic condition prevails for some sites, a more general coupling model is needed. We thus consider the non-isotropic (or cross-coupled) case which allows for different areal and shear coupling coefficients for each gauge (Hodgkinson et al., 2013):

$$\begin{aligned} \begin{pmatrix} e_0 \\ e_1 \\ e_2 \\ e_3 \end{pmatrix} = \begin{pmatrix} c_0 &{} d_{01} cos(2\theta _0) &{} d_{02} sin(2\theta _0) \\ c_1 &{} d_{11} cos(2\theta _1) &{} d_{12} sin(2\theta _1) \\ c_2 &{} d_{21} cos(2\theta _2) &{} d_{22} sin(2\theta _2) \\ c_3 &{} d_{31} cos(2\theta _3) &{} d_{32} sin(2\theta _3) \\ \end{pmatrix} \begin{pmatrix} \epsilon _A^F \\ \gamma _1^F \\ \gamma _2^F \end{pmatrix} \end{aligned}$$
(13)

where \(c_i\), \(d_{i1}\) and \(d_{i2}\) are the areal, differential extension and engineering shear coupling coefficients for gauge \(CH_i\), respectively. The non-isotropic calibration protocol implies strong heterogeneities between gauge responses to areal and shear strain, possibly caused by the overall sensor installation environment (Sect. 2) (Hodgkinson et al., 2013).

In general, the calibration factors of tensor strain signals are constrained by comparing the recorded amplitudes and phases of \(M_2\) and \(O_1\) tidal waveform modeling against theoretical values (Hart et al., 1996; Roeloffs, 2010). In this study, we test an original procedure to carry out the GTSM sensor calibration. We seek a tidal waveform reproduction based on a large set of tidal constituents (Sect. 2) as proposed by Canitano et al. (2018) which we then recombine to get a total waveform, being aware that, after calibration, \(M_2\) and \(O_1\) dominate the waveform reconstruction as shown in (Canitano et al., 2018). In agreement with previous calibration attempts we do not model diurnal and semidiurnal waveforms separately, neglecting a possible cross-coupling frequency dependence. This argument is partly supported by the vicinity of the observed to model ratio values for the \(M_2\) and \(O_1\) tidal components (e.g., Table 2 of (Roeloffs, 2010); Table 3 of (Hsu et al., 2015)), and by studies where such strain data are in agreement with those based on seismic or GPS information (e.g., Takanami et al., 2013; Agustsson et al., 1999).

The developed approach is completely data driven and proposes a new workflow for calibration starting from the raw gauge measurements (Fig. 5). As shear strain signals are difficult to resolve using multi-component strainmeters (Langbein, 2015), because they are particularly subjected to cross-coupling originating from internal inhomogeneities (Hart et al., 1996), we start the calibration by considering a quasi-isotropic coupling model for all sites. However, since the fully isotropic case represents the particular situation in which a common coupling coefficient for shear strain components exists (Eq. (11)), we let our data-driven calibration workflow to point towards this eventuality.

Fig. 5
figure 5

Flowchart depicting the calibration methodology proposed in this work

Full size image

4 Quasi-Isotropic Coupling Calibration

In order to carry out the calibration of the GTSMs under the quasi-isotropic assumption, we follow a two-step approach. Taking advantage of the redundancy of GTSM measures, we first perform a consistency check (Roeloffs, 2010) to assess whether the two relations to express areal strain (Eqs. (1) and (2)) and differential extension (Eqs. (3) and (4)) yield similar tidal waveform time-history. In theory, these two ways to compute strain signals should yield a similar result since they rely on the same assumptions (Sect. 2). However, strain recorded in situ undergoes several perturbations (Harrison, 1976; Canitano et al., 2014) that can strongly affect the gauge responses and the tensor strain signals. If similarity is verified, we can assume weights in Eqs. (1) to (5) to be unitary (i.e., \(g_i=1\)). On the other hand, differences in phase or amplitude between areal strain and differential extension can point towards the need of weighting the gauges before calibration (Hodgkinson et al., 2013). We observe that waveform correlations between \(\epsilon _A^I\) and \(\epsilon _{A0}^I\), and \(\gamma _1^I\) and \(\gamma _{10}^I\) are significant for most of the GTSM sensors, with Pearson correlation coefficient R of approximately 80% to 90% (Table 2). However, only two strainmeters (RNT and RST) show similar waveforms (Fig. 6), and thus require no weighting. To properly weight the gauges for the nine remaining strainmeters, we equalize Eqs. (1) and (2) (or equivalently Eqs. (3) and (4)), as follows:

$$\begin{aligned} e_1 = 2 \times g_0 e_0 + 2 \times g_2 e_2 - 3 \times g_3 e_3 \end{aligned}$$
(14)

where gauge weights \(g_0\), \(g_2\), \(g_3\) are constrained with respect to \(g_1\) (taken as unitary) through a least square minimization. We assess the effectiveness of the weighting through the variance reduction:

$$\begin{aligned} V_R = \dfrac{Var(\epsilon _A^{I,unweight} - \epsilon _{A0}^{I,unweight}) - Var(\epsilon _A^{I,weight} - \epsilon _{A0}^{I,weight})}{Var(\epsilon _A^{I,unweight} - \epsilon _{A0}^{I,unweight})} \end{aligned}$$
(15)

and we proceed similarly for differential extension signals \(\gamma _1^I\) and \(\gamma _{10}^I\). The superscripts unweight and weight refer to the case with \(g_i = 1\) and \(g_i\) estimated through Eq. (14), respectively. The weighting of \(CH_i\) significantly reduces the variance observed during the consistency check (\(V_R\) > 90%). For most of the sites, weights differ by about a factor 2 to 3 with respect to \(g_1\), but ratios of about an order of magnitude are found for SLIN, TAIS and DARB stations (Table 2).

Fig. 6
figure 6

Example of gauge weighting during the consistency check of quasi-isotropic calibration (Eq. (14)) using strain measurement redundancy following Eqs. (1) and (3) (black curve) and Eqs. (2) and (4) (red curve). We show comparisons between the two ways to compute areal strain and differential extension for RNT (with identical gauge weights), BMMT and PFMT stations (coefficients are shown in Table 2)

Full size image
Table 2 Gauge weights \(g_i\), Pearson correlation coefficient R (before and after weighting gauges) and variance reduction \(V_R\) estimated for weighted areal strain and differential extension signals through a consistency check
Full size table

In a second step, we constrain the sensor azimuth using Eq. (12), namely correlating the rotated theoretical strain field \(\epsilon ^{F'}\) (Eq. (9)) with the weighted shear strain components (Eqs. (3), (4) and (5)). In practice, we rotate the synthetic tide tensor with an increment of \(1^{\circ }\) (Eq. (10)) and seek the common angle which gives the highest Pearson coefficient between observed and synthetic shear components (Fig. 7). We assume this angle to represent the azimuth \(\theta _1\) of gauge \(CH_1\). A weak agreement between the shear components curves is symptomatic of a troublesome environment (e.g., JING and SANS, Fig. 7), which makes it harder to clearly identify the azimuth of the instrument. Once the sensor gauges are properly weighted, we estimate directly the quasi-isotropic calibration coefficient for areal strain C via the correlation between weighted areal strain and synthetic tidal waveforms (Sect. 2). To estimate the shear coupling coefficients, we first need to rotate the theoretical and measured strain signals in the same reference system. Then, having the strainmeter oriented, we estimate the shear calibration coefficients \(D_{dif}\) and \(D_{eng}\) using tidal waveform correlations.

Fig. 7
figure 7

Procedure adopted to estimate the instrument azimuth (i.e., orientation of gauge \(CH_1\), vertical gray line) using the joint waveform modeling of differential extension (blue curve) and engineering shear (orange curve) during quasi-isotropic calibration

Full size image

We observe that the quasi-isotropic approach (Fig. 8) allows us to estimate fairly accurately (\(R>85\%\)) the calibration factors for tensor strain signals in the case of five stations (out of eleven) (Tables 3 and 4). Four stations (RST, TAIS, SLIN and CINT) show a good modeling for at least two components (\(R>90\%\)) and one component (usually \(\gamma _1\) or \(\gamma _2\)) is less well calibrated (\(R<75\%\)). Only SANS and JING stations exhibit relatively low calibration quality for two components at least (\(R<60-70\%\)). To improve the calibration of the shear signals we now enhance the complexity of our calibration approach and test a fully cross-coupled model.

Table 3 Pearson correlation coefficient estimated for tensor strain components using a quasi-isotropic coupling calibration approach
Full size table
Table 4 Calibration coefficients and sensor orientation (gauge \(CH_1\) azimuth) estimated for tensor strain components using a quasi-isotropic coupling calibration approach
Full size table
Table 5 Pearson correlation coefficient estimated for tensor strain components using a non-isotropic coupling calibration approach
Full size table
Fig. 8
figure 8

Calibration of areal strain (upper panel), differential extension (central panel) and engineering shear (lower panel) following a quasi-isotropic coupling approach: a TSUN, b DARB, and c RST. The black curve represents the theoretical tidal waveforms (computed using Gotic2) and the red curve shows the calibrated strain signal

Full size image
Fig. 9
figure 9

Example of calibration using a non-isotropic coupling calibration approach for JING station. (Top) Calibration of gauges \(CH_i\) following Eq. (13). (Bottom) Reconstitution of tensor strain signals (areal strain (a), differential extension (b) and engineering shear (c)) resulting from the inversion of the coupling matrix (Eq. (16)). The black curve represents the theoretical tidal waveforms and the red curve shows the calibrated strain signal

Full size image

5 Cross-Coupling Calibration

In order to improve the calibration for some stations, we consider a non-isotropic coupling model (Fig. 5), which consists in resolving the linear system of Eq. (13). Once the coupling coefficients are known for every gauge (upper panels in Figs. 9 and 10), it is possible to invert the coupling matrix to obtain the calibration matrix:

$$\begin{aligned} \begin{pmatrix} \epsilon _A^F \\ \gamma _1^F \\ \gamma _2^F \\ \end{pmatrix} = \begin{pmatrix} C_{0} &{} C_{1} &{} C_{2} &{} C_{3} \\ D^{dif}_{10} &{} D^{dif}_{11} &{} D^{dif}_{12} &{} D^{dif}_{13} \\ D^{eng}_{20} &{} D^{eng}_{21} &{} D^{eng}_{22} &{} D^{eng}_{23} \\ \end{pmatrix} \begin{pmatrix} e_0 \\ e_1 \\ e_2 \\ e_3 \\ \end{pmatrix} \end{aligned}$$
(16)

As the coupling matrix is non-squared, some approximations are needed, and a Moore-Penrose pseudoinverse is applied (Hodgkinson et al., 2013). Note that this method does not allow us to estimate the sensor orientation, thus we use values estimated via the quasi-isotropic calibration (see Table 4).

Fig. 10
figure 10

Same as Fig. 9 for SANS strainmeter

Full size image

Applying the calibration matrix of Eq. (16) to the tidal extraction signals, we obtain the tensor strain components, that then can be compared with theoretical tidal signals to check the accuracy of the estimated calibration coefficients (Tables 5 and 6). For most of the stations, the non-isotropic protocol keeps the high degree of correlation for areal strain found via the quasi-isotropic approach. In particular, the approach also allows to strongly improve the calibration for TAIS sensor (\(R> 98\%\)) (Fig. 5) and a reasonable calibration improvement for SANS is found (\(R> 70\%\)) (Fig. 10). On the other hand, the protocol tends to slightly degrade the calibration of at least one tensor strain component for CINT and SLIN (\(< 10\%\)) while improving other signals (\(\gamma _1\) for CINT and \(\epsilon _A\) for SLIN).

Table 6 Calibration coefficients estimated for tensor strain components using a non-isotropic coupling calibration approach
Full size table

6 Discussion

In this study, we develop a protocol to calibrate the GTSM array deployed in Taiwan based on the modeling of the Earth and ocean tidal signals for a large range of tidal constituents (Fig. 5). The protocol starts by assuming the simplest calibration conditions, then we add complexity to the model depending on the quality of the strain data. Despite allowing a large number of free parameters (12 calibration factors) under the assumption of strong cross-coupling between gauges (Hart et al., 1996; Hodgkinson et al., 2013), the cross-coupled calibration approach (Sect. 5) shows marginal improvements for tensor strain calibration compared with the quasi-isotropic approach (\(\sim \) 5% to 10% for most stations) (Tables 3 and 5). Only JING and SANS sensors really benefit from a cross-coupled model for the calibration of the shear strain components \(\gamma _1\) and \(\gamma _2\).

The quasi-isotropic calibration proposed in Sect. 4, which relies on a relatively simple coupling model (3 coupling parameters), is generally suitable to resolve the orientation and the calibration of the tensor signals for the GTSM sensors in Taiwan (Table 3) provided that strain gauges are properly weighted before calibration. However, only four sites (RNT, RST, TAIS and PFMT) show a positive coupling coefficient for areal strain, while we observe a phase delay of approximately 180\(^{\circ }\) between observed and theoretical areal strain signals for other stations (\(C<0\)) (Table 4). Evidence for tidal areal signal anticorrelation has been previously observed among several GTSMs of the NOTA (Roeloffs, 2010). It may be related to an unexpectedly large sensitivity of sensor gauges to vertical formation strain (Roeloffs, 2010) but also to a possible effect of pore-fluid pressure (Roeloffs, 1996). Although being designed to respond only to horizontal deformation, GTSM sensors may experience coupling with vertical formation strain (Roeloffs, 2010). The underlying cause is unknown but vertical coupling is undesirable because it degrades the sensor response to tectonic strain while enhancing the response to surface loading, possibly leading to the necessity of a different calibration matrix for tectonic strains and surface loads (Roeloffs, 2010). Formation fluid pressure can impact the areal strain tides recorded by the strainmeter if pore-fluid flow can occur on the time-scale of diurnal or semi-diurnal tides (Roeloffs, 1996). The complex rainfall dynamics (Hsu et al., 2015; Mouyen et al., 2017) related to the rough surface topography and complex lithology of Taiwan (Kao & Milliman, 2008) may likely favor fluid flow at diverse time-scales. Overall a deeper understanding of these perturbations is limited by the lack of information about the GTSM siting and the absence of co-located pore-pressure measurements.

Besides proving to be successful for calibrating areal strain signals, the quasi-isotropic approach allows to calibrate reasonably well the shear components for nine stations (\(R> \sim ~80\%\)) (Table 3). In general, we observe that shear coupling factors for differential extension \(D_{dif}\) is larger than for engineering shear \(D_{eng}\) by a factor of 1.3 to 3 (Table 4). Interestingly, we only infer positive coupling coefficients for tidal shear strain calibration. The positive correlation between observed and theoretical shear strain waveforms may thus suggest that shear strain tides are much less affected by vertical strain or pore-fluid effects than areal strain tides (Roeloffs, 2010). However, we emphasize that because of the difficulty to resolve shear strain signals with tensor strainmeters (Hart et al., 1996; Langbein, 2015), the latter should be considered with care for modeling of geophysical processes, in particular for seismic source analysis (Lin et al., 2023).

We now discuss the case of TAIS site for which calibration results are strongly different from other stations. Indeed, TAIS shows an almost perfect correlation for shear components (Table 4) and a common shear coupling coefficient is found while it is also the only site for which areal strain is poorly constrained by the quasi-isotropic model (\(R\sim ~50\%\)) (Table 3). Conversely, areal tidal strain is strongly constrained via a non-isotropic calibration approach (Table 5) and a perfect anticorrelation is found for tidal waveforms between each protocol. Comparing the areal strain response to seasonal hydrological perturbations (rainfall episodes and groundwater level variations) under \(\epsilon _A^{quasi}\) and \(\epsilon _A^{cross}\) calibrations (Fig. 11), we aim to further investigate TAIS behaviour. The elastic rainfall load is associated to volumetric compression (Mouyen et al., 2017) followed by a groundwater redistribution which can be modeled assuming a poroelastic medium. In undrained conditions, the pore-pressure increases during compression, while it decreases during dilatation. If the undrained conditions do not apply, as during the fluid flow within the poroelastic medium, a pore-pressure increase leads to a dilatation of the rocks, while a pore-pressure decrease leads to a contraction of the rocks. As a consequence, the groundwater recharge of an aquifer (a poroelastic medium) is accompanied by an expansion of the rocks, while the discharge leads to a shrink of the rocks (e.g., Wang, 2000). However, the response of a strainmeter installed in a poro-elastic medium is not trivial. In some cases, the sign of the volumetric strain measured by the strainmeter could be opposite to this of the surrounding rocks. This occurs when the strainmeter behaves like an elastic inclusion inserted into a poroelastic medium (Segall et al., 2003). This greatly complicates the interpretation of the strainmeter response, however we can make two different conjectures for TAIS:

  1. 1.

    Under non-isotropic calibration \(\epsilon _A^{cross}\) the sensor records strain contraction (\(<0\)) during groundwater recharge, and expansion (\(>0\)) during discharge, i.e. the opposite response of a poroelastic medium (Segall et al., 2003). After a phase of steady-state response preceding rainfall (undeformed condition; phase (i)), a small expansion possibly related to atmospheric pressure drop during tropical typhoons is observed (ii). This phase is rapidly followed by the large ground compression (iii), caused by the mass loading of rainwater (Mouyen et al., 2017) which precedes the long and slow expansion (iv), mostly driven by aquifer discharge. This model likely reflects the case of a sensor installed in a properly sealed borehole located near an active aquifer (Hsu et al., 2015; Canitano et al., 2021).

  2. 2.

    Under quasi-isotropic calibration \(\epsilon _A^{quasi}\), the sensor reflects the expected strain evolution of the surrounding rocks which behave as a poroelastic medium (Segall et al., 2003). Undeformed phase (i) is followed by a rapid contraction (ii) which represents the medium elastic response to rainfall loading. Then, the strainmeter records rock expansion as groundwater pressure rises during rainfall diffusion or aquifer recharge (iii) followed by a contraction due to the draining process or aquifer discharge (iv) (Segall et al., 2003; Chen et al., 2021)

Fig. 11
figure 11

a Areal strain response of TAIS sensor to groundwater level perturbations under \(\epsilon _A^{quasi}\) (red curve) and \(\epsilon _A^{cross}\) (magenta curve) calibrations. The blue curve shows groundwater level variations recorded by station 10040111 (15 km away from TAIS). TAIS shows a substantial response (\(\sim \) 10–15 \(\mu strain\)) to the large annual groundwater fluctuations (\(\sim 10\) m over Taiwan) (Hsu et al., 2021). b Areal strain response and groundwater level variations (see a for details) to heavy rainfall episodes from July 18 to September 30 2008. Daily cumulated rainfall time-series (green dashed lines) are recorded at C1M480 rain gauge (\(\sim \) 2 km from TAIS). (c) Focus on the two heavy rainfall events in July 2008. Vertical black dashed lines mark the four different phases of TAIS response to environmental perturbations (see Sect. 6)

Full size image

7 Conclusions

The complex dynamics of surface and subsurface hydrological processes under semi-tropical climate conditions conjugated with the rough surface topography of Taiwan could have impacted the sensor deployment, pushing the installation conditions astray from the optimal ones. However, we demonstrate that a relatively simple quasi-isotropic approach (3 calibration coefficients) based on tidal waveform modeling is suitable to resolve the orientation and the calibration of the tensor signals for the GTSM sensors in Taiwan. Nonetheless, we observe that a high correlation degree does not necessarily reflect the genuine response of the instrument, in particular when the latter is subjected to complex nonlinear interactions between rainfall and groundwater variations (Zadro & Braitenberg, 1999). Moreover, as claimed by (Roeloffs, 2010), a strong coupling with vertical strain may point towards the need to use different calibration matrices for surface loads and tectonic strains. Therefore, calibration results should be analyzed in light of the perturbations that may affect them, and alternative methods should be used to ensure the accuracy and reliability of strain calibration and measurements. The high-fidelity response of borehole strainmeter in the seismic frequency range (Canitano et al., 2017) offers a calibration window depleted from major environmental disturbances and pore-fluid perturbations that can be used for a seismo-geodetic calibration (Bonaccorso et al., 2016; Currenti et al., 2017) in the future. Overall, despite the efforts required for their installation and calibration, we believe that this study demonstrates that borehole strainmeters can benefit research in a wide range of geophysical processes in Taiwan and in other active regions (e.g., Linde et al., 1993; Durand et al., 2022; Lin et al., 2023).