A mathematical description of the Weber nucleus as a classical and quantum mechanical system

Abstract

Wilhelm Weber’s electrodynamics is an action-at-a-distance theory which has the property that equal charges inside a critical radius become attractive. Weber’s electrodynamics inside the critical radius can be interpreted as a classical Hamiltonian system whose kinetic energy is, however, expressed with respect to a Lorentzian metric. In this article we study the Schrödinger equation associated with this Hamiltonian system, and relate it to Weyl’s theory of singular Sturm–Liouville problems.

1 Introduction

1.1 Weber electrodynamics

Wilhelm Weber’s electrodynamics is a today largely forgotten action-at-a-distance theory of electrodynamics. An interesting aspect of the theory is that while opposite charges always attract each other, equal charges are repulsing each other outside a critical distance $r_c$, but become attracting, too, at distances smaller than $r_c$. This led to Weber’s planetary atomic model which Weber published, among other models, posthumously [17]. A detailed account of this model can be found in [4, 5].

The history of Weber’s electrodynamics indeed reminds us on a fairy tale. Wilhelm Weber is famous for his discovery together with Rudolf Kohlrausch on the connection between electrodynamics and the velocity of light. This connection appears in Weber’s action at a distance theory quite different from the theory of Maxwell. How Weber’s electrodynamics leads to a complementary description of the classical electrodynamical phenomena is described in the book “Weber’s electrodynamics" by André Koch Torres Assis [3]. Differences occur if one considers instead of closed circuits as well open circuits. From Weber’s force law Ampère’s force law for current elements can be derived which allows as well transverse Ampère forces. Peter Graneau at MIT examined experimentally such phenomena as explained in the book “Newtonian Electrodynamics" he wrote jointly with his son Neal Graneau. Different from the theory of Maxwell–Lorentz in Weber’s electrodynamics fields do not carry energy. For that reason Weber’s Lagrangian differs as well from the Darwin Lagrangian. A phenomenon which does not have an analogon in the theory of Maxwell–Lorentz is the occurence of a critical radius at which the force between protons changes from attracting to repulsing. This is reminiscent of the Euler-Tricomi equation.

In this paper we treat the Weber nucleus from a mathematical point of view.

It is surprising that the complementary approach of Weber to electrodynamics got forgotten. Wilhelm Weber and Hermann von Helmholtz didn’t get along with each other. Helmholtz studied vortices which led to the theory of vortex atoms of Lord Kelvin. These vortex atoms had a great impact on the development of knot theory in mathematics but as well are the reason for one of the most absurd stories in the history of physics. Felix Klein blamed himself in his book “Geschichte der Mathematik im 19. Jahrhundert" for having explained to Karl Friedrich Zöllner, a phanatic admirer of Wilhelm Weber, that every knot in four dimensions can be unknotted. In order to disprove the theory of vortex atoms Zöllner tried with the help of a spiritualist medium to prove the existence of a fourth dimension. The elderly Wilhelm Weber participated as well at these spiritualist sessions and his complementary theory got forgotten in Europe soon. It was different in the US. A famous person which concerned himself with Weber’s electrodynamics is Vannevar Bush, the Science advisor of president Roosevelt, or the above mentioned Peter Graneau.

Given a positive charge at the center, the Weber Lagrangian, see [15, 18], for a second positive charge influenced by the one in the center is given in polar coordinates by the formula

$$\begin{aligned} L_{\textrm{W}}(r,\phi ,v_r,v_\phi ) =\frac{1}{2}( v_r^2+r^2 v_\phi ^2) {-}\frac{1}{r}\bigg (1+\frac{ v_r^2}{2c^2}\bigg ) \end{aligned}$$

where c is the speed of light. The first term is just the usual kinetic energy, but the second term describes a velocity dependent potential. Historically this led to a lot of confusion, in particular, Helmholtz doubted, because of the velocity dependent potential, that energy is preserved. That energy is preserved can easily be seen by changing brackets

$$\begin{aligned} \begin{aligned} L_{\textrm{W}}(r,\phi ,v_r,v_\phi )&=\frac{1}{2}\bigg (1 {-}\frac{1}{c^2r}\bigg ) v_r^2 +\frac{1}{2} r^2 v_\phi ^2 {-}\frac{1}{r} \\&=\frac{1}{2}\left( g_{rr}\, v_r^2 +g_{\phi \phi }\, v_\phi ^2\right) -\frac{1}{r}. \end{aligned} \end{aligned}$$

(1.1)

Now the potential does not depend on the velocity any more. But the kinetic part is not computed with respect to the flat metric. In fact, the metric gets singular at a critical radius, the Weber radius

$$\begin{aligned} r_c=1/c^2 \end{aligned}$$

where c is the speed of light. Outside the critical radius the metric is Riemannian, while inside it becomes Lorentzian.

Although the changing of brackets is mathematically trivial, the interpretation of Weber’s Lagrangian as a velocity independent Coulomb potential in a curved Lorentzian or Riemannian space seems to be first discussed in our previous paper [6]. This interpretation finally opens the door to actually write down a Schrödinger equation for the Weber nucleus, namely by replacing the kinetic part by the Laplace-Beltrami operator but now with respect to the Lorentzian metric. The discussion of the properties of the Schrödinger equation is the topic of the present paper.

1.1.1 Outline and main result

In Sect. 2 we study the classical motion. In particular, we see that inside the Weber nucleus there are no periodic orbits, but instead the trajectories start spiraling into the origin (the collision locus).

In Sect. 3 the Lorentzian interpretation of Weber’s Lagrangian, given by formula (1.1), enables us to find the Schrödinger equation for Weber electrodynamics by replacing the Lorentzian kinetic energy by its Laplace-Beltrami operator.

In Sect. 3.2 we separate the wave function into the radial and the angular part. In Sect. 4 we show that inside the critical radius the radial part satisfies a singular Sturm–Liouville problem with singularities at both ends, one due to the charge at the origin where the potential is singular, and one due to the critical radius where the Lorentz metric is singular.

The classical study of singular Sturm–Liouville problems is due to Hermann Weyl and his famous discovery [20] of a dichotomy between the two cases of limit circle and limit point. Weyl’s theory was further developed in Titchmarsh’s monograph [14]. If both ends are limit point the corresponding Schrödinger operator is self-adjoint, while in the case of limit circle an additional boundary condition has to be chosen [12, Chap. X §3 pp 448]. The main result of this article is

Theorem A

The radial part of Schrödinger’s equation of the Weber nucleus is limit circle at both ends of $(0,r_c)$, namely at the origin $r=0$ and at the critical radius $r=r_c$.

Theorem A is proved in Sect. 4. The case of zero angular momentum $\ell =0$ is Proposition 4.2. The case of non-zero angular momentum $\ell \not =0$ is Proposition 4.4.

The proof of Theorem A differs greatly in the case of zero angular momentum $\ell =0$ and non-zero angular momentum $\ell \not = 0$. This is due to the fact that for vanishing angular momentum the singularity at the origin $r=0$ is regular and therefore the corresponding ode Fuchsian, see e.g. [13, §4.2], while for non-vanishing angular momentum the singularity at $r=0$ is irregular. See [11, Ch. 5 §4] for the notions of regular and irregular singularities of an ode. In the irregular case the behavior close to the singularity is described by a diverging asymptotic series and the solutions start oscillating wildly.

1.1.2 Interpretation

What do we learn from Theorem A and its proof? It is interesting to compare the quantum solutions with the classical solutions. In fact, there are no periodic orbits in the Weber nucleus before regularization. According to Gutzwiller’s trace formula, cf. [7], there should be a relation between the classical periodic orbits and the treatment by Schrödinger’s equation. In view of Theorem A the Schrödinger operator is not self-adjoint, unless one assigns adequate boundary conditions; see [12, Ch. X §3]. Here one discovers an interesting difference between the cases of vanishing and non-vanishing angular momentum.

If the angular momentum vanishes, the singularity at the origin is regular. In this case it is possible to assign natural boundary conditions; see [8, Kap. 3 §7]. In fact, a similar phenomenon happened already for the classical hydrogen atom in case of vanishing angular momentum; see [8, Kap. 3 §9]. For the Weber nucleus the classical solutions for vanishing angular momentum are collisions. Collisions can be regularized so that one obtains periodic orbits.

For non-vanishing angular momentum the singularity at the origin is not regular. Close to the origin the eigenfunctions of the Schrödinger equation, for any choice of boundary condition, start oscillating wildly. In this case it is not clear how to put natural boundary conditions. On the classical side a similar phenomenon happens. Namely, for non-vanishing angular momentum the classical solutions start spiraling into the origin. In this case it is not clear how to regularize them.

It would be interesting to find a semi-classical interpretation, see [7], of this phenomenon which makes the Weber nucleus an intriguing dynamical system worth of further explorations.

2 The classical motion

Before we embark on the quantum mechanical treatment of the Weber nucleus we discuss its classical motion, see also [16] and [4, 5, §6.4].

As we explained in the introduction the relative motion of two equal charges is described in polar coordinates $(r,\phi )$ by the Weber Lagrangian $L=L_{\textrm{W}}$ in (1.1), that is

$$\begin{aligned} \begin{aligned} L(r,\phi ,v_r,v_\phi )&= \frac{1}{2}\left( \frac{r-r_c}{r}\, {v_r}^2+r^2 {v_\phi }^2\right) -\frac{1}{r} \end{aligned} \end{aligned}$$

where c is the speed of light and the critical radius

$$\begin{aligned} r_c:= 1/c^2 \end{aligned}$$

is called the Weber radius. Note that the metric describing the kinetic energy is Riemannian above the critical radius, and Lorentz below. The conjugate momenta are

$$\begin{aligned} p_r:=\frac{{\partial }L}{{\partial }\dot{r}} = \left( 1-\frac{1}{c^2r}\right) \dot{r} =\left( \frac{r-r_c}{r}\right) \dot{r},\qquad p_\phi :=\frac{{\partial }L}{{\partial }{{\dot{\phi }}}} = r^2{{\dot{\phi }}}. \end{aligned}$$

The Euler-Lagrange equation $\frac{d}{dt}\frac{{\partial }L}{{\partial }{{\dot{\phi }}}}=\frac{{\partial }L}{{\partial }\phi }$, namely $\dot{p}_\phi =0$, yields conservation of angular momentum

$$\begin{aligned} \ell :=r^2{{\dot{\phi }}} = p_\phi = \textrm{const}\end{aligned}$$

while $\frac{d}{dt}\frac{{\partial }L}{{\partial }\dot{r}}=\frac{{\partial }L}{{\partial }r}$, namely $\frac{d}{dt}\bigl (\frac{r-r_c}{r}\bigr )\cdot \dot{r}+\left( \frac{r-r_c}{r}\right) \ddot{r}=$, becomes

$$\begin{aligned} \left( \frac{1}{c^2}-1\right) \ddot{r} = \frac{\dot{r}^2}{2c^2r^2} - \frac{\ell ^2}{r^3} - \frac{1}{r^2}. \end{aligned}$$

Note that the factor $\frac{1}{c^2}-1 = \frac{r_c-r}{r}$ in front of $\ddot{r}$ is positive below the critical radius, and negative above. The Euler-Lagrange equations are equivalent to Hamilton’s equations for the Weber Hamiltonian

$$\begin{aligned} \begin{aligned} H(r,\phi ,p_r,p_\phi ) = p_r\dot{r}+p_\phi {{\dot{\phi }}} - L&= \frac{1}{2}\left( \frac{(r-r_c)\dot{r}^2}{r} + \frac{\ell ^2}{r^2}\right) + \frac{1}{r} \\&= \frac{1}{2}\left( \frac{rp_r^2}{r-r_c} + \frac{p_\phi ^2}{r^2}\right) + \frac{1}{r}. \end{aligned} \end{aligned}$$

(2.2)

To determine the motions, we rewrite the conservation of energy equation

$$\begin{aligned} H = \frac{1}{2}\left( \frac{(r-r_c)\dot{r}^2}{r} + \frac{\ell ^2}{r^2}\right) + \frac{1}{r} = h = \textrm{const}\end{aligned}$$

as

$$\begin{aligned} \dot{r}^2 = \frac{\ell ^2+2r-2hr^2}{r(r_c-r)}. \end{aligned}$$

(2.3)

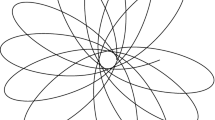
In the following we only discuss the radial component r, not the angular component $\phi$ which in case that the angular momentum $\ell :=r^2{{\dot{\phi }}}$ does not vanish is responsible for the spiraling mentioned in Fig. 1.

Fig. 1

Interpretation of results—classical and quantum solution types

Fig. 2

Radial component case 1—Energy $h\le 0$

Case 1: $h\le 0$–Fig. 2. Then the enumerator in equation (2.3) is positive, so there are no solutions with $r>r_c$. For $r<r_c$ equation (2.3) implies that $\dot{r}^2>2/r_c$ is bounded away from 0. Thus the solutions move in finite time between the poles at 0 and $r_c$.

Taking advantage of the fact that the velocity at the origin and at the critical radius even explodes, we can give a more refined analysis as follows. Consider first the approach to $r_c$. For $r<r_c$ close to $r_c$ we have approximately

$$\begin{aligned} \dot{r} \approx \pm \frac{k}{\sqrt{r_c-r}} \end{aligned}$$

with $k=\sqrt{\ell ^2/r_c+2-2hr_c}>0$. The solution of the ODE $\dot{r} =\pm k/\sqrt{r_c-r}$ with initial condition $r(0)=r_0<r_c$ close to $r_c$ is given by

$$\begin{aligned} r(t) = r_c - \left( (r_c-r_0)^{3/2}\mp \frac{3}{2} kt\right) ^{2/3}. \end{aligned}$$

Note that the solution can be continued continuously (but not $C^1$) beyond time T, of collision with the origin, to bounce back at $r_c$ and move toward the origin $r=0$. In contrast, it has yet not been studied if there is a geometric regularization at the origin $r=0$.

Consider next the approach to $r=0$. Suppose first that $\ell \ne 0$. Then for $r>0$ close to 0 we have approximately

$$\begin{aligned} \dot{r} \approx \pm \frac{k}{\sqrt{r}} \end{aligned}$$

(2.4)

with $k=\sqrt{\ell ^2/r_c}>0$. The solution of $\dot{r} = \pm \frac{k}{\sqrt{r}}$ with initial condition $r(0)=r_0>0$ close to 0 is given by

$$\begin{aligned} r(t) = \left( r_0^{3/2}\pm \frac{3}{2} kt\right) ^{2/3}, \end{aligned}$$

which approaches 0 in finite (positive or negative) time T. Note that the solution can be continued continuously (but not $C^1$) beyond time T to bounce back at 0 and move toward the critical radius $r_c$.

If $\ell =0$, then for $r>0$ close to 0 we have approximately

$$\begin{aligned} \dot{r} \approx \pm \sqrt{2/r_c} = \pm \sqrt{2}\, c, \end{aligned}$$

so the solution approaches 0 in finite time with approximately constant speed $\sqrt{2}\, c$ (the Weber constant). Note that the solution can be continued continuously (but not $C^1$) beyond time T, of collision with the origin,

Case 2: $h>0$. Then equation (2.3) can be written as

$$\begin{aligned} \dot{r}^2 = \frac{2h(r-r_+)(r-r_-)}{r(r-r_c)},\qquad \text {with}\quad r_\pm (\ell ) = \frac{1\pm \sqrt{1+2h\ell ^2}}{2h}. \end{aligned}$$

(2.5)

Since $r_+>\frac{1}{h}>0$ and $r_-\le 0$, we need to distinguish the three subcases $r_+<r_c$, $r_+=r_c$ and $r_+>r_c$. Note that $r_+<r_c$ is equivalent to $h>h_c$ for the critical energy

$$\begin{aligned} h_c = V_\textrm{eff}(r_c) = \frac{\ell ^2}{2r_c^2} + \frac{1}{r_c}, \end{aligned}$$

(2.6)

where $V_\textrm{eff}(r) = \ell ^2/2r^2 + 1/r$ is the effective potential.

Fig. 3

Case 2a—Energy $h\le 0$ and $r_+\in (0,r_c)$

Case 2a: $r_+<r_c$ (or equivalently $h>h_c$)–Fig. 3. Then the right hand side in equation (2.5) is negative for $r\in (r_+,r_c)$, so solutions cannot enter this region. Solutions in the region $(0,r_+)$ move in finite time between 0 and $r_+$.

To see this, consider first the approach to $r_+$. For $r<r_+$ close to $r_+$ we have approximately

$$\begin{aligned} \dot{r} \approx \pm k\sqrt{r_+-r} \end{aligned}$$

with $k=\sqrt{2h(r_+-r_-)/r_+(r_c-r_+)}>0$. Thus the solution with initial condition $r(0)=r_0<r_+$ close to $r_+$ is approximately given by

$$\begin{aligned} r(t) = r_+ - \left( (r_+-r_0)^{1/2}\mp \frac{1}{2} kt\right) ^{2}, \end{aligned}$$

which approaches $r_+$ in finite (positive or negative) time T at speed zero. Note that the solution can be continued smoothly beyond time T to reflect back at $r_+$ and move toward the origin $r=0$.

Consider next the approach to $r=0$. Suppose first that $\ell \ne 0$, and thus $r_-<0$. Then for $r>0$ close to 0 we have approximately, cf. (2.4),

$$\begin{aligned} \dot{r} \approx \pm \frac{k}{\sqrt{r}} \end{aligned}$$

with $k=\sqrt{-2hr_+r_-/r_c}>0$, so the solution approaches 0 in finite time as in Case 1. If $\ell =0$, then for $r>0$ close to 0 we have approximately (Case 1 again)

$$\begin{aligned} \dot{r} \approx \pm \sqrt{2hr_+/r_c} = \pm \sqrt{2}c, \end{aligned}$$

so the solution reaches 0 in finite time with approximately constant speed $\sqrt{2}c$.

Solutions in the region $(r_c,\infty )$ approach $r_c$ in finite (positive or negative) time (similarly to the approach to $r_c$ in Case 1). In the other time direction they move to $\infty$ with asymptotic speed $\sqrt{2h}$ (since the right hand side in (2.5) converges to 2h as $r\rightarrow \infty$).

Fig. 4

Case 2b—Energy $h\le 0$ and $r_+>r_c$

Case 2b: $r_+>r_c$ (or equivalently $h<h_c$)–Fig. 4. Then the right hand side in equation (2.5) is negative for $r\in (r_c,r_+)$, so solutions cannot enter this region. Solutions in the region $(0,r_c)$ move in finite time between 0 and $r_c$ as in Case 1 above. Solutions in the region $(r_+,\infty )$ approach $r_+$ at speed zero in finite (positive or negative) time (where they reflect back smoothly similarly to the approach to $r_+$ in Case 2a), while in the other time direction they again move to $\infty$ with asymptotic speed $\sqrt{2h}$.

Fig. 5

Case 2c—Energy $h\le 0$ and $r_+=r_c$

Case 2c: $r_+=r_c$ (or equivalently $h=h_c$)–Fig. 5. Then (2.5) simplifies to $\dot{r}^2=2h(1-\frac{r_-}{r})\ge 2h>0$, so solutions approach 0 in finite (positive or negative) time with infinite speed ($\ell \not =0$) or finite speed $\sqrt{2h}$ ($\ell =0$), while in the other time direction they move to $\infty$ with asymptotic speed $\sqrt{2h}$. In particular, this is the only case in which solutions pass through the critical radius.

We summarize this discussion in

Theorem 2.1

The relative motion of two equal charges in the plane under their mutual Weber force is as follows, depending on their energy h compared to the critical energy $h_c$.

1:

For $h\le 0$ solutions inside the critical radius $r_c$ move in finite time between 0 and $r_c$, and there are no solutions outside the critical radius.

2b:

For $0<h<h_c$ solutions inside the critical radius move in finite time between 0 and $r_c$, while solutions outside the critical radius move to $\infty$ as $t\rightarrow \pm \infty$ without reaching $r_c$.

2a:

For $h>h_c$ solutions inside the critical radius move to 0 in finite time in both time directions without reaching $r_c$, while solutions outside the critical radius move to $r_c$ in finite time in one time direction and to $\infty$ in infinite time in the other time direction.

2c:

For $h=h_c$ solutions move to 0 in finite time in one time direction and to $\infty$ in infinite time in the other time direction; in particular, this is the only case in which solutions pass through the critical radius. $\square$

3 Derivation of the nuclear Weber–Schrödinger equation

Let $r_c=1/c^2$ be the Weber radius and let

$$\begin{aligned} {{\mathbb {R}}}_\times :=(0,\infty )\setminus \{r_c\},\qquad {{\mathbb {R}}}^2_\times :={{\mathbb {R}}}^2\setminus \{0,x^2+y^2=r_c^2\} \end{aligned}$$

be the Weber “half line” and “plane”, respectively. In polar coordinates $(r,\phi )\in {{\mathbb {R}}}_\times \times {{\mathbb {R}}}/2\pi {{\mathbb {Z}}}$ on ${{\mathbb {R}}}^2_\times$ the Weber metric and cometric are the diagonal matrizes

$$\begin{aligned} \left( g_{ij}\right) =\begin{pmatrix}\frac{r-r_c}{r}&{}0\\ 0&{}r^2\end{pmatrix} , \qquad \left( g^{ij}\right) =\begin{pmatrix}\frac{r}{r-r_c}&{}0\\ 0&{}\frac{1}{r^2}\end{pmatrix} . \end{aligned}$$

(3.7)

The entries are the coefficients in the Weber Lagrangian (1.1) and Hamiltonian (2.2), respectively. The Weber plane is the Riemannian manifold $({{\mathbb {R}}}^2_\times , g)$.

3.1 Laplace-Beltrami operator on Weber plane

The Laplace-Beltrami operator applied to a function f is in local coordinates of any domain manifold given by

$$\begin{aligned} \Delta f =\frac{1}{\sqrt{\left| g\right| }} {\partial }_i\left( \sqrt{\left| g\right| } g^{ij} {\partial }_j f\right) \end{aligned}$$

where $|g|:=\left| \det g\right|$ and the Einstein sum convention applies.

Lemma 3.1

The Laplace-Beltrami operator in polar coordinates acts by

$$\begin{aligned} \begin{aligned} \Delta f&=\frac{{\partial }_r\Bigl (r^\frac{3}{2}\frac{\left| r-r_c\right| ^\frac{1}{2}}{r-r_c}\,{\partial }_r f\Bigr )}{\sqrt{r\left| r-r_c\right| }} +\frac{1}{r^2}\,{\partial }_{\phi \phi } f \\&=\left( \frac{3}{2}\, \frac{1}{r-r_c}-\frac{1}{2}\,\frac{r}{(r-r_c)^2}\right) {\partial }_r f +\frac{r}{r-r_c}\,{\partial }_{rr} f +\frac{1}{r^2}\,{\partial }_{\phi \phi } f \end{aligned} \end{aligned}$$

(3.8)

on functions f on the Weber plane $({{\mathbb {R}}}^2_\times ,g)$.

Proof

With $\left| g\right| =r\left| r-r_c\right|$ and due to the diagonal form of g we obtain

$$\begin{aligned} \begin{aligned} \Delta f&=\frac{{\partial }_r\left( \sqrt{r\left| r-r_c\right| }\,\frac{r}{r-r_c}\,{\partial }_r f\right) +{\partial }_\phi \left( \sqrt{r\left| r-r_c\right| }\,\frac{1}{r^2}\,{\partial }_\phi f\right) }{\sqrt{r\left| r-r_c\right| }} \\&=\frac{{\partial }_r\left( \sqrt{r\left| r-r_c\right| }\frac{r}{r-r_c}\right) \cdot {\partial }_r f +\left( \sqrt{r\left| r-r_c\right| }\frac{r}{r-r_c}\right) {\partial }_{rr} f}{\sqrt{r\left| r-r_c\right| }} +\frac{1}{r^2}\,{\partial }_{\phi \phi } f . \end{aligned} \end{aligned}$$

It remains to calculate the term ${\partial }_r(\dots )$, namely

$$\begin{aligned} \begin{aligned} \frac{{\partial }_r\Bigl (r^\frac{3}{2} \frac{\left| r-r_c\right| ^\frac{1}{2}}{r-r_c} \Bigr )}{\sqrt{r\left| r-r_c\right| }}&= \frac{\tfrac{3}{2}\, r^\frac{1}{2}\,\frac{r-r_c}{\left| r-r_c\right| ^\frac{3}{2}} +r^\frac{3}{2}(-\tfrac{1}{2})\frac{1}{\left| r-r_c\right| ^\frac{3}{2}}}{r^\frac{1}{2} \left| r-r_c\right| ^\frac{1}{2}} \\&=\frac{3}{2}\,\frac{1}{r-r_c}-\frac{1}{2}\,\frac{r}{(r-r_c)^2} \end{aligned} \end{aligned}$$

(3.9)

and this proves the lemma. $\square$

3.2 Separation into radial and angular part

On the Weber plane $({{\mathbb {R}}}^2_\times ,g)$ with coordinates $(r,\phi )$ consider the Laplace-Beltrami operator $\Delta$ given by (3.8). The Schrödinger equation is the pde

$$\begin{aligned} -\frac{1}{2} \Delta \psi +\frac{1}{r}\psi =E\psi \end{aligned}$$

(3.10)

for complex-valued functions $\psi :{{\mathbb {R}}}^2_\times \rightarrow {{\mathbb {C}}}$ and reals E. Separation of variables

$$\begin{aligned} \psi (r,\phi )=R(r)Y(\phi ) \end{aligned}$$

and abbreviating $\dot{R}:={\partial }_r R$ and $Y^\prime :={\partial }_\phi Y$ translates Schrödinger’s equation to

$$\begin{aligned} \begin{aligned} -\,\frac{Y}{2}\, \frac{{\partial }_r\Bigl (r^\frac{3}{2}\frac{\left| r-r_c\right| ^\frac{1}{2}}{r-r_c}\,{\partial }_r R\Bigr )}{\sqrt{r\left| r-r_c\right| }} -\frac{R}{2}\,\frac{1}{r^2}\, Y^{\prime \prime }+\frac{1}{r}\, RY =E RY. \end{aligned} \end{aligned}$$

Multiply this equation by $\frac{r^2}{RY}$ and reorder to obtain

$$\begin{aligned} \begin{aligned} -\,\frac{r^2}{2R}\, \frac{{\partial }_r\Bigl (r^\frac{3}{2}\frac{\left| r-r_c\right| ^\frac{1}{2}}{r-r_c}\,{\partial }_r R\Bigr )}{\sqrt{r\left| r-r_c\right| }} +r -r^2 E =\frac{1}{2}\,\frac{Y^{\prime \prime }}{Y} . \end{aligned} \end{aligned}$$

(3.11)

Note that the left hand side, a function of r only, is in fact constant, because the right hand side does not depend on r. Analogously the right hand side, a function of $\phi$ only, is equal to a constant, say $-\ell$.

3.2.1 Angular equation for Y

The right hand side (RHS) of (3.11) is equal to a constant, say $-\ell$, hence

$$\begin{aligned} Y^{\prime \prime }(\phi )=-2\ell Y(\phi ). \end{aligned}$$

The ode has a solution $Y(\phi )=c e^{i\sqrt{2\ell }\phi }$ for $c\in {{\mathbb {R}}}$. Periodicity $Y(\phi )=Y(\phi +2\pi )$ tells that $e^{2\pi i\sqrt{2\ell }}=1$ or equivalently $\sqrt{2\ell }=k\in {{\mathbb {N}}}_0$. Thus

$$\begin{aligned} Y(\phi )=c e^{i k\phi },\qquad c\in {{\mathbb {R}}},\quad k=\sqrt{2\ell }\in {{\mathbb {N}}}_0. \end{aligned}$$

(3.12)

4 Inside critical radius

4.1 Radial equation for R—zero angular momentum $\ell =0$

The left hand side (LHS) of (3.11) is equal to a constant $-\ell =-\frac{k^2}{2}$ where $k\in {{\mathbb {N}}}_0$. Multiplication by $\frac{-R}{r^2}$ leads to the ode

$$\begin{aligned} \frac{{\partial }_r\Bigl (r^\frac{3}{2}\frac{\left| r-r_c\right| ^\frac{1}{2}}{{ r-r_c}}\,{\partial }_r R\Bigr )}{2\sqrt{r\left| r-r_c\right| }} -\frac{1}{r}\, R -\frac{\ell }{r^2}\, R =-ER \end{aligned}$$

for functions $R:{{\mathbb {R}}}_\times \rightarrow {{\mathbb {C}}}$ of the variable r and a constant $E\in {{\mathbb {R}}}$. From now on we focus on the region inside the critical radius, because there our two protons have the property – spectacular when contrasted with the mainstream Coulomb law – to attract each other thanks to the Weber force law. Because ${ r-r_c}<0$ is negative, abbreviating $\dot{R}:={\partial }_r R$ the ode becomes

$$\begin{aligned} \begin{aligned} ER&= \frac{{\partial }_r\Bigl (\frac{r^\frac{3}{2}}{\sqrt{r_c-r}}\,{\partial }_r R\Bigr )}{2\sqrt{r(r_c-r)}} +\frac{1}{r}\, R { \,\,+\,\frac{\ell }{r^2}\, R}\\&=\frac{1}{2}\,\frac{r}{r_c-r}\, {\ddot{R}} +\left( \frac{3}{4}\,\frac{1}{r_c-r}+\frac{1}{4}\,\frac{r}{(r_c-r)^2}\right) \dot{R} +\frac{1}{r}\, R { \,\,+\,\frac{\ell }{r^2}\, R} \end{aligned} \end{aligned}$$

(4.13)

where ${ \ell =k^2/2}$ for any given $k\in {{\mathbb {N}}}_0$, see (3.12). Alternatively, this ode for the unkown function $R:(0,r_c)\rightarrow {{\mathbb {C}}}$ takes on the Sturm–Liouville normal form

$$\begin{aligned} \left( p{\dot{R}}\right) ^{{\cdot }}+qR=w E R \end{aligned}$$

(4.14)

where ${\dot{c}}$ means $\frac{d}{dr}$ and where in case ${ \ell =0}$ the functions w, q, p are given by

$$\begin{aligned} w=2\sqrt{r(r_c-r)},\quad q=2\sqrt{\frac{r_c-r}{r}}=\frac{w}{r},\quad p=\frac{r^\frac{3}{2}}{\sqrt{r_c-r}}=\frac{2r}{q}=\frac{2r^2}{w}. \end{aligned}$$

4.1.1 Singular Sturm–Liouville theory

A Sturm–Liouville problem of the form (4.14) on a closed interval $[0,r_c]$ is called regular if the coefficient $p:[0,r_c]\rightarrow {{\mathbb {R}}}$ is a continuous and non-vanishing function, the coefficient $w:[0,r_c]\rightarrow (0,\infty )$ is continuous and positive, and $q:[0,r_c]\rightarrow {{\mathbb {R}}}$ is continuous. If at the boundary of the interval $[0,r_c]$ at least one of the coefficients p, q, or w becomes infinite or p or w approach zero, then the Sturm–Liouville problem is called singular.

For singular Sturm–Liouville problems Weyl introduced in [20] a dichotomy into limit circle and limit point. Given an end point 0 or $r_c$, the singular Sturm–Liouville problem is called limit circle if all solutions of the homogeneous problem

$$\begin{aligned} \left( p{\dot{R}}\right) ^{{\cdot }}+qR=0 \end{aligned}$$

(4.15)

close to the given end point are of class $L^2$. Otherwise, the problem is called limit point. For more information see e.g. [1, p. 277], [9, XII.3], or [10, III §1].

Remark 4.1

(Sturm–Liouville theory) Later, in Sect. 4.2, when we deal with the case of non-zero angular momentum ($\ell \not =0$) we will encounter special cases of Sturm–Liouville equations—Bessel equations. Excellent accounts of the history of Sturm–Liouville theory, surveys, and even a catalogue can be found in the collection of papers [1, p. 277]. We recommend these papers for further references. Without the extensive tables and property lists in [2, §9] one would get nowhere, in finite time, in Sect. 4.2.

The main result of this Sect. 4.1 is the

Proposition 4.2

(Zero angular momentum – limit circle on $(0,r_c)$) The singular Sturm–Liouville problem given by the 1-dimensional Weber Schrödinger equation (4.17) on the interval $(0,r_c)$ is

• a) limit circle at the left origin boundary singularity 0;

• b) limit circle at the right critical radius boundary singularity $r_c$.

Proof

a) Sect. 4.1.1. b) Sect. 4.1.2. $\square$

4.1.2 Type ’limit circle’ at the origin

For non-zero angular momentum ($\ell \not = 0$) already the classical solutions behave not nicely inside the critical radius, they spiral into the origin singularity, cf. Theorem 2.1. So in a first step to prove Theorem A we restrict to the case of angular momentum $\ell =0$. As mentioned above we consider the region inside the critical radius $r_c:=\frac{1}{c^2}$, in symbols $r\in (0,r_c)$.

In the following we show that for zero angular momentum ($\ell =0$) the singular Sturm–Liouville problem (4.13) on $(0,r_c)$, equivalently (4.14), is of type limit circle at the boundary singularity $r=0$.

Remark 4.3

The property limit circle does not depend on the choice of the constant E; see e.g. [9, Thm. XII.3.2] or [10, III Le. 1.1]. Thus we choose $E=0$. By [10, p. 22] limit circle at a boundary singularity $r_*$ is equivalent to not being limit point at $r_*$ which, by [10, Rmk. on p. 23], is equivalent to all solutions being $L^2$ near $r_*$.

Setup (Case $E=0$). Equation (4.13) for $\ell =0$, multiplied by $\frac{2(r_c-r)}{r}$, gets

$$\begin{aligned} {\ddot{R}} +\left( \frac{3}{2}\,\frac{1}{r}+\frac{1}{2}\,\frac{1}{r_c-r}\right) \dot{R} +2\,\frac{r_c-r}{r^2}\, R =0 \end{aligned}$$

(4.16)

or, equivalently, after reordering¹

$$\begin{aligned} {\ddot{R}} +\frac{3}{2r}\,\dot{R} +\frac{2r_c}{r^2}\, R =\underbrace{ -\frac{1}{2(r_c-r)}\, \dot{R} +\frac{2}{r}\, R}_{=: b} . \end{aligned}$$

(4.17)

Step 1 (Homogeneous equation). First let us solve equation (4.17) in case the RHS b is zero: The Ansatz $f(r):=r^k$ leads to $k^2+\frac{1}{2} k+2r_c=0$, hence

$$\begin{aligned} k_1=-\frac{1}{4}-\sqrt{\frac{1}{16}-2r_c} {\mathop {\approx }\limits ^{>}}-\frac{1}{2},\quad k_2=-\frac{1}{4}+\sqrt{\frac{1}{16}-2r_c}{\mathop {\approx }\limits ^{<}} 0. \end{aligned}$$

So $2k_i>-1$ for $i=1,2$. Thus two solutions of (4.17) for $b=0$ are given by

$$\begin{aligned} u(r):=r^{k_1},\qquad v(r):=r^{k_2} \end{aligned}$$

and they are $L^2$ near 0 since $2k_i>-1$. It is useful to calculate the sums

$$\begin{aligned} k_2+k_1=-\frac{1}{2},\qquad k_2-k_1=\sqrt{\frac{1}{4}-8r_c}. \end{aligned}$$

and the Wronskian

$$\begin{aligned} W=W(r):=u\dot{v}-\dot{u} v =(k_2-k_1) r^{k_2+k_1-1} =(k_2-k_1) r^{-\frac{3}{2}}. \end{aligned}$$

Observe that the product $r^{\frac{3}{2}} W(r)=k_2-k_1$ is a constant.

Step 2 (Inhomogeneous equation). Given constants $\alpha ,\beta \in {{\mathbb {R}}}$, abbreviate $r_0:=r_c/2$, then the solution R to (4.17) with

$$\begin{aligned} R(r_0)=\alpha u(r_0)+\beta v(r_0),\qquad \dot{R}(r_0)=\alpha \dot{u}(r_0)+\beta \dot{v}(r_0) \end{aligned}$$

(4.18)

is given by the formula (see e.g. [9, Exc. IV.5.3 p. 81])

$$\begin{aligned} \begin{aligned} R(r):&=\alpha u(r)+\beta v(r) +\int _{r_0}^r\frac{u(s)v(r)-u(r)v(s)}{{ s^{3/2}}\, W(s)} \, { s^{3/2}}\, b(s)\, ds \\&{\mathop {=}\limits ^{1}}\alpha r^{k_1}+\beta r^{k_2} +\int _{r_0}^r \frac{s^{k_1} r^{k_2}-r^{k_1} s^{k_2}}{k_2-k_1} \left( -\frac{1}{2} \frac{s^\frac{3}{2}}{r_c-s}\, { \dot{R}} +s^\frac{1}{2} 2R\right) ds \\&{\mathop {=}\limits ^{2}}\alpha r^{k_1}+\beta r^{k_2} -\int _r^{r_0} \frac{s^{-k_2} r^{k_2}-r^{k_1} s^{-k_1}}{k_2-k_1}\, 2R\; ds \\&\quad +\frac{1}{2} \int _r^{r_0} \frac{s^{-k_2} r^{k_2}-r^{k_1} s^{-k_1}}{k_2-k_1} \,\frac{s}{r_c-s}\, { \dot{R}}\, ds \\&{\mathop {=}\limits ^{3}}\alpha r^{k_1}+\beta r^{k_2} -\int _r^{r_0} \frac{(r/s)^{k_2}-(r/s)^{k_1}}{k_2-k_1}\, 2R(s) \, ds \\&\quad +\frac{1}{2}\,\frac{(r/r_0)^{k_2}-(r/r_0)^{k_1}}{k_2-k_1}\, \frac{r_0}{r_c-r_0}\, { R(r_0)} \\&\quad +\frac{1}{2} \int _r^{r_0} \frac{k_2(r/s)^{k_2}-k_1 (r/s)^{k_1}}{k_2-k_1} \,{\frac{1}{r_c-s}}\, R(s)\, ds \\&\quad -\frac{1}{2} \int _r^{r_0} \frac{(r/s)^{k_2}-(r/s)^{k_1}}{k_2-k_1} \, {\frac{r_c}{(r_c-s)^2}}\, R(s)\, ds \end{aligned} \end{aligned}$$

(4.19)

for every $r\in (0,r_0]$. Step 1 uses definition (4.17) of b, in step 2 we interchange limits of integration and catch a minus sign, and step 3 is by partial integration.

Consider the $L^2$ functions on $(0,r_0]$, where $r_0:=\frac{r_c}{2}$, given by

$$\begin{aligned} h_1(r):={{\tilde{\alpha }}} r^{k_1}+{{\tilde{\beta }}} r^{k_2},\qquad h_2(r):=\gamma r^{k_1}+\delta r^{k_2} \end{aligned}$$

where the constants are defined by

$$\begin{aligned} {{\tilde{\alpha }}}:=|\alpha |+\frac{r_0 { R(r_0)}}{2 r_0^{k_1}(k_2-k_1)(r_c-r_0)},\quad {{\tilde{\beta }}}:=|\beta |+\frac{r_0 { R(r_0)}}{2 r_0^{k_2}(k_2-k_1)(r_c-r_0)} \end{aligned}$$

and

$$\begin{aligned} \gamma :=2\frac{r_0^{-k_1}}{k_2-k_1} +\frac{1}{2}\,\frac{k_1 r_0^{-k_1}}{k_2-k_1}\, {\frac{2}{r_c}} +\frac{1}{2}\,\frac{r_0^{-k_1}}{k_2-k_1}\, {\frac{4}{r_c}} \end{aligned}$$

and

$$\begin{aligned} \delta :=2\frac{r_0^{-k_2}}{k_2-k_1} +\frac{1}{2}\,\frac{k_1 r_0^{-k_2}}{k_2-k_1}\, {\frac{2}{r_c}} +\frac{1}{2}\,\frac{r_0^{-k_2}}{k_2-k_1}\, {\frac{4}{r_c}}. \end{aligned}$$

With the $L^2$ functions $h_1$ and $h_2$ on $(0,r_0]$ we get from (4.19), using ${\frac{1}{r_c-s}\le \frac{2}{r_c}}$ and Cauchy-Schwarz, the estimate

$$\begin{aligned} \begin{aligned} \left| R(r)\right|&\le h_1(r) +h_2(r) \int _{r}^{r_0}\left| R(s)\right| ds \\&= h_1(r)+h_2(r)\Vert R\cdot { 1}\Vert _1(r) \\&\le h_1(r)+h_2(r)\Vert R\Vert _2(r) \cdot {\sqrt{r_0}}\\ \end{aligned} \end{aligned}$$

(4.20)

for every $r\in (0,r_0]$, note that ${\sqrt{r_0}} \le 1$, and where

$$\begin{aligned} \Vert R\Vert _p(r):=\left( \int _r^{r_0}\left| R(s)\right| ^p\, ds\right) ^{\frac{1}{p}} \end{aligned}$$

for $p\ge 1$ and $r\in (0,r_0]$. Taking squares we get that

$$\begin{aligned} \begin{aligned} R(r)^2&\le h_1(r)^2+2 h_1(r) h_2(r) \Vert R\Vert _2(r) + h_2(r)^2\Vert R\Vert _2(r)^{\, 2} \\&\le 2 h_1(r)^2 + 2 h_2(r)^2\Vert R\Vert _2(r)^{\, 2} \end{aligned} \end{aligned}$$

for every $r\in (0,r_0]$. Therefore

$$\begin{aligned} \begin{aligned} \underbrace{\Vert R\Vert _2(r)^{\, 2}}_{=:U(r)} :&=\int _r^{r_0} R(s)^2\, ds \\&\le 2 \int _r^{r_0} h_1(s)^2\, ds +2 \int _r^{r_0} h_2(s)^2\Vert R\Vert _2(s)^{\, 2}\, ds \\&=\underbrace{2\Vert h_1\Vert _2(r)^{\, 2}}_{\le 2\Vert h_1\Vert _2^2=:\alpha } +\int _r^{r_0} \underbrace{2 h_2(s)^2}_{=:\beta (s)}\underbrace{\Vert R\Vert _2(s)^{\, 2}}_{=U(s)}\, ds \end{aligned} \end{aligned}$$

for every $r\in (0,r_0]$ where $\Vert h_1\Vert _2:=\Vert h_1\Vert _{L^2(0,r_0)}<\infty$. So by Gronwall’s lemma

$$\begin{aligned} \underbrace{\Vert R\Vert _2(r)^{\, 2}}_{U(r)} \le \underbrace{2\Vert h_1\Vert _2^2}_{\alpha }\, \exp \left( \int _r^{r_0} \underbrace{2 h_2(s)^2}_{\beta (s)} ds\right) \le 2\Vert h_1\Vert _2^2\, e^{2\Vert h_2\Vert _2^2} =:\gamma \end{aligned}$$

for every $r\in (0,r_0]$. Thus $\Vert R\Vert _2^2\le \gamma$. This shows that any solution R of (4.17), independent of the choice of initial conditions (4.18), is $L^2$ near the boundary singularity 0. By Remark 4.3 this proves part a) in Proposition 4.2.

4.1.3 Type ’limit circle’ at the critical radius

To prove Proposition 4.2 b) it suffices to treat the case $E=0$ by Remark 4.3.

Setup (Case $E=0$). Reordering (4.16) for singularities $\frac{1}{r-r_c}$ we get the ode

$$\begin{aligned} {\ddot{R}} +\frac{1}{2(r_c-r)}\, \dot{R} +\frac{3}{2r}\,\dot{R} =\underbrace{ -\frac{r_c-r}{r^2}\, 2R }_{=: b} \end{aligned}$$

(4.21)

for functions R on $[r_0,r_c)$ where $r_0:=\frac{r_c}{2}$.

Step 1 (Homogeneous equation). First let us solve equation (4.21) in case the RHS $b=0$ is zero: Two solutions of (4.21) for $b=0$ are given by²

$$\begin{aligned} u(r)\equiv 1,\qquad v(r):=\int _{r_0}^r s^{-3/2}\sqrt{r_c-s}\, ds \end{aligned}$$

(4.22)

and

$$\begin{aligned} W(r):=u\dot{v}-\dot{u} v=\dot{v} =r^{-3/2}\sqrt{r_c-r}. \end{aligned}$$

is their Wronskian. Since $r_c-r_0=r_c/2$ we get that the function

$$\begin{aligned} \left| v(r)\right| \le (r_c-r_0) r_0^{-3/2} \sqrt{r_c-r_0}=1 \end{aligned}$$

is bounded, hence $L^2$, on the interval $[r_0,r_c)$.

Step 2 (Inhomogeneous equation). Given constants $\alpha ,\beta \in {{\mathbb {R}}}$, the solution R to (4.21) with initial conditions

$$\begin{aligned} R(r_0)=\alpha u(r_0)+\beta v(r_0),\qquad \dot{R}(r_0)=\alpha \dot{u}(r_0)+\beta \dot{v}(r_0) \end{aligned}$$

(4.23)

is given for $r\in [r_0,r_c)$ by the definition in (4.19). On $[r_0,r_c)$ we estimate

$$\begin{aligned} \begin{aligned} |R(r)|&\le |\alpha |\cdot 1+|\beta |\cdot 1 +\left| \int _{r_0}^r\frac{v(r)-v(s)}{s^{-3/2}\sqrt{r_c-s}} \, \frac{r_c-s}{s^2}\, 2R(s) \, ds\right| \\&\le c_1+c_2 \int _{r_0}^r\left| R(s)\right| ds . \end{aligned} \end{aligned}$$

Here inequality one uses that $\Vert u\Vert _\infty =\Vert 1\Vert _\infty =1$ and $\Vert v\Vert _\infty =1$. Inequality two holds with $c_1:=|\alpha |+|\beta |$ and with $c_2=1$. Set $I:=[r_0,r_c)$ to estimate

$$\begin{aligned} 2\sup _{r\in I}(r-r_0) \sup _{s\in I}\frac{|v(r)|+|v(s)|}{\sqrt{s}} \, \sqrt{r_c-s} \le 2 \frac{r_c}{2}\,\frac{2\Vert v\Vert _\infty }{\sqrt{r_0}}\,\sqrt{r_c/2} =2r_c\ll 1=:c_2. \end{aligned}$$

Since $c_1,c_2$ are constants, a special case of Gronwall gives

$$\begin{aligned} |R(r)|\le c_1e^{c_2(r-r_0)}\le c_1e^{r_c/2}. \end{aligned}$$

for $r\in [r_0,r_c)$. Thus any solution R of (4.21) on $[r_0,r_c)$ is uniformly bounded, thus $L^2$. By Remark 4.3 this proves part b) of Proposition 4.2.

4.2 Equation for R—non-zero angular momentum $\ell \not =0$

For non-zero angular momentum already the classical solutions behave not nicely inside the critical radius, they spiral into the origin singularity, cf. Theorem 2.1. In this subsection we restrict again to the region inside the critical radius $r_c:=\frac{1}{c^2}$, in symbols $r\in (0,r_c)$.

Recall that separating the equal charge Schrödinger equation (3.10), Ansatz $\psi =R(r)Y(\phi )$, leads to equation (4.13) for R, namely

$$\begin{aligned} \begin{aligned} ER&= \frac{{\partial }_r\Bigl (\frac{r^\frac{3}{2}}{\sqrt{r_c-r}}\,{\partial }_r R\Bigr )}{2\sqrt{r(r_c-r)}} +\frac{1}{r}\, R +\frac{\ell }{r^2}\, R\\&=\frac{1}{2}\,\frac{r}{r_c-r}\, {\ddot{R}} +\left( \frac{3}{4}\,\frac{1}{r_c-r}+\frac{1}{4}\,\frac{r}{(r_c-r)^2}\right) \dot{R} +\frac{1}{r}\, R +\frac{\ell }{r^2}\, R \end{aligned} \end{aligned}$$

(4.24)

for $r\in (0,r_c)$. Here $\ell =k^2/2$ for $k\in {{\mathbb {N}}}$; cf. (3.12). Alternatively, the equation is

$$\begin{aligned} \left( p{\dot{R}}\right) ^{{\cdot }}+qR=w E R \end{aligned}$$

(4.25)

for functions R on $(0,r_c)$ and where ${\dot{c}}$ denotes $\frac{d}{dr}$ and with

$$\begin{aligned} w=2\sqrt{r(r_c-r)},\qquad q=\frac{w}{r}\left( 1+\frac{\ell }{r}\right) ,\qquad p=\frac{r^\frac{3}{2}}{\sqrt{r_c-r}}. \end{aligned}$$

Note that $\frac{w}{r}=2\sqrt{\frac{r_c-r}{r}}$.

The main result of this Sect. 4.2 is the

Proposition 4.4

(Non-zero angular momentum – limit circle on $(0,r_c)$) The singular Sturm–Liouville problem given by the 1-dimensional Weber Schrödinger equation (4.27) on the interval $(0,r_c)$ is

• a) limit circle at the left origin boundary singularity 0;

• b) limit circle at the right critical radius boundary singularity $r_c$.

Proof

a) Sect. 4.2.1. b) Sect. 4.2.2. $\square$

4.2.1 Type ’limit circle’ at the origin ($\rho =\infty$)

In the following we show that for non-zero angular momentum ($\ell \not =0$) the singular Sturm–Liouville problem (4.24) on $(0,r_c)$, equivalently (4.25), is of type limit circle at the boundary singularity $x=0$. By Remark 4.3 it suffices to consider the case $E=0$.

Setup (Case $E=0$). Equation (4.24), multiplied by $\frac{2(r_c-r)}{r}$, becomes

$$\begin{aligned} {\ddot{R}} +\left( \frac{3}{2}\,\frac{1}{r}+\frac{1}{2}\,\frac{1}{r_c-r}\right) \dot{R} +2\,\frac{r_c-r}{r^2}\, R +2\,\frac{\ell (r_c-r)}{r^3}\, R =0 \end{aligned}$$

(4.26)

or, equivalently, after reordering we get the ode

$$\begin{aligned} {\ddot{R}} +\frac{3}{2r}\,\dot{R} +\frac{2r_c}{r^2}\, R+\frac{2r_c \ell }{r^3}\, R = -\frac{1}{2(r_c-r)}\, \dot{R} +2\left( \frac{1}{r}+\frac{\ell }{r^2}\right) \, R \end{aligned}$$

(4.27)

for functions R on $(0,r_c)$ and where $\ell =k^2/2$ for a given $k\in {{\mathbb {N}}}$; see (3.12). It is useful to change variables. Recall that $r_c:=1/c^2$. Suppose R satisfies (4.27). Then in the new variable

$$\begin{aligned} \rho :(0,r_c)\rightarrow (c^2,\infty ),\quad r\mapsto 1/r \end{aligned}$$

the function given by $f(\rho ):=R(r(\rho ))$ satisfies the ode³

$$\begin{aligned} f^{\prime \prime }+\frac{1}{2\rho } f^\prime +\frac{2r_c}{\rho ^2}f+\frac{2r_c\ell }{\rho } f = \underbrace{ \frac{1}{2\rho ^2} \frac{1}{(\frac{\rho }{c^2}-1)} f^\prime +\frac{2}{\rho ^3} f+\frac{2\ell }{\rho ^2} f }_{=:b(\rho )} \end{aligned}$$

(4.28)

for $\rho \in (c^2,\infty )$ and where $\ell =k^2/2$ for a given $k\in {{\mathbb {N}}}$.

Step 1 (Homogeneous equation). To solve (4.28) for $b=0$ suppose f is a solution. The Ansatz $f(\rho )=\rho ^\alpha w(\rho )$ with $\alpha \in {{\mathbb {R}}}$ leads to the ode

$$\begin{aligned} w^{\prime \prime } +\left( 2\alpha +\frac{1}{2}\right) \frac{w^\prime }{\rho } +\biggl ((\underbrace{\alpha (\alpha -1)+\frac{\alpha }{2}}_{=\alpha (\alpha -\frac{1}{2})} +2r_c\biggr )\frac{w}{\rho ^2} +2\ell r_c\frac{w}{\rho }=0 \end{aligned}$$

for $\rho \in (c^2,\infty )$. For $\alpha =-\frac{1}{4}$ the coefficient of $w^\prime$ vanishes and we get the ode

$$\begin{aligned} w^{\prime \prime }+\left( \frac{3}{16}+2r_c\right) \frac{w}{\rho ^2} +2\ell r_c\frac{w}{\rho }=0 \end{aligned}$$

for functions $w=w(\rho )$ with $\rho \in (c^2,\infty )$. This ode is of the form

$$\begin{aligned} w^{\prime \prime } +\left( \frac{\lambda ^2}{4\rho }+\frac{1-\nu ^2}{4\rho ^2}\right) w =0,\qquad \lambda ^2=8\ell r_c=\left( \frac{2k}{c}\right) ^2,\quad \nu ^2=\frac{1-32 r_c}{4} \end{aligned}$$

(4.29)

where $k\in {{\mathbb {N}}}$ by (3.12). Solutions are given by $w(\rho )=\rho ^\frac{1}{2}\,{{\mathcal {C}}}_\nu (\lambda \rho ^\frac{1}{2})$, see [2, 9.1.51 p. 362], where for ${{\mathcal {C}}}_\nu$ one can choose e.g. Bessel functions $J_\nu$ or Weber functions⁴$Y_\nu$, formulas for which are given in [2, 9.1.2 and 9.1.10–11]. So

$$\begin{aligned} {{\tilde{u}}}:=\rho ^\frac{1}{2}\, J_\nu (\lambda \rho ^\frac{1}{2}), \qquad \tilde{v}:=\rho ^\frac{1}{2}\, Y_\nu (\lambda \rho ^\frac{1}{2}) \end{aligned}$$

are two solutions of (4.29).

Due to our Ansatz $f=\rho ^{-\frac{1}{4}} w$ two solutions of (4.28) for $b=0$ are given by

$$\begin{aligned} u:=\rho ^\frac{1}{4}\, J_\nu (\lambda \rho ^\frac{1}{2}), \quad v:=\rho ^\frac{1}{4}\, Y_\nu (\lambda \rho ^\frac{1}{2}), \qquad \lambda =\tfrac{2k}{c},\quad \nu =\tfrac{1}{2}\sqrt{1-\tfrac{32}{c^2}}{\mathop {<}\limits ^{\approx }}\tfrac{1}{2} \end{aligned}$$

(4.30)

where $k\in {{\mathbb {N}}}$; see (3.12). The Wronskian of u and v is given by

$$\begin{aligned} W(\rho ):=W(u,v)|_\rho :=u v^\prime -u^\prime v = \tfrac{\lambda }{2}\, W(J_\nu ,Y_\nu )|_{\lambda \rho ^\frac{1}{2}} =\frac{1}{\pi \rho ^\frac{1}{2}} \end{aligned}$$

Step one is calculation, step two uses that $W(J_\nu ,Y_\nu )|_s=\frac{2}{\pi s}$ by [2, 9.1.16].

Step 2 (Inhomogeneous equation). Let $\rho _0:=2c^2\in (c^2,\infty )$. Given constants $\alpha ,\beta \in {{\mathbb {R}}}$ and from (4.30) the solutions u, v of the homogeneous ($b=0$) version of (4.28), then the solution f to equation (4.28) with initial conditions

$$\begin{aligned} f(1)=\alpha u(1)+\beta v(1),\qquad f^\prime (1)=\alpha u^\prime (1)+\beta v^\prime (1) \end{aligned}$$

(4.31)

is given for $\rho \in [2c^2,\infty )$ by the formula (see e.g. [9, Exc. IV.5.3 p. 81])

$$\begin{aligned} \begin{aligned} f(\rho ):&=\alpha u(\rho )+\beta v(\rho ) +\int _{\rho _0}^\rho \frac{u(s)v(\rho )-u(\rho )v(s)}{W(s)}\, b(s)\, ds \\&=\alpha \rho ^\frac{1}{4} J_\nu (\lambda \rho ^\frac{1}{2}) +\beta \rho ^\frac{1}{4} Y_\nu (\lambda \rho ^\frac{1}{2})\\&\quad +\pi \rho ^\frac{1}{4} Y_\nu (\lambda \rho ^\frac{1}{2}) \int _{\rho _0}^\rho s^\frac{3}{4} J_\nu (\lambda s^\frac{1}{2}) \left( \frac{f^\prime (s)}{2s^2(\frac{s}{c^2}-1)} +\tfrac{2+2\ell s}{s^3} f(s) \right) ds\\&\quad -\pi \rho ^\frac{1}{4} J_\nu (\lambda \rho ^\frac{1}{2}) \int _{\rho _0}^\rho s^\frac{3}{4} Y_\nu (\lambda s^\frac{1}{2}) \left( \frac{f^\prime (s)}{2s^2(\frac{s}{c^2}-1)} +\tfrac{2+2\ell s}{s^3} f(s) \right) ds \\&=\alpha \rho ^\frac{1}{4} J_\nu (\lambda \rho ^\frac{1}{2}) +\beta \rho ^\frac{1}{4} Y_\nu (\lambda \rho ^\frac{1}{2}) \\&\quad +2\pi \rho ^\frac{1}{4} Y_\nu (\lambda \rho ^\frac{1}{2}) \int _{\rho _0}^\rho \frac{(1+\ell s) J_\nu (\lambda s^\frac{1}{2})}{s^{3-\frac{3}{4}}} f(s) \, ds\\&\quad -2\pi \rho ^\frac{1}{4} J_\nu (\lambda \rho ^\frac{1}{2}) \int _{\rho _0}^\rho \frac{(1+\ell s) Y_\nu (\lambda s^\frac{1}{2})}{s^{3-\frac{3}{4}}} f(s)\, ds\\&\quad +\tfrac{\pi }{2}\rho ^\frac{1}{4}\int _{\rho _0}^\rho \frac{Y_\nu (\lambda \rho ^\frac{1}{2}) J_\nu (\lambda { s}^\frac{1}{2}) -Y_\nu (\lambda { s}^\frac{1}{2}) J_\nu (\lambda \rho ^\frac{1}{2})}{{ s}^\frac{5}{4}(\frac{{ s}}{c^2}-1)} f^\prime ({ s})\, d{ s} \end{aligned} \end{aligned}$$

(4.32)

We wish to show that every solution R of (4.27) is $L^2$ near the origin, say on $(0,r_0]\subset (0,r_c)$ where $r_0:=\frac{1}{\rho _0}=\frac{1}{2} r_c$. For $r(\rho )=\frac{1}{\rho }$ and $f(\rho ):=R(r(\rho ))$ we get

$$\begin{aligned} \int _0^{r_0} R(r)^2\, dr =\int _{\rho _0}^\infty \frac{f(\rho )^2}{\rho ^2}\, d\rho =\int _{\rho _0}^\infty F(\rho )^2\, d\rho ,\qquad F(\rho ):=\frac{|f(\rho )|}{\rho } . \end{aligned}$$

(4.33)

To show finiteness of the integral in (4.33) we need to estimate (4.32) and for this it is crucial to understand boundedness and, more crucially, decay behavior of the Bessel functions $J_\nu$ and their cousins $Y_\nu$. People not familiar with them might wish to have a look at their graphs, for instance in the appropriate Wiki, to see that these resemble cosine and sine functions with some decay factor – which actually is $1/\sqrt{\rho }=1/\rho ^{\frac{2}{4}}$. It is this exponent of the decay factor which translates in (4.36) into a power smaller than 1/2 in $\rho ^{ 1/4}$ which is necessary to have $\beta (\rho )$ be integrable on $(\rho _0,\infty )$. So in the end $\gamma$ in (4.37) is indeed finite.

Remark 4.5

(Boundedness and decay of Bessel functions) Recall that $\nu {\mathop {\approx }\limits ^{<}}\frac{1}{2}$, see (4.30). Hence assertion (i) holds by [2, 9.1.60 p. 362].

• (i) $|J_\nu |\le 1$ on $[0,\infty )$. As $(c^2,\infty )$ is far out, $|J_\nu |$ is very small by [2, 9.2.5].

• (ii) $|Y_\nu |\le 1$ on $(c^2,\infty )=(\frac{1}{r_c},\infty )$⁵: By [2, 9.1.2 & 9.1.62] we get that

  $$\begin{aligned} \begin{aligned} \left| Y_\nu (\rho )\right|&=\left| J_\nu (\rho )\frac{\cos (\nu \pi )}{\sin (\nu \pi )}-J_{-\nu }(\rho )\right| \\&\le \cot (\nu \pi )+\frac{2^\nu }{c^{2\nu }\, \Gamma (1-\nu )}\\&\le \cot (\nu \pi )+\frac{1}{c^{\nu }}=: c_Y \end{aligned} \end{aligned}$$

  We used for the $\Gamma$ function that $\Gamma (1-\nu )\approx \Gamma (\frac{1}{2})>1$. In fact $c_Y>0$ is very close to zero: Indeed $c^\nu \approx \sqrt{3}\cdot 10^4$ and $\nu \pi$ is smaller but very close to $x=\frac{\pi }{2}$ where cosine is zero and sine is one.

• (iii) Asymptotic decay$J_\nu (\rho ),Y_\nu (\rho )\sim 1/\rho ^{\frac{2}{4}}$ as $\rho \rightarrow \infty$. By [2, 9.2.1] we get

  $$\begin{aligned} J_\nu (\rho )\in \sqrt{\tfrac{2}{\pi \rho }} \left( \cos (\rho -\tfrac{\nu \pi }{2}-\tfrac{\pi }{4})+O(\tfrac{1}{\rho }) \right) . \end{aligned}$$

  (4.34)

  For $Y_\nu$ use sine. By definition there are constants $\rho _1,C_1>1$ such that

  $$\begin{aligned} |J_\nu (\rho )| \le \frac{C_1}{\rho ^{\frac{2}{4}}} \left| \cos (\rho -\tfrac{\nu \pi }{2}-\tfrac{\pi }{4})+\tfrac{1}{\rho }\right| \le \frac{C_1}{\rho ^{\frac{2}{4}}} \end{aligned}$$

  for every $\rho \ge \rho _1$ and similarly for $Y_\nu$ (using sine and same constant names). In the second inequality one might have to enlarge the constants.

We use the bounds (i–ii), the crucial one (iii), and (4.32) to get the estimate

$$\begin{aligned} \begin{aligned} \frac{|f(\rho )|}{\rho }&\le \frac{|\alpha |+|\beta |}{\rho ^\frac{3}{4}} +\frac{4\pi C_1}{\rho ^\frac{3}{4}}\int _{\rho _0}^\rho \left( \frac{|f(s)|}{s^\frac{9}{4}} +\frac{\ell |f(s)|}{s^{{\frac{5}{4}}+{\frac{2}{4}}}} \right) ds\\&\quad +\frac{\pi }{2\rho ^\frac{3}{4}} \left| \int _{\rho _0}^\rho \left( \frac{{ J_\nu (\lambda s^\frac{1}{2})}}{{ s^\frac{5}{4}(\frac{s}{c^2}-1)}} f^\prime (s) \right) ds\right| \\&\quad +\frac{\pi }{2\rho ^\frac{3}{4}} \left| \int _{\rho _0}^\rho \left( \frac{Y_\nu (\lambda s^\frac{1}{2})}{s^\frac{5}{4}(\frac{s}{c^2}-1)} f^\prime (s) \right) ds\right| \\ \end{aligned} \end{aligned}$$

(4.35)

for every $\rho \in [\rho _0,\infty )$. Next we carry out partial integration for one of the two terms in (4.35), say the ${ J_\nu }$ term, the $Y_\nu$ term being analogous and leading to exactly the same estimate. Note that $s\ge \rho _0$ implies $\frac{s}{c^2}-1\ge \frac{\rho _0}{c^2}-1=2-1$. Partial integration, the unit bound $|J_\nu |\le 1$, and the crucial decay (iii) tell that

$$\begin{aligned} \begin{aligned} g(\rho ):&= \left| \int _{\rho _0}^\rho \left( \frac{J_\nu (\lambda s^\frac{1}{2})}{s^\frac{5}{4}(\frac{s}{c^2}-1)} f^\prime (s) \right) ds \right| \\&= \Biggl | \frac{J_\nu (\lambda \rho ^\frac{1}{2})f(\rho )}{\rho ^{\frac{5}{4}}(\frac{\rho }{c^2}-1)} -\frac{J_\nu (\lambda \rho _0^\frac{1}{2})f(\rho _0)}{\rho _0^{\frac{5}{4}}}\\&\quad +\int _{\rho _0}^\rho \frac{{ J_\nu (\lambda s^\frac{1}{2})} \left( \frac{5}{4}s^\frac{1}{4} (\frac{s}{c^2}-1)+{s^\frac{5}{4}}\right) }{s^\frac{5}{2}(\frac{s}{c^2}-1)^2} f(s)\, ds \\&\quad -\int _{\rho _0}^\rho \frac{J_\nu ^\prime (\lambda s^\frac{1}{2}) \frac{\lambda }{2\sqrt{s}}\, { s^\frac{5}{4} (\frac{s}{c^2}-1)}}{s^\frac{5}{2}(\frac{s}{c^2}-1)^2} f(s)\, ds \Bigg |\\&\le \left( \frac{|f(\rho _0|}{c^2} +\frac{|f(\rho )|}{\rho ^\frac{5}{4}} +C_1\int _{\rho _0}^\rho \frac{|{ f(s)}|}{s^{{\frac{5}{4}}+{\frac{2}{4}}}} \,ds \; +\tfrac{\lambda }{2}\int _{\rho _0}^\rho \underbrace{|J_\nu ^\prime (\lambda s^\frac{1}{2})|}_{\le 2} \cdot \frac{|{f(s)}|}{s^\frac{7}{4}} \, ds \right) . \end{aligned} \end{aligned}$$

Indeed, by the recurrence relation in [2, 9.1.27] and since $|J_\mu |\le 1$ on $[0,\infty )$ for $\mu \ge 0$ by [2, 9.1.60], we get for $s\ge \rho _0=2 c^2$ and with $\lambda =2k/c$ that

$$\begin{aligned} | J_\nu ^\prime (\lambda s^\frac{1}{2})| =\left| -J_{\nu +1}(\lambda s^\frac{1}{2}) +\frac{\nu }{\lambda s^\frac{1}{2}} J_{\nu }(\lambda s^\frac{1}{2})\right| \le 1+ \frac{\nu }{(2k/c) \sqrt{2} c}< 1+\frac{1}{4}. \end{aligned}$$

Hence for each $k\in {{\mathbb {N}}}$ we obtain the estimate

$$\begin{aligned} g(\rho ) \le \frac{|f(\rho _0|}{c^2} +\frac{|f(\rho )|}{\rho ^\frac{5}{4}} +\int _{\rho _0}^\rho \left( C_1+\tfrac{2k}{c}\right) \frac{|f(s)|}{s^{{\frac{5}{4}}+{\frac{2}{4}}}} \,ds \end{aligned}$$

for every $\rho \ge \rho _0=2c^2 \gg 2\pi$. Set $\gamma _0/2:=|\alpha |+|\beta |+|f(\rho _0)|$ to finally get

$$\begin{aligned} \frac{|f(\rho )|}{\rho } \le \frac{\gamma _0}{2\rho ^\frac{3}{4}} +\frac{1}{2} \frac{|f(\rho )|}{\rho } +\frac{2\pi C_1(1+k+k^2)}{\rho ^\frac{3}{4}} \int _{\rho _0}^\rho \frac{|f(s)|}{s^{{\frac{5}{4}}+{\frac{2}{4}}}} \,ds \end{aligned}$$

and therefore

$$\begin{aligned} F(\rho ):=\frac{|f(\rho )|}{\rho } \le \frac{\gamma _0}{\rho ^\frac{3}{4}} +\frac{12\pi C_1 k^2}{\rho ^\frac{3}{4}} \int _{\rho _0}^\rho \frac{|f(s)|}{s^{{\frac{5}{4}}+{\frac{2}{4}}}} \,ds \end{aligned}$$

for every $\rho \ge \rho _0$. Set $c_k:=(12\pi C_1 k^2)^2$ and square the expression to obtain

$$\begin{aligned} \begin{aligned} F(\rho )^2&\le \frac{2\gamma _0^2}{\rho ^\frac{3}{2}} +\frac{2c_k}{\rho ^\frac{3}{2}} \left( \int _{\rho _0}^\rho \frac{1}{s^{{\frac{1}{4}}+{\frac{2}{4}}}} \cdot F(s)\,ds\right) ^2\\&\le \underbrace{\frac{2\gamma _0^2}{\rho ^\frac{3}{2}}}_{=:h(\rho )} +\underbrace{8 c_k \frac{\rho ^{\frac{1}{4}} -{\rho _0}^{\frac{1}{4}}}{\rho ^\frac{3}{2}}}_{=:\beta (\rho )} \int _{\rho _0}^\rho F(s)^2\,ds \end{aligned} \end{aligned}$$

(4.36)

for every $\rho \ge \rho _0$. The second inequality is by Cauchy-Schwarz. Define

$$\begin{aligned} \Vert F\Vert _p(t):=\left( \int _{\rho _0}^t F(s)^p\,ds\right) ^\frac{1}{p} \end{aligned}$$

for $p\ge 1$ and $t\ge \rho _0$. Integrate (4.36) to obtain the estimate

$$\begin{aligned} \begin{aligned} \underbrace{\Vert F\Vert _2(t)^2}_{=:U(t)}: =\int _{\rho _0}^t F(\rho )^2\,d\rho \le \underbrace{\Vert h\Vert _1(t)}_{\le \alpha } +\int _{\rho _0}^t \beta (\rho ) \underbrace{\Vert F\Vert _2(\rho )^2}_{U(\rho )}\, d\rho \end{aligned} \end{aligned}$$

for every $t\ge \rho _0$ and where $\alpha :=\Vert h\Vert _{L^1(\rho _0,\infty )}<\infty$. So by Gronwall’s lemma

$$\begin{aligned} \underbrace{\Vert F\Vert _2(t)^{\, 2}}_{= U(t)} \le \alpha \exp \biggl (\int _{\rho _0}^t \beta (s)\, ds\biggr ) \le \alpha \exp \biggl (\int _{\rho _0}^\infty \beta (s) \, ds\biggr ):=\gamma <\infty \end{aligned}$$

(4.37)

for any $t\ge \rho _0$. The constant $\gamma$ is finite, because the integral $\int _{\rho _0}^\infty \frac{1}{s^{5/4}}\, ds<\infty$ is. Thus $\gamma \ge \Vert F\Vert _{L^2(\rho _0,\infty )}^2=\Vert R\Vert _{L^2(0,r_0)}^2$ by (4.33). This proves that any solution R of (4.27) on $(0,r_c)$, independent of the choice of initial conditions (cf. (4.31)), is $L^2$ near the boundary singularity 0. By Remark 4.3 this proves a) in Proposition 4.4.

4.2.2 Type ’limit circle’ at the critical radius

To prove Proposition 4.4 b) it suffices to treat the case $E=0$ by Remark 4.3.

Setup (Case $E=0$). Reorder (4.27) to get the ode

$$\begin{aligned} {\ddot{R}} +\frac{1}{2(r_c-r)}\, \dot{R} +\frac{3}{2r}\,\dot{R} =\underbrace{-\frac{(r_c-r)(r+\ell )}{r^3}\, 2R}_{=:b(r)} \end{aligned}$$

(4.38)

for functions R on $[r_0,r_c)$ where $r_0:=\frac{r_c}{2}$ and where $\ell =k^2/2$ for a given $k\in {{\mathbb {N}}}$; see (3.12). For $\ell =0$ the ode reduces to (4.21) which we had solved for $b=0$.

Step 1 (Homogeneous equation). We already solved equation (4.38) for $b=0$. Recall that solutions are $u\equiv 1$ and v in (4.22), that $|v|\le 1$, and that their Wronskian is $W(r)=r^{-3/2}\sqrt{r_c-r}$.

Step 2 (Inhomogeneous equation). Given constants $\alpha ,\beta \in {{\mathbb {R}}}$, the solution R to (4.21) with initial conditions

$$\begin{aligned} R(r_0)=\alpha u(r_0)+\beta v(r_0),\qquad \dot{R}(r_0)=\alpha \dot{u}(r_0)+\beta \dot{v}(r_0) \end{aligned}$$

(4.39)

is given for $r\in [r_0,r_c)$ by the definition in (4.19). On $[r_0,r_c)$ we estimate

$$\begin{aligned} \begin{aligned} |R(r)|&\le |\alpha |+|\beta | +\left| \int _{r_0}^r\frac{v(r)-v(s)}{s^{-3/2}\sqrt{r_c-s}} \, \frac{(r_c-s)(s+\ell )}{s^3}\, 2R(s) \, ds\right| \\&\le c_1+c_2\int _{r_0}^r\left| R(s)\right| ds . \end{aligned} \end{aligned}$$

Here inequality one uses that $\Vert u\Vert _\infty =\Vert 1\Vert _\infty =1$ and $\Vert v\Vert _\infty =1$. Inequality two holds with $c_1:=|\alpha |+|\beta |$ and $c_2:=2r_c$. To get $c_2$ let $I:=[r_0,r_c)$, note that

$$\begin{aligned} \begin{aligned} 2\sup _{r\in I}(r-r_0) \sup _{s\in I} \frac{|v(r)|+|v(s)|}{s^{3/2}} \, \sqrt{r_c-s} (s+\ell )&\le 2 \frac{r_c}{2}\,\frac{2\Vert v\Vert _\infty }{r_0^{3/2}}\, \sqrt{\frac{r_c}{2}} (r_c+\ell )\\&\le 4(1+\ell )=:c_2. \end{aligned} \end{aligned}$$

Since $c_1,c_2$ are constants, a special case of Gronwall gives

$$\begin{aligned} |R(r)|\le c_1e^{c_2(r-r_0)}\le c_1e^{c_2r_c/2}=c_1e^{2(1+\ell )/c^2}. \end{aligned}$$

for $r\in [r_0,r_c)$. Thus any solution R of (4.21) on $[r_0,r_c)$ is uniformly bounded, thus $L^2$. By Remark 4.3 this proves part b) of Proposition 4.4.