1 Introduction

In this research paper, our focus is on investigating the controllability of linear time delay differential equations. It is important to differentiate between the notions of function controllability and controllability in Euclidean space (relative controllability) for these equations. This distinction arises because although the solutions of these equations are trajectories in Euclidean space, the natural “state space” is actually a function space. For the purposes of this study, we limit our discussion to controllability in Euclidean space. Furthermore, unlike in the case of ordinary differential equations, it is necessary to also distinguish between the concepts of complete controllability and null controllability when it comes to controllability in Euclidean space.

Chyung and Lee initially explored the concept of complete controllability in Euclidean space, focusing on a linear controlled hereditary system described by multi-delay differential equations [1]. In 1967, Kirillova and Curakova [2] introduced algebraic criteria for the null controllability of linear autonomous time-delay differential equations in Euclidean space. Building upon this work, Gabasov and Curakova [3] demonstrated that the conditions derived in [2] are not only necessary but also sufficient for achieving complete controllability, see also [4, 5]. Weiss [6] extended the understanding of controllability by obtaining an algebraic sufficient condition for time-varying differential-difference equations, encompassing the findings of Buckalo [7] as a special case. Recently, Choudhury [8] published results closely related to those presented by Gabasov and Curakova [3].

In recent decades, the field of fractional calculus has experienced significant advancements due to its broad range of applications in various scientific and engineering domains. Mathematical tools derived from fractional calculus have proven to be highly effective in describing numerous real-world phenomena. These applications encompass diverse areas such as fluid dynamics, archeology, electrode-electrolyte polarization, transmission modeling, control theory of continuous/discrete dynamical systems, electrical networks, optics, signal processing, and more.

The controllability analysis for fractional linear delay systems is typically based on fractional calculus and control theory. Fractional calculus extends the concept of derivatives and integrals to non-integer orders, allowing the modeling and analysis of systems with fractional dynamics. Fractional delay systems introduce additional complexity due to the presence of fractional orders in the system’s dynamics.

The controllability of fractional linear delay systems depends on various factors, including the system’s structure, the fractional orders of the delays, and the available control inputs. Fractional order delays can lead to rich and intricate dynamics, and analyzing controllability in such systems can be challenging. Techniques such as fractional differential equations, fractional Laplace transforms, and fractional control theory are commonly used to analyze the controllability properties of fractional linear delay systems.

It is important to note that the field of fractional calculus and fractional control theory is still an active area of research. Developing efficient analysis techniques and control strategies for fractional linear delay systems is an ongoing topic of investigation, and different approaches may be employed depending on the specific system characteristics and requirements.

In recent times, numerous researchers have focused on examining the controllability of various systems that are described by integro-differential equations with fractional order. To delve deeper into this topic, we suggest interested readers to explore the works of several authors [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], as well as the additional sources mentioned in those references.

We are going to study the relative controllability of a linear fractional system with delay

$$\begin{aligned} \left\{ \begin{array}{c} {^{C}}D_{0^{+}}^{\alpha }y\left( t\right) =Ay\left( t\right) +By\left( t-h\right) +Cu\left( t\right) ,\ \ t\in \left( 0,T\right] ,\ h>0,\\ y\left( 0\right) =y_{0},\ \ y\left( t\right) =\varphi \left( t\right) ,\ \ -h\le t<0. \end{array} \right. \end{aligned}$$
(1.1)

Here \({^{C}}D_{0^{+}}^{\alpha }\) is the Caputo fractional derivative, \(0<\alpha \le 1,\) A, B are \(d\times d\) constant matrices, C is an \(d\times r\) constant matrix. We assume that the initial condition \(\varphi \left( t\right) \) is continuous on the interval \(\left[ -h,0\right] \) and an admissible control \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R} ^{r}\right) ,\ p>1.\)

In 2015, Mur and Henriquez [22] extended the results on null controllability of [2] to the Caputo fractional time-delay linear system. They obtained algebraic criteria for the null controllability of linear autonomous fractional time-delay differential equations (1.1) in Euclidean space. We extend to system (1.1) the algebraic criterion of relative controllability established in [3] for the classical differential system associated to (1.1).

The proof of algebraic criterion for the relative controllability for linear differential systems, known as Kalman’s criterion, relies on two important results.

  • The first result is the integral representation formula for the solution of a Cauchy problem in a nonhomogeneous system. This formula expresses the solution x(t) as the sum of two terms: the exponential of the system matrix A multiplied by the initial condition \(x_{0}\), and an integral involving the matrix exponential and the control input u(s). The matrix exponential, denoted as exp(At), is defined as a power series involving the matrix A. It starts with the identity matrix I, and each term in the series is a power of A divided by the corresponding factorial.

  • The second result is the Cayley-Hamilton theorem, which states that for a given constant \(n\times n\) matrix A, every power of A from the nth power onward can be expressed as a linear combination of a finite number of matrices: the identity matrix \(I,A,A^{2}\), and so on up to \(A^{n-1}\).

These two results are significant in the research on controllability and serve as motivation for further exploration. In this study we use the following analogues of these two results to obtain an algebraic criterion for the relative controllability of fractional system (1.1):

  • representation of solution expressed using delayed Mittag-Leffler matrix function \(Y_{h,\alpha ,\alpha }^{A,B}\)and delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\), which are defined by means of determining function \(Q_{k+1}\left( jh\right) \) in [26], see Theorem 1. It is important to emphasize that the studies conducted in [15, 22] focused on the solution representations for the Caputo fractional delay differential equations (1.1). However, the explicit forms of \(Y_{h,\alpha ,\alpha }^{A,B}\) and \(X_{h,\alpha ,\alpha }^{A,B}\) were not provided in that paper. Consequently, we are unable to utilize this representation for deriving the Kalman-type criterion;

  • analogue of the Cayley-Hamilton theorem for the determining function \(Q_{k+1}\left( jh\right) \), which is proved in Lemma 4.

Another criterion for the relative controllability for fractional linear time-delay systems is a necessary and sufficient condition in terms of the Gramian matrix. The expected Gramian matrix is

$$\begin{aligned} W\left( 0,T\right) =\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr. \end{aligned}$$

Since delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\) has singularities at the points 0, h, 2h, ..., \(W\left( 0,T\right) \) does not converges and is not well-defined. To neutralize the singular points we introduce a new \(\alpha \)-Gramian matrix

$$\begin{aligned} G_{\alpha }\left( 0,T\right) :=\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr, \end{aligned}$$

see Definition 7, which is well-defined for all \(0<\alpha \le 1 \), but is not symmetric matrix, see Lemma 6. Using a newly defined \(\alpha \)-Gramian matrix \(G_{\alpha }\left( 0,T\right) \) we prove a necessary and sufficient condition for the relative controllability.

The main contributions of this article are as follows:

  • We employ a method based on the delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\), as outlined in Lemma 3, which deals with the sequential Riemann-Liouville derivative of this function. Additionally, we establish an analogue of the Cayley-Hamilton theorem for the determining function \(Q_{k+1}\left( jh\right) \). Utilizing these tools, we demonstrate a Kalman-type algebraic criterion for the fractional linear time-delay systems, where the fractional order \(0<\alpha \le 1\) ranges between 0 and 1.

  • We introduce a condition for relative controllability of linear fractional time-delay systems (1.1), which is characterized by a newly introduced \(\alpha \)-Gramian matrix, denoted as \(G_{\alpha }\left( 0,T\right) \). This condition is both necessary and sufficient for assessing relative controllability. Using Gramian matrix we define a control which transfer the system from any initial state to any final state within a given time.

This paper is organized in four sections. In Section 2 we study properties of the determining function and prove analogue of the Cayley-Hamilton theorem. In Section 3, we prove Kalman type algebraic criterion for the fractional linear delay system in terms of determining function. Moreover, we introduce an \(\alpha \)-Gramian matrix and prove a new criterion in terms of \(\alpha \)-Gramian matrix \(G_{\alpha }\left( 0,T\right) \). Finally, in Section 4 we apply our results to study the relative controllability of some concrete systems.

2 Determining function and Cayley-Hamilton theorem

We first recall some definitions and lemmas.

Definition 1

[27] Let \(0<\alpha <1.\) The Riemann-Liouville fractional integral \(I_{T^{-}}^{\alpha }y\) is defined by

$$\begin{aligned} I_{T^{-}}^{\alpha }y\left( t\right) =\frac{1}{\varGamma \left( \alpha \right) }\int _{t}^{T}\left( r-t\right) ^{\alpha -1}y\left( r\right) dr,\ \ \ t<T. \end{aligned}$$

The Riemann-Liouville fractional derivatives \({^{RL}}D_{0^{+}}^{\alpha }y\) and \({^{RL}}D_{T^{-}}^{\alpha }y\) are defined by

$$\begin{aligned} {^{RL}}D_{0^{+}}^{\alpha }y\left( t\right)&=\frac{1}{\varGamma \left( 1-\alpha \right) }\frac{d}{dt}\int _{0}^{t}\left( t-r\right) ^{-\alpha }y\left( r\right) dr,\ \ \ t>0,\\ {^{RL}}D_{T^{-}}^{\alpha }y\left( t\right)&=-\frac{1}{\varGamma \left( 1-\alpha \right) }\frac{d}{dt}\int _{t}^{T}\left( r-t\right) ^{-\alpha }y\left( r\right) dr,\ \ \ t<T, \end{aligned}$$

respectively. The Caputo fractional derivative \({^{C}}D_{0^{+}}^{\alpha }y\) is defined by

$$\begin{aligned} {^{C}}D_{0^{+}}^{\alpha }y\left( t\right) =\frac{1}{\varGamma \left( 1-\alpha \right) }\int _{0}^{t}\left( t-r\right) ^{-\alpha }\frac{d}{dr}y\left( r\right) dr,\ \ \ t>0. \end{aligned}$$

Lemma 1

[27] If \(\alpha \ge 0\) and \(\gamma >-1\), then

$$\begin{aligned} \left( ^{RL}D_{T^{-}}^{\alpha }\left( T-s\right) ^{\gamma }\right) \left( t\right)&=\frac{\varGamma \left( \gamma +1\right) }{\varGamma \left( \gamma -\alpha +1\right) }\left( T-t\right) ^{\gamma -\alpha },\ \ \ \alpha \ge 0,\gamma >-1,\\ \left( ^{RL}D_{T^{-}}^{\alpha }\left( T-s\right) ^{\alpha -1}\right) \left( t\right)&=0. \end{aligned}$$

Next, we present a specific form of the fundamental matrix that will be valuable for future sections. The Mittag-Leffler function, which is an extension of the exponential function, plays a crucial role in this context. The purely delayed Mittag-Leffler matrix function, which incorporates delays, is defined in the reference [28]. Additionally, more recent research, as cited in [26, 29] has focused on the study of delayed perturbations of Mittag-Leffler type matrix functions. This paper introduces and examines the delayed perturbation of Mittag-Leffler type matrix function and \(\alpha \)-exponential matrix function through the use of a determining matrix equation for \(Q_{k}\left( jh\right) :\)

$$\begin{aligned} Q_{k+1}\left( jh\right)&=AQ_{k}\left( jh\right) +BQ_{k}\left( jh-h\right) ,\nonumber \\ Q_{0}\left( jh\right)&=Q_{k}\left( -h\right) =\varTheta ,\ \ Q_{1}\left( 0\right) =I,\nonumber \\ k&=0,1,2,...,j=0,1,2,..., \end{aligned}$$
(2.1)

where I is an identity, \(\varTheta \) is a zero matrix. It is obvious that \(Q_{k+1}\left( jh\right) \) satisfies the following equation:

$$\begin{aligned} Q_{k+1}\left( jh\right) =Q_{k}\left( jh\right) A+Q_{k}\left( jh-h\right) B, \end{aligned}$$

and \(Q_{k+1}\left( jh\right) =\varTheta \) for \(j\ge k+1>1.\)

The matrix family \(\left\{ Q_{k+1}\left( jh\right) :k,j\in \mathbb {N} \cup \left\{ 0\right\} \right\} \subset \mathbb {R}^{d\times d}\) plays a role as a kernel for the delayed perturbation of Mittag-Leffler matrix function and delayed \(\alpha \)-exponential matrix function.

Apply the Laplace transform in

$$\begin{aligned} \left\{ \begin{array}{c} {^{C}}D_{0^{+}}^{\alpha }Y\left( t\right) =AY\left( t\right) +BY\left( t-h\right) ,\ \ t\in \left( 0,T\right] ,\ h>0,\\ Y\left( 0\right) =I,\ Y\left( t\right) =\varTheta ,\ \ -h\le t<0. \end{array}\right. \end{aligned}$$

It is shown in [22] that

$$\begin{aligned} \lambda ^{\alpha }\widehat{Y}\left( \lambda \right) -\lambda ^{\alpha -1}I=A\widehat{Y}\left( \lambda \right) +e^{-\lambda h}B\widehat{Y}\left( \lambda \right) . \end{aligned}$$

Then

$$\begin{aligned} \widehat{Y}\left( \lambda \right) =\lambda ^{\alpha -1}\left( \lambda ^{\alpha }-A-e^{-\lambda h}B\right) ^{-1}, \end{aligned}$$

where \(\widehat{Y}\left( \lambda \right) \) is the Laplace transform of \(Y\left( t\right) \). Let \(X\left( t\right) \) be the inverse Laplace transform of

$$\begin{aligned} \widehat{X}\left( \lambda \right) =\left( \lambda ^{\alpha }-A-e^{-\lambda h}B\right) ^{-1}. \end{aligned}$$

Then

$$\begin{aligned} Y\left( t\right)&=L^{-1}\left\{ \lambda ^{\alpha -1}\left( \lambda ^{\alpha }-A-e^{-\lambda h}B\right) ^{-1}\right\} ,\\ X\left( t\right)&=L^{-1}\left\{ \left( \lambda ^{\alpha }-A-e^{-\lambda h}B\right) ^{-1}\right\} . \end{aligned}$$

Here \(L^{-1}\) is the inverse Laplace transform. In [26, 29], the explicit formulas for \(Y\left( t\right) \) and \(X\left( t\right) \) are given and it is shown that

$$\begin{aligned} Y\left( t\right) =Y_{h,\alpha ,1}^{A,B}\left( t\right) ,\ \ \ X\left( t\right) =X_{h,\alpha ,\alpha }^{A,B}\left( t\right) , \end{aligned}$$

see Definitions 2 and 3.

Definition 2

Let \(\alpha ,\beta >0,\ t\in \mathbb {R}_{\ge 0}=\left[ 0,\infty \right) \). Delayed perturbation of two parameter Mittag-Leffler type matrix function \(Y_{h,\alpha ,\beta }^{A,B}\) generated by A, B is defined by

$$\begin{aligned} Y_{h,\alpha ,\beta }^{A,B}\left( t\right) :=\left\{ \ \begin{array}{l} \sum \limits _{i=0}^{\infty }Q_{i+1}\left( 0\right) \dfrac{t^{i\alpha }}{\varGamma \left( i\alpha +\beta \right) }+\sum \limits _{i=1}^{\infty } Q_{i+1}\left( h\right) \dfrac{\left( t-h\right) ^{i\alpha }}{\varGamma \left( i\alpha +\beta \right) }\\ +...+\sum \limits _{i=m}^{\infty }Q_{i+1}\left( mh\right) \dfrac{\left( t-mh\right) ^{i\alpha }}{\varGamma \left( i\alpha +\beta \right) }, \end{array}\ \ \ \ \right. \end{aligned}$$

where \(\ mh<t\le \left( m+1\right) h,\ \ m\in \mathbb {N}\cup \left\{ 0\right\} .\)

We can derive the following important properties of \(Y_{h,\alpha ,\beta }^{A,B}\left( t\right) \) and

\(\left\{ Q_{k+1}\left( jh\right) :k,j\in \mathbb {N}\cup \left\{ 0\right\} \right\} \) :

  • If \(j\ge k+1\) for \(k>0\), then \(Q_{k+1}\left( jh\right) =\varTheta \). Therefore, a matrix family \(\left\{ Q_{k+1}\left( jh\right) :k,j\in \mathbb {N}\cup \left\{ 0\right\} \right\} \subset \mathbb {R}^{d\times d}\) is a lower triangular matrix.

  • For arbitrary (commutative or non-commutative) real matrices \(A,B\in \mathbb {R}^{d\times d}\), a matrix family \(\left\{ Q_{k+1}\left( jh\right) :k,j\in \mathbb {N}\cup \left\{ 0\right\} \right\} \subset \mathbb {R}^{d\times d}\) is satisfying \(Q_{k+1}\left( jh\right) =AQ_{k}\left( jh\right) +BQ_{k}\left( jh-h\right) )\) for \(k,j\in \mathbb {N}\cup \left\{ 0\right\} \).

  • For arbitrary commutative real matrices \(A,B\in \mathbb {R}^{d\times d}\), i.e., \(AB=BA\), a matrix family \(\left\{ Q_{k+1}\left( jh\right) :k,j\in \mathbb {N}\cup \left\{ 0\right\} \right\} \subset \mathbb {R}^{d\times d}\) satisfies \(Q_{k+1}\left( jh\right) =\left( {\begin{array}{c}k\\ j\end{array}}\right) A^{k-j}B^{j}\), \(k,j\in \mathbb {N}\cup \left\{ 0\right\} \).

  • If \(B=\varTheta \), then for any \(\mathbb {N}\cup \left\{ 0\right\} \), \(Q_{k+1}\left( jh\right) = {\left\{ \begin{array}{ll} A^{k},\quad j=0,\\ \varTheta ,\quad j\in \mathbb {N}. \end{array}\right. } \) and \(Y_{h,\alpha ,\beta }^{A,B}\) becomes a Mittag-Leffler matrix function: \(Y_{h,\alpha ,\beta }^{A,B}\left( t\right) =\sum \limits _{i=0}^{\infty } A^{i}\dfrac{t^{i\alpha }}{\varGamma \left( i\alpha +\beta \right) }=E_{\alpha ,\beta }\left( At^{\alpha }\right) \) for \(t\ge 0\), see [27, p.53].

  • If \(A=\varTheta \), then for any \(k,j\in \mathbb {N}\cup \left\{ 0\right\} \), \(Q_{k+1}\left( jh\right) = {\left\{ \begin{array}{ll} B^{j},\quad k=j,\\ \varTheta ,\quad k\ne j \end{array}\right. } \) and \(Y_{h,\alpha ,\beta }^{A,B}\) becomes the pure delayed Mittag-Leffler matrix function \(Y_{h,\alpha ,\beta }^{A,B}\left( t\right) =\sum \limits _{k=0}^{\infty }B^{k}\dfrac{\left( t-kh\right) _{+}^{k\alpha }}{\varGamma \left( k\alpha +\beta \right) }\) for \(t\ge 0,\) where \(\left( t\right) _{+}:=\max \left( 0,t\right) \).

  • \(Y_{h,\alpha ,\beta }^{A,B}\left( \cdot \right) \) is a continuous function on \(\left[ 0,\infty \right) .\)

Next we define delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\), which is delayed counterpart of \(e_{\alpha ,\alpha }\left( At^{\alpha }\right) =t^{\alpha -1}E_{\alpha ,\alpha }\left( At^{\alpha }\right) ,\) see [27, p.50].

Definition 3

[29] Let \(\alpha >0,t\in \mathbb {R}_{\ge 0}\). Delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\) generated by A, B is defined by

$$\begin{aligned} X_{h,\alpha ,\alpha }^{A,B}\left( t\right)&:=t^{\alpha -1}\sum \limits _{i=0}^{\infty }Q_{i+1}\left( 0\right) \dfrac{t^{i\alpha }}{\varGamma \left( i\alpha +\alpha \right) }\\&\quad +\left( t-h\right) ^{\alpha -1}\sum \limits _{i=1}^{\infty }Q_{i+1}\left( h\right) \dfrac{\left( t-h\right) ^{i\alpha }}{\varGamma \left( i\alpha +\alpha \right) }\\&\quad +...+\left( t-mh\right) ^{\alpha -1}\sum \limits _{i=m}^{\infty } Q_{i+1}\left( mh\right) \dfrac{\left( t-mh\right) ^{i\alpha }}{\varGamma \left( i\alpha +\alpha \right) }, \end{aligned}$$

where \(mh<t\le \left( m+1\right) h,\ \ m\in \mathbb {N}\cup \left\{ 0\right\} .\)

Remark 1

By definition the function \(X_{h,\alpha ,\alpha }^{A,B}\left( \cdot \right) \), \(0<\alpha <1\), is continuous on \(\mathbb {R}_{\ge 0}\backslash \left\{ mh:m\in \mathbb {N}\cup \left\{ 0\right\} \right\} \).

Let us introduce the following notations:

$$\begin{aligned} Y_{h,\alpha ,\beta }^{k}\left( t-kh\right)&:=\sum \limits _{i=k}^{\infty }Q_{i+1}\left( kh\right) \dfrac{\left( t-kh\right) _{+}^{i\alpha }}{\varGamma \left( i\alpha +\beta \right) },\\ X_{h,\alpha ,\alpha }^{k}\left( t-kh\right)&:=\left( t-kh\right) ^{\alpha -1}\ Y_{h,\alpha ,\alpha }^{k}\left( t-kh\right) \\&=\left( t-kh\right) ^{\alpha -1}\sum \limits _{i=k}^{\infty }Q_{i+1}\left( kh\right) \dfrac{\left( t-kh\right) _{+}^{i\alpha }}{\varGamma \left( i\alpha +\alpha \right) }. \end{aligned}$$

Now we introduce a shift operator \(T^{h}\left( h\in \mathbb {R}\right) \) which takes a function f on \(\mathbb {R}\) to its translation \(f_{h}:\)

$$\begin{aligned} T^{h}f\left( t\right) =e^{h\frac{d}{dt}}f:=f\left( t+h\right) . \end{aligned}$$

Say, if \(f\left( t\right) =t^{k}\) then \(e^{-mh\frac{d}{dt}}f=f\left( t-mh\right) =\left( t-mh\right) ^{k}.\)

Using the shift operator we can give an equivalent definition of \(Y_{h,\alpha ,\beta }^{A,B}\) and \(X_{h,\alpha ,\alpha }^{A,B}.\) As it is shown in [26], Definitions 2, 3 and 4 are equivalent.

Definition 4

[26, 29] Delayed Mittag-Leffler type matrix functions \(Y_{h,\alpha ,\beta }^{A,B}\) and delayed \(\alpha \)-exponential matrix function \(X_{h,\alpha ,\alpha }^{A,B}\)generated by A, B are defined by

$$\begin{aligned} Y_{h,\alpha ,\beta }^{A,B}\left( t\right)&:=\sum \limits _{k=0}^{\infty }\left( A+Be^{-h\frac{d}{dt}}\right) ^{k}\frac{\left( t\right) _{+}^{\alpha k}}{\varGamma \left( \alpha k+\beta \right) },\\ X_{h,\alpha ,\alpha }^{A,B}\left( t\right)&:=\sum \limits _{k=0}^{\infty }\left( A+Be^{-h\frac{d}{dt}}\right) ^{k}\frac{\left( t\right) _{+}^{\alpha k+\alpha -1}}{\varGamma \left( \alpha k+\alpha \right) } ,\ \ \ t \in \mathbb {R}_{\ge 0}, \end{aligned}$$

where \(\left( t\right) _{+}:=\max \left( 0,t\right) \).

It is clear that

$$\begin{aligned} \left\| Y_{h,\alpha ,\beta }^{A,B}\left( t\right) \right\|&\le \sum \limits _{k=0}^{\infty }\left( \left\| A\right\| +\left\| B\right\| e^{-h\frac{d}{dt}}\right) ^{k}\frac{\left( t\right) _{+}^{\alpha k}}{\varGamma \left( \alpha k+\beta \right) }\nonumber \\&\le \sum \limits _{k=0}^{\infty }\left( \left\| A\right\| +\left\| B\right\| \right) ^{k}\frac{t^{\alpha k}}{\varGamma \left( \alpha k+\beta \right) }\nonumber \\&=E_{\alpha ,\beta }\left( \left( \left\| A\right\| +\left\| B\right\| \right) t^{\alpha }\right) . \end{aligned}$$
(2.2)

Definition 5

A function \(y:\left[ -h,T\right] \rightarrow \mathbb {R}^{d}\) is said to be a solution of (1.1) if y is continuous on \(\left[ 0,T\right] ,\) conditions \(y\left( 0\right) =y_{0},\ \ y\left( t\right) =\varphi \left( t\right) ,\ \ -h\le t<0,\) are satisfied, and the equation

$$\begin{aligned} y\left( t\right)&=Y_{h,\alpha ,1}^{A,B}\left( t\right) \varphi \left( 0\right) +\int _{-h}^{\min \left( 0,t-h\right) }X_{h,\alpha ,\alpha } ^{A,B}\left( t-s-h\right) B\varphi \left( s\right) ds\nonumber \\&\quad +\int _{0}^{t}X_{h,\alpha ,\alpha }^{A,B}\left( t-s\right) Cu\left( s\right) ds \end{aligned}$$
(2.3)

is valued for \(0<t\le T\).

Theorem 1

[29] Let \(0<\alpha \le 1\) and \(p>\frac{1}{\alpha }\). For any admissible control \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R} ^{r}\right) \), there exists a unique continuous solution y on \(\left( 0,T\right] \) to (1.1).

By taking \(\alpha =1\) the system (1.1) reduces to a classical order delay system and solution representation (2.3) coincides with the classical one, see [30, 31].

Let us present two lemmas that will be used in the proof of the main results.

Lemma 2

The function \(X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) \) satisfies the following equation

$$\begin{aligned} ^{RL}D_{T^{-}}^{\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right)&=AX_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) +BX_{h,\alpha ,\alpha } ^{A,B}\left( T-t-h\right) , \\ \lim _{t\rightarrow T^{-}}\ I_{T^{-}}^{1-\alpha }\ \left( X_{h,\alpha ,\alpha }^{A,B}\left( T-s\right) \right) \left( t\right)&=I. \end{aligned}$$

Proof

Taking the Riemann-Liouville fractional derivative \(D_{T^{-}}^{\alpha }\) and using the formulas

$$\begin{aligned} \left( ^{RL}D_{T^{-}}^{\alpha }\left( T-s\right) ^{\gamma }\right) \left( t\right) =\frac{\varGamma \left( \gamma +1\right) }{\varGamma \left( \gamma -\alpha +1\right) }\left( T-t\right) ^{\gamma -\alpha },\ \ \ \alpha \ge 0,\gamma >-1, \end{aligned}$$

and

$$\begin{aligned} \left( ^{RL}D_{T^{-}}^{\alpha }\left( T-s\right) ^{\alpha -1}\right) \left( t\right) =0, \end{aligned}$$

we have

$$\begin{aligned}&{^{RL}}D_{T^{-}}^{\alpha }\ X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) \\&\quad = {^{RL}}D_{T^{-}}^{\alpha }\sum \limits _{k=0}^{\infty }\ \sum \limits _{0\le i\le k}Q_{k+1}\left( ih\right) \dfrac{\left( T-t-ih\right) _{+} ^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad = \sum \limits _{k=1}^{\infty }\ \sum \limits _{0\le i\le k}Q_{k+1}\left( ih\right) \dfrac{\left( T-t-ih\right) _{+}^{k\alpha -1}}{\varGamma \left( k\alpha \right) }\\&\quad =\sum \limits _{k=0}^{\infty }\ \sum \limits _{0\le i\le k+1}Q_{k+2}\left( ih\right) \dfrac{\left( T-t-ih\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad = A\sum \limits _{k=0}^{\infty }\ \sum \limits _{0\le i\le k+1}Q_{k+1}\left( ih\right) \dfrac{\left( T-t-ih\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\\&\qquad +B\sum \limits _{k=0}^{\infty }\ \sum \limits _{0\le i\le k+1}Q_{k+1}\left( ih-h\right) \dfrac{\left( T-t-ih\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad = AX_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) +B\sum \limits _{k=0} ^{\infty }\ \sum \limits _{0\le i\le k}Q_{k+1}\left( ih\right) \dfrac{\left( T-t-h-ih\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad = AX_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) +BX_{h,\alpha ,\alpha }^{A,B}\left( T-t-h\right) \\&\quad =\left( A+Be^{h\frac{d}{dt}}\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) . \end{aligned}$$

Next, we prove the second equality:

$$\begin{aligned}&\lim _{t\rightarrow T^{-}}\ I_{T^{-}}^{1-\alpha }\ \left( X_{h,\alpha ,\alpha }^{A,B}\left( T-s\right) \right) \left( t\right) \\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ \ \lim _{t\rightarrow T^{-} }\ \int _{t}^{T}\left( r-t\right) ^{-\alpha }\left( \sum \limits _{k=0} ^{\infty }\left( A+Be^{-h\frac{d}{dt}}\right) ^{k}\frac{\left( T-r\right) _{+}^{\alpha k+\alpha -1}}{\varGamma \left( \alpha k+\alpha \right) }\right) dr\\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ \lim _{t\rightarrow T^{-}} \ \int _{t}^{T}\left( r-t\right) ^{-\alpha }\ \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \dfrac{\left( T-r\right) ^{k\alpha +\alpha -1} }{\varGamma \left( k\alpha +\alpha \right) }dr\\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \ \lim _{t\rightarrow T^{-}}\ \int _{t}^{T} \dfrac{\left( r-t\right) ^{-\alpha }\left( T-r\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }dr\\&\quad = \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \ \lim _{t\rightarrow T^{-}}\ \frac{\left( T-t\right) ^{k\alpha }}{\varGamma \left( k\alpha +1\right) }=Q_{1}\left( 0\right) =I. \end{aligned}$$

\(\square \)

For \(jh<T-s\le \left( j+1\right) h,\) define

$$\begin{aligned} X_{j}\left( T-s\right) :=\ ^{RL}D_{T-}^{m\alpha }X_{h,\alpha ,\alpha } ^{A,B}\left( T-s\right) =\sum _{i=0}^{j}Q_{m+1}\left( ih\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) . \end{aligned}$$

Lemma 3

We have

$$\begin{aligned}{} & {} ^{RL}D_{T-}^{m\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-s\right) =\sum _{i=0}^{m}Q_{m+1}\left( ih\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) , \end{aligned}$$
(2.4)
$$\begin{aligned}{} & {} \lim _{t\rightarrow \left( T-jh\right) ^{-}}\ I_{\left( T-jh\right) ^{-} }^{1-\alpha }\ \left( X_{j}\left( T-s\right) -X_{j-1}\left( T-s\right) \right) \left( t\right) =Q_{m+1}\left( jh\right) , \end{aligned}$$
(2.5)

where \({^{RL}}D_{T-}^{m\alpha }\ X_{h,\alpha ,\alpha }^{A,B}\) is the sequential Riemann-Liouville fractional derivative of order m.

Proof

Case \(m=0\) is obvious. Case \(m=1,\) is proved in Lemma 2

$$\begin{aligned} ^{RL}D_{T^{-}}^{\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right)&=\left( A+Be^{h\frac{d}{dt}}\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) \\&=Q_{2}\left( 0\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) +Q_{2}\left( 1\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-t-h\right) . \end{aligned}$$

We use mathematical induction (2.4). Assume that it is true for \(m=n\), then for \(m=n+1\) we have

$$\begin{aligned}&{^{RL}}D_{T^{-}}^{\left( n+1\right) \alpha }X_{h,\alpha ,\alpha } ^{A,B}\left( T-t\right) \\&\quad = (^{RL}D_{T^{-}}^{\alpha })\ ^{RL}D_{T^{-}}^{n\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-t\right) \\&\quad ={^{RL}}D_{T^{-}}^{\alpha }\sum _{i=0}^{n}Q_{n+1}\left( ih\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) \\&\quad = \sum _{i=0}^{n}Q_{n+1}\left( ih\right) {^{RL}}D_{T^{-}}^{\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) \\&\quad = \sum _{i=0}^{n}Q_{n+1}\left( ih\right) \left[ AX_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) +BX_{h,\alpha ,\alpha }^{A,B}\left( T-s-h-ih\right) \right] \\&\quad = \sum _{i=0}^{n}Q_{n+1}\left( ih\right) AX_{h,\alpha ,\alpha } ^{A,B}\left( T-s-ih\right) \\&\qquad +\sum _{i=1}^{n+1}Q_{n+1}\left( ih-h\right) BX_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) \\&\quad = \sum _{i=0}^{n+1}\left[ Q_{n+1}\left( ih\right) A+Q_{n+1}\left( ih-h\right) B\right] X_{h,\alpha ,\alpha }^{A,B}\left( T-s-ih\right) \\&\quad = \sum _{i=0}^{n+1}Q_{n+2}\left( ih\right) X_{h,\alpha ,\alpha } ^{A,B}\left( T-s-ih\right) . \end{aligned}$$

In order to prove (2.5) we use (2.4). Using the equality

$$\begin{aligned} X_{j}\left( T-s\right) -X_{j-1}\left( T-s\right) =Q_{m+1}\left( jh\right) X_{h,\alpha ,\alpha }^{A,B}\left( T-s-jh\right) , \end{aligned}$$

we get

$$\begin{aligned}&\lim _{t\rightarrow \left( T-jh\right) ^{-}}\ I_{\left( T-jh\right) ^{-} }^{1-\alpha }\ \left( X_{j}\left( T-s\right) -X_{j-1}\left( T-s\right) \right) \left( t\right) \\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ Q_{m+1}\left( jh\right) \\&\qquad \times \lim _{t\rightarrow \left( T-jh\right) ^{-}}\ \int _{t}^{T-jh}\left( r-t\right) ^{-\alpha }\left( X_{h,\alpha ,\alpha }^{A,B}\left( T-r-jh\right) \right) dr\\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ Q_{m+1}\left( jh\right) \ \lim _{t\rightarrow \left( T-jh\right) ^{-}}\ \int _{t}^{T-jh}\left( r-t\right) ^{-\alpha }\\&\qquad \times \left( \ \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \dfrac{\left( T-r-jh\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\right) dr\\&\quad =\frac{1}{\varGamma \left( 1-\alpha \right) }\ Q_{m+1}\left( jh\right) \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \ \\&\qquad \times \ \lim _{t\rightarrow \left( T-jh\right) ^{-}} \ \int _{t}^{T-jh}\dfrac{\left( r-t\right) ^{-\alpha }\left( T-r-jh\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }dr\\&\quad = Q_{m+1}\left( jh\right) \sum \limits _{k=0}^{\infty }\ Q_{k+1}\left( 0\right) \ \lim _{t\rightarrow \left( T-jh\right) ^{-}}\ \frac{\left( T-t-jh\right) ^{k\alpha }}{\varGamma \left( k\alpha +1\right) }\ \\&\quad =Q_{m+1}\left( jh\right) Q_{1}\left( 0\right) =Q_{m+1}\left( jh\right) . \end{aligned}$$

\(\square \)

Next lemma is analogue of Cayley-Hamilton theorem for the determining function \(Q_{k+1}\left( jh\right) .\) Similar result can be found, for example, in [32].

Lemma 4

For any p, \(d\le p<\infty ,\) the following equality holds:

$$\begin{aligned}&rank \left\{ Q_{k+1}\left( lh\right) C:k=0,1,...,d-1\right\} \\&=rank \left\{ Q_{k+1}\left( jh\right) C:k=0,1,...,p;~j=0,1,...,l\right\} . \end{aligned}$$

Proof

It can be easily shown that (see [26])

$$\begin{aligned} \left( A+sB\right) ^{k}=\sum \limits _{j=0}^{k}s^{j}Q_{k+1}\left( jh\right) . \end{aligned}$$

The characteristic equation of matrix \(A+sB\) has the form

$$\begin{aligned} \varDelta \left( \lambda \right)&:=\det \left( \lambda I-A-sB\right) \nonumber \\&=\lambda ^{n}+p_{1}\left( s\right) \lambda ^{n-1}+...+p_{n}\left( s\right) =0. \end{aligned}$$
(2.6)

The coefficients \(p_{k}\left( s\right) \) in (2.6) depend on the variable s and are written in the form

$$\begin{aligned} p_{i}\left( s\right) =\sum \limits _{j=0}^{i}p_{ij}s^{j}. \end{aligned}$$

Therefore

$$\begin{aligned} \varDelta \left( A+sB\right) =\sum _{i=0}^{d}p_{i}\left( s\right) \lambda ^{n-i}=\sum _{i=0}^{d}\sum \limits _{j=0}^{i}p_{ij}\left( A+sB\right) ^{d-i}s^{j}=0. \end{aligned}$$
(2.7)

Taking into account that \(p_{00}=1\), we can represent the above equation in the form

$$\begin{aligned} \left( A+sB\right) ^{d}+\sum _{i=1}^{d}\sum \limits _{j=0}^{i}p_{ij}\left( A+sB\right) ^{d-i}s^{j}=0. \end{aligned}$$

It follows that

$$\begin{aligned} \sum \limits _{j=0}^{d}s^{j}Q_{d+1}\left( jh\right) C+\sum _{i=1}^{d} \sum \limits _{j=0}^{i}p_{ij}\sum \limits _{l=0}^{d-i}s^{l}Q_{d-i+1}\left( lh\right) Cs^{j}=0. \end{aligned}$$

Comparing the coefficients of \(s^{j}\) and having in mind that \(Q_{d+1}\left( jh\right) =\varTheta \), \(j\ge d+1\) and \(Q_{d+1}\left( s\right) =\varTheta \), \(s<0\), we get

$$\begin{aligned} Q_{d+1}\left( lh\right) C=-\sum _{i=1}^{d}\sum \limits _{j=0}^{i} p_{ij}Q_{d-i+1}\left( \left( l-j\right) h\right) C,\ \ 0\le l\le n. \end{aligned}$$

Therefore, matrices \(Q_{d+1}\left( lh\right) C\) are linearly dependent on the matrices \(Q_{d-i+1}\left( jh\right) C\) for \(j=0,1,...,l\).

Thus, the lemma is proven for \(p=d\). The validity of the lemma in the general case can be proved by induction for p. \(\square \)

It should be stressed out that if \(j=0, d=r\), and \(C=I\) then \(Q_{k+1}\left( 0\right) =A^{k}\) and Lemma 4 becomes the Cayley-Hamilton theorem:

$$\begin{aligned} {rank }\left\{ A^{k}:k=0,1,...,d-1\right\} ={rank }\left\{ A^{k}:k=0,1,...,p\right\} \end{aligned}$$

for \(p\ge d\).

3 Relative controllability

3.1 Controllability \(\alpha \)-Gramian

We introduce the following concept of controllability.

Definition 6

The system (1.1) is said to be relatively controllable on \(\left[ 0,T\right] \) if for every \(y_{0}\in \mathbb {R}^{d},\) \(\varphi \in C\left( \left[ -h,0\right] ,\mathbb {R}^{d}\right) \) and for every \(y_{T}\in \mathbb {R}^{d}\) there exists a control \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \), \(p>\frac{1}{\alpha }\), such that \(y\left( T,y_{0},\varphi ,u\right) =y_{T}.\)

The representation formula (2.3) leads us to introduce the mapping \(C_{0}^{T}:L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \rightarrow \mathbb {R}^{d}\) given by

$$\begin{aligned} C_{0}^{T}u:=\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr. \end{aligned}$$

In what follows, without loss of generality, we assume that \(mh<T\le \left( m+1\right) h\) for some \(m\in \mathbb {N\cup }\left\{ 0\right\} \) and we denote q the conjugate exponent of p: \(\frac{1}{p}+\frac{1}{q}=1.\)

Lemma 5

Let \(0<\alpha \le 1\) and \(p>\frac{1}{\alpha }\). The linear operator

\(C_{0}^{T}:L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \rightarrow \mathbb {R}^{d}\) is bounded.

Proof

Indeed, for any \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \) and \(\frac{1}{p}+\frac{1}{q}=1\), using the inequality (2.2) we have

$$\begin{aligned} \left\| C_{0}^{T}u\right\|&\le \int _{0}^{T}\left\| X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right\| \left\| C\right\| \left\| u\left( r\right) \right\| dr\\&\le \left\| C\right\| \int _{0}^{T}\sum \limits _{k=0\ }^{\infty } \ \sum \limits _{i=0}^{k}\left\| Q_{k+1}\left( ih\right) \right\| \dfrac{\left( T-r-ih\right) _{+}^{k\alpha +\alpha -1}}{\varGamma \left( k\alpha +\alpha \right) }\left\| u\left( r\right) \right\| dr\\&\le \left\| C\right\| \sum \limits _{k=0\ }^{\infty }\ \sum \limits _{i=0}^{k}\left\| Q_{k+1}\left( ih\right) \right\| \dfrac{T^{k\alpha }}{\varGamma \left( k\alpha +\alpha \right) }\int _{0}^{T}\left( T-r-ih\right) _{+}^{\alpha -1}\left\| u\left( r\right) \right\| dr\\&\le \left\| C\right\| \sum \limits _{k=0}^{\infty }\ \left( \left\| A\right\| +\left\| B\right\| \right) ^{k}\frac{T^{k\alpha }}{\varGamma \left( k\alpha +\alpha \right) }\int _{0}^{T}\left( T-r-kh\right) _{+}^{\alpha -1}\left\| u\left( r\right) \right\| dr\\&\le \left\| C\right\| \sum \limits _{k=0}^{\infty }\ \left( \left\| A\right\| +\left\| B\right\| \right) ^{k}\frac{T^{k\alpha }}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad \times \left( \int _{0}^{T}\left( T-r-kh\right) _{+}^{q\left( \alpha -1\right) }dr\right) ^{\frac{1}{q}}\left( \int _{0}^{T}\left\| u\left( r\right) \right\| ^{p}dr\right) ^{\frac{1}{p}}\\&=\left\| C\right\| \sum \limits _{k=0}^{\infty }\ \left( \left\| A\right\| +\left\| B\right\| \right) ^{k}\frac{T^{k\alpha }}{\varGamma \left( k\alpha +\alpha \right) }\\&\quad \times \left( \frac{\left( T-r-kh\right) _{+}^{q\left( \alpha -1\right) +1}}{q\left( \alpha -1\right) +1}\right) ^{\frac{1}{q} }\left( \int _{0}^{T}\left\| u\left( r\right) \right\| ^{p}dr\right) ^{\frac{1}{p}}\\&\le \left\| C\right\| E_{\alpha ,\alpha }\left( \left( \left\| A\right\| +\left\| B\right\| \right) T^{\alpha }\right) \\&\quad \times \left( \frac{\left( T-r\right) _{+}^{q\left( \alpha -1\right) +1}}{q\left( \alpha -1\right) +1}\right) ^{\frac{1}{q} }\left( \int _{0}^{T}\left\| u\left( r\right) \right\| ^{p}dr\right) ^{\frac{1}{p}}. \end{aligned}$$

Here \(q\left( \alpha -1\right) +1=\frac{p\alpha -1}{p-1}>0\). \(\square \)

Theorem 2

The system (1.1) is relatively controllable at time T if and only if \(\eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0\), \(r\in \left[ 0,T\right] \backslash \left\{ 0,h,2h,...,mh\right\} ,\) implies that \(\eta =0.\)

Proof

\(\left( \Longrightarrow \right) \) Assume that system (1.1) is relatively controllable at time T and

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ r\in \left[ 0,T\right] \backslash \left\{ 0,h,2h,...,mh\right\} . \end{aligned}$$

Let \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \). Then

$$\begin{aligned} \eta ^{\intercal }\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr=0. \end{aligned}$$

Since u was arbitrarily chosen, this implies that \(\eta \in \left( {\text {Im}}C_{0}^{T}\right) ^{\perp }=\left( \mathbb {R}^{d}\right) ^{\perp }=\left\{ 0\right\} \).

\(\left( \Longleftarrow \right) \) Conversely, assume that system (1.1) is relatively not controllable, that is, exists \(\eta \ne 0\) such that \(\eta \in \left( {\text {Im}}C_{0}^{T}\right) ^{\perp }\). Proceeding as above we have

$$\begin{aligned} \eta ^{\intercal }\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr=0 \end{aligned}$$

for all \(u\in L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) \). Let \(V_{l}\subset \left( T-\left( l+1\right) h,T-lh\right) \) be measurable set and \(u_{0}\in \mathbb {R}^{r}\). We define \(u_{l}\left( s\right) =\chi _{V_{l} }\left( s\right) u_{0}\), where \(\chi _{V_{l}}\) stands for the characteristic function of \(V_{l}\). Then

$$\begin{aligned} \eta ^{\intercal }\int _{V_{l}}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr=0. \end{aligned}$$

Applying the mean value theorem, we deduce that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \text {a.e. }r\in \left( T-\left( l+1\right) h,T-lh\right) . \end{aligned}$$

Since the function \(\eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C\) is continuous on \(\left( T-\left( l+1\right) h,T-lh\right) \) and \(u_{0}\in \mathbb {R}^{r}\) was arbitrarily chosen, we obtain that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \text { }r\in \left[ 0,T\right] \backslash \left\{ 0,h,2h,...,mh\right\} . \end{aligned}$$

\(\square \)

A necessary and sufficient condition for relative controllability in terms of the Gramian matrix typically involves analyzing the properties of this matrix, such as its positive definiteness. Thus, by examining the properties of the controllability Gramian matrix, one can derive necessary and sufficient conditions for relative controllability in the context of fractional linear time-delay systems. This criterion provides valuable insights into the controllability properties of such systems, aiding in their analysis and control design.

Consider nondelayed system (1.1), the case when \(B=\varTheta :\)

$$\begin{aligned} \left\{ \begin{array}{c} {^{C}}D_{0^{+}}^{\alpha }y\left( t\right) =Ay\left( t\right) +Cu\left( t\right) ,\ \ t\in \left( 0,T\right] ,\ h>0,\\ y\left( 0\right) =y_{0},\ \ y\left( t\right) =\varphi \left( t\right) ,\ \ -h\le t<0. \end{array} \right. \end{aligned}$$

In this case

$$\begin{aligned} X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) =\left( T-r\right) ^{\alpha -1}E_{\alpha ,\alpha }\left( A\left( T-r\right) ^{\alpha }\right) . \end{aligned}$$

In nondelayed case, in the literature [23, 24] there are the following definitions of the Gramian matrix

$$\begin{aligned} W\left( 0,T\right)&=\int _{0}^{T}\left( T-r\right) ^{2\left( \alpha -1\right) }E_{\alpha ,\alpha }\left( T-r\right) CC^{\intercal }\left( E_{\alpha ,\alpha }\left( T-r\right) \right) ^{\intercal }dr,\\ W_{1}\left( 0,T\right)&=\int _{0}^{T}\left( T-r\right) ^{1-\alpha }\left[ \left( T-r\right) ^{2\left( \alpha -1\right) }E_{\alpha ,\alpha }\left( T-r\right) C\right. \\&\quad \times \left. C^{\intercal }\left( E_{\alpha ,\alpha }\left( T-r\right) \right) ^{\intercal }\right] dr,\\ W_{2}\left( 0,T\right)&=\int _{0}^{T}\left( T-r\right) ^{2\left( 1-\alpha \right) }\left[ \left( T-r\right) ^{2\left( \alpha -1\right) }E_{\alpha ,\alpha }\left( T-r\right) C\right. \\&\quad \times \left. C^{\intercal }\left( E_{\alpha ,\alpha }\left( T-r\right) \right) ^{\intercal }\right] dr. \end{aligned}$$

\(W\left( 0,T\right) \) is well-defined for \(\frac{1}{2}<\alpha \le 1\), \(W_{1}\left( 0,T\right) \) and \(W_{2}\left( 0,T\right) \) are well-defined for every \(\alpha \in \left( 0,1\right] \). The addition of \(\left( T-r\right) ^{1-\alpha }\) and \(\left( T-r\right) ^{2\left( 1-\alpha \right) }\) play a neutralizer of singularity at \(r=T\) for \(W_{1}\left( 0,T\right) \) and \(W_{2}\left( 0,T\right) \), respectively, and is sufficient for the convergence of Gramians \(W_{1}\left( 0,T\right) \) and \(W_{2}\left( 0,T\right) \). But in the delayed system (1.1), it is not the case. At first glance, analogues of \(W\left( 0,T\right) ,W_{1}\left( 0,T\right) ,W_{2}\left( 0,T\right) \) for the system (1.1) would be

$$\begin{aligned} W\left( 0,T\right)&=\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr,\\ W_{1}\left( 0,T\right)&=\int _{0}^{T}\left( T-r\right) ^{1-\alpha }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr,\\ W_{2}\left( 0,T\right)&=\int _{0}^{T}\left( T-r\right) ^{2\left( 1-\alpha \right) }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr, \end{aligned}$$

since \(X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) =\left( T-r\right) ^{\alpha -1}E_{\alpha ,\alpha }\left( A\left( T-r\right) ^{\alpha }\right) \), in nondelayed case. The following example shows that, the addition of \(\left( T-r\right) ^{1-\alpha }\) and \(\left( T-r\right) ^{2\left( 1-\alpha \right) }\) does not play a neutralizer of singularities at \(r=T-h,\ r=T-2h,...\).

Example 1

Consider the following simple control problem:

$$\begin{aligned} ^{C}D_{0^{+}}^{\frac{1}{10}}x\left( t\right)&=x\left( t\right) +x\left( t-1\right) +u\left( t\right) ,\ \ \ 0<t\le T=2,\\ x\left( t\right)&=1,\ \ \ -1\le t\le 0. \end{aligned}$$

In this case, \(A=1,\ B=1\), \(C=1,\alpha =\frac{1}{10},\ h=1\), \(Q_{k+1}\left( jh\right) =\left( \begin{array}{c} k\\ j \end{array} \right) \). The matrix \(X_{1,\frac{1}{10},\frac{1}{10}}^{1,1}\left( 2-r\right) \) has the following form

$$\begin{aligned} X_{1,\frac{1}{10},\frac{1}{10}}^{1,1}\left( 2-r\right)&=\sum \limits _{k=0}^{\infty }\sum \limits _{j=0}^{k}\left( \begin{array}{c} k\\ j \end{array} \right) \frac{\left( 2-r-j\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) }\\&=\sum \limits _{k=0}^{\infty }\frac{\left( 2-r\right) ^{\frac{1}{10} k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) } +\sum \limits _{k=1}^{\infty }\frac{\left( 1-r\right) ^{\frac{1}{2}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) }. \end{aligned}$$

It is clear that

$$\begin{aligned} W\left( 0,2\right)&=\int _{0}^{2}\left( \sum \limits _{k=0}^{\infty } \frac{\left( 2-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) }+\sum \limits _{k=1}^{\infty }\frac{\left( 1-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10} k+\frac{1}{10}\right) }\right) ^{2}dr\\&=\int _{0}^{2}\frac{\left( 2-r\right) ^{-\frac{18}{10}}}{\varGamma \left( \frac{1}{10}\right) }dr+...,\\ W_{1}\left( 0,2\right)&=\int _{0}^{2}\left( 2-r\right) ^{\frac{9}{10} }\left( \sum \limits _{k=0}^{\infty }\frac{\left( 2-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) } +\sum \limits _{k=1}^{\infty }\frac{\left( 1-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) }\right) ^{2}dr\\&=\int _{0}^{2}\left( 2-r\right) ^{\frac{9}{10}}\frac{\left( 1-r\right) ^{-\frac{16}{10}}}{\varGamma ^{2}\left( \frac{2}{10}\right) }dr+...,\\ W_{2}\left( 0,2\right)&=\int _{0}^{2}\left( 2-r\right) ^{\frac{18}{10} }\left( \sum \limits _{k=0}^{\infty }\frac{\left( 2-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) } +\sum \limits _{k=1}^{\infty }\frac{\left( 1-r\right) ^{\frac{1}{10}k-\frac{9}{10}}}{\varGamma \left( \frac{1}{10}k+\frac{1}{10}\right) }\right) ^{2}dr\\&=\int _{0}^{2}\left( 2-r\right) ^{\frac{18}{10}}\frac{\left( 1-r\right) ^{-\frac{16}{10}}}{\varGamma ^{2}\left( \frac{2}{10}\right) }dr+.... \end{aligned}$$

and all expected Gramian matrices \(W\left( 0,2\right) ,\) \(W_{1}\left( 0,2\right) \), \(W_{2}\left( 0,2\right) \) diverge. The terms \(\left( T-r\right) ^{1-\alpha }\) and \(\left( T-r\right) ^{2\left( 1-\alpha \right) }\) remove singularity of the first series only and for the second series we need another neutralizer, say \(\left( T-r-h\right) ^{1-\alpha }=\left( 1-r\right) ^{\frac{9}{10}}\).

Following the example provided, let us introduce a novel Gramian matrix, called the \(\alpha \)-Gramian matrix, that is applicable for all values within the range \(0<\alpha \le 1\).

Definition 7

We define the controllability \(\alpha \)-Gramian of the control problem (1.1) as the nonsymmetric \(d\times d\) matrix

$$\begin{aligned} G_{\alpha }\left( 0,T\right)&=W_{1}\left( 0,T\right) :=\int _{0} ^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr\\&=\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal } \\&\quad \times \left( \sum \limits _{l=0}^{m}\left( T-r-lh\right) _{+}^{1-\alpha } X_{h,\alpha ,\alpha }^{l}\left( T-r-lh\right) \right) ^{\intercal }dr. \end{aligned}$$

Remark 2

It is important to emphasize that \(G_{\alpha }\left( 0,T\right) \) is not symmetric matrix, although it becomes symmetric matrix when \(B=\varTheta \) or \(\alpha =1\). Since the integral part of the solution of (1.1) contains \(X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \) in order to define a control, see (3.3), that transfers the system from any point \(y_{0}\) to arbitrary point \(y_{T},\) it is necessary to define the Gramian matrix as nonsymmetric. This Gramian matrix specification is the only acceptable option for the control system (1.1).

Lemma 6

For \(0<\alpha \le 1\) the \(\alpha \)-Gramian \(G_{\alpha }\left( 0,T\right) \) is well defined.

Proof

Indeed,

$$\begin{aligned}&\left\| G_{\alpha }\left( 0,T\right) \right\| \\&\quad \le \int _{0}^{T}\left\| X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }\right\| dr\\&\quad =\int _{0}^{T}\sum \limits _{j=0}^{m}\left( T-r-jh\right) ^{\alpha -1}Y_{h,\alpha ,\alpha }^{j}\left( T-r-jh\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr\\&\quad \le \left\| Y_{h,\alpha ,\alpha }^{A,B}\left( T\right) \right\| \left\| C\right\| ^{2}\int _{0}^{T}\sum \limits _{j=0}^{m}\left( T-r-jh\right) ^{\alpha -1}dr\left\| Y_{h,\alpha ,\alpha }^{j}\left( T\right) \right\| \\&\quad \le \left\| Y_{h,\alpha ,\alpha }^{A,B}\left( T\right) \right\| \left\| C\right\| ^{2}\sum \limits _{j=0}^{m}\frac{\left( T-r-jh\right) ^{\alpha }}{\alpha }\left\| Y_{h,\alpha ,\alpha }^{j}\left( T\right) \right\| \\&\quad \le \frac{T^{\alpha }}{\alpha }\left\| Y_{h,\alpha ,\alpha }^{A,B}\left( T\right) \right\| \left\| C\right\| ^{2}\sum \limits _{j=0} ^{m}\left\| Y_{h,\alpha ,\alpha }^{j}\left( T\right) \right\| . \end{aligned}$$

\(\square \)

Now, we present out first main result: a necessary and sufficient condition for the relative controllability in terms of \(\alpha \)-Gramian matrix.

Theorem 3

Let \(0<\alpha \le 1\). The system (1.1) is relatively controllable at time T if and only if

$$\begin{aligned} G_{\alpha }\left( 0,T\right) =\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr \end{aligned}$$

is nonsingular.

Proof

\(\left( \Longrightarrow \right) \) Assume that system (1.1) is relatively controllable and that the \(\alpha \)-Gramian \(G_{\alpha }\left( 0,T\right) \) is singular. Then there exists \(\eta \in \mathbb {R}^{d} \backslash \left\{ 0\right\} \) such that

$$\begin{aligned}&\eta ^{\intercal }G_{\alpha }\left( 0,T\right) \eta =\int _{0}^{T}\ \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\nonumber \\&\quad \times \left( \sum \limits _{l=0}^{m}\left( T-r-lh\right) _{+}^{1-\alpha } X_{h,\alpha ,\alpha }^{l}\left( T-r-lh\right) \right) ^{\intercal }\eta dr=0. \end{aligned}$$
(3.1)

Let \(\omega \left( r\right) =\eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C\) an \(\omega ^{l}\left( r\right) =C^{\intercal }\left( X_{h,\alpha ,\alpha }^{l}\left( T-r-lh\right) \right) ^{\intercal }\eta \). Then from (3.1), it follows that

$$\begin{aligned} 0&=\sum \limits _{l=0}^{m}\int _{0}^{T}\left( T-r-lh\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr \\&\ge \sum \limits _{l=0} ^{m}\int _{0}^{T}\left( T-r-mh\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr\\&=\int _{0}^{T}\left( T-r-mh\right) _{+}^{1-\alpha }\omega \left( r\right) \sum \limits _{l=0}^{m}\omega ^{l}\left( r\right) dr \\&=\int _{0}^{T}\left( T-r-mh\right) _{+}^{1-\alpha }\left\| \omega \left( r\right) \right\| ^{2}dr\\&=\int _{0}^{T-mh}\left( T-r-mh\right) ^{1-\alpha }\left\| \omega \left( r\right) \right\| ^{2}dr. \end{aligned}$$

Therefore \(\omega \left( r\right) =0\), almost everywhere on \(\left[ 0,T-mh\right] \). Since

$$\begin{aligned} \omega \left( r\right) =\eta ^{\intercal } X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C \end{aligned}$$

is continuous on \(\left[ 0,T-mh\right) ,\) \(\omega \left( r\right) =0\) on \(\left[ 0,T-mh\right) .\)

Similarly,

$$\begin{aligned} 0&=\sum \limits _{l=0}^{m}\int _{0}^{T}\left( T-r-lh\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr\\&=\sum \limits _{l=0}^{m}\int _{T-mh}^{T}\left( T-r-lh\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr\\&=\sum \limits _{l=0}^{m}\int _{T-mh}^{T}\left( T-r-lh\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr\\&\ge \sum \limits _{l=0}^{m}\int _{T-mh}^{T}\left( T-r-\left( m-1\right) h\right) _{+}^{1-\alpha }\omega \left( r\right) \omega ^{l}\left( r\right) dr\\&=\int _{T-mh}^{T-\left( m-1\right) h}\left( T-r-\left( m-1\right) h\right) _{+}^{1-\alpha }\omega \left( r\right) \sum \limits _{l=0}^{m} \omega ^{l}\left( r\right) dr\\&=\int _{T-mh}^{T-\left( m-1\right) h}\left( T-r-\left( m-1\right) h\right) _{+}^{1-\alpha }\left\| \omega \left( r\right) \right\| ^{2}dr. \end{aligned}$$

Therefore \(\omega \left( r\right) =0\), on \(\left( T-mh,T-mh+h\right) \). Repeating we have \(\omega \left( r\right) =0\), on

$$\begin{aligned} \left[ 0,T-mh\right) \cup _{l=1}^{m}\left( T-\left( m-l+1\right) h,T-\left( m-l\right) h\right) =\left[ 0,T\right] \backslash \left\{ h,2h,...,mh\right\} . \end{aligned}$$

Therefore, \(\omega \left( r\right) =0\), almost everywhere on \(\left[ 0,T\right] \). From the relative controllability of the system (1.1), it follows that for the initial state \(y_{0}=0\) and the final state \(y_{T}=\eta \), there exists a control function u which steers the solution y from 0 to \(\eta \), during the time interval \(\left[ 0,T\right] \). Hence, from (3.1) we have

$$\begin{aligned} \eta =\int _{0}^{T}X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr, \end{aligned}$$

and

$$\begin{aligned} \left\| \eta \right\| ^{2}=\eta ^{\intercal }\eta =\int _{0}^{T} \ \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) Cu\left( r\right) dr=\int _{0}^{T}\omega \left( r\right) u\left( r\right) dr. \end{aligned}$$
(3.2)

Since \(\omega \left( r\right) =0\), almost everywhere on \(\left[ 0,T\right] \), (3.2) implies that \(\eta =0\), which is a contradiction with \(\eta \ne 0 \).

\(\left( \Longleftarrow \right) \) Let \(y_{T}\in \mathbb {R}^{d}\) be the desired final state. If \(G_{\alpha }\left( 0,T\right) \) is invertible, then the control function

$$\begin{aligned} \widehat{u}\left( r\right)&=C^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }\left( G_{\alpha }\left( 0,T\right) \right) ^{-1}\nonumber \\&\quad \times \left( y_{T}-Y_{h,\alpha ,1}^{A,B}\left( T\right) y_{0} -\int _{-h}^{0}X_{h,\alpha ,\alpha }^{A,B}\left( T-s-h\right) B\varphi \left( s\right) ds\right) \end{aligned}$$
(3.3)

is well defined and belongs to \(L^{p}\left( \left[ 0,T\right] ,\mathbb {R}^{r}\right) ,\) even it is continuous on \(\left[ 0,T\right] \). Moreover, inserting the control \(\widehat{u}\) into (1.1) we get

$$\begin{aligned} y\left( T\right)&=Y_{h,\alpha ,1}^{A,B}\left( T\right) y_{0} +\int _{-h}^{0}X_{h,\alpha ,\alpha }^{A,B}\left( T-r-h\right) B\varphi \left( r\right) dr\\&\quad +\int _{0}^{T}\ X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) CC^{\intercal }\left( Y_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) \right) ^{\intercal }dr\left( G_{\alpha }\left( 0,T\right) \right) ^{-1}\\&\quad \times \left( y_{T}-Y_{h,\alpha ,1}^{A,B}\left( T\right) y_{0} -\int _{-h}^{0}X_{h,\alpha ,\alpha }^{A,B}\left( T-s-h\right) B\varphi \left( s\right) ds\right) \\&=Y_{h,\alpha ,1}^{A,B}\left( T\right) y_{0}+\int _{-h}^{0} X_{h,\alpha ,\alpha }^{A,B}\left( T-r-h\right) B\varphi \left( r\right) dr\\&\quad +G_{\alpha }\left( 0,T\right) \left( G_{\alpha }\left( 0,T\right) \right) ^{-1}\\&\quad \times \left( y_{T}-Y_{h,\alpha ,1}^{A,B}\left( T\right) y_{0} -\int _{-h}^{0}X_{h,\alpha ,\alpha }^{A,B}\left( T-s-h\right) B\varphi \left( s\right) ds\right) \\&=y_{T}. \end{aligned}$$

Hence, the control \(\widehat{u}\) steers the solution of the system (1.1) to the desired value \(y_{T}\). \(\square \)

3.2 Kalman-type criterion

Finally, we prove our second main result: the Kalman-type criterion for the relative controllability.

Theorem 4

Let \(0<\alpha \le 1\). A necessary and sufficient condition for the system (1.1) to be relatively controllable on \(\left[ 0,T\right] \) is that the matrix

$$\begin{aligned} \widehat{Q}_{d}\left( T\right) =\left\{ Q_{1}\left( jh\right) C,Q_{2}\left( jh\right) C,...,Q_{d}\left( jh\right) C:jh\in \left[ 0,T\right] \right\} \end{aligned}$$

has rank d : 

$$\begin{aligned} {rank }\,\widehat{Q}_{d}\left( T\right) =d. \end{aligned}$$

Proof

a) Sufficiency:

Suppose that

$$\begin{aligned} \text {rank }\,\left\{ Q_{1}\left( jh\right) C,Q_{2}\left( jh\right) C,...,Q_{d}\left( jh\right) C:jh\in \left[ 0,T\right] \right\} =d, \end{aligned}$$

but \({\text {Im}}L_{0}^{T}\ne \mathbb {R}^{d}\), that is the system (1.1) is not relatively controllable on \(\left[ 0,T\right] \). Then by Theorem 2 there exists \(0\ne \eta \in \mathbb {R}^{d}\) such that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \ \text { on}\ r\in \left[ 0,T\right] \backslash \left\{ 0,h,2h,...,mh\right\} . \end{aligned}$$
(3.4)

It follows that

$$\begin{aligned} \eta ^{\intercal }\left[ \lim _{t\rightarrow T^{-}}\ I_{T^{-}}^{1-\alpha }\ \left( X_{h,\alpha ,\alpha }^{A,B}\left( T-s\right) \right) \left( t\right) \right] C=\eta ^{\intercal }Q_{1}\left( 0\right) C=\eta ^{\intercal }C=0. \end{aligned}$$

By Lemma 3 (3.4) implies that

$$\begin{aligned}&\eta ^{\intercal }\left[ \lim _{t\rightarrow \left( T-jh\right) ^{-} }\ I_{\left( T-jh\right) ^{-}}^{1-\alpha }\ \left( X_{j}\left( T-s\right) -X_{j-1}\left( T-s\right) \right) \left( t\right) \right] C\\&\quad =\eta ^{\intercal }Q_{m+1}\left( jh\right) C=0, \end{aligned}$$

for \(m=0,1,2...,\) \(j=0,1,2,....\) Thus the vector \(\eta \) is orthogonal to all columns of \(\widehat{Q}_{n}\left( T\right) ,\) which is a contradiction. Hence \({\text {Im}}C_{0}^{T}=\mathbb {R}^{d}\).

b) Necessity:

First we show that controllability implies that

$$\begin{aligned} \widehat{Q}_{\infty }\left( T\right)&=\left\{ Q_{1}\left( jh\right) C,Q_{2}\left( jh\right) C,...,Q_{n}\left( jh\right) C,...:jh\in \left[ 0,T\right) \right\} , \\ \text {rank }\,\widehat{Q}_{\infty }\left( T\right)&=d. \end{aligned}$$

This means that the number of linearly independent columns in the sequence

$$\begin{aligned} \left\{ Q_{1}\left( jh\right) C,Q_{2}\left( jh\right) C,...,Q_{n}\left( jh\right) C,...:jh\in \left[ 0,T\right) \right\} \end{aligned}$$

is equal to d. Suppose the contrary that there exists \(0\ne \eta \in \mathbb {R}^{d}\) such that

$$\begin{aligned} \eta ^{\intercal }Q_{i+1}\left( jh\right) C=0,\ \ i=0,1,2...,\ jh\in \left[ 0,T\right) . \end{aligned}$$

The function \(X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C\) is piecewise analytic on \(\left[ 0,T\right] \), i.e. analytic except at isolated points of \(\left[ 0,T\right] ,\) which are \(T,T-h,T-2h,\) etc. On the other hand the function \(X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C\) vanishes for \(r>T\). It follows that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{0}\left( T-r\right) C=\sum _{j=0}^{\infty }\eta ^{\intercal }Q_{j+1}\left( 0\right) C\dfrac{\left( T-r\right) ^{\alpha j+\alpha -1}}{\varGamma \left( \alpha j+\alpha \right) }=0,\ \text { a. e. on}\ \left[ 0,T\right] . \end{aligned}$$

So

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \text { a. e. on}\ \left[ T-h,T\right] . \end{aligned}$$

Repeating this, we obtain

$$\begin{aligned}{} & {} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=\eta ^{\intercal }\left[ X_{h,\alpha ,\alpha }^{0}\left( T-r\right) +X_{h,\alpha ,\alpha }^{1}\left( T-r\right) \right] C\\{} & {} \quad =\sum _{j=0}^{\infty }\eta ^{\intercal }Q_{j+1}\left( 0\right) C\dfrac{\left( T-r\right) ^{\alpha j+\alpha -1}}{\varGamma \left( \alpha j+\alpha \right) } +\sum _{j=1}^{\infty }\eta ^{\intercal }Q_{j+1}\left( h\right) C\dfrac{\left( T-r-h\right) ^{\alpha j+\alpha -1}}{\varGamma \left( \alpha j+\alpha \right) }\\{} & {} \quad =0,\ \ \ \text { a. e. on}\ \left[ 0,T-h\right] . \end{aligned}$$

It follows that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \text {a. e. on}\ \left[ T-2h,T-h\right] . \end{aligned}$$

Repeating these, we have that there exists \(0\ne \eta \in \mathbb {R}^{d}\) such that

$$\begin{aligned} \eta ^{\intercal }X_{h,\alpha ,\alpha }^{A,B}\left( T-r\right) C=0,\ \ \text {a. e. on}\ \left[ 0,T\right] . \end{aligned}$$

This is a contradiction. This means that the relative controllability implies that rank \(\widehat{Q}_{\infty }\left( T\right) =d.\)

It remains to show that rank\(\ \widehat{Q}_{\infty }\left( T\right) =d\) implies that rank\(\widehat{Q}_{d}\left( T\right) =d,\) which follows from Lemma 4. Indeed, by Lemma 4 the matrices \(Q_{m+1}\left( jh\right) \) for \(m+1\ge d\) are linearly dependent on the matrices \(Q_{i+1}\left( lh\right) \) for \(i=0,...,d-2,\) \(l=0,1,...,j\).

$$\begin{aligned}&{rank }\left\{ Q_{m+1}\left( jh\right) C:m=0,1,...,d-1\right\} \\&\quad ={rank }\left\{ Q_{m+1}\left( lh\right) C:p\ge d\ \ m=0,1,...,p;~l=0,1,...,j\right\} . \end{aligned}$$

\(\square \)

In the next two corollaries we consider two special cases separately: (i) nondelayed case \(B=\varTheta ,\) (ii) purely delay case \(A=\varTheta \).

Corollary 1

[23] Let \(0<\alpha \le 1\). Assume that in the system (1.1) \(B=\varTheta \). A necessary and sufficient condition for complete Euclidean space controllability on \(\left[ 0,T\right] \) is that the matrix

$$\begin{aligned} \left\{ C\ AC\ ...\ A^{d-1}C\right\} \end{aligned}$$

has rank d.

Theorem 4 presents a novelty, even in the context of purely delayed fractional linear systems.

Corollary 2

Let \(0<\alpha \le 1\). Assume that in the system (1.1) \(A=\varTheta \). A necessary and sufficient condition for complete Euclidean space controllability on \(\left[ 0,T\right] \) is that the matrix

$$\begin{aligned} \left\{ C\ BC\ ...\ B^{d-1}C\right\} \end{aligned}$$

has rank d.

Proof

According to Theorem 4, it is enough to show that

$$\begin{aligned} \widehat{Q}_{d}\left( T\right) =\left\{ C\ BC\ ...\ B^{d-1}C\right\} . \end{aligned}$$

Indeed, since in the system (1.1) \(A=\varTheta \), the determining equation becomes

$$\begin{aligned} Q_{k+1}\left( jh\right) =\left\{ \begin{array}{ll} B^{k}, &{} \quad k=j,\\ \varTheta , &{}\quad k\ne j. \end{array}\ \ \right. \end{aligned}$$

and

$$\begin{aligned} \widehat{Q}_{d}\left( T\right)&=\left\{ Q_{1}\left( jh\right) ,Q_{2}\left( jh\right) ,...,Q_{d}\left( jh\right) :jh\in \left[ 0,T\right] \right\} \\&=\left\{ C\ BC\ ...\ B^{d-1}C\right\} . \end{aligned}$$

\(\square \)

It should be noted that comparable result were achieved in [10], when the value of \(\alpha =1\).

4 Examples

Example 2

Let us have the differential equation of third degree with a constant delay:

$$\begin{aligned} \left\{ \begin{array}{c} D_{0^{+}}^{\alpha }y\left( t\right) =Ay\left( t\right) +By\left( t-h\right) +Cu\left( t\right) ,\ \ t\in \left( 0,T\right] ,\ h>0,\\ y\left( 0\right) =y_{0},\ \ y\left( t\right) =\varphi \left( t\right) ,\ \ -h\le t<0, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} A=\left( \,\begin{array}{lll} 1&{} 0 &{} 0\\ 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array}\, \right) ,\ \ \ B=\left( \, \begin{array}{lll} 1 &{} 2 &{} 3\\ 0 &{} 1 &{} 2\\ 0 &{} 0 &{} 1 \end{array}\, \right) ,\ \ \ C=\left( \begin{array}{c} 0\\ 0\\ 1 \end{array}\right) . \end{aligned}$$

We want to know whether this system is relatively controllable. Let us check the necessary and sufficient condition. First, we will find the matrix \(\widehat{Q}_{3}\left( T\right) \):

$$\begin{aligned} \widehat{Q}_{3}\left( T\right)&=\left\{ C\ AC\ BC\ A^{2}C\ \left( AB+BA\right) C\ B^{2}C\ ...\ A^{2}B^{2}C\right\} \\&=\left( \,\begin{array}{lll} 0 &{} 3 &{} 0\\ 0 &{} 2 &{} 0\\ 1 &{} 2 &{} 1 \end{array} \begin{array}{llll} 6 &{} 10 &{} ... &{} 10\\ 7 &{} 4 &{} ... &{} 24\\ 2 &{} 4 &{} ... &{} 1 \end{array}\ \ \right) . \end{aligned}$$

We have rank \(\widehat{Q}_{3}\left( T\right) =3\) , so the system is relatively controllable.

Example 3

Let us have the differential equation of third degree with a constant delay:

$$\begin{aligned} \left\{ \begin{array}{c} D_{0^{+}}^{\alpha }y\left( t\right) =Ay\left( t\right) +By\left( t-h\right) +Cu\left( t\right) ,\ \ t\in \left( 0,T\right] ,\ h>0,\\ y\left( 0\right) =y_{0},\ \ y\left( t\right) =\varphi \left( t\right) ,\ \ -h\le t<0, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} A=\left( \begin{array}{lll} 1 &{} 0 &{} 0\\ 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right) ,\ \ \ B=\left( \begin{array}{lll} 1 &{} 2 &{} 3\\ 0 &{} 1 &{} 2\\ 0 &{} 0 &{} 1 \end{array} \right) ,\ \ \ C=\left( \begin{array}{lll} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

First, we will find the matrix \(\widehat{Q}_{3}\left( T\right) \):

$$\begin{aligned} \widehat{Q}_{3}\left( T\right)&=\left\{ C\ AC\ BC\ A^{2}C\ \left( AB+BA\right) C\ B^{2}C\ ...\ A^{2}B^{2}C\right\} \\&=\left( \begin{array}{lll} 1 &{} 0 &{} 0\\ 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \begin{array}{lll} 1 &{} 2 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \begin{array}{lll} 1 &{} 0 &{} 0\\ 2 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \begin{array}{lll} 4 &{} 4 &{} 0\\ 2 &{} 4 &{} 0\\ 0 &{} 0 &{} 0 \end{array}\right. \\&\ \ \ \ \left. \begin{array}{lll} 1 &{} 4 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \ ... \begin{array}{lll} 1 &{} 4 &{} 0\\ 2 &{} 9 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

We have rank \(\widehat{Q}_{3}\left( T\right) =2\), so sufficient condition is not implemented so we can not conclude if the system is relatively controllable.

Example 4

Consider the time-invariant system (1.1). Choose \(\alpha =\frac{1}{3},\) \(A=\left( \begin{array}{ll} 0 &{} 1\\ 0 &{} 0 \end{array} \right) ,\ B=\varTheta ,\ C=\left( \begin{array}{c} 2\\ 1 \end{array} \right) ,\ \ T=1, \ \ h=0.\) Now we apply Theorem 3 to prove that the system (1.1) is controllable. First,

$$\begin{aligned} G_{\alpha }\left( 0,1\right)&=\int _{0}^{1}X_{0,\frac{1}{3},\frac{1}{3} }^{A,B}\left( 1-r\right) CC^{\intercal }\left( Y_{0,\frac{1}{3},\frac{1}{3} }^{A,B}\left( 1-r\right) \right) ^{\intercal }dr\\&=\int _{0}^{1}\sum \limits _{i=0}^{\infty }A^{i}\dfrac{\left( 1-s\right) ^{i\frac{1}{3}-\frac{1}{3}}}{\varGamma \left( i\frac{1}{3}+\frac{1}{3}\right) }CC^{\intercal }\sum \limits _{i=0}^{\infty }\left( A^{\intercal }\right) ^{i}\dfrac{\left( 1-s\right) ^{i\frac{1}{3}}}{\varGamma \left( i\frac{1}{3}+\frac{1}{3}\right) }ds. \end{aligned}$$

By computation,

$$\begin{aligned} \sum \limits _{i=0}^{\infty }A^{i}\dfrac{\left( 1-s\right) ^{i\frac{1}{3}} }{\varGamma \left( i\frac{1}{3}+\frac{1}{3}\right) }&=\frac{1}{\varGamma \left( \frac{1}{3}\right) }I+\frac{1}{\varGamma \left( \frac{2}{3}\right) }A\left( 1-s\right) ^{\frac{1}{3}},\\ I&=\left( \begin{array}{ll} 1 &{} 0\\ 0 &{} 1 \end{array} \right) ,\ \ CC^{\intercal }=\left( \begin{array}{c} 2\\ 1 \end{array} \right) \left( 2\ \ 1\right) =\left( \begin{array}{ll} 4 &{} 2\\ 2 &{} 1 \end{array} \right) ,\\ \sum \limits _{i=0}^{\infty }\left( A^{\intercal }\right) ^{i}\dfrac{\left( 1-s\right) ^{i\frac{1}{3}-\frac{1}{3}}}{\varGamma \left( i\frac{1}{3}+\frac{1}{3}\right) }&=\frac{\left( 1-s\right) ^{-\frac{1}{3}}}{\varGamma \left( \frac{1}{3}\right) }I+\frac{1}{\varGamma \left( \frac{2}{3}\right) }A^{\intercal },\\ G_{\alpha }\left( 0,1\right)&=\int _{0}^{1}\left( \frac{\left( 1-s\right) ^{-\frac{1}{3}}}{\varGamma \left( \frac{1}{3}\right) }I+\frac{1}{\varGamma \left( \frac{2}{3}\right) }A^{\intercal }\right) \\&\quad \times \ \left( \begin{array}{ll} 4 &{} 2\\ 2 &{} 1 \end{array} \right) \left( \frac{1}{\varGamma \left( \frac{1}{3}\right) } I+\frac{\left( 1-s\right) ^{\frac{1}{3}}}{\varGamma \left( \frac{2}{3}\right) }A\right) ds\\&=\int _{0}^{1}\frac{\left( 1-s\right) ^{-\frac{1}{3}}}{\varGamma ^{2}\left( \frac{1}{3}\right) }\left( \begin{array}{ll} 4 &{} 2\\ 2 &{} 1 \end{array}\right) +\frac{1}{\varGamma \left( \frac{2}{3}\right) \varGamma \left( \frac{1}{3}\right) }\left( \begin{array}{ll} 4 &{} 1\\ 1 &{} 0 \end{array}\right) \\&\quad +\frac{3\left( 1-s\right) ^{\frac{1}{3}}}{4\varGamma ^{2}\left( \frac{2}{3}\right) }\left( \begin{array}{ll} 1 &{} 0\\ 0 &{} 0 \end{array} \right) ds\\&=\left( \begin{array}{ll} \frac{6}{\varGamma ^{2}\left( \frac{1}{3}\right) }+\frac{4}{\varGamma \left( \frac{2}{3}\right) \varGamma \left( \frac{1}{3}\right) }+\frac{3}{5\varGamma ^{2}\left( \frac{2}{3}\right) } &{} \frac{3}{\varGamma ^{2}\left( \frac{1}{3}\right) }+\frac{1}{\varGamma \left( \frac{2}{3}\right) \varGamma \left( \frac{1}{3}\right) }\\ \frac{3}{\varGamma ^{2}\left( \frac{1}{3}\right) }+\frac{1}{\varGamma \left( \frac{2}{3}\right) \varGamma \left( \frac{1}{3}\right) } &{} \frac{3}{4\varGamma ^{2}\left( \frac{1}{3}\right) } \end{array}\right) \\&=\left( \begin{array}{ll} 1.3885 &{}0.6131\\ 0.6131 &{} 0.1045 \end{array}\right) . \end{aligned}$$

It is obvious that \(G_{\alpha }\left( 0,1\right) \) is nonsingular and

$$\begin{aligned} \left( G_{\alpha }\left( 0,1\right) \right) ^{-1}=\left( \begin{array}{ll} -0.4529 &{} 2.6581\\ 2.6581 &{} -6.0200 \end{array}\right) . \end{aligned}$$

Thus by Lemma 3, the system is relatively controllable. The control

$$\begin{aligned} u(s)&=C^{\intercal }\left( Y_{0,\frac{1}{3},\frac{1}{3}}^{A,B}\left( 1-r\right) \right) ^{\intercal }\left( G_{\alpha }\left( 0,1\right) \right) ^{-1}\left( y_{1}-Y_{0,\frac{1}{3},1}^{A,B}\left( 1\right) y_{0}\right) \\&=\left( \frac{2}{\varGamma \left( \frac{1}{3}\right) }+\frac{\left( 1-s\right) ^{\frac{1}{3}}}{\varGamma \left( \frac{2}{3}\right) },\frac{1}{\varGamma \left( \frac{1}{3}\right) }\right) \left( \begin{array}{ll} -0.4529 &{} 2.6581\\ 2.6581 &{} -6.0200 \end{array} \ \ \right) \left( \begin{array}{c} 3-\frac{1}{\varGamma \left( \frac{1}{3}\right) }\\ 3-\frac{1}{\varGamma \left( \frac{1}{3}\right) } \end{array}\right) \end{aligned}$$

transfers the system form \(y_{0}\) to the point \(y_{1}\).

On the other hand,

$$\begin{aligned} \text {rank}\widehat{Q}_{2}\left( T\right) =\text {rank}\left( C\ AC\right) =\text {rank}\left( \begin{array}{ll} 2 &{} 1\\ 1 &{} 0 \end{array} \ \ \right) =2. \end{aligned}$$

Thus by Theorem 4, the system is relatively controllable.

Example 5

Consider the time-invariant system (1.1). Choose \(\alpha =\frac{2}{3},\) \(A=\left( \begin{array}{lll} -1 &{} -4 &{} -2\\ 0 &{} 6 &{} 1\\ 1 &{} 7 &{} 1 \end{array} \right) , B=\varTheta , \ C=\left( \begin{array}{c} 2\\ 0\\ 1 \end{array} \right) .\) Now we apply Theorem 4 to prove that the system (1.1) is controllable.

$$\begin{aligned} \text {rank}\widehat{Q}_{3}\left( T\right) =\text {rank}\left( C\ AC\ A^{2} C\right) =\text {rank}\left( \begin{array}{lll} 2 &{} -4 &{} 6\\ 0 &{} -1 &{} 7\\ 1 &{} 1 &{} -12 \end{array} \right) =3. \end{aligned}$$

By Theorem 4, the system is relatively controllable.

Fig. 1
figure 1

Graph of solution y(t) to the system (4.1) with \(u=0\)

Full size image
Fig. 2
figure 2

Graph of solution y(t) to the system (4.1) with u(r)

Full size image

Example 6

Consider the following system:

$$\begin{aligned} ^{C}D_{0^{+}}^{\frac{1}{5}}x\left( t\right)&=x\left( t\right) +x\left( t-0.5\right) +u\left( t\right) ,\ \ \ 0<t\le T=1,\nonumber \\ x\left( t\right)&=1,\ \ \ -1\le t\le 0. \end{aligned}$$
(4.1)

In this case, \(A=1,\ B=1\), \(C=1,\alpha =\frac{1}{5},\ h=0.5\), \(Q_{k+1}\left( jh\right) =\left( \begin{array}{c} k\\ j \end{array} \right) \). The matrices \(X_{1,\frac{1}{10},\frac{1}{10}}^{1,1}\left( 1-r\right) ,\) \(Y_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right) \) and \(Y_{\frac{1}{2},\frac{1}{5},1}^{1,1}\left( 1-r\right) \) have the following form

$$\begin{aligned} X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right)&=\sum \limits _{k=0}^{\infty }\sum \limits _{j=0}^{k}\left( \begin{array}{c} k\\ j \end{array} \right) \frac{\left( 1-r-\frac{1}{2}j\right) _{+}^{\frac{1}{5}k-\frac{1}{5}}}{\varGamma \left( \frac{1}{5}k+\frac{1}{5}\right) },\\ Y_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right)&=\sum \limits _{k=0}^{\infty }\sum \limits _{j=0}^{k}\left( \begin{array}{c} k\\ j \end{array} \right) \frac{\left( 1-r-\frac{1}{2}j\right) _{+}^{\frac{1}{5}k}}{\varGamma \left( \frac{1}{5}k+\frac{1}{5}\right) },\\ Y_{\frac{1}{2},\frac{1}{5},1}^{1,1}\left( 1-r\right)&=\sum \limits _{k=0}^{\infty }\sum \limits _{j=0}^{k}\left( \begin{array}{c} k\\ j \end{array} \right) \frac{\left( 1-r-\frac{1}{2}j\right) _{+}^{\frac{1}{5}k}}{\varGamma \left( \frac{1}{5}k+1\right) }. \end{aligned}$$

In this case, \(\alpha \)-Gramian is defined as

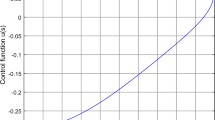
$$\begin{aligned} G_{\alpha }\left( 0,1\right) =\int _{0}^{1}X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right) Y_{\frac{1}{2},\frac{1}{5},\frac{1}{5}} ^{1,1}\left( 1-r\right) dr, \end{aligned}$$

the control which transfers the system form \(y\left( 0\right) =1\) to \(y\left( 1\right) =5\) is defined as

$$\begin{aligned} u\left( r\right)&=Y_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right) \left( G_{\alpha }\left( 0,1\right) \right) ^{-1} \\&\quad \times \left( 5-Y_{\frac{1}{2},\frac{1}{5},1}^{1,1}\left( 1\right) -\int _{-0.5} ^{0}X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 0.5-s\right) ds\right) , \end{aligned}$$

and \(y\left( t\right) \) is the trajectory of (4.1) with control starts from the initial point 1 and reaches the final point 5 in [0, 1].

$$\begin{aligned} y\left( t\right)&=Y_{\frac{1}{2},\frac{1}{5},1}^{1,1}\left( 1\right) +\int _{-0.5}^{0}X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( t-0.5-s\right) ds\\&\quad +\int _{0}^{t}X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( t-r\right) Y_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 1-r\right) dr\left( G_{\alpha }\left( 0,1\right) \right) ^{-1}\\&\quad \times \left( 5-Y_{\frac{1}{2},\frac{1}{5},1}^{1,1}\left( 1\right) -\int _{-0.5}^{0}X_{\frac{1}{2},\frac{1}{5},\frac{1}{5}}^{1,1}\left( 0.5-s\right) ds\right) . \end{aligned}$$

Next we give the numerical simulation of the state with and without control function for the system (4.1).

Fig. 1 represents the trajectory of (4.1) with \(u=0\).

Fig. 2 represents the trajectory of (4.1) with control u(r) starts from the initial point 1 and reaches the final point 5 in [0, 1].

5 Conclusions and future directions

In this paper, our focus was on exploring the relative controllability of systems governed by linear fractional differential equations incorporating state delay. We introduced a novel counterpart to the Cayley-Hamilton theorem. Leveraging a delayed perturbation of the Mittag-Leffler function, along with a determining function and an analog of the Cayley-Hamilton theorem, we established an algebraic Kalman-type rank criterion for assessing the relative controllability of fractional linear differential equations with state delay. Moreover, we articulated necessary and sufficient conditions for relative controllability criteria concerning linear fractional time-delay systems, expressed in terms of a new Gramian matrix. Furthermore, practical examples were provided to demonstrate the proposed criteria for controllability, and controls were designed accordingly.

In our future endeavors, we aim to explore the Lyapunov-type, finite-time and exponential stability, and relative controllability of Caputo-type fractional order time-delay linear/nonlinear deterministic/stochastic systems.