No CrossRef data available.
Article contents
Ideals with componentwise linear powers
Part of:
Algebraic combinatorics
General commutative ring theory
Computational aspects and applications
Published online by Cambridge University Press: 12 March 2024
Abstract
Let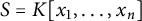 
$S=K[x_1,\ldots ,x_n]$ be the polynomial ring over a field K, and let A be a finitely generated standard graded S-algebra. We show that if the defining ideal of A has a quadratic initial ideal, then all the graded components of A are componentwise linear. Applying this result to the Rees ring 
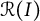$\mathcal {R}(I)$ of a graded ideal I gives a criterion on I to have componentwise linear powers. Moreover, for any given graph G, a construction on G is presented which produces graphs whose cover ideals 
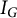$I_G$ have componentwise linear powers. This, in particular, implies that for any Cohen–Macaulay Cameron–Walker graph G all powers of 
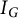$I_G$ have linear resolutions. Moreover, forming a cone on special graphs like unmixed chordal graphs, path graphs, and Cohen–Macaulay bipartite graphs produces cover ideals with componentwise linear powers.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
Takayuki Hibi is partially supported by JSPS KAKENHI 19H00637. Somayeh Moradi is supported by the Alexander von Humboldt Foundation.
References
Aramova, A., Herzog, J., and Hibi, T.,
Ideals with stable Betti numbers
. Adv. Math. 152(2000), 72–77.CrossRefGoogle Scholar
Erey, N.,
Powers of ideals associated to
$\left({C}_4,2{K}_2\right)$
-free graphs
. J. Pure Appl. Algebra 223(2019), no. 7, 3071–3080.CrossRefGoogle Scholar
$\left({C}_4,2{K}_2\right)$
-free graphs
. J. Pure Appl. Algebra 223(2019), no. 7, 3071–3080.CrossRefGoogle ScholarHà, H. T. and Van Tuyl, A.,
Powers of componentwise linear ideals: the Herzog–Hibi–Ohsugi conjecture and related problems
. Res. Math. Sci. 9(2022), 22.CrossRefGoogle Scholar
Herzog, J. and Hibi, T.,
Componentwise linear ideals
. Nagoya Math. J. 153(1999), 141–153.CrossRefGoogle Scholar
Herzog, J. and Hibi, T.,
Distributive lattices, bipartite graphs and Alexander duality
. J. Algebraic Combin. 22(2005), 289–302.CrossRefGoogle Scholar
Herzog, J., Hibi, T., and Moradi, S.,
Componentwise linear powers and the
$x$
-condition
. Math. Scand. 128(2022), 401–433.CrossRefGoogle Scholar
$x$
-condition
. Math. Scand. 128(2022), 401–433.CrossRefGoogle ScholarHerzog, J., Hibi, T., and Ohsugi, H.,
Powers of componentwise linear ideals
. In: Fløystad, G., Johnsen, T., and Knutsen, A. (eds.), Combinatorial aspects of commutative algebra and algebraic geometry, Abel Symposia, 6, Springer, Berlin, 2011, pp. 49–60.CrossRefGoogle Scholar
Herzog, J., Hibi, T., and Ohsugi, H., Binomial ideals, Graduate Texts in Mathematics, 279, Springer, Cham, 2018.CrossRefGoogle Scholar
Herzog, J., Hibi, T., and Zheng, X.,
Monomial ideals whose powers have a linear resolution
. Math. Scand. 95(2004), 23–32.CrossRefGoogle Scholar
Herzog, J., Reiner, V., and Welker, V.,
Componentwise linear ideals and Golod rings
. Michigan Math. J. 46(1999), 211–223.CrossRefGoogle Scholar
Hibi, T., Higashitani, A., Kimura, K., and O’Keefe, A. B.,
Algebraic study on Cameron–Walker graphs
. J. Algebra 422(2015), 257–269.CrossRefGoogle Scholar
Kumar, A. and Kumar, R.,
On the powers of vertex cover ideals
. J. Pure. Appl. Algebra 226(2022), no. 1, 106808.CrossRefGoogle Scholar
Römer, T., On minimal graded free resolutions. Ph.D. dissertation, Universität Duisburg-Essen, 2001.Google Scholar
Yanagawa, K.,
Alexander duality for Stanley–Reisner rings and squarefree
${\mathbb{N}}^n$
-graded modules
. J. Algebra 225(2000), 630–645.CrossRefGoogle Scholar
${\mathbb{N}}^n$
-graded modules
. J. Algebra 225(2000), 630–645.CrossRefGoogle Scholar