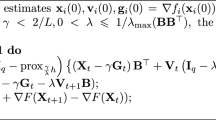Appendix 1: Details about experiments and other results
In this section we provide details about our experiments as well as results about training and test loss. For each experiment, we set our network topology as a special ring network, where \(W= (w_{i,j})\) and the only nonzero elements are given by:
$$\begin{aligned} w_{i,i} = a,\ w_{i,i+1}=w_{i,i-1} = \frac{1-a}{2},\ \text { for some }a\in (0,1). \end{aligned}$$
Here we overload the notation and set \(w_{n,n+1}= w_{n,1}, w_{1,0}=w_{1,n}\). Note that a is the unique parameter that determines the weight matrix and will be specified in each experiment.
1.1 Synthetic data
1.1.1 Logistic regression on synthetic data
In this experiment, on node i we have:
$$\begin{aligned}&f_i(\lambda ,\tau ^*(\lambda )) = \sum _{(x_e,y_e)\in {\mathcal {D}}_i'}\psi (y_ex_e^{{\textsf{T}}}\tau ^*(\lambda )),\\&g_i(\lambda ,\tau ) = \sum _{(x_e,y_e)\in {\mathcal {D}}_i}\psi (y_ex_e^{{\textsf{T}}}\tau ) + \frac{1}{2}\tau ^{{\textsf{T}}}\text {diag}(e^{\lambda })\tau , \end{aligned}$$
where \(e^{\lambda }\) is element-wise, \(\text {diag}(v)\) denotes the diagonal matrix generated by vector v, and \(\psi (x) = \log (1+e^{-x})\). \({\mathcal {D}}_i'\) and \({\mathcal {D}}_i\) represent validation set and training set on node i. Following the setup in [24], we first randomly generate \(\tau ^*\in {\mathbb {R}}^{p}\) and the noise vector \(\epsilon \in {\mathbb {R}}^{p}\). For the data point \((x_e, y_e)\) on node i, each element of \(x_e\) is sampled from the normal distribution with mean 0, variance \(i^2\). \(y_e\) is then set by \(y_e = \text {sign}(x_e^{{\textsf{T}}}\tau ^* + m\epsilon )\), where \(\text {sign}\) denotes the sign function and \(m=0.1\) denotes the noise rate. In the experiment we choose \(p = q = 50,\) and the number of inner-loop and outer-loop iterations as 10 and 100 respectively. N, the number of iterations of the JHIP oracle 1 is 20. The stepsizes are \(\eta _x=\eta _y=\gamma = 0.01.\) The number of agents n is chosen as 20, and the weight parameter \(a=0.4\) (Fig. 3).
1.2 Real-world data
1.2.1 Logistic regression on 20 Newsgroup dataset
In this experiment, on node i we have:
$$\begin{aligned}&f_i(\lambda , \tau ^*(\lambda ))= \frac{1}{|{\mathcal {D}}^{(i)}_{val}|}\sum _{(x_e,y_e)\in {\mathcal {D}}^{(i)}_{val}}L(x_e^{{\textsf{T}}}\tau ^*, y_e), \\&g_i(\lambda , \tau )= \frac{1}{|{\mathcal {D}}_{tr}^{(i)}|}\sum _{(x_e,y_e)\in {\mathcal {D}}^{(i)}_{tr}}L(x_e^{{\textsf{T}}}\tau , y_e) + \frac{1}{cp} \sum _{i=1}^{c}\sum _{j=1}^{p}e^{\lambda _j}\tau _{ij}^2, \end{aligned}$$
where \(c=20\) denotes the number of topics, \(p=101631\) is the feature dimension, L is the cross entropy loss, \({\mathcal {D}}_{val}\) and \({\mathcal {D}}_{tr}\) are the validation and training data sets, respectively. Our codes can be seen as decentralized versions of the one provided in [13].
We first set inner and outer stepsizes \(\eta _x=\eta _y=100\) (the same as the ones used in [13]), and then compare its performance with different stepsizes. We set the number of inner-loop iterations \(T = 10,\) the number of outer-loop iterations \(K=30,\) the number of agents \(n=20,\) and the weight parameter \(a=0.33\). At the end of jth outer-loop iteration we use the average \(\overline{\tau _j} = \frac{1}{n}\sum _{i=1}^{n}\tau _{i,j}\) as the model parameter and then do the classification on the test set to get the test accuracy (Fig. 4).
1.2.2 Data hyper-cleaning on MNIST
In this experiment, on node i we have:
$$\begin{aligned} f_i(\lambda , \tau )&= \frac{1}{\vert {\mathcal {D}}^{(i)}_{val}\vert }\sum _{(x_e,y_e)\in {\mathcal {D}}^{(i)}_{val}}L(x_e^{{\textsf{T}}}\tau , y_e), \\ g_i(\lambda , \tau )&= \frac{1}{\vert {\mathcal {D}}^{(i)}_{tr}\vert }\sum _{(x_e,y_e)\in {\mathcal {D}}^{(i)}_{tr}}\sigma (\lambda _e)L(x_e^{{\textsf{T}}}\tau , y_e) + C_r\Vert \tau \Vert ^2, \end{aligned}$$
where L is the cross-entropy loss and \(\sigma (x)= (1+e^{-x})^{-1}\) is the sigmoid function. The number of inner-loop iterations T and outer-loop iterations K are set as 10 and 30, respectively. The number of agents \(n=20\) and the weight parameter \(a=0.5\). Following [13, 53] the regularization parameter \(C_r\) is set as 0.001. We first choose stepsizes similar to those in [13] and then set larger stepsizes. In each iteration we evaluate the norm of the hypergradient at the average of the hyperparameters \({\bar{\lambda }}\), and plot the logarithm (base 10) of the norm of the hypergradient versus iteration number in Fig. 2 (Figs. 5, 6).
Appendix 2: Convergence analysis
In this section we provide the proofs of convergence results. For convenience, we first list the notation below.
$$\begin{aligned}&W := (w_{ij}) \text { is symmetric doubly stochastic, and } \rho := \max \left( |\lambda _2|, |\lambda _n|\right) < 1 \\&X_k := \left( x_{1,k},x_{2,k},\ldots ,x_{n,k}\right) ,\ {{\bar{x}}}_k := \frac{1}{n}\sum _{i=1}^{n}x_{i,k},\\&\partial \Phi (X_k) := \left( {\hat{\nabla }} f_1(x_{1,k}, y_{1,k}^{(T)}),\ldots ,{\hat{\nabla }} f_n(x_{n,k}, y_{n,k}^{(T)})\right) ,\\&\partial \Phi (X_k;\phi ) := \left( {\hat{\nabla }} f_1(x_{1,k}, y_{1,k}^{(T)};\phi _{1,k}),\ldots ,{\hat{\nabla }} f_n(x_{n,k}, y_{n,k}^{(T)};\phi _{n,k})\right) \\&\overline{\partial \Phi (X_k)} := \frac{1}{n}\sum _{i=1}^{n}{\hat{\nabla }}f_{i}(x_{i,k}, y_{i,k}^{(T)}),\ \overline{\partial \Phi (X_k;\phi )} := \frac{1}{n}\sum _{i=1}^{n}{\hat{\nabla }}f_{i}(x_{i,k}, y_{i,k}^{(T)}; \phi _{i,k}), \\&q_{i,k} := x_{i,k} - {{\bar{x}}}_k,\ r_{i,k} := u_{i,k} - {{\bar{u}}}_k, \\&Q_k := \left( q_{1,k}, q_{2,k},\ldots ,q_{n,k}\right) ,\ R_k := \left( r_{1,k},r_{2,k},\ldots ,r_{n,k}\right) \in {\mathbb {R}}^{p\times n}, \\&S_K := \sum _{k=1}^{K}\Vert Q_k\Vert ^2,\ T_K := \sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2,\ E_K := \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert ^2, \\&A_K := \sum _{j=0}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(T)} - y_i^*(x_{i,j})\Vert ^2, B_K := \sum _{j=0}^{K}\sum _{i=1}^{n}\Vert v_{i,j}^* - v_{i,j}^{(0)}\Vert ^2, \\&v_{i,j}^* = \left( \nabla _y^2g_i(x_{i,j},y_i^*(x_{i,j}))\right) ^{-1}\nabla _y f_i(x_{i,j},y_i^*(x_{i,j})), \\&\delta _y := (1 - \eta _y\mu )^2,\ \delta _{\kappa } := \left( \frac{\sqrt{\kappa } - 1}{\sqrt{\kappa } + 1}\right) ^2. \end{aligned}$$
We first introduce a few lemmas that are useful in the proofs.
Lemma 1
For any \(p, q, r\in {\mathbb {N}}_+\) and matrix \(A\in {\mathbb {R}}^{p\times q}, B\in {\mathbb {R}}^{q\times r}\), we have:
$$\begin{aligned} \Vert AB\Vert \le \min \left( \Vert A\Vert _2\cdot \Vert B\Vert , \Vert A\Vert \cdot \Vert B^{{\textsf{T}}}\Vert _2\right) . \end{aligned}$$
Lemma 2
For any matrix \(A = (a_1,a_2,\ldots ,a_q)\in {\mathbb {R}}^{p\times q}\), we have:
$$\begin{aligned} \Vert a_j\Vert ^2\le \Vert A\Vert _2^2 \le \Vert A\Vert ^2 = \sum _{i=1}^{q}\Vert a_i\Vert ^2,\ \forall {j}\in \{1,2,\ldots ,q\}. \end{aligned}$$
For one-step gradient descent, we have the following result (see, e.g., Lemma 10 in [34] and Lemma 3 in [46]).
Lemma 3
Suppose f(x) is \(\mu\)-strongly convex and \(L-smooth\). For any x and \(\eta <\frac{2}{\mu + L}\), define \(x^+ = x - \eta \nabla f(x),\ x^*=\mathop {\mathrm {arg\,min}}\limits f(x)\). Then we have
$$\begin{aligned} \Vert x^+ - x^*\Vert \le (1-\eta \mu )\Vert x-x^*\Vert . \end{aligned}$$
The following lemma is a common result in decentralized optimization (e.g., [15, Lemma 4]).
Lemma 4
Suppose Assumption 2.2 holds. We have for any integer \(k\ge 0\),
$$\begin{aligned} \left\| W^{k} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right\| _2\le \rho ^k. \end{aligned}$$
Proof
Assume \(1=\lambda _1>\lambda _2\ge \cdots \ge \lambda _n>-1\) are eigenvalues of W. Since \(W^{k}{\textbf{1}}_n{\textbf{1}}^{\top }_n = {\textbf{1}}_n{\textbf{1}}^{\top }_nW^k\), we know \(W^k\) and \({\textbf{1}}_n{\textbf{1}}^{\top }_n\) are simultaneously diagonalizable. Hence there exists an orthogonal matrix P such that
$$\begin{aligned} W^k = P\text {diag}(\lambda _i^k)P^{-1},\quad \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}=P\text {diag}(1,0,0,\ldots ,0)P^{-1}, \end{aligned}$$
and thus:
$$\begin{aligned} \left\| W^{k} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right\| _2 = \left\| P(\text {diag}(\lambda _i^{k}) - \text {diag}(1,0,0,\ldots ,0) )P^{-1}\right\| _2\le \max \left( |\lambda _2|^k, |\lambda _n|^k\right) . \end{aligned}$$
By definition of rho, the proof is complete. \(\square\)
The following three lemmas are adopted from Lemma 2.2 in [12]:
Lemma 5
(Hypergradient) Define \(\Phi _i(x):= f_i(x, y^*(x))\), where \(y^*(x) = {\mathrm{arg~min}}_{y\in {\mathbb {R}}^{q}}g(x,y)\). Under Assumption 2.1 we have:
$$\begin{aligned} \nabla \Phi _i(x) = \nabla _x f_i(x,y^*(x)) - \nabla _{xy} g(x,y^*(x))\left( \nabla _y^2g(x,y^*(x))\right) ^{-1}\nabla _y f_i(x,y^*(x)). \end{aligned}$$
Moreover, \(\nabla \Phi _i\) is Lipschitz continuous:
$$\begin{aligned} \Vert \nabla \Phi _i(x_1) - \nabla \Phi _i(x_2)\Vert \le L_{\Phi }\Vert x_1 - x_2\Vert , \end{aligned}$$
with the Lipschitz constant given by:
$$\begin{aligned} L_{\Phi } = L + \frac{2L^2 + L_{g,2}L_{f,0}^2 }{\mu } + \frac{LL_{f,0}L_{g,2}+L^3 + L_{g,2}L_{f,0}L }{\mu ^2} + \frac{L_{g,2}L^2L_{f,0}}{\mu ^3} = \Theta (\kappa ^3). \end{aligned}$$
Remark
if Assumption 2.3 does not hold, then this hypergradient is completely different from the local hypergradient:
$$\begin{aligned} \nabla f_i(x, y_i^*(x)) = \nabla _x f_i(x,y_i^*(x)) - \nabla _{xy} g_i(x,y_i^*(x))\left( \nabla _y^2g_i(x,y_i^*(x))\right) ^{-1}\nabla _y f_i(x,y_i^*(x)), \end{aligned}$$
(11)
where \(y_i^*(x)={\mathrm{arg~min}}_{y\in {\mathbb {R}}^{q}}g_i(x,y)\).
Lemma 6
Define:
$$\begin{aligned} {\bar{\nabla }} f_i(x, y) = \nabla _x f_i(x,y) - \nabla _{xy} g(x,y) \left( \nabla _y^2g(x,y)\right) ^{-1}\nabla _y f_i(x,y). \end{aligned}$$
Under the Assumption 2.1 we have:
$$\begin{aligned} \Vert {\bar{\nabla }} f_i(x, y) - {\bar{\nabla }} f_i({\tilde{x}}, {\tilde{y}}) \Vert \le L_{f}\Vert (x,y) - ({\tilde{x}}, {\tilde{y}})\Vert , \end{aligned}$$
where the Lipschitz constant is given by:
$$\begin{aligned} L_{f} = L + \frac{L^2}{\mu } + L_{f,0}\left( \frac{L_{g,2}}{\mu } + \frac{L_{g,2}L}{\mu ^2} \right) = \Theta (\kappa ). \end{aligned}$$
Lemma 7
Suppose Assumption 2.1 holds. We have:
$$\begin{aligned} \Vert y_i^*(x_1) - y_i^*(x_2)\Vert \le \kappa \Vert x_1 - x_2\Vert ,\quad \forall i\in \{1,2,\ldots ,n\}. \end{aligned}$$
These lemmas reveal some nice properties of functions in bilevel optimization under Assumption 2.1. We will make use of these lemmas in our theoretical analysis.
Lemma 8
Suppose Assumption 2.1 holds. If the iterates satisfy:
$$\begin{aligned} {{\bar{x}}}_{k+1} = {{\bar{x}}}_k - \eta _x\overline{\partial \Phi (X_k)},\quad \text {where } 0<\eta _x\le \frac{1}{L_{\Phi }}, \end{aligned}$$
then we have the following inequality holds:
$$\begin{aligned}\frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 &\le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) \nonumber \\&\quad+ \frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2. \end{aligned}$$
(12)
Proof
Since \(\Phi (x)\) is \(L_{\Phi }\)-smooth, we have:
$$\begin{aligned}&\Phi ({{\bar{x}}}_{k+1}) - \Phi ({{\bar{x}}}_k) \\&\quad \le \nabla \Phi ({{\bar{x}}}_k)^{{\textsf{T}}}(-\eta _x\overline{\partial \Phi (X_k)}) + \frac{L_{\Phi }\eta _x^2}{2}\Vert \overline{\partial \Phi (X_k)}\Vert ^2 \\&\quad =\frac{L_{\Phi }\eta _x^2}{2}\Vert \overline{\partial \Phi (X_k)}\Vert ^2 - \eta _x \nabla \Phi ({{\bar{x}}}_k)^{{\textsf{T}}}\overline{\partial \Phi (X_k)} \\&\quad =\frac{L_{\Phi }\eta _x^2}{2}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + \left( \frac{L_{\Phi }\eta _x^2}{2} - \eta _x\right) \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\qquad +\,(L_{\Phi }\eta _x^2- \eta _x) \nabla \Phi (\bar{x}_k)^{{\textsf{T}}}(\overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)) \\&\quad \le \frac{L_{\Phi }\eta _x^2}{2}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + \left( \frac{L_{\Phi }\eta _x^2}{2} - \eta _x\right) \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\qquad +\, (\eta _x - L_{\Phi }\eta _x^2)\left( \frac{1}{2}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + \frac{1}{2}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \right) \\&\quad = \frac{\eta _x}{2} \Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 -\frac{\eta _x}{2}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2, \end{aligned}$$
where the second inequality is due to Young’s inequality and \(\eta _x\le \frac{1}{L_{\Phi }}\). Therefore, we have:
$$\begin{aligned} \begin{aligned} \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2&\le \frac{2}{\eta _x}(\Phi ({{\bar{x}}}_k) - \Phi ({{\bar{x}}}_{k+1})) + \Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2. \end{aligned} \end{aligned}$$
(13)
Summing (13) over \(k=0,\ldots ,K\), yields:
$$\begin{aligned} \sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \le \frac{2}{\eta _x}(\Phi ({{\bar{x}}}_0) - \Phi ({{\bar{x}}}_{k+1})) + \sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2, \end{aligned}$$
which completes the proof. \(\square\)
We have the following lemma which provides an upper bound for \(E_K\):
Lemma 9
In each iteration, if we have \({{\bar{x}}}_{k+1} = {{\bar{x}}}_k - \eta _x\overline{\partial \Phi (X_k)}\), then the following inequality holds:
$$\begin{aligned} E_K \le 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}. \end{aligned}$$
Proof
By the definition of \(E_K\), we have:
$$\begin{aligned} E_K&= \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert ^2 = \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - {{\bar{x}}}_j + {{\bar{x}}}_j - \bar{x}_{j-1} + {{\bar{x}}}_{j-1} - x_{i,j-1}\Vert ^2 \\&= \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert q_{i,j} -\eta _x(\overline{\partial \Phi (X_{j-1})} - \nabla \Phi ({{\bar{x}}}_{j-1})) - \eta _x\nabla \Phi ({{\bar{x}}}_{j-1}) - q_{i,j-1}\Vert ^2 \\&\le 4\sum _{j=1}^{K}\sum _{i=1}^{n}(\Vert q_{i,j}\Vert ^2 + \eta _x^2\Vert \overline{\partial \Phi (X_{j-1})} - \nabla \Phi (\bar{x}_{j-1}))\Vert ^2 \\&\quad +\, \eta _x^2\Vert \nabla \Phi ({{\bar{x}}}_{j-1})\Vert ^2 + \Vert q_{i,j-1}\Vert ^2) \\&\le 4\sum _{j=1}^{K}(\Vert Q_j\Vert ^2 + \Vert Q_{j-1}\Vert ^2 +\, n\eta _x^2\Vert \overline{\partial \Phi (X_{j-1})} - \nabla \Phi ({{\bar{x}}}_{j-1})\Vert ^2 + n\eta _x^2\Vert \nabla \Phi (\bar{x}_{j-1})\Vert ^2) \\&\le 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}(\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + \Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2) \\&= 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}, \end{aligned}$$
where the second inequality is by the definition of \(Q_j\), the third inequality is by the definition of \(S_K\) and \(Q_0 = 0\), the last equality is by the definition of \(T_{K-1}.\) \(\square\)
Next we give bounds for \(A_K\) and \(B_K\).
Lemma 10
Suppose Assumptions 2.1 and 2.3 hold. If \(\eta _y, T\) and N in Algorithm 3 and 4 satisfy:
$$\begin{aligned} 0<\eta _y< \frac{2}{\mu + L},\quad \delta _y^T< \frac{1}{3},\quad \delta _{\kappa }^N <\frac{1}{8\kappa }, \end{aligned}$$
(14)
then the following inequalities hold:
$$\begin{aligned} A_K\le 3\delta _y^T(c_1 + 2\kappa ^2E_K),\quad B_K\le 2c_2 + 2d_1A_{K-1} + 2d_2E_K, \end{aligned}$$
where the constants are defined as follows:
$$\begin{aligned}&c_1 = \sum _{i=1}^{n}\Vert y_{i,0}^{(0)} - y_i^*(x_{i,0})\Vert ^2,\ c_2 = \sum _{i=1}^{n}\Vert v_{i,0}^* - v_{i,0}^{(0)}\Vert ^2, \nonumber \\&d_1 = 4(1+\sqrt{\kappa })^2\left( \kappa + \frac{L_{g,2} L_{f,0}}{\mu ^2}\right) ^2=\Theta (\kappa ^3), \nonumber \\&d_2 = 2\left( \kappa ^2 + \frac{2L_{f,0}\kappa }{\mu } + \frac{2L_{f,0}\kappa ^2}{\mu }\right) ^2 = \Theta (\kappa ^4). \end{aligned}$$
(15)
Proof
For each term in \(A_K\) we have
$$\begin{aligned} \begin{aligned}\Vert y_{i,j}^{(T)} - y_i^*(x_{i,j})\Vert ^2 &= \Vert y_{i,j}^{(T-1)} - \eta _y\nabla _y g(x_{i,j}, y_{i,j}^{(T-1)}) - y_i^*(x_{i,j}) \Vert ^2 \\& \le (1 - \eta _y\mu )^2\Vert y_{i,j}^{(T-1)} - y_i^*(x_{i,j})\Vert ^2\le \delta _y^T \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2, \end{aligned} \end{aligned}$$
(16)
where the first inequality uses Lemma 3. We further have:
$$\begin{aligned} \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 &= \Vert y_{i,j-1}^{(T)} - y_i^*(x_{i,j-1}) + y_i^*(x_{i,j-1}) - y_i^*(x_{i,j})\Vert ^2 \\& \le 2(\Vert y_{i,j-1}^{(T)} - y_i^*(x_{i,j-1})\Vert ^2 + \Vert y_i^*(x_{i,j-1}) - y_i^*(x_{i,j})\Vert ^2) \\& \le 2\delta _y^T \Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2 + 2\kappa ^2\Vert x_{i,j-1} - x_{i,j}\Vert ^2 \\& < \frac{2}{3}\Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2 + 2\kappa ^2\Vert x_{i,j-1} - x_{i,j}\Vert ^2, \end{aligned}$$
where the second inequality is by (16) and Lemma 7, and the last inequality is by the condition (14). Taking summation on both sides, we get
$$\begin{aligned}&\sum _{j=1}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 \\&\quad \le \frac{2}{3}\sum _{j=1}^{K}\sum _{i=1}^{n}\Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2 + 2\kappa ^2\sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert ^2 \\&\quad \le \frac{2}{3} \sum _{j=0}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 + 2\kappa ^2E_K \\&\quad \le \frac{2}{3} c_1 + \frac{2}{3}\sum _{j=1}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 + 2\kappa ^2E_K, \end{aligned}$$
which directly implies:
$$\begin{aligned} \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 \le 2c_1 + 6\kappa ^2E_K. \end{aligned}$$
(17)
Combining (16) and (17) leads to:
$$\begin{aligned} A_K =&\sum _{j=0}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{T} - y_i^*(x_{i,j})\Vert ^2\le \delta _y^T \sum _{j=0}^{K}\sum _{i=1}^{n}\Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2 \\ \le&\delta _y^T (c_1 + 2c_1 + 6\kappa ^2E_K) = 3\delta _y^T(c_1 + 2\kappa ^2E_K). \end{aligned}$$
We then consider the bound for \(B_K\). Recall that:
$$\begin{aligned} v_{i,k}^* = \left( \nabla _y^2g_i(x_{i,k},y_i^*(x_{i,k}))\right) ^{-1}\nabla _y f_i(x_{i,k},y_i^*(x_{i,k})), \end{aligned}$$
which is the solution of the linear system \(\nabla _y^2g_i(x_{i,k},y_i^*(x_{i,k}))v = \nabla _y f_i(x_{i,k},y_i^*(x_{i,k}))\) in the AID-based approach in Algorithm 2. Note that \(v_{i,k}^*\) is a function of \(x_{i,k}\), and it is \((\kappa ^2 + \frac{2L_{f,0}L}{\mu ^2} + \frac{2L_{f,0}L\kappa }{\mu ^2})\)-Lipschitz continuous with respect to \(x_{i,k}\) [13]. For each term in \(B_K\), we have:
$$\begin{aligned}&\Vert v_{i,j}^* - v_{i,j}^{(0)}\Vert ^2 \\&\quad \le 2(\Vert v_{i,j-1}^* - v_{i,j-1}^{(N)}\Vert ^2 + \Vert v_{i,j}^* - v_{i,j-1}^*\Vert ^2 ) \\&\quad \le 4(1+\sqrt{\kappa })^2\left( \kappa + \frac{L_{g, 2} L_{f,0}}{\mu ^2}\right) ^2\Vert y_{i,j-1}^{(T)} - y_i^*(x_{i,j-1})\Vert ^2 \\&\qquad + 4\kappa \left( \frac{\sqrt{\kappa } - 1}{\sqrt{\kappa } + 1}\right) ^{2N}\Vert v_{i,j-1}^* - v_{i,j-1}^{(0)}\Vert ^2 + 2\left( \kappa ^2 + \frac{2L_{f,0}L(1+\kappa )}{\mu ^2}\right) ^2 \Vert x_{i,j} - x_{i,j-1}\Vert ^2, \end{aligned}$$
where the second inequality follows [13, Lemma 4]. Taking summation over i, j, we get
$$\begin{aligned} \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert v_{i,j}^* - v_{i,j}^{(0)}\Vert ^2\le d_1 A_{K-1} + 4\kappa \delta _\kappa ^N B_{K-1} + d_2E_K\le d_1 A_{K-1} + \frac{1}{2}B_{K} + d_2E_K, \end{aligned}$$
(18)
where the last inequality holds since we pick N such that \(4\kappa \delta _\kappa ^N <\frac{1}{2}\). Therefore, we can get:
$$\begin{aligned} B_K\le c_2 + d_1 A_{K-1} + \frac{1}{2}B_{K} + d_2E_K\quad \Rightarrow \quad B_K\le 2c_2 + 2d_1A_{K-1} + 2d_2E_K, \end{aligned}$$
which completes the proof. \(\square\)
The following lemmas give bounds on \(\sum \Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\) in (13).We first consider the case when the Assumption 2.3 holds. In this case, the outer loop computes the hypergradient via AID based approach. Therefore, we borrow [13, Lemma 3] and restate it as follows.
Lemma 11
[13, Lemma 3] Suppose Assumptions 2.1 and 2.3 hold, then we have:
$$\begin{aligned}&\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)}) - \nabla f_i(x_{i,j}, y_i^*(x_{i,j})) \Vert ^2\\&\hspace{6em}\le \Gamma \Vert y_i^*(x_{i,j}) - y_{i, j}^{(T)}\Vert ^2 + 6L^2\kappa \left( \frac{\sqrt{\kappa } -1 }{\sqrt{\kappa } + 1}\right) ^{2N}\Vert v_{i,j}^* - v_{i,j}^{(0)}\Vert ^2 \end{aligned}$$
where the constant \(\Gamma\) is
$$\begin{aligned} \Gamma = 3L^2 + \frac{3L_{g,2}^2L_{f,0}}{\mu ^2} + 6L^2(1+\sqrt{\kappa })^2\left( \kappa + \frac{L_{g,2}L_{f,0}}{\mu ^2}\right) ^2=\Theta (\kappa ^3). \end{aligned}$$
Next, we bound \(\sum \Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\) under Assumption 2.3.
Lemma 12
Suppose Assumptions 2.1 and 2.3 hold. We have:
$$\begin{aligned} \begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 \le \frac{2L_{\Phi }^2}{n}S_K + \frac{2\Gamma }{n}A_K + \frac{12L^2\kappa }{n}\delta _\kappa ^NB_K. \end{aligned} \end{aligned}$$
(19)
Proof
Under Assumption 2.3 we know \(g_i = g\), and thus from (5) and (6) we have
$$\begin{aligned} \nabla \Phi _i({{\bar{x}}}_k) = \nabla f_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k)). \end{aligned}$$
Therefore, we have
$$\begin{aligned}&\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 = \frac{1}{n^2}\left\| \sum _{i=1}^{n}\left( {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla f_i({{\bar{x}}}_k, y^*(\bar{x}_k))\right) \right\| ^2 \\&\quad \le \frac{1}{n}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla f_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k))\Vert ^2 \\&\quad \le \frac{2}{n}\sum _{i=1}^n( \Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla f_i(x_{i,k}, y_i^*(x_{i,k}) )\Vert ^2 \\&\qquad +\, \Vert \nabla f_i(x_{i,k}, y_i^*(x_{i,k})) - \nabla f_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k)) \Vert ^2 ) \\&\quad \le \frac{2}{n}\sum _{i=1}^n (\Gamma \Vert y_i^*(x_{i,k}) - y_{i, k}^{(T)}\Vert ^2 + 6L^2\kappa \delta _\kappa ^N\Vert v_{i,k}^* - v_{i,k}^{(0)}\Vert ^2 + L_{\Phi }^2\Vert x_{i,k} - {{\bar{x}}}_k\Vert ^2) \\&\quad \le \frac{2\Gamma }{n}\sum _{i=1}^n\Vert y_i^*(x_{i,k}) - y_{i, k}^{(T)}\Vert ^2 + \frac{12L^2\kappa }{n}\delta _\kappa ^N\sum _{i=1}^{n}\Vert v_{i,k}^* - v_{i,k}^{(0)}\Vert ^2 + \frac{2L_{\Phi }^2}{n}\Vert Q_k\Vert ^2 , \end{aligned}$$
where the first inequality follows from the convexity of \(\Vert \cdot \Vert ^2\), the third inequality follows from Lemma 11 and Assumption 2.3, the last inequality is by Lemma 5:
$$\begin{aligned} \Vert \nabla f_i(x_{i,k}, y^*(x_{i,k})) - \nabla f_i({{\bar{x}}}_k, y^*(\bar{x}_k)) \Vert ^2=\Vert \nabla \Phi _i(x_{i,k}) - \nabla \Phi _i({{\bar{x}}}_k)\Vert ^2 \le L_{\Phi }^2\Vert q_{i,k}\Vert ^2. \end{aligned}$$
Taking summation on both sides, we get:
$$\begin{aligned} \sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 \le \frac{2L_{\Phi }^2}{n}S_K + \frac{2\Gamma }{n}A_K + \frac{12L^2\kappa }{n}\delta _\kappa ^NB_K. \end{aligned}$$
\(\square\)
We now consider the case when Assumption 2.3 does not hold. In this case, our target in the lower level problem is
$$\begin{aligned} y^*({{\bar{x}}}_k) = \mathop {\mathrm {arg\,min}}\limits _{y}\frac{1}{n}\sum _{i=1}^{n}g_i({{\bar{x}}}_k, y). \end{aligned}$$
(20)
However, the update in our decentralized algorithm (e.g. line 8 of Algorithm 3) aims at solving
$$\begin{aligned} {\tilde{y}}_k^* := \mathop {\mathrm {arg\,min}}\limits _{y}\frac{1}{n}\sum _{i=1}^{n}g_i(x_{i,k}, y), \end{aligned}$$
(21)
which is completely different from our target (20). To resolve this problem, we introduce the following lemma to characterize the difference:
Lemma 13
The following inequality holds:
$$\begin{aligned} \Vert {\tilde{y}}_k^* - y^*({{\bar{x}}}_k)\Vert \le \frac{\kappa }{n}\sum _{i=1}^{n}\Vert x_{i,k} - {{\bar{x}}}_k\Vert \le \frac{\kappa }{\sqrt{n}} \Vert Q_k\Vert . \end{aligned}$$
Proof
By optimality conditions of (20) and (21), we have:
$$\begin{aligned} \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,k}, {\tilde{y}}_k^*) = 0,\quad \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, y^*(\bar{x}_k)) = 0. \end{aligned}$$
Combining with the strongly convexity and the smoothness of \(g_i\) yields:
$$\begin{aligned}&\left\| \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, {\tilde{y}}_k^*)\right\| \\&\quad = \left\| \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, {\tilde{y}}_k^*) - \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k))\right\| \ge \mu \Vert {\tilde{y}}_k^* - y^*({{\bar{x}}}_k)\Vert , \\&\left\| \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, {\tilde{y}}_k^*)\right\| \\&\quad = \left\| \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i({{\bar{x}}}_k, {\tilde{y}}_k^*) - \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,k}, {\tilde{y}}_k^*) \right\| \le \frac{L}{n}\sum _{i=1}^{n}\Vert x_{i,k} - {{\bar{x}}}_k\Vert . \end{aligned}$$
Therefore, we obtain the following inequality:
$$\begin{aligned} \Vert {\tilde{y}}_k^* - y^*({{\bar{x}}}_k)\Vert \le \frac{\kappa }{n} \sum _{i=1}^{n}\Vert x_{i,k} - {{\bar{x}}}_k\Vert =\frac{\kappa }{n} \sum _{i=1}^{n}\Vert q_{i,k}\Vert \le \frac{\kappa }{\sqrt{n}} \Vert Q_k\Vert , \end{aligned}$$
where the last inequality is by Cauchy–Schwarz inequality. \(\square\)
Notice that in the inner loop of Algorithms 3, 4 and 5, i.e., Lines 4–11 of Algorithms 3 and 4, and Lines 4–10 of Algorithm 5, \(y_{i,k}^{(T)}\) converges to \({\tilde{y}}_k^*\) and the rates are characterized by [34, 36, 46, 55] (e.g., Corollary 4.7. in [55], Theorem 10 in [35] and Theorem 1 in [46]). We include all the convergence rates here.
Lemma 14
Suppose Assumption 2.3 does not hold. We have:
Here \(C_1, C_2\) are positive constants and \(\alpha _1\in (0,1)\).
Besides, the JHIP oracle (Algorithm 1) also performs standard decentralized optimization with gradient tracking in deterministic case (Algorithms 3, 4) and stochastic case (Algorithm 5). We have:
Lemma 15
In Algorithm 1, we have:
-
For deterministic case, there exists a constant \(\gamma\) such that if \(\gamma _t \equiv \gamma\) then
$$\begin{aligned} \Vert Z_i^{(t)}-Z^*\Vert ^2 \le C_3\alpha _2^t.\quad \text {(See }[34]\text {).} \end{aligned}$$
-
For stochastic case and there exists a diminishing stepsize sequence \(\gamma _t = {\mathcal {O}}(\frac{1}{t})\), such that
$$\begin{aligned} \frac{1}{n}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert Z_i^{(t)}-Z^*\Vert ^2\right] \le \frac{C_4}{t}.\quad \text {(See }[36]\text {)}. \end{aligned}$$
Here \(C_3, C_4\) are positive constant, and \(\alpha _2\in (0,1)\). Here the optimal solution is denoted by \((Z^*)^{{\textsf{T}}}= \left( \sum _{i=1}^{n}J_i\right) \left( \sum _{i=1}^{n}H_i\right) ^{-1}\).
For simplicity we define:
$$\begin{aligned} C = \max \left( C_1,C_2,C_3,C_4\right) ,\quad \alpha = \max \left( \alpha _1,\alpha _2\right) . \end{aligned}$$
Since the objective functions mentioned in Lemma 14 (the lower level function g) and 15 (the objective in (9)) are strongly convex, we know C and \(\alpha\) only depend on \(L, \mu , \rho\) and the stepsize (only when it is a constant). For example \(\alpha _2\) in Lemma 15 only depends on the spectral radius of \(H_i\), smallest eigenvalue of \(H_i\), \(\rho\) and \(\gamma\).
For heterogeneous data (i.e., no Assumption 2.3) on g we have a different error estimation. We first notice that for each JHIP oracle, the following lemma holds:
Lemma 16
Suppose Assumptions 2.1 holds. In Algorithm 3 and 4 we have:
$$\begin{aligned}&\Vert \left( Z_{k}^*\right) ^{{\textsf{T}}}- \nabla _{xy} g({{\bar{x}}}_k, {\tilde{y}}_k^*)\left( \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right) ^{-1}\Vert _2^2\\&\hspace{10em}\le \frac{2L_{g,2}^2(1 + \kappa ^2)}{\mu ^2}\left( \frac{1}{n}\Vert Q_k\Vert ^2 + \frac{1}{n}\sum _{j=1}^{n}\Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2\right) , \end{aligned}$$
where \(Z_{k}^*\) denotes the optimal solution of Algorithm 1 in iteration k:
$$\begin{aligned} \left( Z_{k}^*\right) ^{{\textsf{T}}}= \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _{xy} g_j(x_{j,k}, y_{j,k}^{(T)})\right) \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\right) ^{-1}. \end{aligned}$$
Proof
Notice that we have
$$\begin{aligned}&\Vert \left( Z_{k}^*\right) ^{{\textsf{T}}}- \nabla _{xy} g({{\bar{x}}}_k, {\tilde{y}}_k^*)\left[ \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right] ^{-1}\Vert _2^2 \\&\quad \le 2\left\| \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _{xy} g_j(x_{j,k}, y_{j,k}^{(T)}) - \nabla _{xy} g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right) \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\right) ^{-1}\right\| _2^2 \\&\qquad +\,2\left\| \nabla _{xy} g({{\bar{x}}}_k, {\tilde{y}}_k^*)\left[ \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\right) ^{-1} -\left( \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right) ^{-1}\right] \right\| _2^2 \\&\quad \le \frac{2L_{g,2}^2}{n\mu ^2}\sum _{j=1}^{n}(\Vert x_{j,k} - {{\bar{x}}}_k\Vert ^2 + \Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2) \\&\qquad +\, \frac{2L_{g,1}^2L_{g,2}^2}{n\mu ^4}\sum _{j=1}^{n}(\Vert x_{j,k} - {{\bar{x}}}_k\Vert ^2 + \Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2) \\&\quad \le \frac{2L_{g,2}^2(1 + \kappa ^2)}{\mu ^2}\left( \frac{1}{n}\Vert Q_k\Vert ^2 + \frac{1}{n}\sum _{j=1}^{n}\Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2\right) \end{aligned}$$
where the second inequality holds due to Assumption 2.1 and the following inequality:
$$\begin{aligned}&\left\| \left( \frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\right) ^{-1} -\left( \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right) ^{-1}\right\| _2^2 \\&\quad =\bigg \Vert \bigg (\frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\bigg )^{-1}\cdot \\&\qquad \bigg (\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*) - \frac{1}{n}\sum _{j=1}^{n}\nabla _y^2g_j(x_{j,k}, y_{j,k}^{(T)})\bigg )\left( \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)\right) ^{-1}\bigg \Vert _2^2 \\&\quad \le \frac{L_{g,2}^2}{n\mu ^4}\sum _{j=1}^{n}(\Vert x_{j,k} - \bar{x}_k\Vert ^2 + \Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2). \end{aligned}$$
\(\square\)
Lemma 17
Suppose Assumption 2.1 holds. In Algorithm 3 and 4 we have:
$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)\Vert ^2 \nonumber \\&\quad \le \frac{18L_{f,0}^2L_{g,2}^2(1 + \kappa ^2)}{n\mu ^2}\Vert Q_k\Vert ^2 + \frac{6L_{f,0}^2}{n}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2 \nonumber \\&\quad +\, \left( 6 + 6L^2\kappa ^2 + \frac{12L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \left( \frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - \tilde{y}_k^*\Vert ^2\right) . \end{aligned}$$
(22)
Proof
Note that
$$\begin{aligned} {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)})&= \nabla _x f_i(x_{i,k},y_{i,k}^{(T)}) -\left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}), \\ {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)&= \nabla _x f_i(x_{i,k}, {\tilde{y}}_k^*) - \nabla _{xy} g(x_{i,k}, {\tilde{y}}_k^*)\nabla _y^2g(x_{i,k}, {\tilde{y}}_k^*)^{-1}\nabla _yf_i(x_{i,k},{\tilde{y}}_k^*). \end{aligned}$$
Then we know
$$\begin{aligned}&{\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)\\&\quad = \nabla _x f_i(x_{i,k},y_{i,k}^{(T)}) - \nabla _x f_i(x_{i,k}, {\tilde{y}}_k^*) \\&\qquad - \left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}) + \left( Z_{k}^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}) \\&\qquad - \left( Z_{k}^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}) + \left( Z_{k}^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},{\tilde{y}}_k^*) \\&\qquad - \left( Z_{k}^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},{\tilde{y}}_k^*) + \nabla _{xy} g({{\bar{x}}}_k,{\tilde{y}}_k^*)\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}\nabla _y f_i(x_{i,k}, {\tilde{y}}_k^*) \\&\qquad - \nabla _{xy} g({{\bar{x}}}_k,{\tilde{y}}_k^*)\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}\nabla _y f_i(x_{i,k}, {\tilde{y}}_k^*) \\&\qquad + \nabla _{xy} g(x_{i,k}, {\tilde{y}}_k^*)\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}\nabla _y f_i(x_{i,k},{\tilde{y}}_k^*) \\&\qquad -\nabla _{xy} g(x_{i,k}, {\tilde{y}}_k^*)\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}\nabla _y f_i(x_{i,k},{\tilde{y}}_k^*) \\&\qquad + \nabla _{xy} g(x_{i,k}, {\tilde{y}}_k^*)\nabla _y^2g(x_{i,k}, {\tilde{y}}_k^*)^{-1}\nabla _y f(x_{i,k},{\tilde{y}}_k^*), \end{aligned}$$
which gives
$$\begin{aligned}&\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)\Vert ^2 \\&\quad \le 6 \left(\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2 + L_{f,0}^2\Vert Z_{i,k}^{(N)} - Z_{k}^*\Vert ^2 + L^2\Vert \left( Z_{k}^*\right) ^{{\textsf{T}}}\Vert _2^2\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2 \right. \\&\left. \qquad +L_{f,0}^2\Vert \left( Z_{k}^*\right) ^{{\textsf{T}}}- \nabla _{xy} g({{\bar{x}}}_k, {{\tilde{y}}}_k^*)\nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}\Vert _2^2 + \frac{L_{g,2}^2L_{f,0}^2}{\mu ^2}\Vert x_{i,k} - {{\bar{x}}}_k\Vert ^2 \right. \\&\left. \qquad + L^2L_{f,0}^2\Vert \nabla _y^2g({{\bar{x}}}_k, {\tilde{y}}_k^*)^{-1}- \nabla _y^2g(x_{i,k}, {\tilde{y}}_k^*)^{-1}\Vert _2^2 \right) \\&\quad \le 6 \left(\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2 + L_{f,0}^2\Vert Z_{i,k}^{(N)} - Z_{k}^*\Vert ^2 + \frac{L^4}{\mu ^2}\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2 \right. \\& \left. \qquad + \frac{2L_{f,0}^2L_{g,2}^2(1 + \kappa ^2)}{\mu ^2}\left( \frac{1}{n}\Vert Q_k\Vert ^2 + \frac{1}{n}\sum _{j=1}^{n}\Vert y_{j,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2\right)\right. \\&\left. \qquad + \frac{L_{g,2}^2L_{f,0}^2}{\mu ^2}\Vert x_{i,k}-{{\bar{x}}}_k\Vert ^2 + \frac{L^2L_{f,0}^2L_{g,2}^2}{\mu ^4}\Vert x_{i,k} - {{\bar{x}}}_k\Vert ^2 \right). \end{aligned}$$
The second inequality uses Lemma 16, Assumption 2.1. Taking summation on both sides and using Lemma 15, we know
$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)\Vert ^2 \\&\quad \le \frac{18L_{f,0}^2L_{g,2}^2(1 + \kappa ^2)}{n\mu ^2}\Vert Q_k\Vert ^2 + \frac{6L_{f,0}^2}{n}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2 \\&\qquad + \left( 6 + 6L^2\kappa ^2 + \frac{12L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \left( \frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - \tilde{y}_k^*\Vert ^2\right) . \end{aligned}$$
\(\square\)
Lemma 18
Suppose Assumption 2.3 does not hold, then in Algorithms 3 and 4 we have:
$$\begin{aligned} \begin{aligned}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 &\le \frac{(1+\kappa ^2)}{n} \cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \Vert Q_k\Vert ^2 \\&\quad +12C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] . \end{aligned} \end{aligned}$$
(23)
Proof
We have
$$\begin{aligned}&\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 = \frac{1}{n^2}\left\| \sum _{i=1}^{n}\left( {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla f_i({{\bar{x}}}_k, y^*(\bar{x}_k))\right) \right\| ^2 \nonumber \\&\quad \le \frac{1}{n}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla f_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k))\Vert ^2 \nonumber \\&\quad \le \frac{2}{n}\sum _{i=1}^n( \Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) - {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*))\Vert ^2 + \Vert {\bar{\nabla }} f_i(x_{i,k}, {\tilde{y}}_k^*)- \nabla f_i({{\bar{x}}}_k, y^*({{\bar{x}}}_k)) \Vert ^2) \nonumber \\&\quad \le \frac{36L_{f,0}^2L_{g,2}^2(1 + \kappa ^2)}{n\mu ^2}\Vert Q_k\Vert ^2 \nonumber \\&\qquad + 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - {{\tilde{y}}}_k^*\Vert ^2 \nonumber \\&\qquad + \frac{12L_{f,0}^2}{n}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2 + \frac{2}{n}\sum _{i=1}^{n}(L_{f}^2\Vert x_{i,k} - \bar{x}_k\Vert ^2 + L_{f}^2\Vert {\tilde{y}}_k^* - y^*({{\bar{x}}}_k)\Vert ^2) \nonumber \\&\quad \le 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - {{\tilde{y}}}_k^*\Vert ^2 \nonumber \\&\qquad + \frac{12L_{f,0}^2}{n}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2 + \frac{(1+\kappa ^2)}{n}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \Vert Q_k\Vert ^2, \end{aligned}$$
(24)
where the third inequality is due to Lemma 17 and Lemma 6, and the fourth inequality is by Lemma 13. Notice that \(\frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2\) in the first term denotes the error of the inner loop iterates. In both DBO (Algorithm 3) and DBOGT (Algorithm 4), the inner loop performs a decentralized gradient descent with gradient tracking. By Lemmas 14 and 15, we have the error bounds \(\frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - {\tilde{y}}_k^*\Vert ^2\le C\alpha ^T\) and \(\frac{1}{n}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2\le C\alpha ^N\), which complete the proof. \(\square\)
1.1 Proof of the DBO convergence
In this section we will prove the following convergence result of the DBO algorithm:
Theorem 19
In Algorithm 3, suppose Assumptions 2.1 and 2.2 hold. If Assumption 2.3 holds, then by setting \(0<\eta _x\le \frac{1-\rho }{130L_{\Phi }},\ 0<\eta _y< \frac{2}{\mu + L},\ T=\Theta (\kappa \log \kappa ),\ N=\Theta (\sqrt{\kappa }\log \kappa )\), we have:
$$\begin{aligned}&\frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 \le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x))+ \eta _x^2\cdot \frac{1272L_{\Phi }^2L_{f,0}^2(1+\kappa )^2}{(1-\rho )^2} + \frac{C_1}{K+1}. \end{aligned}$$
If Assumption 2.3 does not hold, then by setting \(0< \eta _x\le \frac{1}{L_{\Phi }}, \eta _y^{(t)} = {\mathcal {O}}(\frac{1}{t})\), we have:
$$\begin{aligned}\frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi (\bar{x}_j)\Vert ^2 &\le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) \\&\quad + \eta _x^2\left( \frac{18L_{f,0}^2L_{g,2}^2}{\mu ^2} + L_{f}^2\right) \frac{4(1+\kappa ^2)((1+\kappa )^2 + C\alpha ^N)L_{f,0}^2 }{(1-\rho )^2}+ \tilde{C_1}, \end{aligned}$$
where \(C_1 = \Theta (1), C = \Theta (1)\) and \(\tilde{C_1} = {\mathcal {O}}(\alpha ^T + \alpha ^N)\).
We first consider bounding the consensus error estimation for DBO:
Lemma 20
In Algorithm 3, we have
$$\begin{aligned} S_{K}:= \sum _{k=1}^{K}\Vert Q_k\Vert ^2< \frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2. \end{aligned}$$
Proof
Note that the x update can be written as
$$\begin{aligned} X_k = X_{k-1}W - \eta _x\partial \Phi (X_{k-1}), \end{aligned}$$
which indicates
$$\begin{aligned} {{\bar{x}}}_k = {{\bar{x}}}_{k-1} - \eta _x\overline{\partial \Phi (X_{k-1})}. \end{aligned}$$
By definition of \(q_{i,k}\), we have
$$\begin{aligned} q_{i,k+1}&= \sum _{j=1}^{n}w_{ij}x_{j,k} - \eta _x {\hat{\nabla }}f(x_{i,k}, y_{i,k}^{(T)}) - ({{\bar{x}}}_k - \eta _x\overline{\partial \Phi (X_k)} ) \\&=\sum _{j=1}^{n}w_{ij}(x_{j,k} - {{\bar{x}}}_k) - \eta _x({\hat{\nabla }}f(x_{i,k}, y_{i,k}^{(T)}) - \overline{\partial \Phi (X_k)}) \\&= Q_kWe_i - \eta _x\partial \Phi (X_k)\left( e_i - \frac{{\textbf{1}}_n}{n} \right) , \end{aligned}$$
where the last equality uses the fact that W is symmetric. Therefore, for \(Q_{k+1}\) we have
$$\begin{aligned} Q_{k+1}&= Q_kW - \eta _x\partial \Phi (X_k)\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \\&=\left( Q_{k-1}W - \eta _x\partial \Phi (X_{k-1})\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \right) W - \eta _x\partial \Phi (X_k)\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \\&=Q_0W^{k+1} - \eta _x\sum _{i=0}^{k}\left( \partial \Phi (X_{i})\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) W^{k-i}\right) \\&=-\eta _x\sum _{i=0}^{k}\partial \Phi (X_{i})\left( W^{k-i} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) , \end{aligned}$$
where the last equality is obtained by \(Q_0 = 0\) and \({\textbf{1}}_n{\textbf{1}}^{\top }_n W = {\textbf{1}}_n{\textbf{1}}^{\top }_n.\) By Cauchy–Schwarz inequality, we have the following estimate
$$\begin{aligned}&\Vert Q_{k+1}\Vert ^2 = \eta _x^2 \Vert \sum _{i=0}^{k} \partial \Phi (X_{i})\left( W^{k-i} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \Vert ^2\\&\quad \le \eta _x^2 \left( \sum _{i=0}^{k} \Vert \partial \Phi (X_{i})\left( W^{k-i} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \Vert \right) ^2 \\&\quad \le \eta _x^2 \left( \sum _{i=0}^{k} \Vert \partial \Phi (X_{i})\Vert \Vert \left( W^{k-i} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \Vert _2\right) ^2 \\&\quad \le \eta _x^2 \left( \sum _{i=0}^{k}\rho ^{k-i}\Vert \partial \Phi (X_i)\Vert ^2 \right) \left( \sum _{i=0}^{k}\frac{1}{\rho ^{k-i}}\left\| W^{k-i} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right\| _2^2\right) \\&\quad \le \eta _x^2 \left( \sum _{i=0s}^{k}\rho ^{k-i}\Vert \partial \Phi (X_i)\Vert ^2\right) \left( \sum _{i=0}^{k}\rho ^{k-i}\right) < \frac{\eta _x^2}{1-\rho }\left( \sum _{i=0}^{k}\rho ^{k-i}\Vert \partial \Phi (X_i)\Vert ^2\right) \\&\quad = \frac{\eta _x^2}{1-\rho }\left( \sum _{j=0}^{k}\rho ^{k-j}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2\right) = \frac{\eta _x^2}{1-\rho }\sum _{i=1}^{n}\sum _{j=0}^{k}\rho ^{k-j}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2. \end{aligned}$$
where the fourth inequality is obtained by Lemma 4. Summing the above inequality yields
$$\begin{aligned} S_K&= \sum _{k=0}^{K-1}\Vert Q_{k+1}\Vert ^2< \frac{\eta _x^2}{1-\rho }\sum _{k=0}^{K-1}\sum _{i=1}^{n}\sum _{j=0}^k\rho ^{k-j}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 \nonumber \\&=\frac{\eta _x^2}{1-\rho }\sum _{j=0}^{K-1}\sum _{i=1}^{n}\sum _{k=j}^{K-1}\rho ^{k-j}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2\nonumber \\&< \frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2, \end{aligned}$$
(25)
where the second equality holds since we can change the order of summation. \(\square\)
1.1.1 Case 1: Assumption 2.3 holds
We first consider the case when Assumption 2.3 holds.
Lemma 21
Suppose Assumptions 2.1 and 2.3 hold, then we have:
$$\begin{aligned} \Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2\le 2(L^2\kappa \delta _\kappa ^N\Vert v_{i,j}^{(0)}- v_{i,j}^*\Vert ^2 + (1+\kappa )^2L_{f,0}^2). \end{aligned}$$
Proof
Notice that we have:
$$\begin{aligned}&\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 \le 2\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)}) - {\bar{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 + 2\Vert {\bar{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 \\&\quad \le 2\Vert \nabla _{xy} g_i(x_{i,j},y_{i,j}^{(T)})(v_{i,j}^{(N)} - v_{i,j}^*)\Vert ^2 \\&\qquad + 2\Vert \nabla _x f_i(x_{i,j}, y_{i,j}^{(T)}) - \nabla _{xy} g_i(x_{i,j}, y_{i,j}^{(T)}) \left( \nabla _y^2g_i(x_{i,j}, y_{i,j}^{(T)})\right) ^{-1}\nabla _y f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 \\&\quad \le 2(L^2\Vert v_{i,j}^{(N)} - v_{i,j}^*\Vert ^2 + (L_{f,0} + \frac{L}{\mu }L_{f,0})^2)\le 2(L^2\kappa \delta _\kappa ^N\Vert v_{i,j}^{(0)}- v_{i,j}^*\Vert ^2 + (1+\kappa )^2L_{f,0}^2), \end{aligned}$$
where the second inequality is via the Assumption 2.1, and the last inequality is based on the convergence result of CG for the quadratic programming, e.g., eq. (17) in [24]. \(\square\)
Next we obtain the upper bound for \(S_K\).
Lemma 22
Suppose Assumptions 2.1 and 2.3 hold, then we have:
$$\begin{aligned} S_K < \frac{2\eta _x^2}{(1-\rho )^2} (L^2\kappa \delta _\kappa ^NB_{K-1} + nK(1+\kappa )^2L_{f,0}^2). \end{aligned}$$
Proof
By Lemmas 20 and 21, we have:
$$\begin{aligned} S_K <&\frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 \\ \le&\frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}2(L^2\kappa \delta _\kappa ^N\Vert v_{i,j}^{(0)}- v_{i,j}^*\Vert ^2 + (1+\kappa )^2L_{f,0}^2) \\ =&\frac{2\eta _x^2}{(1-\rho )^2} (L^2\kappa \delta _\kappa ^NB_{K-1} + nK(1+\kappa )^2L_{f,0}^2), \end{aligned}$$
which completes the proof. \(\square\)
We are ready to prove the main results in Theorem 19. We first summarize main results in Lemmas 22, 10 and 9:
$$\begin{aligned} S_{K}&< \frac{2\eta _x^2}{(1-\rho )^2} (L^2\kappa \delta _\kappa ^NB_{K-1} + nK(1+\kappa )^2L_{f,0}^2), \nonumber \\ A_K&\le 3\delta _y^T(c_1 + 2\kappa ^2E_K),\ B_K\le 2c_2 + 2d_1A_{K-1} + 2d_2E_K, \nonumber \\ E_K&\le 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}. \end{aligned}$$
(26)
The next lemma proves the first part of Theorem 19.
Lemma 23
Suppose the assumptions of Lemma 10 hold. Furthermore, if we set \(N = \Theta (\sqrt{\kappa }\log \kappa ), T=\Theta (\kappa \log \kappa ), \eta _x = {\mathcal {O}}(\kappa ^{-3})\) such that:
$$\begin{aligned}&\delta _{\kappa }^N<\min \left( \frac{L_{\Phi }^2}{L^2\kappa (4d_1\kappa ^2 + 2d_2)}, \kappa ^{-6}\right) =\Theta (\kappa ^{-6}),\\&\delta _y^T<\min \left( \frac{L_{\Phi }^2}{12\Gamma \kappa ^2}, \kappa ^{-5}, \frac{1}{3}\right) =\Theta (\kappa ^{-5}),\ \eta _x< \frac{1-\rho }{130L_{\Phi }}, \end{aligned}$$
we have:
$$\begin{aligned}&\frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 \le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \eta _x^2\cdot \frac{1272L_{\Phi }^2L_{f,0}^2(1+\kappa )^2}{(1-\rho )^2} + \frac{C_1}{K+1}, \end{aligned}$$
where the constant is given by:
$$\begin{aligned} C_1&= 106L_{\Phi }^2\cdot \frac{6\eta _x^2}{(1-\rho )^2}L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n}\\&= \Theta (\eta _x^2\delta _{\kappa }^{N}\kappa ^{12} + \kappa ^5\delta _y^T) = \Theta (1). \end{aligned}$$
Proof
For \(B_K\) we know:
$$\begin{aligned} B_K&\le 2c_2 + 2d_1A_K + 2d_2E_K \le 2c_2 + \frac{2}{3}d_1(3c_1 + 6\kappa ^2E_K) + 2d_2E_K \nonumber \\&= 2c_2 + 2d_1c_1 + (4d_1\kappa ^2 + 2d_2)E_K. \end{aligned}$$
(27)
We first eliminate \(B_K\) in the upper bound of \(S_K\). Pick N, T such that:
$$\begin{aligned} \delta _{\kappa }^N\cdot (4d_1\kappa ^2 + 2d_2)\cdot L^2\kappa<L_{\Phi }^2\quad \Rightarrow \quad \delta _{\kappa }^N< \frac{L_{\Phi }^2}{L^2\kappa (4d_1\kappa ^2 + 2d_2)}. \end{aligned}$$
(28)
Therefore, we have
$$\begin{aligned} S_K&\le \frac{2\eta _x^2}{(1-\rho )^2}(L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + L^2\kappa \delta _{\kappa }^N(4d_1\kappa ^2 + 2d_2)E_K + nK(1+\kappa )^2L_{f,0}^2) \\&\le \frac{2\eta _x^2}{(1-\rho )^2}(L_{\Phi }^2 E_K + L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2), \end{aligned}$$
where in the first inequality we use (27) to eliminate \(B_K\). Next we eliminate \(E_K\) in this bound. By the definition of \(\eta _x\), we know:
$$\begin{aligned} \eta _x<\frac{(1-\rho )}{4\sqrt{2}L_{\Phi }}\quad \Rightarrow \quad \frac{16\eta _x^2L_{\Phi }^2}{(1-\rho )^2}<\frac{1}{2}, \end{aligned}$$
which, together with (26), yields
$$\begin{aligned} S_{K}&\le \frac{2\eta _x^2}{(1-\rho )^2}(L_{\Phi }^2(8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}) \nonumber \\&\quad + L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2) \nonumber \\&< \frac{1}{2}S_K + \frac{2\eta _x^2}{(1-\rho )^2}(4n\eta _x^2L_{\Phi }^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2L_{\Phi }^2T_{K-1} \nonumber \\&\quad + L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2). \end{aligned}$$
(29)
The above inequality indicates
$$\begin{aligned} S_K&\le \,\frac{4\eta _x^2}{(1-\rho )^2}\left( 4n\eta _x^2L_{\Phi }^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2L_{\Phi }^2T_{K-1}\right) \nonumber \\&\quad +\, \frac{4\eta _x^2}{(1-\rho )^2}\left( L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2\right) . \end{aligned}$$
(30)
Note that we have
$$\begin{aligned} \delta _y^T<\frac{L_{\Phi }^2}{12\Gamma \kappa ^2}\quad \Rightarrow \quad \delta _y^T\cdot 6\kappa ^2\cdot 2\Gamma < L_{\Phi }^2. \end{aligned}$$
(31)
Define
$$\begin{aligned} \Lambda = \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n}. \end{aligned}$$
By Lemma 12,
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2\le \frac{2L_{\Phi }^2}{n}S_K + \frac{2\Gamma }{n}A_K + \frac{12L^2\kappa }{n}\delta _\kappa ^NB_K \\&\quad \le \frac{2L_{\Phi }^2}{n}S_K + \left( \frac{2\Gamma }{n}\cdot 6\kappa ^2\delta _y^T + \frac{12L^2\kappa }{n}\cdot \delta _{\kappa }^N\cdot (4d_1\kappa ^2 + 2d_2)\right) E_K \\&\qquad +\, \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 6d_1c_1\delta _y^T) + 6\Gamma c_1\delta _y^T}{n} \\&\quad \le \frac{2L_{\Phi }^2}{n}S_K + \left( \frac{L_{\Phi }^2}{n} + \frac{12L_{\Phi }^2}{n}\right) E_K + \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n} \\&\quad \le \frac{2L_{\Phi }^2}{n}S_K + \frac{13L_{\Phi }^2}{n}\left( 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}\right) + \Lambda \\&\quad < \frac{106L_{\Phi }^2}{n}S_K + 52\eta _x^2L_{\Phi }^2 \left( \sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_{K}\right) + \Lambda \\&\quad \le \left( \frac{106L_{\Phi }^2}{n}\cdot \frac{16nL_{\Phi }^2\eta _x^4}{(1-\rho )^2} + 52\eta _x^2L_{\Phi }^2\right) \left( \sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_K\right) \\&\qquad +\, \frac{106L_{\Phi }^2}{n}\cdot \frac{4\eta _x^2}{(1-\rho )^2}\left( L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2\right) + \Lambda , \end{aligned}$$
where the second inequality is by (26) and (27), the third inequality is by (28) and (31), the fourth inequality is obtained by (26) and the last inequality is by (30). Note that the definition of \(\eta _x\) also indicates:
$$\begin{aligned} 106L_{\Phi }^2\cdot \frac{16L_{\Phi }^2\eta _x^4}{(1-\rho )^2} + 52\eta _x^2L_{\Phi }^2 < \frac{1}{3}. \end{aligned}$$
Therefore,
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2<\frac{1}{3}\left( \sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + T_K\right) \\&\quad +\frac{106L_{\Phi }^2}{n}\cdot \frac{4\eta _x^2}{(1-\rho )^2}(L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + nK(1+\kappa )^2L_{f,0}^2) + \Lambda ,\\ \end{aligned}$$
which leads to
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\\&\quad \le \frac{1}{2}T_K + 106L_{\Phi }^2\cdot \frac{6\eta _x^2}{(1-\rho )^2}\left( \frac{L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)}{n} + K(1+\kappa )^2L_{f,0}^2\right) \\&\qquad +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n}. \end{aligned}$$
Combining this bound with (12), we can obtain
$$\begin{aligned} T_{K}&\le \frac{2}{\eta _x}(\Phi ({{\bar{x}}}_0) - \inf _{x}\Phi (x)) + \sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 \\&\le \frac{2}{\eta _x}(\Phi ({{\bar{x}}}_0) - \inf _{x}\Phi (x)) + \eta _x^2\cdot \frac{636L_{\Phi }^2L_{f,0}^2(1+\kappa )^2}{(1-\rho )^2}K + \frac{1}{2}T_K + \frac{1}{2}C_1, \end{aligned}$$
which implies
$$\begin{aligned}&\frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2\\&\quad \le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \eta _x^2\cdot \frac{1272L_{\Phi }^2L_{f,0}^2(1+\kappa )^2}{(1-\rho )^2} + \frac{C_1}{K+1}. \end{aligned}$$
The constant \(C_1\) satisfies
$$\begin{aligned} \frac{1}{2}C_1&= 106L_{\Phi }^2\cdot \frac{6\eta _x^2L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)}{n(1-\rho )^2} +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n}\\&= {\mathcal {O}}(\eta _x^2\delta _{\kappa }^{N}\kappa ^{12} + \kappa ^5\delta _y^T) = {\mathcal {O}}(1). \end{aligned}$$
Moreover, we notice that by setting
$$\begin{aligned} N = \Theta (\sqrt{\kappa }\log \kappa ),\ T=\Theta (\kappa \log \kappa ),\ \eta _x = \Theta (K^{-\frac{1}{3}}\kappa ^{-\frac{8}{3}}),\ \eta _y = \frac{1}{\mu + L}, \end{aligned}$$
for sufficiently large K the conditions on algorithm parameters in Lemma 23 hold and
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 = {\mathcal {O}}\left( \frac{\kappa ^{\frac{8}{3}}}{K^{\frac{2}{3}}}\right) , \end{aligned}$$
which proves the first case of Theorems 3.1 and 19. \(\square\)
1.1.2 Case 2: Assumption 2.3 does not hold
Now we consider the case when Assumption 2.3 does not hold.
Lemma 24
$$\begin{aligned} S_{K}< \frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\Vert ^2 < \frac{\eta _x^2L_{f,0}^2}{(1-\rho )^2}nK\left( 2(1+\kappa )^2 + 2C\alpha ^N\right) . \end{aligned}$$
Proof
The first inequality follows from Lemma 20. For the second one observe that:
$$\begin{aligned}&\Vert {\hat{\nabla }}f_i(x_{i,j},y_{i,j}^{(T)})\Vert = \left\| \nabla _x f_i(x_{i,k},y_{i,k}^{(T)}) -\left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)})\right\| \\&\quad \le \Vert \nabla _x f_i(x_{i,k},y_{i,k}^{(T)})\Vert + \Vert (Z_{i,k}^{(N)} - Z_k^*)^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)})\Vert + \Vert \left( Z_k^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)})\Vert \\&\quad \le \left( 1 + \left\| \left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}- \left( Z_k^*\right) ^{{\textsf{T}}}\right\| _2 + \kappa \right) L_{f,0}, \end{aligned}$$
where we use \(\left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\) to denote the output of Algorithm 1 in outer loop iteration k of agent i, and \(\left( Z_k^*\right) ^{{\textsf{T}}}\) denotes the optimal solution. By Cauchy–Schwarz inequality we know:
$$\begin{aligned} \Vert {\hat{\nabla }}f_i(x_{i,j},y_{i,j}^{(T)})\Vert ^2&\le (1+\kappa +\Vert \left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}- \left( Z_k^*\right) ^{{\textsf{T}}}\Vert _2)^2L_{f,0}^2\\&\le (2(1+\kappa )^2 + 2\Vert \left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}- \left( Z_k^*\right) ^{{\textsf{T}}}\Vert _2^2)L_{f,0}^2\\&\le (2(1+\kappa )^2+2C\alpha ^N)L_{f,0}^2, \end{aligned}$$
which completes the proof. \(\square\)
Taking summation on both sides of (23) and applying Lemma 24 we know:
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 \\&\quad \le \frac{(1+\kappa ^2)}{n}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) S_K \\&\qquad + 12(K+1)C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] \\&\quad \le \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \frac{(1+\kappa ^2)\eta _x^2L_{f,0}^2}{(1-\rho )^2}K(2(1+\kappa )^2 + 2C\alpha ^N) + (K+1){{\tilde{C}}}_1, \end{aligned}$$
where we define:
$$\begin{aligned} \tilde{C_1} = 12C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] = {\mathcal {O}}(\alpha ^T + \alpha ^N). \end{aligned}$$
The above inequality together with (12) gives
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\\&\quad \le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) + \frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\quad \le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) \\&\hspace{3em}+ \frac{4\eta _x^2(1+\kappa ^2)L_{f,0}^2 }{(1-\rho )^2}((1+\kappa )^2 + C\alpha ^N)\left( \frac{18L_{f,0}^2L_{g,2}^2}{\mu ^2} + L_{f}^2\right) + \tilde{C_1}. \end{aligned}$$
Moreover, if we choose
$$\begin{aligned} N = \Theta (\log K),\ T=\Theta (\log K),\ \eta _x = \Theta (K^{-\frac{1}{3}}\kappa ^{-\frac{8}{3}}),\ \eta _y^{(t)} = \Theta (1) \end{aligned}$$
then we can get:
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 = {\mathcal {O}}\left( \frac{\kappa ^{\frac{8}{3}}}{K^{\frac{2}{3}}}\right) , \end{aligned}$$
which proves the second case of Theorems 3.1 and 19.
1.2 Proof of the convergence of DBOGT
In this section we will prove the following convergence result of Algorithm 4
Theorem 25
In Algorithm 4, suppose Assumptions 2.1 and 2.2 hold. If Assumption 2.3 holds, then by setting \(0< \eta _x<\frac{(1-\rho )^2}{8L_{\Phi }},\ 0<\eta _y< \frac{2}{\mu + L},\ T = \Theta (\kappa \log \kappa ),\ N = \Theta (\sqrt{\kappa }\log \kappa )\), we have:
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2\le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \frac{C_2}{K+1}. \end{aligned}$$
If Assumption 2.3 does not hold, then by setting
$$\begin{aligned} 0<\eta _x<\min \left( \frac{(1-\rho )^2}{14\kappa L_f}, \frac{\mu (1-\rho )^2}{21L_{f,0}L_{g,2}\kappa }\right) ,\ \eta _y=\Theta (1), \end{aligned}$$
we have:
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi (\bar{x}_j)\Vert ^2\le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) +{\tilde{C}}_2. \end{aligned}$$
Here \(C_2 = \Theta (1)\) and \({\tilde{C}}_2 = \Theta (\alpha ^T + \alpha ^N + \frac{1}{K+1})\).
We first bound the consensus estimation error in the following lemma.
Lemma 26
In Algorithm 4, we have the following inequality holds:
$$\begin{aligned} S_K \le \frac{\eta _x^2}{(1-\rho )^4}\left(\sum _{j=1}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)}) \Vert ^2 + \Vert \partial \Phi (X_0)\Vert ^2\right). \end{aligned}$$
Proof
From the updates of x and u, we have:
$$\begin{aligned} {{\bar{u}}}_k = {{\bar{u}}}_{k-1} + \overline{\partial \Phi (X_k)} - \overline{\partial \Phi (X_{k-1})},\quad {{\bar{u}}}_0 = \overline{\partial \Phi (X_0)},\quad {{\bar{x}}}_{k+1} = {{\bar{x}}}_k - \eta _x{{\bar{u}}}_k, \end{aligned}$$
which implies:
$$\begin{aligned} {{\bar{u}}}_k = \overline{\partial \Phi (X_k)},\quad {{\bar{x}}}_{k+1} = \bar{x}_k - \eta _x\overline{\partial \Phi (X_k)}. \end{aligned}$$
Hence by definition of \(q_{i,k+1}\):
$$\begin{aligned} q_{i,k+1} =&\, x_{i,k+1} - {{\bar{x}}}_{k+1} =\sum _{j=1}^{n}w_{ij}x_{j,k} - \eta _x u_{i,k} - {{\bar{x}}}_k + \eta _x{{\bar{u}}}_k\\ =&\sum _{j=1}^{n}w_{ij}(x_{j,k} - {{\bar{x}}}_k) - \eta _x(u_{i,k} - {{\bar{u}}}_k)\\ =&\sum _{j=1}^{n}w_{ij}q_{j,k} - \eta _xr_{i,k} =Q_{k}We_i - \eta _x R_k e_i. \\ \end{aligned}$$
Therefore, we can write the update of the matrix \(Q_{k+1}\) as
$$\begin{aligned} Q_{k+1} = Q_kW - \eta _x R_k,\quad Q_1 = -\eta _x R_0. \end{aligned}$$
Note that \(Q_{k+1}\) takes the form of
$$\begin{aligned} Q_{k+1} = (Q_{k-1}W - \eta _x R_{k-1})W - \eta _x R_k = -\eta _x\sum _{i=0}^{k}R_iW^{k-i}. \end{aligned}$$
(32)
We then compute \(r_{i,k}\) as following
$$\begin{aligned}&r_{i,k+1} = u_{i,k+1} - {{\bar{u}}}_{k+1} \\&\quad = \sum _{j=1}^{n}w_{ij}u_{j,k} + {\hat{\nabla }} f_i(x_{i,k+1},y_{i,k+1}^{(T)}) - {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)}) - {{\bar{u}}}_k - (\overline{\partial \Phi (X_{k+1})} - \overline{\partial \Phi (X_{k})})\\&\quad =\sum _{j=1}^{n}w_{ij}(u_{j,k} - {{\bar{u}}}_k) + (\partial \Phi (X_{k+1}) - \partial \Phi (X_{k}))\left( e_i - \frac{{{\textbf {1}}}_n}{n}\right) \\&\quad = R_kWe_i + (\partial \Phi (X_{k+1}) - \partial \Phi (X_{k}))\left( e_i - \frac{{{\textbf {1}}}_n}{n}\right) . \end{aligned}$$
The matrix \(R_{k+1}\) can be written as
$$\begin{aligned} R_{k+1}&= R_kW + (\partial \Phi (X_{k+1}) - \partial \Phi (X_{k}))(I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}) \nonumber \\&=R_0W^{k+1} + \sum _{j=0}^k(\partial \Phi (X_{j+1}) - \partial \Phi (X_{j}))\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) W^{k-j} \nonumber \\&=\partial \Phi (X_0)\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) W^{k+1} + \sum _{j=0}^k(\partial \Phi (X_{j+1}) - \partial \Phi (X_{j}))\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) W^{k-j} \nonumber \\&=\sum _{j=0}^{k+1}(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1}))\left( I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) W^{k+1-j}, \end{aligned}$$
(33)
where the third equality holds because of the initialization \(u_{i,0} = {\hat{\nabla }} f_i(x_{i,0},y_{i,0}^{(T)})\) and we denote \(\partial \Phi (X_{-1})=0\). Plugging (33) into (32) yields
$$\begin{aligned} Q_{k+1}&= -\eta _x\sum _{i=0}^{k}\sum _{j=0}^{i}(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1})) \left(I - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n} \right)W^{k-j} \\&=-\eta _x\sum _{j=0}^{k}\sum _{i=j}^{k}(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1})) \left(W^{k-j} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n} \right) \\&=-\eta _x\sum _{j=0}^{k}(k+1-j)(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1})) \left(W^{k-j} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n} \right), \end{aligned}$$
where the second equality is obtained by \({\textbf{1}}_n{\textbf{1}}^{\top }_n W = {\textbf{1}}_n{\textbf{1}}^{\top }_n\) and switching the order of the summations. Therefore, we have
$$\begin{aligned}\Vert Q_{k+1}\Vert ^2 &= \eta _x^2\left\| \sum _{j=0}^{k}(k+1-j)(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1}))\left( W^{k-j} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \right\| ^2 \nonumber \\& \le \eta _x^2\left( \sum _{j=0}^k\left\| (k+1-j)(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1}))\left( W^{k-j} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right) \right\| \right) ^2 \nonumber \\& \le \eta _x^2\left( \sum _{j=0}^k\left\| (k+1-j)(\partial \Phi (X_{j}) - \partial \Phi (X_{j-1}))\right\| \left\| W^{k-j} - \frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right\| _2\right) ^2 \nonumber \\& \le \eta _x^2 \left( \sum _{j=0}^{k} \rho ^{k-j}(k+1-j)\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2\right) \cdot \nonumber \\&\qquad \left( \sum _{j=0}^{k}\frac{(k+1-j)}{\rho ^{k-j}}\left\| W^{k-j}-\frac{{\textbf{1}}_n{\textbf{1}}^{\top }_n}{n}\right\| _2^2\right) \nonumber \\& \le \eta _x^2\left( \sum _{j=0}^{k} \rho ^{k-j}(k+1-j)\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2\right) \left( \sum _{j=0}^{k}(k+1-j)\rho ^{k-j}\right) \nonumber \\& < \frac{\eta _x^2}{(1-\rho )^2}\left( \sum _{j=0}^{k} \rho ^{k-j}(k+1-j)\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2\right) , \end{aligned}$$
(34)
where the second inequality is by Lemma 1, the third inequality is by Lemma 4, and the last inequality uses the fact that:
$$\begin{aligned} \sum _{j=0}^{k}(k+1-j)\rho ^{k-j} = \sum _{m=0}^{k}(m+1)\rho ^m = \frac{1 - (k+2)\rho ^{k+1} + (k+1)\rho ^{k+2}}{(1-\rho )^2}<\frac{1}{(1-\rho )^2}. \end{aligned}$$
(35)
Summing (34) over \(k=0,\ldots , K-1\), we get:
$$\begin{aligned} S_K&= \sum _{k=0}^{K-1}\Vert Q_{k+1}\Vert ^2\\&\le \frac{\eta _x^2}{(1-\rho )^2}\left( \sum _{k=0}^{K-1}\sum _{j=0}^{k} \rho ^{k-j}(k+1-j)\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2\right) \\&=\frac{\eta _x^2}{(1-\rho )^2}\left( \sum _{j=0}^{K-1}\sum _{k=j}^{K-1} \rho ^{k-j}(k+1-j)\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2\right) \\&<\frac{\eta _x^2}{(1-\rho )^4}\sum _{j=0}^{K-1}\Vert \partial \Phi (X_{j}) - \partial \Phi (X_{j-1})\Vert ^2 \\&= \frac{\eta _x^2}{(1-\rho )^4}\left( \sum _{j=1}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)}) \Vert ^2 + \Vert \partial \Phi (X_0)\Vert ^2\right) , \\ \end{aligned}$$
which completes the proof. \(\square\)
1.2.1 Case 1: Assumption 2.3 holds
When Assumption 2.3 holds, we have the following lemmas.
Lemma 27
Under Assumption 2.3, the following inequality holds for Algorithm 4:
$$\begin{aligned}&\sum _{j=1}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)})\Vert ^2\\&\hspace{6em}\le 6\Gamma A_{K-1} + 36L^2\kappa \delta _\kappa ^NB_{K-1} + 3L_{\Phi }^2E_{K-1}. \end{aligned}$$
Moreover, we have:
$$\begin{aligned} S_K \le \frac{\eta _x^2}{(1-\rho )^4}(6\Gamma A_{K-1} + 36L^2\kappa \delta _\kappa ^NB_{K-1} + 3L_{\Phi }^2E_{K-1} + \Vert \partial \Phi (X_0)\Vert ^2). \end{aligned}$$
Proof
For each term, we know that for \(j\ge 1\):
$$\begin{aligned}&\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)}) \Vert ^2 \\&\quad \le 3(\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - \nabla \Phi _i(x_{i,j})\Vert ^2 + \Vert \nabla \Phi _i(x_{i,j}) - \nabla \Phi _i(x_{i,j-1}) \Vert ^2\\&\qquad + \Vert \nabla \Phi _i(x_{i,j-1}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)})\Vert ^2) \\&\quad \le 3(\Gamma (\Vert y_i^*(x_{i,j}) - y_{i, j}^{(T)}\Vert ^2 + \Vert y_i^*(x_{i,j-1}) - y_{i, j-1}^{(T)}\Vert ^2) \\&\qquad + 6L^2\kappa \delta _\kappa ^N(\Vert v_{i,j}^* - v_{i,j}^{(0)}\Vert ^2 + \Vert v_{i,j-1}^* - v_{i,j-1}^{(0)}\Vert ^2) + L_{\Phi }^2\Vert x_{i,j} - x_{i,j-1}\Vert ^2), \end{aligned}$$
where the last inequality uses Lemmas 11 and 5. Taking summation (\(j=1,2,\ldots ,K-1\) and \(i=1,2,\ldots ,n\)) on both sides, we have:
$$\begin{aligned}&\sum _{j=1}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)})\Vert ^2 \\&\quad \le 6\Gamma A_{K-1} + 36L^2\kappa \delta _\kappa ^NB_{K-1} + 3L_{\Phi }^2E_{K-1}. \end{aligned}$$
Together with Lemma 26, we can prove the second inequality for \(S_K\). \(\square\)
The above lemma together with Lemma 10 and 9 gives
$$\begin{aligned} S_K&\le \frac{\eta _x^2}{(1-\rho )^4}(6\Gamma A_{K-1} + 36L^2\kappa \delta _\kappa ^NB_{K-1} + 3L_{\Phi }^2E_{K-1} + \Vert \partial \Phi (X_0)\Vert ^2) \nonumber \\ A_K&\le \delta _y^T (3c_1 + 6\kappa ^2E_K)\quad B_K\le 2c_2 + 2d_1A_{K-1} + 2d_2E_K \nonumber \\ E_K&\le 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}. \end{aligned}$$
(36)
Now we can obtain the following result.
Lemma 28
Suppose Assumptions 2.1, 2.2 and 2.3 hold. Set:
$$\begin{aligned}&\delta _y^{T}<\min \left( \frac{L_{\Phi }^2}{72\kappa ^2\Gamma }, \kappa ^{-5}\right) =\Theta (\kappa ^{-5}),\\&\delta _{\kappa }^N<\min \left( \frac{L_{\Phi }^2}{72L^2\kappa (4d_1\kappa ^2 + 2d_2)}, \kappa ^{-4}\right) =\Theta (\kappa ^{-4}),\ \eta _x<\frac{(1-\rho )^2}{8L_{\Phi }}. \end{aligned}$$
For Algorithm 4, we have:
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \frac{C_2}{K+1}, \end{aligned}$$
where the constant is defined as:
$$\begin{aligned} \frac{1}{2}C_2&= \frac{15\eta _x^2L_{\Phi }^2}{n(1-\rho )^4}(\Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1))\\&\quad +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n} \\&=\Theta (\eta _x^2\kappa ^6 + (\eta _x^2\kappa ^6 + 1)(\kappa ^5\delta _y^T + \kappa ^4\delta _{\kappa }^N)) = \Theta (1). \end{aligned}$$
Proof
We first bound \(B_K\) as
$$\begin{aligned} \begin{aligned} B_K&\le 2c_2 + 2d_1A_K + 2d_2E_K \le 2c_2 + \frac{2}{3}d_1(3c_1 + 6\kappa ^2E_K) + 2d_2E_K \\&= 2c_2 + 2d_1c_1 + (4d_1\kappa ^2 + 2d_2)E_K. \end{aligned} \end{aligned}$$
(37)
Next we eliminate \(A_K\) and \(B_K\) in the upper bound of \(S_K\). Choose N, T such that
$$\begin{aligned}&\delta _y^T\cdot 6\kappa ^2\cdot 6\Gamma< \frac{L_{\Phi }^2}{2},\quad \delta _{\kappa }^N\cdot (4d_1\kappa ^2 + 2d_2)\cdot 36L^2\kappa <\frac{L_{\Phi }^2}{2}, \end{aligned}$$
which implies
$$\begin{aligned} \begin{aligned}&\delta _y^{T}< \frac{L_{\Phi }^2}{72\kappa ^2\Gamma },\quad \delta _{\kappa }^N< \frac{L_{\Phi }^2}{72L^2\kappa (4d_1\kappa ^2 + 2d_2)}. \end{aligned} \end{aligned}$$
(38)
By (36) and the, we have
$$\begin{aligned} S_K\le \frac{\eta _x^2}{(1-\rho )^4}(4L_{\Phi }^2E_{K-1} + \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)). \end{aligned}$$
Next we eliminate \(E_{K-1}\) in this bound. The definition of \(\eta _x\) gives \(\eta _x<\frac{(1-\rho )^2}{8L_{\Phi }}\), which implies \(\frac{32L_{\Phi }^2\eta _x^2}{(1-\rho )^4}<\frac{1}{2}.\) Together with (36) and \(E_{K-1}\le E_K\), we have:
$$\begin{aligned} S_{K}&\le \frac{\eta _x^2}{(1-\rho )^4}\left( 4L_{\Phi }^2(8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}\right) \\&\qquad + \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) ) \\&\le \frac{1}{2}S_K + \frac{\eta _x^2}{(1-\rho )^4}\left( 4L_{\Phi }^2(4n\eta _x^2\sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K}\right) \\&\qquad +\, \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) ), \end{aligned}$$
which immediately implies
$$\begin{aligned} \begin{aligned} S_K&< \frac{2\eta _x^2}{(1-\rho )^4}(16n\eta _x^2L_{\Phi }^2\left( \sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_{K}\right) \\&\qquad + \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) ). \end{aligned} \end{aligned}$$
(39)
Moreover, by (19) we have
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2\le \frac{2L_{\Phi }^2}{n}S_K + \frac{2\Gamma }{n}A_K + \frac{12L^2\kappa }{n}\delta _{\kappa }^NB_K \\&\quad \le \frac{2L_{\Phi }^2}{n}S_K + \left( \frac{L_{\Phi }^2}{6n} + \frac{L_{\Phi }^2}{6n}\right) E_K + \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n} \\&\quad \le \frac{2L_{\Phi }^2}{n}S_K + \frac{L_{\Phi }^2}{3n}\left( 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}\right) \\&\qquad +\, \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n}\\&\quad < \frac{5L_{\Phi }^2}{n}S_K + \frac{4\eta _x^2L_{\Phi }^2}{3}\left( \sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_{K}\right) \\&\qquad +\, \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n} \\&\quad \le \left( \frac{5L_{\Phi }^2}{n}\cdot \frac{32nL_{\Phi }^2\eta _x^4}{(1-\rho )^4} + \frac{4\eta _x^2L_{\Phi }^2}{3}\right) \left( \sum _{j=0}^{K}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_K\right) \\&\qquad +\, \frac{5L_{\Phi }^2}{n}\cdot \frac{2\eta _x^2}{(1-\rho )^4}\left( \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)\right) \\&\qquad +\, \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n}, \end{aligned}$$
where the second inequality is by (36), (37) and (38), and the third inequality uses (36). Note that \(\eta _x\) satisfies:
$$\begin{aligned} \eta _x<\frac{(1-\rho )^2}{8L_{\Phi }}\quad \Rightarrow \quad \frac{160L_{\Phi }^4\eta _x^4}{(1-\rho )^4} + \frac{8\eta _x^2L_{\Phi }^2}{3} < \frac{1}{3}. \end{aligned}$$
Therefore, we have:
$$\begin{aligned}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 &\le \frac{1}{3}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + \frac{1}{3}T_K \\&\quad + \frac{10\eta _x^2L_{\Phi }^2}{n(1-\rho )^4}(\Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)) \\&\quad + \frac{12L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 6\Gamma c_1\delta _y^T}{n}, \end{aligned}$$
which leads to
$$\begin{aligned}&\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2\\&\quad \le \frac{1}{2}T_K + \frac{15\eta _x^2L_{\Phi }^2}{n(1-\rho )^4}\left( \Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)\right) \\&\qquad +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n}. \end{aligned}$$
Recall (12), we have
$$\begin{aligned} \frac{1}{K+1}T_K&\le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \frac{1}{2(K+1)}T_K + \frac{1}{2(K+1)}C_2. \\ \end{aligned}$$
Therefore, we get
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2\le \frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0)-\inf _x \Phi (x)) + \frac{C_2}{K+1}, \end{aligned}$$
where the constant is defined as following
$$\begin{aligned} \frac{1}{2}C_2&= \frac{15\eta _x^2L_{\Phi }^2}{n(1-\rho )^4}(\Vert \partial \Phi (X_0)\Vert ^2 + 18\Gamma c_1\delta _y^T + 36L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1)) \\&\qquad +\frac{18L^2\kappa \delta _{\kappa }^N(2c_2 + 2d_1c_1) + 9\Gamma c_1\delta _y^T}{n} \\&=\Theta (\eta _x^2\kappa ^6 + (\eta _x^2\kappa ^6 + 1)(\kappa ^5\delta _y^T + \kappa ^4\delta _{\kappa }^N)) = \Theta (1). \end{aligned}$$
Then if we choose
$$\begin{aligned} T=\Theta (\kappa \log \kappa ), N=\Theta (\sqrt{\kappa }\log \kappa ), \eta _x = \Theta (\kappa ^{-3}), \eta _y = \frac{1}{\mu + L}, \end{aligned}$$
then the restrictions on algorithm parameters in Lemma 28 hold and we have
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 = {\mathcal {O}}\left( \frac{1}{K}\right) , \end{aligned}$$
which proves the first case of Theorems 3.2 and 25. \(\square\)
1.2.2 Case 2: Assumption 2.3 does not hold
We first give a bound for \(\Vert {\tilde{y}}_{j}^* - {\tilde{y}}_{j-1}^*\Vert\) in the following lemma.
Lemma 29
Recall that \({\tilde{y}}_j^* = \mathop {\mathrm {arg\,min}}\limits \frac{1}{n}\sum _{i=1}^{n}g_i(x_{i,j}, y)\). We have:
$$\begin{aligned} \Vert {\tilde{y}}_j^* - {\tilde{y}}_{j-1}^*\Vert ^2\le \frac{\kappa ^2}{n}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert ^2. \end{aligned}$$
Proof
The proof technique is similar to Lemma 13. Consider:
$$\begin{aligned}&\Vert \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j-1}, {\tilde{y}}_j^*)\Vert \\&\quad = \Vert \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j-1}, {\tilde{y}}_j^*) - \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j-1}, {\tilde{y}}_{j-1}^* )\Vert \ge \mu \Vert {\tilde{y}}_j^* - {\tilde{y}}_{j-1}^* \Vert , \\&\Vert \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j-1}, {\tilde{y}}_j^*)\Vert \\&\quad = \Vert \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j-1}, {\tilde{y}}_j^*) - \frac{1}{n}\sum _{i=1}^{n}\nabla _yg_i(x_{i,j}, {\tilde{y}}_j^*) \Vert \le \frac{L}{n}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert , \end{aligned}$$
which implies:
$$\begin{aligned} \Vert {\tilde{y}}_j^* - {\tilde{y}}_{j-1}^* \Vert ^2\le \frac{\kappa ^2}{n^2}\left( \sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert \right) ^2\le \frac{\kappa ^2}{n}\sum _{i=1}^{n}\Vert x_{i,j}-x_{i,j-1}\Vert ^2. \end{aligned}$$
\(\square\)
Lemma 30
Suppose \(\eta _x\) satisfies
$$\begin{aligned} \eta _x \le \frac{\mu (1-\rho )^2}{21L_{f,0}L_{g,2}\kappa }. \end{aligned}$$
(40)
When the Assumption 2.3 does not hold, we have for Algorithm 4:
$$\begin{aligned} S_K&\le \frac{2\eta _x^2}{(1-\rho )^4}\left[ 3L_f^2(1+\kappa ^2)\sum _{j=1}^{K-1}\sum _{i=1}^{n}E_{K-1} + \Vert \partial \Phi (X_0)\Vert ^2\right] \\&\quad +\frac{72nKC\eta _x^2}{(1-\rho )^4}\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) \end{aligned}$$
Proof
We first notice that
$$\begin{aligned}&\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)}) \Vert ^2\\&\quad \le 3\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\bar{\nabla }} f_i(x_{i,j}, {\tilde{y}}_j^*)\Vert ^2 +3\Vert {\bar{\nabla }} f_i(x_{i,j}, {\tilde{y}}_j^*) - {\bar{\nabla }} f_i(x_{i,j-1}, {\tilde{y}}_{j-1}^*)\Vert ^2 \\&\qquad + 3\Vert {\bar{\nabla }} f_i(x_{i,j-1}, {\tilde{y}}_{j-1}^*) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)})\Vert ^2. \end{aligned}$$
Taking summation on both sides and using Lemma 17, we have
$$\begin{aligned}&\frac{1}{n}\sum _{j=1}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)}) - {\hat{\nabla }} f_i(x_{i,j-1}, y_{i,j-1}^{(T)})\Vert ^2\\&\quad \le \frac{108L_{f,0}^2L_{g,2}^2(1 + \kappa ^2)}{n\mu ^2}S_{K-1} \\&\qquad + 36(K-1)\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{1}{n}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - {{\tilde{y}}}_k^*\Vert ^2\\&\qquad + 36(K-1)CL_{f,0}^2\alpha ^N + \frac{3L_f^2}{n}\sum _{j=1}^{K-1}\sum _{i=1}^{n}(\Vert x_{i,j}-x_{i,j-1}\Vert ^2 + \Vert {\tilde{y}}_j^* - {\tilde{y}}_{j-1}^*\Vert ^2)\\&\quad \le \frac{(1-\rho )^4}{2n\eta _x^2}S_{K-1}+36KC\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) \\&\qquad +\frac{3L_f^2(1+\kappa ^2)}{n}E_{K-1}, \end{aligned}$$
where the second inequality uses Lemma 14, 29 and (40). This completes the proof together with Lemma 26. \(\square\)
Lemma 31
When the Assumption 2.3 does not hold, we further have for Algorithm 4:
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\quad \le \frac{(1+\kappa ^2)}{n(K+1)}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) S_K \\&\qquad + 12C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] . \end{aligned}$$
Proof
Note that the above inequality is a direct result of Lemma 18. \(\square\)
Now we are ready to provide the convergence rate. Recall that from Lemma 30, 9 and inequality (12), we have:
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \nonumber \\&\quad \le \frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) + \frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2, \nonumber \\&S_K \le \frac{2\eta _x^2}{(1-\rho )^4}\left( 3L_f^2(1+\kappa ^2)E_{K-1} + \Vert \partial \Phi (X_0)\Vert ^2\right) \nonumber \\&\qquad +\frac{72nKC\eta _x^2}{(1-\rho )^4}\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) , \nonumber \\&E_K \le 8S_K + 4n\eta _x^2\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + 4n\eta _x^2T_{K-1}. \end{aligned}$$
(41)
The following lemma proves the convergence results in Theorem 25.
Lemma 32
Suppose the Assumption 2.3 does not hold. We set \(\eta _x\) as
$$\begin{aligned} \eta _x<\min \left( \frac{(1-\rho )^2}{14\kappa L_f},\ \frac{\mu (1-\rho )^2}{21L_{f,0}L_{g,2}\kappa }\right) . \end{aligned}$$
(42)
Then we have:
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\le \frac{6}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) + \frac{\Vert \partial \Phi (X_0)\Vert ^2 }{K+1} +{\tilde{C}}_2, \end{aligned}$$
where the constant is given by:
$$\begin{aligned} \frac{{\tilde{C}}_2}{6} =&\, 6L^2(1+\kappa ^2)C\alpha ^T + 6L_{f,0}^2C\alpha ^N \\&\quad + 2L_f^2(1 + \kappa ^2)\cdot \frac{2\eta _x^2}{(1-\rho )^4}\left[ 6L^2(1 + \kappa ^2)nC\alpha ^T + 6nL_{f,0}^2C\alpha ^N + \frac{\Vert \partial \Phi (X_0)\Vert ^2}{K+1}\right] \\&=\Theta \left(\alpha ^T + \alpha ^N + \frac{1}{K+1} \right). \end{aligned}$$
Proof
We first eliminate \(E_{K-1}\) in the upper bound of \(S_K\). Note that (42) implies
$$\begin{aligned} \frac{2\eta _x^2}{(1-\rho )^4}\cdot 3L_f^2(1+\kappa ^2)\cdot 8<\frac{1}{2}, \end{aligned}$$
which together with \(E_{K-1}\le E_K\) and the upper bounds of \(S_K\) and \(E_K\) in (41) gives
$$\begin{aligned} S_K&\le \frac{1}{2}\left( S_K + \frac{\eta _x^2}{2}\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + \frac{\eta _x^2}{2}T_{K-1}\right) + \frac{2\eta _x^2}{(1-\rho )^4}\Vert \partial \Phi (X_0)\Vert ^2\\&\quad + \frac{2\eta _x^2}{(1-\rho )^4}\left( 36nKC\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) \right) . \end{aligned}$$
Hence we know
$$\begin{aligned} S_K&\le \frac{\eta _x^2}{2}\sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + \frac{\eta _x^2}{2}T_{K-1} + \frac{4\eta _x^2}{(1-\rho )^4}\Vert \partial \Phi (X_0)\Vert ^2 \\&\quad + \frac{4\eta _x^2}{(1-\rho )^4}\left( 36nKC\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) \right) . \end{aligned}$$
By Lemma 31, we have
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\nonumber \\&\quad \le \frac{(1+\kappa ^2)}{n(K+1)}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) S_K \nonumber \\&\qquad +\, 12C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] \nonumber \\&\quad \le \frac{1}{3(K+1)}\left( \sum _{j=0}^{K-1}\Vert \overline{\partial \Phi (X_{j})} - \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 + T_{K-1}\right) + \frac{\tilde{C}_2}{3}, \end{aligned}$$
(43)
where the second inequality holds since we have (42), which implies
$$\begin{aligned} \eta _x^2(1+\kappa ^2)\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \le \frac{1}{4}. \end{aligned}$$
The constant is defined as:
$$\begin{aligned} \frac{{\tilde{C}}_2}{3}&=\, 12C\left[ \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right] + \frac{1}{(1-\rho )^4}\frac{\Vert \partial \Phi (X_0)\Vert ^2}{n(K+1)}\\&\quad + \frac{1}{(1-\rho )^4}\left( 36C\left( \left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \alpha ^T + L_{f,0}^2\alpha ^N\right) \right) \\&=\Theta \left(\alpha ^T + \alpha ^N + \frac{1}{K+1} \right). \end{aligned}$$
From (43) we know
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2< \frac{{\tilde{C}}_2}{2} + \frac{1}{2(K+1)}T_{K-1}. \end{aligned}$$
Combining the above inequality, Lemma 8, and \(T_{K-1}\le T_K\), we have
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}\Vert \nabla \Phi (\bar{x}_k)\Vert ^2<\frac{2}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x)) + \frac{{\tilde{C}}_2}{2} + \frac{1}{2(K+1)}T_K. \end{aligned}$$
Hence
$$\begin{aligned} \frac{1}{K+1}T_K<\frac{4}{\eta _x(K+1)}(\Phi ({{\bar{x}}}_0) - \inf _x\Phi (x))+{\tilde{C}}_2. \end{aligned}$$
Furthermore, by setting
$$\begin{aligned} N = \Theta (\log K),\ T = \Theta (\log K),\ \eta _x=\Theta (\kappa ^{-3}),\ \eta _y=\Theta (1) \end{aligned}$$
we have
$$\begin{aligned} \frac{1}{K+1}\sum _{j=0}^{K}\Vert \nabla \Phi ({{\bar{x}}}_j)\Vert ^2 = {\mathcal {O}}\left( \frac{1}{K}\right) , \end{aligned}$$
which proves the second case of Theorems 3.2 and 25. \(\square\)
1.3 Proof of the convergence of DSBO
In this section we will prove the convergence result of the DSBO algorithm.
Theorem 33
In Algorithm 5, suppose Assumptions 2.1 and 2.2 hold. If Assumption 2.3 holds, then by setting \(M = \Theta (\log K),\ T = \Omega (\kappa \log \kappa ),\ \beta \le \min \left( \frac{\mu }{\mu ^2 + \sigma _{g,2}^2},\ \frac{1}{L}\right) ,\ \eta _x\le \frac{1}{L_{\Phi }},\ \eta _y< \frac{2}{\mu + L}\), we have:
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\quad \le \frac{2}{\eta _x(K+1)}({\mathbb {E}}\left[ \Phi ({{\bar{x}}}_0)\right] -\inf _x \Phi (x)) + \frac{3\eta _y L_f^2 \sigma _{g,1}^2}{\mu } + \frac{3\eta _x^2 L_{\Phi }^2 }{(1-\rho )^2}{\tilde{C}}_f^2 + L\eta _x{\tilde{\sigma }}_f^2 + C_3. \end{aligned}$$
If Assumption 2.3 does not hold, then by setting \(\eta _x\le \frac{1}{L_{\Phi }},\ \eta _y^{(t)} = {\mathcal {O}}(\frac{1}{t})\), we have:
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\quad \le \frac{2}{\eta _x(K+1)}({\mathbb {E}}\left[ \Phi (\overline{x_{0}})\right] - \inf _x\Phi (x)) + \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \frac{\eta _x^2(1+\kappa ^2)}{(1-\rho )^2}{\tilde{C}}_f^2 \\&\qquad +L\eta _x\left( 4\sigma _f^2(1+\kappa ^2) + (8L_{f,0}^2 + 4\sigma _f^2)\frac{C}{N}\right) + {\tilde{C}}_3. \end{aligned}$$
Here \(C = \Theta (1),\ C_3 = \Theta (\eta _x^2 + \frac{1}{K+1})\) and \({\tilde{C}}_3 = {\mathcal {O}}\left( \frac{1}{T}+\alpha ^N\right)\).
We first define the following filtration:
$$\begin{aligned}&{\mathcal {F}}_k = \sigma \left( \bigcup _{i=1}^{n}\{x_{i,0}, x_{i,1},\ldots ,x_{i,k}\}\right) , \\&{\mathcal {G}}_{i,j}^{(t)} = \sigma \left( \{y_{i,l}^{(s)}: 0\le l\le j, 0\le s\le t\}\bigcup \{x_{i,l}: 0\le l\le j\}\right) . \end{aligned}$$
Then in both cases we have the following lemma.
Lemma 34
If \(\eta _x\le \frac{1}{L_{\Phi }}\), then we have:
$$\begin{aligned}&{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\quad \le \frac{2}{\eta _x}({\mathbb {E}}\left[ \Phi ({{\bar{x}}}_k)\right] - {\mathbb {E}}\left[ \Phi ({{\bar{x}}}_{k+1})\right] ) + {\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\qquad + L\eta _x {\mathbb {E}}\Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2. \end{aligned}$$
Proof
In each iteration of Algorithm 5, we have:
$$\begin{aligned} {{\bar{x}}}_{k+1} = {{\bar{x}}}_k - \eta _x \overline{\partial \Phi (X_k;\phi )}. \end{aligned}$$
(44)
The \(L_{\Phi }\)-smoothness of \(\Phi\) indicates that
$$\begin{aligned} \Phi ({{\bar{x}}}_{k+1}) - \Phi ({{\bar{x}}}_k) \le \nabla \Phi (\bar{x}_k)^{{\textsf{T}}}(-\eta _x\overline{\partial \Phi (X_k;\phi )}) + \frac{L_{\Phi }\eta _x^2}{2}\Vert \overline{\partial \Phi (X_k;\phi )}\Vert ^2. \end{aligned}$$
Taking conditional expectation with respect to \({\mathcal {F}}_k\) on both sides, we have the following
$$\begin{aligned}&{\mathbb {E}}\left[ \Phi ({{\bar{x}}}_{k+1})\vert {\mathcal {F}}_k \right] - \Phi (\bar{x}_k)\\&\quad \le \nabla \Phi ({{\bar{x}}}_k)^{{\textsf{T}}}(-\eta _x{\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] ) + \frac{L_{\Phi }\eta _x^2}{2} {\mathbb {E}}\left[ \Vert \overline{\partial \Phi (X_k;\phi )}\Vert ^2\vert {\mathcal {F}}_k\right] \\&\quad =-\frac{\eta _x}{2}(\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 + \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2 - \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2) \\&\qquad + \frac{L_{\Phi }\eta _x^2}{2}(\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2 + {\mathbb {E}}\left[ \Vert \overline{\partial \Phi (X_k; \phi )} - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2\vert {\mathcal {F}}_k\right] ) \\&\quad = \left( \frac{L_{\Phi }\eta _x^2}{2} - \frac{\eta _x}{2}\right) \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2 \\&\qquad + \frac{L_{\Phi }\eta _x^2}{2} {\mathbb {E}}\left[ \Vert \overline{\partial \Phi (X_k; \phi )} - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2\vert {\mathcal {F}}_k\right] \\&\qquad - \frac{\eta _x}{2}(\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 - \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2) \\&\quad \le \frac{L_{\Phi }\eta _x^2}{2} {\mathbb {E}}\left[ \Vert \overline{\partial \Phi (X_k; \phi )} - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2\vert {\mathcal {F}}_k\right] \\&\qquad -\frac{\eta _x}{2}(\Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 - \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2), \end{aligned}$$
where the second inequality holds since we pick \(\eta _x\le \frac{1}{L}\). Thus we can take expectation again and use tower property to obtain:
$$\begin{aligned}&\frac{\eta _x}{2}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \nonumber \\&\quad \le {\mathbb {E}}\left[ \Phi ({{\bar{x}}}_k)\right] - {\mathbb {E}}\left[ \Phi (\bar{x}_{k+1})\right] + \frac{\eta _x}{2}{\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \nonumber \\&\qquad +\frac{L_{\Phi }\eta _x^2}{2} {\mathbb {E}}\Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2. \end{aligned}$$
(45)
which completes the proof. \(\square\)
1.3.1 Case 1: Assumption 2.3 holds
Lemma 35
Suppose \(\beta \le \frac{1}{L}\) and Assumption 2.3 holds, we have:
$$\begin{aligned} \left\| {\mathbb {E}}\left[ {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - {\bar{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)})\right\| _2 \le L_{f,0}(1-\beta \mu )^M\kappa . \end{aligned}$$
Proof
We first consider the expectation
$$\begin{aligned}&{\mathbb {E}}\left[ {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] \nonumber \\&\quad = \nabla _xf_i(x_{i,k}, y_{i,k}^{(T)})\nonumber \\&\qquad - \beta \nabla _{xy}g(x_{i,k}, y_{i,k}^{(T)})\sum _{j=0}^{M-1} \big (I - \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)}) \big )^j\nabla _yf_i(x_{i,k}, y_{i,k}^{(T)}). \end{aligned}$$
(46)
Notice that for the finite sum we have:
$$\begin{aligned}\beta \sum _{j=0}^{M-1} \left( I - \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)}) \right) ^j &= \beta \left( \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)})\right) ^{-1}\left( I - (I - \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)}))^M\right) \\& =\left( \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)})\right) ^{-1}\left( I - (I - \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)}))^M\right) , \end{aligned}$$
which implies:
$$\begin{aligned} \left\| \beta \sum _{j=0}^{M-1} \left( I - \beta \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)}) \right) ^j - \left( \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)})\right) ^{-1}\right\| _2\le \frac{ (1-\beta \mu )^M}{\mu }. \end{aligned}$$
(47)
The above inequality and the fact that
$$\begin{aligned} {\bar{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)}) = \nabla _xf_i(x_{i,k}, y_{i,k}^{(T)}) - \nabla _{xy}g(x_{i,k}, y_{i,k}^{(T)})\left( \nabla _y^2g(x_{i,k}, y_{i,k}^{(T)})\right) ^{-1}\nabla _yf_i(x_{i,k}, y_{i,k}^{(T)}) \end{aligned}$$
imply
$$\begin{aligned} \left\| {\mathbb {E}}\left[ {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - {\bar{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)})\right\| _2 \le L_{f,0}(1-\beta \mu )^M\kappa , \end{aligned}$$
which completes the proof. \(\square\)
Lemma 36
Under Assumption 2.3, we have:
$$\begin{aligned}&\sum _{k=0}^{K}\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\nonumber \\&\quad \le 3 \left((K+1)L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{L_f^2}{n}A_K + \frac{L_{\Phi }^2}{n}S_K \right). \end{aligned}$$
(48)
Proof
We first bound each component of the gradient error as
$$\begin{aligned}&\Vert {\mathbb {E}}\left[ {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - \nabla \Phi _i({{\bar{x}}}_k)\Vert ^2 \\&\quad \le 3(\Vert {\mathbb {E}}\left[ {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - {\bar{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)})\Vert ^2 \\&\qquad +\Vert {\bar{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)}) - \nabla f_i(x_{i,k}, y_i^*(x_{i,k}))\Vert ^2+\Vert \nabla f_i(x_{i,k}, y_i^*(x_{i,k})) - \nabla \Phi _i({{\bar{x}}}_k)\Vert ^2) \\&\quad \le 3(L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + L_f^2\Vert y_{i,k}^{(T)} - y_i^*(x_{i,k})\Vert ^2 + L_{\Phi }^2\Vert x_{i,k} - {{\bar{x}}}_k\Vert ^2), \end{aligned}$$
where the second inequality is obtained by Lemmas 35 and 5. Taking summation on both sides over \(i=1,\ldots ,n\), we have:
$$\begin{aligned}&\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 \\&\quad \le \frac{1}{n}\sum _{i=1}^{n}\Vert {\mathbb {E}}\left[ {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - \nabla \Phi _i({{\bar{x}}}_k)\Vert ^2 \\&\quad \le 3\left( L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{L_f^2}{n} \sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - y_i^*(x_{i,k})\Vert ^2 + \frac{L_{\Phi }^2}{n} \sum _{i=1}^{n}\Vert x_{i,k} - {{\bar{x}}}_k\Vert ^2\right) . \\ \end{aligned}$$
Taking summation on both sides over \(k=0,\ldots ,K\), we know
$$\begin{aligned}&\sum _{k=0}^{K}\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\\&\quad \le 3 \left((K+1)L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{L_f^2}{n}A_K + \frac{L_{\Phi }^2}{n}S_K \right), \end{aligned}$$
which completes the proof. \(\square\)
The following lemma characterizes the variance of the hypergradient estimation.
Lemma 37
Suppose \(\beta\) in Algorithm 2 satisfies
$$\begin{aligned} \beta \le \min \left( \frac{\mu }{\mu ^2 + \sigma _{g,2}^2},\ \frac{1}{L}\right) \end{aligned}$$
(49)
Under Assumptions 2.1–2.4, we have:
$$\begin{aligned} \begin{aligned} {\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k})\vert {\mathcal {F}}_k\right] - {\hat{\nabla }} f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k})\Vert ^2\right]&\le {\tilde{\sigma }}_f^2, \\ {\mathbb {E}}\left[ \Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2\right]&\le \frac{{\tilde{\sigma }}_f^2}{n}, \end{aligned} \end{aligned}$$
(50)
where the constants are defined as
$$\begin{aligned} {\tilde{\sigma }}_f^2 = \sigma _{f,1}^2 + \frac{2(\sigma _{g,2}^2 + L^2)(\sigma _{f,1}^2 + L_{f,0}^2)}{\mu ^2} = {\mathcal {O}}(\kappa ^2). \end{aligned}$$
Proof
We first notice that in the stochastic case of Algorithm 2 under Assumption 2.3, for each agent i we have
$$\begin{aligned} H_M\cdot \nabla _yf_i(x, y;\phi ^{(0)}) = \beta \sum _{s=0}^{M-1}\prod _{n=1}^{s}(I - \beta \nabla _y^2g_i(x, y;\phi ^{(M+1-n)}))\nabla _yf_i(x, y;\phi ^{(0)}). \end{aligned}$$
(51)
For \(m=1, 2,\ldots , M-1\) we define
$$\begin{aligned}&A = \nabla _y^2 g_i(x,y),\ A_m = \nabla _y^2g_i(x, y;\phi ^{(m+1)}),\ b_0 = \nabla _yf_i(x, y;\phi ^{(0)}), \\&x_m = \beta \sum _{s=0}^{m-1}\prod _{n=1}^{s}(I - \beta A_{m-n})b_0,\ x_0 = 0, \end{aligned}$$
which gives
$$\begin{aligned} x_{m+1} = (I - \beta A_m)x_m + \beta b_0. \end{aligned}$$
(52)
For simplicity in the proof of this lemma we denote by \({\mathbb {E}}_0\) the conditional expectation given \(\phi ^{(0)}\). In other words we have \({\mathbb {E}}_0\left[ x\right] = {\mathbb {E}}\left[ x\vert \phi ^{(0)}\right]\) for any random vector (or matrix) x. From (52) we know
$$\begin{aligned} \Vert {\mathbb {E}}_0\left[ x_m\right] \Vert = \beta \left\| \sum _{n=1}^{M-1}\left( I - \beta A\right) ^nb_0\right\| = \left\| A^{-1}\left( I - (I - \beta A)^M\right) b_0\right\| \le \frac{\Vert b_0\Vert }{\mu }. \end{aligned}$$
(53)
Combining (52) and (53), we know
$$\begin{aligned}&{\mathbb {E}}_0\left[ \Vert x_{m+1} - {\mathbb {E}}_0\left[ x_{m+1}\right] \Vert ^2\right] \\&\quad = {\mathbb {E}}_0\left[ \Vert (I - \beta A)(x_m - {\mathbb {E}}_0\left[ x_m\right] ) + \beta (A - A_m)x_m\Vert ^2\right] \\&\quad = {\mathbb {E}}_0\left[ \Vert (I - \beta A)(x_m - {\mathbb {E}}_0\left[ x_m\right] )\Vert ^2\right] + \beta ^2{\mathbb {E}}_0\left[ \Vert (A-A_m)x_m\Vert ^2\right] \\&\quad \le (1-\beta \mu )^2{\mathbb {E}}_0\left[ \Vert x_m - {\mathbb {E}}_0\left[ x_m\right] \Vert ^2\right] + \beta ^2\sigma _{g,2}^2({\mathbb {E}}_0\left[ \Vert x_m - {\mathbb {E}}_0\left[ x_m\right] \Vert ^2\right] + \Vert {\mathbb {E}}_0\left[ x_m\right] \Vert ^2) \\&\quad \le (1-\beta \mu ){\mathbb {E}}_0\left[ \Vert x_m - {\mathbb {E}}_0\left[ x_m\right] \Vert ^2\right] + \frac{\beta ^2\sigma _{g,2}^2\Vert b_0\Vert ^2}{\mu ^2} \\&\quad \le (1-\beta \mu )^{m+1}{\mathbb {E}}\left[ \Vert x_0 - {\mathbb {E}}_0\left[ x_0\right] \Vert ^2\right] + \frac{\beta ^2\sigma _{g,2}^2\Vert b_0\Vert ^2}{\mu ^2}\left( \sum _{i=0}^{m}(1-\beta \mu )^i\right) \le \frac{\beta \sigma _{g,2}^2\Vert b_0\Vert ^2}{\mu ^3}. \end{aligned}$$
The second equality uses the independence, the second inequality uses (49), and the third inequality repeats the second inequality for m times. From the above inequality we know that the variance of \(x_m\), namely, (51), has bounded variance since
$$\begin{aligned} {\mathbb {E}}\left[ \Vert x_{M} - {\mathbb {E}}_0\left[ x_{M}\right] \Vert ^2\right] \le \frac{\beta \sigma _{g,2}^2{\mathbb {E}}\left[ \Vert b_0\Vert ^2\right] }{\mu ^3}\le \frac{\beta \sigma _{g,2}^2(\sigma _{f,1}^2 + L_{f,0}^2)}{\mu ^3}\le \frac{\sigma _{f,1}^2 + L_{f,0}^2}{\mu ^2}, \end{aligned}$$
where the second inequality uses Assumption 2.1 and the third inequality uses (49). We further know from the above conclusion and (53) that
$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\left[ \Vert x_M - {\mathbb {E}}\left[ x_M\right] \Vert ^2\right] \\&\quad \le {\mathbb {E}}\left[ \Vert x_M\Vert ^2\right] = {\mathbb {E}}\left[ \Vert x_M - {\mathbb {E}}_0\left[ x_M\right] \Vert ^2\right] + {\mathbb {E}}\left[ \Vert {\mathbb {E}}_0\left[ x_M\right] \Vert ^2\right] \le \frac{2(\sigma _{f,1}^2 + L_{f,0}^2)}{\mu ^2}. \end{aligned} \end{aligned}$$
(54)
Hence in Algorithm 2 (stochastic case under Assumption 2.3) we have the following decomposition:
$$\begin{aligned}{\hat{\nabla }} f_i - {\mathbb {E}}\left[ {\hat{\nabla }} f_i\right] &= \nabla _xf_i(x, y;\phi ^{(0)}) - \nabla _x f_i(x,y) + \nabla _{xy}g_i(x,y){\mathbb {E}}\left[ x_M\right] - \nabla _{xy}g_i(x, y;\phi ^{(1)})x_{M} \\& = \nabla _xf_i(x, y;\phi ^{(0)}) - \nabla _x f_i(x,y) + (\nabla _{xy}g_i(x,y) - \nabla _{xy}g_i(x, y;\phi ^{(1)}))x_{M} \\&\quad + \nabla _{xy}g_i(x,y)({\mathbb {E}}\left[ x_M\right] - x_M), \end{aligned}$$
which implies
$$\begin{aligned}&{\mathbb {E}}\left[ \left\| {\hat{\nabla }} f_i - {\mathbb {E}}\left[ {\hat{\nabla }} f_i\right] \right\| ^2\vert x, y\right] \\&\quad = {\mathbb {E}}\left[ \Vert \nabla _xf_i(x, y;\phi ^{(0)}) - \nabla _x f_i(x,y)\Vert ^2\vert x, y\right] \\&\qquad + {\mathbb {E}}\left[ \Vert (\nabla _{xy}g_i(x,y) - \nabla _{xy}g_i(x, y;\phi ^{(1)}))x_{M}\Vert ^2\vert x, y\right] \\&\qquad + {\mathbb {E}}\left[ \Vert \nabla _{xy}g_i(x,y)({\mathbb {E}}\left[ x_M\right] - x_M)\Vert ^2\vert x, y\right] \\&\quad \le \sigma _{f,1}^2 + (\sigma _{g,2}^2 + L^2){\mathbb {E}}\left[ \Vert x_M\Vert ^2\right] \le \sigma _{f,1}^2 + \frac{2(\sigma _{g,2}^2 + L^2)(\sigma _{f,1}^2 + L_{f,0}^2)}{\mu ^2} = {{\tilde{\sigma }}}_f^2, \end{aligned}$$
where the first inequality uses the independence between different samples, the first inequality uses Assumptions 2.1 and 2.4 and the second inequality uses (54). Hence we know the first inequality of (50) holds. Furthermore the second inequality of (50) is true since for any n independent random vectors \(v_1,\ldots ,v_n\) with variance bounded by \(\sigma _v^2\) if we define \({{\bar{v}}} = \frac{1}{n}\sum _{i=1}^{n}v_i\) we have
$$\begin{aligned} {\mathbb {E}}\left[ \Vert {{\bar{v}}} - {\mathbb {E}}\left[ {{\bar{v}}}\right] \Vert ^2\right] = \frac{1}{n^2}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert v_i-{\mathbb {E}}\left[ v_i\right] \Vert ^2\right] \le \frac{\sigma _v^2}{n}. \end{aligned}$$
\(\square\)
The following lemmas give the estimation bound of \(A_K\) and \(S_K\) in the stochastic case.
Lemma 38
In Algorithm 5, we have
$$\begin{aligned} {\mathbb {E}}\left[ S_{K}\right]&< \frac{\eta _x^2}{(1-\rho )^2}\sum _{j=0}^{K-1}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert {\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)};\phi _{i,j})\Vert ^2\right] \le \frac{\eta _x^2nK}{(1-\rho )^2}{\tilde{C}}_f^2, \end{aligned}$$
where the constant is defined as
$$\begin{aligned} {\tilde{C}}_f^2 = \left( L_{f,0} + \frac{LL_{f,1}}{\mu } +\frac{ LL_{f,1}}{\mu } \right) ^2 + {\tilde{\sigma }}_f^2 = {\mathcal {O}}(\kappa ^2). \end{aligned}$$
Proof
Observe that in this stochastic case, we can replace \({\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)})\) with \({\hat{\nabla }}f_i(x_{i,j}, y_{i,j}^{(T)};\phi _{i,j})\) in Lemma 20 to get the first inequality. For the second inequality, we adopt the bound in Lemma 2 of [14]. \(\square\)
Lemma 39
Set parameters in Algorithm 5 as
$$\begin{aligned} \eta _y< \frac{2}{\mu + L},\quad \delta _y^{T}\le \frac{1}{3}. \end{aligned}$$
(55)
Then we have the following inequalities
$$\begin{aligned} {\mathbb {E}}\left[ A_K\right] \le \delta _y^{T}(2{\mathbb {E}}\left[ c_1\right] + 6\kappa ^2{\mathbb {E}}\left[ E_K\right] ) + \frac{\eta _y nK\sigma _{g,1}^2}{\mu },\ {\mathbb {E}}\left[ E_K\right] \le \frac{9n\eta _x^2K{\tilde{C}}_f^2}{(1-\rho )^2}. \end{aligned}$$
Proof
The proof is based on Lemma 10. Taking conditional expectation with respect to the filtration \({\mathcal {G}}_{i,j}^{(t-1)}\), we get
$$\begin{aligned}&{\mathbb {E}}\left[ \Vert y_{i,j}^{(t)} - y_i^*(x_{i,j})\Vert ^2\vert {\mathcal {G}}_{i,j}^{(t-1)}\right] \\&\quad = {\mathbb {E}}\left[ \Vert y_{i,j}^{(t-1)} - \eta _y\nabla _y g(x_{i,j}, y_{i,j}^{(t-1)};\xi _{i,j}^{(t-1)}) - y_i^*(x_{i,j}) \Vert ^2\vert {\mathcal {G}}_{i,j}^{(t-1)}\right] \\&\quad = \Vert y_{i,j}^{(t-1)} - \eta _y\nabla _y g(x_{i,j}, y_{i,j}^{(t-1)}) - y_i^*(x_{i,j})\Vert ^2 \\&\qquad + \eta _y^2{\mathbb {E}}\left[ \Vert \nabla _y g(x_{i,j}, y_{i,j}^{(t-1)}) - \nabla _y g(x_{i,j}, y_{i,j}^{(t-1)};\xi _{i,j}^{(t-1)})\Vert ^2\vert {\mathcal {G}}_{i,j}^{(t-1)}\right] \\&\quad \le (1 - \eta _y\mu )^2\Vert y_{i,j}^{(t-1)} - y_i^*(x_{i,j})\Vert ^2 + \eta _y^2\sigma _{g,1}^2, \end{aligned}$$
where the inequality uses Lemma 3. Taking expectation on both sides and using the tower property, we have
$$\begin{aligned}&{\mathbb {E}}\left[ \Vert y_{i,j}^{(T)} - y_i^*(x_{i,j})\Vert ^2\right] \nonumber \\&\quad \le (1 - \eta _y\mu )^2{\mathbb {E}}\left[ \Vert y_{i,j}^{(T-1)} - y_i^*(x_{i,j})\Vert ^2\right] + \eta _y^2\sigma _{g,1}^2 \nonumber \\&\quad \le (1 - \eta _y\mu )^{2T}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] + \eta _y^2\sigma _{g,1}^2\sum _{s=0}^{T-1}(1 - \eta _y\mu )^{2s} \nonumber \\&\quad \le \delta _y^{T}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] + \frac{\eta _y\sigma _{g,1}^2}{\mu }. \end{aligned}$$
(56)
Moreover, by the warm-start strategy, we have \(y_{i,j}^{(0)} = y_{i,j-1}^{(T)}\) and thus
$$\begin{aligned}&{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] \nonumber \\&\quad = {\mathbb {E}}\left[ \Vert y_{i,j-1}^{(T)} - y_i^*(x_{i,j-1}) + y_i^*(x_{i,j-1}) - y_i^*(x_{i,j})\Vert ^2\right] \nonumber \\&\quad \le 2{\mathbb {E}}\left[ \Vert y_{i,j-1}^{(T)} - y_i^*(x_{i,j-1})\Vert ^2\right] + 2{\mathbb {E}}\left[ \Vert y_i^*(x_{i,j-1}) - y_i^*(x_{i,j})\Vert ^2\right] \nonumber \\&\quad \le 2\delta _y^{T} {\mathbb {E}}\left[ \Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2\right] + 2\kappa ^2{\mathbb {E}}\left[ \Vert x_{i,j-1} - x_{i,j}\Vert ^2\right] \nonumber \\&\quad \le \frac{2}{3}{\mathbb {E}}\left[ \Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2\right] + 2\kappa ^2{\mathbb {E}}\left[ \Vert x_{i,j-1} - x_{i,j}\Vert ^2\right] , \end{aligned}$$
(57)
where the second inequality is by Lemma 7 and (57) and the last inequality is by (55). Taking summation over i, j, we have:
$$\begin{aligned}&\sum _{j=1}^{K}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] \\&\quad \le \frac{2}{3} \sum _{j=1}^{K}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert y_{i,j-1}^{(0)} - y_i^*(x_{i,j-1})\Vert ^2\right] + 2\kappa ^2{\mathbb {E}}\left[ E_K\right] \\&\quad \le \frac{2}{3}{\mathbb {E}}\left[ c_1\right] + \frac{2}{3}\sum _{j=1}^{K}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] + 2\kappa ^2{\mathbb {E}}\left[ E_K\right] , \end{aligned}$$
which leads to
$$\begin{aligned} \sum _{j=1}^{K}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] \le 2{\mathbb {E}}\left[ c_1\right] + 6\kappa ^2{\mathbb {E}}\left[ E_K\right] . \end{aligned}$$
(58)
Combining (58) with (56) and taking summation over i, j, we have
$$\begin{aligned} {\mathbb {E}}\left[ A_K\right]&\le \delta _y^{T}\sum _{j=1}^{K}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert y_{i,j}^{(0)} - y_i^*(x_{i,j})\Vert ^2\right] + \frac{\eta _y nK\sigma _{g,1}^2}{\mu } \\&\le \delta _y^{T}(2{\mathbb {E}}\left[ c_1\right] + 6\kappa ^2{\mathbb {E}}\left[ E_K\right] ) + \frac{\eta _y nK\sigma _{g,1}^2}{\mu }. \end{aligned}$$
Recall that for \(E_K\) we have:
$$\begin{aligned} E_K&= \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - x_{i,j-1}\Vert ^2 \\&= \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert x_{i,j} - {{\bar{x}}}_j + {{\bar{x}}}_j - {{\bar{x}}}_{j-1} + {{\bar{x}}}_{j-1} - x_{i,j-1}\Vert ^2 \\&= \sum _{j=1}^{K}\sum _{i=1}^{n}\Vert q_{i,j} -\eta _x\overline{\partial \Phi (X_{j-1};\phi )} - q_{i,j-1}\Vert ^2\\&\le 3\sum _{j=1}^{K}\sum _{i=1}^{n}(\Vert q_{i,j}\Vert ^2 + \eta _x^2\Vert \overline{\partial \Phi (X_{j-1};\phi )}\Vert ^2 + \Vert q_{i,j-1}\Vert ^2) \\&\le 3\sum _{j=1}^{K}(\Vert Q_j\Vert ^2 + \Vert Q_{j-1}\Vert ^2 + \eta _x^2\Vert \overline{\partial \Phi (X_{j-1};\phi )}\Vert ^2 \\&\le 6S_K + \frac{3\eta _x^2}{n}\sum _{j=0}^{K-1}\sum _{i=1}^{n}\Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)};\phi _{i,j})\Vert ^2. \end{aligned}$$
Taking expectation on both sides yields
$$\begin{aligned} {\mathbb {E}}\left[ E_K\right]&\le 6{\mathbb {E}}\left[ S_K\right] + \frac{3\eta _x^2}{n}\sum _{j=0}^{K-1}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert {\hat{\nabla }} f_i(x_{i,j}, y_{i,j}^{(T)};\phi _{i,j})\Vert ^2 \right] \\&\le \frac{6\eta _x^2nK}{(1-\rho )^2}{\tilde{C}}_f^2 + 3\eta _x^2K {\tilde{C}}_f^2 = \frac{9n\eta _x^2K{\tilde{C}}_f^2}{(1-\rho )^2},\\ \end{aligned}$$
which completes the proof. \(\square\)
Next, we prove the main convergence results in Theorem 33. Taking expectation on both sides in (48), we have:
$$\begin{aligned} \begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi (\bar{x}_k)\Vert ^2\right] \\&\quad \le 3\left( L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{L_f^2}{n(K+1)}{\mathbb {E}}\left[ A_K\right] + \frac{L_{\Phi }^2}{n(K+1)}{\mathbb {E}}\left[ S_K\right] \right) \\&\quad \le C_3 + \frac{3\eta _y L_f^2 \sigma _{g,1}^2}{\mu } + \frac{3\eta _x^2L_{\Phi }^2 }{(1-\rho )^2}{\tilde{C}}_f^2, \end{aligned} \end{aligned}$$
(59)
where the constant is defined as:
$$\begin{aligned} C_3&= 3L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{3L_f^2}{n(K+1)}\delta _y^{T}(2{\mathbb {E}}\left[ c_1\right] + 6\kappa ^2{\mathbb {E}}\left[ E_K\right] ) \\&\le 3L_{f,0}^2(1-\beta \mu )^{2M}\kappa ^2 + \frac{3L_f^2}{n(K+1)}\delta _y^{T}\left( 2{\mathbb {E}}\left[ c_1\right] +\frac{54\kappa ^2n\eta _x^2K{\tilde{C}}_f^2}{(1-\rho )^2}\right) \\&=\Theta (\delta _{\beta }^{M}\kappa ^2 + \eta _x^2\delta _y^T\kappa ^8). \end{aligned}$$
Here we denote \(\delta _{\beta } = (1-\beta \mu )^2\) for simplicity. Therefore, we set \(M = \Theta (\log K)\) and \(T = \Theta (\log \kappa )\) such that \(C_3 = \Theta (\eta _x^2 + \frac{1}{K+1})\). Recall that (45) yields:
$$\begin{aligned}&{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\quad \le \frac{2}{\eta _x}\left( {\mathbb {E}}\left[ \Phi ({{\bar{x}}}_k)\right] - {\mathbb {E}}\left[ \Phi ({{\bar{x}}}_{k+1})\right] \right) + {\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\qquad +L\eta _x{\mathbb {E}}\Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2. \end{aligned}$$
Taking summation on both sides and using (59) and Lemma 37, we have
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi (\bar{x}_k)\Vert ^2\right] &\le \frac{2}{\eta _x(K+1)}({\mathbb {E}}\left[ \Phi (\bar{x}_0)\right] -\inf _x \Phi (x))+ \frac{3\eta _y L_f^2 \sigma _{g,1}^2}{\mu } \\&\quad + \frac{3\eta _x^2 L_{\Phi }^2 }{(1-\rho )^2}{\tilde{C}}_f^2 + \frac{L\eta _x{\tilde{\sigma }}_f^2}{n} + C_3. \end{aligned}$$
By setting
$$\begin{aligned} M = \Theta (\log K),\ T=\Theta (K^{\frac{1}{2}}),\ \eta _x = \Theta (K^{-\frac{1}{2}}),\ \eta _y = \Theta (K^{-\frac{1}{2}}) \end{aligned}$$
we know that the restrictions on algorithm parameters in Lemmas 35, 37, and 39 hold and we have
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] = {\mathcal {O}}\left( \frac{1}{\sqrt{K}}\right) , \end{aligned}$$
which proves the first case of Theorems 3.3 and 33.
1.3.2 Case 2: Assumption 2.3 does not hold
Lemma 40
Suppose the Assumption 2.3 does not hold in Algorithm 5, we have
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi (\bar{x}_k)\Vert ^2\right] \\&\quad \le 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{C}{T} + 12CL_{f,0}^2\alpha ^N \\&\qquad + \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \frac{\eta _x^2(1+\kappa ^2)}{(1-\rho )^2}{\tilde{C}}_f^2. \end{aligned}$$
Proof
Denote by \({\hat{Z}}_{i,k}^{(N)}\) the output of each stochastic JHIP oracle 1 in Algorithm 5. Then
$$\begin{aligned} {\mathbb {E}}\left[ {\hat{Z}}_{i,k}^{(N)}\right] =Z_{i,k}^{(N)}, \end{aligned}$$
which implies
$$\begin{aligned} {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] = \overline{\partial \Phi (X_k)}. \end{aligned}$$
Hence we can follow the same process in case 2 of DBO to get (24) and thus
$$\begin{aligned}&\sum _{k=0}^{K}\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi ({{\bar{x}}}_k)\Vert ^2 = \sum _{k=0}^{K}\Vert \overline{\partial \Phi (X_k)} - \nabla \Phi (\bar{x}_k)\Vert ^2 \\&\quad \le 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{1}{n}\sum _{k=0}^{K}\sum _{i=1}^{n}\Vert y_{i,k}^{(T)} - \tilde{y}_k^*\Vert ^2 \\&\qquad + \frac{12L_{f,0}^2}{n}\sum _{k=0}^{K}\sum _{i=1}^{n}\Vert Z_{i,k}^{(N)} - Z_k^*\Vert ^2+ \frac{(1+\kappa ^2)}{n}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) S_K. \\&\quad \le 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{(K+1)C}{T} + 12(K+1)CL_{f,0}^2\alpha ^N\\&\qquad + \frac{(1+\kappa ^2)}{n}\cdot \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) S_K. \end{aligned}$$
The second inequality uses Lemmaa 14 and 15. Taking expectation, multiplying by \(\frac{1}{K+1}\), and using Lemma 38 we complete the proof. \(\square\)
The next lemma characterizes the variance of the gradient estimation.
Lemma 41
Suppose the Assumption 2.3 does not hold in Algorithm 5, then there exists \(\gamma _t = {\mathcal {O}}\left( \frac{1}{t}\right)\) such that
$$\begin{aligned} {\mathbb {E}}\Vert \overline{\partial \Phi (X_k; \phi )} - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2 \le 4\sigma _f^2(1+\kappa ^2) + (8L_{f,0}^2 + 4\sigma _f^2)\frac{C}{N}. \end{aligned}$$
Proof
Recall that we have:
$$\begin{aligned}&{\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi ) = \nabla _x f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) -\left[ {\hat{Z}}_{i,k}^{(N)}\right] ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) \\&{\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) = \nabla _x f_i(x_{i,k},y_{i,k}^{(T)}) -\left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}). \end{aligned}$$
By introducing intermediate terms we have
$$\begin{aligned}&{\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi ) - {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)}) \\&\quad = \nabla _x f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) - \nabla _x f_i(x_{i,k},y_{i,k}^{(T)}) - \left[ {\hat{Z}}_{i,k}^{(N)}\right] ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) \\&\qquad + \left( Z_k^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)})- \left( Z_k^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) \\&\qquad + \left( Z_k^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}) - \left( Z_k^*\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}) + \left( Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)}). \end{aligned}$$
Hence we know
$$\begin{aligned}&\Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi ) - {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)})\Vert ^2 \\&\quad \le 4\Vert \nabla _x f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) - \nabla _x f_i(x_{i,k},y_{i,k}^{(T)})\Vert ^2\\&\qquad +4\Vert \left( {\hat{Z}}_{i,k}^{(N)} - Z_k^* \right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)})\Vert ^2 \\&\qquad +4\Vert \left( Z_k^*\right) ^{{\textsf{T}}}(\nabla _y f_i(x_{i,k},y_{i,k}^{(T)};\phi _{i,k}^{(0)}) - \nabla _y f_i(x_{i,k},y_{i,k}^{(T)}))\Vert ^2\\&\qquad +4\Vert \left( Z_k^* - Z_{i,k}^{(N)}\right) ^{{\textsf{T}}}\nabla _y f_i(x_{i,k},y_{i,k}^{(T)})\Vert ^2. \end{aligned}$$
For the first term and the third term we use \({\mathbb {E}}\left[ \Vert \nabla f_i(x,y;\phi ) - \nabla f_i(x,y)\Vert ^2\right] \le \sigma _f^2\). For the second term (and the fourth term) we use the fact that stochastic (and deterministic) decentralized algorithm achieves sublinear rate (Lemma 15). Without loss of generality we can set C such that: \(\max \left( \frac{1}{n}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert {\hat{Z}}_{i,k}^{(N)} - Z_k^*\Vert ^2\right] , \Vert Z_{i,k}^{(N)}-Z_k^*\Vert ^2\right) \le \frac{C}{N}\). For partial gradients in the second and fourth terms, we use Assumption 2.1 and the fact that
$$\begin{aligned} {\mathbb {E}}\left[ \Vert X\Vert ^2\right] = {\mathbb {E}}\left[ \Vert X - {\mathbb {E}}\left[ X\right] \Vert ^2\right] + \Vert {\mathbb {E}}\left[ X\right] \Vert ^2 \end{aligned}$$
for any random vector X. Taking summation and expectation on both sides, we have
$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi ) - {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)})\Vert ^2\right] \\&\quad \le 4\sigma _f^2 + 4(L_{f,0}^2 + \sigma _f^2)\frac{C}{N} + \frac{4L^2}{\mu ^2}\sigma _f^2 + 4L_{f,0}^2\frac{C}{N}, \end{aligned}$$
which, together with
$$\begin{aligned}&{\mathbb {E}}\Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2\\&\quad \le \frac{1}{n}\sum _{i=1}^{n}{\mathbb {E}}\left[ \Vert {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)};\phi ) - {\hat{\nabla }}f_i(x_{i,k}, y_{i,k}^{(T)})\Vert ^2\right] , \end{aligned}$$
proves the lemma. \(\square\)
Now we are ready to give the final proof. Taking summation on both sides of (45) and putting Lemma 40 and 41 together we know:
$$\begin{aligned}&\frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] \\&\quad \le \frac{1}{K+1}\big (\frac{2}{\eta _x}({\mathbb {E}}\left[ \Phi (\overline{x_{0}})\right] - \inf _x\Phi (x)) +\sum _{k=0}^{K}{\mathbb {E}}[\Vert {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] - \nabla \Phi (\bar{x}_k)\Vert ^2]\big ) \\&\qquad +\frac{L\eta _x}{K+1} \sum _{k=0}^{K}{\mathbb {E}}\Vert \left[ \overline{\partial \Phi (X_k; \phi )}\right] - {\mathbb {E}}\left[ \overline{\partial \Phi (X_k; \phi )}\vert {\mathcal {F}}_k\right] \Vert ^2 \\&\quad \le \frac{2}{\eta _x(K+1)}({\mathbb {E}}\left[ \Phi (\overline{x_{0}})\right] - \inf _x\Phi (x)) \\&\qquad +12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{C}{T} + 12CL_{f,0}^2\alpha ^N \\&\qquad + \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \frac{\eta _x^2(1+\kappa ^2)}{(1-\rho )^2}{\tilde{C}}_f^2 +L\eta _x \left(4\sigma _f^2(1+\kappa ^2) + (8L_{f,0}^2 + 4\sigma _f^2)\frac{C}{N}\right) \\&\quad = \frac{2}{\eta _x(K+1)}({\mathbb {E}}\left[ \Phi (\overline{x_{0}})\right] - \inf _x\Phi (x)) + \left( \frac{36L_{f,0}^2L_{g,2}^2}{\mu ^2} + 2L_{f}^2\right) \frac{\eta _x^2(1+\kappa ^2)}{(1-\rho )^2}{\tilde{C}}_f^2 \\&\qquad + L\eta _x\left( 4\sigma _f^2(1+\kappa ^2) + (8L_{f,0}^2 + 4\sigma _f^2)\frac{C}{N}\right) + {\tilde{C}}_3, \end{aligned}$$
which completes the proof. Here the constant is defined as
$$\begin{aligned} {\tilde{C}}_3 = 12\left( 1 + L^2\kappa ^2 + \frac{2L_{f,0}^2L_{g,2}^2(1+\kappa ^2)}{\mu ^2}\right) \cdot \frac{C}{T} + 12CL_{f,0}^2\alpha ^N = {\mathcal {O}}\left( \frac{1}{T}+\alpha ^N\right) . \end{aligned}$$
By setting
$$\begin{aligned} N=\Theta (\log K),\ T=\Theta (K^{\frac{1}{2}}),\ \eta _x = \Theta (K^{-\frac{1}{2}}),\ \eta _y^{(t)} = {\mathcal {O}}\left( \frac{1}{t}\right) ,\ \end{aligned}$$
we have:
$$\begin{aligned} \frac{1}{K+1}\sum _{k=0}^{K}{\mathbb {E}}\left[ \Vert \nabla \Phi ({{\bar{x}}}_k)\Vert ^2\right] = {\mathcal {O}}\left( \frac{1}{\sqrt{K}}\right) , \end{aligned}$$
which proves the second case of Theorems 3.3 and 33.