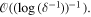Abstract
Waves in the plane, punctured by excision of a small disk with radius much smaller than the wavelength, can be modified by being forced to vanish on the boundary of the disk. Such waves exhibit a logarithmically thin 'pinprick', and logarithmically weak oscillations persisting far away. As the radius vanishes, these modifications become asymptotically invisible. Examples are punctured plane waves, and a punctured unit disk; in the latter case, the pinprick causes a logarithmic shift in the eigenvalues. It is conjectured that the plane can be densely covered with asymptotically invisible pinpricks, and that there are analogous phenomena in higher dimensions. The curious phenomenon of pinpricks is not hard to understand, and would be worth presenting in graduate courses on waves.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In the anatomy of waves, zeros are important. Examples are Dirichlet boundary conditions, nodal lines in 2D and surfaces in 3D for real waves, and their counterparts in complex scalar waves, namely points and lines of phase singularity. The aim here is to explore a simple type of zero.
Consider 2D for definiteness, and consider waves 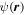 that vanish at points in the plane
that vanish at points in the plane 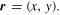 Point zeros of several types have already been studied. In complex scalar waves, they occur naturally, as phase singularities (also called wave dislocations or wave vortices [1–8]). In the Šeba quantum billiard [9], they can be created by a particular boundary condition corresponding to a Dirac delta potential, whose significance is that it can introduce wave chaos in systems where the classical dynamics is not chaotic—for example for free motion in a punctured rectangle. In the Aharonov–Bohm effect [10, 11], a line of magnetic flux generates a different type of zero, around which there is a phase change [12]. Mathematically, the Šeba and Aharonov–Bohm zeros can be regarded as self-adjoint extensions of the quantum Hamiltonian in the punctured plane [13]. In addition, plane-wave superpositions forced to vanish at points on a boundary [14] constitute an effective numerical method for computing mode wavefunctions and eigenvalues.
Point zeros of several types have already been studied. In complex scalar waves, they occur naturally, as phase singularities (also called wave dislocations or wave vortices [1–8]). In the Šeba quantum billiard [9], they can be created by a particular boundary condition corresponding to a Dirac delta potential, whose significance is that it can introduce wave chaos in systems where the classical dynamics is not chaotic—for example for free motion in a punctured rectangle. In the Aharonov–Bohm effect [10, 11], a line of magnetic flux generates a different type of zero, around which there is a phase change [12]. Mathematically, the Šeba and Aharonov–Bohm zeros can be regarded as self-adjoint extensions of the quantum Hamiltonian in the punctured plane [13]. In addition, plane-wave superpositions forced to vanish at points on a boundary [14] constitute an effective numerical method for computing mode wavefunctions and eigenvalues.
The zero considered here is different, and much simpler. A disk of small radius 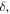 centred on a chosen point, is excised, and
centred on a chosen point, is excised, and 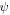 is required to vanish on its boundary, i.e. on a small circle of radius
is required to vanish on its boundary, i.e. on a small circle of radius 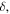 and the influence of this condition as
and the influence of this condition as 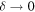 is studied. The result is that the zero differs from the ambient ('unperturbed') wave inside a logarithmically thin tube, outside which there are logarithmically weak ripples. The limit
is studied. The result is that the zero differs from the ambient ('unperturbed') wave inside a logarithmically thin tube, outside which there are logarithmically weak ripples. The limit 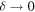 is singular, and can be regarded as a special case of the Šeba billiard boundary condition. In the limit
is singular, and can be regarded as a special case of the Šeba billiard boundary condition. In the limit 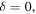 the zero is infinitely thin; it is asymptotically invisible, and we call it a 'logarithmic pinprick'. The limit
the zero is infinitely thin; it is asymptotically invisible, and we call it a 'logarithmic pinprick'. The limit 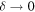 suggests application of perturbation theory. But this is not straightforward because the limit is a singular perturbation, so it is clearer to work with explicit solutions.
suggests application of perturbation theory. But this is not straightforward because the limit is a singular perturbation, so it is clearer to work with explicit solutions.
Section 2 gives the general theory of the pinprick. Section 3 gives two examples: section 3.1 describes a pinprick in a plane wave; section 3.2 describes a pinprick in a circular billiard (a disk with Dirichlet boundary conditions), where the eigenvalues (energy levels) are logarithmically shifted. The concluding section 4 discusses some extensions: peppering the plane densely with pinpricks, and analogous effects in higher dimensions; also, a note about limits.
The pinprick phenomenon is not immediately obvious, and the underlying analysis is not difficult. Therefore it would be an instructive exercise, worth presenting to students at the graduate level.
2. General pinprick theory
A sufficiently general setting is: free waves in the plane 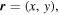 satisfying the Helmholtz equation with wavelength
satisfying the Helmholtz equation with wavelength 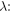

We excise a disk of radius 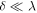 centred on a chosen point
centred on a chosen point 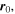 and require
and require 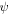 to vanish on its boundary (figure 1):
to vanish on its boundary (figure 1):

If the ambient wave, i.e. the wave before imposing the zero condition, is 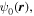 the zero condition can be most simply accommodated, sufficiently accurately, by adding a small multiple of the Bessel function of the second kind,
the zero condition can be most simply accommodated, sufficiently accurately, by adding a small multiple of the Bessel function of the second kind, 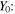

This is an exact solution of the linear equation (2.1) because it is the sum of two exact solutions. But it is an approximation to the boundary condition (2.2). On the circle 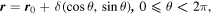
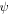 differs from zero by
differs from zero by 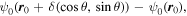 which is of order
which is of order 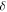 for
for 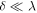 and therefore negligible. This is further justified in the appendix, by showing that the discrepancy can be eliminated by a series of corrections, each corresponding to a much thinner pinprick and weaker accompanying oscillations.
and therefore negligible. This is further justified in the appendix, by showing that the discrepancy can be eliminated by a series of corrections, each corresponding to a much thinner pinprick and weaker accompanying oscillations.
Figure 1. Logarithmic form of the pinprick close to the zero at 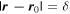 .
.
Download figure:
Standard image High-resolution imageClose to  i.e. for small
i.e. for small 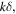 we can replace both Bessel functions by their small-argument limiting forms (see equation (10.8.2) of [15], including the logarithmic and constant terms), so
we can replace both Bessel functions by their small-argument limiting forms (see equation (10.8.2) of [15], including the logarithmic and constant terms), so

where, in terms of the Euler constant 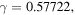

This is the asymptotic form of  close to the pinprick, and our main result, illustrated in figure 1.
close to the pinprick, and our main result, illustrated in figure 1.
Far from  i.e. away from the pinprick, the Bessel function
i.e. away from the pinprick, the Bessel function 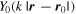 in (2.3) oscillates, indicating persistent undulations decorating the ambient wave. In the next section we will see that for small
in (2.3) oscillates, indicating persistent undulations decorating the ambient wave. In the next section we will see that for small 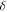 this influence is weak; we also describe a slight generalisation.
this influence is weak; we also describe a slight generalisation.
3. Examples
3.1. Plane wave
For an ambient plane wave in the 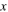 direction, with wavelength
direction, with wavelength 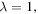 punctured at the origin, i.e.
punctured at the origin, i.e.

the pinpricked wave (2.3) is

Figure 2 shows the intensity
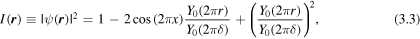
and the phase  for two values of
for two values of 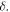 The thinness of the pinprick is evident in (a), (b).
The thinness of the pinprick is evident in (a), (b).
Figure 2. Intensity and phase of the pinpricked plane wave (3.2) for  (a), (c), (e), and
(a), (c), (e), and 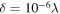 (b), (d), (f). (a), (b): intensities
(b), (d), (f). (a), (b): intensities 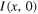 (red) and
(red) and  (black); (c), (d): intensity I(x, y); (e), (f): phase argψ(x, y), colour-coded by hue.
(black); (c), (d): intensity I(x, y); (e), (f): phase argψ(x, y), colour-coded by hue.
Download figure:
Standard image High-resolution imageFigures 2(a)–(d) show that the distant oscillations are surprisingly persistent even for 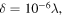 and slower and stronger in
and slower and stronger in 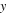 than
than 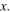 By contrast, (e), (f) show that the effect on the phase is comparatively weaker, illustrating the fact that pinpricks are not phase singularities (around which the phase would change by a nonzero multiple of
By contrast, (e), (f) show that the effect on the phase is comparatively weaker, illustrating the fact that pinpricks are not phase singularities (around which the phase would change by a nonzero multiple of 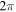 ).
).
Close to the zero, the limiting form of the intensity is (see 2.4)

From this it follows that the intensity halfwidth of the pinprick has radius

Far from the pinprick, large-argument Bessel asymptotics (section 10.17(i) of [15]) gives the asymptotic intensity oscillations along the 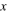 axis:
axis:
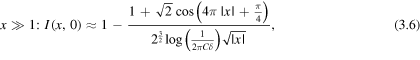
and along the 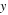 axis:
axis:
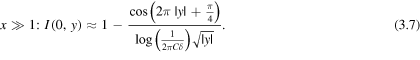
These agree to visual accuracy with the exact oscillations in figures 2(a) and (b) (comparison not shown).
For simplicity, an important aspect of the oscillations was not mentioned until now. In the pinprick formula (2.3), the replacement
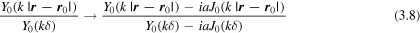
leaves the small 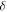 behaviour close to the pinprick unchanged, but alters the oscillations. For the particular choice
behaviour close to the pinprick unchanged, but alters the oscillations. For the particular choice 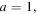 the factor is
the factor is

involving the Bessel function of the third kind. This choice corresponds to the oscillations representing outgoing radiation. In the appendix we will return to this generalisation.
3.2. Circular billiard
Consider azimuthally symmetric waves 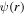 in the unit disk with Dirichlet boundary conditions,
in the unit disk with Dirichlet boundary conditions, 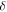 -punctured at the centre
-punctured at the centre 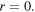 The ambient modes, nonvanishing at
The ambient modes, nonvanishing at  and vanishing at
and vanishing at  are the zero-order Bessel functions with zeros
are the zero-order Bessel functions with zeros  where
where 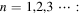

The punctured modes in the annulus 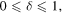 with perturbed eigenvalues
with perturbed eigenvalues 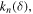 exactly satisfying (2.1) with the boundary condition (2.2), are
exactly satisfying (2.1) with the boundary condition (2.2), are
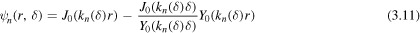
(in this case (2.3) is exact.) The eigenvalues 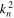 of the operator in (2.1), with the stated Dirichlet boundary condition at
of the operator in (2.1), with the stated Dirichlet boundary condition at  are determined by
are determined by

Figures 3 and 4 show the punctured modes for 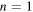 and
and  The pinpricks are clearly visible in figures 3(d) and 4(d), even for
The pinpricks are clearly visible in figures 3(d) and 4(d), even for 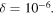 Away from the pinpricks, the modes are visibly altered for
Away from the pinpricks, the modes are visibly altered for 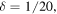 and hardly so for
and hardly so for 
Figure 3. Punctured circle billiard mode 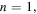 for (a), (b):
for (a), (b): 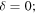 (c,d):
(c,d): 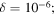 (e), (f):
(e), (f): 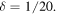 Figures (a), (c), (e) show the radial dependence (red), and the unperturbed wave (dashed), and figures (b), (d), (f) are 3D renderings.
Figures (a), (c), (e) show the radial dependence (red), and the unperturbed wave (dashed), and figures (b), (d), (f) are 3D renderings.
Download figure:
Standard image High-resolution imageFigure 4. As figure 3, for 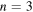 .
.
Download figure:
Standard image High-resolution imageThe shift in the eigenvalues, 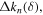 can be easily calculated numerically, or perturbatively from (3.12):
can be easily calculated numerically, or perturbatively from (3.12):
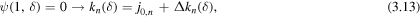
where, using 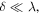

Figure 5 shows the fractional eigenvalue shifts as functions of 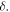
Figure 5. Fractional eigenvalue shifts 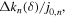 from (3.14).
from (3.14).
Download figure:
Standard image High-resolution imageThe formula (3.12) can be simplified using the approximation

This is the asymptotics for  but it can be used even for
but it can be used even for 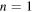 where the ratio is 0.9822; similarly, we can approximate
where the ratio is 0.9822; similarly, we can approximate 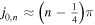 (accurate to 2% even for
(accurate to 2% even for 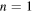 ). Thus the fractional shift of the
). Thus the fractional shift of the  (pinpricked) mode
(pinpricked) mode 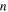 is
is

The factor 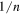 shows that the eigenvalue shift for fixed small
shows that the eigenvalue shift for fixed small 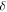 gets smaller as
gets smaller as  increases, as illustrated in figure 5 for
increases, as illustrated in figure 5 for 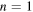 and
and 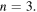
4. Concluding remarks
The foregoing has considered a single pinprick, but it is clear that the plane can be  punctured at more than one place. Indeed, a dense peppering of the plane with zeros can be envisaged, which would be invisible in the limit
punctured at more than one place. Indeed, a dense peppering of the plane with zeros can be envisaged, which would be invisible in the limit 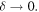 How dense? I conjecture that in the limit as
How dense? I conjecture that in the limit as 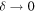 the pinpricks can form a set of fractal dimension
the pinpricks can form a set of fractal dimension 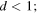 dimension
dimension 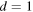 is excluded because this would include Dirichlet conditions along a line, which would certainly not be invisible.
is excluded because this would include Dirichlet conditions along a line, which would certainly not be invisible.
For waves in three-dimensional space, asymptotically invisible pinpricks would form lines, arbitrarily curved, possibly closed, linked or knotted, and arbitrarily numerous. In addition, there can be point zeros, based on excising small spheres of radius 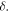 The theory is similar, with
The theory is similar, with 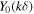 replaced by the spherical Bessel function
replaced by the spherical Bessel function 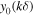 [15], so the radius (intensity half-width) of the pinpricks would be
[15], so the radius (intensity half-width) of the pinpricks would be  rather than
rather than 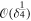 as in (3.5). Extension to higher space dimensions
as in (3.5). Extension to higher space dimensions  is clear: asymptotically invisible pinpricks can be created, with codimensions
is clear: asymptotically invisible pinpricks can be created, with codimensions 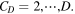
Complementary to pinpricks would be positive spikes ('prickles') instead of zeros. To create these is simple: instead of the negative modification (2.3), add 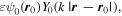 with
with 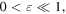 to the ambient wave. As
to the ambient wave. As 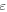 decreases to zero, the prickles get asymptotically invisible.
decreases to zero, the prickles get asymptotically invisible.
A note about limits. The emphasis here is the pinprick limit 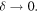 Other limits need not commute with it. For example, if the
Other limits need not commute with it. For example, if the 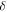 -excised disk is in a region of the plane with a rectangular perimeter, or if the plane is compactified into a 2-torus, the system is the Sinai billiard [16], whose geometrical ('classical') trajectories exhibit chaos: exponential separation of infinitesimally close initial trajectories as
-excised disk is in a region of the plane with a rectangular perimeter, or if the plane is compactified into a 2-torus, the system is the Sinai billiard [16], whose geometrical ('classical') trajectories exhibit chaos: exponential separation of infinitesimally close initial trajectories as 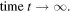 This obviously does not commute with
This obviously does not commute with 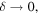 because as
because as 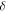 gets smaller the chaos gets longer to develop, and when
gets smaller the chaos gets longer to develop, and when 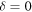 it never does. And in the wave version, the eigenvalues for finite
it never does. And in the wave version, the eigenvalues for finite 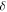 reflect the classical chaos by exhibiting random-matrix statistics [17–19]. The
reflect the classical chaos by exhibiting random-matrix statistics [17–19]. The 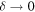 limit also does not commute with the classical limit
limit also does not commute with the classical limit 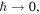 which in this case corresponds to the short-wave limit
which in this case corresponds to the short-wave limit 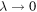 of high excited states: as
of high excited states: as 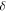 gets smaller, it is necessary to search higher in the spectrum in order to see the random-matrix statistics (this is discussed in appendix C of [17]).
gets smaller, it is necessary to search higher in the spectrum in order to see the random-matrix statistics (this is discussed in appendix C of [17]).
Acknowledgments
I thank the Beijing Institute for Mathematical Sciences and Applications (BIMSA) and Peking University for hospitality while this work was carried out. My research was supported by the Leverhulme Trust.
Data availability statement
No new data were created or analysed in this study.
Appendix
Appendix. Corrections to the pinprick formula (2.3)
Here we show how the boundary condition (2.2) can be satisfied exactly. Setting 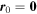 and
and 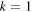 for convenience, we expand the ambient wave in circular-harmonic solutions of (2.1), using polar coordinates:
for convenience, we expand the ambient wave in circular-harmonic solutions of (2.1), using polar coordinates:

(For the example wave (3.1), 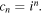 ) The approximation (2.3) corresponds to modifying the term
) The approximation (2.3) corresponds to modifying the term 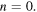
The boundary condition at 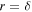 can be satisfied exactly for each
can be satisfied exactly for each 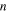 separately, by adding a contribution to
separately, by adding a contribution to 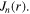 The modification depends on other boundary conditions that the exact
The modification depends on other boundary conditions that the exact 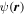 must satisfy. For a real wave, as in section 3.2, the modification is
must satisfy. For a real wave, as in section 3.2, the modification is

For the infinite plane, the modification can be any combination of incoming and outgoing waves, depending on the radiation condition. For the outgoing choice, it involves Bessel functions of the third kind, as described for 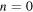 at the end of section 3.1, and can be conveniently written
at the end of section 3.1, and can be conveniently written

For 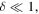 the difference between the coefficients in (A.2) and (A.3) disappears; the small argument limiting forms of the Bessel functions [15] gives
the difference between the coefficients in (A.2) and (A.3) disappears; the small argument limiting forms of the Bessel functions [15] gives
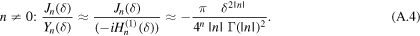
For 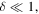 these
these 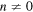 coefficients are
coefficients are 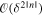 and therefore negligible in comparison with the
and therefore negligible in comparison with the 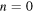 coefficient, which (see (2.4)) is
coefficient, which (see (2.4)) is  Therefore the
Therefore the 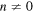 corrections correspond to thinner pinpricks, reflecting the familiar s wave scattering of scalar waves by infinitesimal obstacles.
corrections correspond to thinner pinpricks, reflecting the familiar s wave scattering of scalar waves by infinitesimal obstacles.
For 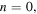 the real and outgoing modifications are different for the
the real and outgoing modifications are different for the 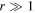 oscillations. In the example in section 3.1 we have chosen the real modification in equation (3.2), but the order of magnitude of the oscillations is the same for the outgoing case: both vanish as
oscillations. In the example in section 3.1 we have chosen the real modification in equation (3.2), but the order of magnitude of the oscillations is the same for the outgoing case: both vanish as