On Boundary Conditions for Magnetohydrodynamic Waves in Flux Tubes with a Pressure Jump

Starting from the observation that quite a number of papers on magneto-acoustic waves in solar magnetic flux tubes exploit the approximation that the kinetic pressure is negligible compared to the magnetic pressure in the loop, β = 0, Yelagandula (2023) (to be cited as Y23), for β ≠ 0 proposes to replace the boundary condition for the radial displacement ξ,

$$\begin{eqnarray}&&[[{\boldsymbol{n}}\cdot {\rm{}}\,{\rm{\xi }}]]=0\Rightarrow [[\xi ]]=0\qquad (\mathrm{at}\ r=a),\end{eqnarray} \tag{ 1 }$$

by a similar boundary condition on the radial magnetic field perturbation Q. Here, the notation is used of the textbook by Goedbloed & Poedts (2004) (to be cited as GP04) since Y23 refers to Equation (1) as coming from that textbook, and expresses doubts on its validity. It may be convenient for some readers to also refer to the newer version of that book by Goedbloed et al. (2019) (to be cited as GKP19). In the notation of GP04 and GKP19, the subscripts 0 for the equilibrium quantities and 1 for the perturbations are omitted by exploiting different symbols, in particular ξ and Q (instead of the velocity perturbation v ₁ ≡ ∂ξ/∂t and the magnetic field perturbation B ₁ exploited by Y23). Moreover, radial components of these vectors are indicated by the scalars ξ and Q, whereas double square brackets indicate the jump of the quantity enclosed. Note that all these expressions refer to cylindrical geometry where the normal n to the equilibrium boundary surface points in the radial direction. According to Y23, replacing the boundary condition (1) by [[Q]] = 0 at r = a should be appropriate for flux tubes with a pressure jump at that boundary, β ≠ 0, and also would do justice to the more fundamental nature of the variable Q  ≡  B ₁. The fact that the boundary condition [[ξ]] = 0 is then no longer satisfied is to be taken for granted.

We can agree with the remark that the magnetic field perturbation Q is the most fundamental quantity in magnetohydrodynamics. In fact, the linearized form obtained from the time-integrated laws of Faraday and Ampère presents an intricate relation between the magnetic field perturbation Q and the plasma displacement vector ξ,

$$\begin{eqnarray}&&{\boldsymbol{Q}}={\rm{\nabla }}\times ({\rm{}}\,{\rm{\xi }}\times {\boldsymbol{B}}).\end{eqnarray} \tag{ 2 }$$

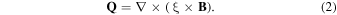
For cylindrical geometry with Fourier harmonics $\exp [i(m\theta +{kz})]$, its radial component reads:

$$\begin{eqnarray}&&Q=i\,F\xi ,\qquad F\equiv {{mB}}_{\theta }/r+{{kB}}_{z},\end{eqnarray} \tag{ 3 }$$

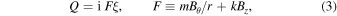
where F is the parallel gradient operator, central to all MHD wave phenomena. It guarantees that the magnetic field moves with the plasma (as frequently stated, "the magnetic field is frozen into the plasma"). A consequence is that the magnetic field, which is tangential to the equilibrium magnetic surfaces, also remains tangential to the magnetic surfaces when they are perturbed. This holds for all magnetic surfaces, including the one under discussion at the pressure discontinuity at r = a. In equilibrium, that pressure jump is balanced by jumps of the magnetic field produced by surface currents,

$$\begin{eqnarray}&&[[{B}_{\theta }]]=-{j}_{z}^{* },\qquad [[{B}_{z}]]={j}_{\theta }^{* }.\end{eqnarray} \tag{ 4 }$$

Observing the boundary condition (1), this implies a jump of Q,

$$\begin{eqnarray}&&[[Q]]=i[[F]]\xi =i\left\{(m/r)[[{B}_{\theta }]]+k[[{B}_{z}]]\right\}\xi ,\end{eqnarray} \tag{ 5 }$$

but not of ξ! It is important to notice that this equation is not a boundary condition, but just a consequence of the flux conservation Equation (2), or (3), valid everywhere, here applied to points on the boundary. This expression appears to bear no resemblance to the fact that the magnetic field should be tangential to the magnetic surfaces. Hence, the normal component of the total magnetic field should vanish, n  ·  B  = 0, whereas the expression for the radial magnetic field perturbation Q is only part of the answer. Transformation of the normality condition from the unperturbed to the perturbed position is still needed. This is the complicated part to which we will come.

But, first of all, it needs to be stressed that ignoring the boundary condition (1) in Y23 is a fatal mistake. This boundary condition ensures that, with compression, the inner and outer plasma do not move into each other and, with decompression, the two plasmas do not move apart leaving a void in between. The new boundary condition [[Q]] = 0 proposed by Y23 directly contradicts Equation (5) and, hence, the boundary condition (1). Returning to the need to transform the normality condition, it is instructive to compare Figure 1 of Y23 with Figure 6.17 of GP04 (or Figure 6.13 of GKP19). That first figure of Y23 shows how the wrong boundary condition on Q is obtained from the usual pill box geometry of classical electrodynamics, applied to a fixed boundary, whereas our figure refers to the entirely non-trivial relationship between the unperturbed and the perturbed boundary. It is not accidental that, in our textbooks, the discussion of the simple looking boundary condition (1) (Equation (6.144) of GP04 or Equation (6.135) of GKP19) is preceded by the extensive exposition in Section 6.6.1 on "Boundary conditions at the interface." Omitting the algebraic details of that section, we just present the two essential steps in the reduction of the normality condition:

$$\begin{eqnarray}&&\begin{array}{l}0={\boldsymbol{n}}\cdot {\boldsymbol{B}}\approx [{{\boldsymbol{n}}}_{0}-({\rm{\nabla }}{\rm{}}\,{\rm{\xi }})\cdot {{\boldsymbol{n}}}_{0}+{{\boldsymbol{n}}}_{0}\,{{\boldsymbol{n}}}_{0}\cdot ({\rm{\nabla }}{\rm{}}\,{\rm{\xi }})\cdot {{\boldsymbol{n}}}_{0}]\\ \quad \cdot \ ({{\boldsymbol{B}}}_{0}+{\boldsymbol{Q}}+{\rm{}}\,{\rm{\xi }}\cdot {\rm{\nabla }}{{\boldsymbol{B}}}_{0})\approx {{\boldsymbol{n}}}_{0}\cdot \left[{\boldsymbol{Q}}-{\rm{\nabla }}\times ({\rm{}}\,{\rm{\xi }}\times {{\boldsymbol{B}}}_{0})\right].\end{array}\end{eqnarray} \tag{ 6 }$$

Here, n ₀ is the normal to the unperturbed surface and B ₀ is the equilibrium magnetic field at that position. The outermost right-hand side (rhs) of this equation shows that the condition (2) (and, hence, the consequences (3)–(5) for cylindrical geometry) ensures that the perturbed magnetic field remains tangential to the magnetic surfaces. The approximation signs indicate that the expressions are only valid to first order in ξ. This is also the case for the boundary condition (1) since ξ itself is by definition a first order quantity, so that higher order contributions may be neglected. Hence, the misleadingly simple form of the first interface condition ( 1 ). This simplicity does not carry over to the derivation of the boundary condition on the total pressure perturbation Π. There, the normality condition returns in a different form, and Y23 again exploits the wrong pill box argument assuming a fixed instead of a moving boundary. From Equation (6.147) of GP04 (or Equation (6.137) of GKP19), the appropriate form of the second interface condition reads:

$$\begin{eqnarray}\begin{array}{rcl}[[{\rm{\Pi }}]] & = & -[[{\boldsymbol{n}}\cdot {\rm{\nabla }}(p+\tfrac{1}{2}{B}^{2})]]\,{\boldsymbol{n}}\cdot {\rm{}}\,{\rm{\xi }}\Rightarrow [[{\rm{}}\,{\rm{\Pi }}]]\\ & = & \ -[[(p+\tfrac{1}{2}{B}^{2})^{\prime} ]]\,\xi =[[{B}_{\theta }^{2}/r]]\,\xi \quad {\rm{(at}}\ r=a).\end{array}\end{eqnarray} \tag{ 7 }$$

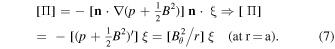
Here, Π ≡ − γ p∇ · ξ − ξ · ∇p +  B  ·  Q indicates the total pressure perturbation, whereas the left expression refers to general and the right one to cylindrical geometries. The equilibrium jumps on the rhs of the equality signs of Equation (7) are missing in the wrong boundary condition (30) of Y23. Notice that the jump $[[{B}_{\theta }^{2}/r]]$ is precisely the one responsible for the external kink mode instability of the sharp boundary model of the z-pinch, which was a concern in the early days of nuclear fusion research.

In conclusion, replacing the two boundary conditions (1) and (7) by [[Q]] = 0 and [[Π]] = 0, supposed by Y23 to provide a more appropriate description for the magnetohydrodynamic waves in a flux tube with a pressure jump at the boundary, is fundamentally wrong. The results of that paper should be discarded. In particular, a classification of the different waves resulting from the modified dispersion equations thus obtained for β ≠ 0, which would supersede the standard classification obtained for β = 0, is illusory. Apart from posing the wrong boundary conditions, it also ignores the much more complicated part of solving the differential equation for the magnetohydrodynamic waves with pressure terms present, so that the slow magneto-sonic waves enter and the Bessel function solutions exploited in the standard case in general no longer apply. The virtue of the standard classification is that it avoids those complications by restricting the wavevectors to be dominantly perpendicular to the magnetic field and β to be small enough to allow neglect of the Alfvén and slow wave contributions. There is nothing wrong with that.

DIFFER is part of the institutes organization of NWO (the Netherlands Science Organization). S.P. is supported by the projects C14/19/089 (C1 project internal Funds KU Leuven), G.0B58.23N and G.0025.23N (Weave) (FWO-Vlaanderen), 4000134474 (CIDEX, ESA Prodex-12) and Belspo project B2/191/P1/SWIM.