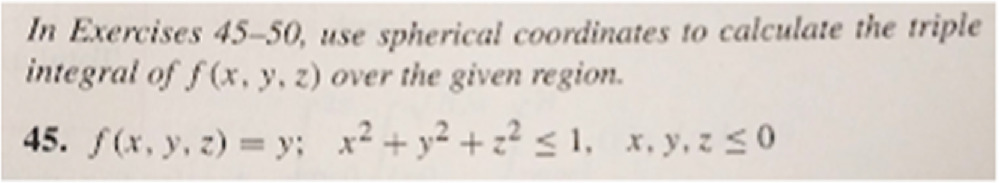Abstract
Upper-division undergraduate physics coursework necessitates a firm grasp on and fluid use of mathematical knowledge, including an understanding of non-cartesian (specifically polar, spherical and cylindrical) coordinates and how to use them. A limited body of research into physics students' thinking about coordinate systems suggests that even for upper-division students, understanding of coordinate system concepts is emergent. To more fully grasp upper-division physics students' incoming understanding of non-cartesian coordinates, the prevalence of non-cartesian content in seven popular Calculus textbooks was studied. Using content analysis techniques, a coding scheme was developed to gain insight into the presentation of coordinate system content both quantitatively and qualitatively. An initial finding was that non-cartesian basis unit vectors were absent in all but one book. A deeper analysis of three of the calculus textbooks showed that cartesian coordinates comprise an overwhelming proportion of the textbooks' content and that qualitatively the cartesian coordinate system is presented as the default coordinate system. Quantitative and qualitative results are presented with implications for how these results might impact physics teaching and research at the middle and upper-division.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
1.1. Motivation and literature review
The ability to communicate mathematically and quantitatively are fundamental skills necessary to succeed in physics. In fact, student success in undergraduate physics courses has been generally correlated with their prior mathematical knowledge and performance [1–6]. Such skills become even more important in upper-division physics courses, such as classical mechanics, quantum mechanics, electromagnetic theory, and thermodynamics, where the mathematics necessary for these courses is much more involved and complex than introductory level coursework [7–11] and mathematical models and physical principles inform each other and students' understanding of physics in more interwoven ways [12–14]. As such, physics students often struggle with the mathematics essential to upper-division coursework [15, 16]. The manner in which the language of mathematics is used in mathematics courses and in physics courses differ in ways that have been characterized as the two disciplines speaking different dialects of the same language, or even speaking two different languages [12]. While communities of physicists and mathematicians might use the same word when referring to a particular mathematical entity, they may struggle to understand the full definition and implications of the other group's use of the word. This myriad of factors informs research efforts to consider students' understanding and employment of mathematics at the upper-division level in physics. Therefore, within both a broader call for additional educational research to be conducted at the upper-division in physics [17] and a larger effort to study students use and understanding of math in the upper-division [18], an effort is underway to develop a research-informed curriculum for a mathematical methods course for undergraduate physics majors. This paper focuses on a preliminary portion of that effort by investigating Calculus textbooks for the prevalence of non-cartesian coordinates and unit vector content.
Many upper-division physics textbooks contain explicit instruction on unit vectors and unit vector notation in both cartesian and non-cartesian coordinate systems, particularly in the disciplines of electromagnetic theory [7] and classical mechanics [8–11]. These mathematical tools are later used within those textbooks to describe physical phenomena such as position, velocity, forces, electric and magnetic fields, etc., in both cartesian and non-cartesian coordinates with and without the associated unit vectors. The presence of this mathematical instruction early in many upper-division textbooks conveys an understanding by the authors that students need to have an ability to use these tools later in the textbook.
Literature in math contexts have suggested that, in general, student understanding of non-cartesian coordinate systems is weak. Montiel, Vidakovic, and colleagues have performed several studies specifically on student understanding of functions in polar coordinates, which demonstrated that student understanding of functions and other mathematical concepts are often tied to the coordinate system in which they were initially taught, cartesian [19, 20]. Moore, Paoletti, and Musgrave [21] studied mathematics students who had previously taken mathematics through Calculus III, and observed difficulties with polar coordinates, specifically student difficulties with the ordered pair (r, θ), which reads (dependent, independent) in comparison to the cartesian ordered pair (x,y) which reads (independent, dependent), when there are functional dependencies for each. Further, Moore et al claimed that when students had difficulty with polar coordinate systems, they would return to employing ideas from cartesian coordinate systems to their thinking about polar systems.
In physics, Sayre and Wittmann [22] studied students in a junior-level Classical Mechanics course and found that students' understanding of the polar coordinate system was under formation and flexible (more plastic, in their terminology), than students' understanding of cartesian coordinate systems. Their results demonstrate that students often start a problem presuming a cartesian coordinate system, and furthermore, persist in using the cartesian coordinate system even when a polar coordinate system serves the question better. Hinrichs [23] surveyed upper-division undergraduate and graduate physics students at four different institutions asking them to write algebraic expressions for position vectors in spherical coordinates for four points all a distance of 5 units from the origin. The correct answer for all points is 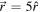 , which is subtle because
, which is subtle because 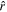 represents a different direction for each point on a cartesian axis or if one were to use cartesian unit vectors. Nearly half of respondents gave an answer in the cartesian-imitating form
represents a different direction for each point on a cartesian axis or if one were to use cartesian unit vectors. Nearly half of respondents gave an answer in the cartesian-imitating form 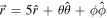 . Hinrichs referred to this type of response as 'pattern-matching.' Farlow, Vega, Loverude, and Christensen [24] replicated Hinrichs's results through think-aloud interviews on a similar question. All of their interview subjects gave similar pattern-matched responses to questions about polar and spherical position vector expressions. The case study subject in their study showed examples of activating resources consistent with cartesian coordinates while constructing such expressions.
. Hinrichs referred to this type of response as 'pattern-matching.' Farlow, Vega, Loverude, and Christensen [24] replicated Hinrichs's results through think-aloud interviews on a similar question. All of their interview subjects gave similar pattern-matched responses to questions about polar and spherical position vector expressions. The case study subject in their study showed examples of activating resources consistent with cartesian coordinates while constructing such expressions.
Work by Pepper, Chasteen, Pollock and Perkins [25, 26] has tied student difficulties with certain mathematical concepts and techniques to their difficulties in upper-division Electricity and Magnetism. Manogue, Browne, Dray, and Edwards [27] has done similar work to Pepper et al, specifically focusing on student difficulties with Ampere's Law, and how mathematical background informs that particular physical application. Additionally, Schermerhorn and Thompson [28, 29] have done work exploring some of the challenges students face while thinking about differential elements in non-cartesian coordinates and developed some instructional materials that used vector calculus concepts to help mitigate some of the challenges students face within that domain in the context of electromagnetic theory.
Vega et al [30] found that student thinking regarding basis unit vectors in polar coordinates was often conflated with or informed by the motion of an object rather than the mathematical rules for basis unit vectors. Farlow et al [24] performed a case-study analysis of a single student, identifying and organizing the student's resources into groups thematically based on the question the student was answering when that resource activated. That case study subject demonstrated multiple examples of disagreement with their previously stated and productively activated ideas and demonstrated a still emerging understanding of the mathematical consequences of non-cartesian basis unit vectors' directions being location-dependent.
In summary, there is body of work linking success in physics courses to students' mathematical ability and background. While most of this work comes from the introductory level, there are studies at the upper-division that further demonstrate this link. Additionally, it is clear that both math and physics students struggle with concepts in non-cartesian coordinate systems and often employing methodology or resources tied to cartesian coordinates, which may be due to these concepts being introduced to them in cartesian coordinates [24]. We believe this serves as the initiation of a broader conversation about what students are taught in calculus classes and how that instruction impacts how physics instructors should introduce specific topics in their upper-division physics courses (see section 4.8).
1.2. Research questions
Students' mathematics understanding is vital to their success in physics, we seek to study mathematics instruction regarding the different types of coordinate systems and their associated vector concepts students' receive before they reach upper-division physics courses. The work presented here characterizes Calculus textbooks that are presumed to convey concepts regarding cartesian, polar, spherical, and cylindrical coordinates. We conducted an analysis of multivariable calculus content within several popular calculus textbooks to answer the following questions:
- (1)Compared to cartesian coordinates, to what extent are non-cartesian coordinates represented in multivariable calculus textbooks?
- (2)What are the natures of the presentation and application of the various coordinate systems?
- (3)To what extent are mathematical topics/concepts (i.e. unit vectors, multiple integration, etc) presented in different coordinate systems?
The first question quantitatively considers how much multivariable textbook content overall is based in each coordinate system. The second question qualitatively seeks to determine the skills assumed and/or required of certain coordinate systems. The third question examines the initial and general presentation of individual mathematical concepts or topics and their relationship to different coordinate systems.
More generally, this textbook analysis sheds light on the mathematical background students entering upper-division physics classes will likely have regarding coordinate systems. Doing so gives physics faculty an empirically-based 'starting point' for their upper-division physics course content and allowing them to meet students where they are.
2. Methodology
Seven multivariable calculus textbooks [31–38] (see table 1) were selected due to their prevalence in Multivariable Calculus classrooms. The textbooks were selected based on their popularity among Calculus III textbooks according to a best sellers list on Amazon (during the summer of 2017). While other sampling methods could be considered, the goal was to categorize the most commonly used textbooks in contemporary Calculus courses and we are confident that this meets the needs of our study. These textbooks were analyzed using content analysis techniques [39]. Also, Boas's mathematical methods in the physical sciences textbook [31], a commonly used mathematical methods in physics textbook, was analyzed, specifically to serve as a reference of what a mathematical methods in physics course might require with respect to non-cartesian coordinate systems. The Boas textbook was not used when calculating means and other statistics across textbooks because it serves as a reference of comparison, and its content and purpose are fundamentally different from the other textbooks.
Table 1. Calculus textbooks reviewed.
| Author(s) | Book Title | Edition | Year | |
|---|---|---|---|---|
| 1 | Boas, ML | Mathematical methods in physical sciences | 3 | 2006 |
| 2 | Briggs, W, Cochran, L, Gillett, B, Schulz, E | Calculus early transcendentals | 2 | 2015 |
| 3 | Goldstein, LJ, Lay, DC, Schneider, DI, Asmar, NH | Calculus ans its applications | 14 | 2018 |
| 4 | Larson, R, Edwards, B | Calculus | 11 | 2018 |
| 5 | McCallum, WG, Hughes-Hallet, D, Flath, D, Mumford, D., Gleason, AM, Osgood, BG et al | Calculus multivariable | 6 | 2013 |
| 6 | Rogawski, J, Adams, C | Calculus | 3 | 2015 |
| 7 | Stewart, J | Calculus: early transcendentals | 8 | 2016 |
| 8 | Thomas, GB, Weir, MD, Hass, J | Thomas' calculus early transcendentals single variable with second-order differential equations | 1 | 2011 |
Several qualitative aspects were examined across the textbooks. To determine where and how non-cartesian content was presented, both the content and the structure were examined. The structure of the content was examined to identify the particular chapters/topics which employed non-cartesian coordinates and then to examine how those topics/chapters presented non-cartesian coordinate systems, in particular, in relation to cartesian coordinate systems.
Each book was initially reviewed to determine whether there were any instances where non-cartesian coordinate systems were explicitly stated, or where the variables associated with a non-cartesian coordinate system were used. If non-cartesian content was present, that chapter was tagged for a more in-depth review.
After this initial round of analysis, it was clear that both quantitative and qualitative analysis would be necessary. Quantitative questions primarily require a 'chapter-based' unit of analysis: in order to determine the proportions of chapters and subsections with non-cartesian content it was necessary to determine the number of sections/chapters that contained such content out of the total numbers of sections/chapters. The qualitative questions are aimed toward determining the nature of the presentation of content, necessitating a 'topic-based' unit of analysis.
For chapter-based analysis, once a chapter was tagged as having non-cartesian content, an analysis of where and to what extent non-cartesian coordinates exist within a chapter was completed. Specific attention was given to when non-cartesian coordinates are introduced, and how the particular behavior and characteristics unique to those coordinate systems was presented. Results reported in this paper on the proportion of content from cartesian and non-cartesian coordinate systems came from this chapter-based analysis. This chapter-based analysis also served as a starting point to discern the nature and type of problems in non-cartesian coordinates mathematics students are expected to solve.
Analyzing the data by topics allowed the specific concepts to stand out more clearly since they might occur within the same chapter in one book, but in different chapters, or not at all, in another textbook. By distinguishing the data by topic rather than chapters, it is also easier to determine whether particular topics were introduced in cartesian or non-cartesian coordinates first, and whether the topics were introduced in distinct sections or in the same section. Moore et al [21] reported that a mathematical concept may continue to carry some associations from the coordinate system in which it was introduced, therefore, it was noted if a concept/topic was introduced in non-cartesian coordinates before, coinciding with, or after its introduction in cartesian coordinate systems (in distinct subsections). Results reported in this paper on the nature and order of presentation of content primarily come from this topic-based analysis.
In order to determine the prevalence of different coordinate systems, three different types of items were coded: (1) definitions, theorems, and properties; (2) worked example problems; (3) exercises. Definitions, theorems, and properties that were boxed separately from the main body text were examined, as these are items that textbook authors are attempting to make the most salient. Additionally, example problems were coded, as these examples model procedural approaches to both students and instructors. Finally, textbook problems were coded, because these constitute the work given to students as assignments.
Each item's content was evaluated to determine what coordinate system it employed across multiple characteristics. A coding scheme was designed addressing five different characteristics with regard to these particular items. Three of the characteristics were very explicit and were applicable to all items. The last two characteristics were item-specific, and the last item required a slightly higher level of interpretation than the other items.
First, the notation used was assessed: specifically, attempting to understand and record what coordinates were used within each item. If x, y, and/or z was used, cartesian notation was marked. If r and θ were used in 2D problems, polar notation was marked. If r, θ, and/or z were used in 3D problems, cylindrical notation was marked. If ρ, θ, and/or ϕ, were used, spherical notation was marked.
Next, any explicit mention of a coordinate system within an item is recorded. Specifically, an explicit mention might take the form of a particular definition or property within specific coordinate systems, or instructions to use specific coordinate systems. Some problems specifically requested students to decide between using particular coordinate systems. These problems were recorded separately.
Third, the coordinate system denoted by the notation of any item's accompanying figure(s) is recorded. No code was made for items without figures.
The fourth characteristic was specifically for worked example problems, and focused on the coordinate system used in the presented solution. If there was only a transformation from one coordinate system within the example, and the second coordinate system was used for the rest of the problem, the second coordinate system would be recorded, since it was the one predominantly used. However, if two coordinate systems were both used beyond a straightforward conversion or transformation, it would be recorded that multiple coordinate systems were used.
The fifth characteristic was for exercises and problems for students to work themselves. It centers around the idea of 'cue-ing.' Items can have particular cues that strongly imply that a particular coordinate system would be best to use to solve a problem. Identifying these cues requires more interpretation from the coder. The cues that were marked were only those that were very obvious, specifically including forms of the equation for a circle, cylinder, and sphere in cartesian coordinates, or the words 'circle,' 'cylinder,' 'sphere,' or 'cone,' in cartesian coordinates. If there was explicit direction in the textbook to use a particular coordinate system, a cue would not be recorded.
These five characteristics are meant to be a simple but complete categorization of the ways in which a coordinate system could be represented within a textbook item. After the coding scheme was developed and revised, two of the authors coded a subset of the textbook sections independently. The interrater reliability for that sample was 96%. This high level of interrater reliability assured that a single author could code the remaining sections.
In order to avoid coding all the examples, problems, and graphics from every chapter, several textbooks were compared, and it was determined that many chapters of the textbooks did not include non-cartesian coordinate systems at all. Accordingly, after examining two textbooks, Stewart's [37] and Rogawski and Adams's [36] in their entirety, only the chapters including non-cartesian coordinate systems were examined further, including topics on vector geometry, vector functions, and multiple integration.
3. Results
Presented here are the data from our analysis with commentary and discussion to follow in section 4.
3.1. Representation of topics in non-cartesian coordinate systems
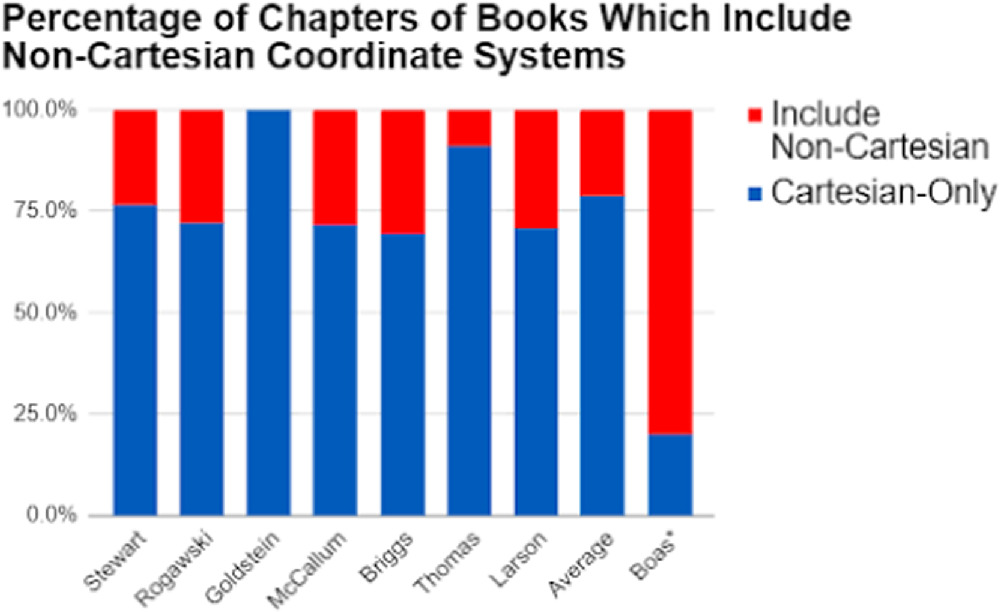
Proportional results for inclusion of cartesian and non-cartesian problems by topic are shown in figure 1. Note that 'Not included' refers to the topics that were not referred to in a textbook at all. Also of note is that many of these concepts arose within the same chapters—the common chapter themes were variants of coordinate geometry, vector geometry, vector calculus, and multiple integration. Figure 2 illustrates the percentage of chapters which include any instance of non-cartesian coordinates by book. Across the multivariable calculus textbooks we assessed, on average, 78.7% of chapters contained cartesian-only content. Boas, the mathematical methods in physics textbook we assessed had 20% of chapters, or 3 out of 15, that contained cartesian-only content.
Figure 1. Total proportions of coordinate system content inclusion, by topic, across all reviewed textbooks.
Download figure:
Standard image High-resolution imageFigure 2. On average over 75% of the chapters in the analyzed calculus books contained only cartesian-coordinate content. *The Boas Math Methods [31] textbook was included in this chart for comparison and is not used in the data analysis.
Download figure:
Standard image High-resolution image3.2. Prevalence of different coordinate systems in chapters that include non-cartesian coordinates
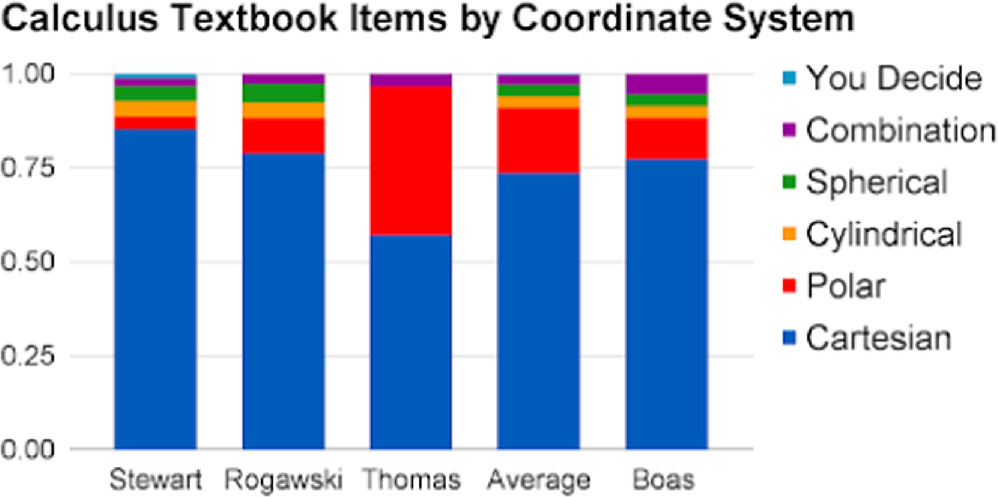
Figure 3 illustrates the proportion of coordinate systems across textbook items. Note that the data in figure 3 is not representative of each textbook as a whole, as only the chapters that included non-cartesian coordinate systems were coded qualitatively. Therefore, figure 3 must also be read with an understanding of figure 2, which denotes which chapters do not include any instance of non-cartesian coordinates.
Figure 3. Of the roughly 25% of textbook chapters that contained any non-cartesian-coordinate content, the bulk of the content was still cartesian in nature. Additionally, only one textbook provided any opportunity for students to determine which coordinate system was most advantageous for a given situation.
Download figure:
Standard image High-resolution imageFor the three Multivariable Calculus books we coded in-depth 81.7% of notation used was cartesian, 83.7% of figures used favored cartesian, and 79.4% of example solutions were cartesian. 20.7% of instructions stated to use cartesian coordinates, and 24.7% of problems were coded for using strong cues that indicated which specific coordinate system to use. Again, these data are only for those items within chapters that feature any non-cartesian coordinates at all. These numbers do not include the notation, figures, and solutions which used both cartesian and non-cartesian content.
3.3. Qualitative trends
Among all the Calculus textbooks, mathematical topics that include non-cartesian coordinates (with the exception of Vector Fields) are introduced in separate subsections from the cartesian discussion of the topic, and are universally introduced later. In Boas, the mathematical methods in physics textbook, similar trends of cartesian coordinates preceding non-cartesian coordinates are observed. However, Boas incorporates non-cartesian coordinates more organically within subsections and chapters. A second trend observed in the data communicates an assumed default of cartesian coordinates: within all the calculus books, there were 28 subsections with explicit language denoting non-cartesian coordinate systems or a technique for them and none explicitly denoting cartesian coordinate systems.
4. Discussion
4.1. Prevalence of non-cartesian coordinate material
The key takeaway from this work is the overwhelming prevalence of cartesian coordinates in the Calculus textbooks. Across the three books coded, on average, 81.7% of notation of coded content used cartesian, 82.5% of figures used cartesian, and 80.5% of example solutions were in cartesian. The notation and the figures demonstrate a cartesian-centric presentation of content and establishes cartesian coordinates as the default coordinate system. This trend was also observed in worked example solutions, conveying that problems are most often expected to be solved in cartesian coordinates. The relatively small number of instructions and problem cues in cartesian, 20.7% and 24.7% respectively, further establish cartesian as the default system, whereas problems using non-cartesian coordinate systems require specific instructions or cues. In summary, across all seven books, approximately 20% of the chapters contain non-cartesian content. Of those 20% of chapters, on average roughly 26% of that content is non-cartesian for the three books we analyzed on an item-by-item basis.
The cartesian-centric nature of these textbooks does not support students on a trajectory into upper-division physics courses. These courses expect students to utilize the symmetry of a system to choose the most useful or convenient coordinates and unit vectors for each situation [31–38].
4.2. Presentation of non-cartesian coordinate material
Within the Calculus textbooks, non-cartesian coordinates do not appear until seven or more chapters into each book. In all books, all topics with the exception of Vector Fields were introduced using cartesian coordinates. In all the books which included vector fields, they were introduced in a single, stand-alone subsection where all coordinate systems were employed. Previous research demonstrates that learning a topic in one coordinate system can often transfer coordinate system-specific ideas about the topic to a coordinate system in which those transferred ideas are not appropriate [19–21]. Therefore, it is logical that students learning material from these textbooks, which introduce topics in cartesian coordinate systems, are likely to transfer ideas from cartesian coordinate systems to non-cartesian coordinate systems. Such transfer aligns with previous physics education research within upper-division physics courses [23, 24]. Such transfers can create barriers to students' ability to understand and solve problems best suited for non-cartesian coordinates in upper-division physics courses. For example, students might hold the idea that the time derivatives of unit vectors stay constant over time, something true for unit vectors in cartesian coordinates but not for unit vectors in non-cartesian coordinates, both of which can be seen in Farlow et al [24].
Most topics in non-cartesian coordinate systems were introduced in distinct subsections from their original introduction. As a result, students are only given explicit opportunities to consider non-cartesian coordinates in a limited number of cases. Therefore, because of the way the material was presented, students had fewer opportunities to choose between different coordinate systems for particular problems, a skill often required in upper-division physics coursework.
4.3. Coordinate system choice
It is notable that exercises asking for students to decide between two or more coordinate systems only arose in one textbook, Stewart [37]. Furthermore, even though coordinate choice was present in this book, these exercises made up only 1.1% of the coded items in chapters which include non-cartesian content. Additionally, only 3.4% of coded items in chapters which include non-cartesian content involved a combination of multiple coordinate systems. We take these data to claim that most of the non-cartesian coordinate content presented was somewhat surface level, as very few problems required students to choose between coordinate systems or to consider multiple coordinate systems when reading the book. These results suggest that, in their multivariable calculus coursework, students have very little experience with choosing the best coordinate system to use for particular situations. In contrast, upper-division physics textbooks regularly contain problems that do not provide a particular coordinate system to solve the problem with, and instead ask students to use their knowledge of symmetries to solve the problem [7–11] (an example of this will be presented below in section 4.7). Students' lack of experience with choosing particular coordinate systems paired with the cartesian-centric nature of these multivariable calculus textbooks may contribute to students' reasoning illustrated in Vega et al [30] and Farlow et al [24] in which students sometimes resort to cartesian coordinates when posed with physics problems rather than choosing coordinates based strictly on geometries.
4.4. Content of non-cartesian coordinate material present
When students are given an opportunity to practice with non-cartesian content, the examples and exercises tend to present the material in a surface-level manner. As an example of surface-level problems, we mean problems that only require a conversion between two coordinate systems, most commonly where the choice of coordinates that are being converted are explicitly named in the problem or use variables associated with a particular system. The example from page 881 of Rogawski and Adams (3rd edition) [36] in figure 4 represents a typical textbook exercise. It explicitly states which coordinate system students should use to solve problems, and indicates through the variables used, that the equation given is in cartesian coordinates.
Figure 4. An example exercise from Calculus by Rogawski and Adams [36]—section 16.4, page 881—showcasing the explicit nature of instruction predominantly present in calculus textbooks when non-cartesian content is expected to be used. This presentation is in contrast to physics textbooks where it is often left to the reader to determine which coordinate system is appropriate and why.
Download figure:
Standard image High-resolution imageThese problems are more surface level than more advanced content often required in upper-division physics courses, requiring only simple conversion and integration rather than a more nuanced understanding of non-cartesian coordinate systems. In upper-division physics textbooks, students are expected to not only solve the problem, but choose the coordinates and unit vectors that will allow them to solve the problem. An example of this can be seen below in section 4.7.
4.5. Three dimensions and non-cartesian coordinate systems
Three-dimensional non-cartesian coordinate systems are even less prevalent than polar coordinate systems, with an average of 17.6% of polar content, 5.4% of cylindrical content, and 2.7% of spherical content over the coded content within the chapters that were not solely cartesian in the multivariable calculus books. Surprisingly, three-dimensional basis unit vectors were not introduced in any of the multivariable calculus books. Only one book, Rogawski and Adams [36], introduced polar unit vectors. In our conversations with physics faculty and other education researchers this may be the most surprising result. The fact that most students coming out of a calculus sequence will have never seen non-cartesian unit vectors is rather alarming. These proportions contrast starkly to the representation of these topics in upper-division physics courses. As mentioned previously, in upper-division physics courses, students are often faced with three dimensional problems that require or are vastly simplified by their use of non-cartesian coordinates. Many of the relevant expressions are written in unit-vector notation. Many of these problems involve symmetries in the spherical and cylindrical directions due to physical phenomena like fields of charges and solenoids or wires.
4.6. Synthesizing results
This sample of calculus textbooks consistently presents mathematical concepts first in cartesian coordinates and then presents the same concept in other coordinate systems later, often in separate sections. They also present content with the built-in assumption that cartesian coordinates are the default coordinates, not requiring any explicit instruction or statement. Whereas problems using non-cartesian coordinate systems are nearly always accompanied by explicit instructions to do so. This structuring provides answers to the qualitative aspects of research questions 2 and 3: non-cartesian coordinate systems are predominantly presented after and as translations of cartesian coordinates and as tools to be used when instructed to do so. Individual mathematical concepts, such as unit vectors, are also first introduced in the cartesian coordinate system and then later their behavior is explained in non-cartesian coordinates, if such non-cartesian behavior is explained at all.
When these quantitative and qualitative findings are considered together, a hidden curriculum emerges. Hidden Curriculum refers to a set of educational theories initially developed in the 1960s and 1970s [40–45]. These theories assert that a hidden curriculum constitutes material which students are expected to learn but are not explicitly taught and/or material of which students learn implicitly through the context of the explicit content: how and when content is presented and/or through the norms and practices of their academic environments [46]. Increasing the awareness of the hidden curricula within explicit curricula has been an ongoing effort within both mathematics [47, 48] and physics [49, 50]. Given the data presented in this review, the overwhelming cartesian-centric nature and the concurrent surface-level applications of non-cartesian coordinate systems do communicate the expectations outlined in multivariable calculus textbooks and set cartesian coordinates as the default coordinate system. Such expectations differ from those students' encounter in upper-division physics coursework.
4.7. Implications
The most immediate implication of this work is for instructors of upper-division physics courses. As mentioned previously, non-cartesian coordinates and non-cartesian unit vectors are utilized extensively in the upper-division physics curriculum. Many common mechanics textbooks—like Taylor [8], Thornton and Marion [9], Kleppner and Kolenkow [10], and Fowles and Cassiday [11]—and Griffiths's Introduction to Electrodynamics [7] explicitly introduce non-cartesian coordinates and their associated basis unit vectors in their first chapters. The tasks for students in these courses can convey very different expectations about a student's familiarity with non-cartesian coordinates than what's required in their Multivariable Calculus mathematics coursework. As an example, consider the fifth physics problem in Chapter 2 from Griffiths EM textbook.
The question asks students to determine the electric field due to a uniform circular charge distribution at a point on the z-axis above the plane of that distribution (figure 5). The problem statement does not specify which coordinates or basis vectors (unit vectors) are best for solving the problem. Recall that our analysis shows that selecting the best coordinates-type problems are only present in two of the textbooks, and thus represent an exceptionally small number of problems in the Calculus textbook. It is, therefore, a task with which students likely have little preparation. The 'cues' within the Griffiths problem are also ambiguous compared to those we observed in the calculus textbooks. While the solution intends students to use cylindrical coordinates with cylindrical unit vectors or cartesian coordinates with cartesian unit vectors, the problem labels the radius with the symbol r, a coordinate typically reserved for polar or polar spherical coordinates in Griffith's text.
Figure 5. This image is used in problem 2.5 of Griffiths EM textbook [7]. The reader is asked to determine the electric field at point P due to a uniform circular charge distribution of radius r. This problem can be simplified by leveraging physical principles, but the full analytic solution requires deep understanding about various spatial coordinate systems. Such spatial understanding is in contrast to typical calculus textbook exercise (see figure 4) that often give explicit instruction as to which coordinate system(s) is required or expected.
Download figure:
Standard image High-resolution imageAssuming the student does elect to solve the problem using cylindrical coordinates, the problem's initial mathematical setup is relatively straightforward. However, a correct solution cannot be obtained staying in cylindrical coordinates and unit vectors unless a shortcut that leverages physical principles—in this case the components of the electric field parallel to the plane of the loop summing to zero—is used to eliminate the ' term' of the integral. If a student sets up the integral properly and just 'does the math' the answer will be incorrect. If a student did not realize this physical shortcut, then the initial cylindrical model would have to be translated into cartesian coordinates (or the problem initially set up in cartesian) where three integrals are evaluated, showing that the x- and y-components' integrals equal zero around the loop and the z-component integral is non-zero.
term' of the integral. If a student sets up the integral properly and just 'does the math' the answer will be incorrect. If a student did not realize this physical shortcut, then the initial cylindrical model would have to be translated into cartesian coordinates (or the problem initially set up in cartesian) where three integrals are evaluated, showing that the x- and y-components' integrals equal zero around the loop and the z-component integral is non-zero.
This problem requires fluency with the various coordinate systems and their limitations, the ability to translate between coordinate systems, and the ability to construct mathematical models using unit vector notation. It also includes an additional possibility of using physical reasoning to simplify the solution process. This problem is offered early in the second chapter of a twelve chapter physics textbook. It demonstrates the gap between the level of understanding of non-cartesian coordinate systems expected of students in upper-division physics courses and the understanding conveyed and expected across a number of Calculus textbooks.
The ultimate goal of this work is to inform the development of research-informed curricula for a mathematical methods in physics course. A goal of the developed materials will be to bridge what students have likely been taught and understand from mathematics courses with what is expected of them in the upper-division physics level.
Additionally, this work lays out a methodological framework for identifying the extent to which other concepts are introduced within mathematics textbooks. Further analysis of additional topics could further inform physics instructors about what students are being taught and the tools they are more likely to have upon entering a math methods course, or an upper-division physics course.
4.8. Authors' insights for upper-division physics instructors
The suggestions in this subsection are based on the authors intuition garnered from years of experience in both physics education research and research in undergraduate mathematics education. This intuition is formed, in part, by a deep understanding of the data presented in this paper and other work showing physics students' emerging understanding on non-cartesian coordinates and non-cartesian vector concepts [22–24, 30]. Whenever physics instructors ask students to engage with a problem or a topic that necessitates students use non-cartesian coordinates and/or non-cartesian unit vectors, faculty should expect that additional time should be committed to instruction on those topics explicitly. Before embarking directly on those non-cartesian ideas, collect data on the students' understanding of cartesian unit vectors and conduct some formative assessments in class. Provide appropriate instruction based on their feedback and build from ideas of cartesian unit vectors and extend those ideas to spherical and cylindrical unit vectors and coordinates. Students' understanding about non-cartesian coordinates might be limited to converting cartesian coordinates to non-cartesian coordinates and, in some cases, be limited to applying how cartesian unit vectors behave when moving to non-cartesian unit vectors. More fundamentally, it is important to realize that students likely have little-to-no prior instruction on or intuition about thinking in non-cartesian coordinates or using non-cartesian unit vectors.
5. Limitations and future work
A few limitations of this work are worth considering. Categorical content analysis was only performed on four of the eight textbooks reviewed. However, upon examination of the other textbooks we are confident the ones we analyzed were representative of the larger sample. Moreover, the review is specifically of textbooks, which may not perfectly represent what instructors teach and what students learn in a multivariable calculus classroom. Looking at a number of textbooks gives a broad sense of what resources multivariable calculus instructors and students have, but does not examine how the textbook is used as a resource for calculus instructors and students.
These limitations are to be addressed in future work, in which interviews will be conducted with Multivariable Calculus instructors. Moreover, interviews and focus groups will be conducted with multivariable calculus students. We have also created a survey assessing student thinking regarding cartesian coordinates and unit vectors that was given after all instruction in multivariable calculus and the analysis of which will be the subject of a future publication.
The most significant steps ahead for this work will be the creation and testing of curricular materials for the mathematical methods course and other upper-division physics courses. We believe this work along our other research outcomes will lay the groundwork for developing such research-informed curriculum. While our plans have been to utilize resources and framing [51–54] as the theoretical underpinnings of this curriculum development, through the review process of this paper, we've begun to think more broadly. Duval [55] raises a number of issues relevant to the translation of mathematical notation to essential understanding. His work might more fully inform the question of why students are having challenges with non-cartesian content due to the notation involved and how we might address those challenges. Furthermore, we can consider Lemke's use of semiotics as a framework for understanding meaning-making of symbols in contexts beyond math and science may provide more insight into student thinking within the use of math in physics [56]. The work of Doran may serve as a useful guide, as he uses Lemke's framework to make claims about the affordances of images and language in mathematics for use in physics knowledge [57]. As this work progresses into its next phases, a great deal of consideration can be given to these new ideas.
6. Conclusion
Through reviewing seven multivariable calculus textbooks using content analysis techniques, the data show that mathematical topics in these texts are predominantly represented using the cartesian coordinate system. This study demonstrates that topics in non-cartesian coordinate systems are predominantly introduced in textbooks both separately and subsequent to those topics in cartesian coordinate systems. Moreover, the chapters that do include non-cartesian coordinates include very few exercises that ask students to consider multiple coordinate systems or ask them to decide what coordinate system is most appropriate for a specific exercise. This surface-level coverage demonstrates a difference between the types of problems students have mathematical preparation for and the types of problems students are expected to solve in upper-division physics courses.
Cartesian coordinate systems were much less frequently explicitly named or stated to use than non-cartesian coordinate systems, despite the overwhelming prevalence of cartesian coordinate systems in textbooks. The explicit naming of non-cartesian systems and the lack of naming cartesian systems implies that when a coordinate system is not characterized, students will expect and/or use cartesian coordinates. Overall, in the textbooks reviewed, cartesian coordinate systems were predominantly the first introduced, the most used, and the default when solving problems. Thus, students entering upper-division physics courses are likely to bring limited or still emerging understandings of non-cartesian coordinate systems. Further, their ideas about specific mathematical concepts might be tied to how those concepts behave in cartesian coordinates. These findings will inform efforts to develop targeted curriculum to help students bridge the gap between how these concepts are used in math courses and how they are used in upper-division physics courses. However, in the interim, it is also important for current upper-division physics course instructors to be aware of the still developing understanding their students are likely to have about coordinates and unit vectors.
Acknowledgments
Funding for this research was provided by NSF DUE #1406035, NSF DUE #1156974, NSF DUE #1560142. Thank you to grant collaborators Dr Michael E Loverude, Dr John Thompson, Dr Benjamin Schermerhorn, and Samantha Gisi; NDSU CiDER REU Program; NDSU Physics Department and STEM-Ed PhD Program; and Dr John Buncher for insightful feedback on this work.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).