Abstract
The Double Asteroid Redirection Test (DART) mission impacted Dimorphos, the satellite of binary near-Earth asteroid (65803) Didymos, on 2022 September 26 UTC. We estimate the changes in the orbital and physical properties of the system due to the impact using ground-based photometric and radar observations, as well as DART camera observations. Under the assumption that Didymos is an oblate spheroid, we estimate that its equatorial and polar radii are 394 ± 11 m and 290 ± 16 m, respectively. We estimate that the DART impact instantaneously changed the along-track velocity of Dimorphos by −2.63 ± 0.06 mm s−1. Initially, after the impact, Dimorphos's orbital period had changed by −32.7 minutes ± 16 s to 11.377 ± 0.004 hr. We find that over the subsequent several weeks the orbital period changed by an additional 34 ± 15 s, eventually stabilizing at 11.3674 ± 0.0004 hr. The total change in the orbital period was −33.25 minutes ±1.5 s. The postimpact orbit exhibits an apsidal precession rate of 6.7 ± 0 2 day−1. Under our model, this rate is driven by the oblateness parameter of Didymos, J2, as well as the spherical harmonics coefficients, C20 and C22, of Dimorphos's gravity. Under the assumption that Dimorphos is a triaxial ellipsoid with a uniform density, its C20 and C22 estimates imply axial ratios, a/b and a/c, of about 1.3 and 1.6, respectively. Preimpact images from DART indicate Dimorphos's shape was close to that of an oblate spheroid, and thus our results indicate that the DART impact significantly altered the shape of Dimorphos.
2 day−1. Under our model, this rate is driven by the oblateness parameter of Didymos, J2, as well as the spherical harmonics coefficients, C20 and C22, of Dimorphos's gravity. Under the assumption that Dimorphos is a triaxial ellipsoid with a uniform density, its C20 and C22 estimates imply axial ratios, a/b and a/c, of about 1.3 and 1.6, respectively. Preimpact images from DART indicate Dimorphos's shape was close to that of an oblate spheroid, and thus our results indicate that the DART impact significantly altered the shape of Dimorphos.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The Double Asteroid Redirection Test (DART) mission was the first planetary defense demonstration mission to test the effectiveness of a kinetic impactor to deflect an asteroid (Cheng et al. 2016). The spacecraft was launched on 2021 November 24 UTC from the Vandenberg Space Force Base in California, and after a roughly 10 month cruise, it impacted Dimorphos, the satellite of binary near-Earth asteroid Didymos, on 2022 September 26 at 23:14 UTC (Daly et al. 2023). Goldstone radar observations about 12 hr after impact provided the first estimate of the orbital period change of Dimorphos of −36 ± 15 minutes (Thomas et al. 2023). Subsequent optical and radar observations over a timespan of about 2 weeks refined the period change estimate to −33.0 ± 1.0 minutes (Thomas et al. 2023). This orbital period change corresponds to a momentum transfer efficiency, β, between 2.2 and 4.9 (Cheng et al. 2023). Using images taken by the Didymos Reconnaissance and Asteroid Camera for Optical navigation (DRACO) on board the DART spacecraft, Daly et al. (2024) estimate the axes of the best-fitting Dimorphos ellipsoid to be 173 × 170 × 113 m prior to the DART impact. Elsewhere, Barnouin et al. (2023) used DRACO and the Light Italian Cubesat for Imaging of Asteroids (LICIACube) imagery to obtain the best-fitting ellipsoid of Didymos as 818 × 796 × 590 m.
The impact and the aftermath were observed by several ground-based observatories as well as spacecraft, including the Lucy spacecraft (H. Weaver et al. 2023, in preparation) and the LICIACube, which was released 15 days prior to impact (Dotto & Zinzi 2023). Using the Hubble Space Telescope, Li et al. (2023) monitored the complex evolution of the ejecta under the influence of gravity and solar radiation pressure starting about 15 minutes after impact for about 19 days. The observations not only provided insight into the kinetic impactor technique of asteroid deflection but also shed light on the formation and evolution of active asteroids.
Moskovitz et al. (2024) continued photometric observations of the system until 2023 February, extending the observational data arc by about 4 months beyond that used in Thomas et al. (2023). Here we show that the additional data reveal more complex dynamical effects and enable estimation of higher-order terms in the gravitational fields of Didymos and Dimorphos. In this work, we used the same general estimation approach as described in Naidu et al. (2022) and Thomas et al. (2023), although fitting the extended data set required a higher-fidelity dynamical model (Section 2) and more precise measurements of the mutual event times (Section 3).
Our approach differs from Scheirich et al. (2024) in terms of the observables, models, and fitting algorithm. The method of Scheirich et al. (2024) fits the entire primary-subtracted lightcurve, including portions that are outside the mutual events, whereas we model only mutual event times observed in the primary-subtracted lightcurves. In addition to lightcurves, we also fit radar delay and Doppler measurements as well as DART spacecraft observations that were taken on approach to the Didymos system. Our orbital model contains additional parameters such as the absolute dimensions of Dimorphos and Didymos, the J2 of Didymos, and the ΔV of Dimorphos due to the DART impact.
2. Dimorphos Orbital Model
For the preimpact orbit, we used the same dynamical model as that described in Naidu et al. (2022) and Thomas et al. (2023). We assumed Dimorphos is a point mass on a modified circular Keplerian orbit about Didymos. The sole non-Keplerian effect was an additional term to capture the drift in mean motion of Dimorphos due to nongravitational forces such as binary YORP. The mean anomaly (M) and mean motion (n) of Dimorphos at time t < timp (time of DART impact) are given by
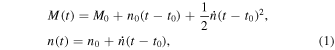
where M0 and n0 are the mean anomaly and mean motion at the epoch t0 and  is the rate of change of mean motion.
is the rate of change of mean motion.
We treat the effect of DART on the Dimorphos orbit as an instantaneous, impact-induced velocity change (ΔV) in the radial (ΔVR ) and transverse (ΔVT ) directions. Since the DART velocity vector was almost aligned to the plane of the mutual orbit (Daly et al. 2023), we assumed no velocity change in the normal direction (ΔVN ), thus keeping the problem planar and simplifying the postimpact orbit integration.
We obtain the state (i.e., position and velocity) of Dimorphos immediately after impact by adding the impulse (ΔV) to the velocity at impact from the preimpact orbit. We used this state as the initial condition for integrating the postimpact orbit. This approach maintains position continuity across the DART impact and guarantees self-consistency between the preimpact and postimpact positions of Dimorphos, which is not necessarily the case when fitting separate preimpact and postimpact orbits as was done in Thomas et al. (2023).
To integrate the postimpact orbit, we assumed Didymos to be an oblate spheroid and Dimorphos to be a triaxial ellipsoid. With these assumptions, we derived the equations of motion following the planar full two-body problem formulation described by Scheeres (2009).
The potential energy for the system shown in Figure 1 is defined as
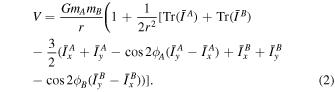
Here mA
and mB
are the masses of the primary and secondary, 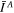 and
and 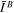 are the mass-normalized inertia tensors of the primary and the secondary, ϕA
and ϕB
are the orientation angles of the primary and secondary with respect to the inertial frame, and r is the distance between the two objects. For a triaxial ellipsoid,
are the mass-normalized inertia tensors of the primary and the secondary, ϕA
and ϕB
are the orientation angles of the primary and secondary with respect to the inertial frame, and r is the distance between the two objects. For a triaxial ellipsoid, 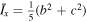 and
and 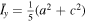 , where a, b, and c are the semiaxes of the ellipsoid from longest to shortest. Since we assume Didymos to be an oblate spheroid, we have
, where a, b, and c are the semiaxes of the ellipsoid from longest to shortest. Since we assume Didymos to be an oblate spheroid, we have 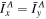 , and the orientation angle of Didymos is ϕA
= 0. We can also replace the moments of inertia with spherical harmonics coefficients, C20 and C22, using the following relations:
, and the orientation angle of Didymos is ϕA
= 0. We can also replace the moments of inertia with spherical harmonics coefficients, C20 and C22, using the following relations:
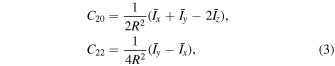
where R is the longest semiaxis of the body (circumscribing radius).
Figure 1. The planar full two-body problem from Scheeres (2009).
Download figure:
Standard image High-resolution imageUsing Equations (2) and (3) and the equations in Section 2.3 in Scheeres (2009) and introducing a time-dependent, draglike transverse acceleration 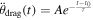 (described in Section 5), we can derive the following equations of motion:
(described in Section 5), we can derive the following equations of motion:
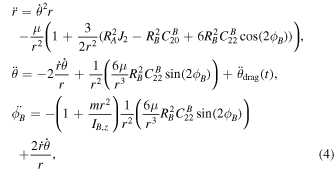
where m = mA
mB
/(mA
+ mB
) is the reduced mass of the system, μ = G(mA
+ mB
), RA
and RB
are the circumscribing radii of the primary and the secondary, 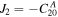 , and
, and 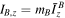 .
.
We tested the importance of solar tides on the mutual orbit and found them to be negligible due to the proximity of the two bodies compared to the distance of the Sun. Solar tides arise from small differences in the solar gravitational force on the two bodies.
3. Observations
Our main observational data set consists of the start and end times of occultations and eclipses, collectively known as mutual events, that are evident in primary-subtracted photometric lightcurves of the Didymos–Dimorphos binary system. The observations and data reduction and the processing to extract the primary-subtracted lightcurves are described in Pravec et al. (2006, 2022) and Moskovitz et al. (2024).
There are four kinds of mutual events that cause temporary dips in the brightness of the primary-subtracted lightcurves. These events are
- 1.primary eclipses (secondary casting shadows on the primary),
- 2.secondary eclipses (primary casting shadows on the secondary),
- 3.primary occultations (secondary obscuring illuminated portions of the primary), and
- 4.secondary occultations (primary obscuring illuminated portions of the secondary).
The shapes and depths of the mutual events vary depending on the geometry of the Sun, the observer, and the Didymos system. Under certain conditions there can also be partial events, where only a fraction of the secondary body causes the mutual event, or overlapping events, where an eclipse and an occultation overlap in time.
For primary events, i.e., events when the primary is being occulted or eclipsed by the secondary, we measured times when the center of mass (COM) of Dimorphos would have entered or exited a mutual event. The measurements were made with the help of a photometric model described in Section 4. The model generates synthetic primary-subtracted lightcurves corresponding to observed mutual events and marks times on the synthetic lightcurves when the secondary COM crosses the terminator or the lit limb. This method allowed us to measure the times more accurately than we did using our simpler measurement method in Naidu et al. (2022) and Thomas et al. (2023). Using the synthetic lightcurves as a guide, we measured corresponding COM crossing times in the observed lightcurves. We assigned 1σ uncertainties of 25% of the time taken by the event to reach full depth. The assigned errors are conservative and take into account measurement errors as well as limitations of the assumed models.
For secondary events, we used the method outlined in Naidu et al. (2022) to measure the times when the brightness drop was half the full event depth. These times correspond to moments when half of the flux from Dimorphos is occulted or eclipsed. Like the primary events, we assigned 1σ uncertainties to be 25% of the time from the onset of the mutual event until it reached full depth. We used the observational model of Naidu et al. (2022) to compute corresponding synthetic observations required for orbit determination. However, we replaced the phase correction model with the photometric model described in Section 4. The phase correction model described in Naidu et al. (2022) assumed Lambertian scattering, which we found was not able to produce the observed events with adequate fidelity.
The choice of event start and stop times as an observable (as opposed to using all of the observed lightcurve's photometric data points) simplifies the model used by the orbit determination process for generating synthetic data points corresponding to the observations, speeding up the orbit determination process. Because of this simplification, we did not use partial events in which the COM of Dimorphos did not take part in the mutual event.
Our mutual event observation times are available at Naidu & Chesley (2023). We also used the positions of Dimorphos relative to Didymos measured in radar delay-Doppler images, radar echo power spectra, and images taken by DRACO on board the DART spacecraft. These data sets are available at Naidu & Chesley (2023) and described in Thomas et al. (2023).
4. Photometric Model
We developed a photometric model to generate synthetic mutual events corresponding to observed events. To estimate the brightness of the system at a given time, we first generated a snapshot of the system in the plane of sky by using SPK 7 files to position Dimorphos, the Sun, and the Earth relative to Didymos. We assumed both bodies to be oblate spheroids, with the Didymos size based on our estimate. For the Dimorphos shape, we used the best-fitting ellipsoid given in Daly et al. (2024), scaled up by 6% to match the observed event depths. We projected these shapes as ellipses in the plane of the sky.
We divided the region of the plane of the sky containing the Didymos system into a grid of pixels with a resolution of 6 m pixel–1. Using a grid with finer resolution does not have a perceptible effect on the mutual event times. We computed the brightness of each pixel by integrating the brightness of the surface beneath that pixel, taking into account if the surface was occulted or eclipsed by the other body.
To compute the brightness profile of the surface of each body, we computed the incidence and emission angles using the relative positions of the Sun and the Earth and used the Lommel–Seeliger photometric scattering model (Seeliger 1884; Hapke 2012) as described in Huang et al. (2017). For the model parameters, we used the mean values for S-type asteroids reported by Huang et al. (2017).
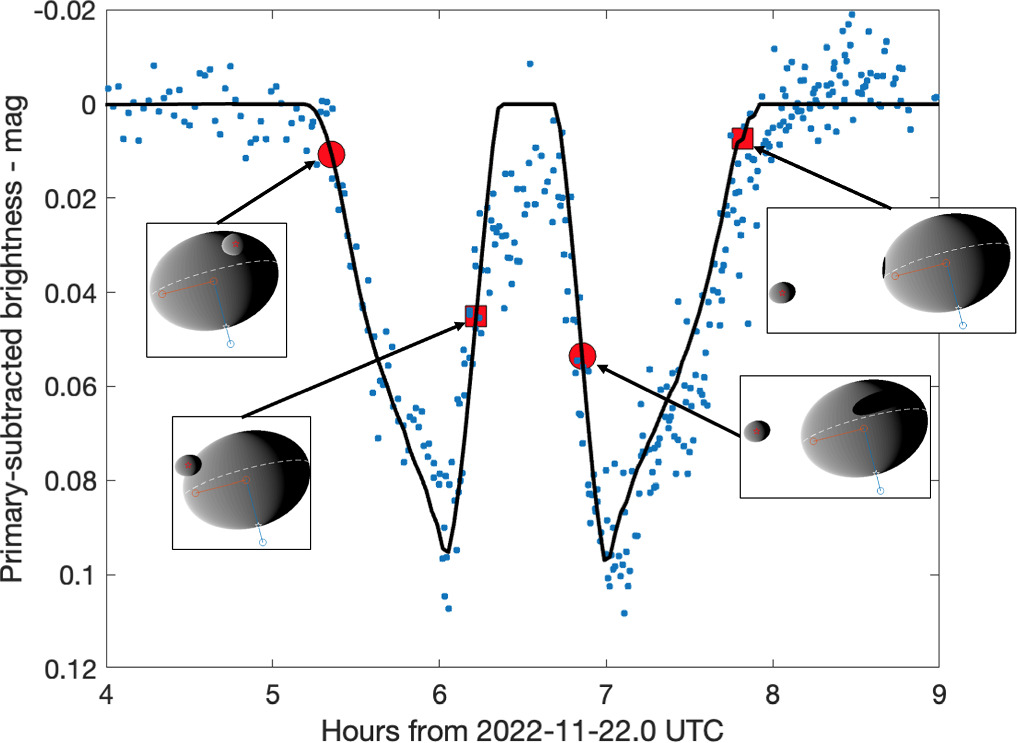
We stepped through the time frames covering the observed mutual events and computed the brightness of the system at each time step to generate synthetic primary-subtracted lightcurves. As an example, Figure 2 compares the observation and model for two primary mutual events and shows that our model is able to reasonably reproduce the observed mutual events.
Figure 2. Photometric measurements (dots) from Moskovitz et al. (2024) of a primary occultation (left minimum) and primary eclipse (right minimum) overlaid with our photometric model (black curve) described in Section 4. Red circles (squares) show the times when the COM of Dimorphos, or the COM shadow, entered (exited) the mutual event. Inset figures show the system configuration corresponding to these event start and stop times.
Download figure:
Standard image High-resolution imageFor primary events, we define the start and end of the events by the time, as seen from Earth, that the center of Dimorphos (for primary occultations) or the shadow of its center (for primary eclipses) crosses either the terminator or the limb of Didymos. Figure 2 plots these times for an example primary occultation and eclipse pair and depicts the binary configuration at each of these times. We used these synthetic lightcurves to estimate the relative depths in the primary-subtracted lightcurve of these start and end times. Our measured event times were the times in the observed lightcurves when the event brightness reached the corresponding depth.
As mentioned above, secondary events were handled somewhat differently from primary events. We defined the secondary start and end times as the times that the brightness crossed half of the full depth for that event. We used our photometric model to identify these "half-depth" times for each event in order to compute a time correction based on the Lomell–Seeliger model. These half-depth times were compared to the times that the COM of Dimorphos entered or exited the eclipse or occultation condition in order to derive a time correction due to a nonzero phase angle. In our measurement model, we applied these time corrections to the COM occultation/eclipse times, which are computed from the model's orbit and body sizes using SPICE routines, to obtain the model half-depth times, which are readily measured in the observational data.
5. Orbit Fit
We used differential corrections to estimate the best-fit model parameters (Milani & Gronchi 2009). In this case, we iteratively corrected the estimated parameters using Equation (1) of Naidu et al. (2022) until we reach a minima in the cost function, which is the sum of the χ2 of the observations and the a priori constraints. The detailed description of our orbit fitting method can be found in Naidu et al. (2022) and Thomas et al. (2023); however, we replaced the orbital model used in those papers with the one described in Section 2. Our estimated parameters were M0, n0,  , the ecliptic longitude and latitude of the orbit (and rotation) pole (λ, β), preimpact semimajor axis (a), ΔVT
, ΔVR
, Didymos J2, libration rate at impact
, the ecliptic longitude and latitude of the orbit (and rotation) pole (λ, β), preimpact semimajor axis (a), ΔVT
, ΔVR
, Didymos J2, libration rate at impact 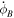 ,
, 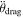 parameters A and τ, and the ellipsoid semiaxis dimensions of Didymos (aA
= bA
and cA
) and Dimorphos (aB
, bB
, and cB
).
parameters A and τ, and the ellipsoid semiaxis dimensions of Didymos (aA
= bA
and cA
) and Dimorphos (aB
, bB
, and cB
).
We applied a priori constraints of aA = bA = 404 ± 20 m based on Barnouin et al. (2023) and aB = 86.5 ± 10 and cB = 56.5 ± 10 m from Daly et al. (2023). To allow for reshaping due to the DART impact, we did not apply constraints on bB ; however, we did constrain the volume of Dimorphos to be within 5% of the value in Daly et al. (2023) of 0.00174 km3. We used the ellipsoidal shape of Didymos published in Barnouin et al. (2023) to compute an a priori value for J2 of 0.094, for which we assumed a 1σ uncertainty of ±10%. A priori constraints are effectively treated as observational constraints and passed through the orbit determination filter.
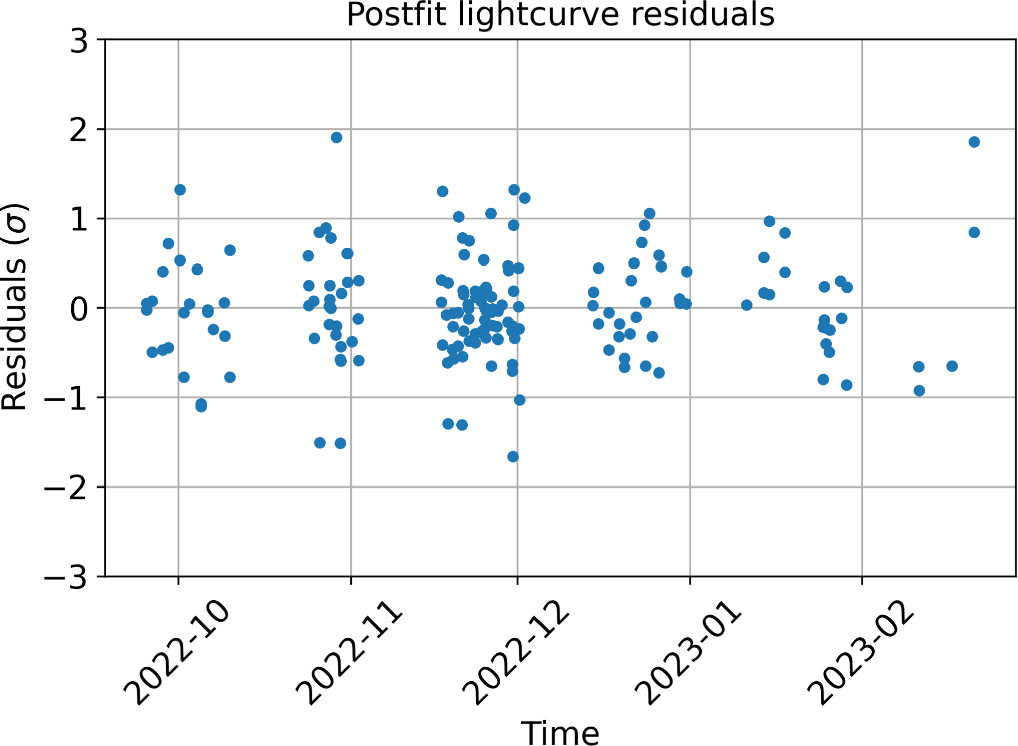
The residuals of the lightcurve mutual events from the best-fit solution using the model described in Section 2 but neglecting 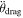 are shown in Figure 3. The residuals within each lunation appear to be biased with a trend in the residuals from positive in the L1 lunation to negative in L5. To investigate the source of this trend, we attempted to fit mutual orbits using shorter data arcs. Figure 4 shows the best-fit ΔP values from these fits. The trend suggests that ΔP continued to decrease after L0, possibly following an exponential curve. However, there are not enough data to rule out alternative decay models, such as a step function.
are shown in Figure 3. The residuals within each lunation appear to be biased with a trend in the residuals from positive in the L1 lunation to negative in L5. To investigate the source of this trend, we attempted to fit mutual orbits using shorter data arcs. Figure 4 shows the best-fit ΔP values from these fits. The trend suggests that ΔP continued to decrease after L0, possibly following an exponential curve. However, there are not enough data to rule out alternative decay models, such as a step function.
Figure 3. Residuals of mutual event times using the best-fit model described in Section 2, neglecting an exponential decay term 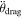 . The dotted line (not a fit) highlights the approximate trend in the residuals. The plot contains six groups of data points, each group taken within a single lunation. The lunations are labeled as L0 to L5.
. The dotted line (not a fit) highlights the approximate trend in the residuals. The plot contains six groups of data points, each group taken within a single lunation. The lunations are labeled as L0 to L5.
Download figure:
Standard image High-resolution imageFigure 4. Estimated ΔP as a function of mid-time of data arc. Uncertainties are 1σ. The corresponding data arc is noted next to each data point. The best-fit constant ΔP (orange), linearly changing ΔP (green), and exponentially decaying ΔP (red) are overlaid.
Download figure:
Standard image High-resolution imageWe hypothesize that a possible cause of the changing orbit period could be an exponentially decaying draglike force acting on the secondary after the DART impact. Since the DART impact released debris into the system on unstable orbits, any particles that are ejected from the system through gravitational interaction with Dimorphos would remove angular momentum from the Dimorphos orbit. This would have the effect of reducing Dimorphos's semimajor axis and orbital period further, and this phenomenon would naturally decay exponentially as the system cleared of debris. See Richardson et al. (2023) for a fuller discussion of this explanation for period decay.
In order to simulate such an exponentially decaying draglike force, we added a term, 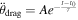 , to the transverse acceleration in Equation (4), where τ is the time constant of the acceleration and A is the associated acceleration at impact. Both A and τ are estimated parameters in our model. As we show below, this additional model feature substantially improved fits to the observational data.
, to the transverse acceleration in Equation (4), where τ is the time constant of the acceleration and A is the associated acceleration at impact. Both A and τ are estimated parameters in our model. As we show below, this additional model feature substantially improved fits to the observational data.
6. Results and Discussion
Table 1 shows the best-fit parameters and their formal 1σ uncertainties for our solution JPL 547, 8 which uses the dynamical model described in Section 2. Table 2 compares solution 547 to the results from Naidu et al. (2020, 2022), Scheirich et al. (2024). All values are consistent within ∼1σ.
Table 1. Best-fit Parameters of Solution JPL 547
| Parameter | Estimate | A Priori Constraint |
|---|---|---|
| Estimated Parameters | ||
| λ (deg) | 310 ± 3 | ⋯ |
| β (deg) | −80.7 ± 0.5 | ⋯ |
| a (km) | 1.189 ± 0.017 | ⋯ |
| M0 (deg) | 174 ± 3 | ⋯ |
| n0 (rad s−1) | (1.464019 ± 0.000002) × 10−4 | ⋯ |
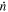 (rad s−2) (rad s−2) | (4.8 ± 0.6) × 10−18 | ⋯ |
| ΔVR (mm s−1) | 0.3 ± 0.4 | 0.4 ± 0.4 |
| ΔVT (mm s−1) | −2.63 ± 0.06 | ⋯ |
| aA (m) | 394 ± 11 | 404 ± 20 |
| cA (m) | 290 ± 16 | ⋯ |
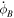 (rad s−1) (rad s−1) | (−1.2 ± 1.5) × 10−5 | ⋯ |
| J2 | 0.090 ± 0.008 | 0.094 ± 0.0094 |
| aB (m) | 96 ± 6 | 86.5 ± 10 |
| bB (m) | 74 ± 4 | See note |
| cB (m) | 59 ± 7 | 56.5 ± 10 |
| A (rad s−2) | (4 ± 4) × 10−14 | ⋯ |
| τ (days) | 12 ± 7 | ⋯ |
| Derived Parameters | ||
| Pimp− (hr) | 11.921493 ± 0.000016 | ⋯ |
| Pimp+ (hr) | 11.377 ± 0.004 | ⋯ |
| P (hr) | 11.3674 ± 0.0004 | ⋯ |
| ΔPimp+ (minutes) | −32.7 ± 0.3 (±16 s) | ⋯ |
| ΔP∞ (minutes) | −33.25 ± 0.03 (±1.5 s) | ⋯ |
| ΔP∞ − ΔPimp+ (s) | 34 ± 15 | ⋯ |
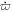 (deg day−1) (deg day−1) | 6.7 ± 0.2 | ⋯ |
| Eccentricity | 0.0274 ± 0.0015 | ⋯ |
| GMsys (m3 s−2) | 35.4 ± 1.5 | ⋯ |
| System bulk density ρ (kg m−3) | 2790 ± 140 | ⋯ |
| aB /bB | 1.300 ±0.010 | ⋯ |
| aB /cB | 1.6 ± 0.3 | ⋯ |
| bB /cB | 1.3 ± 0.2 | ⋯ |
| a/aA | 3.02 ± 0.08 | ⋯ |
| Dimorphos volume (km3) | 0.00174 ± 0.00009 | 0.001740 ± 0.000087 |
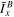 (km2) (km2) | (1.78 ± 0.07) × 10−3 | ⋯ |
 (km2) (km2) | (2.53 ± 0.10) × 10−3 | ⋯ |
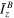 (km2) (km2) | (2.93 ± 0.4) × 10−3 | ⋯ |
| C20 B | −0.08 ± 0.03 | ⋯ |
| C22 B | 0.0204 ± 0.0005 | ⋯ |
| A × τ (rad s−1) | (4.1 ± 1.9) × 10−8 | ⋯ |
Note. The solution epoch is the time of the DART impact, 2022 September 26 23:14:24.183 UTC. Uncertainties on the estimates and a priori constraints are 1σ. GMsys = μ = G(mA
+ mB
). Pimp− is the preimpact period at impact. Pimp+ is the postimpact period at impact. P∞ is the stabilized value of the postimpact period after a few months (several τ periods).  is the postimpact apsidal precession rate. Tabulated eccentricity is the mean postimpact geometric eccentricity. The Dimorphos semiaxis bB
is effectively constrained by an a priori constraint on the satellite volume.
is the postimpact apsidal precession rate. Tabulated eccentricity is the mean postimpact geometric eccentricity. The Dimorphos semiaxis bB
is effectively constrained by an a priori constraint on the satellite volume.
Download table as: ASCIITypeset image
Table 2. Comparison between Naidu et al. (2020, 2022), Scheirich et al. (2024), and JPL 547
| Parameter | This Paper | Scheirich et al. (2024) | Naidu et al. (2020) | Naidu et al. (2022) |
|---|---|---|---|---|
| λ (deg) | 310 ± 3 | 310.0 ± 5.0 | See note | 310 ± 15 |
| β (deg) | −80.7 ± 0.5 | −80.4 ± 0.6 | −89 ± 10 | −76 ± 4 |
| a/aA | 3.02 ± 0.08 | 2.92 ± 0.07 | 3.01 ± 0.2 | Not estimated |
| a (km) | 1.189 ± 0.017 | 1.150 ± 0.03 | 1.19 ± 0.03 | 1.2 (see note) |
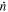 (rad s−2) (rad s−2) | (4.8 ± 0.6) × 10−18 | (4.6 ± 1.2) × 10−18 | Not estimated | (5 ± 1) × 10−18 |
| Pimp− (hr) | 11.921493 ± 0.000016 | 11.92149 ± 0.00003 | 11.93 ± 0.01 | 11.921487 ± 0.000028 |
| Pimp+ (hr) | 11.377 ± 0.004 | 11.3751 ± 0.0017 | ⋯ | ⋯ |
| P∞ (hr) | 11.3674 ± 0.0004 | 11.3675 ± 0.0004 | ⋯ | ⋯ |
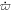 (deg day−1) (deg day−1) | 6.7 ± 0.2 | 7.3 ± 0.7 | ⋯ | ⋯ |
Note. The solution epoch is the time of the DART impact, 2022 September 26 23:14:24.183 UTC. Uncertainties are 1σ. The value of a for Scheirich et al. (2024) was derived from their estimate of the semimajor axis to primary diameter ratio and the Didymos dimensions from Table 1. Using the Scheirich et al. (2024) ratio and equatorial radius of Barnouin et al. (2023) leads to a = 1.178 + / − 0.030 km. The λ value in Naidu et al. (2020) covers almost all longitudes since β is close to the ecliptic south pole. Naidu et al. (2022) does not estimate a but uses a value consistent with Naidu et al. (2020).
Download table as: ASCIITypeset image
Comparing Figures 3 and 5 makes clear that including the drag acceleration removes the bias and the trend from postimpact lightcurve residuals, and the residuals are roughly Gaussian. The timescale, τ, for the period change is about 12 ± 7 days, which is suggestive of the system's e-folding time for debris-clearing. The final ΔP of −33.25 ± 0.03 minutes is not strongly sensitive to the value of τ but depends on the product A × τ, which is estimated (Table 1) with ∼2σ significance.
Figure 5. Residuals of mutual event times from the best-fit solution in Table 1. The notable trend in the residuals seen in Figure 3 has been removed by adopting the draglike dissipation 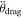 .
.
Download figure:
Standard image High-resolution imageFigure 6 shows the histogram of the residuals for each type of mutual event time. For context, our mean mutual event time uncertainties were variable, with a mean and standard deviation of 11 ± 6 minutes, and the residuals themselves had a mean and rms of 0.02 ± 0.57σ. Every histogram, except the ones showing secondary occultations, have means consistent with 0 and appear similar to a normal distribution. The apparent bias in the secondary occultation timings is likely due to modeling inadequacies or measurement errors.
Figure 6. Histogram of the residuals for each type of event time. PE and PO stand for primary eclipse and primary occultation. SE and SO stand for secondary eclipse and secondary occultation.
Download figure:
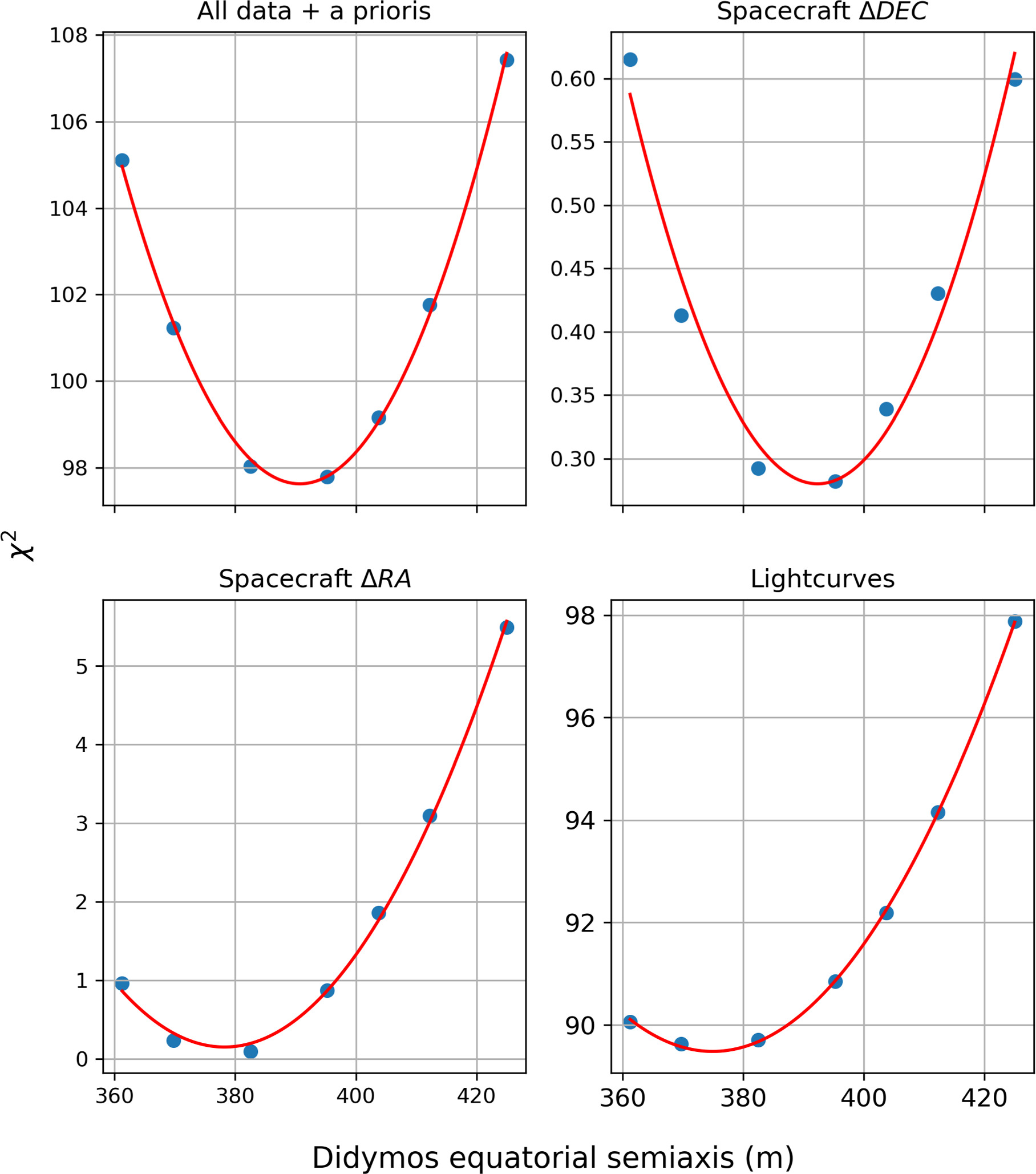
Standard image High-resolution imageOur best-fit value for the radius of the Didymos equator, 394 ± 11 m, differs by ∼1σ from the Barnouin et al. (2023) equator, which is 409 × 398 m. Figure 7 shows how various χ2 values of the fit vary with the radius of the Didymos equator aA . The results indicate that our observations favor a radius of aA = 380 m. But in the fit, we are applying an a priori constraint of 404 ± 20 m to the radius based on the mean of the Barnouin et al. equator. Given that DART and LICIACube imaging sampled only a small fraction of the Didymos surface, the a priori uncertainty is a conservative, ad hoc estimate of shape uncertainty. With this constraint, the overall χ2 is minimized at our estimated value of aA = 394 m.
Figure 7. χ2s as a function of the primary equatorial radius of Didymos. "All data" refers to all the data (lightcurve + radar + spacecraft/DRACO) used in the orbit fit.
Download figure:
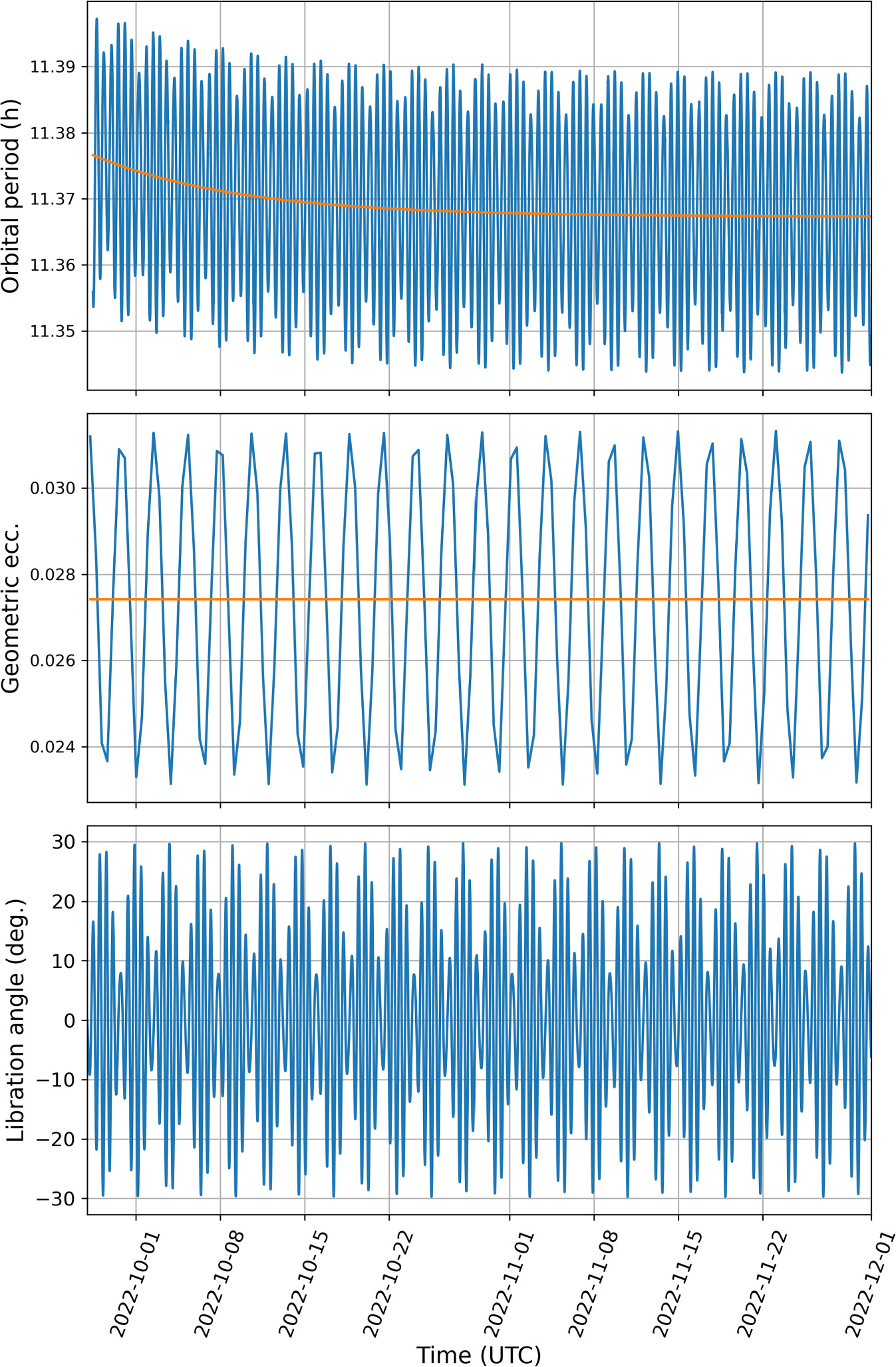
Standard image High-resolution imageThe postimpact orbit is significantly non-Keplerian because of the presence of gravitational harmonics and librational effects in the equations of motion given in Equation (4) (Meyer et al. 2021). As a result, the Dimorphos orbit undergoes periodic variations in the eccentricity and orbital period that are driven by the mean motion, apsidal precession, and satellite libration (Figure 8). The orbital period variations are superimposed on the period change due to the exponentially decaying draglike acceleration (Figure 8). In contrast, the mean eccentricity is not affected by the decaying transverse acceleration.
Figure 8. Postimpact orbital period (top), geometric eccentricity (middle), and libration angle (bottom) derived from the best-fit orbit of Dimorphos as a function of time, beginning at the time of the DART impact. We measure orbital period as the time between consecutive crossings of an inertial reference direction in the orbit plane. Orange curves show the best-fit exponential curve to the orbital period and the mean geometric eccentricity.
Download figure:
Standard image High-resolution imagePrior to impact, the elongation of the Dimorphos equator was found to be rather low (Daly et al. 2024), there was not a strong driver for librational excitation, and the system was believed to have been fully relaxed (Agrusa et al. 2022; Richardson et al. 2022). However, it is likely that the impact changed  by imparting an angular impulse on Dimorphos. Moreover, the impact also changed the shape of Dimorphos, which would presumably cause the new long axis of the satellite to be misaligned from the primary–secondary line, implying a nonzero ϕB
shortly after impact, though the reshaping would not have been instantaneous (Nakano et al. 2024). In our fits, there is some sensitivity to the libration rate
by imparting an angular impulse on Dimorphos. Moreover, the impact also changed the shape of Dimorphos, which would presumably cause the new long axis of the satellite to be misaligned from the primary–secondary line, implying a nonzero ϕB
shortly after impact, though the reshaping would not have been instantaneous (Nakano et al. 2024). In our fits, there is some sensitivity to the libration rate 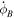 at impact, and so we did estimate a value (Table 1), but the significance of the estimate is modest. There is a correlation between the value of
at impact, and so we did estimate a value (Table 1), but the significance of the estimate is modest. There is a correlation between the value of 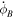 and J2, and so including this in the fit presumably allowed J2 to vary as needed in the estimate. We did not find sensitivity to the phase of libration at impact, which we arbitrarily set to 0. We did not explore the possible range of libration modes (Naidu & Margot 2015) and amplitudes; however, as indicated by Figure 9 and the bottom panel of Figure 8, the libration amplitude was around 30°.
and J2, and so including this in the fit presumably allowed J2 to vary as needed in the estimate. We did not find sensitivity to the phase of libration at impact, which we arbitrarily set to 0. We did not explore the possible range of libration modes (Naidu & Margot 2015) and amplitudes; however, as indicated by Figure 9 and the bottom panel of Figure 8, the libration amplitude was around 30°.
Figure 9. Postimpact libration angle vs. libration velocity of the best-fit orbit of Dimorphos. The star shows the state at impact, which corresponds to ϕB = −1.2 × 10−5 rad s−1 listed in Table 1. The libration amplitude is about 30°.
Download figure:
Standard image High-resolution imageThe best-fit exponential curve to the orbital period measurements yields a postimpact period at the moment of impact Pimp+ = 11.377 ± 0.004 hr (Figure 8). After a few weeks, the period settles to P∞ = 11.3674 ± 0.0004 hr. This implies that the ΔP decreased by an additional 34 ± 15 s after the impact and the total ΔP∞ = −33.25 minutes ± 1.5 s. The 1.5 s uncertainty on ΔP satisfies the DART Level 1 requirement to measure ΔP with an uncertainty of ≤7.3 s (Rivkin et al. 2021).
We estimate that the postimpact apsidal precession rate of Dimorphos is 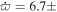 0
0 2 day−1. The precession rate is influenced by the J2 of Didymos as well as the C20 and C22 gravity field coefficients of Dimorphos, which are related to the elongation and oblateness of Dimorphos. The apsidal precession rate expected from the estimated J2 alone is roughly twice the estimated precession rate, indicating that the C20 and C22 of Dimorphos have a significant influence on apsidal precession.
2 day−1. The precession rate is influenced by the J2 of Didymos as well as the C20 and C22 gravity field coefficients of Dimorphos, which are related to the elongation and oblateness of Dimorphos. The apsidal precession rate expected from the estimated J2 alone is roughly twice the estimated precession rate, indicating that the C20 and C22 of Dimorphos have a significant influence on apsidal precession.
Our estimated Didymos J2 of 0.090 ± 0.008 is perfectly consistent with our estimate of the Didymos shape (aA and cA from Table 1), which yields J2 = 0.091, assuming a uniform density oblate spheroid. We note that the a posteriori uncertainty on our J2 estimate is only modestly reduced from the a priori uncertainty, indicating that the a posteriori uncertainty is largely reflective of the a priori. We emphasize that these two values of J2, one from gravity and the other from shape, are not constrained to match each other, and yet they both moved in the same direction and by almost the same amount with respect to the J2 a priori constraint of 0.094 derived using the dimensions from Barnouin et al. (2023). The implication is that our estimates are suggestive of a uniform density for Didymos, but given the uncertainties, the evidence is not definitive.
Assuming that Dimorphos is a triaxial ellipsoid with uniform density, we estimate postimpact ellipsoid extents of (192 ± 12) × (148 ± 9) × (117 ± 15) m. The dimension along the intermediate axis varies significantly from the preimpact value of 170 ± 4 m published in Daly et al. (2024), which suggests significant reshaping due to the DART impact. These dimensions imply that Dimorphos changed from an oblate spheroid to an elongated ellipsoid with aB /bB = 1.300 ± 0.010. We note that, due to correlations in the covariance matrix, the ratio aB /bB has a higher relative precision than the marginal uncertainties on aB and bB . Observations by the upcoming Hera mission (Michel et al. 2022) should be able to test this by estimating the new shape. We point out that the mean cross-sectional area of our Dimorphos shape estimate is ∼3% higher than that of Daly et al. (2024), which is consistent with the 6% scaling that we applied to the Daly et al. shape when running our detailed photometric model (Section 4).
The impulsive effect of the DART impact is represented by the estimated transverse change in velocity ΔVT = −2.63 ± 0.06 mm s−1, which has a relative uncertainty of only 2%. A simplistic analysis, assuming that the bulk densities of Didymos and Dimorphos were the same and that the relative velocities of the spacecraft and Dimorphos were coaligned, would predict ΔVT ∼ 1 mm s−1. The major discrepancy between this naive prediction and the estimated value is due to the added momentum of escaping ejecta, which is often modeled through the momentum enhancement factor β. For a far more detailed analysis and full discussion, see Cheng et al. (2023).
In contrast to ΔVT , there is little signal in the data for estimating ΔVR as evidenced by the fact that the a posteriori sigma is little changed from the a priori value.
We emphasize that our stated uncertainties throughout this report are conditional on the assumptions that underlie the observational and dynamical modeling. Wherever these assumptions are poor and the true dynamics or observations are affected by unmodeled effects, the stated uncertainties will underestimate the errors in our estimates. A few of the key assumptions in question are as follows.
- 1.Planar dynamics. The use of the planar full-body problem eliminates the possibility of orbital inclination with respect to the equator of Didymos. This assumption also enforces the assumption that the poles of both the primary and secondary, as well as the orbit, are aligned. This coalignment removes the possibility of nonprincipal axis rotation of Dimorphos, a possibility proposed by Agrusa et al. (2021) and Scheirich et al. (2024).
- 2.Smooth dynamics. While we do allow satellite libration, and in principle even circulation, our dynamics are modeled as smooth and follow Equation (4), including the exponentially decaying
 . This means that episodic effects such as boulder collisions or chaotic transitions in eccentricity are disallowed.
. This means that episodic effects such as boulder collisions or chaotic transitions in eccentricity are disallowed. - 3.Ellipsoidal shapes. We have not used detailed shape models, either for observational modeling or in the system dynamics. Didymos is treated as an ellipsoid of revolution and Dimorphos as a triaxial ellipsoid. On the observational side, this affects the timing and duration of mutual events and the interpretation of the DART optical navigation imagery. For the dynamics, we are sensitive only to gravitational effects, and so shape assumptions should not compromise the estimates but can easily cloud their interpretation.
We have no rigorous means of estimating the impact of any mismodeling on the errors in our estimates or their associated uncertainties, but a factor of 1.5× could be a reasonable scale factor on some of our uncertainties. However, the quality of our fits is good enough that we see no need to invoke, for example, a dramatically more complicated dynamics than we have presented here. In the course of this effort, we have made many solutions, and we find that some of the estimates hold up remarkably well to dynamical model variations and differing observational treatments. In particular, the various estimates of the orbital period and changes to the orbital period appear robust. Also, the shape of Dimorphos, and in particular the ratio aB /bB , which has a relative uncertainty of better than 1%, has consistently fallen close to a value of 1.3.
Residuals for range, Doppler, and spacecraft astrometry are provided in Naidu & Chesley (2023). The next opportunity for obtaining photometric lightcurves of Didymos is in mid-2024. Using solution 547, we estimate that the 1σ uncertainties of mutual event times in 2024 June range from roughly 30 to 45 minutes. These uncertainties are larger than the ∼10 minute observational uncertainties typically seen in previous measurements. Therefore, measurements of mutual event times in 2024 should help to refine the mutual orbit of Dimorphos and reduce prediction uncertainties at the time of the arrival of the Hera mission in late 2026.
7. Conclusion
The successful execution of the DART mission, culminating in the impact on Dimorphos, the satellite of binary near-Earth asteroid Didymos, marked a significant milestone in planetary defense and asteroid science. In this paper, we have presented a comprehensive analysis of the orbital and physical characteristics of Dimorphos following the DART impact, shedding light on the complex dynamics and transformations within the binary system.
Our findings reveal significant insights into the aftermath of the DART impact.
- 1.Orbital changes. The DART impact led to an instantaneous change in Dimorphos's along-track velocity, causing an initial reduction of its orbital period by approximately 32.7 minutes, a number that fed directly into efforts to estimate the momentum enhancement coefficient β (Cheng et al. 2023). Over the following few months, the orbital period continued to decline, eventually stabilizing at 11.3674 ± 0.0004 hr, resulting in a total postimpact period change of −33.25 minutes ± 1.5 s.
- 2.Apsidal precession. We estimated the apsidal precession rate of Dimorphos's orbit, which is influenced by the oblateness parameter (J2) of Didymos and the axial ratios (a/b and a/c) of Dimorphos. Our results indicate a postimpact precession rate of
 0
0 2 day−1. The contribution of Dimorphos's shape to this precession rate underscores the complex dynamics of the full two-body problem.
2 day−1. The contribution of Dimorphos's shape to this precession rate underscores the complex dynamics of the full two-body problem. - 3.Reshaping of Dimorphos. The DART impact had a profound impact on Dimorphos's shape. The postimpact measurements revealed an elongated ellipsoidal shape with an equatorial axis ratio of ∼1.3, representing a significant departure from its preimpact oblate spheroid shape. This reshaping points to the possibility that satellite libration may be an important feature of the system dynamics worthy of further exploration.
- 4.Exponential period change. The evolving orbital period of Dimorphos suggests the presence of an exponentially decaying draglike force acting on the satellite. This force presumably arises from gravitational interactions of Dimorphos with the impact-generated debris and is consistent with the idea that it takes time for a binary system to settle after a kinetic impact event. From this perspective, our time constant of 12 ± 7 days is an indicator of the e-folding time for this process at Didymos.
In summary, the DART mission and the subsequent analysis presented in this paper have unveiled the complex dynamics and associated changes to binary asteroid systems following a kinetic impact event. These insights not only advance our understanding of the response of small celestial bodies to such an event but also have implications for planetary defense strategies against potentially hazardous near-Earth asteroids.
Acknowledgments
A portion of this work was conducted at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004). This work was supported by the DART mission, NASA contract 80MSFC20D0004. The work by P.P. and P.S. was supported by the Grant Agency of the Czech Republic, grant 20-04431S.
© 2023. All rights reserved.